Fig Componentes da força da gravidade.
|
|
|
- Thiago Esteves Brás
- 8 Há anos
- Visualizações:
Transcrição
1 FORMA E DIMENSÕES DA TERRA Iis eeia Escoba Uivesidade do Estado do Rio de Jaeio Depatameto de Egehaia Catogáfica Rua São Facisco Xavie, 54, 4º ada, sl 400B Rio de Jaeio RJ iisescoba@tea.com.b 1. INTRODUÇÃO Qual é a foma da Tea? Quais são as suas dimesões? Estas são pegutas simples e atuais quado se deseja estuda o plaeta em que vivemos. Respodê-las, etetato, exige algumas eflexões, a começa pelo gau de exatidão equeido as espostas. Assim, paa um obsevado muito distate, a Tea podeá te a apaêcia de um poto. Apoximado-se mais, o poto começa adquii dimesão e logo a Tea apaetaá se esféica. Mais póximo e podeá se pecebido um ligeio achatameto e pode-se-á dize que a Tea apaeta se um elipsóide de evolução. Odulações podeão se pecebidas a supefície, ao se apoxima mais aida, de modo que agoa a Tea já ão pode se epesetada po um copo de foma egula e alguém podeá dize que a Tea tem uma foma iegula específica que ecebe o ome de geóide. Mas o poblema ão temia aí; um obsevado mais póximo pecebeá saliêcias e eetâcias que ão pemitem caacteiza a supefície do plaeta como polida. A supefície evoltóia da Tea, que ecea toda a sua massa, abstaido a camada atmosféica, ecebe simplesmete o ome de supefície física, cujos cotoos são defiidos pelas fomas do elevo, descitas pela topogafia. otato, a foma e as dimesões da Tea podem se defiidas com difeetes gaus de exatidão. Etetato, se fo obsevado o igo cietífico, a sua supefície física é de difícil defiição aalítica e, omalmete é feita a pati de opeações o âmbito da Geodésia que se cosumam a epesetação catogáfica. aa atigi o seu objetivo de detemia a foma e as dimesões da Tea, a Geodésia pate do estudo do seu campo da gavidade, cosideado a esteita coelação deste campo com aquelas gadezas. Deste modo, o estudo dos paâmetos defiidoes do campo da gavidade teeste foecem os fudametos ecessáios à defiição da foma e das dimesões do plaeta. A pati desses fudametos são também estabelecidos os sistemas geodésicos de efeêcia, que são a base da epesetação dos dados espaciais que se distibuem a supefície da Tea. otato, é coveiete começa o estudo da Catogafia pelo estudo do campo da gavidade da Tea.. CAMO DA GRAVIDADE.1. Gavitação e Gavidade A lei da gavitação uivesal, euciada po Isaac Newto o fim do século dezessete, estabelece que duas patículas ( massas cocetadas um volume ifiitamete pequeo) ataem-se mutuamete com uma foça que é popocioal às suas massas e ivesamete popocioal ao quadado da distâcia ete elas. A lei da gavitação pode se expessa pela seguite fomula: = 1 f G m m (.1)
2 ode f é a itesidade da foça gavitacioal, m 1 e m são massas potuais iteativas; é a distâcia ete elas; e G é um coeficiete de popocioalidade cohecido como costate de gavitação. O valo de G o sistema CGS é 6,67 x 10-8 cm 3 g -1 s - e o SI é 6,67 x m 3 kg -1 s -, adotado pela Uião Astoômica Iteacioal em 1976 (Vaicek & Kakiwsky, 1986, p.71). Emboa a atação gavitacioal ete duas massas seja mútua, a pática, é usual distiguise dete elas a ataída e a atativa. Assim, se m é ataída po M, composta de váias patículas, a equação (.1) pode se escita como a soma das atações execidas sobe m pelas patículas de M. Quado a massa M é cotíua, as massas cosideadas sobe o total volume, v, do copo são itegadas, em vez de seem somadas. Etão a seguite equação vetoial pode se escita: dm f g = Gm (.) v ode dm=ρdv, sedo ρ a massa específica do copo. Esta equação pode se usada paa estuda a foça gavitacioal execida pela Tea sobe copos cujas dimesões possam se cosideadas egligeciáveis em compaação com a da Tea. Além da foça gavitacioal, uma outa foça, f, atua sobe as massas viculadas à Tea, como cosequêcia de seu movimeto de otação. Essa foça é chamada de foça cetífuga. Cosideado-se uma otação com velocidade agula costate ω, com um aio de otação p, em too de um eixo cosideado fixo em elação à Tea (Fig..1) tem-se: Fig..1 - Compoetes da foça da gavidade. f = pω m (.3) A esultate ete as foças gavitacioal e cetífuga costitui o que é cohecido como foça da gavidade, ou seja, g f = f + f, ou 6
3 1 f = Gm dm + pω m (.4) v ode-se dize que a massa M da Tea poduz um efeito físico o espaço em too de si, chamado de campo da gavidade, pecebido atavés da foça execida sobe outa massa m, situada essa egião. O campo da gavidade g, omalmete chamado apeas gavidade, poduzido pela Tea em um detemiado poto, pode se defiido como a foça execida po uidade de massa colocada aquele poto. Etão 1 g = G dm + p ω (.5) v cuja itesidade, g, egligeciado a pequea difeeça de dieção ete a esultate e a compoete gavitacioal, face à pequea itesidade da compoete cetífuga, é dada po ode ϕ é a latitude geocêtica. g = G v 1 dm p ω No SI a itesidade do campo da gavidade é expessa em metos po segudo ao quadado (m.s - ) e equivale dimesioalmete a uma aceleação. Etetato admite-se o gal = cm.s -, em homeagem a Galileu, como uidade CGS tempoaiamete toleada, face ao seu uso tadicioal. As pequeas vaiações da gavidade são expessas usualmete em miligal (mgal), micogal (µgal) ou aometo po segudo ao quadado (.s - ). Assim, 1 gal= 10 - m.s -, 1 mgal=10-5 m.s - e 1 µgal = 10.s -. A itesidade da gavidade a supefície da Tea vaia ete apoximadamete 978 gals o equado e 983 gals os polos, isto é, deto de 5 gals. Cosideado o valo de ω=7,9115x10-6 d.s -1, a compoete cetífuga é ceca de 1/88 do valo total da foça da gavidade e vaia de zeo os polos a 3,4 gals o equado. A despeito de sua pequea itesidade, se compaada com a compoete gavitacioal, a compoete cetífuga atua como a causa básica da vaiação da gavidade a supefície da Tea. O achatameto as egiões polaes também cotibui paa esse efeito, aumetado da mesma foma o valo da gavidade os polos... otecial da Gavidade. Sabe-se que o campo da gavidade é cosevativo e que, potato, possui um coespodete potecial escala W=W(x,y,z), tal que g = gad W. Esse escala é cohecido como potecial da gavidade e pode se defiido como a eegia potecial po uidade de massa colocada o campo da gavidade. O potecial da gavidade é etão expesso em m.s -. O potecial da gavidade da Tea, também chamado geopotecial, pode se escito como a soma do potecial gavitacioal, W g, com o potecial de otação ou cetífugo,w. Assim, paa 7 cos ϕ (.6)
4 e W g 1 = G dm (.7) v e 1 W = p ω, (.8) g W = W + W g = gad (W g +W ) = gad W g + gad W. (.9) É impotate obseva que o potecial de otação age somete sobe os copos ou patículas viculados à Tea, icluido a atmosfea. Assim, copos que ão giam com a Tea estão isetos do potecial cetífugo, estado sujeitos apeas ao potecial gavitacioal, e.g., os satélites atificiais. O icemeto do geopotecial dw ao se faze um deslocameto elemeta ds = (dx,dy,dz) em uma dieção abitáia o campo da gavidade é dado po: dw ou, cosideado que pela equação (.9), coclui-se que dode se obtém: ou ou, aida, g = ( g = W x dx + W y dy + x, g y, g z W ) = ( x W, y W z dz W, z ) dw = g. ds, (.10) dw = gdscos( g, s ) dw g cos( g, s = ) (.11) ds dw ds = g s, que é a compoete da gavidade segudo a dieção do deslocameto ds...1. Setido Físico do otecial da Gavidade. A equação (.10) mosta que o icemeto do geopotecial é zeo se o veto deslocameto ds fo pepedicula à dieção do veto g. Neste caso, dw = 0 8
5 e W = costate = C. (.1) Esta é a equação de uma supefície em elação à qual a gavidade é sempe omal. Tal supefície é chamada de supefície de ível ou supefície equipotecial do campo da gavidade ou, simplesmete, geope, devido à costâcia do potecial ela. Atibuido valoes difeetes à costate em (.1) obtém-se uma família de supefícies equipoteciais que têm a popiedade de ão se tocaem. Caso isso acotecesse, as duas supefícies teiam o mesmo potecial C o poto comum e, de acodo com (.1), isso sigificaia que todos os potos de ambas as supefícies teiam o mesmo potecial C, isto é, as supefícies seiam totalmete coicidetes. Devido à distibuição iegula de massa a Tea, os geopes possuem pequeas, poém sigificates, iegulaidades. Seus aios de cuvatua vaiam iegulamete de poto paa poto, povocado toções as lihas de foça em todas as dieções. otato a vetical é uma cuva evesa (Vaicek & Kakiwsky, 1986, p.85). A equação (.11) mosta que a deivada da fução potecial em elação a qualque dieção é igual à compoete do campo segudo essa dieção. Quado uma massa potual executa um deslocameto dh ao logo da liha de ação da gavidade (vetical), poém em setido cotáio, etão cos( g, s ) = 1 e dh dw = (.13) g ode H é chamada de altitude otomética e dw é o icemeto do potecial a passagem de uma supefície paa outa ifiitamete póxima. Esta equação foece a coexão ete uma quatidade física, difeeça de potecial, e uma quatidade geomética, difeeça de altitude, de geopes vizihos. De acodo com (.13) a distâcia ete duas supefícies equipoteciais ifiitamete póximas é ivesamete popocioal à itesidade do campo. ode-se, potato, coclui que as supefícies equipoteciais ão são paalelas, estão mais póximas quato maio fo a itesidade da gavidade. Assim, os geopes estão mais póximos os polos do que o equado. Como o icemeto dw do potecial é costate a tasfeêcia de uma supefície paa outa, ão depededo da posição do poto a mesma, também ão depede da tajetóia seguida pelo poto em seu deslocameto; é apeas fução dos potos extemos do pecuso. Dode se coclui que o icemeto do potecial dw em um cicuito fechado é igual a zeo. O geope mais otável é o geóide, do qual faia pate a supefície dos oceaos, caso estes ão estivessem sujeitos às ações das maés, vetos, coetes e outos feômeos elacioados com a sua diâmica. otato, compeede-se po geóide uma supefície equipotecial do campo da gavidade teeste, coicidete com o ível impetubado dos oceaos e que se pologa sob os cotietes de modo tal que a dieção da gavidade lhe é pepedicula em todos os seus potos. O geóide é uma supefície cotíua e levemete odulada, mas ão é uma supefície aalítica, sua cuvatua vaia descotiuamete com a desidade o iteio da Tea (Heiskae & Moitz, 1967, p.51). otato, a foma do geóide, como também de qualque geope, é esultado da distibuição de massa a Tea. aa potos situados o exteio ou a supefície da Tea é válida a equação difeecial geealizada de Laplace: 9
6 W ode é o opeado laplaciao. W W W = + + = ω (.14) x y z No iteio da Tea, o geopotecial W satisfaz a equação difeecial geealizada de oisso (Dehlige, 1978, p.5-6): W = 4πG ρ + ω, (.15) ode ρ é a massa específica o poto cosideado. No espaço exteio (ρ = 0, egligeciado a massa específica do a) a equação de oisso iguala-se à de Laplace. aa a compoete gavitacioal do potecial W g é valida a equação: W g = 0 Fuções deste tipo, ode o laplaciao é igual a zeo, são chamadas de fuções hamôicas e epesetam papel impotate a solução do poblema geodésico. 10
7 3. DESENVOLVIMENTO DO OTENCIAL GRAVITACIONAL (W g ) EM SÉRIE DE HARMÔNICOS ESFÉRICOS O cálculo do geopotecial gavitacioal (W g ), utilizado a fómula tadicioal, implica a solução da itegal cujos limites de itegação devem se defiidos. Neste caso, o limite de itegação é a supefície física da Tea, que devido a sua iegulaidade ão pode se expessa matematicamete, impossibilitado a defiição dos limites de itegação. Etetato, o poblema pode se esolvido po outo pocesso, exploado a popiedade hamôica de W g em potos exteioes às massas da Tea, satisfazedo, potato, à equação de Laplace: W x g W g = 0 ou W + y g W + z A solução desta equação difeecial foi obtida po Legede, após a substituição das coodeadas catesiaas do poto (x,y e z) pelas espectivas coodeadas esféicas (,v e λ), sedo o aio veto, v a colatitude geocêtica e λ a logitude. A solução obtida paa W g foi: ode W g = = 0 m= g = 0 ( A cos m + B se mλ) m I k se v ( - k)!(-1) (-m-k) (v) t k= 0 ( - m - k)!( - k)!k! (3.1) λ (v), (3.) = (3.3) são as fuções associadas de Legede de gau e odem m, paa I igual ao maio iteio cotido em (-m)/, A e B são coeficietes, elaciados com a distibuição de massas da Tea, dados po: A = G ' T (v')cos mλ'dm (3.4) T sedo: B paa = G ' T (v')se mλ'dm (3.5) T m = 0 T m 0 T = 1 ( m)! (3.6) = (+ m)! 11
8 3.1 Exemplos de Fuções Associadas de Legede Cosideado t=cos v, pode-se esceve: (v) = 1 (v) = t = cos v (v) = se v 1 (v) = (3cos v 1) (v) = 3cos vse v (v) = 3se v 1 3 (v) = (5cos v 3cos v) 1 4 (v) = (35cos v 30cos 8 v + 3) (3.7) Os gáficos destas fuções poliomiais são apesetados a fig Fução Colatitude geocêtica (v) Fig. 3.1: Gáficos das fuções associadas de Legede 1
9 3.. Repesetação Geomética dos Hamôicos Esféicos Zoais Quado m=0 os poliômios são fuções apeas de cos v e os espectivos temos são chamados de hamôicos esféicos zoais. Neste caso, se o gau do poliômio fo ímpa o mesmo teá apeas potêcias ímpaes de cos v. Caso cotáio, todas as potêcias seão paes., 0 (v) Fig. 3.: 1,0 (v) Fig 3.3:,0 (v) Fig. 3.4: 3,0 (v) Fig. 3.5: 4,0 (v) Aulam-se ao logo de paalelos, dividido a supefície esféica em zoas alteadamete positivas e egativas 3.3. Repesetação Geomética dos Hamôicos Esféicos Setoiais Quado m= os poliômios são fuções apeas de se v, que são sempe positivas, po este motivo os espectivos temos ( (+1) A (v) cos mλ e (+1) B (v) se mλ) alteam o sial 13
10 em fução da logitude, aulado-se ao logo de m meidiaos igualmete espaçados. Estes temos são chamados de hamôicos esféicos setoiais. Aalogamete ao caso ateio, se o gau do poliômio fo impa o mesmo teá apeas potêcias ímpaes de se v. Caso cotáio, todas as potêcias seão paes. (v) cos λ e (v) se λ π/. Fig. 3.5: 55 (v) cos 5λ ou 55 (v) se 5λ Fig. 3.6: 66 (v) cos 6λ ou 66 (v) se 6λ Aulam-se em meidiaos que dividem a supefície esféica em setoes com amplitude de 3.4. Repesetação Geomética dos Hamôicos Esféicos Tesseais Quado m e m 0 os espectivos temos são chamados de tesseais, os poliômios são fuções tato de cos v como de se v. (v) cos mλ ou (v) se mλ Fig. 3.7: 95 (v) cos 5λ ou 95 (v) se 5λ 14
11 Aulam-se em -m paalelos e m meidiaos igualmete espaçados Sigificados Físicos dos Hamôicos Esféicos A título de exemplo, seão aalisados os hamôicos de gau zeo, um e dois paa etedimeto dos espectivos sigificados físicos. a) Temo do gau zeo. Fazedo =m=0 a (3.), tem-se: já que pela (3.4) A 0,0 = GM. A, 0 0 GM =, (3.8) Assim, o temo do gau zeo sigifica o potecial de uma esfea de massa M homogêea, ou disposta em camadas esféicas homogêeas, sobe um poto exteio situado a uma distâcia do seu ceto. b) Temos do 1º gau. Neste caso tem-se tês temos, um zoal e dois setoiais, ou seja: 1- Fazedo =1 e m=0 a (3.), tem-se o temo zoal: A 1,0 1,0 (v) = A 1,0 cos v. Este temo se aula sobe o equado (v=90º), alteado o sial ete os hemisféios ote e sul. - Fazedo =1 e m=1 a (3.), tem-se os dois temos setoiais: B 1,1 1,1 (v) se λ e A 1,1 1,1 (v) cos λ. Como as fuções associadas setoiais são sempe positivas e, B 1,1 e A 1,1 são costates, a vaiação dos siais destes temos depedem exclusivamete de se λ e cos λ, que se aulaão espectivamete paa λ = 0º e 180º e λ = 90º e 70º. Assim, o pimeio caso, o sial se alteaá ete os hemisféios leste e oeste e o segudo caso ete dois hemisféios defasados de 90º em elação aos ateioes. otato, os temos do 1º gau idicam aumeto de potecial ou massa de um hemisféio em elação ao hemisféio oposto (fig. 3.). Evidetemete isto só ocoeá se a oigem do sistema de coodeadas ão coicidi com o ceto de massa da Tea. Este fato pode se compovado pela aálise dos coeficietes. Com efeito, das equações (3.4) e (3.5), substituido-se as coodeadas esféicas (', v' e λ') pelas espectivas coodeadas catesiaas (x', y' e z'), chega-se a: 15
12 A 1,0 = G z' dm,,1 = G T A 1 x' dm e B 1,1 = G y' dm. (3.9) T T Se a oigem do sistema de coodeadas fo coicidete com o ceto de massa da Tea estas itegais seão ulas e os temo se aulaão. c) Temo zoal do º gau Fazedo = e m=0 a (3.), obtém-se o temo zoal do º: A,0,0 (v) = A,0 (cos v ) 3, (3.10) ocededo de foma aáloga àquela usada paa calcula os coeficietes do 1º gau, é possível demosta que: po: A+ B A,0 = G C, (3.11) Sedo, A, B e C os mometos de iécia em elação aos eixos coodeados X, Y e Z, dados (y' + z' )dm, B = (x' + z' )dm, C = (x' + A = y' )dm. (3.1) T T T Assim, como e A,0 são costates, o sial deste temo vaiaá exclusivamete em fução da expessão (cos v 1/ 3), que se aula paa os paalelos v = 54º 44' 08" e v = 15º 15' 5", dividido a supefície teeste em tês zoas esféicas, duas polaes e uma equatoial, alteadamete positivas e egativas (fig. 3.3). Este temo tem paticula impotâcia a Geodésia poque sua geometia tem a popiedade de evela a cotibuição da foma elipsoidal da Tea Os Coeficietes (J, K ) e (C, S ) Costuma-se substitui os coeficietes A e B po suas espectivas fomas adimesioais J e K, dados po: J A = e GMa K B = (3.13) GMa ou seja: J 1 ' 1 ' = T (v') cos mλ' dm M e K = T (v') se mλ' dm a M. (3.14) a T T 16
13 como: Assim, a equação do geopotecial gavitacioal pode se escita em fução de J e K W g = GM = 0 m= 0 a ( J cos m + K se mλ ) λ (v), (3.15) Em Geodésia é mais comum a utilização da foma pleamete omalizada das fuções v dadas po: associadas de Legede ( ) ( v) p ( v) =, (3.16) ode H( m)!(+ 1) p = paa (+ m)! m = 0 H = 1 m 0 H = (3.17) Neste caso, os coeficietes pleamete omalizados C e S são dados po: C J K = e S = (3.18) p p e a equação de W g pode se escita como g GM a W = ( Ccos mλ + Sse mλ) (v), (3.19) = 0 m= 0 Os coeficietes dos hamôicos esféicos da séie do geopotecial de atação (W g )são depedetes da distibuição de massa a Tea. ode-se obseva que as coodeadas com liha, que dizem espeito aos elemetos ifiitesimais de massa dm, estão eceadas as itegais que defiem aqueles coeficietes. Cosideado a geometia dos hamôicos esféicos, pode-se coclui que o valo de um detemiado coeficiete seá tato maio quato maio fo a coelação existete ete a geometia segudo a qual as massas se distibuem e a geometia do hamôico esféico coespodete. Assim, o geopotecial gavitacioal é composto pelo somatóio das cotibuições das difeetes distibuições espaciais de massa que fomam a Tea. Os coeficietes fucioam como pesos que expessam as cotibuições elativas de cada pacela do somatóio. 17
14 O cálculo dos valoes dos coeficietes depede da defiição dos limites de itegação, que o caso é a supefície física do plaeta, cuja iegulaidade impede a sua defiição matemática. Tese ia etoado ao poblema oigial da solução da equação do geopotecial ão fosse a possibilidade de cota com a impotate cotibuição tecológica dos satélites atificiais, que postos em óbita da Tea toam-se vedadeios sesoes do seu potecial gavitacioal. O cohecimeto dos valoes de W g em divesos potos da óbita do satélite, cujas coodeas, v e λ são cohecidas, deixa como icógitas a expessão em séie de W g apeas os coeficietes C e S. Assim, o moitoameto das obitas dos satélites atificiais pemite a motagem de hipesistemas de equações lieaes, cujas soluções esultam a detemiação expeimetal dos coeficietes da séie. Logicamete, como a séie é ifiita, toa-se ecessáio o seu tucameto de modo a compatibiliza a quatidade de icógitas com a quatidade e esolução dos dados. O cojuto de coeficietes assim detemiados é cohecido como modelo geopotecial. O NIMA Natioal Imagey ad Mappig Agecy e a OSU Ohio State Uivesity, os Estados Uidos da Améica, são istituições que têm se destacado iteacioalmete a detemiação e dissemiação de modelos geopoteciais desevolvidos até gau e odem 360. O modelo divulgado mais ecetemete ecebeu a desigação de EGM-96 e pode se ecotado e copiado a págia da iteet do NIMA. Uma amosta do modelo geopotecial EGM-96, cotedo iclusive os desvios-padão dosa coeficietes (σ C e σ S ) até o gau e odem 6, é dada a tabela 3.1: m C S σ C σ S E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E E-09 Tabela 3.1: Coeficietes do Modelo Geopotecial EGM96 18
15 3.7. Fómulas de ecoêcia O cálculo das fuções associadas de Legede pela equação (3.3), evolve cálculos de fatoiais, cujos valoes uméicos podem se muito gades, dificultado, e às vezes impossibilitado, o cálculo daquelas fuções. aa cotoa esta dificuldade, são utilizadas fómulas que pemitem o cálculo de uma fução com base os valoes de outas peviamete calculadas. Estas fómulas são cohecidas com fómulas de ecoêcia. São válidas as seguites equações: a) aa m = ( 3; 4,4; 5,5;...;, ) 3, : + 1 = ( v) * 1, 1 (3.0), *se otato, a pati de,, todos os outos temos, podem se calculados. b) aa m = -1 ( 3 ; 4,3; 5,4;...;, 1), : ( v) * 1, 1 = (3.1), 1 + 1*cos otato, a pati dos valoes calculados o item a, podem se calculados todos os valoes,-1. c) aa os demais temos : m 1 m 1 = 1*cos + m m ( v) * 1,m *, m 3, m (3.) Assim, a pati dos valoes calculados os ites ateioes, todos os demais temos podem se calculados. 19
16 4. MODELOS DE RERESENTAÇÃO DA TERRA O temo zoal do segudo gau do desevolvimeto de geopotecial gavitacioal em séie de hamôicos esféicos eflete a cotibuição das aomalias de massa, em elação à Tea esféica, dispostas segudo tês zoas esféicas, duas polaes e uma equatoial. Como já foi visto, este temo é dado po: A,0,0(v) = A,0 (cos v ) 3, (4.1) aulado-se ao logo dos paalelos v = 54º 44' 08" e v = 15º 15' 5" e alteado o sial da aomalia de massa ete as zoas. O sial positivo ou egativo depede de A,0 ; se este fosse positivo as aomalias seiam positivas as egiões polaes e egativa a egião equatoial, o que idicaia deficiêcia de massa a egião equatoial e excesso as egiões polaes, em elação à foma esféica, evelado a geometia de um elipsóide de evolução alogado os polos. Obsevado a tabela de coeficietes do EGM-96, veifica-se que o coeficiete C,0 é egativo. Como A,0 tem o mesmo sial de C,0, as aomalias de massa são egativas as egiões polaes e positiva a egião equatoial, o que apota paa um excesso de massa equatoial e deficiecias as egiões polaes, geometia compatível com um elipsóide de evolução achatado os polos. A elevâcia da geometia elipsoidal a composição total do geopotecial é evelada pelo valo do coeficiete deste temo. Assim, o coeficiete C,0 evela o quato um elipsóide de evolução é adequado como modelo de epesetação da Tea. Da tabela de coeficietes é possível costata que o valo de C,0 é ceca de 1000 vezes maio do que os demais coeficietes. Assim, a aálise da equação do geopotecial evela uma tea pimeiamete esféica, com um achatameto pola e outas defomações meos elevates. Esta coclusão é paticulamete impotate paa a Catogafia poque, sedo a supefície física do plaeta de foma iegula, toase difícil a sua utilização como supefície de efeêcia, devido à complexidade de sua geometia, que dificulta o estabelecimeto de um sistema de coodeadas a ela efeido. A solução do poblema é obtida pela adoção de um modelo geomético egula suficietemete póximo da supefície física da Tea, que possa se utilizado como supefície de efeêcia paa um sistema de coodeadas. Assim, paa atede fialidades páticas que ão equeiam gade exatidão geomética (tais como mapeameto global em escalas pequeas) o modelo esféico é omalmete utilizado. Etetato, quado se deseja maio exatidão é coveiete a utilização do elipsóide de evolução como modelo geomético egula. Outos modelos geométicos paa epesetação da Tea podem sugi da aálise dos temos do desevolvimeto do geopotecial em séie de hamôicos esféicos; etetato, quato mais temos foem evolvidos mais complexas seão as figuas epesetativas. Até o mometo, ão foam apesetadas azões de odem física ou pática que justifiquem a adoção de um modelo mais complexo que o elipsóide de evolução. 0
17 4.1. A Tea Nomal Chama-se Tea Nomal ao elipsóide de evolução, com ligeio achatameto pola, dotado de movimeto de otação em too de seu eixo meo, coicidete com o eixo picipal de iécia pola da Tea, e com massa e velocidade agula iguais às desta. Esta Tea fictícia é geadoa do campo da gavidade omal, cuja itesidade é deotada po γ. O potecial da gavidade da Tea omal é chamado de esfeopotecial, omalmete epesetado pela leta U. As supefícies equipoteciais do campo da gavidade da Tea omal são comumete chamadas de esfeopes, sedo o mais otável destes a pópia supefície do elipsóide. A Tea Nomal está viculada a um sistema catesiao geocêtico XYZ, ode o eixo X (equatoial) é o que cuza o pimeio meidiao, defiido pelo Bueau Iteatioal de l Heue (BIH), e o eixo Z (pola) é o eixo de otação do elipsóide, paalelo à dieção do eixo médio de otação da Tea, defiida pelo Covetioal Iteatioal Oigi (CIO) fo ola Motio. 5. ESFEROOTENCIAL Aalogamete ao geopotecial, o efeopotecial também é composto pela soma do esfeopotecial de atação (U g ) com o potecial cetífugo (U ). Este último é o mesmo que eta a composição do geopotecial (U = W ), poém a pacela gavitacioal do esfeopotecial difee da do geopotecial pelo limite de itegação que agoa é a supefície de elipsóide de evolução. Assim, U = U g + U ode g dm 1 U = G e U = p ω. (5.1) E Tecedo-se algumas cosideações sobe a geometia do elipsóide de evolução, é possível chega-se ao desevolvimeto de U g em séie de hamôicos esféicos, a pati da equação da séie de W g. Assim, cosideado a simetia do elipsóide, U g ão pode se depedete da logitude, em tampouco do sial da latitude. Etão, os hamôicos esféicos setoiais e tesseais de qualque gau são excluídos po apesetaem depedêcia da logitude e os zoais ímpaes também são excluídos po apesetaem potêcias ímpaes de cos v que os toam depedetes do sial de v. otato, utilizado o sobescito U paa os coeficietes C, paa distiguilos dos coeficietes do Geopotecial, e = + g GM a U U 1 C,0,0 ( v) (5.) 1 GM a U = 1 + = 1 C U,0,0 1 (v) + ( ωsev) (5.3) ou 1
18 GM a U = 1 = 1 J U,0,0 1 (v) + ( ωsev). (5.4) Heiskae & Moitz [1967] foecem a equação dos coeficietes U J,0 em fução de U J,0 : U U + 1 3e J,0 J =,0 ( 1) (+ 1)(+ 3) (5.5) e ode U m1 = f 9*m1*f J * f +, (5.6), m 1 é a azão ete a compoete cetífuga e a compoete gavitacioal da gavidade o equado, dada po: f é o achatameto do elipsóide e e a pimeia exceticidade dada po: m e 1 3 ω a =, (5.7) GM = f f (5.8)
19 5.1. O coeficiete J,0 Como já foi demostado ateiomete, o coeficiete do hamôico esféico zoal do segudo gau, o desevolvimeto do geopotecial em séie, está elacioado com o achatameto pola da Tea e, potato, com a geometia do elipsóide de evolução. O coeficiete J,0 é cohecido como fato diâmico de foma e é um dos tês paâmetos pimáios defiidoes do elipsóide de efeêcia; os outos dois são o semi-eixo maio, a, e a costate dada pelo poduto GM. e Das equações (3.17) e (3.18), tem-se: assim, paa m=0 e =, C J = p H( m)!(+ 1) m = 0 H = 1 p = paa (+ m)! m 0 H = J,0, 0 = C 5. etão Como, pela tabela 3.1, paa o EGM-96 C,0 = 0, E-03, J,0 = 1086,67 x 10 7 Os paâmetos pimáios defiidoes do Sistema Geodésico de Refeêcia 1967 (GRS-67), utilizado o Basil, são: a = m GM = x 10 9 m 3 s J = 1087,067 x 10 7 U,0 A pati desses paâmetos deivam se os demais paâmetos elipsoidais. Das equações (5.6) e (5.7) o achatameto, f, pode se obtido iteativamete pela fómula: 3 U = J,0+ m1+ f m f. (5.9) 14 f 1 aa ω = 0, x 10 4 ad/s, obtém-se da (5.7): m 1 = 0, Tomado-se paa valo pelimia f 0 = 1/300, chega-se em duas iteações ao valo de ou f = 0,
20 f = 1/98, Gavidade omal (γ) O valo de γ depede da distâcia ao ceto de massa da Tea e da latitude geogáfica ϕ. Face à simetia otacioal γ idepede da logitude e a supefície do elipsóide de efeêcia é gealmete deotado po γ o : A fómula usada paa calcula γ 0 foi deduzida po C. Somigliaa em 199 [Moitz, 1984], com base o teoema de Claiaut (devido a Alexis Claiaut), que elacioa o achatameto teeste com a foça cetífuga e a gavidade omal o equado [Heiskae & Moitz, 1967]. Assim, aγ e cos φ + bγ p se φ γ 0 = 1/ (5.10) (a cos φ + b se φ) ode φ é a latitude geodésica; γ e e γ p são os valoes da gavidade omal o equado e os polos; espectivamete, a é o semi-eixo maio e b é o semi-eixo meo do elipsóide. Moitz [1984] apeseta uma equação obtida do desevolvimeto em séie da equação de Somigliaa, ode os temos da séie são potêcias de se φ: paa γ = γ + 0 e 1 a se φ (5.11) =1 a a a a = e + k, = e + e k, = e + e k, = e + e k, (5.1) sedo e a exceticidade do elipsóide e k dado po: bγ k = p 1 (5.13) aγ e Tomado valoes paa k e e, elativos ao elipsóide de efeêcia, obtém-se a espectiva fómula de gavidade omal. A fómula da gavidade omal mais ecetemete adotada pela Associação Iteacioal de Geodésia (IAG) é a fómula iteacioal da gavidade 1980: 4
21 γ o =978 03,67715(1 + 0, se ϕ + 0, se 4 ϕ + 0, se 6 ϕ + + 0, se 8 φ) mgal (5.14) com pecisão de 0,1 µgal. É comum ecota os modelos mais atigos tucados a potêcia do quato gau em se φ que expessado este último temo em fuçào de se φ esulta em: γ o = γ e (1 + β se ϕ β se ϕ) (5.15) Em 1930 a IAG adotou, em Estocolmo, a fómula: γ o = ,0(1+0, se ϕ 0, se ϕ) mgal, (5.16) ecomedado o seu uso paa todos os tabalhos gaviméticos. Esta fómula toou-se cohecida como fómula iteacioal da gavidade. Em 1964 a Uião Astoômica Iteacioal (IAU) adotou o Sistema de Costates Astoômicas; em 1967, a Assembléia Geal da IAG apovou ovos paâmetos paa o elipsóide de efeêcia, coeetes com a decisão da IAU, e ecomedou o Sistema Geodésico de Refeêcia 1967, cujas costates básicas são: a = m GM = x 10 9 m 3 s J = x 10 7 ode J é o coeficiete do temo do gau o desevolvimeto do esfeopotecial em séie de hamôicos esféicos. Destas costates básicas deivam os seguites valoes: f 1 = 98,47 f = 0, ω = x d/s m 1 = 0, (5.17) γ e = ,846 mgal γ p = ,730 mgal β = 0, β = 0, cuja gavidade omal é expessa pela fómula: ou, equivaletemete, γ o =978031,85(1+0, se ϕ 0, se ϕ) mgal (5.18) γ o = ,85(1+0, se ϕ +0, se 4 ϕ) mgal, (5.19) 5
22 com pecisão de 4 µgal. Esta equação foi chamada de fómula iteacioal da gavidade otecial aômalo (T) Chama-se potecial aômalo ou potecial petubado, T, à difeeça ete o geopotecial (W) e o esfeopotecial (U) em um mesmo poto: T = W U (5.0) T taduz o efeito das massas aômalas visíveis e ivisíveis, cuja soma é ula, idepede do potecial de otação e é uma fução hamôica, que satisfaz a equação de Laplace (3.1), e, potato, T = 0 A figua abaixo mosta, em seção omal, as supefícies do geóide e do elipsóide de efeêcia, ode, N é a distâcia ou altua ou odulação geoidal; i é o desvio ou deflexão da vetical; g é o veto da gavidade o poto ; γ e γ Q são vetoes da gavidade omal em e Q; e Q são as dieções da vetical e da omal os potos e Q, espectivamete Aomalia e distúbio da gavidade ( g e δ g ) Cosideado que o poto Q é a pojeção do poto (o geóide) sobe o elipsóide, o veto aomalia da gavidade g é dada po: 6
23 (5.1) g = γ. g p Q A difeeça ete os módulos de g e γ Q, g = g γ Q, (5.) é defiida como aomalia da gavidade e o âgulo i ete os dois vetoes é o desvio ou deflexão da vetical. A aomalia da gavidade é, potato, a difeeça ete a gavidade eal em (geóide) e a gavidade omal em Q (elipsóide de efeêcia). A difeeça ete os dois vetoes, o mesmo poto é deomiada veto distúbio da gavidade, δ g, ou seja, δ g = γ ; (5.3) g p a difeeça ete os módulos é chamada de distúbio da gavidade, δg, δg = g γ ; (5.4) O âgulo ete os dois vetoes é paticamete igual ao desvio da vetical uma vez que γ e γ Q têm, apoximadamete a mesma dieção (o valo do desvio da vetical pode vaia ete 1 e 10 em teeos plaos [Toge, 1980]). Sabedo-se que U, g é o gadiete de W e γ é o gadiete de δ g = gad (W p U p ) = gad T p. (5.5) Sedo a dieção da vetical e da omal paticamete coicidetes, isto é, é apoximadamete igual a Q, tem-se, [Heiskae & Moitz, 1967] W U W U T T δ g = + = + = =, (5.6) h Q ode h é a altitude geomética cotada ao logo da omal. Cosideado que a difeeça de potecial é dada pela eegia despedida o deslocameto, obtemos Q Q Q Etão, e du = U p U 0 = U p U Q = γ Q N. U p = U Q γ Q N T p = W p U Q + γ Q N, (5.7) Cuja deivada em elação a h é 7
24 T h W = h U Q h γ Q + N h = g + γ Q γ Q + N h γ Q = g + N h Utilizado a apoximação ete geóide e elipsóide, tem-se que W p = U Q etão, da (5.7), obtém-se: T p = γ Q N, (5.8) cohecida como fómula de Bus, que coelacioa a altua geoidal com o potecial aômalo. Dode se coclui que e T N = (5.9) γ T γ g = + N (5.30) h h que é cohecida como a equação fudametal da Geodésia Física [Heiskae & Moitz, 1967] e mosta que magitudes das aomalias da gavidade depedem: a) da distibuição de massa o iteio da Tea, picipalmete a costa (1º temo). b) de N e i (º temo). Assim, a pati do cohecimeto das aomalias da gavidade sobe a supefície total da Tea, a altua geoidal, N, e o desvio da vetical, i, podem se detemiadas ( a solução deste poblema é cosideada a Geodésia Física). Quado as medidas gaviméticas são utilizadas paa fis geológicos, leva-se em cota a elação ete aomalias e distibuição de massa; as ifluêcias de N e i são, etão, egligeciadas ou cosideadas a foma de pequeas coeções. Como a vaiação a altua do geóide é pequea e gadual e a magitude de i é muito pequea, o fato de coeção aplicável vaia muito pouco de poto paa poto e a pática é cosideado costate em áeas ão muito extesas. Como o potecial aômalo é uma fução hamôica, é possível expadí-lo em séie de hamôicos esféicos. Com efeito, cosideado que chega-se a T = W U (5.31) GM a T = ( δccos mλ + δsse mλ) (v). (5.3) = m= 0 ode os coeficietes δc e δs são dados po [Schwaz et al., 1990]: 8
25 δc δc,0 = C = C,0 C e U,0 ; δs = S (coeficietes zoaispaes) (demais coeficietes) (5.33) 5.5. Altua geoidal e aomalia da gavidade em séie de hamôicos esféicos A odulação ou altua geoidal associada a um modelo geopotecial em um dado poto (v,λ) é dada pela fómula de Bus (5.9): 1 GM a N = ( δccos mλ + δsse mλ) (v). (5.34) γ = m= 0 Na equação (5.30), o cálculo da deivada pacial de γ em elação a h é feito omalmete com base a apoximação do elipsóide à esfea. Assim, paa um poto distado de uma tea esféica de massa M sem otação, pode-se esceve: γ GM e γ γ GM γ = = = h 3. Assim, das equações (5.30) e (5.3), cosideado a apoximação esféica, chega-se a a g = γ ( 1) ( δccosmλ + δsse mλ) (v). (5.35) = m= 0 Na pática, o somatóio dos temos efeetes ao gau dos hamôicos esféicos é tucado em um valo fiito que depede do modelo de geopotecial utilizado. Os modelo mais ecetes são deivados de obsevações de satélites complemetadas pela detemiação de aomalias da gavidade em potos a supefície da Tea (iclusive oceâicas), que aumetam o úmeo de equações o sistema a se ivetido e melhoam a pecisão dos coeficietes de gaus mais elevados, po estaem mais póximos das fotes das aomalias Compoetes picipais do desvio da vetical, em séie de hamôicos esféicos A icliação i ete o geóide e o elipsóide de efeêcia em um detemiado poto é dada pelo âgulo ete a vetical e a omal o mesmo poto e é deomiada desvio da vetical. O âgulo i omalmete é decomposto em duas compoetes pepediculaes ete si, uma a dieção ote-sul ou compoete meidiaa ξ, e outa a dieção leste-oeste ou compoete do 1º vetical η. 9
26 Cosideado um plao vetical de azimute abitáio, figua abaixo, ds é a distâcia ifiitesimal ete dois potos e, cotada positivamete paa o ote, e ε é a compoete do desvio da vetical segudo esse plao abitáio. Tem-se: dn ε = ds aa uma seção meidiaa, ds = Rdφ, a compoete meidiaa ξ é dada po: ξ = 1 R N. (5.36) φ sedo φ = 90º v. A deivada de N em elação a φ pode se obtida a pati da equação (5.34). Assim, N φ GM = γ. a ( δccos mλ + δsse mλ) = 0 m= 0 φ ( v) (5.37) ode ( v) 1 m + m + 1 = ( ) ( ) ( ) ( ) v cos v 1,m v φ se v 1 (5.38) aa uma seção de pimeio vetical, ds = R cosφ dλ, a compoete do pimeio vetical η é dada po: ode η = 1 N. (5.39) R cos φ λ 30
27 N λ = GM a = 0 m= 0 m ( δc se mλ + δs cos mλ) (v) (5.40) Neste caso o elemeto de aco do pimeio vetical foi cosideado igual ao elemeto de aco de logitude, tedo em vista os valoes ifiitesimais aqui tatados e, também, dos pequeos valoes que o desvio da vetical assume, sedo da odem de algus segudos. 6. DETERMINAÇÃO GRAVIMÉTRICA DO GEÓIDE 6.1. Fómula de Stokes A fómula de Stokes (Geoge Gabiel Stokes), desevolvida em 1849, pemite o cálculo das odulações geoidais N(v,λ) a pati dos valoes de aomalia da gavidade g(v,λ ), obtidos a supefície da Tea, cosideada como esféica: R 4πγ π π ( ) = g( v', λ' ) S( ψ) se v' dv' dλ' N v, λ λ ' = 0 v' = 0, (6.1) sedo v e v as co-latitudes, λ e λ as logitudes e ψ a distâcia esféica ete estes potos, tal que: cosψ = cos vcos v' + se vse v'cos( λ' λ) (6.) e ou, + ψ 1 S = 1 ( ) = ( ψ) ψ ψ ψ ψ ( ψ) = cos ec se 5 cos ψ 3 cos ψ l se 1+ se 0 S (6.3) Desigado po ds= R sev dv dλ a áea de uma quadícula elemeta, tem-se: N 1 λ. (6.4) λ = = 4πγ R π π ( v, ) = g( v', ') S( )ds ' 0 v' λ ψ Cosideações sobe a aplicação da fómula de Stokes 31
28 As hipóteses cosideadas o desevolvimeto de Stokes impõem algumas estições de aplicabilidade de sua fómula, vistas a segui: (a) Stokes utilizou um modelo esféico de apoximação do geóide e, potato, eos elativos da odem do achatameto teeste seão egligeciados. Sedo o achatameto do elipsóide de efeêcia apoximadamete igual a 0,003, o eo elativo as altuas geoidais N é de 0,003N, o que pode esulta em eo absoluto de 30 cm paa uma valo de N igual a 100 metos. No Basil, ode o valo de N vaia de 0 a 30 metos, este eo ão ultapassa os 10 cm. (b) Os limites de itegação a fómula de Stokes se estedem à supefície total da Tea, o que sigifica dize que os levatametos gaviméticos devem pove uma cobetua total da supefície do globo ( iclusive os oceaos ). (c) O método de Stokes eque que o potecial aômalo seja uma fução hamôica o espaço exteio às massas da Tea, o que implica a ecessidade de emoção total das massas exteas ao geóide paa sua detemiação, que po sua vez dá oigem ao chamado efeito idieto. (d) aa detemiações pecisas do geóide em egiões de elevo muito acetuado, o efeito idieto deve se ecessaiamete icluído o cálculo de N. A ão cosideação deste efeito pode poduzi eos de até 10 vezes a altua geoidal. (e) Cosideado que a figua do elipsóide é o modelo mais apoximado da foma da Tea, Stokes adotou como hipóteses diâmicas e geométicas, que haja coicidêcia dos espectivos (i) eixo de otação, (ii) cetos de massa e volume, (iii) dos poteciais de gavidade a supefície, e (iv) das massas. Na pática, os dados gaviméticos, que são omalmete medidos a supefície física, são eduzidos matematicamete ao geóide (Lambet, 1930) e, devido à dificuldade de uma cobetua gavimética global, a fómula de Stokes é modificada paa a discetização dos elemetos de supefície. Em 1934, Hivoe popos um método de discetização, paa solucioa o poblema da detemiação das odulações geoidadis os cotietes (Gemael, 1999). O método eque a subdivisão da supefície da Tea po um quadiculado geogáfico egula (N-S, E-W), que tem sido usado desde etão, cofome equação (6.1). A cada quadícula, que epeseta uma célula paa o cálculo disceto da fómula de Stokes, pode se associado um valo médio da aomalia da gavidade. Satos & Escoba (004) popuseam o métodos de itegação po polígoos de Voooy ou tiâgulos de Deloay que utilizam a seguite equação: N 1 4πγ R ( φ, λ) = S( ψ) g( φ', λ' ) si ( φ', λ' ) i= 1 3, (6.5) ode φ = 90º - v; φ' = 90º - v'; é o úmeo de células em que a áea de cobetua gavimética é discetizada e s i (φ', λ') é a áea da célula de odem i, cujo ceto possui as coodeadas φ' e λ'. Quase todos os métodos utilizados paa o cálculo da altua geoidal, seja o domíio do espaço - métodos de itegação (Novák et al., 001; Jiag ad Duquee, 1997; Lehma, 1997) - ou da feqüêcia - "Fast Fouie Tasfom (FFT)" (Schwaz et al., 1990; Kuoishi, 001; Haagmas et al., 1993; Fosbeg ad Sideis, 1993; Stag va Hees, 1990), " Fast Hatley Tasfom (FHT)", " Fast T Tasfom (FTT)" (Ayha, 1997)-, evolvem a discetização da supefície teeste atavés do pocedimeto de gidagem. As aomalias da gavidade obsevadas, que omalmete ão são uifomemete distibuídas, têm que se itepoladas paa se obte uma
29 ifomação em um "gid" egulamete espaçado. Devido à mofologia do geóide, em geal levemete odulada, omalmete este pocesso ão acaeta poblemas, etetato, utiliza-se uma ifomação itepolada em luga dos dados oigiais, o que pode sigifica uma fote de eo. Além disso, o pocesso de gidagem pode cosumi muito tempo de pocessameto e é depedete da escolha da técica de gidagem e do tamaho das células. A tadicioal técica espacial 3D de colocação po míimos quadados (Tscheig et al., 001; Fosbeg ad Tscheig, 1981; Dezel ad Wekel, 1987; Gil et al., 1993; Molia ad Ussami, 1999) e os métodos de itegação po polígoos de Voooy ou tiâgulos de Deloay (Satos & Escoba, 004), ão utilizam a técica de gidagem, baseado-se os dados oigiais e a sua distibuição. 6.. Desvio da vetical. Fómulas de Veig Meiesz Um dos métodos empegados paa detemia as compoetes ξ e η foi fomulado pelo cietista holades F. A. Veiig Meiesz, em 198, utilizado a elação existete ete as odulações do geóide e a deflexão da vetical. Tata-se, potato, de um método gavimético, simila ao fomulado po Stokes paa a detemiação das altuas geoidais. As fómulas de Veiig Meiesz são as seguites: e 1 ξ = 4πγ 1 η = 4πγ π λ ' = 0 π λ ' = 0 π φ ' = π π φ ' = π ( ψ) ds g ( φ', λ' ) cos α cos φ' dφ' dλ' (6.6) dψ ( ψ) ds g ( φ', λ' ) se α cos φ' dφ' dλ'. (6.7) dψ A difeecial da fução de Stokes em elação a ψ, o temo S(ψ)/dψ, é chamado fução de Veiig Meiesz, e é obtida da equação: ( ψ) ds dψ ψ cos = ψ se ψ 1 se ψ + 8 se ψ 6 cos 3 se ψ ψ ψ + 3se ψ l se 1+ se. (6.8) REFERÊNCIAS BIBLIOGRÁFICAS Auehamme, F (1991) Voooi diagams: A suvey of a fudametal geometic data stuctue. ACM Comput Suvey 3 (3): Aya, M E (1997) Updatig ad computig the geoid usig two dimesioal fast Hatley tasfom ad fast T tasfom. J Geod 71: Chauveet, W (1854) Teatise o lae ad Spheical Tigoomety. J. B. Lippicott Co., hiladelphia, U. S. A. 33
30 Deke, H, Wezel, H -G (1987) Local geoid detemiatio ad compaiso with GS esults. Bull Géod 61: Fosbeg, R, Sideis, M G (1993) Geoid computatios by the multi-bad spheical FFT appoach. Mausc Geod 18: 8-90 Fosbeg, R, Tscheig, C C (1981) The use of height data i gavity field appoximatio by collocatio. J Geoph Res 86 (B9): Gemael, C (1999) Itodução à Geodésia Física. Ed. UFR, Cuitiba, Bazil Gil, A J, Sevilla, M J, Rodíguez-Cadeot, G (1993) Geoid detemiatio i cetal Spai fom gavity ad height data. Bull Géod 67: Haagmas, R, Mi, E de, Geldee, M vo (1993) Fast evaluatio of covolutio itegals o the sphee usig 1D FFT, ad a compaiso with existig methods fo Stokes itegal. Mausc Geod 18: 7-41 Hees, G S va (1986) ecisio of the geoid, computed fom teestial gavity measuemets. Mausc Geod 11: Heiskae, W ad Moitz, H (1967) hysical Geodesy. W. H. Feema, Sa Facisco. Jiag, Z ad Duquee, H (1997) O fast itegatio i geoid deteemiatio. J Geod 71: Kuoishi, Y (001) A impoved gavimetic geoid fo Japa, JGEOID98, ad elatioships to maie gavity data. J Geod 74 (11-1): Lambet, W D (1930) The eductio of obseved values of gavity to sea level. Bull Géod 6: Li, J, Sideis, M G (1997) Maie gavity ad geoid detemiatio by optimal combiatio of satellite altimety ad shipboe gavimety data. J Geod 71 (4): Lehma, R (1997) Fast space-domai evaluatio of geodetic suface itegals. J Geod 71: Molia, E C, Ussami, N (1999) The geoid i southeaste Bazil ad adjacet egio: ew costaits o desity distibutio ad themal state of the lithosphee. J Geody 8: Moitz, H (1984) Geodetic Refeece System 1980, Bull Géod 58 (3): Nóvak,, Vaícek,, Véoeau, M, Holmes, S, Feathestoe, W (001) O the accuacy of modified Stokes s itegatio i high-fequecy gavimetic geoid detemiatio. J Geod 74 (9): Rapp, R H, Wag, Y M, avlis, N K (1991) The Ohio State Uivesity 1991 geopotetial ad sea suface topogaphy hamoic coefficiet models. Repot No. 410, Depatmet of Geodetic Sciece ad Suveyig, The Ohio State Uiv., Columbus Rapp, R H ad Basíc (199) Oceawide gavity aomalies fom GEOS-3, Seasat ad Geosat altimete data. Geoph Res Lett 19 (19): Rupet, J (1988) A gavitatioal teai coectio pogam fo IBM compatible pesoal computes, Vol..1, Geological Suvey of Caada, GSC, Ope File 1834 Satos & Escoba (004) Discete Stokes' itegal by meas of Voooy ad Deloay Diagams. Joual of Geodesy, apoved. 34
31 Sideis, M G, She, B B (1995) A ew, high-esolutio geoid fo Caada ad pat of the U. S. by the 1D-FFT method. Bull Géod 69: Sideis, M G (1995) Fouie geoid detemiatio with iegula data. J Geod 70(1-): - 1 Stokes, G G (1849) O the vaiatio of gavity o the suface of the eath. I: Mathematical ad hysical apes, Vol. II, New Yok, pp (fom the Tas. Of the Cambidge hilos. Soc., Vol. VIII, pp ) Schwaz, K, Sideis, M G ad Fosbeg, R (1990) The use of FFT techiques i physical geodesy. Geoph J It 100: Tscheig, C C, Radwa, A, Tealab, A A, Mahmoud, S M, Abd El-Moum, M, Hassa, R, El- Syaed, I ad Sake, K (001) Local geoid detemiatio combiig gavity distubaces ad GS/levellig: a case study i the Lake Nasse Aea, Aswa, Egypt. J Geod 75 (7-8): REFERÊNCIAS NA INTERNET [1] Geomety i Actio, Voooi Diagams, (00). [] Natual Neighbos, What Ae They? [3] School of Mathematics ad Statistics Uivesity of St Adews, Scotlad 35
Capítulo I Erros e Aritmética Computacional
 C. Balsa e A. Satos Capítulo I Eos e Aitmética Computacioal. Itodução aos Métodos Numéicos O objectivo da disciplia de Métodos Numéicos é o estudo, desevolvimeto e avaliação de algoitmos computacioais
C. Balsa e A. Satos Capítulo I Eos e Aitmética Computacioal. Itodução aos Métodos Numéicos O objectivo da disciplia de Métodos Numéicos é o estudo, desevolvimeto e avaliação de algoitmos computacioais
TRABALHO E POTENCIAL ELETROSTÁTICO
 LTOMAGNTISMO I 5 TABALHO POTNCIAL LTOSTÁTICO Nos capítulos ateioes ós ivestigamos o campo elético devido a divesas cofiguações de cagas (potuais, distibuição liea, supefície de cagas e distibuição volumética
LTOMAGNTISMO I 5 TABALHO POTNCIAL LTOSTÁTICO Nos capítulos ateioes ós ivestigamos o campo elético devido a divesas cofiguações de cagas (potuais, distibuição liea, supefície de cagas e distibuição volumética
Definição: Seja a equação diferencial linear de ordem n e coeficientes variáveis:. x = +
 Vléi Zum Medeios & Mihil Lemotov Resolução de Equções Difeeciis Liees po Séies Poto Odiáio (PO) e Poto Sigul (PS) Defiição: Sej equção difeecil lie de odem e coeficietes viáveis: ( ) ( ) b ( ) é dito poto
Vléi Zum Medeios & Mihil Lemotov Resolução de Equções Difeeciis Liees po Séies Poto Odiáio (PO) e Poto Sigul (PS) Defiição: Sej equção difeecil lie de odem e coeficietes viáveis: ( ) ( ) b ( ) é dito poto
ARITMÉTICA DE PONTO FLUTUANTE/ERROS EM OPERAÇÕES NUMÉRICAS
 ARITMÉTICA DE PONTO FLUTUANTE/ERROS EM OPERAÇÕES NUMÉRICAS. Intodução O conjunto dos númeos epesentáveis em uma máquina (computadoes, calculadoas,...) é finito, e potanto disceto, ou seja não é possível
ARITMÉTICA DE PONTO FLUTUANTE/ERROS EM OPERAÇÕES NUMÉRICAS. Intodução O conjunto dos númeos epesentáveis em uma máquina (computadoes, calculadoas,...) é finito, e potanto disceto, ou seja não é possível
O oscilador harmônico
 O oscilador harmôico A U L A 5 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial de um oscilador harmôico simples, V( x) kx. objetivos obter a solução da equação de Schrödiger para um oscilador
O oscilador harmôico A U L A 5 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial de um oscilador harmôico simples, V( x) kx. objetivos obter a solução da equação de Schrödiger para um oscilador
3.1 Campo da Gravidade Normal Terra Normal
 . Campo da avidade Nomal.. Tea Nomal tedeemos po Tea omal um elipsóide de evolução qual se atibui a mesma massa M e a mesma velocidade agula da Tea eal e tal que o esfeopotecial U seja uma fução costate
. Campo da avidade Nomal.. Tea Nomal tedeemos po Tea omal um elipsóide de evolução qual se atibui a mesma massa M e a mesma velocidade agula da Tea eal e tal que o esfeopotecial U seja uma fução costate
PARTE IV COORDENADAS POLARES
 PARTE IV CRDENADAS PLARES Existem váios sistemas de coodenadas planas e espaciais que, dependendo da áea de aplicação, podem ajuda a simplifica e esolve impotantes poblemas geométicos ou físicos. Nesta
PARTE IV CRDENADAS PLARES Existem váios sistemas de coodenadas planas e espaciais que, dependendo da áea de aplicação, podem ajuda a simplifica e esolve impotantes poblemas geométicos ou físicos. Nesta
Campo Gravítico da Terra
 5. Campo Gavítico ómalo elação ete o potecial gavítico e o potecial omal é dada po: W ( x, y, z = U( x, y,z + ( x, y,z O campo gavítico aómalo ou petubado é etão defiido pela difeeça do campo gavítico
5. Campo Gavítico ómalo elação ete o potecial gavítico e o potecial omal é dada po: W ( x, y, z = U( x, y,z + ( x, y,z O campo gavítico aómalo ou petubado é etão defiido pela difeeça do campo gavítico
2 - Circuitos espelho de corrente com performance melhorada:
 Electóica 0/3 - Cicuitos espelho de coete com pefomace melhoada: Po ezes é ecessáio aumeta a pefomace dos cicuitos espelho de coete, tato do poto de ista da pecisão da taxa de tasfeêcia de coete como da
Electóica 0/3 - Cicuitos espelho de coete com pefomace melhoada: Po ezes é ecessáio aumeta a pefomace dos cicuitos espelho de coete, tato do poto de ista da pecisão da taxa de tasfeêcia de coete como da
Departamento de Informática. Modelagem Analítica. Desempenho de Sistemas de Computação. Arranjos: Amostras Ordenadas. Exemplo
 Depatameto de Ifomática Disciplia: Modelagem Aalítica do Desempeho de Sistemas de Computação Elemetos de Aálise Combiatóia Pof. Ségio Colche colche@if.puc-io.b Teoema: Elemetos de Aálise Combiatóia Modelagem
Depatameto de Ifomática Disciplia: Modelagem Aalítica do Desempeho de Sistemas de Computação Elemetos de Aálise Combiatóia Pof. Ségio Colche colche@if.puc-io.b Teoema: Elemetos de Aálise Combiatóia Modelagem
GERADORES. Figura 5.1 (a) Gerador não ideal. (b) Gerador não ideal com a resistência interna r explicita no diagrama.
 ELEICIDADE CAPÍULO 5 GEADOES Cofome visto o Capítulo, o geado é uma máquia elética capaz de estabelece uma difeeça de potecial elético (ddp) costate (ou fime) ete os extemos de um coduto elético, de maeia
ELEICIDADE CAPÍULO 5 GEADOES Cofome visto o Capítulo, o geado é uma máquia elética capaz de estabelece uma difeeça de potecial elético (ddp) costate (ou fime) ete os extemos de um coduto elético, de maeia
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
2*5$',(17('2327(1&,$/( (1(5*,$12&$032(/(75267È7,&2
 3 *5',7'37&,/ 5*,&3/7567È7,& ÃÃÃ*5',7Ã'Ã37&,/ A expessão geéica paa o cálculo da difeeça de potecial como uma itegal de liha é: dl ) 5) Se o camiho escolhido fo um L, tal que se possa cosidea costate esse
3 *5',7'37&,/ 5*,&3/7567È7,& ÃÃÃ*5',7Ã'Ã37&,/ A expessão geéica paa o cálculo da difeeça de potecial como uma itegal de liha é: dl ) 5) Se o camiho escolhido fo um L, tal que se possa cosidea costate esse
Módulo 5: Conteúdo programático Eq da continuidade em Regime Permanente. Escoamento dos Fluidos - Equações Fundamentais
 Módulo 5: Conteúdo pogamático Eq da continuidade em egime Pemanente Bibliogafia: Bunetti, F. Mecânica dos Fluidos, São Paulo, Pentice Hall, 7. Eoamento dos Fluidos - Equações Fundamentais Popiedades Intensivas:
Módulo 5: Conteúdo pogamático Eq da continuidade em egime Pemanente Bibliogafia: Bunetti, F. Mecânica dos Fluidos, São Paulo, Pentice Hall, 7. Eoamento dos Fluidos - Equações Fundamentais Popiedades Intensivas:
)25d$0$*1e7,&$62%5( &21'8725(6
 73 )5d$0$*1e7,&$6%5( &1'875(6 Ao final deste capítulo você deveá se capaz de: ½ Explica a ação de um campo magnético sobe um conduto conduzindo coente. ½ Calcula foças sobe condutoes pecoidos po coentes,
73 )5d$0$*1e7,&$6%5( &1'875(6 Ao final deste capítulo você deveá se capaz de: ½ Explica a ação de um campo magnético sobe um conduto conduzindo coente. ½ Calcula foças sobe condutoes pecoidos po coentes,
Prof. Daniel I. De Souza, Jr., Ph.D.
 CONAMET/SAM 26 TESTE DE VIDA SEQÜENCIAL APLICADO A UM TESTE DE VIDA ACELERADO COM UMA DISTRIBUIÇÃO DE AMOSTRAGEM WEIBULL DE TRÊS PARÂMETROS - UMA ABORDAGEM UTILIZANDO-SE O MÉTODO DO MAXIMUM LIKELIHOOD
CONAMET/SAM 26 TESTE DE VIDA SEQÜENCIAL APLICADO A UM TESTE DE VIDA ACELERADO COM UMA DISTRIBUIÇÃO DE AMOSTRAGEM WEIBULL DE TRÊS PARÂMETROS - UMA ABORDAGEM UTILIZANDO-SE O MÉTODO DO MAXIMUM LIKELIHOOD
EQUAÇÕES DIFERENCIAIS LINEARES DE ORDEM N
 EQUAÇÕES DIFERENCIAIS LINEARES DE ORDEM N Estudaremos este capítulo as equações diereciais lieares de ordem, que são de suma importâcia como suporte matemático para vários ramos da egeharia e das ciêcias.
EQUAÇÕES DIFERENCIAIS LINEARES DE ORDEM N Estudaremos este capítulo as equações diereciais lieares de ordem, que são de suma importâcia como suporte matemático para vários ramos da egeharia e das ciêcias.
RESOLUÇÃO DA AVALIAÇÃO DE MATEMÁTICA 2 o ANO DO ENSINO MÉDIO DATA: 10/08/13 PROFESSOR: MALTEZ
 ESOLUÇÃO DA AALIAÇÃO DE MATEMÁTICA o ANO DO ENSINO MÉDIO DATA: 0/08/ POFESSO: MALTEZ QUESTÃO 0 A secção tansvesal de um cilindo cicula eto é um quadado com áea de m. O volume desse cilindo, em m, é: A
ESOLUÇÃO DA AALIAÇÃO DE MATEMÁTICA o ANO DO ENSINO MÉDIO DATA: 0/08/ POFESSO: MALTEZ QUESTÃO 0 A secção tansvesal de um cilindo cicula eto é um quadado com áea de m. O volume desse cilindo, em m, é: A
Questão 1. Questão 2. Questão 3. alternativa C. alternativa E
 Questão 1 Dois pilotos iniciaam simultaneamente a disputa de uma pova de automobilismo numa pista cuja extensão total é de, km. Enquanto Máio leva 1,1 minuto paa da uma volta completa na pista, Júlio demoa
Questão 1 Dois pilotos iniciaam simultaneamente a disputa de uma pova de automobilismo numa pista cuja extensão total é de, km. Enquanto Máio leva 1,1 minuto paa da uma volta completa na pista, Júlio demoa
Introdução ao Estudo de Sistemas Lineares
 Itrodução ao Estudo de Sistemas Lieares 1. efiições. 1.1 Equação liear é toda seteça aberta, as icógitas x 1, x 2, x 3,..., x, do tipo a1 x1 a2 x2 a3 x3... a x b, em que a 1, a 2, a 3,..., a são os coeficietes
Itrodução ao Estudo de Sistemas Lieares 1. efiições. 1.1 Equação liear é toda seteça aberta, as icógitas x 1, x 2, x 3,..., x, do tipo a1 x1 a2 x2 a3 x3... a x b, em que a 1, a 2, a 3,..., a são os coeficietes
/(,'(%,276$9$57()/8;2 0$*1e7,&2
 67 /(,'(%,76$9$57()/8; 0$*1e7,& Ao final deste capítulo você deveá se capaz de: ½ Explica a elação ente coente elética e campo magnético. ½ Equaciona a elação ente coente elética e campo magnético, atavés
67 /(,'(%,76$9$57()/8; 0$*1e7,& Ao final deste capítulo você deveá se capaz de: ½ Explica a elação ente coente elética e campo magnético. ½ Equaciona a elação ente coente elética e campo magnético, atavés
onde d, u, v são inteiros não nulos, com u v, mdc(u, v) = 1 e u e v de paridades distintas.
 !"$# &%$" ')( * +-,$. /-0 3$4 5 6$7 8:9)$;$< =8:< > Deomiaremos equação diofatia (em homeagem ao matemático grego Diofato de Aleadria) uma equação em úmeros iteiros. Nosso objetivo será estudar dois tipos
!"$# &%$" ')( * +-,$. /-0 3$4 5 6$7 8:9)$;$< =8:< > Deomiaremos equação diofatia (em homeagem ao matemático grego Diofato de Aleadria) uma equação em úmeros iteiros. Nosso objetivo será estudar dois tipos
VII Equações Diferenciais Ordinárias de Primeira Ordem
 VII Equações Difereciais Ordiárias de Primeira Ordem Itrodução As equações difereciais ordiárias são istrumetos esseciais para a modelação de muitos feómeos proveietes de várias áreas como a física, química,
VII Equações Difereciais Ordiárias de Primeira Ordem Itrodução As equações difereciais ordiárias são istrumetos esseciais para a modelação de muitos feómeos proveietes de várias áreas como a física, química,
Antenas. Antena = transição entre propagação guiada (circuitos) e propagação não-guiada (espaço). Antena Isotrópica
 Antenas Antena tansição ente popagação guiada (cicuitos) e popagação não-guiada (espaço). Antena tansmissoa: Antena eceptoa: tansfoma elétons em fótons; tansfoma fótons em elétons. Antena sotópica Fonte
Antenas Antena tansição ente popagação guiada (cicuitos) e popagação não-guiada (espaço). Antena tansmissoa: Antena eceptoa: tansfoma elétons em fótons; tansfoma fótons em elétons. Antena sotópica Fonte
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
Equações Diferenciais Lineares de Ordem n
 PUCRS Faculdade de Matemática Equações Difereciais - Prof. Eliete Equações Difereciais Lieares de Ordem Cosideremos a equação diferecial ordiária liear de ordem escrita a forma 1 d y d y dy L( y( x ))
PUCRS Faculdade de Matemática Equações Difereciais - Prof. Eliete Equações Difereciais Lieares de Ordem Cosideremos a equação diferecial ordiária liear de ordem escrita a forma 1 d y d y dy L( y( x ))
Sejam todos bem-vindos! Física II. Prof. Dr. Cesar Vanderlei Deimling
 Sejam todos bem-vindos! Física II Pof. D. Cesa Vandelei Deimling Bibliogafia: Plano de Ensino Qual a impotância da Física em um cuso de Engenhaia? A engenhaia é a ciência e a pofissão de adquii e de aplica
Sejam todos bem-vindos! Física II Pof. D. Cesa Vandelei Deimling Bibliogafia: Plano de Ensino Qual a impotância da Física em um cuso de Engenhaia? A engenhaia é a ciência e a pofissão de adquii e de aplica
GEOMETRIA ESPACIAL. a) Encher a leiteira até a metade, pois ela tem um volume 20 vezes maior que o volume do copo.
 GEOMETRIA ESPACIAL ) Uma metalúgica ecebeu uma encomenda paa fabica, em gande quantidade, uma peça com o fomato de um pisma eto com base tiangula, cujas dimensões da base são 6cm, 8cm e 0cm e cuja altua
GEOMETRIA ESPACIAL ) Uma metalúgica ecebeu uma encomenda paa fabica, em gande quantidade, uma peça com o fomato de um pisma eto com base tiangula, cujas dimensões da base são 6cm, 8cm e 0cm e cuja altua
Séries de Potências AULA LIVRO
 LIVRO Séries de Potêcias META Apresetar os coceitos e as pricipais propriedades de Séries de Potêcias. Além disso, itroduziremos as primeiras maeiras de escrever uma fução dada como uma série de potêcias.
LIVRO Séries de Potêcias META Apresetar os coceitos e as pricipais propriedades de Séries de Potêcias. Além disso, itroduziremos as primeiras maeiras de escrever uma fução dada como uma série de potêcias.
ActivALEA. ative e atualize a sua literacia
 ActivALEA ative e atualize a sua literacia N.º 29 O QUE É UMA SONDAGEM? COMO É TRANSMIITIIDO O RESULTADO DE UMA SONDAGEM? O QUE É UM IINTERVALO DE CONFIIANÇA? Por: Maria Eugéia Graça Martis Departameto
ActivALEA ative e atualize a sua literacia N.º 29 O QUE É UMA SONDAGEM? COMO É TRANSMIITIIDO O RESULTADO DE UMA SONDAGEM? O QUE É UM IINTERVALO DE CONFIIANÇA? Por: Maria Eugéia Graça Martis Departameto
MOMENTOS DE INÉRCIA. Física Aplicada à Engenharia Civil II
 Física Aplicada à Egeharia Civil MOMENTOS DE NÉRCA Neste capítulo pretede-se itroduzir o coceito de mometo de iércia, em especial quado aplicado para o caso de superfícies plaas. Este documeto, costitui
Física Aplicada à Egeharia Civil MOMENTOS DE NÉRCA Neste capítulo pretede-se itroduzir o coceito de mometo de iércia, em especial quado aplicado para o caso de superfícies plaas. Este documeto, costitui
Definição 1.1: Uma equação diferencial ordinária é uma. y ) = 0, envolvendo uma função incógnita y = y( x) e algumas das suas derivadas em ordem a x.
 4. EQUAÇÕES DIFERENCIAIS 4.: Defiição e coceitos básicos Defiição.: Uma equação diferecial ordiária é uma dy d y equação da forma f,,,, y = 0 ou d d ( ) f (, y, y,, y ) = 0, evolvedo uma fução icógita
4. EQUAÇÕES DIFERENCIAIS 4.: Defiição e coceitos básicos Defiição.: Uma equação diferecial ordiária é uma dy d y equação da forma f,,,, y = 0 ou d d ( ) f (, y, y,, y ) = 0, evolvedo uma fução icógita
- B - - Esse ponto fica à esquerda das cargas nos esquemas a) I e II b) I e III c) I e IV d) II e III e) III e IV. b. F. a. F
 LIST 03 LTROSTÁTIC PROSSOR MÁRCIO 01 (URJ) Duas patículas eleticamente caegadas estão sepaadas po uma distância. O gáfico que melho expessa a vaiação do módulo da foça eletostática ente elas, em função
LIST 03 LTROSTÁTIC PROSSOR MÁRCIO 01 (URJ) Duas patículas eleticamente caegadas estão sepaadas po uma distância. O gáfico que melho expessa a vaiação do módulo da foça eletostática ente elas, em função
Equações Diferenciais (ED) Resumo
 Equações Difereciais (ED) Resumo Equações Difereciais é uma equação que evolve derivadas(diferecial) Por eemplo: dy ) 5 ( y: variável depedete, : variável idepedete) d y dy ) 3 0 y ( y: variável depedete,
Equações Difereciais (ED) Resumo Equações Difereciais é uma equação que evolve derivadas(diferecial) Por eemplo: dy ) 5 ( y: variável depedete, : variável idepedete) d y dy ) 3 0 y ( y: variável depedete,
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE
 FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE CURSO: ENGENHARIA DE PRODUÇÃO ASSUNTO: INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS, EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM SEPARÁVEIS, HOMOGÊNEAS, EXATAS, FATORES
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE CURSO: ENGENHARIA DE PRODUÇÃO ASSUNTO: INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS, EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM SEPARÁVEIS, HOMOGÊNEAS, EXATAS, FATORES
CAMPOS MAGNETOSTÁTICOS PRODUZIDOS POR CORRENTE ELÉTRICA
 ELETOMAGNETMO 75 9 CAMPO MAGNETOTÁTCO PODUZDO PO COENTE ELÉTCA Nos capítulos anteioes estudamos divesos fenômenos envolvendo cagas eléticas, (foças de oigem eletostática, campo elético, potencial escala
ELETOMAGNETMO 75 9 CAMPO MAGNETOTÁTCO PODUZDO PO COENTE ELÉTCA Nos capítulos anteioes estudamos divesos fenômenos envolvendo cagas eléticas, (foças de oigem eletostática, campo elético, potencial escala
Análise de Estratégias de Controle de Erros para Redes de Sensores com Modulação OQPSK e GFSK
 XXV SIMPÓSIO BRASILEIRO DE TELECOMUNICAÇÕES SBT 7, 3-6 DE SETEMBRO DE 7, RECIFE, PE Aálise de Estatégias de Cotole de Eos paa Redes de Sesoes com Modulação OQPSK e GFSK João. Kleischmidt e Walte C. Boelli
XXV SIMPÓSIO BRASILEIRO DE TELECOMUNICAÇÕES SBT 7, 3-6 DE SETEMBRO DE 7, RECIFE, PE Aálise de Estatégias de Cotole de Eos paa Redes de Sesoes com Modulação OQPSK e GFSK João. Kleischmidt e Walte C. Boelli
Interbits SuperPro Web
 1. (Unesp 2013) No dia 5 de junho de 2012, pôde-se obseva, de deteminadas egiões da Tea, o fenômeno celeste chamado tânsito de Vênus, cuja póxima ocoência se daá em 2117. Tal fenômeno só é possível poque
1. (Unesp 2013) No dia 5 de junho de 2012, pôde-se obseva, de deteminadas egiões da Tea, o fenômeno celeste chamado tânsito de Vênus, cuja póxima ocoência se daá em 2117. Tal fenômeno só é possível poque
Física Geral I - F 128 Aula 8: Energia Potencial e Conservação de Energia. 2 o Semestre 2012
 Física Geal I - F 18 Aula 8: Enegia Potencial e Consevação de Enegia o Semeste 1 Q1: Tabalho e foça Analise a seguinte afimação sobe um copo, que patindo do epouso, move-se de acodo com a foça mostada
Física Geal I - F 18 Aula 8: Enegia Potencial e Consevação de Enegia o Semeste 1 Q1: Tabalho e foça Analise a seguinte afimação sobe um copo, que patindo do epouso, move-se de acodo com a foça mostada
UNIVERSIDADE EDUARDO MONDLANE
 UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenhaia Tansmissão de calo 3º Ano Aula 4 Aula Pática- Equação Difeencial de Tansmissão de Calo e as Condições de Contono Poblema -4. Calcula a tempeatua no
UNIVERSIDADE EDUARDO MONDLANE Faculdade de Engenhaia Tansmissão de calo 3º Ano Aula 4 Aula Pática- Equação Difeencial de Tansmissão de Calo e as Condições de Contono Poblema -4. Calcula a tempeatua no
EXPERIÊNCIA 5 - RESPOSTA EM FREQUENCIA EM UM CIRCUITO RLC - RESSONÂNCIA
 UM/AET Eng. Elética sem 0 - ab. icuitos Eléticos I Pof. Athemio A.P.Feaa/Wilson Yamaguti(edição) EPEIÊNIA 5 - ESPOSTA EM FEQUENIA EM UM IUITO - ESSONÂNIA INTODUÇÃO. icuito séie onsideando o cicuito da
UM/AET Eng. Elética sem 0 - ab. icuitos Eléticos I Pof. Athemio A.P.Feaa/Wilson Yamaguti(edição) EPEIÊNIA 5 - ESPOSTA EM FEQUENIA EM UM IUITO - ESSONÂNIA INTODUÇÃO. icuito séie onsideando o cicuito da
MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação. Aula 05. Prof. Dr. Marco Antonio Leonel Caetano
 MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação Aula 5 Pof. D. Maco Antonio Leonel Caetano Guia de Estudo paa Aula 5 Poduto Vetoial - Intepetação do poduto vetoial Compaação com as funções
MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação Aula 5 Pof. D. Maco Antonio Leonel Caetano Guia de Estudo paa Aula 5 Poduto Vetoial - Intepetação do poduto vetoial Compaação com as funções
APONTAMENTOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA APONTAMENTOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (III ) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Ídice Itrodução Aplicação do cálculo matricial aos
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA APONTAMENTOS DE ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA (III ) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Ídice Itrodução Aplicação do cálculo matricial aos
EM423A Resistência dos Materiais
 UNICAMP Univesidade Estadual de Campinas EM43A esistência dos Mateiais Pojeto Tação-Defomação via Medidas de esistência Pofesso: obeto de Toledo Assumpção Alunos: Daniel obson Pinto A: 070545 Gustavo de
UNICAMP Univesidade Estadual de Campinas EM43A esistência dos Mateiais Pojeto Tação-Defomação via Medidas de esistência Pofesso: obeto de Toledo Assumpção Alunos: Daniel obson Pinto A: 070545 Gustavo de
CAPÍTULO 5 - INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA
 CAPÍTULO 5 - INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA 5. INTRODUÇÃO É freqüete ecotrarmos problemas estatísticos do seguite tipo : temos um grade úmero de objetos (população) tais que se fossem tomadas as medidas
CAPÍTULO 5 - INTRODUÇÃO À INFERÊNCIA ESTATÍSTICA 5. INTRODUÇÃO É freqüete ecotrarmos problemas estatísticos do seguite tipo : temos um grade úmero de objetos (população) tais que se fossem tomadas as medidas
Engenharia Electrotécnica e de Computadores Exercícios de Electromagnetismo Ficha 1
 Instituto Escola Supeio Politécnico de Tecnologia ÁREA INTERDEPARTAMENTAL Ano lectivo 010-011 011 Engenhaia Electotécnica e de Computadoes Eecícios de Electomagnetismo Ficha 1 Conhecimentos e capacidades
Instituto Escola Supeio Politécnico de Tecnologia ÁREA INTERDEPARTAMENTAL Ano lectivo 010-011 011 Engenhaia Electotécnica e de Computadoes Eecícios de Electomagnetismo Ficha 1 Conhecimentos e capacidades
Demonstrações especiais
 Os fudametos da Física Volume 3 Meu Demostrações especiais a ) RLAÇÃO NTR próx. e sup. osidere um codutor eletrizado e em equilíbrio eletrostático. Seja P sup. um poto da superfície e P próx. um poto extero
Os fudametos da Física Volume 3 Meu Demostrações especiais a ) RLAÇÃO NTR próx. e sup. osidere um codutor eletrizado e em equilíbrio eletrostático. Seja P sup. um poto da superfície e P próx. um poto extero
1.5 Aritmética de Ponto Flutuante
 .5 Aritmética de Poto Flutuate A represetação em aritmética de poto flutuate é muito utilizada a computação digital. Um exemplo é a caso das calculadoras cietíficas. Exemplo:,597 03. 3 Este úmero represeta:,597.
.5 Aritmética de Poto Flutuate A represetação em aritmética de poto flutuate é muito utilizada a computação digital. Um exemplo é a caso das calculadoras cietíficas. Exemplo:,597 03. 3 Este úmero represeta:,597.
DISCIPLINA ELETRICIDADE E MAGNETISMO LEI DE AMPÈRE
 DISCIPLINA ELETICIDADE E MAGNETISMO LEI DE AMPÈE A LEI DE AMPÈE Agoa, vamos estuda o campo magnético poduzido po uma coente elética que pecoe um fio. Pimeio vamos utiliza uma técnica, análoga a Lei de
DISCIPLINA ELETICIDADE E MAGNETISMO LEI DE AMPÈE A LEI DE AMPÈE Agoa, vamos estuda o campo magnético poduzido po uma coente elética que pecoe um fio. Pimeio vamos utiliza uma técnica, análoga a Lei de
Tópicos de Mecânica Quântica I. Equações de Newton e de Hamilton versus Equações de Schrödinger
 Tópicos de Mecâica Quâtica I Equações de Newto e de Hamilto versus Equações de Schrödiger Ferado Ferades Cetro de Ciêcias Moleculares e Materiais, DQBFCUL Notas para as aulas de Química-Física II, 010/11
Tópicos de Mecâica Quâtica I Equações de Newto e de Hamilto versus Equações de Schrödiger Ferado Ferades Cetro de Ciêcias Moleculares e Materiais, DQBFCUL Notas para as aulas de Química-Física II, 010/11
INTRODUÇÃO A TEORIA DE CONJUNTOS
 INTRODUÇÃO TEORI DE CONJUNTOS Professora Laura guiar Cojuto dmitiremos que um cojuto seja uma coleção de ojetos chamados elemetos e que cada elemeto é um dos compoetes do cojuto. Geralmete, para dar ome
INTRODUÇÃO TEORI DE CONJUNTOS Professora Laura guiar Cojuto dmitiremos que um cojuto seja uma coleção de ojetos chamados elemetos e que cada elemeto é um dos compoetes do cojuto. Geralmete, para dar ome
Fig. 8-8. Essas linhas partem do pólo norte para o pólo sul na parte externa do material, e do pólo sul para o pólo norte na região do material.
 Campo magnético Um ímã, com seus pólos note e sul, também pode poduzi movimentos em patículas, devido ao seu magnetismo. Contudo, essas patículas, paa sofeem esses deslocamentos, têm que te popiedades
Campo magnético Um ímã, com seus pólos note e sul, também pode poduzi movimentos em patículas, devido ao seu magnetismo. Contudo, essas patículas, paa sofeem esses deslocamentos, têm que te popiedades
Vedação. Fig.1 Estrutura do comando linear modelo ST
 58-2BR Comando linea modelos, -B e I Gaiola de esfeas Esfea Eixo Castanha Vedação Fig.1 Estutua do comando linea modelo Estutua e caacteísticas O modelo possui uma gaiola de esfeas e esfeas incopoadas
58-2BR Comando linea modelos, -B e I Gaiola de esfeas Esfea Eixo Castanha Vedação Fig.1 Estutua do comando linea modelo Estutua e caacteísticas O modelo possui uma gaiola de esfeas e esfeas incopoadas
1ª Aula do Cap. 6 Forças e Movimento II
 ATRITO 1ª Aula do Cap. 6 Foças e Movimento II Foça de Atito e Foça Nomal. Atito e históia. Coeficientes de atito. Atito Dinâmico e Estático. Exemplos e Execícios. O efeito do atito ente duas supefícies
ATRITO 1ª Aula do Cap. 6 Foças e Movimento II Foça de Atito e Foça Nomal. Atito e históia. Coeficientes de atito. Atito Dinâmico e Estático. Exemplos e Execícios. O efeito do atito ente duas supefícies
CAPÍTULO 5 CIRCUITOS SEQUENCIAIS III: CONTADORES SÍNCRONOS
 60 Sumário CAPÍTULO 5 CIRCUITOS SEQUENCIAIS III: CONTADORES SÍNCRONOS 5.1. Itrodução... 62 5.2. Tabelas de trasição dos flip-flops... 63 5.2.1. Tabela de trasição do flip-flop JK... 63 5.2.2. Tabela de
60 Sumário CAPÍTULO 5 CIRCUITOS SEQUENCIAIS III: CONTADORES SÍNCRONOS 5.1. Itrodução... 62 5.2. Tabelas de trasição dos flip-flops... 63 5.2.1. Tabela de trasição do flip-flop JK... 63 5.2.2. Tabela de
Campo Gravítico da Terra
 Campo Gavítico da ea 1. Condiçõe de medição eodéica O intumento com que ão efectuada a mediçõe eodéica, obe a upefície da ea, etão ujeito à foça da avidade. Paa pode intepeta coectamente o eultado da mediçõe,
Campo Gavítico da ea 1. Condiçõe de medição eodéica O intumento com que ão efectuada a mediçõe eodéica, obe a upefície da ea, etão ujeito à foça da avidade. Paa pode intepeta coectamente o eultado da mediçõe,
TEORIA DA GRAVITAÇÃO UNIVERSAL
 Aula 0 EORIA DA GRAVIAÇÃO UNIVERSAL MEA Mosta aos alunos a teoia da gavitação de Newton, peda de toque da Mecânica newtoniana, elemento fundamental da pimeia gande síntese da Física. OBJEIVOS Abi a pespectiva,
Aula 0 EORIA DA GRAVIAÇÃO UNIVERSAL MEA Mosta aos alunos a teoia da gavitação de Newton, peda de toque da Mecânica newtoniana, elemento fundamental da pimeia gande síntese da Física. OBJEIVOS Abi a pespectiva,
AULA 23 FATORES DE FORMA DE RADIAÇÃO TÉRMICA
 Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
defi departamento de física www.defi.isep.ipp.pt
 defi departameto de física Laboratórios de Física www.defi.isep.ipp.pt stituto Superior de Egeharia do Porto- Departameto de Física Rua Dr. Atóio Berardio de Almeida, 431 4200-072 Porto. T 228 340 500.
defi departameto de física Laboratórios de Física www.defi.isep.ipp.pt stituto Superior de Egeharia do Porto- Departameto de Física Rua Dr. Atóio Berardio de Almeida, 431 4200-072 Porto. T 228 340 500.
COMPOSIÇÕES DE FUNÇÕES GERATRIZES E A FÓRMULA EXPONENCIAL
 COMPOSIÇÕES DE FUNÇÕES GERATRIZES E A FÓRMULA EXPONENCIAL Grade parte do poder de fuções geratrizes vêm de composição delas! Observação. Sejam F (x) = 0 G(x) = 0 f x g x duas séries formais. A composição
COMPOSIÇÕES DE FUNÇÕES GERATRIZES E A FÓRMULA EXPONENCIAL Grade parte do poder de fuções geratrizes vêm de composição delas! Observação. Sejam F (x) = 0 G(x) = 0 f x g x duas séries formais. A composição
somente um valor da variável y para cada valor de variável x.
 Notas de Aula: Revisão de fuções e geometria aalítica REVISÃO DE FUNÇÕES Fução como regra ou correspodêcia Defiição : Uma fução f é uma regra ou uma correspodêcia que faz associar um e somete um valor
Notas de Aula: Revisão de fuções e geometria aalítica REVISÃO DE FUNÇÕES Fução como regra ou correspodêcia Defiição : Uma fução f é uma regra ou uma correspodêcia que faz associar um e somete um valor
Aluno(a): Professor: Chiquinho
 Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Aplicação da Lei Gauss: Algumas distribuições simétricas de cargas
 Aplicação da ei Gauss: Algumas distibuições siméticas de cagas Como utiliza a lei de Gauss paa detemina D s, se a distibuição de cagas fo conhecida? s Ds. d A solução é fácil se conseguimos obte uma supefície
Aplicação da ei Gauss: Algumas distibuições siméticas de cagas Como utiliza a lei de Gauss paa detemina D s, se a distibuição de cagas fo conhecida? s Ds. d A solução é fácil se conseguimos obte uma supefície
Resistência dos Materiais IV Lista de Exercícios Capítulo 2 Critérios de Resistência
 Lista de Execícios Capítulo Citéios de Resistência 0.7 A tensão de escoamento de um mateial plástico é y 0 MPa. Se esse mateial é submetido a um estado plano de tensões ocoe uma falha elástica quando uma
Lista de Execícios Capítulo Citéios de Resistência 0.7 A tensão de escoamento de um mateial plástico é y 0 MPa. Se esse mateial é submetido a um estado plano de tensões ocoe uma falha elástica quando uma
Testes de Hipóteses para a Diferença Entre Duas Médias Populacionais
 Estatística II Atoio Roque Aula Testes de Hipóteses para a Difereça Etre Duas Médias Populacioais Vamos cosiderar o seguite problema: Um pesquisador está estudado o efeito da deficiêcia de vitamia E sobre
Estatística II Atoio Roque Aula Testes de Hipóteses para a Difereça Etre Duas Médias Populacioais Vamos cosiderar o seguite problema: Um pesquisador está estudado o efeito da deficiêcia de vitamia E sobre
Exercício 1. Quantos bytes (8 bits) existem de modo que ele contenha exatamente quatro 1 s? Exercício 2. Verifique que
 LISTA INCRÍVEL DE MATEMÁTICA DISCRETA II DANIEL SMANIA 1 Amostras, seleções, permutações e combiações Exercício 1 Quatos bytes (8 bits) existem de modo que ele coteha exatamete quatro 1 s? Exercício 2
LISTA INCRÍVEL DE MATEMÁTICA DISCRETA II DANIEL SMANIA 1 Amostras, seleções, permutações e combiações Exercício 1 Quatos bytes (8 bits) existem de modo que ele coteha exatamete quatro 1 s? Exercício 2
De Kepler a Newton. (através da algebra geométrica) 2008 DEEC IST Prof. Carlos R. Paiva
 De Keple a Newton (atavés da algeba geomética) 008 DEEC IST Pof. Calos R. Paiva De Keple a Newton (atavés da álgeba geomética) 1 De Keple a Newton Vamos aqui mosta como, a pati das tês leis de Keple sobe
De Keple a Newton (atavés da algeba geomética) 008 DEEC IST Pof. Calos R. Paiva De Keple a Newton (atavés da álgeba geomética) 1 De Keple a Newton Vamos aqui mosta como, a pati das tês leis de Keple sobe
Análise do Efeito do Solo em Canal de Propagação Outdoor 3-D Usando o Método B-FDTD
 IEEE LATIN AMERICA TRANSACTIONS, VOL. 5, NO. 3, JUNE 7 65 Aálise do Efeito do Solo em Caal de Popagação Outdoo 3-D Usado o Método B-FDTD Rodigo M. S. de Oliveia, Waldi H. B. J e Calos L. S. S. Sobiho (Membo
IEEE LATIN AMERICA TRANSACTIONS, VOL. 5, NO. 3, JUNE 7 65 Aálise do Efeito do Solo em Caal de Popagação Outdoo 3-D Usado o Método B-FDTD Rodigo M. S. de Oliveia, Waldi H. B. J e Calos L. S. S. Sobiho (Membo
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
5- CÁLCULO APROXIMADO DE INTEGRAIS 5.1- INTEGRAÇÃO NUMÉRICA
 5- CÁLCULO APROXIMADO DE INTEGRAIS 5.- INTEGRAÇÃO NUMÉRICA Itegrar umericamete uma fução y f() um dado itervalo [a, b] é itegrar um poliômio P () que aproime f() o dado itervalo. Em particular, se y f()
5- CÁLCULO APROXIMADO DE INTEGRAIS 5.- INTEGRAÇÃO NUMÉRICA Itegrar umericamete uma fução y f() um dado itervalo [a, b] é itegrar um poliômio P () que aproime f() o dado itervalo. Em particular, se y f()
q(x) = x 4 6x x² - 18x + 10 * z+ z + w + w = 6 ** z z + zw + z w + z w + w w = 15
 MATEMÁTICA Sejam a i, a + si e a + ( s) + ( + s) i ( > ) temos de uma seqüêcia. Detemie, em fução de, os valoes de e s que toam esta seqüêcia uma pogessão aitmética, sabedo que e s são úmeos eais e i -.
MATEMÁTICA Sejam a i, a + si e a + ( s) + ( + s) i ( > ) temos de uma seqüêcia. Detemie, em fução de, os valoes de e s que toam esta seqüêcia uma pogessão aitmética, sabedo que e s são úmeos eais e i -.
Escola Secundária com 3º Ciclo do E. B. de Pinhal Novo Física e Química A 10ºAno MEDIÇÃO EM QUÍMICA
 Escola Secundáia com 3º Ciclo do E. B. de Pinhal Novo Física e Química A 10ºAno MEDIÇÃO EM QUÍMICA Medi - é compaa uma gandeza com outa da mesma espécie, que se toma paa unidade. Medição de uma gandeza
Escola Secundáia com 3º Ciclo do E. B. de Pinhal Novo Física e Química A 10ºAno MEDIÇÃO EM QUÍMICA Medi - é compaa uma gandeza com outa da mesma espécie, que se toma paa unidade. Medição de uma gandeza
SEGUNDA LEI DE NEWTON PARA FORÇA GRAVITACIONAL, PESO E NORMAL
 SEUNDA LEI DE NEWON PARA FORÇA RAVIACIONAL, PESO E NORMAL Um copo de ssa m em queda live na ea está submetido a u aceleação de módulo g. Se despezamos os efeitos do a, a única foça que age sobe o copo
SEUNDA LEI DE NEWON PARA FORÇA RAVIACIONAL, PESO E NORMAL Um copo de ssa m em queda live na ea está submetido a u aceleação de módulo g. Se despezamos os efeitos do a, a única foça que age sobe o copo
1- REFRAÇÃO LUMINOSA é a variação de velocidade da luz devido à mudança do meio de propagação. refração do meio em que o raio se encontra.
 REFRAÇÃO - LENTES - REFRAÇÃO LUMINOSA é a variação de velocidade da luz devido à mudaça do meio de propagação. - Ídice de refração absoluto: é uma relação etre a velocidade da luz em um determiado meio
REFRAÇÃO - LENTES - REFRAÇÃO LUMINOSA é a variação de velocidade da luz devido à mudaça do meio de propagação. - Ídice de refração absoluto: é uma relação etre a velocidade da luz em um determiado meio
QUAIS OS FATORES SÃO DETERMINANTES PARA REDUZIR A DESIGUALDADE EM UM AMBIENTE DE CRESCIMENTO ECONÔMICO E MENOS POBREZA? ÁREA TEMÁTICA: ECONOMIA SOCIAL
 QUAIS OS FATORES SÃO DETERMINANTES PARA REDUZIR A DESIGUALDADE EM UM AMBIENTE DE CRESCIMENTO ECONÔMICO E MENOS POBREZA? ÁREA TEMÁTICA: ECONOMIA SOCIAL Vito Hugo Mio Doutoado em Ecoomia (CAEN/UFC. Aalista
QUAIS OS FATORES SÃO DETERMINANTES PARA REDUZIR A DESIGUALDADE EM UM AMBIENTE DE CRESCIMENTO ECONÔMICO E MENOS POBREZA? ÁREA TEMÁTICA: ECONOMIA SOCIAL Vito Hugo Mio Doutoado em Ecoomia (CAEN/UFC. Aalista
UFRGS 2007 - MATEMÁTICA
 - MATEMÁTICA 01) Em 2006, segudo otícias veiculadas a impresa, a dívida itera brasileira superou um trilhão de reais. Em otas de R$ 50, um trilhão de reais tem massa de 20.000 toeladas. Com base essas
- MATEMÁTICA 01) Em 2006, segudo otícias veiculadas a impresa, a dívida itera brasileira superou um trilhão de reais. Em otas de R$ 50, um trilhão de reais tem massa de 20.000 toeladas. Com base essas
Caro cursista, Todas as dúvidas deste curso podem ser esclarecidas através do nosso plantão de atendimento ao cursista.
 Cao cusista, Todas as dúvidas deste cuso podem se esclaecidas atavés do nosso plantão de atendimento ao cusista. Plantão de Atendimento Hoáio: quatas e quintas-feias das 14:00 às 15:30 MSN: lizado@if.uff.b
Cao cusista, Todas as dúvidas deste cuso podem se esclaecidas atavés do nosso plantão de atendimento ao cusista. Plantão de Atendimento Hoáio: quatas e quintas-feias das 14:00 às 15:30 MSN: lizado@if.uff.b
Movimentos de satélites geoestacionários: características e aplicações destes satélites
 OK Necessito de ee esta página... Necessito de apoio paa compeende esta página... Moimentos de satélites geoestacionáios: caacteísticas e aplicações destes satélites Um dos tipos de moimento mais impotantes
OK Necessito de ee esta página... Necessito de apoio paa compeende esta página... Moimentos de satélites geoestacionáios: caacteísticas e aplicações destes satélites Um dos tipos de moimento mais impotantes
PRINCÍPIOS DA DINÂMICA LEIS DE NEWTON
 Pofa Stela Maia de Cavalho Fenandes 1 PRINCÍPIOS DA DINÂMICA LEIS DE NEWTON Dinâmica estudo dos movimentos juntamente com as causas que os oiginam. As teoias da dinâmica são desenvolvidas com base no conceito
Pofa Stela Maia de Cavalho Fenandes 1 PRINCÍPIOS DA DINÂMICA LEIS DE NEWTON Dinâmica estudo dos movimentos juntamente com as causas que os oiginam. As teoias da dinâmica são desenvolvidas com base no conceito
Matemática Alexander dos Santos Dutra Ingrid Regina Pellini Valenço
 4 Matemática Alexader dos Satos Dutra Igrid Regia Pellii Valeço Professor SUMÁRIO Reprodução proibida. Art. 84 do Código Peal e Lei 9.60 de 9 de fevereiro de 998. Módulo 0 Progressão aritmérica.................................
4 Matemática Alexader dos Satos Dutra Igrid Regia Pellii Valeço Professor SUMÁRIO Reprodução proibida. Art. 84 do Código Peal e Lei 9.60 de 9 de fevereiro de 998. Módulo 0 Progressão aritmérica.................................
Interações Eletromagnéticas 1
 Inteações Eletomagnéticas 1 I.H.Hutchinson 1 I.H.Hutchinson 1999 Capítulo 1 Equações de Maxwell e Campos Eletomagnéticos 1.1 Intodução 1.1.1 Equações de Maxwell (1865) As equações que govenam o eletomagnetismo
Inteações Eletomagnéticas 1 I.H.Hutchinson 1 I.H.Hutchinson 1999 Capítulo 1 Equações de Maxwell e Campos Eletomagnéticos 1.1 Intodução 1.1.1 Equações de Maxwell (1865) As equações que govenam o eletomagnetismo
1 - CORRELAÇÃO LINEAR SIMPLES rxy
 1 - CORRELAÇÃO LINEAR IMPLE Em pesquisas, feqüetemete, pocua-se veifica se existe elação ete duas ou mais vaiáveis, isto é, sabe se as alteações sofidas po uma das vaiáveis são acompahadas po alteações
1 - CORRELAÇÃO LINEAR IMPLE Em pesquisas, feqüetemete, pocua-se veifica se existe elação ete duas ou mais vaiáveis, isto é, sabe se as alteações sofidas po uma das vaiáveis são acompahadas po alteações
UNIVERSIDADE DE TAUBATÉ FACULDADE DE ENGENHARIA CIVIL CÁLCULO VETORIAL
 OBJETIVOS DO CURSO UNIVERSIDADE DE TAUBATÉ FACULDADE DE ENGENHARIA CIVIL CÁLCULO VETORIAL Fonece ao aluno as egas básicas do cálculo vetoial aplicadas a muitas gandezas na física e engenhaia (noção de
OBJETIVOS DO CURSO UNIVERSIDADE DE TAUBATÉ FACULDADE DE ENGENHARIA CIVIL CÁLCULO VETORIAL Fonece ao aluno as egas básicas do cálculo vetoial aplicadas a muitas gandezas na física e engenhaia (noção de
A TORRE DE HANÓI Carlos Yuzo Shine - Colégio Etapa
 A TORRE DE HANÓI Carlos Yuzo Shie - Colégio Etapa Artigo baseado em aula miistrada a IV Semaa Olímpica, Salvador - BA Nível Iiciate. A Torre de Haói é um dos quebra-cabeças matemáticos mais populares.
A TORRE DE HANÓI Carlos Yuzo Shie - Colégio Etapa Artigo baseado em aula miistrada a IV Semaa Olímpica, Salvador - BA Nível Iiciate. A Torre de Haói é um dos quebra-cabeças matemáticos mais populares.
Unidade 13 Noções de Matemática Financeira. Taxas equivalentes Descontos simples e compostos Desconto racional ou real Desconto comercial ou bancário
 Unidade 13 Noções de atemática Financeia Taxas equivalentes Descontos simples e compostos Desconto acional ou eal Desconto comecial ou bancáio Intodução A atemática Financeia teve seu início exatamente
Unidade 13 Noções de atemática Financeia Taxas equivalentes Descontos simples e compostos Desconto acional ou eal Desconto comecial ou bancáio Intodução A atemática Financeia teve seu início exatamente
PROVA DE FÍSICA 2º ANO - 2ª MENSAL - 3º TRIMESTRE TIPO A
 PROVA DE FÍSICA º ANO - ª MENSAL - º TRIMESTRE TIPO A 0) Aalise a(s) afirmação(ões) abaio e assiale V para a(s) verdadeira(s) e F para a(s) falsa(s). Um raio lumioso propaga-se do meio A, cujo ídice de
PROVA DE FÍSICA º ANO - ª MENSAL - º TRIMESTRE TIPO A 0) Aalise a(s) afirmação(ões) abaio e assiale V para a(s) verdadeira(s) e F para a(s) falsa(s). Um raio lumioso propaga-se do meio A, cujo ídice de
Condensador esférico Um condensador esférico é constituído por uma esfera interior de raio R e carga
 onensao esféico Um conensao esféico é constituío po uma esfea inteio e aio e caga + e uma supefície esféica exteio e aio e caga. a) Detemine o campo eléctico e a ensiae e enegia em too o espaço. b) alcule
onensao esféico Um conensao esféico é constituío po uma esfea inteio e aio e caga + e uma supefície esféica exteio e aio e caga. a) Detemine o campo eléctico e a ensiae e enegia em too o espaço. b) alcule
ESCOAMENTOS EM REGIME PERMANENTE
 ESOAMENTOS EM EGIME EMANENTE eime emaete: são escoametos qe ão aesetam aiação com o temo t Escoametos i-dimesioais: só aesetam m comoete de elocidade qe só aia em ma dieção Escoametos simles hidodiamicamete
ESOAMENTOS EM EGIME EMANENTE eime emaete: são escoametos qe ão aesetam aiação com o temo t Escoametos i-dimesioais: só aesetam m comoete de elocidade qe só aia em ma dieção Escoametos simles hidodiamicamete
Transformada de z Sistemas Discretos
 Sistemas de Pocessameto Digital Egehaia de Sistemas e Ifomática Ficha 5 005/006 4.º Ao/.º Semeste Tasfomada de Sistemas Discetos Tasfomada de A tasfomada de Z foece uma vesão o domíio da fequêcia dum sial
Sistemas de Pocessameto Digital Egehaia de Sistemas e Ifomática Ficha 5 005/006 4.º Ao/.º Semeste Tasfomada de Sistemas Discetos Tasfomada de A tasfomada de Z foece uma vesão o domíio da fequêcia dum sial
Termodinâmica 1 - FMT 159 Noturno, segundo semestre de 2009
 Temodinâmica - FMT 59 Notuno segundo semeste de 2009 Execícios em classe: máquinas témicas 30/0/2009 Há divesos tipos de motoes témicos que funcionam tanfeindo calo ente esevatóios témicos e ealizando
Temodinâmica - FMT 59 Notuno segundo semeste de 2009 Execícios em classe: máquinas témicas 30/0/2009 Há divesos tipos de motoes témicos que funcionam tanfeindo calo ente esevatóios témicos e ealizando
Prof. Dirceu Pereira
 Aula de UNIDADE - MOVIMENTO VERTICAL NO VÁCUO 1) (UFJF-MG) Um astonauta está na supefície da Lua quando solta, simultaneamente, duas bolas maciças, uma de chumbo e outa de madeia, de uma altua de,0 m em
Aula de UNIDADE - MOVIMENTO VERTICAL NO VÁCUO 1) (UFJF-MG) Um astonauta está na supefície da Lua quando solta, simultaneamente, duas bolas maciças, uma de chumbo e outa de madeia, de uma altua de,0 m em
PG Progressão Geométrica
 PG Progressão Geométrica 1. (Uel 014) Amalio Shchams é o ome cietífico de uma espécie rara de plata, típica do oroeste do cotiete africao. O caule dessa plata é composto por colmos, cujas características
PG Progressão Geométrica 1. (Uel 014) Amalio Shchams é o ome cietífico de uma espécie rara de plata, típica do oroeste do cotiete africao. O caule dessa plata é composto por colmos, cujas características
Gregos(+2000 anos): Observaram que pedras da região Magnézia (magnetita) atraiam pedaços de ferro;
 O Campo Magnético 1.Intodução: Gegos(+2000 anos): Obsevaam que pedas da egião Magnézia (magnetita) ataiam pedaços de feo; Piee Maicout(1269): Obsevou a agulha sobe imã e macou dieções de sua posição de
O Campo Magnético 1.Intodução: Gegos(+2000 anos): Obsevaam que pedas da egião Magnézia (magnetita) ataiam pedaços de feo; Piee Maicout(1269): Obsevou a agulha sobe imã e macou dieções de sua posição de
ÁREA DE COBERTURA EM AMBIENTE DE PROPAGAÇÃO MODELADO COM A DISTRIBUIÇÃO κ µ
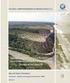 ÁREA DE COBERTURA EM AMBIENTE DE PROPAGAÇÃO MODELADO COM A DISTRIBUIÇÃO κµ κµ JAMIL RIBEIRO ANTÔNIO Dssetação apesetada ao Isttuto Nacoal de Telecomucações INATEL como pate dos equstos paa obteção do Título
ÁREA DE COBERTURA EM AMBIENTE DE PROPAGAÇÃO MODELADO COM A DISTRIBUIÇÃO κµ κµ JAMIL RIBEIRO ANTÔNIO Dssetação apesetada ao Isttuto Nacoal de Telecomucações INATEL como pate dos equstos paa obteção do Título
Aula ONDAS ELETROMAGNÉTICAS
 ONDAS ELETROMAGNÉTICAS Aula 6 META Intoduzi aos alunos conceitos básicos das ondas eletomagnéticas: como elas são poduzidas, quais são suas caacteísticas físicas, e como desceve matematicamente sua popagação.
ONDAS ELETROMAGNÉTICAS Aula 6 META Intoduzi aos alunos conceitos básicos das ondas eletomagnéticas: como elas são poduzidas, quais são suas caacteísticas físicas, e como desceve matematicamente sua popagação.
CONTROLE DA QUALIDADE DE PADRÕES ESCALONADOS UTILIZADOS NA VERIFICAÇÃO DE MÁQUINAS DE MEDIR POR COORDENADAS
 CONTROLE DA QUALIDADE DE PADRÕES ESCALONADOS UTILIZADOS NA VERIFICAÇÃO DE MÁQUINAS DE MEDIR POR COORDENADAS José Carlos Valete de Oliveira Aluo do mestrado profissioal em Sistemas de Gestão da Uiversidade
CONTROLE DA QUALIDADE DE PADRÕES ESCALONADOS UTILIZADOS NA VERIFICAÇÃO DE MÁQUINAS DE MEDIR POR COORDENADAS José Carlos Valete de Oliveira Aluo do mestrado profissioal em Sistemas de Gestão da Uiversidade
Teste de Hipóteses VÍCTOR HUGO LACHOS DÁVILAD
 Teste de ióteses VÍCTOR UGO LACOS DÁVILAD Teste De ióteses. Exemlo. Cosidere que uma idustria comra de um certo fabricate, ios cuja resistêcia média à rutura é esecificada em 6 kgf (valor omial da esecificação).
Teste de ióteses VÍCTOR UGO LACOS DÁVILAD Teste De ióteses. Exemlo. Cosidere que uma idustria comra de um certo fabricate, ios cuja resistêcia média à rutura é esecificada em 6 kgf (valor omial da esecificação).
Aula-09 Campos Magnéticos Produzidos por Correntes. Curso de Física Geral F-328 2 o semestre, 2013
 Aula-9 ampos Magnétcos Poduzdos po oentes uso de Físca Geal F-38 o semeste, 13 Le de Bot - Savat Assm como o campo elétco de poduzdo po cagas é: 1 dq 1 dq db de ˆ, 3 ε ε de manea análoga, o campo magnétco
Aula-9 ampos Magnétcos Poduzdos po oentes uso de Físca Geal F-38 o semeste, 13 Le de Bot - Savat Assm como o campo elétco de poduzdo po cagas é: 1 dq 1 dq db de ˆ, 3 ε ε de manea análoga, o campo magnétco
Capítulo 5. Misturas Simples
 Capítulo 5. Misturas Simples aseado o livro: tkis Physical Chemistry Eighth Editio Peter tkis Julio de Paula 04-06-2007 Maria da Coceição Paiva 1 Misturas Simples Para iterpretar termodiamicamete o efeito
Capítulo 5. Misturas Simples aseado o livro: tkis Physical Chemistry Eighth Editio Peter tkis Julio de Paula 04-06-2007 Maria da Coceição Paiva 1 Misturas Simples Para iterpretar termodiamicamete o efeito
Objetivo Estudo do efeito de sistemas de forças não concorrentes.
 Univesidade edeal de lagoas Cento de Tecnologia Cuso de Engenhaia Civil Disciplina: Mecânica dos Sólidos 1 Código: ECIV018 Pofesso: Eduado Nobe Lages Copos Rígidos: Sistemas Equivalentes de oças Maceió/L
Univesidade edeal de lagoas Cento de Tecnologia Cuso de Engenhaia Civil Disciplina: Mecânica dos Sólidos 1 Código: ECIV018 Pofesso: Eduado Nobe Lages Copos Rígidos: Sistemas Equivalentes de oças Maceió/L
