INE ESTATÍSTICA APLICADA I - TURMA GABARITO LISTA DE EXERCÍCIOS SOBRE AMOSTRAGEM E PLANEJAMENTO DA PESQUISA

Transcrição

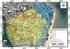
1 INE ESTATÍSTICA APLICADA I - TURMA GABARITO LISTA DE EXERCÍCIOS SOBRE AMOSTRAGEM E PLANEJAMENTO DA PESQUISA 1. Aalise as situações descritas abaixo e decida se a pesquisa deve ser feita por amostragem ou por ceso, justificado sua resposta. a) Numa liha de produção de empacotameto de café, observar o peso dos pacotes produzidos. Se houver possibilidade de agregar uma balaça automática ao processo produtivo pode-se utilizar ceso. Pois como ão se trata de teste destrutivo, e peso dos pacotes é importate para a imagem da empresa (e para ão haver desperdício) todos os pacotes podem ser medidos. b) Em uma sala de aula composta por 4 aluos, aalisar suas idades. Ceso, porque a população é pequea, apeas 4 elemetos. c) Observar se a água de uma lagoa está cotamiada. Amostragem. É o míimo cotraproducete retirar toda a água da lagoa para exame de sua cotamiação. d) Verificar a carga horária diária de trabalho dos fucioários da coziha de um restaurate. Ceso, por razões políticas, para que iguém se sita prejudicado, além da população ser pequea e acessível. e) Num lote de cabos de aço, verificar a resistêcia dos mesmos à tração. Amostragem. O teste é destrutivo. f) Pesquisa de opiião eleitoral para goverador do estado de São Paulo. Amostragem. A ecessidade de rápido processameto exige amostragem, devido ao grade tamaho da população que toraria muito leta a obteção dos resultados, além de muito cara.. Aalise os plaos de amostrages apresetados abaixo. Você cocorda com a maeira como foram elaborados? Justifique. Apresete as soluções que julgar ecessárias. a)para aalisar os laboratórios de pesquisa quato ao seu ivestimeto a aquisição de tecologia de pota, foram eviados questioários e aalisadas as respostas daqueles que respoderam o questioário. Não. Apeas os que respoderam serão cosiderados. Deveriam ser etrevistados os resposáveis pelos laboratórios sorteados em uma amostragem probabilística. b) Para aalisar o perfil dos clietes de um baco, foram aalisados ao logo de um mês 4 clietes por dia, retirados da fila do caixa, variado sistematicamete o horário da coleta. Sim. Mostra o perfil dos clietes ao logo do mês e mesmo ao logo do dia, mas apeas dos clietes que usam os serviços de caixa covecioal c) Para ser cohecida a opiião dos estudates da UFSC sobre o Joral Uiversitário, foram colhidas as opiiões de 4 estudates da última fase do curso de Joralismo daquela istituição. Não. Se o objetivo é cohecer a opiião dos aluos da UFSC sobre o joral, aluos de todos os cursos deveriam ser ouvidos, o plao está icoerete com o objetivo da pesquisa. Deveria ser selecioada uma amostra cotedo itegrates de todos os cursos da UFSC, podedo ser estratificada por fase predomiate (quato mais tempo a UFSC maior a probabilidade de ter cotato com o joral e acompahar sua evolução, o que pode ser relevate). d) Há iteresse em medir o ídice de lumiosidade das salas de aula da UFSC. A coleta de dados será feita em todos os cetros da UFSC, durate os períodos diuro e oturo, as salas que estiveram desocupadas o mometo da pesquisa. Cada cetro será visitado apeas uma vez. Não. O problema reside em medir a lumiosidade apeas as salas desocupadas o mometo da pesquisa, e em ão retorar aos cetros mais de uma vez. É preciso medir os ídices de lumiosidade os períodos matutio, vespertio e oturo, levado em cota também a posição solar das salas (selecioar as salas a pesquisar com as platas dos cetros de esio, que devem estar dispoíveis o ETUSC ou a Prefeitura Uiversitária). 1

2 e) As costates reclamações dos usuários motivaram a direção da Biblioteca Cetral da UFSC a realizar uma pesquisa sobre o ível de ruído em suas depedêcias. O ruído será medido em todas as seções da Biblioteca, a primeira e a peúltima semaas do semestre, de seguda à sábado, durate todo o horário de fucioameto. Não. Por que apeas a primeira e a peúltima semaa do semestre? O ideal seria realizar medidas em todas as semaas. f) No cotrole de qualidade de uma fábrica de peças, que trabalha 4 horas por dia, sete dias por semaa, um item produzido é retirado de cada máquia, a cada meia hora, para avaliação. O procedimeto é feito durate todo o dia, ao logo da semaa. Sim. Com este procedimeto é possível retratar a qualidade do processo ao logo do tempo (levado em cota os diferetes turos, operários, codições ambietais), e idetificar evetuais problemas, possibilitado a sua preveção e correção. g) O Comado de um Batalhão da PMSC quer cohecer a opiião das pessoas que residem em sua área de atuação, o ituito de formular ovas escalas de policiameto ostesivo. Para tato serão feitas etrevistas com as pessoas que se passarem a pé pela frete do Batalhão, de seguda à sexta das 8:3 às 1: horas e das 14: às 17:3 horas durate duas semaas. Não. Os que ão passarem a pé pela frete do batalhão, e os horários estabelecidos, ão terão a meor possibilidade de serem ouvidos, o que pode comprometer a cofiabilidade dos resultados da pesquisa. Seria ecessário obter uma listagem das residêcias, utilizar algum mecaismo de sorteio aleatório para selecioar algumas e etrevistar os moradores sobre a ecessidade de policiameto ostesivo. h) Com a fialidade de estudar o perfil dos cosumidores de um supermercado, observaram-se os cosumidores que compareceram ao supermercado o primeiro sábado do mês. Não. E os que forem ao supermercado em outros dias da semaa, ou mesmo em outros sábados do mês? Não terão chace de participar da pesquisa, o que poderá comprometer os resultados. A coleta de dados precisa ser feita todos os dias, ao logo do horário de atedimeto, e por pelo meos um mês (para avaliar o efeito das diferetes datas de pagameto o cosumo dos clietes). i) Com a fialidade de estudar o perfil dos cosumidores de um supermercado, fez-se a coleta de dados durate um mês, tomado a cada dia um cosumidor de cada fila de cada caixa, variado-se sistematicamete o horário de coleta dos dados. Possibilita captar todo o movimeto mesal, e o movimeto durate o dia (ver item h). j) Para avaliar a qualidade dos ites que saem de um liha de produção, observaram-se todos os ites das 14 às 14 horas e trita miutos. Não. Supoha que algo acoteça às 14h31mi. Um evetual problema somete seria otado quado a avaliação fosse repetida, e etão os prejuízos poderiam ser muito grades. k) Para avaliar a qualidade dos ites que saem de uma liha de produção, observou-se um item a cada meia hora, durate todo o dia. Sim. Com este plao todo o processo produtivo é moitorado (de forma semelhate à vista o item f), possibilitado a detecção mais rápida de evetuais problemas. l) Para estimar a porcetagem de empresas que ivestiram em ovas tecologias o último ao, eviou-se um questioário a todas as empresas de um estado. A amostra foi formada pelas empresas que respoderam o questioário. Não. Provavelmete os respodetes são justamete as empresas que ivestiram em tecologia, o que poderia dar a falsa impressão de que a situação está bem melhor do que realmete está. Uma forma de cotorar este problema seria coduzir a pesquisa por telefoe: obtém-se uma listagem das empresas por porte e ramo de atuação (via FIESC, Fecomércio, CDL's), selecioa-se uma amostra aleatória (estratificada por ramo e porte) e aplica-se um questioário com aqueles que poderiam forecer iformações cofiáveis sobre o ivestimeto em tecologia (ver item a).

3 3. Aalise as situações abaixo e determie qual é o tipo de amostragem a ser usado em cada caso, e explique por quê. a) Parte da população é iacessível e trata-se de um estudo prelimiar. Amostragem ão probabilística, a esmo. Como ão há acesso a toda a população seria impossível aplicar uma amostragem probabilística, e como se trata de estudo prelimiar a ão probabilística é aceitável. b) Todos os elemetos da população podem ser pesquisados, mas ão há recursos para a sua listagem total. Sabe-se também que a população subdivide-se em subgrupos semelhates (para os quais há uma listagem). Amostragem probabilística por coglomerados. Há acesso a toda a população (mas ão há recursos para listar todos os elemetos) e a população divide-se em grupos homogêeos (que podem ser listados). c) Sabe-se que toda a população é acessível, e que é homogêea. A amostra deve ser obtida rapidamete. Amostragem probabilística sistemática. Há acesso a toda a população (pressupõe-se que haja listagem), que é homogêea. A amostragem sistemática, com o sorteio do poto de partida e a retirada de elemetos a itervalos regulares possibilita um processameto mais rápido do que a aleatória simples. d) Uma empresa atua em três mercados distitos. Dispõe de uma listagem com os omes e edereços de todos os clietes. Pretede pesquisar qual seria a evetual demada de um ovo produto. Precisa fazer isso rapidamete (ão há tempo para ceso). Amostragem probabilística estratificada proporcioal. Não há tempo para um ceso. Há acesso a toda a população (há listagem), que pode ser cosiderada dividida em três estratos (mercados). Como se deseja cohecer a demada por um ovo produto é preciso obter iformações precisas, o que pode ser obtido com uma amostra proporcioal ao tamaho de cada estrato. e) A reitoria da UFSC quer cohecer as difereças básicas etre as idéias de professores, servidores e aluos sobre a istituição. Dispõe de listas com todos os professores, aluos e servidores. Amostragem probabilística estratificada uiforme. Há acesso a toda a população (listagem), e supõe-se que há uma divisão em 3 estratos (embora detro dos estratos supoha-se uma certa homogeeidade). Como há iteresse em comparar os estratos (as opiiões dos seus itegrates) ão há ecessidade de obter uma amostra proporcioal, bastado retirar a mesma quatidade de cada estrato. 4. Uma população é composta por 96 elemetos que estão ordeados. Se devesse ser retirada uma amostra sistemática de elemetos desta população, como você procederia? Na amostragem sistemática o primeiro passo é obter o itervalo de retirada k, sabedo o tamaho da população (N = 96) e o tamaho da amostra ( = ). N 96 k 148 Como k é iteiro ão há ecessidade de ajustes. A cada 148 elemetos da população retira-se um para fazer parte da amostra, até completar os que devem compô-la. Deve-se sortear o poto de partida das retiradas, para garatir que todos terão chace de pertecer à amostra: os primeiros 148 elemetos devem receber úmeros de 1 a 148. Vamos supor que a fução ALEATÓRIOENTRE do Calc (com argumetos de 1 a 148) desse o resultado 44): etão o poto de partida será o quadragésimo quarto elemeto da lista. A amostra etão será composta pelos úmeros: 44, 19, 34, 488, 636, 784, 93, 18, 18, 1376, 154, 167, 18, 1968, 116, 64, 41, 56, 856 (totalizado elemetos). 5.Uma amostragem etre os estudates de ciêcias da computação, egeharia de produção e egeharia de automação foi realizada da seguite maeira: cosiderou-se cada curso como um estrato, e fez-se retirada proporcioal. O curso de computação possui 35 aluos, o de egeharia 3

4 de produção 45 aluos e o curso de automação possui aluos. Do curso de computação foram aalisados 4 aluos. Qual o úmero total de aluos aalisados a amostra? Trata-se de amostragem probabilística estratificada proporcioal, idicado que o úmero de elemetos de cada estrato que fazem parte da amostra é proporcioal ao tamaho do estrato a população. A população é composta por 15 aluos ( ), com os seguites percetuais para cada curso: computação = (35/15) 1 = 34,15% egeharia de produção = (475/15) 1 = 46,34% automação = (/15) 1 = 19,51% Etão, os 4 aluos de computação correspodem a 34,15% da amostra, fazedo uma regra de três simples podemos obter o total de elemetos da amostra: > 34,15%? > 1% E ecotramos 1,98, praticamete igual a Numa sala de aula temos 36 homes e 8 mulheres. Faça uma amostragem estratificada proporcioal de tamaho 16 cosiderado o sexo como variável estratificadora. Quatos de cada sexo serão aalisados? Temos que avaliar as proporções de cada estrato o total de 64 (36 + 8). Homes = (36/64) 1 = 56,5% Mulheres = (8/64) 1 = 43,75% Basta aplicar os percetuais acima ao tamaho da amostra (16): Homes =, = 9 Mulheres =, = 7 Etão serão pesquisados 9 homes e 7 mulheres. A retirada detro de cada estrato pode ser feita com amostra aleatória simples. 7. A biblioteca do CEPM apreseta-se dividida em sete grades seções (que podem ser cosiderados como estratos ou coglomerados, depededo do caso): direito (com títulos), técicas policiais (com 1 títulos), psicologia/sociologia (com 9 títulos), documetos sobre a PMSC (com 9 títulos), lígua portuguesa (com 6 títulos), obras de referêcia- eciclopédias e dicioários (com 4 títulos), e outros- matemática, estatística, ciêcias (com 1 títulos). A direção quer cohecer a idade média dos títulos, através do ao de edição, para determiar se há ecessidade de reovação do acervo. Vamos executar vários plaos de amostragem, todos podem ser feitos através da fução ALEATÓRIOENTRE do Calc. Há um total de 7 títulos: 1 a (direito - D), 1 a 3 (técicas policiais - TP), 31 a 41 (psicologia/sociologia - P/S), 411 a 5 (documetos sobre a PMSC - DP), 51 a 56 (lígua portuguesa - LP), 561 a 6 (obras de referêcia - R), 61 a 7 (outros - O). a) Selecioar uma amostra aleatória simples de 7 títulos. Supoha os títulos umerados de acordo com a ordem do euciado: de 1 a títulos de metodologia de esio, de 1 a 3 títulos de metodologia de esio especial, etc. Amostragem aleatória simples. Precisamos ecotrar 7 úmeros etre 1 e 7 a tabela de úmeros aleatórios (agrupado 4 dígitos, pois o valor máximo é 7). Vamos registrar, pelo úmero, a que categoria o livro pertece. Usado a fução ALEATÓRIOENTRE do Calc, com argumetos de 1 a 7, costituido 7 células, poderíamos obter: 648 (O), 645 (TP), 4 (TP), 4499 (DP), 947 (D), 347 (P/S), 3544 (P/S), 1318 (D), 1851 (D), 63 (O), 4194 (DP), 159 (D), 4989 (DP), 4354 (DP), 5419 (LP), 5487 (LP), 343 (TP), 14 (D), 696 (D), 387 (P/S), 774 (D), 15 (TP), 133 (D), 16 (D), 598 (LP), 4611 (DP), 18 (D), 591 (TP), 5 (TP), 39 (P/S), 3875 (P/S), 1863 (D), 335 (P/S), 3798 (P/S), 145(D),6571 (O), 311 (TP), 46 (D), 4556 (DP), 147 (D), 3674 (P/S), 94 (D), 39 (P/S), 55(LP), 18 (TP), 1748 (D), 5417 (LP), 118 (D), 533 (D), 519 (LP), 6956 (O), 171 (D), 364 (P/S), 93 (D), 411 (TP), 6644 (O), 57 (LP), 759 (TP), 3817 (P/S), 1539 (D), 997 (D), 3334(P/S), 488 (P/S), 461 (DP), 3356 (P/S), 483 (DP), 4779 (DP), 831 (TP), 496 (TP), 471 (DP). 4

5 Repare que ehum livro de obras de referêcia (etre 561 e 6) foi selecioado, ão obstate o sorteio ão ser viciado: livros de direito, 1 de técicas policiais, 14 de psicologia/sociologia, 1 de documeto da PMSC, 7 de lígua portuguesa e 5 de outros. b) Repetir o item aterior, usado amostragem sistemática. Sabemos o tamaho da população (N = 7) e o tamaho da amostra ( = 7), calculamos etão o itervalo de retirada: k = N/ = 7/7 = 1. A cada 1 elemetos, retiramos um para fazer parte da amostra. Precisamos sortear o poto de partida: escolher, por sorteio, um úmero etre 1 e 7. Podemos usar a fução ALEATÓRIOENTRE do Calc, com argumetos de 1 a 1, poderíamos obter 39, que passa a ser o poto de partida. Etão a amostra será composta por: 39 (D), 139 (D), 39 (D), 339 (D), 439 (D), 539 (D), 639 (D), 739 (D), 839 (D), 939 (D), 139 (D), 1139 (D), 139 (D), 1339 (D), 1439(D), 1539(D), 1639(D), 1739(D), 1839(D), 1939(D), 39 (TP), 139 (TP), 39(TP), 339(TP), 439(TP), 539(TP), 639(TP), 739 (TP), 839 (TP), 939 (TP), 339(TP), 3139(TP), 339(P/S),3339(P/S), 3439(P/S), 3539(P/S), 3639(P/S), 3739(P/S),3839 (P/S), 3939(P/S), 439(P/S), 4139(DP), 439(DP), 4339(DP), 4439(DP), 4539(DP), 4639(DP),4739(DP), 4839(DP), 4939(DP), 539(LP), 5139(LP), 539(LP), 5339(LP), 5439(LP), 5539(LP), 5639(R), 5739(R), 5839(R), 5939(R), 639(O), 6139(O), 639(O), 6339(O), 6439(O), 6539(O), 6639(O), 6739(O), 6839(O), 6939(O). c) Selecioar uma amostra estratificada proporcioal de 7 títulos. O primeiro passo é defiir o quato cada estrato represeta da população, para saber quatos elemetos da amostra ( = 7) virão de cada um deles. Direito = (/7) 1 = 8,57% (etão 8,57% da amostra virá deste estrato, livros). Técicas policiais = (1/7) 1 = 17,14% (1 livros da amostra virão desta seção). Psicologia/sociologia = (9/7) 1 = 1,86% (9 livros da amostra virão desta seção). Documetos sobre a PMSC = (9/7) 1 = 1,86% (9 livros da amostra virão desta seção). Lígua portuguesa = (6/7) 1 = 8,57% (6 livros da amostra virão desta seção). Obras de referêcia = (4/7) 1 = 5,71% (4 livros da amostra virão desta seção). Outros = (1/7) 1 = 14,8% (1 livros da amostra virão desta seção). Detro de cada estrato podemos selecioar a amostra utilizado a amostragem sistemática, descrita o item b: basta defiir os itervalos de retirada para cada estrato (com o tamaho de cada estrato sedo N e os tamahos de amostra defiidos acima como ). d) Extrair uma amostra aleatória de 7 títulos através de amostragem de coglomerados em dois estágios: o primeiro selecioar seções, e o segudo estágio 35 títulos de cada coglomerado selecioado. Seleção de coglomerados. Cosideremos as seções como coglomerados, há 7 deles, vamos umerá-los: Direito - 1 Técicas policiais - Psicologia/sociologia - 3 Documetos sobre a PMSC - 4 Lígua portuguesa - 5 Referêcia - 6 Outros - 7 Temos que selecioar dois: precisamos obter dois úmeros de 1 dígito (etre 1 e 7) através da fução ALEATÓRIOENTRE do Calc. Poderíamos ter ecotrado 6 e 7: os coglomerados sorteados serão Referêcia e Outros. Detro de cada um deles podemos selecioar 35 elemetos, vejamos o procedimeto o coglomerado Referêcia, que tem 4 títulos (umerados de 561 a 6). N = 4 =35 k = N/ = 4/35 = 11,43 O valor de k é fracioário, e como ão podemos modificar devemos descartar por sorteio 15 elemetos do coglomerado de Referêcia, restado 385 elemetos, resultado em k = 11. O sorteio pode ser realizado procurado por 15 úmeros de 4 dígitos etre 561 e 6 através da fução ALEATÓRIOENTRE do Calc. Após remover estes elemetos reordea-se a lista e retiram-se os 35 elemetos da amostra propriamete dita, usado o procedimeto visto a letra b. Observe que os coglomerados sorteados ão cotêm exatamete os livros mais importates da biblioteca. e) Compare os resultados e comete sobre as semelhaças e ou difereças. Qual dos ites terá um resultado mais preciso, por quê? 5

6 Os resultados das amostrages sistemática e estratificada proporcioal são bastate razoáveis, pois as amostras obtidas icluíram vários elemetos de todas as seções. Não obstate o resultado mais preciso é o da estratificada proporcioal, por preservar a amostra a proporcioalidade das seções a população, e por garatir que todos os estratos estejam presetes a amostra: esta retirou livros de direito, equato a sistemática retirou apeas 11, por exemplo. A amostragem aleatória simples apreseta títulos de quase todas as áreas, mas é aida meos precisa do que a sistemática (uma área ão teve elemetos selecioados). Mas a meos precisa foi a de coglomerados, que sorteou livros apeas das seções de referêcia e outros: isso ocorreu meramete por acaso, o mesmo poderia ter acotecido a aleatória simples, pois ambas supõem que a população é homogêea. 8. O mapa seguite simboliza os domicílios de um bairro. Os quadros grades correspodem aos quarteirões, divididos em duas localidades (estratos) do bairro. Os úmeros detro dos quadrados meores (domicílios), correspodem ao úmero de cômodos do domicílio, que é a variável a ser observada, uma amostra de domicílios Estrato A Estrato B Para resolver este exercício umere os domicílios de cada quarteirão, da esquerda para a direita, e de cima para baixo, resultado em domicílios de 1 a 9 (ode os domicílios de 1 a 6 estão o estrato A, e os de 61 a 9 o estrato B. a) Igorado os estratos, selecioar uma amostra aleatória simples de 9 domicílios. Aotar o úmero de cômodos dos domicílios selecioados a amostra. Obtedo 9 úmeros aleatórios de dígitos (etre 1 e 9) pela fução ALEATÓRIOENTRE do Calc, poderíamos ecotrar: 8, 6, 48, 6, 45, 4,, 84, 4. Os úmeros de cômodos serão etão:, 8, 4, 6, 3, 5, 3, 5, 5. b) Selecioar uma amostra estratificada proporcioal de 9 domicílios. Aotar o úmero de cômodos dos domicílios selecioados a amostra. O estrato A tem 6 domicílios, represetado /3 da população, e o estrato B tem 3, represetado 1/3. Como a amostra deve ter 9 domicílios, 6 virão do estrato A e 3 do estrato B. Através da fução ALEATÓRIOENTRE do Calc podemos obter 6 úmeros aleatórios de dígitos (etre 1 e 6), por exemplo: 54, 11, 48, 9, 8, 8. Etão, do estrato A teremos: 5,, 4,, e 5 cômodos. Através da fução ALEATÓRIOENTRE do Calc podemos obter 3 úmeros aleatórios de dígitos (etre 61 e 9) por exemplo: 8, 63, 83. Etão, do estrato B teremos: 7, 7, e 7 cômodos. Amostra completa: 5,, 4,,, 5, 7, 7, 7. 6

7 c) Extrair uma amostra aleatória de tamaho 9, através de uma amostragem de coglomerados em dois estágios. No primeiro estágio selecioe 3 quarteirões e, o segudo estágio, 3 domicílios em cada coglomerado selecioado. Aotar o úmero de cômodos dos domicílios selecioados a amostra. Atribuem-se úmeros de 1 a 9 aos quarteirões, da esquerda para a direita e de cima para baixo. Através da fução ALEATÓRIOENTRE do Calc podemos obter 3 úmeros de 1 dígito (de 1 a 9), por exemplo:, 5. Foram selecioados os quarteirões e 5 (ambos do estrato A...). Vamos etão selecioar 3 domicílios em cada um deles. O coglomerado cotém os domicílios umerados de 11 a. Através da fução ALEATÓRIOENTRE do Calc podemos obter 3 úmeros de dígitos (de 11 a ), por exemplo: 18, 11, 19. Etão, do coglomerado teremos: 4,, e 3 cômodos. O coglomerado 5 cotém os domicílios umerados de 41 a 5. Através da fução ALEATÓRIOENTRE do Calc podemos obter 3 úmeros de dígitos (de 41 a 5), por exemplo: 48, 45, 44. Etão, do coglomerado 5 teremos: 4, 3 e 4 cômodos. Amostra completa: 4,, 3, 4, 3, 4. d) Comparar os resultados e cometar sobre as evetuais semelhaças ou discrepâcias. Qual dos ites terá um resultado mais preciso, por quê? Os resultados mais precisos serão obtidos com a amostragem estratificada proporcioal, que garate a proporcioalidade dos estratos a amostra, torado-a mais represetativa. Os resultados da amostragem aleatória simples são bastate próximos: 7 domicílios do estrato A e do B (cotra 6 do A e 3 do B a estratificada). A amostragem por coglomerados obteve o pior resultado, pois foram sorteados apeas coglomerados do estrato A: mas, tal resultado ocorreu apeas por acaso, a aleatória simples também poderíamos ter obtido apeas domicílios do estrato A, ou apeas do estrato B. A vatagem da estratificada proporcioal é a garatia de que todos os estratos estarão presetes a amostra, quado a população NÃO é homogêea (o que ocorre este problema). 9. Será feito um levatameto por amostragem de uma população de famílias, para a realização de uma pesquisa. a) Calcule o tamaho míimo de uma amostra para que se teha um erro amostral máximo de 5%. 1 1 N , e (,5) N 4 b) Supodo a população dividida em estratos iguais, qual o tamaho míimo de amostra para se ter um erro amostral máximo de 5% em cada estrato? O valor de N será igual a 1 (/): 1 1 N ,71 86 (59 elemetos) e (,5) N 1 4 c) Qual seria o erro amostral em cada estrato do item b, se o tamaho da amostra em cada estrato fosse simplesmete o valor defiido o item a dividido por? Vamos fazer o camiho iverso: a partir de (que vale 334/ = 167), supodo N = 1, ecotrar o e = 1 = 167/833 =, , isolado e : e, 75 (7,5%) e 1. Repetir o exercício 9 para os seguites tamahos de população: a) 4 famílias. b) famílias c) 4 famílias 7

8 Basta repetir o procedimeto do exercício 13, os resultados: a) 364 elemetos, 668 elemeto, 7,39%. b) 393 elemetos, 77 elemetos, 7,1%. c) 4 elemetos, 8 elemetos, 7,5% 11. A um mês das eleições, um dos cadidatos a goverador de RR ecomedou a você uma pesquisa eleitoral. O estado tem 6 eleitores cocetrados basicamete em 3 cidades (e estas costumam ter tedêcias eleitorais diferetes). Esboce o plaejameto da pesquisa idicado apeas: a) População b) Variáveis de Iteresse c) Se a pesquisa deve ser feita por amostragem ou por ceso e por quê. a) População. Eleitores com domicílio eleitoral as três pricipais cidades de RR. São para estas pessoas que queremos geeralizar os resultados da pesquisa. b) As variáveis de iteresse. A opiião eleitoral pode ser idicada através de duas variáveis: o cadidato preferido (em quem o eleitor votaria), e o cadidato rejeitado (em quem o eleitor NÃO votaria). Seriam medidas através de uma escala de opções, ode seriam listados os omes dos cadidatos (o caso de uma pesquisa estimulada). c) A pesquisa deve ser feita por amostragem. Estamos a um mês das eleições, para que o resultado da pesquisa seja útil para os estrategistas políticos, e para os eleitores, o processameto precisa ser rápido, exigido a utilização de amostragem. 1. Para medir o ível de satisfação dos espectadores a rede Multicaal de TV a cabo ecomedou ao IVOP (Istituto de Verificação de Opiião Pública) uma pesquisa com 1 pessoas selecioadas ao acaso detre os 1 assiates de SC. a) Qual é o tipo de amostragem utilizada? A amostra solicitada é represetativa da população? É sigificativa? Justifique a sua resposta. Trata-se de amostragem probabilística aleatória simples. A amostra pode ão ser represetativa da população, pois regiões iteiras do estado podem, apeas por acaso, ão ser represetadas a amostra. Quato ao tamaho, aparetemete parece ser um bom úmero, teríamos que defiir o erro amostral tolerável: se a população realmete fosse homogêea, usado 5% de erro amostral a amostra deveria ter 399 elemetos. Como tem 1 elemetos, pressupõe-se que é sigificativa, mas APENAS se a população puder ser cosiderada homogêea, o que é arriscado. b) Como você procederia para realizar a pesquisa por amostragem? Explicite, detalhado o plao de amostragem. Seria ecessário obter mais detalhes da população. O recomedável seria ao meos dividir o estado por regiões geográficas e realizar uma amostragem probabilística estratificada proporcioal, selecioado elemetos em fução do percetual de assiates de cada região. c) Que istrumeto de coleta de dados você utilizaria? Esboce o istrumeto com o máximo dez questões. Como se trata de uma pesquisa de opiião é preciso utilizar um questioário para obtê-las dos assiates. O questioário poderia ser elaborado procurado obter opiiões sobre a variedade de caais, programação em si, qualidade da imagem e do som, atedimeto do 8, cobraça, etc. d) Se o istrumeto de coleta foi eviado por correio, e 1 pessoas respoderam. Você cosidera esta taxa de resposta adequada? O que você pesa desta maeira de realizar a pesquisa? Não. A taxa de resposta é muito pequea (,1% do total de assiates). O questioário pelo correio costuma ter uma taxa de resposta muito baixa, e este caso, em que há provavelmete os úmeros dos telefoes dos assiates uma pesquisa por telefoe seria mais recomedada. 13. O govero de um Estado brasileiro ecomedou uma pesquisa de opiião ao IVOP (Istituto de Verificação de Opiião Pública). O objetivo da pesquisa era descobrir qual era a opiião dos habitates do Estado (cerca de 4 milhões de pessoas) sobre a atual admiistração após aos de govero. O IVOP idetificou cico regiões o Estado: a Capital (que cocetra 6% da população) 8

9 e quatro regiões o iterior. Devido ao maior percetual de habitates decidiu-se realizar a pesquisa apeas a Capital, e adotou-se a estratégia de potos de fluxo: foram colocados etrevistadores em 3 potos estratégicos da cidade durate 3 dias com istruções sobre que tipos de pessoas (sexo, faixa etária, etc) deveriam abordar: em cada poto deveriam ser etrevistadas 4 pessoas, das quais 5% deveriam ser homes com até 3 aos, 5% mulheres com até 3 aos, 5% homes com mais de 3 aos e 5% mulheres com mais de 3 aos. Estas pessoas deveriam respoder ao questioário abaixo: Você ão cocorda que a atual admiistração estadual está dado mais ateção ao problema da saúde? ( ) SIM ( )NÃO ( )NÃO SABE Você acredita que a atual admiistração estadual está aplicado melhor o diheiro público? ( ) SIM ( )NÃO ( )NÃO SABE Você ão cocorda que um bom goverate teha o direito de se reeleger? ( ) SIM ( )NÃO ( )NÃO SABE Após realizar a pesquisa o govero divulgou que 7,6% dos habitates estavam satisfeitos com a atual admiistração estadual. a) Você cocorda com a forma como a pesquisa foi coduzida? Por quê? Você mudaria algo? JUSTIFIQUE. Não cocordo com o modo como a pesquisa foi coduzida. Deveriam ter sido realizadas etrevistas as 5 regiões do estado, e a metodologia de passates evetuais simplesmete impede que aqueles que ão passaram pelos potos de coleta sejam selecioados, IMPOSSIBILITANDO a geeralização estatística dos resultados obtidos para a população de eleitores. b) O questioário aplicado é adequado? Por quê? Se achar que ão elabore um questioário (máximo de 1 questões). O questioário ão é adequado. As questões 1 e 3 estão cofusas, e todas estão iduzido o etrevistado a maifestar-se favoravelmete ao govero: bastaria retirar o "ão" as pergutas 1 e 3, o "mais" a questão 1, o "melhor" a questão e o "bom" a questão 3. c) Qual é a sua opiião sobre o resultado da pesquisa? É cofiável? JUSTIFIQUE. Os resultados de tal pesquisa ão são cofiáveis. A amostragem usada ão é probabilística, é viesada (por selecioar pessoas apeas a capital do estado), e o questioário está cofuso e iduzido os etrevistados. 9