A Transformada de Laplace
|
|
|
- Edson Gabeira Bergmann
- 6 Há anos
- Visualizações:
Transcrição
1 UFPEL IFM/DME - Equaçõ Difrnciai Tranformada ingrai: A Tranformada d Laplac Uma da difrn manira d rolvr quaçõ difrnciai linar é conidrar a chamada ranformada ingrai. Uma ranformada ingral é uma rlação qu ranforma uma função m oura mdian uma ingração. Ou ja, T é uma ranformada ingral qu ranforma a função f m F não pod r crio: b T(f(= K (, f ( d, a ond f é uma função dada qu é ranformada m F por mio da ingral dfinida indicada. A função F é chamada ranformada d f K é o núclo da ranformação T. O inr é uilizar a ranformada para ranformar um problma m f num problma m F (por mio d uma ranformada convnin, rolvr o problma m F (ond l dv r mai impl ou d olução conhcida não obr a olução m f mdian a ranformada invra. Exim difrn ipo d ranformada ingrai, cada uma apropriada para um cro conxo iuacional. No cao da ranformada d Laplac, o núclo é K(,= -, da forma, a ranformada á rlacionada à quaçõ difrnciai linar d coficin conan. Tranformada d Laplac A Tranformação d Laplac é uma ranformação linar qu auxilia na rolução d quaçõ difrnciai qu rprnam iuaçõ problma ou fnômno qu urgm no ambin profiional. O méodo d rolvr quaçõ por mio da ranformada d Laplac coni m rê apa principai: i inicialmn a quação difrncial é ranformada numa quação algébrica, mdian o cálculo da ranformada d Laplac d cada um do mmbro da quação difrncial, ii m guida a quação algébrica é rolvida por mio d manipulaçõ algébrica, obndo- uma olução da quação algébrica, iii a olução da quação algébrica é ranformada na olução procurada da quação difrncial uilizando- a ranformação invra d Laplac. E méodo é vanajoo m rlação a ouro méodo, poi lva m cona a condiçõ iniciai dd o início, m ncidad d drminar primiro a olução gral para dpoi obr a olução qu aifaz a condiçõ dada. Além dio, a ranformação d Laplac é pcialmn úil na buca d olução d quaçõ difrnciai qu rprnam iuaçõ d naurza dconínua ou impuliva, dcria por funçõ ccionalmn conínua. Chama- ranformação d Laplac (proco qu ranforma a ranformação L qu a cada função f, ral dfinida m (,, aifazndo drminada condiçõ (conínua por par d ordm xponncial: vr p. / do livro da bibliografia aocia a função
2 F : XR - f( d ond X é o conjuno do valor d para o quai a ingral imprópria convrg. A ranformação d Laplac d f é dnoada por L(f, ond L(f=F( ou L(f( = F( quando qur chamar anção para a variávl indpndn d f. Exmplo: S f é a função f : (, R dfinida por f( =, não a ranformada d Laplac d f é a função F:XR dada por - d = /, para. Aim, L(=/ para. D um modo gral, f : (, R não a ranformada d Laplac d f é a função F:XR dada por - f(d = F( S f( = a,, a R, não a ranformada d Laplac d f é dada por: (a- d = /(-a, para a. D manira análoga é poívl calcular a ranformada d Laplac d divra funçõ. Na maioria do cao da aplicaçõ é poívl calcular L(f como foi fio no xmplo anrior a parir do cálculo da ingral imprópria qu a dfin. O orma qu nvolvm a xiência da ranformada d Laplac d funçõ rão omiido, m prjuízo para noo objivo. Para maior dalh podm r conulado o livro indicado na bibliografia. Uma vz qu noa ma é uilizar a ranformação d Laplac para rolvr problma nvolvndo quaçõ difrnciai, farmo uo d uma abla qu coném a ranformada da principai funçõ qu aparcm na aplicaçõ. É imporan ralar qu a ranformada d Laplac d uma função, quando xi é única, qu dua funçõ conínua êm a mma ranformada d Laplac, não la ão iguai, ou ja, L(f=L(g não f = g, para um dado inrvalo ond m nido dfinir L(f L(g, (orma d Lrch. Propridad da Tranformada d Laplac A ranformação d Laplac poui vária propridad a parir da quai é poívl calcular a ranformada d alguma funçõ d manira mai fácil. Uma dla é a L linaridad: a ranformação d Laplac é uma ranformação linar, io é, f g admim L(f L(g, não L(af+bg = al(f + bl(g, para a,b R.
3 (oura propridad podm r nconrada no manual, livro da bibliografia. Propridad do Dlocamno: Muliplicar uma função por b é quivaln a ubiuir por -b na xprão d ua função ranformada. Ex.: L (cox. Calcul ( x L cox : Ex.: Ex.: L (nx. Calcul ( x L nx : 9 x L (cohx. Calcul L( cohx Exrcício Conul uma abla nconr a ranformada d Laplac da guin funçõ, conidrando a propridad linar da ranformação d Laplac: f( = f( = n( f( =. co( f( = k, k R f( = - co( f( = - n(. 7g( = n ( 8f( =, 9f(x = x + x - x g(y = y + -y q( = n( (x = x - Calcul, com auxílio da abla a guin ranformada: al(, bl( -, cl(n, dl(co, L(coh, fl(,nh, gl( -, hl( -, il( - co, jl( n, kl( - coh, ll(+ -, ml(,-, nl( +co-, ol(/+- - /, pl( -, co,, ql( -, m(/, rl( -, nh, L(co-n, L(/co-/n, ul(, vl(n+co,. Rpoa xrcício : - :, 9 k ( (,, 7 ( ( (
4 Rpoa xrcício : a, b, c, d, 9, f 9, g -, h (, i (, j 8 (, k (, l (, m, (, n ( ( (, o (, p, (,,, q / (, / 9, r (,, ( (, / ( ( (, u 9, v ( ( (, (, Tranformada Invra d Laplac Chama- ranformação invra d Laplac a ranformação L - (ranformação invra d L - qu a cada função F : XR, F(= f( d, aocia a função f: (,, ou ja, F( é a ranformada d Laplac d f(, não f( é a ranformada invra d Laplac d F(, ou ja, F( = L(f( não a ranformada invra d Laplac d F, qu rá dnoada por L - (F( é f(, ou ainda : F( = L(f( L - (F( = f(. Para calcular L - d uma função, rá uilizada uma abla d ranformada d Laplac. Exmplo: L - ( + = - poi L( - = + L - ( = n( poi L(n( = + + A ranformação L - é linar, ou ja, L - (af+bg = a L - (F + b L - (G = af( + bg(, ond L(f( = F( L(g( = G(. À vz, é ncário fazr alguma manipulaçõ algébrica na função dada.
5 Numrador: Muliplicar dividir plo mmo faor. Ex.: L - Ex.: L - Dnominador: Complar quadrado. Ex.: x +x+=(x+ + Ex.: L - Ex.: L - 8 Ex.: L - Ex.: L - 8 Exrcício Conidrando a propridad dfinição da ranformação invra d Laplac, nconr a ranformada invra d Laplac da guin funçõ: F(= F(= F(= H(= G(= - G(= 7 F(= - 8 G(= G( = + F(= + F(= F(= - G(= G(= H(= , H(= (- -
6 7 G(= H(= - 9 G(= F(=, - F(= - Rpoa: G(= H(= n(x nx co x x x x nh x 7 x 8 coh x nh x 9 x+x x+x cox+nx 7 x x x co x n x x ( x x x x 7 8 x x x x x x 8 ( n co 9 co x n x cox. x x coh nh x n 8x 8 x x co x n x co x n x Tranformada d drivada: S L(f( = F(, na condiçõ já aprnada, não mo: L(f (n ( = n L(f( - n - f( - n - f '( - n - f ''( f (n - ( - f (n - ( dd qu f ua drivada jam conínua para N, para N ral poiivo, d ordm xponncial para drminado valor d M, M. Exmplo: L(y' = L(y - y( L(y'' = L(y - y( - y'( Como fica L(y'''? A dmonração da propridad linar da ranformada d drivada podm r fia a parir da dfinição do oprador L ão nconrada no livro indicado na bibliografia. Exrcício
7 Tranform a quaçõ difrnciai abaixo m quaçõ algébrica mdian a uilização da ranformação d Laplac ua propridad: a y'+,y=, y(= olução: y(x=/(- -,x + -,x b y'+,y= y(= olução: y(x= -,x c q'+,q= q(=9 olução: q(=9 -, d I'+,I= I(= olução: I(=(- -, z'+,z=,x z(= olução: z(x=,x-,+, -,x f q'+,q= q(=, olução: q(=, -, +- g I'+I+,= I(= olução: I(=-/(- -8 h y'-y= y(= olução: y(x= x i y'-y= x y(= olução: y(x=x x j y''+y= y(=; y'(= olução: y(x=cox+nx Exrcício d aplicação d Tranformada d Laplac Rolva a quaçõ difrnciai abaixo: a y' ' 7y' y, y (, y' ( b q' q co, q ( c y' ' y' y, y (, y' ( d y' y nh, y ( y' y coh, y ( Rpoa: a Fraçõ parciai: A=, B=-/ C=/, olução: b Fraçõ parciai: A=/, B=/ C=-/, olução: c Fraçõ parciai: A=/, B-/ C=-, olução: d Fraçõ parciai: A=-/, B=/ C=/, olução: y( 8 co n n co. q( y( y( 7
8 Fraçõ parciai: A=/, B=/ C=-/, olução: y( Uando ranformada d Laplac, nconr a olução da guin quaçõ difrnciai: a. y'+y=, y(= olução: y(= -/ b. y'-7y=, y(= olução: y(= 7 - c.y''+y=, y(= y'(= olução: y(=co d. y''-y'=, y(= y'(=- olução: y(=-. y''+y'+y=, y(= y'(= olução: y(= - (+ f. y''-y'+y=, y(= y'(= olução: y(= g. z''+z'+z=x -x, z(= z'(= olução: z(x= ( +x+,x -x h. q''+q'-q=, q(= q'(=- olução: q(= - + i. x''+x=n, x(= x'(= olução: x(=/n-/n. Um circuio RCL ligado m éri com uma riência d ohm, um capacior d capaciância, farad uma induância d, hnry não m não aplicada. Drmin a corrn no circuio a carga inicial, no capacior é, C a corrn inicial é nula. Rpoa: I(=(/( A função H(= é a função d ranfrência num circuio abro. A rpoa ao ima é ( dada por L - (H(=y(. Enconr a rpoa ao ima, n cao, io é, y(. Qual o valor da rpoa ao ima quando = gundo? Rpoa: y(=,-,co y(=, +. S L(q(= nconr q(, io é, a função qu rprna a carga m cada inan. 8 Faça o mmo para a função qu rprna a corrn no circuio. Rpoa: q(= - co+ - n i(=- - n. S L(I(=, calcul a corrn m cada inan. ( ( Rpoa: I(= +co+n 8
9 7. A função G(= é a função d ranfrência num circuio abro. A rpoa ao ( - ( ima é dada por L - (G(=y(. Enconr a rpoa ao ima, n cao, io é, y(. Rpoa: y(=co- + Funçõ Sccionalmn Conínua Uma função é chamada ccionalmn conínua m um inrvalo (a,b, a função for conínua m cada ubinrvalo d (a,b o limi larai d f, m cada um do ubinrvalo for finio. Exmplo: Em cada cao a guir, boc o gráfico da função vrifiqu qu la é ccionalmn conínua, no inrvalo ond á dfinida. f( = g( = h( = - f( = - h( = - r( = n, > 9
10 Alguma funçõ ccionalmn conínua aparcm m quaçõ difrnciai qu rprnam problma d ngnharia. Uma dla é a chamada função calão uniário ou função impulo. Ela é dnoada dfinida por: u a ( = a a Faça o gráfico da função u a (. a A ranformada d Laplac da função u a ( é dada por: L(u a ( = -a / a (confira na abla. Exrcício Faça o gráfico calcul a ranformada d Laplac da funçõ guin: f( = u ( g( = u ( h( = - u ( f( = +u ( h( = u / ( h( = u (- u ( 7 r( = u (-u ( 8 u(=- u ( Em cada xrcício a guir, crva numa forma mai implificada a funçõ indicada faça o gráfico d cada uma dla. a u ( b u (n c u (co(- d u (n u / ((-/ fu ((- g-u ( h u, ( -, + Equaçõ Difrnciai Envolvndo Funçõ Sccionalmn Conínua Para rolvr quaçõ difrnciai nvolvndo funçõ ccionalmn conínua é ncário calcular a ranformada invra d funçõ qu nvolvm o rmo -a. Aim vamo udar o rulado guin, qu é um orma imporan dnro da oria d ranformada d Laplac. Sja F( = L(f(, para a ja c. Da forma f(=l - (F(. Enão: L(u a (f(-a = -a Lf(, a, ou ja, como f( = L - (F(, a xprão pod r cria aim: u a (f(-a = L - ( -a F(.
11 A parir d rulado é poívl calcular a ranformada invra da funçõ qu aparcrão na rolução da quaçõ difrnciai qu nvolvm funçõ ccionalmn conínua. Exrcício Conidrando o concio dfiniçõ anrior, calcul a ranformada invra d Laplac da funçõ guin. Expr a função f(=l - (F(, indicando o inrvalo ond la muda d comporamno faça o gráfico da função obida, m cada cao. F( = - /(+ G( = - /( + F( = - /(+ F( = - / G( = - /( + H( = -/ /( + 7 F( = (- - / 8 G( = - /( + 9 H( = (+ - / H( = - /(- G( = - /(+ F( = (+ - / T( = - /( -+ F( = - /( ++ G( = - /( + G( = -/ /( - 7 R( = (-/ (+/( + 8H( = (-/ (-/( Rpoa: u ( -+ u (,n(- u ( [ ] u (,( u ( n( u, ( n (, 7 u ( ( 8 u ( [co( ] 9 u( ( 9 u ( ( [ ] u u( (,( u ( ( u( [ n,7( ],7
12 u ( co ( u coh (,, ( 7 u ( [co ( n ( ] 8 u ( ( Rolva a quaçõ abaixo, uilizando a ranformada d Laplac. a y''+y = y(= y'(= Rpoa: y(=co [, ;,+,7 para [, ] co para [, b y''+y = f(x ond f(x= x x y(= y'(= Rpoa: y(=u ((-co(-+co( c y''+y'+y = y( = y'( = Rpoa: y(=-u ((- -+ d y'+y = y( = Rpoa: y(=(- - -u ((- - y''+y = / y( = y'( = / Rpoa: y(=+n-co+u / ((-co(-
13 Conidr a função d ranfrência d uma malha abra, dada por -/ (, + G(= (, Calcul a rpoa do ima a um ímulo inicial, qu é rprnada por y( = L - (G(. Qual o valor da rpoa do ima para =, para =? Rpoa: y u ( (co (, n (, (, Idm para a funçõ guin: a G( = - ( +( + -, c F( = ( +, - ( - b G( = (, +( + - d H(= ( Rpoa:,( ( a y ( u ( b,9 y ( u ( (, 9,9,( c,, y ( u (, d, y( u (,( n,7(,7 Exrcício Exra: Um circuio RC m E(=u (, riência d ohm, capaciância d - farad inicialmn uma carga d coulomb no capacior. Enconr a função qu dá a carga a função qu dá a corrn m cada inan. Calcul a carga para = para =. Rpoa: q (,u ( ( Enconr a corrn m = num circuio RL ond R= ohm, L= hnry, E(=-u (, ndo qu a corrn inicial no circuio é nula. Rpoa: I ( ( u( (
14 Enconr a oluçao da quação difrncial ' y y com condição inicial y(=, aravé da ranformada d Laplac. Ecrva a olução numa forma mai implificada faç a o gráfico da função nrada. Rpoa: ( ( ( ( u y Enconr a olução da quação difrncial ' ' y y com condiçõ iniciai y(= y (=, aravé da ranformada d Laplac. Ecrva a olução numa forma mai implificada. Faça o gráfico da função nrada nconr y(: Rpoa: ( co ( co ( u y Num circuio RC, R= ohm, C=, farad E(=u (-u (. Supondo qu a carga inicial ja d coulomb, nconr a carga m cada inan d mpo, crvndo-a numa forma mai implificada faça o gráfico da função nrada: Rpoa:, (, ( ( u u q
3. TRANSFORMADA DE LAPLACE. Prof. JOSÉ RODRIGO DE OLIVEIRA
 3 TRNSFORMD DE LPLCE Prof JOSÉ RODRIGO DE OLIVEIR CONCEITOS BÁSICOS Númro complxo: ond α β prncm ao nº rai Módulo fa d um númro complxo Torma d Eulr: b a an a co co n n Prof Joé Rodrigo CONCEITOS BÁSICOS
3 TRNSFORMD DE LPLCE Prof JOSÉ RODRIGO DE OLIVEIR CONCEITOS BÁSICOS Númro complxo: ond α β prncm ao nº rai Módulo fa d um númro complxo Torma d Eulr: b a an a co co n n Prof Joé Rodrigo CONCEITOS BÁSICOS
que representa uma sinusoide com a amplitude modulada por uma exponencial. Com s real, tem-se,
 Curo d Engnharia Elcrónica d Compuador - Elcrónica III Frquência Complxa rvião n Conidr- a xprão, σ v V co qu rprna uma inuoid com a ampliud modulada por uma xponncial. Com ral, m-, n σ>0 a ampliud d v
Curo d Engnharia Elcrónica d Compuador - Elcrónica III Frquência Complxa rvião n Conidr- a xprão, σ v V co qu rprna uma inuoid com a ampliud modulada por uma xponncial. Com ral, m-, n σ>0 a ampliud d v
A TRANSFORMADA DE LAPLACE
 A TRANSFORMADA DE APACE Prof M Ayron Barboni SUMÁRIO INTRODUÇÃO TRANSFORMADA DE APACE Dfinição Cálculo da ranformada d aplac Exrcício rolvido 4 4 Exrcício propoo 8 TRANSFORMADA INVERSA DE APACE 9 Exrcício
A TRANSFORMADA DE APACE Prof M Ayron Barboni SUMÁRIO INTRODUÇÃO TRANSFORMADA DE APACE Dfinição Cálculo da ranformada d aplac Exrcício rolvido 4 4 Exrcício propoo 8 TRANSFORMADA INVERSA DE APACE 9 Exrcício
Em termos temporais há duas formas possíveis de operação dos sistemas: estacionária e dinâmica.
 INTRODUÇÃO N curo ão arnada uada frramna ncária ara a análi do comoramno dinâmico d ima (roco oraçõ uniária) da ngnharia química. Numa abordagm baan imlia, m rmo do númro d alavra uilizada, orm abrangn
INTRODUÇÃO N curo ão arnada uada frramna ncária ara a análi do comoramno dinâmico d ima (roco oraçõ uniária) da ngnharia química. Numa abordagm baan imlia, m rmo do númro d alavra uilizada, orm abrangn
Teoria de Controle (sinopse) 4 Função de matriz. J. A. M. Felippe de Souza
 Toria d Conrol (sinops) 4 Função d mariz J. A. M. Flipp d Souza Função d mariz Primiramn vamos dfinir polinómio d mariz. Dfinição: Polinómio d mariz (quadrada) Sja p(λ)um polinómio m λd grau n (finio),
Toria d Conrol (sinops) 4 Função d mariz J. A. M. Flipp d Souza Função d mariz Primiramn vamos dfinir polinómio d mariz. Dfinição: Polinómio d mariz (quadrada) Sja p(λ)um polinómio m λd grau n (finio),
log 2, qual o valor aproximado de 0, 70
 UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
1ª. Lei da Termodinâmica para um Volume de Controle
 ª. Li da Trmodinâmica ara um Volum d Conrol Grand ar do roblma d inr na ngnharia nol ima abro, ou ja, ima no quai há fluo d maa araé d ua fronira. É, orano, connin obrmo uma rão da ª. Li álida ara ima
ª. Li da Trmodinâmica ara um Volum d Conrol Grand ar do roblma d inr na ngnharia nol ima abro, ou ja, ima no quai há fluo d maa araé d ua fronira. É, orano, connin obrmo uma rão da ª. Li álida ara ima
Aula Teórica nº 32 LEM-2006/2007. Prof. responsável de EO: Mário J. Pinheiro. Oscilações eléctricas num circuito RLC
 Aula órica nº 3 LEM-6/7 Prof. rponávl d EO: Mário J. Pinhiro Ocilaçõ lécrica num circuio RLC Conidr- agora um condnador inicialmn carrgado com a carga q qu no inan é dcarrgado obr um circuio lécrico d
Aula órica nº 3 LEM-6/7 Prof. rponávl d EO: Mário J. Pinhiro Ocilaçõ lécrica num circuio RLC Conidr- agora um condnador inicialmn carrgado com a carga q qu no inan é dcarrgado obr um circuio lécrico d
MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação. Aula 07. Prof. Dr. Marco Antonio Leonel Caetano
 MESTRADO EM MACROECONOMIA FINANÇAS Disiplina d Compuação Aula 7 Prof. Dr. Maro Anonio Lonl Caano Guia d Esudo para Aula 7 Vors Linarmn Indpndns - Vrifiação d vors LI - Cálulo do Wronsiano Equaçõs Difrniais
MESTRADO EM MACROECONOMIA FINANÇAS Disiplina d Compuação Aula 7 Prof. Dr. Maro Anonio Lonl Caano Guia d Esudo para Aula 7 Vors Linarmn Indpndns - Vrifiação d vors LI - Cálulo do Wronsiano Equaçõs Difrniais
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
 Uivridad Salvador UNIFACS Curo d Egharia Méodo Mmáico Aplicado / Cálculo Avaçado / Cálculo IV Profa: Ilka Rouça Frir A Traformada d Laplac Txo : Irodução. Dfiição. Codiçõ d Exiêcia. Propridad. Irodução
Uivridad Salvador UNIFACS Curo d Egharia Méodo Mmáico Aplicado / Cálculo Avaçado / Cálculo IV Profa: Ilka Rouça Frir A Traformada d Laplac Txo : Irodução. Dfiição. Codiçõ d Exiêcia. Propridad. Irodução
TRANSFORMADA DE LAPLACE- PARTE I
 TRNSFORMD DE LLE- RTE I Eor. d Barro. INTRODUÇÃO odmo dfiir a Traformada d Laplac como uma opração mamáica qu covr uma fução d variávl ral m uma fução d variávl complxa: Od, F f d i f é uma fução ral da
TRNSFORMD DE LLE- RTE I Eor. d Barro. INTRODUÇÃO odmo dfiir a Traformada d Laplac como uma opração mamáica qu covr uma fução d variávl ral m uma fução d variávl complxa: Od, F f d i f é uma fução ral da
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
 Univridad Salvador UNIFACS Curo d Engnharia Método Matmático Alicado / Cálculo Avançado / Cálculo IV Profa: Ilka Rbouça Frir A Tranformada d Lalac Txto 3: Dlocamnto obr o ixo t. A Função Dgrau Unitário.
Univridad Salvador UNIFACS Curo d Engnharia Método Matmático Alicado / Cálculo Avançado / Cálculo IV Profa: Ilka Rbouça Frir A Tranformada d Lalac Txto 3: Dlocamnto obr o ixo t. A Função Dgrau Unitário.
Questão. Sinais periódicos e não periódicos. Situação limite. Transformada de Fourier de Sinais Contínuos
 Qusão Srá possívl rprsnar sinais não priódicos como soma d xponnciais? ransformada d Fourir d Sinais Conínuos jorg s. marqus, jorg s. marqus, Sinais priódicos não priódicos Siuação limi Um sinal não priódico
Qusão Srá possívl rprsnar sinais não priódicos como soma d xponnciais? ransformada d Fourir d Sinais Conínuos jorg s. marqus, jorg s. marqus, Sinais priódicos não priódicos Siuação limi Um sinal não priódico
TRASITÓRIOS PARTE 2. 1 Fluxo magnético. 2 Ímã permanente. 2 Ímã. 3 Fluxo magnético de um condutor retilíneo 27/4/2015
 7/4/5 TTÓO PTE 7/4/5 7/4/5 Fluxo magnéico Ímã prmann N há corrn lérica [], xi fluxo magnéico. há fluxo magnéico [Wb], xi corrn lérica. 7/4/5 7/4/5 4 Ímã Da mma forma qu não lérica fluxo lérico ão inparávi,
7/4/5 TTÓO PTE 7/4/5 7/4/5 Fluxo magnéico Ímã prmann N há corrn lérica [], xi fluxo magnéico. há fluxo magnéico [Wb], xi corrn lérica. 7/4/5 7/4/5 4 Ímã Da mma forma qu não lérica fluxo lérico ão inparávi,
Este texto trata do estudo analítico de sistemas de controle. Falando de forma geral, ele consiste de quatro partes:
 . Mamáica.. Sima Fíico Modlo E o raa do udo analíico d ima d conrol. Falando d forma gral, l coni d quaro par:. Modlagm. Dnvolvimno d quaçõ mamáica. Análi 4. Projo E capíulo dicu a dua primira par. A diinção
. Mamáica.. Sima Fíico Modlo E o raa do udo analíico d ima d conrol. Falando d forma gral, l coni d quaro par:. Modlagm. Dnvolvimno d quaçõ mamáica. Análi 4. Projo E capíulo dicu a dua primira par. A diinção
7 Solução de um sistema linear
 Toria d Conrol (sinops 7 Solução d um sisma linar J. A. M. Flipp d Souza Solução d um sisma linar Dfinição 1 G(,τ mariz cujos lmnos g ij (,τ são as rsposas na i ésima saída ao impulso aplicado na j ésima
Toria d Conrol (sinops 7 Solução d um sisma linar J. A. M. Flipp d Souza Solução d um sisma linar Dfinição 1 G(,τ mariz cujos lmnos g ij (,τ são as rsposas na i ésima saída ao impulso aplicado na j ésima
Capítulo 2.1: Equações Lineares 1 a ordem; Método dos Fatores Integrantes
 Capíulo.1: Equaçõs Linars 1 a ordm; Méodo dos Faors Ingrans Uma EDO d primira ordm m a forma gral d f, ond f é linar m. Exmplo: a Equaçõs com coficins consans; a b b Equaçõs com coficins variavis: d p
Capíulo.1: Equaçõs Linars 1 a ordm; Méodo dos Faors Ingrans Uma EDO d primira ordm m a forma gral d f, ond f é linar m. Exmplo: a Equaçõs com coficins consans; a b b Equaçõs com coficins variavis: d p
ANALISE DE CIRCUITOS DE 1 a E 2 a. J.R. Kaschny ORDENS
 ANAISE DE IRUITOS DE a E a J.R. Kaschny ORDENS Inrodução As caracrísicas nsão-corrn do capacior do induor inroduzm as quaçõs difrnciais na anális dos circuios léricos. As is d Kirchhoff as caracrísicas
ANAISE DE IRUITOS DE a E a J.R. Kaschny ORDENS Inrodução As caracrísicas nsão-corrn do capacior do induor inroduzm as quaçõs difrnciais na anális dos circuios léricos. As is d Kirchhoff as caracrísicas
RESPOSTA TEMPORAL. 1. Motivação. 2. Solução homogênea. Calcular a resposta temporal de sistemas dinâmicos LIT na forma SS.
 Euaro Lobo Luoa Cabral RESPOST TEMPORL. Moiação Calcular a rpoa mporal ima inâmico LT na forma SS. Rpoa mporal prmi analiar comporamno inâmico o ima no omínio o mpo. Dua oluçõ: Solução homogêna rpoa à
Euaro Lobo Luoa Cabral RESPOST TEMPORL. Moiação Calcular a rpoa mporal ima inâmico LT na forma SS. Rpoa mporal prmi analiar comporamno inâmico o ima no omínio o mpo. Dua oluçõ: Solução homogêna rpoa à
CÁLCULO II MATEMÁTICA PARFOR LISTA DE EXERCICIOS PARA A PROVA SUBSTITUTIVA
 CÁLCULO II MATEMÁTICA PARFOR LISTA DE EXERCICIOS PARA A PROVA SUBSTITUTIVA ) Drmin as Primiivas das funçõs abaio: a) b) ( ) ) ( ) d) ln ) 6ln 6 f) (sn( ) os( )) os( ) sn( ) g) h) / arg ( ) i) j) k) (sn(
CÁLCULO II MATEMÁTICA PARFOR LISTA DE EXERCICIOS PARA A PROVA SUBSTITUTIVA ) Drmin as Primiivas das funçõs abaio: a) b) ( ) ) ( ) d) ln ) 6ln 6 f) (sn( ) os( )) os( ) sn( ) g) h) / arg ( ) i) j) k) (sn(
Efeito da pressão decrescente da atmosfera com o aumento da altitude
 Efio da prssão dcrscn da amosfra com o aumno da aliud S lançarmos um projéil com uma vlocidad inicial suficinmn ala l aingirá aliuds ond o ar é mais rarfio do qu próximo à suprfíci da Trra Logo a rsisência
Efio da prssão dcrscn da amosfra com o aumno da aliud S lançarmos um projéil com uma vlocidad inicial suficinmn ala l aingirá aliuds ond o ar é mais rarfio do qu próximo à suprfíci da Trra Logo a rsisência
Análises de sistemas no domínio da frequência
 prmno d Engnhri Químic d Prólo UFF iciplin: TEQ0- COTROLE E PROCESSOS náli d im no domínio d frquênci Prof inok Boorg Rpo d Frquênci Cliqu pr dir o ilo do xo mr COCEITO: Coni d um méodo gráfico-nlíico
prmno d Engnhri Químic d Prólo UFF iciplin: TEQ0- COTROLE E PROCESSOS náli d im no domínio d frquênci Prof inok Boorg Rpo d Frquênci Cliqu pr dir o ilo do xo mr COCEITO: Coni d um méodo gráfico-nlíico
7. Aplicação do Principio do Máximo
 7. Aplicação do Principio do Máximo Ns capiulo vamos implmnar um algorimo qu uiliz a oria do Principio do Máximo para drminar o conjuno dos sados aingívis. Com o rsulados obidos vamos nar fazr um parallo
7. Aplicação do Principio do Máximo Ns capiulo vamos implmnar um algorimo qu uiliz a oria do Principio do Máximo para drminar o conjuno dos sados aingívis. Com o rsulados obidos vamos nar fazr um parallo
ZEROS DE SISTEMAS MIMO
 Edardo Lobo Loa abral ZEROS DE SISTEMAS MIMO. Zro d ranmião O cálclo do ro d m ima SISO é rmamn impl d r fado, poi ão a raí do polinômio do nmrador d a fnção d ranfrência. Por mplo, conidr o ima dinâmico
Edardo Lobo Loa abral ZEROS DE SISTEMAS MIMO. Zro d ranmião O cálclo do ro d m ima SISO é rmamn impl d r fado, poi ão a raí do polinômio do nmrador d a fnção d ranfrência. Por mplo, conidr o ima dinâmico
TRANSFORMADA DE LAPLACE Conceitos e exemplos
 TRANSFORMADA DE LAPLACE Conceio e exemplo Diciplina MR7 A finalidade dea apoila é dar o conceio da ranformada de Laplace, eu uo na olução de problema e por fim um aprendizado do méodo de reoluçõe. Muia
TRANSFORMADA DE LAPLACE Conceio e exemplo Diciplina MR7 A finalidade dea apoila é dar o conceio da ranformada de Laplace, eu uo na olução de problema e por fim um aprendizado do méodo de reoluçõe. Muia
enquanto que um exemplo de e.d.p. é uma equação do tipo potencial
 6- EDO s: TEORIA E TRATAMENTO NUMÉRICO Inrodução Muios problmas imporans significaivos da ngnharia, das ciências físicas das ciências sociais, formulados m rmos mamáicos, igm a drminação d uma função qu
6- EDO s: TEORIA E TRATAMENTO NUMÉRICO Inrodução Muios problmas imporans significaivos da ngnharia, das ciências físicas das ciências sociais, formulados m rmos mamáicos, igm a drminação d uma função qu
EQUAÇÕES DIFERENCIAIS APLICADAS EM MODELOS DE COMPARTIMENTOS
 EQUAÇÕES DIFERENCIAIS APLICADAS EM MODELOS DE COMPARTIMENTOS Tiago Novllo d Brio Fcilcam, iago-novllo@homail.com ald dos Sanos Coquiro Fcilcam, vcoquiro@yahoo.com.br Rosangla Tixira Guds UTFPR, r_guds@homail.com
EQUAÇÕES DIFERENCIAIS APLICADAS EM MODELOS DE COMPARTIMENTOS Tiago Novllo d Brio Fcilcam, iago-novllo@homail.com ald dos Sanos Coquiro Fcilcam, vcoquiro@yahoo.com.br Rosangla Tixira Guds UTFPR, r_guds@homail.com
Amostragem de sinais contínuos
 Amoragm inai conínuo 0.8 0.6 0.4 0. 0 0 0. 0. 0.3 0.4 0.5 0.6 0.7 0.8 0.9 SS MIEIC 008/009 Programa SS Sinai Sima aula Sima Linar Invarian aula Análi Fourir (mpo conínuo 3 aula Análi Fourir (mpo icro aula
Amoragm inai conínuo 0.8 0.6 0.4 0. 0 0 0. 0. 0.3 0.4 0.5 0.6 0.7 0.8 0.9 SS MIEIC 008/009 Programa SS Sinai Sima aula Sima Linar Invarian aula Análi Fourir (mpo conínuo 3 aula Análi Fourir (mpo icro aula
ESZO Fenômenos de Transporte
 Univridad Fdral do ABC ESZO 001-15 Fnôno d Tranpor Profa. Dra. Ana Maria Prira No ana.no@ufabc.du.br Bloco A, orr 1, ala 637 1ª Li da Trodinâica para olu d Conrol ESZO 001-15_Ana Maria Prira No 1ª Li da
Univridad Fdral do ABC ESZO 001-15 Fnôno d Tranpor Profa. Dra. Ana Maria Prira No ana.no@ufabc.du.br Bloco A, orr 1, ala 637 1ª Li da Trodinâica para olu d Conrol ESZO 001-15_Ana Maria Prira No 1ª Li da
Equações de Maxwell. Métodos Eletromagnéticos. Equações de Maxwell. Equações de Maxwell
 Méodos Elromagnéicos agoso d 9 Fundamnos Equaçõs d Mawll no domínio do mpo da frqüência Onda plana édison K. ao Equaçõs d Mawll Todos os fnômnos lromagnéicos obdcm às quaçõs mpíricas d Mawll. b d h j ond
Méodos Elromagnéicos agoso d 9 Fundamnos Equaçõs d Mawll no domínio do mpo da frqüência Onda plana édison K. ao Equaçõs d Mawll Todos os fnômnos lromagnéicos obdcm às quaçõs mpíricas d Mawll. b d h j ond
MEEC Mestrado em Engenharia Electrotécnica e de Computadores. MCSDI Modelação e Controlo de Sistemas Dinâmicos. Exercícios de.
 EEC rado Engnharia Elroénia d Copuador CDI odlação Conrolo d ia Dinâio Exríio d Função Driiva Conuno d xríio laborado plo don Joé Tnriro ahado JT, anul ano ilva, Víor Rodrigu da Cunha VRC Jorg Erla da
EEC rado Engnharia Elroénia d Copuador CDI odlação Conrolo d ia Dinâio Exríio d Função Driiva Conuno d xríio laborado plo don Joé Tnriro ahado JT, anul ano ilva, Víor Rodrigu da Cunha VRC Jorg Erla da
Oscilações amortecidas
 Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
3º) Equação do tipo = f ( y) dx Solução: 2. dy dx. 2 =. Integrando ambos os membros, dx. dx dx dy dx dy. vem: Ex: Resolva a equação 6x + 7 = 0.
 0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
ANO LECTIVO 2001/2002
 ANO LECTIVO 00/00 ª Fas, ª Chamada 00 Doss rapêuicas iguais d um cro anibióico são adminisradas, pla primira vz, a duas pssoa: a Ana o Carlos Admia qu, duran as doz primiras horas após a omada simulâna
ANO LECTIVO 00/00 ª Fas, ª Chamada 00 Doss rapêuicas iguais d um cro anibióico são adminisradas, pla primira vz, a duas pssoa: a Ana o Carlos Admia qu, duran as doz primiras horas após a omada simulâna
SOLUÇÃO NUMÉRICA DAS EQUAÇÕES DE PROBABILIDADES DE TRANSIÇÃO DE PROCESSOS SEMI MARKOVIANOS UTILIZANDO TRANSFORMADAS DE LAPLACE
 Pquia Opracional na Socidad: Educação, Mio Ambin Dnvolvimno SOLUÇÃO NUMÉRICA DAS EQUAÇÕES DE PROBABILIDADES DE TRANSIÇÃO DE PROCESSOS SEMI MARKOVIANOS UTILIZANDO TRANSFORMADAS DE LAPLACE Márcio Joé da
Pquia Opracional na Socidad: Educação, Mio Ambin Dnvolvimno SOLUÇÃO NUMÉRICA DAS EQUAÇÕES DE PROBABILIDADES DE TRANSIÇÃO DE PROCESSOS SEMI MARKOVIANOS UTILIZANDO TRANSFORMADAS DE LAPLACE Márcio Joé da
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
 PR UNIVERSIDADE TECNOÓGICA FEDERA DO PARANÁ OBSERVAÇÃO: O TEXTO É ADAPTADO DO IVRO: BRONSON. R. Modrna introdução à quaçõ difrniai. tradução d Alfrdo Alv d Faria, rvião ténia Robrto Romano. São Paulo:
PR UNIVERSIDADE TECNOÓGICA FEDERA DO PARANÁ OBSERVAÇÃO: O TEXTO É ADAPTADO DO IVRO: BRONSON. R. Modrna introdução à quaçõ difrniai. tradução d Alfrdo Alv d Faria, rvião ténia Robrto Romano. São Paulo:
Seção 2.1: Equações lineares; Fator integrante
 Capíulo Sção.: Equaçõs linars; Faor ingran Uma EDO d primira ordm é da forma d d f ond f é linar na variávl. Alguns mplos ípicos ds ipo d quaçõs com coficins consans saõ a b ou quaçõs com coficins variávis:
Capíulo Sção.: Equaçõs linars; Faor ingran Uma EDO d primira ordm é da forma d d f ond f é linar na variávl. Alguns mplos ípicos ds ipo d quaçõs com coficins consans saõ a b ou quaçõs com coficins variávis:
INSTITUTO POLITÉCNICO DE VISEU. f x = x em relação à partição do intervalo. em 4 subintervalos de igual amplitude e tal que o ponto ω
 INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA Dparamno Mamáica Disciplina Anális Mamáica Curso Engnharia Informáica º Smsr º Ficha nº : Cálculo ingral m IR Drmin a soma d Rimann da função
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA Dparamno Mamáica Disciplina Anális Mamáica Curso Engnharia Informáica º Smsr º Ficha nº : Cálculo ingral m IR Drmin a soma d Rimann da função
1. A TRANSFORMADA DE LAPLACE
 Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Equaçõ Difrciai - Traformada d Laplac A TRANSFORMADA DE LAPLACE Dfiição: Sja f() uma fução ral dfiida para > Eão a raformada d Laplac d f(), doada por L [ ( ) ] f é dfiida por: L [ f ( ) ] F( ) f( )d,
Total. UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Departamento de Matemática Pura e Aplicada MAT Turma A /2 Prova da área IIA
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma A - 7/ Prova da área IIA - 5 6 7 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma A - 7/ Prova da área IIA - 5 6 7 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou
Total. UFRGS INSTITUTO DE MATEMÁTICA Departamento de Matemática Pura e Aplicada MAT Turma A /1 Prova da área IA
 UFRGS INSTITUTO DE MATEMÁTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma A - 6/ Prova da área IA - 6 7 8 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou qualquer ouro recuro
UFRGS INSTITUTO DE MATEMÁTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma A - 6/ Prova da área IA - 6 7 8 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou qualquer ouro recuro
Total. UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Departamento de Matemática Pura e Aplicada MAT Turma D /2 Prova da área IA
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT6 - Turma D - 6/ Prova da área IA - 5 6 7 Toal Nome: Gabario Regra Gerai: Não é permiido o uo de calculadora, elefone
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT6 - Turma D - 6/ Prova da área IA - 5 6 7 Toal Nome: Gabario Regra Gerai: Não é permiido o uo de calculadora, elefone
3. Análise de Circuitos Elétricos Simples
 REDES CIRCUITOS: 3. Anális d Circuios Eléricos Simpls A inrconxão d dois ou mais lmnos d circuios simpls forma uma rd lérica. S a rd ivr plo mnos um caminho fchado, la é ambém um circuio lérico. ELEMENTO
REDES CIRCUITOS: 3. Anális d Circuios Eléricos Simpls A inrconxão d dois ou mais lmnos d circuios simpls forma uma rd lérica. S a rd ivr plo mnos um caminho fchado, la é ambém um circuio lérico. ELEMENTO
( 1). β β. 4.2 Funções Densidades Con2nuas
 4 Funçõs Dnsidads Connuas Dnsidad Eponncial A dnsidad ponncial é u:lizada comumn para sablcr sruuras d probabilidads m primnos cujos nos são siuados na ra ral [, ] Uma aplicação gral comum corrspond à
4 Funçõs Dnsidads Connuas Dnsidad Eponncial A dnsidad ponncial é u:lizada comumn para sablcr sruuras d probabilidads m primnos cujos nos são siuados na ra ral [, ] Uma aplicação gral comum corrspond à
Análise Matemática III
 João Paulo Pais d Almida Ilda Marisa d Sá Ris Ana Esr da Viga Rodrigus Víor Luis Prira d Sousa Anális Mamáica III Dparamno d Mamáica Escola Suprior d Tcnologia d Gsão Insiuo Poliécnico d Bragança Smbro
João Paulo Pais d Almida Ilda Marisa d Sá Ris Ana Esr da Viga Rodrigus Víor Luis Prira d Sousa Anális Mamáica III Dparamno d Mamáica Escola Suprior d Tcnologia d Gsão Insiuo Poliécnico d Bragança Smbro
TÓPICOS. ordem; grau; curvas integrais; condições iniciais e fronteira. 1. Equações Diferenciais. Conceitos Gerais.
 Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR A =
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 4 EQUAÇÕES DIFERENCIAIS LINEARES Formas canónicas d Jordan () Para cada uma das matrizs A
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 4 EQUAÇÕES DIFERENCIAIS LINEARES Formas canónicas d Jordan () Para cada uma das matrizs A
TRASITÓRIOS PARTE 1 CAPACITÂNCIA CAPACITÂNCIA CAPACITÂNCIA CAPACITÂNCIA CAPACITÂNCIA. 0 q elétron. Itens. 1 Carga elétrica.
 // TÂN TTÓO T TÂN // // TÂN n. nrgia poncial lérica..trabalho lérico..oncial lérico..tnão lérica.. arga lérica..apaciância lérica.. Força lérica..náli mporal.. ampo lérico.. rmiividad lérica ar.. Fluxo
// TÂN TTÓO T TÂN // // TÂN n. nrgia poncial lérica..trabalho lérico..oncial lérico..tnão lérica.. arga lérica..apaciância lérica.. Força lérica..náli mporal.. ampo lérico.. rmiividad lérica ar.. Fluxo
Análise Matemática IV
 Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA
 Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES
 PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
Aula 1, Experiência 1 Circuitos CA e Caos
 Noas d aula: www.fap.if.usp.br/~hbarbosa LabFlx: www.dfn.if.usp.br/curso/labflx Profa. Eloisa Szano loisa@dfn.if.usp.br Ramal: 7 Pllron Aula, Expriência ircuios A aos Prof. Hnriqu Barbosa hbarbosa@if.usp.br
Noas d aula: www.fap.if.usp.br/~hbarbosa LabFlx: www.dfn.if.usp.br/curso/labflx Profa. Eloisa Szano loisa@dfn.if.usp.br Ramal: 7 Pllron Aula, Expriência ircuios A aos Prof. Hnriqu Barbosa hbarbosa@if.usp.br
Análise Matemática IV
 Análie Maemáica IV Problema para a Aula Práica Semana. Calcule a ranformada de Laplace e a regiõe de convergência da funçõe definida em 0 pela expreõe eguine: a f = cha b f = ena Reolução: a Aendendo a
Análie Maemáica IV Problema para a Aula Práica Semana. Calcule a ranformada de Laplace e a regiõe de convergência da funçõe definida em 0 pela expreõe eguine: a f = cha b f = ena Reolução: a Aendendo a
Função Exponencial: Conforme já vimos, o candidato natural à função exponencial complexa é dado pela função. f z x iy f z e cos y ie sen y.
 Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Capítulo 2.1: Equações Lineares; Método dos Fatores Integrantes
 Capíulo.: Equaçõs Linars; Méodo dos Faors Ingrans Uma EDO d primira ordm m a forma gral d d f ond f é linar m. Emplos inclum quaçõs com coficins consans a ou quaçõs com coficins variavis: d d b p g Capíulo.:
Capíulo.: Equaçõs Linars; Méodo dos Faors Ingrans Uma EDO d primira ordm m a forma gral d d f ond f é linar m. Emplos inclum quaçõs com coficins consans a ou quaçõs com coficins variavis: d d b p g Capíulo.:
Equações de Maxwell na Forma Fasorial
 quaçõs d Mawll na Forma Fasorial N s o raa-s das quaçõs d Mawll na forma fasorial as rlaçõs consiuivas m mios mariais, as quais srão amplamn mprga- das ao longo o o, por raar-s d uma podrosa frramna mamáica
quaçõs d Mawll na Forma Fasorial N s o raa-s das quaçõs d Mawll na forma fasorial as rlaçõs consiuivas m mios mariais, as quais srão amplamn mprga- das ao longo o o, por raar-s d uma podrosa frramna mamáica
Física IV. Instituto de Física - Universidade de São Paulo. Aula: Interferência
 Física IV Insiuo d Física - Univrsidad d São Paulo Profssor: Valdir Guimarãs -mail: valdirg@if.usp.br Aula: Inrfrência Inrfrência d ondas Inrfrência d ondas O qu aconc quando duas ondas s combinam ou inrfrm
Física IV Insiuo d Física - Univrsidad d São Paulo Profssor: Valdir Guimarãs -mail: valdirg@if.usp.br Aula: Inrfrência Inrfrência d ondas Inrfrência d ondas O qu aconc quando duas ondas s combinam ou inrfrm
Escoamento incompressível, tubo rígido I
 Balanço d aa: coano incorívl, ubo ríido I ) 0 ) Balanço d ono linar: Inrando nr a oiçõ, rula: vaão voluérica conan na oição d d ) nθ d ) ) uda d rão á cooa d uda d rão or nria oncial ravidad), nria cinéica
Balanço d aa: coano incorívl, ubo ríido I ) 0 ) Balanço d ono linar: Inrando nr a oiçõ, rula: vaão voluérica conan na oição d d ) nθ d ) ) uda d rão á cooa d uda d rão or nria oncial ravidad), nria cinéica
EXPERIÊNCIA 7 MEDIDA DE INDUTÂNCIA POR ONDA RETANGULAR
 UMCCE Eng. Elérca m - ab. Crco Elérco Prof. Wlon Yamag EXPEÊNC 7 MEDD DE NDUÂNC PO OND ENGU NODUÇÃO O objvo báco da xprênca é mdr a ndânca a rênca d ma bobna zando ma onda ranglar. O prncípo da mdção é
UMCCE Eng. Elérca m - ab. Crco Elérco Prof. Wlon Yamag EXPEÊNC 7 MEDD DE NDUÂNC PO OND ENGU NODUÇÃO O objvo báco da xprênca é mdr a ndânca a rênca d ma bobna zando ma onda ranglar. O prncípo da mdção é
6 Resposta do Sistema Não-Linear
 6 Roa do Sima Não-Linar A quaçõ d movimno 4.1 arnam não-linaridad goméria inrial m virud do movimno do êndulo. Ao onidrar a não-linaridad, o ima aa a não ouir uma olução fhada. Aim, dv- rourar uma olução
6 Roa do Sima Não-Linar A quaçõ d movimno 4.1 arnam não-linaridad goméria inrial m virud do movimno do êndulo. Ao onidrar a não-linaridad, o ima aa a não ouir uma olução fhada. Aim, dv- rourar uma olução
Cálculo de Autovalores, Autovetores e Autoespaços Seja o operador linear tal que. Por definição,, com e. Considere o operador identidade tal que.
 AUTOVALORES E AUTOVETORES Dfiniçõs Sja um oprador linar Um vtor, é dito autovtor, vtor próprio ou vtor caractrístico do oprador T, s xistir tal qu O scalar é dnominado autovalor, valor próprio ou valor
AUTOVALORES E AUTOVETORES Dfiniçõs Sja um oprador linar Um vtor, é dito autovtor, vtor próprio ou vtor caractrístico do oprador T, s xistir tal qu O scalar é dnominado autovalor, valor próprio ou valor
FENOMENOS DE TRANSPORTE 2 o Semestre de 2013 Prof. Maurício Fabbri
 FENOMENOS DE TRANSPORTE o Smsr d 03 Prof. Maurício Fabbri 3ª SÉRIE DE EXERCÍCIOS Transpor d calor por convcção O ransin ponncial simpls Consrvação da nrgia 0-3. O coficin d ransfrência d calor Lia o marial
FENOMENOS DE TRANSPORTE o Smsr d 03 Prof. Maurício Fabbri 3ª SÉRIE DE EXERCÍCIOS Transpor d calor por convcção O ransin ponncial simpls Consrvação da nrgia 0-3. O coficin d ransfrência d calor Lia o marial
2. Processo Estocástico para o Preço do Gás Natural
 . Proco ocáico para o Prço do Gá Naural Viando proporcionar uma ba para a comprnão do fundamno da modologia d drminação d prço do GN, é analiado o modlo d doi faor d chwarz mih 000 qu pod r uilizado para
. Proco ocáico para o Prço do Gá Naural Viando proporcionar uma ba para a comprnão do fundamno da modologia d drminação d prço do GN, é analiado o modlo d doi faor d chwarz mih 000 qu pod r uilizado para
Capítulo 3 Transmissão de Sinais e Filtragem
 Capíulo 3 Transmissão d Sinais Filragm 3.1 Rsposa d Sismas Linars Invarians no Tmpo No diagrama d blocos da Figura 3.1-1, é o sinal d nrada é o sinal d saída. Elmnos qu armaznam nrgia ouros ios inrnos
Capíulo 3 Transmissão d Sinais Filragm 3.1 Rsposa d Sismas Linars Invarians no Tmpo No diagrama d blocos da Figura 3.1-1, é o sinal d nrada é o sinal d saída. Elmnos qu armaznam nrgia ouros ios inrnos
Justifique todas as passagens
 ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
1. (2,0) Um cilindro circular reto é inscrito em uma esfera de raio r. Encontre a maior área de superfície possível para esse cilindro.
 Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Universidade Salvador UNIFACS Cursos de Engenharia Métodos Matemáticos Aplicados / Cálculo Avançado / Cálculo IV Profa: Ilka Rebouças Freire
 Univeridade Salvador UNIFACS Curo de Engenharia Método Matemático Aplicado / Cálculo Avançado / Cálculo IV Profa: Ila Rebouça Freire A Tranformada de Laplace Texto 0: A Tranformada Invera. A Derivada da
Univeridade Salvador UNIFACS Curo de Engenharia Método Matemático Aplicado / Cálculo Avançado / Cálculo IV Profa: Ila Rebouça Freire A Tranformada de Laplace Texto 0: A Tranformada Invera. A Derivada da
FUNÇÕES DE UMA VARIÁVEL COMPLEXA
 FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
Transformada Inversa de Laplace. Prof. Eng. Antonio Carlos Lemos Júnior
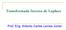 Tanfomada Inva d Lalac Pof Eng nonio Calo Lmo Júnio GEND Tanfomada Inva d Lalac Excício Conol d Sima Mcânico Tanfomada Inva d Lalac Obivo: O obivo da ção é faz uma odução à Tanfomada Inva d Lalac ua alicação
Tanfomada Inva d Lalac Pof Eng nonio Calo Lmo Júnio GEND Tanfomada Inva d Lalac Excício Conol d Sima Mcânico Tanfomada Inva d Lalac Obivo: O obivo da ção é faz uma odução à Tanfomada Inva d Lalac ua alicação
A DERIVADA DE UM INTEGRAL
 A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,
A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,
Sinais e Sistemas Lineares
 ES 43 Sinais Sismas Sinais Sismas Linars Prof. Aluizio Fauso Ribiro Araújo Dpo. of Sismas d Compuação Cnro d Informáica - UFPE Capíulo Sinais Sismas Eng. da Compuação Conúdo Sinais Tamanho d um Sinal Opraçõs
ES 43 Sinais Sismas Sinais Sismas Linars Prof. Aluizio Fauso Ribiro Araújo Dpo. of Sismas d Compuação Cnro d Informáica - UFPE Capíulo Sinais Sismas Eng. da Compuação Conúdo Sinais Tamanho d um Sinal Opraçõs
ANÁLISE MATEMÁTICA IV A =
 Instituto uprior Técnico Dpartamnto d Matmática cção d Álgbra Anális ANÁLIE MATEMÁTICA IV FICHA 5 ITEMA DE EQUAÇÕE LINEARE E EQUAÇÕE DE ORDEM UPERIOR À PRIMEIRA () Considr a matriz A 3 3 (a) Quais são
Instituto uprior Técnico Dpartamnto d Matmática cção d Álgbra Anális ANÁLIE MATEMÁTICA IV FICHA 5 ITEMA DE EQUAÇÕE LINEARE E EQUAÇÕE DE ORDEM UPERIOR À PRIMEIRA () Considr a matriz A 3 3 (a) Quais são
Aula Expressão do produto misto em coordenadas
 Aula 15 Nsta aula vamos xprssar o produto misto m trmos d coordnadas, analisar as propridads dcorrnts dssa xprssão fazr algumas aplicaçõs intrssants dos produtos vtorial misto. 1. Exprssão do produto misto
Aula 15 Nsta aula vamos xprssar o produto misto m trmos d coordnadas, analisar as propridads dcorrnts dssa xprssão fazr algumas aplicaçõs intrssants dos produtos vtorial misto. 1. Exprssão do produto misto
Capítulo IV TRANSFORMADAS DE LAPLACE
 Cpíulo IV TRANSFORMADAS DE LAPLACE Cpíulo IV Trnormd d Lplc Cpíulo IV O méodo d rnormd d Lplc rolv quçõ dirncii corrpondn problm d vlor inicil problm d vlor ronir O proco d olução coni m rê po principi:
Cpíulo IV TRANSFORMADAS DE LAPLACE Cpíulo IV Trnormd d Lplc Cpíulo IV O méodo d rnormd d Lplc rolv quçõ dirncii corrpondn problm d vlor inicil problm d vlor ronir O proco d olução coni m rê po principi:
EQUAÇÕES DIFERENCIAIS NOTAS DE AULA
 Minisério da Educação Univrsidad Tcnológica Fdral do Paraná Campus Curiiba Grência d Ensino Psquisa Dparamno Acadêmico d Mamáica EQUAÇÕES DIFERENCIAIS NOTAS DE AULA Prof. a Paula Francis Bnvids Equaçõs
Minisério da Educação Univrsidad Tcnológica Fdral do Paraná Campus Curiiba Grência d Ensino Psquisa Dparamno Acadêmico d Mamáica EQUAÇÕES DIFERENCIAIS NOTAS DE AULA Prof. a Paula Francis Bnvids Equaçõs
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
VARIÁVEIS ALEATÓRIAS DISCRETAS. Vamos agora analisar em detalhe algumas variáveis aleatórias discretas, nomeadamente:
 98 99 VARIÁVEIS ALEATÓRIAS DISCRETAS Vamos agora analisar m dalh algumas variávis alaórias discras, nomadamn: uniform Brnoulli binomial binomial ngaiva (ou d Pascal) gomérica hirgomérica oisson mulinomial
98 99 VARIÁVEIS ALEATÓRIAS DISCRETAS Vamos agora analisar m dalh algumas variávis alaórias discras, nomadamn: uniform Brnoulli binomial binomial ngaiva (ou d Pascal) gomérica hirgomérica oisson mulinomial
= 0. O campo electrostático não tem fontes de circulação, não roda.
 Aula Tórica nº 3-7 Prof. Rsponsávl: Mário J. Pinhiro 1. Opradors difrnciais (conclusão) Exrcício 1: Provar qu rot gradu = 1. Usando coordnadas cartsianas. rot u x u y u z U U grad U = = u x +... = x y
Aula Tórica nº 3-7 Prof. Rsponsávl: Mário J. Pinhiro 1. Opradors difrnciais (conclusão) Exrcício 1: Provar qu rot gradu = 1. Usando coordnadas cartsianas. rot u x u y u z U U grad U = = u x +... = x y
r = (x 2 + y 2 ) 1 2 θ = arctan y x
 Sção 0: Equação d Laplac m coordnadas polars Laplaciano m coordnadas polars. Sja u = ux, y uma função d duas variávis. Dpndndo da rgião m qu a função stja dfinida, pod sr mais fácil trabalhar com coordnadas
Sção 0: Equação d Laplac m coordnadas polars Laplaciano m coordnadas polars. Sja u = ux, y uma função d duas variávis. Dpndndo da rgião m qu a função stja dfinida, pod sr mais fácil trabalhar com coordnadas
6.1: Transformada de Laplace
 6.: Tranformada de Laplace Muio problema práico da engenharia envolvem iema mecânico ou elérico ob ação de força deconínua ou de impulo. Para ee ipo de problema, o méodo vio em Equaçõe Diferenciai I, ão
6.: Tranformada de Laplace Muio problema práico da engenharia envolvem iema mecânico ou elérico ob ação de força deconínua ou de impulo. Para ee ipo de problema, o méodo vio em Equaçõe Diferenciai I, ão
estados. Os estados são influenciados por seus próprios valores passados x
 3 Filtro d Kalman Criado por Rudolph E. Kalman [BROWN97] m 1960, o filtro d Kalman (FK) foi dsnvolvido inicialmnt como uma solução rcursiva para filtragm linar d dados discrtos. Para isto, utiliza quaçõs
3 Filtro d Kalman Criado por Rudolph E. Kalman [BROWN97] m 1960, o filtro d Kalman (FK) foi dsnvolvido inicialmnt como uma solução rcursiva para filtragm linar d dados discrtos. Para isto, utiliza quaçõs
Funções reais de n variáveis reais
 Apoio às aulas MAT II 8--6 INSTITUTO SUPERIOR DE CONTABILIDADE E ADMINISTRAÇÃO DE LISBOA LICENCIATURA EM GESTÃO MATEMÁTICA II APOIO ÀS AULAS DE FUNÇÕES REAIS DE MAIS DE UMA VARIÁVEL REAL 5/6 Manul Marins
Apoio às aulas MAT II 8--6 INSTITUTO SUPERIOR DE CONTABILIDADE E ADMINISTRAÇÃO DE LISBOA LICENCIATURA EM GESTÃO MATEMÁTICA II APOIO ÀS AULAS DE FUNÇÕES REAIS DE MAIS DE UMA VARIÁVEL REAL 5/6 Manul Marins
4. Modelos matemáticos de crescimento
 2 Sumário (3ª aula) Exrcícios d consolidação (coninuação) 4. Modlos mamáicos d crscimno 4..Progrssão ariméica (variação absolua consan) 4.2.Progrssão goméricas (variação rlaiva consan) Exrcício 2) Compaibiliz
2 Sumário (3ª aula) Exrcícios d consolidação (coninuação) 4. Modlos mamáicos d crscimno 4..Progrssão ariméica (variação absolua consan) 4.2.Progrssão goméricas (variação rlaiva consan) Exrcício 2) Compaibiliz
Total. UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Departamento de Matemática Pura e Aplicada MAT Turma C /2 Prova da área IIA
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma C - 7/ Prova da área IIA - 5 6 7 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Deparameno de Maemáica Pura e Aplicada MAT68 - Turma C - 7/ Prova da área IIA - 5 6 7 Toal Nome: Regra Gerai: Não é permiido o uo de calculadora, elefone ou
Módulo III Capacitores
 laudia gina ampos d arvalho Módulo apacitors apacitors: Dnomina-s condnsador ou capacitor ao conjunto d condutors dilétricos arrumados d tal manira qu s consiga armaznar a máxima quantidad d cargas létricas.
laudia gina ampos d arvalho Módulo apacitors apacitors: Dnomina-s condnsador ou capacitor ao conjunto d condutors dilétricos arrumados d tal manira qu s consiga armaznar a máxima quantidad d cargas létricas.
R é o conjunto dos reais; f : A B, significa que f é definida no conjunto A (domínio - domain) e assume valores em B (contradomínio range).
 f : A B, significa qu f é dfinida no conjunto A (domínio - domain) assum valors m B (contradomínio rang). R é o conjunto dos rais; R n é o conjunto dos vtors n-dimnsionais rais; Os vtors m R n são colunas
f : A B, significa qu f é dfinida no conjunto A (domínio - domain) assum valors m B (contradomínio rang). R é o conjunto dos rais; R n é o conjunto dos vtors n-dimnsionais rais; Os vtors m R n são colunas
3.5 Métodos Numéricos para a Solução de Problemas de Contorno
 3.5 Métd Numéric ara a Sluçã d Prblma d Cntrn Equaçõ difrnciai rdinária Eml 3.7. Difuã-raçã m uma artícula catalítica ra: Figura 3.6. Partícula catalítica férica. Balanç d maa: (tad tacinári, itérmic)
3.5 Métd Numéric ara a Sluçã d Prblma d Cntrn Equaçõ difrnciai rdinária Eml 3.7. Difuã-raçã m uma artícula catalítica ra: Figura 3.6. Partícula catalítica férica. Balanç d maa: (tad tacinári, itérmic)
Tabela 1 Relações tensão-corrente, tensão-carga e impedância para capacitoers, resistores e indutores.
 Modelagem Maemáica MODELOS MATEMÁTICOS DE CIRCUITOS ELÉTRICOS O circuio equivalene à rede elérica com a quai rabalhamo coniem baicamene em rê componene lineare paivo: reiore, capaciore e induore. A Tabela
Modelagem Maemáica MODELOS MATEMÁTICOS DE CIRCUITOS ELÉTRICOS O circuio equivalene à rede elérica com a quai rabalhamo coniem baicamene em rê componene lineare paivo: reiore, capaciore e induore. A Tabela
Enunciados equivalentes
 Lógica para Ciência da Computação I Lógica Matmática Txto 6 Enunciados quivalnts Sumário 1 Equivalência d nunciados 2 1.1 Obsrvaçõs................................ 5 1.2 Exrcícios rsolvidos...........................
Lógica para Ciência da Computação I Lógica Matmática Txto 6 Enunciados quivalnts Sumário 1 Equivalência d nunciados 2 1.1 Obsrvaçõs................................ 5 1.2 Exrcícios rsolvidos...........................
Apêndice Matemático. Se este resultado for inserido na expansão inicial (A1.2), resulta
 A Séris Intgrais d Fourir Uma função priódica, d príodo 2, = + 2 pod sr xpandida m séri d Fourir no intrvalo <
A Séris Intgrais d Fourir Uma função priódica, d príodo 2, = + 2 pod sr xpandida m séri d Fourir no intrvalo <
TRANSFORMADA DE LAPLACE
 TRANSFORMADA DE LAPLACE Nt cpítulo trtmo d um método d rolução d quçõ difrncii linr d ordm n com coficint contnt condiçõ inici, ou j, trnformd d Lplc.. Dfinição Sj f(t) um função dd pr t, uponhmo qu f
TRANSFORMADA DE LAPLACE Nt cpítulo trtmo d um método d rolução d quçõ difrncii linr d ordm n com coficint contnt condiçõ inici, ou j, trnformd d Lplc.. Dfinição Sj f(t) um função dd pr t, uponhmo qu f
10. EXERCÍCIOS (ITA-1969 a ITA-2001)
 . EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
. EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
UTFPR Termodinâmica 1 Análise Energética para Sistemas Abertos (Volumes de Controles)
 UTFPR Trmodinâmica 1 Análi Enrgética para Sitma Abrto (Volum d Control) Princípio d Trmodinâmica para Engnharia Capítulo 4 Part 1 Objtivo Dnvolvr Ilutrar o uo do princípio d conrvação d maa d nrgia na
UTFPR Trmodinâmica 1 Análi Enrgética para Sitma Abrto (Volum d Control) Princípio d Trmodinâmica para Engnharia Capítulo 4 Part 1 Objtivo Dnvolvr Ilutrar o uo do princípio d conrvação d maa d nrgia na
TEORMA DA FUNÇÃO INVERSA. Teorema 2. Dada f : Ω ab
 TEORMA DA FUNÇÃO INVERSA Torma Dada f : Ω ab R n R n (n função com drivadas parciais contínuas m P Ω Suponhamos qu dt(jf((p Então xist ɛ > uma bola abrta B B(P ɛ uma função g : B R n (B f(ω com todas as
TEORMA DA FUNÇÃO INVERSA Torma Dada f : Ω ab R n R n (n função com drivadas parciais contínuas m P Ω Suponhamos qu dt(jf((p Então xist ɛ > uma bola abrta B B(P ɛ uma função g : B R n (B f(ω com todas as
Índices Físico do Solo e Estado das areias e argilas
 Univridad d Várza Grand Índic Fíico do Solo Etado da aria argila Diciplina: Mcânica do olo Prof.: Marcl Sna Campo nagl@gmail.com Índic Fíico Elmnto Contituint d um olo O olo é um matrial contituído por
Univridad d Várza Grand Índic Fíico do Solo Etado da aria argila Diciplina: Mcânica do olo Prof.: Marcl Sna Campo nagl@gmail.com Índic Fíico Elmnto Contituint d um olo O olo é um matrial contituído por
Transformada de Fourier em tempo discreto
 Capítulo 2*: Transformada d Fourir m tmpo discrto Prof. Alan Ptrônio Pinhiro Univrsidad Fdral d Ubrlândia Faculdad d Engnharia Elétrica alanptronio@ufu.br *Basado no capítulo 5 do livro txto: Sinais Sistmas
Capítulo 2*: Transformada d Fourir m tmpo discrto Prof. Alan Ptrônio Pinhiro Univrsidad Fdral d Ubrlândia Faculdad d Engnharia Elétrica alanptronio@ufu.br *Basado no capítulo 5 do livro txto: Sinais Sistmas
