Funções reais de n variáveis reais
|
|
|
- Sabrina Assunção Lopes
- 6 Há anos
- Visualizações:
Transcrição
1 Apoio às aulas MAT II 8--6 INSTITUTO SUPERIOR DE CONTABILIDADE E ADMINISTRAÇÃO DE LISBOA LICENCIATURA EM GESTÃO MATEMÁTICA II APOIO ÀS AULAS DE FUNÇÕES REAIS DE MAIS DE UMA VARIÁVEL REAL 5/6 Manul Marins Carla Marino Ana Jorg Funçõs rais d n variávis rais Cama-s unção ral d variávis rais a oda a aplicação d um conjuno R R. Ao conjuno cama-s domínio da unção. Sjam R. As variávis são as variávis indpndns é a variávl dpndn. Ao conjuno R: cama-s conradomínio d. Cama-s gráico d ao subconjuno dr : : 8--6 CI/ FR 5/6
2 Apoio às aulas MAT II 8--6 Funçõs rais d n variávis rais Noas: - S a unção or dinida por uma prssão analíica o su domínio é o conjuno d ponos ond a prssão analíica sará dinida. - o gráico d é uma curva d R. S o gráico d é uma supríci dr. Por simpliicação odo o capíulo rá por bas unçõs d variávis podndo acilmn sr gnralizado para as n variávis CI/ FR Domínio Emplo - Drmin o domínio da unção D D ln ( ) {( ) IR :( ) ( > ) ( ) } {( ) IR :( ) ( < ) ( ) } A primira quação rprsna o rior d uma circunrência d raio ; a sgunda quação rprsna o inrior d uma circunrência d raio ; a rcira quação rprsna a bissriz dos quadrans impars CI/ FR 5/6
3 Apoio às aulas MAT II 8--6 Domínio Emplo - Rprsnação gomérica: É considrada válida a ára marcada a amarlo a circunrência inrior cada com a cção dos ponos da bissriz CI/5FR5 Domínio Emplo - Drmin o domínio rprsn-o gomricamn da D D sguin unção ( ) ln {( ) IR :( > ) ( ) } {( ) IR :( ) ( ) } {( ) IR :( ) ( [ ;])} Rprsnação gomérica: 8--6 CI/6 FR6 5/6
4 Apoio às aulas MAT II 8--6 Domínio Emplo - Drmin o domínio rprsn-o gomricamn da unção ( ) ln D D ( ) IR : > ( ) {( ) IR :[(( ) ( > ) ) ( ( ) ( < ) )] ( < ) } Rprsnação gomérica: 8--6 CI/7 FR7 Limi coninuidad Diz-s qu L é o limi da unção quando nd para rprsna-s por quando L Lim ( ) ( ab) ( ) δ > ε > : D ( ) ( ab ) < ε ( ) L < δ NOTA: Em R as vizinanças d um pono são círculos dinidos no plano sndo as disâncias mdidas pla órmula uclidiana (co s ouvr indicação prssa m conrário) rprsnam-s da orma aprsnada CI/8 FR8 5/6
5 Apoio às aulas MAT II 8--6 Limi coninuidad As propridads opraórias dos limis o orma da unicidad concidos para unçõs rais d uma variávl ral são igualmn válidos para unçõs dnvariávis indpndns. Diz-s qu uma unção é conínua no pono s. sá dinida no pono com. m limi no pono ss limi é igual a é ó lim ( ) ( ) ( ) 8--6 CI/9 FR9 Drivadas parciais Dada a unção d duas variávis indpndns é possívl drivar m unção d cada uma dlas. Dsigna-s por drivada parcial m ordm a da unção num pono rprsna-s por ( ) Como sndo ( ab) Lim ( b) ( ab) ( a b) ( ab) a Lim a Dsigna-s por drivada parcial m ordm a da unção num pono rprsna-s por ( ) Como sndo ( ab) Lim ( a ) ( ab) ( ab ) ( ab) b Lim a 8--6 CI/ FR 5/6 5
6 Apoio às aulas MAT II 8--6 Drivadas parciais Camam-s drivadas parciais da unção às unçõs ( ) ( ) qu êm por domínio o conjuno dos ponos ond ( ) m as rspivas drivadas parciais inias m cada pono domínio oma os valors ( ) ( ). dss Emplo - Drmin usando a dinição as drivadas parciais da unção dinida por no pono () ( ) ( ) Lim Lim ( ) ( ) ( ) ( ) ( ) ( ) 7 6 ( )( ) Lim Lim 7 Lim ( ) CI/ FR Emplo Coninuação ( ) Lim Drivadas parciais ( ) ( ) ( ) ( ) Lim Lim ( ) Lim 7 Lim 7 Lim NOTA: As rgras d drivação manêm-s vrdadiras. ( ) Torma: S uma unção m drivadas parciais conínuas num pono la é conínua nss pono 8--6 CI/ FR 5/6 6
7 Apoio às aulas MAT II 8--6 Drivadas parciais Emplo - Drmin a drivada parcial m ordm a da unção Usando a dinição: ( ) ( ) ( ) ( ) ( ) Lim Lim Lim ( ) Lim Lim Lim 8--6 CI/ FR Drivadas parciais Usando as rgras d drivação (m ordm a sa compora-s como variávl como uma qualqur consan): ( ) ( ) ( ) ( ) 8--6 CI/ FR 5/6 7
8 Apoio às aulas MAT II / CI/5 FR5 CI/5 Drivadas parciais Emplo - Drmin as drivadas parciais da unção ln Usando as rgras d drivação m ordm a sa compora-s como variávl como uma qualqur consan: ln 8--6 CI/6 FR6 CI/6 Drivadas parciais Coninuação do Ercício - Em ordm a sa compora-s como variávl como uma qualqur consan: ln
9 Apoio às aulas MAT II / CI/7 FR7 CI/7 Drivada da Função composa Considr-s a unção sjam Ψ. Num ponoa sjam Ψ. Enão a drivada da unção m ordm a num pono é dada por a a a Considr-s a unção sjam Ψ. Num pono sjam Ψ. Enão as drivadas parciais da unção m ordm a num pono são dadas por ab ab ab ab r ab r ab r 8--6 CI/8 FR8 CI/8 Drivada da Função composa Emplo - Sja sjam. Calcul. ; ; ; ;
10 Apoio às aulas MAT II 8--6 Drivada da Função composa Emplo - Sja sjam ln. w Calcul. ( ) ; ( ) w w ( w) ; ( w) ; ( w) ; ( w) ( w) ( ) ( w) ( ) ( w) ( ) w w w w ; w w w w w w ( ln w) ( ln w) 8--6 CI/9 FR9 w w w w ( w) ( ) ( w) ( ) ( w) w w ( ) w w w ( ln w) 6 w ; 6 Função Implícia Dada a quação do ipo Φ ond a cada par d valors d do domínio da quação corrspond um um só valor d z diz-s qu a quação din d orma implícia a unção. Torma da Função Implícia Sja R R um abro : R uma unção al qu:.. (a unção rspivas drivadas d ª ordm são coninuas).. Enão din impliciamn a variávl como unção das variávis numa vizinança do pono ( ). ( ) ( ) ( ) ( ) ( ) ( ) 8--6 CI/ FR 5/6
11 Apoio às aulas MAT II 8--6 Função Implícia Emplo Considr a unção ln. Mosr qu a quação φ din impliciamn como unção das variávis numa vizinança do pono () calcul para ss pono. º Passo: Vriicar qu o pono P prnc à curvaφ ϕ ( ) ln º Passo A unção assim como as suas ª drivadas são coninuas (unção polinomial unção logarímica) logo a unção é d class. ϕ ϕ z º Passo: ( ) (?) z ϕ z z ( ) ( ) Enão a unção din impliciamn como unção das variávis numa vizinança do pono () 8--6 CI/ FR Enão: z ( ) ( ) ϕ ϕ ϕ z ϕ ( ) ( ) ( ) ( ) Função Implícia z z z z z ( ) ( ) 8--6 CI/ FR 5/6
12 Apoio às aulas MAT II 8--6 Função Homogéna Uma unção ( ) diz-s omogéna d grau s só s R R ( ) Emplo - Mosr qu a unção é omogéna dscubra o su grau d omognidad. ( ) ( ) ( ) Logo a unção é omogéna d grau CI/ FR Função Homogéna Emplo Rlaivamn à unção do mplo vriiqu a sguin igualdad (d Eulr) Ond é uma unção omogéna d grau ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( ) ( ) 8--6 CI/ FR 5/6
13 Apoio às aulas MAT II 8--6 Drivadas Parciais d Ordm Suprior à ª Dada a unção s isirm num pono s sas admiirm drivada m ordm rspivamn a a num pono a ssa drivada cama-s drivada d sgunda ordm d m ordma oua rspivamn. Rprsnam-s por S admiir drivada m ordm a num pono D a ssa drivada cama-s drivada d sgunda ordm d m ordm a a. D igual modo s din a drivada d sgunda ordm d a m ordm a. Esas úlimas drivadas camam-s drivadas cruzadas CI/5 FR5 Drivadas Parciais d Ordm Suprior à ª Assim rprsnadas por: as drivadas parciais d ª ordm da unção são ( ) O dsnvolvimno anrior mosra qu o númro d drivadas parciais crsc ponncialmn m unção da ordm ou sja: Drivadas parciais d ª ordm ; }... Drivadas parciais d ª ordm ; Drivadas parciais d ª ordm 8 ; c CI/6 FR6 5/6
14 Apoio às aulas MAT II 8--6 Drivadas Parciais d Ordm Suprior à ª Emplo - Drmin as drivadas parciais d ª ordm da unção ( ) ( ) ( ) ( ) ( ) ( ) ( ) 8--6 CI/7 FR7 Drivadas Parciais d Ordm Suprior à ª Torma d Scwarz Sja D R R um pono inrior a D. S as parciais drivadas são dinidas numa vizinança do pono s é conínua m não ambém sá dinida m ab ( ) 8--6 CI/8 FR8 5/6
15 Apoio às aulas MAT II 8--6 Drivadas Parciais d Ordm Suprior à ª Dada a unção dsigna-s por Mariz Hssiana a mariz H ( ) ( ) Viso raar-s d uma mariz quadrada é possívl alar no su drminan dsignado por Hssiano. Torma S a unção vriica o orma d Scwarz a mariz Hssiana é uma mariz simérica CI/9 FR9 Ermos rlaivos Sja : R R um pono inrior a. i) diz-s um máimo rlaivo d s isir uma vizinança d ab al qu. i) diz-s um máimo absoluo d s iii) diz-s um mínimo rlaivo d s isir uma vizinança d al qu. iv) diz-s um mínimo absoluo d s 8--6 CI/ FR 5/6 5
16 Apoio às aulas MAT II 8--6 Ermos rlaivos Sjam R R ( ). S diz-s qu é um pono criico ou um pono d sacionaridad d. Torma Sja R R suponamos qu m um rmo rlaivo no pono prncn ao inrior d qu odas as drivadas parciais d ism no pono ( ). Enão é um pono críico d CI/ FR Torma Ermos rlaivos Dada a unção sja pono críico da unção sja H mariz Hssiana associada. Enão: i. S < > não ( ) é um máimo rlaivo ii. d. S > > não é um mínimo rlaivo d. iii. S < não é um pono d sla d. iv. S nada s pod concluir sobr o pono CI/ FR 5/6 6
17 Apoio às aulas MAT II / CI/ FR Ermos rlaivos CI/ Emplo - Drmin classiiqu os rmos rlaivos da unção dinida por. Ponos críicos: CI/ FR Ermos rlaivos CI/ Emplo Coninuação Os ponos () (9) são ponos críicos da unção; Pono O pono é um pono d sla. Pono (9) Logo 9 5 é um máimo da unção. 9 6 < H < > H
18 Apoio às aulas MAT II / CI/5 FR5 Ermos rlaivos CI/5 Emplo - Sja a unção dinida por. Vriiqu qu a unção m rmos rlaivos classiiqu-os. Ponos críicos: 8--6 CI/6 FR6 Ermos rlaivos CI/6 Emplo Coninuação - Os ponos ( ) ( ) () são ponos críicos da unção. Pono ( ) Logo é um máimo rlaivo da unção. Pono ( ): Enão é um máimo rlaivo da unção. 96 < > H 96 < > H
19 Apoio às aulas MAT II / CI/7 FR7 Ermos rlaivos CI/7 Emplo Coninuação Pono (): Esudo diro - Euando o sudo por aproimação do pono ao longo das ras : : Os limis dircionais êm sinais conrários logo ism valors maiors mnors qu a unção m orno do pono (); Assim () é um pono d sla da unção. H 8--6 CI/8 FR8 Ermos rlaivos CI/8 Emplo - Sja a unção dinida pla sguin prssão. Vriiqu qu m rmos rlaivos classiiqu-os { } : IR D ) ( D
20 Apoio às aulas MAT II 8--6 Emplo Coninuação Ermos rlaivos Como não prnc ao domínio o pono () é o único pono críico da unção. H ( ) 6 ( ) > Logo 6 é um mínimo rlaivo da unção. 6 > 8--6 CI/9 FR9 Bibliograia. Ana Sá Bno Louro.. Cálculo Dirncial m R Uma inrodução. Dparamno d Mamáica. FCT/UNL.. Larson Hoslr Edwards. 6. Cálculo. Volum. Oiava Edição. McGraw- Hill CI/ FR 5/6
Derivadas parciais de ordem superior à primeira. Teorema de Schwarz.
 Drivadas parciais d ordm suprior à primira. Torma d Scwarz. As drivadas das primiras drivadas são as sgundas drivadas assim sucssivamnt. Então, para uma unção d duas variávis podmos considrar, s istirm,
Drivadas parciais d ordm suprior à primira. Torma d Scwarz. As drivadas das primiras drivadas são as sgundas drivadas assim sucssivamnt. Então, para uma unção d duas variávis podmos considrar, s istirm,
INSTITUTO POLITÉCNICO DE VISEU. f x = x em relação à partição do intervalo. em 4 subintervalos de igual amplitude e tal que o ponto ω
 INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA Dparamno Mamáica Disciplina Anális Mamáica Curso Engnharia Informáica º Smsr º Ficha nº : Cálculo ingral m IR Drmin a soma d Rimann da função
INSTITUTO POLITÉCNICO DE VISEU ESCOLA SUPERIOR DE TECNOLOGIA Dparamno Mamáica Disciplina Anális Mamáica Curso Engnharia Informáica º Smsr º Ficha nº : Cálculo ingral m IR Drmin a soma d Rimann da função
log 2, qual o valor aproximado de 0, 70
 UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1/3
 FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsn o s raciocínio d orma clara, indicando odos os cálclos q ivr d ar odas as jsiicaçõs ncssárias. Qando, para m rslado, não é pdida ma aproimação,
FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsn o s raciocínio d orma clara, indicando odos os cálclos q ivr d ar odas as jsiicaçõs ncssárias. Qando, para m rslado, não é pdida ma aproimação,
Grupo I. 1) Calcule os integrais: (4.5) 2) Mostre que toda a equação do tipo yf( xydx ) xg( xydy ) 0
 Mamáica III / ºSmsr Grupo I ) Calcul os ingrais: a) b) D () ( ) dd sndo D d d d d (.) ) Mosr qu oda a quação do ipo f( d ) g( d ) s ransforma numa quação d variávis sparadas fazndo a subsiuição (.) ) A
Mamáica III / ºSmsr Grupo I ) Calcul os ingrais: a) b) D () ( ) dd sndo D d d d d (.) ) Mosr qu oda a quação do ipo f( d ) g( d ) s ransforma numa quação d variávis sparadas fazndo a subsiuição (.) ) A
TÓPICOS. EDO de variáveis separadas. EDO de variáveis separáveis. EDO homogénea. 2. Equações Diferenciais de 1ª Ordem.
 ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ - UTFPR CAMPUS CORNÉLIO PROCÓPIO
 MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
Seja f uma função r.v.r. de domínio D e seja a R um ponto de acumulação de
 p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
Questão. Sinais periódicos e não periódicos. Situação limite. Transformada de Fourier de Sinais Contínuos
 Qusão Srá possívl rprsnar sinais não priódicos como soma d xponnciais? ransformada d Fourir d Sinais Conínuos jorg s. marqus, jorg s. marqus, Sinais priódicos não priódicos Siuação limi Um sinal não priódico
Qusão Srá possívl rprsnar sinais não priódicos como soma d xponnciais? ransformada d Fourir d Sinais Conínuos jorg s. marqus, jorg s. marqus, Sinais priódicos não priódicos Siuação limi Um sinal não priódico
VI- MOMENTOS E FUNÇÃO GERATRIZ DE MOMENTO.
 VI- MOMENTOS E FUNÇÃO GERATRIZ DE MOMENTO. 6.- ESPERANÇA DE UMA FUNÇÃO: CASO DISCRETO: E[g()] i g( i )(i ) CASO CONTÍNUO: E [g()] 6.- MOMENTO: + - g(). () d DEFINIÇÃO DE MOMENTOS: srado Din-s momno d uma
VI- MOMENTOS E FUNÇÃO GERATRIZ DE MOMENTO. 6.- ESPERANÇA DE UMA FUNÇÃO: CASO DISCRETO: E[g()] i g( i )(i ) CASO CONTÍNUO: E [g()] 6.- MOMENTO: + - g(). () d DEFINIÇÃO DE MOMENTOS: srado Din-s momno d uma
Cálculo Numérico. Integração Numérica. Prof: Reinaldo Haas
 Cálculo Numérico Intgração Numérica Pro: Rinaldo Haas Intgração Numérica Em dtrminadas situaçõs, intgrais são diícis, ou msmo impossívis d s rsolvr analiticamnt. Emplo: o valor d é conhcido apnas m alguns
Cálculo Numérico Intgração Numérica Pro: Rinaldo Haas Intgração Numérica Em dtrminadas situaçõs, intgrais são diícis, ou msmo impossívis d s rsolvr analiticamnt. Emplo: o valor d é conhcido apnas m alguns
MESTRADO EM MACROECONOMIA e FINANÇAS Disciplina de Computação. Aula 07. Prof. Dr. Marco Antonio Leonel Caetano
 MESTRADO EM MACROECONOMIA FINANÇAS Disiplina d Compuação Aula 7 Prof. Dr. Maro Anonio Lonl Caano Guia d Esudo para Aula 7 Vors Linarmn Indpndns - Vrifiação d vors LI - Cálulo do Wronsiano Equaçõs Difrniais
MESTRADO EM MACROECONOMIA FINANÇAS Disiplina d Compuação Aula 7 Prof. Dr. Maro Anonio Lonl Caano Guia d Esudo para Aula 7 Vors Linarmn Indpndns - Vrifiação d vors LI - Cálulo do Wronsiano Equaçõs Difrniais
( 1). β β. 4.2 Funções Densidades Con2nuas
 4 Funçõs Dnsidads Connuas Dnsidad Eponncial A dnsidad ponncial é u:lizada comumn para sablcr sruuras d probabilidads m primnos cujos nos são siuados na ra ral [, ] Uma aplicação gral comum corrspond à
4 Funçõs Dnsidads Connuas Dnsidad Eponncial A dnsidad ponncial é u:lizada comumn para sablcr sruuras d probabilidads m primnos cujos nos são siuados na ra ral [, ] Uma aplicação gral comum corrspond à
7. Aplicação do Principio do Máximo
 7. Aplicação do Principio do Máximo Ns capiulo vamos implmnar um algorimo qu uiliz a oria do Principio do Máximo para drminar o conjuno dos sados aingívis. Com o rsulados obidos vamos nar fazr um parallo
7. Aplicação do Principio do Máximo Ns capiulo vamos implmnar um algorimo qu uiliz a oria do Principio do Máximo para drminar o conjuno dos sados aingívis. Com o rsulados obidos vamos nar fazr um parallo
para Z t (lembre que = 1 B)
 Economria III ANE59 Lisa d Ercícios d Economria d Séris mporais Pro. Rogério Siva d Maos (Juho 6) Si: www.uj.br/rogrio_maos A. MODELOS ARIMA. Escrva por nso:. ARMA(,) para. ARMA(,) para X. ( B B ) Z (
Economria III ANE59 Lisa d Ercícios d Economria d Séris mporais Pro. Rogério Siva d Maos (Juho 6) Si: www.uj.br/rogrio_maos A. MODELOS ARIMA. Escrva por nso:. ARMA(,) para. ARMA(,) para X. ( B B ) Z (
Derivada Escola Naval
 Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
CÁLCULO I 2º Semestre 2011/2012. Duração: 1 hora e 30 minutos
 NOVA SCHOOL OF BSINESS AND ECONOMICS CÁLCLO I º Smsr / TESTE INTERMÉDIO Tópi d rsolução Abril Duração: ora miuos Não é prmiido o uso d calculadoras. Não pod dsagraar as olas do uciado. Rspoda d orma jusiicada
NOVA SCHOOL OF BSINESS AND ECONOMICS CÁLCLO I º Smsr / TESTE INTERMÉDIO Tópi d rsolução Abril Duração: ora miuos Não é prmiido o uso d calculadoras. Não pod dsagraar as olas do uciado. Rspoda d orma jusiicada
5.10 EXERCÍCIO pg. 215
 EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
Efeito da pressão decrescente da atmosfera com o aumento da altitude
 Efio da prssão dcrscn da amosfra com o aumno da aliud S lançarmos um projéil com uma vlocidad inicial suficinmn ala l aingirá aliuds ond o ar é mais rarfio do qu próximo à suprfíci da Trra Logo a rsisência
Efio da prssão dcrscn da amosfra com o aumno da aliud S lançarmos um projéil com uma vlocidad inicial suficinmn ala l aingirá aliuds ond o ar é mais rarfio do qu próximo à suprfíci da Trra Logo a rsisência
( ) π π. Corolário (derivada da função inversa): Seja f uma função diferenciável e injectiva definida num intervalo I IR.
 Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
FUNÇÕES DE UMA VARIÁVEL COMPLEXA
 FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
APONTAMENTOS DE COMPLEMENTOS DE MATEMÁTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA APONTAMENTOS DE COMPLEMENTOS DE MATEMÁTICA (REVISÕES SOBRE FUNÇÕES REAIS DE VARIÁVEL REAL) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Rvisõs sobr unçõs
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA APONTAMENTOS DE COMPLEMENTOS DE MATEMÁTICA (REVISÕES SOBRE FUNÇÕES REAIS DE VARIÁVEL REAL) ÁREA DEPARTAMENTAL DE ENGENHARIA CIVIL Rvisõs sobr unçõs
enquanto que um exemplo de e.d.p. é uma equação do tipo potencial
 6- EDO s: TEORIA E TRATAMENTO NUMÉRICO Inrodução Muios problmas imporans significaivos da ngnharia, das ciências físicas das ciências sociais, formulados m rmos mamáicos, igm a drminação d uma função qu
6- EDO s: TEORIA E TRATAMENTO NUMÉRICO Inrodução Muios problmas imporans significaivos da ngnharia, das ciências físicas das ciências sociais, formulados m rmos mamáicos, igm a drminação d uma função qu
Memorize as integrais imediatas e veja como usar a técnica de substituição.
 Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
CÁLCULO DIFERENCIAL E INTEGRAL II MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS VARIÁVEIS. Figura 1: Pontos de máximo e mínimo
 Introdução S CÁLCULO DIFERENCIAL E INTEGRAL II MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS VARIÁVEIS é uma unção d duas variávis ntão dizmos qu 1 a b é no máimo igual a a Gomtricamnt o gráico d tm um máimo quando:
Introdução S CÁLCULO DIFERENCIAL E INTEGRAL II MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS VARIÁVEIS é uma unção d duas variávis ntão dizmos qu 1 a b é no máimo igual a a Gomtricamnt o gráico d tm um máimo quando:
4. Modelos matemáticos de crescimento
 2 Sumário (3ª aula) Exrcícios d consolidação (coninuação) 4. Modlos mamáicos d crscimno 4..Progrssão ariméica (variação absolua consan) 4.2.Progrssão goméricas (variação rlaiva consan) Exrcício 2) Compaibiliz
2 Sumário (3ª aula) Exrcícios d consolidação (coninuação) 4. Modlos mamáicos d crscimno 4..Progrssão ariméica (variação absolua consan) 4.2.Progrssão goméricas (variação rlaiva consan) Exrcício 2) Compaibiliz
1.1 O Círculo Trigonométrico
 Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Teoria de Controle (sinopse) 4 Função de matriz. J. A. M. Felippe de Souza
 Toria d Conrol (sinops) 4 Função d mariz J. A. M. Flipp d Souza Função d mariz Primiramn vamos dfinir polinómio d mariz. Dfinição: Polinómio d mariz (quadrada) Sja p(λ)um polinómio m λd grau n (finio),
Toria d Conrol (sinops) 4 Função d mariz J. A. M. Flipp d Souza Função d mariz Primiramn vamos dfinir polinómio d mariz. Dfinição: Polinómio d mariz (quadrada) Sja p(λ)um polinómio m λd grau n (finio),
TÓPICOS. ordem; grau; curvas integrais; condições iniciais e fronteira. 1. Equações Diferenciais. Conceitos Gerais.
 Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
1 Capítulo 2 Cálc l u c lo l I ntegra r l l em m R
 píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos
píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos
Funções de Várias Variáveis (FVV) UFABC, 2019-Q1
 Funçõs d Várias Variávis (FVV UFABC, 209-Q Pr Hazard 4 Drivadas Toal, Dircional Parcial 4. Drivadas a rspio d um vor. Dfinição 4.. Sja A R n um abro, sja f: A R, P A v R n. Digamos qu f é drivávl (ou difrnciávl
Funçõs d Várias Variávis (FVV UFABC, 209-Q Pr Hazard 4 Drivadas Toal, Dircional Parcial 4. Drivadas a rspio d um vor. Dfinição 4.. Sja A R n um abro, sja f: A R, P A v R n. Digamos qu f é drivávl (ou difrnciávl
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES
 PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
ANALISE DE CIRCUITOS DE 1 a E 2 a. J.R. Kaschny ORDENS
 ANAISE DE IRUITOS DE a E a J.R. Kaschny ORDENS Inrodução As caracrísicas nsão-corrn do capacior do induor inroduzm as quaçõs difrnciais na anális dos circuios léricos. As is d Kirchhoff as caracrísicas
ANAISE DE IRUITOS DE a E a J.R. Kaschny ORDENS Inrodução As caracrísicas nsão-corrn do capacior do induor inroduzm as quaçõs difrnciais na anális dos circuios léricos. As is d Kirchhoff as caracrísicas
Capítulo V. Derivação. 5.1 Noção de derivada. Seja f uma função real de variável real. Definição: Seja. e f definida numa vizinhança do ponto x = a.
 Capítulo V Drivação 5. Noção d drivada Sja uma unção ral d variávl ral. Dinição: Sja a D dinida numa vizinhança do ponto a. Diz-s qu é drivávl ou dirnciávl m ( ) ( a) a a a s ist é inito o it Est it (quando
Capítulo V Drivação 5. Noção d drivada Sja uma unção ral d variávl ral. Dinição: Sja a D dinida numa vizinhança do ponto a. Diz-s qu é drivávl ou dirnciávl m ( ) ( a) a a a s ist é inito o it Est it (quando
Exame de Matemática Página 1 de 6. obtém-se: 2 C.
 Eam d Matmática -7 Página d 6. Simplificando a prssão 9 ( ) 6 obtém-s: 6.. O raio r = m d uma circunfrência foi aumntado m 5%. Qual foi o aumnto prcntual da ára da sgunda circunfrência m comparação com
Eam d Matmática -7 Página d 6. Simplificando a prssão 9 ( ) 6 obtém-s: 6.. O raio r = m d uma circunfrência foi aumntado m 5%. Qual foi o aumnto prcntual da ára da sgunda circunfrência m comparação com
VARIÁVEIS ALEATÓRIAS DISCRETAS. Vamos agora analisar em detalhe algumas variáveis aleatórias discretas, nomeadamente:
 98 99 VARIÁVEIS ALEATÓRIAS DISCRETAS Vamos agora analisar m dalh algumas variávis alaórias discras, nomadamn: uniform Brnoulli binomial binomial ngaiva (ou d Pascal) gomérica hirgomérica oisson mulinomial
98 99 VARIÁVEIS ALEATÓRIAS DISCRETAS Vamos agora analisar m dalh algumas variávis alaórias discras, nomadamn: uniform Brnoulli binomial binomial ngaiva (ou d Pascal) gomérica hirgomérica oisson mulinomial
A DERIVADA DE UM INTEGRAL
 A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,
A DERIVADA DE UM INTEGRAL HÉLIO BERNARDO LOPES Rsumo. O cálculo o valor a rivaa um ingral ocorr com cra frquência na via profissional físicos, químicos, ngnhiros, conomisas ou biólogos. É frqun, conuo,
Curso de linguagem matemática Professor Renato Tião. 3. Sendo. 4. Considere as seguintes matrizes:
 Curso d linguagm mamáica Profssor Rnao Tião 1 PUCRS. No projo Sobrmsa Musical, o Insiuo d Culura da PUCRS raliza aprsnaçõs smanais grauias para a comunidad univrsiária. O númro d músicos qu auaram na aprsnação
Curso d linguagm mamáica Profssor Rnao Tião 1 PUCRS. No projo Sobrmsa Musical, o Insiuo d Culura da PUCRS raliza aprsnaçõs smanais grauias para a comunidad univrsiária. O númro d músicos qu auaram na aprsnação
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO
 UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
UFPB CCEN DEPARTAMENTO DE MATEMÁTICA CÁLCULO DIFERENCIAL I 5 a LISTA DE EXERCÍCIOS PERÍODO 0 Nos rcícios a) ), ncontr a drivada da função dada, usando a dfinição a) f ( ) + b) f ( ) c) f ( ) 5 d) f ( )
7 Solução de um sistema linear
 Toria d Conrol (sinops 7 Solução d um sisma linar J. A. M. Flipp d Souza Solução d um sisma linar Dfinição 1 G(,τ mariz cujos lmnos g ij (,τ são as rsposas na i ésima saída ao impulso aplicado na j ésima
Toria d Conrol (sinops 7 Solução d um sisma linar J. A. M. Flipp d Souza Solução d um sisma linar Dfinição 1 G(,τ mariz cujos lmnos g ij (,τ são as rsposas na i ésima saída ao impulso aplicado na j ésima
Resolução do exame de Análise Matemática I (24/1/2003) Cursos: CA, GE, GEI, IG. 1ª Chamada
 Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
Proposta de teste de avaliação
 Proposta d tst d avaliação Matmática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Cadrno (é prmitido o uso d calculadora) Na rsposta aos itns d scolha múltipla, slcion a opção corrta. Escrva, na
Proposta d tst d avaliação Matmática A. O ANO DE ESCOLARIDADE Duração: 90 minutos Data: Cadrno (é prmitido o uso d calculadora) Na rsposta aos itns d scolha múltipla, slcion a opção corrta. Escrva, na
Equações de Maxwell. Métodos Eletromagnéticos. Equações de Maxwell. Equações de Maxwell
 Méodos Elromagnéicos agoso d 9 Fundamnos Equaçõs d Mawll no domínio do mpo da frqüência Onda plana édison K. ao Equaçõs d Mawll Todos os fnômnos lromagnéicos obdcm às quaçõs mpíricas d Mawll. b d h j ond
Méodos Elromagnéicos agoso d 9 Fundamnos Equaçõs d Mawll no domínio do mpo da frqüência Onda plana édison K. ao Equaçõs d Mawll Todos os fnômnos lromagnéicos obdcm às quaçõs mpíricas d Mawll. b d h j ond
Justifique todas as passagens
 ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
ā Prova d Cálculo II - MAT2 - IOUSP /2/204 Nom : GABARITO N ō USP : Profssor : Oswaldo Rio Branco d Olivira Justifiqu todas as passagns Q 2 4 5 Total N. Considr a função f : R 2 R dfinida por f(x,y) =
a) (0.2 v) Justifique que a sucessão é uma progressão aritmética e indique o valor da razão.
 MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
λ, para x 0. Outras Distribuições de Probabilidade Contínuas
 abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
Capítulo 3 Transmissão de Sinais e Filtragem
 Capíulo 3 Transmissão d Sinais Filragm 3.1 Rsposa d Sismas Linars Invarians no Tmpo No diagrama d blocos da Figura 3.1-1, é o sinal d nrada é o sinal d saída. Elmnos qu armaznam nrgia ouros ios inrnos
Capíulo 3 Transmissão d Sinais Filragm 3.1 Rsposa d Sismas Linars Invarians no Tmpo No diagrama d blocos da Figura 3.1-1, é o sinal d nrada é o sinal d saída. Elmnos qu armaznam nrgia ouros ios inrnos
3º) Equação do tipo = f ( y) dx Solução: 2. dy dx. 2 =. Integrando ambos os membros, dx. dx dx dy dx dy. vem: Ex: Resolva a equação 6x + 7 = 0.
 0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
Função Exponencial: Conforme já vimos, o candidato natural à função exponencial complexa é dado pela função. f z x iy f z e cos y ie sen y.
 Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Ficha 2. 1 Polinómios de Taylor de um campo escalar. 1.1 O primeiro polinómio de Taylor.
 Aulas Práticas d Matmática II Mstrado m Arquitctura o Smstr Fica 1 Polinómios d Talor d um campo scalar. Rcord qu os polinómios d Talor são uma important frramnta para studar o comportamnto d uma função
Aulas Práticas d Matmática II Mstrado m Arquitctura o Smstr Fica 1 Polinómios d Talor d um campo scalar. Rcord qu os polinómios d Talor são uma important frramnta para studar o comportamnto d uma função
ANO LECTIVO 2001/2002
 ANO LECTIVO 00/00 ª Fas, ª Chamada 00 Doss rapêuicas iguais d um cro anibióico são adminisradas, pla primira vz, a duas pssoa: a Ana o Carlos Admia qu, duran as doz primiras horas após a omada simulâna
ANO LECTIVO 00/00 ª Fas, ª Chamada 00 Doss rapêuicas iguais d um cro anibióico são adminisradas, pla primira vz, a duas pssoa: a Ana o Carlos Admia qu, duran as doz primiras horas após a omada simulâna
Definição de Área entre duas curvas - A área A entre região limitada pelas curvas. x onde f e g são contínuas e x g x
 Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para
Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para
LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA
 Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Seção 2.1: Equações lineares; Fator integrante
 Capíulo Sção.: Equaçõs linars; Faor ingran Uma EDO d primira ordm é da forma d d f ond f é linar na variávl. Alguns mplos ípicos ds ipo d quaçõs com coficins consans saõ a b ou quaçõs com coficins variávis:
Capíulo Sção.: Equaçõs linars; Faor ingran Uma EDO d primira ordm é da forma d d f ond f é linar na variávl. Alguns mplos ípicos ds ipo d quaçõs com coficins consans saõ a b ou quaçõs com coficins variávis:
{ : 0. Questões de resposta de escolha múltipla. Grupo I 1. ( ) D = x f x x D. Resposta: D. lim = 3, pode-se concluir que o
 Grupo I Qustõs d rsposta d scolha múltipla { : 0 f }. ( ) D = f D g f ( ) 0 [, + [. Como f tm domínio \{ 5}, é contínua f ( ) gráfico d f não admit assimptotas vrticais. 5 Rsposta: D lim =, pod-s concluir
Grupo I Qustõs d rsposta d scolha múltipla { : 0 f }. ( ) D = f D g f ( ) 0 [, + [. Como f tm domínio \{ 5}, é contínua f ( ) gráfico d f não admit assimptotas vrticais. 5 Rsposta: D lim =, pod-s concluir
sen( x h) sen( x) sen xcos h sen hcos x sen x
 MAT00 Cálculo Difrcial Itgral I RESUMO DA AULA TEÓRICA Livro do Stwart: Sçõs 3., 3.4 3.8. DEMONSTRAÇÕES Nssa aula srão aprstadas dmostraçõs, ou sboços d dmostraçõs, d algus rsultados importats do cálculo
MAT00 Cálculo Difrcial Itgral I RESUMO DA AULA TEÓRICA Livro do Stwart: Sçõs 3., 3.4 3.8. DEMONSTRAÇÕES Nssa aula srão aprstadas dmostraçõs, ou sboços d dmostraçõs, d algus rsultados importats do cálculo
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 21 DE JULHO Grupo I. Questões
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 63) ª FASE 1 DE JULHO 014 Grupo I Qustõs 1 3 4 6 7 8 Vrsão 1 C B B D C A B C Vrsão B C C A B A D D 1 Grupo II 11 O complo
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 63) ª FASE 1 DE JULHO 014 Grupo I Qustõs 1 3 4 6 7 8 Vrsão 1 C B B D C A B C Vrsão B C C A B A D D 1 Grupo II 11 O complo
FENOMENOS DE TRANSPORTE 2 o Semestre de 2013 Prof. Maurício Fabbri
 FENOMENOS DE TRANSPORTE o Smsr d 03 Prof. Maurício Fabbri 3ª SÉRIE DE EXERCÍCIOS Transpor d calor por convcção O ransin ponncial simpls Consrvação da nrgia 0-3. O coficin d ransfrência d calor Lia o marial
FENOMENOS DE TRANSPORTE o Smsr d 03 Prof. Maurício Fabbri 3ª SÉRIE DE EXERCÍCIOS Transpor d calor por convcção O ransin ponncial simpls Consrvação da nrgia 0-3. O coficin d ransfrência d calor Lia o marial
Lista 5: Regras de Derivação
 Univrsidad Fdral do Val do São Francisco Câmpus Juaziro BA Colgiado d Engnharia Elétrica Prof. Pdro Macário d Moura Cálculo Difrncial Intgral Lista : Rgras d Drivação 0. Calcular as drivadas das prssõs
Univrsidad Fdral do Val do São Francisco Câmpus Juaziro BA Colgiado d Engnharia Elétrica Prof. Pdro Macário d Moura Cálculo Difrncial Intgral Lista : Rgras d Drivação 0. Calcular as drivadas das prssõs
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 2/4
 FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsnt o s raciocínio d orma clara, indicando todos os cálclos q tivr d tar todas as jstiicaçõs ncssárias. Qando, para m rsltado, não é pdida
FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsnt o s raciocínio d orma clara, indicando todos os cálclos q tivr d tar todas as jstiicaçõs ncssárias. Qando, para m rsltado, não é pdida
Matemática C Extensivo V. 7
 Matmática C Extnsivo V 7 Exrcícios 0) 0 0) D 0 Falsa B A 4 0 6 0 4 6 4 6 0 Vrdadira A + B 0 0 + 4 6 7 04 Vrdadira A B 0 0 4 6 6 4 08 Vrdadira dt ( A) dt (A) 9 ( ) 9 dt (B) 9 0 6 Vrdadira A A 0 0 0 0 0
Matmática C Extnsivo V 7 Exrcícios 0) 0 0) D 0 Falsa B A 4 0 6 0 4 6 4 6 0 Vrdadira A + B 0 0 + 4 6 7 04 Vrdadira A B 0 0 4 6 6 4 08 Vrdadira dt ( A) dt (A) 9 ( ) 9 dt (B) 9 0 6 Vrdadira A A 0 0 0 0 0
O modelo Von Bertalanffy adaptado para suínos de corte
 O modlo Von Bralanffy adapado para suínos d cor Lucas d Olivira nro Fdral d Educação Fdral Tcnológica EFET-MG.5-, Av. Amazonas 525 - Nova Suíça - Blo Horizon - MG - Brasil E-mail: lucasdolivira@gmail.com
O modlo Von Bralanffy adapado para suínos d cor Lucas d Olivira nro Fdral d Educação Fdral Tcnológica EFET-MG.5-, Av. Amazonas 525 - Nova Suíça - Blo Horizon - MG - Brasil E-mail: lucasdolivira@gmail.com
Probabilidade II Aula 6
 obabilidad II Aula 6 Março d 9 Mônica Barros, DSc Conúdo Mais sobr momnos condicionais Cálculo d valors srados aravés do condicionamno numa variávl rlação nr valors srados condicionais incondicionais fórmulas
obabilidad II Aula 6 Março d 9 Mônica Barros, DSc Conúdo Mais sobr momnos condicionais Cálculo d valors srados aravés do condicionamno numa variávl rlação nr valors srados condicionais incondicionais fórmulas
k m d 2 x m z = x + iy, d 2 z m Essa mesma equação também pode ser escrita assim: dt 2 + ω2 0z = F 0 Veja que interessante a propriedade seguinte:
 Oscilaçõs forçadas Dpois d tr visto coo são as oscilaçõs aortcidas, agora você pod facilnt ntndr as oscilaçõs forçadas. Aqui vou ignorar a dissipação apnas introduzir ua força oscilant ao sista assa-ola.
Oscilaçõs forçadas Dpois d tr visto coo são as oscilaçõs aortcidas, agora você pod facilnt ntndr as oscilaçõs forçadas. Aqui vou ignorar a dissipação apnas introduzir ua força oscilant ao sista assa-ola.
10. EXERCÍCIOS (ITA-1969 a ITA-2001)
 . EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
. EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
Equações Diferenciais Lineares
 Equaçõs Diriais Liars Rordmos a orma gral d uma quação dirial liar d ordm a d d d d a a a, I d d m qu as uçõs a i são idpdts da variávl. S, a quação diz-s liar homogéa. Caso otrário, diz-s liar omplta.
Equaçõs Diriais Liars Rordmos a orma gral d uma quação dirial liar d ordm a d d d d a a a, I d d m qu as uçõs a i são idpdts da variávl. S, a quação diz-s liar homogéa. Caso otrário, diz-s liar omplta.
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Quadro de Respostas das Questões de Múltipla Escolha Valor: 65 pontos Alternativa/Questão Rascunho A B C D E. 1 e.
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
Oscilações amortecidas
 Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
Álgebra. Matrizes. . Dê o. 14) Dada a matriz: A =.
 Matrizs ) Dada a matriz A = Dê o su tipo os lmntos a, a a ) Escrva a matriz A, do tipo x, ond a ij = i + j ) Escrva a matriz A x, ond a ij = i +j ) Escrva a matriz A = (a ij ) x, ond a ij = i + j ) Escrva
Matrizs ) Dada a matriz A = Dê o su tipo os lmntos a, a a ) Escrva a matriz A, do tipo x, ond a ij = i + j ) Escrva a matriz A x, ond a ij = i +j ) Escrva a matriz A = (a ij ) x, ond a ij = i + j ) Escrva
Secção 8. Equações diferenciais não lineares.
 Scção 8. Equaçõs difrnciais não linars. (Farlow: Sc. 8. a 8.3) Esa scção srá ddicada às EDOs não linars, as quais são gralmn d rsolução analíica difícil ou msmo impossívl. Não vamos porano nar rsolvê-las
Scção 8. Equaçõs difrnciais não linars. (Farlow: Sc. 8. a 8.3) Esa scção srá ddicada às EDOs não linars, as quais são gralmn d rsolução analíica difícil ou msmo impossívl. Não vamos porano nar rsolvê-las
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 REC2010 MICROECONOMIA II SEGUNDA PROVA (2011) ROBERTO GUENA (1) Considr uma indústria m concorrência prfita formada por mprsas idênticas. Para produzir, cada mprsa dv arcar com um custo quas fixo F = 1.
REC2010 MICROECONOMIA II SEGUNDA PROVA (2011) ROBERTO GUENA (1) Considr uma indústria m concorrência prfita formada por mprsas idênticas. Para produzir, cada mprsa dv arcar com um custo quas fixo F = 1.
/ :;7 1 6 < =>6? < 7 A 7 B 5 = CED? = DE:F= 6 < 5 G? DIHJ? KLD M 7FD? :>? A 6? D P
 26 a Aula 20065 AMIV 26 Exponncial d matrizs smlhants Proposição 26 S A SJS ntão Dmonstração Tmos A SJS A % SJS SJS SJ % S ond A, S J são matrizs n n ", (com dt S 0), # S $ S, dond ; A & SJ % S SJS SJ
26 a Aula 20065 AMIV 26 Exponncial d matrizs smlhants Proposição 26 S A SJS ntão Dmonstração Tmos A SJS A % SJS SJS SJ % S ond A, S J são matrizs n n ", (com dt S 0), # S $ S, dond ; A & SJ % S SJS SJ
Capítulo 2.1: Equações Lineares 1 a ordem; Método dos Fatores Integrantes
 Capíulo.1: Equaçõs Linars 1 a ordm; Méodo dos Faors Ingrans Uma EDO d primira ordm m a forma gral d f, ond f é linar m. Exmplo: a Equaçõs com coficins consans; a b b Equaçõs com coficins variavis: d p
Capíulo.1: Equaçõs Linars 1 a ordm; Méodo dos Faors Ingrans Uma EDO d primira ordm m a forma gral d f, ond f é linar m. Exmplo: a Equaçõs com coficins consans; a b b Equaçõs com coficins variavis: d p
Estatística II. Aula 8. Prof. Patricia Maria Bortolon, D. Sc.
 Estatística II Aula 8 Pro. Patricia Maria Bortolon, D. Sc. Tsts Qui Quadrado Objtivos da Aula 8 Nsta aula, você aprndrá: Como quando utilizar o tst qui-quadrado para tablas d contingência Como utilizar
Estatística II Aula 8 Pro. Patricia Maria Bortolon, D. Sc. Tsts Qui Quadrado Objtivos da Aula 8 Nsta aula, você aprndrá: Como quando utilizar o tst qui-quadrado para tablas d contingência Como utilizar
Capítulo 6 Decaimento Radioativo
 Física das Radiaçõs Dosimria Capíulo 6 Dcaimno Radioaivo Dra. Luciana Tourinho Campos Programa acional d Formação m Radiorapia Inrodução Inrodução Consan d dcaimno Vida-média mia-vida Rlaçõs nr núclo pai
Física das Radiaçõs Dosimria Capíulo 6 Dcaimno Radioaivo Dra. Luciana Tourinho Campos Programa acional d Formação m Radiorapia Inrodução Inrodução Consan d dcaimno Vida-média mia-vida Rlaçõs nr núclo pai
Função do 2 o Grau. Uma aplicação f der emr
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
Matemática IME-2007/ a QUESTÃO. 2 a QUESTÃO COMENTA
 Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
1. A soma de quaisquer dois números naturais é sempre maior do que zero. Qual é a quantificação correcta?
 Abuso Sual nas Escolas Não dá para acitar Por uma scola livr do SID A Rpública d Moçambiqu Matmática Ministério da Educação ª Época ª Class/0 Conslho Nacional d Eams, Crtificação Equivalências 0 Minutos
Abuso Sual nas Escolas Não dá para acitar Por uma scola livr do SID A Rpública d Moçambiqu Matmática Ministério da Educação ª Época ª Class/0 Conslho Nacional d Eams, Crtificação Equivalências 0 Minutos
Equações não lineares processo iterativo
 Equaçõs não linars procsso itrativo Sja uma função considr-s a quação =0. A solução da quação dsigna-s por rai da quação ou por ro da função () y Sucssão itrativa: 0,,, 3, 0 3 0 3 4 = Prtndmos qu a sucssão
Equaçõs não linars procsso itrativo Sja uma função considr-s a quação =0. A solução da quação dsigna-s por rai da quação ou por ro da função () y Sucssão itrativa: 0,,, 3, 0 3 0 3 4 = Prtndmos qu a sucssão
1. (2,0) Um cilindro circular reto é inscrito em uma esfera de raio r. Encontre a maior área de superfície possível para esse cilindro.
 Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
TÓPICOS DE MATEMÁTICA PROF.: PATRÍCIA ALVES
 TÓPICOS DE MATEMÁTICA PROF.: PATRÍCIA ALVES 33 MATRIZES 1. Dê o tipo d cada uma das sguints prtncm às diagonais principais matrizs: scundárias d A. 1 3 a) A 7 2 7. Qual é o lmnto a 46 da matriz i j 2 j
TÓPICOS DE MATEMÁTICA PROF.: PATRÍCIA ALVES 33 MATRIZES 1. Dê o tipo d cada uma das sguints prtncm às diagonais principais matrizs: scundárias d A. 1 3 a) A 7 2 7. Qual é o lmnto a 46 da matriz i j 2 j
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 21 DE JULHO 2014 Grupo I.
 Associação d Profssors d Matmática Contactos: Rua Dr João Couto, nº 7-A 100-6 Lisboa Tl: +1 1 716 6 90 / 1 711 0 77 Fa: +1 1 716 64 4 http://wwwapmpt mail: gral@apmpt PROPOSTA DE RESOLUÇÃO DA PROVA DE
Associação d Profssors d Matmática Contactos: Rua Dr João Couto, nº 7-A 100-6 Lisboa Tl: +1 1 716 6 90 / 1 711 0 77 Fa: +1 1 716 64 4 http://wwwapmpt mail: gral@apmpt PROPOSTA DE RESOLUÇÃO DA PROVA DE
01.Resolva as seguintes integrais:
 INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
Adriano Pedreira Cattai
 Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
Questões para o concurso de professores Colégio Pedro II
 Qustõs para o concurso d profssors Colégio Pdro II Profs Marilis, Andrzinho Fábio Prova Discursiva 1ª QUESTÃO Jhosy viaja com sua sposa, Paty, sua filha filho para a Rgião dos Lagos para curtir um friadão
Qustõs para o concurso d profssors Colégio Pdro II Profs Marilis, Andrzinho Fábio Prova Discursiva 1ª QUESTÃO Jhosy viaja com sua sposa, Paty, sua filha filho para a Rgião dos Lagos para curtir um friadão
Exercício 2. Calcule. f (x)<0 e f (x) e M 2 = f (0.5) =1.3 Logo
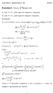 Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5
 P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
Análise Matemática II
 Análise Maemáica II Exame/Tese 3 - de Junho de 5 Licenciaura em Eng. Informáica e de Compuadores Nome: Número: Exame: Todas as pergunas Tese: Pergunas 5, 6, 7, 8 e 9 Indique na erceira coluna da abela
Análise Maemáica II Exame/Tese 3 - de Junho de 5 Licenciaura em Eng. Informáica e de Compuadores Nome: Número: Exame: Todas as pergunas Tese: Pergunas 5, 6, 7, 8 e 9 Indique na erceira coluna da abela
Identifique todas as folhas Folhas não identificadas NÃO SERÃO COTADAS. Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I
 Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
a) 1. b) 0. c) xnw. d) q (Espm 2014) Se a matriz 7. (Pucrs 2014) Dadas as matrizes A = [ 1 2 3] a) 18 b) 21 c) 32 d) 126 e) 720 Se a matriz M=
![a) 1. b) 0. c) xnw. d) q (Espm 2014) Se a matriz 7. (Pucrs 2014) Dadas as matrizes A = [ 1 2 3] a) 18 b) 21 c) 32 d) 126 e) 720 Se a matriz M= a) 1. b) 0. c) xnw. d) q (Espm 2014) Se a matriz 7. (Pucrs 2014) Dadas as matrizes A = [ 1 2 3] a) 18 b) 21 c) 32 d) 126 e) 720 Se a matriz M=](/thumbs/54/33471810.jpg) Dtrminant. (Upg 4) Considrando as matrizs abaixo, sndo dt A = 5, dtb= dtc=, assinal o qu for orrto. x z x y x A =,B= 4 5 x+ z y C= ) x+ y+ z= 4 ) A C= 4) B C= 4 8) y = x 6) 6 4 A+ B= 6 5 T. (Uds 4) S A
Dtrminant. (Upg 4) Considrando as matrizs abaixo, sndo dt A = 5, dtb= dtc=, assinal o qu for orrto. x z x y x A =,B= 4 5 x+ z y C= ) x+ y+ z= 4 ) A C= 4) B C= 4 8) y = x 6) 6 4 A+ B= 6 5 T. (Uds 4) S A
UFJF ICE Departamento de Matemática Cálculo I Terceira Avaliação 10/07/2010 FILA A Aluno (a): Matrícula: Turma:
 UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/07/00 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha.
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação 0/07/00 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha.
Análise Matemática III
 João Paulo Pais d Almida Ilda Marisa d Sá Ris Ana Esr da Viga Rodrigus Víor Luis Prira d Sousa Anális Mamáica III Dparamno d Mamáica Escola Suprior d Tcnologia d Gsão Insiuo Poliécnico d Bragança Smbro
João Paulo Pais d Almida Ilda Marisa d Sá Ris Ana Esr da Viga Rodrigus Víor Luis Prira d Sousa Anális Mamáica III Dparamno d Mamáica Escola Suprior d Tcnologia d Gsão Insiuo Poliécnico d Bragança Smbro
INTRODUÇÃO À ESTATÍSTICA
 INTRODUÇÃO À ESTATÍSTICA ERRATA (capítulos 1 a 6 CAP 1 INTRODUÇÃO. DADOS ESTATÍSTICOS Bnto Murtira Carlos Silva Ribiro João Andrad Silva Carlos Pimnta Pág. 10 O xmplo 1.10 trmina a sguir ao quadro 1.7,
INTRODUÇÃO À ESTATÍSTICA ERRATA (capítulos 1 a 6 CAP 1 INTRODUÇÃO. DADOS ESTATÍSTICOS Bnto Murtira Carlos Silva Ribiro João Andrad Silva Carlos Pimnta Pág. 10 O xmplo 1.10 trmina a sguir ao quadro 1.7,
COLEÇÃO DARLAN MOUTINHO VOL. 04 RESOLUÇÕES. com. voce
 COLEÇÃO DARLAN MOUTINHO VOL. 04 RESOLUÇÕES RESOLUÇÃO A1 Primiramnt, dividimos a figura B m dois triângulos B1 B2, um altura d 21 m bas d 3 m outro altura bas mdindo 15 m. Mosaico 1: Tmos qu os dois triângulos
COLEÇÃO DARLAN MOUTINHO VOL. 04 RESOLUÇÕES RESOLUÇÃO A1 Primiramnt, dividimos a figura B m dois triângulos B1 B2, um altura d 21 m bas d 3 m outro altura bas mdindo 15 m. Mosaico 1: Tmos qu os dois triângulos
