Processamento Digital de Sinais
|
|
|
- Madalena de Oliveira da Conceição
- 8 Há anos
- Visualizações:
Transcrição
1 Procssmto Digitl Siis Mrclo Bsílio Joquim São Crlos -
2 Íic Aprstção i Cpítulo Siis Sistms tmpo iscrto. Itroução. Siis Tmpo Discrto. Siis tmpo iscrto básicos.. Squêci mostr uitári.. Squêci gru uitário.. Squêci pocil..4 Squêci soil 4.4 Algums fiiçõs sobr siis tmpo iscrto 6.4. Ergi 6.4. Potêci 6.4. Squêcis simétrics ti-simétrics 8.5 Sistms tmpo iscrto 8.5. Sistms lirs tmpo iscrto 9.5. Sistms lirs ivrits o slocmto.5. Sistms cusis.5.4 Sistms stávis.5.5 Rprstção m igrm blocos os sistms tmpo iscrto.5.6 Sistms lirs iscrtos ivrits o slocmto.5.7 Som covolução.5.7. Propris covolução sistms LID Cusli stbili m sistms lirs ivrits o slocmto 5.6 Equção lir ifrçs com coficits costts 7.6. Solução qução ifrçs 7.6. Rspost o impulso 9.7 Rprstção siis sistms iscrtos o omíio frquêci.8 Trsform Fourir pr squêcis.8. Espctro si rgi.8. Propris trsform Fourir pr siis iscrtos 5 Ercícios Cpítulo Amostrgm siis 5. Siis tmpo iscrto 5. Amostrgm siis 5. Torm mostrgm 6.4 Covrsão t mostrgm 9 Ercícios 44 Cpítulo A trsform 45. Itroução 45.. Dfiição covrgêci 45.. Rgião covrgêci 46.. Propris rgião covrgêci 5. Trsform ivrs 5.. Métoo forml pl itgrl cotoro 5.. Métoo por ispção 5.. Métoo por psão m frçõs prciis Métoo por psão m séri potêcis Métoo pl ivisão log 58.4 Propris trsform Liri 59
3 .4. Dslocmto o tmpo Difrcição X() Multiplicção por um squêci pocil Complo cojugo um squêci Rvrsão o tmpo Covolução squêcis Torm o vlor iicil Torm o vlor fil 6.4. Torm covolução compl 6.4. Torm Prsvl 6.5 Aplicção m sistms lirs 6.5. Rprstção um sistm utilio trsform 6.5. Fução o sistm prtir qução ifrçs 6.5. Estbili cusli Obtção rspost m frquêci prtir o gráfico polos ros 65 Ercícios 67 Cpítulo 4 Trsform iscrt Fourir 7 4. Itroução 7 4. Trsform Fourir pr tmpos iscrtos 7 4. Trsform Discrt Fourir Trsform Discrt Fourir Ivrs Propris TDF Prioici Liri Dslocmto circulr () Dslocmto circulr m X() TDF squêcis ris Covolução circulr Covolução lir Uso DFT m ális spctrl 8 Ercícios 84 Cpítulo 5 Filtros Digitis Itroução Projto filtros igitis com rspost o impulso ifiit - IIR Métoo por proimção s rivs Métoo por ivriâci o impulso Métoo por trsformção bilir 9 5. Fmíli filtros lógicos Rspost Buttrworth Espcificçõs pr o projto filtros pss-bis Rspost Chbyshv Filtros Elípticos 5..4 Filtros Bssl Emplo projto um filtro IIR Plo métoo por proimção s rivs Métoo por trsformção bilir Projto filtros igitis com rspost o impulso fiit - FIR 5.5. Dfiição um filtro FIR 5.5. Coição fs lir 5.5. Loclição os ros um filtro FIR com fs lir 5.6 Projto filtros FIR por jls 5.7 Projto filtros FIR utilio jl Kisr Projto filtros FIR por mostrgm m frquêci 9 Ercícios Cpítulo 6 Projtos otimios filtros 5
4 6. Projto filtros FIR quirippl 5 6. Aproimção Pé 6. Métoo Proy 6.4 Projto filtros FIR plo métoo os míimos quros 4 Bibliogrfi 9 Apêics A Jls 4 A FFT 45 A Fórmuls tbls 5
5 Aprstção Procssmto igitl siis (PDS) é o trtmto qu s plic um sil tmpo iscrto. Est procssmto é cuto por mios igitis: computors ou procssors igitis. Com o vto os computors o iício éc 6, com o svolvimto lgoritmos como o trsform rápi Fourir - FFT (Coly Tuy 965), tm iício um ov tp o cmpo trtmto siis sus plicçõs. O svolvimto os microprocssors (éc 97) os procssors igitis (éc 98): mplirm s plicçõs PDS. Por volt 975 tm-s publicção os primiros livros importts o ssuto: Ophim, A. V. Schfr, R. W., Digitl Sigl Procssig. Rbir & Gol, Thory Applictios of Digitl Sigl Procssig. A mior prt os siis cotros são cotíuos o tmpo, por mplo, áuio, vío, tmprtur. Assim, pr o trtmto igitl, tm-s cssi covrtr s iformçõs m siis létricos tmpo cotíuos por mio trsutors m sgui igitlir sts siis, isto é: covrtr o tmpo cotíuo pr o tmpo iscrto (igitl) utilio covrsors AD. Os pricipis compots um sistm DSP típico são mostros figur. (t) Filtro (I) AD DSP DA Filtro (II) y(t) (t) () Filtro I: Filtro ti-lisig AD: Covrsor lógico igitl DSP: Computor igitl ou procssor igitl siis DA: Covrsor igitl lógico Filtro II: Filtro ti-imgig (filtro rcostrução) Figur : Compots um sistm pr procssmto igitl siis. Algums vtgs DSP: Progrmbili: Um implmtção m PDS é mis flívl, s qu é mis fácil s moificr (o softwr po sr tulio, rfito ou moifico). Estbili Rptibili: Aprst mlhor quli o sil, stbili rptibili o smpho o sistm, pois o sistm é rprsto form igitl implmtção é trvés lgoritmos qu ão pm tolrâci compots, vlhcimto, tc. Aplicçõs spciis: Algus procssmtos são rlios com mis ficiêci form igitl: comprssão, filtros com fs lir. Agums svtgs DSP: ão é coômico m plicçõs simpls: os covrsors AD DA, m grl crcm o sistm. Limitção m frquêci, cosumo lto potêci. Algums plicçõs DSP Grvção igitl áuio.
6 Comprssão siis vo áuio pr plicçõs m tlfoi igitl, rmmto m CD. Implmtção mom. Eriqucimto imgm comprssão. Síts fl rcohcimto. Prição siis ou sís sistms. Cotrol. Bioghri. Gofísic Est tto tm como objtivo prstr os luos iicits um borgm os tópicos básicos mtéri procssmto igitl siis. Aluos Eghri Elétric têm cssi trr o mrco trblho com lgum cohcimto básico PDS. A itção é prstr um tto itroutório pr sr utilio m cursos grução s árs Eghri Elétric, Eghri Computção árs fis, o ist cssi s trblhr com siis sistms tmpo iscrto. o cpítulo são itrouios os cocitos siis sistms tmpo iscrto como trblhr com sts os omíios o tmpo frquêci. São prstos tmbém os sistms lirs tmpo iscrtos sus frrmts mtmátics ális. o cpítulo são itrouios o cocito mostrgm prióic siis, o torm mostrgm sus fitos. Os cpítulos 4 são rsrvos, rspctivmt, pr prstção trsform trsform iscrt Fourir (TDF) com mplo plicção m ális spctrl. A trsform rápi Fourir, trvés o lgoritmo cimção o tmpo, é prst o pêic A-, pr os itrssos m cohcr tl lgoritmo. E os cpítulos 5 6 são utilios pr o stuo projtos filtros igits. o cpítulo 5 são stuos os projtos clássicos filtros sltivos m frquêci utilio os filtros com rspost o impulso ifiit (IIR) os projtos filtros com rspost o impulso fiit (FIR): projto por jls por mostrgm m frquêci. o cpítulo 6 são prstos lgus projtos otimios filtros, icluio o lgoritmo Prs-McClll pr filtros FIR os métoos proimção Pé, Proy métoo os míimos quros pr filtros IIR. Pr uilir o stuo outros ois pêics são icluíos: um pr jls (A-) um com formuls tbls utilis m PDS (A-). Mrclo Bsilio Joquim
7 - - Cpítulo SIAIS E SISTEMAS DE TEMPO DISCRETO. Itroução Um sil po sr fiio como um quti físic, vrit o tmpo qu trsport iformção rspito o comportmto um sistm. Em grl, l é rprsto mtmticmt como um fução um ou mis vriávis ipts (tmpo, spço, tc.), porém, st stuo, ls srão mitis fuçõs com somt um vriávl ipt, o tmpo. O moo mis comum s clssificr um sil é ivii-lo m us importts clsss. Os trmiísticos os ltórios. Os siis trmiísticos são quls utilios pr propósitos tsts, molgm crctrição sistms. Dtr ls po-s stcr: os siis soiis, o qur, fução gru uitário, fução impulso, tc. Els são bm fiios m grl rprstos ou scritos por um fução mtmátic ou gráfic, o s cohc o su vlor m qulqur istt tmpo, prst, psso ou futuro. Amplitu, frquêci fs são os sus pricipis prâmtros. sgu ctgori rcm os siis iformção proprimt itos quls provits tur, tis como: siis vo, áuio, vío, tmprtur, os igitis tmbém o ruío. Dvio à tur ltóri, ls só pom sr scritos utilio como fumto tori probbilis lgums propris qu prstm, como por mplo, stciori trvés lgums méis tis como: vlor méio, vlor qurático méio, vriâci svio prão, fução utocorrlção spctro si potêci. A vriávl ipt tmbém é um outr quti muito importt pr clssificr os siis. Os siis tmpo cotíuo são clssificos por um vriávl ipt qu po ssumir qulqur vlor tro um fi cotíu qu po s str té o ifiito; sts siis são chmos mis rrmt lógicos. Já os siis tmpo iscrto são fiios m istts tmpos iscrtos, t, Z. A vriávl ipt ssum vlors iscrtos, provvlmt ão umrávl, portto ls são rprstos por um squêci úmros. A mplitu o sil tmbém po sr iscrt ou cotíu. o cso iscrto l é quti, isto é proim pr um vlor prtct um cojuto fiito mplitus m sgui coific igitlmt. st cso têm-s os siis igitis, o tto mplitu quto o tmpo são qutis iscrts. st stuo, miori s vs ão s frá hum rfrêci com rlção à mplitu, form tl qu os siis srão mitios tmpo iscrto, ms cuj mplitu po ssumir qulqur vlor tro um fi cotíu prtct os úmros ris. Um sistm po sr fiio como um ispositivo qu rli um oprção mtmátic m um sil. Como um mplo sistm po s citr um filtro utilio pr ruir ruío ou itrfrêcis m um sil plico m su tr. Os sistms pom sr clssificos o msmo moo qu os siis. Sistms cotíuos ou lógicos são quls m qu s trs sís são siis tmpo cotíuo. Os iscrtos são quls cujs trs sís são siis tmpo iscrto os igitis são quls cujs trs sís são siis igitis. Quo s pss um sil trvés um sistm imos qu l foi procsso, í o om procssmto siis. st cpítulo srão stuos os pricipis cocitos propris pr siis sistms tmpo iscrto.. Siis tmpo iscrto Os siis tmpo iscrto são m grl, origios trvés mostrgm o sil cotíuo, cujo itrvlo mostrgm é costt spcifico plo torm yquist, qu srá stuo o
8 - - cpítulo. Como um mplo um sil cotíuo um tmpo iscrto, cosir o sguit sil pocil, t () t (.) Est sil é fiio pr qulqur istt tmpo o itrvlo - < t <, como mostr figur..., so portto um sil tmpo cotíuo. Amitio gor, qu st sil é fiio somt os istts t :, ±, ±,..., como mostr figur..b, tão st ovo sil pss sr tmpo iscrto. st cso tm-s qu, ( t ) t, ±, ±, L (.).5 ( ) ( b ).5 t Figur.: Rprstção gráfic o sil s quçõs (.) (.). figur..b o sil iscrto é rprsto por rts (ris) prlls o io tmpo iscrto. Obsrv qu s spcific rspito o sil mostro tr ois itrvlos jcts t t pois vriávl é fii somt pr vlors iscrtos. Isto ão implic qu l ão prst vlors sts itrvlos, ms somt qu ão é fiio. Os istts tmpo são rgulrmt spços tis qu t T (T é chmo itrvlo ou príoo mostrgm). A otção comumt utili pr st tipo sil é () (T ) o sil pss sr rprsto por um squêci úmros {()}. Amitio, por mplo, qução (.) T, s, tm-s sguit squêci,. ( ), ±, ±, L (.) Como foi comto cim, um sil tmpo iscrto é ssocio um squêci úmros {()} como quls covciolmt utilis m mtmátic. Assim é itrsst spcificr s oprçõs básics qu s rlim com squêcis. () Som squêcis ( ) ( ) ( ) y Som-s mostr com mostr s squêcis iiviuis. Obsrv qu sts squêcis vm prstr o msmo tmho. o cso squêcis com tmhos ifrts o problm po sr rsolvio crscto-s ros à squêci mor tmho. (b) Prouto squêcis ( ) ( ). ( ) y Multiplic-s mostr por mostr s squêcis iiviuis. Obsrv qu, como triormt, sts squêcis vm prstr o msmo tmho. (c) Multiplicção por um sclr α y ( ) α( )
9 - - Multiplic-s c lmto squêci por α. () Atrso m um squêci y ( ) ( ) Em qu, é um úmro itiro positivo qulqur. Obsrv qu o istt, y() (- ), ssim, y() stá trs por mostrs m rlção à (). S for um úmro gtivo tão s i qu y() stá vç por mostrs m rlção ().. Siis tmpo iscrto básicos Eistm lgus siis iscrtos qu são muito utilios o svolvimto tori procssmto igitl siis o stuo, molgm tst sistms. Algus sts siis são fiios sguir... Squêci mostr uitári, δ( ) (.4), Est tipo sil ou squêci smph o msmo ppl qu fução impulso uitário δ(t) smph os sistms cotíuos o tmpo. El tmbém é chmo, sm istição com os sistms cotíuos, fução impulso, impulso uitário ou pulso uitário. Qulqur squêci () po sr rprst por um squêci por fuçõs mostrs uitáris tis qu: ( ) L δ( ) δ( ) δ( ) δ( ) δ ( ) L (.5) m qu: ()... Squêci gru uitário, u ( ) (.6), < Est squêci é muito útil quo s prt istiguir íics positivos (tmpo positivo) os gtivos. Itificmos ssim, os siis cusis, isto é, siis qu são ulos pr <, ou sj, qu prstm vlors somt pr íics positivos. Pr st squêci s sguits rlçõs são vális:.. Squêci pocil ( ) δ( ) δ( ) u (.7) ( ) u( ) u( ) δ (.8)
10 - 4 - ( ) α (.9) Est squêci é muito utili m procssmto igitl siis. El prc com frquêci o stuo sistms lirs tmpo iscrto. Um sistm lir primir orm prst como rspost o impulso um fução pocil, como srá visto mis it. Um squêci pocil cusl é rprst como bio, ( ) α u( ) (.) ssim, l prst toos os sus vlors ulos pr <. o cso α < l tom form um pocil mortci com mostr figur Squêci soil Figur.: Sil pocil. Um sil soil tmpo iscrto é um oscilção hrmôic qu po sr prss por um s forms mostrs bio, ( ) A cos( πf φ) A cos( w φ) (.) ( ) As( πf φ) As( w φ) (.) j ( ) ( πfφ) j( w φ) A A (.) A qução (.) rprst form compl sói s outrs us triors rprstm s forms ris. Est sil possui três prâmtros qu o crctrim compltmt: mplitu A, frquêci w o âgulo fs φ Figur.: Sil soil tmpo iscrto. É cssário fr um obsrvção importt com rlção à frquêci os siis cotíuos os iscrtos. As ltrs miúsculs Ω F srão utilis pr rprstr s frquêcis lógics s miúsculs w f srão utilis pr rprstr s frquêcis igitis. st cso w tm ui rios por mostr f ui ciclos por mostr stão rlcios por: w πf (.4)
11 - 5 - As frquêcis lógics igitis stão rlcios plo príoo ou pl frquêci mostrgm o sil como sgu, F f FT (.5) F m qu, T é o príoo mostrgm o sil. Obsrv qu quo for cssário trmir frquêci um sil lógico qu grou o mostro bst multiplicr frquêci igitl pl mostrgm. Pr mostrr st rsulto, cosir o sguit sil soil tmpo cotíuo, ( t) A cos( πft φ) Amitio qu s colh um mostr st sil c T sguos tão o sil mostro srá o por: ( T ) A cos( πft φ) Cosiro f FT, como iico pl qução (.5), tm-s qu: ( ) A cos( πf φ) Propris um sil soil tmpo iscrto ) Siis soiis cujs frquêcis são sprs por múltiplos itiros π são iêticos. [( w πm ) φ] cos[ w πm φ] cos[ w φ] cos b) A t mis lt oscilção pr siis tmpo iscrto é obti quo w π ou f.5. Pr provr st propri, cosir um squêci () tl qu: ( ) A cos( w ), m qu : < < π w Sj um outr squêci (), com frquêci mior qu π, tl qu: ( ) A cos[ ( w π) ] Assim, pricípio, frquêci () sri w π, ms st firmção ão é vrir pois: ( ) A cos[ ( w π) ] A cos[ ( w π π) ] Pl propri trior, propri () i rlmbro qu fução cosso é pr tm-s qu: ( ) A cos[ ( w π) ] A cos[ ( π w ) ] Assim, frquêci st sil srá π - w, logo l prtc o itrvlo (,π). Portto frquêci oscilção mis lt é obti quo w π. c) Um sil soil iscrto é prióico s somt s frquêci for um úmro rciol.
12 - 6 - Dfiição: S um squêci () é prióic, com príoo, tão () srá igul (), m qu é o mor itiro qu stisf rlção () (). Sj: S () é prióic tão: ( ) A cos( πf ) ( ) A cos( πf ) A cos[ πf ( )] A cos( πf πf ) Obsrv qu pl propri () rlção cim é vrir s istir um úmro M, itiro tl qu: f πm f π Portto f v sr um úmro rciol pr squêci sr prióic. ) Um sil soil po sr obtio pls rlçõs Eulr: j θ jθ M cos ( θ) (.6.) j θ jθ s( θ ) (.6.b) j θ ( θ) j s( θ) j cos (.7).4 Algums fiiçõs sobr siis tmpo iscrto.4. Ergi A rgi um sil tmpo iscrto é fii pl sguit qução: E ( ) (.8) S o sil () prstr rgi fiit l é chmo sil rgi. Os siis urção fiit, isto é, quls qu prstm somt mostrs ão uls, têm smpr rgi fiit. Os siis urção ifiit qu prstm rgi fiit são crctrios por vlors mostrs qu tm ro coform t ifiito..4. Potêci ( ), coform E < (.9) Em grl, os siis prióicos os procssos ltórios prstm rgi ifiit. Pr sts csos é propri fiição potêci méi qu é pl sguit qução:
13 - 7 - P lim ( ) (.) S o sil é prióico, com príoo fumtl, tão potêci méi é fii por: ( ) P (.) α Emplo : Dtrmi rgi o sguit sil: ( ) A u( ), : α < α A ( ) α α α A A A E Emplo : Dtrmi potêci squêci gru uitário u(). P lim u ( ) lim lim / lim / Emplo : Dtrmi potêci um sil complo, composto pl som us compots soiis, com frquêcis w w ifrts, tis qu: ( ) A A m qu, A A são costts ris positivs. - Cálculo () ( A A )( A A ) * ( ) ( ) ( ) A A A A - Cálculo Potêci P lim A A j( w w ) j( w w ) ( ) j( w w ) j( w w ) [ A A A A ( )] A A lim j( w w ) j( w w ) ( ) j( w w ) lim j( w w ) j( w w Emio o limit: ( ) ) L lim Portto: P A A Po-s mostrr tmbém qu pr M sóis compls istits potêci méi srá:
14 - 8 - P M A (.) st mplo form cosiros siis soiis complos. Pr situção m qu s tm M siis soiis ris com frquêcis istits, potêci méi srá por: P M A (.).4.. Squêcis simétrics ti-simétrics Sj () um squêci compl * () o su cojugo. Um squêci é chm simétric (pr) s: ( ) * ( ) Um squêci é omi ti-simétric (impr) s: ( ) * ( ) É possívl tmbém obtr um squêci simétric () ou um ti-simétric o () prtir um squêci qulqur () trvés s sguits prssõs: [ ] * ( ) ( ) ( ) (.4) o [ ] * ( ) ( ) ( ) (.5).5 Sistms tmpo iscrto Os sistms tmpo iscrto são fiios o msmo moo qu os sistms cotíuos. Els são fiios mtmticmt como um trsformção qu s opr m um squêci tr () prouio um squêci sí y() chm rspost o sistm à citção (). Est trsformção é rprst pl sguit rlção: [ ( )] y ( ) T (.6) m qu o opror T[.] rprst trsformção su rprstção gráfic é fit plo igrm blocos mostro figur bio. () T[()] y() Figur.4: Rprstção um sistm tmpo iscrto. Emplo 4: Sgu sguir lgus mplos sistms tmpo iscrto qu são muito utilios m procssmto igitl siis: ) Sistm trso y ( ) ( ) (.7)
15 - 9 - Amitio um úmro itiro positivo, st sistm trs (sloc) o sil tr por mostrs. o cso sr gtivo l vç pl msm quti mostrs. b) Acumulor O sistm cumulor clcul som toos os vlors pssos tr té o istt prst (tul). El é fiio pl sguit qução: ( ) ( ) y (.8) Isolo o trmo orm prssão cim s tm qu: y ( ) ( ) ( ) Obsrv qu o sguo trmo qução cim rprst sí trs mostr. Assim: ( ) ( ) y( ) y (.9) A qução (.9) justific o trmo cumulor, pois sí p o vlor prst tr o vlor trior y(-) sí. Além isso, su rspost ão é uicmt trmi pl tr, ms p s coiçõs iiciis o sistm, isto é, o sto o sistm ts s plicr citção. Cosiro, por mplo, qu o sistm qu é plico fução u(), po-s obsrvr qu sí p y(-). - mitio y(-) tm-s: y ( ) u( ) y( ) - mitio y(-) tm-s: ( ) y ( ) u( ) y( ) ( ) Obsrv qu os rsultos triors mostrm qu sí p y(-). Frqutmt, quo s coiçõs iiciis são uls, isto é, y(-) y(-)..., o sistm é ito str m rpouso (ou rlo). c) Sistm sm mmóri Um sistm sm mmóri é qul cuj sí p somt tr o istt. Por mplo, o sistm fiio pl qução (.) ão tm mmóri..5. Sistms lirs tmpo iscrto ( ) [ ( ) ] y (.) Um sistm lir tmpo iscrto (qu srá brvio pl sigl (LTD) é qul qu obc o pricípio suprposição, isto é: Amitio y (), y (),..., y M () s rsposts o sistm corrspots, rspctivmt, às citçõs (), (),..., m (), tão o sistm é lir s somt s :
16 - - T T [ ( ) ( ) ( ) ] T[ ( ) ] T[ ( ) ] L T[ ( ) ] L M M [ ( ) ( ) ( ) ] y ( ) y ( ) L y ( ) L M M M M (.) m qu, M é um úmro itiro qulqur,,..., M são costts. Emplo 5: Emplos ois sistms lirs: ) O sistm y() () é lir pois: [ ( ) ( ) ] [ ( ) ( ) ] ( ) ( ) y ( ) y ( ) T b) O cumulor fiio pl qução (.8) é um sistm lir pois: y ( ) [ ( ) ( ) ] ( ) ( ) y ( ) y ( ).5. Sistms lirs ivrits o slocmto Um sistm LTD ivrit o slocmto é qul cuj crctrístic ão vri com o slocmto provoco tr. Assim, um sistm LTD é ivrit o slocmto s somt s: T [ ( )] y( ). (.) M M Emplo 6: Emplos sistms ivrits vrits o slocmto: Sj y (, ) sí o sistm quo s plico m su tr um squêci ( ) ) O ifrcior, y() () (-) é ivrit o slocmto pois: y (, ) ( ) ( ) y( ). b) O sistm y() () é vrit o slocmto pois quo é plico (- ) tm-s: y (, ) ( ) y( ) ( ) ( ) c) O sistm y() (-) é vrit o slocmto pois: Sj: ( ) ( ), tão: y ( ) ( ) ( ) y( ) ) O comprssor y() (M) é vrit o slocmto ão sr qu M. Sj: ( ) ( ), tão:.5. Sistms cusis y ( ) ( M) ( M ) y( )
17 - - Um sistm é chmo cusl s o sil prst su sí y(), m qulqur istt, p somt os vlors os istts pssos sí os istts prst pssos tr {(), (-), (-),...}, ão p os vlors futuros {(), (),..., y(),...}. Um outr fiição muito usul pr os sistms cusis é qu sgu: Um sistm é chmo cusl s pr qulqur istt su sí o istt p os vlors tr pr. Emplo 7: Emplos sistms cusis: ) y ( ) ( ) ( ) ) y ( ) ( ) ) y ( ) ( ) by( ) Emplo 8: Emplos sistms ão cusis: ) y ( ) ( ) ( 4) ) y ( ) ( ) ) y( ) ( ) 4) y( ) ( ).5.4 Sistms stávis Um sistm m rpouso, é stávl s somt s pr um squêci tr limit tm-s um sí limit, isto é: m qu B B y são costts fiits. Emplo 9: Emplos sistms stávis ) y( ( ) ( ) ) y ( ) [ ( ) ] ) y ( ) ( M) Emplo : O cumulor é um sistm istávl. ( ) B < y( ) B <, (.) y ( ) ( ) Sj () u() qu é limit, pois o vlor máimo fução gru uitário é. Etão: y
18 - - y ( ) u( ), <, Obsrv qu mbor sj fiito, ão ist um vlor fio pr B y, como fiição m (.), tl qu: ( ) B y <..5.5 Rprstção m igrm blocos os sistms tmpo iscrto Srá útil st prt fr um pqu itroução à rprstção por igrm blocos os sistms LDT, pois l fcilit o stuo su implmtção. As pricipis oprçõs m sistms tmpo iscrto são mostrs plos blocos bio. ) Bloco somor () y() () () () b) Bloco multiplicor () y() (). () () c) Bloco multiplicor por costt () () y() () ) Bloco slocor mostrs () - y() ( ) Em qu - é um opror trso qu sloc () por mostrs o sil. Est rsulto ficrá prt o stuo trsform, o cpítulo. Emplo : Rprst trvés igrm blocos o sguit sistm: y ( ) y( ). 5( ). 5( ) Rrrjo qução cim moo s coomir um bloco multiplicor tm-s qu: y ( ) y( ). 5[ ( ) ( ) ]
19 - - ().5 y() - - (-) y(-) Figur.5: Digrm m blocos o sistm..5.6 Sistms lirs iscrtos ivrits o slocmto As fiiçõs s triormt clssificm os sistms quto às su propris ctgoris tis como: liri, ivriâci o slocmto ou o tmpo, cusli stbili. Os sistms lirs iscrtos ivrits o slocmto qu srão brvios por LID São os mis importts sts sistms. Els são crctrios o omíio o tmpo por su rspost à fução mostr (ou impulso) uitári como srá visto sguir, prssão grl qu rlcio tr sí tis sistms é pl som covolução. Pr s trmir rspost o sistm um citção tr () qulqur, srá mitio qu h() é rspost o sistm LID à fução mostr uitári. Como foi visto triormt, vj qução (.5), um squêci () po sr scrit como um som por fuçõs mostrs uitáris, tl qu: ( ) ( ) δ( ) (.4) Assim, por fiição, rspost um sistm vio à citção tr () srá por: ( ) [ ( )] y T T ( ) δ( ) (.5) Como por hipóts, o sistm é lir, tão, plico o pricípio suprposição tm-s qu: y ( ) ( ) T[ δ( ) ] Como, tmbém por hipóts, o sistm é mitio sr ivrit o slocmto, tão rspost á citção δ(-) srá h(-), logo, ( ) ( ) h( ) y (.6) Obsrv qu tr sí stão rlcios trvés h(), como cosquêci, um sistm LID é crctrio compltmt pl su rspost á fução mostr uitári, h(). Assim, um v qu é fução h(), po-s trmir squêci sí y() vio à citção tr () trvés qução (.6). A qução (.5) é cohci plo om som covolução ou simplsmt covolução tr () h(), so rprst plo opror *, isto é,.5.7 A som covolução y( ( ) h( ) ( ).\ (.7)
20 - 4 - Supoh qu s qur clculr sí o sistm m um istt qulqur,. Utilio qução (.6) tm-s qu: y ( ) ( ) h( ) (.8) Obsrv st qução qu som é rli os íics ão os íics, lém isso, st íic é ivrtio rspost o impulso o sistm. Dss moo po-s rsumir como sgu s oprçõs volvis som covolução: i. Rbt-s h() m toro pr s obtr h(-), ii. Dsloc-s h(-) por mostrs á irit, s for um úmro positivo (ou à squr s for gtivo), iii. Multiplic-s c lmto () por h( ) pr s obtr squêci ()h( ), iv. Somm-s toos os vlors squêci prouto pr s obtr y( ), v. Rptm-s os pssos cim pr toos os vlors possívis moo obtr-s y(). Emplo : Dtrmi som covolução tr s sguits squêcis: h() {,,, -} () {,,, }. O úmro m grito iic o vlor squêci pr o íic. - Rbtimto h(): h(-) {-,,, } - Cálculo y(): h ( ) ( ) y ( ) 4 - Cálculo y() h ( ) ( ) 4 y () 8 - o fil, clculo covolução pr -,,,..., 5, obtmos y(). Pr os outros vlors os rsultos são ulos. y() {, 4, 8, 8,, -, -} ot st mplo qu o tmho squêci () é M 4, o tmho h() é 4 o y() é L 7. Como rgr grl tm-s qu pr squêci tmho fiito covolução prou um squêci fiit tmho: L M. (.9) Um outr obsrvção importt é qu pr os sistms cotíuos, lirs ivrits o tmpo, rlção tr tr sí é rgi pl itgrl covolução, st cso é possívl somt stur
21 - 5 - o comportmto tórico sts sistms. Já os sistms LID são rgios pl som covolução m qu é possívl, ão somt stur o comportmto tórico, ms tmbém rliá-lo utilio procssors igitis trvés implmtção um lgoritmo qu rsolv qução (.6) Propris covolução sistms LID ) A som covolução é comuttiv, isto é, b) A covolução é ssocitiv, isto é, ( ) ( ) * h( ) h( ) * ( ) h( ) ( ) y (.4) ( ) [ ( ) * h ( ) ]* h ( ) ( )* [ h ( ) * h ( ) ] y (.4) Est propri é itrprt o sguit moo: Dois sistms itrcoctos m csct corrspom um sistm quivlt cuj rspost o impulso é covolução s rsposts o impulso iiviuis os ois sistms. () h () h () y() () h ()*h () y() c) A covolução é istributiv, isto é, Figur.6: Itrprtção li ssocitiv. ( ) ( ) * h ( ) ( ) * h ( ) ( ) * [ h ( ) h ( ) ] y (.4) Dois sistms m prllo corrspom um sistm cuj rspost o impulso é som s rsposts iiviuis os sistms. h () () y() h ()h () () y() h () Figur.7: Itrprtção li istributiv..5.8 Cusli stbili m sistms LID Pr os sistms lirs iscrtos ivrits o slocmto, s propris cusli stbili pom sr protmt vrifics trvés ális rspost o impulso o sistm. ) Cusli Cosir sí um sistm LID m um o istt. Dss moo: y ( ) h( ) ( ) Dsobro qução cim m us quçõs tm-s qu:
22 - 6 - y y ( ) h( ) ( ) h( ) ( ) ( ) [ L h( ) ( ) h( ) ( ) ] [ h( ) ( ) h( ) ( ) L] O primiro trmo tr colchts volv os vlors futuros (): ( ), ( ),... Como o sistm é cusl su rspost ão po pr sts vlors (futuros), ssim, o primiro trmo v sr ulo. Pr qu ls sjm ulos v-s tr portto: h(-) h(-)..., ou sj rspost o impulso v stisfr sguit coição: ( ), < h (.4) Amitio qu s stj trblho com um sistm cusl, os limits somtóri covolução pom sr moificos moo rfltir coição stblci pl qução (.4). ( ) ( ) h( ) h( ) ( ) y (.44) lém isso, s squêci tr () tmbém for cusl, tão: y ( ) ( ) h( ) h( ) ( ) (.44) b) Estbili A stbili é tmbém um propri muito importt sr vrific implmtção um sistm. Como posto triormt, um sistm é stávl s pr um tr limit sí tmbém srá limit. ovmt, utilio qução covolução mitio qu () B <, tão móulo squêci sí é, ms, por hipóts () B, tão: ( ) h( ) ( ) y (.45) y ( ) h( ) ( ) ( ) B h( ) y. Assim, pr qu o sil sí sj limito v-s tr qu: ( ) B < h. (.46) h Portto, pr qu um sistm LID sj stávl, rspost o impulso v sr bsolutmt somávl. Est é um coição cssári suficit, lém isso l iic qu h() v sr mortci, isto é, cir pr ro coform s proim o ifiito.
23 - 7 - A rspost o impulso um sistm tmpo iscrto srv tmbém pr clssificá-los m rlção à su urção: - Os sistms FIR (brvição o iglês fiit impuls rspos) são quls cuj rspost o impulso é fiit, isto é têm urção limit. - Os sistms IIR (brvição o iglês ifiit impuls rspos), isto é, quls cuj rspost o impulso é ifiit. Est omcltur srá muito utili m projto filtros igitis. Obsrv qu os sistms FIR são smpr stávis, pois h() prst urção fiit..6 Equção lir ifrçs com coficits costts Um s forms s scrvr um sistm LID é trvés su rspost o impulso cosqutmt trvés som covolução, cotuo, miori os csos é cssário ou sjávl prssr o comportmto o sistm m trmos os vlors prst pssos o sil tr, tmbém os vlors pssos o sil sí. Pomos rprstr os sistms iscrtos trvés qução lir ifrçs. st cso o sistm é protmt implmto trvés blocos somors, multiplicors trso. Além isso, l srv como bs pr obtção rspost m frquêci o sistm, como srá visto mis it. A form grl pr um sistm LID scrito trvés um qução lir ifrçs é por: y ( ) y( ) b ( ) M (.47) m qu os coficits b são prâmtros costts o sistm. Um form quivlt scrvr st sistm é trvés qução bio: y M ( ) b ( ) (.48) m qu é mitio sr igul, o limit somtóri é chmo orm o sistm. Obsrv qu qução (.47) prss rspost o sistm LID como um som por os vlors pssos y(), y(-), y(-),..., y(-), os vlors prst pssos, (), (-),..., (-M), por isso st qução tmbém é chm rcursiv pois sí p vlors triors tr sí. Além isso pr s trmir y() é cssário o cohcimto s coiçõs iiciis o sistm, isto é, y(-), y(-),..., y(-). A qução (.47) é form grl um qução lir ifrçs rprst um sistm cuj rspost o impulso é ifiit (sistm IIR). o cso sistms com rspost o impulso fiit (sistms FIR), sí p somt os vlors prsts pssos tr. Dss moo, :,,..., fic fácil mostrr qu rspost o impulso h() é plos próprios coficits b, ou sj: h ( ) b,,, L, M, cso cotrário (.49) Emplo : Dtrmi qução ifrçs pr o sistm cumulor: y ( ) ( )
24 - 8 - y ( ) ( ) ( ) y( ) ( ) Assim, st sistm é rprsto por um qução lir ifrçs tl qu compro com qução (.48) tmos:,, M b. () y() y(-) - Figur.8: Digrm m blocos o cumulor..6. Solução qução ifrçs A solução qução ifrçs, qução (.47), é compost us prts: A rspost turl (ou homogê), y (), qu é vi um tr ul, (), rspost prticulr (ou forç) y p (), vi um tr ão ul. A rspost totl o sistm é o rsulto s us rsposts triors. y ( ) y ( ) y ( ) (.5) Pr s trmir y() é cssário o cohcimto s coiçõs iiciis o sistm, isto é, o cohcimto y(-), y(-),..., y(-). S s coiçõs iiciis são uls o sistm stá m rpouso, pois ão há rmmto rgi s mmóris o sistm. p A rspost turl A rspost turl é solução qução homogê, El prst sguit form: ( ) y (.5) y ( ) i c iri (.5) Em qu r i são s rís o poliômio crctrístico o sistm: i i r (.5) Rsolvo qução cim clculmos r i os coficits c i são trmios moo stisfr s coiçõs iiciis. Pr o cso m qu um ri é rpti M vs, vm-s crsctr os trmos: r j, r j M j, L, r (.54) A rspost prticulr (forç)
25 - 9 - A rspost forç é solução qução ifrçs mitio um tr ifrt ro. Como stmos mitio um sistm lir, rspost é obti supoo qu sí th msm form tr, por mplo, pr um tr soil sí tmbém srá soil provvlmt moific m mplitu fs plo sistm. A tbl bio rsum s soluçõs pr s trs mis comus utilis os sistms. Tbl : Solução prticulr pr lgums trs. Etr Solução prticulr (costt) c (costt) c w φ cos w c s w cos( ) ( ) ( ) c Emplo 4: Dtrmi rspost totl o sistm LID rprsto pl qução ifrçs: y ( ) 4y( ) ( ) quo plicmos tr fução gru uitário. Amit s sguits coiçõs iiciis: y(-) y(-). Obsrv qu -4 - Rspost turl: r 4 r ± portto: y ( ) c ( ) c ( ) - Rspost prticulr: obsrv qu tr vl pr, logo y p ( ) c. Substituio qução ifrçs tm-s: 4c c y c p ( ), - Rspost totl: y( ) y ( ) y ( ) c ( ) c ( ) p As costts c c são trmis utilio s coiçõs iiciis. Assim, y y 4 4 ( ) c ( ) c ( ) c c ( I ) ( ) c ( ) c ( ) c c ( II ) Combio s quçõs (i) (II) tm-s qu: c c 8 Portto rspost totl srá: y 4 4 / ( ) 4( ) ( ) 8.6. Rspost o impulso
26 - - A rspost o impulso um sistm po sr cotr trvés rspost o gru uitário, supoo qu o sistm stj m rpouso, isto é, com coiçõs iiciis uls. Amitio s() como rspost m rpouso à fução gru, tão, pl qução (.8), rspost o impulso srá h() s() s(-). Emplo 5: Dtrmi rspost o impulso o sistm o o mplo 4. Pr trmir rspost o impulso mitimos y(-) y(-), logo, y y 4 4 ( ) c ( ) c ( ) c c ( I ) ( ) c ( ) c ( ) c c ( II ) Combio s quçõs (i) (II) tm-s qu: c c / Assim, rspost totl srá: s( ) ( ) ( ) E rspost o impulso srá h() s() s(-): h ( ) ( ) ( ).7 Rprstção siis sistms iscrtos o omíio frquêci Dvio o fto qu quo o sil tr é soil sí um sistm lir é tmbém um sil soil com msm frquêci tr, mplitu fs trmis plo sistm, rprstção siis trvés compots soiis ou tão pociis compls é muito usul tori prátic sistms lirs. Cosir um sistm LDI, com rspost o impulso h(), m cuj tr é plic um squêci pocil compl form: ( ), : < < (.55) A sí o sistm srá pl som covolução tr tr () rspost o impulso o sistm h() tl qu: Como o íic ão tr somtóri, ( ) ( ) ( h ) y (.56) Vmos fiir sguit fução: ( ) h( ) y (.57)
27 - - ( ) h( ) H (.58) Est fução é chm Rspost m Frquêci o sistm. Obsrv qu l scrv ltrção mplitu pocil compl,, m fução su frquêci. A qução (.58) mis é qu trsform Fourir squêci h(). Assim, pomos scrvr qu sí o sistm srá: ( ) H ( ) y (.59) A sí, y(), é um pocil compl msm form qu tr, ms moific pl mplitu fs H( ). Fic ssim prt qu H( ) crctri compltmt um sistm lir. Em grl, rprst-s rspost o sistm por um rspost mplitu (móulo H( )) um rspost fs tl qu: H j H ( ) H ( ) ( ) (.6) O trmo H( ) trmi mplificção (s H( ) > ) ou tução (s H( ) < ) qu o sistm impõ o sil tr o trmo H( ) trmi quti slocmto fs impost o sil soil tr. Assim o móulo rspost m frquêci, H( ) é chmo rspost mplitu o sistm o trmo H( ) é chmo rspost fs Emplo 6: Cosir o sistm trso: y() ( ). Aplico squêci pocil compl () tr st sistm tm-s qu: y ( ) ( ) Compro qução cim com (.59), cocluímos qu rspost m frquêci o sistm srá por: H ( ) H H ( ) ( ) w O cocito rspost m frquêci pr os sistms lirs ivrits o tmpo é o msmo, tto pr os sistms cotíuos como pr os iscrtos. Cotuo, rspost m frquêci pr os iscrtos tm um ifrç fumtl, l é smpr prióic, com príoo igul π. Pr obsrvr st crctrístic cosir um frquêci w w π qução (.6). Assim: j ( ( w π) j ) ( ) ( w π ) H h h( ) como -jπ cos(π) js(π), tão: jπ j ( ( wπ) H ) h( ) H ( ) (.6) Portto H( ) é prióic, com príoo π. Dss moo, por coviêci simplici l srá smpr prss m um os itrvlos bio:
28 - - w < π π < w π ou f <.5 < f.5 Emplo 7: Dtrmi rspost m frquêci o sistm cuj rspost o impulso é bio, tmbém squêci sí, quo squêci tr é por: () A jπ/. h ( ) u( ) - Cálculo rspost m frquêci o sistm, qução (.58): H ( ) h( ) - Dtrmição squêci sí, qução (.59): y jπ / jπ / jπ / j ( ) ( ). jπ / j( π / H A A A A ). j Est mplo mostr qu sí cotiu so um pocil compl com msm frquêci tr, com um slocmto fs provoco plo sistm igul. rios um ltrção mplitu plo ftor /. As msms coclusõs srim vlis s tr foss um squêci soil rl. S tr o sistm cosistir mis qu um sil soil plic-s o pricípio suprposição..8 Trsform Fourir pr squêcis O pr trsforms Fourir pr um squêci ou sil iscrto () é fiio pls sguits quçõs: ( ) ( ) X (.6) π π ( ) X ( ) w. (.6) π A qução (.6) é trsform Fourir irt pr squêcis ou siis iscrtos, tmbém chm qução ális, qução (.6) é trsform Fourir ivrs ou qução síts pois rprou () prtir su spctro frquêci. A trsform X( ) é um fução compl portto é usul scrvê-l form polr, isto é, X j X ( ) X ( ) ( ). (.64) O móulo trsform é cohcio como spctro mplitu, fs como spctro fs. O spctro fs ão é trmio uicmt, s qu qulqur itiro múltiplo π po sr somo à fs sm ftr o rsulto fil. Em grl, trmi-s o vlor pricipl, itifico por
29 - - ARG[X( )] com vlors tr ± π. Como iscutio sção trior, tto o spctro fs como o mplitu são prióicos com príoo π. Um prgut qu s origi urt o cálculo trsform é: Qul clss siis tmpo iscrto qu po sr rprst pl trsform Fourir? st cso v-s lisr covrgêci trsform. Pr qu trsform ist, qução (.6) v covrgir, isto é, coição bio v sr stisfit: Obsrv qu: ( ) < : w < π X (.65) ( ) ( ) ( ) X, ( ) ( ) < X. (.66) Portto, coição suficit pr qu trsform Fourir ist é qu () sj bsolutmt somávl. Emplo 8: Dtrmi trsform Fourir squêci () u(). X ( ) ( ) Obsrv qu séri cim é um progrssão gométric com rão -. Amitio qu - <, o qu é quivlt mitir qu <, tm-s qu: X ( ) (.67) A coição trior < implic squêci () é bsolutmt somávl, grtio covrgêci uiform séri Um obsrvção importt s fr é qu istm lgums squêcis qu ão grtm coição qução (.66), ms msmo ssim é possívl cotrr su trsform Fourir. Em prticulr, é possívl rlr st coição clculr trsform Fourir squêcis cuj rgi é ifiit. Eistm outros csos o s squêcis ão são m bsolutmt somávis, m têm rgi fiit, ms é possívl clculr trsform fo uso fução impulso uitário. (Vj Ophim, 989, mplo pp 49)..8. Espctro si rgi Foi fiio sção.. qu rgi um sil é por: E * ( ) ( ) ( )
30 - 4 - Utilio fiição trsform ivrs Fourir, qução (.6), trsform Fourir ivrs o cojugo um squêci é, π π * ( ) X ( ) w π substituio qução cim s tm qu: E * π * ( ) X ( ) π π Troco orm s oprçõs somtóri com itgrl, π * E X π π w ( ) ( ) w Obsrv qu quti tr prêtsis é trsform Fourir (). Assim, rgi () po sr trmi utilio su trsform Fourir, ou sj, π π π ( ) X ( ) w X ( ) * E X w π π π (.68) A quti: ( ) X ( ) S (.69) rprst istribuição rgi squêci () m fução frquêci por isso msmo l é chm Espctro Dsi Ergi () Emplo 9: Dtrmi trsform Fourir o spctro si rgi squêci, ( ) A,, < M c. c. Amitio qu M sj um úmro fiito, () é bsolutmt somávl portto prst trsform Fourir, pois, Cálculo X( ): X M ( ) A M A < M M ( ) ( M A A A ) / sw / O móulo fs o spctro são: swm /
31 - 5 - X swm / A, π w < π ( ) X ( ) w( m ) / sw / M A, w O spctro si rgi é o plo quro o móulo X( ), ssim: S ( ) swm / A sw / 5 4 -π -4π/M -π/m π/m 4 π/m w π - w -π -4π/M -π/m π/m 4π/M π Figur.9: Espctro mplitu fs pr o mplo 7, mitio A M Propris trsform Fourir pr siis iscrtos o cálculo trsform Fourir, o cohcimto utilição crts propris fcilitm o uso itrprtção os rsultos. ) Simtri Quo o sil stisf crts propris simtri o omíio o tmpo, sts impom crts propris trsform. Ats listr sts propris cosir s sguits fiiçõs: [ ] * Squêci cojug simétric: ( ) ( ) ( ) ( ) * Squêci cojug ti-simétric: ( ) ( ) ( ) ( ) o * * o Propris simtri. * ( ) * X ( ) {( ( ) } X ( ). Im{ ( ) } X o ( ) 4. ( ) X ( ) [ ] (.7) (.7) (.7) R (.7) j (.74) (.75) R
32 ( ) jx ( ) Amitio () um squêci rl tm-s X( ) é: (.76) * 6. Cojug simétric: X ( ) X ( ) 7. A su prt rl é pr: X R ( ) X R( ( ) 8. A su prt imgiári é ímpr: X ( ) X ( ) 9. O su móulo é pr: X ( ) X ( ). A su fs é ímpr: X ( ) X ( ) b) Propris torms gris o I I (.77) (.78) (.79) I (.8) (.8) Além s propris simtri, têm-s tmbém outrs propris muito importts qu rlciom oprçõs com squêcis fcilitm o uso obtção rsultos tóricos com siis sistms. Ests propris são lists bio sm procupção m prová-ls. Ds qu ls são similrs o cso trsform Fourir pr siis cotíuos rcom-s como rcício prov sts propris.. Liri ( ) by( ) X ( ) by ( ) (.8). Dslocmto o omíio o tmpo ( ) X ( ). Dslocmto o omíio frquêci (.8) ( ) j ( ) ( w ) X w (.84) 4. Rvrsão o tmpo ( ) X ( ) (.85) 5. Difrcição o omíio frquêci 6. Torm Prsvl ( ) j X ( ) (.86) w Est torm rlcio o cálculo rgi o sil o omíio o tmpo com o cálculo o omíio frquêci (vr spctro si rgi sção.7.) π ( ) X ( ) E w π π (.87)
33 - 7 - π * * ( ) y ( ) X ( ) Y ( ) π π w (.88) 7. Torm covolução ( ) * y( ) X ( ) Y ( ) (.89) 8. Torm moulção ou jlmto jθ * j ( ) ( ) ( ) ( ( wθ X Y )) w π π θ π (.9) Emplo : Dtrmi trsform Fourir sguit squêci, ( ) : < Pr rsolvr st mplo vmos prssr () como som us squêcis, () (),,, ( ) ( ) <,, < A trsform Fourir squêci () já foi clcul o mplo 6 vl: X ( ) - Cálculo X ( ): X ( ) ( ) Aplico o torm liri tm-s qu: X ( ) X( ) X ( ) Como <, o spctro fs é ulo pois X( ) é rl smpr positiv. cos w.5 () (b) - -π - - π (c) w w Figur.: () squêci (), (b) spctro mplitu; (c) spctro fs pr o mplo 9.
34 - 8 - Emplo : Dtrmi o móulo fs fução o sistm o filtro méi móvl, o pl qução ifrçs bio: y ( ) { ( ) ( ) ( ) } Obsrv qu st é um filtro FIR (rspost o impulso fiit), sí p somt vlors prsts ou pssos tr. Assim, Clculo trsform Fourir: Portto: h ( ) δ( ) δ( ) δ( ) { } cos w H ( ) H ( ) cos w φ ( ), π, w π / π / < w < π.5.5 -π -π / -π / π / π / π π -π -π -π / -π / π / π / π Figur.: Espctro mplitu fs pr o mplo. os ois mplos cim s po obsrvr qu rspost mplitu é um fução pr frquêci fs é um fução ímpr. A rprstção um sil o omíio frquêci é importt pr s obsrvr lisr o cotúo frquêcis um sil ou um sistm. Em procssmto siis st iformção é muito importt usul. Por mplo, ális fitos filtrgm, v-s mir cohcr o comportmto o sil sr filtro o omíio frquêci, quli smpho os filtros tmbém é stblci liso rspost m frquêci sts. Quo s sj trsmitir siis m um cl tlcomuicçõs v-s cohcr su rspost m frquêci pr qu, bso-s st
35 - 9 - iformção, sj possívl ciir qu fi ou grupo frquêcis pom sr trsmitis trvés o cl com pouc istorção. A tbl, mostr bio, rlcio lgums squêcis básics frqutmt utilis m procssmto siis, jutmt com sus rspctivs trsforms Fourir. Tbl : Prs trsforms Fourir. Squêci. δ (). ) δ (. u( ) : < Trsform Fourir 4. ( ) π δ( w π) 5. r s w ( ) u( ) : r < s w r cos w r 6. s w, w < w π, w < w π 7. 8., < M ( ), cso cotrário s wm / s w / ( M ) / π δ( w w π)
36 - - Ercícios. Cosir squêci () (5-)[u() u(-5)]. Dsh: ) () b) y () (-) c) y () (-) ) y () (-). Um sil iscrto é fiio por:, ( ), c. c. () Dtrmi squêci () sh o sil. (b) Dsh o sil (-). (c) Dsh o sil (). () Dsh o sil ().u().. Dsh s sguits squêcis: () () cos[(π/)] (b) () cos[(π/6)] (c) () u() u(-5) () () (.5) u() () () u() 4. Pr os its () (b) o rcício trior, mitio T., trmi os siis cotíuos o tmpo qu grrm s squêcis. 5. Eprss os siis bio m trmos fuçõs prõs. (miti qu ls sjm soiis). () () (b) (){,,,,,,,...} 6. Eprss squêci bio m fução fuçõs gru uitário pors. ( ),,,, c. c. 7. Pr c um os siis bio, sboc () trmi E ou P M.
37 - - π / () ( ) u( ) (b) ( ) cos[ π( 6) / 6]{ u( 6) u( 6 )} 8. Dtrmi covolução pr os sguits prs siis: ) ( ) {, } h( ) {,, } b) ( ) δ( ) h( ) {,, } c) ( ) α u( ) h( ) β u( ) α β ) ( ) h( ) α u( ) 9. Dtrmi rspost o impulso os sistms os bio. (cosir coiçõs iiciis uls) () y ( ) ( ) ( ) 4( ) ( 4) (b) y ( ).5( ) ( ).5( ).5( ) (c) y ( ) ( ) y( ) () y ( ) ( ) y( ) () y ( ) ( ) ( ) y( ) (f) y ( ) ( ) y( ) y( ) 4 (g) y ( ) ( ) ( ) y( ) y( ) 4. Pr c sistm bio trmi s ls são ou ão: lirs, ivrits o slocmto, cusis, stávis, com ou sm mmóri. Prov s propris ou forç um cotr mplo cotr rspost o impulso. () y ( ) ( ) y( ) (b) ( ), pr y( ) ( ), ímpr (c) y ( ) ( ) (), ( ) > y ( ) ( ), ( ), ( ) < () y ( ) (). Pr os sistms bio cotr rspost o impulso, rspost m frquêci (simplifiqu o máimo possívl qução), sboc o spctro mplitu scrv m trmos gris o fito filtrgm m um sil. () y ( ) ( ) y( ) (b) y ( ) ( ) ( ) y( ) (c) y ( ) { ( ) ( ) ( ) } 4 () y ( ) ( ) ( ) ( ) ( ) ( 4)
38 - -. Cosir o sistm LID scrito pl sguit qução ifrçs: y ( ) ( ) ( ) ( ) () Dtrmi h(), (b) Dtrmi H( ), (c) Ecotr rspost st sistm à tr {,.5,.5 }. Cosir o sistm SLI scrito pl sguit qução ifrçs: y ( ) ( ) ( ).5y( ) () Dtrmi h(), (b) Dtrmi H( ), (c) Ecotr rspost st sistm à tr () u() () Digrm m blocos o sistm. 4. Cosir o sistm cusl LID scrito pl sguit qução ifrçs: y ( ) y( ) ( ) b( ) Ecotr o vlor b pr qu su rspost m mplitu sj costt pr qulqur frquêci. Est tipo filtro é chmo pss tuo. 5. Clcul trsform Fourir s sguits squêcis:, 5 () (), cso cotrário (b) ( ) ( ) { u( ) u( 8)} (c), ( ),, c. c. () π π ( ) cos 5 () y( ) j ( ) (f) y( ) ( )* ( ) 6. Dtrmi qução ifrçs qu crctri o sistm cuj rspost m frquêci é por: () (b) (c) H ( H ( H ( ) ) ) 4
39 S rspost o gru uitário um sistm lir ivrit o slocmto é: s ( ) u( ), > δ. Dtrmi rspost o impulso h() st sistm. ot qu: ( ) u( ) u( ) h( ) s( ) s( ) 8. Cosir o filtro igitl bio. Amitio um frquêci mostrgm igul 8 H, trmi s frquêcis cort ifrior suprior lrgur b o filtro lógico quivlt. Ercícios o computor: 9. Utilio o Mtlb gr sh os siis bio: () () cos[(π/)]u() :, 5 (b) () u() u(-5) (c) () δ() () () (.5) u() () () u() (f) ruío brco gussio com vlor méio ro svio prão igul. (g) Ruío brco com istribuição uiform tr, tr.5.5. Cosir o sguit sistm LID: y( ) ( ) ( ) L ( ) { } () Dtrmi H( ) tmbém o móulo fs, (b) Utili o Mtlb pr shr o móulo fs ( w π ) mitio 4, 5,. (c) Comt os rsultos.. Cosir o sguit sistm LID: y ( ) { ( ) ( ) ( ) } Utili o Mtlb pr shr (utili fução gráfic stm) sí y() mitio: (), ( ), c. c. π (b) ( ) s u( ) 4
40 - 4 -
41 - 5 - Cpítulo AMOSTRAGEM DE SIAIS.. Siis tmpo iscrto Os siis tmpo iscrto prstm vlors fiios somt m trmios istts o tmpo. Grlmt ls provêm siis (ou fuçõs) o tmpo cotíuo qu são mios ou grvos m itrvlos tmpo rgulrmt spços. s últims écs sts siis ssumirm gr importâci vio o svolvimto ltrôic igitl os computors pssois. Por sr impossívl itrouir os cotíuos os computors igitis, qulqur sil ou o cssit sr rprsto por um cojuto úmros pr procssmto postrior. S prtrmos trblhr com siis tmpo iscrto, primirmt vmos mostrr o su quivlt tmpo cotíuo. prátic oprção mostrgm é cut por um covrsor AD (covrsor lógico-igitl) qu iclui tmbém qutição s mplitus s mostrs igitlição. Assim, sí o covrsor AD é um séri vlors igitis. A oprção rvrs pr rcostrução um sil cotíuo prtir sus mostrs é cohci como covrsão igitl lógic (DA). A tori mostrgm tm um ppl muito importt o smpho qulqur sistm procssmto igitl siis. st cpítulo srá prst um brv iscussão sobr tori mostrgm siis, qu stblc s coiçõs básics pr qu um sil tmpo cotíuo sj rprsto uicmt por sus mostrs toms m istts tmpo rgulrmt spços... A mostrgm siis A tori mostrgm é bs mtmátic pr s obtr um sil () tmpo iscrto prtir um sil (t) tmpo cotíuo. A obtção um squêci mostrs () prtir um sil (t) cotíuo o tmpo po sr rprst pl sguit rlção: ( ) ( t) ( T ) t T. m qu T é chmo príoo mostrgm, é um úmro prtct o cojuto os úmros itiros. O ivrso st príoo, F /T, é chmo frquêci mostrgm, com ui m mostrs por sguo ou m H. A squêci úmros () é lgums vs ot por vtor {()}, - < <, m qu () é o -ésimo lmto squêci. Um mplo um sil tmpo iscrto é mostro figur., m qu s mostrs são toms m itrvlos rgulrmt spços por T sguos s ris prpiculrs o io o tmpo rprstm o sil tmpo iscrto. ot qu tr ois itrvlos tmpo sucssivos é fiio sobr o sil. T () (t) t Figur.: Sil mostro. Um mir s visulir o procsso mostrgm é ilustro plo igrm blocos figur.. O sil tmpo cotíuo (t) é plico um multiplicor. Est sil é multiplico por um squêci prióic impulsos rgulrmt spços por T sguos p(t), chmo trm impulsos, tl qu:
42 - 6 - () t δ( t ) sí o multiplicor tmos o sguit sil: p T. () t () t p() t ( T ) ( t T ) ( T ) δ. (t) (T ) p(t) Figur.: Rprstção o procsso mostrgm. A multiplicção o sil plos impulsos covrt (t) m um sil tmpo iscrto, form um squêci úmros () m qu os vlors s mostrs são ios pl vriávl itir, ou sj, ( ) ( ) T T.4 Assim, como visto o cpítulo, mitio, squêci () po sr scrit como um som impulsos uitários poros tl qu: ( ) ( ) δ( ) ( ) δ( ) ( ) δ( ) L.5 ou sj, () po sr cosir um squêci úmros (um vtor), qu m últim ális rprst o sil origil. Est squêci úmros po sr trsmiti ou tão rm m um computor pr o procssmto (trtmto) igitl o sil. Tbl : Vlors tblos ou rmos rltivos o sil rl. sil o istt () () () () 4 (4) M M Obsrv qu o sil, ou squêci (), é iscrto o tmpo, ms os sus vlors ou mplitus pr c íic tmpo prtcm o cmpo os úmros ris... O torm mostrgm O fito mostrgm m um sil é mlhor liso o omíio frquêci utilio trsform Fourir (Joquim Srtori, ). Sb-s tori Fourir qu trsform fução trm impulsos m (.) é por:
43 - 7 - δ π ( t T ) δ( Ω Ω ) T m qu Ω π/t. A trsform Fourir o sil qução (.), qu é o prouto us fuçõs, srá pl covolução tr s trsforms (t) p(t):, ssim: X ( Ω) X ( Ω) * P( Ω).6 π m qu X (Ω) é trsform Fourir o sil mostro. Assim, X π ( Ω) X ( Ω) * δ( Ω Ω ) π troco orm somtóri com covolução tm-s, portto, X T ( Ω) X ( Ω) * δ( Ω Ω ) T,, X ( Ω) X ( Ω Ω ) T.7 ot qu o spctro o sil mostro é prióico, com príoo Ω, pois stmos o omíio frquêci. El cosist um úmro ifiito cópis o spctro X(Ω), o sil tmpo cotíuo. Ests cópis são rgulrmt spçs pl frquêci mostrgm Ω. A figur., mostr um mplo mostrgm siis cosiro o omíio frquêci. Aliso qução (.7) com o uílio figur.., pomos obsrvr qu s cópis rptis o spctro (t) pom s sobrpor. Primirmt vmos obsrvr qu pr qu sts cópis ão itrfirm ums com s outrs, o spctro (t) v sr limito m um frquêci máim. Sj Ω M frquêci máim o sil sr mostro. Obsrvo figur..c ot-s clrmt qu pr ão hvr suprposição spctrl v-s tr qu: Ω Ω Ω.8 M Dss moo, pr qu ão hj suprposição, frquêci mostrgm v sr o míimo o obro frquêci máim o sil, isto é, M Ω Ω M.9 S coição cim ão é stisfit, ou sj, Ω < Ω M, s cópis o spctro (t) s suprpõm, cuso pr o formto o spctro origil. Obsrv ilustrção figur... Est fômo é cohcio litrtur como lisig (suprposição spctrl). st cso o spctro origil é prio ão po mis sr rcupro prtir o sil mostro.
44 - 8 - X(Ω) () -Ω M Ω M P(Ω) (b) -Ω -Ω Ω Ω Ω > Ω M X (Ω) (c) -Ω -Ω M Ω M Ω Ω < Ω M X (Ω) Ω -Ω M () -Ω Figur.: Efito mostrgm o omíio frquêci. st cso X(Ω) é o spctro o sil cotíuo o tmpo, X (Ω) é o spctro o sil mostro. Por outro lo s coição m (.9) é stisfit o spctro origil b básic (m toro frquêci ro) é mtio iltro po sr rcupro trvés um filtrgm por um filtro pssbis il com frquêci cort Ω /. Ω X(Ω) () -Ω M Ω M Ω > Ω M X (Ω) (b) -Ω -Ω M Ω M Ω Ω / Ω -Ω M Figur.4: Espctro o sil origil sil mostro sm lisig. Com s cosirçõs cim, pomos gor ucir fcilmt o torm mostrgm como sgu: S (t) é um sil stritmt b limit, isto é, X ( ), Ω > Ω M Ω, tão st sil (t) po sr rcupro prtir sus mostrs (T ) s: π Ω Ω T M.
45 - 9 - A frquêci Ω M é chm frquêci yquist, frquêci míim mostrgm, Ω M, é chm t yquist. Toos os siis cotros os sistms físicos uc são, stritmt flo, b limit, ssim, ts o procsso mostrgm é comum filtrr o sil (filtro ti-lisig) fim s miimir rgi o sil cim frquêci yquist (limitr o sil m b), pr, ss moo, miimir o fito o lisig qu ocorr urt covrsão lógico-igitl. X (Ω) X(Ω) -Ω -Ω M Ω M Ω (T A ) H(Ω) (t) -Ω M Ω M H(Ω) Ω Ω c Ω M ou Ω c Ω / -Ω C C Figur.5: Rcostrução o sil: filtrgm o sil mostro rcuprção o sil origil. Algums cosirçõs prátics rli impulsos com urção ul ão istm. prátic mostrgm é rli trvés um circuito mostror-sguror. O sil mostro é proimo por um proimção m grus tr ois istts jcts mostrgm, m sgui qutio. st cso o filtro rcostrução v sr lvmt moifico pr compsr proimção m grus (opphim 979, Joquim, ). Como ito triormt, pr ssgurr qu ão hj ocorrêci suprposição spctrl (lisig), o sil ts sr mostro é filtro fim limitá-lo m b, m um frquêci máim, por mplo, Ω M. Est filtro é chmo filtro ti-lisig, srv tmbém pr limitr o ruío prst o sil tmpo cotíuo, ts o procsso covrsão lógico-igitl. El srv tmbém pr fcilitr o projto prático o filtro rcostrução, qu ão prst um trsição brupt tr b pssgm tução, t mostrgm é fit lvmt suprior à yquist. figur.5 H(Ω) rprst um filtro rcostrução il. O ouvio humo é cp itificr frquêcis tr H H. Pr siis áuio frquêci mostrgm é proi m 44. H m v 4 H. Em tlfoi 9% rgi o sil fl stá prst m frquêcis té.4 H, qu é suficit pr prsrvr quli s covrsçõs, t mostrgm é proi m 8 H m v 6.8 H, prmitio um b gur. H qu fcilit o projto prático o filtro rcostrução. Em psquis t mostrgm é muits vs lv pr H..4. Covrsão t mostrgm Em lgums plicçõs spciis, como por mplo lgus tipos coificção b, ist cssi moificção t mostrgm um squêci (). Pomos ruir ou umtr t mostrgm por um trmio ftor itiro, ou tão moificá-l por um ftor rciol. Est procsso é cohcio como covrsão t mostrgm po sr rlio irtmt o sil tmpo iscrto Rução t mostrgm por um ftor itiro
46 - 4 - A rução t mostrgm por um ftor itiro, M, é fit tomo tos s mostrs o sil múltipls M, isto é, ( ) ( t) ( MT ) ( M ) t MT. Obsrv qu, pr o sil r-mostro, o ovo príoo mostrgm é MT. Fic clro qu st oprção po rsultr m lisig (suprposição spctrl). Clculo trsform o sil r-mostro ( t) ( ) MT tm-s qu: X ( ) Ω MT Ω X Ω M. st cso ov frquêci mostrgm é Ω /M, qu é mor o qu Ω. Assim, pr s prvir suprposição spctrl o sil () vri sr filtro ts covrsão mostrgm. o omíio frquêci igitl trsform Fourir ( ) ( M ) Ω w / MT,pós lgum mipulção mtmátic po sr mostr qu: ( ) M j ( ( wπ )/ M X ), mitio qu X. M o cso cotíuo, pr s vitr suprposição spctrl, o sil (t) vri sr filtro por um filtro pss-bis com frquêci cort igul à mt ov frquêci mostrgm, Ω /M. Como, m grl, já stmos trblho o tmpo iscrto, tão filtrmos o sil iscrto () por um filtro igitl pss-bis com gho uitário frquêci cort igitl, tl qu, w c Ω T M π M.4 O procsso filtrgm igitl sguio rução mostrgm é chmo um cimor é ilustro plo igrm blocos figur.6. Assim, o procsso rução t mostrgm por um ftor M, primirmt squêci é filtr por um filtro igitl com gho uitário frquêci cort igul π/m m sgui f-s oprção scrit pl qução (.). () FPB π/m M r () Figur.6: Dcimor. Aumto t mostrgm por um ftor itiro Supoh qu s qur umtr t mostrgm um squêci (), mostr com um príoo T sguos, por um ftor L, m qu L é um úmro itiro. A ov squêci, i (), po sr obti prtir () trvés sguit trsformção: ( ) T i.5 L L
47 - 4 - por: Obsrv qu s mostrs i (m), com íics múltiplos itiros tis qu m L (m), são s ( L) ( ) i.6 Pomos cocluir tão qu qução (.6) p () crscto ~ L - ros tr c tl qu: i us mostrs jcts (), ou sj, tmos um ov squêci ( ) ( / L), ~, ± L, ± L, L i ( )..7, cso cotrário A figur.7., mostr bio, ilustr st oprção. T (t) ~ i ( ) () t (b) i ( ) t T /L Figur.7: Itrpolção o omíio o tmpo. portto, Clculo trsform Fourir squêci ( ) X ~ i ( ) ~ i ( ) ( ) ~ jlw X i ( ) X ( ) Obsrv qu X~ ( ) é um vrsão X ( ) i ~ i qução (.7) tm-s qu, jlw.8, comprimi por um ftor scl L. Ests us trsforms stão ilustrs figur.8b.8c. Obsrvo st figur pomos cocluir qu pr s obtr i () bst crir um squêci como qução (.7) m sgui filtrá-l com um filtro pssbis igitl com gho L cort m w c π/l. O uso o gho L po sr justifico oto qu, como stmos comprimio o sil o omíio frquêci por um ftor L limio s compots frquêci tr π/l π - π/l, rgi o sil imiuirá por um ftor igul L. Assim, stblco o gho o filtro itrpolor igul L rgi o sil itrpolo é mti igul à o origil. O sil itrpolo o omíio o tmpo é mostro figur.7.b.
Associação de Resistores e Resistência Equivalente
 Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos
Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos
TÉCNICAS DE INTEGRAÇÃO. 1.1 Integrais por Substituição Mudança de Variáveis
 UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis
UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis
Curso: Engenharia Industrial Elétrica. Análise de variáveis Complexas MAT 216 Turma: 01
 urso: Egharia Idustrial Elétrica Aális d variávis omplas MAT 6 Profssora: Edmary S B Araújo Turma: Lista d Provas Rspodu Jsus: Em vrdad, m vrdad t digo: qum ão ascr da água do Espírito ão pod trar o rio
urso: Egharia Idustrial Elétrica Aális d variávis omplas MAT 6 Profssora: Edmary S B Araújo Turma: Lista d Provas Rspodu Jsus: Em vrdad, m vrdad t digo: qum ão ascr da água do Espírito ão pod trar o rio
1 Introdução e Base Matemática
 J. A. M. Flipp Souz Iroução Bs Mmáic Iroução Bs Mmáic Iroução Bs Mmáic 3. O úmro imgiário 3. Númros complxos 4.3 Oprçõs com úmros complxos 9.4 O so o co-so.5 A qução Eulr 5.6 A g 7.7 As ivrss so, co-so
J. A. M. Flipp Souz Iroução Bs Mmáic Iroução Bs Mmáic Iroução Bs Mmáic 3. O úmro imgiário 3. Númros complxos 4.3 Oprçõs com úmros complxos 9.4 O so o co-so.5 A qução Eulr 5.6 A g 7.7 As ivrss so, co-so
conjunto dos números inteiros. conjunto dos números que podem ser representados como quociente de números inteiros.
 Cpítulo I Noçõs Eltrs d Mtátic. Oprçõs co frcçõs, Equçõs Iquçõs Tipos d úros {,,,,,6, } cojuto dos úros turis. 0 { 0} {,,,, 0,,,, } cojuto dos úros itiros., 0 0 p : p, q q cojuto dos úros rciois ou frccioários,
Cpítulo I Noçõs Eltrs d Mtátic. Oprçõs co frcçõs, Equçõs Iquçõs Tipos d úros {,,,,,6, } cojuto dos úros turis. 0 { 0} {,,,, 0,,,, } cojuto dos úros itiros., 0 0 p : p, q q cojuto dos úros rciois ou frccioários,
Módulo 03. Determinantes. [Poole 262 a 282]
![Módulo 03. Determinantes. [Poole 262 a 282] Módulo 03. Determinantes. [Poole 262 a 282]](/thumbs/74/70829060.jpg) Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
= 1, independente do valor de x, logo seria uma função afim e não exponencial.
 6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0
6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0
O Uso da Álgebra Linear nas Equações Diferenciais
 Uso d Álgr ir s Equçõs ifriis íi Gri ol úi Rsd rir Bofim Fuldd d mái FT Uivrsidd Fdrl d Urlâdi UFU 88 - Urlâdi ril d 8 Rsumo Álgr ir é um supor mmáio pr muis árs d iêi Vrmos omo lgus d sus rsuldos podm
Uso d Álgr ir s Equçõs ifriis íi Gri ol úi Rsd rir Bofim Fuldd d mái FT Uivrsidd Fdrl d Urlâdi UFU 88 - Urlâdi ril d 8 Rsumo Álgr ir é um supor mmáio pr muis árs d iêi Vrmos omo lgus d sus rsuldos podm
Geometria Analítica e Álgebra Linear
 Geometri Alític e Álgebr Lier 8. Sistems Lieres Muitos problems ds ciêcis turis e sociis, como tmbém ds egehris e ds ciêcis físics, trtm de equções que relciom dois cojutos de vriáveis. Um equção do tipo,
Geometri Alític e Álgebr Lier 8. Sistems Lieres Muitos problems ds ciêcis turis e sociis, como tmbém ds egehris e ds ciêcis físics, trtm de equções que relciom dois cojutos de vriáveis. Um equção do tipo,
Métodos Computacionais em Engenharia DCA0304 Capítulo 4
 Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d
Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d
RESOLUÇÃO DE EQUAÇÕES POR MEIO DE DETERMINANTES
 RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.
RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.
4.1 Método das Aproximações Sucessivas ou Método de Iteração Linear (MIL)
 4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
PSI-2432: Projeto e Implementação de Filtros Digitais Projeto Proposto: Conversor de taxas de amostragem
 PSI-2432: Projto Implmntação d Filtros Digitais Projto Proposto: Convrsor d taxas d amostragm Migul Arjona Ramírz 3 d novmbro d 2005 Est projto consist m implmntar no MATLAB um sistma para troca d taxa
PSI-2432: Projto Implmntação d Filtros Digitais Projto Proposto: Convrsor d taxas d amostragm Migul Arjona Ramírz 3 d novmbro d 2005 Est projto consist m implmntar no MATLAB um sistma para troca d taxa
Código PE-ACSH-2. Título:
 CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu
CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu
Lista 3 - Resolução. 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os.
 GN7 Introução à Álgr Linr Prof n Mri Luz List - Rsolução Vrifiqu s os proutos ixo stão m finios, m so firmtivo, lul-os ) [ / ] / ) / [ / ] ) ) Solução ) orm primir mtriz é x sgun é x, logo o prouto stá
GN7 Introução à Álgr Linr Prof n Mri Luz List - Rsolução Vrifiqu s os proutos ixo stão m finios, m so firmtivo, lul-os ) [ / ] / ) / [ / ] ) ) Solução ) orm primir mtriz é x sgun é x, logo o prouto stá
4.21 EXERCÍCIOS pg. 176
 78 EXERCÍCIOS pg 7 Nos rcícios d clculr s drivds sucssivs t ordm idicd, 5 7 IV V 7 c d c, 5, 8 IV V VI 8 8 ( 7) ( 8), ( ) ( ) '' ( ) ( ) ( ) ( ) 79 5, 5 8 IV, 8 7, IV 8 l, 9 s, 7 8 cos IV V VI VII 5 s
78 EXERCÍCIOS pg 7 Nos rcícios d clculr s drivds sucssivs t ordm idicd, 5 7 IV V 7 c d c, 5, 8 IV V VI 8 8 ( 7) ( 8), ( ) ( ) '' ( ) ( ) ( ) ( ) 79 5, 5 8 IV, 8 7, IV 8 l, 9 s, 7 8 cos IV V VI VII 5 s
CAPÍTULO 3. Exercícios é contínua, decrescente e k 2 positiva no intervalo [ 3, [. De ln x 1 para x 3, temos. dx 3.
 CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)
CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)
8 = 1 GRUPO II. = x. 1 ln x
 Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim
Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim
, então ela é integrável em [ a, b] Interpretação geométrica: seja contínua e positiva em um intervalo [ a, b]
![, então ela é integrável em [ a, b] Interpretação geométrica: seja contínua e positiva em um intervalo [ a, b] , então ela é integrável em [ a, b] Interpretação geométrica: seja contínua e positiva em um intervalo [ a, b]](/thumbs/39/18525051.jpg) Interl Deinid Se é um unção de, então su interl deinid é um interl restrit à vlores em um intervlo especíico, dimos, O resultdo é um número que depende pens de e, e não de Vejmos deinição: Deinição: Sej
Interl Deinid Se é um unção de, então su interl deinid é um interl restrit à vlores em um intervlo especíico, dimos, O resultdo é um número que depende pens de e, e não de Vejmos deinição: Deinição: Sej
TÓPICOS. Números complexos. Plano complexo. Forma polar. Fórmulas de Euler e de Moivre. Raízes de números complexos.
 Not m: litur dsts potmtos ão disps d modo lgum litur tt d iliogrfi pricipl d cdir Chm-s tção pr importâci do trlho pssol rlir plo luo rsolvdo os prolms prstdos iliogrfi, sm cosult prévi ds soluçõs proposts,
Not m: litur dsts potmtos ão disps d modo lgum litur tt d iliogrfi pricipl d cdir Chm-s tção pr importâci do trlho pssol rlir plo luo rsolvdo os prolms prstdos iliogrfi, sm cosult prévi ds soluçõs proposts,
MATEMÁTICA A - 12o Ano Funções - Teorema de Bolzano Propostas de resolução
 MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos
MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos
Lista de Exercícios 9 Grafos
 UFMG/ICEx/DCC DCC111 Mtmáti Disrt List Exríios 9 Gros Ciênis Exts & Engnhris 1 o Smstr 2018 1. O gro intrsção um olção onjuntos A 1, A 2,..., A n é o gro qu tm um vérti pr um os onjuntos olção tm um rst
UFMG/ICEx/DCC DCC111 Mtmáti Disrt List Exríios 9 Gros Ciênis Exts & Engnhris 1 o Smstr 2018 1. O gro intrsção um olção onjuntos A 1, A 2,..., A n é o gro qu tm um vérti pr um os onjuntos olção tm um rst
Ánálise de Fourier tempo discreto
 Fculdd d Eghri Áális d Fourir tpo discrto 4.5.5.5.5.5.5 -.5 -.5 - - -8-6 -4-4 6 8 - - -5 5 5 5 SS MIEIC 8/9 Progr d SS Fculdd d Eghri Siis Sists uls Sists Lirs Ivrits uls Aális d Fourir (tpo cotíuo) uls
Fculdd d Eghri Áális d Fourir tpo discrto 4.5.5.5.5.5.5 -.5 -.5 - - -8-6 -4-4 6 8 - - -5 5 5 5 SS MIEIC 8/9 Progr d SS Fculdd d Eghri Siis Sists uls Sists Lirs Ivrits uls Aális d Fourir (tpo cotíuo) uls
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Fculdde de Enenhri, Arquiteturs e Urnismo FEAU Pro. Dr. Serio Pillin IPD/ Físic e Astronomi V Ajuste de curvs pelo método dos mínimos qudrdos Ojetivos: O ojetivo dest ul é presentr o método
Cálculo Numérico Fculdde de Enenhri, Arquiteturs e Urnismo FEAU Pro. Dr. Serio Pillin IPD/ Físic e Astronomi V Ajuste de curvs pelo método dos mínimos qudrdos Ojetivos: O ojetivo dest ul é presentr o método
Capítulo 3: Limite de uma Função e Continuidade
 Cpítulo : mt d um Fução Cotudd - Noção d mt d um Fução Noção Itutv Isttuto d Cêcs Ets - Dprtmto d Mtmátc Cálculo I Proª Mr Jult Vtur Crvlho d Arujo Emplo : Cosdr ução dd pr todo rl Obsrv os vlors d ução
Cpítulo : mt d um Fução Cotudd - Noção d mt d um Fução Noção Itutv Isttuto d Cêcs Ets - Dprtmto d Mtmátc Cálculo I Proª Mr Jult Vtur Crvlho d Arujo Emplo : Cosdr ução dd pr todo rl Obsrv os vlors d ução
Matemática 1 Professor Paulo Cesar Pfaltzgraff Ferreira. Sumário
 Mtemátic Professor Pulo Cesr Pfltgrff Ferreir i Sumário Uidde Revisão de Tópicos Fudmetis do Esio Médio... 0. Apresetção... 0. Simologi Mtemátic mis usul... 0. Cojutos Numéricos... 0. Operções com Números
Mtemátic Professor Pulo Cesr Pfltgrff Ferreir i Sumário Uidde Revisão de Tópicos Fudmetis do Esio Médio... 0. Apresetção... 0. Simologi Mtemátic mis usul... 0. Cojutos Numéricos... 0. Operções com Números
Cálculo Diferencial II Lista de Exercícios 1
 Cálculo Difrncil II List d Ercícios 1 CONJUNTO ABERTO E PONTOS DE ACUMULAÇÃO 1 Vrifiqu quis dos conjuntos sguir são brtos m (, ) 1 (, ) 0 (, ) 0 (, ) 0 1 Dtrmin o conjunto d pontos d cumulção do conjunto
Cálculo Difrncil II List d Ercícios 1 CONJUNTO ABERTO E PONTOS DE ACUMULAÇÃO 1 Vrifiqu quis dos conjuntos sguir são brtos m (, ) 1 (, ) 0 (, ) 0 (, ) 0 1 Dtrmin o conjunto d pontos d cumulção do conjunto
CAPÍTULO 9 COORDENADAS POLARES
 Luiz Frncisco d Cruz Drtmnto d Mtmátic Uns/Buru CAPÍTULO 9 COORDENADAS POLARES O lno, tmbém chmdo d R, ond R RR {(,)/, R}, ou sj, o roduto crtsino d R or R, é o conjunto d todos os rs ordndos (,), R El
Luiz Frncisco d Cruz Drtmnto d Mtmátic Uns/Buru CAPÍTULO 9 COORDENADAS POLARES O lno, tmbém chmdo d R, ond R RR {(,)/, R}, ou sj, o roduto crtsino d R or R, é o conjunto d todos os rs ordndos (,), R El
SISTEMAS DE TEMPO DISCRETO DESCRITO POR EQUAÇÕES A DIFERENÇA
 SISTEMAS DE TEMPO DISCRETO DESCRITO POR EQUAÇÕES A DIFEREÇA ( ( x( Coeficiete costte. ( ( x ( Coeficiete vriável (depedete do tempo. Aplicmos x( pr e cosidermos codição iicil ( ( ( M ( ( ( ( x( x( ( x(
SISTEMAS DE TEMPO DISCRETO DESCRITO POR EQUAÇÕES A DIFEREÇA ( ( x( Coeficiete costte. ( ( x ( Coeficiete vriável (depedete do tempo. Aplicmos x( pr e cosidermos codição iicil ( ( ( M ( ( ( ( x( x( ( x(
Soluções E-Procurement
 Soluçõs -Procurm Móulos Vgs Aprsção Dspss Tomé A. Gl Jro/2003 Sumáro: Soluçõs - Procurm 2 Soluçõs - Procurm m xrp 3 Prcps Vgs 4 Solução 5 Móulo vgs 7 Móulo Rlóros Aprsção spss 8 Cls 9 Cocos Ús 10 www.scrgl.com
Soluçõs -Procurm Móulos Vgs Aprsção Dspss Tomé A. Gl Jro/2003 Sumáro: Soluçõs - Procurm 2 Soluçõs - Procurm m xrp 3 Prcps Vgs 4 Solução 5 Móulo vgs 7 Móulo Rlóros Aprsção spss 8 Cls 9 Cocos Ús 10 www.scrgl.com
Física Computacional 5
 Física Computacioal 5. Drivaas com irças iitas a. O cocito rivaa mos simpls qu o itgral b. Cálculo umérico a rivaa com irças iitas c. Um outro cocito Equação Dircial Oriária. Solução aalítica as EDO liars.
Física Computacioal 5. Drivaas com irças iitas a. O cocito rivaa mos simpls qu o itgral b. Cálculo umérico a rivaa com irças iitas c. Um outro cocito Equação Dircial Oriária. Solução aalítica as EDO liars.
Adição dos antecedentes com os consequentes das duas razões
 Adição dos ntcdnts com os consqunts ds dus rzõs Osrv: 0 0 0 0, ou sj,, ou sj, 0 Otnh s trnsformds por mio d dição dos ntcdnts com os consqünts: ) ) ) 0 0 0 0 0 0 0 0 ) 0 0 0 0 ) 0 0 0 0 ) Osrv gor como
Adição dos ntcdnts com os consqunts ds dus rzõs Osrv: 0 0 0 0, ou sj,, ou sj, 0 Otnh s trnsformds por mio d dição dos ntcdnts com os consqünts: ) ) ) 0 0 0 0 0 0 0 0 ) 0 0 0 0 ) 0 0 0 0 ) Osrv gor como
Semelhança e áreas 1,5
 A UA UL LA Semelhnç e áres Introdução N Aul 17, estudmos o Teorem de Tles e semelhnç de triângulos. Nest ul, vmos tornr mis gerl o conceito de semelhnç e ver como se comportm s áres de figurs semelhntes.
A UA UL LA Semelhnç e áres Introdução N Aul 17, estudmos o Teorem de Tles e semelhnç de triângulos. Nest ul, vmos tornr mis gerl o conceito de semelhnç e ver como se comportm s áres de figurs semelhntes.
1 Fórmulas de Newton-Cotes
 As nots de ul que se seguem são um compilção dos textos relciondos n bibliogrfi e não têm intenção de substitui o livro-texto, nem qulquer outr bibliogrfi. Integrção Numéric Exemplos de problems: ) Como
As nots de ul que se seguem são um compilção dos textos relciondos n bibliogrfi e não têm intenção de substitui o livro-texto, nem qulquer outr bibliogrfi. Integrção Numéric Exemplos de problems: ) Como
SISTEMAS DE TEMPO DISCRETO DESCRITO POR EQUAÇÕES A DIFERENÇA
 SISTEMAS DE TEMPO DISCRETO DESCRITO POR EQUAÇÕES A DIFEREÇA Coeficiete costte. SISTEMAS LIT CARACTERIZADOS POR EQUAÇÕES A DIFEREÇA COM COEFICIETES COSTATES Sistems descritos por equções difereç com coeficiete
SISTEMAS DE TEMPO DISCRETO DESCRITO POR EQUAÇÕES A DIFEREÇA Coeficiete costte. SISTEMAS LIT CARACTERIZADOS POR EQUAÇÕES A DIFEREÇA COM COEFICIETES COSTATES Sistems descritos por equções difereç com coeficiete
Transformada z. A transformada z é a TFTD da sequência r -n x[n] e a ROC é determinada pelo intervalo de valores de r para os quais.
![Transformada z. A transformada z é a TFTD da sequência r -n x[n] e a ROC é determinada pelo intervalo de valores de r para os quais. Transformada z. A transformada z é a TFTD da sequência r -n x[n] e a ROC é determinada pelo intervalo de valores de r para os quais.](/thumbs/84/89187131.jpg) Trsformd A TFTD de um sequêci é: Pr covergir série deve ser solutmete somável. Ifelimete muitos siis ão podem ser trtdos: A trsformd é um geerlição d TFTD que permite o trtmeto desses siis: Ζ Defiição:
Trsformd A TFTD de um sequêci é: Pr covergir série deve ser solutmete somável. Ifelimete muitos siis ão podem ser trtdos: A trsformd é um geerlição d TFTD que permite o trtmeto desses siis: Ζ Defiição:
Física 1 Capítulo 3 2. Acelerado v aumenta com o tempo. Se progressivo ( v positivo ) a m positiva Se retrógrado ( v negativo ) a m negativa
 Físic 1 - Cpítulo 3 Movimento Uniformemente Vrido (m.u.v.) Acelerção Esclr Médi v 1 v 2 Movimento Vrido: é o que tem vrições no vlor d velocidde. Uniddes de celerção: m/s 2 ; cm/s 2 ; km/h 2 1 2 Acelerção
Físic 1 - Cpítulo 3 Movimento Uniformemente Vrido (m.u.v.) Acelerção Esclr Médi v 1 v 2 Movimento Vrido: é o que tem vrições no vlor d velocidde. Uniddes de celerção: m/s 2 ; cm/s 2 ; km/h 2 1 2 Acelerção
9.1 Indutores e Indutância
 Cpítuo 9 Indutânci 9.1 Indutores e Indutânci Neste cpítuo, estudmos os indutores e sus indutâncis, cujs proprieddes decorrem diretmente d ei de indução de Frdy. Cpcitores: Recpitução Lembre-se que, no
Cpítuo 9 Indutânci 9.1 Indutores e Indutânci Neste cpítuo, estudmos os indutores e sus indutâncis, cujs proprieddes decorrem diretmente d ei de indução de Frdy. Cpcitores: Recpitução Lembre-se que, no
ESTABILIDADE. Pólos Zeros Estabilidade
 ESTABILIDADE Pólo Zero Etbilidde Itrodução Um crcterític importte pr um item de cotrole é que ele ej etável. Se um etrd fiit é plicd o item de cotrole, etão íd deverá er fiit e ão ifiit, ito é, umetr em
ESTABILIDADE Pólo Zero Etbilidde Itrodução Um crcterític importte pr um item de cotrole é que ele ej etável. Se um etrd fiit é plicd o item de cotrole, etão íd deverá er fiit e ão ifiit, ito é, umetr em
AGRUPAMENTO DE ESCOLAS DE MORTÁGUA Geometria Ficha de Trabalho Nº 02 10º Ano
 AGUPAMENO DE EOLA DE MOÁGUA Gomti Fih lho Nº 0 0º Ano Osv igu o lo... Ini so istm: ois plnos ppniuls us ts plls um t post um plno um t snt o plno FIH us ts não omplns. s oons os vétis... Qul posição ltiv
AGUPAMENO DE EOLA DE MOÁGUA Gomti Fih lho Nº 0 0º Ano Osv igu o lo... Ini so istm: ois plnos ppniuls us ts plls um t post um plno um t snt o plno FIH us ts não omplns. s oons os vétis... Qul posição ltiv
MATRIZES. Matriz é uma tabela de números formada por m linhas e n colunas. Dizemos que essa matriz tem ordem m x n (lê-se: m por n), com m, n N*
 MTRIZES DEFINIÇÃO: Mtriz é um tl d númros formd por m linhs n coluns. Dizmos qu ss mtriz tm ordm m n (lê-s: m por n), com m, n N* Grlmnt dispomos os lmntos d um mtriz ntr prêntss ou ntr colchts. m m m
MTRIZES DEFINIÇÃO: Mtriz é um tl d númros formd por m linhs n coluns. Dizmos qu ss mtriz tm ordm m n (lê-s: m por n), com m, n N* Grlmnt dispomos os lmntos d um mtriz ntr prêntss ou ntr colchts. m m m
POLINÔMIOS. Definição: Um polinômio de grau n é uma função que pode ser escrita na forma. n em que cada a i é um número complexo (ou
 POLINÔMIOS Definição: Um polinômio de gru n é um função que pode ser escrit n form P() n n i 0... n i em que cd i é um número compleo (ou i 0 rel) tl que n é um número nturl e n 0. Os números i são denomindos
POLINÔMIOS Definição: Um polinômio de gru n é um função que pode ser escrit n form P() n n i 0... n i em que cd i é um número compleo (ou i 0 rel) tl que n é um número nturl e n 0. Os números i são denomindos
Definição: Seja a equação diferencial linear de ordem n e coeficientes variáveis:. x = +
 Vléi Zum Medeios & Mihil Lemotov Resolução de Equções Difeeciis Liees po Séies Poto Odiáio (PO) e Poto Sigul (PS) Defiição: Sej equção difeecil lie de odem e coeficietes viáveis: ( ) ( ) b ( ) é dito poto
Vléi Zum Medeios & Mihil Lemotov Resolução de Equções Difeeciis Liees po Séies Poto Odiáio (PO) e Poto Sigul (PS) Defiição: Sej equção difeecil lie de odem e coeficietes viáveis: ( ) ( ) b ( ) é dito poto
Material Teórico - Módulo Triângulo Retângulo, Lei dos Senos e Cossenos, Poĺıgonos Regulares. Razões Trigonométricas no Triângulo Retângulo.
 Mtril Tórico - Módulo Triângulo Rtângulo, Li dos Snos ossnos, Poĺıgonos Rgulrs Rzõs Trigonométrics no Triângulo Rtângulo Nono no utor: Prof Ulisss Lim Prnt Rvisor: Prof ntonio min M Nto Portl d OMEP 1
Mtril Tórico - Módulo Triângulo Rtângulo, Li dos Snos ossnos, Poĺıgonos Rgulrs Rzõs Trigonométrics no Triângulo Rtângulo Nono no utor: Prof Ulisss Lim Prnt Rvisor: Prof ntonio min M Nto Portl d OMEP 1
CASA DE DAVI CD VOLTARÁ PARA REINAR 1. DEUS, TU ÉS MEU DEUS. E B C#m A DEUS, TU ÉS MEU DEUS E SENHOR DA TERRA
 S VI VOLTRÁ PR RINR 1. US, TU ÉS MU US #m US, TU ÉS MU US SNHOR TRR ÉUS MR U T LOUVRI #m SM TI NÃO POSSO VIVR M HGO TI OM LGRI MOR NST NOV NÇÃO #m #m OH...OH...OH LVNTO MINH VOZ #m LVNTO MINHS MÃOS #m
S VI VOLTRÁ PR RINR 1. US, TU ÉS MU US #m US, TU ÉS MU US SNHOR TRR ÉUS MR U T LOUVRI #m SM TI NÃO POSSO VIVR M HGO TI OM LGRI MOR NST NOV NÇÃO #m #m OH...OH...OH LVNTO MINH VOZ #m LVNTO MINHS MÃOS #m
Geometricamente, um esboço da interpolante g(x) sobre a função f(x) é visto na figura 3.1.
 4 APROXIMAÇÃO DE FUNÇÕES 4- INTERPOAÇÃO POINOMIA Itroução: A iterpolção Iterpolr um ução () cosiste em proimr ess ução por um outr ução g() escolhi etre um clsse e uções eii priori e que stisç lgums propriees
4 APROXIMAÇÃO DE FUNÇÕES 4- INTERPOAÇÃO POINOMIA Itroução: A iterpolção Iterpolr um ução () cosiste em proimr ess ução por um outr ução g() escolhi etre um clsse e uções eii priori e que stisç lgums propriees
Análise de Sistemas Discretos por Transformada-z
 ES Siis Sists Aális d Sists Discrtos por Trsford- Prof. Aliio Fsto Ribiro Arúo Dpto. of Sists d Coptção Ctro d Iforátic - UFPE Cpítlo Siis Sists Eg. d Coptção Itrodção A Trsford- Cotúdo A Trsford Ivrs
ES Siis Sists Aális d Sists Discrtos por Trsford- Prof. Aliio Fsto Ribiro Arúo Dpto. of Sists d Coptção Ctro d Iforátic - UFPE Cpítlo Siis Sists Eg. d Coptção Itrodção A Trsford- Cotúdo A Trsford Ivrs
Simbolicamente, para. e 1. a tem-se
 . Logritmos Inicilmente vmos trtr dos ritmos, um ferrment crid pr uilir no desenvolvimento de cálculos e que o longo do tempo mostrou-se um modelo dequdo pr vários fenômenos ns ciêncis em gerl. Os ritmos
. Logritmos Inicilmente vmos trtr dos ritmos, um ferrment crid pr uilir no desenvolvimento de cálculos e que o longo do tempo mostrou-se um modelo dequdo pr vários fenômenos ns ciêncis em gerl. Os ritmos
Sinais e Sistemas Mecatrónicos
 Sinis Sistms Mctrónicos Anális d Sistms no Domínio do Tmpo José Sá d Cost José Sá d Cost T11 - Anális d Sistms no Tmpo - Rsp. stcionári 1 Crctrizção d rspost stcionário A crctrizção d rspost stcionári
Sinis Sistms Mctrónicos Anális d Sistms no Domínio do Tmpo José Sá d Cost José Sá d Cost T11 - Anális d Sistms no Tmpo - Rsp. stcionári 1 Crctrizção d rspost stcionário A crctrizção d rspost stcionári
Escola de Engenharia de Lorena - USP Cinética Química Capítulo 01 Introdução a Cinética
 1.1 - ITODUÇÃO O termo ciétic está relciodo movimeto qudo se pes ele prtir de seu coceito físico. tretto, s reções químics, ão há movimeto, ms sim mudçs de composição do meio reciol, o logo d reção. Termodiâmic
1.1 - ITODUÇÃO O termo ciétic está relciodo movimeto qudo se pes ele prtir de seu coceito físico. tretto, s reções químics, ão há movimeto, ms sim mudçs de composição do meio reciol, o logo d reção. Termodiâmic
Transporte de solvente através de membranas: estado estacionário
 Trnsporte de solvente trvés de membrns: estdo estcionário Estudos experimentis mostrm que o fluxo de solvente (águ) em respost pressão hidráulic, em um meio homogêneo e poroso, é nálogo o fluxo difusivo
Trnsporte de solvente trvés de membrns: estdo estcionário Estudos experimentis mostrm que o fluxo de solvente (águ) em respost pressão hidráulic, em um meio homogêneo e poroso, é nálogo o fluxo difusivo
1º semestre de Engenharia Civil/Mecânica Cálculo 1 Profa Olga (1º sem de 2015) Função Exponencial
 º semestre de Engenhri Civil/Mecânic Cálculo Prof Olg (º sem de 05) Função Eponencil Definição: É tod função f: R R d form =, com R >0 e. Eemplos: = ; = ( ) ; = 3 ; = e Gráfico: ) Construir o gráfico d
º semestre de Engenhri Civil/Mecânic Cálculo Prof Olg (º sem de 05) Função Eponencil Definição: É tod função f: R R d form =, com R >0 e. Eemplos: = ; = ( ) ; = 3 ; = e Gráfico: ) Construir o gráfico d
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
 PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Prof Mc ARMANDO PAULO DA SILVA Prof Mc JOSÉ DONIZETTI DE LIMA INTEGRAIS IMPRÓPRIAS A TRANSFORMADA DE LAPLACE g ()d = lim R R g()d o limit it Qudo o limit it
PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ Prof Mc ARMANDO PAULO DA SILVA Prof Mc JOSÉ DONIZETTI DE LIMA INTEGRAIS IMPRÓPRIAS A TRANSFORMADA DE LAPLACE g ()d = lim R R g()d o limit it Qudo o limit it
Primeira Prova de CTC-20 Estruturas Discretas 24/09/2009 Prof. Carlos Henrique Q. Forster
 Primir Prov CTC-0 Estruturs Disrts 4/09/009 Pro Crlos nriqu Q Forstr om: GABARITO 40 pontos Consir Z n { 0 n } Z é um grupo on é oprção ou-xlusivo Mostr qu oprção ou-xlusivo it--it m plvrs 3 its orm um
Primir Prov CTC-0 Estruturs Disrts 4/09/009 Pro Crlos nriqu Q Forstr om: GABARITO 40 pontos Consir Z n { 0 n } Z é um grupo on é oprção ou-xlusivo Mostr qu oprção ou-xlusivo it--it m plvrs 3 its orm um
CRYSTTIAN ARANTES PAIXÃO TRANSPORTE ELETRÔNICO EM SISTEMAS DE BAIXA DIMENSIONALIDADE
 CRYSTTAN ARANTES PAXÃO TRANSPORTE ELETRÔNCO EM SSTEMAS DE BAXA DMENSONALDADE Moogrfi d grdução prstd o Dprtmto d Ciêci d Computção d Uivrsidd Fdrl d Lvrs como prt ds igêcis do curso d Ciêci d Computção
CRYSTTAN ARANTES PAXÃO TRANSPORTE ELETRÔNCO EM SSTEMAS DE BAXA DMENSONALDADE Moogrfi d grdução prstd o Dprtmto d Ciêci d Computção d Uivrsidd Fdrl d Lvrs como prt ds igêcis do curso d Ciêci d Computção
TÓPICOS. Melhor aproximação. Projecção num subespaço. Mínimo erro quadrático.
 Not m: litur dsts pontmntos não dispns d modo lgum litur tnt d iliogrfi principl d cdir Chm-s tnção pr importânci do trlho pssol rlizr plo luno rsolvndo os prolms prsntdos n iliogrfi, sm consult prévi
Not m: litur dsts pontmntos não dispns d modo lgum litur tnt d iliogrfi principl d cdir Chm-s tnção pr importânci do trlho pssol rlizr plo luno rsolvndo os prolms prsntdos n iliogrfi, sm consult prévi
ln xdx 1 TÉCNICAS DE INTEGRAÇÃO
 Cpítlo Técnics d Inrção - TÉCNICAS DE INTEGRAÇÃO. INTEGRAÇÃO POR PARTES Um técnic d inrção mito útil é inrção por prts, q dpnd d fórml pr difrncil d m prodto. Sjm f g fnçõs difrnciávis d. Então, pl rgr
Cpítlo Técnics d Inrção - TÉCNICAS DE INTEGRAÇÃO. INTEGRAÇÃO POR PARTES Um técnic d inrção mito útil é inrção por prts, q dpnd d fórml pr difrncil d m prodto. Sjm f g fnçõs difrnciávis d. Então, pl rgr
0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:
![0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é: 0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:](/thumbs/95/123353134.jpg) - Rção orm zro: Es ipo rção ão po sr lmr (., ão há rção!), so poro ipo ν, logo, mos qu, i Igrção, pr 4 ) (, cocrção m um mpo é: 5 6 7 Eq. () 8 (Nos mplos i supori qu ). 9 - Rçõs orm : S loci rção é rmi
- Rção orm zro: Es ipo rção ão po sr lmr (., ão há rção!), so poro ipo ν, logo, mos qu, i Igrção, pr 4 ) (, cocrção m um mpo é: 5 6 7 Eq. () 8 (Nos mplos i supori qu ). 9 - Rçõs orm : S loci rção é rmi
c.c. É a função que associa a cada x X(S) um número f(x) que deve satisfazer as seguintes propriedades:
 Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj um vriávl ltóri com conjunto d vlors (S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. É função qu ssoci
Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj um vriávl ltóri com conjunto d vlors (S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. É função qu ssoci
1. DISPOSITIVOS SEMICONDUTORES
 . DISPOSIIOS SMICODUORS. Itroução: isositivos ltrôicos Fisicmt, são struturs cujo comortmto létrico romit : s PROPRIDDS DOS MRIIS DS IRFCS os PRÂMROS GOMÉRICOS COSRUIOS Plcs mtálics Por xmlo, um strutur
. DISPOSIIOS SMICODUORS. Itroução: isositivos ltrôicos Fisicmt, são struturs cujo comortmto létrico romit : s PROPRIDDS DOS MRIIS DS IRFCS os PRÂMROS GOMÉRICOS COSRUIOS Plcs mtálics Por xmlo, um strutur
VARIÁVEIS ALEATÓRIAS CONTÍNUAS. Vamos agora estudar algumas variáveis aleatórias contínuas e respectivas propriedades, nomeadamente:
 86 VARIÁVIS ALATÓRIAS CONTÍNUAS Vmos gor studr lgums vriávis ltóris contínus rspctivs propridds, nomdmnt: uniform ponncil norml qui-qudrdo t-studnt F DISTRIBUIÇÃO UNIFORM Considr-s qu função dnsidd d proilidd
86 VARIÁVIS ALATÓRIAS CONTÍNUAS Vmos gor studr lgums vriávis ltóris contínus rspctivs propridds, nomdmnt: uniform ponncil norml qui-qudrdo t-studnt F DISTRIBUIÇÃO UNIFORM Considr-s qu função dnsidd d proilidd
Aula 16 p. 1. 1:for Cada v V do 2: Make_Set(v) 3:for cada aresta (u, v) E do. 1:if Find_Set(u)=Find_Set(v)then. 5: Union(u, v)
 Estrutur d Ddos pr Cojutos Aul 16 Estrutur d ddos pr Cojutos Disjutos Prof. Mro Aurélio Stfs mro m dt.ufms.r www.dt.ufms.r/ mro Complxidd srá mdid m fução: úmro d oprçõs Mk_St m úmro totl d oprçõs Mk_St,
Estrutur d Ddos pr Cojutos Aul 16 Estrutur d ddos pr Cojutos Disjutos Prof. Mro Aurélio Stfs mro m dt.ufms.r www.dt.ufms.r/ mro Complxidd srá mdid m fução: úmro d oprçõs Mk_St m úmro totl d oprçõs Mk_St,
TRIGONOMETRIA. A trigonometria é uma parte importante da Matemática. Começaremos lembrando as relações trigonométricas num triângulo retângulo.
 TRIGONOMETRIA A trigonometri é um prte importnte d Mtemátic. Começremos lembrndo s relções trigonométrics num triângulo retângulo. Num triângulo ABC, retângulo em A, indicremos por Bˆ e por Ĉ s medids
TRIGONOMETRIA A trigonometri é um prte importnte d Mtemátic. Começremos lembrndo s relções trigonométrics num triângulo retângulo. Num triângulo ABC, retângulo em A, indicremos por Bˆ e por Ĉ s medids
# D - D - D - - -
 1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
Encontro na casa de Dona Altina
 Ano 1 Lagdo, Domingo, 29 d junho d 2014 N o 2 Encontro na casa d Dona Altina Na última visita dos studants da UFMG não foi possívl fazr a runião sobr a água. Houv um ncontro com a Associação Quilombola,
Ano 1 Lagdo, Domingo, 29 d junho d 2014 N o 2 Encontro na casa d Dona Altina Na última visita dos studants da UFMG não foi possívl fazr a runião sobr a água. Houv um ncontro com a Associação Quilombola,
Electromagnetismo e Óptica
 Elctromgntismo Óptic Lbortório 1 Expriênci d Thomson OBJECTIVOS Obsrvr o fito d forç d Lorntz. Mdir o cmpo d indução mgnétic produzido por bobins d Hlmholtz. Dtrminr xprimntlmnt o vlor d rlção crg/mss
Elctromgntismo Óptic Lbortório 1 Expriênci d Thomson OBJECTIVOS Obsrvr o fito d forç d Lorntz. Mdir o cmpo d indução mgnétic produzido por bobins d Hlmholtz. Dtrminr xprimntlmnt o vlor d rlção crg/mss
ELETROPNEUMÁTICA E SEGURANÇA DAS MÁQUINAS NOVA DIRETIVA 2006/42/CE NORMAS NF EN/CEI 62061 - EN ISO 13849-1
 ELETRONEUMÁTICA E SEGURANÇA DAS MÁQUINAS NOVA DIRETIVA 2006/42/CE NORMAS NF EN/CEI 62061 - EN ISO 13849-1 SEGURANÇA DAS MÁQUINAS rincípio d sgurnç ds máquins: Grntir sgurnç súd ds pssos xposts durnt instlção,
ELETRONEUMÁTICA E SEGURANÇA DAS MÁQUINAS NOVA DIRETIVA 2006/42/CE NORMAS NF EN/CEI 62061 - EN ISO 13849-1 SEGURANÇA DAS MÁQUINAS rincípio d sgurnç ds máquins: Grntir sgurnç súd ds pssos xposts durnt instlção,
Cálculo II. Eliezer Batista Elisa Zunko Toma Márcio Rodolfo Fernandes Silvia Martini de Holanda Janesch
 Cálculo II Eliezer Btist Elis Zuko Tom Márcio Rodolfo Ferdes Silvi Mrtii de Hold Jesch ª Edição Floriópolis, Govero Federl Presidete d Repúblic: Dilm V Rousseff Miistro de Educção: Aloízio Mercdte Coordedor
Cálculo II Eliezer Btist Elis Zuko Tom Márcio Rodolfo Ferdes Silvi Mrtii de Hold Jesch ª Edição Floriópolis, Govero Federl Presidete d Repúblic: Dilm V Rousseff Miistro de Educção: Aloízio Mercdte Coordedor
1 Instituto de Geografia e Ordenamento do Território da Universidade de Lisboa (IGOT-UL) 2 Instituto Superior de Agronomia Universidade de Lisboa
 MODELOS ESPACIALMENTE EXPLÍCITOS DE ANÁLISE DE DINÂMICAS LOCAIS: O CASO DA VEGETAÇÃO NATURAL POTENCIAL NO APOIO AO PLANEAMENTO E ORDENAMENTO TERRITORIAL Frncsco Gutrrs1, Eusébo Rs1, Crlos Nto1 José Crlos
MODELOS ESPACIALMENTE EXPLÍCITOS DE ANÁLISE DE DINÂMICAS LOCAIS: O CASO DA VEGETAÇÃO NATURAL POTENCIAL NO APOIO AO PLANEAMENTO E ORDENAMENTO TERRITORIAL Frncsco Gutrrs1, Eusébo Rs1, Crlos Nto1 José Crlos
1. VARIÁVEL ALEATÓRIA 2. DISTRIBUIÇÃO DE PROBABILIDADE
 Vriáveis Aletóris 1. VARIÁVEL ALEATÓRIA Suponhmos um espço mostrl S e que cd ponto mostrl sej triuído um número. Fic, então, definid um função chmd vriável letóri 1, com vlores x i2. Assim, se o espço
Vriáveis Aletóris 1. VARIÁVEL ALEATÓRIA Suponhmos um espço mostrl S e que cd ponto mostrl sej triuído um número. Fic, então, definid um função chmd vriável letóri 1, com vlores x i2. Assim, se o espço
Experiência n 2 1. Levantamento da Curva Característica da Bomba Centrífuga Radial HERO
 8 Expriência n 1 Lvantamnto da Curva Caractrística da Bomba Cntrífuga Radial HERO 1. Objtivo: A prsnt xpriência tm por objtivo a familiarização do aluno com o lvantamnto d uma CCB (Curva Caractrística
8 Expriência n 1 Lvantamnto da Curva Caractrística da Bomba Cntrífuga Radial HERO 1. Objtivo: A prsnt xpriência tm por objtivo a familiarização do aluno com o lvantamnto d uma CCB (Curva Caractrística
NESS-A TOUCH SCREEN 7" C/ MODEM
 6 7 8 9 0 QUIPMNTOS ONTROLOS OMPRSSOR LTRNTIVO // LTRÇÃO LYOUT-IM MUTI PR SOPOST OTÃO MRÊNI LLN9 0 07/0/ LTRÇÃO O MOM O LYOUT LOUV 7 0 06// INLUSÃO O ORINTTIVO O LÇO OMUNIÇÃO IO V. 00 8/0/ INIIL TOS R.
6 7 8 9 0 QUIPMNTOS ONTROLOS OMPRSSOR LTRNTIVO // LTRÇÃO LYOUT-IM MUTI PR SOPOST OTÃO MRÊNI LLN9 0 07/0/ LTRÇÃO O MOM O LYOUT LOUV 7 0 06// INLUSÃO O ORINTTIVO O LÇO OMUNIÇÃO IO V. 00 8/0/ INIIL TOS R.
Elementos de Análise Financeira Fluxos de Caixa Séries Uniformes de Pagamento
 Elemetos de Aálise Ficeir Fluxos de Cix Séries Uiformes de Pgmeto Fote: Cpítulo 4 - Zetgrf (999) Mtemátic Ficeir Objetiv 2ª. Ed. Editorção Editor Rio de Jeiro - RJ Séries de Pgmetos - Defiição Defiição:
Elemetos de Aálise Ficeir Fluxos de Cix Séries Uiformes de Pgmeto Fote: Cpítulo 4 - Zetgrf (999) Mtemátic Ficeir Objetiv 2ª. Ed. Editorção Editor Rio de Jeiro - RJ Séries de Pgmetos - Defiição Defiição:
Sistemas e Sinais (LEIC) Resposta em Frequência
 Sismas Siais (LEIC Rsposa m Frquêcia Carlos Cardira Diaposiivos para acompahamo da bibliografia d bas (Srucur ad Irpraio of Sigals ad Sysms, Edward A. L ad Pravi Varaiya Sumário Dfiiçõs Sismas sm mmória
Sismas Siais (LEIC Rsposa m Frquêcia Carlos Cardira Diaposiivos para acompahamo da bibliografia d bas (Srucur ad Irpraio of Sigals ad Sysms, Edward A. L ad Pravi Varaiya Sumário Dfiiçõs Sismas sm mmória
, onde F n é uma força de tracção e d o alongamento correspondente. F n [N] -1000 -2000
![, onde F n é uma força de tracção e d o alongamento correspondente. F n [N] -1000 -2000 , onde F n é uma força de tracção e d o alongamento correspondente. F n [N] -1000 -2000](/thumbs/26/7541439.jpg) º Tst d CONTROLO DE SISTEMS (TP E PRO) Licciatura m Eg.ª Mcâica Prof. Rsposávl: Pdro Maul Goçalvs Lourti d bril d 00 º Smstr Duração: hora miutos. Tst com cosulta. Rsolução. Cosidr o sistma rprstado a
º Tst d CONTROLO DE SISTEMS (TP E PRO) Licciatura m Eg.ª Mcâica Prof. Rsposávl: Pdro Maul Goçalvs Lourti d bril d 00 º Smstr Duração: hora miutos. Tst com cosulta. Rsolução. Cosidr o sistma rprstado a
Taxi: Opção mais rápida e cara. Deve ser evitada, a não ser que você privilegie o conforte
 Vi vijr pr? Situ-s com nosss dics roportos trns mtrôs Chgd m Avião: Aroporto Hthrow: Situdo crc 20 km ost um dos mis movim ntdos d Europ possui cinco trminis Dpois pssr pls formlids imigrção pgr su bggm
Vi vijr pr? Situ-s com nosss dics roportos trns mtrôs Chgd m Avião: Aroporto Hthrow: Situdo crc 20 km ost um dos mis movim ntdos d Europ possui cinco trminis Dpois pssr pls formlids imigrção pgr su bggm
Professores Edu Vicente e Marcos José Colégio Pedro II Departamento de Matemática Potências e Radicais
 POTÊNCIAS A potênci de epoente n ( n nturl mior que ) do número, representd por n, é o produto de n ftores iguis. n =...... ( n ftores) é chmdo de bse n é chmdo de epoente Eemplos =... = 8 =... = PROPRIEDADES
POTÊNCIAS A potênci de epoente n ( n nturl mior que ) do número, representd por n, é o produto de n ftores iguis. n =...... ( n ftores) é chmdo de bse n é chmdo de epoente Eemplos =... = 8 =... = PROPRIEDADES
Alteração da seqüência de execução de instruções
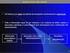 Iníci Busc d próxim Excut Prd Cicl busc Cicl xcuçã Prgrm Sqüênci instruçõs m mmóri Trdutr : Cmpilr X Intrprtr / Linkditr Cnvrt prgrm-fnt m prgrm bjt (lingugm máqui) Prgrm cmpil = mis rápi Prgrm Intrprt
Iníci Busc d próxim Excut Prd Cicl busc Cicl xcuçã Prgrm Sqüênci instruçõs m mmóri Trdutr : Cmpilr X Intrprtr / Linkditr Cnvrt prgrm-fnt m prgrm bjt (lingugm máqui) Prgrm cmpil = mis rápi Prgrm Intrprt
3 Proposição de fórmula
 3 Proposição fórmula A substituição os inos plos juros sobr capital próprio po sr um important instrumnto planjamnto tributário, sno uma rução lgal a tributação sobr o lucro. Nos últimos anos, a utilização
3 Proposição fórmula A substituição os inos plos juros sobr capital próprio po sr um important instrumnto planjamnto tributário, sno uma rução lgal a tributação sobr o lucro. Nos últimos anos, a utilização
Como a x > 0 para todo x real, segue que: a x = y y 1. Sendo f -1 a inversa de f, tem-se que f -1 (y)= log a ( y y 1 )
 .(TA - 99 osidere s firmções: - Se f: é um fução pr e g: um fução qulquer, eão composição gof é um fução pr. - Se f: é um fução pr e g: um fução ímpr, eão composição fog é um fução pr. - Se f: é um fução
.(TA - 99 osidere s firmções: - Se f: é um fução pr e g: um fução qulquer, eão composição gof é um fução pr. - Se f: é um fução pr e g: um fução ímpr, eão composição fog é um fução pr. - Se f: é um fução
CÁLCULO I. Exibir o cálculo de algumas integrais utilizando a denição.
 CÁLCULO I Prof Mrcos Diiz Prof Adré Almeid Prof Edilso Neri Prof Emerso Veig Prof Tigo Coelho Aul o : A Itegrl de Riem Objetivos d Aul Deir itegrl de Riem; Exibir o cálculo de lgums itegris utilizdo deição
CÁLCULO I Prof Mrcos Diiz Prof Adré Almeid Prof Edilso Neri Prof Emerso Veig Prof Tigo Coelho Aul o : A Itegrl de Riem Objetivos d Aul Deir itegrl de Riem; Exibir o cálculo de lgums itegris utilizdo deição
5(6,67Ç1&,$(&$3$&,7Æ1&,$
 59 5(6,67Ç&,$(&$3$&,7Æ&,$ ÃÃ5(6,67Ç&,$Ã(Ã/(,Ã'(Ã+0 No pítulo 6 efinimos ução J σ omo seno um ensie e oente e onução. Multiplino mos os los po um áe S, el fiá: J.S σs (A (8. σs (A (8. Se o mpo elétio fo
59 5(6,67Ç&,$(&$3$&,7Æ&,$ ÃÃ5(6,67Ç&,$Ã(Ã/(,Ã'(Ã+0 No pítulo 6 efinimos ução J σ omo seno um ensie e oente e onução. Multiplino mos os los po um áe S, el fiá: J.S σs (A (8. σs (A (8. Se o mpo elétio fo
fundamental do cálculo. Entretanto, determinadas aplicações do Cálculo nos levam a formulações de integrais em que:
 Cpítulo 8 Integris Imprópris 8. Introdução A eistênci d integrl definid f() d, onde f é contínu no intervlo fechdo [, b], é grntid pelo teorem fundmentl do cálculo. Entretnto, determinds plicções do Cálculo
Cpítulo 8 Integris Imprópris 8. Introdução A eistênci d integrl definid f() d, onde f é contínu no intervlo fechdo [, b], é grntid pelo teorem fundmentl do cálculo. Entretnto, determinds plicções do Cálculo
b 2 = 1: (resp. R2 e ab) 8.1B Calcule a área da região delimitada pelo eixo x, pelas retas x = B; B > 0; e pelo grá co da função y = x 2 exp
 8.1 Áres Plns Suponh que cert região D do plno xy sej delimitd pelo eixo x, pels rets x = e x = b e pelo grá co de um função contínu e não negtiv y = f (x) ; x b, como mostr gur 8.1. A áre d região D é
8.1 Áres Plns Suponh que cert região D do plno xy sej delimitd pelo eixo x, pels rets x = e x = b e pelo grá co de um função contínu e não negtiv y = f (x) ; x b, como mostr gur 8.1. A áre d região D é
DIAGRAMA DE INTERLIGAÇÃO DE AUTOMAÇÃO NESS P2 COM SENSORES NESS P2 SEM SENSORES
 0 QUIPMTOS OTROLOS OMPRSSOR PRUSO IRM ITRLIÇÃO UTOMÇÃO 0.0.. SS P OM SSORS 0.0..0 SS P SM SSORS /0/ ILUSÃO O MOLO SM SSORS 0/0/ LTRÇÃO MR O TRSUTOR ORRT URO URO /0/ RVISÃO S IMSÕS O LYOUT /0/ LTRÇÃO O
0 QUIPMTOS OTROLOS OMPRSSOR PRUSO IRM ITRLIÇÃO UTOMÇÃO 0.0.. SS P OM SSORS 0.0..0 SS P SM SSORS /0/ ILUSÃO O MOLO SM SSORS 0/0/ LTRÇÃO MR O TRSUTOR ORRT URO URO /0/ RVISÃO S IMSÕS O LYOUT /0/ LTRÇÃO O
Recordando produtos notáveis
 Recordndo produtos notáveis A UUL AL A Desde ul 3 estmos usndo letrs pr representr números desconhecidos. Hoje você sbe, por exemplo, que solução d equção 2x + 3 = 19 é x = 8, ou sej, o número 8 é o único
Recordndo produtos notáveis A UUL AL A Desde ul 3 estmos usndo letrs pr representr números desconhecidos. Hoje você sbe, por exemplo, que solução d equção 2x + 3 = 19 é x = 8, ou sej, o número 8 é o único
Grafos. Luís Antunes. Grafos dirigidos. Grafos não dirigidos. Definição: Um grafo em que os ramos não são direccionados.
 Luís Antuns Grfos Grfo: G=(V,E): onjunto vértis/nós V um onjunto rmos/ros E VxV. Rprsntção visul: Grfos não irigios Dfinição: Um grfo m qu os rmos não são irionos. Grfos irigios Dfinição: Um grfo m qu
Luís Antuns Grfos Grfo: G=(V,E): onjunto vértis/nós V um onjunto rmos/ros E VxV. Rprsntção visul: Grfos não irigios Dfinição: Um grfo m qu os rmos não são irionos. Grfos irigios Dfinição: Um grfo m qu
FUNÇÃO EXPONENCIAL. a 1 para todo a não nulo. a. a. a a. a 1. Chamamos de Função Exponencial a função definida por: f( x) 3 x. f( x) 1 1. 1 f 2.
 49 FUNÇÃO EXPONENCIAL Professor Lur. Potêcis e sus proprieddes Cosidere os úmeros ( 0, ), mr, N e, y, br Defiição: vezes por......, ( ), ou sej, potêci é igul o úmero multiplicdo Proprieddes 0 pr todo
49 FUNÇÃO EXPONENCIAL Professor Lur. Potêcis e sus proprieddes Cosidere os úmeros ( 0, ), mr, N e, y, br Defiição: vezes por......, ( ), ou sej, potêci é igul o úmero multiplicdo Proprieddes 0 pr todo
P R E G Ã O P R E S E N C I A L N 145/2010
 P R E G Ã O P R E S E N C I A L N 145/2010 D A T A D E A B E R T U R A : 2 9 d e d e z e m b r o d e 2 0 1 0 H O R Á R I O : 9:0 0 h o r a s L O C A L D A S E S S Ã O P Ú B L I C A: S a l a d a C P L/
P R E G Ã O P R E S E N C I A L N 145/2010 D A T A D E A B E R T U R A : 2 9 d e d e z e m b r o d e 2 0 1 0 H O R Á R I O : 9:0 0 h o r a s L O C A L D A S E S S Ã O P Ú B L I C A: S a l a d a C P L/
unesp ARITMÉTICA DE PONTO FLUTUANTE
 usp CAMUS DE GUARATINGUETÁ Computção Cálculo Numérco rof. G.J. d S - Dpto. d Mtmátc Ed.. CAÍTULO ARITMÉTICA DE ONTO LUTUANTE.. Rprstção d Númros um Sstm d Artmétc d oto lutut O Sstm Computcol d Artmétc
usp CAMUS DE GUARATINGUETÁ Computção Cálculo Numérco rof. G.J. d S - Dpto. d Mtmátc Ed.. CAÍTULO ARITMÉTICA DE ONTO LUTUANTE.. Rprstção d Númros um Sstm d Artmétc d oto lutut O Sstm Computcol d Artmétc
Resolução A primeira frase pode ser equacionada como: QUESTÃO 3. Resolução QUESTÃO 2 QUESTÃO 4. Resolução
 (9) - www.elitecmpins.com.br O ELITE RESOLVE MATEMÁTICA QUESTÃO Se Améli der R$, Lúci, então mbs ficrão com mesm qunti. Se Mri der um terço do que tem Lúci, então est ficrá com R$, mis do que Améli. Se
(9) - www.elitecmpins.com.br O ELITE RESOLVE MATEMÁTICA QUESTÃO Se Améli der R$, Lúci, então mbs ficrão com mesm qunti. Se Mri der um terço do que tem Lúci, então est ficrá com R$, mis do que Améli. Se
Definição de Termos Técnicos
 Dfinição d Trmos Técnicos Eng. Adriano Luiz pada Attack do Brasil - THD - (Total Harmonic Distortion Distorção Harmônica Total) É a rlação ntr a potência da frqüência fundamntal mdida na saída d um sistma
Dfinição d Trmos Técnicos Eng. Adriano Luiz pada Attack do Brasil - THD - (Total Harmonic Distortion Distorção Harmônica Total) É a rlação ntr a potência da frqüência fundamntal mdida na saída d um sistma
2 Mbps (2.048 kbps) Telepac/Sapo, Clixgest/Novis e TV Cabo; 512 kbps Cabovisão e OniTelecom. 128 kbps Telepac/Sapo, TV Cabo, Cabovisão e OniTelecom.
 4 CONCLUSÕES Os Indicadors d Rndimnto avaliados nst studo, têm como objctivo a mdição d parâmtros numa situação d acsso a uma qualqur ára na Intrnt. A anális dsts indicadors, nomadamnt Vlocidads d Download
4 CONCLUSÕES Os Indicadors d Rndimnto avaliados nst studo, têm como objctivo a mdição d parâmtros numa situação d acsso a uma qualqur ára na Intrnt. A anális dsts indicadors, nomadamnt Vlocidads d Download
PROVA DE MATEMÁTICA - TURMAS DO
 PROVA DE MATEMÁTICA - TURMAS DO o ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - MARÇO DE 0. ELABORAÇÃO: PROFESSORES ADRIANO CARIBÉ E WALTER PORTO. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 0. (UDESC SC)
PROVA DE MATEMÁTICA - TURMAS DO o ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - MARÇO DE 0. ELABORAÇÃO: PROFESSORES ADRIANO CARIBÉ E WALTER PORTO. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 0. (UDESC SC)
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
TÓPICOS DE RESOLUÇÃO DO EXAME DE CÁLCULO I
 Faculdad d Ecoomia Uivrsidad Nova d Lisboa TÓPICOS DE RESOLUÇÃO DO EXAME DE CÁLCULO I Ao Lctivo 7-8 - º Smstr Eam Fial d 1ª Época m d Juho d 8 Duração: horas 3 miutos É proibido usar máquias d calcular
Faculdad d Ecoomia Uivrsidad Nova d Lisboa TÓPICOS DE RESOLUÇÃO DO EXAME DE CÁLCULO I Ao Lctivo 7-8 - º Smstr Eam Fial d 1ª Época m d Juho d 8 Duração: horas 3 miutos É proibido usar máquias d calcular
Aula 9 Limite de Funções
 Alise Mtemátic I Aul 9 Limite de Fuções Ao cdémico 017 Tem 1. Cálculo Dierecil Noção ituitiv e deiição de ite. Eemplos de ites. Limites lteris. Proprieddes. Bibliogri Básic Autor Título Editoril Dt Stewrt,
Alise Mtemátic I Aul 9 Limite de Fuções Ao cdémico 017 Tem 1. Cálculo Dierecil Noção ituitiv e deiição de ite. Eemplos de ites. Limites lteris. Proprieddes. Bibliogri Básic Autor Título Editoril Dt Stewrt,
Integrais. A integral indefinida de uma função f(t) é representada como. Por outro lado, a integral definida, representada como
 J. A. M. Flipp d Soz Igris (rsmo l) Igris A igrl idfiid d m fção f() é rprsd como f ( τ) Por oro ldo, igrl dfiid, rprsd como f ( τ), f ( τ) τ o f ( τ) dτ 3 d fz Som d Rim q clcl ár so crv m m irvlo m dfiido
J. A. M. Flipp d Soz Igris (rsmo l) Igris A igrl idfiid d m fção f() é rprsd como f ( τ) Por oro ldo, igrl dfiid, rprsd como f ( τ), f ( τ) τ o f ( τ) dτ 3 d fz Som d Rim q clcl ár so crv m m irvlo m dfiido
Transporte Vestiário Higiene Pessoal Poupança
 Álgbr Mricil PRTE LGUMS CONSDERÇÕES TEORCS MTRZES Noção d mriz Mrizs formm um impor cocio m mmáic, d spcil uso o sudo d rsformçõs lirs mriiz é um bl d lmos disposos m lih colus Mriz m é um bl d m úmros
Álgbr Mricil PRTE LGUMS CONSDERÇÕES TEORCS MTRZES Noção d mriz Mrizs formm um impor cocio m mmáic, d spcil uso o sudo d rsformçõs lirs mriiz é um bl d lmos disposos m lih colus Mriz m é um bl d m úmros
Reforço Orientado. Matemática Ensino Médio Aula 4 - Potenciação. Nome: série: Turma: t) (0,2) 4. a) 10-2. b) (-2) -2. 2 d) e) (0,1) -2.
 Reforço Orientdo Mtemátic Ensino Médio Aul - Potencição Nome: série: Turm: Exercícios de sl ) Clcule s potêncis, em cd qudro: r) b) (-) Qudro A s) t) (0,) Qudro B - b) (-) - e) (-,) g) (-) h) e) (0,) -
Reforço Orientdo Mtemátic Ensino Médio Aul - Potencição Nome: série: Turm: Exercícios de sl ) Clcule s potêncis, em cd qudro: r) b) (-) Qudro A s) t) (0,) Qudro B - b) (-) - e) (-,) g) (-) h) e) (0,) -
