Soluções E-Procurement

Código PE-ACSH-2. Título:

CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu

RESOLUÇÃO DE EQUAÇÕES POR MEIO DE DETERMINANTES

RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.

Planejamento Estratégico

Pljmo Esrégco Iformvo o Pljmo Esrégco Usc Ao 1 Nº 1 Fvrro 2009 Pljmo Esrégco Iformvo o Pljmo Esrégco Usc Mssão Eucr, por mo o so, psqus xsão, pr promovr qul susbl o mb v. A Usc, por mo os gsors rprss Ror,

Módulo 03. Determinantes. [Poole 262 a 282]

Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost

A formulação representada pelas equações (4.1)-(4.3) no método de elementos finitos é denominada de formulação forte (strong formulation).

4. Fomlção Mcl o Méoo Elmos Fos s cpílo sá ps fomlção mcl o méoo lmos fos pos plcção o méoo lv ssms lgécos q pom s ogzos fom mcl p poso solção po éccs mécs pops p c po qção fcl: lípc pólc o hpólc. O poo

RESPOSTA DO SISTEMA. Resposta em Regime Transitório Resposta em Regime Permanente

RESPOSTA DO SISTEMA Rsps m Rgm Trsór Rsps m Rgm Prm Exmpls d ssms d prmr rdm Tqu d águ crld pr um bó Tx d vrçã lur é prprcl (H-h) dh k( H h) k h H ( ) Ssm RC, cpcr m sér cm rssr dv C RC ( V V C ) V C RC

Espaço de Estados. Modelo de Estado: y(t) = saída u(t) = entrada. função de transferência em cadeia fechada (f.t.c.f) :

Epço Eo Eqo or corolo covcol - rlção r í-r, o fção rfrêc, o corolo moro - crção qçõ o m m rmo qçõ frc ªorm q pom r com m qção frcl ª orm form mrcl. O o oção mrcl mplfc m mo rprção mmác m qçõ. O mo úmro

Associação de Resistores e Resistência Equivalente

Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos

ORGANIZAÇÃO DIDÁTICA DO PROCESSO DE ENSINO, APRENDIZAGEM E DESENVOLVIMENTO: O PLANEJAMENTO. Prof. Dr. Roberto Valdés Puentes

ORGANIZAÇÃO DIDÁTICA DO PROCESSO DE ENSINO, APRENDIZAGEM E DESENVOLVIMENTO: O PLANEJAMENTO Prf. Dr. Rbr Vdés Pus PPGED/FACED/UFU rbrpus@fcd.ufu.br MOMENTOS DO PROCESSO DE ENSINO, APRENDIZAGEM E DESENVOLVIMENTO

Prgrmçã O Mu s u Év r, p r l ém f rcr s s i g ns «vi s i t s cl áss i cs» qu cri m s p nt s c nt ct nt r s di v rs s p úb l ic s qu vi s it m s c nt ú d s d s u ri c s p ó l i, p r cu r, c nc m i t nt

Agrupamento de Escolas Drª Laura Ayres

cár rª r yrs, Qrtr, lé tífc-místc êcs clgs 11º 1 r fs Vz 15 X X X X X X X 9405 2 r s más 16 X X X X X X X 11481 3 r chz rt 16 X X X X X X X 11596 4 árbr f mrl rrã 15 X X X X X X X 11597 5 c f ckhm rrs

1 Instituto de Geografia e Ordenamento do Território da Universidade de Lisboa (IGOT-UL) 2 Instituto Superior de Agronomia Universidade de Lisboa

MODELOS ESPACIALMENTE EXPLÍCITOS DE ANÁLISE DE DINÂMICAS LOCAIS: O CASO DA VEGETAÇÃO NATURAL POTENCIAL NO APOIO AO PLANEAMENTO E ORDENAMENTO TERRITORIAL Frncsco Gutrrs1, Eusébo Rs1, Crlos Nto1 José Crlos

Situação Atual e Perspectivas das Culturas do Cará (Dioscorea sp.) e do Taiá (Colocasia esculenta) no Sul do Brasil

Sção Al Prspcvs s Clrs o Crá (Doscor sp.) o Tá (Colocs scl) o Sl o Brsl Jrz José V Müllr 1 Iroção A proção crá á o á-jpão é rlz promm m pqs proprs, como m v complmr o ssm provo. O cosmo é rlzo prcplm por

9. MODELAGEM DE CONVERSORES: MODELO DA CHAVE PWM

Fns Chs C. 9 Mlgm nrsrs: ml h PWM J. A. Pml 9. MOEAGEM E CONERSORES: MOEO A CHAE PWM As lgs báss nrsrs CCCC ssum um h nrl ur nãnrl sss lmns lnrs nrns n m. A njun ss us hs r nm h PWM [9.]. O bj ns íul é

# D - D - D - - -

1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18

+ = x + 3y = x 1. x + 2y z = Sistemas de equações Lineares

Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn

(22) Data do Depósito: 08/05/2012. (43) Data da Publicação: 12/04/2016 (RPI 2362)

INPI (21) BR 102012010884-4 A2 (22) Dt d Dpósit: 08/05/2012 *BR102012010884A Rpúblic Fdrtiv d Brsil Ministri d Dsnvlvimnt, Indústri d Cmrci Extrir Institut Ncinl d Prpridd Industril (43) Dt d Publicçã:

Processamento Digital de Sinais

Procssmto Digitl Siis Mrclo Bsílio Joquim São Crlos - Íic Aprstção i Cpítulo Siis Sistms tmpo iscrto. Itroução. Siis Tmpo Discrto. Siis tmpo iscrto básicos.. Squêci mostr uitári.. Squêci gru uitário..

TÓPICOS EM MATEMÁTICA AVANÇADA PARA A ENGENHARIA: Álgebra Linear, Geometria Analítica, Cálculo e Equações Diferenciais,

UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE TECNOLOGIA/SETOR DE CIÊNCIAS EXATAS DEPARTAMENTO DE ENGENHARIA CIVIL/ DEPARTAMENTO DE MATEMÁTICA PROGRAMA DE PÓS-GRADUAÇÃO EM MÉTODOS NUMÉRICOS EM ENGENHARIA TÓPICOS

Lista de Exercícios 9 Grafos

UFMG/ICEx/DCC DCC111 Mtmáti Disrt List Exríios 9 Gros Ciênis Exts & Engnhris 1 o Smstr 2018 1. O gro intrsção um olção onjuntos A 1, A 2,..., A n é o gro qu tm um vérti pr um os onjuntos olção tm um rst

Conceitos básicos População É constutuida por todos os elementos que são passíveis de ser analisados de tamanho N

sísc Coceos áscos opulção É cosuud por odos os elemeos que são pssíves de ser lsdos de mho mosrgem Sucojuo d populção que é eecvmee lsdo com um ddo mho mosr leór mosr ode cd elemeo d populção êm hpóeses

Primeira Prova de CTC-20 Estruturas Discretas 24/09/2009 Prof. Carlos Henrique Q. Forster

Primir Prov CTC-0 Estruturs Disrts 4/09/009 Pro Crlos nriqu Q Forstr om: GABARITO 40 pontos Consir Z n { 0 n } Z é um grupo on é oprção ou-xlusivo Mostr qu oprção ou-xlusivo it--it m plvrs 3 its orm um

II L ATA N. 19/XIV. Conselheiro Fernando da Costa Soares.

jf II L Comissão Ncionl Eliçõs ATA N. 19/XIV Tv lugr no di vint qutro jniro dois mil doz, sssão númro znov d Comissão Ncionl Eliçõs, n sl runiõs sit n Av. D. Crlos 1, n. 128 7. ndr, m Lisbo, sob prsidênci

MECANISMOS DE REAÇÕES

/4/7 MECSMS DE REÇÕES rof. Hrly. Mrins Filho Rçõs lmnrs Rçõs qu concm m pns um p são rçõs lmnrs. molculri rção lmnr é o númro moléculs qu rgm. Rção lmnr unimolculr: C molécul m um proili inrínsc s compor

NESS-A TOUCH SCREEN 7" C/ MODEM

6 7 8 9 0 QUIPMNTOS ONTROLOS OMPRSSOR LTRNTIVO // LTRÇÃO LYOUT-IM MUTI PR SOPOST OTÃO MRÊNI LLN9 0 07/0/ LTRÇÃO O MOM O LYOUT LOUV 7 0 06// INLUSÃO O ORINTTIVO O LÇO OMUNIÇÃO IO V. 00 8/0/ INIIL TOS R.

conjunto dos números inteiros. conjunto dos números que podem ser representados como quociente de números inteiros.

Cpítulo I Noçõs Eltrs d Mtátic. Oprçõs co frcçõs, Equçõs Iquçõs Tipos d úros {,,,,,6, } cojuto dos úros turis. 0 { 0} {,,,, 0,,,, } cojuto dos úros itiros., 0 0 p : p, q q cojuto dos úros rciois ou frccioários,

DIAGRAMA DE INTERLIGAÇÃO DE AUTOMAÇÃO EXXA -SL

3 4 7 8 9 0 QUIPMNTOS ONTROLOS XX SL (L44) - RJ4- /SNSORS - IM SOPOR 30.400.83.7 XX SL (L44) - RJ4- /SNSORS - IM MUTIR 30.400.84. IRM INTRLIÇÃO UTOMÇÃO XX -SL 3 0// INTIIÇÃO OS SNSORS UMI PRSSÃO /03/4

MATEMÁTICA A - 12o Ano Funções - Teorema de Bolzano Propostas de resolução

MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos

Sistemas e Sinais (LEIC) Resposta em Frequência

Sismas Siais (LEIC Rsposa m Frquêcia Carlos Cardira Diaposiivos para acompahamo da bibliografia d bas (Srucur ad Irpraio of Sigals ad Sysms, Edward A. L ad Pravi Varaiya Sumário Dfiiçõs Sismas sm mmória

TRANSFORMAÇÕES CONTÍNUAS

TRANSFORMAÇÕES CONTÍNUAS Tscçõs o mo U, 0 0 odo scção o mo odo voução U, 0 HU, 0 Hmoo, H, dd do mo U fução d H U, H 0 0 H gdo do guo ds scçõs o mo [ H, U, ] 0 0 H 0 H 0, 0 H cos do movmo: E, g, cosv-s

PROVA NACIONAL ESCRITA DE MATEMÁTICA

PROVA NACIONAL ESCRITA DE MATEMÁTICA Equip Rsposávl Pl Elorção Corrção d Prov: Prof. Douor Sérgio Brrir Prof.ª Douor Cri Lmos Durção d Prov: 0 miuos. Tolrâci: 30 miuos Coção: 00 PONTOS Escol d Proviêci

que indica que, através do operador H, pode-se determinar y(t) para qualquer u(t).

8. REPRESENÇÃO NO ESPÇO DE ESDOS 8. Coco so ( prsção srá f o omío o mpo coío; s frçs com o cso scro são pqs srão prss posrorm). rprsção r/sí m ssm lr só é ál qo, o mpo cl, o ssm sá o so scoáro. ssm é ál

Transporte Vestiário Higiene Pessoal Poupança

Álgbr Mricil PRTE LGUMS CONSDERÇÕES TEORCS MTRZES Noção d mriz Mrizs formm um impor cocio m mmáic, d spcil uso o sudo d rsformçõs lirs mriiz é um bl d lmos disposos m lih colus Mriz m é um bl d m úmros

Manhã Tarde Noite. Sala 252 - Escola cultura e Sociedade II para o curso de Pedagogia, Prof. Lino.

S g n d Mnhã Td No Sl 251 LD Rpsnção m S Hll, dscpln do PPGE, Po. Mác Ondn. Sl 252 EBOPP T1 o nvsl, Po.ª Eln, 50 lnos. Sl 253 Pojo Novos Cmnhos Poª Glsn Sl 254 Fndmnos SócoHsóco Flosócos d Edcção T5 p

Uniforme Exponencial Normal Gama Weibull Lognormal. t (Student) χ 2 (Qui-quadrado) F (Snedekor)

Prof. Lorí Vili, Dr. vili@pucrs.br vili@m.ufrgs.br hp://www.pucrs.br/fm/vili/ hp://www.m.ufrgs.br/~vili/ Uniform Exponncil Norml Gm Wibull Lognorml (Sudn) χ (Qui-qudrdo) F (Sndkor) Um VAC X é uniform no

CASA DE DAVI CD VOLTARÁ PARA REINAR 1. DEUS, TU ÉS MEU DEUS. E B C#m A DEUS, TU ÉS MEU DEUS E SENHOR DA TERRA

S VI VOLTRÁ PR RINR 1. US, TU ÉS MU US #m US, TU ÉS MU US SNHOR TRR ÉUS MR U T LOUVRI #m SM TI NÃO POSSO VIVR M HGO TI OM LGRI MOR NST NOV NÇÃO #m #m OH...OH...OH LVNTO MINH VOZ #m LVNTO MINHS MÃOS #m

Matrizes - Teoria ...

Mrzs - Tor Mrz Rgulr Mrz Rgulr d ord por é u qudro fordo por los dsposos lhs olus ou s Rprsros u rz d lhs olus por Os los d rz srão dfdos por u lr o dos íds o prro íd d lh o sgudo íd olu à qu pr o lo Iguldd

MÉTODOS NUMÉRICOS. Integração Numérica. por Chedas Sampaio. Época 2002/2003. Escola Náutica I.D.Henrique 1de 33

Métodos umércos - ntegrção umérc Escol áutc.d.henrque MÉTODOS UMÉRCOS ntegrção umérc por Cheds Smpo Époc /3 Escol áutc.d.henrque de 33 Sumáro Regrs áscs Regrs do Rectngulo Regr do Trpézo Regr de Smpson

ELETRÔNICO. PERFIS DE INVESTIMENTO (abril 2013)

INFORMATIVO ELETRÔNICO M 2013 O PLANO DE PREVIDÊNCIA DO SISTEMA UNICRED Íc: GERENCIANDO PARA CRESCER 1. RENTABILIDADE DOS PERFIS DE INVESTIMENTO DO PLANO PRECAVER 2. EM JUNHO VOCÊ PODE MUDAR SEU DE INVESTIMENTO

PREÇOS APLICÁVEIS ÀS CHAMADAS DESTINADAS A SERVIÇOS NÃO GEOGRÁFICOS DE OUTROS OPERADORES

PREÇOS APLICÁVEIS ÀS CHAMADAS DESTINADAS A SERVIÇOS NÃO GEOGRÁFICOS DE OUTROS OPERADORES OPS DE DESTINO SERVIÇ O DE DESTIN O REDE MÓVEL DE ORIGEM (Fixa/ Móvl/ Ambas) DATA DE EFEITOS Cadência d taxação

8 = 1 GRUPO II. = x. 1 ln x

Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim

Disciplina: Programação 1 Professor: Paulo César Fernandes de Oliveira, BSc, PhD. Lista de Exercícios JavaScript 8 (revisão)

Disiplin: Progrmção 1 Profssor: Pulo Césr Frnns Olivir, BS, PhD List Exríios JvSript 8 (rvisão) 1. O qu ont o s xutr progrm ixo? jvsript: - funtion utorizr(snh){ if(snh == "luno"){ lrt("bm-vino!"); ls{

Alteração da seqüência de execução de instruções

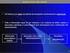Iníci Busc d próxim Excut Prd Cicl busc Cicl xcuçã Prgrm Sqüênci instruçõs m mmóri Trdutr : Cmpilr X Intrprtr / Linkditr Cnvrt prgrm-fnt m prgrm bjt (lingugm máqui) Prgrm cmpil = mis rápi Prgrm Intrprt

ESCOLA SUPERIOR DE TECNOLOGIA

Dprtnto Mtátic Disciplin Anális Mtátic II Curso Engnhri do Abint º Sstr º Fich nº 6: Equçõs difrnciis d vriávis sprds správis, totis cts, co fctor intgrnt hoogéns d ª ord. Coptição ntr spécis E hbitts

Electromagnetismo e Óptica

Elctromgntismo Óptic Lbortório 1 Expriênci d Thomson OBJECTIVOS Obsrvr o fito d forç d Lorntz. Mdir o cmpo d indução mgnétic produzido por bobins d Hlmholtz. Dtrminr xprimntlmnt o vlor d rlção crg/mss

ESTADO-MAIOR DO EXÉRCITO OBJETIVO ROTEIRO XXXXXXXXXXXXXXXXXX

STO-MOR O XÉRCTO OBJTVO 5 PRSTR OS PRCPS SPCTOS S STRUÇÕS GRS PR CORRSPOÊC O XÉRCTO B10- G-01.001 S STRUÇÕS GRS PR OS TOS MSTRTVOS O XÉRCTO - B10-G-01.003 1 / 23 2 / 23 XXXXXXXXXXXXXXXXXX ROTRO do CS CS/GP

CD CORAÇÃO DA NOIVA - 1. O SENHOR É BOM INTR:E D A/C# C7+ B E D A/C# O SENHOR É BOM C7+ B E SEU AMOR DURA PARA SEMPRE ELE É BOM...

C CORÇÃO NOIV - 1. O SNHOR É OM INTR: /C# C7+ /C# O SNHOR É OM C7+ SU MOR UR PR SMPR L É OM... Letra e Música: avi Silva C CORÇÃO NOIV - 2. SNTO É O TU NOM M TO TRR S OUVIRÁ UM NOVO SOM UM CNÇÃO MOR PRCORRRÁ

PROPRIEDADES DO ELIPSÓIDE

. Elis grdor N Godsi é o lisóid d rvolução (ª roximção) qu srv como rfrênci no osicionmnto godésico; N mior rt dos cálculos d Godsi Gométric é usd gomtri do Elisóid d volução; O Elisóid é formdo l rvolução

Mackenzie Voluntario. Caro apoiador, Redes sociais: 8668 de 30/11/1981), que atua em solo brasileiro há 141 anos.

C, O Mkz Vlá é m j sl Mkz, sm fs lvs (D º 8668 3/11/1981), q m sl bsl há 141 s. Iml m 24, m m l fl ssblz, mblz g s s ss gs, gss, lbs, fsss, ls, gs ls, fs, s, mgs fmls m mvm xmçã s ms q bgm s ss m, lém

21/07/2015 13:36:51 ARTE MODA ARTE ARQUITETURA ARQUITETURA ENTRETENIMENTO MODA DESTINO GASTRONOMIA GASTRONOMIA MODA POLINÉSIA FRANCESA. CAPA 24.

R 3 R R D S VL L Ó S L U D K LÃ W -S / 3 SH FW -S Ã P UL F S SP / / : 8:3 3// 8/ 3/ : 6: SPCL - PRU C VCÊ UC VU.in 7 R Ú 8 9 - R$,,9 R$ CP.in S D PP R S G GS S - R$, 9 R D : : U Q R VG D R SÃ PU L FS H

INSTRUÇÕES DE MONTAGEM REF.: REF.: VT-801

NSTRUÇÕS D MONTM R.: R.: VT-8 VT-8 R.: L-8 R.: L-8 MPORTNT: PRODUTO BRCDO COM CPS D MDP MD 15MM UNDOS M D 3MM COM PNTUR ULTRVOLT. RRMNTS 20 MN COL NDÚSTR COMÉRCO D MÓVS LTD RU RLNDO BCCN, 6 BRRO VNDOS

O Uso da Álgebra Linear nas Equações Diferenciais

Uso d Álgr ir s Equçõs ifriis íi Gri ol úi Rsd rir Bofim Fuldd d mái FT Uivrsidd Fdrl d Urlâdi UFU 88 - Urlâdi ril d 8 Rsumo Álgr ir é um supor mmáio pr muis árs d iêi Vrmos omo lgus d sus rsuldos podm

6. Características de Funcionamento Análise Dimensional e Semelhança

6. Crctrístcs Fucomto Aáls msol Smlhç 6.. Grzs Crctrístcs o Fucomto O ucomto um áqu Hráulc stá rtmt ssoco grzs qu mtém um crt pêc tr s. Ests grzs são oms grzs crctrístcs o ucomto. Etr ls pomos ctr: ) Grzs

Variáveis aleatórias Conceito de variável aleatória

Variávis alatórias Muitos primtos alatórios produzm rsultados ão-uméricos. Ats d aalisá-los, é covit trasformar sus rsultados m úmros, o qu é fito através da variávl alatória, qu é uma rgra d associação

Visão Geral Métodos construtivos Métodos construtivos O Mercado Visão de Negócios Alguns números Principais diferenciais

Shw C TÓPICOS Vã Gl Mé cv Mé cv O Mc Vã Ngóc Alg ú Pcp fc Rl N vç Pc Q fz Vã Gl A ESTRUTURA ECOLÓGICA CONSTRUTORA, g c l é c cçã à v pcpçã q lz écc clógc. Sb p v é pf pívl v, p g cl c fã. N çã ppc c, c

!" # $$ " " '# " *+,!$%!-"( "%&'%"($ )%" !" #$% " &"% '(%&!" ) '%" *+( $&"% +"", -$. &) $% /.")" /

!" # $$ "!" #$% " &"% '(%&!" ) '%" *+( $&"% +"", -$. &) $% /.")" #%"0&"#"1$!"%"2&% 3 "%&'%"($ )%" " '# " *+,!$%!-"( /4 56673 Livros Grátis http://www.livrosgratis.com.br Milhares de livros grátis para

Março 2017 *Consulte-nos condições de pagamento a prestações I

L A N E M U SR IN O I R Ó A RO ã i c i F 0 mm sjurss s * r M d 3 é S t Mr 07 *Csult-s cdiõs d pgmt prstõs. 800 83 4 5 I www.dtlxprss.pt ã Prm URBINA PREMIUM PACK DE IMPRESSÃO - 4 Elit HD Putty - 4 Elit

1 Capítulo 2 Cálc l u c lo l I ntegra r l l em m R

píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos

Roteiro de de Trabalho com com o AQUA AQUA REDE REDE

Rtir d d Trblh cm cm AQUA AQUA REDE REDE Prt Prt I I Iníci Iníci AutCAD Lnçr Lnçr s s pnts pnts ct ct d d Rd Rd Lnçr Lnçr s s trchs trchs brts brts lignd lignd smpr smpr d d Mntnt Mntnt pr pr Jusnt Jusnt

TÓPICOS. Integração complexa. Integral de linha. Teorema de Cauchy. Fórmulas integrais de Cauchy.

No m, liur dss pomos ão disps d modo lgum liur d iliogri pricipl d cdir hm-s à ção pr imporâci do rlho pssol rlir plo luo rsolvdo os prolms prsdos iliogri, sm ul prévi ds soluçõs proposs, ális compriv

DIAGRAMA DE INTERLIGAÇÃO DE AUTOMAÇÃO NESS LRC MULTILINHAS C/ IHM

4 5 6 7 8 9 0 QUIPNOS ONROLOS 5 LINS RSRIOS OU LINS ONLOS LIN RSRIOS IR INRLIÇÃO UOÇÃO NSS LR ULILINS O I 8 0/0/5 URÇÃO LRÇÃO OS UNIUS, RPOSIIONNO O POLI LRÇÂO N LIS RIIS LOUV 7 7 0/0/5 LRO O LYOU, SUSIUIO

1 Introdução e Base Matemática

J. A. M. Flipp Souz Iroução Bs Mmáic Iroução Bs Mmáic Iroução Bs Mmáic 3. O úmro imgiário 3. Númros complxos 4.3 Oprçõs com úmros complxos 9.4 O so o co-so.5 A qução Eulr 5.6 A g 7.7 As ivrss so, co-so

4. Análise de Sistemas de Controle por Espaço de Estados

Sisma para vrificação Lógica do Corolo Dzmro 3 4. ális d Sismas d Corol por Espaço d Esados No capiulo arior, vimos qu a formulação d um Prolma Básico d Corolo Ópimo Liar, ra cosidrado um sisma diâmico

Aula 1. Apontamentos Teórico-Práticos de Algoritmia Avançada LEI/ISEP Métodos de Pesquisa Carlos Ramos

Méts Psqus u 1 1 Prr Pru qu stá rt ét Prr Pru é ttr vçr st r st té qu s tr suçã É u ét qu s s çõs ts r rçã rrt, s sr qu s rçã t r squ O ét Prr Pru rst vt tr us rqusts trs ór O ét é té qu r rs qu t várs

(22) Data do Depósito: 11/02/2015. (43) Data da Publicação: 24/01/2017

INPI (21) BR 102015003018-5 A2 (22) Dt do Dpósito: 11/02/2015 *BR102015003018A Rpúblic Fdrtiv do Brsil Ministério d Indústri, Comércio Extrior Srviços Instituto Ncionl d Propridd Industril (43) Dt d Publicção:

ESTIMATIVA: é o valor numérico obtido para o estimador numa certa amostra.

I- STIMAÇÃO D PARÂMTROS 9 INTRODUÇÃO: Sj,,, um mostr ltór com fução (dsdd d proldd cohcd, sj d θ um vtor dos prâmtros dst vrávl ltór Assm θ {θ, θ,, θ k } os k prâmtros qu chmmos d spço d prâmtros dotdo

Oscilações amortecidas

Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa

Teoria dos Grafos Aula 11

Tori dos Gros Aul Aul pssd Gros om psos Dijkstr Implmntção Fil d prioridds Hp Aul d hoj MST Algoritmos d Prim Kruskl Propridds d MST Dijkstr (o próprio) Projtndo um Rd $ $ $ $ $ Conjunto d lolidds (x.

Figura 1. m. Responda às seguintes questões:

UIVERSIDADE DE LISBOA ISIUO SUPERIOR ÉCICO Vbrções e Ruído º Exme /5-5 de Jero de 5 (sem cosul) Problem (6 vl.) Fgur Cosdere o mecsmo de gru de lberdde reresedo fgur, que se ecor su osção cl de equlíbro

INSTRUÇÕES DE MONTAGEM

NSTRUÇÕS D MONTM R.: VT-815 R.: L-822 MPORTNT: PRODUTO BRCDO COM CPS D MDP MD 15MM UNDOS M D 3MM COM PNTUR ULTRVOLT. RRMNTS 20 MN COL NDÚSTR COMÉRCO D MÓVS LTD RU RLNDO BCCN, 6 BRRO VNDOS CX POSTL 847

Mecânica & Ondas. Módulo 10: O Oscilador harmónico. J. Seixas

Mcânc & Onds Oscldor hrónco Spls Co ro Forçdo Oscldors copldos qução ds onds Módulo : O Oscldor hrónco J. Ss Prlnr: Poncs U forç dz - s consrv v s s u l qu du F d Por plo, grvdd é consrv v dgz F g F -

( ) 2. Eletromagnetismo I Prof. Dr. Cláudio S. Sartori - CAPÍTULO VIII Exercícios 1 ˆ ˆ ( ) Idl a R. Chamando de: x y du. tg θ

Elromgnismo Prof. Dr. Cláudio S. Srori - CPÍTUO V Ercícios Emplo Cálculo do cmpo mgnéico d um fio d comprimno prcorrido por um corrn léric num pono P(,,. dl - r + + r dl d P(,, r r + + ( ( r r + + r r

INSTRUÇÕES DE MONTAGEM

NSTRUÇÕS D MONTM R.: VT-732 R.: VT-735 R.: VT-737 R.: L-738 R.: L-739 R.: L-740 MPORTNT: PRODUTO BRCDO COM CPS D MDP MD 15MM UNDOS M D 3MM COM PNTUR ULTRVOLT. RRMNTS 20 MN COL NDÚSTR COMÉRCO D MÓVS LTD

CAPÍTULO 3. Exercícios é contínua, decrescente e k 2 positiva no intervalo [ 3, [. De ln x 1 para x 3, temos. dx 3.

CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)

Capítulo 9. Chopper(conversor CC-CC)

píulo 9 onrsor nrodução hoppr(conrsor rg Alimnção: nsão ix rg: nsão riál Equiln d um rnsormdor A A nsão d síd do conrsor pod sr mior ou mnor qu nsão d nrd Normlmn uilizdos m limnção d disposiios lromcânicos

Métodos Computacionais em Engenharia DCA0304 Capítulo 4

Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d

tr EU H."i Ed <Ft En ,-t;dt.'j oa 5 F.> ?-.ES >.= ii EN -</9Fl _FU ca pla a- c)-e a-t- .Pi ce* ir. F. FT* te l^' ooo\ Q.a tr o^q Et C) slb Ca rr vti

?/ :; : 5 G VJ. iiu'. \..c G 3.;i.. f) \J + '= il 'i rl c pl _ ii >.= h:,;.'j e < n."i r r. 1! ' nr 9 ^^, r.!. l k J J l = r*r ( r f = 9 >,i r!.?. b r r &'= b 9 c l f l^' T*.i ir.. Gr

TEORIA MICROECONÔMICA I N

CENTRO DE CIÊNCIAS SOCIAIS DEPARTAMENTO DE ECONOMIA ECO 3 TEORIA MICROECONÔMICA I N PROFESSOR: JULIANO ASSUNÇÃO TURMA: JA Minimizção de Custos. Conts com Co-Dougls. Considere um firm que produz o produto

Aulas práticas: Introdução à álgebra geométrica

Auls prátics: Introdução à álgr gométric Prolm Mostr qu ár A do prllogrmo d figur nx é dd por A= = αβ αβ y β α α β β A = αβ αβ α x α β = α + α, = β + β = = αβ + αβ = = ( αβ αβ)( ) = + = = 0 = = = 0 = Prolm

Lista 3 - Resolução. 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os.

GN7 Introução à Álgr Linr Prof n Mri Luz List - Rsolução Vrifiqu s os proutos ixo stão m finios, m so firmtivo, lul-os ) [ / ] / ) / [ / ] ) ) Solução ) orm primir mtriz é x sgun é x, logo o prouto stá

INSTRUÇÕES DE MONTAGEM

NSTRUÇÕS D MONTM VT-732 VT-735 VT-737 L-738 L-739 L-740 MPORTNT: PRODUTO BRCDO COM CPS D MDP MD 15MM UNDOS M D 3MM COM PNTUR ULTRVOLT. RRMNTS 20 MN COL NDÚSTR COMÉRCO D MÓVS LTD RU RLNDO BCCN, 6 BRRO VNDOS

APARADOR BUFFET RETRÔ 90

TEÇÃ ESTE PRUT Ã PE SER RRST PRR UET RETRÔ 90 ESÕES PRUT / ESS PRUT L / W X P/ X / H - 800 x 4 x 762 12 2 11 1 2 11 1 13 S: TS S PEÇS SÃ UERS. EX: 1915X-X (nº da peça) US ESPES LPEZ- Pano limpo umedecido

Redes Bayesianas. » Microsoft: em 1993 contratam Eric Horvitz, David Heckerman e Jack Breese

Rds Bss Rds Bss São dgrms qu orgzm o cohcmto um dd ár trvés d um mpmto tr cuss ftos Os sstms sdos m rds Bss são cpzs d grr utomtcmt prdçõs ou dcsõs msmo stução d stêc d lgums pçs d formção Mrcos mportts:»

2º ano Avaliação Mensal MAIO

2º ano Avaliação Mensal MAIO Cap. 07- Troca de bilhetes- Páginas 7 até 12. Cap. 08- Animais da fauna brasileira- Páginas 17 até 25 e 28 e 29. Cap. 09- Barata tonta e barata esperta- Páginas 30 até 39 e

DIMENSÕES DO PRODUTO / DIMENSIONS PRODUCT F2 11

RK RTRÔ 85 INSÕS PRUT / INSINS PRUT L / W x P/ x / - 1620 x 388 x 547 ST PRUT NÃ P SR RRST S: TS S PÇS SÃ NURS. X: 1915X-X 05 (nº da peça) 2 1 08 1 05 UIS SPIIS LIPZ- Pano limpo umedecido em água e sabão

RESOLUÇÃO Matemática APLICADA FGV Administração - 06-06-10

QUESTÃO 1 VESTIBULAR FGV 2010 JUNHO/2010 RESOLUÇÃO DAS 10 QUESTÕES DE MATEMÁTICA DA PROVA DA TARDE - MÓDULO DISCURSIVO São curiosos os números. Às vezes é mis útil rredondá-los do que trblhr com seu vlor

Arquitetura de Sistemas Web

Arquittura d Sistmas Wb Rprsntação dsign arquittural d sistmas Wb Uso da UML Visõs Arquitturais Basa na tação d Jim Conalln WAE UML Rfrência Jim Conalln. Building Wb Application with UML Addison-Wsly,

Avaliação externa/avaliação interna: o equilíbrio necessário

4º Étco Intrg São Pulo, 22 d gosto d 2009 Avlção xtrn/avlção ntrn: o qulíbro ncssáro Nílson José Mchdo Unvrsdd d São Pulo Fculdd d Educção njmchd@usp.br www.nlsonjosmchdo.nt Avlção: qustõs fundmnts - O

PLANEAMENTO E PROGRAMAÇÃO DO TREINO DE ATLETAS DE ½ FUNDO E FUNDO

PLM PGMÇÃ LS ½ F F SPÊS BLÓGS S SÂS ½ F F 800M 1500M 3000M SÂS 5000M 10000M ½ M. M. L L FQÊ.Í L Z ÍVL B B LÁ SV B XSV 22 LÁ SV 14 B XSV FQ.. MX. 8 MS SV 6 B XSV FQ.. MX. -15 4 3 B B ÓB GLL. B B LPLÍ 2

PLR Por quê? d L i i q u e z b l d d R t i i e n a a e b d E i t a d d d P t i i ro u v a e é l l d B F t i R t u s c a e r n c a e p o e su a o

.. u p v g c C C O ) F h C I ( É, - p c c ç u u g w w p g c u F C I ã ) A U E ( C D h W k N f N h C F. z c v p ç p g u ) k M U ( E ã A M ) P S ( M P S E k M G p v h F C O ã b S Apc gc Agc Ag c R z O v

ANÁLISE DE ESTRUTURAS I

IST - DECvl Deprtmento de Engenhr Cvl NÁISE DE ESTRUTURS I Tels de nálse de Estruturs Grupo de nálse de Estruturs IST, 0 Formuláro de es IST - DECvl Rotções: w w θ θ θ θ n θ n n Relção curvtur-deslocmento:

PLANEJAMENTO PEDAGÓGICO PP

1. Ifmçõs Gs PLAEJAEO PEDAGÓGICO PP 1.1. ucíp: 1.2. UF: 1.3. ês/a Pcm PP: 1.4. m Rspsávl pl Elbç PP: 1.5. Cg Rspsávl pl Elbç PP: 1.6. E-ml Rspsávl (fm ps um): 1.7. Eç: 1.7.1. Cmplm: 1.7.2. CEP: 1.8. lf

Problema do Caixeiro Viajante. Solução força bruta. Problema do Caixeiro Viajante. Projeto e Análise de Algoritmos. Problema do Caixeiro Viajante

Projto Anális Aloritmos Prolm o Cixiro Vijnt Altirn Sors Silv Univrsi Frl o Amzons Instituto Computção Prolm o Cixiro Vijnt Um vim (tour) m um ro é um ilo qu pss por toos os vértis. Um vim é simpls quno

3 Solução Analítica Exata para Viga Infinita no Caso Linear

37 3 Solução Alítc Ext pr Vg It o Cso Lr st cpítulo são borddos os procdmtos pr rsolução d qução (.4, pr o cso spcíco d um vg prsmátc d comprmto to. st sstm os dslocmtos rotçõs tdm pr o zro à mdd qu s

Criando Valor para o Negócio com a Solução SAP para Gestão de Capital Humano

Crian Valor o Ngócio a SAP Gstão Capital Hno Grans Grans Dsafi Dsafi na na Gstão Gstão Rcurs Rcurs Hn Hn Gstão Talnt Gstão Talnt Atrair rtr o talnto quan o mrca é Atrair Atrair Atrair rtr rtr rtr talnto

4.21 EXERCÍCIOS pg. 176

78 EXERCÍCIOS pg 7 Nos rcícios d clculr s drivds sucssivs t ordm idicd, 5 7 IV V 7 c d c, 5, 8 IV V VI 8 8 ( 7) ( 8), ( ) ( ) '' ( ) ( ) ( ) ( ) 79 5, 5 8 IV, 8 7, IV 8 l, 9 s, 7 8 cos IV V VI VII 5 s

Transformada de Laplace. Prof. Eng. Antonio Carlos Lemos Júnior

Trormd d plc Pro. Eg. oio Crlo mo Júior GEND Diição d Trormd d plc Trormd d plc d lgu ii Propridd d Trormd d plc Exrcício Corol d Sm Mcâico Trormd d plc Obivo: O obivo d ção é zr um irodução à Trormd d

RESULTADO FINAL OPTATIVAS INTERCURSO

Ç Ã B S F PVS S 2014/2 ome atrícula urso S GÇVS SG204104 SÇÃ ÊSS S P SG208080 G P H SG207287 BÁB G H SG204772 ÇÃ BY FGS SG207806 ÇÃ FÍS B S V SG207988 S - ÍG PGS PS S SG208360 QÍ V F SG204632 H V GÇVS

Porcentagem (testemunha) Ano 1 (1) Ano 2 (2) Ano 3 (3) Média g/s/a (4) kg/ha/ano (5) g/s/a kg/ha/ano g/s/a kg/ha/ano g/s/a kg/ha/ano

Clones Parentais IAC 40 RRIM 608 (AVROS 33 x Tjir 1) x AVROS 1279 (AVROS 156 x AVROS 374) IAC 56 RRIM 608 (AVROS 33 x Tjir 1) x Fx 3810 (F 4542 x AVROS 363) IAC 300 RRIM 605 (Tjir 1 x PB 49) x AVROS 363

EM NOME DO PAI ====================== j ˆ«. ˆ««=======================

œ» EM NOME O PI Trnscçã Isbel rc Ver Snts Pe. Jãzinh Bm & # #6 8 j. j... Œ. ll { l l l l n me d Pi e d Fi lh ed_es & #. 2. #. _. _ j.. Œ. Œ l l l j {.. l. pí t Sn t_ mém Sn t_ mém LÓRI O PI Trnscçã Isbel