Física IV para a Escola Politécnica (Engenharia Elétrica) TURMA 3
|
|
|
- Denílson Mendes Alvarenga
- 6 Há anos
- Visualizações:
Transcrição
1 Física IV para a Escola Politécica (Egearia Elétrica) TURMA 3 Professor: Dr. Marcos A. G. Alvarez Departaeto de Física Nuclear (DFN) IFUSP Edifício Oscar Sala (sala 46) Escaio alvarez@if.usp.br IVRO: Pricípios de Física (Óptica e Física Modera) Rayod A. Serway / Jo W. Jewett Jr. Volue 4
2 PROVA P Capítulos 8 e 9 Serway/Jewett vol. 4 CAPÍTUO 8: Física Quâtica Radiação de corpo egro e a Teoria de Plack O Efeito Foto-Elétrico O Efeito Copto Fótos e Odas Eletroagéticas Propriedades Odulatórias das Partículas A Partícula Quâtica Eperiêcia de Dupla Feda
3 CAPÍTUO 8: Física Quâtica O Pricípio da Icerteza Mecâica Quâtica Ua Partícula e ua Caia A Equação de Scrödiger Tuelaeto através de ua Barreira de Eergia Potecial ista de eercícios sugerida Capítulo 8: 8.4,., 3, 4, 5, 6, 9, 0,, 33, 35, 38, 4, 43, 5
4 A partícula quâtica Ates: odelos corpusculares (partículas co carga e assa) odelos odulatórios (odas) Depois: Efeito Foto-Elétrico & Copto Tato a luz coo as partículas tê propriedades corpusculares e odulatórias De Broglie p p v
5 EXEMPO 8.5 O coprieto de oda de u elétro Calcule o coprieto de oda de De Broglie para u elétro deslocado-se co ua velocidade de: v sedo 7 e / e v s 9. 3 Kg
6 EXEMPO 8.5 O coprieto de oda de u elétro Calcule o coprieto de oda de De Broglie para u elétro deslocado-se co ua velocidade de: v sedo 7 e / s 9. 3 Kg Solução e v ( 3 ) ( 7 ) 9. Kg.0 / s J s 7.8 Este coprieto de oda correspode ao coprieto de oda típico dos raios-x
7 Eeplo 3- Eisberg & Resick: Coprieto de oda de ua bola Qual é o coprieto de oda de De Broglie de ua bola de beisebol co ua assa de Kg ovedo-se a ua velocidade de /s J s p v.0kg s
8 Eeplo 8.7: Ua carga acelerada Ua partícula de carga q e assa é acelerada a partir do repouso por ua difereça de potecial V. Supodo que a partícula desloca-se co velocidade ão relativística, ecotre seu coprieto de oda de de Broglie. v p vv q V Calcule o coprieto de oda de de Broglie de u elétro acelerado por ua difereça de potecial de 50V. p q e e.6 p 9 9. C 3 Kg
9 Eeplo 8.7: Ua carga acelerada Ua partícula de carga q e assa é acelerada a partir do repouso por ua difereça de potecial V. Supodo que a partícula co velocidade ão relativística, ecotre seu coprieto de oda de de Broglie. p ( ) q,, V v p v p v q V q V q V eu A p q V q V ou eu A
10 Calcule o coprieto de oda de de Broglie de u elétro acelerado por ua difereça de potecial de 50V J s eu A 9.6 C 9. Kg 50V 3 carga assa ENTIDADES CORPUSCUARES
11 Resultados eperietais deveria ostrar que elétros são difratados pelos plaos de u cristal de aeira siilar aos raios-x, sedo portato aplicável a codição de Bragg. ( ) dseθ,,3... O coprieto de oda que deveos associar aos elétros é previsto pela ipótese de De Broglie, segudo a qual: ( ) dseθ,,3... p v
12 Ua característica essecial de ua partícula é que ela está localizada o espaço. O prieiro passo é ostrar que podeos costruir ua etidade localizada a partir de cosiderações odulatórias. Iagie traçar ua oda ao logo do eio co ua de suas cristas localizadas e 0. 0
13 ogo ua seguda oda de esa aplitude as co ua frequêcia diferete, poré tabé co ua de suas cristas e 0. Frequêcias diferetes e Aplitudes que coicide e 0 O resultado da superposição dessas duas odas é u batieto pois as odas estão alteradaete e fase e fora de fase.
14 Iterferêcia etre odas está coectada à (difereça de) fase etre as odas. A difereça de fase etre duas odas pode udar Iterferêcia costrutiva Dois casos etreos de iterferêcia Iterferêcia destrutiva
15 Iterferêcia de duas odas co esa aplitude e esa frequêcia Padrão de iterferêcia cotíuo o tepo oda de cor preta é estacioária Iterferêcias costrutivas e destrutivas etre odas está coectada à (difereça de) fase etre as odas. Duas odas pode ter distitas frequêcias (coprietos de oda). A difereça de fase etre duas odas pode udar. Cosiderado duas odas co distitas frequêcias e esa aplitude (A), eiste ua aplitude (A) áia para a aplitude de ua iterferêcia costrutiva.
16 Iterferêcia de duas odas co esa aplitude e diferetes frequêcias Padrão de iterferêcia descotíuo o tepo (a) Ua oda idealizada co ua úica frequêcia eata é a esa por todo o espaço e e todo istate; (b) se são cobiadas duas odas ideais co frequêcias ligeiraete diferetes, surge (b)batietos (posições alteradaete e fase e fora de fase)
17 Se adicioaos odas, de odo que suas cristas coicida co as deais odas e 0, a pequea região de iterferêcia costrutiva é deoiada pacote de oda. Iterferêcia áia e 0 Esta é ua região localizada do espaço que é diferete de todas as outras. Aquí, podeos assuir (aproiar) o pacote de odas coo/por ua partícula.
18 O padrão de batietos da figura da esquerda co ua fução evoltória sobreposta (figura da direita). Cada vez que ocorre u áio de aplitude se diz que ocorreu u batieto.
19 Cosidere duas odas co aplitudes iguais, as frequêcias diferetes f e f. Podeos represetar estas odas ateáticaete coo: ( ) ( ) ( ) ( ) b a b a b a t k A t k A y y y k f t k A y t k A y cos cos cos cos trigooétrica fora a cos cos Pricípio de Superposição e cos e cos. ω ω π π ω ω ω a b ( ) ( ) ( ) ( ) t k k t k A t k t k t k t k A y t k b t k a b a cos cos cos cos teos : e sedo cos cos cos cos ω ω ω ω ω ω ω ω ω a b O segudo fator co-seo represeta ua oda co u úero de oda e frequêcia iguais às édias dos valores das odas idividuais.
20 k ω k + k ω + ω Acos t cos t O segudo fator co-seo represeta ua oda co u úero de oda e frequêcia iguais às édias dos valores das odas idividuais. O fator etre colcetes represeta a evoltória da oda, coo ostrado Observe que este fator tabé te a fora ateática de ua oda ( k ω t) e y A ( k ω t) y Acos cos Esta oda descrita pela fução evoltória pode deslocar-se o espaço co ua velocidade diferete das odas idividuais.
21 Coo u eeplo etreo dessa possibilidade, iagie cobiar duas odas idêticas deslocado-se e direções opostas. As duas odas desloca-se co a esa velocidade escalar, as a evoltória te ua velocidade ula, pois costruíos ua oda estacioária
22 ( ) ( ) ( ) ( ) t k A t k A y y y k f t k A y t k A y cos cos pelo Pricípio de Superposição e cos e cos ω ω π π ω ω ω t k k t k A cos cos ω ω ω
23 Para ua oda idividual, a velocidade é dada pela equação: fase Que é defiida coo velocidade de fase porque é a taa de progressão de ua crista e ua úica oda, que é u poto de fase fia. v fase ω k v ω k π π ω πf e k T ω coeficiete de variável teporal"t" v fase vg k coeficiete de variável espacial"" ω k O subscrito g a velocidade idica que ela é usualete deoiada velocidade de grupo ou a velocidade do pacote de odas (o grupo de odas) que costruíos. Ode teos ua cobiação de frequêcias (ω) e coprietos de oda () variáveis etre diferetes odas.
24 Para ua superposição de u úero uito grade odas para forar u pacote de odas, teos a razão: dk d g ω v Vaos ultiplicar o uerador e o deoiador por ћ ode ћ/π: aalisado separadaete o d d ) ( ω ω aalisado separadaete o uerador e o deoiador dp de k d d p k E f f k d d dk d g g ) ( ) ( v ) ( ) ( v ω π π π π ω ω ω
25 Coo estaos eplorado a possibilidade de que a evoltória das odas cobiadas represete a partícula, se cosideraos ua partícula livre deslocado-se co ua velocidade v que é pequea coparada co a velocidade da luz. A eergia da partícula é sua eergia ciética: p difereciado co relação a p E v p g v de dp v d dp p ( p) Assi, podeos assuir a aalogia etre a velocidade do pacote de oda e a velocidade de ua partícula p v
26 Os pacotes de oda são costruídos coo ua superposição liear de odas plaas de diferetes oetos lieares «p». p ( ) p Neste caso, cada copoete do pacote de odas viaja co sua velocidade característica, coecida coo velocidade de fase.
27 Novaete a Eperiêcia da Dupla Feda Ates: odelos corpusculares (partículas co carga e assa) odelos odulatórios (odas) Depois: Efeito Foto-Elétrico & Copto Tato a luz coo as partículas tê propriedades corpusculares e odulatórias De Broglie p p v
28 Novaete a Eperiêcia da Dupla Feda Vaos laçar elétros cotra ua dupla feda Cosidere u feie paralelo de elétros oo-eergéticos (oo-croáticos) icidido sobre ua dupla feda. As larguras das fedas são pequeas? coparadas co o coprieto de oda do elétro O detector de elétros é colocado be loge das fedas a ua distâcia uito aior que d (distâcia de separação etre as fedas).
29 ACEITÁVE???
30 Efeito esperado Teoria Clássica Se o detector coletar elétros por u tepo veos u típico padrão de iterferêcia de oda e teros do úero de elétros por iuto. Não se espera tal coportaeto se cosideraos os elétros - partículas. Esta é ua evidêcia de que os elétros estão iterferido segudo feôeos ao eos siilares aos odulatórios.
31 Efeito esperado Teoria Clássica Se o detector coletar elétros por u tepo veos u típico padrão de iterferêcia de oda e teros do úero de elétros por iuto. Não se espera tal coportaeto se cosideraos os elétros - partículas. Esta é ua evidêcia de que os elétros estão iterferido segudo feôeos ao eos siilares aos odulatórios.
32 Efeito esperado Teoria Clássica Efeito observado Teoria Quâtica
33 Se iagiaros elétro(s) o feie produzido pequeas odas e fase quado alcaça ua das fedas Utilizado a teoria odulatória do Capítulo 7, etão: F dseθ represeta u íio de iterferêcia, e F dseθ represeta u áio de iterferêcia F dseθ
34 F dseθ Coo o coprieto de oda do elétro é dado por:, para θ pequeo p seθ θ p d teos : Coo isso se respeita fica ostrada a F dseθ atureza dual do elétro. Iterferêcia destrutiva
35 F dseθ Coo o coprieto de oda do elétro é dado por:, para θ pequeo teos : p seθ θ p d Coo isso se respeita fica ostrada a atureza dual do elétro. F dseθ Iterferêcia costrutiva
36 Assi, os elétros são detectados coo partículas e u certo poto e algu istate de tepo. Mas a probabilidade de cegada a esse poto é deteriada pela itesidade de duas odas que iterfere.
37 Eercício 8.4 É usado u osciloscópio odificado para realizar ua eperiêcia de iterferêcia de elétros. Elétros icide sobre u par de fedas estreitas separadas por µ. As badas brilates o padrão de iterferêcia estão separadas por 0,400 sobre ua tela a 0,0 c das fedas. Deterie a difereça de potecial através da qual os elétros fora acelerados para forar este padrão. dse θ p e v e K v e V e e
38 É usado u osciloscópio odificado para realizar ua eperiêcia de iterferêcia de elétros. Elétros icide sobre u par de fedas estreitas separadas por µ. As badas brilates o padrão de iterferêcia estão separadas por 0,400 sobre ua tela a 0,0 c das fedas. Deterie a difereça de potecial através da qual os elétros fora acelerados para forar este padrão. Cosiderado a prieira bada brilate teos: dseθ tgθ dseθ K V v e 0.00 e v v e e e e e v e e ( 8 ) 6.0 se( 0.00) e e V ( 34 ) 6.63 J s ( 9 )( 3 )( ) C 9. Kg J C V 5V
39 EXERCÍCIO O que acotece quado ua feda é coberta
40 EXERCÍCIO Se ua feda é coberta, se observa ua curva siétrica co seu pico ao redor da feda aberta áio cetral do padrão de difração de feda úica. A figura ostra gráficos das cotages de elétros por iuto (probabilidade de cegada de elétros) co a feda superior () ou iferior () fecada.
41 RESUMINDO Se a feda está aberta e a feda fecada por u certo tepo e depois iverteos durate o eso itervalo de tepo obteos os padrões e azul É iportate observar Que é copletaete diferete do padrão e que as duas fedas estão abertas (curva co vários picos). Não eiste ais ua probabilidade áia de cegada e θ0 (curva azul) Desaparece o padrão de iterferêcia e o resultado acuulado é a soa dos resultados idividuais.
42 COMO PODEMOS IDENTIFICAR POR ONDE O EÉTRON PASSA QUANDO AS DUAS FENDAS ESTÃO ABERTAS????
43 Quado as duas fedas estão abertas ossa ituição tede a iduzir-os a que o elétro passa pela feda OU pela feda. Padrão de iterferêcia siilar ao de duas odas oocroáticas coeretes Os resultados eperietais idicados pelo padrão de iterferêcia co uitos picos cotradize isso. PRINCÍPIO DE HUYGENS Portato, a coclusão de que o elétro é localizado e atravessa apeas ua feda quado as duas fedas são abertas está errada. Coclusão difícil pois vai e cotra da ossa ituição.
44 U elétro iterage co as duas fedas siultaeaete. É ipossível deteriar por qual feda passa o elétro. Se tetaros deteriar eperietalete qual feda o elétro atravessou, o siples ato da edida destruirá o padrão de iterferêcia. Podeos apeas afirar que o elétro passa pelas duas fedas.
45 O PRINCÍPIO DA INCERTEZA Sepre que se ede a posição ou a velocidade de ua partícula e u certo istate, icertezas eperietais estão icluídas as edidas. De acordo co a ecâica clássica ão á u liite para o aueto da precisão (diiuição da icerteza) dos procedietos eperietais.
46 O PRINCÍPIO DA INCERTEZA A Mecâica Quâtica prevê que é fudaetalete ipossível edir siultâeaete a posição () e o oeto (pv) de ua partícula co precisão ifiita. Se são feitas ua edida da posição de ua partícula co ua icerteza ( ) e ua edida siultâea do seu oeto co ua icerteza ( p) o produto das duas icertezas uca pode ser eor que ћ/: i p i π
47 Cosidere ua partícula para a qual coeceos eataete o coprieto de oda. De acordo co as relações de de Broglie : Coeceríaos o oeto co precisão ifiita. Eistiria por todo o espaço ua oda co o coprieto de oda. Qualquer região ao logo dessa oda sigifica a esa coisa que qualquer outra região. p
48 Se os pergutaos, ode está a partícula represetada por esta oda? Neua localização especial o espaço ao logo da oda poderia ser idetificada co a partícula, pois todos os potos ao logo da oda são idêticos. Assi teos ua icerteza ifiita a posição da partícula. U coecieto perfeito do oeto custa toda a iforação quato à posição. p cte
49 E coparação, cosidere agora ua partícula co algua icerteza o oeto, de tal fora que seja possível u itervalo de oetos p o que iplica u itervalo de coprietos de oda. p p Assi a partícula ão é represetada por u úico coprieto de oda, as por ua cobiação de coprietos de oda este itervalo. Esta cobiação fora u pacote de odas
50 Para deteriar a posição da partícula, podeos dizer que ela está e algu poto a região defiida pelo pacote de oda, pois eite ua ítida difereça etre esta região e o restate do espaço. Assi ao perder parte da iforação quato ao oeto da partícula, gaaos iforação sobre sua posição.
51 Eeplo 8.8 ocalizado u elétro É edida a velocidade de u elétro coo sedo: e Detro de quais liites pode-se deteriar a posição desse elétro ao logo da direção de seu vetor velocidade? v v e 3 (5.0 ± 0.003%) s (5000,00 ± 0.5) s p e e v e ( 3 ) 9. Kg p p
52 Eeplo 8.8 ocalizado u elétro É edida a velocidade de u elétro coo sedo: e Detro de quais liites pode-se deteriar a posição desse elétro ao logo da direção de seu vetor velocidade? Solução: O oeto do elétro é: p v e e v v e 3 (5.0 ± 0.003%) s (5000,00 ± 0.5) s ( ) ( ) Kg 5 Kg s Assuido a icerteza do oeto, coo sedo igual à icerteza da velocidade Teos: 3 Kg p p.37 Pode-se agora calcular a icerteza íia a posição usado-se o valor de p a equação: p p J s kg s s s 0.384
53 Eercício 7: U elétro e u projétil tê, cada u, ua velocidade de agitude 500/s eata co aproiação de 0.00%. Detro de quais liites poderíaos deteriar a posição dos corpos ao logo da direção da velocidade? Coecedo os valores das respectivas assas: p e p 9. v Kg p π Kg
54 Eercício 7: U elétro e u projétil tê, cada u, ua velocidade de agitude 500/s eata co aproiação de 0.00%. Detro de quais liites poderíaos deteriar a posição dos corpos ao logo da direção da velocidade? Coecedo os valores das respectivas assas: 3 Para o elétro: e 9. p p e e v v ( -3 )( )( 4 ) 9. Kg 500 / s Kg s ( 34 ) 6.63 J s. 6 4π p 3 Kg 4π 4.56 s Para o projétil: p v 0.000Kg p e e 4π p ( )( )( 4 ) 500 / s.00 v.0 3 Kg s p 0.000Kg ( 34 ) 6.63 J s π.0 3 Kg s Kg
55 A fora ateática do pricípio da icerteza afira que o produto das icertezas a posição e o oeto sepre será aior que u valor íio. Pode ser gerada ua outra fora do pricípio da icerteza recosiderado a figura co o tepo o eio o lugar da posição. Podeos cosiderar os esos arguetos, utilizados para o coprieto de oda (oeto) e a posição, o doíio teporal. As variáveis correspodetes seria a frequêcia e o tepo. A frequêcia está relacioada co a eergia por: E f e o pricípio de icerteza E t esta fora é :
56 Se cobiaos u grade úero de odas a probabilidade de u valor positivo a fução de oda e qualquer poto é a esa que a probabilidade de u valor egativo. Iterferêcia áia e 0 Se cada oda ova é adicioada de odo que sua crista coicida co as deais odas e 0, a pequea região de iterferêcia costrutiva é deoiada pacote de oda. Esta é ua região localizada do espaço que é diferete de todas as outras. Aquí, podeos assuir o pacote de odas coo ua partícula.
57 CAPÍTUO 8: Física Quâtica O Pricípio da Icerteza Iterpretação da Mecâica Quâtica Ua partícula livre e e ua caia Fução de Oda e Valor Esperado A Equação de Scrödiger Tuelaeto através de ua Barreira de Eergia Potecial ista de eercícios sugerida Capítulo 8: 8.4,., 3, 4, 5, 6, 9, 0,, 33, 35, 38, 4, 43, 5
58 UMA INTERPRETAÇÃO DA MECÂNICA QUÂNTICA Aalogias perite tratar radiação eletroagética coo corpúsculo Vios que o úero de elétros (portador de carga) por uidade de tepo é proporcioal à itesidade de correte elétrica. I dq dt (derivada - taa de variação de carga co o tepo) Defiição de carga está oralete relacioada co elétros, prótos, íos. Defiição de correte: fluo de carga por uidade de tepo. Supoaos que a carga q se ove através de ua seção trasversal A de u arae (fio), e u tepo t, etão a itesidade de correte I através do arae é dada por: NQ C I( A) t s C e úero de elétros
59 UMA INTERPRETAÇÃO DA MECÂNICA QUÂNTICA Aalogaete, cosiderado o fóto coo portador de radiação eletroagética, o úero de fótos (NF) por uidade de área (A-D) volue (V-3D) é proporcioal à itesidade da radiação: I( A) NQ t C s 8 C 6.4 e NF probabilidade Iα α V V Dito de outra aeira, a probabilidade de ecotrar u fóto por uidade de volue, e ua certa região do espaço, e u certo istate de tepo é proporcioal ao úero de fótos por uidade de volue Recordado que a itesidade da radiação eletroagética é proporcioal ao quadrado do capo elétrico: I α E α probabilidade V
60 Odas eletroagéticas trasporta eergia e a taa de fluo de eergia atravessado ua uidade de área A é descrita pelo vetor de poitig S r CalculadoS para ua oda eletroagética plaa. r r r r 0 E e B são perpediculares etre sí E B EB, assi este caso: S S EB, sedo B µ 0 0 cb µ Isso ivolvea a 0 B µ 0 a E c A édia teporalde equações para Desta fora,o valor édio de I E µ c S E S tabé podeos forular: édia teporalde cos a E µ c 0 cb µ a 0 ( k ωt) r S por u ou ais ciclos é a itesidade. S que é igual a ou a itesidade da oda é : µ. r E S que se aplicaa istate de tepo. r B
61 A probabilidade por uidade de volue de localizar ua partícula associada co essa radiação (o fóto) pode ser assuida coo proporcioal ao quadrado de ua aplitude da oda. r E r (, t) E cos( k ωt) I α E (, t) E cos ( k ωt) 0 I α E α probabilidade V E a k (, t) π k π ωt ωt Assuido a dualidade oda-partícula, a probabilidade de ecotrar ua partícula, por uidade de volue, pode ser assuida proporcioal ao quadrado da aplitude da oda represetado a partícula.
62 p ψ (, y, z) v,p, E ψ (, y, z, t)
63 Na verdade, a aplitude da oda associada a ua partícula ão é ua gradeza física e portato ão é esurável coo é o capo elétrico para ua oda eletroagética. A úica coeão é a aalogia dada pela equação: I α E α probabilidade α V A Coo resutado disso, caaos siplesete a aplitude da oda associada à partícula de aplitude de probabilidade ou de fução de oda
64 A fução de oda é a descrição ateática ais copleta possível para u sistea regido pela ecâica quâtica. Na ecâica clássica a descrição copleta de u sistea cosistia e deteriar a posição e a velocidade de todas as partículas e, co esta descrição, ser possível prever todos os ovietos futuros e passados do sistea. Na ecâica quâtica ão se pode deteriar todas as gradezas desejadas co a esa certeza (Pricípio da Icerteza). De acordo co a ecâica quâtica, a descrição do sistea teria ao ível da fução de oda, co a idéia de probabilidade de ecotrar a partícula e ua posição.
65 ( ) dv r A fução de oda ψ, y, z r é ua ferraeta ateática (, y, z) criada a partir de eis da Física que coté (gera) iforação espacial da partícula. Ua fução de oda ais copleta deve depeder tabé do tepo, represetada por ua epressão do tipo: ψ (, y, z, t) Já vios que, a equação de de Broglie relacioa o oeto de ua partícula co seu coprieto de oda. p Se ua partícula livre ideal te u oeto p coecido co precisão sua fução de oda é ua oda seoidal co coprieto de oda: + e a partícula te ua probabilidade igual de estar e qualquer poto do espaço p
66 A fução de oda para tal partícula livre deslocado-se ao logo do eio pode ser escrita a fora: ψ Ebora ão podeos edir ψ, podeos edir ua desidade de probabilidade que é a probabilidade relativa por uidade de volue de ecotrar a partícula e qualquer poto de volue. Ψ Substituido dv por d e r por teos: P ( ) d ψ d ( ) Ase Ase( k) r d r ( r) V π r, dv r (, y z) Coo a partícula te que estar e algu lugar do espaço Ao logo do eio a soa das probabilidades sobre todos os valores de é + ψ d 0% Qualquer fução de oda que satisfaça esta codição é dita oralizada +
67 A fução de oda para tal partícula livre deslocado-se ao logo do eio pode ser escrita a fora depedete do tepo coo: ψ π (, t) Ase πft Ase( k ωt) Ebora ão podeos edir ψ, podeos edir a desidade de probabilidade que é a probabilidade relativa por uidade de volue de ecotrar a partícula e qualquer poto de volue. Ψ Substituido dv por d e r por teos: P ( ) d ψ d r d r ( r) V r, dv r (, y z) Coo a partícula te que estar e algu lugar do espaço Ao logo do eio a soa das probabilidades sobre todos os valores de é + ψ d Qualquer fução de oda que satisfaça esta codição é dita oralizada
68 Ebora ão seja possível especificar a posição de ua partícula co certeza absoluta, é possível, através de ψ especificar a probabilidade de observá-la e ua pequea região ao redor de u certo poto. A probabilidade de ecotrar a partícula o itervalo a b (a<<b) é: P b ab ψ d a Esta probabilidade é a área sobre a curva de ψ e fução de etre os potos a e b. Eperietalete esta probabilidade é fiita. O valor desta probabilidade te que estar etre 0 e (cojuto dos úeros reais positivos).
69 Eercício 33 - Seção 8.9: Ua iterpretação da Mecâica Quâtica U elétro livre te ua fução de oda: Ode está e etros. Ecotre: (a) o coprieto de oda de De Broglie (b) o oeto liear (c) a eergia ciética e elétro-volt ψ ( ) ( ) Ase 5.00 ψ ( ) Ase p K J p π J s Kg ev
70 Eercício 33 - Seção 8.9: Ua iterpretação da Mecâica Quâtica U elétro livre te ua fução de oda: Ode está e etros. Ecotre: (a) o coprieto de oda de De Broglie (b) O oeto liear (c) A eergia ciética e elétro-volt π a ψ Ase Ase 5.00 π etão, 5.00 π ( ) ( ) ( ) ( b) ( c) K p p Kg J s 5.7 ( 4 ) 5.7 Kg 9. 3 s Kg 4.5 kg 7 s J J J ev 95.5eV
71 Eercício 3 - Seção 8.9: Ua iterpretação da Mecâica Quâtica A fução de oda para ua partícula livre é: ψ ( ) π ( a + a ) para a > 0 e - < < + Deterie a probabilidade de que a partícula esteja localizada e algu lugar etre -a e +a Sabedo que: d arctg a + a a
72 Eercício 3 - Seção 8.9: Ua Iterpretação da Mecâica Quâtica A fução de oda para ua partícula livre é: Deterie a probabilidade de que a partícula esteja localizada e algu lugar etre -a e +a ( ) < + < > + - e 0 para a ) ( a a π ψ ( ) ( ) ( ) [ ] 4 4 ta ta ta π π π π π π ψ P a a a d a a P a a a a a a
73 UMA PARTÍCUA EM UMA CAIXA (a) Ua partícula de assa e velocidade v, sedo refletida para a frete e para tras etre duas paredes ipeetráveis. (b) A fução eergia potecial para o sistea.
74 UMA PARTÍCUA EM UMA CAIXA Ua partícula de assa, velocidade v e oeto pv sedo refletida para a frete e para trás etre duas paredes ipeetráveis, ode a fução eergia de potecial é represetada por u poço de potecial de zero a ifiito.
75 UMA PARTÍCUA EM UMA CAIXA, a qual te que satisfazer as codições de cotoro as paredes π ( ) ( ) Ase π π π ψ π ψ 0 0 ( ) ( ) Ase Ase Ase Ase π π π ψ π π π π π ψ 3 3 ; ; 0
76 UMA PARTÍCUA EM UMA CAIXA p,,3...) ( 8 p v E Quatização de eergia
77 EXEMPO 8.9: U elétro ligado. U elétro esta cofiado etre duas paredes ipeetráveis separados por 0.. Deterie as eergias peritidas da partícula para os estados quâticos descritos por,,3. e 3 Kg 9. p,,3...) ( 8 v p E
78 EXEMPO 8.9: U elétro ligado. U elétro esta cofiado etre duas paredes ipeetráveis separados por 0.. Deterie as eergias peritidas da partícula para os estados quâticos descritos por,,3. p E v.5 8 J p para, teos : E e Kg 8 9.4eV 8 ( -34 ) 6.63 J s ( -3 ) ( ) 9. Kg (,,3...)
79 EXERCÍCIO 35, seções 8. e 8., A partícula quâtica e ua caia sob codições de cotoro U elétro está cotido e ua caia uidiesioal co largura de 0.0. (a) Trace u diagraa dos íveis de eergia para o elétro co íveis até 4. (b) Ecotre os coprietos de oda de todos os fótos que pode ser eitidos pelo elétro ao realizar trasições espotâeas que poderia levá-lo, evetualete, do estado 4 para o estado, cosiderado d d p d d E p d 8d (,,3...)
80 p E d d p p,,3...) ( substitido e, ( ) ( ) ( ) ( ) ( ) ( )( ) ev ev E ev d J d Kg s J d E d d E ,,3...) (
81 p E d d p p,,3...) ( substitido e, ( ) ( ) ( ) ( ) ( ) ( )( ) ev ev E ev d J d Kg s J d E d d E ,,3...) (
82 p E d d p p,,3...) ( substitido e, ( ) ( ) ( ) ( ) ( ) ( )( ) ev ev E ev d J d Kg s J d E d d E ,,3...) (
83 p E d d p p,,3...) ( substitido e, ( ) ( ) ( ) ( ) ( ) ( )( ) ev ev E ev d J d Kg s J d E d d E ,,3...) (
84 EXERCÍCIO 35, seções 8. e 8., A partícula quâtica e ua caia sob codições de cotoro U elétro está cotido e ua caia uidiesioal co largura de 0.0. (b) Ecotre os coprietos de oda de todos os fótos que pode ser eitidos pelo elétro ao realizar trasições espotâeas que poderia levá-lo, evetualete, do estado 4 para o estado Resposta: Quado o elétro salta do estado para o estado ele libera a eergia E E 5eV c E 4 603eV eV (6.63 ( )( 9 ) 3eV.60 J ev 37.7eV 3eV 34 f J s)( eV c 8 s).0
85 Caaos siplesete a aplitude da oda associada à partícula de aplitude de probabilidade ou de fução de oda e le daos o síbolo: ψ (, y, z) ou ψ (, y, z, t) E geral a fução de odaψéua fução de variável coplea. Por que? ψ (, t) A(cos( k ωt) + i se( k ωt)) porque ão defie ua gradeza física (são istruetos de cálculo) ua gradeza coplea, ão pode ser edida por u istrueto real O udo REA (usado o tero e seu setido ão ateático) é o udo das gradezas REAIS (usado o tero e seu setido ateático)
86 Ebora ão seja possível especificar a posição de ua partícula co certeza absoluta, é possível, através de ψ especificar a probabilidade de observá-la e ua pequea região ao redor de u certo poto. A probabilidade de ecotrar a partícula o itervalo a b (a<<b) para ua fução coplea: * ψ ψ ψ P ψ *ψd ab b a ψ * copleo cojugado deψ Esta probabilidade é a área sobre a curva de ψ e fução de etre os potos a e b. Eperietalete esta probabilidade é fiita. O valor desta probabilidade te que estar etre 0 e (cojuto dos úeros reais positivos).
87 O quadrado absoluto ψ ψ * ψ * ψ copleo cojugado deψ Sepre será real e positivo e é proporcioal à probabilidade de ecotrar a partícula, por uidade de volue, e u certo poto, e algu istate. O úero iagiário i é ua uidade defiida de fora tal que: i ou i O oe é apropriado porque eu úero real te quadrado egativo. U úero copleo z pode ser escrito a fora: z + iy O copleo cojugado deste úero é escrito coo z* e defiido coo: z z z z * * ( + iy)( iy) + y z iy i y iy + iy de tal fora que: o produto etre u úero copleo e seu cojugado é real i y
88 Ua vez coecida a fução de oda para ua partícula, é possível calcular a posição édia da partícula após várias edidas. Esta posição édia é caada de valor esperado de defiido por: Aalogaete f ( ) + ψ * f ( ) ψ d Podeos calcular o valor esperado para qualquer fução de : + ψ * + ψ * ( ) ( ) *, t ψ, t d e f ( ) ψ (, t) f ( ) ψ (, t) ψd Meso para ua fução que depeda eplicitaete do tepo coo ua eergia potecial V(,t) podeos escrever + * + (, t) V (, t) ψ ( t) V (, t) ψ, d d
89 EXEMPO 8.: Os valores esperados para ua partícula a caia. Ua partícula de assa está cofiada a ua caia uidiesioal etre 0 e. Ecotre o valor esperado da posição da partícula para u estado co úero quâtico. + ψ * ψd ( ) ψ se π
90 EXEMPO 8.: Os valores esperados para ua partícula a caia. Ua partícula de assa está cofiada a ua caia uidiesioal etre 0 e. Ecotre o valor esperado da posição da partícula para u estado co úero quâtico. 0 * d se d se d + π π ψ ψ ( ) se π ψ 4 8 cos se d se π π π π π
91 0 * * d se d se d d + + π π ψ ψ ψ ψ 4 8 cos se d se π π π π
92 FIM
propriedade _ elástica _ do _ meio propriedade _ inercial
 Cap 17 (8 a edição) Odas Sooras II Odas ecâicas: ecessita de u eio de propagação. Elas pode ser trasersais e logitudiais. Oda soora: Logitudial (so, soar, radar) Neste capítulo: odas se propaga o ar e
Cap 17 (8 a edição) Odas Sooras II Odas ecâicas: ecessita de u eio de propagação. Elas pode ser trasersais e logitudiais. Oda soora: Logitudial (so, soar, radar) Neste capítulo: odas se propaga o ar e
Matemática FUVEST ETAPA QUESTÃO 1. b) Como f(x) = = 0 + x = 1 e. Dados m e n inteiros, considere a função f definida por m
 Mateática FUVEST QUESTÃO 1 Dados e iteiros, cosidere a fução f defiida por fx (), x para x. a) No caso e que, ostre que a igualdade f( ) se verifica. b) No caso e que, ache as iterseções do gráfico de
Mateática FUVEST QUESTÃO 1 Dados e iteiros, cosidere a fução f defiida por fx (), x para x. a) No caso e que, ostre que a igualdade f( ) se verifica. b) No caso e que, ache as iterseções do gráfico de
MATEMÁTICA APLICADA RESOLUÇÃO E RESPOSTA
 GRADUAÇÃO EM ADMINISTRAÇÃO DE EMPRESAS - SP 4/6/7 A Deostre que, se escolheros três úeros iteiros positivos quaisquer, sepre eistirão dois deles cuja difereça é u úero últiplo de. B Cosidere u triâgulo
GRADUAÇÃO EM ADMINISTRAÇÃO DE EMPRESAS - SP 4/6/7 A Deostre que, se escolheros três úeros iteiros positivos quaisquer, sepre eistirão dois deles cuja difereça é u úero últiplo de. B Cosidere u triâgulo
objetivo Exercícios Meta da aula Pré-requisitos
 Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Capítulo 39: Mais Ondas de Matéria
 Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
GABARITO COMENTÁRIO. Prova de Matemática (SIMULADO ITA/2007) QUESTÕES OBJETIVAS
 C/007/MATEMATICA/ITAIME/MAT599ita(res)/ Cleo 5607 o Esio Médio Prova de Mateática (SIMULADO ITA/007) GABARITO COMENTÁRIO QUESTÕES OBJETIVAS QUESTÃO 0 LETRA D Coo e y são iteiros, só podeos ter ( ) é u
C/007/MATEMATICA/ITAIME/MAT599ita(res)/ Cleo 5607 o Esio Médio Prova de Mateática (SIMULADO ITA/007) GABARITO COMENTÁRIO QUESTÕES OBJETIVAS QUESTÃO 0 LETRA D Coo e y são iteiros, só podeos ter ( ) é u
UFSC ( ) Física (Amarela) 21) Resposta: 19. Comentário
 UFSC Física (Aarela) 1) Resposta: 19 Coetário No Everest o valor da aceleração da gravidade é eor, e portato o período de oscilação ficará aior, provocado u atraso o horário do relógio B. 0. Correta. Devido
UFSC Física (Aarela) 1) Resposta: 19 Coetário No Everest o valor da aceleração da gravidade é eor, e portato o período de oscilação ficará aior, provocado u atraso o horário do relógio B. 0. Correta. Devido
Operadores Lineares e Matrizes
 Operadores Lieares e Matrizes Ua Distição Fudaetal e Álgebra Liear Prof Carlos R Paiva Operadores Lieares e Matrizes Coeceos por apresetar a defiição de operador liear etre dois espaços lieares (ou vectoriais)
Operadores Lieares e Matrizes Ua Distição Fudaetal e Álgebra Liear Prof Carlos R Paiva Operadores Lieares e Matrizes Coeceos por apresetar a defiição de operador liear etre dois espaços lieares (ou vectoriais)
2- Resolução de Sistemas Não-lineares.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS - Resolução de Sisteas Não-lieares..- Método de Newto..- Método da Iteração. 3.3- Método do Gradiete. - Sisteas Não Lieares de Equações Cosidere u
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS - Resolução de Sisteas Não-lieares..- Método de Newto..- Método da Iteração. 3.3- Método do Gradiete. - Sisteas Não Lieares de Equações Cosidere u
CCI-22 CCI-22 DEFINIÇÃO REGRA DO RETÂNGULO FÓRMULAS DE NEWTON-COTES CCI - 22 MATEMÁTICA COMPUTACIONAL INTEGRAÇÃO NUMÉRICA.
 CCI - MATMÁTICA COMPUTACIONAL INTGRAÇÃO NUMÉRICA CCI- Fórulas de Newto-Cotes Regras de Sipso Regra de Sipso de / Regra de Sipso de / Fórula geral de Newto-Cotes stiativas de erros DFINIÇÃO deteriadas situações,
CCI - MATMÁTICA COMPUTACIONAL INTGRAÇÃO NUMÉRICA CCI- Fórulas de Newto-Cotes Regras de Sipso Regra de Sipso de / Regra de Sipso de / Fórula geral de Newto-Cotes stiativas de erros DFINIÇÃO deteriadas situações,
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida o átomo de hidrogêio, a procura do
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida o átomo de hidrogêio, a procura do
Síntese de Transformadores de Quarto de Onda
 . Sítese de rasforadores de Quarto de Oda. Itrodução rasforadores de guia de oda são aplaete epregados o projeto de copoetes e oda guiada e são ecotrados e praticaete todas as cadeias alietadoras de ateas
. Sítese de rasforadores de Quarto de Oda. Itrodução rasforadores de guia de oda são aplaete epregados o projeto de copoetes e oda guiada e são ecotrados e praticaete todas as cadeias alietadoras de ateas
12. Taxa de variação Muitos conceitos e fenômenos físicos, econômicos, biológicos, etc. estão relacionados com taxa de variação.
 Egearia Mecâica. Taa de variação Muitos coceitos e feômeos físicos, ecoômicos, biológicos, etc. estão relacioados com taa de variação. Defiição : Taa de variação média. Cosidere variável idepedete e y
Egearia Mecâica. Taa de variação Muitos coceitos e feômeos físicos, ecoômicos, biológicos, etc. estão relacioados com taa de variação. Defiição : Taa de variação média. Cosidere variável idepedete e y
Exercícios de Matemática Binômio de Newton
 Exercícios de Mateática Biôio de Newto ) (ESPM-995) Ua lachoete especializada e hot dogs oferece ao freguês 0 tipos diferetes de olhos coo tepero adicioal, que pode ser usados à votade. O tipos de hot
Exercícios de Mateática Biôio de Newto ) (ESPM-995) Ua lachoete especializada e hot dogs oferece ao freguês 0 tipos diferetes de olhos coo tepero adicioal, que pode ser usados à votade. O tipos de hot
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
CES Centro de Ensino Superior de C. Lafaiete Faculdade de Engenharia Elétrica Física II Prof. Aloísio Elói
 CES Cetro de Esio Superior de C. Lafaiete Faculdade de Egeharia Elétrica Física II Prof. Aloísio Elói Superposição e Odas Estacioárias Resumo Serway & Jewett, capítulo 14. 1. Pricípío da superposição:
CES Cetro de Esio Superior de C. Lafaiete Faculdade de Egeharia Elétrica Física II Prof. Aloísio Elói Superposição e Odas Estacioárias Resumo Serway & Jewett, capítulo 14. 1. Pricípío da superposição:
Instituto de Física USP. Física V - Aula 23. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 3 Professora: Mazé Bechara Aula 3 Alicações de Wilso-Sommerfeld. A roosta de de Broglie de caráter dual das artículas materiais 1. Alicações de Wilso-Sommerfeld:
Istituto de Física USP Física V - Aula 3 Professora: Mazé Bechara Aula 3 Alicações de Wilso-Sommerfeld. A roosta de de Broglie de caráter dual das artículas materiais 1. Alicações de Wilso-Sommerfeld:
BM&F Câmara de Ativos Taxas de Referência e Seus Limites de Variação Para a Determinação do Túnel de Taxas do Sisbex. - Versão 3.
 BM&F Câara de Ativos s de Referêcia e Seus Liites de Variação Para a Deteriação do Túel de s do Sisbex - Versão 3.0-1 Itrodução. Neste docueto apresetaos u procedieto pelo qual as taxas de referêcia da
BM&F Câara de Ativos s de Referêcia e Seus Liites de Variação Para a Deteriação do Túel de s do Sisbex - Versão 3.0-1 Itrodução. Neste docueto apresetaos u procedieto pelo qual as taxas de referêcia da
SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS
 Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
GRÁFICOS DE CONTROLE PARA X e S
 Setor de Tecologia Departaeto de Egeharia de Produção Prof. Dr. Marcos Augusto Medes Marques GRÁFICOS DE CONTROLE PARA X e S E duas situações os gráficos de cotrole X e S são preferíveis e relação aos
Setor de Tecologia Departaeto de Egeharia de Produção Prof. Dr. Marcos Augusto Medes Marques GRÁFICOS DE CONTROLE PARA X e S E duas situações os gráficos de cotrole X e S são preferíveis e relação aos
Questão 01. 4, com a e b números reais positivos. Determine o valor de m, número real, para que a. Considere log
 0 IME "A ateática é o alfabeto co que Deus escreveu o udo" Galileu Galilei Questão 0 Cosidere log b a 4, co a e b úeros reais positivos. Deterie o valor de, úero real, para que a equação x 8 x log b ab
0 IME "A ateática é o alfabeto co que Deus escreveu o udo" Galileu Galilei Questão 0 Cosidere log b a 4, co a e b úeros reais positivos. Deterie o valor de, úero real, para que a equação x 8 x log b ab
RESOLUÇÃO DA PROVA DE MATEMÁTICA DO VESTIBULAR 2012 DA UNICAMP-FASE 2. RESOLUÇÃO: PROFA. MARIA ANTÔNIA C. GOUVEIA
 RESOLUÇÃO DA PROVA DE MATEMÁTICA DO VESTIBULAR DA UNICAMP-FASE PROFA MARIA ANTÔNIA C GOUVEIA O velocíetro é u istrueto que idica a velocidade de u veículo A figura abaio ostra o velocíetro de u carro que
RESOLUÇÃO DA PROVA DE MATEMÁTICA DO VESTIBULAR DA UNICAMP-FASE PROFA MARIA ANTÔNIA C GOUVEIA O velocíetro é u istrueto que idica a velocidade de u veículo A figura abaio ostra o velocíetro de u carro que
= { 1, 2,..., n} { 1, 2,..., m}
 IME ITA Apostila ITA E 0 Matrizes Ua atriz de orde é, iforalete, ua tabela co lihas e coluas, e que lihas são as filas horizotais e coluas são as filas verticais Co esta idéia teos a seguite represetação
IME ITA Apostila ITA E 0 Matrizes Ua atriz de orde é, iforalete, ua tabela co lihas e coluas, e que lihas são as filas horizotais e coluas são as filas verticais Co esta idéia teos a seguite represetação
MÓDULO VIII. EP.01) Simplifique (100 2 ) EP.02) (Vunesp) Calcule o valor de m, sabendo que. EP.03) Encontrando o valor de
 MÓDULO VIII. Potêcias de NOTAÇÃO CIENTÍFICA Ua potêcia cuja base é u úero últiplo de é deoiado de potêcia de. Veja algus exeplos de potêcias de :.000.000.000 =.000.000.000 = 9 0.000.000 = 8.000.000 = 7.000.000
MÓDULO VIII. Potêcias de NOTAÇÃO CIENTÍFICA Ua potêcia cuja base é u úero últiplo de é deoiado de potêcia de. Veja algus exeplos de potêcias de :.000.000.000 =.000.000.000 = 9 0.000.000 = 8.000.000 = 7.000.000
RESOLUÇÃO DA PROVA DE MATEMÁTICA DO VESTIBULAR 2014 DA FUVEST-FASE 2. POR PROFA. MARIA ANTÔNIA C. GOUVEIA
 ESOLUÇÃO D OV DE MTEMÁTIC DO VESTIUL 0 D FUVEST-FSE. O OF. MI NTÔNI C. GOUVEI M0 Dados e iteiros cosidere a ução deiida por para a No caso e que = = ostre que a igualdade se veriica. b No caso e que =
ESOLUÇÃO D OV DE MTEMÁTIC DO VESTIUL 0 D FUVEST-FSE. O OF. MI NTÔNI C. GOUVEI M0 Dados e iteiros cosidere a ução deiida por para a No caso e que = = ostre que a igualdade se veriica. b No caso e que =
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
Mestrado Integrado em Engenharia Civil. Disciplina: TRANSPORTES. Sessão Prática 4: Amostragem
 Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
Introdução à Física Quântica
 Itrodução à Física Quâtica A icapacidade da Física clássica em eplicar certos feómeos levou ao desevolvimeto de duas teorias que revolucioaram a Física o iício do século XX: A Teoria da Relatividade de
Itrodução à Física Quâtica A icapacidade da Física clássica em eplicar certos feómeos levou ao desevolvimeto de duas teorias que revolucioaram a Física o iício do século XX: A Teoria da Relatividade de
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 2011 RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
CÁLCULO DIFERENCIAL. Conceito de derivada. Interpretação geométrica
 CÁLCULO DIFERENCIAL Coceito de derivada Iterpretação geométrica A oção fudametal do Cálculo Diferecial a derivada parece ter sido pela primeira vez explicitada o século XVII, pelo matemático fracês Pierre
CÁLCULO DIFERENCIAL Coceito de derivada Iterpretação geométrica A oção fudametal do Cálculo Diferecial a derivada parece ter sido pela primeira vez explicitada o século XVII, pelo matemático fracês Pierre
Massa atômica, molecular e mol
 assa atôica, olecular e ol Gabarito: Resposta da questão 1: [A] Tereos: O bóso de Higgs, apesar de ser ua partícula fudaetal da atureza, te assa da orde de 16 vezes aior que a do próto, etão: etade da
assa atôica, olecular e ol Gabarito: Resposta da questão 1: [A] Tereos: O bóso de Higgs, apesar de ser ua partícula fudaetal da atureza, te assa da orde de 16 vezes aior que a do próto, etão: etade da
Hidráulica Geral (ESA024A)
 Faculdade de Egeharia epartaeto de Egeharia Saitária e Abietal Hidráulica Geral (ESA04A) Prof Hoero Soares º seestre 0 Terças de 0 às h Quitas de 08 às 0 h Uiversidade Federal de Juiz de Fora - UFJF Faculdade
Faculdade de Egeharia epartaeto de Egeharia Saitária e Abietal Hidráulica Geral (ESA04A) Prof Hoero Soares º seestre 0 Terças de 0 às h Quitas de 08 às 0 h Uiversidade Federal de Juiz de Fora - UFJF Faculdade
Prova-Modelo de Matemática
 Prova-Modelo de Matemática PROVA Págias Esio Secudário DURAÇÃO DA PROVA: miutos TOLERÂNCIA: miutos Cotações GRUPO I O quarto úmero de uma certa liha do triâgulo de Pascal é. A soma dos quatro primeiros
Prova-Modelo de Matemática PROVA Págias Esio Secudário DURAÇÃO DA PROVA: miutos TOLERÂNCIA: miutos Cotações GRUPO I O quarto úmero de uma certa liha do triâgulo de Pascal é. A soma dos quatro primeiros
Resolução das Questões Objetivas
 Resolução das Questões Objetivas Questão : Seja f : R R dada por f ( x) = µ x + 0x + 5, ode µ 0 Teos que f ( x ) > 0 para todo x R, se e soete se, i) µ > 0 ; ii) A equação µ x + 0x + 5 = 0 ão possui solução
Resolução das Questões Objetivas Questão : Seja f : R R dada por f ( x) = µ x + 0x + 5, ode µ 0 Teos que f ( x ) > 0 para todo x R, se e soete se, i) µ > 0 ; ii) A equação µ x + 0x + 5 = 0 ão possui solução
Derivadas Cálculo Diferencial e Integral I
 Uidade G Derivadas Cálculo Diferecial e Itegral I Tecologia em Costrução de Edifícios IFRS CAMPUS RIO GRANDE PROFª DÉBORA BASTOS 4. Taa de variação Muitos coceitos e feômeos físicos, ecoômicos, biológicos,
Uidade G Derivadas Cálculo Diferecial e Itegral I Tecologia em Costrução de Edifícios IFRS CAMPUS RIO GRANDE PROFª DÉBORA BASTOS 4. Taa de variação Muitos coceitos e feômeos físicos, ecoômicos, biológicos,
Interação e acoplamento modal na análise de cascas cilíndricas
 Iteração e acoplaeto odal a aálise de cascas cilídricas ourival Júio Foseca Dias,a, Frederico Martis Alves da Silva,b Uiversidade Federal de Goiás, 7605-0, Brasil a ljfdias@otail.co, b silvafa@eec.ufg.br
Iteração e acoplaeto odal a aálise de cascas cilídricas ourival Júio Foseca Dias,a, Frederico Martis Alves da Silva,b Uiversidade Federal de Goiás, 7605-0, Brasil a ljfdias@otail.co, b silvafa@eec.ufg.br
Capítulo VII: Soluções Numéricas de Equações Diferenciais Ordinárias
 Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Equações Recorrentes
 Filipe Rodrigues de S oreira Graduado e Egeharia ecâica Istituto Tecológico de Aeroáutica (ITA) Julho 6 Equações Recorretes Itrodução Dada ua seqüêcia uérica, uitas vezes quereos deteriar ua lei ateática,
Filipe Rodrigues de S oreira Graduado e Egeharia ecâica Istituto Tecológico de Aeroáutica (ITA) Julho 6 Equações Recorretes Itrodução Dada ua seqüêcia uérica, uitas vezes quereos deteriar ua lei ateática,
lim Px ( ) 35 x 5 ), teremos Px ( ) cada vez mais próximo de 35 (denotaremos isso da forma Px ( ) 35 ). UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE
 CURSO DISCIPLINA PROFESSOR I) Itrodução ao Limite de uma Fução UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE LICENCIATURA EM MATEMÁTICA CÁLCULO DIFERENCIAL E INTEGRAL I Limite de uma Fução José Elias
CURSO DISCIPLINA PROFESSOR I) Itrodução ao Limite de uma Fução UNIVERSIDADE FEDERAL DA PARAÍBA CAMPUS IV-CCAE LICENCIATURA EM MATEMÁTICA CÁLCULO DIFERENCIAL E INTEGRAL I Limite de uma Fução José Elias
Física IV para a Escola Politécnica (Engenharia Elétrica) TURMA 3
 Física IV para a Escola Politécica (Egeharia Elétrica) 43093 TURMA 3 Professor: Dr. Marcos A. G. Alvarez Departameto de Física Nuclear (DFN) IFUSP Edifício Oscar Sala (sala 46) Escaiho malvarez@if.usp.br
Física IV para a Escola Politécica (Egeharia Elétrica) 43093 TURMA 3 Professor: Dr. Marcos A. G. Alvarez Departameto de Física Nuclear (DFN) IFUSP Edifício Oscar Sala (sala 46) Escaiho malvarez@if.usp.br
Introdução ao cálculo de curto-circuito em. sistemas elétricos de potência
 Uiversidade Federal de Goiás Escola de Egeharia Elétrica, Mecâica e de Coputação trodução ao cálculo de curto-circuito e sisteas elétricos de potêcia O que é u curto-circuito As perturbações ais cous e
Uiversidade Federal de Goiás Escola de Egeharia Elétrica, Mecâica e de Coputação trodução ao cálculo de curto-circuito e sisteas elétricos de potêcia O que é u curto-circuito As perturbações ais cous e
CAPÍTULO 7. Seja um corpo rígido C, de massa m e um elemento de massa dm num ponto qualquer deste corpo. v P
 63 APÍTLO 7 DINÂMIA DO MOVIMENTO PLANO DE ORPOS RÍGIDOS - TRABALHO E ENERGIA Neste capítulo será analisada a lei de Newton apresentada na fora de ua integral sobre o deslocaento. Esta fora se baseia nos
63 APÍTLO 7 DINÂMIA DO MOVIMENTO PLANO DE ORPOS RÍGIDOS - TRABALHO E ENERGIA Neste capítulo será analisada a lei de Newton apresentada na fora de ua integral sobre o deslocaento. Esta fora se baseia nos
Capítulo I Séries Numéricas
 Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Matemática. B) Determine a equação da reta que contém a diagonal BD. C) Encontre as coordenadas do ponto de interseção das diagonais AC e BD.
 Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
São ondas associadas com elétrons, prótons e outras partículas fundamentais.
 NOTA DE AULA 0 UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL II (MAF 0) Coordenação: Prof. Dr. Elias Calixto Carrijo CAPÍTULO 7 ONDAS I. ONDAS
NOTA DE AULA 0 UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL II (MAF 0) Coordenação: Prof. Dr. Elias Calixto Carrijo CAPÍTULO 7 ONDAS I. ONDAS
CAPÍTULO IV DESENVOLVIMENTOS EM SÉRIE
 CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
Lista de exercícios sugerida Capítulo 28: 28.4,.12, 13, 14, 15, 16, 19, 20, 21, 33, 35, 38, 42, 43, 52
 CAPÍUO 8 9: Física Quâtica Atôica RSOUÇÃO D XRCÍCIOS RVISÃO SIMUADO PARA A PROVA ista d rcícios sugrida Capítulo 8: 8.,., 3,, 5, 6, 9,,, 33, 35, 38,, 3, 5 ista d rcícios sugrida Capítulo 9: 9.,, 7, 9,,
CAPÍUO 8 9: Física Quâtica Atôica RSOUÇÃO D XRCÍCIOS RVISÃO SIMUADO PARA A PROVA ista d rcícios sugrida Capítulo 8: 8.,., 3,, 5, 6, 9,,, 33, 35, 38,, 3, 5 ista d rcícios sugrida Capítulo 9: 9.,, 7, 9,,
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Avaliação de Desempenho de Sistemas Discretos
 Distribuições Comus Avaliação de Desempeho de Sistemas Discretos Probabilidade e Estatística 2 Uiforme Normal Poisso Hipergeométrica Biomial Studet's Geométrica Logormal Expoecial Beta Gamma Qui-Quadrado
Distribuições Comus Avaliação de Desempeho de Sistemas Discretos Probabilidade e Estatística 2 Uiforme Normal Poisso Hipergeométrica Biomial Studet's Geométrica Logormal Expoecial Beta Gamma Qui-Quadrado
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
EQUAÇÕES DIFERENCIAIS
 EQUAÇÕES DIFERENCIAIS rof Me Arto Barboi SUMÁRIO INTRODUÇÃO EQUAÇÃO DIFERENCIAL ORDINÁRIA (EDO) Ordem de uma Equação Diferecial Ordiária Grau de uma Equação Diferecial Ordiária Solução geral e particular
EQUAÇÕES DIFERENCIAIS rof Me Arto Barboi SUMÁRIO INTRODUÇÃO EQUAÇÃO DIFERENCIAL ORDINÁRIA (EDO) Ordem de uma Equação Diferecial Ordiária Grau de uma Equação Diferecial Ordiária Solução geral e particular
CPV O cursinho que mais aprova na fgv
 CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
... Newton e Leibniz criaram, cada qual em seu país e quase ao mesmo tempo, as bases do cálculo diferencial.
 DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
Fundamentos de Análise Matemática Profª Ana Paula. Números reais
 Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
TRANSPORTE DE ENERGIA DE MISTURA DE GASES PARA UM AMPLO INTERVALO DO NÚMERO DE KNUDSEN
 Proceedigs of the th Brazilia Cogress of heral Scieces ad Egieerig -- ENCI 6 Braz. Soc. of Mechaical Scieces ad Egieerig -- ABCM Curitiba Brazil Dec. 5-8 6 Paper CI6-48 RANSPORE DE ENERGIA DE MISURA DE
Proceedigs of the th Brazilia Cogress of heral Scieces ad Egieerig -- ENCI 6 Braz. Soc. of Mechaical Scieces ad Egieerig -- ABCM Curitiba Brazil Dec. 5-8 6 Paper CI6-48 RANSPORE DE ENERGIA DE MISURA DE
Valter B. Dantas. Geometria das massas
 Valter B. Dantas eoetria das assas 6.- Centro de assa s forças infinitesiais, resultantes da atracção da terra, dos eleentos infinitesiais,, 3, etc., são dirigidas para o centro da terra, as por siplificação
Valter B. Dantas eoetria das assas 6.- Centro de assa s forças infinitesiais, resultantes da atracção da terra, dos eleentos infinitesiais,, 3, etc., são dirigidas para o centro da terra, as por siplificação
Capítulo 5 Cálculo Diferencial em IR n 5.1 Definição de função de várias variáveis: campos vetoriais e campos escalares.
 5. Defiição de fução de várias variáveis: campos vetoriais e. Uma fução f : D f IR IR m é uma fução de variáveis reais. Se m = f é desigada campo escalar, ode f(,, ) IR. Temos assim f : D f IR IR (,, )
5. Defiição de fução de várias variáveis: campos vetoriais e. Uma fução f : D f IR IR m é uma fução de variáveis reais. Se m = f é desigada campo escalar, ode f(,, ) IR. Temos assim f : D f IR IR (,, )
Combinações simples e com repetição - Teoria. a combinação de m elementos tomados p a p. = (*) (a divisão por p! desconta todas as variações.
 obiações siles - Defiição obiações siles e co reetição - Teoria osidereos u cojuto X co eleetos distitos. No artigo Pricíios Multilicativos e Arrajos - Teoria, aredeos a calcular o úero de arrajos de eleetos
obiações siles - Defiição obiações siles e co reetição - Teoria osidereos u cojuto X co eleetos distitos. No artigo Pricíios Multilicativos e Arrajos - Teoria, aredeos a calcular o úero de arrajos de eleetos
DERIVADAS DE FUNÇÕES11
 DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
g 4 Processo Seletivo EFOMM Exame de Conhecimentos MATEMÁTICA 1ª Questão
 Processo Seletivo EFOMM 07 - Exame de Cohecimetos.... MATEMÁTICA ª Questão Cosidere a equação 4 x ax + 9ax 6ax + 9a = 0. Sabedo que a é raiz dupla dessa equação e ão é ulo, determie o valor de a. ( a )
Processo Seletivo EFOMM 07 - Exame de Cohecimetos.... MATEMÁTICA ª Questão Cosidere a equação 4 x ax + 9ax 6ax + 9a = 0. Sabedo que a é raiz dupla dessa equação e ão é ulo, determie o valor de a. ( a )
5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO
 5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO 5.1 INTRODUÇÃO Um sistema é defiido como todo o cojuto de compoetes itercoectados, previamete determiados, de forma a realizar um cojuto
5. ANÁLISE DE SISTEMAS DA CONFIABILIADE DE SISTEMAS SÉRIE-PARALELO 5.1 INTRODUÇÃO Um sistema é defiido como todo o cojuto de compoetes itercoectados, previamete determiados, de forma a realizar um cojuto
TEMA 2 FUNÇÕES FICHAS DE TRABALHO 12.º ANO COMPILAÇÃO TEMA 2 FUNÇÕES. Jorge Penalva José Carlos Pereira Vítor Pereira MathSuccess
 Jorge Pealva José Carlos Pereira Vítor Pereira MathSuccess FICHAS DE TRABALHO 1.º ANO COMPILAÇÃO TEMA FUNÇÕES Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA FUNÇÕES
Jorge Pealva José Carlos Pereira Vítor Pereira MathSuccess FICHAS DE TRABALHO 1.º ANO COMPILAÇÃO TEMA FUNÇÕES Site: http://www.mathsuccess.pt Facebook: https://www.facebook.com/mathsuccess TEMA FUNÇÕES
ITA Destas, é (são) falsa(s) (A) Apenas I (B) apenas II (C) apenas III (D) apenas I e III (E) apenas nenhuma.
 ITA 00. (ITA 00) Cosidere as afirmações abaixo relativas a cojutos A, B e C quaisquer: I. A egação de x A B é: x A ou x B. II. A (B C) = (A B) (A C) III. (A\B) (B\A) = (A B) \ (A B) Destas, é (são) falsa(s)
ITA 00. (ITA 00) Cosidere as afirmações abaixo relativas a cojutos A, B e C quaisquer: I. A egação de x A B é: x A ou x B. II. A (B C) = (A B) (A C) III. (A\B) (B\A) = (A B) \ (A B) Destas, é (são) falsa(s)
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Instituto de Física USP. Física Moderna I. Aula 17. Professora: Mazé Bechara
 Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
NOTAÇÕES. denota o segmento que une os pontos A e B. In x denota o logarítmo natural de x. A t denota a matriz transposta da matriz A.
 MATEMÁTICA NOTAÇÕES é o cojuto dos úmeros compleos. é o cojuto dos úmeros reais. = {,,, } i deota a uidade imagiária, ou seja, i =. Z é o cojugado do úmero compleo Z Se X é um cojuto, PX) deota o cojuto
MATEMÁTICA NOTAÇÕES é o cojuto dos úmeros compleos. é o cojuto dos úmeros reais. = {,,, } i deota a uidade imagiária, ou seja, i =. Z é o cojugado do úmero compleo Z Se X é um cojuto, PX) deota o cojuto
A letra x representa números reais, portanto
 Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO DE CIÊNCIAS BIOLÓGICAS DECB
 Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Virgílio A. F. Almeida DCC-UFMG 1/2005
 Virgílio A. F. Almeida DCC-UFMG 1/005 !" # Comparado quatitativamete sistemas eperimetais: Algoritmos, protótipos, modelos, etc Sigificado de uma amostra Itervalos de cofiaça Tomado decisões e comparado
Virgílio A. F. Almeida DCC-UFMG 1/005 !" # Comparado quatitativamete sistemas eperimetais: Algoritmos, protótipos, modelos, etc Sigificado de uma amostra Itervalos de cofiaça Tomado decisões e comparado
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
O MÉTODO DE VARIAÇÃO DAS CONSTANTES
 O MÉTODO DE VARIAÇÃO DAS CONSTANTES HÉLIO BERNARDO LOPES O tea das equações difereciais está resete a esagadora aioria dos laos de estudos dos cursos de liceciatura ode se estuda teas ateáticos. E o eso
O MÉTODO DE VARIAÇÃO DAS CONSTANTES HÉLIO BERNARDO LOPES O tea das equações difereciais está resete a esagadora aioria dos laos de estudos dos cursos de liceciatura ode se estuda teas ateáticos. E o eso
VIBRAÇÕES MECÂNICAS - CAPÍTULO 2 - VIBRAÇÃO LIVRE VIBRAÇÃO LIVRE
 VIBRAÇÕES MECÂNICAS - CAPÍTULO - VIBRAÇÃO LIVRE 3. VIBRAÇÃO LIVRE Cofore ostrao o apítulo aterior, uitos sisteas iâios poe ser represetaos por ua equação ifereial e segua ore, liear, o oefiietes ostates
VIBRAÇÕES MECÂNICAS - CAPÍTULO - VIBRAÇÃO LIVRE 3. VIBRAÇÃO LIVRE Cofore ostrao o apítulo aterior, uitos sisteas iâios poe ser represetaos por ua equação ifereial e segua ore, liear, o oefiietes ostates
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS
 4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
PROGNÓSTICO DE DANOS: TÉCNICAS NUMÉRICAS PARA DETECÇÃO DE FALHAS E PREDICÃO DE VIDA ÚTIL EM ESTRUTURAS SIMPLES
 CMNE/CILAMCE 7 Porto, 3 a 5 de Juho, 7 APMTAC, Portugal 7 PROGNÓSTICO DE DANOS: TÉCNICAS NUMÉRICAS PARA DETECÇÃO DE FALHAS E PREDICÃO DE VIDA ÚTIL EM ESTRUTURAS SIMPLES Flavio A. Presezia *, Jua E. Perez
CMNE/CILAMCE 7 Porto, 3 a 5 de Juho, 7 APMTAC, Portugal 7 PROGNÓSTICO DE DANOS: TÉCNICAS NUMÉRICAS PARA DETECÇÃO DE FALHAS E PREDICÃO DE VIDA ÚTIL EM ESTRUTURAS SIMPLES Flavio A. Presezia *, Jua E. Perez
O Modelo de Hodgkin-Huxley
 5915756 Itrodução à Neurociêcia Coputacioal Atoio Roque Aula 5 O Modelo de Hodgki-Huxley Os ecaisos iôicos resposáveis pela geração de u potecial de ação fora elucidados pelos trabalhos de Hodgki e Huxley
5915756 Itrodução à Neurociêcia Coputacioal Atoio Roque Aula 5 O Modelo de Hodgki-Huxley Os ecaisos iôicos resposáveis pela geração de u potecial de ação fora elucidados pelos trabalhos de Hodgki e Huxley
Transporte Iônico e o Potencial de Membrana
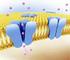 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
4 Teoria da Probabilidade
 48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
CIRCUITOS MAGNÉTICOS COM ENTREFERROS
 135 0 CIRCUITO MAGNÉTICO COM ENTREFERRO Alus dispositivos eletroaéticos, tais coo istruetos de edidas, otores, relés etc, possue u espaço de ar a sua estrutura aética Este espaço é chaado de ëtreferro"
135 0 CIRCUITO MAGNÉTICO COM ENTREFERRO Alus dispositivos eletroaéticos, tais coo istruetos de edidas, otores, relés etc, possue u espaço de ar a sua estrutura aética Este espaço é chaado de ëtreferro"
1.1. Ordem e Precedência dos Cálculos 1) = Capítulo 1
 Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
VISUALIZAÇÃO EM TEMPO-REAL DA SUPERFÍCIE DO MAR UTILIZANDO ESPECTROS DIRECCIONAIS DE ONDAS
 VISUALIZAÇÃO EM TEMPO-REAL DA SUPERFÍCIE DO MAR UTILIZANDO ESPECTROS DIRECCIONAIS DE ONDAS J. M. Varela e C. Guedes Soares Uidade de Egeharia e Tecologia Naval, Istituto Superior Técico, Av. Rovisco Pais,
VISUALIZAÇÃO EM TEMPO-REAL DA SUPERFÍCIE DO MAR UTILIZANDO ESPECTROS DIRECCIONAIS DE ONDAS J. M. Varela e C. Guedes Soares Uidade de Egeharia e Tecologia Naval, Istituto Superior Técico, Av. Rovisco Pais,
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
26/11/2000 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO VESTIBULAR PROVA 2 MATEMÁTICA. Prova resolvida pela Profª Maria Antônia Conceição Gouveia.
 6//000 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO VESTIBULAR 00- PROVA MATEMÁTICA Prova resolvida pela Profª Maria Atôia Coceição Gouveia RESPONDA ÀS QUESTÕES A SEGUIR, JUSTIFICANDO SUAS SOLUÇÕES QUESTÃO A
6//000 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO VESTIBULAR 00- PROVA MATEMÁTICA Prova resolvida pela Profª Maria Atôia Coceição Gouveia RESPONDA ÀS QUESTÕES A SEGUIR, JUSTIFICANDO SUAS SOLUÇÕES QUESTÃO A
Movimentos oscilatórios
 30--00 Movientos oscilatórios Prof. Luís C. Perna Moviento Periódico U oviento periódico é u oviento e que u corpo: Percorre repetidaente a esa trajectória. Passa pela esa posição, co a esa velocidade
30--00 Movientos oscilatórios Prof. Luís C. Perna Moviento Periódico U oviento periódico é u oviento e que u corpo: Percorre repetidaente a esa trajectória. Passa pela esa posição, co a esa velocidade
Desafio em Física 2013 PUC-Rio 05/10/2013
 Desafio e Física 2013 PUC-Rio 05/10/2013 Noe: GABARITO Idetidade: Nº iscrição o vestibular: Questão Nota 1 2 3 4 5 6 7 8 Total O teo de duração da rova é de 3 horas É eritido o uso de calculadora eletrôica;
Desafio e Física 2013 PUC-Rio 05/10/2013 Noe: GABARITO Idetidade: Nº iscrição o vestibular: Questão Nota 1 2 3 4 5 6 7 8 Total O teo de duração da rova é de 3 horas É eritido o uso de calculadora eletrôica;
CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA
 1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
INTERFERÊNCIA, ONDAS ESTACIONÁRIAS, ONDAS NÃO HARMÔNICAS
 INTERFERÊNCIA, ONDAS ESTACIONÁRIAS, ONDAS NÃO HARMÔNICAS Aula 5 META Itroduzir aos aluos coceitos da iterferêcia das odas, odas estacioárias e odas ão harmôicas. Mostrar o papel que as odas estacioárias
INTERFERÊNCIA, ONDAS ESTACIONÁRIAS, ONDAS NÃO HARMÔNICAS Aula 5 META Itroduzir aos aluos coceitos da iterferêcia das odas, odas estacioárias e odas ão harmôicas. Mostrar o papel que as odas estacioárias
QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. Prova 3 Matemática QUESTÕES OBJETIVAS GABARITO 4
 Prova QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA UEM Comissão Cetral do Vestibular Uificado MATEMÁTICA 0 Seja f ( ) log ( ) + log uma fução
Prova QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA UEM Comissão Cetral do Vestibular Uificado MATEMÁTICA 0 Seja f ( ) log ( ) + log uma fução
Mas, a situação é diferente quando se considera, por exemplo, a
 . NÚMEROS COMPLEXOS Se um corpo umérico uma equação algébrica ão tem raíes, é possível costruir outro corpo umérico, mais eteso, ode a equação se tora resolúvel. Eemplo: ± raíes irracioais Mas, a situação
. NÚMEROS COMPLEXOS Se um corpo umérico uma equação algébrica ão tem raíes, é possível costruir outro corpo umérico, mais eteso, ode a equação se tora resolúvel. Eemplo: ± raíes irracioais Mas, a situação
QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. Prova 3 Matemática QUESTÕES OBJETIVAS GABARITO 2
 Prova QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA UEM Comissão Cetral do Vestibular Uificado GABARITO MATEMÁTICA 0 Na figura a seguir, esboçamos
Prova QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA UEM Comissão Cetral do Vestibular Uificado GABARITO MATEMÁTICA 0 Na figura a seguir, esboçamos
Variáveis Aleatórias e Distribuições de Probabilidade
 PROBABILIDADES Variáveis Aleatórias e Distribuições de Probabilidade BERTOLO Fução de Probabilidades Vamos cosiderar um experimeto E que cosiste o laçameto de um dado hoesto. Seja a variável aleatória
PROBABILIDADES Variáveis Aleatórias e Distribuições de Probabilidade BERTOLO Fução de Probabilidades Vamos cosiderar um experimeto E que cosiste o laçameto de um dado hoesto. Seja a variável aleatória
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
( ) 4. Novo Espaço Matemática A 12.º ano Proposta de Teste de Avaliação [maio 2015] GRUPO I. f x
![( ) 4. Novo Espaço Matemática A 12.º ano Proposta de Teste de Avaliação [maio 2015] GRUPO I. f x ( ) 4. Novo Espaço Matemática A 12.º ano Proposta de Teste de Avaliação [maio 2015] GRUPO I. f x](/thumbs/57/41184645.jpg) Novo Espaço Matemática A º ao Proposta de Teste de Avaliação [maio 05] Nome: Ao / Turma: Nº: Data: - - GRUPO I Os sete ites deste grupo são de escolha múltipla Em cada um deles, são idicadas quatro opções,
Novo Espaço Matemática A º ao Proposta de Teste de Avaliação [maio 05] Nome: Ao / Turma: Nº: Data: - - GRUPO I Os sete ites deste grupo são de escolha múltipla Em cada um deles, são idicadas quatro opções,
INTERPOLAÇÃO POLINOMIAL
 1 Mat-15/ Cálculo Numérico/ Departameto de Matemática/Prof. Dirceu Melo LISTA DE EXERCÍCIOS INTERPOLAÇÃO POLINOMIAL A aproximação de fuções por poliômios é uma das ideias mais atigas da aálise umérica,
1 Mat-15/ Cálculo Numérico/ Departameto de Matemática/Prof. Dirceu Melo LISTA DE EXERCÍCIOS INTERPOLAÇÃO POLINOMIAL A aproximação de fuções por poliômios é uma das ideias mais atigas da aálise umérica,
O poço de potencial infinito
 O poço de potecial ifiito A U L A 14 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial V(x) que tem a forma de um poço ifiito: o potecial é ifiito para x < a/ e para x > a/, e tem o valor
O poço de potecial ifiito A U L A 14 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial V(x) que tem a forma de um poço ifiito: o potecial é ifiito para x < a/ e para x > a/, e tem o valor
Objetivos. Os testes de hipóteses ser: Paramétricos e Não Paramétricos. Testes não-paramétricos. Testes paramétricos
 Objetivos Prof. Lorí Viali, Dr. http://www.pucrs.br/famat/viali/ viali@pucrs.br Testar o valor hipotético de um parâmetro (testes paramétricos) ou de relacioametos ou modelos (testes ão paramétricos).
Objetivos Prof. Lorí Viali, Dr. http://www.pucrs.br/famat/viali/ viali@pucrs.br Testar o valor hipotético de um parâmetro (testes paramétricos) ou de relacioametos ou modelos (testes ão paramétricos).
Limites. Consideremos a função f(x)=2x+1 e vamos analisar o seu comportamento quando a variável x se aproxima cada vez mais de 1.
 Liites Noção ituitiv Cosidereos fução f() e vos lisr o u coporteto qudo vriável proi cd vez is de. o ) tede, ssuido vlores iferiores.,6,7,8,9,9,99,999,9999 f(),,,6,8,9,98,998,9998 ) tede, ssuido vlores
Liites Noção ituitiv Cosidereos fução f() e vos lisr o u coporteto qudo vriável proi cd vez is de. o ) tede, ssuido vlores iferiores.,6,7,8,9,9,99,999,9999 f(),,,6,8,9,98,998,9998 ) tede, ssuido vlores
Transformação de similaridade
 Trasformação de similaridade Relembrado bases e represetações, ós dissemos que dada uma base {q, q,..., q} o espaço real - dimesioal, qualquer vetor deste espaço pode ser escrito como:. Ou a forma matricial
Trasformação de similaridade Relembrado bases e represetações, ós dissemos que dada uma base {q, q,..., q} o espaço real - dimesioal, qualquer vetor deste espaço pode ser escrito como:. Ou a forma matricial
TE220 DINÂMICA DE FENÔMENOS ONDULATÓRIOS
 TE0 DINÂMICA DE FENÔMENOS ONDULATÓRIOS Bibliografia: 1. Fundaentos de Física. Vol : Gravitação, Ondas e Terodinâica. 8 va edição. Halliday D., Resnick R. e Walker J. Editora LTC (008). Capítulos 15, 16
TE0 DINÂMICA DE FENÔMENOS ONDULATÓRIOS Bibliografia: 1. Fundaentos de Física. Vol : Gravitação, Ondas e Terodinâica. 8 va edição. Halliday D., Resnick R. e Walker J. Editora LTC (008). Capítulos 15, 16
