objetivo Exercícios Meta da aula Pré-requisitos
|
|
|
- Thomas Bergmann Freire
- 7 Há anos
- Visualizações:
Transcrição
1 Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado os coteúdos das Aulas a 5, do Módulo. Pré-requisitos Os coteúdos das Aulas a 5 desta disciplia.
2 Itrodução à Mecâica Quâtica Exercícios. BARREIRA DE POTENCIAL (AULAS E ).. Um feixe de elétros de ev icide sobre uma barreira de potecial retagular de 4 ev de altura e m de espessura. (a) Qual é a probabilidade de trasmissão T? (b) Qual seria o valor de T para elétros de 6eV? (a) Trata-se do caso em que a eergia é meor que a altura da barreira. Podemos usar a Equação (.8) deduzida a Aula : T = + ( k + K ) seh ( Ka) 4k K ( ) V seh Ka = + 4E( V E), ( ) = em que K = m V E h 7, m. Substituido os valores a fórmula, obtemos T =, 6. (b) Agora temos a eergia maior que a altura da barreira, etão usamos a Equação (.) da Aula : T = + ( ) em que k = m E V h 7, m. Substituido os valores a fórmula, obtemos T =, 83. k k ( k a) se V k se ( a) = + 4k k 4E( E V ) ( ) =,.. Supodo que podemos ajustar a espessura da barreira do exercício..a, qual o valor da mesma para que elétro, de cada icidetes, tuelasse através dela? 74 C E D E R J
3 Podemos usar a Equação (.8) da Aula para obter uma expressão para a espessura a: ( ) E( V E) T 4 a = seh K V AULA 6 MÓDULO Usado T = /, E = ev, V = 4 ev e K = 7, m, obtemos a =.576 m..3. Um próto e um dêutero (que possui duas vezes a massa do próto), ambos com uma eergia ciética de 3MeV, icidem sobre uma barreira de fm de espessura e altura igual a MeV. Calcule a probabilidade de trasmissão para cada uma destas partículas. ( ) V Ka seh Usamos ovamete a expressão T = +. 4E( V E) No caso do próto, usamos m =,67 7 kg e obtemos 4 K = m( V. Substituido a fórmula, E) h = 5, 8 m obtemos T = 3, 5. Já o caso do dêutero, temos K = 8, 4 m e T =,5 7. Veja que, se aumetarmos a massa apeas por um fator, a probabilidade de tuelameto dimiui por duas ordes de magitude! C E D E R J 75
4 Itrodução à Mecâica Quâtica Exercícios O POÇO DE POTENCIAL FINITO (AULA 3).. Um elétro está o iterior de um poço quadrado de ev de profudidade. a. Se a eergia do estado fudametal do eletro o poço é de 8 ev, calcule a largura do poço. b. Repita o item aterior para o caso em que 8 ev seja a eergia do primeiro estado excitado. a. Usado a Equação (3.7), temos kta ka K, que relacioa a eergia e a largura de um poço quadrado o caso de uma solução par (como a do estado fudametal). Usado as defiições de k e K, temos: Deste modo, ( ) = ( ) = me m V E K V E k = K, = = h h k E ka ta ( ka ) = =, 46 + π (em radiaos) ode =,,,.... Assim, há vários valores possíveis da largura a que satisfazem os dados do problema. No etato, ote que aida ão impusemos a codição de que este é o estado fudametal (o estado par com meor eergia). Os diferetes valores possíveis de a correspodem a diferetes estados pares, todos com eergia de 8 ev, mas apeas um deles deve ser o estado fudametal para o poço correspodete. Note que, quato mais largo o poço, maior o úmero de estados ligados. Ou seja, se aumetarmos muito a largura do poço, certamete itroduziremos estados pares com eergia meor que 8 ev. Assim, o valor de para o qual o estado em questão é o estado fudametal deve correspoder à meor largura de poço possível, ou seja, =. Obtemos etão a =, 93. Como k me 9, 8, 6 k = = 34 h, m =,45 m, etão obtemos fialmete a = 6,4 m. b. No caso do primeiro estado excitado, temos de usar a Equação ( ) = (3.5), kcot ka K, que se refere a fuções de oda ímpares. Repetido o procedimeto do item aterior, obtemos: ka cot ( ka ) = =, 3 + π (em radiaos) 76 C E D E R J
5 ode, ovamete, =,,,.... Pela mesma argumetação aterior, escolhemos = (estamos em busca do estado ímpar de meor eergia). 4, 6 Obtemos etão a = =, 8 m. k AULA 6 MÓDULO! A atividade a seguir é opcioal, pois requer do aluo um cohecimeto básico de programação... Crie um pequeo programa de computador que calcule as eergias dos estados ligados de um elétro em um poço quadrado fiito. Seu programa deve ter aproximadamete a seguite estrutura:. Defia a massa do elétro, costate de Plack, a altura e a largura do poço.. Varie a eergia E em passos muito pequeos desde até V, e calcule k e K. 3. Em cada passo, verifique se as Equações (3.5) (para estados ímpares) ou (3.7) (para estados pares) são satisfeitas, detro de uma certa tolerâcia. O POÇO DE POTENCIAL INFINITO (AULA 4) 3.. Faça uma estimativa da eergia de poto zero de um êutro em um úcleo, tratado-o como se estivesse em um poço quadrado ifiito de largura igual a um diâmetro uclear de 4 m (Eisberg-Resick, Problema, Capítulo 6). C E D E R J 77
6 Itrodução à Mecâica Quâtica Exercícios A eergia de poto zero é a eergia do estado fudametal ( = ) do poço ifiito: E. Usado a = -4 m e = h π ma m =,67 7 kg, obtemos E =, MeV. 3.. a. Para uma partícula em uma caixa, mostre que a difereça fracioal de eergia etre autovalores adjacetes é E + =. E b. Use essa fórmula para discutir o limite clássico do sistema (Eisberg-Resick, Problema, Capítulo 6). a. Usado a fórmula (4.) para as auto-eergias do poço ifiito, E π ma = h, temos: E E E = E E + ( + ) + = = b. O limite clássico é obtido para grades úmeros quâticos. Nesse limite, deve haver uma correspodêcia etre os resultados quâticos e os clássicos. Pela fórmula obtida o item aterior, o limite de grades úmeros quâticos ( ), a difereça fracioal tede a zero. Ou seja, tora-se imperceptível a quatização da eergia, o que está de acordo com a Mecâica Clássica, já que, para uma partícula clássica detro de um poço, qualquer valor positivo da eergia é possível. 78 C E D E R J
7 3.3. Calcule os valores esperados x, p, x, p para o estado com = 3 do poço ifiito e comete sobre cada resultado. AULA 6 MÓDULO A fução de oda ormalizada para = 3 é dada pela Equação (4.) da Aula 4: 3π ψ. Calculado os valores esperados: 3( x) = cos a a x 3π x = x x x dx = x. a a x ψ * ψ dx 3( ) 3( ) cos = a Para qualquer autofução do poço ifiito, é sempre uma fução par, de modo que a desidade de probabilidade de ecotrarmos a partícula em x é sempre igual que em x. Sedo assim, o valor mais provável para a posição da partícula tem de ser em x =. a ψ ( ) x ih 3π 3π p = x i x dx = x a a a x 3π ψ * 3( ) h ψ 3( ) cos si x dx = a a A partícula tem probabilidade igual de se mover para a direita ou para a esquerda. Portato, o mometo liear médio deve ser ulo. a 3π x x x x dx x a a x dx a = ψ * 3( ) ψ 3( ) = cos = = 8π Com esse resultado, podemos obter a icerteza a medida da posição: x = x x, 8a, um pouco meor que a largura do poço, como deveria ser. a a 77, a p a 9π h 3π = x x dx x a a a x 9π h 3 3 = ψ * ( ) h ψ ( ) cos dx = a a, O valor esperado de p poderia também ser obtido a partir do autovalor da eergia e usado E = p /m. A partir do valor obtido, podemos calcular a 3π h icerteza o mometo: p = p p =. Podemos, etão, verificar a h o pricípio da icerteza para esse estado quâtico: x p, 6h >. C E D E R J 79
8 Itrodução à Mecâica Quâtica Exercícios O OSCILADOR HARMÔNICO (AULA 5) 4.. A costate de força restauradora (costate de mola) k para vibrações iteratômicas de uma molécula diatômica típica é de aproximadamete 3 J/m. Use esse valor para fazer uma estimativa da eergia de poto zero das vibrações moleculares (Eisberg-Resick, Problema 9, Capítulo 6). A eergia de poto zero de um oscilador harmôico simples é dada por. hω Para obtermos a freqüêcia, precisamos estimar a massa da molécula (de forma mais rigorosa, a massa reduzida para o movimeto relativo de vibração). Obviamete, essa massa varia de acordo com a molécula, mas podemos tomar cerca vezes a massa do próto como uma ordem de gradeza para uma molécula formada por átomos leves. Sedo assim, a freqüêcia é ω =,4 4 rad/s, e a eergia é =,8 ev. hω 4.. a. Faça uma estimativa da difereça em eergia etre o estado fudametal e o primeiro estado excitado de vibração da molécula do exercício aterior. b. A partir dessa estimativa, determie a eergia do fóto emitido quado a molécula faz uma trasição etre o primeiro estado excitado e o estado fudametal. c. Determie também a freqüêcia do fóto e compare-a com a freqüêcia de oscilação clássica do sistema. d. Em qual região do espectro eletromagético está a radiação emitida? 8 C E D E R J
9 a. As auto-eergias do oscilador harmôico quâtico são dadas pela Equação (5.): E = ( + ) hω. Assim, a difereça de eergia etre dois íveis cosecutivos quaisquer, iclusive etre o estado fudametal e o primeiro estado excitado, é igual a hω. Portato, o caso da molécula cosiderada a atividade aterior, temos hω =, 6 ev. b. A eergia do fóto emitido quado a molécula faz a trasição etre dois estados quâticos é precisamete a difereça de eergias etre os dois estados, que calculamos o item aterior. c. Pela relação de Eistei, a frequêcia do fóto é ν = E h, ode E é a sua eergia, calculada o item aterior. Sedo assim, a frequêcia do fóto é idêtica à freqüêcia de vibração da molécula. Podemos eteder este resultado a partir do eletromagetismo clássico. Uma molécula é composta por elétros e úcleos, que cotêm carga elétrica. Quado a molécula oscila, as oscilações de carga dão origem a odas eletromagéticas (fótos) de mesma freqüêcia, de forma semelhate ao que ocorre em uma atea. d. Usado a relação de Eistei com E =,6 ev, temos ν = E h = 3,8 3 Hz ou comprimeto de oda de = c/ = 7,7 µm. Esta radiação está a faixa do ifravermelho. É por este motivo que a espectroscopia a região do ifravermelho é uma das técicas mais poderosas o estudo de moléculas. AULA 6 MÓDULO 4.3. Um pêdulo, costituído por uma massa de kg o extremo de uma barra leve de m, oscila com uma amplitude de, m. Calcule as seguites gradezas: a. freqüêcia de oscilação; b. eergia de oscilação; c. valor aproximado do úmero quâtico para a oscilação; d. separação etre eergias possíveis adjacetes; e. separação em distâcia etre os máximos adjacetes a fução desidade de probabilidade em toro do poto de equilíbrio (Eisberg- Resick, Problema 3, Capítulo 6). C E D E R J 8
10 Itrodução à Mecâica Quâtica Exercícios a. A frequêcia do pêdulo é dada por =, 5Hz. g ν = = π l π 9, 8m/s m b. Pela Mecâica Clássica, a eergia de oscilação é dada por E = mω A, ode A é a amplitude do movimeto. Usado os dados do problema, temos E = ( ) ( ) = 5 π,, 4, 9 J. c. Usado a relação E = + temos h = + E hω ν, = = hν 4, , 34,, Note que um sistema clássico correspode, detro de uma descrição quâtica, a úmeros quâticos absurdamete altos. d. A separação etre íveis adjacetes é hω = 3, 3 34 J =,5 5 ev. Esta difereça de eergias é tão pequea que é impossível de ser medida. Ou seja, é impossível afirmar, para valores tão altos do úmero quâtico, se o oscilador está realmete o ível ou o ível +. e. O úmero de máximos da desidade de probabilidade para um estado do oscilador harmôico com úmero quâtico é igual a +. Assim, o úmero de máximos é também aproximadamete igual a,4 3. Supodo que os os máximos adjacetes estão igualmete espaçados etre si ao logo da trajetória do pêdulo, a distâcia etre dois máximos adjacetes é igual a, 33, 4 m. 3, 4 Esta é também uma distâcia impossível de ser medida. INFORMAÇÃO SOBRE A PRÓXIMA AULA Na próxima aula, iiciaremos o Módulo 3 de ossa disciplia, que trata de sistemas quâticos em três dimesões. 8 C E D E R J
Instituto de Física USP. Física Moderna. Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física Modera Aula 5 Professora: Mazé Bechara Aula 5 A equação de Schroediger para estados estacioários ligados. Aplicação o movimeto uidimesioal. 1. Aplicação : os auto estados
Istituto de Física USP Física Modera Aula 5 Professora: Mazé Bechara Aula 5 A equação de Schroediger para estados estacioários ligados. Aplicação o movimeto uidimesioal. 1. Aplicação : os auto estados
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida o átomo de hidrogêio, a procura do
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida o átomo de hidrogêio, a procura do
Capítulo 39: Mais Ondas de Matéria
 Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
Aula-10 Mais Ondas de Matéria II
 http://www.bugma3.com/physics/ Aula-0 Mais Odas de Matéria II Física Geral F-48 Partícula em uma Caixa ( poço ) Vamos resolver a equação de Schrödiger para uma partícula cofiada a uma caixa de paredes
http://www.bugma3.com/physics/ Aula-0 Mais Odas de Matéria II Física Geral F-48 Partícula em uma Caixa ( poço ) Vamos resolver a equação de Schrödiger para uma partícula cofiada a uma caixa de paredes
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
UNIVERSIDADE DE SÃO PAULO Escola de Engenharia de Lorena EEL
 UNIVERSIDADE DE SÃO PAULO Escola de Egeharia de Lorea EEL LOB101 - FÍSICA IV Prof. Dr. Durval Rodrigues Juior Departameto de Egeharia de Materiais (DEMAR) Escola de Egeharia de Lorea (EEL) Uiversidade
UNIVERSIDADE DE SÃO PAULO Escola de Egeharia de Lorea EEL LOB101 - FÍSICA IV Prof. Dr. Durval Rodrigues Juior Departameto de Egeharia de Materiais (DEMAR) Escola de Egeharia de Lorea (EEL) Uiversidade
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara AVISO 1. Já se ecotra a págia da disciplia o TEC 3 para ser etregue até 9/5. Aula O Modelo Atômico de Bohr 1. As hipóteses do modelo de Bohr
Istituto de Física USP Física V - Aula Professora: Mazé Bechara AVISO 1. Já se ecotra a págia da disciplia o TEC 3 para ser etregue até 9/5. Aula O Modelo Atômico de Bohr 1. As hipóteses do modelo de Bohr
-0,4-0,6 -0,9 -1,5 -3,4 -13,6 EXERCÍCIOS
 EXERCÍCIOS FÍSICA MODERNA ÁTOMO DE BOHR PROF. MARENGÃO. (UFRN) Um átomo de hidrogêio, ao passar de um estado quâtico para outro, emite ou absorve radiação eletromagética de eergias bem defiidas. No diagrama
EXERCÍCIOS FÍSICA MODERNA ÁTOMO DE BOHR PROF. MARENGÃO. (UFRN) Um átomo de hidrogêio, ao passar de um estado quâtico para outro, emite ou absorve radiação eletromagética de eergias bem defiidas. No diagrama
Instituto de Física USP. Física Moderna I. Aula 17. Professora: Mazé Bechara
 Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Introdução à Física Quântica
 Itrodução à Física Quâtica A icapacidade da Física clássica em eplicar certos feómeos levou ao desevolvimeto de duas teorias que revolucioaram a Física o iício do século XX: A Teoria da Relatividade de
Itrodução à Física Quâtica A icapacidade da Física clássica em eplicar certos feómeos levou ao desevolvimeto de duas teorias que revolucioaram a Física o iício do século XX: A Teoria da Relatividade de
Instituto de Física USP. Física Moderna I. Aula 20. Professora: Mazé Bechara
 Istituto de Física USP Física Modera I Aula 20 Professora: Mazé Bechara Satos FC tricampeão paulista Aula 20 A oda da partícula material e o pricípio de icerteza 1. Odas de de Broglie - aplicações: (a)
Istituto de Física USP Física Modera I Aula 20 Professora: Mazé Bechara Satos FC tricampeão paulista Aula 20 A oda da partícula material e o pricípio de icerteza 1. Odas de de Broglie - aplicações: (a)
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Dentro, a/2 < x < a/2: com: Ondas com a mesma amplitude nos 2 sentidos. Elas se combinam formando uma onda estacionária. Então podemos fazer A = B:
 Poços de potecial: E < V Detro a/ < < a/: ψ com: i i Ae + Be me p Odas com a mesma amplitude os setidos. Elas se combiam formado uma oda estacioária. Etão podemos fazer A B: ψ ψ i i + e B e Bʹ cos e Bʹ
Poços de potecial: E < V Detro a/ < < a/: ψ com: i i Ae + Be me p Odas com a mesma amplitude os setidos. Elas se combiam formado uma oda estacioária. Etão podemos fazer A B: ψ ψ i i + e B e Bʹ cos e Bʹ
Instituto de Física USP. Física V - Aula 23. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 3 Professora: Mazé Bechara Aula 3 Alicações de Wilso-Sommerfeld. A roosta de de Broglie de caráter dual das artículas materiais 1. Alicações de Wilso-Sommerfeld:
Istituto de Física USP Física V - Aula 3 Professora: Mazé Bechara Aula 3 Alicações de Wilso-Sommerfeld. A roosta de de Broglie de caráter dual das artículas materiais 1. Alicações de Wilso-Sommerfeld:
FÍSICA MODERNA I AULA 14
 Uiversidade de São Paulo Istituto de Física FÍSICA MODERNA I AULA 14 Profa. Márcia de Almeida Rizzutto Pelletro sala 114 rizzutto@if.usp.br 1o. Semestre de 014 Moitor: Gabriel M. de Souza Satos Págia do
Uiversidade de São Paulo Istituto de Física FÍSICA MODERNA I AULA 14 Profa. Márcia de Almeida Rizzutto Pelletro sala 114 rizzutto@if.usp.br 1o. Semestre de 014 Moitor: Gabriel M. de Souza Satos Págia do
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
O poço de potencial infinito
 O poço de potecial ifiito A U L A 14 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial V(x) que tem a forma de um poço ifiito: o potecial é ifiito para x < a/ e para x > a/, e tem o valor
O poço de potecial ifiito A U L A 14 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial V(x) que tem a forma de um poço ifiito: o potecial é ifiito para x < a/ e para x > a/, e tem o valor
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
>> cm f < Hz. Sólido: meio contínuo
 Capítulo IV. VIBRAÇÕES NOS SÓIDOS CRISTAINOS Alargameto do coceito de sólido: ovo modelo Átomos que vibram colectivamete quado excitados A vibração global pode ser represetada por uma ONDA que se propaga
Capítulo IV. VIBRAÇÕES NOS SÓIDOS CRISTAINOS Alargameto do coceito de sólido: ovo modelo Átomos que vibram colectivamete quado excitados A vibração global pode ser represetada por uma ONDA que se propaga
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 7 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER INDEPENDENTE DO TEMPO Primeira Edição junho de 2005 CAPÍTULO 07 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 7 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER INDEPENDENTE DO TEMPO Primeira Edição junho de 2005 CAPÍTULO 07 SOLUÇÕES DA EQUAÇÃO DE SCHRÖDINGER
Física IV Poli Engenharia Elétrica: 15ª Aula (07/10/2014)
 Física V Poi Egeharia Eétrica: 15ª Aua (7/1/14) Prof. Avaro Vaucci Na útima aua vimos: Partícua presa a um poço de potecia ifiito (1D) Equação de Schrödiger (U = ): d dx m E K ; K me ikx Soução:. A' e
Física V Poi Egeharia Eétrica: 15ª Aua (7/1/14) Prof. Avaro Vaucci Na útima aua vimos: Partícua presa a um poço de potecia ifiito (1D) Equação de Schrödiger (U = ): d dx m E K ; K me ikx Soução:. A' e
O Átomo de Hidrogênio
 Física IV Poli geharia létrica: 11ª Aula (3/08/014) Pro. Alvaro Vaucci Na última aula vimos: h eito Compto: ' 0 (1 cos ) ( Lei decompto) mc e Ou seja, um óto (comportameto corpuscular), além de possuir
Física IV Poli geharia létrica: 11ª Aula (3/08/014) Pro. Alvaro Vaucci Na última aula vimos: h eito Compto: ' 0 (1 cos ) ( Lei decompto) mc e Ou seja, um óto (comportameto corpuscular), além de possuir
NOTAS DE AULAS DE FÍSICA MODERNA
 NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 SOLUÇÕES DA EQUAÇÃO DE SCHORÖDINGER INDEPENDENTE DO TEMPO Edição de junho de 2014 CAPÍTULO 06 SOLUÇÕES DA EQUAÇÃO DE SCRÖDINGER INDEPENDENTE
NOTAS DE AULAS DE FÍSICA MODERNA Prof. Carlos R. A. Lima CAPÍTULO 6 SOLUÇÕES DA EQUAÇÃO DE SCHORÖDINGER INDEPENDENTE DO TEMPO Edição de junho de 2014 CAPÍTULO 06 SOLUÇÕES DA EQUAÇÃO DE SCRÖDINGER INDEPENDENTE
. Dessa forma, quanto menor o MSE, mais a imagem
 Uiversidade Federal de Perambuco CI / CCEN - Área II 1 o Exercício de Cálculo Numérico ( 18 / 06 / 2014 ) Aluo(a) 1- Questão 1 (2,5 potos) Cosidere uma imagem digital como uma matriz bidimesioal de dimesões
Uiversidade Federal de Perambuco CI / CCEN - Área II 1 o Exercício de Cálculo Numérico ( 18 / 06 / 2014 ) Aluo(a) 1- Questão 1 (2,5 potos) Cosidere uma imagem digital como uma matriz bidimesioal de dimesões
Mas o que deixou de ser abordado na grande generalidade desses cursos foi o estudo dos produtos infinitos, mesmo que só no caso numérico real.
 Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
CPV O cursinho que mais aprova na fgv
 CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
CPV O cursiho que mais aprova a fgv FGV ecoomia a Fase 0/dezembro/0 MATEMÁTICA 0. Chamaremos de S() a soma dos algarismos do úmero iteiro positivo, e de P() o produto dos algarismos de. Por exemplo, se
Séries e Equações Diferenciais Lista 02 Séries Numéricas
 Séries e Equações Difereciais Lista 02 Séries Numéricas Professor: Daiel Herique Silva Defiições Iiciais ) Defia com suas palavras o coceito de série umérica, e explicite difereças etre sequêcia e série.
Séries e Equações Difereciais Lista 02 Séries Numéricas Professor: Daiel Herique Silva Defiições Iiciais ) Defia com suas palavras o coceito de série umérica, e explicite difereças etre sequêcia e série.
Distribuições Amostrais
 9/3/06 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/09/06 3:38 ESTATÍSTICA APLICADA I - Teoria
9/3/06 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/09/06 3:38 ESTATÍSTICA APLICADA I - Teoria
1 a Lista de PE Solução
 Uiversidade de Brasília Departameto de Estatística 1 a Lista de PE Solução 1. a) Qualitativa omial. b) Quatitativa discreta. c) Quatitativa discreta. d) Quatitativa cotíua. e) Quatitativa cotíua. f) Qualitativa
Uiversidade de Brasília Departameto de Estatística 1 a Lista de PE Solução 1. a) Qualitativa omial. b) Quatitativa discreta. c) Quatitativa discreta. d) Quatitativa cotíua. e) Quatitativa cotíua. f) Qualitativa
Distribuições Amostrais
 7/3/07 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/07/07 09:3 ESTATÍSTICA APLICADA I - Teoria
7/3/07 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/07/07 09:3 ESTATÍSTICA APLICADA I - Teoria
Séries de Fourier. As séries de Fourier são séries cujos termos são funções sinusoidais.
 Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
binomial seria quase simétrica. Nestas condições será também melhor a aproximação pela distribuição normal.
 biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
Eletromagnetismo II 1 o Semestre de 2007 Noturno - Prof. Alvaro Vannucci
 Eletromagetismo 1 o Semestre de 7 Noturo - Prof. Alvaro Vaucci 1 a aula 7/fev/7 ivros-texto: eitz-milford Griffiths Vamos relembrar as 4 equações básicas do Eletromagetismo 1 a ) ei de Gauss: O Fluxo do
Eletromagetismo 1 o Semestre de 7 Noturo - Prof. Alvaro Vaucci 1 a aula 7/fev/7 ivros-texto: eitz-milford Griffiths Vamos relembrar as 4 equações básicas do Eletromagetismo 1 a ) ei de Gauss: O Fluxo do
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO
 CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Iformática para o Esio de Física CONTEUDISTA: Carlos Eduardo Aguiar AULA
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Iformática para o Esio de Física CONTEUDISTA: Carlos Eduardo Aguiar AULA
GABARITO DO GE5 ONDAS ESTACIONÁRIAS, BATIMENTOS E EFEITO DOPPLER
 GABARTO DO GE ONDAS ESTACONÁRAS, BATMENTOS E EFETO DOPPLER.9 Exercícios de Fixação G.E..9.1) Duas odas 1 e estão presetes em uma corda: y 1 (3 mm) se [(, rad/m)x - (1,7 rad/s)t] y (3 mm) se [(, rad/m)x
GABARTO DO GE ONDAS ESTACONÁRAS, BATMENTOS E EFETO DOPPLER.9 Exercícios de Fixação G.E..9.1) Duas odas 1 e estão presetes em uma corda: y 1 (3 mm) se [(, rad/m)x - (1,7 rad/s)t] y (3 mm) se [(, rad/m)x
Mestrado Integrado em Engenharia Civil. Disciplina: TRANSPORTES. Sessão Prática 4: Amostragem
 Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
g 4 Processo Seletivo EFOMM Exame de Conhecimentos MATEMÁTICA 1ª Questão
 Processo Seletivo EFOMM 07 - Exame de Cohecimetos.... MATEMÁTICA ª Questão Cosidere a equação 4 x ax + 9ax 6ax + 9a = 0. Sabedo que a é raiz dupla dessa equação e ão é ulo, determie o valor de a. ( a )
Processo Seletivo EFOMM 07 - Exame de Cohecimetos.... MATEMÁTICA ª Questão Cosidere a equação 4 x ax + 9ax 6ax + 9a = 0. Sabedo que a é raiz dupla dessa equação e ão é ulo, determie o valor de a. ( a )
Capítulo 3. Sucessões e Séries Geométricas
 Capítulo 3 Sucessões e Séries Geométricas SUMÁRIO Defiição de sucessão Mootoia de sucessões Sucessões itadas (majoradas e mioradas) Limites de sucessões Sucessões covergetes e divergetes Resultados sobre
Capítulo 3 Sucessões e Séries Geométricas SUMÁRIO Defiição de sucessão Mootoia de sucessões Sucessões itadas (majoradas e mioradas) Limites de sucessões Sucessões covergetes e divergetes Resultados sobre
Introdução ao Qui-Quadrado
 Técicas Laboratoriais de Física Lic. Física e g. Biomédica 007/08 Capítulo X Teste do Qui-quadrado, Itrodução ao qui-quadrado Defiição geral do qui-quadrado Graus de liberdade e reduzido abilidade do 66
Técicas Laboratoriais de Física Lic. Física e g. Biomédica 007/08 Capítulo X Teste do Qui-quadrado, Itrodução ao qui-quadrado Defiição geral do qui-quadrado Graus de liberdade e reduzido abilidade do 66
Matemática. B) Determine a equação da reta que contém a diagonal BD. C) Encontre as coordenadas do ponto de interseção das diagonais AC e BD.
 Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
Como se decidir entre modelos
 Como se decidir etre modelos Juliaa M. Berbert Quado uma curva é lei de potecia? O procedimeto amplamete usado para testar movimetação biológica a fim de ecotrar padrões de busca como Voos de Levy tem
Como se decidir etre modelos Juliaa M. Berbert Quado uma curva é lei de potecia? O procedimeto amplamete usado para testar movimetação biológica a fim de ecotrar padrões de busca como Voos de Levy tem
ESCOLA BÁSICA DE ALFORNELOS
 ESCOLA BÁSICA DE ALFORNELOS FICHA DE TRABALHO DE MATEMÁTICA 9.º ANO VALORES APROXIMADOS DE NÚMEROS REAIS Dado um úmero xe um úmero positivo r, um úmero x como uma aproximação de x com erro iferior a r
ESCOLA BÁSICA DE ALFORNELOS FICHA DE TRABALHO DE MATEMÁTICA 9.º ANO VALORES APROXIMADOS DE NÚMEROS REAIS Dado um úmero xe um úmero positivo r, um úmero x como uma aproximação de x com erro iferior a r
Virgílio Mendonça da Costa e Silva
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
Sumário. 2 Índice Remissivo 11
 i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
Capítulo 5- Introdução à Inferência estatística. (Versão: para o manual a partir de 2016/17)
 Capítulo 5- Itrodução à Iferêcia estatística. (Versão: para o maual a partir de 2016/17) 1.1) Itrodução.(222)(Vídeo 39) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar
Capítulo 5- Itrodução à Iferêcia estatística. (Versão: para o maual a partir de 2016/17) 1.1) Itrodução.(222)(Vídeo 39) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar
Capítulo 5- Introdução à Inferência estatística.
 Capítulo 5- Itrodução à Iferêcia estatística. 1.1) Itrodução.(184) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar coclusões acerca da população de ode se extraiu a amostra.
Capítulo 5- Itrodução à Iferêcia estatística. 1.1) Itrodução.(184) Na iferêcia estatística, aalisamos e iterpretamos amostras com o objetivo de tirar coclusões acerca da população de ode se extraiu a amostra.
Avaliação de Desempenho de Sistemas Discretos
 Distribuições Comus Avaliação de Desempeho de Sistemas Discretos Probabilidade e Estatística 2 Uiforme Normal Poisso Hipergeométrica Biomial Studet's Geométrica Logormal Expoecial Beta Gamma Qui-Quadrado
Distribuições Comus Avaliação de Desempeho de Sistemas Discretos Probabilidade e Estatística 2 Uiforme Normal Poisso Hipergeométrica Biomial Studet's Geométrica Logormal Expoecial Beta Gamma Qui-Quadrado
Séries de Fourier. As séries de Fourier são séries cujos termos são funções sinusoidais.
 Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Física Moderna II
 Física Modera II - 4300376 http://disciplias.stoa.usp.br/course/view.php?id=666 Sala 08, Ala ; Segudas, 1 3 h; Quartas, 19 1 h. º Semestre 01 - Noturo Prof. Marcos Nogueira Martis Ed. Basílio Jafet, sala
Física Modera II - 4300376 http://disciplias.stoa.usp.br/course/view.php?id=666 Sala 08, Ala ; Segudas, 1 3 h; Quartas, 19 1 h. º Semestre 01 - Noturo Prof. Marcos Nogueira Martis Ed. Basílio Jafet, sala
O oscilador harmônico
 O oscilador harmôico A U L A 5 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial de um oscilador harmôico simples, V( x) kx. objetivos obter a solução da equação de Schrödiger para um oscilador
O oscilador harmôico A U L A 5 Meta da aula Aplicar o formalismo quâtico ao caso de um potecial de um oscilador harmôico simples, V( x) kx. objetivos obter a solução da equação de Schrödiger para um oscilador
Exercícios de DSP: 1) Determine se os sinais abaixo são periódicos ou não e para cada sinal periódico, determine o período fundamental.
 Exercícios de DSP: 1) Determie se os siais abaixo são periódicos ou ão e para cada sial periódico, determie o período fudametal a x[ ] = cos( 0,15 π ) 1 18 b x [ ] = Re{ e } Im{ } jπ + e jπ c x[ ] = se(
Exercícios de DSP: 1) Determie se os siais abaixo são periódicos ou ão e para cada sial periódico, determie o período fudametal a x[ ] = cos( 0,15 π ) 1 18 b x [ ] = Re{ e } Im{ } jπ + e jπ c x[ ] = se(
Radiação térmica Física Moderna 1 Aula 2 1
 Radiação térmica Maxwell, 1873 odas eletromagéticas (teoria) Correte alterada produção de odas com comportameto aálogo ao da luz (reflexão, refração, difração, iterferêcia,...) Hertz, 1887 comprovação
Radiação térmica Maxwell, 1873 odas eletromagéticas (teoria) Correte alterada produção de odas com comportameto aálogo ao da luz (reflexão, refração, difração, iterferêcia,...) Hertz, 1887 comprovação
Análise Infinitesimal II LIMITES DE SUCESSÕES
 -. Calcule os seguites limites Aálise Ifiitesimal II LIMITES DE SUCESSÕES a) lim + ) b) lim 3 + 4 5 + 7 + c) lim + + ) d) lim 3 + 4 5 + 7 + e) lim + ) + 3 f) lim + 3 + ) g) lim + ) h) lim + 3 i) lim +
-. Calcule os seguites limites Aálise Ifiitesimal II LIMITES DE SUCESSÕES a) lim + ) b) lim 3 + 4 5 + 7 + c) lim + + ) d) lim 3 + 4 5 + 7 + e) lim + ) + 3 f) lim + 3 + ) g) lim + ) h) lim + 3 i) lim +
Fundamentos de Análise Matemática Profª Ana Paula. Sequência Infinitas
 Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Química 5 aula 1. aula 2 COMENTÁRIOS ATIVIDADES PARA SALA COMENTÁRIOS ATIVIDADES PROPOSTAS. 7. ( F ) Raios x são prejudiciais aos pacientes.
 Química 5 aula 1 1. A alterativa icorreta ecotra-se em a, pois para a ideia de átomo idivisível, o que é por todo errado.. Atualmete, sabe-se que átomos do mesmo elemeto químico podem apresetar diferetes
Química 5 aula 1 1. A alterativa icorreta ecotra-se em a, pois para a ideia de átomo idivisível, o que é por todo errado.. Atualmete, sabe-se que átomos do mesmo elemeto químico podem apresetar diferetes
MAE Introdução à Probabilidade e Estatística II Resolução Lista 1
 MAE 229 - Itrodução à Probabilidade e Estatística II Resolução Lista 1 Professor: Pedro Moretti Exercício 1 (a) Fazer histograma usado os seguites dados: Distribuição de probabilidade da variável X: X
MAE 229 - Itrodução à Probabilidade e Estatística II Resolução Lista 1 Professor: Pedro Moretti Exercício 1 (a) Fazer histograma usado os seguites dados: Distribuição de probabilidade da variável X: X
Eletromagnetismo II. 15 a Aula. Professor Alvaro Vannucci
 Eletromagetismo II 5 a Aula Professor Alvaro Vaucci Na última aula, vimos... Icidêcia oblíqua: ( meios dielétricos) θi θr siθi (Lei da eflexão) siθ t (Lei de Sell) Obtivemos os Coeficietes de Fresel (
Eletromagetismo II 5 a Aula Professor Alvaro Vaucci Na última aula, vimos... Icidêcia oblíqua: ( meios dielétricos) θi θr siθi (Lei da eflexão) siθ t (Lei de Sell) Obtivemos os Coeficietes de Fresel (
Sequências Reais e Seus Limites
 Sequêcias Reais e Seus Limites Sumário. Itrodução....................... 2.2 Sequêcias de Números Reais............ 3.3 Exercícios........................ 8.4 Limites de Sequêcias de Números Reais......
Sequêcias Reais e Seus Limites Sumário. Itrodução....................... 2.2 Sequêcias de Números Reais............ 3.3 Exercícios........................ 8.4 Limites de Sequêcias de Números Reais......
Sucessão ou Sequência. Sucessão ou seqüência é todo conjunto que consideramos os elementos dispostos em certa ordem. janeiro,fevereiro,...
 Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Fundamentos de Análise Matemática Profª Ana Paula. Números reais
 Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
Dessa forma, concluímos que n deve ser ímpar e, como 120 é par, então essa sequência não possui termo central.
 Resoluções das atividades adicioais Capítulo Grupo A. a) a 9, a 7, a 8, a e a 79. b) a, a, a, a e a.. a) a, a, a, a 8 e a 6. 9 b) a, a 6, a, a 9 e a.. Se a 9 e a k são equidistates dos extremos, etão existe
Resoluções das atividades adicioais Capítulo Grupo A. a) a 9, a 7, a 8, a e a 79. b) a, a, a, a e a.. a) a, a, a, a 8 e a 6. 9 b) a, a 6, a, a 9 e a.. Se a 9 e a k são equidistates dos extremos, etão existe
FÍSICA MODERNA I AULA 11 - REVISÃO
 Uiversidade de São Paulo Istituto de Física FÍSICA MODERNA I AULA - REVISÃO Profa. Márcia de Almeida Rizzutto Pelletro sala 4 rizzutto@if.usp.br o. Semestre de 04 Moitor: Gabriel M. de Souza Satos Págia
Uiversidade de São Paulo Istituto de Física FÍSICA MODERNA I AULA - REVISÃO Profa. Márcia de Almeida Rizzutto Pelletro sala 4 rizzutto@if.usp.br o. Semestre de 04 Moitor: Gabriel M. de Souza Satos Págia
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON 5.1 MODELO MATEMÁTICO E SOLUÇÃO ANALÍTICA
 Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS.
 TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS. 1.1 Objectivos Medir gradezas físicas, utilizado os istrumetos adequados. Apresetar correctamete os resultados das medições, ao ível da utilização
TRABALHO1 MEDIÇÕES, ALGARISMOS SIGNIFICATIVOS E ERROS. 1.1 Objectivos Medir gradezas físicas, utilizado os istrumetos adequados. Apresetar correctamete os resultados das medições, ao ível da utilização
Professor Mauricio Lutz LIMITES
 LIMITES ) Noção ituitiva de ites Seja a fução f ( ) +. Vamos dar valores de que se aproimem de, pela sua direita (valores maiores que ) e pela esquerda (valores meores que ) e calcular o valor correspodete
LIMITES ) Noção ituitiva de ites Seja a fução f ( ) +. Vamos dar valores de que se aproimem de, pela sua direita (valores maiores que ) e pela esquerda (valores meores que ) e calcular o valor correspodete
CAPÍTULO IV DESENVOLVIMENTOS EM SÉRIE
 CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
Algoritmos de Iluminação Global
 Sistemas Gráficos/ Computação Gráfica e Iterfaces Objectivo: calcular a cor de cada poto a partir da ilumiação directa de uma fote de luz, mais a soma de todas as reflexões das superfícies próximas. Nos
Sistemas Gráficos/ Computação Gráfica e Iterfaces Objectivo: calcular a cor de cada poto a partir da ilumiação directa de uma fote de luz, mais a soma de todas as reflexões das superfícies próximas. Nos
Estacionariedade e correlação temporal em dados financeiros
 Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
ESTIMAÇÃO POR INTERVALO (INTERVALOS DE CONFIANÇA)
 06 ETIMÇÃO OR INTERVLO (INTERVLO DE CONINÇ) Cada um dos métodos de estimação potual permite associar a cada parâmetro populacioal um estimador. Ora a cada estimador estão associadas tatas estimativas diferetes
06 ETIMÇÃO OR INTERVLO (INTERVLO DE CONINÇ) Cada um dos métodos de estimação potual permite associar a cada parâmetro populacioal um estimador. Ora a cada estimador estão associadas tatas estimativas diferetes
Transporte Iônico e o Potencial de Membrana
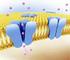 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
CÁLCULO I. Exibir o cálculo de algumas integrais utilizando a denição;
 CÁLCULO I Prof Edilso Neri Júior Prof Adré Almeida Aula o 9: A Itegral de Riema Objetivos da Aula Deir a itegral de Riema; Exibir o cálculo de algumas itegrais utilizado a deição; Apresetar fuções que
CÁLCULO I Prof Edilso Neri Júior Prof Adré Almeida Aula o 9: A Itegral de Riema Objetivos da Aula Deir a itegral de Riema; Exibir o cálculo de algumas itegrais utilizado a deição; Apresetar fuções que
CONCEITOS DE VIBRAÇÃO
 CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
Capítulo I Séries Numéricas
 Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Exercícios de Aprofundamento Matemática Progressão Aritmética e Geométrica
 Exercícios de Aprofudameto Matemática Progressão Aritmética e b. (Fuvest 05) Dadas as sequêcias a 4 4, b, c a a e d, b defiidas para valores iteiros positivos de, cosidere as seguites afirmações: I. a
Exercícios de Aprofudameto Matemática Progressão Aritmética e b. (Fuvest 05) Dadas as sequêcias a 4 4, b, c a a e d, b defiidas para valores iteiros positivos de, cosidere as seguites afirmações: I. a
MAE Introdução à Probabilidade e Estatística II Resolução Lista 2
 MAE 9 - Itrodução à Probabilidade e Estatística II Resolução Lista Professor: Pedro Moretti Exercício 1 Deotado por Y a variável aleatória que represeta o comprimeto dos cilidros de aço, temos que Y N3,
MAE 9 - Itrodução à Probabilidade e Estatística II Resolução Lista Professor: Pedro Moretti Exercício 1 Deotado por Y a variável aleatória que represeta o comprimeto dos cilidros de aço, temos que Y N3,
O poço de potencial finito
 O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
O poço de potencial finito A U L A 13 Meta da aula Aplicar o formalismo quântico ao caso de um potencial V(x) que tem a forma de um poço (tem um valor V 0 para x < -a/ e para x > a/, e um valor 0 para
1.1. Ordem e Precedência dos Cálculos 1) = Capítulo 1
 Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
Capítulo. Aritmética e Expressões Algébricas O estudo de cálculo exige muito mais que o cohecimeto de limite, derivada e itegral. Para que o apredizado seja satisfatório o domíio de tópicos de aritmética
; 2N 2N.! " j %.(1 & q)2 N & j.q j. j!(2n & j)!
 DERIVA GENÉTICA Seja uma população de tamaho fiito N, costate ao logo das gerações; sejam aida p e q as freqüêcias dos alelos A e a de um loco autossômico a geração ; como o tamaho da população é costate,
DERIVA GENÉTICA Seja uma população de tamaho fiito N, costate ao logo das gerações; sejam aida p e q as freqüêcias dos alelos A e a de um loco autossômico a geração ; como o tamaho da população é costate,
n ) uma amostra aleatória da variável aleatória X.
 - Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
- Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
3. Seja C o conjunto dos números complexos. Defina a soma em C por
 Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Universidade São Judas Tadeu Faculdade de Tecnologia e Ciências Exatas Laboratório de Física e Química
 Uiversidade São Judas Tadeu Faculdade de Tecologia e Ciêcias Exatas Laboratório de Física e Química Aálise de Medidas Físicas Quado fazemos uma medida, determiamos um úmero para caracterizar uma gradeza
Uiversidade São Judas Tadeu Faculdade de Tecologia e Ciêcias Exatas Laboratório de Física e Química Aálise de Medidas Físicas Quado fazemos uma medida, determiamos um úmero para caracterizar uma gradeza
Lista de Exercícios #4 Assunto: Variáveis Aleatórias Contínuas
 . ANPEC 8 - Questão Seja x uma variável aleatória com fução desidade de probabilidade dada por: f(x) = x, para x f(x) =, caso cotrário. Podemos afirmar que: () E[x]=; () A mediaa de x é ; () A variâcia
. ANPEC 8 - Questão Seja x uma variável aleatória com fução desidade de probabilidade dada por: f(x) = x, para x f(x) =, caso cotrário. Podemos afirmar que: () E[x]=; () A mediaa de x é ; () A variâcia
Representação de Números em Ponto Flutuante
 Represetação de Números em Poto Flutuate OBS: Esta aula é uma reprodução, sob a forma de slides, da aula em vídeo dispoibilizada pelo prof. Rex Medeiros, da UFRN/ECT, em https://youtu.be/ovuymcpkoc Notação
Represetação de Números em Poto Flutuate OBS: Esta aula é uma reprodução, sob a forma de slides, da aula em vídeo dispoibilizada pelo prof. Rex Medeiros, da UFRN/ECT, em https://youtu.be/ovuymcpkoc Notação
PTC 2549 SISTEMAS TELEFÔNICOS
 PTC 9 SISTMS TLFÔICOS GBRITO D PRIMIR LIST D RCÍCIOS /3/ Questão ) s ecessidades de comuicação etre duas localidades e B são de. e 3. chamadas por dia, para os setidos B e B respectivamete, com uma duração
PTC 9 SISTMS TLFÔICOS GBRITO D PRIMIR LIST D RCÍCIOS /3/ Questão ) s ecessidades de comuicação etre duas localidades e B são de. e 3. chamadas por dia, para os setidos B e B respectivamete, com uma duração
4 Teoria da Probabilidade
 48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
Análise Matemática I 2 o Exame
 Aálise Matemática I 2 o Exame Campus da Alameda LEC, LET, LEN, LEM, LEMat, LEGM 29 de Jaeiro de 2003, 3 horas Apresete todos os cálculos e justificações relevates I. Cosidere dois subcojutos de R, A e
Aálise Matemática I 2 o Exame Campus da Alameda LEC, LET, LEN, LEM, LEMat, LEGM 29 de Jaeiro de 2003, 3 horas Apresete todos os cálculos e justificações relevates I. Cosidere dois subcojutos de R, A e
Probabilidade II Aula 9
 Coteúdo Probabilidade II Aula 9 Maio de 9 Môica Barros, D.Sc. Estatísticas de Ordem Distribuição do Máximo e Míimo de uma amostra Uiforme(,) Distribuição do Máximo e Míimo caso geral Distribuição das Estatísticas
Coteúdo Probabilidade II Aula 9 Maio de 9 Môica Barros, D.Sc. Estatísticas de Ordem Distribuição do Máximo e Míimo de uma amostra Uiforme(,) Distribuição do Máximo e Míimo caso geral Distribuição das Estatísticas
Universidade Federal do Maranhão Centro de Ciências Exatas e Tecnologia Coordenação do Programa de Pós-Graduação em Física
 Uiversidade Federal do Marahão Cetro de Ciêcias Exatas e Tecologia Coordeação do Programa de Pós-Graduação em Física Exame de Seleção para Igresso o 1º. Semestre de 2011 Disciplia: Mecâica Clássica 1.
Uiversidade Federal do Marahão Cetro de Ciêcias Exatas e Tecologia Coordeação do Programa de Pós-Graduação em Física Exame de Seleção para Igresso o 1º. Semestre de 2011 Disciplia: Mecâica Clássica 1.
CPV O cursinho que mais aprova na FGV
 O cursiho que mais aprova a FGV FGV ecoomia a Fase 0/dezembro/00 MATEMÁTICA 0. Se P é 0% de Q, Q é 0% de R e S é 0% de R, etão P S é igual a: 0 c 0. Dado um petágoo regular ABCDE, costrói-se uma circuferêcia
O cursiho que mais aprova a FGV FGV ecoomia a Fase 0/dezembro/00 MATEMÁTICA 0. Se P é 0% de Q, Q é 0% de R e S é 0% de R, etão P S é igual a: 0 c 0. Dado um petágoo regular ABCDE, costrói-se uma circuferêcia
Prof. Celso Módulo 12 Resposta em freqüência-diagrama de Nyquist RESPOSTA EM FREQÜÊNCIA-DIAGRAMA DE NYQUIST
 Prof. Celso Módulo Resposta em freqüêcia-diagrama de Nyquist RESPOSTA EM FREQÜÊNCIA-DIAGRAMA DE NYQUIST O diagrama de Nyquist ou diagrama polar é um gráfico do módulo de G pelo âgulo de fase de G em coordeadas
Prof. Celso Módulo Resposta em freqüêcia-diagrama de Nyquist RESPOSTA EM FREQÜÊNCIA-DIAGRAMA DE NYQUIST O diagrama de Nyquist ou diagrama polar é um gráfico do módulo de G pelo âgulo de fase de G em coordeadas
Série Trigonométrica de Fourier
 studo sobre a Série rigoométrica de Fourier Série rigoométrica de Fourier Uma fução periódica f( pode ser decomposta em um somatório de seos e seos eqüivaletes à fução dada f ( o ( ( se ( ) ode: o valor
studo sobre a Série rigoométrica de Fourier Série rigoométrica de Fourier Uma fução periódica f( pode ser decomposta em um somatório de seos e seos eqüivaletes à fução dada f ( o ( ( se ( ) ode: o valor
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
Processamento Digital de Sinais Lista de Exercícios Suplementares 3-1 quad. 2012
 Processameto Digital de Siais - Lista de Exercícios Suplemetares 3- Marcio Eisecraft abril 01 Processameto Digital de Siais Lista de Exercícios Suplemetares 3-1 quad 01 1 (1041) [OPPENHEIM, p 603] Supoha
Processameto Digital de Siais - Lista de Exercícios Suplemetares 3- Marcio Eisecraft abril 01 Processameto Digital de Siais Lista de Exercícios Suplemetares 3-1 quad 01 1 (1041) [OPPENHEIM, p 603] Supoha
Física B Semi-Extensivo V. 4
 Semi-Extesio V 4 Exercícios ) 9 Correta correta Como os dois estão emitido sos com a mesma altura, as freqüêcias emitidas pelo iolio e pela flauta são iguais 4 Correta 8 Correta 6 Correta correta Tato
Semi-Extesio V 4 Exercícios ) 9 Correta correta Como os dois estão emitido sos com a mesma altura, as freqüêcias emitidas pelo iolio e pela flauta são iguais 4 Correta 8 Correta 6 Correta correta Tato
Aula 5 Teorema central do limite & Aplicações
 Diâmica Estocástica Aula 5 Teorema cetral do limite & Aplicações Teorema cetral do limite Se x é tal que: x 0 e ( xv é fiita,,..., x x, x,...,, 3 x variáveis aleatórias idepedetes com a mesma distribuição
Diâmica Estocástica Aula 5 Teorema cetral do limite & Aplicações Teorema cetral do limite Se x é tal que: x 0 e ( xv é fiita,,..., x x, x,...,, 3 x variáveis aleatórias idepedetes com a mesma distribuição
MAE116 Noções de Estatística
 Exercício 1 A Secretaria de Saúde de um muicípio vem realizado um programa educativo etre as gestates mostrado a importâcia da amametação. Para averiguar a eficácia do programa pretede-se realizar uma
Exercício 1 A Secretaria de Saúde de um muicípio vem realizado um programa educativo etre as gestates mostrado a importâcia da amametação. Para averiguar a eficácia do programa pretede-se realizar uma
