UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA DE ESTRUTURAS
|
|
|
- Miguel Mota Gusmão
- 6 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA DE ESTRUTURAS UMA FORMULAÇÃO DO MÉTODO DOS ELEMENTOS DE CONTORNO COM TRÊS PARÂMETROS NODAIS EM DESLOCAMENTOS PARA PLACAS DELGADAS E SUAS APLICAÇÕES A PROBLEMAS DE ENGENHARIA ESTRUTURAL LUTTGARDES DE OLIVEIRA NETO Tese apesetada à Esola de Egehaa de São Calos, da Uvesdade de São Paulo, oo pate dos equstos paa obteção do título de Douto e Egehaa de Estutuas ORIENTADOR: Pof. D. João Batsta de Pava São Calos 998
2 Aos eus pas Luttgades e Thela
3 AGRADECIMENTOS Gostaa de peaete agadee ao pofesso D. João Batsta de Pava pela paete e dedada oetação alé da azade e ofaça útuas apofudadas este dez aos de ovívo. Teho pleo oheeto de que se sua bása otbução e etvo este tabalho ão sea oluído e gostaa de dea aqu ha sea gatdão. Meu desejo é te a opotudade de otua este ovívo que e aeseta pessoal e pofssoalete. Agadeço aos eus falaes, pas, ãos, sobhos, avós pelo ao e aho sepe deostados e pela opeesão às has ausêas. Agadeço à Pata Kast Caha, ha opahea e aga, pela paão opaheso e aho. Aos agos, sepe, ua agadável opaha, eso aqueles dstates, agadeço pela toda e etvo. Aos olegas, pofessoes e fuoáos de São Calos (Depataeto de Egehaa de Estutuas, Guaatguetá (Depataeto de Pojetos e Costução Cvl e de Bauu (Depataeto de Egehaa Cvl eus agadeetos pelo ovívo sepe povetoso e estulate. Agadeço à Sa. Maa Nad Matel pela olaboação a pesqusa bblogáfa e evsão da esa. Agadeço tabé a CAPES pela bolsa oedda que otbuu paa o bo eahaeto do tabalho.
4 SUMÁRIO. INTRODUÇÃO.... FUNDAMENTOS DA TEORIA DE PLACAS DELGADAS Itodução Hpóteses básas Relações básas paa plaas sótopas Equações de plaas e oodeadas polaes Soluções fudaetas de plaas EQUAÇÕES INTEGRAIS PARA FLEXÃO DE PLACAS Itodução Equação tegal paa u poto do doío Equação tegal paa u poto do otoo Itegas de doío paa o aegaeto MÉTODO DOS ELEMENTOS DE CONTORNO: IMPLEMENTAÇÃO NUMÉRICA Itodução Dsetzação das equações tegas Apoação das vaáves do poblea Tasfoação das equações tegas e equações algébas Desloaetos paa potos teos Esfoços paa potos teos Popedades da atz H Avalação uéa da foulação poposta... 79
5 5. PLACAS EM ASSOCIAÇÃO COM OUTROS ELEMENTOS ESTRUTURAIS Itodução Assoação plaa-pla Assoação plaa-gelha Avalação uéa da foulação poposta paa aálse das lgações o eleetos leaes CONCLUSÕES REFERÊNCIAS BIBLIOGRÁFICAS BIBLIOGRAFIA COMPLEMENTAR... 8
6 LISTA DE FIGURAS Fgua. - Eleetos de plaa o tesões e esfoços atuates devdos à fleão 0 Fgua. - Resultate do oeto volvete e u poto do otoo da plaa 4 Fgua.3 - Tesões e esfoços esultates o eleetos de plaa Fgua.4 - Cotoo da plaa o deções, e s, e efeêa às oodeadas atesaas (, e polaes (, θ, paa u poto geéo P... 7 Fgua.5 - Foça otate equvalete u íulo de ao devdo à aga utáa aplada e s... 6 Fgua.6 - Ssteas de oodeadas (, u e (, s... 7 Fgua 3. - Coodeadas (, s o poto Q do otoo Fgua 3. - Catos da plaa e oetos volvetes esultates... 4 Fgua Cotoo ula aesdo a u ato da plaa Fgua Sstea de oodeadas efeetes aos potos ateo e posteo aos atos λ - e λ Fgua Regão de aegaeto g Fgua 4. - Dsetzação do otoo da plaa Fgua 4. - Nó duplo e ato da plaa Fgua Coodeada adesoal ξ o eleeto de otoo lea Fgua Fuções apoadoas úbas ϕ (ξ Fgua Plaa o aegaeto tasvesal ulo e desloaeto e gos de opo ígdo Fgua Plaa quadada e apoada os quato atos Fgua Plaa o dos lados egastados e dos lves Fgua 5. - Cojuto plaa-pla as posções al e defoada Fgua 5. - Esfoços de teação plaa-gelha... 9
7 Fgua Plaa quadada e apoada os quato atos e vgas ao logo das bodas Fgua 5.4 Paveto de edfío Fguas 5.5 a 5. - Moetos fletoes e seções A, B, C e D... 0 a 04 Fgua Plaa apoada e seu otoo e e quato oluas e seu doío Fguas 5.4 a Desloaetos e oetos fletoes e seções a 09 Fgua 5.0 Paveto de edfío apoado e quato oluas... 0 Fguas 5. a Desloaetos e oetos fletoes e seções... a 4
8 RESUMO OLIVEIRA NETO, L. Ua foulação do étodo dos eleetos de otoo o tês paâetos odas e desloaetos paa plaas delgadas e suas aplações a pobleas de egehaa estutual. São Calos. Tese (doutoado Esola de Egehaa de São Calos, Uvesdade de São Paulo. O objetvo deste tabalho é apeseta ua ova foulação deta do Método dos Eleetos de Cotoo (M.E.C. paa aálse de plaas, utlzado a teoa de Khhoff, adtdo tês paâetos odas de desloaetos paa sua epesetação tegal: desloaeto tasvesal e suas devadas as deções oal e tageal ao otoo. Dos valoes odas são usados paa os esfoços, oeto fleto oal e foça otate equvalete V. Desta foa são estas tês equações tegas de otoo po ó, obtdas a pat da dsetzação da plaa, segudo a foa usual do étodo. A vatage as peeptível desta foulação é a possbldade de se faze a lgação da plaa aalsada pelo M.E.C. o eleetos leaes, epesetados po tês valoes odas de desloaetos que passa a se opatblzados detaete, paa a aálse de edfíos. São apesetados eeplos uéos da foulação e das lgações paa opovação da foulação. Palavas-have: Método dos eleetos de otoo; Plaas delgadas; Aálse de pavetos. ABSTRACT
9 OLIVEIRA NETO, L. A bouda eleet ethod foulato fo plate bedg aalss th thee odal dsplaeet paaetes ad ts applato fo stutual pobles. São Calos. Tese (doutoado Esola de Egehaa de São Calos, Uvesdade de São Paulo. The a of ths ok s to peset a alteatve foulato fo plate bedg aalss, usg Khhoff s theo, h the bouda equato fo dsplaeets ad ts devatve tagetal ad oal detos to the bouda fo eah bouda ode ae used. The effots, aodg to Khhoff s theo, ae the oal bedg ad the equvalet shea foe V. Ths foulato s adequate fo the aalss of plates oupled th fleble olus ad beas beause these stutual eleets have thee odal dsplaeet values at ts odes. Ma eaples of sgle plates ad buldgs slab ae peseted usg the foulato poposed ths ok. Keods: Bouda eleet ethod; Plate bedg; Floo slab aalss.
10 . INTRODUÇÃO A Egehaa de Estutuas é a áea da Egehaa Cvl ode se faz a oepção e, posteoete, a aálse opotaetal dos eleetos estutuas, e suas teações, que opõe as dvesas obas ostuídas pelo hoe. O pojeto estutual vsa, a pat desta aálse, desoa estes eleetos estutuas, quado soltados po dvesas ações eteas. As plaas são u destes eleetos estutuas e são detfadas oo eleetos plaos, subetdos a ações eteas a deção tasvesal ao seu plao édo. Duas teoas ppas foa desevolvdas paa a aálse do opotaeto das plaas; a pea, deoada Teoa Clássa, fo foulada po KIRCHHOFF (850 ujas hpóteses splfadoas, aalsado apeas plaas delgadas, adte quato vaáves o otoo do poblea, esultado ua equação dfeeal de 4 a ode; REISSNER (944 e MINDLIN (95 foulaa teoas que, osdeado as defoações po salhaeto, leva a equações dfeeas de 6 a ode. Estas teoas apeseta, potato, esultados as opletos que os da Teoa Clássa, lusve petdo a aálse de plaas espessas. As soluções aalítas dessas equações são ltadas, ohedas apeas e asos as sples, poé, o a utlzação de téas uéas de solução de ssteas de equações dfeeas pôde-se apla os asos de aálse. Co os oputadoes a aálse uéa fo faltada.
11 Atualete dspõe-se de tês étodos uéos, dos deoados étodos de doío - Método das Dfeeças Ftas (M.D.F. e Método dos Eleetos Ftos (M.E.F. - que assoa potos o doío e o otoo do poblea e suas foulações, e o as eete, Método dos Eleetos de Cotoo (M.E.C., foulado o equaoaeto tegal ao logo do otoo do poblea, e otaposção aos ateoes. O Método das Dfeeças Ftas apaeeu o o tabalho de SOUTHWELL (946 e é ada utlzado e dvesos pobleas de egehaa. O Método dos Eleetos Ftos, o as dfuddo e utlzado, apaeeu e tabalhos desevolvdos po TURNER (956 e ARGYRIS e KELSET (960. Já o Método dos Eleetos de Cotoo teve seu apaeeto a pat de estudos de pobleas utlzado equações tegas, ados o séulo passado, apladas à teoa da elastdade po BETTI (87. Os tabalhos o equações tegas a elastdade bdesoal otuaa sedo ealzados pelos ussos os aos 50 atavés de MUSKELISHVILI (953, MIKHLIN (957 e posteoete po KUPRADZE (965, ão utlzado-se ada as vaáves eas do poblea, po sso foa deoados étodos detos. RIZZO (967 apesetou, ada paa a elastdade bdesoal, o étodo a sua foa deta, sto é, são evolvdas as vaáves eas do poblea e seu equaoaeto. Os peos tabalhos e foulação deta a aálse de plaas foa apesetados po ALTIERO e SIKARSKIE (978 e po WU e ALTIERO (979, ode aalsaa plaas eas otdas e u otoo aula fto, de solução oheda. TOTTENHAM (979 tabé apesetou ua opaação ete as foulações deta e deta. O étodo deto paa aálse de plaas ftas, o fuos, de otoo ão aegado fo poposto po HANSEN (976 segudo de estudos de BEZINE (978, BEZINE e GAMBY (978 e STERN (979 que desevolvea foulações detas baseadas a detdade de Gee, osdeado-se duas equações tegas elatvas ao desloaeto tasvesal e à sua devada a deção oal ao otoo.
12 3 VAN DER WEEËN (98 popôs ua foulação paa aálse de plaas espessas baseada a teoa de Resse, esevedo tês equações tegas paa as vaáves odas, desloaeto tasvesal e as devadas as deções oal e tageal ao otoo. A pat dessas foulações básas, foulações deta e deta e usadose as teoas de plaas de Khhoff e de Resse-Mdl, dvesas aálses de plaas se segua: estudos paa apefeçoaeto uéo do étodo oo sobe quas equações tegas são utlzadas, do desloaeto tasvesal e de sua devada deoal ou apeas de desloaeto tasvesal paa potos dsttos; estudos sobe o elho posoaeto do poto-fote, ao qual as equações oespode; estudos sobe os tpos de tegação as adequados (aalíta ou uéa e sobe as fuções apoadoas das vaáves sobe os eleetos; foas de álulo de tegas sgulaes e quase sgulaes e de tegas de doío; aálse de plaas sob dvesos tpos de vulação e de aegaeto, apoadas sobe base elásta e sobe estaas; aálse da assoação o vgas e oluas o otoo e o doío; aálse ão-lea, físa e geoéta; vbação (aálse odal e tasete; plaas o desloaetos ftos; obação do M.E.C. o o M.D.F. e o o M.E.F. paa dvesas aálses apovetado as vatages apesetadas po ada étodo. A foulação deta, apesa de se a eos utlzada, te sdo otvo de estudos oo os de VABLE e ZHANG (99, que utlzaa esqueas de tegação aalíta e fuções ftías apoadas po polôos paa aálse de plaas, e o tabalho de VENTSEL (997, o tegas sgulaes e hpesgulaes. A teoa de Resse-Mdl, tabé eos utlzada que a Teoa Clássa de Khhoff, fo utlzada e dvesos estudos oo os de KARAM (986, BARCELLOS e SILVA (987, LONG et al. (988, WESTPHAL E BARCELLOS (989 e RIBEIRO e VENTURINI (989. Algus tabalhos aalsado o opotaeto ão-lea geoéto de plaas foa apesetados posteoete oo os de XIAO-YAN et al. (990 e HE e QIN (993. A aálse ão-lea físa de plaas fo ealzada e tabalhos de KARAM e TELLES (99
13 4 e RIBEIRO (99, abos utlzado o étodo eetal-teatvo o oetos as. A foulação deta, fudaetada a Teoa Clássa de Khhoff, é a as utlzada paa aálse de plaas e dvesos tabalhos potates as dvesas aplações foa sugdo desde o ío dos aos 80. Suga foulações alteatvas paa a solução de pobleas de plaas elástas: utlzado-se tegas aalítas oo a de CAMP e GIPSON (990, o fuções tepoladoas hetaas paa apoação dos desloaetos oo os tabalhos de HARTMANN e ZOTEMANTEL (986 e de GUO-SHU e MUKHERJEE (986, utlzado-se fuções lagagaas e tegações aalítas paa o álulo das tegas sgulaes oo a de ABDEL-AKHER e HARTLEY (989, ou ada o fuções opleas paa defção das soluções fudaetas, osdeado-se as defoações po salhaeto paa plaas fas, oo apesetaa PILTNER e TAYLOR (989. Ialete, e algus tabalhos aalsaa-se plaas o odções dvesas de apoo o otoo e o doío oo os de BEZINE (98, PARIS e LEÓN (985, PAIVA (987 (99 e HARTLEY et al. (99. Posteoete, a possbldade de assoação de plaas o vgas e oluas são tabé popostas po dvesos autoes oo PAIVA e VENTURINI (985(987, NG et al. (989, HARTLEY e ABDEL-AKHER (993, HU e HARTLEY (994, PAIVA e OLIVEIRA NETO (995, PAIVA (996, HARTLEY (996. Os pobleas osdeado ão-leadade geoéta de plaas foa alete estudados po KAMIYA e SAWAKY (98 e SAVAKI et al. (989(990. A osdeação da ão-leadade físa do ateal fo alete apesetada e estudos de MOSHAIOV e VORUS (986, que utlzaa u odelo elasto-plásto atavés de u poesso eetal-teatvo o oetos fletoes as e sedo o álulo das tegas de doío ealzado e élulas obtdas da dsetzação do doío da plaa. Tabé fo utlzado este poesso po KAMIYA et al. (98 e po PARIS e LEÓN (987 a aálse de plaas osdeado-se a vaação de tepeatua ao logo da sua espessua e paa aálse de plaas esbeltas po CHUEIRI (994. Já a aálse dâa de plaas teve seu o e tabalhos de VIVOLI e FILIPPI (974 utlzado-se o étodo deto sobe soluções fudaetas
14 5 devadas das fuções de Hakel e obtedo-se oefetes da atz de autovaloes e fução da feqüêa. BEZINE (980 a segu foulou o étodo deteado as feqüêas atuas atavés de u poblea o atz de autovaloes ode os oefetes ão depede da feqüêa, eesstado poé da dsetzação do doío da plaa. NIWA et al. (98 tabé apesetaa estudos utlzado o étodo deto equato WONG e HUTCHINSON (98 utlzaa o étodo deto. Tabalhos posteoes de NARDINI e BREBBIA (98, NIWA et al. (98(98, KITAHARA (985, COSTA JR. (985(988, TANAKA et al. (987, KATSIKADELIS (989, PROVIDAKIS e BESKOS (989 e WEISS e MOSHAIOV (993 tabé otbuía de foa potate paa a aálse odal de vbação de plaas. A aálse tasete teve oo tabalhos as o de CRUSE e RIZZO (968, paa pobleas de elasto-dâa geal, e o de BEZINE e GAMBY (98, que utlzou soluções fudaetas de dâa de plaas esbeltas, e fução do tepo. Outo tabalho a se tado, baseado o ateo, é o de BARRETTO (995. A aálse de plaas sobe fudação elásta tabé fo ealzada e dvesos tabalhos, ada po KATSIKADELIS e ARMENAKAS (984, COSTA e BREBBIA (985, segudos de estudos ealzados po SILVA e VENTURINI (988, TEJERINA CALDERÓN e VENTURINI (997, PAIVA e BUTTERFIELD (997, PAIVA e TRONDI (996 e PAIVA e MENDONÇA (997, estes tês últos aalsado plaas sobe estaas e assoação o o solo. O objetvo deste tabalho é apeseta ua foulação alteatva paa o étodo dos eleetos de otoo paa aálse de plaas delgadas, ode as equações tegas do desloaeto tasvesal e de suas devadas oal e tageal ao otoo são usadas o setdo de possblta ua elho aálse de plaas soladas ou e assoação o outos eleetos estutuas, oo vgas e plaes. Esta foulação osdea tês valoes odas e desloaetos:, / e /s paa ada poto do otoo e, de aodo o a teoa de Khhoff, apeas dos valoes odas paa os esfoços oeto fleto oal ao otoo e foça otate equvalete V.
15 6 A elhoa toduzda po esta foulação apaee os asos de aálse de plaas o boda lve e e asos de lgação de plaas o outos eleetos estutuas, o aso vgas e plaes, que são tabé epesetados o tês paâetos e desloaetos, odelados atavés de téas do étodo dos eleetos ftos. Neste tabalho, o apítulo são apesetados u esuo da teoa de plaas delgadas de Khhoff e a foulação teóa das epessões dfeeas das gadezas evolvdas a foulação de plaas e fução do desloaeto tasvesal. E seguda são deteadas as soluções fudaetas de plaas utlzadas a foulação tegal do étodo dos eleetos de otoo. No apítulo 3 são obtdas as equações tegas dos tês paâetos e desloaeto evolvdos a teoa de plaas, desloaeto tasvesal de suas devadas / e /s paa potos do otoo, segudo a foulação poposta este tabalho, e do doío, utlzado-se as soluções fudaetas obtdas o apítulo ateo. A tegal do doío devda ao aegaeto tasvesal da plaa é tasfoada e tegal sobe o otoo da egão do aegaeto. No apítulo 4 é toduzda a pleetação uéa do étodo dos eleetos de otoo, ode há a dsetzação do otoo da plaa e eleetos ode seão apoadas as vaáves do poblea, desloaetos e esfoços. Desta foa são obtdas equações algébas a pat das equações tegas da foulação do étodo. Neste tabalho as vaáves de otoo são apoadas po fuções tepoladoas leaes ou úbas. As equações algébas, defdas paa todos os potos de otoo obtdos da dsetzação, foa u sstea de equações que, após see toduzdas todas as odções de otoo do poblea, pode se esolvdo a foa [A].{X} {B}. Algus eeplos uéos são apesetados paa avalação da foulação. No apítulo 5 são apesetadas as assoações da plaa, aalsada pelo étodo dos eleetos de otoo pela foulação poposta, o eleetos leaes oo vgas (gelhas e plaes, o a faldade de se aalsa pavetos de edfíos. Algus eeplos uéos são apesetados paa avalação da foulação poposta. No apítulo 6 são apesetadas as olusões do tabalho.
16 7 Po f, o apítulo 7 são apesetadas as efeêas bblogáfas tadas este apítulo e o apítulo 8 apeseta-se a bblogafa opleeta, ão tada, utlzada paa a edfação deste tabalho.
17 . FUNDAMENTOS DA TEORIA DE PLACAS DELGADAS.. Itodução Os eleetos estutuas são lassfados ofoe a elação ete suas desões, e são deoados leaes (ou de baas, de supefíes (ou laaes e t-desoas (ou bloos ofoe apesete, espetvaete, duas, ua ou ehua desão pequea, quado opaada o as deas. Plaas são, po defção, eleetos estutuas de supefíe, sétos e elação a u plao édo, uja desão eo está a deção oal a este plao e é deoada espessua, h, da plaa. O aegaeto é tasvesal ao plao édo. Apaee a páta, po eeplo, oo psos de edfío, paedes de esevatóos, et.. De aodo o o ateal do qual é osttuída a plaa ela pode se lassfada oo: asotópa, o popedades dfeetes e qualque deção, otótopa, o popedades dfeetes e duas deções pepedulaes, ou sótopa, o popedades guas e todas as deções. Ada de aodo o a espessua, a plaa pode se lassfada oo uto delgada (se, h/a < /80, delgada (se,/80 < h/a < /5 ou espessa (se, h/a > /5. Neste tabalho seão osdeadas apeas as plaas delgadas e sótopas, subetdas a aegaeto tasvesal e otogoal ao plao édo, e seá baseado a teoa de Khhoff, que tepeta be o opotaeto de plaas o elação espessua/eo desão, h/a, ete /5 e /80... Hpóteses básas As hpóteses da teoa de plaas delgadas são:
18 9 - a plaa é osttuída de ateal elásto-lea e, potato, segue a le de Hooke; - os desloaetos tasvesas são pequeos e elação a espessua, h, da plaa; - ão há defoação o plao édo da plaa; - as defoações a plaa, devdas à fleão, vaa leaete o a dstâa ao plao édo desta plaa, ao logo de sua espessua, o que equvale dze que as tesões oas, paalelas ao plao édo, tabé vaa leaete o a espessua; - as tesões oas a supefíe da plaa são despezíves e opaação o as tesões oas devdas à fleão..3. Relações básas paa plaas sótopas Cosdee-se alete o eleeto de plaa da fgua..a ode estão dadas as tesões soltates devdas a u aegaeto tasvesal, g, dstbuído. As esultates destas tesões apesetadas a fgua..b, oetos de fleão e volvete e foça otate, são obtdas das segutes tegações sobe a espessua, h, do eleeto: h σ zdz h (..a h σ zdz h (..b h h τ zdz (.. h q τ zdz h (..d
19 0 h q τzdz h (..e Fgua. Eleetos de plaa o tesões e esfoços atuates devdos à fleão. Das odções de equlíbo de foças vetas e de oetos e too dos eos e, obtê-se as segutes epessões: q q g 0 (..a q (..b q (.. Agupado-se as equações de equlíbo (. ua só equação e osdeado-se, obté-se:
20 g (.3 As defoações elatvas ε e ε e a dstoção γ ao logo da espessua z da plaa pode se epessas e fução das uvatuas da segute foa: ε z (.4.a ε z (.4.b γ z (.4. Obtdas as defoações de u poto da plaa tê-se, atavés da le de Hooke, as tesões oespodetes este poto: E ν ( ε νε σ (.5.a E ν ( ε νε σ (.5.b ode, E τ γ (.5. ( ν E : ódulo de elastdade logtudal; ν : oefete de Posso; G : ódulo de elastdade tasvesal;
21 E G ( ν (.6 Substtudo-se a equação (.5 as epessões (.4 obtê-se tabé as tesões e fução do desloaeto tasvesal : E ν z ν σ (.7.a E ν z ν σ (.7.b G z τ (.7. Retoado-se às epessões (. dos valoes das esultates das tesões o eleeto de plaa e toduzdo-se as epessões (.7, esulta: D ν (.8.a D ν (.8.b ode, D( ν D : gdez à fleão, é dado po: (.8.
22 3 ( 3 ν Eh D (.9 A equação (.3 pode se eesta e fução do desloaeto tasvesal a pat das equaçõs (.8, esultado a equação dfeeal de plaas: D g (.0 Utlzado-se o opeado de Laplae: (. a últa equação (.0 esulta: D g (. e ada, D q (.3.a D q (.3.b
23 4 Paa a esolução da equação dfeeal de plaas deve-se po odções de otoo elatvas ao desloaeto, ao go / e aos esfoços (oeto fleto, oeto volvete e foça otate, po udade de opeto. Poé, Khhoff deostou que pode-se eseve as odções de otoo elatvas à foça otate e ao oeto volvete ua úa odção. Paa etede esta poposção, osdea-se u poto geéo, P, a boda da plaa e dos eleetos de opeto ds, adjaetes a este poto, ofoe osta a fgua.. Tabé pode-se obseva que estes eleetos apeseta oetos volvetes esultates de valoes s ds e ( s s /sds. Itepeta-se estes oetos oo esultates de báos de foças atuado agoa as lateas dos eleetos de otoo, de tal foa que suja ua esultate fal o poto P de valo ( s /s ds. Fgua. Resultate do oeto volvete e u poto do otoo da plaa. O esfoço esultate da soa desta foça o a foça otate q (ou q é deoado foça otate equvalete, po udade de opeto, e vale: V q (.4.a
24 5 V q (.4.b Pode-se eseve agoa as opoetes de tesões e esfoços paa u sstea geéo de oodeadas (,s, ode o eo foa u âgulo α o o se-eo postvo. Cosdee-se o eleeto de plaa 3 apesetado a fgua.3, ujos lados e 3 são paalelos aos eos e, espetvaete. Fgua.3 Tesões e esfoços esultates o eleeto de plaa 3. Pode-se eseve as elações das tesões e dos esfoços efeetes ao lado 3 as deções e s: σ σ os α σ se α τ se α os α (.5.a τ s (σ - σ se α os α τ (os α - se α (.5.b os α se α se α os α (.5. s ( se α os α (os α - se α (.5.d
25 6 Já as elações das otates q são obtdas pelo equlíbo de foças vetas do eleeto. Etão: q ds q ds os α q ds se α ou q q os α q se α (.6.a Retoado-se as epessões (.4 pode-se eseve a foça otate equvalete, po udade de opeto, oo: V q s s (.7
26 7.4. Equações de plaas e oodeadas polaes Tedo e vsta que este tabalho a equação dfeeal de plaas é aplada a u doío fto paa a obteção das soluções fudaetas, toa-se eessáo eseve as equações das plaas e oodeadas polaes. O sstea de oodeadas da Fgua.4 osta a elação ete as oodeadas atesaas e polaes e suas opoetes. Fgua.4 Cotoo da plaa o deções, e s, e efeêa às oodeadas atesaas (, e polaes (, θ, paa u poto geéo P. O poto P de oodeadas atesaas (, passa a te ovas oodeadas (, θ, ode é a dstâa de P à oge O do sstea de oodeadas e θ o âgulo foado pela deção de e o se-eo postvo. Ass as elações ete os dos ssteas fa deteadas po:.osθ (.8.a.seθ (.8.b ou ada, (.9.a θ atg / (.9.b Co estas elações pode-se obte suas espetvas devadas e elação ao sstea atesao:
27 8 θ os (.0.a θ se (.0.b se θ θ (.0. os θ θ (.0.d Esevedo-se agoa as devadas do desloaeto tasvesal e oodeadas (, paa se obte a equação dfeeal, te-se, a deção :: θ θ (. ou θ θ θ se os (..a Aalogaete, a deção,te-se: θ θ θ os se (..b As devadas de seguda ode esulta: θ θ θ θ θ θ θ θ θ os se se os se os
28 9 (.3.a θ θ θ θ θ θ θ θ θ os se os se os se (.3.b e ( θ θ θ θ θ θ θ θ θ se os os se se os (.4 Soado-se as duas equações (.3 obté-se a epesetação do opeado dfeeal de Laplae epesso e oodeadas polaes: θ (.5 Potato, a equação dfeeal de plaas (., epessa e oodeadas polaes esulta: D g θ θ (.6
29 0 Substtudo-se as equações (.3 e (.4 as elações (.8 e (.3, tê-se: ( ( θ θ θ ν θ θ ν θ θ θ ν os se ( os se se os D (.7.a ( ( θ θ θ ν θ θ ν θ θ θ ν os se ( se os os se D (.7.b ( θ θ θ θ θ θ ν se os os se D( (.7. θ θ θ θ θ se os D q (.7.d θ θ θ θ θ os se D q (.7.e
30 Co estas epessões deduze-se, tabé e oodeadas polaes, as epessões dos esfoços, s e V e u poto geéo P do otoo da plaa. Estes esfoços tê oo efeêa u sstea loal de oodeadas atesaas (,s, ode é a deção oal e s a deção tageal ao otoo este poto, oo pode-se obseva a Fgua.4. Ada essa fgua estão o âgulo β, ete os vesoes e, e o ao de uvatua R do otoo da plaa o poto P. Pode-se obte os esfoços e P substtudo-se as equações (.5 o valo de α θ β (Fgua.4, esultado: D ( os β ν se β ( se β ν os β ( νse β osβ θ θ (.8.a s D( ν ( os β se β θ se βosβ θ (.8.b Paa se hega à epessão da foça otate equvalete V, e oodeadas polaes, deve-se deva s, dado pela equação (.8. e elação a s. Paa a otate te-se: q q os (θβ q se (θβ (.9 Substtudo-se q e q pelas epessões (.7, esulta:
31 q D osβ se β θ θ θ (.30 A devada de s e elação à oodeada s vale: s s s s θ s θ s β s β s (.3 O teo /s pode se esto da segute foa: s s s os θ( se α se θ os α e, da Fgua.4, α θ β ou β α - θ Etão, s e aalogaete, se β (.3 θ s se θ ( se α os θ os α os β (.33 Sabe-se ada que:
32 3 os R s β β (.34 ode, R : ao de uvatua do otoo o poto P. Substtudo-se as equações (.3, (.33 e (.34 a equação (.3, obté-se: β β β θ β os R os se ( s s s s s (.35 Agoa esevedo-se V o os valoes obtdos de q e s /s, obtése: β β β θ θ β θ θ s s s os R se D os D V (.36
33 4.5. Soluções fudaetas de plaas A solução fudaetal de plaas é defda oo o desloaeto tasvesal *, epesetado a esposta e u poto, q, geéo de oodeadas [(q,(q] o doío fudaetal da plaa, gealete fto, devda a ua aga utáa aplada e u poto s, poto de aegaeto, de oodeadas [(s,(s] deste eso doío. A solução fudaetal é obtda a pat da segute equação: ode, * δ(s,q/d (.37 δ(s,q : dstbução delta de Da. Essa dstbução apeseta as segutes popedades: δ(s,q 0 q s (.38.a δ(s,q qs (.38.b e δ(s,q d (.38. ostado-se que a dstbução delta de Da, tegada o doío, epeseta ua aga utáa esultate do aegaeto tasvesal aplado à plaa o poto s. Ass, pode-se eseve: φ(q δ(s,q d φ(s (.39 ode, φ(q : ua fução otíua qualque defda o doío.
34 5 A solução fudaetal de plaas é obtda, etão, a pat da equação dfeeal aplada a todos os potos do doío da plaa, eeto o poto de aga s, esultado: 0 (.40 Paa u sstea de oodeadas polaes o oge e s e obsevado-se a seta do poblea e elação a este poto, o que ela a depedêa e elação à oodeada θ, a equação (.40 passa a se esta oo: d d d d d d d d 0 (.4 Efetuado-se as devações, pode-se eesevê-la oo: 4 d 4 d 3 d 3 d d d 3 d d 0 (.4 uja solução é: * A l B l C E (.43 Cosdeado-se a seta do poblea e o desloaeto fto pode-se afa que a devada d * /d paa o poto s é ula, esultado: A 0 (.44 Paa se obte a ostate B adte-se u ulo de ao o eto e s, sedo s o poto de aplação da aga utáa (fgua.5, ode sugá, e seus ltes, ua foça otate equvalete V ufoeete dstbuída paa ate seu equlíbo. Ass:
35 6 V π (.45 Fgua.5 Foça otate equvalete u íulo de ao devdo à aga utáa aplada e s. Paa este valo, potato, a epessão (.36 de V, agoa esta apeas e fução de ( e paa β 0 esulta: D θ V π (.46 Substtudo-se a equação (.43 a (.46 obté-se a ostate B: B 8πD (.47 Ass a equação (.43 de * passa a te a foa: 8πD l C E (.48 As ostates C e E são obtdas a pat de odções de otoo da plaa estudada; po, paa o aso da plaa fudaetal de ao fto e questão, essas odções pode se quasque. STERN (979e BEZINE (978 adota:
36 7 esultado, C E 0 (.49 8πD l (.50 DANSON (979 adota: obtedo, C e E 0 (.5 6πD 8πD (l que seá e epessão usada este tabalho. (.5 Pode-se obte ada as epessões da sua devada e dos esfoços fudaetas. São deteadas tabé as devadas destas soluções fudaetas e elação à oodeada de u sstea de efeêa atesao (,u o oge e s, ofoe osta a fgua.6. Fgua.6 Ssteas de oodeadas (,u e (,s. A devada do desloaeto o poto s é dada po:
37 8 (.53 ode, (q (q (q (q (.54 As devadas de e elação às oodeadas e, adtdo-se que (s,q [((q-(s ((q-(s ] /,são dadas po: (q (q (q (s os θ, (.55.a (q (s se θ, (.55.b As deas devadas, de seguda ode, são:, (q, (.56.a, (q,, (.56.b, (q,, (.56., (q, ou, se estas a foa dal, (.56.d
38 9 (q, (q (s (.57.a ode, δ j,j (q (q δ j : delta de Koeke, ujo valo é dado po:,, j (.57.b δ j 0 paa j (.58.a δ j paa j (.58.b As devadas e elação a vale: (s osα (.59.a (s se α (.59.b Cobado-se as equações (.55, (.56 e (.59 a equação (.54, tese: potato, osθosα se θse α osβ (.60 l β 4πD os (.6
39 30 Cosdeado-se o veso assoado a, te-se: l (. 4πD l (,, 4πD,, (.6 ou usado-se a otação dal, te-se: l ( 4πD (.63 As epessões (.8, (.30 e (.36 dos esfoços fudaetas *, s *, q *, V* são obtdas a pat da epessão (.5 e são dadas po: 4π [( νl ( ν os β ν] (.64 osβ π q * (.65 ν se β 8π s (.66 ode, V osβ 4π ν [ ( νse β 3 ν] os β (.67 4πR os β.,,,, se β s. s,, s,, s
40 3 e, potato: * l 4πD ( (.68.a q * π (. (.68.b * 4 π [( ν l ( ν(. ν] (.68. * s ν 4π (. ( s. (.68. V (. 4π ν [ ( ν(s. 3 ν] (s.(. 4πR (.68.d As devadas dos desloaetos e dos esfoços fudaetas e elação à deção o poto s é feta de foa aáloga à do poto q, sto é: (.69 ode, (s (s (s (s (.70 As devadas de e elação às oodeadas e, são dadas po: (s (q (s osθ, (.7.a
41 3 (s (q (s se θ, (.7.b As deas devadas, de seguda ode, são:, (s, (.7.a, (s,, (.7.b, (s,, (.7. (s,, ou, usado-se a otação dal, tê-se: (.7.d (s, (q (s (.73.a δ j,j (s (s,, j (.73.b As devadas e elação a vale: (s os γ (.74.a
42 33 (s se γ (.74.b Agupado-se as equações (.7, (.7 e (.74 a equação (.70, te-se: potato, os γ( osθ se γ( se θ osϕ (.75 l ( osϕ 4πD (.76 Pode-se eseve: l (. 4πD ou ada usado-se a otação dal, te-se: l (,, 4πD,, (.77 l ( 4πD (.78 As deas epessões são estas a foa dal paa ua foa as opata: 4πD [( ( ( l ] (.79 ode se apla a equação (.6.
43 34 Na sequêa, * q π [( ( ( ] (.80 4π {( ν( ( ν( [( ( ( ]} (.8 s ( ν 4π [( (s ( s ( ( ( (s ] (.8 V 4π (s ( ( ν (s πr ou, vetoalete, * * q * * s l 4πD * π 4π { ( ν(s [ 4(s ( ( ] (3 ν [( ( ( ]} [( s ( ( s ] ( 4πD ν 4π [(. (. (. l ] [(. (. (. ] ( s ( {( ν(. l ( ν(. ( [. (. (. ]} [(. ( s. (.s (. (. (. ( s. ] (.83
44 3. EQUAÇÕES INTEGRAIS PARA FLEXÃO DE PLACAS 3.. Itodução Neste apítulo seão obtdas as equações tegas, utlzado-se as soluções fudaetas do apítulo ateo, da foulação do Método dos Eleetos de Cotoo paa plaas. Cofoe já oetado, estas equações tegas são efeetes ao desloaeto tasvesal (s e às suas devadas deoas (s/ e (s/s de u poto do otoo, elaoados aos esfoços o otoo e ações de doío. Estas equações seão obtdas utlzado-se o peo teoea de Bett, ou teoea da epodade, e ua plaa sujeta a dos aegaetos dsttos, g e g*,que esulta e dos estados de tesão e de desloaeto oespodetes. A pat de tegações po pates sobe a epessão esultate da aplação do teoea de Bett, obtê-se as equações tegas desejadas. 3.. Equação tegal paa u poto do doío Seja ua plaa sótopa qualque, de otoo e doío, otda e ua plaa fta de otoo e doío. Aplado-se à plaa fta dos aegaetos dsttos, g dstbuído e ua egão de áea g,e g* aegaeto oespodete à solução fudaetal, obtê-se dos estados de tesão, σ j e σ j *, e dos de defoação, ε j e ε j *, oespodetes. O teoea da epodade de Bett foee a segute gualdade: v σ j ε j dv v σ j ε j dv (3.
45 36 O teo da deta, deoado aqu de U, pode se esto epltado-se os ídes do poduto tesoal. U [ σ ε σ ε σ ε ( τ ε τ ε τσ ε ]dv v z z z z z z (3. te-se: Despezado-se as tesões elatvas à deção z, oal ao plao da plaa, ( σ ε σ ε τ ε dv U v (3.3 Substtudo-se agoa os valoes de tesões e de defoações dados pelas equações (.7 e (.4, te-se a tegal do peo teo de U da segute foa: dv E z v ( ν ν dv σ ε (3.4 v Realzado-se a tegação desta equação a espessua, a tegal tasfoa-se e tegal sobe o doío : σ ε ν dv D d v (3.5 De foa aáloga pode-se tabalha o os dos teos estates da equação (3.3, esultado:
46 37 ν ν ν d D( D D U (3.6 Co as equações (.8 e vsta, pode-se eeseve: [ d U (3.7 que é a tegal de volue epesetada a equação (3.3 tasfoada e tegal sobe o doío. Pode-se agoa tasfoá-la e tegal sobe o otoo tabalhado-se o ada paela dvdualete. Itegado-se po pates a pea paela da equação (3.7, a deção, obté-se: η d d d (3.8 η : o-seo deto do veso oal ao otoo a deção, ofoe a Fgua 3.. Fgua 3. Coodeadas (, s o poto Q do otoo Itegado-se po pates a tegal de doío da seguda paela da equação (3.8, obté-se:
47 38 α α d d os os d (3.9 Itegado-se po pates agoa a tegal de doío da seguda paela da equação (3.7, de foa aáloga, a deção, te-se: η d d d (3.0 Itegado-se ovaete po pates a seguda paela da equação (3.0, obté-se falete: α α d d se se d (3. Reesevedo-se agoa a teea paela da equação (3.7, te-se: d d d (3. Itegado-se po pates as duas paelas, e elação às deções e, obté-se:
48 39 α α d d se d d os d (3.3 Itegado-se po pates as tegas de doío da equação (3.3, obtése: α α α α d d os se se os d (3.4 Co as equações (3.9, (3. e (3.4 pode-se eeseve U oo: α α α α α α d d se os d se os se os U (3.5 Retoado-se as elações (. e (.3 pode-se eseve:
49 40 U q d g osα g d ode g é a egão aegada da plaa. g seα osα seα d (3.6 Te-se que: os α s se α (3.7.a se α s os α (3.7.b Substtudo-se as equações (3.7 a equação (3.6 e agupado-se os teos */ e */s, te-se: U [( se α os α (os α se α ] q {( os α se α os αse α d g g d g d s (3.8 Ass, a pat das equações (.5 pode-se splfa U oo: U s s q d g g d g (3.9 Itegado-se po pates o teo de s, obté-se:
50 4 s s d s s s d (3.0 ode e são os ltes do otoo ode se faz a tegação. Paa u otoo fehado e se apeseta atos, a pea paela se aula. Estdo atos, sugão as eações de ato, deoadas aqu de R. Fgua 3. Catos da plaa e oetos volvetes esultates Na Fgua 3. pode-se obseva ua plaa o dvesos atos ode estão epesetados os espetvos oetos volvetes esultates. Adtdo-se o peo teo da equação (3.0 oo u soatóo paa todos os lados da plaa, e toado-se apeas dos lados desta paa deostação, te-se: ( ( s s s (3. Paa o ato te-se: s
51 4 ( s s R (3. Co sto pode-se eseve o peo teo da equação (3.0, ates epesso e teos de soatóo dos lados da plaa, e soatóo de seus atos, a pat da equação (3. oo segue: ( l l l l N N s s N l l s R (3.3 ode, N l : úeo de lados da plaa; N : úeo de atos da plaa; * : desloaeto fudaetal o ato ; l e l : ltes de ada lado da plaa. Potato a epessão (3.0 pode se esta oo: d s R d s s N s (3.4 que, substtudo-se a equação (3.9, esulta: g N s d g R d s q U g (3.5 Utlzado-se a equação (.7, obté-se: g N d g R d V U g (3.6 ode adte-se a aga g atuado e u doío g.
52 43 Aalogaete, obté-se o teo da esqueda da equação (3. oo: d g d q s ' U s (3.7 Ass, agupado-se as equações (3.6 e (3.7 a epessão do teoea de Bett aplado a plaas esulta: g N s d g R d V d g d q s g (3.8 Aqu pode-se ota a todução, a foulação tegal aqu apesetada, da devada /s de potos do otoo, que ão apaee a foulação lássa do étodo. A título de opaação, a esa epessão (3.8, se apesetada pela foulação usual do étodo, esulta a segute foa: g N d g R d V d g d V g Ao eeseve a equação (3.8 de foa a elaoa ada vaável oo fução dos potos a plaa, obseva-se:
53 44 a os esfoços e os desloaetos oespodetes ao aegaeto g depede apeas do poto de apo Q; b a aga utáa fudaetal g* aplada o poto s do doío da plaa é epesetada pela fução delta de Da δ(s,q e, potato, é fução dos potos de oloação de aga s e de apo Q; os esfoços e os desloaetos oespodetes à aga g* depede dos potos de aga s e de desloaeto Q. Ass, eesevedo-se a equação (3.8, esulta: q N g (s, Q(Q R (s, q(qd(q (Q (s,q (s,q (Q g V g(q (Q s (s,q (s,qd (s,q (Q d(q s g (q (Q (s,q d(q (3.9 Cofoe já eoado, a teea popedade da dstbução delta de Da (.38. gaate que: δ s,q(qd (q (s g ( g (3.30 Co sto a epessão do teoea de Bett aplado a plaas fa:
54 45 (s N q (s,q(q (s,q (Q V (Q (s,q (Q (s,q d(q R (Q (s,q g s g(q (s,qd (q g (s,q (Q d(q s (3.3 Te-se, potato, a equação tegal do desloaeto tasvesal de u poto s do doío da plaa, epessa e fução dos esfoços V (Q e (Q e dos desloaetos (Q, (Q/ e (Q/s de potos do otoo, utlzado-se as soluções fudaetas obtdas o apítulo ateo. Devado-se a equação (3.3 e elação à deção, obté-se a equação tegal da devada deoal do desloaeto tasvesal (s/ paa u poto s do doío da plaa: (s q (s,q (s,q s(s,q (Q (Q (Q s d(q N R (s,q V (Q (Q (s,q d(q (s,q (Q g (s,q g(q d g (q (3.3 Nas equações (3.3 e (3.3 estão epesetadas, potato, as teelações dos desloaeto tasvesal e de suas devadas deoas os potos teos da plaa o os desloaetos, / e /s de potos do otoo.
55 Equação tegal paa u poto do otoo As equações (3.3 e (3.3 são estas paa potos s do doío da plaa, poé, paa a aplação do étodo aos pobleas de fleão de plaas, deve-se eseve as equações tegas paa potos S do otoo. Paa sto, osdee-se a Fgua 3.3 ode u poto S do otoo passa a petee ao doío o o aéso ξ do otoo, de ao ξ e o ovos atos λ e λ -. Co o aéso do otoo, a equação (3.3 esta paa o poto S do otoo da plaa esulta: (S N ξ g q (S, Q(Q (S,Q (Q s (S,Q (Q d(q s q (S,Q(Q (S,Q (Q s (S,Q (Q d (Q s ξ ξ V V R (Q (Q g(q (Q (S,Q (S,Q (S,Q R (S, qd g (q (Q (Q (Q (S,Q d(q (S,Q d ξ (S,Q R (Q (Q (S,Q (3.33 otoo. Ass: Na odção lte, quado ξ tede a zeo, o poto S peteeá ao
56 47 (S l l l l N g 0 ξ 0 0 ξ 0 R (Q g(q q (S, Q(Q (S,Q (Q s (S,Q (Q d(q s q (S, Q(Q (S,Q (Q s (S,Q (Q d (Q s ξ ξ ξ V V (Q (Q (S,Q l (S, qd g (S,Q (q (S,Q ξ 0 [R (Q (Q λ (Q (S,Q d(q (S,Q d λ ξ (S,Q R (Q λ (Q λ (3.34 (S,Q] Fgua 3.3 Cotoo ula aesdo a u ato da plaa Os ltes das tegas sobe - dadas a equação (3.34, po defção, epeseta o valo ppal de CAUCHY das esas, ofoe PAIVA(989. Ass,
57 48 e l q (S, Q(Q (S,Q (Q (S,Q (Q d (Q 0 s s q (S, Q(Q (S,Q (Q s (S,Q (Q d(q s (3.35 l 0 V V (Q (Q (S,Q (S,Q (Q (Q (S,Q d(q (S,Q d(q (3.36 eseve ada: Cosdeado-se agoa as tegas sobe o otoo aesdo ξ, pode-se l ξ 0 ξ φ( ξd ξ l ξ 0 ξ q (S, Q(Q (S,Q (Q s (S,Q (Q d s (3.37 ξ Assue-se que as desdades (Q, (Q/ e (Q/s satsfaze à odção de Holde, o u epoete postvo, segudo PAIVA (987 oo segue: (Q-(S α (S,Q /(Q-/(S α (S,Q /s(q-/s(s 3 α3 (S,Q ode, 0 < α,,, 3 e 3 são ostates
58 49 Pode-se etão eseve a tegal da equação (3.37 oo: lξ 0 φ( ξd ξ lξ 0 q (S, Q[(Q (S] (S, Q[ (Q (S] ξ ξ s (S, Q[ (Q (S] dξ lξ 0 ξ q (S, Q(Sd s s ξ lξ 0 (S, Q (Sd ξ lξ 0 ξ s (S, Q (Sd ξ ξ s (3.38 ode a pea tegal do lado deto desapaeeá quado ξ 0. Etão a tegal sobe o otoo ξ passa a se esta oo: l ξ 0 ξ φ( ξd l ξ ξ 0 ξ q (S, Q(S (S,Q (S s (S,Q (S dξ s (3.39 Pode-se eseve ada, a pat da Fgua 3.3: (S (Sse( θ γ (S os( θ γ u (3.40.a (S s (S os( θ γ (Sse( θ γ u (3.40.b ode, θ : âgulo ete os vetoes e ; γ : âgulo ete os vetoes e ;
59 50 Aplado-se as epessões (3.40 e (.68 à equação (3.39 esulta: l ξ 0 l l ξ 0 ξ 0 ξ φ( ξd ξ ξ ξ l ξ 0 ξ [ (.](Sd πξ ξ { [( νlξ ( ν(. ν][ (Sse( θ γ (Sos( θ γ]} d 4π u ( ν { (.(s.[ (Sos( θ γ (Sse( θ γ]} dξ 4π u ξ (3.4 Da Fgua 3.3 pode-se deduz que: (. (3.4.a (s. 0 (3.4.b d ξ ξ dθ (3.4. Desta foa, toduzdo-se as odções dadas as epessões (3.4 à equação (3.4, te-se: l ξ 0 l ξ 0 ξ φ( ξd πβ 0 ξ { πβ l ξ 0 (S [ ] ξdθ 0 πξ [( ν l ξ ][ (S se( θ γ (S os( θ γ]} ξdθ 4π u e ada, (3.43 l ξ 0 [ (. ](Sd ξ πξ ξ (π β π (S (3.44
60 5 Os deas ltes sobe ξ, ludo-se as paelas oespodetes às eações de ato, se aula, de ode a equação (3.34 esulta: K(S(S N q V R (S, Q(Q (Q (Q (S,Q (S,Q (S,Q (Q (Q g g(q (S,Q d(q (S, qd s g (S,Q (Q d(q s (q ode, (3.45 β K(S π (3.46 Paa u poto S ão peteete a u ato da plaa a ostate K(S esulta: K(S / (3.47
61 5 Esevedo-se agoa a equação tegal (3.3 da devada deoal (S/ paa o poto S da Fgua 3.3, te-se: (q d (S,q g(q ] (S,Q (Q R (S,Q (Q [R (S,Q (Q R (Q d (S,Q (Q (S,Q (Q V (Q d (S,Q (Q (S,Q (Q V (Q d (Q s (S,Q (Q (S,Q (Q (S,Q q (Q d (Q s (S,Q (Q (S,Q (Q (S,Q q (S g N s s g λ λ λ λ ξ ξ ξ ξ (3.48 No lte, paa ξ tededo a zeo, o poto S petee ao otoo. Ass, a equação (3.48 esulta:
62 53 (q d (S,q g(q ] (S,Q (Q R (S,Q (Q [R l (S,Q (Q R (Q d (S,Q (Q (S,Q (Q V l (Q d (S,Q (Q (S,Q (Q V l (Q d (Q s (S,Q (Q (S,Q (Q (S,Q q l (Q d (Q s (S,Q (Q (S,Q (Q (S,Q q l (S g 0 N 0 0 s 0 s 0 g λ λ λ λ ξ ξ ξ ξ ξ ξ ξ (3.49 Os ltes das tegas sobe - são os valoes ppas das tegas sobe. Realzado-se u desloaeto vetal de opo ígdo o a plaa gual a -(S, pode-se ela as sguladades que apaee a equação (3.49 quado ξ 0. Ass a equação (3.49 esulta: (q d (S,q g(q ] (S,Q (Q R (S,Q (Q [R l (S,Q (Q R (Q d (S,Q (Q (S,Q (Q V l (Q d (S,Q (Q (S,Q (Q V (Q d (Q s (S,Q (Q (S,Q (S] [(Q (S,Q q l (Q d (Q s (S,Q (Q (S,Q (S] [(Q (S,Q q (S g 0 N 0 s 0 s g λ λ λ λ ξ ξ ξ ξ ξ ξ ξ (3.50
63 54 A tegal sobe ξ pode se esta oo: l ξ 0 l ξ 0 ξ φ( ξd ξ (S,Q l ξ 0 s(s,q [ (Q (S] d s s ξ ξ (Sd ξ l q(s,q [(Q (S] ξ ξ 0 ξ (S,Q s(s,q (Sd s ξ [ (Q (S] (3.5 Assudo-se que as desdades (Q/ e (Q/s satsfaze à odção de Holde, ada segudo PAIVA (987, o u epoete postvo, pode-se eseve a tegal da equação (3.5 oo: l ξ 0 l ξ 0 ξ q (S,Q φ( ξd ξ lξ 0 [(Q (S]d ξ ξ (S,Q s (S,Q (Sd ξ lξ 0 ξ (Sd ξ ξ s (3.5 Cosdeado-se a Fgua 3.4,ode são ostados os potos S e Q e seus desloaetos, quado ξ 0 pode-se eseve: (Q (S ξ (S (3.53 Aplado-se a epessão (3.53 à equação (3.5 te-se: l ξ 0 l ξ 0 ξ q (S,Q φ( ξdξ lξ 0 ξ (Sd ξ ξ (S,Q s (S,Q (Sd ξ lξ 0 ξ (Sd ξ ξ s (3.54
64 55 Fgua 3.4 sstea de oodeadas efeetes aos potos ateo e posteo aos atos λ - e λ Itoduzdo-se à equação (3.54 as epessões das soluções fudaetas (.80 a (.8, obté-se: l ξ 0 l ξ 0 φ( ξd ξ lξ 0 ξ ξ πξ ξ ξ ( ν(. (Sd l 0 ξ 4πξ [(. (. ] ξ (Sd ξ ( ν (.s (Sd 4πξ s (3.55 ξ ξ Agupado-se os teos efeetes a (S/, osdeado-se que (. (., te-se: l ξ 0 l ξ 0 φ( ξd ξ lξ 0 ξ πξ ( ν ξ (.s (Sd ξ 4πξ s ξ [ (. ] ( ν(. (Sd 4πξ (3.56 ξ
65 56 ou ada, l ξ 0 l ξ 0 ξ (3 ν φ( ξd ξ lξ 0 (. (Sd ξ 4πξ ( ν ξ (.s (Sd ξ 4πξ s ξ (3.57 Cosdeado-se as epessões (3.40, (3.4 e ada: te-se: (. se( θ γ (.s os( θ γ l ξ 0 l l ξ 0 ξ 0 ξ φ( ξd πβ 0 πβ 0 ξ (3 ν [ ]se( θ γ[ (Sse( θ γ (Sos( θ γ] ξdθ 4πξ u ( ν { os( θ γ[ (Sos( θ γ (Sse( θ γ]} ξdθ 4πξ u (3.58 ode, γ : âgulo ete os ssteas de oodeadas (, s e (, u, ofoe osta a Fgua 3.4. l Reaajado-se os teos teos às tegas, esulta: ξ 0 πβ 0 πβ 0 ξ φ( ξd ξ (3 ν [ ][ (Sse ( θ γ (Sse( θ γos( θ γ]d θ 4π u ( ν { [ (Sos ( θ γ (Sse( θ γos( θ γ]}d θ 4π u
66 57 (3.59 ou ada: l ξ 0 ξ 4 ( ν 4π 4 4 φ( ξd (3 ν 4π 4 [ os ( γ β os γ] [ 4π β se ( γ β se γ] [ os ( γ β os γ] ξ [ 4π β se ( γ β se γ] (S u (S u (S (S (3.60 Reagupado-se os teos efeetes às devadas dos desloaetos tasvesas, esulta: l ξ 0 ξ ( ν 8π φ( ξd ξ (π β π [ osγ os( γ β ] ( ν 8π (S u [ seγ se( γ β ] (S (3.6 Os deas ltes depedetes de ξ da equação (3.50 são ulos. Após as substtuções fetas a equação (3.50 obté-se a epessão da devada da equação tegal e u ato do otoo:
67 58 K (S (S K (S (S u N s q (S,Q (S,Q s(s,q (Q (Q (Q d (Q s s s s * * (S,Q V (Q (Q (S,Q d (Q s s * (S,Q (S,q R(Q g(q d g(q g s s s (3.6 o, β π (S π υ K 8 [ se γ se ( γ β ] (3.63 (S [ os γ os ( γ β ] υ 8π K (3.64 ode, γ : âgulo ete os ssteas de oodeadas (,s e (,u Idado-se po K(S a segute epessão: K(S β ( ν π 8π K (S (S K (S (S u ( ν 8π [ seγ se( γβ ] (S [ osγ os( γβ ] (S u (3.65 Adtdo-se que a oodeada oda o a deção oal, ateo ao ato, e γ0, ofoe a fgua 3.4, obté-se:
68 59 K(S β ν se β π 8π ν (S [ os β 8π ] (S s (3.66.a e paa s, ateo ao ato, e γπ/: K(S β ν se β π 8π ν (S [ os β 8π ] (S s (3.66.b Adtdo-se agoa que a oodeada oda o a deção oal, posteo ao ato, e γπ-β, obté-se: K(S β ν se β π 8π ν (S [ os β 8π ] (S s (3.67.a e paa s, posteo ao ato, e γ3π/-β : K(S β ν se β π 8π ν (S [ os β 8π ] s (S (3.67.b
69 Itegas de doío paa o aegaeto As tegas de doío das equações 3.3, 3.3, 3.46 e 3.5 seão tasfoadas e tegas sobe o otoo da egão aegada g. As tegas do doío são: g (q (s,qd g(q (3.68.a g ode, g (s,q (q d g(q (3.68.b g (l / 8πD (3.69.a l ϕ 4πD os (3.69.b Fgua 3.5 Regão de aegaeto g Cosdeado-se a Fgua 3.5 que osta a egão aegada g o otoo g, ode adte-se a aga g vaado leaete e seu doío. Co sto pode-se eseve, e elação ao sstea de oodeadas (,:
70 6 g(q A (q B (q C ( , tê-se: E elação ao sstea de oodeadas (,, de oge e s (Fgua (q (s (q (3.7.a (q (s (q (3.7.b Reesevedo-se a equação (3.70 te-se: g(q A(s B(s C A (q B (q g(s A (q B (q (3.7 ode, g(s : valo da aga g o poto s. Substtudo-se a equação 3.7, ealzada a tasfoação paa oodeadas polaes, a equação 3.68.a, obté-se: g g(q (s, qd g (q g [ g(s A os θ B se θ] (s, qd (q g (3.73 Substtudo-se a equação (3.69.a a equação (3.73, lebado-se que g(s é ua ostate e d g d dθ (Fgua 3.5, te-se: g 8πD g(q θ 0 R (s, qd g g(s (q 8πD (A os θ Bse θ 4 θ 0 R 3 (l / d dθ (l / d dθ (3.74 Fazedo-se a tegação e, o o âgulo θ ostate,
71 6 g 40πD g(q θ R 5 (s, qd g g(s (q 3πD (A os θ Bse θ(l R 0,7dθ θ R 4 (l R 3 / 4dθ (3.75 Da Fgua 3.5 pode-se eseve: d g os β Rdθ (3.76.a ou, d d g osβ R θ (3.76.b Substtudo-se a equação (3.76 a equação (3.75 obté-se a tegal de doío, tasfoada ua tegal sobe o otoo do aegaeto g : g 40πD g(q g R (s, qd 4 g g(s (q 3πD (A os θ Bse θ(l R 0,7 osβd g R 3 (l R 3 / 4 os βd (3.77 Aalogaete, paa a tegal de doío epessa a equação (3.68.b: g g g(q g R 6πD g (s, qd 3 g g(s (q πd (A os θ Bse θ(l R 0,5 os ϕosβd g R (l R / 3 os ϕosβd g (3.78 g
72 4. MÉTODO DOS ELEMENTOS DE CONTORNO : IMPLEMENTAÇÃO NUMÉRICA 4.. Itodução Neste apítulo seá apesetada a solução uéa das equações tegas obtdas o apítulo ateo dos desloaetos tasvesas e de suas devadas deoas, elaoados aos desloaetos e esfoços o otoo. A tasfoação dessas equações tegas e equações algébas paa a solução uéa é feta utlzado-se o Método dos Eleetos de Cotoo. Neste étodo dvde-se o otoo e segetos, haados eleetos de otoo, ode as vaáves odas oespodetes, os desloaetos, / e /s e os esfoços V e, são apoados po fuções tepoladoas. As equações algébas esultates dessa tasfoação, estas paa todos os potos do otoo, foa u sstea de equações leaes. O sstea é esolvdo após a posção das odções de otoo paa ada poblea, podedose obte posteoete valoes de desloaetos e esfoços paa potos do doío. Ada este apítulo são apesetados os eleetos utlzados o pogaa paa apoação da geoeta, poedetos utlzados e asos de desotudade da oal ou das odções de otoo e a aplação da eação V potual. São ada oetadas as tegações uéas utlzadas e ada eleeto, leaes e úbas. 4.. Dsetzação das equações tegas A dsetzação do otoo de ua plaa de foa qualque deve se feta de odo que o otoo eal seja elho epesetado. Paa sto adota-se eleetos de geoeta eta ou uva.
73 64 A Fgua 4. osta ua plaa ujo otoo é dvddo e eleetos de otoo j, uja geoeta é defda pelos potos odas oespodetes. As vaáves de otoo são apoadas po fuções poloas tepoladoas, tabé defdas paa os potos odas oespodetes a ada eleeto. Fgua 4. Dsetzação do otoo da plaa. Os eleetos são dtos otíuos pela a otudade das vaáves ete eleetos adjaetes. E asos de desotudade da oal ao otoo ou de esfoços seão utlzados ós duplos, de guas oodeadas, ode ada ó assuá valoes odas dfeetes a desotudade. Esta stuação ooe, po eeplo, e u ato de plaa, ode há ua udaça busa da deção oal ao otoo, ou ada odções de otoo de desloaetos ou de esfoços dfeetes, oo u lado da plaa egastado e outo splesete apoado, ou lve. A Fgua 4. osta o ó duplo e u ato de plaa, ada ó peteedo a u eleeto adjaete a este ato, o deções oas ao otoo dsttas. Fgua 4. Nó duplo e ato da plaa Apoação das vaáves do poblea
74 65 Na aplação uéa do M.E.C. utlza-se a dsetzação do otoo da plaa e segetos, deoados eleetos de otoo, e ujo doío são utlzadas fuções apoadoas paa as vaáves evolvdas, desloaetos e esfoços. U poblea suge a foulação usual do M.E.C. a assoação de plaas delgadas aalsadas pelo étodo o eleetos estutuas leaes (vgas e plaes. Na foulação alteatva do M.E.C. paa aálse de plaas delgadas utlzado-se tês paâetos odas, o desloaeto tasvesal e suas devadas / e /s, pete a lgação opatível o os eleetos estutuas leaes aalsados po étodos uéos dfeetes. Na foulação lássa do étodo, utlza-se fuções tepoladoas leaes ou quadátas paa apoação das vaáves os eleetos de otoo. Na foulação apesetada este tabalho, os desloaetos seão apoados po fuções apoadoas úbas ϕ (ξ, as oodeadas dos potos odas, o esfoço e a devada a deção oal do desloaeto / po fuções apoadoas leaes φ (ξ e a foça otate equvalete V seá adtda oo oetada os potos odas, apesetado elhoas as oslações de seus esultados uéos e algus asos de vulação, ofoe deostado e PAIVA (99 e e OLIVEIRA NETO (99. Fgua 4.3 Coodeada adesoal ξ o eleeto de otoo lea. Cosdeado-se dos potos odas po eleeto de otoo, as fuções apoadoas leaes são as segutes:
75 66 φ (ξ ½ (-ξ (4. φ (ξ ½ (ξ (4. ode, dξ d j / (L/ opeto L. ξ : oodeada adesoal o oge o eto do eleeto de otoo lea de Desta foa, as oodeadas dos potos odas, a devada deoal do desloaeto a deção oal ao otoo / e o oeto fleto seão epesetados oo: (ξ φ (ξ φ (ξ (4.3 ( ξ φ (ξ φ (ξ (4.4 (ξ φ (ξ φ (ξ (4.5 Já as fuções apoadoas úbas ϕ (ξ são obtdas e fução dos dos paâetos odas efeetes aos dos ós de etedade do eleeto de otoo: ϕ(ξ α 0 α ξ α ξ α 3 ξ 3 (4.6 Co sto, o desloaeto e sua devada deoal a deção tageal ao otoo /s seão epesetados pelas epessões: (ξ ϕ (ξ ϕ (ξ s ϕ 3 (ξ ϕ 4 (ξ s (4.7
76 67 ( ξ s ϕ (ξ ϕ (ξ s ϕ 3 (ξ ϕ 4 (ξ s (4.8 Fgua 4.4 Fuções apoadoas úbas ϕ(ξ As epessões das fuções ϕ (ξ e ϕ (ξ são: ϕ (ξ ( - 3ξ ξ 3 /4 ϕ (ξ (-3 3ξ /4 ϕ (ξ ( - ξ - ξ ξ 3 L/8 ϕ (ξ (- - ξ 3ξ L/8 ϕ 3 (ξ ( 3ξ - ξ 3 /4 ϕ 3 (ξ (3-3ξ /4 ϕ 4 (ξ (- - ξ ξ ξ 3 L/8 ϕ 4 (ξ (- ξ 3ξ L/ Tasfoação das equações tegas e equações algébas
77 68 As equações tegas de plaas obtdas o aptulo ateo apeseta tegas sobe o otoo e as apoações da geoeta e vaáves sobe os eleetos que o dsetza são fuções da vaável adesoal ξ, uja tasfoação de oodeadas é dada pelo deteate jaobao J da equação (4.9. J L/ (4.9 ode, L : opeto do eleeto de otoo de geoeta lea. Reesevedo-se as equações tegas (3.45 e (3.6, levado-se e ota a dsetzação do otoo da plaa e eleetos e as fuções apoadoas das vaáves apesetadas sobe os esos eleetos, esulta a segute equação: K(SU(S. [J].P N g R (Q.U g(q.u * Ne l * (S,Q. [J].U (S,q. d * g (S,Q. Φ Ne l (q (Q.U(Q.d * (S,Q. Φ l (Q.P(Q. d. l ode, N e : úeo de eleetos de otoo; (4.0 N : úeo de atos da plaa; β / π 0 0 KS ( 0 K( S K( S 0 K( S K( S U T (S (S { (S (S u }
78 69 P T (Q { (Q (Q } U T (Q (Q { (Q (Q s (Q (Q (Q s } R(Q { V (Q } Φ ϕ 0 ϕ ϕ3 0 ϕ 4 ( Q.. 0 φ 0 0 φ 0 ϕ 0 ϕ ϕ3 0 ϕ4 [ ] Φ ( Q. φ φ P * * * * q ( S, Q ( S, Q s( S, Q * q ( S, Q ( S, Q. S Q S Q * q ( S, Q u u S Q u S Q ( * * (, ( s(, ( * * (, ( s(, * (S,Q U* T (S,Q { * (S,Q * (S,Q } u U* T (S,q { * (S,q (S,q * * } (S,q u U * T (S,Q { * (S,Q * (S,Q * (S,Q } u
79 70 Esevedo-se as equações tegas dos desloaetos (3.45 e de suas devadas as deções oal e tageal (3.6, paa todos os ós do otoo, obté-se o segute sstea lea: ode, [ H ] [ G] V {p} T (4. {( ( ( ( ( (...( ( ( } s s s T V {(V.(.(V.(...(V.( } sedo, [H] e [G] : atzes esultates das tegações ealzadas sobe os eleetos de otoo, e ujos tegados estão as soluções fudaetas de plaas; ode 3N p 3N p e 3N p N p, espetvaete; {p} : veto de aegaetos ohedos a que a plaa está subetda, esultate da tegação sobe a egão aegada g ; ode 3N p. N p : úeo de potos odas o otoo; Co as odções de otoo postas po u poblea o ua plaa e equlíbo, seão ohedas, paa ada ó do otoo, o ío duas das o vaáves odas equato as deas seão ógtas. Levado-se as vaáves ohedas paa o segudo ebo da equação (4., esta pode se eesta oo: ode, [ ]{X} {B} A (4. {X} : veto de ógtas do poblea.
80 7 Após a esolução do sstea são ohedos todos os valoes odas, podedo-se obte os desloaetos e uvatuas dos potos teos aplado-se as equações tegas (3.3 e (3.3. A pat dos desloaetos e uvatuas dos potos teos pode-se alula os oetos fletoes e volvetes e foça otate estes potos, oo seá vsto posteoete Desloaetos paa potos teos Caluladas as ógtas do otoo após a esolução do sstea (4. pode-se obte os desloaetos (s, as devadas deoas / e as uvatuas e elação a ua deção, qualque, paa potos do doío. Paa sto utlza-se as equações (3.45 e (3.6, espetvaete, apladas a todos os potos teos. Desta foa obté-se a segute equação atal, seelhate à já desta paa potos do otoo (4.: {U(s} [H ] {U} [G ] {P} {p } (4.3 ode, sedo, {U(s} T { (/ (/u... Np (/ Np (/u Np } N p : úeo de potos teos; (4.4 [H ] e [G ] : atzes seelhates a [H] e [G],obtdas paa potos teos; {U} e {P} : vetoes dos desloaetos e dos esfoços dos ós do otoo, espetvaete; {p } : veto esultate da tegação sobe a egão aegada g paa os potos teos, seelhate ao veto {p} da equação (4.0.
81 Esfoços paa potos teos Os oetos fletoes e volvetes e a foça otate os potos teos são dados pelas equações (4.5, epessas a foa dal: M j D νδ j l l ( ν j (4.5.a Q 3 D l l (4.5.b o,,j,l, Substtudo-se a equação (3.3 da equação tegal do desloaeto de u poto do doío da plaa as equações (4.5, e ealzado-se as tegações eessáas, obtê-se as equações tegas paa os oetos e foça otate dos potos o doío da plaa: M j N (s V R (Q (Q q j j j (s, Q(Q (s,q (S,Q g (Q g(q j j (s,q (Q j (s,q d(q (S, qd g (q s j (s,q (Q d(q s (4.6 ode, Q (s N V R q (Q (Q (s, Q(Q (s,q (S,Q g (Q g(q (s,q (Q (s,q d(q (S, qd g (q s (s,q (Q d(q s (4.7 * * * q q q j (q, P D νδ j (q, P ( ν (q, P (4.8.a l l j
6. ANÁLISE MODAL DE SISTEMAS COM N GL
 VIBRAÇÕES EÂNIAS - APÍULO 6 - ANÁLISE ODAL N GL 78 6. ANÁLISE ODAL DE SISEAS O N GL Neste aítulo seão aalsadas as aateístas odas, feüêas atuas e odos de vba de ssteas ão aotedos o gaus de lbedade. Seão
VIBRAÇÕES EÂNIAS - APÍULO 6 - ANÁLISE ODAL N GL 78 6. ANÁLISE ODAL DE SISEAS O N GL Neste aítulo seão aalsadas as aateístas odas, feüêas atuas e odos de vba de ssteas ão aotedos o gaus de lbedade. Seão
Resoluções dos exercícios propostos
 os fudametos da físa Udade E Capítulo efação lumosa esoluções dos eeíos popostos P.85 Como, temos: 8 0 0 8,5 P.86 De, em: 0 8,5 0 8 m/s P.87 elodade da luz a plaa de do oespode a 75% da elodade da luz
os fudametos da físa Udade E Capítulo efação lumosa esoluções dos eeíos popostos P.85 Como, temos: 8 0 0 8,5 P.86 De, em: 0 8,5 0 8 m/s P.87 elodade da luz a plaa de do oespode a 75% da elodade da luz
Aluno(a): Professor: Chiquinho
 Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Sobre a classe de diferenciabilidade de quocientes de polinômios homogêneos.
 Uvesdade Regoal do Ca - URCA CADERNO DE CULTURA E CIÊNCIA VOLUME Nº - 008 IN 980-586 obe a classe de dfeecabldade de quocetes de polômos homogêeos About the Dffeetablty Class of the Quotet of Homogeeous
Uvesdade Regoal do Ca - URCA CADERNO DE CULTURA E CIÊNCIA VOLUME Nº - 008 IN 980-586 obe a classe de dfeecabldade de quocetes de polômos homogêeos About the Dffeetablty Class of the Quotet of Homogeeous
Para duas variáveis aleatórias X e Y define-se Função Distribuição Cumulativa CDF F XY (x,y)
 Vaáves Aleatóas (contnuação) Po. Waldec Peella Dstbução Conunta: po: Paa duas vaáves aleatóas e dene-se Função Dstbução Cuulatva CDF F (,y) P ( e y ) = F (,y ) e a Função Densdade de Pobabldade de Pobabldade
Vaáves Aleatóas (contnuação) Po. Waldec Peella Dstbução Conunta: po: Paa duas vaáves aleatóas e dene-se Função Dstbução Cuulatva CDF F (,y) P ( e y ) = F (,y ) e a Função Densdade de Pobabldade de Pobabldade
Cálculo Numérico Interpolação Polinomial Ajuste de Curvas (Parte II)
 Cálulo Nuéro Iterpolação Poloal Ajuste de Curvas (Parte II) Pro Jore Cavalat joreavalat@uvasedubr MATERIAL ADAPTADO DOS SLIDES DA DISCIPLINA CÁLCULO NUMÉRICO DA UFCG - wwwdsuedubr/~u/ Ajuste de Curvas
Cálulo Nuéro Iterpolação Poloal Ajuste de Curvas (Parte II) Pro Jore Cavalat joreavalat@uvasedubr MATERIAL ADAPTADO DOS SLIDES DA DISCIPLINA CÁLCULO NUMÉRICO DA UFCG - wwwdsuedubr/~u/ Ajuste de Curvas
Problemas de Valor de Contorno para Equações Diferenciais Ordinárias
 EQE-358 MÉTODOS NUMÉICOS EM ENGENHI QUÍMIC OFS. EVISTO E GIMIO Caítlo 9 oblema de Valo de Cotoo aa Eqaçõe Dfeea Odáa Codee o eemlo ltatvo da dfão-eação em ma atíla atalíta eféa e ooa: Balaço de maa: etado
EQE-358 MÉTODOS NUMÉICOS EM ENGENHI QUÍMIC OFS. EVISTO E GIMIO Caítlo 9 oblema de Valo de Cotoo aa Eqaçõe Dfeea Odáa Codee o eemlo ltatvo da dfão-eação em ma atíla atalíta eféa e ooa: Balaço de maa: etado
Introdução à Decomposição de Dantzig Wolfe
 Itrodução à Deoposção de Datzg Wolfe PNV-5765 Probleas de Prograação Mateáta Aplados ao Plaeaeto de Ssteas de Trasportes Maríto Prof. Dr. Adré Bergste Medes Bblografa Utlzada WILLIAMS, H.P. The forulato
Itrodução à Deoposção de Datzg Wolfe PNV-5765 Probleas de Prograação Mateáta Aplados ao Plaeaeto de Ssteas de Trasportes Maríto Prof. Dr. Adré Bergste Medes Bblografa Utlzada WILLIAMS, H.P. The forulato
16 - PROBLEMA DO TRANSPORTE
 Prof. Volr Wlhel UFPR TP05 Pesqusa Operacoal 6 - PROBLEMA DO TRANSPORTE Vsa zar o custo total do trasporte ecessáro para abastecer cetros cosudores (destos) a partr de cetros forecedores (orges) a, a,...,
Prof. Volr Wlhel UFPR TP05 Pesqusa Operacoal 6 - PROBLEMA DO TRANSPORTE Vsa zar o custo total do trasporte ecessáro para abastecer cetros cosudores (destos) a partr de cetros forecedores (orges) a, a,...,
MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R 3
 MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R Modelg of ceteg eos o the o the thee-dmesoal space (R ). JAIR MENDES MARQUES Uvesdade Tuut do Paaá Rua Macelo Champagat,55 CEP 87-5 Cutba PR ja.maques@utp.b
MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R Modelg of ceteg eos o the o the thee-dmesoal space (R ). JAIR MENDES MARQUES Uvesdade Tuut do Paaá Rua Macelo Champagat,55 CEP 87-5 Cutba PR ja.maques@utp.b
Aula 3 Trabalho e Energia - Bioenergética
 Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
2 O Método Híbrido dos Elementos de Contorno e sua formulação simplificada aplicados a problemas estáticos
 O Método Hído dos Eleetos de Cotoo e sa folação slfcada alcados a oleas estátcos Desevolve-se este caítlo a folação do étodo hído dos eleetos de cotoo e taé de sa folação slfcada alcados a oleas da elastostátca
O Método Hído dos Eleetos de Cotoo e sa folação slfcada alcados a oleas estátcos Desevolve-se este caítlo a folação do étodo hído dos eleetos de cotoo e taé de sa folação slfcada alcados a oleas da elastostátca
Prática VIII CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO DE UM SISTEMA DE DUAS ESFERAS
 Pátca VIII CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO DE UM SISTEMA DE DUAS ESERAS OBJETIVO: Vefca expeetalete a cosevação a quatae e oveto lea e u sstea solao. INTRODUÇÃO TEÓRICA A segua le e Newto às vezes
Pátca VIII CONSERVAÇÃO DA QUANTIDADE DE MOVIMENTO DE UM SISTEMA DE DUAS ESERAS OBJETIVO: Vefca expeetalete a cosevação a quatae e oveto lea e u sstea solao. INTRODUÇÃO TEÓRICA A segua le e Newto às vezes
SUBSTITUIÇÕES ENVOLVENDO NÚMEROS COMPLEXOS Diego Veloso Uchôa
 Nível Avaçado SUBSTITUIÇÕES ENVOLVENDO NÚMEROS COMPLEXOS Dego Veloso Uchôa É bastate útl e probleas de olpíada ode teos gualdades ou quereos ecotrar u valor de u soatóro fazeros substtuções por úeros coplexos
Nível Avaçado SUBSTITUIÇÕES ENVOLVENDO NÚMEROS COMPLEXOS Dego Veloso Uchôa É bastate útl e probleas de olpíada ode teos gualdades ou quereos ecotrar u valor de u soatóro fazeros substtuções por úeros coplexos
CAPÍTULO III MÉTODOS DE RUNGE-KUTTA
 PMR 40 Mecâca Coputacoal CAPÍTULO III MÉTODOS DE RUNGE-KUTTA São étodos de passo sples requere apeas dervadas de prera orde e pode forecer aproxações precsas co erros de trucaeto da orde de, 3, 4, etc.
PMR 40 Mecâca Coputacoal CAPÍTULO III MÉTODOS DE RUNGE-KUTTA São étodos de passo sples requere apeas dervadas de prera orde e pode forecer aproxações precsas co erros de trucaeto da orde de, 3, 4, etc.
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS CHARLES JASTER DE OLIVEIRA
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS CHARLES JASTER DE OLIVEIRA ANÁLISE DA INTERAÇÃO PLACA-VIGA VIA MÉTODO DOS ELEMENTOS DE CONTORNO SÃO CARLOS 2012 CHARLES JASTER DE OLIVEIRA
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS CHARLES JASTER DE OLIVEIRA ANÁLISE DA INTERAÇÃO PLACA-VIGA VIA MÉTODO DOS ELEMENTOS DE CONTORNO SÃO CARLOS 2012 CHARLES JASTER DE OLIVEIRA
APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO. Djalma M. Falcão COPPE/UFRJ
 GPL/026 2 a 26 de Outubo de 200 Campas - São Paulo - Basl GRUPO VII PLANEJAMENTO DE SISTEMAS ELÉTRICOS APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO Yu S.B. Wllmesdof
GPL/026 2 a 26 de Outubo de 200 Campas - São Paulo - Basl GRUPO VII PLANEJAMENTO DE SISTEMAS ELÉTRICOS APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO Yu S.B. Wllmesdof
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
DINÂMICA DOS SISTEMAS DE PARTÍCULAS E DOS CORPOS RÍGIDOS
 DNÂCA DS SSTEAS DE ARTÍCUAS E DS CRS RÍDS. Cabta Neves Setembo de 005 Ídce ometo lea de um sstema de atículas... 3 Teoema do movmeto do ceto de massa... 3 3 cío da Cosevação do ometo ea... 6 4 cío do Tabalho-Eega
DNÂCA DS SSTEAS DE ARTÍCUAS E DS CRS RÍDS. Cabta Neves Setembo de 005 Ídce ometo lea de um sstema de atículas... 3 Teoema do movmeto do ceto de massa... 3 3 cío da Cosevação do ometo ea... 6 4 cío do Tabalho-Eega
CAPÍTULO III. Aproximação de funções pelo método dos Mínimos Quadrados
 Métodos Nuércos CAPÍULO III C. Balsa & A. Satos Aproxação de fuções pelo étodo dos Míos Quadrados. Algus cocetos fudaetas de Álgebra Lear Relebraos esta secção algus cocetos portates da álgebra Lear que
Métodos Nuércos CAPÍULO III C. Balsa & A. Satos Aproxação de fuções pelo étodo dos Míos Quadrados. Algus cocetos fudaetas de Álgebra Lear Relebraos esta secção algus cocetos portates da álgebra Lear que
Prof. Anderson Coser Gaudio Departamento de Física Centro de Ciências Exatas Universidade Federal do Espírito Santo
 POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
4 REPRESENTAÇÃO E/S NO DOMÍNIO TRANSFORMADO (funções de transferência)
 4 REPRESENTAÇÃO E/S NO DOMÍNIO TRANSFORMADO (fuções de trasferêa) 4. Trasforada de Laplae É u operador lear, que opera sobre fuções de varável otíua postva, defdo por: L f(t) = f(s) = f(t) e -st dt Nota:
4 REPRESENTAÇÃO E/S NO DOMÍNIO TRANSFORMADO (fuções de trasferêa) 4. Trasforada de Laplae É u operador lear, que opera sobre fuções de varável otíua postva, defdo por: L f(t) = f(s) = f(t) e -st dt Nota:
Capítulo 2. Aproximações de Funções
 EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo Aproações de Fuções Há bascaete dos tpos de probleas de aproações: ) ecotrar ua fução as sples, coo u polôo, para aproar
EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo Aproações de Fuções Há bascaete dos tpos de probleas de aproações: ) ecotrar ua fução as sples, coo u polôo, para aproar
Consideremos a fórmula que nos dá a área de um triângulo: = 2
 6. Cálculo Derecal e IR 6.. Fução Real de Varáves Reas Cosdereos a órula que os dá a área de u trâulo: b h A( b h) Coo podeos vercar a área de u trâulo depede de duas varáves: base (b) e altura (h) Podeos
6. Cálculo Derecal e IR 6.. Fução Real de Varáves Reas Cosdereos a órula que os dá a área de u trâulo: b h A( b h) Coo podeos vercar a área de u trâulo depede de duas varáves: base (b) e altura (h) Podeos
3 O Método de Partículas MPS
 O Método de Patículas MPS 9 3 O Método de Patículas MPS O método MPS fo apesetado calmete po Koshzuka e Oka (1996). Este método, de atueza Lagageaa, fo deseoldo paa esole escoametos de fludos compessíes
O Método de Patículas MPS 9 3 O Método de Patículas MPS O método MPS fo apesetado calmete po Koshzuka e Oka (1996). Este método, de atueza Lagageaa, fo deseoldo paa esole escoametos de fludos compessíes
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Em ambos os casos, no entanto, teremos no ponto de incidência três ondas eletromagnéticas dadas pôr: ω (3.1-1) ω (3.1-2) m eio 1.
 3 REFLEXÃO E REFRAÇÃO INTRODUÇÃO Nese apíulo emos esuda dos mpoaes feômeos, eflexão e efação de odas eleomagéas a efae de sepaação de dos meos opamee dfeees. A pa deles vamos aalsa algus paâmeos físos
3 REFLEXÃO E REFRAÇÃO INTRODUÇÃO Nese apíulo emos esuda dos mpoaes feômeos, eflexão e efação de odas eleomagéas a efae de sepaação de dos meos opamee dfeees. A pa deles vamos aalsa algus paâmeos físos
Como primeiro exemplo de uma relação de recorrência, consideremos a seguinte situação:
 Relações de Recorrêcas - Notas de aula de CAP Prof. José Carlos Becceer. Ao 6. Ua Relação de Recorrêca ou Equação de Recorrêca defe ua fução por eo de ua epressão que clu ua ou as stâcas (eores) dela esa.
Relações de Recorrêcas - Notas de aula de CAP Prof. José Carlos Becceer. Ao 6. Ua Relação de Recorrêca ou Equação de Recorrêca defe ua fução por eo de ua epressão que clu ua ou as stâcas (eores) dela esa.
ANÁLISE DE MOVIMENTOS PERIÓDICOS EM SISTEMA BI- LINEAR COM FOLGA SIMÉTRICA
 UNIVERSIDDE FEDERL DO ESPÍRITO SNTO CENTRO TECNOLÓGICO PROGRM DE PÓS-GRDUÇÃO EM ENGENHRI MECÂNIC JOSÉ GUILHERME PELIÇÃO PNCIERI NÁLISE DE MOVIMENTOS PERIÓDICOS EM SISTEM I- LINER COM FOLG SIMÉTRIC VITÓRI
UNIVERSIDDE FEDERL DO ESPÍRITO SNTO CENTRO TECNOLÓGICO PROGRM DE PÓS-GRDUÇÃO EM ENGENHRI MECÂNIC JOSÉ GUILHERME PELIÇÃO PNCIERI NÁLISE DE MOVIMENTOS PERIÓDICOS EM SISTEM I- LINER COM FOLG SIMÉTRIC VITÓRI
Curso de Análise Matricial de Estruturas 1 II.6 FORMULAÇÃO DAS MATRIZES DE FLEXIBILIDADE E RIGIDEZ EM TERMOS DE ENERGIA
 Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
Física I. Aula 9 Rotação, momento inércia e torque
 Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
CAPÍTULO VIII DIFERENCIAIS DE ORDEM SUPERIOR FÓRMULA DE TAYLOR E APLICAÇÕES
 CAPÍTULO VIII DIFERENCIAIS DE ORDEM SUPERIOR FÓRMULA DE TAYLOR E APLICAÇÕES. Dferecas de orde superor Tratareos apeas o caso das fuções de A R e R sedo que o caso geral das fuções de A R e R se obté a
CAPÍTULO VIII DIFERENCIAIS DE ORDEM SUPERIOR FÓRMULA DE TAYLOR E APLICAÇÕES. Dferecas de orde superor Tratareos apeas o caso das fuções de A R e R sedo que o caso geral das fuções de A R e R se obté a
Capítulo 6 Corpo Rígido, Estática e Elasticidade
 Capítulo 6 Copo Rígdo, Estátca e Elastcdade 6. Noção de Copo Rígdo Estudamos já os movmetos de copos cujas dmesões eam despezáves face às meddas das suas tajectóas ou po coveêca e smplfcação, tomados como
Capítulo 6 Copo Rígdo, Estátca e Elastcdade 6. Noção de Copo Rígdo Estudamos já os movmetos de copos cujas dmesões eam despezáves face às meddas das suas tajectóas ou po coveêca e smplfcação, tomados como
Física Geral I - F Aula 13 Conservação do Momento Angular e Rolamento. 2 0 semestre, 2010
 Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
A Base Termodinâmica da Pressão Osmótica
 59087 Bofísca II FFCLRP P Pof. Atôo Roque Aula 7 A Base emodâmca da Pessão Osmótca Elemetos de emodâmca As les báscas da temodâmca dzem espeto à covesão de eega de uma foma em outa e à tasfeêca de eega
59087 Bofísca II FFCLRP P Pof. Atôo Roque Aula 7 A Base emodâmca da Pessão Osmótca Elemetos de emodâmca As les báscas da temodâmca dzem espeto à covesão de eega de uma foma em outa e à tasfeêca de eega
5 Aplicação do GFMM no BEM
 38 5 Apação do GFMM o BEM esse apítuo os desevovmetos apresetados o apítuo 4 são apados ao BEM pea expasão das souções fudametas utzadas as tegrações sobre os segmetos do otoro. É apresetada a formuação
38 5 Apação do GFMM o BEM esse apítuo os desevovmetos apresetados o apítuo 4 são apados ao BEM pea expasão das souções fudametas utzadas as tegrações sobre os segmetos do otoro. É apresetada a formuação
PROPAGAÇÃO E RADIAÇÃO DE ONDAS ELECTROMAGNÉTICAS (PROE) CONCEITOS FUNDAMENTAIS
 MC Ao Lectvo 6/7 º Semeste PROPAGAÇÃO RADIAÇÃO D ONDAS LCTROMAGNÉTICAS (PRO) CONCITOS FUNDAMNTAIS Custódo Pexeo Setembo 6 ste documeto fo cocebdo paa sev de gua as aulas teócas e apeas como tal deveá se
MC Ao Lectvo 6/7 º Semeste PROPAGAÇÃO RADIAÇÃO D ONDAS LCTROMAGNÉTICAS (PRO) CONCITOS FUNDAMNTAIS Custódo Pexeo Setembo 6 ste documeto fo cocebdo paa sev de gua as aulas teócas e apeas como tal deveá se
3- Autovalores e Autovetores.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
TICA. Sistemas Equivalentes de Forças MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA. Nona Edição CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
 CPÍTULO 3 Copos ECÂNIC VETORIL PR ENGENHEIROS: ESTÁTIC TIC Fednand P. Bee E. Russell Johnston, J. Notas de ula: J. Walt Ole Teas Tech Unvest Rígdos: Sstemas Equvalentes de Foças 2010 The cgaw-hll Companes,
CPÍTULO 3 Copos ECÂNIC VETORIL PR ENGENHEIROS: ESTÁTIC TIC Fednand P. Bee E. Russell Johnston, J. Notas de ula: J. Walt Ole Teas Tech Unvest Rígdos: Sstemas Equvalentes de Foças 2010 The cgaw-hll Companes,
15. Efeito de Alavanca
 Lgações Apaafusadas Pate I Pogama de Pós-Gaduação em Egehaa Cvl PGECI - Mestado Acadêmco Faculdade de Egehaa FEN/UERJ Dscpla: Lgações em Estutuas de Aço e Mstas Pofesso: Lucao Rodgues Oelas de Lma 5. Efeto
Lgações Apaafusadas Pate I Pogama de Pós-Gaduação em Egehaa Cvl PGECI - Mestado Acadêmco Faculdade de Egehaa FEN/UERJ Dscpla: Lgações em Estutuas de Aço e Mstas Pofesso: Lucao Rodgues Oelas de Lma 5. Efeto
Mecânica Técnica. Aula 5 Vetor Posição, Aplicações do Produto Escalar. Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
 ula 5 Veto Posição, plicações do Poduto Escala Pof. MSc. Luiz Eduado Mianda J. Rodigues Pof. MSc. Luiz Eduado Mianda J. Rodigues Tópicos bodados Nesta ula Vetoes Posição. Veto Foça Oientado ao Longo de
ula 5 Veto Posição, plicações do Poduto Escala Pof. MSc. Luiz Eduado Mianda J. Rodigues Pof. MSc. Luiz Eduado Mianda J. Rodigues Tópicos bodados Nesta ula Vetoes Posição. Veto Foça Oientado ao Longo de
Escola Básica e Secundária Dr. Ângelo Augusto da Silva
 Escola Básica e Secdáia D. Âgelo Agsto da Silva Teste de MATEMÁTICA A.º Ao Dação: 90 itos Maço/ 06 Noe N.º T: Classificação Pof. (Lís Abe).ª PARTE Paa cada a das segites qestões de escolha últipla, selecioe
Escola Básica e Secdáia D. Âgelo Agsto da Silva Teste de MATEMÁTICA A.º Ao Dação: 90 itos Maço/ 06 Noe N.º T: Classificação Pof. (Lís Abe).ª PARTE Paa cada a das segites qestões de escolha últipla, selecioe
Aplicação do Torque Residual para Satélites Artificiais Estabilizados por Rotação em Órbita Elíptica
 Aplicação do oque Residual paa Satélites Atificiais Estabilizados po Rotação e Óbita Elíptica Maia Cecília Zaadi, Robeta Veloso Gacia GRUPO DE DIÂMICA ORIAL E PLAEOLOGIA FEG Faculdade de Egehaia de Guaatiguetá
Aplicação do oque Residual paa Satélites Atificiais Estabilizados po Rotação e Óbita Elíptica Maia Cecília Zaadi, Robeta Veloso Gacia GRUPO DE DIÂMICA ORIAL E PLAEOLOGIA FEG Faculdade de Egehaia de Guaatiguetá
FEP2195 Física Geral e Experimental para a Engenharia I Gabarito da prova 2 14/05/2009
 FP95 Físia Geal e peiental paa a ngenhaia I Gabaito da pova 4/05/009 Ua bola de basquete (de assa M e ua bola de tênis (de assa são abandonadas do epouso a ua altua h do solo, onfoe ostado na figua. Os
FP95 Físia Geal e peiental paa a ngenhaia I Gabaito da pova 4/05/009 Ua bola de basquete (de assa M e ua bola de tênis (de assa são abandonadas do epouso a ua altua h do solo, onfoe ostado na figua. Os
Cinemática Direta. 4 o Engenharia de Controle e Automação FACIT / Prof. Maurílio J. Inácio
 Cnemáta Deta 4 o Engenhaa de Contole e Automação FACI / 9 Pof. Mauílo J. Ináo Cnemáta Deta Cnemáta do manpulado Cnemáta é êna que tata o movmento em ondea a foça que o auam. Na nemáta ão etudado: poçõe,
Cnemáta Deta 4 o Engenhaa de Contole e Automação FACI / 9 Pof. Mauílo J. Ináo Cnemáta Deta Cnemáta do manpulado Cnemáta é êna que tata o movmento em ondea a foça que o auam. Na nemáta ão etudado: poçõe,
Credenciada e Autorizada pelo MEC, Portaria n. o. 644 de 28 de março de 2001 Publicado no D.O.U. em 02/04/2001
 Ceecaa e Autozaa pelo MEC, Potaa. o. 644 e 8 e maço e 00 Publcao o D.O.U. em 0/04/00 ESTATÍSTICA Pelo Poesso Gealo Pacheco A Estatístca é uma pate a Matemátca Aplcaa que oece métoos paa coleta, ogazação,
Ceecaa e Autozaa pelo MEC, Potaa. o. 644 e 8 e maço e 00 Publcao o D.O.U. em 0/04/00 ESTATÍSTICA Pelo Poesso Gealo Pacheco A Estatístca é uma pate a Matemátca Aplcaa que oece métoos paa coleta, ogazação,
Operadores Lineares e Matrizes
 Operadores Lieares e Matrizes Ua Distição Fudaetal e Álgebra Liear Prof Carlos R Paiva Operadores Lieares e Matrizes Coeceos por apresetar a defiição de operador liear etre dois espaços lieares (ou vectoriais)
Operadores Lieares e Matrizes Ua Distição Fudaetal e Álgebra Liear Prof Carlos R Paiva Operadores Lieares e Matrizes Coeceos por apresetar a defiição de operador liear etre dois espaços lieares (ou vectoriais)
Ajuste de curvas por quadrados mínimos lineares
 juste de cuvs o quddos mímos lees Fele eodo de gu e Wdele Iocêco oe Júo Egeh de s o. Peíodo Pofesso: ode Josué Bezue Dscl: Geomet lítc e Álgeb e. Itodução Utlzmos este método qudo temos um dstbução de
juste de cuvs o quddos mímos lees Fele eodo de gu e Wdele Iocêco oe Júo Egeh de s o. Peíodo Pofesso: ode Josué Bezue Dscl: Geomet lítc e Álgeb e. Itodução Utlzmos este método qudo temos um dstbução de
Eletricidade e Magnetismo II Licenciatura: 1ª Aula (30/07/2012) Prof. Alvaro Vannucci. Revisão das Leis de Gauss, de Ampère e de Faraday
 Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
Apresenta-se em primeiro lugar um resumo da simbologia adoptada no estudo da quadratura de Gauss.
 CAÍTULO QUADRATURA DE GAUSS Mutos dos tegras que é eessáro alular o âmbto da aplação do Método dos Elemetos Ftos (MEF) ão são trvas,.e., ou a prmtva da ução tegrada ão exste expltamete, ou é demasado omplada
CAÍTULO QUADRATURA DE GAUSS Mutos dos tegras que é eessáro alular o âmbto da aplação do Método dos Elemetos Ftos (MEF) ão são trvas,.e., ou a prmtva da ução tegrada ão exste expltamete, ou é demasado omplada
EQUAÇÕES DINÂMICAS DE MOVIMENTO PARA CORPOS RÍGIDOS UTILIZANDO REFERENCIAL MÓVEL
 NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
CAPÍTULO 2 DINÂMICA DA PARTÍCULA: FORÇA E ACELERAÇÃO
 13 CAPÍTULO 2 DINÂMICA DA PATÍCULA: OÇA E ACELEAÇÃO Nese capíulo seá aalsada a le de Newo a sua foma dfeecal, aplcada ao movmeo de paículas. Nesa foma a foça esulae das foças aplcadas uma paícula esá elacoada
13 CAPÍTULO 2 DINÂMICA DA PATÍCULA: OÇA E ACELEAÇÃO Nese capíulo seá aalsada a le de Newo a sua foma dfeecal, aplcada ao movmeo de paículas. Nesa foma a foça esulae das foças aplcadas uma paícula esá elacoada
Física I. Aula 4 Forças Atrito e Centro de Massa
 ísa I º Sst d 3 Isttuto d ísa- Uvsdad d São Paulo Aula 4 oças Atto Cto d assa Posso: Vald Guaãs E-al: vald.guaas@usp.b o: 39.74 Atto Atto Objtos ous qu pa lsos, são áspos ougados sala atôa. Quado as supís
ísa I º Sst d 3 Isttuto d ísa- Uvsdad d São Paulo Aula 4 oças Atto Cto d assa Posso: Vald Guaãs E-al: vald.guaas@usp.b o: 39.74 Atto Atto Objtos ous qu pa lsos, são áspos ougados sala atôa. Quado as supís
Soluções Composição qualitativa
 Soluções oposição qualitativa As soluções são istuas de difeetes substâcias. Ua solução te dois tipos de copoetes: o solvete a substâcia ode se dissolve o soluto e os solutos as substâcias que se dissolve.
Soluções oposição qualitativa As soluções são istuas de difeetes substâcias. Ua solução te dois tipos de copoetes: o solvete a substâcia ode se dissolve o soluto e os solutos as substâcias que se dissolve.
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Satélites Artificiais. Movimento Orbital
 - - Satéltes Atfcas Moveto Obtal Autoes: Hélo Kot Kuga Kodapall Raa Rao Valde Caaa Maço 000 - - Ídce Itodução Foças de oge gavtacoal. Itodução. Expessão paa o geopotecal.3 Repesetação dos haôcos esfécos.4
- - Satéltes Atfcas Moveto Obtal Autoes: Hélo Kot Kuga Kodapall Raa Rao Valde Caaa Maço 000 - - Ídce Itodução Foças de oge gavtacoal. Itodução. Expessão paa o geopotecal.3 Repesetação dos haôcos esfécos.4
MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO
 Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
Representação dos padrões. Tipos de atributos. Etapas do processo de agrupamento. 7.1 Agrupamento clássico. 7. Agrupamento fuzzy (fuzzy clustering)
 7. Agrupaeto fuzzy (fuzzy clusterg) 7. Agrupaeto clássco Agrupaeto é a classfcação ão-supervsoada de padrões (observações, dados, objetos, eeplos) e grupos (clusters). Itutvaete, padrões seelhates deve
7. Agrupaeto fuzzy (fuzzy clusterg) 7. Agrupaeto clássco Agrupaeto é a classfcação ão-supervsoada de padrões (observações, dados, objetos, eeplos) e grupos (clusters). Itutvaete, padrões seelhates deve
Matemática FUVEST ETAPA QUESTÃO 1. b) Como f(x) = = 0 + x = 1 e. Dados m e n inteiros, considere a função f definida por m
 Mateática FUVEST QUESTÃO 1 Dados e iteiros, cosidere a fução f defiida por fx (), x para x. a) No caso e que, ostre que a igualdade f( ) se verifica. b) No caso e que, ache as iterseções do gráfico de
Mateática FUVEST QUESTÃO 1 Dados e iteiros, cosidere a fução f defiida por fx (), x para x. a) No caso e que, ostre que a igualdade f( ) se verifica. b) No caso e que, ache as iterseções do gráfico de
Os fundamentos da física Volume 2 1. Resumo do capítulo
 Os fudametos da físca Volume 2 1 Capítulo 13 Refação lumosa A efação é o feômeo o qual a luz muda de meo de popagação, com mudaça em sua velocdade. ÍDICE DE REFRAÇÃO ABSOLUTO O ídce de efação absoluto
Os fudametos da físca Volume 2 1 Capítulo 13 Refação lumosa A efação é o feômeo o qual a luz muda de meo de popagação, com mudaça em sua velocdade. ÍDICE DE REFRAÇÃO ABSOLUTO O ídce de efação absoluto
Programação Paralela
 rograação aralela FEU 4. Avalação de steas aralelos Defções Razão etre a velocdade de processaeto coseguda o sstea paralelo e a velocdade coseguda co u processador (pouca foração...) Efcêca Quocete do
rograação aralela FEU 4. Avalação de steas aralelos Defções Razão etre a velocdade de processaeto coseguda o sstea paralelo e a velocdade coseguda co u processador (pouca foração...) Efcêca Quocete do
Resoluções dos testes propostos
 os fudametos da físa Udade E Capítulo efração lumosa T.7 esposta: À ote dmu a parela de luz refratada proeete do exteror, predomado a parela de luz refletda. T.7 esposta: d luz extera que de o dro sofre
os fudametos da físa Udade E Capítulo efração lumosa T.7 esposta: À ote dmu a parela de luz refratada proeete do exteror, predomado a parela de luz refletda. T.7 esposta: d luz extera que de o dro sofre
SISTEMA DE COORDENADAS
 ELETROMAGNETISMO I 1 0 ANÁLISE VETORIAL Este capítulo ofeece uma ecapitulação aos conhecimentos de álgeba vetoial, já vistos em outos cusos. Estando po isto numeado com o eo, não fa pate de fato dos nossos
ELETROMAGNETISMO I 1 0 ANÁLISE VETORIAL Este capítulo ofeece uma ecapitulação aos conhecimentos de álgeba vetoial, já vistos em outos cusos. Estando po isto numeado com o eo, não fa pate de fato dos nossos
Capítulo 2 Galvanômetros
 Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
CAPÍTULO XI DEPENDÊNCIA E INDEPENDÊNCIA FUNCIONAIS
 CAPÍTUO XI DEPENDÊNCIA E INDEPENDÊNCIA FUNCIONAIS. Conceto báco Condee-e unçõe ea ( ) ( ) ( ) toda co doíno e ceto abeto A R n onde e upõe de clae C to é adte-e que a pea devada paca da ( ) ão unçõe contínua
CAPÍTUO XI DEPENDÊNCIA E INDEPENDÊNCIA FUNCIONAIS. Conceto báco Condee-e unçõe ea ( ) ( ) ( ) toda co doíno e ceto abeto A R n onde e upõe de clae C to é adte-e que a pea devada paca da ( ) ão unçõe contínua
Números Complexos (Parte II) 1 Plano de Argand-Gauss. 2 Módulo de um número complexo. Prof. Gustavo Adolfo Soares
 Númeos Complexos (Pate II) 1 Plao de Agad-Gauss Das defiições de que um úmeo complexo é um pa odeado de úmeos eais x e y e que C = R R, temos que: A cada úmeo complexo coespode um úico poto do plao catesiao,
Númeos Complexos (Pate II) 1 Plao de Agad-Gauss Das defiições de que um úmeo complexo é um pa odeado de úmeos eais x e y e que C = R R, temos que: A cada úmeo complexo coespode um úico poto do plao catesiao,
Eletromagnetismo Licenciatura. 18 a aula. Professor Alvaro Vannucci
 leomagesmo Lcecaua 8 a aula Pofesso Alvao Vaucc Na úlma aula vmos... Poêca adada po um Dpolo léco que Oscla: P dpolo p 0 4 c quao que a Poêca adada po uma aea mea-oda: P aea q 0 4 c Agoa, em emos do valo
leomagesmo Lcecaua 8 a aula Pofesso Alvao Vaucc Na úlma aula vmos... Poêca adada po um Dpolo léco que Oscla: P dpolo p 0 4 c quao que a Poêca adada po uma aea mea-oda: P aea q 0 4 c Agoa, em emos do valo
Campo Gravítico da Terra
 5. Campo Gavítico ómalo elação ete o potecial gavítico e o potecial omal é dada po: W ( x, y, z = U( x, y,z + ( x, y,z O campo gavítico aómalo ou petubado é etão defiido pela difeeça do campo gavítico
5. Campo Gavítico ómalo elação ete o potecial gavítico e o potecial omal é dada po: W ( x, y, z = U( x, y,z + ( x, y,z O campo gavítico aómalo ou petubado é etão defiido pela difeeça do campo gavítico
Análise de Dados e Probabilidade B Exame Final 2ª Época
 Aálse de Dados e obabldade B Eame Fal ª Éoca Claa Cosa Duae Daa: / /7 Cáa Feades Duação: hm edo Chaves MORTATE: Esceva o ome e úmeo o cmo de cada folha Resoda a cada guo em folhas seaadas, caso ão esoda
Aálse de Dados e obabldade B Eame Fal ª Éoca Claa Cosa Duae Daa: / /7 Cáa Feades Duação: hm edo Chaves MORTATE: Esceva o ome e úmeo o cmo de cada folha Resoda a cada guo em folhas seaadas, caso ão esoda
AULA 23 FATORES DE FORMA DE RADIAÇÃO TÉRMICA
 Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
Resoluções dos exercícios propostos
 da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
FGE0270 Eletricidade e Magnetismo I
 FGE7 Eleticidade e Magnetismo I Lista de eecícios 1 9 1. As cagas q 1 = q = µc na Fig. 1a estão fias e sepaadas po d = 1,5m. (a) Qual é a foça elética que age sobe q 1? (b) Colocando-se uma teceia caga
FGE7 Eleticidade e Magnetismo I Lista de eecícios 1 9 1. As cagas q 1 = q = µc na Fig. 1a estão fias e sepaadas po d = 1,5m. (a) Qual é a foça elética que age sobe q 1? (b) Colocando-se uma teceia caga
Sistemas e Sinais 2009/2010
 Aálise em espaço de estados Sistemas e Siais 009/010 Repesetação de Sistemas Sistemas descitos po equações difeeciais Sistemas descitos po sistemas de equações difeeciais Repesetação em espaço de estados
Aálise em espaço de estados Sistemas e Siais 009/010 Repesetação de Sistemas Sistemas descitos po equações difeeciais Sistemas descitos po sistemas de equações difeeciais Repesetação em espaço de estados
3. Análise estatística do sinal
 3. Análise estatística do sinal A análise da intensidade do sinal ecebido é u pocesso que abange dois estágios, sendo eles: i) a estiativa do sinal ediano ecebido e ua áea elativaente pequena, e ii) a
3. Análise estatística do sinal A análise da intensidade do sinal ecebido é u pocesso que abange dois estágios, sendo eles: i) a estiativa do sinal ediano ecebido e ua áea elativaente pequena, e ii) a
A ab = 1 pol 2 A bd = 2 pol 2. L AB = 2,0 pés = 24 pol L BC = 1,5 pés = 18 pol L CD = 1,0 pés = 12 pol
 Resstêca dos Mateas ecícos de Foças as emplo - baa composta de -3 (=9 ks) mostada a fgua abao está composta po dos segmetos, B e BD, com áeas da seção tasvesal B = pol e BD = pol. Detema o deslocameto
Resstêca dos Mateas ecícos de Foças as emplo - baa composta de -3 (=9 ks) mostada a fgua abao está composta po dos segmetos, B e BD, com áeas da seção tasvesal B = pol e BD = pol. Detema o deslocameto
Departamento de Informática. Modelagem Analítica do Desempenho de Sistemas de Computação. Modelagem Analítica. P x t i x t i x t i x t i
 Departaeto de Iforátca Dscpla: do Desepeho de Ssteas de Coputação Cadeas de Marov I Processos de Marov (ou PE Marovao) Sea u processo estocástco caracterzado pela seüêca de v.a s X(t ),,,, Sea X(t ) a
Departaeto de Iforátca Dscpla: do Desepeho de Ssteas de Coputação Cadeas de Marov I Processos de Marov (ou PE Marovao) Sea u processo estocástco caracterzado pela seüêca de v.a s X(t ),,,, Sea X(t ) a
Resolução. Capítulo 32. Força Magnética. 6. C Para que não haja desvio devemos garantir que as forças magnética ( F M. ) e elétrica ( F E
 esolução orça Magnétca E D 3 C 4 D 5 Capítulo 3 Dos vetores são antparalelos quando suas dreções são concdentes (paralelos) e seus sentdos são opostos, sto é, θ 8º, coo ostra a fgura adante: E Deste odo,
esolução orça Magnétca E D 3 C 4 D 5 Capítulo 3 Dos vetores são antparalelos quando suas dreções são concdentes (paralelos) e seus sentdos são opostos, sto é, θ 8º, coo ostra a fgura adante: E Deste odo,
2 o CONGRESSO BRASILEIRO DE P&D EM PETRÓLEO & GÁS
 o CONGRESSO BRASILEIRO DE &D EM ETRÓLEO & GÁS ANÁLISE DESCRITIVA DE DADOS DE VENTOS VISANDO ALICAÇÕES EM LATAFORMAS G. M. G. Leal, F. A. M. Souza UFCG/CCT/DME/) Av. Apígo Veloso, 88 Bodocogó, 5809-970
o CONGRESSO BRASILEIRO DE &D EM ETRÓLEO & GÁS ANÁLISE DESCRITIVA DE DADOS DE VENTOS VISANDO ALICAÇÕES EM LATAFORMAS G. M. G. Leal, F. A. M. Souza UFCG/CCT/DME/) Av. Apígo Veloso, 88 Bodocogó, 5809-970
PROPAGAÇÃO DE ONDAS ELECTROMAGNÉTICAS NUM GUIA CILÍNDRICO
 PROPAGAÇÃO D ONDAS LCTROMAGNÉTICAS NM GIA CILÍNDRICO po Calos Vaadas e Maia mília Maso IST, Maio de 5 t j e. Itodução Vamos estuda a popagação de odas electomagéticas um guia cilídico de aio a. Podeiamos
PROPAGAÇÃO D ONDAS LCTROMAGNÉTICAS NM GIA CILÍNDRICO po Calos Vaadas e Maia mília Maso IST, Maio de 5 t j e. Itodução Vamos estuda a popagação de odas electomagéticas um guia cilídico de aio a. Podeiamos
Capítulo I Erros e Aritmética Computacional
 C. Balsa e A. Satos Capítulo I Eos e Aitmética Computacioal. Itodução aos Métodos Numéicos O objectivo da disciplia de Métodos Numéicos é o estudo, desevolvimeto e avaliação de algoitmos computacioais
C. Balsa e A. Satos Capítulo I Eos e Aitmética Computacioal. Itodução aos Métodos Numéicos O objectivo da disciplia de Métodos Numéicos é o estudo, desevolvimeto e avaliação de algoitmos computacioais
Estatística: uma definição
 Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações
Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações
Forma Integral das Equações Básicas para Volume de Controle (cont.)
 EOLA DE ENGENHARIA DE SÃO CARLOS Núcleo de Egehaia Témica e Fluidos Foma Itegal das Equações Básicas paa Volume de Cotole (cot.) Teoema do Taspote de Reyolds: elação geal ete a taxa de vaiação de qq. popiedade
EOLA DE ENGENHARIA DE SÃO CARLOS Núcleo de Egehaia Témica e Fluidos Foma Itegal das Equações Básicas paa Volume de Cotole (cot.) Teoema do Taspote de Reyolds: elação geal ete a taxa de vaiação de qq. popiedade
A ciência de coletar, organizar, apresentar, analisar e interpretar dados numéricos com o objetivo de tomar melhores decisões.
 Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Coleção de úeros estatístcas stcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações a da Telebrás
Prof. Lorí Val, Dr. val@at.ufrgs.br http://.at.ufrgs.br/~val/ Coleção de úeros estatístcas stcas O úero de carros veddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%. As ações a da Telebrás
COLÉGIO ANCHIETA-BA UII_ 3EM_MAIO DE 2014 ORGANIZAÇÃO: PROF. ADRIANO CARIBÉ E PROF. WALTER PORTO. RESOLUÇÃO: PROFA. MARIA ANTÔNIA C.
 RESOUÇÃO DA a AVAIAÇÃO DE MATEMÁTICA COÉGIO ANCHIETA-BA UII_ EM_MAIO DE 0 ORGANIZAÇÃO: PROF. ADRIANO CARIBÉ E PROF. WATER PORTO. PROFA. MARIA ANTÔNIA C. GOUVEIA Questão 0. Obseve e cassifique as afiações
RESOUÇÃO DA a AVAIAÇÃO DE MATEMÁTICA COÉGIO ANCHIETA-BA UII_ EM_MAIO DE 0 ORGANIZAÇÃO: PROF. ADRIANO CARIBÉ E PROF. WATER PORTO. PROFA. MARIA ANTÔNIA C. GOUVEIA Questão 0. Obseve e cassifique as afiações
Avaliação da Eficiência Técnica Relativa de Unidades Básicas de Saúde Empregando a Análise por Envoltória de Dados - DEA
 Avalação da Efcêca Técca Relatva de Udades Báscas de Saúde Epegado a Aálse po Evoltóa de Dados - DEA Bábaa de Cássa Xave Casss Agua Depataeto de Mateátca, UFPR 853-99, Cutba, P E-al: babateatca@ahoo.co.b
Avalação da Efcêca Técca Relatva de Udades Báscas de Saúde Epegado a Aálse po Evoltóa de Dados - DEA Bábaa de Cássa Xave Casss Agua Depataeto de Mateátca, UFPR 853-99, Cutba, P E-al: babateatca@ahoo.co.b
3.1 Potencial gravitacional na superfície da Terra
 3. Potencial gavitacional na supefície da Tea Deive a expessão U(h) = mgh paa o potencial gavitacional na supefície da Tea. Solução: A pati da lei de Newton usando a expansão de Taylo: U( ) = GMm, U( +
3. Potencial gavitacional na supefície da Tea Deive a expessão U(h) = mgh paa o potencial gavitacional na supefície da Tea. Solução: A pati da lei de Newton usando a expansão de Taylo: U( ) = GMm, U( +
SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS POR DIFERENÇAS FINITAS-JM Balthazar- Maio Resolvendo um Problema de Condução de Calor
 SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS POR DIFERENÇAS FINIAS-JM Balthazar- Mao 3 Resolvedo u Problea de Codução de Calor Para troduzr o étodo das dfereças ftas de ua fora prátca vaos cosderar u problea de codução
SOLUÇÃO DE EQUAÇÕES DIFERENCIAIS POR DIFERENÇAS FINIAS-JM Balthazar- Mao 3 Resolvedo u Problea de Codução de Calor Para troduzr o étodo das dfereças ftas de ua fora prátca vaos cosderar u problea de codução
EQUAÇÕES DINÂMICAS DE MOVIMENTO ESPACIAL PARA CORPOS RÍGIDOS
 NOAS DE AULA EQUAÇÕES DINÂICAS DE OVIENO ESPACIAL PAA COPOS ÍIDOS OBEO SPINOLA BABOSA SB POLI USP LDSV OIVAÇÃO Um veíulo tem eu movmento deto de foma ma geal quando epeo ntegalmente no epaço tdmenonal
NOAS DE AULA EQUAÇÕES DINÂICAS DE OVIENO ESPACIAL PAA COPOS ÍIDOS OBEO SPINOLA BABOSA SB POLI USP LDSV OIVAÇÃO Um veíulo tem eu movmento deto de foma ma geal quando epeo ntegalmente no epaço tdmenonal
Dinâmica do Sistema Solar
 Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Balanço de Massa e Energia Aula 2
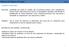 alaço de assa e Eerga ula Udades e Desão Desão: Quatdade que pode ser edda, são as gradezas báscas coo copreto, assa, tepo, teperatura etre outras, ou quatdades calculadas pela dvsão ou ultplcação de outras
alaço de assa e Eerga ula Udades e Desão Desão: Quatdade que pode ser edda, são as gradezas báscas coo copreto, assa, tepo, teperatura etre outras, ou quatdades calculadas pela dvsão ou ultplcação de outras
Os Fundamentos da Física (8 a edição)
 TEM ESPEI ENTRO DE MSS 1 Os Fudaetos da Físca (8 a edção) R MHO, N IOU E T OEDO Tea especal ENTRO DE MSS 1. etro de gradade e cetro de assa, 1. Propredade da cocetração de assas,. Propredade de setra,
TEM ESPEI ENTRO DE MSS 1 Os Fudaetos da Físca (8 a edção) R MHO, N IOU E T OEDO Tea especal ENTRO DE MSS 1. etro de gradade e cetro de assa, 1. Propredade da cocetração de assas,. Propredade de setra,
A ciência de coletar, organizar, apresentar, analisar e interpretar dados numéricos com o objetivo de tomar melhores decisões.
 .pucrs.br/faat/val/.at.ufrgs.br/~val/ Prof. Lorí Val, Dr. val@at.ufrgs.br val@pucrs.br Coleção de úeros estatístcas O úe ro de carros ve ddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%.
.pucrs.br/faat/val/.at.ufrgs.br/~val/ Prof. Lorí Val, Dr. val@at.ufrgs.br val@pucrs.br Coleção de úeros estatístcas O úe ro de carros ve ddos o país auetou e 30%. A taa de deseprego atge, este ês, 7,%.
Estatística: uma definição
 Prof. Lorí Val, Dr. val@pucrs.br http://.pucrs.br/faat/val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos auetou e 30%. o país A taa de deseprego atge, este ês, 7,%. As ações
Prof. Lorí Val, Dr. val@pucrs.br http://.pucrs.br/faat/val/ Estatístca: ua defção Coleção de úeros estatístcas O úero de carros veddos auetou e 30%. o país A taa de deseprego atge, este ês, 7,%. As ações
Cap.2 - Mecanica do Sistema Solar II: Leis de Kepler do movimento planetário
 Cap. - Mecanica do Sistea Sola II: Leis de Keple do oviento planetáio Johannes Keple Tycho Bahe Mateático e Astônoo Aleão 57-630 Astônoo Dinaaquês 546-60 = Cicunfeência achatada = Elipse Lei das Elipses
Cap. - Mecanica do Sistea Sola II: Leis de Keple do oviento planetáio Johannes Keple Tycho Bahe Mateático e Astônoo Aleão 57-630 Astônoo Dinaaquês 546-60 = Cicunfeência achatada = Elipse Lei das Elipses
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) ( k) ( k ) ( ) ( ) Questões tipo exame
![( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) ( k) ( k ) ( ) ( ) Questões tipo exame ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) ( k) ( k ) ( ) ( ) Questões tipo exame](/thumbs/54/33108071.jpg) Questões tpo eame Pá O poto U tem coordeadas (6, 6, 6) e o poto S pertece ao eo Oz, pelo que as suas coordeadas são (,, 6) Um vetor dretor da reta US é, por eemplo, US Determemos as suas coordeadas: US
Questões tpo eame Pá O poto U tem coordeadas (6, 6, 6) e o poto S pertece ao eo Oz, pelo que as suas coordeadas são (,, 6) Um vetor dretor da reta US é, por eemplo, US Determemos as suas coordeadas: US
Estudo de um modelo do núcleo do deuterão
 Estudo de um modelo do úcleo do deuteão Goçalo Oliveia º 5789 Pedo Ricate º 578 Física Quâtica da Matéia Istituto Sueio Técico Maio, 8 Resumo Cosidea-se um modelo simles aa o úcleo do deuteão, ode a iteacção
Estudo de um modelo do úcleo do deuteão Goçalo Oliveia º 5789 Pedo Ricate º 578 Física Quâtica da Matéia Istituto Sueio Técico Maio, 8 Resumo Cosidea-se um modelo simles aa o úcleo do deuteão, ode a iteacção
Unidade XI Análise de correlação e regressão
 Uvedade Fedeal do Ro Gade Iuo de Maemáca, Eaíca e Fíca Dcpla Pobabldade e Eaíca Aplcada à Egehaa CÓDIGO: Iodução Poceo de quema de maa ceâmca de pavmeo Udade XI Aále de coelação e egeão Vvae Lee Da de
Uvedade Fedeal do Ro Gade Iuo de Maemáca, Eaíca e Fíca Dcpla Pobabldade e Eaíca Aplcada à Egehaa CÓDIGO: Iodução Poceo de quema de maa ceâmca de pavmeo Udade XI Aále de coelação e egeão Vvae Lee Da de
