( ) a. 2 e x dx = 2. b. 2 = e dx. e dx e 2 dx. = u. Integrais Exponenciais e Logarítmicas. e dx = e du = e + C dx
|
|
|
- Armando Mendonça Clementino
- 7 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Aplicação da rgra ponncial Intgração d Fnçõs Eponnciais Sja ma fnção difrnciávl d. Intgrais Eponnciais Logarítmicas d + C d d d + C d Rgra Eponncial Simpls Rgra Eponncial Gral Prof.: Rogério Dias Dalla Riva Intgrais Eponnciais Logarítmicas. Aplicação da rgra ponncial.aplicação da rgra ponncial.aplicação da rgra log Emplo : Calcl as intgrais indfinidas a. d d ( + ) b. c. d. Aplicação da rgra ponncial. Aplicação da rgra ponncial Cada ma das rgras d difrnciação d fnçõs ponnciais tm sa rgra d intgração corrspondnt. a. d d Rgra do Múltiplo Constant + C Rgra Eponncial Simpls ( ) b. d d Sja, ntão d d + C Rgra Eponncial Gral
2 . Aplicação da rgra ponncial. Aplicação da rgra ponncial c. ( + ) + d d d + + C Rgra da Soma Rgra Eponncial Simpls da Potência Emplo : Calcl a intgral indfinida d. Aplicação da rgra ponncial. Aplicação da rgra ponncial Emplo : Calcl a intgral indfinida + d Fazndo -, d/d -. Introdzimos o fator (-) no intgrando mltiplicando dividindo por -. d d ( ) d ( ) Mltiplicar dividir por - Pôr a constant -/ m vidência. Aplicação da rgra ponncial. Aplicação da rgra ponncial Fazndo +, ntão d/d. O fator asnt pod sr introdzido no intgrando mdiant mltiplicação divisão por. d d d + C + + C ( ) + + d d Mltiplicar dividir por Introdzir d/d Rgra Eponncial Gral d d d + C + C Introdzir d/d Rgra Eponncial Gral
3 . Aplicação da rgra ponncial. Aplicação da rgra log OBS: Lmbr-s d q não é possívl introdzir ma variávl no intgrando. Assim é q não podmos obtr d mltiplicando dividindo por fatorando /() na intgral; isto é, d ( ) d Intgrais d Fnçõs Logarítmicas Sja ma fnção difrnciávl d. d ln + C d d + C ln Rgra Logarítmica Simpls. Aplicação da rgra log. Aplicação da rgra log Qando introdzimos as Rgras da Potência para intgração nas alas antriors, vimos q las não são válidaspara n -. n+ n d + C, n n + n+ n d d + C, n d n + Rgra Simpls da Potência Rgra Gral da Potência Podmos vrificar ssas rgras por difrnciação. Por mplo, para vrificar q notmos q d ln, d d d [ ln ] ln( ) d d. Aplicação da rgra log. Aplicação da rgra log As Rgras Log prmitm intgrar fnçõs da forma d d OBS: Obsrv os valors absoltos nas Rgras Log. Para os casos spciais m q o não pod sr ngativo, podmos omitir o sinal d valor absolto. Emplo 4: Calcl as intgrais indfinidas a. 4 d b. d c. + d
4 . Aplicação da rgra log. Aplicação da rgra log a. 4 d 4 d 4ln + C b. d ln + C ln + C d Rgra do Múltiplo Constant Rgra Logarítmica Simpls Fazndo, ntão Fazndo, tmos d/d. Podmos introdzir o fator ncssário no intgrando mltiplicando dividindo por. d d d ln + C ln + C Mltiplicar dividir por Introdzir. Aplicação da rgra log. Aplicação da rgra log c. d + ln + C d Fazndo +, ntão Emplo 6: Calcl a intgral indfinida 6 d + ln + + C. Aplicação da rgra log. Aplicação da rgra log Emplo : Calcl a intgral indfinida d Com +, vm d/d. Podmos criar o fator ncssário no intgrando colocando m vidência. 6 d + d + d ln + C ( ) ln + + C Fatorar no intgrando Introdzir 4
5 . Aplicação da rgra log. Aplicação da rgra log OBS: As intgrais às qais s pod aplicar a Rgra Log costmam sr dadas m forma disfarçada. Por mplo, s ma fnção racional tm nmrador d gra não infrior ao do dnominador, dvmos primiro ftar a divisão, obtndo ma part intira ma part fracionária. Obsrv o mplo abaio: d d 6 ln ( ) + d + d C b. Inicialmnt, vamos mltiplicar dividir o intgrandopor. d + + d + ( ) ln + + C d. Aplicação da rgra log. Aplicação da rgra log Emplo 7: Calcl as intgrais indfinidas a. b. c. + d + d + + d c. Dividindo o nmrador plo dnominador: + + d + + d + d + d ( ) + + ln + C. Aplicação da rgra log a. Comcmos scrvndo o intgrando como a soma d três fraçõs + d + d + d + ln + + C
6.1 Definição de Primitiva. Relação entre primitiva e derivadas.
apítlo VI Primitivação 6. Dfinição d Primitiva. Rlação ntr primitiva drivadas. Dada ma fnção F já sabmos dtrminar ma nova fnção F q s obtém da antrior através da drivação. Pnsmos no problma ao contrário:
Limite Escola Naval. Solução:
Limit Escola Naval (EN (A 0 (B (C (D (E é igal a: ( 0 In dt r min ação, do tipo divisão por zro, log o não ist R par q pod sr tão grand qanto qisrmos, pois, M > 0, δ > 0 tal q 0 < < δ > M M A última ha
1.1 O Círculo Trigonométrico
Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
2 x. ydydx. dydx 1)INTEGRAIS DUPLAS: RESUMO. , sendo R a região que. Exemplo 5. Calcule integral dupla. xda, no retângulo
Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
Funções Hiperbólicas Inversas. Funções Hiperbólicas Inversas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Introdução snh D
Resolução do exame de Análise Matemática I (24/1/2003) Cursos: CA, GE, GEI, IG. 1ª Chamada
Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
λ, para x 0. Outras Distribuições de Probabilidade Contínuas
abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
Sala: Rúbrica do Docente: Registo:
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Àlgbra Anális o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I (MEFT, LMAC, MEBiom) o Sm. 0/ 4/Jan/0 Duração: h30mn Instruçõs Prncha os sus dados na
A Regra Geral da Potência
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I A Regra Geral da Potência
1. (2,0) Um cilindro circular reto é inscrito em uma esfera de raio r. Encontre a maior área de superfície possível para esse cilindro.
Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
( ) π π. Corolário (derivada da função inversa): Seja f uma função diferenciável e injectiva definida num intervalo I IR.
Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
TÓPICOS. ordem; grau; curvas integrais; condições iniciais e fronteira. 1. Equações Diferenciais. Conceitos Gerais.
Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
3º) Equação do tipo = f ( y) dx Solução: 2. dy dx. 2 =. Integrando ambos os membros, dx. dx dx dy dx dy. vem: Ex: Resolva a equação 6x + 7 = 0.
0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
Diferenciação Implícita
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Diferenciação Implícita
Fun»c~oesexponenciaiselogar ³tmicas. Uma revis~ao e o n umero e
Aula 9 Fun»c~osponnciaislogar ³tmicas. Uma rvis~ao o n umro Nsta aula farmos uma pquna rvis~ao das fun»c~os f() =a g() =log a, sndo a uma constant ral, a>0 a 6=. Farmos ainda uma aprsnta»c~ao do n umro,
Função do 2 o Grau. Uma aplicação f der emr
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
Integração por Substituição
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Integração por Substituição
Polinômios. 1.Introdução 2.Técnicas de fatoração 3.Fatoração de polinômios de terceiro grau ou de grau superior 4.Teorema do zero racional
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Polinômios Prof.:
Cálculo Numérico. Integração Numérica. Prof: Reinaldo Haas
Cálculo Numérico Intgração Numérica Pro: Rinaldo Haas Intgração Numérica Em dtrminadas situaçõs, intgrais são diícis, ou msmo impossívis d s rsolvr analiticamnt. Emplo: o valor d é conhcido apnas m alguns
( ) ( ) Polinômios. Polinômios. a n x n + a n-1 x n a 1 x + a 0. O Teorema Fundamental da Álgebra afirma que todo polinômio de grau n
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Técnicas de fatoração O
- Função Exponencial - MATEMÁTICA
Postado m 9 / 07 / - Função Eponncial - Aluno(a): TURMA: FUNÇÃO EXPONENCIAL. Como surgiu a função ponncial? a n a n, a R n N Hoj, a idia d s scrvr. ² ou.. ³ nos parc óbvia, mas a utilização d númros indo
Regra de l Hôpital. 1.Formas e limites indeterminados 2.Regra de l Hôpital
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Regra de l Hôpital
Material Teórico - Módulo Equações e Sistemas de Equações Fracionárias. Sistemas de Equações Fracionárias. Oitavo Ano
Matrial Tórico - Módulo Equaçõs Sistmas d Equaçõs Fracionárias Sistmas d Equaçõs Fracionárias Oitavo Ano Autor: Prof Ulisss Lima Parnt Rvisor: Prof Antonio Caminha M Nto Sistmas d quaçõs fracionárias Nssa
Principais Modelos Contínuos
rincipais Modlos Contínuos . Modlo uniform Uma v.a. contínua tm distribuição uniform com parâmtros < s sua função dnsidad d probabilidad é dada por c c f. 0. Var E F 0 0 A função d distribuição acumulada
Integração por Partes
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Integração por Partes
, ou seja, 8, e 0 são os valores de x tais que x e, Página 120
Prparar o Eam 0 07 Matmática A Página 0. Como g é uma função contínua stritamnt crscnt no su domínio. Logo, o su contradomínio é g, g, ou sja, 8,, porqu: 8 g 8 g 8 8. D : 0, f Rsposta: C Cálculo Auiliar:
1. Integração por partes. d dx. 1. Integração por partes
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Integração por Partes
TÓPICOS. EDO de variáveis separadas. EDO de variáveis separáveis. EDO homogénea. 2. Equações Diferenciais de 1ª Ordem.
ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
Cálculo Diferencial e Integral II
Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
Análise Matemática IV
Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
1 1 2π. Área de uma Superfície de Revolução. Área de uma Superfície de Revolução
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Ára d uma Suprfíc
Antiderivadas e Integrais Indefinidas. Antiderivadas e Integrais Indefinidas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Antiderivadas e Integrais
Integral Indefinido - Continuação
- ontinuação Técnicas Intgração (Primitivação) OBJETIVO: Aprsntar técnicas para trminar a função F() conhcia como primitiva tal qu F () f() ou: f() F() As principais técnicas primitivação FUNÇÕES DE UMA
Memorize as integrais imediatas e veja como usar a técnica de substituição.
Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
Exercício 2. Calcule. f (x)<0 e f (x) e M 2 = f (0.5) =1.3 Logo
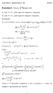Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
Frações Parciais e Crescimento Logístico
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Frações Parciais e
Identifique todas as folhas Folhas não identificadas NÃO SERÃO COTADAS. Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I
Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
Transformada de Fourier
Transformada d orir Séri d orir: Uma fnção priódica pod sr rprsntada pla soma d m conjnto d snos o cosnos d difrnts frqências cada ma mltiplicada por m por m coficint Transformada d orir: Uma fnção não
Razão e Proporção. Noção de Razão. 3 3 lê-se: três quartos lê-se: três para quatro ou três está para quatro
Razão Proporção Noção d Razão Suponha qu o profssor d Educação Física d su colégio tnha organizado um tornio d basqutbol com quatro quips formadas plos alunos da ª séri. Admita qu o su tim foi o vncdor
Funções Hiperbólicas. Funções hiperbólicas. A função seno hiperbólico é definida por
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Função sno hiprbólico
Antiderivadas e Integrais Indefinidas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Antiderivadas e Integrais
a) (0.2 v) Justifique que a sucessão é uma progressão aritmética e indique o valor da razão.
MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
CAPÍTULO 12 REGRA DA CADEIA
CAPÍTULO 12 REGRA DA CADEIA 121 Introdução Em aulas passadas, aprndmos a rgra da cadia para o caso particular m qu s faz a composição ntr uma função scalar d várias variávis f uma função vtorial d uma
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ NOTAS DE AULA ELABORADA POR: Prof. M.Sc. Armando Paulo da Silva Prof. M.Sc. José Doniztti d Lima Equação comparação d igualdad Equação difrncial é uma quação
Matmática A Etnsivo V. 6 Rsolva.) a) Aula. ( ) Função Exponencial. 1.Definição 2.Propriedades 3.Imagem 4.Gráfico 5.Equações exponenciais 6.Inequações exponenciais
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Função Eponencial Prof.:
( ) Função Exponencial. Função Exponencial. x = 0 f(0) = a 0 = 1. x 1 < x 2 f(x 1 ) > f(x 2 ) x a. 1 a ) Na função exponencial f(x) = a x, temos:
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Função Eponencial. Propriedades
log 2, qual o valor aproximado de 0, 70
UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
Equações Exponenciais e Logarítmicas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Equações Exponenciais e Logarítmicas
Matemática C Extensivo V. 7
Matmática C Extnsivo V 7 Exrcícios 0) 0 0) D 0 Falsa B A 4 0 6 0 4 6 4 6 0 Vrdadira A + B 0 0 + 4 6 7 04 Vrdadira A B 0 0 4 6 6 4 08 Vrdadira dt ( A) dt (A) 9 ( ) 9 dt (B) 9 0 6 Vrdadira A A 0 0 0 0 0
Regras do Produto e do Quociente
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Regras do Produto
Matemática IME-2007/ a QUESTÃO. 2 a QUESTÃO COMENTA
Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
Integrais de Funções Trigonométricas. Integrais de Funções Trigonométricas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. As seis integrais
INTEGRAÇÃO MÉTODO DA SUBSTITUIÇÃO
INTEGRAÇÃO MÉTODO DA UBTITUIÇÃO o MUDANÇA DE VARIAVEL PARA INTEGRAÇÃO Emplos Ercícios MÉTODO DA INTEGRAÇÃO POR PARTE Emplos Ercícios7 INTEGRAL DEFINIDA8 Emplos Ercícios REFERÊNCIA BIBLIOGRÁFICA INTRODUÇÃO:
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 2/4
FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsnt o s raciocínio d orma clara, indicando todos os cálclos q tivr d tar todas as jstiicaçõs ncssárias. Qando, para m rsltado, não é pdida
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Inequações Exponenciais e Logarítmicas. Inequações Exponenciais e Logarítmicas. Exemplos:
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Inequações Eponenciais e
( ) d dx. A Regra Geral da Potência. A Regra Geral da Potência
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Para começar, cosideremos
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 2. < arg z < π}.
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
Análise Matemática IV Problemas para as Aulas Práticas
Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA
Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 12º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema II Introdução ao Cálculo Diferencial II
ESCOLA SECUNDÁRIA COM º CICLO D DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tma II Introdução ao Cálculo Difrncial II Aula nº 4 do plano d trabalho nº 9 Rsolvr os rcícios 87, 88, 89, 90 9 os rcícios 9
CAPÍTULO 12. Exercícios a) z sen xy, x 3t e y t 2. 1.º Processo: z sen (3t 3 ) e daí dz dt. 2.º Processo: z x. dz dt. dx dt z. dy dt. .
CAPTULO Ercícios a) sn, 3t t º Procsso: sn 3t 3 ) daí d 9t cos 3t 3 ) º Procsso: d d d Tmos d cos ; 3; cos ; d t daí d 3 cos cos ) t, o sja, d 3t cos 3t 3 6t cos 3t 3, portanto, d 9t cos 3t 3 b) 3, sn
/ :;7 1 6 < =>6? < 7 A 7 B 5 = CED? = DE:F= 6 < 5 G? DIHJ? KLD M 7FD? :>? A 6? D P
26 a Aula 20065 AMIV 26 Exponncial d matrizs smlhants Proposição 26 S A SJS ntão Dmonstração Tmos A SJS A % SJS SJS SJ % S ond A, S J são matrizs n n ", (com dt S 0), # S $ S, dond ; A & SJ % S SJS SJ
Equações Exponenciais e Logarítmicas. Equações Exponenciais e Logarítmicas. Exemplos: Exemplos: a x = b x= log a b. 1) Resolva as equações: ) 5 = 3
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Equações Eponenciais e Logarítmicas.
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
COLÉGIO OBJETIVO JÚNIOR
COLÉGIO OBJETIVO JÚNIOR NOME: N. o : DATA: / /01 FOLHETO DE MATEMÁTICA (V.C. E R.V.) 6. o ANO Est folhto é um rotiro d studo para você rcuprar o contúdo trabalhado m 01. Como l vai srvir d bas para você
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 1/3
FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsn o s raciocínio d orma clara, indicando odos os cálclos q ivr d ar odas as jsiicaçõs ncssárias. Qando, para m rslado, não é pdida ma aproimação,
CAPÍTULO 14. Exemplo : Mostre que y = g(x) = 1 x 2, x 1 está dado de forma implícita na equação x 2 + y 2 1 = 0.
CAPÍTULO 4 TEOREMA DA FUNÇÃO IMPLÍCITA 4 Introdução No studo d funçõs da rta na rta dfinimos qu uma função y = gx x Domg stá dada implicitamnt numa quação nvolvndo as variávis x y s para todo x Domg o
Adriano Pedreira Cattai
Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
ln xdx 1 TÉCNICAS DE INTEGRAÇÃO
Cpítlo Técnics d Inrção - TÉCNICAS DE INTEGRAÇÃO. INTEGRAÇÃO POR PARTES Um técnic d inrção mito útil é inrção por prts, q dpnd d fórml pr difrncil d m prodto. Sjm f g fnçõs difrnciávis d. Então, pl rgr
Estratégias de Integração. Estratégias de Integração
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Estratégias de Integração
Função Exponencial: Conforme já vimos, o candidato natural à função exponencial complexa é dado pela função. f z x iy f z e cos y ie sen y.
Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
EQUAÇÕES DIFERENCIAIS
EQUAÇÕES DIFERENCIAIS No capítulo qu irmos iniciar, studarmos as quaçõs difrnciais, sus aspctos, caractrísticas suas rspctivas soluçõs. Obviamnt sugrm a rsolução d algum tipo d quação nvolvndo drivadas.
10 Encontro de Ensino, Pesquisa e Extensão, Presidente Prudente, 21 a 24 de outubro, 2013
10 Encontro d Ensino, Psquisa Extnsão, Prsidnt Prudnt, 21 a 24 d outubro, 2013 DIFERENCIAÇÃO COMPLEXA E AS CONDIÇÕES DE CAUCHY-RIEMANN Pâmla Catarina d Sousa Brandão1, Frnando Prira Sousa2 1 Aluna do Curso
CÁLCULO DIFERENCIAL E INTEGRAL II MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS VARIÁVEIS. Figura 1: Pontos de máximo e mínimo
Introdução S CÁLCULO DIFERENCIAL E INTEGRAL II MÁXIMOS E MÍNIMOS DE FUNÇÕES DE DUAS VARIÁVEIS é uma unção d duas variávis ntão dizmos qu 1 a b é no máimo igual a a Gomtricamnt o gráico d tm um máimo quando:
Ficha 2. 1 Polinómios de Taylor de um campo escalar. 1.1 O primeiro polinómio de Taylor.
Aulas Práticas d Matmática II Mstrado m Arquitctura o Smstr Fica 1 Polinómios d Talor d um campo scalar. Rcord qu os polinómios d Talor são uma important frramnta para studar o comportamnto d uma função
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ - UTFPR CAMPUS CORNÉLIO PROCÓPIO
MINISÉRIO DA EDUCAÇÃO UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ - UFPR CAMPUS CORNÉLIO PROCÓPIO PR UNIVERSIDADE ECNOLÓGICA FEDERAL DO PARANÁ Noçõs básicas d unçõs d várias variávis FUNÇÕES DE VARIAS VARIÁVEIS
Funções Crescentes e Funções Decrescentes. Funções Crescentes e Funções Decrescentes. Função Crescente. Função Decrescente
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Definição de Função
Material Teórico - Círculo Trigonométrico. Secante, cossecante e cotangente. Primeiro Ano do Ensino Médio
Matrial Tórico - Círculo Trigonométrico Scant, cosscant cotangnt Primiro Ano do Ensino Médio Autor: Prof. Fabrício Siquira Bnvids Rvisor: Prof. Antonio Caminha M. Nto 5 d dzmbro d 08 Invrsas numéricas:
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE ASSUNTO: DERIVADAS E INTEGRAIS DAS FUNÇÕES, TRIGONOMÉTRICAS E HIPÉRBOLICAS INVERSAS
FACULDADE DE ADMINISTRAÇÃO E NEGÓCIOS DE SERGIPE CURSO: ENGENHARIA DE PRODUÇÃO ASSUNTO: DERIVADAS E INTEGRAIS DAS FUNÇÕES, TRIGONOMÉTRICAS E HIPÉRBOLICAS INVERSAS PROFESSOR: MARCOS AGUIAR CÁLCULO I. FUNÇÕES
Derivadas parciais de ordem superior à primeira. Teorema de Schwarz.
Drivadas parciais d ordm suprior à primira. Torma d Scwarz. As drivadas das primiras drivadas são as sgundas drivadas assim sucssivamnt. Então, para uma unção d duas variávis podmos considrar, s istirm,
Área e Teorema Fundamental do Cálculo
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Área e Teorema Fundamental
Extremos e o Teste da Derivada Primeira. Extremos e o Teste da Derivada Primeira
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I 1. Etremos relativos
Derivadas de Ordem Superior
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Derivadas de Ordem
Funções Crescentes e Funções Decrescentes
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Funções Crescentes
Quadro de Respostas das Questões de Múltipla Escolha Valor: 65 pontos Alternativa/Questão Rascunho A B C D E. 1 e.
UFJF ICE Dpartamnto d Matmática Cálculo I Trcira Avaliação /08/0 FILA A Aluno (a): Matrícula: Turma: Instruçõs Grais: - A prova pod sr fita a lápis, cto o quadro d rspostas das qustõs d múltipla scolha,
Extremos e o Teste da Derivada Primeira
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Extremos e o Teste
lim f ( x) Limites Limites
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I 1. O ite de uma função
Oscilações amortecidas
Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
COLEÇÃO DARLAN MOUTINHO VOL. 01 RESOLUÇÕES
COLEÇÃO DRLN MOUTINHO VOL. 01 RESOLUÇÕES PÁGIN 42 39 LETR C Sjam as staçõs, B C, cujos lmntos são as pssoas qu scutavam, plo mnos, uma das staçõs, B ou C. Considr o diagrama abaixo: B 31500 17000 7500
Assíntotas. Assíntotas. Os limites infinitos para a função f(x) = 3/(x 2) podem escrever-se como
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Assíntotas Os limites
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
PR UNIVERSIDADE TECNOÓGICA FEDERA DO PARANÁ OBSERVAÇÃO: O TEXTO É ADAPTADO DO IVRO: BRONSON. R. Modrna introdução à quaçõ difrniai. tradução d Alfrdo Alv d Faria, rvião ténia Robrto Romano. São Paulo:
Formas simplificadas das equações de Navier-Stokes
Formas simplificadas das qaçõs d Navir-Stoks Eqaçõs d camada limit o camadas d cort dlgadas (Bondar lar, tin sar lar qations) Prssão dtrminada plo scoamnto xtrior à rgião viscosa, p Difsão na dircção principal
PROFESSOR (A): ANDRÉ (MAL) DISCIPLINA: MATEMÁTICA DATA: 13 / 06 / matricial AX M em que: ) Sejam A =
ALUNO (A) : PROFESSOR (A): ANDRÉ (MAL) DISCIPLINA: MATEMÁTICA DATA: / 06 / 06 ÁLGEBRA LINEAR: MATRIZES, DETERMINANTES E SISTEMAS. MATRIZES 0-0) Dada a matriz, B, calcul a + -7 0 a a + a. 0) Escrva a matriz