6.1 Definição de Primitiva. Relação entre primitiva e derivadas.
|
|
|
- Kevin Franco di Azevedo
- 5 Há anos
- Visualizações:
Transcrição
1 apítlo VI Primitivação 6. Dfinição d Primitiva. Rlação ntr primitiva drivadas. Dada ma fnção F já sabmos dtrminar ma nova fnção F q s obtém da antrior através da drivação. Pnsmos no problma ao contrário: Dada ma fnção f, srá possívl dtrminar ma otra fnção F tal q F (' ) f ( )? ma tal fnção F chama-s primitiva o intgral d f. Tal como há rgras para a drivação, vamos ncontrar rgras para a primitivação o intgração. Dfinição: Uma fnção F é ma primitiva o intgral d ma fnção f : I IR s F (' ) f ( ), I (I é m intrvalo o rnião finita d intrvalos). Emplo:. F ( ) é ma primitiva d f ( ). G ( ) também é ma primitiva d f ( ). H ( ) 0 também é ma primitiva d f ( ).. Uma primitiva d f ( ) é F( ) sr G( ). D facto, tm-s F '( ) G '( )., otro mplo também pod 90
2 apítlo VI: Primitivação 9 Torma: S F, G são das primitivas d f : I IR, ntão F G difrm apnas nma constant, isto é, ist constant, tal q G( ) F( ), I. Sgndo st torma não s tm ma só primitiva d ma fnção, mas sim ma família d primitivas, cja difrnça ntr las é ma constant. ssim, podmos dizr q ma primitiva é única a mnos d ma constant. Notação: Para indicar ma primitiva gral d f (nos trmos do torma antrior), tiliza-s a notação: Sinal d intgral f ( ) d Fnção a primitivar Indica m ordm a q variávl s vai primitivar Escrv-s f ( ) d F( ) qando F (' ) f ( ). é a constant d intgração. Emplo:. d. d ln( ), > 0. d 6. Primitivas imdiatas. Rgras d primitivação. omo vimos pla dfinição a primitivação o intgração é a opração invrsa da drivação portanto tmos as sgints propridads: F '( ) d F( ) ; d d. ( f ( ) d) f ( ) Esta rlação prmit obtr dirctamnt propridads primitivas d várias fnçõs a partir das propridads tablas d drivação:
3 apítlo VI: Primitivação 9 d d Fórmla d drivação d d d d d d d d d d d d ( ) 0 ( a) a n n ( ) n Fórmla d primitivação 0 d a d a n n d n para ( n ) (*) d ( ln( )) d ln (**) d ( ( )) ( ) ( ) d ( ) ( ( )) ( ) d d ( ) d ( ) ( ) d ( arctg( )) ( arc( )) (a são constants.) d arctg( ) d arc( ) fórmla (*) não é válida para o caso m q n, nss caso aplica-s a fórmla (**). Ercício: d. d Vrifiq q ( ln ) Proposição: Tal como a drivação também a primitivação é ma opração linar, isto é: k. f ( ) d k f ( ) d [ f ( ) g( ) ] d f ( ) d g( ) d
4 apítlo VI: Primitivação 9 Ercício: alcl as sgints primitivas.. d. ( ) d. d Rsolção d. d. d. Nota: S considrarmos > 0 comparmos o gráfico das três difrnts primitivas d f ( ). Os gráfi corrspondm a fnçõs da forma d igais a, 0 -:, para valors Ercício: Dtrmin a primitiva F da fnção f ( ) tal q F(0). Rsolção: º) alclar a primitiva d f : ( ) d d É fácil d vr q ma primitiva d d d é d : ( ) d. d Logo ( ) d F( ). Not-s q a soma das constants, ainda é ma constant,. º) Dtrminar d modo q F ( 0 ) : 0 F(0) 0 d d
5 apítlo VI: Primitivação 9 rsposta é F ( ). Nota: Podmos smpr vrificar s o rsltado d ma primitiva stá o não corrcto, por drivação; Rsltados d ma primitiva aparntmnt distintos podm, na vrdad, difrir ntr si apnas m ma constant; Há fnçõs q apsar d srm lmntars a sa primitiva não é lmntar, por mplo ( ). 6. Primitivação por sbstitição. Já vimos como calclar primitivas d fnçõs simpls a partir da tabla d drivação. Passmos agora a fnçõs mais complicadas. Rgra da adia (o rgra da drivada da fnção composta rvr página 08) para drivação d ma fnção composta é: d d F ( ( ) ) F '( ( )). ' ( ) Rlacionando a rgra da cadia com a primitivação tmos: ( ( ) ). '( ) d F( ( ) F ' ) Emplo: k Sja ( ) f ond k é ma constant difrnt d zro. Prtnd-s dtrminar k k d. Podmos ncarar a fnção f como composta das fnçõs ( ) k ( ) Então, tmos q: k F ( ( ) ) F.
6 apítlo VI: Primitivação 9 k F ( ( ) ) ' ( ) k (drivada da fnção composta). k ' k k d F' ( ( ) ) ' ( ) d [ F( ( ) )] d F( ( ) ) S m vz d k k d tivrmos k d, o problma é d fácil rsolção pois k k k k k d k d d k st intgral já sabmos calclar portanto k d k k. Ercício: a. alcl a primitiva da fnção ( ) Rsolção: Fazndo ( ) vm q f. f ( ) d d ( ) ( ) d ( ) ' ( ) d ( ) b. d Rsolção: Fazndo ( ), ' vm q d ( ) ' d ' c. d Rsolção: Fazndo ( ), ' podmos scrvr o intgral como d, mas só aparc o factor m vz d. Ora st problma rsolv-s mltiplicando o intgral por :
7 apítlo VI: Primitivação 96 d ' d. Ddzimos assim ma fórmla mais gral d primitivação da fnção ponncial: ' d Ora sta fórmla pod, também, sr ddzida tndo m conta q é fnção d : d d ( ) ( ) ( ) '( ) Procdndo d forma análoga tmos: d d d d d d d d d d d d () ' d n '. n ( ) n n () '. d n n ' ' ln () d ln ( ( ) ) '.( ), s n () '. ( ) d ( ) ( ( ) ) ' ( ) () '. ( ) d ( ) ( arctg( ) ) ( arc( ) ) ' (6) d arctg ' ( ) (7) ' d arc( ) Emplo: d a.. ( ) Rsolção:, ', logo Fazndo ( ) ' d 6 ( ) ( ) 6 b. d
8 apítlo VI: Primitivação 97 Rsolção: Fazndo ( ), ', logo / ' d () ( ) d ln O q fizmos nos rcícios antriors foi rconhcr q a fnção intgrando, podia sr scrita como a drivada d ma fnção composta. Esta técnica pod sr sada d ma forma mais sistmática plo chamado Método d sbstitição d variávl para o qal ist ma notação particlarmnt adqada prática: Sponhamos q qrmos calclar ( ) ) f ( '( ) d. d d S () for drivávl tmos '( ) ncarando como m qocint, tmos: d d Então, com sta notação O sja: d ' ( ) d ( ( ) ) ' ( ) d F( ( ) ), s F ' f f f ( ) d F ( ) ( ) d F( ) f. Emplo: d Rsolção: O cálclo dst intgral pod sr fito do sgint modo: onsidramos a sbstitição: d. Então portanto d d d Logo d. d d d d alclamos a primitiva prssa m fnção d :
9 apítlo VI: Primitivação 98 d / omo o nosso objctivo é a dtrminação d ma primitiva d sbstitímos por fim por obtndo: / ( ) / Est é o método d sbstitição para o cálclo d primitivas o intgrais dv sr mprg smpr q o cálclo do intgral f ( ) d for mais simpls. Emplos: alcl os sgints intgrais sando o método d sbstitição: a. d b. d c. d.. ( ) ln d ln ( ) d ( ) f. d 9 d fazndo fazndo ; fazndo ln( ) g. d (faça apnas a sbstitição, a continação da rsolção implica Rsolção: a tilização da técnica d primitivação por parts, q srá dada a sgir). a. d d d S ntão d. d d. Logo d d b. d
10 apítlo VI: Primitivação 99 S ntão d d d Logo d ( ) d ( ) d d. ( ) ln c. d d d d d S ln( ) ntão d d ( ) Logo ln d d d ( ) d ln ln ( ) d. ln ( ) d d d S ln( ) ntão d. d d Logo d d ln ln ln( ) ln ln ( ) ( ). d ( ) S d ntão d d d Logo d d d arctg arctg ( ) ( ) ( ) f. d 9 d S 9 ntão 8 d d d 8 d Logo d d d ln 8 ln 9 8 g. d S d ntão d d. d Mas d não aparc na primitiva. Então tndo m conta q tmos d d d d. Sbstitindo: d d d
11 apítlo VI: Primitivação 00 (a continação da rsolção implica a tilização da técnica d primitivação por parts, q srá dada a sgir). Nota: a partir do momnto m q s sbstiti d por d só pod aparcr na primitiva. 6. Primitivação por parts. rgra para a drivação do prodto d das fnçõs é: Então, m trmos d primitivas tmos: logo, ( fg) d d ( fg) d d f ' g fg' d f g d fg ' d fg f ' g d ' fg ' d. f ' gd fg fg' d sta é a fórmla para o método d primitivação por parts. Nota:. plicámos primitivação por parts qando tmos as condiçõs: Qrmos primitivar m prodto d fnçõs q não consgimos primitivar dirctamnt, f '( ) g( ) d ; onhcmos ma primitiva d f ', f '( ) d f ( ) ; primitiva f ( ) g'( ) d é mais simpls d calclar.. Qando qrmos primitivar m prodto d fnçõs por st método, scolhmos ma fnção para primitivar, m conta os três pontos antriors. f ', otra para drivar, g. Essa scolha dv sr fita tndo Emplos: a. ( ) d 8 Escolhndo f '( ) ( ) tmos 8 ( ) f ( ) pois ( ) ( ) d ; 9 9
12 apítlo VI: Primitivação 0 Escolhndo g ( ) tmos g '( ) plicando a fórmla d primitivação por parts tmos: g 9 8 ( ) ( ) d 9 g f ' f f g ' 9 ( ) d ( ) ( ) Not q: S tivéssmos scolhido f ( ) 8 ' ( ) ( ) g ao aplicar a fórmla d primitivação por parts ficaríamos com ma primitiva mais complicada para calclar. g f ' b. d Escolhndo f '( ) g ( ) tmos plicando a fórmla d primitivação por parts tmos: d g f ' g' f d f ( ) d g '( ). d ( ) c. d Escolhndo f '( ) g ( ) tmos f ( ) d g '( ). plicando o método d primitivação por parts tmos d d g f ' g f g' f Ora a primitiva d também não é imdiata, aplicando novamnt o método d primitivação por parts da sgint forma: fazndo f '( ) g( ) tmos f ( ) d g '( ) portanto d d g f ' Logo ( ) d d
13 apítlo VI: Primitivação 0 Nota: Na sgnda vz q s aplica a fórmla d primitivação por parts dvmos continar a considrar como f ( ) '. Em gral, smpr q é ncssário aplicar rptidamnt o método d primitivação por parts dvmos mantr a scolha d f ' d. arctg( ) d Nota: Nst intgral só tmos ma fnção para intgrar. Mas não sabmos primitivar o arctg ( ). Então para podrmos aplicar intgração por parts olhamos para a fnção a intgrar como.arctg( ). d Então arctg ( ) d. arctg( ) Fazndo f '( ) g ( ) arctg( ) tmos f ( ) d g '( ) plicando a fórmla d primitivação por parts tmos arctg( ) d. arctg( ) d. arctg( ) f ' g. arctg( ). arctg( ) ln d d. ln( ) d (rsolção análoga à antrior) f. ( ) d Escolhndo f '( ) ( ) ( ) g tmos plicando a fórmla d primitivação por parts tmos ( ) d ( ) f ' g f g ( ) f ( ) g' ( ) ( ). ( ( ) ) d f g ' ( ) d
14 apítlo VI: Primitivação 0 plicando novamnt primitivação por parts ( tndo m conta o q foi dito nma nota antrior) tmos q: ssim Nota: ( ) d ( ) f ' g f ( ) g ( ) ( ) ( ) d ( ) ( ) ( ) d f ( ) ( ) d g ' ( ) d ( ) ( ) d d O intgral q aparc no º mmbro é igal ao inicial, ntão podmos passá-lo para o primiro mmbro rsolvr a qação m ordm a ( ) d : ( ) ( ) ( ) d ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d Ercício: alcl as sgints primitivas tilizando primitivação por parts:. ( ) d. d. ( ) ) ln( d. ln( ) d. ( ) d ( ) 6. ( ) d
15 apítlo VI: Primitivação 0 6. Primitivação d fnçõs racionais Vamos comçar por vr três tipos spciais d fnçõs racionais: as fracçõs parciais. Tipo I c ( m b) n c,m,b,n constants m,n 0 Tipo II m ( a b c) n m,a,b,c,n constants b a,n 0 ac < 0 Tipo III m ( a b c) n m,,a,b,c,n constants a,m,n b 0 ac < 0 Tipo I Já sabmos intgrar st tipo d fnçõs. Emplo: d d a. ln b. d 0 ( ) ( ) d ( ) Tipo II Pod sr rdzido por sbstitição a m intgral do tipo rsolvido sando a fórmla d rdção: dt ( ) ( ) n ( ) t n t n ( t ) dt ( t ) t n dt n () n n n q pod sr Nota: no caso m q dt t n tmos arctg(
16 apítlo VI: Primitivação 0 Emplo: d a. 6 (nst caso n ) Not-s q o dnominador não tm zros rais ( < 0) mas podmos scrvê-lo na forma ( t ) ond é constant, compltando o qadrado. ssim, no intgral q stamos a rsolvr tmos: 6 6 ( ) Fazndo Logo t, d dt dt d. d 6 dt ( t ) 0 ( ) dt t ( arctg 0 arctg 0 b. d ( 9 ) O dnominador não tm zros rais. ( ) Fazndo t, dt d tmos d dt ( ) 9 ( 9( t ), dt 8 ( t ) sando a fórmla () tmos q
17 apítlo VI: Primitivação 06 plo q dt t dt t arctg( t, t t ( t ) d dt ( ) 9 ( 9( t ) 8 6 dt ( t ) 9 6 t 8 t arctg ( arctg 9 6 arctg Tipo III Pod sr rdzido à soma d dois intgrais, m do tipo II otro qas imdiato. Emplo: ln a. d d d arctg( ) 6 b. 6 qas imdiato d tipoii O dnominador não tm raízs. Not-s q ( 6 ) 8 6 ( 8) Plo q s pod scrvr: 6 6 d ' ( 8) d 6 8 d d 6 6 ln 6 mplo a ) arctg 0
18 apítlo VI: Primitivação 07 c. d ( 9 ) O dnominador não tm raízs. Not-s q ( 9 ' ) 8 8 ( 8 ) Plo q s pod scrvr: d 8 8 d ( ) ( ) 9 9 ( 9 ) 8 9 imdiato ( ) 6 9 d mplo b ) 9 6 arctg Dcomposição m fracçõs parciais Vamos tntar primir ma dada fnção racional, p q ( ) ( ), como soma d fnçõs racionais. No caso m q o gra d p ( ) é sprior ao d ( ) divisão d polinómios obtndo-s ond d ( ) é o qocint r( ) p q ( ) ( ) ( ) d polinômio q comça-s por fctar o algoritmo da gra r ( ) ( ) r q ( ) < gra q( ) o rsto da divisão. Para intgrar p q ( ) ( ) basta scrvr como soma d fracçõs racionais intgrar cada ma das parclas (como vrmos mais à frn. r q ( ) ( )
19 apítlo VI: Primitivação 08 Obsrvação: Todo o polinómio q ( ), não constant com coficints rais pod sr scrito d modo único (a mnos da ordm dos factors) como prodto d polinómios linars, a b, polinómios qadráti sm raízs rais, a b c ssim podmos factorizar q ( ) do sgint modo: com b ac < 0. q n m m m n nl ( ) ( a ) ( a ) ( a ) ( b c ) ( b c ) ( b c ) k l k k Polinómios linars distintos Notar q a constant q aparc na dcomposição d q ( ) é igal ao coficint do trmo d maior gra d q ( ). Polinómios qadráti distintos (sm raízs rais) omo dcompor p q ( ) ( ) m fracçõs parciais?. omçar por factorizar q( ) d modo q a sa dcomposição nvolva somnt polinómios linars qadráti sm raízs rais.. pliq as sgints rgras: a. Para cada factor ( α ) n com n, a dcomposição m fracçõs parciais nvolv ma soma d n fracçõs parciais da forma ond os α i ' s rprtam constants. ( α ) ( α ) n n b. Para cada factor ( a b c) m com m a b c sm raízs rais, a dcomposição m fracçõs parciais nvolv ma soma d m fracçõs parciais da forma a b c ( a b c) ( a b c) m m m
20 apítlo VI: Primitivação 09 ond os s ' i s ' i rprtam constants.. Os coficints do ponto antrior dtrminam-s plo método dos coficints indtrminados. Vamos agora vr algns mplos q ilstram a dcomposição m fracçõs parciais. Emplo: a. ( ) d Trata-s d m intgral d ma fnção racional cjo dnominador já stá factorizado: pont do factor é pont do factor é Na dcomposição m fracçõs parciais podrmos ncontrar os dnominadors: ( ), ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) omo tmos ma igaldad os dnominadors são igais ntão tmos q tr forçosamnt os nmradors igais, isto é: ( ) ( ) Not q dois polinómios são igais s os coficints d cada potência d são igais. ssim trmos q tr 6 8 Plo q ( ) ( )
21 apítlo VI: Primitivação 0 portanto ( ) ( ) ln ln d d d d b. d Factorização do dnominador: ( )( ) ( )( ) ( ) rais raízs tm não Na dcomposição m fracçõs parciais podrmos ncontrar os dnominadors: (not q cada factor da dcomposição do dnominador tm pont ). tnção! omo ist m polinómio d ª gra sm raízs rais na factorização do dnominador, o nmrador da fracção parcial corrspondnt srá da forma D. ( )( ) ( )( ) ( )( )( ) ( )( )( ) ( ) ( ) ( )( ) ( )( )( ) ( ) ( ) ( )( )( ) ( ) ( ) ( ) ( ) ( )( )( ) D D D D D D D omo tmos ma igaldad os dnominadors são igais ntão tmos q tr forçosamnt os nmradors igais, isto é: ( ) ( ) ( ) ( ) D D Igalando as potências d, tmos
22 apítlo VI: Primitivação D D D Plo q ln ln ln d d d c. ( ) d O dnominador da fracção ( ) já stá factorizado. Na dcomposição m fracçõs parciais podrmos ncontrar os dnominadors: ( ) ( ) (not q o pont do dnominador é maior q ). tnção! omo ist m polinómio d ª gra sm raízs rais na factorização do dnominador, o nmrador da fracção parcial corrspondnt srá da forma. ( ) ( ) ( ) ( )( ) ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) F D E D F E D D F E D F E D omo tmos ma igaldad os dnominadors são igais ntão tmos q tr forçosamnt os nmradors igais, isto é: ( ) ( ) ( ) ( ) F D E D Igalando as potências d, tmos
23 apítlo VI: Primitivação F E D F D E D Plo q ( ) ( ) ( ) ( ) ln d d d d d. d Not q o gra do nmrador é sprior ao gra do dnominador, plo q é ncssário rcorrr ao algoritmo da divisão d polinómios: ssim tmos q ( )( ) ( ) o sja, ( )( ) ( ) ( ) Portanto ( ) d d d
24 apítlo VI: Primitivação Um dos intgrais rsltants é imdiato o otro tm gra do nmrador mnor q o gra do dnominador. Vamos comçar por calclar d. Factorização do dnominador: ( )( ) Na dcomposição m fracçõs parciais podrmos ncontrar os dnominadors: Vamos dcompor a fnção intgrando m fracçõs parciais: ( ) ( ) ( )( ) omo tmos ma igaldad os dnominadors são igais ntão tmos q tr forçosamnt os nmradors igais, isto é: Igalando as potências d, tmos Plo q onclsão: ( ) ( ) d 6 d d ln ln 7 7 d ( ) d d 7 6 ln ln 7 7
25 apítlo VI: Primitivação 6.6 Otras técnicas d primitivação: Primitivas d fnçõs trigonométricas, Sbstitiçõs trigonométricas, Racionalização d algmas d algmas fnçõs Intgração d fnçõs trigonométricas: Vamos agora ocparmo-nos dos intgrais do tipo ond n, m são númros intiros positivos. m n ( ) ( ) d Já sabmos q: ( m, n 0 ) ( ) d ( ) ( m 0, n ) ( ) d ( ) É fácil vr q: n n ( ) ( ) d ( ) ( ) ( ) n d, n n ' Not q s n tmos n ( ) ( ) ( ) ( ) d d o sja, tg ( ) d ln ( ) ' ( ) ( ) d ln ( ) m m ( ) ( ) d ( ) ( ) ( ) m d, m m ' Not q s m tmos n
26 apítlo VI: Primitivação ( ) ( ) d ' ( ) d ln ( ) o sja, cot g( ) d ln ( ) ( ) Emplos: a. ( ) ( ) ( ) ( ) d b. ( ) ( ) ( ) d c. ( ) ( ) ( ) d lgm dos ponts ímpar: Procdimnto: Dstaca-s ma nidad à potência impar o factor rsltant passa-s à cofnção através da fórmla fndamntal da trigonomtria: Emplos: a. ( ) ( ) d [ ] ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) ( ) ( ) ( ) d ( ) ( ) ada m dos intgrais rsltants é imdiato, logo ( ) ( ) ( ) ( ) d d d 6 b. ( ) ( ) d omcmos por scrvr ( ) ( ) ( ) ( )( ) p.par.
27 apítlo VI: Primitivação 6 Pla fórmla fndamntal da trigonomtria tm-s q ( ) ( ) dond ( ) ( ) ( ) ( )( ) ( ) [ ] ssim, 6. p.par qando s dvolv o qadrado fica tdo m fnção d o 6 6 ( ) ( ) d ( ) ( ) ( ) d ( ) ( )[ ] 6 ( ) ( )[ ] d 6 ( ) ( ) [ ( ) ( ) ] d d d ada m dos intgrais rsltants é imdiato, logo, ( ) ( ) ( ) ( ) ( ) ( ) 9 ( ) ( ) ( ) 7 6 ( ) ( ) d 7 9 d d c. ( ) ( ) d [ ] ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) ( ) ( ) ( ) d ( ) ( ) ada m dos intgrais rsltants é imdiato, logo 6 ( ) ( ) ( ) ( ) d 6 d d 7 d. ( ) ( ) d omcmos por scrvr ( ) ( ) ( ) ( )( ) p.par Pla fórmla fndamntal da trigonomtria tm-s q ( ) ( ) dond ssim, ( ) ( ) ( ) ( )( ) ( ) [ ] p.par qando s dvolv o qadrado fica tdo m fnção d o.,
28 apítlo VI: Primitivação ( ) ( ) d ( ) ( ) ( ) d ( ) ( )[ ] 7 ( ) ( )[ ] d 7 ( ) ( ) [ ( ) ( ) ] d 7 9 d d ada m dos intgrais rsltants é imdiato, logo ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) ( ) ( ) 8 7 ( ) ( ) d 8 d d. ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) ( ) passar a ( ) ( ) ( ) d ( ) ( ) ( ) d 6 ( ) ( ) ( ) ( ) d ( ) ( ) ada m dos intgrais rsltants é imdiato, logo 7 ( ) ( ) ( ) ( ) ( ) d 7 d d d f. ( ) ( ) d ( ) ( ) ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) 6 ( ) ( ) d ( ) ( ) ada m dos intgrais rsltants é imdiato fica como rcício d d
29 apítlo VI: Primitivação 8 mbas as potências pars: Rcordar: ( a b) ( a) ( b) ( b) ( a) No caso particlar m q a b tm-s ( a) ( a) ( a) ( a b) ( a) ( b) ( a) ( b) No caso particlar m q a b tm-s ( a) ( a) ( a) omo ( a) ( a) tm-s q ( a) omo ( a) ( a) tm-s q ( a) ( ) ( ) a ( ) ( ) a Emplos: a. ( ) ( ) d ( ) ( ) d [ ( ) ( ) ] ( ) ( ) d ( ) d ( ) d O intgral rsltant é imdiato fica como rcício... d por ( ) b. ( ) ( ) d Not q agora não pod sar a msma técnica da alína antrior porq o pont não é o msmo. Nst caso como stamos a trabalhar com potências pars é ncssário para o arco-dplo através das fórmlas ( ) /o ( ).
30 apítlo VI: Primitivação 9 ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) ( ) ( ( ) )(( ( ) )( ( ) )) ( ) ( ( ) ) ( ) ( ( ) ) ( ) ( ) d ( ) ( ) ( ) 8 d 8 d d d Os intgrais rsltants são imdiatos ficam como rcício... d ( ) ( ) d por ( ) onsidrmos intgrais do tipo m n ( ) ( ) d, n m ( ) ( ) d ond n, m são númros intiros positivos. Já sabmos q: ( ) ( ) ( ) tg d d ln g( ) ( ) ( ) ( ) cot d d ln ( ) É fácil vr q: ( ) ( ) d n ( ) ( ) m d n ( ) ( ) d, n ' n m ( ) ( ) n ( n ) ( ) d, m ' m m ( m ) ( ) Emplos:
31 apítlo VI: Primitivação 0 a. b. c. ( ) d ( ) ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) Para otros ponts: Procdimnto: Usar intgração por parts aplicar fórmlas trigonométricas. Emplos: a. ( ) ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d g f ' sc sc ( ) tg( ) d sc ( ) d ( ) tg( ) ln sc( ) tg( ) b. ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d [ ( ) ] ( ) d ( ) ( ) ( ) d ( ) d ( ) ( ) d ( ) ( ) ( ) sc d Usando a alína antrior a tabla d primitivas facilmnt s concli q ( ) ( ) ( ) tg( ) ln sc( ) tg( ) sc d ( ) d
32 apítlo VI: Primitivação c. ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d [ ( ) ] ( ) d ( ) ( ) ( ) d ( ) ( ) ada m dos intgrais rsltants é imdiato fica como rcício d d.. ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d ( ( ) ) ( ) ( ) ( ) ( ) d ( ) ( ) ( ( ) ) ( ) d ( ) ( ) ( ) d ( ) ( ) d d d ( ( ) ) ( ) ( ) ( ) ( ) ada m dos intgrais rsltants é fácil d calclar fica como rcício ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) ( ) ( ) ( ) d ( ) d ( ) ( ) d ( ( ) ) ( ) ( ) ( ( ) ) ( ) d ( ) d ( ) ( ) d ada m dos intgrais rsltants é imdiato fica como rcício d ( ) ( ) d d d ( ) d f. ( ) ( ) d ( ) ( ) d ( ) ( ) ( ) d ( ( ) ) ( ) d ( ) ( ) ( ) d ( ) ( ) d ada m dos intgrais rsltants é imdiato fica como rcício
33 apítlo VI: Primitivação g. h. i. ( ) ( ) ( ) ( ) d d ( ) ( ) ( ) ( ) ( ) ( ) d d sc d ( ) ( ) ( ) d ( ) d d tg( ) ( ( ) ) ( ) d ( ) ( ) d ( ) ( ) d ( ) ( ) d ( ) Os intgrais rsltants são fácis d calclar ficam como rcício... ( ) ( ) d ( ) ( ) ( ) ( ) ( ) ( ) ( ) d ( ) ( ) d ( ) d d tg g f ' ( ) onsidrmos intgrais do tipo: m n ( ) ( ) d, ond n, m são númros intiros positivos. Para st tipo d intgrais não farmos m stdo astivo ficam apnas qatro mplos: a. b. d d c ( ) ( ) ( ) ( ) ( ) ( ) g ( ) ( ) ln c ( ) d ( ) cot g( ) ( ) ( ) cot d d sc( ) d d
34 apítlo VI: Primitivação c. d. Os intgrais q rsltam são fácis d calclar ficam como rcício ( ) ( ) ( ) d ( ) ( ) ( ) d ( ) d ( ) sc d g f ' O primiro intgral calcla-s sando primitivação por parts, o sgndo é imdiato plo q o rsto da rsolção do rcício fica como rcício. ( ) ( ) d (rcício...) tg tg ( ) d ( ) ( ) d ( ) ( ) ( ) ( ) d ( ) ( ) ( ) d ( ) ( ) ( ) ( ) d ( ) d ( ) ( ) d ( ) ( ) d Estdmos por último os intgrais do tipo ond a, b são rais não nlos. ( a) ( b) d, ( a) ( b) d, ( a) ( b) d Rcordar ( a b) ( a) ( b) ( b) ( a) ( a b) ( a) ( b) ( b) ( a) d ond d ddz q: ( a) ( b) ( a b) ( a) ( b) ( a) ( b) ( a b) ( a) ( b) ( a) ( b) d ond s ddz q: ( a) ( b) ( a b) ( a b) () ( a b) ( a b) ()
35 apítlo VI: Primitivação ( a) ( b) ( a b) ( a b) () Emplos: a. ( ) ( ) d omparando com a fórmla () tmos ( ) ( ) d a b plo q ( 8) ( ) ( 8) ( ) d ( 8) d ( ) Os intgrais q rsltam são imdiatos ficam como rcício... d d b. ( ) ( ) d omparando com a fórmla () tmos ( ) ( ) a b plo q ( ) ( ) d d ( ) d ( ) d Os intgrais q rsltam são imdiatos ficam como rcício... c. ( ) ( ) d
36 apítlo VI: Primitivação Sbstitiçõs Trigonométricas No cálclo d primitivas qando aparcm algns tipos d radicais fazm-s as sbstitiçõs a sgir indicadas: I. Primitivas do tipo: R, a d ond (, a ) R é ma fnção racional a > 0 é fnção d : Sbstitição: a ( Logo, a a ( t ) d a ( t ) dt pois, a a ( a ( t )) a ( ( t )) a ( t ) a ( t ) d dt a ( t ) d a ( t ) dt Nota: No fim da primitiva, para voltar à variávl inicial há q tr m conta o sgint: a ( a ( arc t a ( a a a ( ( a a tndo m conta o º º ponto, podmos fazr a sbstitição d todas as ( t ) ( t ) fnçõs trigonométricas dirctas: tg ( t ) ; cotg ( t ) ; ( t ) ( t ) sc(t ) ; ( t ) c ( t ). ( t )
37 apítlo VI: Primitivação 6 Nota: Podmos fazr a sbstitição a ( nss caso tmos: a a ( d a ( dt. Emplo: d Rsolção: Fazndo ( t ) tmos d ( dt ( : ( t ) d ( t )( ( t )d ( t )dt dt ( t ) ( t ) dt dt t ( t )( t ) omo ( α ) ( α)( α) tmos d t Para voltar à variávl inicial (tal como rfr a Obs.) há q tr m conta q ( ( q t arc(), logo d arc( ). II. Primitivas do tipo: R, a d ond (, a ) R é ma fnção racional a > 0 é fnção d : Sbstitição: asc( Logo, a a tg( d asc( tg( dt
38 apítlo VI: Primitivação 7 sc( ( t ) ( t ) tg ( t ) sc ( t ) tmos: omo ( t ))' sc(t )tg( t ) d dt asc( tg( d asc( tg( dt dividindo por t ( a sc( ) a a ( sc ( ) a tg ( a tg( a Nota: No fim da primitiva, para voltar à variávl inicial há q tr m conta o sgint: a sc( a sc( a a tg( a ( ( a arc t a a ( a a a ( ( ( ( a tndo m conta o º º ponto, podmos fazr a sbstitição d todas as fnçõs trigonométricas dirctas. Emplo: d Rsolção: Fazndo sc( tmos d sc( tg( dt, tg( d omo sc( tg( dt dt sc ( tg( sc( ( dt ( sc ( : sc( ( tg( ( tmos d ( t ).
39 apítlo VI: Primitivação 8 III. Primitivas do tipo: ond (, a ) R, a d R é ma fnção racional a > 0 é fnção d : Sbstitição: atg( Logo, a a sc( d a sc ( dt Porq ( tg( t ))' sc ( t ) d dt ( t ) ( t ) tg ( t ) sc ( t ) tmos: asc ( d a sc ( dt dividindo por t ( a tg( ) a ( tg ( ) a sc ( asc a a Nota: No fim da primitiva, para voltar à variávl inicial há q tr m conta o sgint: a tg( arctg t a a a tg( a sc( a ( a ( ( a ( ( a a a tndo m conta o º º ponto, podmos fazr a sbstitição d todas as fnçõs trigonométricas dirctas. d Emplo: 9 Rsolção: Fazndo tg( tmos d sc ( dt 9 sc( : d 9 sc ( t ) 9 dt sc( t )dt ln sc( t ) tg( t ) ln sc( t ).
40 apítlo VI: Primitivação 9 Ercício: alcl: d. ( ) (sgstão: ( ) ). d. 8 (sgstão: 8 ( ) ( ) ) Racionalização d algmas d algmas fnçõs Vamos vr com podmos racionalizar primitivas q nvolvam as fnçõs () ( ) R( ( ), ( ) )d ond ( ( ),( ) ) R é ma fnção racional: Sbstitição: ond ( ) ( ) d são sbstitídos por: tg t t ( ) t t ( ) d dt t t s igaldads antriors são obtidas das sgints idntidads trigonométricas: tg( ) tg ( ) tg tg ( ). ( ) d obtém-s da forma sgint: tg t arctg( logo, d t dt
41 apítlo VI: Primitivação 0 Emplos: a. d ) ( ) ( Rsolção: Fazndo t tg tmos: tg ln t ln dt t t t t t dt t ) ( ) ( d b. d ) ( )d sc( Rsolção: Fazndo tg tmos: ) tg( ) ln sc( tg tg ln ln ln ln d d d. d ) ( c. ) ( d Rsolção: Fazndo y tg tmos: ( ) tg y dy y dy y y y y dy y y y d.. ) (
42 apítlo VI: Primitivação Ercício: alcl as sgints primitivas: d. ( ) d. ( ) ( ) tg( ). d tg( ) d. ( ) 6.7 Ercícios. alcl as sgints primitivas: a. b. c. d g. d m. d h. ( ) d i. d. d j. ( ). f. ( ). d k. ( ). d l. d d n. ( ) d d o. ( ) d arctg( ) d ( ) d p. ln( ) d q. ( ) d r. d d. Dtrmina as sgints primitivas: a. b. d, fazndo a sbstitição t ; ln( ) d, fazndo a sbstitição ln( ) t ;
43 apítlo VI: Primitivação. alcla os sgints intgrais, tilizando a técnica d primitivação por sbstitição, s ncssário: a. d b. c. d d. ( ) d d. alcl as sgints primitivas, tilizando a primitivação por parts: a. d f. ln( ) d k. ( )( ) d b. d g. ln ( ) d l. arctg( ) d c. ln( ) d h. (ln( )) d m. ( ) d d. ln ( ) d i. ( ) d. d d j. ( ) d. Dtrmin a fnção f dfinida m IR q vrifica as condiçõs f ( ) ln( ) f ( ). 6. alcl os sgints intgrais d fnçõs racionais:
44 apítlo VI: Primitivação 7. Dtrmin a primitiva da fnção π f ( ) q toma o valor, para Dtrmin a fnção f tal q 8 f ''( ), f '() lim f ( ). ( ) 9. alcl os intgrais das sgints fnçõs trigonométricas: a. d b. d. g. cot ( g ) d. ( ) ( ) d h. ( ) ( )( ) d c. tg( ) d ( ) d f. ( ) sc( ) d i. ( ) c d ( ) d j. ( ) d k. sc ( ) d l. ( ) ( ) d m. p. ( ) ( ) d n. ( ) ( ) d q. d o. ( ) ( ) d tg ( )sc( ) d r. ( ) ( ) d s. ( ) ( ) d t. ( ) ( ) d. ( ) ( ) d v. y. tg ( ) d w. ( ) d. ( ) d z.. d ( ( )) d tg ( )sc ( ) d. d 0. alcl as sgints primitivas, tilizando as sbstitiçõs trigonométricas, smpr q ncssário: a. d. b. d. d c. 9 d ( ) 9 d f. d d
45 apítlo VI: Primitivação g. d h. ( ) j. d k. ( ) 9 d i. d l. 9 d ( ) d m. d. alcl os intgrais das sgints fnçõs sando o método q achar mais convnint.
( ) π π. Corolário (derivada da função inversa): Seja f uma função diferenciável e injectiva definida num intervalo I IR.
 Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
Capítlo V: Drivação 9 Corolário (drivada da nção invrsa): Sja ma nção dirnciávl injctiva dinida nm intrvalo I IR Sja I tal q '( ), ntão ( é drivávl m y ) ' ( ) ( y ) '( ) Ercício: Dtrmin a drivada d ()
( ) a. 2 e x dx = 2. b. 2 = e dx. e dx e 2 dx. = u. Integrais Exponenciais e Logarítmicas. e dx = e du = e + C dx
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Aplicação da rgra
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I. Aplicação da rgra
Resolução do exame de Análise Matemática I (24/1/2003) Cursos: CA, GE, GEI, IG. 1ª Chamada
 Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
Rsolução do am d nális Matmática I (//) Cursos: C, GE, GEI, IG ª Chamada Ercício > > como uma função ponncial d bas mnor do qu ntão o gráfico dsta função é o rprsntado na figura ao lado. Esta função é
Limite Escola Naval. Solução:
 Limit Escola Naval (EN (A 0 (B (C (D (E é igal a: ( 0 In dt r min ação, do tipo divisão por zro, log o não ist R par q pod sr tão grand qanto qisrmos, pois, M > 0, δ > 0 tal q 0 < < δ > M M A última ha
Limit Escola Naval (EN (A 0 (B (C (D (E é igal a: ( 0 In dt r min ação, do tipo divisão por zro, log o não ist R par q pod sr tão grand qanto qisrmos, pois, M > 0, δ > 0 tal q 0 < < δ > M M A última ha
TÓPICOS. ordem; grau; curvas integrais; condições iniciais e fronteira. 1. Equações Diferenciais. Conceitos Gerais.
 Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
Not bm, a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliografia principal da cadira hama-s à atnção para a importância do trabalho pssoal a ralizar plo aluno rsolvndo os problmas
1.1 O Círculo Trigonométrico
 Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Elmntos d Cálculo I - 06/ - Drivada das Funçõs Trigonométricas Logarítmicas Prof Carlos Albrto S Soars Funçõs Trigonométricas. O Círculo Trigonométrico Considrmos no plano a cirncunfrência d quação + =,
Transformada de Fourier
 Transformada d orir Séri d orir: Uma fnção priódica pod sr rprsntada pla soma d m conjnto d snos o cosnos d difrnts frqências cada ma mltiplicada por m por m coficint Transformada d orir: Uma fnção não
Transformada d orir Séri d orir: Uma fnção priódica pod sr rprsntada pla soma d m conjnto d snos o cosnos d difrnts frqências cada ma mltiplicada por m por m coficint Transformada d orir: Uma fnção não
ANÁLISE MATEMÁTICA IV A =
 Instituto uprior Técnico Dpartamnto d Matmática cção d Álgbra Anális ANÁLIE MATEMÁTICA IV FICHA 5 ITEMA DE EQUAÇÕE LINEARE E EQUAÇÕE DE ORDEM UPERIOR À PRIMEIRA () Considr a matriz A 3 3 (a) Quais são
Instituto uprior Técnico Dpartamnto d Matmática cção d Álgbra Anális ANÁLIE MATEMÁTICA IV FICHA 5 ITEMA DE EQUAÇÕE LINEARE E EQUAÇÕE DE ORDEM UPERIOR À PRIMEIRA () Considr a matriz A 3 3 (a) Quais são
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR A =
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 4 EQUAÇÕES DIFERENCIAIS LINEARES Formas canónicas d Jordan () Para cada uma das matrizs A
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 4 EQUAÇÕES DIFERENCIAIS LINEARES Formas canónicas d Jordan () Para cada uma das matrizs A
/ :;7 1 6 < =>6? < 7 A 7 B 5 = CED? = DE:F= 6 < 5 G? DIHJ? KLD M 7FD? :>? A 6? D P
 26 a Aula 20065 AMIV 26 Exponncial d matrizs smlhants Proposição 26 S A SJS ntão Dmonstração Tmos A SJS A % SJS SJS SJ % S ond A, S J são matrizs n n ", (com dt S 0), # S $ S, dond ; A & SJ % S SJS SJ
26 a Aula 20065 AMIV 26 Exponncial d matrizs smlhants Proposição 26 S A SJS ntão Dmonstração Tmos A SJS A % SJS SJS SJ % S ond A, S J são matrizs n n ", (com dt S 0), # S $ S, dond ; A & SJ % S SJS SJ
2 x. ydydx. dydx 1)INTEGRAIS DUPLAS: RESUMO. , sendo R a região que. Exemplo 5. Calcule integral dupla. xda, no retângulo
 Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
Intgração Múltipla Prof. M.Sc. Armando Paulo da Silva UTFP Campus Cornélio Procópio )INTEGAIS DUPLAS: ESUMO Emplo Emplo Calcul 6 Calcul 6 dd dd O fato das intgrais rsolvidas nos mplos srm iguais Não é
TÓPICOS. EDO de variáveis separadas. EDO de variáveis separáveis. EDO homogénea. 2. Equações Diferenciais de 1ª Ordem.
 ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
ot bm a litura dsts apontamntos não dispnsa d modo algum a litura atnta da bibliograia principal da cadira Cama-s à atnção para a importância do trabalo pssoal a ralizar plo aluno rsolvndo os problmas
Sala: Rúbrica do Docente: Registo:
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Àlgbra Anális o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I (MEFT, LMAC, MEBiom) o Sm. 0/ 4/Jan/0 Duração: h30mn Instruçõs Prncha os sus dados na
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Àlgbra Anális o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I (MEFT, LMAC, MEBiom) o Sm. 0/ 4/Jan/0 Duração: h30mn Instruçõs Prncha os sus dados na
3º) Equação do tipo = f ( y) dx Solução: 2. dy dx. 2 =. Integrando ambos os membros, dx. dx dx dy dx dy. vem: Ex: Resolva a equação 6x + 7 = 0.
 0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
0 d º) Equação do tipo: f ) d Solução: d d d d f ) f ) d f ) d. Intgrando ambos os mmbros d d d d vm: d d f ) d C d [ f ) d C ]d [ f ) d C] d C d E: Rsolva a quação 6 7 0 d d d º) Equação do tipo f ) :
Memorize as integrais imediatas e veja como usar a técnica de substituição.
 Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
Blém, d maio d 0 aro aluno, om início das intgrais spro qu vocês não troqum as rgras com as da drivada principalmnt d sno d sno. Isso tnho dito assim qu comçamos a studar drivada, lmbra? Mmoriz as intgrais
FICHA de AVALIAÇÃO de MATEMÁTICA A 12.º Ano Versão 2/4
 FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsnt o s raciocínio d orma clara, indicando todos os cálclos q tivr d tar todas as jstiicaçõs ncssárias. Qando, para m rsltado, não é pdida
FICHA d AVALIAÇÃO d MATEMÁTICA A.º Ano Vrsão / Nom: N.º Trma: Aprsnt o s raciocínio d orma clara, indicando todos os cálclos q tivr d tar todas as jstiicaçõs ncssárias. Qando, para m rsltado, não é pdida
Seja f uma função r.v.r. de domínio D e seja a R um ponto de acumulação de
 p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
p-p8 : Continuidad d funçõs rais d variávl ral. Lr atntamnt. Dominar os concitos. Fazr rcícios. Função contínua, prolongávl por continuidad, dscontínua. Classificação d dscontinuidads. Continuidad num
CAPÍTULO 12. Exercícios a) z sen xy, x 3t e y t 2. 1.º Processo: z sen (3t 3 ) e daí dz dt. 2.º Processo: z x. dz dt. dx dt z. dy dt. .
 CAPTULO Ercícios a) sn, 3t t º Procsso: sn 3t 3 ) daí d 9t cos 3t 3 ) º Procsso: d d d Tmos d cos ; 3; cos ; d t daí d 3 cos cos ) t, o sja, d 3t cos 3t 3 6t cos 3t 3, portanto, d 9t cos 3t 3 b) 3, sn
CAPTULO Ercícios a) sn, 3t t º Procsso: sn 3t 3 ) daí d 9t cos 3t 3 ) º Procsso: d d d Tmos d cos ; 3; cos ; d t daí d 3 cos cos ) t, o sja, d 3t cos 3t 3 6t cos 3t 3, portanto, d 9t cos 3t 3 b) 3, sn
Representação de Números no Computador e Erros
 Rprsntação d Númros no Computador Erros Anális Numérica Patrícia Ribiro Artur igul Cruz Escola Suprior d Tcnologia Instituto Politécnico d Stúbal 2015/2016 1 1 vrsão 23 d Fvriro d 2017 Contúdo 1 Introdução...................................
Rprsntação d Númros no Computador Erros Anális Numérica Patrícia Ribiro Artur igul Cruz Escola Suprior d Tcnologia Instituto Politécnico d Stúbal 2015/2016 1 1 vrsão 23 d Fvriro d 2017 Contúdo 1 Introdução...................................
a) (0.2 v) Justifique que a sucessão é uma progressão aritmética e indique o valor da razão.
 MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
MatPrp / Matmática Prparatória () unidad tra curricular / E-Fólio B 8 dzmbro a janiro Critérios d corrção orintaçõs d rsposta Qustão ( val) Considr a sucssão d númros rais dfinida por a) ( v) Justifiqu
5.10 EXERCÍCIO pg. 215
 EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
EXERCÍCIO pg Em cada um dos sguints casos, vriicar s o Torma do Valor Médio s aplica Em caso airmativo, achar um númro c m (a, b, tal qu (c ( a - ( a b - a a ( ; a,b A unção ( é contínua m [,] A unção
ln xdx 1 TÉCNICAS DE INTEGRAÇÃO
 Cpítlo Técnics d Inrção - TÉCNICAS DE INTEGRAÇÃO. INTEGRAÇÃO POR PARTES Um técnic d inrção mito útil é inrção por prts, q dpnd d fórml pr difrncil d m prodto. Sjm f g fnçõs difrnciávis d. Então, pl rgr
Cpítlo Técnics d Inrção - TÉCNICAS DE INTEGRAÇÃO. INTEGRAÇÃO POR PARTES Um técnic d inrção mito útil é inrção por prts, q dpnd d fórml pr difrncil d m prodto. Sjm f g fnçõs difrnciávis d. Então, pl rgr
Análise Matemática IV
 Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
Anális Matmática IV Problmas para as Aulas Práticas Smana 7 1. Dtrmin a solução da quação difrncial d y d t = t2 + 3y 2 2ty, t > 0 qu vrifica a condição inicial y(1) = 1 indiqu o intrvalo máximo d dfinição
LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA
 Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Fadiga dos Matriais Mtálicos Prof. Carlos Baptista Cap. 4 PROPAGAÇÃO DE TRINCAS POR FADIGA LEITURA 1: CAMPO ELÁSTICO PRÓXIMO À PONTA DA TRINCA Qualqur solução do campo d tnsõs para um dado problma m lasticidad
Material Teórico - Círculo Trigonométrico. Secante, cossecante e cotangente. Primeiro Ano do Ensino Médio
 Matrial Tórico - Círculo Trigonométrico Scant, cosscant cotangnt Primiro Ano do Ensino Médio Autor: Prof. Fabrício Siquira Bnvids Rvisor: Prof. Antonio Caminha M. Nto 5 d dzmbro d 08 Invrsas numéricas:
Matrial Tórico - Círculo Trigonométrico Scant, cosscant cotangnt Primiro Ano do Ensino Médio Autor: Prof. Fabrício Siquira Bnvids Rvisor: Prof. Antonio Caminha M. Nto 5 d dzmbro d 08 Invrsas numéricas:
λ, para x 0. Outras Distribuições de Probabilidade Contínuas
 abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
abilidad Estatística I Antonio Roqu Aula 3 Outras Distribuiçõs d abilidad Contínuas Vamos agora studar mais algumas distribuiçõs d probabilidads para variávis contínuas. Distribuição Eponncial Uma variávl
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 2. < arg z < π}.
 Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
Instituto Suprior Técnico Dpartamnto d Matmática Scção d Álgbra Anális ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR LOGARITMOS E INTEGRAÇÃO DE FUNÇÕES COMPLEXAS Logaritmos () Para cada um dos sguints conjuntos
Análise Matemática IV Problemas para as Aulas Práticas
 Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
Anális Matmática IV Problmas para as Aulas Práticas 7 d Abril d 003 Smana 1. Us as quaçõs d cauchy-rimann para dtrminar o conjunto dos pontos do plano complo ond as sguints funçõs admitm drivada calcul
Módulo 04. Vectores em R 2 e R 3. [Poole 003 a 028]
![Módulo 04. Vectores em R 2 e R 3. [Poole 003 a 028] Módulo 04. Vectores em R 2 e R 3. [Poole 003 a 028]](/thumbs/83/87566457.jpg) Módlo 4 [Pool a 8] Vctors m R R Vctors lirs. Sgmnto orintado. Origm xtrmidad. Vctors igais. Vctor simétrico. Soma d ctors. Propridads. Vctor nlo. Prodto d m scalar por m ctor. Propridads. Norma. Vctor
Módlo 4 [Pool a 8] Vctors m R R Vctors lirs. Sgmnto orintado. Origm xtrmidad. Vctors igais. Vctor simétrico. Soma d ctors. Propridads. Vctor nlo. Prodto d m scalar por m ctor. Propridads. Norma. Vctor
Razão e Proporção. Noção de Razão. 3 3 lê-se: três quartos lê-se: três para quatro ou três está para quatro
 Razão Proporção Noção d Razão Suponha qu o profssor d Educação Física d su colégio tnha organizado um tornio d basqutbol com quatro quips formadas plos alunos da ª séri. Admita qu o su tim foi o vncdor
Razão Proporção Noção d Razão Suponha qu o profssor d Educação Física d su colégio tnha organizado um tornio d basqutbol com quatro quips formadas plos alunos da ª séri. Admita qu o su tim foi o vncdor
Oscilações amortecidas
 Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
Oscilaçõs amortcidas Uso d variávl complxa para obtr a solução harmônica ral A grand vantagm d podr utilizar númros complxos para rsolvr a quação do oscilador harmônico stá associada com o fato d qu ssa
Equações não lineares processo iterativo
 Equaçõs não linars procsso itrativo Sja uma função considr-s a quação =0. A solução da quação dsigna-s por rai da quação ou por ro da função () y Sucssão itrativa: 0,,, 3, 0 3 0 3 4 = Prtndmos qu a sucssão
Equaçõs não linars procsso itrativo Sja uma função considr-s a quação =0. A solução da quação dsigna-s por rai da quação ou por ro da função () y Sucssão itrativa: 0,,, 3, 0 3 0 3 4 = Prtndmos qu a sucssão
CAPÍTULO 12 REGRA DA CADEIA
 CAPÍTULO 12 REGRA DA CADEIA 121 Introdução Em aulas passadas, aprndmos a rgra da cadia para o caso particular m qu s faz a composição ntr uma função scalar d várias variávis f uma função vtorial d uma
CAPÍTULO 12 REGRA DA CADEIA 121 Introdução Em aulas passadas, aprndmos a rgra da cadia para o caso particular m qu s faz a composição ntr uma função scalar d várias variávis f uma função vtorial d uma
Função do 2 o Grau. Uma aplicação f der emr
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA. Dfinição Uma aplicação f
Função Exponencial: Conforme já vimos, o candidato natural à função exponencial complexa é dado pela função. f z x iy f z e cos y ie sen y.
 Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
Funçõs Elmntars Função Exponncial: Conform já vimos, o candidato natural à função xponncial complxa é dado pla função Uma v qu : : ( ) x x f x i f cos i sn x f, x. E uma gnraliação para sr útil dv prsrvar
EQUAÇÕES DIFERENCIAIS
 EQUAÇÕES DIFERENCIAIS No capítulo qu irmos iniciar, studarmos as quaçõs difrnciais, sus aspctos, caractrísticas suas rspctivas soluçõs. Obviamnt sugrm a rsolução d algum tipo d quação nvolvndo drivadas.
EQUAÇÕES DIFERENCIAIS No capítulo qu irmos iniciar, studarmos as quaçõs difrnciais, sus aspctos, caractrísticas suas rspctivas soluçõs. Obviamnt sugrm a rsolução d algum tipo d quação nvolvndo drivadas.
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 21 DE JULHO Grupo I. Questões
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 63) ª FASE 1 DE JULHO 014 Grupo I Qustõs 1 3 4 6 7 8 Vrsão 1 C B B D C A B C Vrsão B C C A B A D D 1 Grupo II 11 O complo
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 63) ª FASE 1 DE JULHO 014 Grupo I Qustõs 1 3 4 6 7 8 Vrsão 1 C B B D C A B C Vrsão B C C A B A D D 1 Grupo II 11 O complo
Cálculo Numérico. Integração Numérica. Prof: Reinaldo Haas
 Cálculo Numérico Intgração Numérica Pro: Rinaldo Haas Intgração Numérica Em dtrminadas situaçõs, intgrais são diícis, ou msmo impossívis d s rsolvr analiticamnt. Emplo: o valor d é conhcido apnas m alguns
Cálculo Numérico Intgração Numérica Pro: Rinaldo Haas Intgração Numérica Em dtrminadas situaçõs, intgrais são diícis, ou msmo impossívis d s rsolvr analiticamnt. Emplo: o valor d é conhcido apnas m alguns
Hewlett-Packard MATRIZES. Aulas 01 a 05. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MTRIZES ulas 0 a 05 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE ENTRE
Hwltt-Packard MTRIZES ulas 0 a 05 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE ENTRE
tg 2 x , x > 0 Para determinar a continuidade de f em x = 0, devemos calcular os limites laterais
 UFRGS Instituto d Matmática DMPA - Dpto. d Matmática Pura Aplicada MAT 0 353 Cálculo Gomtria Analítica I A Gabarito da a PROVA fila A 5 d novmbro d 005 Qustão (,5 pontos Vrifiqu s a função f dada abaixo
UFRGS Instituto d Matmática DMPA - Dpto. d Matmática Pura Aplicada MAT 0 353 Cálculo Gomtria Analítica I A Gabarito da a PROVA fila A 5 d novmbro d 005 Qustão (,5 pontos Vrifiqu s a função f dada abaixo
A trajetória sob a ação de uma força central inversamente proporcional ao quadrado da distância
 A trajtória sob a ação d uma força cntral invrsamnt proporcional ao quadrado da distância A força gravitacional a força ltrostática são cntrais proporcionais ao invrso do quadrado da distância ao cntro
A trajtória sob a ação d uma força cntral invrsamnt proporcional ao quadrado da distância A força gravitacional a força ltrostática são cntrais proporcionais ao invrso do quadrado da distância ao cntro
MÉTODOS DE INTEGRAÇÃO
 ÁLULO DIFERENIL E INTEGRL MÉTODOS DE INTEGRÇÃO Nem todas as integrais são imediatas segndo o formlário dado, porém algns métodos simples ajdam a obter as primitivas das fnções qe não têm integração imediata.
ÁLULO DIFERENIL E INTEGRL MÉTODOS DE INTEGRÇÃO Nem todas as integrais são imediatas segndo o formlário dado, porém algns métodos simples ajdam a obter as primitivas das fnções qe não têm integração imediata.
Exercício 2. Calcule. f (x)<0 e f (x) e M 2 = f (0.5) =1.3 Logo
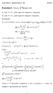 Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
Ercício. Calcul. ln( ) cos d : a) com c.d.c., pla rgra dos trapézios composta; b) com c.d.c., pla rgra d Simpson composta; a) a b., c.d.c rro E T + ε cal + ε dados E T. - f ( ) ln f ET M ( cos ) ; f (
TÉCNICAS DE INTEGRAÇÃO. 1.1 Integrais por Substituição Mudança de Variáveis
 UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis
UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis
Hewlett-Packard MATRIZES. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MTRIZES ulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz no 06 Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE
Hwltt-Packard MTRIZES ulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz no 06 Sumário MTRIZES NOÇÃO DE MTRIZ REPRESENTÇÃO DE UM MTRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDMENTL MTRIZES ESPECIIS IGULDDE
Adriano Pedreira Cattai
 Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
Adriano Pdrira Cattai apcattai@ahoocombr Univrsidad Fdral da Bahia UFBA, MAT A01, 006 3 Suprfíci Cilíndrica 31 Introdução Dfinição d Suprfíci Podmos obtr suprfícis não somnt por mio d uma quação do tipo
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
r = (x 2 + y 2 ) 1 2 θ = arctan y x
 Sção 0: Equação d Laplac m coordnadas polars Laplaciano m coordnadas polars. Sja u = ux, y uma função d duas variávis. Dpndndo da rgião m qu a função stja dfinida, pod sr mais fácil trabalhar com coordnadas
Sção 0: Equação d Laplac m coordnadas polars Laplaciano m coordnadas polars. Sja u = ux, y uma função d duas variávis. Dpndndo da rgião m qu a função stja dfinida, pod sr mais fácil trabalhar com coordnadas
Equações não lineares processo iterativo
 Equaçõs não linars procsso itrativo Sja f() uma função considr s a quação f()=0. A solução da quação dsigna s por raiz da quação ou por zro da função (z) y f() z Sucssão itrativa: 0,,, 3, 0 f() 3 0 3 z
Equaçõs não linars procsso itrativo Sja f() uma função considr s a quação f()=0. A solução da quação dsigna s por raiz da quação ou por zro da função (z) y f() z Sucssão itrativa: 0,,, 3, 0 f() 3 0 3 z
Integral Indefinido - Continuação
 - ontinuação Técnicas Intgração (Primitivação) OBJETIVO: Aprsntar técnicas para trminar a função F() conhcia como primitiva tal qu F () f() ou: f() F() As principais técnicas primitivação FUNÇÕES DE UMA
- ontinuação Técnicas Intgração (Primitivação) OBJETIVO: Aprsntar técnicas para trminar a função F() conhcia como primitiva tal qu F () f() ou: f() F() As principais técnicas primitivação FUNÇÕES DE UMA
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA A DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 635) 2ª FASE 21 DE JULHO 2014 Grupo I.
 Associação d Profssors d Matmática Contactos: Rua Dr João Couto, nº 7-A 100-6 Lisboa Tl: +1 1 716 6 90 / 1 711 0 77 Fa: +1 1 716 64 4 http://wwwapmpt mail: gral@apmpt PROPOSTA DE RESOLUÇÃO DA PROVA DE
Associação d Profssors d Matmática Contactos: Rua Dr João Couto, nº 7-A 100-6 Lisboa Tl: +1 1 716 6 90 / 1 711 0 77 Fa: +1 1 716 64 4 http://wwwapmpt mail: gral@apmpt PROPOSTA DE RESOLUÇÃO DA PROVA DE
FUNÇÕES DE UMA VARIÁVEL COMPLEXA
 FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
FUNÇÕES DE UMA VARIÁVEL COMPLEXA Ettor A. d Barros 1. INTRODUÇÃO Sja s um númro complxo qualqur prtncnt a um conjunto S d númros complxos. Dizmos qu s é uma variávl complxa. S, para cada valor d s, o valor
Identifique todas as folhas Folhas não identificadas NÃO SERÃO COTADAS. Faculdade de Economia Universidade Nova de Lisboa EXAME DE CÁLCULO I
 Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
Idntifiqu todas as folhas Folhas não idntificadas NÃO SERÃO COTADAS Faculdad d Economia Univrsidad Nova d Lisboa EXAME DE CÁLCULO I Ano Lctivo 8-9 - º Smstr Eam Final d ª Época m d Janiro 9 Duração: horas
Derivada Escola Naval
 Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
Drivada Escola Naval EN A drivada f () da função f () = l og é: l n (B) 0 l n (E) / l n EN S tm-s qu: f () = s s 0 s < < 0 s < I - f () só não é drivávl para =, = 0 = II - f () só não é contínua para =
Material Teórico - Módulo Equações e Sistemas de Equações Fracionárias. Sistemas de Equações Fracionárias. Oitavo Ano
 Matrial Tórico - Módulo Equaçõs Sistmas d Equaçõs Fracionárias Sistmas d Equaçõs Fracionárias Oitavo Ano Autor: Prof Ulisss Lima Parnt Rvisor: Prof Antonio Caminha M Nto Sistmas d quaçõs fracionárias Nssa
Matrial Tórico - Módulo Equaçõs Sistmas d Equaçõs Fracionárias Sistmas d Equaçõs Fracionárias Oitavo Ano Autor: Prof Ulisss Lima Parnt Rvisor: Prof Antonio Caminha M Nto Sistmas d quaçõs fracionárias Nssa
Introdução ao Processamento Digital de Sinais Soluções dos Exercícios Propostos Capítulo 6
 Introdução ao Soluçõs dos Exrcícios Propostos Capítulo 6 1. Dadas as squências x[n] abaixo com sus rspctivos comprimntos, ncontr as transformadas discrtas d Fourir: a x[n] = n, para n < 4 X[] = 6 X[1]
Introdução ao Soluçõs dos Exrcícios Propostos Capítulo 6 1. Dadas as squências x[n] abaixo com sus rspctivos comprimntos, ncontr as transformadas discrtas d Fourir: a x[n] = n, para n < 4 X[] = 6 X[1]
E X A M E ª FASE, V E R S Ã O 1 P R O P O S T A D E R E S O L U Ç Ã O
 Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
Prparar o Eam 05 Matmática A E X A M E 0.ª FASE, V E R S Ã O P R O P O S T A D E R E S O L U Ç Ã O. Tm-s qu P A P A P A GRUPO I ITENS DE ESCOLHA MÚLTIPLA 0, 0, 0,. Assim: P B A PB A 0,8 0,8 PB A 0,8 0,
- Função Exponencial - MATEMÁTICA
 Postado m 9 / 07 / - Função Eponncial - Aluno(a): TURMA: FUNÇÃO EXPONENCIAL. Como surgiu a função ponncial? a n a n, a R n N Hoj, a idia d s scrvr. ² ou.. ³ nos parc óbvia, mas a utilização d númros indo
Postado m 9 / 07 / - Função Eponncial - Aluno(a): TURMA: FUNÇÃO EXPONENCIAL. Como surgiu a função ponncial? a n a n, a R n N Hoj, a idia d s scrvr. ² ou.. ³ nos parc óbvia, mas a utilização d númros indo
Enunciados equivalentes
 Lógica para Ciência da Computação I Lógica Matmática Txto 6 Enunciados quivalnts Sumário 1 Equivalência d nunciados 2 1.1 Obsrvaçõs................................ 5 1.2 Exrcícios rsolvidos...........................
Lógica para Ciência da Computação I Lógica Matmática Txto 6 Enunciados quivalnts Sumário 1 Equivalência d nunciados 2 1.1 Obsrvaçõs................................ 5 1.2 Exrcícios rsolvidos...........................
CAPÍTULO 14. Exemplo : Mostre que y = g(x) = 1 x 2, x 1 está dado de forma implícita na equação x 2 + y 2 1 = 0.
 CAPÍTULO 4 TEOREMA DA FUNÇÃO IMPLÍCITA 4 Introdução No studo d funçõs da rta na rta dfinimos qu uma função y = gx x Domg stá dada implicitamnt numa quação nvolvndo as variávis x y s para todo x Domg o
CAPÍTULO 4 TEOREMA DA FUNÇÃO IMPLÍCITA 4 Introdução No studo d funçõs da rta na rta dfinimos qu uma função y = gx x Domg stá dada implicitamnt numa quação nvolvndo as variávis x y s para todo x Domg o
Análise de Fourier tempo contínuo
 nális d Fourir tmpo contínuo 4.5.5.5.5.5.5 -.5 - -.5 - -.5.5.5 -.5 - -.5 - -.5.5.5 SS MIEIC 8/9 nális d Fourir m tmpo contínuo aula d hoj Rsposta d SLITs contínuo a xponnciais Séri d Fourir d sinais priódicos
nális d Fourir tmpo contínuo 4.5.5.5.5.5.5 -.5 - -.5 - -.5.5.5 -.5 - -.5 - -.5.5.5 SS MIEIC 8/9 nális d Fourir m tmpo contínuo aula d hoj Rsposta d SLITs contínuo a xponnciais Séri d Fourir d sinais priódicos
Exercício: Exercício:
 Smântica Opracional Estrutural Smântica Opracional Estrutural O ênfas dsta smântica é nos passos individuais d xcução d um programa A rlação d transição tm a forma rprsnta o primiro passo d xcução do programa
Smântica Opracional Estrutural Smântica Opracional Estrutural O ênfas dsta smântica é nos passos individuais d xcução d um programa A rlação d transição tm a forma rprsnta o primiro passo d xcução do programa
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC200 MICROECONOMIA II PRIMEIRA PROVA (20) () Para cada uma das funçõs d produção
UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ
 PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ NOTAS DE AULA ELABORADA POR: Prof. M.Sc. Armando Paulo da Silva Prof. M.Sc. José Doniztti d Lima Equação comparação d igualdad Equação difrncial é uma quação
PR UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ NOTAS DE AULA ELABORADA POR: Prof. M.Sc. Armando Paulo da Silva Prof. M.Sc. José Doniztti d Lima Equação comparação d igualdad Equação difrncial é uma quação
UNIVERSIDADE DE SÃO PAULO Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto Departamento de Economia
 UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
UNIVERSIDADE DE SÃO PAULO Faculdad d Economia, Administração Contabilidad d Ribirão Prto Dpartamnto d Economia Nom: Númro: REC00 MICROECONOMIA II PRIMEIRA PROVA (0) () Para cada uma das funçõs d produção
RESUMO de LIMITES X CONTINUIDADE. , tivermos que f(x) arbitr
 RESUMO d LIMITES X CONTINUIDADE I. Limits finitos no ponto 1. Noção d Limit Finito num ponto Sjam f uma função x o IR. Dizmos qu f tm it (finito) no ponto x o (m símbolo: f(x) = l IR) quando x convn x
RESUMO d LIMITES X CONTINUIDADE I. Limits finitos no ponto 1. Noção d Limit Finito num ponto Sjam f uma função x o IR. Dizmos qu f tm it (finito) no ponto x o (m símbolo: f(x) = l IR) quando x convn x
FENOMENOS DE TRANSPORTE 2 o Semestre de 2012 Prof. Maurício Fabbri 2ª SÉRIE DE EXERCÍCIOS
 FENOMENOS DE TRANSPORTE o Smstr d 0 Prof. Maurício Fabbri ª SÉRIE DE EXERCÍCIOS 0. O coficint d transfrência d calor Transport d calor por convcção O transint ponncial simpls Consrvação da nrgia Lia o
FENOMENOS DE TRANSPORTE o Smstr d 0 Prof. Maurício Fabbri ª SÉRIE DE EXERCÍCIOS 0. O coficint d transfrência d calor Transport d calor por convcção O transint ponncial simpls Consrvação da nrgia Lia o
log 2, qual o valor aproximado de 0, 70
 UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
UNIERSIDADE FEDERAL DE ITAJUBÁ GABARITO DE FUNDAMENTOS DA MATEMÁTICA PROA DE TRANSFERÊNCIA INTERNA, EXTERNA E PARA PORTADOR DE DIPLOMA DE CURSO SUPERIOR // CANDIDATO: CURSO PRETENDIDO: OBSERAÇÕES: Prova
1. (2,0) Um cilindro circular reto é inscrito em uma esfera de raio r. Encontre a maior área de superfície possível para esse cilindro.
 Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Gabarito da a Prova Unificada d Cálculo I- 15/, //16 1. (,) Um cilindro circular rto é inscrito m uma sfra d raio r. Encontr a maior ára d suprfíci possívl para ss cilindro. Solução: Como o cilindro rto
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Univrsidad Fdral do Rio d Janiro Instituto d Matmática Dpartamnto d Matmática Gabarito da Prova Final d Cálculo Difrncial Intgral II - 07-I (MAC 8 - IQN+IFN+Mto, 6/06/07 Qustão : (.5 pontos Rsolva { xy.
Univrsidad Fdral do Rio d Janiro Instituto d Matmática Dpartamnto d Matmática Gabarito da Prova Final d Cálculo Difrncial Intgral II - 07-I (MAC 8 - IQN+IFN+Mto, 6/06/07 Qustão : (.5 pontos Rsolva { xy.
4.1 Método das Aproximações Sucessivas ou Método de Iteração Linear (MIL)
 4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
4. Método das Aproimaçõs Sucssivas ou Método d Itração Linar MIL O método da itração linar é um procsso itrativo qu aprsnta vantagns dsvantagns m rlação ao método da bisscção. Sja uma função f contínua
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5
 P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
P R O P O S T A D E R E S O L U Ç Ã O D O E X A M E T I P O 5 GRUPO I ITENS DE ESCOLHA MÚLTIPLA 1. Agrupando num bloco a Ana, a Bruna, o Carlos, a Diana o Eduardo, o bloco os rstants st amigos prmutam
Principais Modelos Contínuos
 rincipais Modlos Contínuos . Modlo uniform Uma v.a. contínua tm distribuição uniform com parâmtros < s sua função dnsidad d probabilidad é dada por c c f. 0. Var E F 0 0 A função d distribuição acumulada
rincipais Modlos Contínuos . Modlo uniform Uma v.a. contínua tm distribuição uniform com parâmtros < s sua função dnsidad d probabilidad é dada por c c f. 0. Var E F 0 0 A função d distribuição acumulada
Matemática IME-2007/ a QUESTÃO. 2 a QUESTÃO COMENTA
 Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
Matmática a QUESTÃO IME-007/008 Considrando qu podmos tr csto sm bola, o númro d maniras d distribuir as bolas nos três cstos é igual ao númro d soluçõs intiras não-ngativas da quação: x + y + z = n, na
Módulo de Círculo Trigonométrico. Secante, Cossecante e Cotangente. 1 a série E.M.
 Módulo d Círculo Trigonométrico Scant, Cosscant Cotangnt a séri EM Círculo Trigonométrico Scant, Cosscant Cotangnt Exrcícios Introdutórios ] π Exrcício Sja α ; π tal qu sn α, dtrmin, s xistir, o rsultado
Módulo d Círculo Trigonométrico Scant, Cosscant Cotangnt a séri EM Círculo Trigonométrico Scant, Cosscant Cotangnt Exrcícios Introdutórios ] π Exrcício Sja α ; π tal qu sn α, dtrmin, s xistir, o rsultado
Cálculo Diferencial e Integral II
 Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
Cálculo Difrncial Intgral II Lista 7 - Rsumo a Toria A Rgra a Caia No stuo funçõs uma variávl usamos a Rgra a Caia para calcular a rivaa uma função composta Nst caso sno w f uma função ifrnciávl sno g
Exame de Matemática Página 1 de 6. obtém-se: 2 C.
 Eam d Matmática -7 Página d 6. Simplificando a prssão 9 ( ) 6 obtém-s: 6.. O raio r = m d uma circunfrência foi aumntado m 5%. Qual foi o aumnto prcntual da ára da sgunda circunfrência m comparação com
Eam d Matmática -7 Página d 6. Simplificando a prssão 9 ( ) 6 obtém-s: 6.. O raio r = m d uma circunfrência foi aumntado m 5%. Qual foi o aumnto prcntual da ára da sgunda circunfrência m comparação com
Questões para o concurso de professores Colégio Pedro II
 Qustõs para o concurso d profssors Colégio Pdro II Profs Marilis, Andrzinho Fábio Prova Discursiva 1ª QUESTÃO Jhosy viaja com sua sposa, Paty, sua filha filho para a Rgião dos Lagos para curtir um friadão
Qustõs para o concurso d profssors Colégio Pdro II Profs Marilis, Andrzinho Fábio Prova Discursiva 1ª QUESTÃO Jhosy viaja com sua sposa, Paty, sua filha filho para a Rgião dos Lagos para curtir um friadão
indicando (nesse gráfico) os vectores E
 Propagação Antnas Eam 5 d Janiro d 6 Docnt Rsponsávl: Prof Carlos R Paiva Duração: 3 horas 5 d Janiro d 6 Ano Lctivo: 5 / 6 SEGUNDO EXAME Uma onda lctromagnética plana monocromática é caractrizada plo
Propagação Antnas Eam 5 d Janiro d 6 Docnt Rsponsávl: Prof Carlos R Paiva Duração: 3 horas 5 d Janiro d 6 Ano Lctivo: 5 / 6 SEGUNDO EXAME Uma onda lctromagnética plana monocromática é caractrizada plo
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 12º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema II Introdução ao Cálculo Diferencial II
 ESCOLA SECUNDÁRIA COM º CICLO D DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tma II Introdução ao Cálculo Difrncial II Aula nº 4 do plano d trabalho nº 9 Rsolvr os rcícios 87, 88, 89, 90 9 os rcícios 9
ESCOLA SECUNDÁRIA COM º CICLO D DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tma II Introdução ao Cálculo Difrncial II Aula nº 4 do plano d trabalho nº 9 Rsolvr os rcícios 87, 88, 89, 90 9 os rcícios 9
Fun»c~oesexponenciaiselogar ³tmicas. Uma revis~ao e o n umero e
 Aula 9 Fun»c~osponnciaislogar ³tmicas. Uma rvis~ao o n umro Nsta aula farmos uma pquna rvis~ao das fun»c~os f() =a g() =log a, sndo a uma constant ral, a>0 a 6=. Farmos ainda uma aprsnta»c~ao do n umro,
Aula 9 Fun»c~osponnciaislogar ³tmicas. Uma rvis~ao o n umro Nsta aula farmos uma pquna rvis~ao das fun»c~os f() =a g() =log a, sndo a uma constant ral, a>0 a 6=. Farmos ainda uma aprsnta»c~ao do n umro,
v 4 v 6 v 5 b) Como são os corte de arestas de uma árvore?
 12 - Conjuntos d Cort o studarmos árors gradoras, nós stáamos intrssados m um tipo spcial d subgrafo d um grafo conxo: um subgrafo qu mantiss todos os értics do grafo intrligados. Nst tópico, nós stamos
12 - Conjuntos d Cort o studarmos árors gradoras, nós stáamos intrssados m um tipo spcial d subgrafo d um grafo conxo: um subgrafo qu mantiss todos os értics do grafo intrligados. Nst tópico, nós stamos
PARTE 6 DERIVADAS PARCIAIS
 PARTE 6 DERIVADAS PARCIAIS 6.1 Introdução Vamos falar agora das drivadas parciais d uma função ral d várias variávis rais, f : Dom(f) R n R. Para simplificar, vamos comçar com uma função m R, para só dpois
PARTE 6 DERIVADAS PARCIAIS 6.1 Introdução Vamos falar agora das drivadas parciais d uma função ral d várias variávis rais, f : Dom(f) R n R. Para simplificar, vamos comçar com uma função m R, para só dpois
1. A soma de quaisquer dois números naturais é sempre maior do que zero. Qual é a quantificação correcta?
 Abuso Sual nas Escolas Não dá para acitar Por uma scola livr do SID A Rpública d Moçambiqu Matmática Ministério da Educação ª Época ª Class/0 Conslho Nacional d Eams, Crtificação Equivalências 0 Minutos
Abuso Sual nas Escolas Não dá para acitar Por uma scola livr do SID A Rpública d Moçambiqu Matmática Ministério da Educação ª Época ª Class/0 Conslho Nacional d Eams, Crtificação Equivalências 0 Minutos
10. EXERCÍCIOS (ITA-1969 a ITA-2001)
 . EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
. EXERCÍCIOS (ITA-969 a ITA-) - (ITA - 969) Sjam f() = + g() = duas funçõs rais d variávl ral. Então (gof)(y ) é igual a: a) y y + b) (y ) + c) y + y d) y y + ) y - (ITA -97) Sjam A um conjunto finito
FILTROS. Assim, para a frequência de corte ω c temos que quando g=1/2 ( )= 1 2 ( ) = 1 2 ( ) e quando = 1 2
 FILTROS Como tmos visto, quando tmos lmntos rativos nos circuitos, as tnsõs sobr os lmntos d um circuitos m CA são dpndnts da frquência. Est comportamnto m circuitos montados como divisors d tnsão prmit
FILTROS Como tmos visto, quando tmos lmntos rativos nos circuitos, as tnsõs sobr os lmntos d um circuitos m CA são dpndnts da frquência. Est comportamnto m circuitos montados como divisors d tnsão prmit
CRITÉRIOS GERAIS DE CLASSIFICAÇÃO
 Eam Final Nacional d Matmática A Prova 65.ª Fas Ensino Scundário 09.º Ano d Escolaridad Dcrto-Li n.º 9/0, d 5 d julho Critérios d Classificação 0 Páginas CRITÉRIOS GERAIS DE CLASSIFICAÇÃO A classificação
Eam Final Nacional d Matmática A Prova 65.ª Fas Ensino Scundário 09.º Ano d Escolaridad Dcrto-Li n.º 9/0, d 5 d julho Critérios d Classificação 0 Páginas CRITÉRIOS GERAIS DE CLASSIFICAÇÃO A classificação
Ficha de Trabalho Matemática 12ºano Temas: Trigonometria ( Triângulo rectângulo e círculo trigonométrico) Proposta de correcção
 COLÉGIO PAULO VI Ficha d Trabalho Matmática ºano Tmas: Trigonomtria ( Triângulo rctângulo círculo trigonométrico) Proposta d corrcção Rlmbrar qu um radiano é, m qualqur circunfrência, a amplitud do arco
COLÉGIO PAULO VI Ficha d Trabalho Matmática ºano Tmas: Trigonomtria ( Triângulo rctângulo círculo trigonométrico) Proposta d corrcção Rlmbrar qu um radiano é, m qualqur circunfrência, a amplitud do arco
Cálculo de Autovalores, Autovetores e Autoespaços Seja o operador linear tal que. Por definição,, com e. Considere o operador identidade tal que.
 AUTOVALORES E AUTOVETORES Dfiniçõs Sja um oprador linar Um vtor, é dito autovtor, vtor próprio ou vtor caractrístico do oprador T, s xistir tal qu O scalar é dnominado autovalor, valor próprio ou valor
AUTOVALORES E AUTOVETORES Dfiniçõs Sja um oprador linar Um vtor, é dito autovtor, vtor próprio ou vtor caractrístico do oprador T, s xistir tal qu O scalar é dnominado autovalor, valor próprio ou valor
Matemática C Extensivo V. 7
 Matmática C Extnsivo V 7 Exrcícios 0) 0 0) D 0 Falsa B A 4 0 6 0 4 6 4 6 0 Vrdadira A + B 0 0 + 4 6 7 04 Vrdadira A B 0 0 4 6 6 4 08 Vrdadira dt ( A) dt (A) 9 ( ) 9 dt (B) 9 0 6 Vrdadira A A 0 0 0 0 0
Matmática C Extnsivo V 7 Exrcícios 0) 0 0) D 0 Falsa B A 4 0 6 0 4 6 4 6 0 Vrdadira A + B 0 0 + 4 6 7 04 Vrdadira A B 0 0 4 6 6 4 08 Vrdadira dt ( A) dt (A) 9 ( ) 9 dt (B) 9 0 6 Vrdadira A A 0 0 0 0 0
R é o conjunto dos reais; f : A B, significa que f é definida no conjunto A (domínio - domain) e assume valores em B (contradomínio range).
 f : A B, significa qu f é dfinida no conjunto A (domínio - domain) assum valors m B (contradomínio rang). R é o conjunto dos rais; R n é o conjunto dos vtors n-dimnsionais rais; Os vtors m R n são colunas
f : A B, significa qu f é dfinida no conjunto A (domínio - domain) assum valors m B (contradomínio rang). R é o conjunto dos rais; R n é o conjunto dos vtors n-dimnsionais rais; Os vtors m R n são colunas
01.Resolva as seguintes integrais:
 INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
INSTITUTO DE MATEMÁTICA -UFBA DEPARTAMENTO DE MATEMÁTICA MAT A CÁLCULO A a LISTA DE EXERCÍCIOS Atualizada m 7..Rsolva as sguints intgrais: 5.).).).) sn().5) sn cos.) tg 5 sc.7).8).9) ln 5.) arctg.).).).).7)
Definição de Área entre duas curvas - A área A entre região limitada pelas curvas. x onde f e g são contínuas e x g x
 Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para
Aula Capítulo 6 Aplicaçõs d Intração (pá. 8) UFPA, d junho d 5 Ára ntr duas curvas Dinição d Ára ntr duas curvas - A ára A ntr rião limitada plas curvas a y plas rtas a,, é ond são contínuas A a d y para
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES
 PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
PARTE 8 DERIVADAS PARCIAIS DE ORDENS SUPERIORES 8.1 Drivadas Parciais d Ordns Supriors Dada a função ral d duas variávis f : Dom(f) R 2 R X = ) f(x) = f ) aprndmos antriormnt como construir suas drivadas
Universidade da Beira Interior Departamento de Matemática. Ficha de exercícios nº2: Algoritmo Simplex Primal.
 Ano lctivo: 8/9 Univrsidad da ira Intrior Dpartamnto d Matmática INVESTIGAÇÃO OPERACIONAL Ficha d rcícios nº: Algoritmo Simpl Primal. Cursos: Economia. Considr o sguint conjunto d soluçõs admissívis: {,
Ano lctivo: 8/9 Univrsidad da ira Intrior Dpartamnto d Matmática INVESTIGAÇÃO OPERACIONAL Ficha d rcícios nº: Algoritmo Simpl Primal. Cursos: Economia. Considr o sguint conjunto d soluçõs admissívis: {,
Aula Expressão do produto misto em coordenadas
 Aula 15 Nsta aula vamos xprssar o produto misto m trmos d coordnadas, analisar as propridads dcorrnts dssa xprssão fazr algumas aplicaçõs intrssants dos produtos vtorial misto. 1. Exprssão do produto misto
Aula 15 Nsta aula vamos xprssar o produto misto m trmos d coordnadas, analisar as propridads dcorrnts dssa xprssão fazr algumas aplicaçõs intrssants dos produtos vtorial misto. 1. Exprssão do produto misto
Hewlett-Packard MATRIZES. Aulas 01 a 06. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz
 Hwltt-Packard MATRIZES Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MATRIZES NOÇÃO DE MATRIZ REPRESENTAÇÃO DE UMA MATRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDAMENTAL MATRIZES ESPECIAIS IGUALDADE
Hwltt-Packard MATRIZES Aulas 0 a 06 Elson Rodrigus, Gabril Carvalho Paulo Luiz Sumário MATRIZES NOÇÃO DE MATRIZ REPRESENTAÇÃO DE UMA MATRIZ E SEUS ELEMENTOS EXERCÍCIO FUNDAMENTAL MATRIZES ESPECIAIS IGUALDADE

 Matmática A Etnsivo V. 6 Rsolva.) a) Aula. ( )
Matmática A Etnsivo V. 6 Rsolva.) a) Aula. ( )