Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
|
|
|
- Nathalia Valverde Jardim
- 7 Há anos
- Visualizações:
Transcrição
1 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM
2 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para cada um dos úmeros bomas abaxo, ecotre outro de mesmo valor e a mesma lha do Trâgulo de Pascal Por exemplo, a b c d 7 0 Exercíco Calcule os úmeros Bomas abaxo: a b c d Exercíco Determe o coefcete de a x o desevolvmeto de x + ; b x o desevolvmeto de x + ; c x o desevolvmeto de x + ; d x o desevolvmeto de x + Exercíco + : + a Se b Se c Se d Se Em cada tem abaxo, determe o valor de e ; + e 6; + 8 e 6; + 6 e 6 + Exercíco Determe o valor de + + se: a + 6 e 9; + b + e 66; + c + e + + Dca: Use que Exercíco 6 Determe o coefcete de x o desevolvmeto de x + Veja exercíco 0 Exercíco 7 Determe o coefcete de x o desevolvmeto de x + Exercíco 8 Determe o úmero de termos o desevolvmeto de cada um dos bômos abaxo: a x + y b x + y c x + y 7 d x + y Exercíco 9 No desevolvmeto de x + y 00, qual o vgésmo termo se o desevolvmeto for feto em potêcas de expoetes crescetes em x? Exercíco 0 Determe o coefcete depedete de y o desevolvlmeto dos segutes bômos: a y + y b c y + y 6 y + y Exercíco Ecotre a soma dos possíves valores de p que satsfazem: a p + p b p + p c p + 6 p d p + p Exercícos de Fxação Exercíco Qual o coefcete de x + o desevolvmeto de x + x? Exercíco Quatos termos racoas aparecem o desevolvmeto de + 0? Exercíco Calcule aproxmadamete, 00 0 usado o Teorema Bomal Exercíco Calcule aproxmadamete, 00 0 usado o Teorema Bomal Exercíco 6 Calcule o valor da soma: S Exercíco 7 Determe o termo cetral do desevolvmeto de x 8 x Exercíco 8 Determe o coefcete de x o desevolvmeto de x + x matematca@obmeporgbr
3 Exercíco 9 Para que valores de o desevolvmeto de x x possu um termo depedete de x Exercícos de Aprofudameto e de Exames Exercíco 0 Exercíco + Mostre que + Mostre que + +!!! Exercíco O termo depedete de x o desevolvmeto de x 0 x é gual a: a 0 b 0 c 0 d 0 e 0 Exercíco Desevolvedo-se o bômo Px + x, podemos dzer que a soma de seus coefcetes é a 6 b c d 0 e 8 Exercíco A expressão + é gual a: a 60 b 690 c 7 d 8 e 60 Exercíco A soma dos coefcetes de todos os termos do desevolvmeto de x y 0 é gual a: a 0 b c 9 d e 9 Exercíco 6 Sedo um úmero real postvo, o tercero termo do desevolvmeto de x +, ordeado segudo expoetes decrescetes de x, é 66x 0 Assm, é correto afrmar que é gual a:, deter- a /66 b /6 c /8 d / e / Exercíco 7 Se + 6 me o valor de a b 6 c 9 d e 8 Exercíco 8 O termo depedete de x o desevolvmeto do bômo x x é x Exercíco 9 Sabedo que x e y são úmeros postvos x y e x + x y + 6x y + xy + y 6, podemos coclur que: a x 7/6 b x 6/ c x / d x / e x / Exercíco 0 A respeto das combações a e b, temos que, para cada,,, a dfereça a b é gual a:! a + a b e + a Exercíco + a c + a d + a Sabedo que é de 0 a soma dos coefcetes do polômo em x e y, obtdo pelo desevolvmeto do bômo x + y m, temos que o úmero de arrajos sem repetção de m elemetos, tomados a, é: a 80 b 90 c 70 d 00 e 60 Exercíco cos x 0 Em [0, π], se α é a maor raz da equação cos x + cos x cos x + 0, etão se α vale: a b c 0 d / e / Exercíco Cosdere a equação, o cojuto dos úmero reas, x + x + x x + x + 7x etão x 6 vale: a 6 b 0 c 6 d 6 6 e 6 Exercíco No desevolvmeto de [x + /x], N, os coefcetes bomas do quarto e do décmotercero termos são guas Etão o termo depedete de x é o: a décmo b décmo-prmero c oo d décmo-segudo e sexto Exercíco Para cada, temos que + + é gual a: a 79 b 97 c 89 e 6 7 d 76 a b c d + e + matematca@obmeporgbr
4 Exercíco 6 A soma de todos os coefcetes do desevolvmeto de x y 7 é: a 0 b c d 7 e 9777 Exercíco 7 O coefcete de x o polômo px x x + é: a 0 b 0 c 00 d 0 e 80 Exercíco 8 Se o tercero termo do desevolvmeto de a + b é a b, etão o sexto termo é: a a b b a b c a b d 7ab 6 e 7a b Exercíco 9 Sejam α e β úmeros reas Supoha que ao desevolvermos αx + βy, os coefcetes dos moômos x y e x y sejam guas a 0 e 70, respectvamete Nestas codções, assale a opção que cotém o valor de α β a / b / c / d e / Exercíco 0 Todas as captas de um país estão terlgadas por estradas pavmetadas, de acordo com o segute crtéro: uma úca estrada lga duas captas Com a cração de duas ovas captas, fo ecessára a costrução de mas de estradas pavmetadas para que todas as captas cotuassem lgadas com o mesmo crtéro Determe o úmero cal de estradas Exercíco Um cofre eletrôco possu um pael com dez teclas umércas e pode ser aberto por meo da dgtação, em qualquer ordem, de três teclas dsttas detre ses habltadas prevamete pelo fabrcate Cosdere o úmero máxmo de cojutos de três teclas que abrem o cofre Na fgura em destaque, as teclas azus represetam as habltadas prevamete Exercíco Mostre que: m m r r r m r Se o fabrcate reduzsse para cco o úmero de teclas habltadas, havera etre elas um total de m cojutos dsttos de três teclas dsttas para abrr o cofre Calcule o valor de m Exercíco Desevolvedo-se a expressão [x + /xx /x] 6, obtém-se como termo depedete de x o valor: matematca@obmeporgbr
5 a 9 7 a 7 b 6 c 6 d Respostas e Soluções b c d a Pelo desevolvmeto de Newto, o coefcete de x é dado por 6 b Pelo desevolvmeto de Newto, o coefcete de x é dado por 8 c Pelo desevolvmeto de Newto, o coefcete de x é dado por 90 d Pelo desevolvmeto de Newto, o coefcete de x é dado por 80 Pela relação de Stfel, temos: Portato, basta somar os valores dados em cada tem a 70 b c 8 d Usado a dca, segue que: Temos etão a 9 66 b 6 c 6 6 Pelo desevolvmeto de Newto, o coefcete de x é dado por 7 Pelo desevolvmeto de Newto, o coefcete de x é dado por Como a + b a b, o desevolvmeto 0 de tal bômo possu + termos Portato, as respostas são: a b 6 c 8 d 9 Desevolvedo em potêcas de expoete crescete, temos x + y x y 00 Portato, o vgésmo 0 00 termo é x 9 y a b c No desevolvmeto do Bômo de Newto, o termo geérco será da forma y y Assm o termo depedete ocorre quado, ou seja, 6 Portato o coefcete procurado é No desevolvmeto do Bômo de Newto, o termo 6 geérco será da forma y y 6 Assm o termo depedete ocorre quado 6, ou seja, 6 Portato o coefcete procurado é 6 60 No desevolvmeto do Bômo de Newto, o termo geérco será da forma y y Assm o termo depedete ocorre quado, ou seja, 96 Portato o coefcete procurado é Para que temos l ou l, sso l os gera tpcamete dos casos em cada equação: a b No prmero caso, p + p, ou seja, p No segudo caso, p + p, ou seja, p Portato a soma procurada é 7; No prmero caso, p + p, ou seja, p No segudo caso, p + p, ou seja, p Portato a soma procurada é ; matematca@obmeporgbr
6 c d No prmero caso, p + 6 p, ou seja, p No segudo caso, p + 6 p, ou seja, p Portato a soma procurada é ; No prmero caso, p + p, ou seja, p No segudo caso p + p, ou seja, p 6 Portato a soma procurada é ; Em vrtude da multplcação por x, todos os termos do desevolvmeto de x + x terão expoete pelo meos a varável x Portato, se <, o coefcete de x + será zero Se, o coefcete de x + o produto dado é gual ao coefcete de x + x em x +, ou seja, No desevolvmeto do Bômo de Newto, o termo 0 geérco terá a forma 0 Quado é par, tato quato 0 são racoas Quado é ímpar, , 0 sedo 9 racoal Como 0 é rracoal, o produto ateror também é um úmero rracoal Portato, os termos do desevolvmeto são racoas apeas quado é par e, cosequetemete, exstem 6 termos racoas o desevolvmeto bomal Se a e h 0, 00, temos, 00 0 a + h 0 0 a 0 + a 9 h + 0 a 0 + a 9 h, 00 0 a 8 h + Fzemos a aproxmação ateror usado que as potêcas h, com >, estão muto próxmas de zero bem como os termos geércos 0 a0 h assocados a elas Usado uma calculadora, ote que, 00 0, 0077 Repetdo a estratéga do exercíco ateror, se a e h 0, 00, temos, 00 0 a + h 0 0 a 0 + a 9 h + 0 a 0 + a 9 h, 0 0 a 8 h + Fzemos a aproxmação ateror usado que as potêcas h, com >, estão muto próxmas de zero bem como os termos geércos 0 a0 h assocados a elas Usado uma calculadora, ote que, 00 0, Pelo desevolvmeto bomal de Newto: S O termo geérco do desevolvmeto bomal é dado por x x 8 O x termo cetral pode ser obtdo fazedo 8/ e é 8 dado por x 70x 8 Temos x + x x + x + x + x x + x + x + x Basta etão determarmos o coefcete de x em cada um dos termos aterores No prmero, seu coefecete é No segudo, é e o tercero é Portato, o coefcete de x o produto é O termo geérco do desevolvmeto bomal é dado por x x x Para que exste um termo depedete de x, devemos ter da forma para algum tero ão egatvo 0 Prmera Solução + + +! +!! + +!!! matematca@obmeporgbr
7 Seguda Solução Cosdere um grupo de + craças e o segute problema: De quatas formas podemos escolher + delas para partcparem de uma vagem sabedo que uma das escolhdas também receberá um prêmo especal extra? Podemos resolver esse problema de duas formas A prmera delas é escolher calmete as + craças, sso + pode ser feto de formas, e posterormete, escolher detre as selecoadas aquela que receberá o prêmo, + sso pode ser feto de + formas Pelo prcípo multplcatvo, temos + escolhas possíves A + + seguda forma sera calmete escolher a craça que gahará o prêmo e que evtavelmete estará a vagem, sso pode ser feto de + formas, e em seguda, escolhermos as outras craças, detre as que sobraram, de formas Novamete, pelo prcípo multplcatvo, o total de escolhas possíves é + Portato, como as duas cotages devem produzr úmeros guas, temos Basta agora dvdr equação por + para coclurmos o desejado Aplcado o exercíco ateror, podemos escrever: +! 0!!! Extraído da Ama 0 O termo geérco do desevolvmeto bomal é da forma 0 0 x x x 0 Para o termo depedete de x, devemos ter 0 0, ou seja, Portato, o coefcete procurado é Resposta letra B Extraído da FGV 0 O termo geérco do desevolvmeto bomal é da forma x Ao substturmos x por, obteremos apeas o coefcete e, cosequetemete, a soma de todos eles é dada por + Resposta letra C ITA 00 Se a e b, temos a + b a b a b a b a b b + a b + a b FGV 008 O termo geérco do desevolvmeto 0 bomal é da forma x y 0 Ao substturmos x e y por, obteremos apeas o coefcete de cada termo e, cosequetemete, a soma de todos eles é dada por 0 Resposta letra B 6 FGV 007 O desevolvmeto pelo Bômo de Newto ordeado segudo expoetes decrescetes de x é: x + x + x + x 0 + Igualado o tercero termo forecdo o eucado ao ecotrado a expressão ateror, temos 0 66, ou seja, /0 Como é postvo, devemos ter / e a resposta é a letra E 7 FGV 00 Pela relação de Stfel, Para ocorrer tal gualdade etre elemetos de uma mesma lha do Trâgulo de Pascal, devemos ter 6, ou seja, 8 Resposta letra E 8 ITA 00 O termo geérco do desevolvmeto bomal é dado por x x x /6 x / 6 matematca@obmeporgbr
8 Para o termo depedete de x, devemos ter 0, ou seja, Portato, o coefcete procurado é: Resposta letra E 9 FGV 00 Temos / x + x y + 6x y + xy + y x + y Como x e y são reas postvos, segue que x + y Resolvedo o sstema: x + y x y ecotramos como soluções x / e y / Resposta letra E 0 ITA 00 Prmera Solução a b!!!!! +!! +!! + a Seguda Solução Pelo exercíco 0, temos a b a ITA 00 Para ecotrarmos a soma dos coefcetes da expasão bomal de x + y m, basta fazermos x y, obtedo + m m Sabedo que tal valor é 0, podemos coclur que m 0 Portato o úmero de arrajos sem repetção de 0 elemetos tomados dos a dos é Resposta letra B Maceze 999 Pelo desevolvmeto do Bômo de Newto, a expressão dada é equvalete a cos x 0, ou seja, cos x No tervalo [0, π], a maor solução é α π Portato, se α se π Resposta letra A Pelo desevolvmeto do Bômo de Newto, o membro do lado esquerdo é equvalete a x + x Portato, x 7x, ou seja, x e x 6 0 Resposta letra B Maceze 999 A gualdade dada etre os coefcetes bomas mecoados o eucado os permte coclur que Portato, + O termo geérco do desevolvmeto bomal possu a etão a forma x x O termo x depedete de x ocorre quado 0, ou seja, e o termo depedete de x é o sexto Resposta letra E ITA 99 Se, temos j0 j0 j + j j + j j + j0 j+ j j + j0 Como é úmero real, podemos coclur que j0 j0 j j j + A resposta é a letra A j 0 6 FEI 99 Basta fazer x y, obtedo 7 Resposta letra B 7 matematca@obmeporgbr
9 7 UFCE Os termos de grau e o desevolvmeto bomal x + são x e x Pela propredade de dstrbutvdade, o termo de grau o produto dado é x x 80x Portato, o coefcete procurado é 80 8 PUC-RS O tercero termo, segudo potêcas crescetes de b, é da forma a b Comparado com o coefcete dado, temos, ou seja 7 O 7 sexto termo é dado por a b a b a b Resposta letra C 9 UFCE Pelo desevolvmeto do Bômo de Newto, temos xα yβ 0x y xα yβ 70x y Dvddo os coefcetes da prmera equação pelos da seguda, obtemos Resposta letra E α β α β O termo depedete de x ocorre quado 0, ou 6 seja, Portato, o coefcete procurado é 0 Iremos provar a gualdade usado uma cotagem dupla Cosdere o problema de cotarmos o úmero de maeras de escolhermos m bolas, detre um grupo de bolas guas, para serem ptadas de preto e, em seguda, escolhermos r dessas m bolas que serão ptadas de preto para receberem também uma lstra da cor azul O úmero de maeras de escolhermos as bolas que serão ptadas de preto é Em seguda, o úmero m de maeras de escolhermos m dessas bolas que serão m ptadas de preto para receberem a lstra azul é r Pelo prcípo multplcatvo, o total de escolhas é m m r Outra maera de resolver o problema é calmete escolhermos logo as r bolas que serão ptadas de preto e que vão receber a lstra azul, sso pode ser feto de r maeras Em seguda, das r bolas restates, basta escolhermos as m r bolas que serão ptadas apeas r de preto Isso pode ser feto de Pelo prcípo m r r multplcatvo, o total de escolhas é r m r Como as duas cotages devem produzr úmeros guas, obtemos assm o resultado do eucado 0 UERJ 0 Adaptado Cada uma das ovas cdades deverá ser lgada a cada uma das cdades e assm de cada uma delas partrão ovas estradas Além dsso, precsamos ur essas duas ovas por uma estrada Portato, +, ou seja, 0 O total de estradas o íco era 0 6 e m UERJ 00 Temos 6 m FGV-SP Temos Portato, [x + /xx /x] 6 x x x x 6 x Produzdo por Arqumedes Curso de Eso cotato@cursoarqumedescom 8 matematca@obmeporgbr
tica Professor Renato Tião
 Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Introdução à Teoria dos Números Notas 1 Os Princípios da Boa Ordem e de Indução Finita Prof Carlos Alberto S Soares
 Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
RESUMO E EXERCÍCIOS NÚMEROS COMPLEXOS ( )
 NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
Oitava Lista de Exercícios
 Uversdade Federal Rural de Perambuco Dscpla: Matemátca Dscreta I Professor: Pablo Azevedo Sampao Semestre: 07 Otava Lsta de Exercícos Lsta sobre defções dutvas (recursvas) e prova por dução Esta lsta fo
Uversdade Federal Rural de Perambuco Dscpla: Matemátca Dscreta I Professor: Pablo Azevedo Sampao Semestre: 07 Otava Lsta de Exercícos Lsta sobre defções dutvas (recursvas) e prova por dução Esta lsta fo
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Como CD = DC CD + DC = 0
 (9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
(9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
x n = n ESTATÍSTICA STICA DESCRITIVA Conjunto de dados: Organização; Amostra ou Resumo; Apresentação. População
 ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
PLANO PROBABILIDADES Professora Rosana Relva DOS. Números Inteiros e Racionais COMPLEXOS NÚMEROS COMPLEXOS NÚMEROS COMPLEXOS NÚMEROS COMPLEXOS
 Professor Luz Atoo de Carvalho PLANO PROBABILIDADES Professora Rosaa Relva DOS Números Iteros e Racoas COMPLEXOS rrelva@globo.com Número s 6 O Número Por volta de 00 d.c a mpressão que se tha é que, com
Professor Luz Atoo de Carvalho PLANO PROBABILIDADES Professora Rosaa Relva DOS Números Iteros e Racoas COMPLEXOS rrelva@globo.com Número s 6 O Número Por volta de 00 d.c a mpressão que se tha é que, com
Atividades Práticas Supervisionadas (APS)
 Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Relatório 2ª Atividade Formativa UC ECS
 Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
MEDIDAS DE DISPERSÃO:
 MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
Licenciatura em Ciências USP/ Univesp funções polinomiais 4
 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Tabela 1 Números de acidentes /mês no Cruzamento X em CG/07. N de acidentes / mês fi f
 Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
Estatística: Aplicação ao Sensoriamento Remoto SER ANO Estimação Pontual
 Estatístca: Aplcação ao Sesorameto Remoto SER 04 - ANO 08 Estmação Potual Camlo Daleles Reó camlo@dp.pe.br http://www.dp.pe.br/~camlo/estatstca/ Iferêca Estatístca Cosdere o expermeto: retram-se 3 bolas
Estatístca: Aplcação ao Sesorameto Remoto SER 04 - ANO 08 Estmação Potual Camlo Daleles Reó camlo@dp.pe.br http://www.dp.pe.br/~camlo/estatstca/ Iferêca Estatístca Cosdere o expermeto: retram-se 3 bolas
2. MODELO DETALHADO: Relações de Recorrência. Exemplo: Algoritmo Recursivo para Cálculo do Fatorial Substituição Repetida
 . MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
. MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
QUESTÕES DISCURSIVAS Módulo 01 (com resoluções)
 QUESTÕES DISCURSIVAS Módulo 0 (com resoluções D (Fuvest-SP/00 Nos tens abaxo, denota um número complexo e a undade magnára ( Suponha a Para que valores de tem-se? b Determne o conjunto de todos os valores
QUESTÕES DISCURSIVAS Módulo 0 (com resoluções D (Fuvest-SP/00 Nos tens abaxo, denota um número complexo e a undade magnára ( Suponha a Para que valores de tem-se? b Determne o conjunto de todos os valores
Exercícios - Sequências de Números Reais (Solução) Prof Carlos Alberto S Soares
 Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
Matemática Ficha de Trabalho
 Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
? Isso é, d i= ( x i. . Percebeu que
 Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Capitulo 1 Resolução de Exercícios
 S C J S C J J C FORMULÁRIO Regme de Juros Smples 1 1 S C 1 C S 1 1.8 Exercícos Propostos 1 1) Qual o motate de uma aplcação de R$ 0.000,00 aplcados por um prazo de meses, à uma taxa de 2% a.m, os regmes
S C J S C J J C FORMULÁRIO Regme de Juros Smples 1 1 S C 1 C S 1 1.8 Exercícos Propostos 1 1) Qual o motate de uma aplcação de R$ 0.000,00 aplcados por um prazo de meses, à uma taxa de 2% a.m, os regmes
Olá, amigos concursandos de todo o Brasil!
 Matemátca Facera ICMS-RJ/008, com gabarto cometado Prof. Wager Carvalho Olá, amgos cocursados de todo o Brasl! Veremos, hoje, a prova do ICMS-RJ/008, com o gabarto cometado. - O artgo º da Le.948 de 8
Matemátca Facera ICMS-RJ/008, com gabarto cometado Prof. Wager Carvalho Olá, amgos cocursados de todo o Brasl! Veremos, hoje, a prova do ICMS-RJ/008, com o gabarto cometado. - O artgo º da Le.948 de 8
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
NÚMEROS COMPLEXOS. z = a + bi,
 NÚMEROS COMPLEXOS. DEFINIÇÃO No cojuto dos úmeros reas R, temos que a = a. a é sempre um úmero ão egatvo para todo a. Ou seja, ão é possível extrar a ra quadrada de um úmero egatvo em R. Dessa mpossbldade
NÚMEROS COMPLEXOS. DEFINIÇÃO No cojuto dos úmeros reas R, temos que a = a. a é sempre um úmero ão egatvo para todo a. Ou seja, ão é possível extrar a ra quadrada de um úmero egatvo em R. Dessa mpossbldade
13 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL
 3 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL Como vto em amotragem o prmero bmetre, etem fatore que fazem com que a obervação de toda uma população em uma pequa eja mpratcável, muta veze em vrtude
3 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL Como vto em amotragem o prmero bmetre, etem fatore que fazem com que a obervação de toda uma população em uma pequa eja mpratcável, muta veze em vrtude
Análise Combinatória I
 Aálise Combiatória I O pricípio fudametal da cotagem ada mais é que a maeira mais simples possível de determiar de quatas maeiras diferetes que um eveto pode acotecer. Se eu, por exemplo, estiver pitado
Aálise Combiatória I O pricípio fudametal da cotagem ada mais é que a maeira mais simples possível de determiar de quatas maeiras diferetes que um eveto pode acotecer. Se eu, por exemplo, estiver pitado
INTRODUÇÃO A ESTATÍSTICA
 Hewlett-Packard INTRODUÇÃO A ESTATÍSTICA Aulas 01 e 06 Elso Rodrgues, Gabrel Carvalho e Paulo Luz Sumáro Defções... 1 EXERCÍCIOS FUNDAMENTAIS... 1 Meddas de tedêca cetral... 1 Méda artmétca smples... 1
Hewlett-Packard INTRODUÇÃO A ESTATÍSTICA Aulas 01 e 06 Elso Rodrgues, Gabrel Carvalho e Paulo Luz Sumáro Defções... 1 EXERCÍCIOS FUNDAMENTAIS... 1 Meddas de tedêca cetral... 1 Méda artmétca smples... 1
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
MAE0229 Introdução à Probabilidade e Estatística II
 Exercíco Cosdere a dstrbução expoecal com fução de desdade de probabldade dada por f (y; λ) = λe λy, em que y, λ > 0 e E(Y) = /λ Supor que o parâmetro λ pode ser expresso proporcoalmete aos valores de
Exercíco Cosdere a dstrbução expoecal com fução de desdade de probabldade dada por f (y; λ) = λe λy, em que y, λ > 0 e E(Y) = /λ Supor que o parâmetro λ pode ser expresso proporcoalmete aos valores de
Números Complexos. 2. (IME) Seja z um número complexo de módulo unitário que satisfaz a condição z 2n 1, onde n é um número inteiro positivo.
 Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
UNICAMP - 2004. 2ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
REGESD Prolic Matemática e Realidade- Profª Suzi Samá Pinto e Profº Alessandro da Silva Saadi
 REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
Estatística. 2 - Estatística Descritiva
 Estatístca - Estatístca Descrtva UNESP FEG DPD Prof. Edgard - 0 0- ESTATÍSTICA DESCRITIVA Possblta descrever as Varáves: DESCRIÇÃO GRÁFICA MEDIDAS DE POSIÇÃO MEDIDAS DE DISPERSÃO MEDIDAS DE ASSIMETRIA
Estatístca - Estatístca Descrtva UNESP FEG DPD Prof. Edgard - 0 0- ESTATÍSTICA DESCRITIVA Possblta descrever as Varáves: DESCRIÇÃO GRÁFICA MEDIDAS DE POSIÇÃO MEDIDAS DE DISPERSÃO MEDIDAS DE ASSIMETRIA
DISTRIBUIÇÃO HIPERGEOMÉTRICA
 7 DISTRIBUIÇÃO HIPERGEOMÉTRICA Cosdere-se uma população fta costtuída por N elemetos dstrbuídos por duas categoras eclusvas e eaustvas de dmesões M e N M, respectvamete. Os elemetos da prmera categora
7 DISTRIBUIÇÃO HIPERGEOMÉTRICA Cosdere-se uma população fta costtuída por N elemetos dstrbuídos por duas categoras eclusvas e eaustvas de dmesões M e N M, respectvamete. Os elemetos da prmera categora
Curso Mentor. Radicais ( ) www.cursomentor.wordpress.com. Definição. Expoente Fracionário. Extração da Raiz Quadrada. Por definição temos que:
 Curso Metor www.cursometor.wordpress.com Defiição Por defiição temos que: Radicais a b b a, N, Observação : Se é par devemos ter que a é positivo. Observação : Por defiição temos:. 0 0 Observação : Chamamos
Curso Metor www.cursometor.wordpress.com Defiição Por defiição temos que: Radicais a b b a, N, Observação : Se é par devemos ter que a é positivo. Observação : Por defiição temos:. 0 0 Observação : Chamamos
Métodos iterativos. Capítulo O Método de Jacobi
 Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
BINÔMIO DE NEWTON. O desenvolvimento da expressão 2. a b é simples, pois exige somente quatro multiplicações e uma soma:
 07 BINÔMIO DE NEWTON O desevolvimeto da epressão a b é simples, pois eige somete quatro multiplicações e uma soma: a b a b a b a ab ba b a ab b O desevolvimeto de a b é uma tarefa um pouco mais trabalhosa,
07 BINÔMIO DE NEWTON O desevolvimeto da epressão a b é simples, pois eige somete quatro multiplicações e uma soma: a b a b a b a ab ba b a ab b O desevolvimeto de a b é uma tarefa um pouco mais trabalhosa,
16/03/2014. IV. Juros: taxa efetiva, equivalente e proporcional. IV.1 Taxa efetiva. IV.2 Taxas proporcionais. Definição:
 6// IV. Juros: taxa efetva, equvalete e proporcoal Matemátca Facera Aplcada ao Mercado Facero e de Captas Professor Roaldo Távora IV. Taxa efetva Defção: É a taxa de juros em que a udade referecal de seu
6// IV. Juros: taxa efetva, equvalete e proporcoal Matemátca Facera Aplcada ao Mercado Facero e de Captas Professor Roaldo Távora IV. Taxa efetva Defção: É a taxa de juros em que a udade referecal de seu
Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira INEP Ministério da Educação MEC. Índice Geral de Cursos (IGC)
 Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Material Teórico - Módulo de MATEMÁTICA FINANCEIRA. Financiamentos. Primeiro Ano do Ensino Médio
 Materal Teórco - Módulo de MATEMÁTICA FINANCEIRA Facametos Prmero Ao do Eso Médo Autor: Prof Fracsco Bruo Holada Autor: Prof Atoo Camha Muz Neto 20 de agosto de 2018 1 Itrodução Neste materal, remos aplcar
Materal Teórco - Módulo de MATEMÁTICA FINANCEIRA Facametos Prmero Ao do Eso Médo Autor: Prof Fracsco Bruo Holada Autor: Prof Atoo Camha Muz Neto 20 de agosto de 2018 1 Itrodução Neste materal, remos aplcar
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Requisitos metrológicos de instrumentos de pesagem de funcionamento não automático
 Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Matemática C Semiextensivo V. 2
 Matemátca C Semetesvo V. Eercícos 0) Através da observação dreta do gráfco, podemos coclur que: a) País. b) País. c) 00 habtates. d) 00 habtates. e) 00 0 0 habtates. 0) C Através do gráfco, podemos costrur
Matemátca C Semetesvo V. Eercícos 0) Através da observação dreta do gráfco, podemos coclur que: a) País. b) País. c) 00 habtates. d) 00 habtates. e) 00 0 0 habtates. 0) C Através do gráfco, podemos costrur
Cursos de Licenciatura em Ensino de Matemática e de EGI. Teoria de Probabilidade
 Celso Albo FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhaguee, Av. de Moçambque, km, Tel: +258 240078, Fax: +258 240082, Maputo Cursos de Lcecatura em Eso de Matemátca
Celso Albo FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhaguee, Av. de Moçambque, km, Tel: +258 240078, Fax: +258 240082, Maputo Cursos de Lcecatura em Eso de Matemátca
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
Capítulo 1 PORCENTAGEM
 Professor Joselas Satos da Slva Matemátca Facera Capítulo PORCETAGEM. PORCETAGEM A porcetagem ada mas é do que uma otação ( % ) usada para represetar uma parte de cem partes. Isto é, 20% lê-se 20 por ceto,
Professor Joselas Satos da Slva Matemátca Facera Capítulo PORCETAGEM. PORCETAGEM A porcetagem ada mas é do que uma otação ( % ) usada para represetar uma parte de cem partes. Isto é, 20% lê-se 20 por ceto,
RACIOCÍNIO LÓGICO / ESTATÍSTICA LISTA 2 RESUMO TEÓRICO
 RACIOCÍIO LÓGICO - Zé Carlos RACIOCÍIO LÓGICO / ESTATÍSTICA LISTA RESUMO TEÓRICO I. Cocetos Icas. O desvo médo (DM), é a méda artmétca dos desvos de cada dado da amostra em toro do valor médo, sto é x
RACIOCÍIO LÓGICO - Zé Carlos RACIOCÍIO LÓGICO / ESTATÍSTICA LISTA RESUMO TEÓRICO I. Cocetos Icas. O desvo médo (DM), é a méda artmétca dos desvos de cada dado da amostra em toro do valor médo, sto é x
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Total Bom Ruim Masculino
 UNIDADE I - ESTUDO DIRIGIDO Questão - Classfque as varáves em qualtatva (omal ou ordal ou quattatva (cotíua ou dscreta: a. População: aluos de uma Uversdade. Varável: cor dos cabelos (louro, castaho, ruvo,
UNIDADE I - ESTUDO DIRIGIDO Questão - Classfque as varáves em qualtatva (omal ou ordal ou quattatva (cotíua ou dscreta: a. População: aluos de uma Uversdade. Varável: cor dos cabelos (louro, castaho, ruvo,
Desigualdades (por Iuri de Silvio ITA-T11)
 Desigualdades (por Iuri de Silvio ITA-T) Apresetação O objetivo desse artigo é apresetar as desigualdades mais importates para quem vai prestar IME/ITA, e mostrar como elas podem ser utilizadas a resolução
Desigualdades (por Iuri de Silvio ITA-T) Apresetação O objetivo desse artigo é apresetar as desigualdades mais importates para quem vai prestar IME/ITA, e mostrar como elas podem ser utilizadas a resolução
e represente as no plano Argand-Gauss.
 PROFESSOR: Cládo Das BANCO DE QUESTÕES MATEMÁTICA ª SÉRIE ENSINO MÉDIO ============================================================================================== - Determe o módlo dos segtes úmeros
PROFESSOR: Cládo Das BANCO DE QUESTÕES MATEMÁTICA ª SÉRIE ENSINO MÉDIO ============================================================================================== - Determe o módlo dos segtes úmeros
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
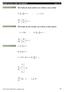 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
Estudo das relações entre peso e altura de estudantes de estatística através da análise de regressão simples.
 Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
CÁLCULO DE RAÍZES DE EQUAÇÕES NÃO LINEARES
 CÁLCULO DE RAÍZES DE EQUAÇÕES NÃO LINEARES Itrodução Em dversos camos da Egehara é comum a ecessdade da determação de raízes de equações ão leares. Em algus casos artculares, como o caso de olômo, que
CÁLCULO DE RAÍZES DE EQUAÇÕES NÃO LINEARES Itrodução Em dversos camos da Egehara é comum a ecessdade da determação de raízes de equações ão leares. Em algus casos artculares, como o caso de olômo, que
Matemática. Binômio de Newton. Professor Dudan.
 Matemática Biômio de Newto Professor Duda www.acasadococurseiro.com.br Matemática BINÔMIO DE NEWTON Defiição O biômio de Newto é uma expressão que permite calcular o desevolvimeto de (a + b), sedo a +
Matemática Biômio de Newto Professor Duda www.acasadococurseiro.com.br Matemática BINÔMIO DE NEWTON Defiição O biômio de Newto é uma expressão que permite calcular o desevolvimeto de (a + b), sedo a +
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
Sucessão ou Sequência. Sucessão ou seqüência é todo conjunto que consideramos os elementos dispostos em certa ordem. janeiro,fevereiro,...
 Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Curso Metor www.cursometor.wordpress.com Sucessão ou Sequêcia Defiição Sucessão ou seqüêcia é todo cojuto que cosideramos os elemetos dispostos em certa ordem. jaeiro,fevereiro,...,dezembro Exemplo : Exemplo
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
QUESTÕES DISCURSIVAS Módulo
 QUESTÕES DISCURSIVAS Módulo 0 009 D (FUVEST-SP 008 A fgura ao lado represeta o úero + o plao coplexo, sedo a udade agára Nessas codções, a detere as partes real e agára de e b represete e a fgura a segur
QUESTÕES DISCURSIVAS Módulo 0 009 D (FUVEST-SP 008 A fgura ao lado represeta o úero + o plao coplexo, sedo a udade agára Nessas codções, a detere as partes real e agára de e b represete e a fgura a segur
Regressão Simples. Parte III: Coeficiente de determinação, regressão na origem e método de máxima verossimilhança
 Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
5n 3. 1 nsen(n + 327) e)
 Exercícios 1 Mostre, utilizado a defiição, que as seguites sucessões são limitadas: 2 4 50 a) b) 3 +16 1 5 3 2 c) 1 4( 1) 8 5 d) 100 5 3 2 + 2( 1) 1 4( 1) 8 1 se( + 327) e) f) 5 3 2 4 4 2 2 Mostre, utilizado
Exercícios 1 Mostre, utilizado a defiição, que as seguites sucessões são limitadas: 2 4 50 a) b) 3 +16 1 5 3 2 c) 1 4( 1) 8 5 d) 100 5 3 2 + 2( 1) 1 4( 1) 8 1 se( + 327) e) f) 5 3 2 4 4 2 2 Mostre, utilizado
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
M = C( 1 + i.n ) J = C.i.n. J = C((1+i) n -1) MATEMÁTICA FINANCEIRA. M = C(1 + i) n BANCO DO BRASIL. Prof Pacher
 MATEMÁTICA 1 JUROS SIMPLES J = C.. M C J J = M - C M = C( 1 +. ) Teste exemplo. ados com valores para facltar a memorzação. Aplcado-se R$ 100,00 a juros smples, à taxa omal de 10% ao ao, o motate em reas
MATEMÁTICA 1 JUROS SIMPLES J = C.. M C J J = M - C M = C( 1 +. ) Teste exemplo. ados com valores para facltar a memorzação. Aplcado-se R$ 100,00 a juros smples, à taxa omal de 10% ao ao, o motate em reas
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
d s F = m dt Trabalho Trabalho
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
1. Conceitos básicos de estatística descritiva 1.3. Noção de extracção aleatória e de probabilidade
 Sumáro (3ª aula). Cocetos báscos de estatístca descrtva.3. Noção de etracção aleatóra e de probabldade.4 Meddas de tedêca cetral.4. Méda artmétca smples.4. Méda artmétca poderada.4.3 Méda artmétca calculada
Sumáro (3ª aula). Cocetos báscos de estatístca descrtva.3. Noção de etracção aleatóra e de probabldade.4 Meddas de tedêca cetral.4. Méda artmétca smples.4. Méda artmétca poderada.4.3 Méda artmétca calculada
Apostila de Introdução Aos Métodos Numéricos
 Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
ESTATÍSTICA Exame Final 1ª Época 3 de Junho de 2002 às 14 horas Duração : 3 horas
 Faculdade de cooma Uversdade Nova de Lsboa STTÍSTIC xame Fal ª Época de Juho de 00 às horas Duração : horas teção:. Respoda a cada grupo em folhas separadas. Idetfque todas as folhas.. Todas as respostas
Faculdade de cooma Uversdade Nova de Lsboa STTÍSTIC xame Fal ª Época de Juho de 00 às horas Duração : horas teção:. Respoda a cada grupo em folhas separadas. Idetfque todas as folhas.. Todas as respostas
S S S S 5. Uma pessoa deposita em um banco, no fim de cada mês, durante 5 meses, a quantia de R$ 200,00. 1,05 1
 CopyMarket.com Todos os dretos reservados. ehuma parte desta publcação poderá ser reproduzda sem a autorzação da Edtora. Título: Matemátca Facera e Comercal utores: Roberto Domgos Mello e Carlos Eduardo
CopyMarket.com Todos os dretos reservados. ehuma parte desta publcação poderá ser reproduzda sem a autorzação da Edtora. Título: Matemátca Facera e Comercal utores: Roberto Domgos Mello e Carlos Eduardo
AULA Espaços Vectoriais Estruturas Algébricas.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resolvedo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resolvedo os problemas
AULA Produto interno em espaços vectoriais reais ou complexos Produto Interno. Norma. Distância.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
PROVA 2 Cálculo Numérico. Q1. (2.0) (20 min)
 PROVA Cálculo Numérco Q. (.0) (0 mn) Seja f a função dada pelo gráfco abaxo. Para claro entendmento da fgura, foram marcados todos os pontos que são: () raízes; () pontos crítcos; () pontos de nflexão.
PROVA Cálculo Numérco Q. (.0) (0 mn) Seja f a função dada pelo gráfco abaxo. Para claro entendmento da fgura, foram marcados todos os pontos que são: () raízes; () pontos crítcos; () pontos de nflexão.
( ) ( ) ( ) ( ) ( ) 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Introdução.
 55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
CADERNO 1 (É permitido o uso de calculadora gráfica.)
 Proposta de teste de avalação [mao 09] Nome: Ao / Turma: N.º: Data: - - Não é permtdo o uso de corretor. Deves rscar aqulo que pretedes que ão seja classfcado. A prova clu um formuláro. As cotações dos
Proposta de teste de avalação [mao 09] Nome: Ao / Turma: N.º: Data: - - Não é permtdo o uso de corretor. Deves rscar aqulo que pretedes que ão seja classfcado. A prova clu um formuláro. As cotações dos
CAP. 5 DETERMINANTES 5.1 DEFINIÇÕES DETERMINANTE DE ORDEM 2 EXEMPLO DETERMINANTE DE ORDEM 3
 DETERMINNTES CP. DETERMINNTES. DEFINIÇÕES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é por defção plcção: : M IK IK ( ) DETERMINNTES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é
DETERMINNTES CP. DETERMINNTES. DEFINIÇÕES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é por defção plcção: : M IK IK ( ) DETERMINNTES DETERMINNTE DE ORDEM O ermte de um mtrz qudrd de ordem é
CAPÍTULO 2 - Estatística Descritiva
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
ANÁLISE DE ERROS. Todas as medidas das grandezas físicas deverão estar sempre acompanhadas da sua dimensão (unidades)! ERROS
 ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
Centro de massa, momento linear de sistemas de partículas e colisões
 Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Teoria Elementar da Probabilidade. a) Cada experiência poderá ser repetida indefinidamente sob condições essencialmente inalteradas.
 Estatístca 47 Estatístca 48 Teora Elemetar da Probabldade SPECTOS PERTINENTES À CRCTERIZÇÃO DE UM EXPERIÊNCI LETÓRI MODELOS MTEMÁTICOS DETERMINÍSTICOS PROBBILÍSTICOS PROCESSO (FENÓMENO) LETÓRIO - Quado
Estatístca 47 Estatístca 48 Teora Elemetar da Probabldade SPECTOS PERTINENTES À CRCTERIZÇÃO DE UM EXPERIÊNCI LETÓRI MODELOS MTEMÁTICOS DETERMINÍSTICOS PROBBILÍSTICOS PROCESSO (FENÓMENO) LETÓRIO - Quado
Forma padrão do modelo de Programação Linear
 POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
Grande Conjuntos de Dados. Organização; Resumo; Apresentação. Amostra ou População. Defeitos em uma linha de produção
 Prof. Lorí Val, Dr. val@pucr.br http://www.pucr.br/~val/ Grade Cojuto de Dado Orgazação; Reumo; Apreetação. Amotra ou População Defeto em uma lha de produção Lacado Deeho Torto Deeho Torto Lacado Torto
Prof. Lorí Val, Dr. val@pucr.br http://www.pucr.br/~val/ Grade Cojuto de Dado Orgazação; Reumo; Apreetação. Amotra ou População Defeto em uma lha de produção Lacado Deeho Torto Deeho Torto Lacado Torto
MATEMÁTICA PARA CONCURSOS II
 MATEMÁTICA PARA CONCURSOS II Módulo III Neste Módulo apresetaremos um dos pricipais assutos tratados em cocursos públicos e um dos mais temíveis por parte dos aluos: Progressão Aritmética e Progressão
MATEMÁTICA PARA CONCURSOS II Módulo III Neste Módulo apresetaremos um dos pricipais assutos tratados em cocursos públicos e um dos mais temíveis por parte dos aluos: Progressão Aritmética e Progressão
ESTATÍSTICA APLICADA À ZOOTECNIA
 ESTATÍSTICA APLICADA À ZOOTECNIA Eucldes Braga MALHEIROS *. INTRODUÇÃO.a) Somatóras e Produtóros Sejam,, 3,...,, valores umércos. A soma desses valores (somatóra) pode ser represetada por: = = = =. e o
ESTATÍSTICA APLICADA À ZOOTECNIA Eucldes Braga MALHEIROS *. INTRODUÇÃO.a) Somatóras e Produtóros Sejam,, 3,...,, valores umércos. A soma desses valores (somatóra) pode ser represetada por: = = = =. e o
