Licenciatura em Ciências USP/ Univesp funções polinomiais 4
|
|
|
- Brenda Sintra Cabral
- 7 Há anos
- Visualizações:
Transcrição
1 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos Gráfcos da Fução Quadrátca 4.5 Gráfcos das fuções polomas 4.6 Raízes das fuções polomas 4.7 Raízes da Fução Quadrátca 4.8 Máxmos e Mímos da Fução Quadrátca Lcecatura em Cêcas USP/ Uvesp fuções polomas 4
2 4.1 Potecação Lcecatura em Cêcas USP/Uvesp 53 Ates de abordar as fuções polomas, devemos troduzr uma operação com úmeros reas deomada potecação. Assm, defmos a potêca do úmero a, represetada por a (com N*), como o resultado do produto sucessvo do úmero a vezes, ou seja, Assm, defmos a 3 como: a a a a 3 a 4.1 vezes = a a a ou seja, o produto sucessvo de a três vezes. O resultado da potecação de um úmero real é um outro úmero real. Por exemplo, = 333 = 39 = = = 3 9= A potecação de um úmero, caracterzada pela potêca, é uma operação bastate smples sempre que a potêca evolva úmeros teros postvos. 4. Fuções Polomas de grau A operação potecação permte-os defr uma ampla classe de fuções, deomadas geercamete fuções polomas. Por exemplo, a fução cúbca, ou fução polomal de tercero grau é defda de forma aáloga à potecação uma vez que a fução da forma: 3 f ( x) = x 4.4 assoca ao valor x da varável depedete, um valor para a varável depedete o qual é determado da própra varável depedete: f ( x) = ( x x x) 4.5 fuções polomas 4
3 54 Lcecatura em Cêcas USP/Uvesp Um exemplo smples de fução cúbca é aquela que expressa o volume de uma esfera como fução do seu rao. Nesse caso a depedêca do volume em relação ao rao R, se escreve: V = 4π 3 Aalogamete, podemos defr uma fução evolvedo uma potêca arbtrára,, da varável depedete (cosderado-se, até esse poto, apeas úmeros teros e postvos). Ela será represetada por: R f x = x x x x vezes 4.7 Um polômo de grau é defdo como uma soma ou combações leares de fuções da forma 4.7, sto é, ele é defdo pela expressão geral: P x = a f x + a f x + + a f x + a Ou, aalogamete 1 P x = ax + a x ax+ a Ou seja, um polômo de grau pode ser defdo como uma soma de polômos de graus varado de um até, P ( x) = ax = Da defção acma, temos que a fução afm é, por defção, um polômo de prmero grau, ou seja, P x = ax+ a Fgura 4.1: Gráfco de uma fução polomal do prmero grau, ou fução afm. / Fote: Cepa TERRA E UNIVERSO Fudametos da Matemátca I
4 Lcecatura em Cêcas USP/Uvesp 55 Por exemplo, a velocdade escalar de uma partícula de massa m sujeta a uma força costate F atuado ao logo de uma curva é dada, como fução do tempo t decorrdo, por: F V t t V m = Nesse caso, a varável depedete, x, é o tempo, acma desgado por t, equato os parâmetros a 1 e a 0 são, respectvamete, a aceleração da partícula (a 1 = F/m) e a sua velocdade cal (V (t = 0) = V 0 ). Um polômo é cosderado par se: = ( ) P x P x 4.13 em cujo caso, deve ser ecessaramete um úmero par e todos os coefcetes das potêcas ímpares devem ser ulas. Por exemplo, o polômo: 4 4 P x = x 13x é um polômo par. Um polômo é dto ímpar, se: = ( ) P x P x 4.15 A codção ecessára e sufcete para que sso acoteça é a de que deve ser, ecessaramete, um úmero ímpar, bem como todos os coefcetes das potêcas pares devem ser ulos. Assm, o polômo P x = x 13x + 36x 4.16 é um polômo ímpar. fuções polomas 4
5 56 Lcecatura em Cêcas USP/Uvesp 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca A fução polomal do segudo grau cotém, além dos termos leares já aalsados, um termo quadrátco a varável x. Assm, a forma mas geral do polômo do segudo grau é: y( x) = ax + bx + c 4.17 Na expressão acma, empregamos a forma covecoal de apresetar as fuções quadrátcas, ou seja, em termos de parâmetros desgados pelas letras a, b e c. As costates a, b e c são deomadas, respectvamete, coefcete quadrátco, coefcete lear e coefcete costate ou termo lvre. O coefcete quadrátco é o úco que ão pode ser ulo, pos, esse caso, a equação sera do prmero grau. O gráfco de um polômo do segudo grau é uma parábola. O movmeto dos projétes a superfíce terrestre provê mas de um exemplo de gradezas que depedem quadratcamete, umas das outras. Por exemplo, a coordeada y assocada à posção de um projétl depede da coordeada x da segute forma: g x x y( x) + v + y v y0 0 0x v0x 4.18 ode g é a aceleração da gravdade, y 0 é o valor da coordeada y quado do íco do movmeto, sto é, quado x = 0, e a velocdade cal do projétl tem compoetes (v 0x, v 0y ). Fgura 4.: A trajetóra de um projétl é descrta por uma fução quadrátca. / Fote: Cepa TERRA E UNIVERSO Fudametos da Matemátca I
6 Lcecatura em Cêcas USP/Uvesp 57 A segur, escreveremos a expressão 4.17 de uma forma teramete equvalete, e muto útl, como se verá. Admtdo-se o parâmetro a ão ulo (a 0), podemos escrever as segutes gualdades: b c b c b b = + + = + + = a a a a 4a 4a y ax bx c a x x a x x b b c b b b 4ac = a x + x+ + a x = + a 4 a a 4a a 4a b x+ a 4.19 Dode fermos que b = + + = + a a y x ax bx c a x 4.0 ode o termo é dado por = b Embora seja pouco usual, vamos usar, e mutas vezes, essa últma forma da fução quadrátca. Em partcular, se recorrermos a um artfíco defdo como traslação de exos (mudaças de exos a dreção vertcal e horzotal) ela se tora útl para escrever a equação da parábola de uma forma mas smples. De fato, se redefrmos as varáves de acordo com as expressões: 4ac 4.1 b x = x+ a b 4ac y = y a 4. etão, o polômo do segudo grau pode ser escrto, essas ovas varáves, como: = y x ax 4.3 fuções polomas 4
7 58 Lcecatura em Cêcas USP/Uvesp Observe que efetuar traslações ao logo dos exos x e y correspode a realzar uma mudaça do sstema de coordeadas. As trasformações 4. podem ser pesadas como traslações dos exos a dreção horzotal e a dreção vertcal. Assm, medate uma ova escolha de exos, escolha essa defda por 4., podemos reduzr a expressão 4.17 ou 4.0 a uma forma bastate smples. Utlzaremos, dsttamete, qualquer uma das expressões 4.17, 4.0 ou 4.3. De acordo com a expressão 4.17, podemos costatar que a fução polomal sob a forma 4.3 é uma fução par. Isso os leva a uma smetra da parábola. De fato, ela é smétrca em relação à reta dada por: Fgura 4.3: Por meo da traslação de exos, podemos smplfcar a forma da fução quadrátca. / Fote: Cepa x = b a Aálse da Forma Geral dos Gráfcos da Fução Quadrátca Podemos classfcar as parábolas a partr de suas duas característcas. A prmera delas é a cocavdade. A seguda dz respeto ao fato dela terceptar, ou ão, o exo x. Uma fução quadrátca pode exbr dos tpos de cocavdade. A cocavdade é cosderada postva se a curva está vrada para cma. Se ocorrer o oposto, a cocavdade da curva é egatva. Nesse caso dzemos, uma lguagem coloqual, que ela está vrada para baxo. Levado-se em cota ada a forma 4.3, podemos verfcar que a cocavdade é determada pelo sal do parâmetro a da fução. A cocavdade será egatva se o parâmetro a o for. E será postva se o mesmo valer para a. Isso pode ser faclmete costatado aalsado-se Fgura 4.4: A cocavdade da fução depede do sal do parâmetro a. / Fote: Cepa as fguras em cada caso (Fgura 4.4). TERRA E UNIVERSO Fudametos da Matemátca I
8 Lcecatura em Cêcas USP/Uvesp 59 Assm, o parâmetro a determa também o quão aberta ou fechada será a parábola. Quato maor o valor desse parâmetro tato mas aberta será a parábola (vde fgura 4.5). A parábola pode terceptar, ou ão, o exo x. Para determar sob que crcustâcas a curva terceptará o exo x, basta aalsar em que crcustâcas teremos um valor de y gual a zero para um dado valor de x. A tas valores, quado exstem, damos o ome de raízes do polômo. Os potos os quas a parábola cruza o exo x têm coordeadas ( y = 0, x r ), ode x r é uma das raízes do polômo de segudo grau, sto é: Fgura 4.5: Comportameto da parábola quado varamos o parâmetro a. / Fote: Cepa ax + bx + c = 0 r r 4.5 Assm, o gráfco de um polômo do segudo grau pode terceptar duas vezes o exo x (se ele possur duas raízes), terceptar apeas uma vez (o caso de ter apeas uma raz), ou uca terceptá-lo (se ão houver raízes reas). De acordo com aálse que faremos a seção 4.6, tas casos podem ser decddos por meo da relação etre os parâmetros a, b e c. O resultado é o segute: Se Assm, a fução quadrátca > 0 b > 4ac = 0 b = 4ac < 0 b < 4ac Fgura 4.6: Por forma geral para dferetes sas ou valores de Δ. / Fote: Cepa 4.6 y x = x 3x+ 4.7 tercepta o exo x duas vezes e, esse caso, b = 9 > 4ac = 4 1 = 8 fuções polomas 4
9 60 Lcecatura em Cêcas USP/Uvesp ao passo que a fução y x = x x tercepta o exo x apeas uma vez, pos b = 4 = 4ac = = 4. E a fução x y x = jamas tocará o exo x. Esboce o gráfco da fução Exercíco Resolvdo: Problema 1 y = f x = x 6x Resolução: Prmeramete, lembramos que Um modo de resolver o problema proposto sera atrbur algus valores a x e calcular os correspodetes valores de y, costtudo assm uma tabela e, a partr da tabela, costrur o gráfco. Há um modo mas produtvo, porém, que é procurar os potos mas mportates: corte com os exos e o vértce. Lembramos que, esse caso, temos: a = 1, b = 6, c = 5. a. Corte com o exo y: Para ecotrar o valor de y, basta tomar x = 0 a equação Obtemos: y (0) = = Portato, o gráfco corta o exo 0y o poto de coordeadas (0,5) b. Cocavdade: Tedo em vsta que a = 1 > 0, a cocavdade é para cma c. Cortes com o exo 0x: Devemos verfcar se exstem potos a curva tas que y = 0, ou seja, potos x para os quas: x 6x + 5= TERRA E UNIVERSO Fudametos da Matemátca I
10 O valor de é postvo. Lcecatura em Cêcas USP/Uvesp 61 = b ac = = = Portato, esse caso ele tercepta o exo x duas vezes. 4.5 Gráfcos das fuções polomas Gráfcos típcos das fuções polomas são apresetados as fguras abaxo. O polômo da fgura 4.7C é um polômo par. Os demas ão têm uma pardade bem defda. A) B) C) D) Fgura 4.7: Algus gráfcos de fuções polomas / Fote: Cepa fuções polomas 4
11 6 Lcecatura em Cêcas USP/Uvesp Pode-se ver, pelos gráfcos, que as fuções polomas ão são lmtadas, sto é, elas podem crescer defdamete, decrescer defdamete, ou ambos. A curva assocada ao gráfco pode cortar o exo x um certo de úmero de vezes. Esse úmero é gual ou meor do que. Aos valores de x para os quas sso ocorre damos o ome de raízes do polômo. Os polômos, em geral, exbem potos de máxmos ou mímos locas. Por exemplo, o gráfco da fgura 4.7D exbe dos máxmos locas e um mímo local. 4.6 Raízes das fuções polomas A determação das raízes de um polômo de grau se faz medate a solução de uma equação algébrca. De fato, desgado por x a -ésma raz de um polômo, por defção x, deve satsfazer à equação algébrca: 0 P x = 4.34 ou seja, ax + a x ax + a = Podemos ter até soluções reas para tal equação. Não haver solução, em se tratado de úmeros reas, é, também, uma possbldade. O estudo das raízes de um polômo tem desafado os matemátcos. Assm, desde o século XVI, sabe-se a solução para as segutes equações cúbcas e quártcas: x + mx = 0 3 x + px + qx + r = Nos casos mas geras o problema é complexo. O caso mas smples etre todos é aquele em que o polômo é favorável de tal forma a escrevê-lo sob a forma de produtos de polômos de prmero grau: = ( )( ) ( ) P x a x x1 x x x x 4.37 TERRA E UNIVERSO Fudametos da Matemátca I
12 Lcecatura em Cêcas USP/Uvesp 63 Por exemplo, o polômo dado por 4.14 pode ser escrto como = = ( )( + )( 3)( + 3) 4 4 P x x x x x x x 4.38 Fgura 4.8 Gráfco do polômo P 4 dcado suas raízes. / Fote: Cepa Ele tem, portato, quatro raízes. Elas são represetadas pelo cojuto { 3,,,3} 4.39 Fgura 4.9 Gráfco do polômo P 5 dcado suas raízes. / Fote: Cepa O polômo ímpar, dado por 4.16, pode ser escrto como = = ( )( + )( 3)( + 3) P x x x x x x x x x 4.40 Ele tem, portato, cco raízes, costtudo o cojuto de úmeros reas: { 3,, 0,,3} 4.7 Raízes da Fução Quadrátca 4.41 Aalsaremos, a segur, o problema das raízes de uma equação do segudo grau. Ele tem uma solução bastate smples, que se aplca a qualquer fução polomal de segudo grau. A equação que os permte determar as raízes da fução quadrátca, de acordo com a otação da seção precedete, é dada por: ax + bx + c = De 4.0 vemos que ela pode ser escrta como: ( b ac) b ax ( + ) = 0 a 4a fuções polomas 4
13 64 Lcecatura em Cêcas USP/Uvesp E, portato, tas valores, se exstrem, devem satsfazer à detdade: ( b 4ac) b ( x ) a 4a 4a + = 4.44 Ora, como se pode observar, para que exstam valores x que satsfaçam à relação acma, é ecessáro que o lado dreto de 4.44 seja postvo. Isso, por outro lado, fca assegurado se: Tedo em vsta a expressão 4.43, temos obtemos a segute expressão para as raízes: a x b + = a 4a Uma vez que o coefcete a é ão ulo, a equação acma os leva à segute expressão para as raízes: b x + = a 4a 4.47 Dode fermos que para haver raízes reas devemos ter 0. Se > 0 as raízes são dadas pela expressão: b x + =± a a 4.48 Da expressão acma, cocluímos que, depededo do valor de, podemos ter até três possbldades: > 0 duas raízes reas dferetes = 0 duas raízes reas guas (uma úca raz) < 0 ão há razes reas 4.49 TERRA E UNIVERSO Fudametos da Matemátca I
14 Lcecatura em Cêcas USP/Uvesp 65 Assm, para > 0 ecotramos duas raízes dadas pelos valores: b b b ac 1 = = x x a 4a a b b + b ac = + = a 4a a Se, o etato, = 0, as duas raízes se reduzem a uma só. x = x = 1 De 4.50 podemos coclur que a soma das raízes (S ) e o seu produto (P) são dados, respectvamete, por: b a 4.51 b S = x1+ x = a c P = x1 x = a 4.5 Falmete, é fácl verfcar que, em termos das raízes dadas por 4.50, ou 4.51, um polômo do segudo grau pode ser escrto como: b a c a ax + bx + c = a x + x + = a x x1 x x 4.53 Por exemplo, as raízes da fução 4.1, são determadas pela equação: x 3x + = cujas soluções, de acordo com 4.50, são: x1 = = x = = 4.55 fuções polomas 4
15 66 Lcecatura em Cêcas USP/Uvesp equato que a equação x x + 1= Fgura 4.10: Gráfcos de fuções quadrátca exbdo duas, uma e ehuma raz. / Fote: Cepa comporta apeas uma solução, já que esse caso = 0. Tal raz, de acordo com a expressão 4.51, é dada por: x1 = x = = A fução 4.9 ão exbe soluções para as raízes. Não tem, portato, raízes. Exercíco Resolvdo: Problema Determe as raízes do polômo dado por Resolução: Lembrado que o valor de é dado pela expressão 4.49, obtemos = b ac = = = e utlzado os valores dados por 4.58, em 4.50, obtemos as duas raízes a partr da expressão: b ± 6 ± 4 6± 4 x = = = a 1 ou seja, 6 4 x1 = = x = = TERRA E UNIVERSO Fudametos da Matemátca I
16 Lcecatura em Cêcas USP/Uvesp Máxmos e Mímos da Fução Quadrátca Falmete, lembramos que uma parábola exbe um poto o qual a varável y atge um valor máxmo, (ou um valor mímo). Qualquer que seja o caso (máxmo ou mímo), esse valor de y será represetado geercamete por y m. O valor da varável depedete, x, para o qual ocorre o valor máxmo (ou mímo), da fução polomal do segudo grau será desgado por x m. Como a cada par de valores das varáves correspode um poto o plao (x, y), esse poto mu especal da parábola é aquele para o qual as varáves são dadas por: ( x, y ) m m 4.60 Esse poto tem o ome de vértce da parábola. Exste uma forma sstemátca de determar os potos de máxmos e mímos de um polômo do segudo grau. Para sso reescrevemos a equação do segudo grau utlzado a forma 4.0, ou seja, escrevemos: b y = a x+ a 4a 4.61 Da expressão acma, resulta que os máxmos ou mímos da fução quadrátca ocorrerão para os valores de x para os quas o prmero termo etre parêteses do lado dreto se aula, sto é, para valores x m tas que: ou seja, para x m x m b = a b + = 0 a fuções polomas 4
17 68 Lcecatura em Cêcas USP/Uvesp Outro modo de determar a abscssa do vértce é lembrar que, havedo raízes reas, o vértce se stua um poto cuja abscssa é a méda das coordeadas assocadas às raízes: x x + x b a 1 m = = ao passo que o valor de y m, o valor do máxmo, ou mímo, será determado substtudo-se em 4.61 o valor dado por 4.64, ou seja, 4.64 b ym y( xm) = a xm + a 0 = = a 4a 4a 4a 4.65 Obtemos, assm, explctamete: y b = + c 4a 4a Assm, os potos de máxmo, ou mímo, têm coordeadas dadas por: m b b xm, ym =, + c a 4a Os potos de mímo, os vértces, das fuções quadrátcas 4.7, 4.8 e 4.9, são dados, respectvamete, por: Fgura 4.11: Vértces das fuções quadrátcas / Fote: Cepa No caso da fução: 3 1, 1, 0 0, y x x = a abscssa do vértce (x v ) é dada por: ( 6) b xv = = = 3 a TERRA E UNIVERSO Fudametos da Matemátca I
18 Lcecatura em Cêcas USP/Uvesp 69 Equato de 4.66 temos que a coordeada ordeada do vértce poto será dada por: y m 16 = = = 4 4a Exercíco Resolvdo: Problema 3 A fgura 4.1 apreseta o gráfco de uma fução quadrátca. Escreva a equação que defe a fução. Determe as coordeadas do vértce Resolução: Lembrado a forma geral da fução quadrátca y = ax + bx + c, o problema que se coloca é o de determar os coefcetes a, b, e c. Da fgura 4.1 fermos que as raízes são x 1 = 1 e x = 3. Cosderado agora a forma fatorada de uma fução polomal do segudo grau, escrevemos: Fgura 4.1: Gráfco de uma fução quadrátca / Fote: Cepa ( 1) ( 1)( 3) ( 3) y = a x x x x = a x+ x = a x x 4.7 Resta-os, portato, determar o valor do parâmetro a. Para sso, observemos que o gráfco corta o exo 0y o poto (0,), sto é, para x = 0, temos y = : y ( 0) a( 0 0 3) = = 4.73 Dode fermos que 3a = a = Substtudo esse valor de a em (II) obtemos: y = ( x x 3) fuções polomas 4
19 70 Lcecatura em Cêcas USP/Uvesp ou de modo equvalete: 4 = y x x Para determar a posção do vértce, em termos das coordeadas deomadas abscssa e ordeada, lembramos prmeramete que a abscssa do vértce é essecalmete a méda das abscssas das raízes. Assm, esse caso obtemos: x m x1+ x 1+ 3 b 4 = = = = = 1 a 3 Da expressão 4.66, que dá o valor da ordeada assocada ao vértce obtemos: y = = = m 4a Portato, o vértce é o poto (1, 8 3). Observe que, este caso, a cocavdade da parábola é para baxo e a fução admte um valor máxmo que é 8 3. Exercíco Resolvdo: Problema 4 Uma pessoa que costrur um galhero, de forma retagular, usado um muro reto já costruído, como um dos lados do galhero. Dado que essa pessoa tem materal para costrur 60 metros de cerca de uma altura fxa, determe os valores de x e z de modo que a área do galhero seja a maor possível (possa abrgar o maor úmero possível de galhas). TERRA E UNIVERSO Fudametos da Matemátca I Fgura 4.13 / Fote: Cepa
20 Lcecatura em Cêcas USP/Uvesp 71 Resolução: Tedo em vsta que o galhero é retagular, a sua área, deomada y, é dada pelo produto dos lados: O lado z deve ser escrto de forma que leve em cota a lmtação mposta pela dspobldade do materal à dsposção. Assm, escrevemos para a soma dos três lados: Dode cocluímos que, com o materal exstete, a relação etre os lados é dada por: Portato, escrevedo a área da costrução em fução do comprmeto do lado x,obtemos y = xz 4.79 x+ z+ x = z = 60 x 4.81 y = x 60 x = x + 60x 4.8 Como a < 0, a cocavdade da parábola [que é o gráfco de fução y = f (x)] é para baxo e a fução admte um valor máxmo para o valor da abscssa dado por: b 60 x = xm = = = 15 a ( ) 4.83 Assm, para esse valor de x, o valor do outro lado será, em metros, dado por: z = 60 x = = Portato, para que o galhero teha a área máxma, devemos ter: x = 15 metros y = 30 metros 4.85 Fgura 4.14 / Fote: Cepa fuções polomas 4
Fundamentos de Matemática I FUNÇÕES POLINOMIAIS4. Licenciatura em Ciências USP/ Univesp. Gil da Costa Marques
 FUNÇÕES POLINOMIAIS4 Gl da Costa Marques Fudametos de Matemátca I 4.1 Potecação de epoete atural 4. Fuções polomas de grau 4. Fução polomal do segudo grau ou fução quadrátca 4.4 Aálse do gráfco de uma
FUNÇÕES POLINOMIAIS4 Gl da Costa Marques Fudametos de Matemátca I 4.1 Potecação de epoete atural 4. Fuções polomas de grau 4. Fução polomal do segudo grau ou fução quadrátca 4.4 Aálse do gráfco de uma
tica Professor Renato Tião
 Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Regressão Linear - Introdução
 Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Sumário. Mecânica. Sistemas de partículas
 Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Como CD = DC CD + DC = 0
 (9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
(9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
Exercícios - Sequências de Números Reais (Solução) Prof Carlos Alberto S Soares
 Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Matemática Ficha de Trabalho
 Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Construção e Análise de Gráficos
 Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
PLANO PROBABILIDADES Professora Rosana Relva DOS. Números Inteiros e Racionais COMPLEXOS NÚMEROS COMPLEXOS NÚMEROS COMPLEXOS NÚMEROS COMPLEXOS
 Professor Luz Atoo de Carvalho PLANO PROBABILIDADES Professora Rosaa Relva DOS Números Iteros e Racoas COMPLEXOS rrelva@globo.com Número s 6 O Número Por volta de 00 d.c a mpressão que se tha é que, com
Professor Luz Atoo de Carvalho PLANO PROBABILIDADES Professora Rosaa Relva DOS Números Iteros e Racoas COMPLEXOS rrelva@globo.com Número s 6 O Número Por volta de 00 d.c a mpressão que se tha é que, com
AULA Os 4 espaços fundamentais Complemento ortogonal.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
RESUMO E EXERCÍCIOS NÚMEROS COMPLEXOS ( )
 NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
d s F = m dt Trabalho Trabalho
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
Complexidade Computacional da Determinação da Correspondência entre Imagens
 Complexdade Computacoal da Determação da Correspodêca etre Images Adraa Karlstroem Laboratóro de Sstemas Embarcados Departameto de Egehara Mecatrôca Escola Poltécca da Uversdade de São Paulo adraa.karlstroem@pol.usp.br
Complexdade Computacoal da Determação da Correspodêca etre Images Adraa Karlstroem Laboratóro de Sstemas Embarcados Departameto de Egehara Mecatrôca Escola Poltécca da Uversdade de São Paulo adraa.karlstroem@pol.usp.br
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
? Isso é, d i= ( x i. . Percebeu que
 Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
ANÁLISE DE REGRESSÃO E CORRELAÇÃO
 ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
AULA Produto interno em espaços vectoriais reais ou complexos Produto Interno. Norma. Distância.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Números Complexos. 2. (IME) Seja z um número complexo de módulo unitário que satisfaz a condição z 2n 1, onde n é um número inteiro positivo.
 Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
AULA Espaços Vectoriais Estruturas Algébricas.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resolvedo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resolvedo os problemas
NÚMEROS COMPLEXOS. z = a + bi,
 NÚMEROS COMPLEXOS. DEFINIÇÃO No cojuto dos úmeros reas R, temos que a = a. a é sempre um úmero ão egatvo para todo a. Ou seja, ão é possível extrar a ra quadrada de um úmero egatvo em R. Dessa mpossbldade
NÚMEROS COMPLEXOS. DEFINIÇÃO No cojuto dos úmeros reas R, temos que a = a. a é sempre um úmero ão egatvo para todo a. Ou seja, ão é possível extrar a ra quadrada de um úmero egatvo em R. Dessa mpossbldade
Forma padrão do modelo de Programação Linear
 POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
Métodos iterativos. Capítulo O Método de Jacobi
 Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
(1) no domínio : 0 x < 1, : constante não negativa. Sujeita às condições de contorno: (2-a) (2-b) CC2: 0
 EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
UNICAMP - 2004. 2ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
Problemas fundamentais da teoria da aproximação func/onal
 18 GAZETA DE MA TEM ATIÇA 2 5 ) ( A - se) l + (T _ y) * + ( Z - z) K=O p 1 1 " 1 d p 1 df-j pl - p ds T d íj (A'~ «)> -f (Y - y) ft + (2-z)v = - 3 1 e resolve-se rapdamete. X x + Aa + B\ r = y + Aß + Bp,
18 GAZETA DE MA TEM ATIÇA 2 5 ) ( A - se) l + (T _ y) * + ( Z - z) K=O p 1 1 " 1 d p 1 df-j pl - p ds T d íj (A'~ «)> -f (Y - y) ft + (2-z)v = - 3 1 e resolve-se rapdamete. X x + Aa + B\ r = y + Aß + Bp,
Tabela 1 Números de acidentes /mês no Cruzamento X em CG/07. N de acidentes / mês fi f
 Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
ANÁLISE DE ERROS. Todas as medidas das grandezas físicas deverão estar sempre acompanhadas da sua dimensão (unidades)! ERROS
 ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
Apostila de Introdução Aos Métodos Numéricos
 Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Medidas Numéricas Descritivas:
 Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: enchentes
 Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Números Complexos Sumário
 Números Complexos Sumáro. FORMA ALGÉBRICA DOS NÚMEROS COMPLEXOS.. Adção de úmeros complexos... Propredades da operação de adção.. Multplcação de úmeros complexos... Propredades da operação de multplcação..
Números Complexos Sumáro. FORMA ALGÉBRICA DOS NÚMEROS COMPLEXOS.. Adção de úmeros complexos... Propredades da operação de adção.. Multplcação de úmeros complexos... Propredades da operação de multplcação..
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) ( k) ( k ) ( ) ( ) Questões tipo exame
![( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) ( k) ( k ) ( ) ( ) Questões tipo exame ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) [ ] ( ) ( k) ( k ) ( ) ( ) Questões tipo exame](/thumbs/54/33108071.jpg) Questões tpo eame Pá O poto U tem coordeadas (6, 6, 6) e o poto S pertece ao eo Oz, pelo que as suas coordeadas são (,, 6) Um vetor dretor da reta US é, por eemplo, US Determemos as suas coordeadas: US
Questões tpo eame Pá O poto U tem coordeadas (6, 6, 6) e o poto S pertece ao eo Oz, pelo que as suas coordeadas são (,, 6) Um vetor dretor da reta US é, por eemplo, US Determemos as suas coordeadas: US
Introdução à Teoria dos Números Notas 1 Os Princípios da Boa Ordem e de Indução Finita Prof Carlos Alberto S Soares
 Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
MEDIDAS DE DISPERSÃO:
 MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
Atividades Práticas Supervisionadas (APS)
 Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
Centro de massa, momento linear de sistemas de partículas e colisões
 Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
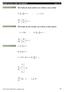 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
b. As medidas de posição mais importantes são as medidas de tendência central. Dentre elas, destacamos: média aritmética, mediana, moda.
 Meddas de Posção Introdução a. Dentre os elementos típcos, destacamos aqu as meddas de posção _ estatístcas que representam uma sére de dados orentando-nos quanto à posção da dstrbução em relação ao exo
Meddas de Posção Introdução a. Dentre os elementos típcos, destacamos aqu as meddas de posção _ estatístcas que representam uma sére de dados orentando-nos quanto à posção da dstrbução em relação ao exo
Curso Mentor. Radicais ( ) www.cursomentor.wordpress.com. Definição. Expoente Fracionário. Extração da Raiz Quadrada. Por definição temos que:
 Curso Metor www.cursometor.wordpress.com Defiição Por defiição temos que: Radicais a b b a, N, Observação : Se é par devemos ter que a é positivo. Observação : Por defiição temos:. 0 0 Observação : Chamamos
Curso Metor www.cursometor.wordpress.com Defiição Por defiição temos que: Radicais a b b a, N, Observação : Se é par devemos ter que a é positivo. Observação : Por defiição temos:. 0 0 Observação : Chamamos
MÉTODO DOS MÍNIMOS QUADRADOS
 MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
( ) ( ) ( ) ( ) ( ) 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Introdução.
 55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
REGRESSÃO LINEAR 05/10/2016 REPRESENTAÇAO MATRICIAL. Y i = X 1i + 2 X 2i k X ni + i Y = X + INTRODUÇÃO SIMPLES MÚLTIPLA
 REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO
 ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal
ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal
3 - ANÁLISE BIDIMENSIONAL
 INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
1. Revisão Matemática
 1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
2-0,0041295**.C 2 + 0,0017052**.T.C
 14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
CAPÍTULO III - POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA
 Polômos de Jacob e CAPÍTULO III - POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA III--)INTRODUÇÃO Para um melhor etedmeto do método da colocação ortogoal e sua relação com o método dos resíduos poderados (MRP),
Polômos de Jacob e CAPÍTULO III - POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA III--)INTRODUÇÃO Para um melhor etedmeto do método da colocação ortogoal e sua relação com o método dos resíduos poderados (MRP),
REGESD Prolic Matemática e Realidade- Profª Suzi Samá Pinto e Profº Alessandro da Silva Saadi
 REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
Intervalo de Confiança para uma Média Populacional
 Estatística II Atoio Roque Aula 5 Itervalo de Cofiaça para uma Média Populacioal Um dos objetivos mais importates da estatística é obter iformação sobre a média de uma dada população. A média de uma amostra
Estatística II Atoio Roque Aula 5 Itervalo de Cofiaça para uma Média Populacioal Um dos objetivos mais importates da estatística é obter iformação sobre a média de uma dada população. A média de uma amostra
CAPÍTULO 5. Ajuste de curvas pelo Método dos Mínimos Quadrados
 CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
Capítulo V - Interpolação Polinomial
 Métodos Numércos C Balsa & A Satos Capítulo V - Iterpolação Polomal Iterpolação Cosdere o segute couto de dados: x : x0 x x y : y y y 0 m m Estes podem resultar de uma sequêca de meddas expermetas, ode
Métodos Numércos C Balsa & A Satos Capítulo V - Iterpolação Polomal Iterpolação Cosdere o segute couto de dados: x : x0 x x y : y y y 0 m m Estes podem resultar de uma sequêca de meddas expermetas, ode
DISTRIBUIÇÃO HIPERGEOMÉTRICA
 7 DISTRIBUIÇÃO HIPERGEOMÉTRICA Cosdere-se uma população fta costtuída por N elemetos dstrbuídos por duas categoras eclusvas e eaustvas de dmesões M e N M, respectvamete. Os elemetos da prmera categora
7 DISTRIBUIÇÃO HIPERGEOMÉTRICA Cosdere-se uma população fta costtuída por N elemetos dstrbuídos por duas categoras eclusvas e eaustvas de dmesões M e N M, respectvamete. Os elemetos da prmera categora
II. Propriedades Termodinâmicas de Soluções
 II. Propredades Termodâmcas de Soluções 1 I. Propredades Termodâmcas de Fludos OBJETIVOS Eteder a dfereça etre propredade molar parcal e propredade de uma espéce pura Saber utlzar a equação de Gbbs-Duhem
II. Propredades Termodâmcas de Soluções 1 I. Propredades Termodâmcas de Fludos OBJETIVOS Eteder a dfereça etre propredade molar parcal e propredade de uma espéce pura Saber utlzar a equação de Gbbs-Duhem
Distribuições de Probabilidades
 Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Determinantes. De nição de determinante de uma matriz quadrada. Determinantes - ALGA - 2004/05 15
 Determnantes - ALGA - 004/05 15 Permutações Determnantes Seja n N Uma permutação p = (p 1 ; p ; : : : ; p n ) do conjunto f1; ; ; ng é um arranjo dos n números em alguma ordem, sem repetções ou omssões
Determnantes - ALGA - 004/05 15 Permutações Determnantes Seja n N Uma permutação p = (p 1 ; p ; : : : ; p n ) do conjunto f1; ; ; ng é um arranjo dos n números em alguma ordem, sem repetções ou omssões
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
CÁLCULO DA DIRECTRIZ
 CÁCUO DA DIRECTRIZ I - Elementos de defnção da polgonal de apoo: - Coordenadas dos vértces da polgonal (M, P ); - Dstânca entre vértces da polgonal ( d); - Rumos dos alnhamentos (ângulo que fazem com a
CÁCUO DA DIRECTRIZ I - Elementos de defnção da polgonal de apoo: - Coordenadas dos vértces da polgonal (M, P ); - Dstânca entre vértces da polgonal ( d); - Rumos dos alnhamentos (ângulo que fazem com a
( x) Método Implícito. No método implícito as diferenças são tomadas no tempo n+1 ao invés de tomá-las no tempo n, como no método explícito.
 PMR 40 Mecâca Computacoal Método Implícto No método mplícto as dfereças são tomadas o tempo ao vés de tomá-las o tempo, como o método explícto. O método mplícto ão apreseta restrção em relação ao valor
PMR 40 Mecâca Computacoal Método Implícto No método mplícto as dfereças são tomadas o tempo ao vés de tomá-las o tempo, como o método explícto. O método mplícto ão apreseta restrção em relação ao valor
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Estabilidade no Domínio da Freqüência
 Establdade o Domío da Freqüêca Itrodução; apeameto de Cotoros o Plao s; Crtéro de Nyqust; Establdade Relatva; Crtéro de Desempeho o Domío do Tempo Especfcado o Domío da Freqüêca; Bada Passate de Sstema;
Establdade o Domío da Freqüêca Itrodução; apeameto de Cotoros o Plao s; Crtéro de Nyqust; Establdade Relatva; Crtéro de Desempeho o Domío do Tempo Especfcado o Domío da Freqüêca; Bada Passate de Sstema;
Capítulo 5: Ajuste de curvas pelo método dos mínimos quadrados
 Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Confiabilidade Estrutural
 Professor Uversdade de Brasíla Departameto de Egehara Mecâca Programa de Pós graduação em Itegrdade Estrutural Algortmo para a Estmatva do Idce de Cofabldade de Hasofer-Ld Cofabldade Estrutural Jorge Luz
Professor Uversdade de Brasíla Departameto de Egehara Mecâca Programa de Pós graduação em Itegrdade Estrutural Algortmo para a Estmatva do Idce de Cofabldade de Hasofer-Ld Cofabldade Estrutural Jorge Luz
Estatística Descritiva
 Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA
 UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
CAPÍTULO 2 - Estatística Descritiva
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
(c) Para essa nova condição de operação, esboce o gráfico da variação da corrente no tempo.
 CONVERSÃO ELETROMECÂNICA DE ENERGIA Lsta de exercícos sobre crcutos magétcos Questão A fgura 1(a mostra um acoador projetado para produzr força magétca. O mesmo possu um úcleo em forma de um C e uma armadura
CONVERSÃO ELETROMECÂNICA DE ENERGIA Lsta de exercícos sobre crcutos magétcos Questão A fgura 1(a mostra um acoador projetado para produzr força magétca. O mesmo possu um úcleo em forma de um C e uma armadura
CAPÍTULO III ANÁLISE DOS DADOS. Para responder à primeira pergunta, observe os dois gráficos abaixo
 CAPÍTULO III ANÁLISE DOS DADOS III.5 Idéias básicas sobre gráficos e modelos Modelos são regras matemáticas que permitem reproduzir um cojuto de valores uméricos a partir de outro ao qual correspodem.
CAPÍTULO III ANÁLISE DOS DADOS III.5 Idéias básicas sobre gráficos e modelos Modelos são regras matemáticas que permitem reproduzir um cojuto de valores uméricos a partir de outro ao qual correspodem.
Avaliação da qualidade do ajuste
 Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Equação e Inequação do 2 Grau Teoria
 Equação e Inequação do Grau Teoria Candidato segue um resumo sobre resolução e discussão de equações e inequações do grau. Bons Estudos! Equação do Grau Onde Uma Equação do Grau é sentença aberta do tipo
Equação e Inequação do Grau Teoria Candidato segue um resumo sobre resolução e discussão de equações e inequações do grau. Bons Estudos! Equação do Grau Onde Uma Equação do Grau é sentença aberta do tipo
Estudo do intervalo de confiança da regressão inversa utilizando o software R
 Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
7 Análise de covariância (ANCOVA)
 Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Oitava Lista de Exercícios
 Uversdade Federal Rural de Perambuco Dscpla: Matemátca Dscreta I Professor: Pablo Azevedo Sampao Semestre: 07 Otava Lsta de Exercícos Lsta sobre defções dutvas (recursvas) e prova por dução Esta lsta fo
Uversdade Federal Rural de Perambuco Dscpla: Matemátca Dscreta I Professor: Pablo Azevedo Sampao Semestre: 07 Otava Lsta de Exercícos Lsta sobre defções dutvas (recursvas) e prova por dução Esta lsta fo
