O método de Equação Integral com Quadratura Gaussiana para otimizar os parâmetros do gráfico de controle multivariado de Somas Acumuladas
|
|
|
- Edite Bardini Galvão
- 8 Há anos
- Visualizações:
Transcrição
1 Unversdade Federal de Santa Catarna Centro Tecnológco Programa de Pós-Graduação em Engenhara de Produção O método de Equação Integral com Quadratura Gaussana para otmzar os parâmetros do gráfco de controle multvarado de Somas Acumuladas Custodo da Cunha Alves Tese de Doutorado Orentador Robert Wayne Samohyl, Ph.D. Floranópols 009
2 Unversdade Federal de Santa Catarna Centro Tecnológco Programa de Pós-Graduação em Engenhara de Produção O método de Equação Integral com Quadratura Gaussana para otmzar os parâmetros do gráfco de controle multvarado de Somas Acumuladas Custodo da Cunha Alves Tese apresentada à Unversdade Federal de Santa Catarna para obtenção do título de Doutor em Engenhara de Produção Orentador: Robert Wayne Samohyl, Ph.D. Floranópols 009
3 3 Catalogação na fonte pela Bbloteca Unverstára da Unversdade Federal de Santa Catarna A474 Alves, Custodo da Cunha O método de Equação Integral com Quadratura Gaussana para otmzar os parâmetros do gráfco de controle multvarado de Somas Acumuladas [ tese] / Custodo da Cunha Alves ; orentador, Robert Wayne Samohyl - Floranópols, SC, f.: l., tabs., grafs. Tese (doutorado - Unversdade Federal de Santa Catarna, Centro Tecnológco. Programa de Pós-Graduação em Engenhara de Produção. Inclu bblografa. Engenhara de produção.. Matemátca para engenhara. 3. Pesqusa operaconal. 4. Estatístca - Controle de qualdade. 5. Planejamento epermental - Estatístca. I. Samohyl, Robert Wayne. II. Unversdade Federal de Santa Catarna. Programa de Pós-Graduação em Engenhara de Produção. III. Título. CDU 658.5
4 4 Custodo da Cunha Alves O método de Equação Integral com Quadratura Gaussana para otmzar os parâmetros do gráfco de controle multvarado de Somas Acumuladas Esta tese fo julgada e aprovada para a obtenção do título de Doutor em Engenhara de Produção no Programa de Pós Graduação em Engenhara de Produção da Unversdade Federal de Santa Catarna Floranópols, 06 de março de 009 Prof. Antôno Sérgo Coelho, Dr Coordenador do Programa de Pós-Graduação em Engenhara de Produção BANCA EXAMINADORA Prof. Adrano Mendonça Souza, Dr Unversdade Federal de Santa Mara Eamnador Eterno Prof. Mlton Procópo de Borba, Dr Unversdade do Estado de SC Eamnador Eterno Prof. Pedro Alberto Barbetta, Dr Unversdade Federal de SC Eamnador/Moderador Prof. Marcelo Menezes Res, Dr Unversdade Federal de SC Eamnador Prof a Vera do Carmo C. de Vargas, Dr a Unversdade Federal de SC Eamnadora Prof. Robert Wayne Samohyl, Ph.D. Unversdade Federal de SC Orentador
5 5 Mnhas homenagens: A mãe de meus flhos, Cecíla, a quem amo, e que se faz sempre amga e companhera Aos meus flhos Cásso, Cassano e Cláudo que me dão alegra e amor Aos meus pas (em memóra que sempre me ajudaram e apoaram ao longo ao longo de toda mnha vda e a quem sempre estare em dívda Ao meu rmão Daro (em memóra por ter despertado em mm o nteresse por Cêncas Eatas As mnhas cnco rmãs que a cada da escrevem uma nova págna na hstóra de nossa famíla
6 6 AGRADECIMENTOS Sntetzar agradecmentos a todos que, de uma manera ou de outra, contrbuíram para a realzação deste trabalho, mostrou ser uma tarefa dfícl. Gostara de dear regstrada aqu mnha mensa gratdão e meu reconhecmento a todos que contrbuíram, dreta ou ndretamente, para o êto deste trabalho. Um agradecmento especal ao meu orentador professor Robert Wayne Samohyl pela amzade, atenção, ncentvo e, prncpalmente, pacênca e dedcação na elaboração deste trabalho. Agradeço anda: aos meus famlares, o apoo constante; ao meu flho prmogênto, Cásso Alves, pela valosa contrbução no desenvolvmento dos programas computaconas propostos neste trabalho; aos professores e funconáros do PPGEP/UFSC com quem tve a oportundade de convver e aprender; aos meus colegas Manoel, Éder, Andréa, Leandro, Guebe e Rodrgo, pela amzade e companhersmo; à colega Elsa, pela amzade e palavras de ncentvo; ao colega Ary, pela enorme colaboração no fornecmento dos dados reas do processo de usnagem utlzado em sua dssertação de mestrado; aos professores Adrano Souza, Vera de Vargas, Pedro Barbetta, Marcelo Res e Mlton de Borba, Robert Samohyl, Rubson Rocha e Evandro da Slva as sugestões propostas para a melhora deste trabalho por ocasão tanto do Eame de Qualfcação quanto da Defesa de Doutorado; aos professores, funconáros e acadêmcos da UNIVILLE e SENAI onde lecono que me encorajaram ao longo de todo o doutorado. Não me refro nnguém em especal para não cometer a njustça de esquecer alguém; à Unversdade Regão de Jonvlle, o ncentvo moral e a ajuda fnancera e, em especal, à professora Sandra Furlan, Pró-Retora de Pesqusa e Pós-Graduação, a quem sou muto grato por sua polítca de valorzação do professor, responsável pelo meu crescmento pessoal e profssonal; A todas as pessoas que não foram nomnalmente menconadas, mas que de alguma forma contrbuíram para vablzar este trabalho.
7 7 BIOGRAFIA DO AUTOR Custodo da Cunha Alves é graduado em Matemátca e possu especalzação em Matemátca Aplcada pela Unversdade da Regão de Jonvlle (UNIVILLE, em 990 e 995, respectvamente. É mestre em Engenhara de Produção pela Unversdade Federal de Santa Catarna (UFSC, em 003. O autor atua como professor de ensno de Matemátca e Estatístca desde 980. Atua, também como nstrutor de ensno na área de Estatístca Industral. É consultor ad hoc da Fundação de Cênca e Tecnologa do Estado de Santa Catarna (FUNCITEC. Trabalhou na Empresa Braslera de Compressores S.A. (EMBRACO, em Jonvlle-SC, de 989 a 998, na área de Controle da Qualdade. Atualmente, é professor de ensno do Departamento de Engenhara de Produção Mecânca da UNIVILLE e SENAI onde lecona as dscplnas de Cálculo Dferencal e Integral, Álgebra Lnear e Geometra Analítca, Estatístca, Pesqusa Operaconal e Controle Estatístco de Processos. Entre seus prncpas nteresses por trabalhos acadêmcos ncluem a pesqusa e o ensno de matemátca e estatístca na engenhara, tas como, técncas de controle estatístco da qualdade, planejamento de epermentos e aplcação da metodologa de pesqusa operaconal a problemas de sstemas de manufatura. É, também, autor e co-autor de artgos técncos nessas áreas publcados em anas de grandes eventos naconas, tas como, Encontro Naconal de Engenhara de Produção (Enegep, Smpóso Naconal de Probabldade e Estatístca (Snape e Smpóso de Engenhara de Produção (Smpep. Atualmente, o autor contnua estudando técncas de controle estatístco com enfoque em aplcações efcentes de projetos de gráfcos de controle unvarados e multvarados de Somas Acumuladas (CUSUM e MCUSUM no montoramento de processos ndustras.
8 8 RESUMO ALVES, C.C. O método de Equação Integral com Quadratura Gaussana para otmzar os parâmetros do gráfco de controle multvarado de Somas Acumuladas. Tese de Doutorado. Programa de Pos-Graduação em Engenhara de Produção e Sstemas. Unversdade Federal de Santa Catarna, 009. O rápdo crescmento das tecnologas de aqusção de dados e a utlzação de computadores têm ncrementado o nteresse pelas técncas de controle estatístco emergentes, tas como os gráfcos de controle multvarados aplcados no montoramento de processos que envolvem o controle smultâneo de característcas da qualdade ou varáves de processo correlaconadas. Neste trabalho propõe-se o método de Equação Integral com Quadratura Gaussana para otmzar os prncpas parâmetros ARL, k e h do gráfco de controle multvarado de Somas Acumuladas (MCUSUM. Este método envolve a dervação analítca de uma equação ntegral, cuja resolução numérca va Quadratura Gaussana possblta ao usuáro obter a solução apromada desses parâmetros utlzando um programa computaconal desenvolvdo a partr deste método. Além dsso, propõe-se também, a partr desta metodologa, uma apromação sstemátca de projetar estatstcamente um gráfco de controle MCUSUM ótmo baseado nestes parâmetros, que mnmze o custo médo de operação. Isso, orenta o usuáro a decdr que tamanho de mudança do vetor de médas é realmente mportante detectar, e tendo sto como base, seleconar aqueles parâmetros ótmos do gráfco MCUSUM que contemplem aspectos estatístcos como a mnmzação do número de falsos alarmes e a mamzação da capacdade de detecção de mudanças reas. Os resultados obtdos deste trabalho revelam o método de Equação Integral proposto como uma ecelente alternatva para otmzar os parâmetros do gráfco MCUSUM por ser um procedmento mas versátl que fornece melhores resultados para o valor de ARL com maor rapdez de cálculo comparado com o método de smulações e a relatva smplcdade de mplementação em um programa computaconal. Palavras-chave: Otmzação de parâmetros, equação ntegral, métodos numércos, gráfco de controle multvarado de somas acumuladas.
9 9 ABSTRACT ALVES, C.C. The Method of Integral Equaton wth Gaussan Quadrature to optmze the parameters of the multvarate cumulatve sum control chart. Doctorate Thess. Programa de Pos-Graduação em Engenhara de Produção e Sstemas. Unversdade Federal de Santa Catarna, 009. The fast growth of data technologes acquston and the use of computers have ncreased the nterest n technques of statstcal emergent control, such as appled multvarate control charts for montorng processes that nvolve the smultaneous control of the qualty characterstcs or process varables correlated. In ths work the method of Integral Equaton wth Gaussan Quadrature to optmze the man parameters ARL, k and h of the multvarate cumulatve sum control chart (MCUSUM s proposed. Ths method nvolves the dervaton of an analytcal ntegral equaton, whose numercal resoluton way Gaussan Quadrature allows the user to obtan the appromate soluton of these parameters usng a computer program developed from ths method. Furthermore, from ths methodology, a systematc approach to desgn a statstcal chart of MCUSUM optmal control based on these parameters, whch mnmzes the average cost of operaton, s also proposed. Ths, gudes the user to decde what sze to change the vector of means s mportant to detect, and takng ths as a base, selectng those parameters MCUSUM great chart that address statstcal ssues such as mnmzng the number of false alarms and mamzng the ablty of detecton of real changes. The results of ths study reveal the method of Integral Equaton proposed as an ecellent alternatve to optmze the parameters of the chart MCUSUM to be a more versatle procedure that provdes better results for the value of ARL wth hgher speed of calculaton compared wth the method of smulatons and the relatve smplcty of mplementaton n a computer program. Keywords: Optmzaton of parameters, ntegral equaton, numercal methods, multvarate cumulatve sum control chart.
10 0 LISTA DE FIGURAS Fgura. Fases da metodologa utlzada no trabalho...3 Fgura. Regão de controle para duas varáves ndependentes analsadas de forma conjunta adaptada de Montgomery Fgura. Regão de controle para duas varáves correlaconadas analsadas de forma conjunta adaptada de Montgomery ( Fgura.3 Forma bdmensonal de prâmde, cone e parabolóde...45 Fgura.4 Valores de ARL dos gráfcos MCUSUM e T de Hotellng para ARLo= Fgura 4. Curvas de ARL do gráfco MCUSUM para n= e ARL o =00, 500 e Fgura 4. Desempenho de ARL dos gráfcos MCUSUM, MEWMA e T de Hotellng...78 Fgura 4.3 Desempenho de ARL do gráfco MCUSUM com aplcação de SIM, MCM e MEI...79 Fgura 4.4 Resumo das etapas para desenvolvmento do projeto estatístco MCUSUM...8 Fgura 4.5 Regões de Máma e mínma potênca de um gráfco de controle...8 Fgura 4.6 Função perda para as característcas da qualdade do eemplo de aplcação...83 Fgura 4.7 Regões de Máma e mínma potênca do MCUSUM do eemplo de aplcação...86 Fgura 4.8 Caa de dálogo com os dados de entrada do eemplo de aplcação...87 Fgura 4.9 Esboço dos furos e do bloco de motor para veículo de passeo...89 Fgura 4.0 Fluo resumdo do processo de usnagem do bloco de motor...90 Fgura 4. Hstograma das característcas da qualdade X e Y (Processo XY...93 Fgura 4. Gráfco de probabldade qu-quadrado (Q-Q plot para os dados do processo XY...94 Fgura 4.3 Correlogramas das característcas da qualdade X e Y (Processo XY...95 Fgura 4.4 Função Autocorrelação (FAC das varáves X com Y (Processo XY...96 Fgura 4.5 Análse de Varânca (ANOVA e Estatístca Descrtva para as varáves X e Y...96 Fgura 4.6 Modelo matemátco para otmzar os pontos de máma e mínma potênca...98 Fgura 4.7 Pontos de máma e mínma potênca para otmzar o gráfco MCUSUM...99 Fgura 4.8 Tela do R para carregar a rotna do gráfco MCUSUM...00
11 Fgura 4.9 Tela do R para eecutar a rotna do gráfco MCUSUM...0 Fgura 4.0 Gráfco MCUSUM do processo XY (furação de acabamento do furo...0 Fgura 4. Hstogramas das característcas da qualdade X, Y e D do Processo XYD...03 Fgura 4. Gráfco de Probabldade Normal das varáves X,Y e D do Processo XYD...04 Fgura 4.3 Gráfco de probabldade qu-quadrado (Q-Q plot para os dados do Processo XYD...05 Fgura 4.4 Correlogramas das característcas da qualdade X, Y e D do Processo XYD...06 Fgura 4.5 Função Autocorrelação (FAC para as varáves X com D e Y e D Fgura 4.6 Análse de Varânca (ANOVA e Estatístca Descrtva para as varáves X e D Fgura 4.7 Análse de Varânca (ANOVA e Estatístca Descrtva para as varáves as vasrávesy e D...08 Fgura 4.8 Gráfco de controle MCUSUM para os dados do processo XYD...0
12 LISTA DE TABELAS Tabela 4. Tabela para a mplementação do algortmo de soma acumulada O parâmetro ótmo do gráfco, k para projetar o MCUSUM e os correspondentes lmtes de controle, h com o mínmo (ARL mín. para p=, ARL sob controle (ARL o de 00, 500 e 000, e város tamanhos de mudança, d...73 Tabela 4. Tabela para a mplementação do algortmo de soma acumulada O parâmetro ótmo do gráfco, k para projetar o MCUSUM e os correspondentes lmtes de controle, h com o mínmo (ARL mín. para p=3, ARL sob controle (ARL o de 00, 500 e 000, e város tamanhos de mudança, d...74 Tabela 4.3 Tabela para a mplementação do algortmo de soma acumulada O parâmetro ótmo do gráfco, k para projetar o MCUSUM e os correspondentes lmtes de controle, h com o mínmo (ARL mín. para p=4, ARL sob controle (ARL o de 00, 500 e 000, e város tamanhos de mudança, d...74 Tabela 4.4 Comparatvo das propredades estatístcas do MCUSUM va MCM MEI Tabela 4.5 Análse de sensbldade: Valores de k e h para o ARL de 00 quando o processo está sob controle e os valores de ARL quando o processo está fora de controle com p= e n=...76 Tabela 4.6 Desempenho de ARL entre gráfcos de controle multvarado....0
13 3 LISTA DE SIGLAS E SÍMBOLOS RL ARL ARL o ARL d MRL SPRT FIR MEI MCM MCU SIM CEP CUSUM FAC ACP f( H o H k h N(0, d o número de amostras coletadas até à emssão de um snal (Run Length número médo de amostras coletadas até à emssão de um snal (Average Run Length número médo de amostras coletadas até a emssão de um snal durante o período sob controle (ARL para o desvo nulo número médo de amostras coletadas até a emssão de um snal que ndque uma stuação de fora de controle (ARL para o desvo d número medano de amostras coletadas até à emssão de um snal Teste Seqüencal da Razão de Probabldades (Sequental Probablty Rato Test Resposta Incal Rápda (Fast Intal Response Método de Equação Integral Método de Cadeas de Markov Múltplos gráfcos CUSUM unvarados Método de Smulação Controle Estatístco de Processos Soma acumulada (Cumulatve Sum Função Autocorrelação Análse de Componentes Prncpas função dstrbução de probabldade da varável aleatóra X hpótese nula hpótese alternatva valor de referênca do gráfco de controle lmte de controle ou ntervalo de decsão padronzado dstrbução normal padronzada com méda zero e desvo padrão untáro probabldade de um erro tpo I probabldade de um erro tpo II tamanho da mudança em undades de desvo padrão vetor de médas vetor de médas para a stuação sob controle vetor de médas para uma stuação de fora de controle
14 4 SUMÁRIO CAPÍTULO INTRODUÇÃO...8. Motvação para aplcação de Gráfcos de Controle Multvarados Tema e Justfcatva Objetvos....4 Método de Trabalho....5 Delmtações da Metodologa Estrutura da Tese...4 CAPÍTULO REVISÃO DE LITERATURA...6. Gráfcos de Controle Estatístco de Processos Multvarados...6. Gráfco de Controle T de Hotellng (Shewhart Multvarado Subgrupos raconas Observações ndvduas multvaradas Gráfco de Controle Multvarado MEWMA Gráfco de Controle Multvarado MCUSUM Gráfco de Controle CUSUM Gráfcos de controle multvarado MCUSUM O ARL - Número Médo de Amostras até a emssão de um snal Método de Equação Integral Método das Cadeas de Markov Método de Smulação Parâmetros dos Gráfcos de Controle CUSUM e MCUSUM Projeto ótmo aplcado para obter os parâmetros do gráfco MCUSUM Método para otmzação dos parâmetros do gráfco MCUSUM Otmzação do MCUSUM baseado em Regões de Máma e Mínma Potênca Integração Numérca Quadratura Gaussana Síntese do Capítulo
15 5 CAPÍTULO 3 METODOLOGIA Introdução Método de Equação Integral com Quadratura Gaussana para otmzação dos parâmetros do gráfco MCUSUM Síntese do Capítulo...68 CAPÍTULO 4 APLICAÇÃO DA METODOLOGIA Introdução Desenvolvmento Epermental da Metodologa Programas Implementados Aplcação do MEI para determnar os parâmetros do gráfco de controle MCUSUM Resultados da aplcação do MEI para os parâmetros do gráfco MCUSUM Projeto estatístco ótmo para um gráfco MCUSUM baseado em ARL e sob a ótca de regões de máma e mínma potênca Eemplo de aplcação para o projeto estatístco ótmo do gráfco MCUSUM baseado em ARL e sob a ótca de regões de máma e mínma potênca Aplcação da metodologa proposta utlzando dados reas de um processo de usnagem Apresentação da empresa Descrção do produto seleconado para análse estatístca multvarada do processo de usnagem Descrção do processo seleconado para o montoramento de característcas da qualdade va gráfco MCUSUM Eploração dos dados do processo para aplcação da metodologa proposta Análse estatístca multvarada dos dados: Processo XY Normaldade Autocorrelação Otmzação dos pontos que delmtam as regões de máma e mínma potênca do gráfco MCUSUM para o processo XY...97
16 Desenvolvmento do gráfco MCUSUM projetado estatstcamente para o processo XY Análse estatístca multvarada dos dados: Processo XYD Normaldade Autocorrelação Projeto ótmo do gráfco MCUSUM em um ponto Síntese do Capítulo... CAPÍTULO 5 CONCLUSÕES Desenvolvmento e Aplcação do Método de Equação Integral Projeto Estatístco Ótmo do Gráfco de Controle MCUSUM Projeto Otmzação do MCUSUM com Regões de Máma e mínma Recursos Computaconas Aplcados e Parâmetros Ótmos obtdos através do MEI Aplcação da Metodologa e Resultados obtdos com a Utlzação de Dados Reas Recomendações para Investgações Futuras...7 REFERÊNCIAS BIBLIOGRÁFICAS...9 APÊNDICE A Integração Gaussana por Polnômos de Legendre...5 APÊNDICE B Teoremas e Demonstrações: Equação Integral para o ARL sob controle...3 APÊNDICE C Dstrbução Normal Multvarada...37 APÊNDICE D Autocorrelação e Establdade Estatístca...44 APÊNDICE E Teste Seqüencal da Razão de Probabldades e Teora da Soma Acumulada em Gráfcos de controle...47 APÊNDICE F A Função Perda de Taguch para a Tomada de Decsões...54 APÊNDICE G Método da Secante...59 APÊNDICE H Interpolação Polnomal...6 APÊNDICE I Relatóros: resultados obtdos com a resolução de modelos matemátcos...63
17 7 APÊNDICE J O R Project e Rotna Desenvolvda para gerar o Gráfco MCUSUM...67 APÊNDICE K Programas Computaconas Desenvolvdos em Ambente Matlab...70 APÊNDICE L Códgo Computaconal dos Programas em Ambente Matlab...84 ANEXO A Dados do processo furação de acabamento do furo para as característcas da qualdade X, Y e D (meddas em mm...93 ANEXO B Parâmetros Ótmos do Gráfco MCUSUM va Método Cadeas de Markov (Tabela...94 ANEXO C Parâmetros Ótmos do Gráfco MCUSUM va Método Cadeas de Markov (Tabela...95 ANEXO D Parâmetros Ótmos do Gráfco MCUSUM va Método Cadeas de Markov (Tabela
18 8 CAPÍTULO INTRODUÇÃO A ndústra atual se encontra dante de uma economa globalzada que estabelece desafos cada vez mas egentes. Hoje em da, nosso competdor pode estar em qualquer lugar do planeta e a sobrevvênca do setor ndustral está baseada na melhora contínua de seus processos e produtos. Dante deste quadro de etrema competênca, a utlzação de ferramentas estatístcas cada vez mas específcas dreconadas ao aperfeçoamento da qualdade tem sdo uma prátca na maor parte das organzações para elevar seus níves de qualdade a um bao custo, permtndo, a longo prazo, a sobrevvênca e a otmzação de cotas de mercado. No século XIX, os esforços para elmnar as varações nerentes ao processo eram mutas vezes bem suceddos devdo à smplcdade de seus produtos manufaturados. Atualmente, estamos atravessando uma tercera revolução ndustral, a revolução da nformação, em que dados estão cada vez mas abundantes e acessíves. Isso, demanda uma maor compledade dos sstemas de fabrcação e montagem que ege uma maor atenção no montoramento das característcas da qualdade para desenvolver um produto cada vez melhor em torno do valor nomnal e dentro das normas técncas egdas. O Controle Estatístco de Processos (CEP e em partcular as técncas de Controle de Qualdade, tas como gráfcos de controle, têm sdo cada vez mas mportantes pelo fato de desempenharem papel prmordal na ndústra moderna. Nas últmas décadas, mudanças consderáves no cenáro econômco mundal tem sdo acompanhada por um crescmento sgnfcatvo de aplcações de técncas de controle da qualdade emergentes tas como o controle estatístco de processos multvarados. A aplcação dessas técncas estatístcas tas como o gráfco de controle multvarado de Somas Acumuladas (MCUSUM, objeto de estudo desse trabalho, tem como alvo proporconar o montoramento efetvo para assegurar a qualdade de processos e produtos ndustras. O aumento da utlzação de técncas de controle estatístco multvarado notadamente nos últmos anos em razão dos números recursos da nformatzação hoje estentes tem sdo fundamental para atender a compledade dos atuas processos ndustras. Estes recursos em procedmentos de controle ndustras têm melhorado sgnfcatvamente a qualdade da produção na ndústra moderna. Na ndústra de manufatura, por eemplo, procedmentos automatzados de nspeção nos permtem obter medções, em cada peça fabrcada, de varáves
19 Capítulo Introdução 9 correlaconadas num mesmo processo tas como a dmensão, peso, etc. Na prátca, este cenáro requer a necessdade do montoramento smultâneo e on-lne de mas de uma característca da qualdade va gráfcos de controle multvarados, uma vez que os recursos dos sstemas de nformação atuas facltam o complamento e o armazenamento de dados utlzados na maora de nossos processos ndustras que nfelzmente são de natureza multvarada. No Brasl, a utlzação de gráfcos de controle com metodologa para processos de multvaráves não tem sdo comum no controle de qualdade ndustral devdo às dfculdades nerentes às técncas multvaradas. Felzmente, com o avanço da nformátca nas últmas décadas, programas de computadores aplcados aos processos de produção têm sdo desenvolvdos para atender as tendêncas mas modernas de métodos de controle estatístcos multvarados que possam aular tas processos na busca pela qualdade. No montoramento de processos ndustras multvarados, mutas vezes se faz necessáro detectar pequenas e moderadas mudanças das varáves correlaconadas, stuação onde são recomendados os gráfcos de controle com memóra, tas como o gráfco multvarado de Somas Acumuladas (MCUSUM e o gráfco de Méda Móvel Eponencalmente Ponderada (MEWMA. Estes gráfcos acumulam a nformação mas recente com nformações anterores e, com sso, detectam pequenas mudanças nos parâmetros de um processo com um número médo de amostras coletadas até à emssão de um snal (ARL menor do que faram os tradconas gráfcos de controle T de Hotellng. O gráfco de controle MCUSUM, focalzado neste trabalho, é consderado uma ferramenta estatístca versátl uma vez que seu processo de decsão basea-se nas somas acumuladas dos resultados e não em observações soladas de amostras. Esta característca torna este gráfco mas sensível para detectar mas rapdamente pequenas trocas no vetor de médas do processo que mplca em menores valores para o ARL. A detecção rápda destas pequenas alterações nos parâmetros de um processo é uma tarefa realmente mportante numa perspectva de aumentar a consstênca da qualdade de processos e produtos. Dante dsso, a otmzação de alguns parâmetros que tornam esse gráfco mas robusto em termos de desempenho de ARL é fundamental para reduzr de forma sgnfcatva a probabldade de falsos alarmes. Este trabalho propõe um projeto estatístco ótmo para o gráfco de controle MCUSUM baseado na otmzação sstemátca de ARL com a melhor combnação dos parâmetros valor de referênca k com o lmte superor de controle h (ntervalo de decsão para assegurar o desempenho deste gráfco. Para determnar o ARL uma equação ntegral é analtcamente dervada. A solução dessa equação é obtda através do método de Equação
20 Capítulo Introdução 0 Integral com Quadratura Gaussana. O procedmento deste projeto ótmo é uma etensão multvarada do gráfco de controle CUSUM unvarado (Gan,99,993 que utlza o método de Equação Integral para determnar os parâmetros ótmos desse gráfco. Além dsso, realzar um estudo comparatvo da otmzação do gráfco MCUSUM em termos de desempenho de ARL va Cadeas de Markov (Lee e Khoo, 006 com o Método de Equação Integral proposto neste trabalho nas mesmas condções e restrto a observações ndvduas com p =, 3 e 4 varáves (característcas da qualdade e para o ARL o de 00, 500 e Motvação para aplcação de Gráfcos de Controle Multvarados Os gráfcos de controle amplamente aplcados ao montoramento de processos são anda, sem dúvda, os tradconas gráfcos que utlzam técncas unvaradas de controle estatístco de processos. Apesar de efcazes, estas ferramentas não são ndcadas em stuações onde se faz necessáro o montoramento smultâneo de duas ou mas característcas da qualdade (ou varáves correlaconadas. Para estas stuações é fundamental a utlzação de gráfcos de controle multvarados na análse estatístca de processos. Na mplementação de um método para montorar dversas varáves, smultaneamente, procura-se uma técnca que preserve essencalmente os seguntes tópcos: Produzr uma únca resposta para constatar que o processo está sob controle estatístco. Manter a probabldade especfcada ( de consderar o processo fora de controle quando na verdade ele não está. Estabelecer o método que leve em consderação a nterdependênca entre as varáves.. Tema e Justfcatva Este trabalho tem como tema prncpal a aplcação do método de Equação Integral com Quadratura Gaussana cuja resolução numérca da equação ntegral dervada analtcamente fornece o ARL. Para seleconar a combnação ótma dos parâmetros k com h que fornece ARL mínmo do gráfco MCUSUM para a mudança do vetor de médas que é mportante detectar utlza-se programas computaconas em ambente Matlab, algortmos de métodos numércos, tas como, a nterpolação polnomal não lnear para obter-se valores ntermedáros tabelados dos parâmetros desejados e o método nteratvo da secante para apromar a solução do lmte superor de controle h. Isso, é fundamental para a análse de
21 Capítulo Introdução sensbldade prelmnar desses parâmetros e mprescndível para projetar estatstcamente o gráfco de controle MCUSUM ótmo. Alguns pesqusadores como Croser (988, Pgnatello e Runger (990, Lowry, Woodall e Champ (99, Nga e Zang (00, etc, têm apresentado tabelas e métodos gráfcos para seleconar parâmetros ótmos de gráfcos multvarados tas como os valores de k, h para algumas magntudes de mudanças. Em aplcações prátcas estes recursos apresentam um número muto reduzdo de stuações sendo portanto, muto lmtada a sua aplcação. O tema proposto nesta tese tem sua relevânca fundamentada na otmzação do gráfco MCUSUM cujo estudo referente a este tema nas últmas décadas dreconado aos gráfcos de controle multvarados T de Hotellng e MEWMA. Pouca atenção tem sdo dreconada ao gráfco de controle multvarado MCUSUM, objeto de estudo deste trabalho. Além dsso, propor uma metodologa cuja seleção dos parâmetros ótmos do gráfco MCUSUM se leve em consderação aspectos estatístcos como a mnmzação do número de falsos alarmes (snalzação da ocorrênca de uma causa especal quando na verdade não houve alteração do processo e por conseqüênca a mamzação da capacdade de detecção de mudanças reas. Para sso, propõe-se uma metodologa que contemple a otmzação sstemátca de parâmetros levando em consderação as regões de máma e mínma potênca do gráfco MCUSUM. Na bblografa consultada só é encontrado a referênca de Woodall (985, que trata análse estatístca de gráfcos de controle segundo a ótca de regões de máma e mínma potênca referdas ao caso unvarado. No caso multvarado para o gráfco MCUSUM, a nvestgação neste sentdo é nula..3 Objetvos O objetvo prncpal deste trabalho é desenvolver o método de Equação Integral com Quadratura Gaussana cujos procedmentos metodológcos ncluem as etapas relaconadas desde a dervação analítca da equação ntegral até sua aplcação para obter a solução apromada de ARL que otmze o gráfco de controle MCUSUM quando o processo está sob controle. Com base nesta nformação, são utlzados outros métodos numércos adequados para estender o estudo deste parâmetro à stuações quando o processo está fora de controle. Além dsso, a mplementação deste método em um ambente ndustral, cuja averguação para valdade prátca é realzada a partr de dados reas resultante do montoramento do vetor de médas de um processo de produção com característcas da qualdade correlaconadas. Os objetvos específcos mas relevantes deste trabalho são os seguntes:
22 Capítulo Introdução a revsar a lteratura sobre gráfcos de controle multvarado de Somas Acumuladas (MCUSUM, suas peculardades e aplcações; b dervar analtcamente uma equação ntegral para otmzar os parâmetros fundamentados no desempenho de ARL do gráfco MCUSUM; c desenvolver o método de Equação Integral com Quadratura Gaussana para otmzar os parâmetros ARL, k e h essencas para projetar estatstcamente o gráfco MCUSUM sob a ótca de regões de máma e mínma potênca; d aplcar um modelo estatístco que possblte encontrar os valores ótmos dos parâmetros do gráfco MCUSUM segundo a flosofa de máma e mínma potênca deste gráfco que mnmze o custo médo de operação; e elaborar um algortmo numérco computaconal utlzando o método de Equação Integral com Quadratura Gaussana sob a ótca de regões de máma e mínma potênca para otmzar os parâmetros do projeto estatístco do gráfco MCUSUM em um ponto para qualquer magntude de mudança do vetor de médas de um processo. Isso, orenta o usuáro a detectar mudanças sgnfcatvas para stuações de varáves correlaconadas e montoradas smultaneamente, tamanho da amostra e ARL dados; f realzar análse de sensbldade para mostrar como vara a probabldade do erro tpo I para dferentes combnações de (k,h da regão ótma do gráfco MCUSUM..4 Método de Trabalho O método de trabalho proposto para o desenvolvmento deste trabalho consttuse na aplcação de técncas útes elaboradas a partr de um modelo matemátco adequado ao controle estatístco de processos multvarados cujas restrções para a otmzação do gráfco MCUSUM ncluem além do ARL os parâmetros k e h, valor de referênca e lmte superor de controle, respectvamente. A metodologa utlzada na presente tese consste na adoção de um referencal teórco ncal do tema proposto para testar a metodologa proposta no escopo do trabalho através de eemplos prátcos da lteratura e de uma aplcação com dados reas para comprovar sua valdade prátca. O desenvolvmento desta metodologa compreende duas fases bem dferencadas. A fase de busca de nformação e planejamento e a fase puramente epermental conforme fgura.
23 Capítulo Introdução 3 I N F O R M A Ç Ã O E P L A N E J A M E N T O Abordagem do Problema Revsão Bblográfca Seleção Técnca (Otmzação T R A B A L H O E X P E R I M E N T A L Conclusões º Estágo: º Estágo: Implementação do Método de Equação Integral Desenvolvmento de Programa Planejamento de Epermentos Epermento Computaconal Análse de Resultados Fgura. Fases da metodologa utlzada neste trabalho A metodologa utlzada na segunda fase consderada como trabalho epermental nca com a mplementação do método de ntegração numérca que ncluem a dervação analítca e a adequação da equação ntegral ao método proposto. Uma vez defnda a equação ntegral para o método é desenvolvdo um programa computaconal (amgável que nos permta otmzar os parâmetros do gráfco MCUSUM. Como o conjunto de possíves combnações de parâmetros (k,h é elevado propõe-se um planejamento de epermentos para poder encontrar em quas condções estes parâmetros otmzam o gráfco MCUSUM. O epermento computaconal é realzado em computadores do Laboratóro de Informátca da Unversdade da Regão de Jonvlle. Uma análse estatístca dos resultados obtdos do epermento computaconal nos
24 Capítulo Introdução 4 permte analsar a nfluênca das dferentes combnações dos parâmetros k com h que assocado ao ARL nterferem na otmzação do gráfco MCUSUM. Por últmo, uma análse de sensbldade da solução ótma desses parâmetros nos leva a etrar as conclusões fnas da nvestgação..5 Delmtações da Metodologa As delmtações da metodologa proposta neste trabalho referem-se a otmzação dos prncpas parâmetros ARL, k e h para projetar estatstcamente o gráfco de controle multvarado de Somas Acumuladas restrto a observações ndvduas devdo a escassez de materal bblográfco referente a esse tpo gráfco para subgrupos raconas. Esta metodologa nclu um modelo matemátco para o projeto do gráfco MCUSUM ótmo com as seguntes restrções: a o lmte superor de controle, h do gráfco MCUSUM para o ARL mínmo é determnado apenas para ARL o de 00, 500 e de 000; b o número p de varáves (característcas da qualdade é consderado apenas com p =, 3 e 4. c a estatístca MCUSUM de controle Y é demarcada num gráfco unlateral com ntervalo de decsão 0 Y h onde 0 e h são respectvamente, os lmtes nferor e superor de controle..6 Estrutura da Tese O presente trabalho está estruturado em cnco capítulos, os quas estão brevemente comentados a segur : O capítulo trata das prelmnares e objetvos do trabalho que ncluem a motvação com sua respectva justfcatva, necessára para o entendmento da stuação em que se aplca o controle estatístco de processos multvarados e para estabelecer-se os objetvos do presente trabalho. O capítulo apresenta o referencal teórco que ncluem a revsão de lteratura sobre gráfco de controle multvarado de Somas Acumuladas (MCUSUM e seus prncpas parâmetros. Além dsso, apresenta os métodos numércos utlzados para apromar estes parâmetros destacando a aplcação do Método de Equação Integral com Quadratura Gaussana, objeto de estudo deste trabalho. O capítulo 3 epõe a metodologa utlzada para alcançar os objetvos dentfcados no capítulo constante no desenvolvmento de modelos que posterormente são otmzados.
25 Capítulo Introdução 5 O capítulo 4 trata do desenvolvmento e da utlzação do programa computaconal (amgável para aplcar o método de Equação Integral com Quadratura Gaussana proposto que otmze os parâmetros essencas do gráfco MCUSUM em ambente ndustral. No capítulo 5 encontram-se as conclusões, ou seja, os resultados mas relevantes obtdos nos capítulos anterores e as recomendações para trabalhos futuros.
26 CAPÍTULO REVISÃO DE LITERATURA. Gráfcos de Controle Estatístco de Processos Multvarados Nas últmas décadas dversas áreas do setor produtvo vêm epermentando acelerados avanços tecnológcos e, desta forma, egndo ferramentas estatístcas cada vez mas específcas para montorar e avalar a atual compledade de seus processos. Este rápdo crescmento em tecnologas de aqusção de dados e o uso de computadores para o montoramento on-lne de processos possbltam, em tempo real, e com menores custos, o montoramento smultâneo de váras característcas da qualdade ou varáves de processo correlaconadas. Dante desta realdade, tem-se verfcado nos últmos anos um crescente nteresse em desenvolver técncas de controle de qualdade mas robustas, que ncorporem todas estas múltplas varáves correlaconadas de uma únca vez tas como os procedmentos de gráfcos de controle estatístco de processos multvarados (Alves, Hennng e Samohyl, 008a. O tradconal método de controle estatístco de processos onde apenas uma característca da qualdade (ou varável é montorada a partr da utlzação de alguns gráfcos de controle unvarados dsponíves tas como Shewhart, CUSUM, EWMA, etc., é anda o mas conhecdo e amplamente aplcado no setor ndustral devdo a sua smplcdade e facldade de operaconalzação (Montgomery, 004. No entanto, são mutas as stuações no cenáro ndustral onde num mesmo processo é necessáro o controle smultâneo e on-lne de duas ou mas característcas da qualdade. Embora a aplcação de gráfcos de controle unvarados a cada varável ndvdual seja uma solução possível pode levar a conclusões errôneas se não levarmos em conta a probabldade conjunta de erro tpo I e a estrutura de correlação entre as varáves consderadas (Ferrer, 005. Suponhamos por eemplo, que se deseja montorar duas varáves normalmente dstrbuídas aplcando a cada uma delas um gráfco X de Shewhart com lmtes de controle stuados segundo o habtual crtéro 3. Se as duas varáves estão sob controle, a probabldade de que uma dessas varáves eceda os lmtes de controle (probabldade de erro tpo I é gual a 0,007. No entanto, a probabldade conjunta de ambas varáves ecederem seus lmtes de controle, smultaneamente quando ambas estão sob controle, é
27 Capítulo Revsão de Lteratura 7 (0,007.(0,007=0, , o que é consderavelmente menor que 0,007. Porém, para o controle conjunto das duas varáves, supondo que são ndependentes, a probabldade de que as duas varáves sejam marcadas fora dos lmtes de controle quando o processo está realmente sob controle é -[(-0,007.(-0,007]=0,0054. Além dsso, a probabldade de que as duas varáves sejam marcadas dentro dos lmtes de controle quando o processo está sob controle é (0,9973.(0,9973= 0, Portanto, a utlzação de dos gráfcos X ndependentes alteram o montoramento smultâneo das duas varáves, consderando que um erro tpo I e a probabldade de um ponto ser representado corretamente não sejam guas aos seus níves anuncados para os gráfcos de controle ndvduas. Essa dstorção no procedmento de montoramento do processo será maor à medda que aumenta o número de varáves que estamos montorando smultaneamente (Montgomery, 004. Em geral, se há p varáves (característcas da qualdade estatstcamente ndependentes para um produto em partcular, e se o gráfco X com probabldade de erro tpo I é mantdo para cada uma, então a verdadera probabldade ( erro tpo I para cada procedmento de controle conjunto,, é: onde ( ' p ( (. p é a probabldade de que todas as varáves sejam representadas no gráfco smultaneamente dentro de seus lmtes de controle (Montgomery, 004. A equação (. pode ser utlzada quando as varáves são ndependentes para determnar os valores aproprados de para cada gráfco de controle quando é fado, e então obter convenentemente os correspondentes lmtes de controle. Para um gráfco de controle multvarado com p característcas de qualdade, a probabldade para que o gráfco ndque uma stuação sob controle no vetor de médas do processo µ o é. No caso em que seja escolhdo de forma que 0, 0035, então p -0,007p é gual a. Quando as p característcas são ndependentes a dferença entre as duas probabldades é pratcamente zero. Portanto, para os gráfcos de controle separados, a probabldade de que cada uma das p médas assume um valor dentro de seus lmtes de controle é p ( 0,007, muto prómo de - 0,007p para o gráfco multvarado. Por eemplo, suponhamos que se pretende controlar smultaneamente a méda do processo para duas característcas da qualdade ndependentes X e X de uma dstrbução normal bvarada. Para montorar ambas as característcas da qualdade pode-se aplcar o gráfco X de Shewhart cujos lmtes de controle são fados segundo o valor de Z Z 0, 0035 para cada p
28 Capítulo Revsão de Lteratura 8 característca. O processo, neste caso, estará sob controle somente se as médas amostras X e X representadas no gráfco estverem dentro de seus respectvos lmtes de controle. Isto equvale a representar o par de médas ( X, X dentro da regão retangular de controle conforme fgura.. Fgura. Regão de controle para duas varáves ndependentes analsadas de forma conjunta adaptada de Montgomery (004 A probabldade que as p = característcas da qualdade sob controle, assumem uma medda dentro de seus lmtes de controle é ( 0,007 0, 995. Porém, quando a probabldade conjunta de ambas as característcas da qualdade, não ecedam seus lmtes de controle é -[(0,007.(]=0,9946. Isto comprova que quando as característcas da qualdade são ndependentes pratcamente não este dferença entre ambas as probabldades (Montgomery, 004. No entanto, quando as característcas da qualdade não forem ndependentes, ou seja, correlaconadas que é o caso mas freqüente em aplcações ndustras, sto representa uma dferença consderável. Neste caso, um procedmento mas compleo, deve ser empregado para determnar o valor aproprado ' e com sso obter corretamente os lmtes de controle. Por smplcdade, contnuamos consderando o caso bvarado supondo que o gráfco X de Shewhart é usado e que ambas varáves (médas X e X seguem uma dstrbução normal bvarada de correlação com vetor de médas µ o = µ e matrz de covarâncas o = respectvamente conhecdos. 0, 0' ( 0,, 0, o = 0, 0, 0, 0, 0,
29 Capítulo Revsão de Lteratura 9 Para sso, um valor deve ser calculado a partr da equação. ' ( ( X ' P[ a ' = p 0, 0, n ( X a a P( a Z a a Z a a a 0, 0, n a ] ' = f ( z, z dzdz (. aa onde n é o tamanho da amostra e f z, z é a função densdade de probabldade de uma ( dstrbução normal padronzada bvarada com correlação. A regão de controle conjunta neste caso, para um determnado valor ', é uma elpse cuja nclnação depende da correlação estente entre as varáves consderadas conforme fgura.. Fgura. Regão de controle para duas varáves correlaconadas analsadas de forma conjunta adaptada de Montgomery (004 Os lmtes de controle fados segundo o crtéro 3 unvarado para as varáves X e X são sobrepostos na elpse para realzar a comparação. A área que representa o processo bvarado sob controle é lmtada pela elpse. Como as duas varáves X e X são dependentes qualquer ponto localzado fora da elpse de controle, ndca a presença de uma causa atrbuível, mesmo que esteja dentro dos lmtes de controle ndvduas para X e X. Os gráfcos de controle estatístco multvarados podem ser separados em dos grupos dstntos: os esquemas de montoramento dreconalmente específcos e os esquemas de montoramento dreconalmente nvarantes. No prmero deles, a dreção específca do
30 Capítulo Revsão de Lteratura 30 deslocamento do vetor de médas o do processo é conhecda vsto que no outro, esta dreção é desconhecda (Pham, 006. Nesta seção, o objetvo maor fo justfcar a pertnênca da utlzação de gráfco de controle estatístco multvarado para montorar smultaneamente duas ou mas característcas da qualdade correlaconadas e meddas sobre o mesmo processo frente à utlzação de gráfcos de controle ndvduas para cada uma das varáves separadamente. Nas seções seguntes, é realzado um estudo pormenorzado dos três prncpas gráfcos de controle atualmente utlzado no controle estatístco de processos multvarados o gráfco T de Hotellng, o gráfco MEWMA e o gráfco MCUSUM.. Gráfco de Controle T de Hotellng (Shewhart Multvarado O procedmento de controle multvarado mas conhecdo e atualmente utlzado para montorar o vetor de médas de um processo é anda o gráfco T de Hotellng. É um procedmento análogo ao gráfco de controle de Shewhart para o caso multvarado. Nesta seção são apresentadas as duas versões do gráfco T de Hotellng: uma para dados em subgrupos raconas, e outra para dados ndvduas... Subgrupos raconas Os gráfcos de controle multvarados são desenvolvdos a partr de medções dos resultados do processo para múltplas varáves. As medções são apresentadas, geralmente, para subgrupos de tens coletados de tal forma que estejam sob atuação de somente causas comuns. São chamados na lteratura de subgrupos raconas. O projeto de desenvolvmento de gráfcos de controle T de Hotellng para subgrupos raconas é separado em duas fases dstntas (Lowry e Montgomery,995. A prmera fase (fase I consste da análse de dados passados com o objetvo de verfcar se o processo estava sob controle estatístco quando os prmeros subgrupos foram obtdos, bem como retrar os pontos suspetos de estarem fora dos lmtes de controle e estmar a dstrbução do processo para teste de pontos futuros. A fase segunte (fase II consste em usar o gráfco de controle para detectar qualquer fuga do processo em relação à sua dstrbução estmada na fase. Para a fase I consdere que obtvemos m subgrupos ndependentes de tamanho n (n>p provenentes de dstrbuções N (, =,,...,m em que os vetores de médas sejam p desconhecdos e cujas matrzes de covarâncas são desconhecdas, mas guas. Nesta prmera fase, precsamos estmar o vetor de médas e a matrz de covarâncas a partr de uma
31 Capítulo Revsão de Lteratura 3 análse de m amostras de tamanho n, tomadas quando se admte que o processo está sob controle estatístco. Esses estmadores para e, são dados respectvamente, por m X (.3 m S (.4 m S m S m m m ( X k X( X k X ' (.5 onde m representa o número de amostras prelmnares de tamanho n retradas do processo e X k é a k-ésma observação p-varável referente a -ésma amostra. Na fase segunte (fase II utlzaremos as estmatvas dos parâmetros para obter a estatístca teste cujo procedmento nesta forma é denomnado gráfco de controle T Hotellng, ou seja: T n( X X S ( X X (.6 onde X e S representam, respectvamente, as estmatvas para o vetor de médas e matrz de covarâncas do processo. Para um gráfco T de Hotellng os lmtes de controle são dados pela escolha de um valor, tal que P(T LIC = -, conforme lmtes de controle quando a fase I é estabelecda. Na fase, os lmtes de controle do gráfco T de Hotellng são dados por: p( m ( n LSC F mn m p LIC = 0, p, mnm p Caso ocorram pontos plotados acma do LSC fasei de (.7 esses pontos são retrados do conjunto de dados e é recalculado um novo LSC fasei para o teste dos pontos remanescentes. Esse processo é realzado até que todos os pontos restantes estejam abao do LSC fasei calculado por últmo. Assummos a partr daí que esses pontos restantes são amostras aleatóras de uma dstrbução N (, e essas nformações serão usadas para a construção do gráfco de p controle para futuras observações do processo (Montgomery, 004. Na fase II, os novos lmtes de controle do gráfco T de Hotellng são dados por: p( m ( n LSC F mn m p, p, mnm p LIC 0 (.8
32 Capítulo Revsão de Lteratura 3 Quando um ponto ecede esse lmte, dzemos que o processo está fora de controle. Alguma causa especal, também chamada de causa assnalável, que não pertence ao sstema de causas comuns do processo deve estar atuando e tem de ser nvestgada. Para os lmtes de controle equações (.7 e (.8, F, p, mnm p representa o percentl da dstrbução F de Snedecor com p e (mn-m-p+ graus de lberdade, obtdo a partr da probabldade de alarme falso adotada... Observações ndvduas multvaradas Em alguns processos a técnca de agrupamento de dados va subgrupos raconas é nadequada de se aplcar, como por eemplo, ndústras de processos (químcas, petroquímcas, de mneração e outras stuações onde podemos consderar um tem como sendo uma porção de materal coletado nstantaneamente de determnada corrente ou de um lote homogêneo de algum produto. Nesse caso, temos geralmente subgrupos de tens de tamanho devdo às restrções de amostragem. Além dsso, a suposção de ndependênca dos tens estara muto comprometda caso se defnsse como amostra um subgrupo de materal do lote ou da corrente. Em ndústra de peças e componentes, a suposção de ndependênca dos tens pode ser adequada, mas às vezes aumenta o custo para se obter medções múltplas de subgrupos de tens. Isso, se justfca pelo elevado tempo de cclo de medção ou pelo seu custo. Observações ndvduas são muto comuns nesses casos (Pham, 006. O projeto de desenvolvmento de gráfcos de controle T de Hotellng para observações ndvduas é separado em duas fases dstntas. A prmera fase consste em um estudo retrospectvo dos dados, que mostra por meo de testes, se o processo está ou não sob controle estatístco quando os dados representam uma amostra de observações tomadas em todos os pontos do processo, ou seja, uma amostra representatva. Por eemplo, uma amostra retrada durante um específco período de tempo. Esta fase é de prmordal mportânca para estabelecer-se o controle estatístco e se encontrar os lmtes de controle aproprados para a fase segunte. Para a fase I consdere o caso em que p característcas correlaconadas estem, são meddas smultaneamente e estão necessaramente sob controle estatístco. Assume-se que estas característcas seguem uma dstrbução normal multvarada p-dmensonal com vetor de médas,,..., e matrz de covarâncas, onde é a méda da -ésma ( p característca e uma matrz de dmensão p p que contém as varâncas-covarâncas das p-característcas. Assumndo que o processo está sob controle nessa fase, os dados obtdos são usados para estmar os verdaderos valores da dstrbução normal e. Suponha que
33 Capítulo Revsão de Lteratura 33 ncalmente se tenha m elementos amostrados, após a retrada dos pontos atípcos restando dessa forma n elementos amostras com n m. Um problema sgnfcatvo, no caso das observações ndvduas é a estmação da matrz de covarâncas do processo. Sullvan e Woodall (996 apresentam crtéros alternatvos para estmar a matrz de covarâncas de processos cujo tamanho da amostra é n=. Esses autores propõem alguns procedmentos para obtenção de S (estmadores que tornam o deslocamento abrupto (mudança súbta no processo e deslocamento gradatvo (tendênca ou mudança gradatva no vetor de médas do processo. Dos desses estmadores merecem destaque. Um deles, é o estmador usual denomnado S, obtdo pela smples combnação de todas as m observações, ou seja, S m m ( X X ( X X (.9 O outro estmador é uma abordagem multvarada do estmador de ampltudes móves (Holmes e Mergen, 993 dado por V V S (.0 ( m onde V é a matrz contendo os vetores lnha das dferenças entre duas observações sucessvas p-varadas dadas por V, =,,3,...m- e S representa a matrz de covarâncas dessas dferenças. Usando S ao nvés de S na estatístca de controle T de Hotellng (.6, obtém-se um gráfco de controle mas sensível a possíves mudanças, abruptas ou gradatvas, no vetor de médas do processo. a observação onde O projeto de desenvolvmento do gráfco de controle estatístco nessas condções para X, utlza a segunte estatístca T de Hotellng para observações ndvduas T ( X X S ( X X (. X e S representam, respectvamente, as estmatvas do vetor de médas e matrz de covarâncas do processo. Nesta prmera fase seleconam-se m amostras prelmnares e representatvas para estabelecer-se o controle estatístco (processo padrão e encontrar os lmtes de controle aproprados. Os lmtes de controle para a estatístca T, nesta fase, segundo Tracy, Young e Mason (99, deve basear-se em uma dstrbução Beta dados por:
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
7. Resolução Numérica de Equações Diferenciais Ordinárias
 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
Controle Estatístico de Qualidade. Capítulo 8 (montgomery)
 Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Introdução e Organização de Dados Estatísticos
 II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Gráficos de controle multivariados: um estudo de caso no setor metalomecânico
 P&D em Engenhara de Produção, Itajubá, v. 10, n. 2, p. 143-156, 2012 Gráfcos de controle multvarados: um estudo de caso no setor metalomecânco Multvarate control charts: case study n the metallurgy mechancal
P&D em Engenhara de Produção, Itajubá, v. 10, n. 2, p. 143-156, 2012 Gráfcos de controle multvarados: um estudo de caso no setor metalomecânco Multvarate control charts: case study n the metallurgy mechancal
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
Palavras-chaves: Gráficos de controle, ambiente R, análise estatística multivariada
 A ntegração de cadeas produtvas com a abordagem da manufatura sustentável. Ro de Janero, RJ, Brasl, 13 a 16 de outubro de 2008 O DESENVOLVIMENTO DE GRÁFICOS DE CONTROLE MCUSUM E MEWMA EM AMBIENTE R COMO
A ntegração de cadeas produtvas com a abordagem da manufatura sustentável. Ro de Janero, RJ, Brasl, 13 a 16 de outubro de 2008 O DESENVOLVIMENTO DE GRÁFICOS DE CONTROLE MCUSUM E MEWMA EM AMBIENTE R COMO
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
O migrante de retorno na Região Norte do Brasil: Uma aplicação de Regressão Logística Multinomial
 O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
Estimativa da Incerteza de Medição da Viscosidade Cinemática pelo Método Manual em Biodiesel
 Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
UTILIZAÇÃO DO MÉTODO DE TAGUCHI NA REDUÇÃO DOS CUSTOS DE PROJETOS. Uma equação simplificada para se determinar o lucro de uma empresa é:
 UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
Controlo Metrológico de Contadores de Gás
 Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS
 Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Rastreando Algoritmos
 Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
REGRESSÃO LOGÍSTICA. Seja Y uma variável aleatória dummy definida como:
 REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
Controle de qualidade de produto cartográfico aplicado a imagem de alta resolução
 Controle de qualdade de produto cartográfco aplcado a magem de alta resolução Nathála de Alcântara Rodrgues Alves¹ Mara Emanuella Frmno Barbosa¹ Sydney de Olvera Das¹ ¹ Insttuto Federal de Educação Cênca
Controle de qualdade de produto cartográfco aplcado a magem de alta resolução Nathála de Alcântara Rodrgues Alves¹ Mara Emanuella Frmno Barbosa¹ Sydney de Olvera Das¹ ¹ Insttuto Federal de Educação Cênca
1 Princípios da entropia e da energia
 1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
www.obconcursos.com.br/portal/v1/carreirafiscal
 www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
Software para Furação e Rebitagem de Fuselagem de Aeronaves
 Anas do 14 O Encontro de Incação Centífca e Pós-Graduação do ITA XIV ENCITA / 2008 Insttuto Tecnológco de Aeronáutca São José dos Campos SP Brasl Outubro 20 a 23 2008. Software para Furação e Rebtagem
Anas do 14 O Encontro de Incação Centífca e Pós-Graduação do ITA XIV ENCITA / 2008 Insttuto Tecnológco de Aeronáutca São José dos Campos SP Brasl Outubro 20 a 23 2008. Software para Furação e Rebtagem
5.1 Seleção dos melhores regressores univariados (modelo de Índice de Difusão univariado)
 5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
Equipas Educativas Para uma nova organização da escola. João Formosinho Joaquim Machado
 Equpas Educatvas Para uma nova organzação da escola João Formosnho Joaqum Machado TRANSFORMAÇÕES NA ESCOLA BÁSICA TRANSFORMAÇÕES NA ESCOLA BÁSICA A expansão escolar e a mplementação das polítcas de nclusão
Equpas Educatvas Para uma nova organzação da escola João Formosnho Joaqum Machado TRANSFORMAÇÕES NA ESCOLA BÁSICA TRANSFORMAÇÕES NA ESCOLA BÁSICA A expansão escolar e a mplementação das polítcas de nclusão
Aula 03 Erros experimentais Incerteza. Aula 03 Prof. Valner Brusamarello
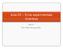 Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
INTRODUÇÃO AO CÁLCULO DE ERROS NAS MEDIDAS DE GRANDEZAS FÍSICAS
 Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
As tabelas resumem as informações obtidas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de informações.
 1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Influência dos Procedimentos de Ensaios e Tratamento de Dados em Análise Probabilística de Estrutura de Contenção
 Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
REGULAMENTO GERAL (Modalidades 1, 2, 3 e 4)
 REGULAMENTO GERAL (Modaldades 1, 2, 3 e 4) 1. PARTICIPAÇÃO 1.1 Podem concorrer ao 11º Prêmo FIEB de Desempenho Socoambental da Indústra Baana empresas do setor ndustral nas categoras MICRO E PEQUENO, MÉDIO
REGULAMENTO GERAL (Modaldades 1, 2, 3 e 4) 1. PARTICIPAÇÃO 1.1 Podem concorrer ao 11º Prêmo FIEB de Desempenho Socoambental da Indústra Baana empresas do setor ndustral nas categoras MICRO E PEQUENO, MÉDIO
XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA NOVO MODELO PARA O CÁLCULO DE CARREGAMENTO DINÂMICO DE TRANSFORMADORES
 XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA Versão 1.0 22 a 25 Novembro de 2009 Recfe - PE GRUPO XIII GRUPO DE ESTUDO DE TRANSFORMADORES, REATORES, MATERIAIS E TECNOLOGIAS
XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA Versão 1.0 22 a 25 Novembro de 2009 Recfe - PE GRUPO XIII GRUPO DE ESTUDO DE TRANSFORMADORES, REATORES, MATERIAIS E TECNOLOGIAS
Apostila de Estatística Curso de Matemática. Volume II 2008. Probabilidades, Distribuição Binomial, Distribuição Normal. Prof. Dr. Celso Eduardo Tuna
 Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Lista de Exercícios de Recuperação do 2 Bimestre. Lista de exercícios de Recuperação de Matemática 3º E.M.
 Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
RODRIGO LUIZ PEREIRA LARA DESEMPENHO DO GRÁFICO DE CONTROLE CUSUM TABULAR PARA O MONITORAMENTO DA MÉDIA
 RODRIGO LUIZ PEREIRA LARA DESEMPENO DO GRÁFICO DE CONTROLE CUSUM TABULAR PARA O MONITORAMENTO DA MÉDIA Dssertação apresentada à Unversdade Federal de Vçosa, como parte das exgêncas do Programa de Pós Graduação
RODRIGO LUIZ PEREIRA LARA DESEMPENO DO GRÁFICO DE CONTROLE CUSUM TABULAR PARA O MONITORAMENTO DA MÉDIA Dssertação apresentada à Unversdade Federal de Vçosa, como parte das exgêncas do Programa de Pós Graduação
Nota Técnica Médias do ENEM 2009 por Escola
 Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
1 INTRODUÇÃO. 1 Segundo Menezes-Filho (2001), brasileiros com ensino fundamental completo ganham, em média, três vezes
 A amplação da jornada escolar melhora o desempenho acadêmco dos estudantes? Uma avalação do programa Escola de Tempo Integral da rede públca do Estado de São Paulo 1 INTRODUÇÃO O acesso à educação é uma
A amplação da jornada escolar melhora o desempenho acadêmco dos estudantes? Uma avalação do programa Escola de Tempo Integral da rede públca do Estado de São Paulo 1 INTRODUÇÃO O acesso à educação é uma
Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Cálculo do Conceito Preliminar de Cursos de Graduação
 Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Análise Econômica da Aplicação de Motores de Alto Rendimento
 Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
2 Máquinas de Vetor Suporte 2.1. Introdução
 Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
I. Introdução. inatividade. 1 Dividiremos a categoria dos jovens em dois segmentos: os jovens que estão em busca do primeiro emprego, e os jovens que
 DESEMPREGO DE JOVENS NO BRASIL I. Introdução O desemprego é vsto por mutos como um grave problema socal que vem afetando tanto economas desenvolvdas como em desenvolvmento. Podemos dzer que os índces de
DESEMPREGO DE JOVENS NO BRASIL I. Introdução O desemprego é vsto por mutos como um grave problema socal que vem afetando tanto economas desenvolvdas como em desenvolvmento. Podemos dzer que os índces de
Universidade do Estado do Rio de Janeiro Instituto de Matemática e Estatística Econometria
 Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
Distribuição de Massa Molar
 Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Estimativa dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro.
 Estmatva dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro. O. L. L. Moraes 1, H. R. da Rocha 2, M. A. Faus da Slva Das 2, O Cabral 3 1 Departamento
Estmatva dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro. O. L. L. Moraes 1, H. R. da Rocha 2, M. A. Faus da Slva Das 2, O Cabral 3 1 Departamento
PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA
 658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
Metodologia IHFA - Índice de Hedge Funds ANBIMA
 Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Sinais Luminosos 2- CONCEITOS BÁSICOS PARA DIMENSIONAMENTO DE SINAIS LUMINOSOS.
 Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
RESOLUÇÃO DE ESTRUTURAS SUBSAL ATRAVÉS DE MIGRAÇÃO RTM
 Copyrght 004, Insttuto Braslero de Petróleo e Gás - IBP Este Trabalho Técnco Centífco fo preparado para apresentação no 3 Congresso Braslero de P&D em Petróleo e Gás, a ser realzado no período de a 5 de
Copyrght 004, Insttuto Braslero de Petróleo e Gás - IBP Este Trabalho Técnco Centífco fo preparado para apresentação no 3 Congresso Braslero de P&D em Petróleo e Gás, a ser realzado no período de a 5 de
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
ÍNDICE NOTA INTRODUTÓRIA
 OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
Palavras-chave: jovens no mercado de trabalho; modelo de seleção amostral; região Sul do Brasil.
 1 A INSERÇÃO E O RENDIMENTO DOS JOVENS NO MERCADO DE TRABALHO: UMA ANÁLISE PARA A REGIÃO SUL DO BRASIL Prscla Gomes de Castro 1 Felpe de Fgueredo Slva 2 João Eustáquo de Lma 3 Área temátca: 3 -Demografa
1 A INSERÇÃO E O RENDIMENTO DOS JOVENS NO MERCADO DE TRABALHO: UMA ANÁLISE PARA A REGIÃO SUL DO BRASIL Prscla Gomes de Castro 1 Felpe de Fgueredo Slva 2 João Eustáquo de Lma 3 Área temátca: 3 -Demografa
ALTERNATIVAS E COMPARAÇÕES DE MODELOS LINEARES PARA ESTIMAÇÃO DA BIOMASSA VERDE DE Bambusa vulgaris NA EXISTÊNCIA DE MULTICOLINEARIDADE
 ADRIANO VICTOR LOPES DA SILVA ALTERNATIVAS E COMPARAÇÕES DE MODELOS LINEARES PARA ESTIMAÇÃO DA BIOMASSA VERDE DE Bambusa vulgars NA EXISTÊNCIA DE MULTICOLINEARIDADE RECIFE-PE Feverero /2008. Lvros Gráts
ADRIANO VICTOR LOPES DA SILVA ALTERNATIVAS E COMPARAÇÕES DE MODELOS LINEARES PARA ESTIMAÇÃO DA BIOMASSA VERDE DE Bambusa vulgars NA EXISTÊNCIA DE MULTICOLINEARIDADE RECIFE-PE Feverero /2008. Lvros Gráts
Sistemas de Filas: Aula 5. Amedeo R. Odoni 22 de outubro de 2001
 Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Análise de Regressão. Profa Alcione Miranda dos Santos Departamento de Saúde Pública UFMA
 Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Despacho Econômico de. Sistemas Termoelétricos e. Hidrotérmicos
 Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Física. Física Módulo 1 Vetores, escalares e movimento em 2-D
 Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
PARTE 1. 1. Apresente as equações que descrevem o comportamento do preço de venda dos imóveis.
 EXERCICIOS AVALIATIVOS Dscplna: ECONOMETRIA Data lmte para entrega: da da 3ª prova Valor: 7 pontos INSTRUÇÕES: O trabalho é ndvdual. A dscussão das questões pode ser feta em grupo, mas cada aluno deve
EXERCICIOS AVALIATIVOS Dscplna: ECONOMETRIA Data lmte para entrega: da da 3ª prova Valor: 7 pontos INSTRUÇÕES: O trabalho é ndvdual. A dscussão das questões pode ser feta em grupo, mas cada aluno deve
RESOLUÇÃO Nº 32/2014/CONEPE. O CONSELHO DO ENSINO, DA PESQUISA E DA EXTENSÃO da Universidade Federal de Sergipe, no uso de suas atribuições legais,
 SERVIÇO PÚBLICO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DE SERGIPE CONSELHO DO ENSINO, DA PESQUISA E DA EXTENSÃO RESOLUÇÃO Nº 32/2014/CONEPE Aprova as Normas Geras do Processo Seletvo para
SERVIÇO PÚBLICO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DE SERGIPE CONSELHO DO ENSINO, DA PESQUISA E DA EXTENSÃO RESOLUÇÃO Nº 32/2014/CONEPE Aprova as Normas Geras do Processo Seletvo para
Energia de deformação na flexão
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
Controle Estatístico de Processos: a questão da autocorrelação, dos erros de mensuração e do monitoramento de mais de uma característica de qualidade
 Controle Estatístco de Processos: a questão da autocorrelação, dos erros de mensuração e do montoramento de mas de uma característca de qualdade Docentes: Maysa S. de Magalhães; Lnda Lee Ho; Antono Fernando
Controle Estatístco de Processos: a questão da autocorrelação, dos erros de mensuração e do montoramento de mas de uma característca de qualdade Docentes: Maysa S. de Magalhães; Lnda Lee Ho; Antono Fernando
ANEXO II METODOLOGIA E CÁLCULO DO FATOR X
 ANEXO II Nota Técnca nº 256/2009-SRE/ANEEL Brasíla, 29 de julho de 2009 METODOLOGIA E ÁLULO DO FATOR X ANEXO II Nota Técnca n o 256/2009 SRE/ANEEL Em 29 de julho de 2009. Processo nº 48500.004295/2006-48
ANEXO II Nota Técnca nº 256/2009-SRE/ANEEL Brasíla, 29 de julho de 2009 METODOLOGIA E ÁLULO DO FATOR X ANEXO II Nota Técnca n o 256/2009 SRE/ANEEL Em 29 de julho de 2009. Processo nº 48500.004295/2006-48
ALGORITMOS GENÉTICOS COMO FERRAMENTA AUXILIAR NA TOMADA DE DECISÃO EM ATIVIDADES DE GESTÃO AGROINDUSTRIAL
 ALGORITMOS GENÉTICOS COMO FERRAMENTA AUXILIAR NA TOMADA DE DECISÃO EM ATIVIDADES DE GESTÃO AGROINDUSTRIAL Danlo Augusto Hereda VIEIRA 1 Celso Correa de SOUZA 2 José Francsco dos REIS NETO 3 Resumo. As
ALGORITMOS GENÉTICOS COMO FERRAMENTA AUXILIAR NA TOMADA DE DECISÃO EM ATIVIDADES DE GESTÃO AGROINDUSTRIAL Danlo Augusto Hereda VIEIRA 1 Celso Correa de SOUZA 2 José Francsco dos REIS NETO 3 Resumo. As
Física. Setor B. Índice-controle de Estudo. Prof.: Aula 23 (pág. 86) AD TM TC. Aula 24 (pág. 87) AD TM TC. Aula 25 (pág.
 Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
MODELAGEM DA FRAÇÃO DE NÃO-CONFORMES EM PROCESSOS INDUSTRIAIS
 versão mpressa ISSN 0101-7438 / versão onlne ISSN 1678-5142 MODELAGEM DA FRAÇÃO DE NÃO-CONFORMES EM PROCESSOS INDUSTRIAIS Ângelo Márco Olvera Sant Anna* Carla Schwengber ten Caten Programa de Pós-graduação
versão mpressa ISSN 0101-7438 / versão onlne ISSN 1678-5142 MODELAGEM DA FRAÇÃO DE NÃO-CONFORMES EM PROCESSOS INDUSTRIAIS Ângelo Márco Olvera Sant Anna* Carla Schwengber ten Caten Programa de Pós-graduação
ESTATÍSTICA. PROBABILIDADES Professora Rosana Relva Números Inteiros e Racionais ESTATÍSTICA. Professor Luiz Antonio de Carvalho
 PROBABILIDADES Professora Rosana Relva Números Interos e Raconas APRESENTAÇÃO ROL:,,, 4, 4,,, DISCRETA : rrelva@globo.com PROGRESSÃO ARITMÉTICA CONTÍNUA PROGRESSÃO ARITMÉTICA DISTRIBUIÇÃO DE REQUÊCIAS
PROBABILIDADES Professora Rosana Relva Números Interos e Raconas APRESENTAÇÃO ROL:,,, 4, 4,,, DISCRETA : rrelva@globo.com PROGRESSÃO ARITMÉTICA CONTÍNUA PROGRESSÃO ARITMÉTICA DISTRIBUIÇÃO DE REQUÊCIAS
PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS DO CEARÁ
 GOVERNO DO ESTADO DO CEARÁ SECRETARIA DO PLANEJAMENTO E GESTÃO - SEPLAG INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE NOTA TÉCNICA Nº 29 PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS
GOVERNO DO ESTADO DO CEARÁ SECRETARIA DO PLANEJAMENTO E GESTÃO - SEPLAG INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE NOTA TÉCNICA Nº 29 PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS
Expressão da Incerteza de Medição para a Grandeza Energia Elétrica
 1 a 5 de Agosto de 006 Belo Horzonte - MG Expressão da ncerteza de Medção para a Grandeza Energa Elétrca Eng. Carlos Alberto Montero Letão CEMG Dstrbução S.A caletao@cemg.com.br Eng. Sérgo Antôno dos Santos
1 a 5 de Agosto de 006 Belo Horzonte - MG Expressão da ncerteza de Medção para a Grandeza Energa Elétrca Eng. Carlos Alberto Montero Letão CEMG Dstrbução S.A caletao@cemg.com.br Eng. Sérgo Antôno dos Santos
PLANEJAMENTO DE GRÁFICOS DE CONTROLE DE REGRESSÃO VIA SIMULAÇÃO
 PLANEJAMENTO DE GRÁFICOS DE CONTROLE DE REGRESSÃO VIA SIMULAÇÃO Ana Carolna Campana Nascmento 1, José Ivo Rbero Júnor 1, Mosés Nascmento 1 1. Professor da Unversdade Federal de Vçosa, Avenda Peter Henr
PLANEJAMENTO DE GRÁFICOS DE CONTROLE DE REGRESSÃO VIA SIMULAÇÃO Ana Carolna Campana Nascmento 1, José Ivo Rbero Júnor 1, Mosés Nascmento 1 1. Professor da Unversdade Federal de Vçosa, Avenda Peter Henr
SEQÜENCIAMENTO DE TAREFAS COM MÁQUINAS PARALELAS, PERMITINDO ATRASOS E COM TEMPOS DE PREPARAÇÃO DE MÁQUINA DEPENDENTES DA SEQÜÊNCIA.
 A pesqusa Operaconal e os Recursos Renováves a 7 de novembro de, Natal-RN SEQÜENCIAMENTO DE TAREFAS COM MÁQUINAS PARALELAS, PERMITINDO ATRASOS E COM TEMPOS DE PREPARAÇÃO DE MÁQUINA DEPENDENTES DA SEQÜÊNCIA.
A pesqusa Operaconal e os Recursos Renováves a 7 de novembro de, Natal-RN SEQÜENCIAMENTO DE TAREFAS COM MÁQUINAS PARALELAS, PERMITINDO ATRASOS E COM TEMPOS DE PREPARAÇÃO DE MÁQUINA DEPENDENTES DA SEQÜÊNCIA.
Testando um Mito de Investimento : Eficácia da Estratégia de Investimento em Ações de Crescimento.
 Testando um Mto de Investmento : Efcáca da Estratéga de Investmento em Ações de Crescmento. Autora: Perre Lucena Rabon, Odlon Saturnno Slva Neto, Valera Louse de Araújo Maranhão, Luz Fernando Correa de
Testando um Mto de Investmento : Efcáca da Estratéga de Investmento em Ações de Crescmento. Autora: Perre Lucena Rabon, Odlon Saturnno Slva Neto, Valera Louse de Araújo Maranhão, Luz Fernando Correa de
TRANSPORTE E ESTOCAGEM DE FUMO UM MODELO DE PROGRAMAÇÃO LINEAR USADO NA TOMADA DE DECISÃO
 TRANSPORTE E ESTOCAGEM DE FUMO UM MODELO DE PROGRAMAÇÃO LINEAR USADO NA TOMADA DE DECISÃO Janaína Poffo Possama janapoffo@gmal.com Unversdade Regonal de Blumenau Rua Antôno da Vega, 0 8902-900 - Blumenau
TRANSPORTE E ESTOCAGEM DE FUMO UM MODELO DE PROGRAMAÇÃO LINEAR USADO NA TOMADA DE DECISÃO Janaína Poffo Possama janapoffo@gmal.com Unversdade Regonal de Blumenau Rua Antôno da Vega, 0 8902-900 - Blumenau
Modelos estatísticos para previsão de partidas de futebol
 Modelos estatístcos para prevsão de partdas de futebol Dan Gamerman Insttuto de Matemátca, UFRJ dan@m.ufrj.br X Semana da Matemátca e II Semana da Estatístca da UFOP Ouro Preto, MG 03/11/2010 Algumas perguntas
Modelos estatístcos para prevsão de partdas de futebol Dan Gamerman Insttuto de Matemátca, UFRJ dan@m.ufrj.br X Semana da Matemátca e II Semana da Estatístca da UFOP Ouro Preto, MG 03/11/2010 Algumas perguntas
UM MODELO DE ALOCAÇÃO DINÂMICA DE CAMINHÕES VISANDO AO ATENDIMENTO DE METAS DE PRODUÇÃO E QUALIDADE
 UM MODELO DE ALOCAÇÃO DINÂMICA DE CAMINHÕES VISANDO AO ATENDIMENTO DE METAS DE PRODUÇÃO E QUALIDADE RESUMO Felppe Perera da Costa, PPGEM/UFOP, Mestrando. felppe@mneral.em.ufop.br Marcone Jamlson Fretas
UM MODELO DE ALOCAÇÃO DINÂMICA DE CAMINHÕES VISANDO AO ATENDIMENTO DE METAS DE PRODUÇÃO E QUALIDADE RESUMO Felppe Perera da Costa, PPGEM/UFOP, Mestrando. felppe@mneral.em.ufop.br Marcone Jamlson Fretas
UNIVERSIDADE PRESBITERIANA MACKENZIE CCSA - Centro de Ciências Sociais e Aplicadas Curso de Economia
 CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
Estatística stica Descritiva
 AULA1-AULA5 AULA5 Estatístca stca Descrtva Prof. Vctor Hugo Lachos Davla oo que é a estatístca? Para mutos, a estatístca não passa de conjuntos de tabelas de dados numércos. Os estatístcos são pessoas
AULA1-AULA5 AULA5 Estatístca stca Descrtva Prof. Vctor Hugo Lachos Davla oo que é a estatístca? Para mutos, a estatístca não passa de conjuntos de tabelas de dados numércos. Os estatístcos são pessoas
ANÁLISE ESTATÍSTICA DE CORRELAÇÕES PVT DE PETRÓLEOS
 UNIVERSIDADE FEDERAL DO ESÍRITO SANTO CENTRO TECNOLÓGICO ROGRAMA DE ÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA GARBEN BRAVIM GOMES ANÁLISE ESTATÍSTICA DE CORRELAÇÕES VT DE ETRÓLEOS VITÓRIA 8 GARBEN BRAVIM GOMES
UNIVERSIDADE FEDERAL DO ESÍRITO SANTO CENTRO TECNOLÓGICO ROGRAMA DE ÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA GARBEN BRAVIM GOMES ANÁLISE ESTATÍSTICA DE CORRELAÇÕES VT DE ETRÓLEOS VITÓRIA 8 GARBEN BRAVIM GOMES
Atribuição Automática de Propagandas a Páginas da Web
 Atrbução Automátca de Propagandas a Págnas da Web Aníso Mendes Lacerda Lara Crstna Rodrgues Coelho Resumo O problema da propaganda dreconada baseada em conteúdo (PDC) consttu-se em atrbur propagandas a
Atrbução Automátca de Propagandas a Págnas da Web Aníso Mendes Lacerda Lara Crstna Rodrgues Coelho Resumo O problema da propaganda dreconada baseada em conteúdo (PDC) consttu-se em atrbur propagandas a
Fast Multiresolution Image Querying
 Fast Multresoluton Image Queryng Baseado no artgo proposto por: Charles E. Jacobs Adan Fnkelsten Davd H. Salesn Propõe um método para busca em um banco de dados de magem utlzando uma magem de consulta
Fast Multresoluton Image Queryng Baseado no artgo proposto por: Charles E. Jacobs Adan Fnkelsten Davd H. Salesn Propõe um método para busca em um banco de dados de magem utlzando uma magem de consulta
FUNÇÃO NO R PARA OBTENÇÃO DO DESENHO D-ÓTIMO EM MODELOS DE MISTURAS COM RESTRIÇÕES
 FUNÇÃO NO R PARA OBTENÇÃO DO DESENHO D-ÓTIMO EM MODELOS DE MISTURAS COM RESTRIÇÕES Edmlson Rodrgues Pnto Leandro Alves Perera Faculdade de Matemátca Faculdade de Matemátca Unversdade Federal de Uberlânda
FUNÇÃO NO R PARA OBTENÇÃO DO DESENHO D-ÓTIMO EM MODELOS DE MISTURAS COM RESTRIÇÕES Edmlson Rodrgues Pnto Leandro Alves Perera Faculdade de Matemátca Faculdade de Matemátca Unversdade Federal de Uberlânda
Suporte Básico para Sistemas de Tempo Real
 Suporte Básco para Sstemas de Tempo Real Escalonamento e Comuncação Sldes elaborados por George Lma, com atualzações realzadas por Ramundo Macêdo Suporte Básco para Sstemas de Tempo-Real Escalonamento
Suporte Básco para Sstemas de Tempo Real Escalonamento e Comuncação Sldes elaborados por George Lma, com atualzações realzadas por Ramundo Macêdo Suporte Básco para Sstemas de Tempo-Real Escalonamento
01. Em porcentagem das emissões totais de gases do efeito estufa, o Brasil é o quarto maior poluidor, conforme a tabela abaixo:
 PROCESSO SELETIVO 7 RESOLUÇÃO MATEMÁTICA Rosane Soares Morera Vana, Luz Cláudo Perera, Lucy Tem Takahash, Olímpo Hrosh Myagak QUESTÕES OBJETIVAS Em porcentagem das emssões totas de gases do efeto estufa,
PROCESSO SELETIVO 7 RESOLUÇÃO MATEMÁTICA Rosane Soares Morera Vana, Luz Cláudo Perera, Lucy Tem Takahash, Olímpo Hrosh Myagak QUESTÕES OBJETIVAS Em porcentagem das emssões totas de gases do efeto estufa,
Capítulo 1: Erros em cálculo numérico
 Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Variabilidade Espacial do Teor de Água de um Argissolo sob Plantio Convencional de Feijão Irrigado
 Varabldade Espacal do Teor de Água de um Argssolo sob Planto Convenconal de Fejão Irrgado Elder Sânzo Aguar Cerquera 1 Nerlson Terra Santos 2 Cásso Pnho dos Res 3 1 Introdução O uso da água na rrgação
Varabldade Espacal do Teor de Água de um Argssolo sob Planto Convenconal de Fejão Irrgado Elder Sânzo Aguar Cerquera 1 Nerlson Terra Santos 2 Cásso Pnho dos Res 3 1 Introdução O uso da água na rrgação
NORMAS DE SELEÇÃO AO DOUTORADO
 1. INSCRIÇÕES PARA SELEÇÃO 1.1. Para a Área de Irrgação e Drenagem Poderão nscrever-se canddatos formados em Engenhara Agrícola, Agronoma, Meteorologa e demas Engenharas, ou em outras áreas afns a crtéro
1. INSCRIÇÕES PARA SELEÇÃO 1.1. Para a Área de Irrgação e Drenagem Poderão nscrever-se canddatos formados em Engenhara Agrícola, Agronoma, Meteorologa e demas Engenharas, ou em outras áreas afns a crtéro
O USO DA INTEGRAL DEFINIDA NO CÁLCULO DA ÁREA ALAGADA DA BARRAGEM DO RIO BONITO
 O USO DA INTEGRAL DEFINIDA NO CÁLCULO DA ÁREA ALAGADA DA BARRAGEM DO RIO BONITO Crstna Martns Paraol crstna@hotmal.com Insttuto Federal Catarnense Rua Prefeto Francsco Lummertz Júnor, 88 88960000 Sombro
O USO DA INTEGRAL DEFINIDA NO CÁLCULO DA ÁREA ALAGADA DA BARRAGEM DO RIO BONITO Crstna Martns Paraol crstna@hotmal.com Insttuto Federal Catarnense Rua Prefeto Francsco Lummertz Júnor, 88 88960000 Sombro
Revisão dos Métodos para o Aumento da Confiabilidade em Sistemas Elétricos de Distribuição
 CIDEL Argentna 2014 Internatonal Congress on Electrcty Dstrbuton Ttle Revsão dos Métodos para o Aumento da Confabldade em Sstemas Elétrcos de Dstrbução Regstraton Nº: (Abstract) Authors of the paper Name
CIDEL Argentna 2014 Internatonal Congress on Electrcty Dstrbuton Ttle Revsão dos Métodos para o Aumento da Confabldade em Sstemas Elétrcos de Dstrbução Regstraton Nº: (Abstract) Authors of the paper Name
MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE
 MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE R. L. S. CANEVESI 1, C. L. DIEL 2, K. A. SANTOS 1, C. E. BORBA 1, F. PALÚ 1, E. A. DA SILVA 1 1 Unversdade Estadual
MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE R. L. S. CANEVESI 1, C. L. DIEL 2, K. A. SANTOS 1, C. E. BORBA 1, F. PALÚ 1, E. A. DA SILVA 1 1 Unversdade Estadual
MAE5778 - Teoria da Resposta ao Item
 MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
Professor Mauricio Lutz CORRELAÇÃO
 Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
INCLUSÃO DE RESTRIÇÕES DINÂMICAS NA ANÁLISE DE FLUXO DE POTÊNCIA ÓTIMO RAFAEL MONTES FONTOURA
 INCLUSÃO DE RESTRIÇÕES DINÂMICAS NA ANÁLISE DE FLUXO DE POTÊNCIA ÓTIMO RAFAEL MONTES FONTOURA DISSERTAÇÃO SUBMETIDA AO CORPO DOCENTE DA COORDENAÇÃO DO PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA DA
INCLUSÃO DE RESTRIÇÕES DINÂMICAS NA ANÁLISE DE FLUXO DE POTÊNCIA ÓTIMO RAFAEL MONTES FONTOURA DISSERTAÇÃO SUBMETIDA AO CORPO DOCENTE DA COORDENAÇÃO DO PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA DA
ELEMENTOS DE CIRCUITOS
 MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
OTIMIZAÇÃO DO FLUXO REVERSO DE PNEUS INSERVÍVEIS ATRAVÉS DE UM MODELO DE LOCALIZAÇÃO DE FACILIDADES: UM ESTUDO DE CASO
 OTIMIZAÇÃO DO FLUXO REVERSO DE PNEUS INSERVÍVEIS ATRAVÉS DE UM MODELO DE LOCALIZAÇÃO DE FACILIDADES: UM ESTUDO DE CASO Felpe Mendonca Gurgel Bandera (UFERSA) felpembandera@hotmal.com Breno Barros Telles
OTIMIZAÇÃO DO FLUXO REVERSO DE PNEUS INSERVÍVEIS ATRAVÉS DE UM MODELO DE LOCALIZAÇÃO DE FACILIDADES: UM ESTUDO DE CASO Felpe Mendonca Gurgel Bandera (UFERSA) felpembandera@hotmal.com Breno Barros Telles
Impactos dos encargos sociais na economia brasileira
 Impactos dos encargos socas na economa braslera Mayra Batsta Btencourt Professora da Unversdade Federal de Mato Grosso do Sul Erly Cardoso Texera Professor da Unversdade Federal de Vçosa Palavras-chave
Impactos dos encargos socas na economa braslera Mayra Batsta Btencourt Professora da Unversdade Federal de Mato Grosso do Sul Erly Cardoso Texera Professor da Unversdade Federal de Vçosa Palavras-chave
Capítulo 1. O plano complexo. 1.1. Introdução. Os números complexos começaram por ser introduzidos para dar sentido à 2
 Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Departamento de Informática. Modelagem Analítica. Modelagem Analítica do Desempenho de Sistemas de Computação. Disciplina: Medida de Probabilidade
 Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
