ÍNDICE NOTA INTRODUTÓRIA
|
|
|
- Samuel Domingos Lisboa
- 8 Há anos
- Visualizações:
Transcrição
1 OGC ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de medção expandda 7 6. Procedmento sequencal de cálculo da ncerteza de medção 7. Referêncas 9 8. Anexo A: Melhor Incerteza (CMC - Calbraton and 9 Measurement Capablty) 9. Anexo B: Glossáro de alguns termos relevantes 9 0. Anexo C: Fontes de ncerteza de medção. Anexo D: Grandezas de entrada correlaconadas. Anexo E: Fatores de expansão provenentes de graus de lberdade efetvos OTA ITRODUTÓRIA Este documento é a tradução do EA-4/0 Evaluaton of the Uncertanty of Measurement n Calbraton, de setembro de 03, publcado pela European Accredtaton (EA), a qual é detentora dos respetvos dretos de reprodução. O EA-4/0 contém suplementos, com exemplos de aplcação para problemas específcos nas dferentes áreas de calbração, que não são objeto de tradução neste documento. O documento EA-4/0 orgnal (em nglês) é de cumprmento obrgatóro prevalecendo a esta tradução, na qual foram ntroduzdas notas IPAC para melhor clarfcação de alguns concetos. Este documento fo preparado por um grupo de trabalho IPAC/IPQ, tendo sdo usado como base de trabalho o documento IPQ Gua para a Expressão da Incerteza de Medção nos Laboratóros de Calbração, entretanto anulado, dado que o mesmo consttuía uma tradução da anteror edção do EA-4/0. ISTITUTO PORTUGUÊS DE ACREDITAÇÃO PORTUGUESE ACCREDITATIO ISTITUTE Rua Antóno Gão,, 5º Tel: Caparca Fax: E-mal: acredta@pac.pt Internet
2 OGC Objetvo O objetvo deste documento é harmonzar a avalação da ncerteza de medção no seo da EA, em complemento dos requstos geras desta, estabelecer as exgêncas específcas no modo de apresentar a ncerteza de medção nos certfcados de calbração emtdos pelos laboratóros acredtados e apoar os organsmos de acredtação na atrbução coerente da melhor ncerteza (CMC Calbraton and Measurement Capablty) aos laboratóros de calbração por eles acredtados. Como as regras expressas por este documento estão de acordo com a polítca do ILAC para a ncerteza em calbração e com as recomendações do Gua para a Expressão da Incerteza na Medção (GUM), a mplementação do EA-4/0 rá também encorajar a acetação global dos resultados de medção europeus.. Introdução. O presente documento estabelece os prncípos e os requstos de avalação da ncerteza de medção na calbração e o modo de a expressar nos certfcados de calbração com base na polítca do ILAC para a ncerteza em calbração estabelecda no ILAC P4 [ref. 5]. O ILAC P4 e o EA-4/0 são de cumprmento obrgatóro para os Organsmos de Acredtação membros da EA. É adotada uma formulação genérca, por forma a ser válda para todas as áreas de calbração. O método delneado poderá ser complementado com recomendações ou nstruções técncas mas específcas para as dferentes áreas de modo a facltar a sua aplcação. o desenvolvmento desses guas suplementares, deverão ser segudos os prncípos geras estabelecdos neste documento, assegurando a harmonzação entre as dferentes áreas.. O presente documento está de acordo com o documento JCGM 00:008 [ref. ], Evaluaton of measurement data Gude to the expresson of uncertanty n measurement (GUM 995 wth mnor correctons). Este documento fo elaborado pelo Comté para Guas em Metrologa, no qual partcpam o BIPM, a IEC, a IFCC, a ILAC, a ISO, a IUPAC, a IUPAP e a OIML. Enquanto o GUM estabelece regras geras para a avalação e expressão da ncerteza da medção que podem ser segudas na maor parte dos domínos das medções físcas, este documento concentra-se no método mas adequado para as medções nos laboratóros de calbração e descreve uma forma não-ambígua e harmonzada de avalação e expressão da ncerteza da medção. o entanto, são acetáves outras abordagens propostas pelo GUM (como por exemplo o método de Monte Carlo). Este documento aborda os seguntes assuntos: Defnções-base para o documento; Métodos para a avalação da ncerteza de medção das grandezas de entrada; Relação entre a ncerteza de medção da grandeza de saída e a ncerteza avalada das grandezas de entrada; Incerteza expandda de medção da grandeza de saída; Procedmento sequencal para cálculo da ncerteza de medção. A avalação da ncerteza de medção em calbração é também tratada em dversos guas de calbração da Euramet dsponíves em Âmbto e defnções ota: Os termos de especal relevânca no texto prncpal estão escrtos em negrto quando aparecem no documento pela prmera vez. O Anexo B contém um glossáro destes termos juntamente com as referêncas.. A expressão de um resultado de medção só está completa quando contém o valor atrbuído à mensuranda e a ncerteza de medção assocada a esse valor. este documento, todas as grandezas que não são completamente conhecdas são tratadas como varáves aleatóras, nclundo as grandezas de nfluênca que possam afetar o valor meddo.. A ncerteza de medção é um parâmetro não negatvo, assocado ao resultado de uma medção, que caracterza a dspersão dos valores que podem ser razoavelmente atrbuídos à mensuranda [ref. 3]. este documento, o termo abrevado ncerteza é usado para referr ncerteza de medção quando não há o rsco de equívoco. Como fontes típcas de ncerteza numa medção ver a lsta dada no Anexo C. Pág. de 4
3 OGC As mensurandas são as grandezas partculares submetdas à medção. a calbração, em regra, lda-se com uma únca mensuranda ou grandeza de saída Y, que depende de um certo número de grandezas de entrada X ( =,,..., ), de acordo com a relação funconal: Y = f (X, X,..., X ) (.) A função modelo f representa o procedmento de medção e o método de avalação. Descreve como os valores da grandeza de saída Y são obtdos a partr das grandezas de entrada X. Em mutos casos, será uma expressão analítca, mas também pode ser um grupo dessas expressões que ncluam correções e fatores de correção para efetos sstemátcos, levando assm a uma relação mas complcada do que uma função explctamente expressa. Além dsso, f pode ser determnada expermentalmente, pode exstr apenas como um algortmo nformátco que tem de ser avalado numercamente, ou pode ser uma combnação de todas estas formas..4 As grandezas de entrada X podem ser agrupadas em duas categoras, de acordo com o modo como foram determnados o valor da grandeza e a ncerteza assocada: (a) As grandezas cuja estmatva e ncerteza assocada são determnadas dretamente na medção. Estes valores podem ser obtdos, por exemplo, de uma smples observação, de observações repetdas, ou de avalação baseada na experênca. Podem envolver a determnação de correções às ndcações de nstrumentos, bem como as correções das grandezas de nfluênca, tas como a temperatura ambente, a pressão atmosférca ou a humdade relatva; (b) As grandezas cuja estmatva e ncerteza assocada são provenentes de orgens externas à medção, tas como as grandezas assocadas aos padrões de medção calbrados, aos materas de referênca certfcados ou aos dados de referênca obtdos de manuas..5 Uma estmatva da mensuranda Y, a estmatva da grandeza de saída desgnada por y, é obtda da equação (.) usando as estmatvas das grandezas de entrada x para os valores das grandezas de entrada X. y = f (x, x,..., x ) (.) Subentende-se que estes valores são as melhores estmatvas das grandezas de entrada e foram corrgdas de todos os efetos sgnfcatvos para o modelo. o caso contráro, as correções necessáras foram ntroduzdas como grandezas de entrada separadas..6 Para uma varável aleatóra, a varânca da sua dstrbução, ou a sua raz quadrada postva, chamada desvopadrão, é utlzada como uma medda da dspersão dos valores. A ncerteza-padrão da medção assocada à estmatva da grandeza de saída ou ao resultado de medção y, desgnada por u(y), é o desvo-padrão da mensuranda Y. Tem de ser determnada a partr das estmatvas x das grandezas de entrada X e das respetvas ncertezas-padrão assocadas u(x ). A ncerteza-padrão assocada a uma estmatva tem a mesma dmensão que a estmatva. Em alguns casos, a ncerteza-padrão relatva da medção pode ser mas aproprada e consste na ncerteza-padrão assocada com uma estmatva dvdda pelo módulo desta estmatva e é, portanto, admensonal. Este conceto não pode ser utlzado se a estmatva for zero. 3 Avalação da ncerteza de medção de estmatvas das grandezas de entrada 3. Consderações geras 3.. A ncerteza de medção assocada às estmatvas das grandezas de entrada é avalada de acordo com o método de avalação Tpo A ou Tpo B. A avalação de Tpo A da ncerteza-padrão é o método de avalação da ncerteza pela análse estatístca de uma sére de observações. este caso, a ncerteza-padrão é o desvo-padrão expermental da méda que decorre de um procedmento de cálculo da méda ou de uma análse de regressão aproprada. A avalação de Tpo B da ncerteza-padrão é o método de avalação de ncerteza por outros meos que não os da análse estatístca de uma sére de observações. este caso, a avalação da ncertezapadrão é baseada noutro conhecmento centífco. ota: Em alguns casos, raramente na calbração, todos os valores possíves de uma grandeza estão sempre do mesmo lado de um determnado valor lmte. Um caso típco é o chamado erro do cosseno. Para o tratamento destes casos especas, ver [ref. ]. 3. Avalação de Tpo A da ncerteza-padrão 3.. A avalação de Tpo A da ncerteza-padrão pode ser aplcada quando váras observações ndependentes tenham sdo efetuadas para uma das grandezas de entrada, nas mesmas condções de medção. Se o processo de Pág. 3 de 4
4 OGC medção tver resolução sufcente, observa-se uma dspersão dos valores obtdos. 3.. Assume-se que a grandeza de entrada X repetdamente medda é a grandeza Q. Quando n observações (n > ) são estatstcamente ndependentes, a estmatva da grandeza Q é q, a méda artmétca dos valores ndvdualmente observados q j (j =,,..., n). q = n n j= q j (3.) A ncerteza de medção assocada à estmatva q é avalada de acordo com um dos seguntes métodos: (a) Uma estmatva da varânca da correspondente dstrbução de probabldade é a varânca expermental s (q) dos valores q j, dada por: n s ( q) = ( q j q) (3.) n j= A raz quadrada postva desta varânca é desgnada desvo-padrão expermental. A melhor estmatva da varânca da méda artmétca q é a varânca expermental da méda, dada por: s ( q) s ( q) = (3.3) n A raz quadrada postva desta varânca é desgnada desvo-padrão expermental da méda. A ncerteza-padrão u( q ) assocada à estmatva da grandeza de entrada q é o desvo-padrão expermental da méda: u ( q) = s( q) (3.4) Atenção: Geralmente, quando o número n de medções repetdas for pequeno (n < 0), terá de se ter em consderação a fabldade da avalação de Tpo A da ncerteza-padrão, expressa pela equação (3.4). Se o número de observações não puder ser aumentado, deverão ser consderados outros meos de avalação da ncerteza-padrão, referdos no texto. (b) Para uma medção bem caracterzada e sob controlo estatístco, a estmatva agrupada da varânca S p pode caracterzar melhor a dspersão do que o desvo-padrão estmado a partr de um número lmtado de observações. estes casos, o valor da grandeza de entrada Q é determnado pela méda artmétca q de um pequeno número de n observações ndependentes, podendo a varânca da méda ser estmada por: sp s ( q) = (3.5) n A ncerteza-padrão assocada é deduzda do valor da equação (3.4). ota IPAC: A varânca agrupada de m séres de observações ndependentes da mesma varável, com m ν s varâncas expermentas s = e ν graus de lberdade cada, é dada por s = p m ν = A varânca agrupada assm obtda possu ν p = m = ν graus de lberdade. 3.3 Avalação de Tpo B da ncerteza-padrão 3.3. A avalação de Tpo B da ncerteza-padrão é o método de avalação da ncerteza assocada a uma estmatva x de uma grandeza de entrada X, por outros meos que os da análse estatístca de uma sére de observações. A ncerteza-padrão u(x ) é avalada por aprecação centífca baseada em toda a nformação dsponível sobre a varabldade possível de X. A esta categora pertencem valores provenentes de: Pág. 4 de 4
5 OGC Dados de medções prévas; Experênca de/ou conhecmento geral do comportamento e propredades de materas e nstrumentos relevantes; Especfcações de fabrcantes; Dados provenentes de calbração e outros certfcados; Incertezas atrbuídas a dados de referênca provenentes de manuas O uso adequado da nformação dsponível para uma avalação de Tpo B da ncerteza-padrão da medção exge dscernmento baseado na experênca e conhecmento específco. É um saber que pode ser aprenddo com a prátca. Uma avalação de Tpo B bem fundamentada pode ser tão fável como uma avalação de Tpo A da ncerteza-padrão, especalmente numa stuação de medção em que a avalação de Tpo A é baseada apenas num número comparatvamente pequeno de observações estatstcamente ndependentes. Os seguntes casos devem ser dstngudos: (a) Se para a grandeza X apenas for conhecdo um únco valor,.e., um únco valor meddo, um valor resultante de uma medção anteror, um valor de referênca de lteratura ou um valor de correção, esse valor deve ser usado como o valor estmado x. A ncerteza-padrão u(x ) assocada a x quando dada, deve ser adotada. De outro modo, deve ser calculada a partr de dados nequívocos da ncerteza. Se não for possível aumentar o número de observações, terá que se consderar uma abordagem dferente para estmar a ncerteza-padrão, de acordo com o referdo em (b). (b) Se for possível assumr uma dstrbução de probabldade para a grandeza X baseada na teora ou na experênca, então, o correspondente valor esperado e a raz quadrada da varânca desta dstrbução, devem ser utlzados como a estmatva de x e a ncerteza-padrão assocada u(x ), respetvamente. (c) Se só for possível estmar os valores lmtes superor e nferor a + e a - da grandeza X (por exemplo, as especfcações do fabrcante de um nstrumento de medção, ntervalo de temperatura, erro de arredondamento ou de truncagem provenente de tratamento automátco), então deve ser usada uma dstrbução de probabldade com densdade de probabldade constante entre esses lmtes (dstrbução de probabldade retangular) para a varabldade possível da grandeza de entrada X. De acordo com (b), teremos: x = ( a+ + a ) (3.6) para os valores estmados respetvos e ( x ) = ( + ) a a u (3.7) para o quadrado da ncerteza-padrão. Se a dferença entre os valores lmte for a, então da equação (3.7) obtém-se: ( x ) a 3 u = (3.8) A dstrbução retangular é uma descrção razoável, em termos de probabldade, na stuação de conhecmento nsufcente da grandeza de entrada X, na ausênca de qualquer outra nformação que não seja a dos seus lmtes de varabldade. Mas, se for conhecdo à pror que os valores centras da grandeza são mas prováves que os valores lmte, deverá ser usada uma dstrbução trangular ou normal. De outro modo, se os valores perto dos valores lmte são mas prováves que os valores próxmos do centro, será mas aproprado utlzar uma dstrbução em forma-de-u. Para a avalação da ncerteza nestes casos, ver [ref.]. 4 Cálculo da ncerteza-padrão da estmatva da grandeza de saída 4. Para grandezas de entrada não correlaconadas entre s, o quadrado da ncerteza-padrão assocado com a estmatva da grandeza de saída y é dado por: Pág. 5 de 4 = u ( y) (4.) = ota: os casos, que raramente acontecem na calbração, onde a função modelo é fortemente não lnear, ou em que alguns dos coefcentes de sensbldade são desprezáves [ver equações (4.) e (4.3)], têm de ser
6 OGC ncluídos termos de ordem superor na equação (4.). Para o tratamento destes casos especas, ver [ref.]. ota IPAC: Para estes casos consderar a Le de Propagação de Incerteza mas genérca, dada por: = = ( ck + cckk ) u ( x ) u ( xk ) = k= + = k= c u ( x ) + ccku( x, xk ) + em que o prmero termo corresponde ao descrto no texto, o segundo termo corresponde à contrbução das correlações exstentes (ver secção 4.6) e o tercero termo corresponde às contrbuções de segunda ordem acma referdas. A grandeza u (y) ( =,,..., ) é a contrbução para a ncerteza-padrão assocada à estmatva da grandeza de saída y, resultando da ncerteza-padrão assocada à estmatva da grandeza de entrada x u (y) = c u(x ) (4.) onde c é o coefcente de sensbldade assocado à estmatva da grandeza de entrada x,.e., a dervada parcal da função modelo f em relação a X, avalada nas estmatvas x da grandeza de entrada, f f (4.3) c = = x X X = x.. X = x 4. O coefcente de sensbldade c descreve como a estmatva da grandeza de saída y é nfluencada pelas varações de cada uma das estmatvas das grandezas de entrada x. Pode ser avalada de acordo com a função modelo f pela equação (4.3) ou através da utlzação de métodos numércos,.e., calculando a varação da estmatva da grandeza de saída y, devda à correspondente varação na estmatva da grandeza de entrada x de +u(x ) e -u(x ), tomando para valor de c a dferença resultante em y dvdda por u(x ). Por vezes, pode ser mas aproprado determnar a varação da estmatva da grandeza de saída y expermentalmente, repetndo a medção, por exemplo, em x ± u(x ). 4.3 O u(x ) é sempre postvo, enquanto que a contrbução de u (y) de acordo com a equação (4.) será postva ou negatva, dependendo do snal do coefcente de sensbldade c. O snal de u (y) tem de ser consderado no caso de grandezas de entrada correlaconadas, ver equação (D4) do Anexo D. 4.4 Se a função modelo f é uma soma ou uma dferença das grandezas de entrada X f ( X, X,... X = p X (4.4) ) = a estmatva da grandeza de saída de acordo com a equação (.) é dada pela correspondente soma ou dferença das estmatvas das grandezas de entrada y = = p x (4.5) onde os coefcentes de sensbldade são guas a p e a equação (4.) é transformada em = p u ( ) (4.6) = x 4.5 Se a função modelo f é um produto ou um quocente das grandezas de entrada X f ( X X,... X ) = c = p, X (4.7) a estmatva da grandeza de saída é também o produto ou o quocente correspondente das estmatvas das grandezas de entrada y = c p x = Os coefcentes de sensbldade, neste caso, são guas a p y/x, obtendo-se uma expressão análoga à equação (4.6) a partr da equação (4.), se forem utlzadas as ncertezas-padrão relatvas w(y) = u(y)/ y e w(x ) = (4.8) Pág. 6 de 4
7 OGC u(x )/ x, = w ( y) = p w ( x ) (4.9) 4.6 Se duas grandezas de entrada X e X k são de algum modo correlaconadas,.e., se forem de alguma forma mutuamente dependentes, a respetva covarânca tem de ser consderada como uma contrbução para a ncerteza (ver Anexo D). A aptdão para consderar o efeto das correlações depende do conhecmento do processo de medção e da avalação da dependênca recíproca das grandezas de entrada. Em geral, deve recordar-se que neglgencar correlações entre grandezas de entrada pode levar a uma ncorreta avalação da ncerteza-padrão da mensuranda. 4.7 A covarânca assocada às estmatvas de duas grandezas de entrada X e X k pode ser consderada nula ou desprezável se: (a) As grandezas de entrada X e X k forem ndependentes, por exemplo, porque foram meddas repetdamente mas não smultaneamente, em experêncas dferentes e ndependentes, ou porque representam grandezas resultantes de avalações dferentes que foram fetas ndependentemente, ou se (b) Tanto as grandezas de entrada X como X k podem ser consderadas constantes, ou se (c) A nformação dsponível for nsufcente para avalar a exstênca de correlação entre as grandezas de entrada X e X k. Por vezes, as correlações podem ser elmnadas através de uma adequada escolha da função modelo. 4.8 A análse da ncerteza de medção - por vezes chamada balanço da ncerteza de medção - deve nclur uma lsta de todas as fontes de ncerteza, juntamente com as ncertezas-padrão de medção assocadas e os respetvos métodos de avalação. Para medções repetdas, o número de observações n tem de ser referdo. Por uma questão de clareza, recomenda-se que os dados relevantes para esta análse sejam apresentados sob a forma de uma tabela. esta tabela, todas as grandezas devem ser referencadas por um símbolo X ou um dentfcador abrevado. Para cada uma dela, devem ser especfcadas, pelo menos, a estmatva x, a ncertezapadrão de medção assocada u(x ), a dstrbução de probabldade, o coefcente de sensbldade c e as dferentes contrbuções para a ncerteza u (y). As undades de medda de cada uma das grandezas devem também ser expressas com os valores numércos ndcados na tabela. 4.9 Um exemplo formal dessa apresentação é dado pela Tabela 4., para o caso de grandezas de entrada não correlaconadas. A ncerteza-padrão assocada ao resultado de medção u(y), dada no canto nferor dreto da tabela, é a raz quadrada da soma dos quadrados de todas as contrbuções para a ncerteza da coluna da dreta. A parte cnzenta da tabela não é preenchda. Tabela 4.: Esquema de apresentação ordenado das grandezas, estmatvas, ncertezas-padrão, dstrbuções de probabldade, coefcentes de sensbldade e contrbuções para a ncerteza-padrão utlzados na análse da ncerteza de uma medção. Grandeza xxx Estmatva xxx Incerteza-padrão xxx Dstrbução de probabldade Coefcente de sensbldade Contrbução para a ncerteza-padrão X x u(x ) c u (y) X x u(x ) c u (y) X x u(x ) c u (y) X x u(x ) c u (y) Y y u(y) 5 Incerteza de medção expandda 5. o seo da EA, fo decddo que os laboratóros de calbração acredtados pelos Organsmos de Acredtação da EA devem expressar uma ncerteza de medção expandda U, obtda medante a multplcação da ncerteza- Pág. 7 de 4
8 OGC padrão u(y) da estmatva da grandeza de saída por um fator de expansão k, U = k u(y) (5.) os casos em que uma dstrbução normal (gaussana) possa ser atrbuída à mensuranda e a ncerteza-padrão assocada à estmatva da grandeza de saída tenha sufcente fabldade, deve ser usado o fator de expansão k =. A ncerteza expandda atrbuída corresponde a uma probabldade de expansão de aproxmadamente 95 %. Estas condções são cumprdas, na maora dos casos encontrados, nos trabalhos de calbração. 5. A hpótese de uma dstrbução normal nem sempre pode ser faclmente confrmada expermentalmente. Contudo, nos casos em que váras componentes da ncerteza (.e. 3), provenentes de dstrbuções de probabldade bem conhecdas de grandezas ndependentes, por exemplo, dstrbuções normas ou dstrbuções retangulares, contrbuam para a ncerteza-padrão assocada à estmatva da grandeza de saída em ampltudes comparáves, as condções do Teorema do Lmte Central estão reundas e pode ser assumdo, com um elevado grau de aproxmação, que a dstrbução da grandeza de saída é normal. 5.3 A fabldade da ncerteza-padrão atrbuída à estmatva da grandeza de saída é determnada pelos seus graus de lberdade efetvos (ver Anexo E). Contudo, os crtéros de fabldade são sempre atngdos nos casos em que nenhuma das contrbuções para a ncerteza é obtda por avalação do Tpo A baseada em menos de dez observações repetdas. 5.4 Se uma destas condções (normaldade ou fabldade sufcente) não for cumprda, o fator de expansão k = pode levar a uma ncerteza expandda que corresponde a uma probabldade de expansão menor que 95 %. estes casos, e de forma a assegurar que o valor da ncerteza expandda apresentado corresponde a uma probabldade de expansão que é dêntca ao caso normal, têm de ser segudos outros procedmentos. O uso de aproxmadamente a mesma probabldade de expansão é essencal sempre que dos resultados de medção de uma dada grandeza têm de ser comparados, por exemplo, quando se avalam os resultados de uma comparação nterlaboratoral ou se avala a conformdade com uma especfcação. 5.5 Mesmo quando se assume uma dstrbução normal, pode ocorrer que a ncerteza-padrão da estmatva da grandeza de saída não seja sufcentemente fável. Se, neste caso, não for prátco aumentar o número de medções repetdas n ou utlzar uma avalação de Tpo B, em vez da do Tpo A de fraca fabldade, deve ser usado o método descrto no Anexo E. 5.6 Para os restantes casos,.e., todos os casos em que a hpótese de uma dstrbução normal não possa ser justfcada, deve ser utlzada nformação sobre a dstrbução de probabldade da estmatva da grandeza de saída, para obter um valor do fator de expansão k que corresponda a uma probabldade de expansão de aproxmadamente 95 %. 6 Procedmento sequencal de cálculo da ncerteza de medção 6. Em seguda, é apresentada uma sequênca para a utlzação prátca deste documento: (a) Expressar em termos matemátcos a dependênca da mensuranda (grandeza de saída) Y em relação às grandezas de entrada X, de acordo com a equação (.). o caso da comparação dreta de dos padrões, a equação pode ser muto smples, por exemplo, Y = X + X. (b) Identfcar e efetuar todas as correções sgnfcatvas. (c) Lstar todas as fontes de ncerteza, na forma de uma análse de ncerteza, de acordo com a secção 4. (d) Calcular a ncerteza-padrão u( q ) para grandezas meddas repetdamente, de acordo com a secção 3.. Pág. 8 de 4 (e) Para valores solados, por exemplo, valores resultantes de medções anterores, valores de correções ou valores da lteratura, adotar as ncertezas-padrão quando são dadas ou podem ser calculadas de acordo com a alínea a) da secção Tomar atenção à forma de representação da ncerteza utlzada. Se não exstrem dados dsponíves, estmar o valor de u(x ) com base na experênca centífca. (f) Para grandezas de entrada cuja dstrbução de probabldade é conhecda ou pode ser assumda, calcular o valor esperado e a ncerteza-padrão u(x ) de acordo com a alínea b) da secção Se só conhecer ou puder estmar os valores lmte superores ou nferores, calcular a ncerteza-padrão u(x ) de acordo com a alínea c) da secção (g) Calcular, para cada grandeza de entrada X, a contrbução u (y) para a ncerteza assocada com a estmatva da grandeza de saída resultante das estmatvas das grandezas de entrada x, de acordo com as equações (4.) e (4.3) e somar os seus quadrados, como descrto na equação (4.), por forma a obter o quadrado da ncerteza-padrão u(y) da mensuranda. Se as grandezas de entrada forem correlaconadas,
9 OGC aplcar o procedmento do Anexo D. (h) Calcular a ncerteza expandda U multplcando a ncerteza-padrão u(y) pelo fator de expansão k, de acordo com a secção 5. () Reportar o resultado da medção, no certfcado de calbração, compreendendo a estmatva y da mensuranda, a ncerteza expandda assocada U e o fator de expansão k, de acordo com a secção 6 do documento ILAC P4 [ref.5]. 7 Referêncas [] JCGM 00:008, GUM 995 wth mnor correctons, Evaluaton of measurement data Gude to the expresson of uncertanty n measurement (dsponível em [] ISO/IEC 705:005, General requrements for the competence of testng and calbraton laboratores. ota IPAC: A versão portuguesa correspondente é a P E ISO/IEC 705: 005: Requstos geras de competênca para laboratóros de ensao e calbração. [3] JCGM 00:0 Internatonal vocabulary of metrology Basc and general concepts and assocated terms (dsponível em ota IPAC: A versão portuguesa correspondente é o Vocabuláro Internaconal de Metrologa Concetos fundamentas e geras e termos assocados (VIM 0) (.a edção luso-braslera, autorzada pelo BIPM, da 3.ª edção nternaconal do VIM - Internatonal Vocabulary of Metrology Basc and general concepts and assocated terms - JCGM 00:0) (Dsponível em [4] ISO 3534-:006, Statstcs-Vocabulary and symbols-part : General statstcal terms and terms used n probablty. [5] ILAC P4:/00, ILAC Polcy for Uncertanty n Calbraton. [6] JCGM 04:009, Evaluaton of measurement data An ntroducton to the Gude to the expresson of uncertanty n measurement and related documents. (dsponível em 8 Anexo A: Melhor Incerteza (CMC - Calbraton and Measurement Capablty) O conceto de Melhor Incerteza (CMC - Calbraton and Measurement Capablty) está cudadosamente estudado na publcação sobre as capacdades de medção e de calbração emtda pelo grupo de trabalho BIPM/ILAC, a 7 de setembro de 007. Esta publcação está ncluída na polítca da ILAC para a ncerteza de medção em calbração, sob a forma de anexo, sendo esta polítca a base para uma abordagem harmonzada do conceto de CMC entre os laboratóros acredtados em todo o mundo [ref. 5]. Os métodos para a avalação da ncerteza descrtos neste documento devem ser utlzados pelos laboratóros acredtados ao estabelecer as respetvas CMC. 9 Anexo B: Glossáro de alguns termos relevantes B B Méda Artmétca ([ref. ] C..9) Méda; Soma dos valores dvdda pelo número de valores. Melhor Incerteza (CMC Calbraton and Measurement Capablty) A Melhor Incerteza é expressa em termos de:. Mensuranda ou materal de referênca;. Método / procedmento de medção / calbração e / ou tpo de nstrumento / materal a ser meddo / calbrado; 3. Intervalo de medção e parâmetros adconas quando aplcáves, por exemplo, a frequênca da tensão elétrca aplcada; 4. Incerteza de medção. Pág. 9 de 4
10 OGC Para uma explcação completa, ver [ref. 5]. B3 Coefcente de Correlação ([ref. ] C3.6). O coefcente de correlação é uma medda da dependênca mútua relatva de duas varáves, gual à razão das respetvas covarâncas e a raz quadrada postva do produto das varâncas. Para uma descrção mas detalhada ver [ref. ]. B4 Covarânca ([ref. ] C 3.4) Medda da dependênca mútua de duas varáves aleatóras, gual ao valor esperado do produto dos desvos dessas duas varáves, relatvamente aos valores esperados respetvos. A defnção completa pode ser encontrada em [ref. ]. B5 Fator de Expansão ([ref. 3] termo.38) úmero maor do que um pelo qual uma ncerteza-padrão combnada é multplcada para se obter uma ncerteza de medção expandda. B6 Probabldade de Expansão ([ref. 3] termo.37) Probabldade de que o conjunto de valores verdaderos duma mensuranda esteja contdo num ntervalo expanddo especfcado. ota: não é utlzado, neste Gua, o termo valor verdadero pelas razões dadas em D.3.5 de [ref. ]; os termos valor de uma mensuranda (ou de uma grandeza) e valor verdadero de uma mensuranda (ou de uma grandeza) são consderados equvalentes, de acordo com o 3.. de [ref. ]. Ver também o capítulo 6 de [ref. 6]. B7 Desvo-Padrão Expermental ([ref. ] 4..) Raz quadrada postva da varânca expermental. B8 Incerteza (de Medção) Expandda ([ref. 3] termo.35) Produto duma ncerteza-padrão combnada por um fator maor do que o número um. B9 Varânca Expermental ([ref. ] 4..) Parâmetro que caracterza a dspersão dos resultados de uma sére de n observações da mesma mensuranda obtda pela equação (3.) do texto. B0 Estmatva de Entrada ([ref. ] 4..4 e C..6) Estmatva de uma grandeza de entrada utlzada na avalação do resultado de uma medção. B Grandeza de Entrada ([ref. ] 4..) Grandeza de que depende a mensuranda, consderada no processo de avalação do resultado de uma medção. B Mensuranda ([ref. 3] termo.3) Grandeza que se pretende medr. B3 Incerteza de Medção ([ref. 3] termo.6) Parâmetro não negatvo que caracterza a dspersão dos valores atrbuídos a uma mensuranda, com base nas nformações utlzadas. B4 Estmatva de Saída ([ref. ] 4..4 e C..6) Resultado de uma medção calculado a partr das estmatvas de entrada através da função modelo. B5 Grandeza de Saída ([ref. ] 4..) Grandeza que representa a mensuranda na avalação de um resultado de medção. B6 Estmatva Agrupada da Varânca (ou Estmatva Combnada da Varânca) ([ref. ] 4..4) Estmatva da varânca expermental obtda a partr de séres consttuídas por um número elevado de Pág. 0 de 4
11 OGC observações da mesma mensuranda em medções bem caracterzadas e controladas estatstcamente. B7 B8 Dstrbução de Probabldade ([ref. ] C..3) Função através da qual se obtém a probabldade de uma varável aleatóra assumr um valor ou pertencer a um dado conjunto de valores. Varável Aleatóra ([ref. ] C..) Varável que pode tomar qualquer dos valores de um dado conjunto de valores e à qual está assocada uma dstrbução de probabldade. B9 Incerteza-Padrão Relatva ([ref. 3] termo.3) Incerteza-padrão de medção dvdda pelo valor absoluto do valor meddo. B0 Coefcente de sensbldade assocado a uma estmatva de entrada ([ref. ] 5..3) Varação dferencal da estmatva de saída, gerada por uma varação dferencal da estmatva de entrada, dvdda pela varação da estmatva de entrada. B Desvo-Padrão ([ref. ] C.) Raz quadrada postva da varânca. B Incerteza-Padrão de Medção ([ref. 3] termo.30) Incerteza de medção expressa na forma dum desvo-padrão. B3 Avalação de Tpo A da Incerteza de Medção ([ref. 3] termo.8) Avalação duma componente da ncerteza de medção por uma análse estatístca dos valores meddos, obtdos sob condções defndas de medção. B4 Avalação de Tpo B da Incerteza de Medção ([ref. 3] termo.9) Avalação duma componente da ncerteza de medção determnada por meos dferentes daquele adotado para uma avalação de tpo A da ncerteza de medção. B5 Balanço de Incerteza ([ref. 3] termo.33) Formulação e apresentação duma ncerteza de medção e de suas componentes, assm como de seu cálculo e combnação. B6 Varânca ([ref. ] C.) Valor esperado do quadrado de uma varável aleatóra centrada. 0 Anexo C: Fontes de ncerteza de medção C A ncerteza de medção de um resultado da medção reflete uma falta de conhecmento completo do valor da mensuranda. O conhecmento completo exge uma nfnta quantdade de nformação. Os fenómenos que contrbuem para a ncerteza e, portanto, para o facto de que o resultado da medção não pode ser caracterzado por um únco valor, são chamados fontes de ncerteza. a prátca, exstem mutas fontes de ncerteza de medção possíves [ref. ], nclundo: (a) Defnção ncompleta da mensuranda; (b) Realzação mperfeta da defnção da mensuranda; (c) Amostragem não representatva - a amostra medda pode não representar a mensuranda defnda; (d) Conhecmento nadequado da nfluênca das condções ambentas ou medção defcente da mesma; (e) Erros de letura dos nstrumentos analógcos; (f) Resolução fnta dos nstrumentos ou lmar de mobldade; (g) Valores nexatos dos padrões e dos materas de referênca; Pág. de 4
12 OGC (h) Valores nexatos de constantes e outros parâmetros obtdos a partr de fontes externas e utlzados no algortmo; () Aproxmações e hpóteses consderadas no método e no procedmento de medção; (j) Varações nas observações repetdas da mensuranda, aparentemente, sob as mesmas condções. C Estas fontes não são necessaramente ndependentes. Algumas das fontes de a) a ) podem contrbur para j). Anexo D: Grandezas de entrada correlaconadas D D Se duas grandezas de entrada X e X k estão correlaconadas,.e., são dependentes entre s, a covarânca assocada às estmatvas x e x k u(x,x k ) = u(x )u(x k )r(x,x k ) ( k) (D.) deve ser consderada como uma contrbução adconal para a ncerteza. O grau de correlação é caracterzado pelo coefcente de correlação r(x,x k ) (onde k e r ). o caso de n pares ndependentes de valores de duas grandezas P e Q, smultaneamente obtdos em medções repetdas, a covarânca assocada com as médas artmétcas p e q é dada por s( p, q) = ( p n( n ) n j= j p)( q j q) (D.) e por substtução r pode ser calculado pela equação (D.). D3 Para grandezas de nfluênca, qualquer grau de correlação tem de ser baseado na experênca. Quando há correlação, a equação (4.) tem de ser substtuída por = k = k= + = c u ( x ) + c c u( x, x ) (D.3) k em que c e c k são os coefcentes de sensbldade defndos pela equação (4.3), ou = u = k= + = + ( y) r( x, x ) (D.4) k k com as contrbuções u (y) para a ncerteza-padrão da estmatva de saída y resultante da ncerteza-padrão da estmatva de entrada x dada pela equação (4.). Deve notar-se que o segundo somatóro dos termos na equação (D.3) ou (D.4) pode tomar o snal negatvo. D4 a prátca, as grandezas de entrada estão frequentemente correlaconadas porque, na avalação dos respetvos valores, é utlzado o mesmo padrão de referênca, nstrumento de medção, dado de referênca ou também o mesmo método de medção, possundo uma ncerteza sgnfcatva. Sem perda de generaldade, suponha que duas grandezas de entrada X e X, estmadas por x e x dependem de um conjunto de varáves ndependentes Q l (l =,,..., L) X = g (Q, Q,..., Q L ) X = g (Q, Q,..., Q L ) (D.5) embora algumas destas varáves possam não aparecer necessaramente em ambas as funções. As estmatvas x e x das grandezas de entrada serão, de alguma forma, correlaconadas mesmo que as estmatvas q l (l =,,..., L) sejam não correlaconadas. A covarânca u(x,x ) assocada às estmatvas x e x é dada por u( x, x L ) = c c u ( q ) (D.6) l l l l = em que c l e c l são os coefcentes de sensbldade dervados das funções g e g, por analoga com a equação (4.3). Dado que só contrbuem para o somatóro aqueles termos cujos coefcentes de sensbldade não sejam desprezáves, a covarânca é zero se não exstr nenhuma varável comum às funções g e g. O coefcente de correlação estmado r(x,x ) assocado às estmatvas x e x é determnado pela equação (D.6) conjugada com a equação (D.). Pág. de 4
13 OGC D5 O exemplo segunte demonstra as correlações exstentes entre valores atrbuídos a dos padrões que são calbrados com o mesmo padrão de referênca. Problema de Medção Dos padrões X e X são comparados com o padrão de referênca Q R, por meo de um sstema de medção capaz de determnar as dferenças z com uma ncerteza-padrão assocada u(z). O valor q R do padrão de referênca é conhecdo com uma ncerteza-padrão u(q R ). Modelo matemátco As estmatvas x e x dependem do valor q R do padrão de referênca e das dferenças observadas z e z, de acordo com as equações x = q R - z x = q R - z (D.7) Incertezas-padrão e covarâncas É suposto que as estmatvas z, z e q R sejam não-correlaconadas porque foram determnadas em medções dferentes. As ncertezas-padrão são calculadas pela equação (4.6) e a covarânca assocada às estmatvas x e x é calculada pela equação (D.6); assumndo que u(z ) = u(z ) = u(z), obtém-se: u (x ) = u (q R )+u (z) u (x ) = u (q R )+u (z) u (x,x ) = u (q R ) (D.8) O coefcente de correlação deduzdo destes resultados é u ( qr ) r x, x ) = (D.9) u ( q ) + u ( z) ( r que vara de 0 a +, em função da razão entre as ncertezas-padrão u(q R ) e u(z). D6 D7 O caso descrto pela equação (D.5) é uma stuação onde a nclusão da correlação na avalação da ncertezapadrão da mensuranda pode ser evtado através da escolha aproprada da função modelo. Introduzndo dretamente as varáves ndependentes Q l, substtundo as varáves orgnas X e X na função modelo f de acordo com as equações de transformação (D.5), orgna uma nova função modelo, que não contém as varáves correlaconadas X e X. Contudo, exstem casos, onde a correlação entre duas grandezas de entrada X e X não pode ser evtada, por exemplo, por utlzar o mesmo nstrumento de medção ou o mesmo padrão de referênca na determnação das estmatvas de entrada x e x e onde não é possível recorrer a equações de transformação para novas varáves ndependentes. Além dsso, se o grau de correlação não for exatamente conhecdo, pode ser útl avalar a máxma nfluênca que esta correlação pode ter, através de um lmte superor da ncerteza-padrão da mensuranda, o que, no caso de outras correlações não terem sdo consderadas, toma a forma de ( + ) + (D.0) r sendo u r (y) a contrbução para a ncerteza-padrão de todas as restantes grandezas de entrada, assumdas como não correlaconadas. ota: A nequação (D.0) é faclmente generalzada para os casos de um ou város grupos com duas ou mas grandezas de entrada correlaconadas. este caso, a soma respetva para o caso mas desfavorável tem de ser ntroduzda na nequação (D.0) para cada grupo de grandezas correlaconadas. Anexo E: Fatores de expansão provenentes de graus de lberdade efetvos Pág. 3 de 4 E A estmatva do fator de expansão k, correspondendo a uma determnada probabldade de expansão requer que seja tda em conta a fabldade da ncerteza-padrão u(y) da estmatva da grandeza de saída y. Isto sgnfca tomar em devda conta a forma como u(y) estma o desvo-padrão assocado ao resultado da medção. a estmatva do desvo-padrão de uma dstrbução normal, o número de graus de lberdade efetvos dessa estmatva, que depende da dmensão da amostra utlzada, é uma medda da fabldade. Do mesmo modo,
14 OGC uma medda adequada de fabldade da ncerteza-padrão da estmatva da grandeza de saída é o número de graus de lberdade efetvos ν ef, que é aproxmadamente representado pela aproprada combnação dos números de graus de lberdade efetvos das suas dferentes contrbuções para a ncerteza u (y). E O procedmento para o cálculo do adequado fator de expansão k, quando se verfcam as condções do Teorema do Lmte Central, compreende os seguntes passos: (a) Obter a ncerteza-padrão assocada à estmatva da grandeza de saída, de acordo com o procedmento sequencal dado na secção 6. (b) Determnar o número de graus de lberdade efetvos ν ef da ncerteza-padrão u(y) assocado à estmatva da grandeza de saída y, através da equação de Welch-Satterthwate ν ef = (E.) 4 u ( y) ν = 4 em que u (y) ( =,,..., ), defndos pela equação (4.), são as contrbuções para a ncerteza-padrão assocadas à estmatva da grandeza de saída y, resultantes das ncertezas-padrão assocadas às estmatvas das grandezas de entrada x, assumdas serem estatístca e mutuamente ndependentes, e ν é o número de graus de lberdade efetvos da componente da ncerteza-padrão u (y). Para uma dada ncerteza-padrão u( q ) obtda por uma avalação de Tpo A como referdo na secção 3., o número de graus de lberdade efetvos é dado por ν = n-. É mas problemátco assocar graus de lberdade com uma ncerteza-padrão u(x ) obtda por uma avalação de Tpo B. Contudo, é prátca corrente efetuar tas avalações de forma a garantr que não fo cometda qualquer subestmação. Se, por exemplo, são defndos lmtes nferor e superor, a - e a +, estes são habtualmente escolhdos, para que a probabldade da grandeza em questão estar fora destes lmtes seja de facto extremamente pequena. esta hpótese, o número de graus de lberdade da ncerteza-padrão u(x ) obtda por uma avalação de Tpo B pode ser consderado como ν. (c) Obter o fator de expansão k consderando os valores da Tabela E.. Esta tabela está baseada numa dstrbução t de Student avalada para uma probabldade de expansão de 95,45 %. Se ν ef calculado não for ntero, o que é normalmente o caso, truncar ν ef para o ntero medatamente nferor. Tabela E.: Fatores de expansão k para dferentes números de graus de lberdade efetvos ν ef ν ef k 3,97 4,53 3,3,87,65,5,43,37,3,8 ν eff k,5,3,,0,8,7,6,5,4,3 ν eff k,,09,07,06,06,05,00 ota IPAC: Ao consderar-se a componente de ncerteza assocada à utlzação de padrões ou de nstrumentos de medção calbrados por uma entdade externa ao laboratóro, e sempre que o respetvo certfcado de calbração não ndque o número de graus de lberdade efetvos da calbração, mas somente para o fator de expansão k =, deverá assumr-se um número de graus de lberdade efetvos gual a 50. Pág. 4 de 4
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
Estimativa da Incerteza de Medição da Viscosidade Cinemática pelo Método Manual em Biodiesel
 Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
7. Resolução Numérica de Equações Diferenciais Ordinárias
 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
Introdução e Organização de Dados Estatísticos
 II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
www.obconcursos.com.br/portal/v1/carreirafiscal
 www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
METROLOGIA E ENSAIOS
 METROLOGIA E ENSAIOS Incerteza de Medção Prof. Aleandre Pedott pedott@producao.ufrgs.br Freqüênca de ocorrênca Incerteza da Medção Dstrbução de freqüênca das meddas Erro Sstemátco (Tendênca) Erro de Repettvdade
METROLOGIA E ENSAIOS Incerteza de Medção Prof. Aleandre Pedott pedott@producao.ufrgs.br Freqüênca de ocorrênca Incerteza da Medção Dstrbução de freqüênca das meddas Erro Sstemátco (Tendênca) Erro de Repettvdade
Aula 03 Erros experimentais Incerteza. Aula 03 Prof. Valner Brusamarello
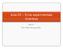 Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
Rastreando Algoritmos
 Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
INTRODUÇÃO AO CÁLCULO DE ERROS NAS MEDIDAS DE GRANDEZAS FÍSICAS
 Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
Princípios do Cálculo de Incertezas O Método GUM
 Prncípos do Cálculo de Incertezas O Método GUM João Alves e Sousa Laboratóro Regonal de Engenhara Cvl - LREC Rua Agostnho Perera de Olvera, 9000-64 Funchal, Portugal. E-mal: jasousa@lrec.pt Resumo Em anos
Prncípos do Cálculo de Incertezas O Método GUM João Alves e Sousa Laboratóro Regonal de Engenhara Cvl - LREC Rua Agostnho Perera de Olvera, 9000-64 Funchal, Portugal. E-mal: jasousa@lrec.pt Resumo Em anos
As tabelas resumem as informações obtidas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de informações.
 1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Influência dos Procedimentos de Ensaios e Tratamento de Dados em Análise Probabilística de Estrutura de Contenção
 Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
2 Incerteza de medição
 2 Incerteza de medção Toda medção envolve ensaos, ajustes, condconamentos e a observação de ndcações em um nstrumento. Este conhecmento é utlzado para obter o valor de uma grandeza (mensurando) a partr
2 Incerteza de medção Toda medção envolve ensaos, ajustes, condconamentos e a observação de ndcações em um nstrumento. Este conhecmento é utlzado para obter o valor de uma grandeza (mensurando) a partr
Distribuição de Massa Molar
 Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Expressão da Incerteza de Medição para a Grandeza Energia Elétrica
 1 a 5 de Agosto de 006 Belo Horzonte - MG Expressão da ncerteza de Medção para a Grandeza Energa Elétrca Eng. Carlos Alberto Montero Letão CEMG Dstrbução S.A caletao@cemg.com.br Eng. Sérgo Antôno dos Santos
1 a 5 de Agosto de 006 Belo Horzonte - MG Expressão da ncerteza de Medção para a Grandeza Energa Elétrca Eng. Carlos Alberto Montero Letão CEMG Dstrbução S.A caletao@cemg.com.br Eng. Sérgo Antôno dos Santos
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
2 Máquinas de Vetor Suporte 2.1. Introdução
 Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Lista de Exercícios de Recuperação do 2 Bimestre. Lista de exercícios de Recuperação de Matemática 3º E.M.
 Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
1 Princípios da entropia e da energia
 1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS
 Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Informação. Nota: Tradução feita por Cláudio Afonso Kock e Sérgio Pinheiro de Oliveira.
 Informação Esta publcação é uma tradução do Gua de Calbração EURAMET Gua para a Estmatva da Incerteza em Medções de Dureza (EURAMET/cg-16/v.01, July 007). Os dretos autoras do documento orgnal pertencem
Informação Esta publcação é uma tradução do Gua de Calbração EURAMET Gua para a Estmatva da Incerteza em Medções de Dureza (EURAMET/cg-16/v.01, July 007). Os dretos autoras do documento orgnal pertencem
PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA
 658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
RM 68 INCERTEZA DE MEDIÇÃO: GUIA PRÁTICO DO AVALIADOR DE LABORATÓRIOS SUMÁRIO 1 OBJETIVO E CAMPO DE APLICAÇÃO 2 REFERÊNCIAS 3 DEFINIÇÕES 4 METODOLOGIA
 RM 68 INCERTEZA DE MEDIÇÃO: GUIA PRÁTICO DO AVALIADOR DE LABORATÓRIOS PROCEDIMENTO DO SISTEMA DE GESTÃO DA QUALIDADE REVISÃO: 05 ABR/013 SUMÁRIO 1 OBJETIVO E CAMPO DE APLICAÇÃO REFERÊNCIAS 3 DEFINIÇÕES
RM 68 INCERTEZA DE MEDIÇÃO: GUIA PRÁTICO DO AVALIADOR DE LABORATÓRIOS PROCEDIMENTO DO SISTEMA DE GESTÃO DA QUALIDADE REVISÃO: 05 ABR/013 SUMÁRIO 1 OBJETIVO E CAMPO DE APLICAÇÃO REFERÊNCIAS 3 DEFINIÇÕES
Controle Estatístico de Qualidade. Capítulo 8 (montgomery)
 Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Apostila de Estatística Curso de Matemática. Volume II 2008. Probabilidades, Distribuição Binomial, Distribuição Normal. Prof. Dr. Celso Eduardo Tuna
 Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
UTILIZAÇÃO DO MÉTODO DE TAGUCHI NA REDUÇÃO DOS CUSTOS DE PROJETOS. Uma equação simplificada para se determinar o lucro de uma empresa é:
 UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
ELEMENTOS DE CIRCUITOS
 MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
Curso de extensão, MMQ IFUSP, fevereiro/2014. Alguns exercício básicos
 Curso de extensão, MMQ IFUSP, feverero/4 Alguns exercíco báscos I Exercícos (MMQ) Uma grandeza cujo valor verdadero x é desconhecdo, fo medda três vezes, com procedmentos expermentas dêntcos e, portanto,
Curso de extensão, MMQ IFUSP, feverero/4 Alguns exercíco báscos I Exercícos (MMQ) Uma grandeza cujo valor verdadero x é desconhecdo, fo medda três vezes, com procedmentos expermentas dêntcos e, portanto,
PROBABILIDADE E ESTATÍSTICA APLICADAS À HIDROLOGIA
 PROBABILIDADE E ESTATÍSTICA APLICADAS À HIDROLOGIA Mauro aghettn Mara Manuela Portela DECvl, IST, 0 PROBABILIDADE E ESTATÍSTICA APLICADAS À HIDROLOGIA Mauro aghettn Professor Assocado, Escola de Engenhara
PROBABILIDADE E ESTATÍSTICA APLICADAS À HIDROLOGIA Mauro aghettn Mara Manuela Portela DECvl, IST, 0 PROBABILIDADE E ESTATÍSTICA APLICADAS À HIDROLOGIA Mauro aghettn Professor Assocado, Escola de Engenhara
Portaria Inmetro nº 248 de 17 de julho de 2008
 INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL - Portara Inmetro nº 248 de 17 de julho de 2008 O PRESIDENTE DO INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL,
INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL - Portara Inmetro nº 248 de 17 de julho de 2008 O PRESIDENTE DO INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL,
Departamento de Informática. Modelagem Analítica. Modelagem Analítica do Desempenho de Sistemas de Computação. Disciplina: Medida de Probabilidade
 Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
REGRESSÃO LOGÍSTICA. Seja Y uma variável aleatória dummy definida como:
 REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
Controlo Metrológico de Contadores de Gás
 Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
A ESTIMATIVA DA INCERTEZA DE MEDIÇÃO PELOS MÉTODOS DO ISO GUM 95 E DE SIMULAÇÃO DE MONTE CARLO
 A ESTIMATIVA DA INCERTEZA DE MEDIÇÃO PELOS MÉTODOS DO ISO GUM 95 E DE SIMULAÇÃO DE MONTE CARLO Paulo Roberto Gumarães Couto INMETRO-DIMCI-DIMEC-LAPRE prcouto@nmetro.gov.br INTRODUÇÃO 3 ISO GUM 95 4. Estmatva
A ESTIMATIVA DA INCERTEZA DE MEDIÇÃO PELOS MÉTODOS DO ISO GUM 95 E DE SIMULAÇÃO DE MONTE CARLO Paulo Roberto Gumarães Couto INMETRO-DIMCI-DIMEC-LAPRE prcouto@nmetro.gov.br INTRODUÇÃO 3 ISO GUM 95 4. Estmatva
Sistemas de Filas: Aula 5. Amedeo R. Odoni 22 de outubro de 2001
 Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Professor Mauricio Lutz CORRELAÇÃO
 Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
MEDIÇÕES DE VIBRAÇÕES NO CORPO HUMANO ESTIMATIVA DA INCERTEZA
 Acústca 008 0 - de Outubro, Combra, Portugal Unversdade de Combra MEDIÇÕES DE VIBRAÇÕES NO CORPO HUMANO ESTIMATIVA DA INCERTEZA Jorge Fradque, Fátma Inglês Drecção Regonal da Economa de Lsboa e Vale do
Acústca 008 0 - de Outubro, Combra, Portugal Unversdade de Combra MEDIÇÕES DE VIBRAÇÕES NO CORPO HUMANO ESTIMATIVA DA INCERTEZA Jorge Fradque, Fátma Inglês Drecção Regonal da Economa de Lsboa e Vale do
Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Cálculo do Conceito Preliminar de Cursos de Graduação
 Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Análise Econômica da Aplicação de Motores de Alto Rendimento
 Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Capítulo 1. O plano complexo. 1.1. Introdução. Os números complexos começaram por ser introduzidos para dar sentido à 2
 Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Sinais Luminosos 2- CONCEITOS BÁSICOS PARA DIMENSIONAMENTO DE SINAIS LUMINOSOS.
 Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
EXPRESSÃO DA INCERTEZA DE MEDIÇÃO
 EXPRESSÃO DA INCERTEZA DE MEDIÇÃO NORMA N o NIT-DICLA-0 APROVADA EM AGO/07 N o 0/30 SUMÁRIO Objetvo Campo de Aplcação 3 Responsabldade 4 Requsto 5 Regstro de Modfcações Anexo Versão Braslera do Documento
EXPRESSÃO DA INCERTEZA DE MEDIÇÃO NORMA N o NIT-DICLA-0 APROVADA EM AGO/07 N o 0/30 SUMÁRIO Objetvo Campo de Aplcação 3 Responsabldade 4 Requsto 5 Regstro de Modfcações Anexo Versão Braslera do Documento
Análise de Regressão. Profa Alcione Miranda dos Santos Departamento de Saúde Pública UFMA
 Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
2 CONSIDERAÇÕES TEÓRICAS
 20 2 CONSIDERAÇÕES TEÓRICAS 2.1. Defnção de gás Um gás é defndo como um fludo cujas condções de temperatura e pressão são superores às do ponto crítco, não podendo haver duas fases presentes em um processo,
20 2 CONSIDERAÇÕES TEÓRICAS 2.1. Defnção de gás Um gás é defndo como um fludo cujas condções de temperatura e pressão são superores às do ponto crítco, não podendo haver duas fases presentes em um processo,
Coordenação Geral de Acreditação
 Coordenação Geral de Acredtação ORIENTAÇÕES PARA APLICAÇÃO DOS REQUISITOS TÉCNICOS DA ABNT NBR ISO/IEC 1705 NA ACREDITAÇÃO DE LABORATÓRIOS DE CALIBRAÇÃO PARA O GRUPO DE SERVIÇO DE FÍSICO-QUÍMICA Documento
Coordenação Geral de Acredtação ORIENTAÇÕES PARA APLICAÇÃO DOS REQUISITOS TÉCNICOS DA ABNT NBR ISO/IEC 1705 NA ACREDITAÇÃO DE LABORATÓRIOS DE CALIBRAÇÃO PARA O GRUPO DE SERVIÇO DE FÍSICO-QUÍMICA Documento
Suporte Básico para Sistemas de Tempo Real
 Suporte Básco para Sstemas de Tempo Real Escalonamento e Comuncação Sldes elaborados por George Lma, com atualzações realzadas por Ramundo Macêdo Suporte Básco para Sstemas de Tempo-Real Escalonamento
Suporte Básco para Sstemas de Tempo Real Escalonamento e Comuncação Sldes elaborados por George Lma, com atualzações realzadas por Ramundo Macêdo Suporte Básco para Sstemas de Tempo-Real Escalonamento
MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE
 MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE R. L. S. CANEVESI 1, C. L. DIEL 2, K. A. SANTOS 1, C. E. BORBA 1, F. PALÚ 1, E. A. DA SILVA 1 1 Unversdade Estadual
MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE R. L. S. CANEVESI 1, C. L. DIEL 2, K. A. SANTOS 1, C. E. BORBA 1, F. PALÚ 1, E. A. DA SILVA 1 1 Unversdade Estadual
3 A técnica de computação intensiva Bootstrap
 A técnca de computação ntensva ootstrap O termo ootstrap tem orgem na expressão de língua nglesa lft oneself by pullng hs/her bootstrap, ou seja, alguém levantar-se puxando seu própro cadarço de bota.
A técnca de computação ntensva ootstrap O termo ootstrap tem orgem na expressão de língua nglesa lft oneself by pullng hs/her bootstrap, ou seja, alguém levantar-se puxando seu própro cadarço de bota.
Universidade do Estado do Rio de Janeiro Instituto de Matemática e Estatística Econometria
 Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
1 a Lei de Kirchhoff ou Lei dos Nós: Num nó, a soma das intensidades de correntes que chegam é igual à soma das intensidades de correntes que saem.
 Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Análise de Incertezas I.B De Paula
 Um bom expermentalsta deve fazer todo o esforço possível para mnmzar os erros de seu expermento. Cabe ao expermentalsta a responsabldade de apresentar uma medda da confabldade de seus dados. amos defnr
Um bom expermentalsta deve fazer todo o esforço possível para mnmzar os erros de seu expermento. Cabe ao expermentalsta a responsabldade de apresentar uma medda da confabldade de seus dados. amos defnr
Metodologia IHFA - Índice de Hedge Funds ANBIMA
 Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Universidade Federal da Bahia Instituto de Física Departamento de Física da Terra e do Meio Ambiente TEXTOS DE LABORATÓRIO T E O R I A D E E R R O S
 Unversdade Federal da Baha Insttuto de Físca Departamento de Físca da Terra e do Meo Ambente TEXTOS DE LABORATÓRIO T E O R I A D E E R R O S Físca I SALVADOR, BAHIA 013 1 Prefáco Esta apostla é destnada
Unversdade Federal da Baha Insttuto de Físca Departamento de Físca da Terra e do Meo Ambente TEXTOS DE LABORATÓRIO T E O R I A D E E R R O S Físca I SALVADOR, BAHIA 013 1 Prefáco Esta apostla é destnada
LQA - LEFQ - EQ -Química Analítica Complemantos Teóricos 04-05
 LQA - LEFQ - EQ -Químca Analítca Complemantos Teórcos 04-05 CONCEITO DE ERRO ALGARISMOS SIGNIFICATIVOS Embora uma análse detalhada do erro em Químca Analítca esteja fora do âmbto desta cadera, sendo abordada
LQA - LEFQ - EQ -Químca Analítca Complemantos Teórcos 04-05 CONCEITO DE ERRO ALGARISMOS SIGNIFICATIVOS Embora uma análse detalhada do erro em Químca Analítca esteja fora do âmbto desta cadera, sendo abordada
Algarismos Significativos Propagação de Erros ou Desvios
 Algarsmos Sgnfcatvos Propagação de Erros ou Desvos L1 = 1,35 cm; L = 1,3 cm; L3 = 1,30 cm L4 = 1,4 cm; L5 = 1,7 cm. Qual destas meddas está correta? Qual apresenta algarsmos com sgnfcado? O nstrumento
Algarsmos Sgnfcatvos Propagação de Erros ou Desvos L1 = 1,35 cm; L = 1,3 cm; L3 = 1,30 cm L4 = 1,4 cm; L5 = 1,7 cm. Qual destas meddas está correta? Qual apresenta algarsmos com sgnfcado? O nstrumento
Energia de deformação na flexão
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
UNIVERSIDADE PRESBITERIANA MACKENZIE CCSA - Centro de Ciências Sociais e Aplicadas Curso de Economia
 CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
IV - Descrição e Apresentação dos Dados. Prof. Herondino
 IV - Descrção e Apresentação dos Dados Prof. Herondno Dados A palavra "dados" é um termo relatvo, tratamento de dados comumente ocorre por etapas, e os "dados processados" a partr de uma etapa podem ser
IV - Descrção e Apresentação dos Dados Prof. Herondno Dados A palavra "dados" é um termo relatvo, tratamento de dados comumente ocorre por etapas, e os "dados processados" a partr de uma etapa podem ser
ANEXO II METODOLOGIA E CÁLCULO DO FATOR X
 ANEXO II Nota Técnca nº 256/2009-SRE/ANEEL Brasíla, 29 de julho de 2009 METODOLOGIA E ÁLULO DO FATOR X ANEXO II Nota Técnca n o 256/2009 SRE/ANEEL Em 29 de julho de 2009. Processo nº 48500.004295/2006-48
ANEXO II Nota Técnca nº 256/2009-SRE/ANEEL Brasíla, 29 de julho de 2009 METODOLOGIA E ÁLULO DO FATOR X ANEXO II Nota Técnca n o 256/2009 SRE/ANEEL Em 29 de julho de 2009. Processo nº 48500.004295/2006-48
RESOLUÇÃO Nº 32/2014/CONEPE. O CONSELHO DO ENSINO, DA PESQUISA E DA EXTENSÃO da Universidade Federal de Sergipe, no uso de suas atribuições legais,
 SERVIÇO PÚBLICO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DE SERGIPE CONSELHO DO ENSINO, DA PESQUISA E DA EXTENSÃO RESOLUÇÃO Nº 32/2014/CONEPE Aprova as Normas Geras do Processo Seletvo para
SERVIÇO PÚBLICO FEDERAL MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE FEDERAL DE SERGIPE CONSELHO DO ENSINO, DA PESQUISA E DA EXTENSÃO RESOLUÇÃO Nº 32/2014/CONEPE Aprova as Normas Geras do Processo Seletvo para
ANÁLISE DE CONFIABILIDADE DO MODELO SCS-CN EM DIFERENTES ESCALAS ESPACIAIS NO SEMIÁRIDO
 ANÁLISE DE CONFIABILIDADE DO MODELO SCS-CN EM DIFERENTES ESCALAS ESPACIAIS NO SEMIÁRIDO J. W. B. Lopes 1 ; E. A. R. Pnhero 2 ; J. R. de Araújo Neto 3 ; J. C. N. dos Santos 4 RESUMO: Esse estudo fo conduzdo
ANÁLISE DE CONFIABILIDADE DO MODELO SCS-CN EM DIFERENTES ESCALAS ESPACIAIS NO SEMIÁRIDO J. W. B. Lopes 1 ; E. A. R. Pnhero 2 ; J. R. de Araújo Neto 3 ; J. C. N. dos Santos 4 RESUMO: Esse estudo fo conduzdo
Variação ao acaso. É toda variação devida a fatores não controláveis, denominadas erro.
 Aplcação Por exemplo, se prepararmos uma área expermental com todo cudado possível e fzermos, manualmente, o planto de 100 sementes seleconadas de um mlho híbrdo, cudando para que as sementes fquem na
Aplcação Por exemplo, se prepararmos uma área expermental com todo cudado possível e fzermos, manualmente, o planto de 100 sementes seleconadas de um mlho híbrdo, cudando para que as sementes fquem na
Aula Características dos sistemas de medição
 Aula - Característcas dos sstemas de medção O comportamento funconal de um sstema de medção é descrto pelas suas característcas (parâmetros) operaconas e metrológcas. Aqu é defnda e analsada uma sére destes
Aula - Característcas dos sstemas de medção O comportamento funconal de um sstema de medção é descrto pelas suas característcas (parâmetros) operaconas e metrológcas. Aqu é defnda e analsada uma sére destes
Análise Fatorial F 1 F 2
 Análse Fatoral Análse Fatoral: A Análse Fatoral tem como prncpal objetvo descrever um conjunto de varáves orgnas através da cração de um número menor de varáves (fatores). Os fatores são varáves hpotétcas
Análse Fatoral Análse Fatoral: A Análse Fatoral tem como prncpal objetvo descrever um conjunto de varáves orgnas através da cração de um número menor de varáves (fatores). Os fatores são varáves hpotétcas
Variabilidade Espacial do Teor de Água de um Argissolo sob Plantio Convencional de Feijão Irrigado
 Varabldade Espacal do Teor de Água de um Argssolo sob Planto Convenconal de Fejão Irrgado Elder Sânzo Aguar Cerquera 1 Nerlson Terra Santos 2 Cásso Pnho dos Res 3 1 Introdução O uso da água na rrgação
Varabldade Espacal do Teor de Água de um Argssolo sob Planto Convenconal de Fejão Irrgado Elder Sânzo Aguar Cerquera 1 Nerlson Terra Santos 2 Cásso Pnho dos Res 3 1 Introdução O uso da água na rrgação
Manual dos Indicadores de Qualidade 2011
 Manual dos Indcadores de Qualdade 2011 1 Dretora de Avalação da Educação Superor Clauda Maffn Grbosk Coordenação Geral de Controle de Qualdade da Educação Superor Stela Mara Meneghel Equpe Técnca: José
Manual dos Indcadores de Qualdade 2011 1 Dretora de Avalação da Educação Superor Clauda Maffn Grbosk Coordenação Geral de Controle de Qualdade da Educação Superor Stela Mara Meneghel Equpe Técnca: José
Física. Física Módulo 1 Vetores, escalares e movimento em 2-D
 Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Prof. Antônio Carlos Fontes dos Santos. Aula 1: Divisores de tensão e Resistência interna de uma fonte de tensão
 IF-UFRJ Elementos de Eletrônca Analógca Prof. Antôno Carlos Fontes dos Santos FIW362 Mestrado Profssonal em Ensno de Físca Aula 1: Dvsores de tensão e Resstênca nterna de uma fonte de tensão Este materal
IF-UFRJ Elementos de Eletrônca Analógca Prof. Antôno Carlos Fontes dos Santos FIW362 Mestrado Profssonal em Ensno de Físca Aula 1: Dvsores de tensão e Resstênca nterna de uma fonte de tensão Este materal
Modelo Logístico. Modelagem multivariável com variáveis quantitativas e qualitativas, com resposta binária.
 Modelagem multvarável com varáves quanttatvas e qualtatvas, com resposta bnára. O modelo de regressão não lnear logístco ou modelo logístco é utlzado quando a varável resposta é qualtatva com dos resultados
Modelagem multvarável com varáves quanttatvas e qualtatvas, com resposta bnára. O modelo de regressão não lnear logístco ou modelo logístco é utlzado quando a varável resposta é qualtatva com dos resultados
ANÁLISE ESTATÍSTICA DE CORRELAÇÕES PVT DE PETRÓLEOS
 UNIVERSIDADE FEDERAL DO ESÍRITO SANTO CENTRO TECNOLÓGICO ROGRAMA DE ÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA GARBEN BRAVIM GOMES ANÁLISE ESTATÍSTICA DE CORRELAÇÕES VT DE ETRÓLEOS VITÓRIA 8 GARBEN BRAVIM GOMES
UNIVERSIDADE FEDERAL DO ESÍRITO SANTO CENTRO TECNOLÓGICO ROGRAMA DE ÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA GARBEN BRAVIM GOMES ANÁLISE ESTATÍSTICA DE CORRELAÇÕES VT DE ETRÓLEOS VITÓRIA 8 GARBEN BRAVIM GOMES
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Eletroquímica 2017/3. Professores: Renato Camargo Matos Hélio Ferreira dos Santos.
 Eletroquímca 2017/3 Professores: Renato Camargo Matos Hélo Ferrera dos Santos http://www.ufjf.br/nups/ Data Conteúdo 07/08 Estatístca aplcada à Químca Analítca Parte 2 14/08 Introdução à eletroquímca 21/08
Eletroquímca 2017/3 Professores: Renato Camargo Matos Hélo Ferrera dos Santos http://www.ufjf.br/nups/ Data Conteúdo 07/08 Estatístca aplcada à Químca Analítca Parte 2 14/08 Introdução à eletroquímca 21/08
O migrante de retorno na Região Norte do Brasil: Uma aplicação de Regressão Logística Multinomial
 O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
Probabilidade e Estatística. Correlação e Regressão Linear
 Probabldade e Estatístca Correlação e Regressão Lnear Correlação Este uma correlação entre duas varáves quando uma delas está, de alguma forma, relaconada com a outra. Gráfco ou Dagrama de Dspersão é o
Probabldade e Estatístca Correlação e Regressão Lnear Correlação Este uma correlação entre duas varáves quando uma delas está, de alguma forma, relaconada com a outra. Gráfco ou Dagrama de Dspersão é o
Exercícios de Física. Prof. Panosso. Fontes de campo magnético
 1) A fgura mostra um prego de ferro envolto por um fo fno de cobre esmaltado, enrolado mutas vezes ao seu redor. O conjunto pode ser consderado um eletroímã quando as extremdades do fo são conectadas aos
1) A fgura mostra um prego de ferro envolto por um fo fno de cobre esmaltado, enrolado mutas vezes ao seu redor. O conjunto pode ser consderado um eletroímã quando as extremdades do fo são conectadas aos
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
CQ110 : Princípios de FQ
 CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
UNIVERSIDADE DE PERNAMBUCO. Física Experimental. Prof o José Wilson Vieira
 UNIVERSIDADE DE PERNAMBUCO ESCOLA POLITÉCNICA DE PERNAMBUCO Físca Expermental Prof o José Wlson Vera wlson.vera@upe.br AULA 01: PROCESSOS DE ANÁLISE GRÁFICA E NUMÉRICA MODELO LINEAR Recfe, agosto de 2015
UNIVERSIDADE DE PERNAMBUCO ESCOLA POLITÉCNICA DE PERNAMBUCO Físca Expermental Prof o José Wlson Vera wlson.vera@upe.br AULA 01: PROCESSOS DE ANÁLISE GRÁFICA E NUMÉRICA MODELO LINEAR Recfe, agosto de 2015
MAE5778 - Teoria da Resposta ao Item
 MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
Incertezas de Medições em Calibrações: aplicações práticas no ambiente hospitalar
 I Congresso Brasileiro de Engenharia Clínica Palestra: Incertezas de Medições em Calibrações: aplicações práticas no ambiente hospitalar São Paulo, 30 de Setembro de 2005 Gilberto Carlos Fidélis Instrutor
I Congresso Brasileiro de Engenharia Clínica Palestra: Incertezas de Medições em Calibrações: aplicações práticas no ambiente hospitalar São Paulo, 30 de Setembro de 2005 Gilberto Carlos Fidélis Instrutor
TERMO DE CONTRATO N 001/2014 - CMM
 \1erra do guaraná" TERMO DE CONTRATO N 001/2014 - CMM CONTRATAÇÃO DE SERVIÇOS DE ACESSO A INTERNET VIA SATÉLITE ATRAVÉS DE LINK DEDICADO, QUE ENTRE SI FAZEM A CÂMRA MUNICIPAL DE MAUÉS E A EMPRESA C H M
\1erra do guaraná" TERMO DE CONTRATO N 001/2014 - CMM CONTRATAÇÃO DE SERVIÇOS DE ACESSO A INTERNET VIA SATÉLITE ATRAVÉS DE LINK DEDICADO, QUE ENTRE SI FAZEM A CÂMRA MUNICIPAL DE MAUÉS E A EMPRESA C H M
TRANSFERÊNCIA DE CALOR NA ENVOLVENTE DA EDIFICAÇÃO
 UNIVERSIDADE FEDERAL DE SANA CAARINA CENRO ECNOLÓGICO DEPARAMENO DE ENGENHARIA CIVIL PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA CIVIL RANSFERÊNCIA DE CALOR NA ENVOLVENE DA EDIFICAÇÃO ELABORADO POR: Martn
UNIVERSIDADE FEDERAL DE SANA CAARINA CENRO ECNOLÓGICO DEPARAMENO DE ENGENHARIA CIVIL PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA CIVIL RANSFERÊNCIA DE CALOR NA ENVOLVENE DA EDIFICAÇÃO ELABORADO POR: Martn
7 - Distribuição de Freqüências
 7 - Dstrbução de Freqüêncas 7.1 Introdução Em mutas áreas há uma grande quantdade de nformações numércas que precsam ser dvulgadas de forma resumda. O método mas comum de resumr estes dados numércos consste
7 - Dstrbução de Freqüêncas 7.1 Introdução Em mutas áreas há uma grande quantdade de nformações numércas que precsam ser dvulgadas de forma resumda. O método mas comum de resumr estes dados numércos consste
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
Programa de Certificação de Medidas de um laboratório
 Programa de Certfcação de Meddas de um laboratóro Tratamento de dados Elmnação de dervas Programa de calbração entre laboratóros Programa nterno de calbração justes de meddas a curvas Tratamento dos resultados
Programa de Certfcação de Meddas de um laboratóro Tratamento de dados Elmnação de dervas Programa de calbração entre laboratóros Programa nterno de calbração justes de meddas a curvas Tratamento dos resultados
Estimativa dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro.
 Estmatva dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro. O. L. L. Moraes 1, H. R. da Rocha 2, M. A. Faus da Slva Das 2, O Cabral 3 1 Departamento
Estmatva dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro. O. L. L. Moraes 1, H. R. da Rocha 2, M. A. Faus da Slva Das 2, O Cabral 3 1 Departamento
CURSO ON-LINE PROFESSOR: VÍTOR MENEZES
 O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
Cap. IV Análise estatística de incertezas aleatórias
 TLF 010/11 Cap. IV Análse estatístca de ncertezas aleatóras Capítulo IV Análse estatístca de ncertezas aleatóras 4.1. Méda 43 4.. Desvo padrão 44 4.3. Sgnfcado do desvo padrão 46 4.4. Desvo padrão da méda
TLF 010/11 Cap. IV Análse estatístca de ncertezas aleatóras Capítulo IV Análse estatístca de ncertezas aleatóras 4.1. Méda 43 4.. Desvo padrão 44 4.3. Sgnfcado do desvo padrão 46 4.4. Desvo padrão da méda
14. Correntes Alternadas (baseado no Halliday, 4 a edição)
 14. orrentes Alternadas (baseado no Hallday, 4 a edção) Por que estudar orrentes Alternadas?.: a maora das casas, comérco, etc., são provdas de fação elétrca que conduz corrente alternada (A ou A em nglês):
14. orrentes Alternadas (baseado no Hallday, 4 a edção) Por que estudar orrentes Alternadas?.: a maora das casas, comérco, etc., são provdas de fação elétrca que conduz corrente alternada (A ou A em nglês):
