7. Resolução Numérica de Equações Diferenciais Ordinárias
|
|
|
- Sérgio Sintra Costa
- 8 Há anos
- Visualizações:
Transcrição
1 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem ser modelados por equações dferencas: equações que envolvem uma função e algumas de suas dervadas. Se uma equação dferencal possu apenas uma varável ndependente então ela é uma equação dferencal ordnára. Eemplos: d d = () + que pode ser escrta como: ' = + " + ( - )' + = (equação dferencal ordnára de ª ordem) Se a equação dferencal envolve mas de uma varável ndependente então ela é uma equação dferencal parcal. Eemplo: u u + = onde u é uma função u(,) Neste capítulo, vamos estudar métodos numércos de solução de equações dferencas ordnáras. 5 Equações Dferencas Ordnáras Uma equação dferencal ordnára de ordem n pode ser escrta como: ( n) ( n ) ( ) = F(, ( ), ' ( ), "( ),..., ( )) [ a, b] A solução desta equação é uma função = f() defnda em [a,b], com n dervadas e que satsfaz a equação. Eemplo. A solução da equação dferencal ordnára de ª ordem = - é a função () = sen() + cos(), pos: () = sen() + cos(); '() = cos() - sen(); "() = -sen() - cos(). Logo: ''() = - (sen() + cos()) = -() Note que, pela notação acma, essa equação devera ser escrta como: () = F(,(), ()) = -(). E uma solução numérca, o que é? É uma função conecda de forma numérca, ou seja, por uma tabela de pontos. = - Método numérco.... ()
2 Equações Dferencas Ordnáras Na verdade, uma equação dferencal ordnára possu uma famíla de soluções. Por eemplo: a solução da equação = - pode se uma função () = asen() + bcos(), pos: '() = acos() - bsen() e "() = -asen() - bcos() = - () Assm, dependendo dos valores de a e b teremos dversas soluções, como lustra a fgura Para que uma equação dferencal tena solução únca é precso mpor condções suplementares. Em geral, uma equação dferencal de ordem n requer n condções suplementares para ter uma únca solução. Com sso, temos dos tpos de problemas: problema de valor ncal (PVI) problema de valor de contorno (PVC) 5 Equações Dferencas Ordnáras Problema de valor ncal (PVI) Equação dferencal de ordem n (n ) e mas n condções dadas pela função e suas dervadas até ordem n-, especfcadas em um mesmo ponto, que corresponde ao valor ncal da varável ndependente. Eemplo. = ( ) + cos(); () = ; () = ; [,]. equação dferencal de ª odem Problema de valor de contorno (PVC) condções ncas observe que a função e sua ª dervada estão especfcadas para o ponto ncal do ntervalo da varável ndependente. Equação dferencal de ordem n (n ) e mas n condções dadas pela função e/ou suas dervadas até ordem n-, especfcadas em pontos dferentes do domíno da varável ndependente. Eemplo. = cos(); () = ; () = ; [,]. observe que, em geral, as condções são especfcadas no contorno do domíno da varável ndependente. 5
3 Problemas de Valor Incal Para problemas de valor ncal, basta consderar apenas equações dferencas de ª ordem, pos uma equação dferencal ordnára de ordem n pode ser transformada faclmente em um sstema de n equações de ª ordem, utlzando mudanças de varáves. Eemplo. Seja o PVI: = + e + + ; ()=; ()=; ()=-; [,]. Fazendo: = = ; () = = = ; () = = = + e + + ; () = - Sstema de equações de ª ordem Portanto, os métodos que vamos estudar para PVIs rão consderar apenas uma equação dferencal de ª ordem: = f(,), com uma condção ncal ( ) =. Quando for precso resolver um problema de ordem n, vamos transformar o problema em um sstema de n equações de ª ordem e aplcar o método a cada uma delas, smultaneamente. 55 Método de Euler Seja uma equação dferencal de ª ordem: = f(,), com uma condção ncal ( ) =. Seja = + - ( =,,...). Pelo teorema de Talor podemos escrever: ( + ) = ( + ) = ( ) + '( ) + "( ξ) ξ (, + ) Portanto, como ( ) = f(,( )), podemos escrever: ( + ) ( ) + f(, ( )) Portanto, com esta epressão do método de Euler, conecdo o valor ( ) (condção ncal) é possível determnar outros valores ( ) ( =,,...) e assm construr uma tabela para a função (). Métodos como o de Euler em que os valores de () podem ser obtdos dretamente são denomnados métodos eplíctos. Além dsto, como ( + ) depende apenas do ponto medatamente precedente (, ( )), tal método é conecdo como de passo smples. Estem métodos em que os valores de () podem ser obtdos somente por teração (métodos mplíctos). Em outros, o valor de ( + ) depende de m pontos medatamente precedentes (métodos de passo múltplo). 56
4 Método de Euler Eemplo. Resolver o PVI: = +; () = ; [.,.5]; =. = +.f(, ) =. + (.)f(.,.) =. + (.)(.(.)+) =.5 = +.f(, ) =.5 + (.)f(.,.5) =.5 + (.)(.(.)+) =. = +.f(, ) =. + (.)f(.,.) =. + (.)(.(.)+) =.56 = +.f(, ) =.56 + (.)f(.,.56) =.56 + (.)(.(.)+) =. 5 = +.f(, ) =. + (.)f(.,.) =. + (.)(.(.)+) = () Solução analítca: () = +- (curva vermela). À medda que a solução avança, os erros vão se tornando maores (pos um ponto da solução depende do ponto anteror). Com um passo menor, o erro será menor. 57 Método de Euler Eemplo. Resolver o PVI: = +; () = ; () = ; [,]; =. Transformando em um sstema com a mudança de varável: = ; = = f (,, ) = () = = f (,, ) = + () = (.) = (.) +.f (., (.), (.)) =. + (.)(.) =. (.) = (.) +.f (., (.), (.)) =. + (.)(.+.) =. (.) = (.) +.f (., (.), (.)) =. + (.)(.) =. (.) = (.) +.f (., (.), (.)) =. + (.)(.+.) =. contnuando () () =
5 Métodos Baseados em Regras de Quadratura Mutos métodos para solução de problemas de valor ncal podem ser obtdos a partr de regras de ntegração numérca, uma vez que para o problema: = f(,) com ( )=, podemos escrever: '( ) d = ] = ( ) ( ) = Por outro lado, pela regra dos trapézos temos: ' ( ) d = [ ' ( ) + ' ( )] + E T Portanto: + f + f [ (, ) (, )] é uma apromação para o valor de () no ponto =. Devemos notar que esta apromação, baseada na regra dos trapézos, consttu um esquema de passo smples (o valor de depende de apenas um valor anteror - ). Entretanto este esquema é mplícto, uma vez que o valor de depende do própro valor. Portanto, neste caso, será necessáro um processo teratvo para determnar o valor de ( =,,...). 59 Métodos Baseados em Regras de Quadratura Para ser obtdo teratvamente é necessáro uma estmatva ncal []. Mutas escolas são possíves para a estmatva ncal. Alguns eemplos são: o valor anteror - o valor de obtdo pelo método de Euler: - + f( -, - ) Dado um valor para [], temos o segunte esquema teratvo: [ n] f f [ n = + [ (, ) + (, ] )] ( n =,,...) Eemplo. Seja o PVI: = ; ()=.5; [,]; =. =.5 [] (estmatva ncal pelo método de Euler):.5 + (.)(.5 ) =.65. Seja ε = -. [] [] []. =.5+ [(.5) + (.65) ] =.6. =.5+ [(.5) + (.6) ] =.67. =.5+ [(.5) + (.67) ] =.67 Valor eato: =(.) (.) = =
6 Métodos de Runge-Kutta Os métodos numércos de resolução de PVIs vstos até aqu tem pouca mportânca prátca. O método de Euler requer um passo muto pequeno para alcançar uma precsão razoável. Já o método baseado na regra dos trapézos, por consttur um esquema mplícto, requer um processo teratvo para determnar cada uma das apromações. Os métodos de Runge-Kutta, ao contráro, são muto empregados na prátca pos possuem as seguntes característcas: são métodos eplíctos de passo smples que alcançam uma boa precsão com passos razoáves. Pela sére de Talor temos: + = ( + ) = ( + ) = ( ) + '( ) + "( ) + E T df(, ) Como = f(,) temos: + ( ) + f (, ) + d = Calcular df(, ) é dfícl pos () é uma função desconecda. d Vamos consderar o polnômo nterpolador de º grau no ntervalo [, + ]: 6 Métodos de Runge-Kutta p() Portanto: escrever: + =.( ) +.(+ ) = [( )(+ ) ( + )( )] + + p '( ) = Usando este resultado, podemos [ ( + ) ( )] Mas, pelo método de Euler, temos: + = + f(, ) e portanto: f( +, + ) = f( +, f(, )). Então: df(, ) [f (+, + ) f(, )] d Portanto: f f f + ( ) + (, ) +. [ ( +, + ) (, )] = + f (, ) + f ( +, + ) Fazendo: + = + f + f + + f [ (, ) (, (, ))] k = f (, ) k = f ( +, + f(, )) = f ( +, + k) + = + k + k [ ] método de Runge-Kutta de º grau 6 6
7 Métodos de Runge-Kutta Eemplo. ' = - ; ()=; [,]; =. + = + k + k [ ] k = f(, ) k = f( +, + k ) k k k =.f(.,.) =.(-.) = -. k =.f(.,.-.) =.f(.,.6) =.(-.) = -.8 (.) =. + (-.-.8)/ =. -. =.66 k =.f(.,.66) =.(-.6) = -.9 k =.f(.,.66-.9) =.f(.,.68) =.(-.968) = -.96 (.) =.66 + ( )/ = = Métodos de Runge-Kutta Eemplo. Resolver o PVI: = +; () = ; () = ; [,]; =. Transformando em um sstema com a mudança de varável: = ; = = f (,, ) = () = = f (,, ) = + () = (.) = (.) + [k +k ]/ (.) = (.) + [k +k ]/ k =.f (.,.,.) =.(.) =. k =.f (.,.,.) =.(.) =. k =.f (.,.+.,.+.) =. k =.f (.,.+.,.+.) =. (.) =. + [.+.]/ =. (.) =. + [.+.]/ =. contnuando mesmo eemplo do método de Euler.. ().. () =
8 Métodos de Runge-Kutta Um dos métodos de Runge-Kutta mas utlzados é o de º grau, dado por: k = f (, ) + = + k [ k + k + k + k 6 ] k f = ( +, + ) k k f = ( +, + ) k = f( +, + k) Eemplo. ' = - ; ()=; [,]; =.5 k k k k Comparando os métodos: º grau º grau Métodos de Passo Múltplo Os métodos de resolução de PVIs vstos anterormente são todos de passo únco, sto é, para calcular + leva-se em conta apenas os valores de f(,) em torno do ponto anteror. Os métodos de passo múltplo levam em conta não apenas o valor de como também pontos anterores -, -,..., -k+ (método de k-passos). A fórmula geral de um método de k-passos é dada por: k k + = α j j+ + β jf j+ j+ j= j= (, ) f j + Dependendo do valor de β tem-se duas classes de métodos de passo múltplo: métodos eplíctos e métodos mplíctos. Se β = então: k k + = α j j+ + β jf j+ = ( α + α αk k+ ) + ( βf + βf β kf k+ ) j= j= ou seja, para determnar o prómo ponto da solução, +, são necessáros os k valores anterores da solução:, -, -,..., -k+, além dos respectvos valores de f( j, j ) (j =, -, -,..., -k+). Portanto, quando β = tem-se um método eplícto de passo múltplo. Se β então, além destes pontos, será necessáro também o valor de f +. Neste caso, para calcular + será precso um esquema teratvo levando, portanto, a um método mplícto de passo múltplo. 66 8
9 Métodos Eplíctos de Passo Múltplo Dada a equação ' = f(,()) podemos obter por ntegração: + ( + ) = ( ) + f(, ( )) d Supondo já conecdos os valores anterores (j =, -,..., -k+), podemos substtur f(,()) por um polnômo nterpolador que passa por estes pontos anterores. Neste caso tem-se uma famíla de métodos (dependendo da escola do grau do polnômo) para resolver a equação dferencal conecdos como métodos de Adams-Basfort. Para k =, o polnômo é do º grau e tem-se um método de º grau: + ( ) = + [ f f d f d f d + = + ( ). ( ) ( ). ] [ ( ) ( ) ] Essas ntegras podem ser calculadas faclmente. Assm: + = + f f f f [ = + ] [ ] (método de Adams-Basfort de º grau). 67 Métodos Eplíctos de Passo Múltplo (de Adams-Basfort) Para k =, o polnômo é do º grau e tem-se o método de º grau: + = + f f + f [ 6 5 ] Para k =, o polnômo é do º grau e tem-se o método de º grau: + = + f f + f f [ ] Para k = 5, o polnômo é do º grau e tem-se o método de 5º grau: + = + f f + f f + f 7 [ ] Pode-se notar que, à medda que aumenta o grau do polnômo nterpolador, aumentam os coefcentes de (j =, -, -,..., -k+) e portanto o método torna-se mas sensível a erros de arredondamento. Os métodos de Adams-Basfort não são auto-ncalzáves, porque necesstam de um conjunto de k pontos anterores da solução para que possam ser aplcados (de níco, tem-se apenas um ponto da solução: a condção ncal). Portanto, para aplcar um método de Adams-Basfort é precso, prmeramente, obter este conjunto ncal de k pontos através de um método de passo únco. 68 9
10 Métodos Implíctos de Passo Múltplo Os métodos mplíctos de passo múltplo são obtdos da mesma forma que os métodos eplíctos, só que agora, β. Tas métodos são conecdos como métodos de Adams-Moulton. Para k = (método de Adams-Moulton de º grau): + f f d = + [ ( ) ( ) + + = + f d f d ] [ + ( ) ( ( ) ( ) + ) ] + + ou seja: + = + f + + f [ Para k = (método de º grau): + = + f+ + f f 5 Para k = (método de º grau): + = + f+ + f f + f 9 Para k = 5 (método de 5º grau): + = + f+ + f f + f f 7 [ ] Pode-se notar que as fórmulas mplíctas são menos sensíves a erros de arredondamento (pos os coefcentes são menores) do que as fórmulas eplíctas, mas necesstam teração. 69 Métodos de Prevsão e Correção Os métodos de passo múltplo possuem algumas característcas nteressantes: Os métodos mplíctos são menos sujetos a erros de arredondamento e apresentam lmtes de erro de truncamento menores que os métodos eplíctos de mesmo grau. Entretanto, nos métodos mplíctos o cálculo de + requer o valor de f + e, portanto, um processo teratvo. Já os métodos eplíctos tem a vantagem de poder calcular + somente com base em valores anterores da solução. Pode-se, então, combnar estes dos tpos de métodos de modo a empregar as vantagens de cada um. Esta combnação é conecda como método de prevsão e correção, que corresponde a: ncalzar o processo por um método de passo únco (por eemplo, um método de Runge-Kutta); calcular o valor de + pelo método de passo múltplo eplícto (valor prevsto); recalcular o valor de + usando o método de passo múltplo mplícto de mesmo grau (valor corrgdo). Portanto, nos métodos de prevsão e correção, o método eplícto (método de Adams-Basfort) é usado como fórmula prevsora e o método mplícto (método de Adams-Moulton) corresponde à fórmula corretora (que pode ser usada váras vezes, até que se consga um resultado consderado satsfatóro). 7
11 Métodos de Prevsão e Correção Eemplo. Seja o PVI: ' = ; () =.5; [,]; =.. Vamos usar um método de prevsão e correção de a ordem, ou seja: ncalzação (RK-): + = + [k + k ]; k = f (, ); k = f( +, + k ) prevsão (AB-): + = + [f f ] / correção (AM-): + = + [f + + f ]/ k =.f(.,.5) =.(.65) =.5 k =.f(.,.5+.5) =.(.689) =.8 (.) =.5 + (.5+.8)/ = ().5 RK- AB- + AM- (.p) =.6 +.[f(.,.65)-f(.,.5)]/ =.776 (.c) =.6 +.[f(.,.776) + f(.,.65)]/ = () Método das Dferenças Fntas Pelo teorema de Talor, podemos escrever o desenvolvmento em sére de uma função () em torno do ponto = como: ( ) ( ) = ( ) + ( ) ' ( ) + "(! ) +... Portanto, o valor de () no ponto = + = +, pode ser escrto como: ( + ) ( + ) = ( ) + ( + )'() + "( ) + L = ( ) + '( ) + "( ) +L! ( + ) ( ) ou seja: = '( ) + "( ) +... ( + ) ( ) Tem-se, portanto: '( ) = + O() onde O() (ldo como ordem de ) ndca que a magntude dos termos restantes depende da ordem de grandeza do valor de. Assm, pode-se escrever: ( ) ( '( ) ) + Dzemos, nesse caso, que () é apromada por uma dferença fnta ascendente, com erro da ordem de. 7
12 Método das Dferenças Fntas Se, no desenvolvmento de Talor: ( ) ( ) = ( ) + ( ) ' ( ) + "(! ) +... substturmos por - teremos: ( ) = ( ) + ( )'( ) + "( ) +... = ( ) '( ) + "( ) +... ( ) ( ) e, portanto: '( ) ( )! Dzemos, nesse caso, que () é apromada por uma dferença fnta descendente, com erro também da ordem de. Uma tercera apromação para () pode ser obtda subtrando-se a epressão para ( - ) da epressão para ( + ), ou seja: ( ou seja: ) = ( ) + '( ) + "( ) L () '( ) + "() ( + ) ( ) logo: '( ) = + ) ( + + L ( + ) ( ) = '( ) + O( ) ( + ) ( ) Portanto: '( ) + O( ) ou seja, () é apromada por uma dferença fnta central, com erro da ordem de. 7 Método das Dferenças Fntas Pode-se obter uma apromação para a dervada segunda (), somando-se as epressões para ( + ) e para ( - ), ou seja: ( ) = ( ) + ' ( ) + " ( ) L + () ' ( ) + "( ) + ) + ( + + L ou seja: ( + ) + ( ) = ( ) + "() + O( ) ( ) ( ) + ( + ) Portanto: " ( ) Esta epressão aproma o valor de () com erro da ordem de. Apromações para dervadas de ordens mas altas podem ser obtdas de forma análoga. O método das dferenças fntas para solução de equações dferencas decorre da substtução, na equação, das dervadas da função pelas suas correspondentes apromações por dferenças fntas. Consderando a notação para desgnar o valor de ( ), temos: Dervada Prmera Segunda Apromação ( + - )/ ( - - )/ ( )/ ( )/ Ordem do Erro 7
13 Método das Dferenças Fntas: Problemas de Valor de Contorno O método das dferenças fntas se aplca muto bem a problemas de valor de contorno. Eemplo. Seja o PVC: = - - e ( + ); ()=; ()=.78; [,]; =.. Nesse caso, a solução será uma tabela da forma: ()..78 Substtundo, na equação dferencal, as dervadas pelas apromações por dferenças fntas (usando, para a dervada prmera, a dferença central, por ser mas eata) obtemos: e = ( + ) =,,, ( + ) + ( ) + ( ) + = e ( + ) =,,, Temos, então: = ( + ) ( ) ( ) e ( + + = + ) = ( + ) + ( ) + ( ) = e ( + ) = ( + ) ( ) ( ) e ( + + = + ) = ( + ) ( ) ( ) e ( = + ) O que é sso? Quas são as ncógntas? 75 Método das Dferenças Fntas: Problemas de Valor de Contorno É um sstema de equações lneares: ( ) (+ ) ( ) ( ) (+ ) ( ) ( ) (+ ) ( ) ( ) = e ( + ) ( + ) e ( + ) e ( + ) e ( + ) ( ) 5 ou seja: = () Nesse caso, não á propagação de erro de um ponto para outro, pos todos os pontos da solução são obtdos de uma vez. A dfculdade, com pequeno, está na dmensão do sstema de equações lneares (por eemplo: =.5 9 equações). 76
14 Método das Dferenças Fntas: Problemas de Valor Incal O método das dferenças fntas também se aplca a problemas de valor ncal. Eemplo. Seja o PVI: ' = - ; ()=; [,]; =.5 Nesse caso, a solução será uma tabela da forma: (). 5 6 Substtundo, na equação dferencal, as dervadas pelas apromações por dferenças fntas (usando, para a dervada prmera, a dferença descendente) obtemos: = =, L,6 Temos, então: = ( ) + ( + ) = ( + ) + ( + ) ( + ) ( + ) ( + ) ( + ) 5 6 = 5 6 ( =, L,6) 77 Método das Dferenças Fntas: Problemas de Valor Incal Substtundo os valores: = ()
15 Método das Dferenças Fntas Nem sempre o método das dferenças fntas leva a um problema lnear. Dependendo da equação dferencal podemos ter um problema não lnear. Eemplo. Seja o PVC: = - ; () = ; ()=.5; [,]; =.. Nesse caso, a solução será uma tabela da forma: ()..5 Substtundo, na equação dferencal, as dervadas pelas apromações por dferenças fntas, obtemos: Teremos, então: = (,,,) = ( + ) = ( =,,,) + +.( ) = + +. ( ) = + +. ( ) = +.5+.(.5 ) = ()
RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS
 Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
1 Princípios da entropia e da energia
 1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
2 Máquinas de Vetor Suporte 2.1. Introdução
 Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
www.obconcursos.com.br/portal/v1/carreirafiscal
 www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Energia de deformação na flexão
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
As tabelas resumem as informações obtidas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de informações.
 1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Introdução e Organização de Dados Estatísticos
 II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
MAE5778 - Teoria da Resposta ao Item
 MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
Física. Física Módulo 1 Vetores, escalares e movimento em 2-D
 Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
REGRESSÃO LOGÍSTICA. Seja Y uma variável aleatória dummy definida como:
 REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
Lista de Exercícios de Recuperação do 2 Bimestre. Lista de exercícios de Recuperação de Matemática 3º E.M.
 Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
01. Em porcentagem das emissões totais de gases do efeito estufa, o Brasil é o quarto maior poluidor, conforme a tabela abaixo:
 PROCESSO SELETIVO 7 RESOLUÇÃO MATEMÁTICA Rosane Soares Morera Vana, Luz Cláudo Perera, Lucy Tem Takahash, Olímpo Hrosh Myagak QUESTÕES OBJETIVAS Em porcentagem das emssões totas de gases do efeto estufa,
PROCESSO SELETIVO 7 RESOLUÇÃO MATEMÁTICA Rosane Soares Morera Vana, Luz Cláudo Perera, Lucy Tem Takahash, Olímpo Hrosh Myagak QUESTÕES OBJETIVAS Em porcentagem das emssões totas de gases do efeto estufa,
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
Flambagem. Cálculo da carga crítica via MDF
 Flambagem Cálculo da carga crítca va MDF ROF. ALEXANDRE A. CURY DEARTAMENTO DE MECÂNICA ALICADA E COMUTACIONAL Flambagem - Cálculo da carga crítca va MDF Nas aulas anterores, vmos como avalar a carga crítca
Flambagem Cálculo da carga crítca va MDF ROF. ALEXANDRE A. CURY DEARTAMENTO DE MECÂNICA ALICADA E COMUTACIONAL Flambagem - Cálculo da carga crítca va MDF Nas aulas anterores, vmos como avalar a carga crítca
Física. Setor B. Índice-controle de Estudo. Prof.: Aula 23 (pág. 86) AD TM TC. Aula 24 (pág. 87) AD TM TC. Aula 25 (pág.
 Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Controle Estatístico de Qualidade. Capítulo 8 (montgomery)
 Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Influência dos Procedimentos de Ensaios e Tratamento de Dados em Análise Probabilística de Estrutura de Contenção
 Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Capítulo 2. APROXIMAÇÕES NUMÉRICAS 1D EM MALHAS UNIFORMES
 Capítulo. Aproxmações numércas 1D em malhas unformes 9 Capítulo. AROXIMAÇÕS NUMÉRICAS 1D M MALHAS UNIFORMS O prncípo fundamental do método das dferenças fntas (MDF é aproxmar através de expressões algébrcas
Capítulo. Aproxmações numércas 1D em malhas unformes 9 Capítulo. AROXIMAÇÕS NUMÉRICAS 1D M MALHAS UNIFORMS O prncípo fundamental do método das dferenças fntas (MDF é aproxmar através de expressões algébrcas
Apostila de Estatística Curso de Matemática. Volume II 2008. Probabilidades, Distribuição Binomial, Distribuição Normal. Prof. Dr. Celso Eduardo Tuna
 Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Rastreando Algoritmos
 Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
CURSO ON-LINE PROFESSOR: VÍTOR MENEZES
 O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
RESOLUÇÃO DE EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE ORDEM 2 HOMOGÊNEAS, COM COEFICIENTES CONSTANTES
 Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Matemática Equações Diferenciais RESOLUÇÃO DE EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE ORDEM HOMOGÊNEAS, COM COEFICIENTES CONSTANTES FORMA
Pontifícia Universidade Católica do Rio Grande do Sul Faculdade de Matemática Equações Diferenciais RESOLUÇÃO DE EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE ORDEM HOMOGÊNEAS, COM COEFICIENTES CONSTANTES FORMA
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
Capítulo 1: Erros em cálculo numérico
 Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Capítulo : Erros em cálculo umérco. Itrodução Um método umérco é um método ão aalítco, que tem como objectvo determar um ou mas valores umércos, que são soluções de um certo problema. Ao cotráro das metodologas
Aula 03 Erros experimentais Incerteza. Aula 03 Prof. Valner Brusamarello
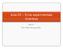 Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
INTRODUÇÃO AO CÁLCULO DE ERROS NAS MEDIDAS DE GRANDEZAS FÍSICAS
 Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Capítulo. Associação de resistores. Resoluções dos exercícios propostos. P.135 a) R s R 1 R 2 R s 4 6 R s 10 Ω. b) U R s i U 10 2 U 20 V
 apítulo 7 da físca Exercícos propostos Undade apítulo 7 ssocação de resstores ssocação de resstores esoluções dos exercícos propostos 1 P.15 a) s 1 s 6 s b) U s U 10 U 0 V c) U 1 1 U 1 U 1 8 V U U 6 U
apítulo 7 da físca Exercícos propostos Undade apítulo 7 ssocação de resstores ssocação de resstores esoluções dos exercícos propostos 1 P.15 a) s 1 s 6 s b) U s U 10 U 0 V c) U 1 1 U 1 U 1 8 V U U 6 U
Despacho Econômico de. Sistemas Termoelétricos e. Hidrotérmicos
 Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
COMPARATIVO ENTRE MÉTODOS DE CÁLCULO DE PERDAS EM TRANSFORMADORES ALIMENTANDO CARGAS NÃO-LINEARES
 COMARAVO ENRE MÉODOS DE CÁLCULO DE ERDAS EM RANSFORMADORES ALMENANDO CARGAS NÃO-LNEARES GUMARÃES, Magno de Bastos EEEC/ UFG/ EQ magnobg@otmal.com. NRODUÇÃO LSA, Luz Roberto EEEC/ UFG lsta@eee.ufg.br NERYS,
COMARAVO ENRE MÉODOS DE CÁLCULO DE ERDAS EM RANSFORMADORES ALMENANDO CARGAS NÃO-LNEARES GUMARÃES, Magno de Bastos EEEC/ UFG/ EQ magnobg@otmal.com. NRODUÇÃO LSA, Luz Roberto EEEC/ UFG lsta@eee.ufg.br NERYS,
Análise de Regressão. Profa Alcione Miranda dos Santos Departamento de Saúde Pública UFMA
 Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
(note que não precisa de resolver a equação do movimento para responder a esta questão).
 Mestrado Integrado em Engenhara Aeroespacal Mecânca e Ondas 1º Ano -º Semestre 1º Teste 31/03/014 18:00h Duração do teste: 1:30h Lea o enuncado com atenção. Justfque todas as respostas. Identfque e numere
Mestrado Integrado em Engenhara Aeroespacal Mecânca e Ondas 1º Ano -º Semestre 1º Teste 31/03/014 18:00h Duração do teste: 1:30h Lea o enuncado com atenção. Justfque todas as respostas. Identfque e numere
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Diferenciais Ordinárias (EDO)
 Resolução Numérica de Equações Diferenciais Ordinárias (EDO) Ivanovitch Medeiros Dantas da Silva Universidade Federal do Rio Grande do Norte Departamento de Engenharia de Computação e Automação DCA0399
Resolução Numérica de Equações Diferenciais Ordinárias (EDO) Ivanovitch Medeiros Dantas da Silva Universidade Federal do Rio Grande do Norte Departamento de Engenharia de Computação e Automação DCA0399
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS (EDO) PROBLEMA DO VALOR INICIAL (PVI)
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS (EDO) PROBLEMA DO VALOR INICIAL (PVI) Introdução Seja a segunte equação derencal: d ( ) ; d para. que é reerencado com o problema do valor ncal. Essa denomnação deve-se
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS (EDO) PROBLEMA DO VALOR INICIAL (PVI) Introdução Seja a segunte equação derencal: d ( ) ; d para. que é reerencado com o problema do valor ncal. Essa denomnação deve-se
Motores síncronos. São motores com velocidade de rotação fixa velocidade de sincronismo.
 Motores síncronos Prncípo de funconamento ão motores com velocdade de rotação fxa velocdade de sncronsmo. O seu prncípo de funconamento está esquematzado na fgura 1.1 um motor com 2 pólos. Uma corrente
Motores síncronos Prncípo de funconamento ão motores com velocdade de rotação fxa velocdade de sncronsmo. O seu prncípo de funconamento está esquematzado na fgura 1.1 um motor com 2 pólos. Uma corrente
Modelos estatísticos para previsão de partidas de futebol
 Modelos estatístcos para prevsão de partdas de futebol Dan Gamerman Insttuto de Matemátca, UFRJ dan@m.ufrj.br X Semana da Matemátca e II Semana da Estatístca da UFOP Ouro Preto, MG 03/11/2010 Algumas perguntas
Modelos estatístcos para prevsão de partdas de futebol Dan Gamerman Insttuto de Matemátca, UFRJ dan@m.ufrj.br X Semana da Matemátca e II Semana da Estatístca da UFOP Ouro Preto, MG 03/11/2010 Algumas perguntas
Interpolação Segmentada
 Interpolação Segmentada Uma splne é uma função segmentada e consste na junção de váras funções defndas num ntervalo, de tal forma que as partes que estão lgadas umas às outras de uma manera contínua e
Interpolação Segmentada Uma splne é uma função segmentada e consste na junção de váras funções defndas num ntervalo, de tal forma que as partes que estão lgadas umas às outras de uma manera contínua e
ALGORITMOS GENÉTICOS COMO FERRAMENTA AUXILIAR NA TOMADA DE DECISÃO EM ATIVIDADES DE GESTÃO AGROINDUSTRIAL
 ALGORITMOS GENÉTICOS COMO FERRAMENTA AUXILIAR NA TOMADA DE DECISÃO EM ATIVIDADES DE GESTÃO AGROINDUSTRIAL Danlo Augusto Hereda VIEIRA 1 Celso Correa de SOUZA 2 José Francsco dos REIS NETO 3 Resumo. As
ALGORITMOS GENÉTICOS COMO FERRAMENTA AUXILIAR NA TOMADA DE DECISÃO EM ATIVIDADES DE GESTÃO AGROINDUSTRIAL Danlo Augusto Hereda VIEIRA 1 Celso Correa de SOUZA 2 José Francsco dos REIS NETO 3 Resumo. As
Cálculo Numérico BCC760 Interpolação Polinomial
 Cálculo Numérco BCC76 Interpolação Polnomal Departamento de Computação Págna da dscplna http://www.decom.ufop.br/bcc76/ 1 Interpolação Polnomal Conteúdo 1. Introdução 2. Objetvo 3. Estênca e uncdade 4.
Cálculo Numérco BCC76 Interpolação Polnomal Departamento de Computação Págna da dscplna http://www.decom.ufop.br/bcc76/ 1 Interpolação Polnomal Conteúdo 1. Introdução 2. Objetvo 3. Estênca e uncdade 4.
I. Introdução. inatividade. 1 Dividiremos a categoria dos jovens em dois segmentos: os jovens que estão em busca do primeiro emprego, e os jovens que
 DESEMPREGO DE JOVENS NO BRASIL I. Introdução O desemprego é vsto por mutos como um grave problema socal que vem afetando tanto economas desenvolvdas como em desenvolvmento. Podemos dzer que os índces de
DESEMPREGO DE JOVENS NO BRASIL I. Introdução O desemprego é vsto por mutos como um grave problema socal que vem afetando tanto economas desenvolvdas como em desenvolvmento. Podemos dzer que os índces de
14. Correntes Alternadas (baseado no Halliday, 4 a edição)
 14. orrentes Alternadas (baseado no Hallday, 4 a edção) Por que estudar orrentes Alternadas?.: a maora das casas, comérco, etc., são provdas de fação elétrca que conduz corrente alternada (A ou A em nglês):
14. orrentes Alternadas (baseado no Hallday, 4 a edção) Por que estudar orrentes Alternadas?.: a maora das casas, comérco, etc., são provdas de fação elétrca que conduz corrente alternada (A ou A em nglês):
Nesse circuito, os dados indicam que a diferença de potencial entre os pontos X e Y, em volts, é a) 3,3 c) 10 e) 18 b) 6,0 d) 12.
 Aprmorando os Conhecmentos de Eletrcdade Lsta 7 Assocação de esstores Prof.: Célo Normando. (UNIFO-97) O resstor, que tem a curva característca representada no gráfco abao, é componente do crcuto representado
Aprmorando os Conhecmentos de Eletrcdade Lsta 7 Assocação de esstores Prof.: Célo Normando. (UNIFO-97) O resstor, que tem a curva característca representada no gráfco abao, é componente do crcuto representado
Equações Diferenciais Ordinárias
 Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Hoje não tem vitamina, o liquidificador quebrou!
 A U A UL LA Hoje não tem vtamna, o lqudfcador quebrou! Essa fo a notíca dramátca dada por Crstana no café da manhã, lgeramente amenzada pela promessa de uma breve solução. - Seu pa dsse que arruma à note!
A U A UL LA Hoje não tem vtamna, o lqudfcador quebrou! Essa fo a notíca dramátca dada por Crstana no café da manhã, lgeramente amenzada pela promessa de uma breve solução. - Seu pa dsse que arruma à note!
Termodinâmica e Termoquímica
 Termodnâmca e Termoquímca Introdução A cênca que trata da energa e suas transformações é conhecda como termodnâmca. A termodnâmca fo a mola mestra para a revolução ndustral, portanto o estudo e compreensão
Termodnâmca e Termoquímca Introdução A cênca que trata da energa e suas transformações é conhecda como termodnâmca. A termodnâmca fo a mola mestra para a revolução ndustral, portanto o estudo e compreensão
CAPÍTULO 1 Exercícios Propostos
 CAPÍTULO 1 Exercícos Propostos Atenção: Na resolução dos exercícos consderar, salvo menção em contráro, ano comercal de das. 1. Qual é a taxa anual de juros smples obtda em uma aplcação de $1.0 que produz,
CAPÍTULO 1 Exercícos Propostos Atenção: Na resolução dos exercícos consderar, salvo menção em contráro, ano comercal de das. 1. Qual é a taxa anual de juros smples obtda em uma aplcação de $1.0 que produz,
Capítulo 1. O plano complexo. 1.1. Introdução. Os números complexos começaram por ser introduzidos para dar sentido à 2
 Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Associação de resistores em série
 Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
ANÁLISE MATRICIAL DE ESTRUTURAS DE BARRAS PELO MÉTODO DE RIGIDEZ
 ANÁISE MATRICIA DE ESTRUTURAS DE BARRAS PEO MÉTODO DE RIGIDEZ A análse matrcal de estruturas pelo método de rgdez compreende o estudo de cnco modelos estruturas báscos: trelça plana, trelça espacal, pórtco
ANÁISE MATRICIA DE ESTRUTURAS DE BARRAS PEO MÉTODO DE RIGIDEZ A análse matrcal de estruturas pelo método de rgdez compreende o estudo de cnco modelos estruturas báscos: trelça plana, trelça espacal, pórtco
Karine Nayara F. Valle. Métodos Numéricos de Euler e Runge-Kutta
 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Professor Orientador: Alberto Berly Sarmiento Vera Belo Horizonte 2012 Karine Nayara F. Valle Métodos Numéricos de Euler e Runge-Kutta Monografia
0.5 setgray0 0.5 setgray1. Mecânica dos Fluidos Computacional. Aula 7. Leandro Franco de Souza. Leandro Franco de Souza p.
 Leandro Franco de Souza lefraso@cmc.usp.br p. 1/1 0.5 setgray0 0.5 setgray1 Mecânca dos Fludos Computaconal Aula 7 Leandro Franco de Souza Leandro Franco de Souza lefraso@cmc.usp.br p. 2/1 Equações Dferencas
Leandro Franco de Souza lefraso@cmc.usp.br p. 1/1 0.5 setgray0 0.5 setgray1 Mecânca dos Fludos Computaconal Aula 7 Leandro Franco de Souza Leandro Franco de Souza lefraso@cmc.usp.br p. 2/1 Equações Dferencas
METROLOGIA E ENSAIOS
 METROLOGIA E ENSAIOS Incerteza de Medção Prof. Aleandre Pedott pedott@producao.ufrgs.br Freqüênca de ocorrênca Incerteza da Medção Dstrbução de freqüênca das meddas Erro Sstemátco (Tendênca) Erro de Repettvdade
METROLOGIA E ENSAIOS Incerteza de Medção Prof. Aleandre Pedott pedott@producao.ufrgs.br Freqüênca de ocorrênca Incerteza da Medção Dstrbução de freqüênca das meddas Erro Sstemátco (Tendênca) Erro de Repettvdade
XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA NOVO MODELO PARA O CÁLCULO DE CARREGAMENTO DINÂMICO DE TRANSFORMADORES
 XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA Versão 1.0 22 a 25 Novembro de 2009 Recfe - PE GRUPO XIII GRUPO DE ESTUDO DE TRANSFORMADORES, REATORES, MATERIAIS E TECNOLOGIAS
XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA Versão 1.0 22 a 25 Novembro de 2009 Recfe - PE GRUPO XIII GRUPO DE ESTUDO DE TRANSFORMADORES, REATORES, MATERIAIS E TECNOLOGIAS
Figura 8.1: Distribuição uniforme de pontos em uma malha uni-dimensional. A notação empregada neste capítulo para avaliação da derivada de uma
 Capítulo 8 Dferencação Numérca Quase todos os métodos numércos utlzados atualmente para obtenção de soluções de equações erencas ordnáras e parcas utlzam algum tpo de aproxmação para as dervadas contínuas
Capítulo 8 Dferencação Numérca Quase todos os métodos numércos utlzados atualmente para obtenção de soluções de equações erencas ordnáras e parcas utlzam algum tpo de aproxmação para as dervadas contínuas
1 A Integral por Partes
 Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
5.1 Seleção dos melhores regressores univariados (modelo de Índice de Difusão univariado)
 5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA
 658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
1 a Lei de Kirchhoff ou Lei dos Nós: Num nó, a soma das intensidades de correntes que chegam é igual à soma das intensidades de correntes que saem.
 Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
Sinais Luminosos 2- CONCEITOS BÁSICOS PARA DIMENSIONAMENTO DE SINAIS LUMINOSOS.
 Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
ÍNDICE NOTA INTRODUTÓRIA
 OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
Sistemas de equações lineares
 Sstemas - ALGA - / Sstemas de equações lneares Uma equação lnear nas ncógntas ou varáves x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b onde a ; a ; :::; a n ; b são constantes
Sstemas - ALGA - / Sstemas de equações lneares Uma equação lnear nas ncógntas ou varáves x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b onde a ; a ; :::; a n ; b são constantes
Equações Diferenciais Ordinárias
 Equações Diferenciais Ordinárias Uma equação diferencial é uma equação que relaciona uma ou mais funções (desconhecidas com uma ou mais das suas derivadas. Eemplos: ( t dt ( t, u t d u ( cos( ( t d u +
Equações Diferenciais Ordinárias Uma equação diferencial é uma equação que relaciona uma ou mais funções (desconhecidas com uma ou mais das suas derivadas. Eemplos: ( t dt ( t, u t d u ( cos( ( t d u +
ASSOCIAÇÃO DE RESISTORES
 Prof(a) Stela Mara de arvalho Fernandes SSOIÇÃO DE ESISTOES ssocação de esstores em Sére Dos ou mas resstores estão assocados em sére quando são percorrdos pela mesma corrente elétrca. omo U D Somando
Prof(a) Stela Mara de arvalho Fernandes SSOIÇÃO DE ESISTOES ssocação de esstores em Sére Dos ou mas resstores estão assocados em sére quando são percorrdos pela mesma corrente elétrca. omo U D Somando
φ(x,y,y',y'',y''',..., d n y/dx n ) = 0 (1) Esta equação é de n-ésima ordem e tem somente uma variável independente, x.
 245 Capítulo 15 Resolução numérica de equações diferenciais Para podermos investigar exemplos de simulação que surgem na Física, Engenharia, Biomatemática etc., estudamos, neste capítulo, alguns métodos
245 Capítulo 15 Resolução numérica de equações diferenciais Para podermos investigar exemplos de simulação que surgem na Física, Engenharia, Biomatemática etc., estudamos, neste capítulo, alguns métodos
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase
 36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
36ª Olimpíada Brasileira de Matemática GABARITO Segunda Fase Soluções Nível 1 Segunda Fase Parte A CRITÉRIO DE CORREÇÃO: PARTE A Na parte A serão atribuídos 5 pontos para cada resposta correta e a pontuação
Equipas Educativas Para uma nova organização da escola. João Formosinho Joaquim Machado
 Equpas Educatvas Para uma nova organzação da escola João Formosnho Joaqum Machado TRANSFORMAÇÕES NA ESCOLA BÁSICA TRANSFORMAÇÕES NA ESCOLA BÁSICA A expansão escolar e a mplementação das polítcas de nclusão
Equpas Educatvas Para uma nova organzação da escola João Formosnho Joaqum Machado TRANSFORMAÇÕES NA ESCOLA BÁSICA TRANSFORMAÇÕES NA ESCOLA BÁSICA A expansão escolar e a mplementação das polítcas de nclusão
Caderno de Exercícios Resolvidos
 Estatístca Descrtva Exercíco 1. Caderno de Exercícos Resolvdos A fgura segunte representa, através de um polígono ntegral, a dstrbução do rendmento nas famílas dos alunos de duas turmas. 1,,75 Turma B
Estatístca Descrtva Exercíco 1. Caderno de Exercícos Resolvdos A fgura segunte representa, através de um polígono ntegral, a dstrbução do rendmento nas famílas dos alunos de duas turmas. 1,,75 Turma B
O migrante de retorno na Região Norte do Brasil: Uma aplicação de Regressão Logística Multinomial
 O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
3 Método Numérico. 3.1 Discretização da Equação Diferencial
 3 Método Numérco O presente capítulo apresenta a dscretação da equação dferencal para o campo de pressão e a ntegração numérca da expressão obtda anterormente para a Vscosdade Newtonana Equvalente possbltando
3 Método Numérco O presente capítulo apresenta a dscretação da equação dferencal para o campo de pressão e a ntegração numérca da expressão obtda anterormente para a Vscosdade Newtonana Equvalente possbltando
Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Exercícios de Física. Prof. Panosso. Fontes de campo magnético
 1) A fgura mostra um prego de ferro envolto por um fo fno de cobre esmaltado, enrolado mutas vezes ao seu redor. O conjunto pode ser consderado um eletroímã quando as extremdades do fo são conectadas aos
1) A fgura mostra um prego de ferro envolto por um fo fno de cobre esmaltado, enrolado mutas vezes ao seu redor. O conjunto pode ser consderado um eletroímã quando as extremdades do fo são conectadas aos
7.4 Precificação dos Serviços de Transmissão em Ambiente Desregulamentado
 64 Capítulo 7: Introdução ao Estudo de Mercados de Energa Elétrca 7.4 Precfcação dos Servços de Transmssão em Ambente Desregulamentado A re-estruturação da ndústra de energa elétrca que ocorreu nos últmos
64 Capítulo 7: Introdução ao Estudo de Mercados de Energa Elétrca 7.4 Precfcação dos Servços de Transmssão em Ambente Desregulamentado A re-estruturação da ndústra de energa elétrca que ocorreu nos últmos
GABARITO ERP19. impedância total em pu. impedância linha em pu; impedância carga em pu; tensão no gerador em pu.
 GABARITO ERP9 Questão mpedânca total em pu. mpedânca lnha em pu; mpedânca carga em pu; tensão no gerador em pu. Assm, tem-se que: ( ). Mas, ou seja: : ( ).. Logo: pu. () A mpedânca da carga em pu,, tem
GABARITO ERP9 Questão mpedânca total em pu. mpedânca lnha em pu; mpedânca carga em pu; tensão no gerador em pu. Assm, tem-se que: ( ). Mas, ou seja: : ( ).. Logo: pu. () A mpedânca da carga em pu,, tem
Professor Mauricio Lutz CORRELAÇÃO
 Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Cálculo do Conceito Preliminar de Cursos de Graduação
 Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Resoluções comentadas de Raciocínio Lógico e Estatística SEFAZ - Analista em Finanças Públicas Prova realizada em 04/12/2011 pelo CEPERJ
 Resoluções comentadas de Raciocínio Lógico e Estatística SEFAZ - Analista em Finanças Públicas Prova realizada em 04/1/011 pelo CEPERJ 59. O cartão de crédito que João utiliza cobra 10% de juros ao mês,
Resoluções comentadas de Raciocínio Lógico e Estatística SEFAZ - Analista em Finanças Públicas Prova realizada em 04/1/011 pelo CEPERJ 59. O cartão de crédito que João utiliza cobra 10% de juros ao mês,
Aula 7: Circuitos. Curso de Física Geral III F-328 1º semestre, 2014
 Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
MAPEAMENTO DA VARIABILIDADE ESPACIAL
 IT 90 Prncípos em Agrcultura de Precsão IT Departamento de Engenhara ÁREA DE MECANIZAÇÃO AGRÍCOLA MAPEAMENTO DA VARIABILIDADE ESPACIAL Carlos Alberto Alves Varella Para o mapeamento da varabldade espacal
IT 90 Prncípos em Agrcultura de Precsão IT Departamento de Engenhara ÁREA DE MECANIZAÇÃO AGRÍCOLA MAPEAMENTO DA VARIABILIDADE ESPACIAL Carlos Alberto Alves Varella Para o mapeamento da varabldade espacal
Universidade do Estado do Rio de Janeiro Instituto de Matemática e Estatística Econometria
 Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
GUSTAVO TERRA BASTOS COMPARAÇÃO DE TÉCNICAS PARA O CÁLCULO DE IDEMPOTENTES GERADORES DE CÓDIGOS ABELIANOS
 GUSTAVO TERRA BASTOS COMPARAÇÃO DE TÉCNICAS PARA O CÁLCULO DE IDEMPOTENTES GERADORES DE CÓDIGOS ABELIANOS Dssertação apresentada à Unversdade Federal de Vçosa, como parte das exgêncas do Programa de Pós-Graduação
GUSTAVO TERRA BASTOS COMPARAÇÃO DE TÉCNICAS PARA O CÁLCULO DE IDEMPOTENTES GERADORES DE CÓDIGOS ABELIANOS Dssertação apresentada à Unversdade Federal de Vçosa, como parte das exgêncas do Programa de Pós-Graduação
CAPÍTULO 7 - ESTIMAÇÃO DE PARÂMETROS
 CAPÍTULO 7 - ESTIMAÇÃO DE PARÂMETROS Nos capítulos anterores analsaram-se város modelos usados na avalação de manancas, tendo-se defndo os respectvos parâmetros. Nas correspondentes fchas de exercícos
CAPÍTULO 7 - ESTIMAÇÃO DE PARÂMETROS Nos capítulos anterores analsaram-se város modelos usados na avalação de manancas, tendo-se defndo os respectvos parâmetros. Nas correspondentes fchas de exercícos
ELEMENTOS DE CIRCUITOS
 MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
ANÁLISE ESTATÍSTICA DE CORRELAÇÕES PVT DE PETRÓLEOS
 UNIVERSIDADE FEDERAL DO ESÍRITO SANTO CENTRO TECNOLÓGICO ROGRAMA DE ÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA GARBEN BRAVIM GOMES ANÁLISE ESTATÍSTICA DE CORRELAÇÕES VT DE ETRÓLEOS VITÓRIA 8 GARBEN BRAVIM GOMES
UNIVERSIDADE FEDERAL DO ESÍRITO SANTO CENTRO TECNOLÓGICO ROGRAMA DE ÓS-GRADUAÇÃO EM ENGENHARIA MECÂNICA GARBEN BRAVIM GOMES ANÁLISE ESTATÍSTICA DE CORRELAÇÕES VT DE ETRÓLEOS VITÓRIA 8 GARBEN BRAVIM GOMES
Controlo Metrológico de Contadores de Gás
 Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
DESENVOLVIMENTO DE UM ALGORITMO PARA RECONS- TRUÇÃO DE IMAGENS UTILIZANDO A TÉCNICA DE TOMO- GRAFIA POR IMPEDÂNCIA ELÉTRICA
 PUCRS PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL PRÓ-REITORIA DE PESQUISA E PÓS-GRADUAÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA E TECNO- LOGIA DE MATERIAIS Facldade de Engenhara Facldade de
PUCRS PONTIFÍCIA UNIVERSIDADE CATÓLICA DO RIO GRANDE DO SUL PRÓ-REITORIA DE PESQUISA E PÓS-GRADUAÇÃO PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA E TECNO- LOGIA DE MATERIAIS Facldade de Engenhara Facldade de
CORRELAÇÃO E REGRESSÃO
 CORRELAÇÃO E REGRESSÃO Constata-se, freqüentemente, a estênca de uma relação entre duas (ou mas) varáves. Se tal relação é de natureza quanttatva, a correlação é o nstrumento adequado para descobrr e medr
CORRELAÇÃO E REGRESSÃO Constata-se, freqüentemente, a estênca de uma relação entre duas (ou mas) varáves. Se tal relação é de natureza quanttatva, a correlação é o nstrumento adequado para descobrr e medr
