TRANSFERÊNCIA DE CALOR NA ENVOLVENTE DA EDIFICAÇÃO
|
|
|
- Vitória Wagner Brandt
- 8 Há anos
- Visualizações:
Transcrição
1 UNIVERSIDADE FEDERAL DE SANA CAARINA CENRO ECNOLÓGICO DEPARAMENO DE ENGENHARIA CIVIL PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA CIVIL RANSFERÊNCIA DE CALOR NA ENVOLVENE DA EDIFICAÇÃO ELABORADO POR: Martn Ordenes, Dr. Roberto Lamberts, PhD. Saulo Güths, PhD. Floranópols, Março de 8.
2 Fone: (48) SUMÁRIO INRODUÇÃO.... O SISEMA INERNACIONAL DE UNIDADES.... DEFINIÇÕES MECANISMOS DE RANSFERÊNCIA DE CALOR Modelo de condução Modelo de convecção Modelo de radação BALANÇO ENERGÉICO...7 CONDUÇÃO.... REGIME PERMANENE.... ANALOGIA ELÉRICA....3 EQUAÇÃO DE DIFUSÃO DE CALOR DIFERENÇAS FINIAS CONVECÇÃO FORÇADA NAURAL CÂMARA DE AR VERICAL NÃO VENILADA RADIAÇÃO RADIAÇÃO EM UMA SUPERFÍCIE RADIAÇÃO ENRE SUPERFÍCIES BIBLIOGRAFIA...4
3 Fone: (48) INRODUÇÃO A envolvente da edfcação ntegra todos os elementos que separam os ambentes nternos das condções clmátcas externas (paredes, janelas, telhado e pso). Ela funcona como uma espéce de fltro ou barrera em que ocorrem trocas de energa térmca (calor), umdade e ar (nfltração e ventlação). O objetvo deste texto pretende descrever os mecansmos de transferênca de calor através de elementos opacos na envolvente. Estes mecansmos defnem o desempenho térmco da edfcação e suas repercussões no consumo energétco e conforto térmco. O conhecmento dos processos físcos que partcpam na envolvente permte avalar a resposta da edfcação frente às mudanças meteorológcas (temperatura, radação solar, vento, etc.) na etapa de projeto e escolher as alternatvas e soluções técncas que garantam um desempenho térmco adequado à localdade em que o edfíco será construído. O estudo da transferênca de calor na envolvente também representa uma ferramenta mportante para dagnostcar o desempenho de uma edfcação exstente. O texto contempla um prmero captulo ntrodutóro que nclu uma descrção do sstema de undades adotado, os prncpas concetos físcos, uma breve explcação dos três mecansmos de transferêncas de calor (Condução, convecção e radação) e a defnção da equação de balanço térmco. Os três capítulos seguntes estão focados em apresentar detalhadamente cada um dos processos físcos de transferênca de calor na envolvente. O texto de Incropera e DeWtt (3), é a base da dscplna e serão adotados os capítulos II, III e V para a parte de condução, os capítulos VI, VII, VIII e IX para a parte de convecção e os capítulos XII e XIII para explca a radação.. O SISEMA INERNACIONAL DE UNIDADES As grandezas termo-físcas utlzadas no estudo da transferênca de calor são especfcadas nas undades do Sstema Internaconal (SI). Este sstema fo defndo em 96 pela a Conferênca Geral de Pesos e Meddas e recomendado como padrão mundal. A defnção das grandezas a utlzar na dscplna e seus símbolos são apresentados na abela. abela Grandezas do SI utlzadas no estudo de transferênca de calor. Grandeza (símbolo) Undade (símbolo) Defnção na base SI Comprmento (l) Metro (m) m Área (A) Metro quadrado (m ) m Volume (V) Metro cúbco (m 3 ) m 3 Massa (m) Qulograma (kg) kg empo (t) Segundo (s) s emperatura () Kelvn (K) K Energa (E) Joule (J) J Potênca (q) Watt (W) J/s Densdade de massa (ρ) --- kg/m 3 Calor específco (c) --- J/(kg K) Condutvdade térmca (λ) --- W/(m K) Resstênca térmca (R) --- W/(m K)
4 Fone: (48) Embora a undade de temperatura no SI seja o Kelvn, o uso da escala Celsus é amplamente dfunddo. O símbolo de grau na desgnação da temperatura em Celsus ( o C) para evtar confund-lo com o C utlzado como undade de carga elétrca (Coulomb). O zero na escala Celsus ( o C) equvale a 73,5 K na escala Kelvn, mantendo uma relação lnear de acordo com a equação. Contudo, a equação mostra que as dferenças de temperaturas (Δ f - ) são equvalentes para as duas escalas e podem ser denotadas em o C ou em K. ( K) ( C) + 73,5 () Além dsso, embora a undade de tempo no SI seja o segundo, outras undades de tempo (mnuto, hora e da) são tão comuns que podem ser utlzadas com o sstema SI. No âmbto do desempenho térmco de edfcações e efcênca energétca é comum encontrar a energa quantfcada em Watthora (Wh). Para facltar a letura de valores numércos e destacar os dígtos sgnfcatvos, utlzam-se os prefxos multplcadores. Estes prefxos são símbolos que permtem expressar valores muto grandes ou muto pequenos sem ter que utlzar potêncas de base ou mutas casas decmas (abela ). abela Prefxos utlzados no Sstema Internaconal (SI) Prefxo Símbolo Valor numérco Yotta Y 4 Zetta Z Exa E 8 Peta P 5 era Gga G 9 Mega M 6 Klo k 3 Hecto h Deca da Dec d Cent c Ml m 3 Mcro μ 6 Nano n 9 Pco p Femto f 5 Atto a 8 Zepto z Yocto y 4 Embora o SI seja recomendado como o padrão nternaconal de meddas, na bblografa é comum encontrar as mesmas grandezas expressadas em undades do sstema nglês (polegadas, graus Fahrenhet, Btu, etc.). Nos cálculos deste texto será utlzado sempre o Sstema Internaconal.
5 Fone: (48) DEFINIÇÕES No estudo da transferênca de calor na envolvente das edfcações, os prmeros concetos a defnr são a temperatura e calor. Estes concetos encontram-se estretamente relaconados. A temperatura está relaconada à quantdade de energa térmca ou calor num sstema. Na medda em que um sstema acumula calor, sua temperatura aumenta. Ao contráro, uma perda de calor provoca uma dmnução da temperatura do sstema. Na escala mcroscópca, este calor corresponde à agtação térmca de átomos e moléculas no sstema. Assm, uma elevação de temperatura corresponde a um aumento da velocdade de agtação térmca dos átomos. A emperatura é a propredade de um materal ou sstema que mplca as noções comuns de "quente" ou "fro". Em geral a matéra com a temperatura maor é dta mas quente. Apesar de todo mundo ter uma compreensão básca do conceto de temperatura, sua defnção precsa não é tão evdente. Ao contráro de outras grandezas, como massa e comprmento, a temperatura é defnda através de um conjunto de condções teórcas (prncípos da termodnâmca), que se afastam dos alcances da dscplna. Porém, é mportante entender que a temperatura é uma grandeza escalar, sto sgnfca que para sua caracterzação é precso apenas conhecer seu módulo ou quantdade. Da mesma forma que a massa, o comprmento e o tempo, na temperatura só é necessáro saber a ntensdade que ela possu. Mas ao contraro da massa e o tempo, a temperatura pode adotar tanto valores postvos como negatvos. Sempre que exstr uma dferença de temperatura em um meo ou entre meos dferentes, ocorre, necessaramente uma transferênca de energa térmca. O Calor (ou fluxo de calor) é defndo então como a taxa de energa térmca transferda por undade de tempo devdo a uma dferença de temperatura. O calor, por tanto, é uma grandeza físca vetoral caracterzada pela ntensdade e orentação espacal (dreção e sentdo). A transferênca de calor ocorre na dreção do gradente de temperatura e no sentdo decrescente da temperatura (de maor a menor temperatura). No sstema SI exste uma undade de energa (térmca, mecânca ou elétrca) defnda como Joule. A taxa de energa (potênca), é por tanto energa/tempo, em que um Joule por segundo é equvalente a um Watt (Fgura ).
6 Fone: (48) Fluxo de calor (q) > Potênca Fluxo de calor > Joules/segundo Watt Fgura Relação entre energa e fluxo de calor Uma notação mportante a consderar quando se trabalha com fluxo de calor é a segunte: q : fluxo de energa calórca por undade de tempo [W] ( J/s W) q : fluxo de energa calórca por undade de tempo e longtude [W/m] q : fluxo de energa calórca por undade de tempo e área [W/m ] q : fluxo de energa calórca por undade de tempo e volume [W/m 3 ] No escopo do estudo da dscplna entende-se frequentemente por densdade de fluxo de calor (q ) a taxa de transferênca de calor em uma dreção defnda por undade de área perpendcular à dreção de transferênca..3 MECANISMOS DE RANSFERÊNCIA DE CALOR.3. MODELO DE CONDUÇÃO A condução esta relaconada ao transporte de energa térmca (calor) em um meo sóldo devdo ao gradente de temperatura. O estudo de transferênca de calor por condução na dscplna encontra-se focado ncalmente a condções smplfcadas, sto é, condução undmensonal em regme permanente em uma parede plana para a qual a dstrbução de temperatura é lnear. Conhecendo a dstrbução de temperaturas no meo, a transferênca de calor por condução ocorre de acordo com a Le de Fourer (Fgura ). > sóldo L q cd q cd λ L (Le de Fourer) λ: condutvdade térmca [W/m K] Fgura Condução de calor na envolvente. A condutvdade térmca é alta em metas ( 7 W/m K) devdo a que os elétrons podem se movmentar lvremente. Os materas sóldos não metálcos não
7 Fone: (48) permtem o movmento de elétrons, smplesmente a vbração molecular, sto faz com que sua condutvdade térmca esteja entre,5 e 3 W/m K. Isolantes térmcos, como o polestreno expanddo (sopor), são compostos de materas de baxa condutvdade térmca (~,4 W/m K), devdo à quantdade de ar ncorporado na estrutura nterna..3. MODELO DE CONVECÇÃO A transferênca de calor por convecção ocorre entre um fluído em movmento e uma superfíce quando os dos se encontram a dferentes temperaturas (Fgura 3). A transferênca acontece tanto pelo movmento molecular aleatóro quanto pelo movmento global do fluído. Ela pode ser natural (ou lvre), msta ou forçada, dependendo das condções de escoamento do fluído. sup > sóldo L q cv q cv h ( sup - ) (Le de Newton) h: coefcente de convecção [W/m K] Fgura 3 Convecção de calor na envolvente O coefcente de convecção é uma constante de proporconaldade que resume as condções nas camadas mas próxmas à superfíce, consderando a geometra da superfíce, a natureza do escoamento (lamnar ou turbulento) e propredades do fluído (densdade, vscosdade, condutvdade térmca e calor específco)..3.3 MODELO DE RADIAÇÃO A radação é um fenômeno superfcal em que o calor emtdo de acordo com a temperatura superfcal do materal (Fgura 4). A energa do campo de radação é transportada por ondas longas eletromagnétcas. Enquanto a transferênca de calor por condução e convecção requer a presença de um meo materal (sóldo ou fluído), a radação ocorre no vácuo, sem precsar de meo. sup q rd ε σ 4 sup (Le de Steffan-Boltzmann) sóldo L q rd σ: cte de Steffan-Boltzmann [W/m K 4 ] ε: emssvdade (adm) Fgura 4 - Radação de calor na envolvente A taxa na qual a energa é lberada por undade de área (W/m ) é conhecda também como poder emssvo, que é prevsto pela Le de Steffan-Boltzmann onde sup deve ser consderada em undades absolutas (K) e σ é a constante de Steffan-Boltzmann
8 Fone: (48) (σ 5,67 x -8 W/m K 4 ). A emssvdade (ε) é uma propredade radante da superfíce que defne uma relação entre a capacdade de emssão do materal comparado com um componente deal, conhecdo como corpo negro ( ε ). Ela depende do tpo de materal usado na superfíce, seu acabamento e sua cor..4 BALANÇO ENERGÉICO O balanço de energa na envolvente da edfcação tem como base a prmera le de termodnâmca, a le da conservação de energa. Esta le estabelece que a quantdade de energa térmca (calor) que entra em um volume de controle - no caso a envolvente (E a ), mas a quantdade de calor gerada no nteror do volume (E g ), menos a quantdade de energa que dexa o volume (E s ) deve ser gual ao aumento da quantdade de energa armazenada (E ar ) no volume de controle (Fgura 5). E s E e E ar E g E ar E s E e E s E s E e E s + E g E ar E g Superfcas Volumétrcas Fgura 5 Conservação de energa (ª Le de termodnâmca) O alcance da dscplna não consdera o estudo de mecansmos de geração de calor na envolvente. Esta smplfcação permte estabelecer o balanço energétco como a dferença entre a energa que ngressa e sa da envolvente deve ser gual à varação de energa (calor armazenado ou lberado) no nteror da envolvente. EXEMPLO. Se lgarmos uma resstênca aquecedora de Ohms em V por mn, dentro de um recpente de l com água a C. Qual a temperatura fnal da água? Potênca (P) fornecda pela resstênca elétrca P U I U R I U: ensão elétrca, Voltagem [Volt] I: Corrente elétrca [Ampère] R: Resstênca elétrca [Ohm] P U /R /.4 Watts.4 J/s
9 Fone: (48) Balanço energétco: E e E s + E g E ar m c ρ V c ( f ) E e, E s E g P t ρ V c ( f ) m: massa [kg] ρ: densdade aparente [kg/m 3 ] V: Volume [m 3 ] c: calor específco [J/kg K] : emperatura [ºC] t: tempo [s].4 6.,. ( f ) > f 34,4 [ºC] Agora, qual a taxa de varação da temperatura? E g ρ V c ( f ) t E g t Δ P m c t m c d dt.4.,. ( /t) > ( /t),4 [ºC/s] Para resolver problemas de transferênca de calor, a palavra chave é balanço energétco e recomenda-se utlzar o segunte esquema de resolução: Modelo: Organze todos os dados do seu problema (revse as undades). Realze um esquema gráfco dentfcando o ponto ou volume de controle (nó ou envolvente) e os fenômenos físcos que partcpam nele. Verfque se suas hpóteses são váldas. Objetvo: Identfque as grandezas físcas a determnar. Le geral: Estabeleça o balanço energétco dentfcando seus componentes no modelo gráfco. Les partculares: Para cada componente, dentfcar o tpo de le que o representa (Fourer, Newton ou Steffan-Boltzmann) e desenvolva a equação de balanço com as relações correspondentes. Solução: Substtua as varáves pelos valores numércos (dados) e execute os cálculos necessáros. Dscussão: Questone os resultados obtdos. Analse se eles são coerentes com a proposta do problema.
10 Fone: (48) EXERCICIOS Para reforçar os concetos ntroduzdos sobre balanço energétco, sugere-se que o aluno trabalhe nos seguntes problemas do texto base (INCROPERA e DEWI, 3). Exemplo. (págna 3) Exemplo. (págna 7) Exemplo.7 (págna 9) Exercíco. (págna ) Exercíco.4 (págna ) Exercíco.6 (págna )
11 Fone: (48) CONDUÇÃO Assm como fo apresentado na ntrodução, a transferênca de calor por condução acontece dentro de um meo sóldo devdo ao gradente de temperatura, defndo como postvo no sentdo de maor a menor temperatura de acordo com a Le de Fourer. Incalmente, o Captulo apresenta o fenômeno de condução sob condções smplfcadas (de forma undmensonal em regme permanente), para depos amplar esta le às condções de regme transente.. REGIME PERMANENE Para entender melhor a Le de Fourer, consdere o expermento apresentado na Fgura 6 em regme permanente. Que um sstema se encontre em regme permanente sgnfca que as condções térmcas (temperatura e fluxo de calor) nas superfíces de contorno não varam ao longo do tempo, tendo atngdo uma stuação de equlbro. Este cenáro mplca que a dstrbução de temperaturas no meo é lnear ( x ou Cte ). x Fgura 6 Condução de calor em regme permanente A Le de Fourer estabelece que o calor transferdo por condução (q) é dretamente proporconal a área (A), a condutvdade térmca do materal (λ) e a dferença de temperatura ( - ); e nversamente proporconal ao comprmento (ou espessura) do materal (L). A equação resume esta le para o caso undreconal. A q λ ( ) L () As propredades termo-físcas de um componente (consderadas fxas) podem ser agrupadas em um termo que defne sua resstênca térmca (R). L R λ A R: Resstênca térmca [(m K)/W] (3)
12 Fone: (48) E o fluxo de calor pode ser resumdo como Δ q (4) R No caso de um componente homogêneo na envolvente como uma parede de concreto, por exemplo, a Le de Fourer pode ser representada de acordo com a Fgura 7. Lembrando que a dreção do fluxo de calor será sempre normal às superfíces, que elas são consderadas sotérmcas e as propredades da parede constantes ao longo do tempo. (x) q x. ANALOGIA ELÉRICA Fgura 7 Condução de calor na parede. As condções de regme permanente permtem estabelecer uma análoga entre a dfusão de calor e a carga elétrca. Assm como uma resstênca elétrca é assocada com uma condução de eletrcdade, uma resstênca térmca pode ser assocada com uma condução de calor (Fgura 8). x λ I U R e Fgura 8 Analoga térmco-elétrca. q Δ R t No caso em que se têm dferentes materas em um mesmo componente da envolvente, pode ser crado um crcuto térmco da mesma forma que um crcuto
13 Fone: (48) elétrco. As regras para calcular resstêncas térmcas equvalentes são as mesmas para somar resstêncas elétrcas em sére e em paralelo (Fgura 9). Sére Paralelo R R R R n n eq R R + R + Req R R R R EXEMPLO. Fgura 9 Cálculo de resstênca térmca equvalente. Calcular a densdade de fluxo de calor na seção da parede. λ λ λ 4,5 [W/m K] λ 3, [W/m K] Prof [m]
14 Fone: (48) , R 4,35 [m, K/W] e R 3, 5 [m K/W],5,,, + + > R eq,45 [m K/W] R eq R R 4,35,5 R 3,,5 (, +,) R4,79 [m K/W] R eqoal R + Req + R4,79 +,45 +,79,6[m K/W] Δ 3 q '' 74,75 [W/m ] A (, +,),6 R t A analoga elétrca pode se estender para os casos de convecção e radação. Para a convecção, a resstênca térmca é defnda como R conv (5) h No caso da radação, a parcela de radação solar que penetra no componente depende de sua absortvdade q rad α: absortvdade [adm.] G: densdade de radação (onda curta) [W/m ] α G A A: área superfcal [m ] (6) E a troca lquda de radação entre a superfíce do componente e o entorno pode ser estmada como q lq 4 4 ε A σ ( ) σ: cte de Steffan-Boltzmann [W/m K 4 ] (7) sup sup vz ε: emssvdade [adm.] : temperatura [K]
15 Fone: (48) EXEMPLO. Calcular as temperaturas superfcas da parede ( e ). L Dados: vz ext : 3 [ºC] vz nt : [ºC] q sol : 5 [W/m ] α:,7 ε:,9 h ext : 5 [W/m K] ext : 3 [ºC] h nt : 8 [W/m K] nt : [ºC] L: [cm] λ: [W/m K] Balanço energétco na superfíce q RAD q + q conv _ ext + qrad qrad _ ext cond q cond q conv_ext q rad_ext (33 ) 4 4 +,7 5,9 σ ( 33 ) +,4,
16 Fone: (48) Balanço energétco na superfíce q conv_nt q q + q cond conv _ nt rad _ nt q cond, 93 +,9 σ (, ) q rad_nt Smplfcando as equações de balanço nas duas superfíces, se tem o segunte sstema: 4 +,4,4 33,4 4 6,87 +,5,5 34 Que resolvendo: 38,3 [ºC] 7,8 [ºC].3 EQUAÇÃO DE DIFUSÃO DE CALOR Como fo vsto no exemplo., a análse de condução de calor vsa o conhecmento da dstrbução de temperaturas em um componente. Uma vez que as temperaturas são conhecdas, o fluxo de calor pode ser determnado pela le de Fourer. A partr do balanço energétco, este capítulo apresenta a metodologa para determnar a equação de dfusão de calor undmensonal conforme o modelo mostrado na Fgura. O resultado é uma equação dferencal, dependente do tempo e posção, cuja solução pode ser obtda a partr de duas condções de contorno e uma condção ncal.
17 Fone: (48) q x Fgura Componente construtvo para análse de dfusão de calor. Balanço energétco em x (Σ E entra - Σ E sa E armazenada ) q q dx dx ( x ) ( x+ ) Δ m c Δt m c d dt (8) Utlzando a expansão de aylor e consderando que m V ρ A dx ρ dx ρ q( x) dq dx dx q( x) dq dx dx ρ c d dt dx dq dx dx ρ c d dt dx dq d ρ c com dx dt d q λ dx d λ dx d dx ρ c d dt d dx λ ρ c d dt
18 Fone: (48) t λ ρ c x Equação de dfusão de calor (Fourer) (9) t α x λ α dfusvdade térmca [m /s] ρ c Observa-se que a pesar do fluxo de calor ser uma grandeza vetoral, ele pode ser ntegrado na equação de dfusão de calor como escalar, sendo que seu sentdo é defndo pelo símbolo (postvo ou negatvo) adotado na convenção. Hpóteses a consderar no uso da equação de dfusão de calor: - Fluxo de calor undmensonal - Duas superfíces planas paralelas - Materal sotrópco e homogêneo - Propredades termo-físcas constantes no tempo (dα/dt ) - Sem geração de calor nterno d dt d α > (x,t) dx Precso conhecer a dstrbução de para um tempo t CONDIÇÃO INICIAL (x,t ) (,t) (L,t) Precso conhecer em dos pontos de x o tempo todo CONDIÇÕES DE CONORNO.4 DIFERENÇAS FINIAS A solução analítca da equação 9 é um problema complexo que está além do alcance da dscplna. Este capítulo apresenta uma solução numérca que utlza uma dscretzação do componente (Fgura ), conhecda como o método de dferenças fntas.
19 Fone: (48) Fgura Dscretzação para dferenças fntas. Para os problemas de condução em regme transente, as soluções podem ser determnadas de forma mplícta e explícta, de acordo com o esquema apresentado na Fgura. Implícto Explícto n n n f (,, ) n + n f ( n, n, n + ) Fgura Métodos de solução para dferenças fntas. O foco de nteresse da dscplna encontra-se no segundo método, em que a temperatura desconhecda ( ) para o tempo futuro é determnada explctamente pelas conhecdas do tempo anteror. Assm, para calcular as temperaturas
20 9 Programa de Pós-Graduação em Engenhara Cvl PPGEC/UFSC Fone: (48) desconhecdas é precso ter as temperaturas ncas em cada nó (condção ncal) e as temperaturas em dos nós durante todo o tempo todo, geralmente as temperaturas nos extremos (condções de contorno). Para todos os pontos a função que determna a temperatura no nstante futuro é o balanço energétco. Para o caso dos elementos nternos, a temperatura 3 (Fgura ) pode ser calculada a partr das temperaturas vznhas prevamente conhecdas (, 3 e 4 ) através do procedmento a segur. Σ E entra - Σ E sa E armazenada t c x x x Δ Δ Δ Δ ) ( ) ( ) ( ρ λ λ () ) ( ) ( t c x Δ Δ + λ ρ com c x t F o Δ Δ ) ( ρ λ ) ( F F F o o o + + (F o : Número de Fourer) No regme transente, as varações bruscas de temperatura podem tornar o sstema de equações nstável. Para evtar esses problemas, o crtéro de establdade é determnado pela exgênca de que todos os coefcentes que acompanham as temperaturas no tempo anteror sejam maores ou guas a zero. No caso de elementos nternos a condção de establdade (convergênca) é o F () Assm, a precsão e convergênca do sstema de equações defne os valores de x e t. A escolha de x é tpcamente baseada na geometra do componente e as exgêncas computaconas. O valor de t deve ser mantdo abaxo de certo lmte, que depende de x e as propredades termo-físcas do materal. Para o caso de elementos superfíces, o balanço energétco consdera as trocas de calor por convecção com o ambente. Analsando o lado esquerdo da Fgura, a temperatura pode ser calculada a partr das temperaturas vznhas prevamente conhecdas ( ext, e ) através do procedmento a segur. Σ E entra - Σ E sa E armazenada t x c x h ext ext Δ Δ Δ ) ( ) ( ) ( ρ λ () ) ( ) ( ) ( x c t x c t h ext ext Δ Δ Δ Δ ρ λ ρ
21 Fone: (48) h Δt ρ c Δx λ Δt ρ c ( Δx) k Δt ρ c ( Δx) h Δt ρ c ( Δx) ext ext + + ext Com B hext Δx e λ B F o hext Δt ρ c Δx ( B Fo Fo ) + Fo + B Fo ext (B : Número de Bot) A mesma condção de establdade (convergênca) é requerda para os elementos superfcas. Assm, o crtéro de convergênca é B F F (3) o o A equação para calcular a temperatura superfcal do lado dreto (nterno) pode ser determnada por analoga com o caso da superfíce esquerda. No método explícto para resolver os problemas de dferenças fntas, quanto menores sejam os valores de x e t maor será a precsão da solução. Porém, dmnundo x aumenta o número de nós em que é feto o balanço energétco e dmnuído t aumenta o número de ntervalo para chegar à solução no tempo fnal Logo, o tempo de smulação e os requermentos computaconas aumentam com a dmnução destes parâmetros. As equações e 3 determnam os valores que podem adotar estes parâmetros e devem ser comparadas para estabelecer qual exgênca é mas rgorosa. Já que B, o valor lmte de F o para a equação 3 é menor do que para a equação (F o / (B +)). O valor de x pode ser determnado a partr da geometra do componente e para garantr a establdade em todos os nós, a equação (3) deve ser utlzada para a escolha do valor máxmo permssível de F o e assm t..5 EXERCÍCIOS Para reforçar os concetos ntroduzdos sobre condução, sugere-se que o aluno trabalhe nos seguntes problemas do texto base (INCROPERA e DEWI, 3). Exercíco.7 (págna 49) Exercíco 3.5 (págna ) Exercíco 3.7 (págna ) Do texto de norma braslera (ABN BR 5-, 3) sugere-se que o aluno calcule a resstênca térmca dos componentes construtvos apresentados nos exemplos C, C3, C5 e C6.
22 Fone: (48) CONVECÇÃO No capítulo, o estudo fo focado na transferênca de calor em um meo sóldo por condução e o fenômeno de convecção fo consderado na analoga térmco-elétrca apenas como uma condção de contorno. Neste captulo será apresentado com mas detalhe o mecansmo de convecção para descrever a transferênca de calor entre uma superfíce e um fludo em movmento sobre a superfíce. Nas equações de balanço energétco desenvolvdas nos capítulos anterores, a resstênca térmca total do sstema é defnda pelas resstêncas térmcas das camadas de ar superfcas e a resstênca à condução do componente (R t R ar_ext + R comp + R ar_nt ), sendo as resstêncas das camadas de ar uma função do coefcente de convecção (h) e da dferença de temperatura entre a superfíce e o ar ( ). O objetvo prncpal no estudo da convecção é determnar o coefcente de convecção (h) para ser utlzado no balanço energétco. A Fgura 3 apresenta um esquema da natureza das trocas de calor por convecção. O fludo que atnge a superfíce a estudar entra com um a velocdade ncal (V ) e temperatura ncal ( ) para escoar de forma aleatóra sobre a superfíce. Consderando que a superfíce encontra-se a uma determnada temperatura ( s ), dferente da temperatura do fludo, ocorrerá uma transferênca de calor entre eles, esta vez por convecção. V, q A s, s s X dx Fgura 3 O problema de transferênca por convecção. Consderando que superfíce está a uma temperatura mas alta que o fluído, a densdade de fluxo de calor local pode ser calculada como q' ' h ( s ) (4) Devdo ás condções de escoamento varam de ponto a ponto ao longo da superfíce, a quantdade de calor transferdo também vara em cada ponto. Por sso a relação 4 referenca uma densdade local de transferênca de calor onde h é o coefcente local de convecção. O fluxo de calor total na superfíce pode ser calculado através da ntegração das densdades locas em toda a superfíce.
23 Fone: (48) q ' das h ( s q ' ) da (5) As As s Pode-se defnr um coefcente de convecção médo ( h ) para toda a superfíce e o fluxo de calor pode ser calculado como q h A ( ) s s (6) O coefcente de convecção médo encontra-se relaconado com o coefcente local através da equação h As As h das (7) E no caso de uma placa plana h h dx (8) L Determnar o coefcente de convecção depende de três parâmetros: Propredades do fluído Geometra da superfíce Condção de escoamento Densdade Vscosdade Condutvdade térmca Calor específco Plana Clíndrca Lamnar urbulento Independentes Para o caso da envolvente de uma edfcação o fluído a consderar será sempre o ar atmosférco (sto delmta a faxa de varação das propredades a utlzar) e a geometra das superfíces sempre planas. Já para poder dentfcar a condção de escoamento que pode estar acontecendo na superfíce da envolvente, é necessáro entender o conceto de camada lmte (Fgura 4).
24 Fone: (48) V δ(x) δ(x) δ c δ t Cnétca érmca Fgura 4 Camadas lmtes (cnétca e térmca). Observado a velocdade de escoamento (V) na Fgura 4 as partículas do ar que estão em contato com a superfíce passam a ter velocdade zero e elas nfluencam as camadas adjacentes para retardar o movmento do fluído, até uma dstânca da superfíce (y δ c ) onde o efeto torna-se desprezível. A espessura da camada lmte cnétca é defnda como o valor para o qual V,99 V. Assm, o escoamento é caracterzado por duas regões dferentes, uma prmera onde a superfíce nfluenca as condções de escoamento gerando altos gradentes de velocdade e uma segunda camada externa em que os gradentes são desprezíves devdo à pouca nfluenca da superfíce. A espessura da camada lmte cnétca depende das condções de atrto local e da vscosdade dnâmca do fluído. Mas é mportante destacar que conforme o fludo avança na superfíce os efetos de vscosdade e atrto penetram cada vez mas no escoamento e a camada lmte aumenta. Sempre que exsta uma dferença de temperatura entre a superfíce e o fludo, exstrá uma camada lmte térmca que ndca quanto penetra a nfluênca das condções térmcas na superfíce no escoamento do fludo. Da mesma forma que no caso cnétco, a camada que está em contato com a superfíce adota a temperatura da superfíce e va nfluencar na temperatura das camadas adjacentes até uma dstânca da superfíce (y δ t ) onde o efeto torna-se desprezível. Outro fator mportante para estmar o coefcente de convecção é determnar se a camada lmte cnétca se encontra em regme lamnar ou turbulento (Fgura 5). Para ter uma stuação de fluxo lamnar, é necessáro que o escoamento do fluído seja altamente organzado, sendo possível dentfcar as lnhas de correntes bem defndas. O escoamento em regme turbulento é caracterzado por um movmento altamente rregular na camada lmte, apresentando flutuações de velocdade (tanto em módulo como em sentdo). Essas varações aumentam as taxas de transferênca de calor por convecção (Fgura 5).
25 Fone: (48) Fgura 5 Escoamento lamnar e turbulento na camada lmte para placa plana (INCROPERA E DEWI, 3). Para saber se o escoamento se encontra em regme lamnar ou turbulento é necessáro trabalhar com o grupo de parâmetros admensonas. Eles descrevem os processos na camada lmte. Um resumo dos prncpas parâmetros admensonas encontra-se na abela 3. O número de Reynolds descreve a relação entre o aumento na quantdade de movmento no fluxo (forças de nérca) e as tensões de csalhamento (forças vscosas) no fluído. Ele permte defnr se o escoamento se encontra em regme lamnar ou turbulento de acordo com a relação: 5 Re x < 5 (turbulento) (9) Para valores baxos de Re x as forças vscosas são sufcentemente altas para mpedr que pequenos dstúrbos no fluído tornem o escoamento turbulento. Por outro lado, com o aumento de Re x, os efetos de nérca começam a ter mportânca podendo desenvolver uma condção de turbulênca. abela 3 Prncpas grupos admensonas para transferênca de calor por convecção. Grupo Equação Interpretação Reynolds (Re) ρ V x Razão entre as forças de nércas e vscosas μ Nusselt (Nu) h L Gradente de temperatura λ f admensonal na superfíce Prandlt (Pr) c μ Razão entre as dfusvdades de p,7 momento e térmca λ Grashof (Gr) 3 g β ( s ) L Razão entre as forças de flutuação e vscosas υ
26 Fone: (48) Contudo, pode-se assumr que a transção de lamnar para turbulento ocorre em um ponto crítco (x c ). Essa posção pode ser determnada a partr de um valor representatvo (5 5 ) para o número de Reynolds como x c 5 μ 5 () ρ V 3. FORÇADA A transferênca de calor por convecção forçada é defnda por um escoamento em que o movmento entre o fluído e a superfíce se mantém medante agentes externos (ventlador, bomba e vento) e não pelas forças de empuxo provocadas por gradentes de temperatura no fluído. A partr de um método empírco em que uma placa plana é aquecda com uma resstênca elétrca para manter s > e controlando a velocdade de escoamento (V ) é possível defnr que o número de Nusselt (que contem o coefcente de convecção) pode ser correlaconado como uma função do número de Reynolds e de Prandlt. Para o fluxo lamnar, os coefcentes de convecção local (h x ) e médo ( h ) podem ser estmados a partr das seguntes relações em função do Nusselt local (Nu x ) e Nusselt médo ( Nu ).,33 Re x 3 Nu Pr () x,664 Re L 3 Nu Pr () No caso do fluxo turbulento o coefcente de convecção local pode ser determnado a partr de: 4 5,96 Rex 3 Nu Pr (3) x Para a zona de transção (ou fluxo msto), o coefcente de convecção médo pode ser determnado a partr de: 4 5,37 Re L 3 Nu ( 87) Pr (4) Para calcular o coefcente de convecção recomenda-se utlzar o segunte esquema de resolução:. Identfcar a geometra de escoamento.. Especfcar a temperatura de referênca aproprada para o fluído e estabelecer as propredades do fluído de acordo com a temperatura de referênca. 3. Decdr se o objetvo é determnar um coefcente local ou médo.
27 Fone: (48) Calcular o número de Reynolds para determnar o tpo de fluxo exstente (lamnar ou turbulento). 5. Isolar o coefcente de convecção nas equações NAURAL Nos casos de convecção natural (ou lvre), a troca de calor também acontece entre um sóldo (superfíce plana) e um fludo (ar), mas o movmento do fludo não é forçado externamente por bombas, ventladores mecâncos ou vento. As stuações de convecção natural são orgnadas por duas forças, o peso própro do fludo (campo gravtaconal) e as forças devdas ao gradente de densdade de massa no fludo relaconado com sua varação de temperatura (Fgura 6). Y u s g, ρ Fgura 6 Convecção natural e camada lmte para fluxo vertcal. No exemplo de convecção lvre em placa plana apresentado na Fgura 6, a temperatura da superfíce é maor que a do ar ( s > ). A camada de ar mas próxma à superfíce adota uma temperatura maor que, sto produz uma expansão do fluído, dmnundo sua densdade de massa. Logo, as forças devdas ao gradente de densdade de massa (forças de empuxo) nduzem uma camada lmte de convecção na qual o fludo aquecdo ascende vertcalmente. A convecção lvre também pode se desenvolver com fluxo descendente sempre que s <. Vsto que as taxas de escoamento em convecção lvre são geralmente menores que as de convecção forçada, a taxa de transferênca de calor entre a superfíce e o fluído também é menor. Isto se traduz em que a camada de ar próxma a superfíce apresenta uma nteressante resstênca térmca. Assm, nos sstemas construtvos de baxa resstênca térmca (5 cm de concreto > resstênca térmca,4 m K/W), a camada nterna de ar pode fornecer uma resstênca térmca maor (,5 m K/W). Consderando um fluxo bdmensonal para a transferênca de calor, em regme permanente e com propredades constantes nas quas a força de gravdade atua na dreção negatva de x., a relação que descreve a convecção natural é X
28 Fone: (48) u v ρ ρ u + v g + x y ρ υ y u (5) Em que as varações de velocdades em cada exo (lado esquerdo) são guas as forças de empuxo em que o escoamento se desenvolve pelo gradente de densdade de massa (prmero termo do lado dreto) e as forças de vscosdade (segundo termo do lado dreto). Se consderarmos que o gradente de densdade de massa é devdo exclusvamente às varações de temperatura, o prmero termo do lado dreto pode ser relaconado com o coefcente de expansão térmca volumétrca (β), que representa a medda na qual a densdade de massa vara em resposta a uma varação de temperatura para uma pressão constante. ρ Δρ ρ ρ β (6) ρ p p ρ Δ ρ Da mesma forma que na convecção forçada, na convecção natural exste também um grupo de parâmetros admensonas que descrevem os processos na camada lmte. A partr da admensonalzação da equação 5, sto é x * x/l e y * y/l, é possível obter o número de Grashof (Gr L ). Gr g β ( s υ ) L 3 (7) O número de Grashof tem o mesmo papel na convecção natural que o número de Reynolds na convecção forçada. O número de Grashof representa a relação entre a força de empuxo e as forças vscosas no fluído. Re ynolds forças _ nercas forças _ vscosas Grashof força _ empuxo forças _ vscosas Na equação 5 observa-se que estão sendo consderados os efetos da velocdade (u e v), da força de empuxo ( ρ) e da vscosdade (υ) o que permte estabelecer que a transferênca de calor é da forma Nu L f (Ra L, Gr L, Pr) Para esses casos, é consderado que os efetos de convecção forçada são comparáves aos de convecção natural. Geralmente, os efetos devem ser consderados em conjunto quando Gr L Re L
29 Fone: (48) Podem ser consderados exclusvamente os efetos do escoamento forçado se Gr L Re << L Podem ser consderados exclusvamente os efetos do escoamento natural se Gr L Re >> L Para a geometra de placa plana, a maor parte dos cálculos de engenhara são apropradas as correlações empírcas da forma Nu h L C (8) k n L Ra L Em que n/4 para escoamento lamnar e n/3 para escoamento turbulento. O número de Raylegh (Ra L ) pode ser defndo como 3 g β ( s ) L RaL GrL Pr (9) υ α Para uma placa plana colocada em posção vertcal, as expressões empírcas estmadas a partr da equação 8 são Nu Nu L L / 4,59 RaL 4 < Ra L < 9 (3) / 3, RaL 9 < Ra L < 3 (3) Para uma placa em posção horzontal e com fluxo ascendente ( s > ) Nu Nu L L / 4,54 RaL 4 < Ra L < 7 (3) / 3,5 RaL 7 < Ra L < (33) E para uma placa horzontal com escoamento descendente ( s < ). Nu L / 4,7 RaL 5 < Ra L < (34) 3.3 CÂMARA DE AR VERICAL NÃO VENILADA Para os espaços de ar fechados em componentes vertcas, como pode ser o caso de paredes de tjolo com furos ou de panés de madera, a transferênca de calor nessas câmaras de ar é devda à condutvdade térmca do ar (condução) e aos efetos de convecção entre as superfíces nternas dos componentes e o ar encerrado (Fgura 7).
30 Fone: (48) conv q t hcv+ cd ( ) q t cond L h h cv + cd cv + kar L Fgura 7 Fluxo de calor em câmara vertcal não ventlada. O coefcente de convecção total ( h cv+ cd ) que ntegra os efetos de condução e convecção pode ser estmado a partr das curvas apresentadas na Fgura 8. Observase que para espaços de espessura pequena (L<,5 m), o movmento do ar na câmara é desprezível, sendo a condutvdade térmca do ar o prncpal responsável pela transferênca de calor. h cv+ cd k ar L L (cm) Fgura 8 Coefcente de transferênca de calor para câmara vertcal não ventlada (HAGENOF, ).
31 Fone: (48) EXERCÍCIOS Para reforçar os concetos ntroduzdos sobre convecção, sugere-se que o aluno trabalhe nos seguntes problemas do texto base (INCROPERA e DEWI, 3). Exemplo 6. (págna 54) Exercíco 7. (págna 98) Exercíco 7.3 (págna 98) Exercíco 7.3 (págna 3) Exemplo 9. (págna 379) Exercíco 9.8 (págna 399)
32 Fone: (48) RADIAÇÃO A transferênca de calor por radação é um fenômeno superfcal, da mesma forma que a convecção, mas com a dferença que não é necessáro de um meo materal para realzar as trocas térmcas. odo materal, seja sóldo ou fluído, emte uma radação de calor de acordo com sua temperatura superfcal. No caso da envolvente de edfcações é de nteresse estudar a radação solar ncdente nas fachadas e a troca lquda de radação entre a envolvente e sua vznhança devda à dferença de temperatura entre elas. 4. RADIAÇÃO EM UMA SUPERFÍCIE Para ntroduzr o fenômeno, a Fgura 9 apresenta uma stuação teórca em que um sóldo encontra-se ncalmente a uma temperatura s, mas alta do que a de sua vznhança e entre eles só exste vácuo. O sóldo começará a dmnur sua temperatura até atngr o equlíbro térmco com sua vznhança. Esse resframento é assocado a uma perda de calor através de uma radação emtda na superfíce do sóldo. Por sua vez, a vznhança recebe a radação emtda pelo sóldo, produzndo-se um aumento na temperatura de sua superfíce. q rad lq vácuo vz sóldo sup > vz sup Fgura 9 Radação entre sóldos devda a gradente de temperatura. odo materal que possua uma temperatura superfcal postva e maor que zero (na escala Kelvn), estará emtndo radação radação ndependente do seu estado (sóldo, lqudo ou gás). Mas o foco no estudo das edfcações está nos materas sóldos em que a emssão de calor por radação acontece nas moléculas que se encontram a uma dstânca não superor a μm da superfíce. Este é o motvo pelo qual o fenômeno de radação é consderado um fenômeno superfcal. A radação térmca é caracterzada de acordo com o comprmento de onda para cada período (Fgura ). A undade de comprmento de onda é o mcron ( μm -6 m). A faxa pertnente á transferênca de calor (, μm) nclu uma parcela da radação ultravoleta (UV) e toda a parte vsível e nfravermelha. O tpo de radação vara conforme ao comprmento de onda, que depende da temperatura da superfíce emssora.
33 Fone: (48) vsível Ultravoleta Infravermelha Mcroonda RADIAÇÃO ÉRMICA, Comprmento [μm] Fgura Espectro de radação para transferênca de calor. A radação emtda por qualquer corpo se propaga em todas as dreções possíves e, da mesma forma, a radação ncdente sobre uma superfíce pode provr de dferentes dreções. Esses fatores fazem da radação um fenômeno físco vetoral com efetos dreconas. as efetos podem ser tratados através do conceto de ntensdade de radação. No caso de superfíces planas (como a envolvente), a ntensdade de radação para cada comprmento de onda pode ser defnda como a taxa de energa radante emtda em uma determnada dreção por undade de área de superfíce emssora normal a essa dreção. A ntensdade de radação tem relação então com a radação emtda e a rradação refletda por uma determnada superfíce. A soma das duas é conhecda como radosdade (Fgura ). Emssão (E) Irradação (G) Irradação refletda Radosdade (J E + G ρ) Fgura Radação, rradação e radosdade. O poder emssvo (E) é a quantdade de radação, emtda em todas as dreções, por undade de área de superfíce. A rradação (G) refere-se à radação ncdente em uma superfíce, provenente de todas as dreções. A radosdade (J) então é o total de energa radante que dexa a superfíce, sto é, a soma da parcela emtda mas a rradação refletda (Gρ) de acordo com a refletvdade do materal (ρ).
34 Fone: (48) A defnção das propredades de materas reas é feta a partr de uma comparação com uma superfíce deal conhecda como Corpo Negro. O corpo negro é um emssor e receptor perfeto de radação (refletvdade zero) que possu as seguntes característcas: Para um determnado comprmento de onda (e temperatura), o corpo negro emte mas energa radante que qualquer outra superfíce; A radação emtda é ndependente de qualquer dreção, ou seja, o corpo negro é um emssor dfuso; O corpo negro absorve toda a radação ncdente, ndependente do comprmento de onda e da dreção. O poder emssvo de um corpo negro (E b ) pode ser calculado segundo a Le de Stefan- Boltzmann, smplesmente conhecendo a temperatura superfcal do corpo negro. E b σ 4 (35) σ 5,67-8 [W/m K 4 ] Constante de Stefan-Boltzmann Contnuando com as superfíces reas, elas têm um poder de emssão que depende de sua emssvdade (ε). Isto é, a razão entre a radação emtda pela superfíce e a radação emtda por um corpo negro na mesma temperatura. A emssvdade de metas é sgnfcatvamente menor se comparado com outros materas de construção opacos para uma temperatura de 3 K (abela 4) abela 4 Emssvdade superfcal para materas de construção. Materal Emssvdade (ε) Alumíno poldo,4 Aço lmpo, Concreto,88,93 jolo (vermelho),93,96 Placa de gesso,9,9 Madera,8,9 A Fgura defne a radosdade como a soma da radação emtda e a rradação refletda. Porém, não toda radação ncdente em uma superfíce (rradação) é refletda. No caso de elementos semtransparentes (como vdro), uma parte da radação é absorvda pelo materal, outra parte é transmtda através do materal e outra é refletda (Fgura ). Para o caso de elemento opacos (como paredes, coberturas e psos) não exste transmssão, a rradação só pode ser absorvda ou refletda.
35 Fone: (48) ρ α Irradação τ α Fgura Absortvdade, refletvdade e transmssvdade. A absortvdade (α), a refletvdade (ρ) e a transmssvdade (τ) são valores admensonas relaconados com um determnado comprmento de onda (λ) e seguem o balanço de radação de acordo com a relação αλ + ρλ + τλ (36) É mportante destacar que nos elementos opacos a refletvdade e a absortvdade podem ser tratados como fenômenos de superfíce e estão estretamente relaconados com a percepção de cor. A sensação de cor percebda pelo olho humano é devda à absorção e reflexão de rradação no espectro vsível provenente do sol ou outra fonte de luz artfcal. Entretanto, é mportante evtar confundr este fenômeno do espectro vsual com o resto do espectro de radação térmca (Fgura ). Por enquanto, a emssão e a absorção de radação foram tratados como dos fenômenos separados em que o prmero depende exclusvamente da temperatura superfcal e o segundo da radação ncdente na superfíce. Porém, sob condções de regme permanente, a emssvdade de um corpo é gual a sua absortvdade. Esta relação, conhecda como a Le de Krchhoff, é defnda para um determnado comprmento de onda. ε λ α λ (37) As superfíces que seguem a relação 37 são conhecdas como superfíces cnza (ou cnzentas). Uma convenção normalmente utlzada na área de desempenho térmco de edfcações é se referr exclusvamente à emssvdade do materal em ondas longas (Infravermelho) e à sua absortvdade no espectro de ondas curtas (radação solar ultravoleta + vsível).
36 Fone: (48) RADIAÇÃO ENRE SUPERFÍCIES No capítulo 4. fo explcado o fenômeno de radação em uma únca superfíce. Nesta parte será apresentado o problema de trocas de radação entre duas ou mas superfíces. Essa troca depende da forma, localzação e orentação das superfíces, assm como das suas propredades radantes (emssvdade e absortvdade) e sua temperatura. Consderando que se trabalhará exclusvamente com superfíces de forma plana, é necessáro prmeramente defnr as característcas geométrcas do problema, ntegrando a localzação e orentação das superfíces através de um parâmetro admensonal conhecdo como Fator de Forma (Fgura 3). A n j θ n θ j R da j da j A j Fgura 3 Característcas geométrcas e radação entre duas superfíces. O Fator de Forma (Fj) determna a fração de radação que sa da superfíce e é nterceptada pela superfíce j, de acordo com a relação: cosθ cosθ F j A A A j π R j da da j (38) A partr da defnção de Fator de Forma podem ser estabelecdas quatro relações mportantes A F A F recprocdade j j j N F j j F j conservação de radação para superfíces convexas F j F para superfíces côncavas para superfíces planas
37 Fone: (48) Para estabelecer a geometra de um problema com N superfíces, sera necessáro calcular N Fatores de Forma. Porém, apoando-se nas relações de recprocdade e conservação de radação é possível evtar calcular esses N fatores dretamente, sendo necessáro determnar apenas N (N-)/ fatores dretamente. EXEMPLO 4. Determnar os fatores de forma de duas esferas concêntrcas. N (superfíces) O problema é defndo através de N fatores de forma > N 4 (F F F F ) Porém, utlzando as relações, será necessáro determnar dretamente N ( N ) N ( N ) ( ) fator de forma F (Côncava) F (udo que sa de é nterceptado por ) A (Recprocdade) > F A F F A A F + F (Conservação radação) > F A A Após ter determnado a geometra do problema é necessáro então nclur as propredades radantes e temperatura superfcal dos elementos para calcular as trocas de radação. Em geral, a radosdade que sa de uma superfíce é devda uma rradação refletda e uma emssão de radação por temperatura. Logo, a superfíce que recebe essa radação pode reflet-la e absorve-la. Para facltar uma prmera aproxmação ao fenômeno, as superfíces partcpantes podem ser consderadas como corpos negros. Assm, a reflexão é excluída e toda a energa radante que sa é
38 Fone: (48) resultado da emssão e toda a radação ncdente em uma superfíce é totalmente absorvda. De acordo com a relação estabelecda na Le de Stefan-Boltzmann para corpos negros, a troca radatva líquda entre duas superfíces pode ser defnda como q j 4 4 A F σ ( ) (39) j j E no caso de três ou mas superfíces, a troca líquda de radação entre a superfíce com as superfíces restantes pode ser calculada através de q N j A F j 4 4 σ ( ) (4) j Porém, o conceto de corpo negro representa uma superfíce radante deal que dfclmente pode ser aplcado nas stuações reas. Para sso, nas superfíces que não são negras é necessáro consderar o fenômeno de reflexão superfcal. Esta análse pode ser abordada a partr de uma superfíce que pertence a um ambente convexo (Fgura 4). Sendo a temperatura, emssvdade e área da superfíce é possível calcular o fluxo térmco radatvo líqudo nela. 3 j j+ N A ε Fgura 4 Modelo de ambente para calcular a radação lquda em uma superfíce. Defnndo a taxa líquda como postva quando a superfíce emte radação, o balanço de energa radante na superfíce pode ser representado como a dferença entre a radosdade (sa) e a rradação (entra). q A J G ) (4) ( A radosdade (J) pode ser detalhada como a soma da emssão mas a rradação refletda. J E + ρ G (4) A emssão de uma superfíce cnza é uma parcela da emssão de um corpo negro. E ε (43) E b
39 Fone: (48) E, a partr da Le de Krchhoff, a refletvdade pode ser consderada como o complemento da emssvdade. ρ α ε (44) Substtundo as equações 43 e 44 na equação 4 e resolvendo para G J ε Eb G (45) ε Substtundo a equação 45 no balanço de energa radante 4 q Eb J ( ε )/ A ε (46) Por outro lado, a taxa líquda na superfce pode ser calculada a partr da troca de radosdade com o resto das superfíces consderando o fator de forma entre elas. q N j A F j ( J J ) (47) j Combnando as equações 46 e 47 é possvel obter uma relação para a radosdade na superfíce com o resto das radosdades, nvolucrando os parâmetros conhecdos (A, ε, F j e E b σ 4 ). Eb J ( ε ) / A ε N j A F j ( J J j ) (48) A equação 48 pode ser aplcada a cada uma das superfíces do ambente e agrupadas de forma matrcal para cada radosdade (J) e suas constantes (a e C) que ntengram os parâmetros conhecdos. a a J.. N J a + a N J.. J a + a N NN J.. J N N C C N (49) A solução matrcal separa o sstema de equações 49 em uma matrz de valores numércos [A], um vetor de varaves [J] e um vetor numérco [C]. [ A] a.. an a a.. N a a N.. NN [ J ] J.. J N [ C] C.. C N
40 Fone: (48) Resumndo o sstema de equações a [A] [J] [C] (5) A solução matrcal é obtda multplcando pela dreta os dos lados da equação 5 pela matrz nversa [A] - [J] [A] - [C] (5) Sendo que a matrz nversa é composta por valores numércos. [ A] b.. bn b b.. N b b N.. NN (5) 4.3 EXERCÍCIOS Para reforçar os concetos ntroduzdos sobre radação, sugere-se que o aluno trabalhe nos seguntes problemas do texto base (INCROPERA e DEWI, 3). Exemplo 3.3 (págna 566) Exemplo 3.4 (págna 57) Exercíco 3. (págna 585)
41 Fone: (48) BIBLIOGRAFIA ABN NBR 5-. Desempenho érmco de Edfcações - Parte : Defnções, símbolos e undades. Janero, 3. ABN NBR 5-. Desempenho érmco de Edfcações - Parte : Métodos de cálculo da transmtânca térmca,da capacdade térmca, do atraso térmco e do fator de calor solar de elementos e componentes de edfcações. Janero, 3. ABN NBR 5-3. Desempenho érmco de Edfcações - Parte 3: Zoneamento Boclmátco Braslero e Dretrzes Construtvas para Habtações Unfamlares de Interesse Socal. Janero, 3. INCROPERA, F; DEWI, D. ransferênca de Calor e Massa. Qunta Edção. LC Lvros écncos e Centífcos Edtora S.A. Ro de Janero, p. LAMBERS, R; DURA, L; PEREIRA, F. Efcênca Energétca nas Edfcações. PW Edtores. São Paulo, p. LIRA, I. ransferenca de calor Apuntes de clase (ICM ). Departamento de Ingenería Mecánca y Metalúrgca, PUC. Santago de Chle, 4. 5 p. HAGENOF, C. Introducton to Buldng Physcs. Studentltteratur. Lund, Suéca,. 4 p.
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
7. Resolução Numérica de Equações Diferenciais Ordinárias
 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
Introdução e Organização de Dados Estatísticos
 II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
Física. Física Módulo 1 Vetores, escalares e movimento em 2-D
 Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
Físca Módulo 1 Vetores, escalares e movmento em 2-D Vetores, Escalares... O que são? Para que servem? Por que aprender? Escalar Defnção: Escalar Grandea sem dreção assocada. Eemplos: Massa de uma bola,
ELEMENTOS DE CIRCUITOS
 MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
MINISTÉRIO D EDUCÇÃO SECRETRI DE EDUCÇÃO PROFISSIONL E TECNOLÓGIC INSTITUTO FEDERL DE EDUCÇÃO, CIÊNCI E TECNOLOGI DE SNT CTRIN CMPUS DE SÃO JOSÉ - ÁRE DE TELECOMUNICÇÕES CURSO TÉCNICO EM TELECOMUNICÇÕES
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Física. Setor B. Índice-controle de Estudo. Prof.: Aula 23 (pág. 86) AD TM TC. Aula 24 (pág. 87) AD TM TC. Aula 25 (pág.
 Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
1 Princípios da entropia e da energia
 1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
1 Prncípos da entropa e da energa Das dscussões anterores vmos como o conceto de entropa fo dervado do conceto de temperatura. E esta últma uma conseqüênca da le zero da termodnâmca. Dentro da nossa descrção
Eletricidade 3. Campo Elétrico 8. Energia Potencial Elétrica 10. Elementos de Um Circuito Elétrico 15. Elementos de Um Circuito Elétrico 20
 1 3º Undade Capítulo XI Eletrcdade 3 Capítulo XII Campo Elétrco 8 Capítulo XIII Energa Potencal Elétrca 10 Capítulo XIV Elementos de Um Crcuto Elétrco 15 Capítulo XV Elementos de Um Crcuto Elétrco 20 Questões
1 3º Undade Capítulo XI Eletrcdade 3 Capítulo XII Campo Elétrco 8 Capítulo XIII Energa Potencal Elétrca 10 Capítulo XIV Elementos de Um Crcuto Elétrco 15 Capítulo XV Elementos de Um Crcuto Elétrco 20 Questões
Distribuição de Massa Molar
 Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Radiação Térmica Processos, Propriedades e Troca de Radiação entre Superfícies (Parte 2)
 Radação Térmca Processos, Propredades e Troca de Radação entre Superfíces (Parte ) Obetvo: calcular a troca por radação entre duas ou mas superfíces. Essa troca depende das geometras e orentações das superfíces,
Radação Térmca Processos, Propredades e Troca de Radação entre Superfíces (Parte ) Obetvo: calcular a troca por radação entre duas ou mas superfíces. Essa troca depende das geometras e orentações das superfíces,
Eletricidade 3 Questões do ENEM. 8. Campo Elétrico 11 Questões do ENEM 13. Energia Potencial Elétrica 15 Questões do ENEM 20
 1 4º Undade Capítulo XIII Eletrcdade 3 Questões do ENEM. 8 Capítulo XIV Campo Elétrco 11 Questões do ENEM 13 Capítulo XV Energa Potencal Elétrca 15 Questões do ENEM 20 Capítulo XVI Elementos de Um Crcuto
1 4º Undade Capítulo XIII Eletrcdade 3 Questões do ENEM. 8 Capítulo XIV Campo Elétrco 11 Questões do ENEM 13 Capítulo XV Energa Potencal Elétrca 15 Questões do ENEM 20 Capítulo XVI Elementos de Um Crcuto
14. Correntes Alternadas (baseado no Halliday, 4 a edição)
 14. orrentes Alternadas (baseado no Hallday, 4 a edção) Por que estudar orrentes Alternadas?.: a maora das casas, comérco, etc., são provdas de fação elétrca que conduz corrente alternada (A ou A em nglês):
14. orrentes Alternadas (baseado no Hallday, 4 a edção) Por que estudar orrentes Alternadas?.: a maora das casas, comérco, etc., são provdas de fação elétrca que conduz corrente alternada (A ou A em nglês):
Energia de deformação na flexão
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Energa de deformação na
Aula 7: Circuitos. Curso de Física Geral III F-328 1º semestre, 2014
 Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Sinais Luminosos 2- CONCEITOS BÁSICOS PARA DIMENSIONAMENTO DE SINAIS LUMINOSOS.
 Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Snas Lumnosos 1-Os prmeros snas lumnosos Os snas lumnosos em cruzamentos surgem pela prmera vez em Londres (Westmnster), no ano de 1868, com um comando manual e com os semáforos a funconarem a gás. Só
Rastreando Algoritmos
 Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
Rastreando lgortmos José ugusto aranauskas epartamento de Físca e Matemátca FFCLRP-USP Sala loco P Fone () - Uma vez desenvolvdo um algortmo, como saber se ele faz o que se supõe que faça? esta aula veremos
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Influência dos Procedimentos de Ensaios e Tratamento de Dados em Análise Probabilística de Estrutura de Contenção
 Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Motores síncronos. São motores com velocidade de rotação fixa velocidade de sincronismo.
 Motores síncronos Prncípo de funconamento ão motores com velocdade de rotação fxa velocdade de sncronsmo. O seu prncípo de funconamento está esquematzado na fgura 1.1 um motor com 2 pólos. Uma corrente
Motores síncronos Prncípo de funconamento ão motores com velocdade de rotação fxa velocdade de sncronsmo. O seu prncípo de funconamento está esquematzado na fgura 1.1 um motor com 2 pólos. Uma corrente
Exercícios de Física. Prof. Panosso. Fontes de campo magnético
 1) A fgura mostra um prego de ferro envolto por um fo fno de cobre esmaltado, enrolado mutas vezes ao seu redor. O conjunto pode ser consderado um eletroímã quando as extremdades do fo são conectadas aos
1) A fgura mostra um prego de ferro envolto por um fo fno de cobre esmaltado, enrolado mutas vezes ao seu redor. O conjunto pode ser consderado um eletroímã quando as extremdades do fo são conectadas aos
UTILIZAÇÃO DO MÉTODO DE TAGUCHI NA REDUÇÃO DOS CUSTOS DE PROJETOS. Uma equação simplificada para se determinar o lucro de uma empresa é:
 UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
www.obconcursos.com.br/portal/v1/carreirafiscal
 www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
UNIVERSIDADE PRESBITERIANA MACKENZIE CCSA - Centro de Ciências Sociais e Aplicadas Curso de Economia
 CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
Receptores elétricos. antes de estudar o capítulo PARTE I
 PARTE I Undade B capítulo 10 Receptores elétrcos seções: 101 Receptor Força contraeletromotrz 102 Crcutos gerador-receptor e gerador-receptor-resstor antes de estudar o capítulo Veja nesta tabela os temas
PARTE I Undade B capítulo 10 Receptores elétrcos seções: 101 Receptor Força contraeletromotrz 102 Crcutos gerador-receptor e gerador-receptor-resstor antes de estudar o capítulo Veja nesta tabela os temas
Notas de Aula de Física
 Versão prelmnar 7 de setembro de Notas de Aula de Físca 7. TRABAO E ENERGIA CINÉTICA... MOVIMENTO EM UMA DIMENSÃO COM FORÇA CONSTANTE... TRABAO EXECUTADO POR UMA FORÇA VARIÁVE... Análse undmensonal...
Versão prelmnar 7 de setembro de Notas de Aula de Físca 7. TRABAO E ENERGIA CINÉTICA... MOVIMENTO EM UMA DIMENSÃO COM FORÇA CONSTANTE... TRABAO EXECUTADO POR UMA FORÇA VARIÁVE... Análse undmensonal...
1 a Lei de Kirchhoff ou Lei dos Nós: Num nó, a soma das intensidades de correntes que chegam é igual à soma das intensidades de correntes que saem.
 Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
2 Máquinas de Vetor Suporte 2.1. Introdução
 Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
Máqunas de Vetor Suporte.. Introdução Os fundamentos das Máqunas de Vetor Suporte (SVM) foram desenvolvdos por Vapnk e colaboradores [], [3], [4]. A formulação por ele apresentada se basea no prncípo de
2 CONSIDERAÇÕES TEÓRICAS
 20 2 CONSIDERAÇÕES TEÓRICAS 2.1. Defnção de gás Um gás é defndo como um fludo cujas condções de temperatura e pressão são superores às do ponto crítco, não podendo haver duas fases presentes em um processo,
20 2 CONSIDERAÇÕES TEÓRICAS 2.1. Defnção de gás Um gás é defndo como um fludo cujas condções de temperatura e pressão são superores às do ponto crítco, não podendo haver duas fases presentes em um processo,
Termodinâmica e Termoquímica
 Termodnâmca e Termoquímca Introdução A cênca que trata da energa e suas transformações é conhecda como termodnâmca. A termodnâmca fo a mola mestra para a revolução ndustral, portanto o estudo e compreensão
Termodnâmca e Termoquímca Introdução A cênca que trata da energa e suas transformações é conhecda como termodnâmca. A termodnâmca fo a mola mestra para a revolução ndustral, portanto o estudo e compreensão
As tabelas resumem as informações obtidas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de informações.
 1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
Resoluções dos testes propostos. T.255 Resposta: d O potencial elétrico de uma esfera condutora eletrizada é dado por: Q 100 9 10 Q 1,0 10 9 C
 apítulo da físca apactores Testes propostos ndade apítulo apactores Resoluções dos testes propostos T.55 Resposta: d O potencal elétrco de uma esfera condutora eletrzada é dado por: Vk 0 9 00 9 0,0 0 9
apítulo da físca apactores Testes propostos ndade apítulo apactores Resoluções dos testes propostos T.55 Resposta: d O potencal elétrco de uma esfera condutora eletrzada é dado por: Vk 0 9 00 9 0,0 0 9
Hoje não tem vitamina, o liquidificador quebrou!
 A U A UL LA Hoje não tem vtamna, o lqudfcador quebrou! Essa fo a notíca dramátca dada por Crstana no café da manhã, lgeramente amenzada pela promessa de uma breve solução. - Seu pa dsse que arruma à note!
A U A UL LA Hoje não tem vtamna, o lqudfcador quebrou! Essa fo a notíca dramátca dada por Crstana no café da manhã, lgeramente amenzada pela promessa de uma breve solução. - Seu pa dsse que arruma à note!
RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS
 Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
Defnções RESOLUÇÃO NUMÉRICA DE EQUAÇÕES DIFERENCIAIS Problemas de Valor Incal PVI) Métodos de passo smples Método de Euler Métodos de sére de Talor Métodos de Runge-Kutta Equações de ordem superor Métodos
ESPELHOS E LENTES ESPELHOS PLANOS
 ESPELHOS E LENTES 1 Embora para os povos prmtvos os espelhos tvessem propredades mágcas, orgem de lendas e crendces que estão presentes até hoje, para a físca são apenas superfíces poldas que produzem
ESPELHOS E LENTES 1 Embora para os povos prmtvos os espelhos tvessem propredades mágcas, orgem de lendas e crendces que estão presentes até hoje, para a físca são apenas superfíces poldas que produzem
XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA NOVO MODELO PARA O CÁLCULO DE CARREGAMENTO DINÂMICO DE TRANSFORMADORES
 XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA Versão 1.0 22 a 25 Novembro de 2009 Recfe - PE GRUPO XIII GRUPO DE ESTUDO DE TRANSFORMADORES, REATORES, MATERIAIS E TECNOLOGIAS
XX SNPTEE SEMINÁRIO NACIONAL DE PRODUÇÃO E TRANSMISSÃO DE ENERGIA ELÉTRICA Versão 1.0 22 a 25 Novembro de 2009 Recfe - PE GRUPO XIII GRUPO DE ESTUDO DE TRANSFORMADORES, REATORES, MATERIAIS E TECNOLOGIAS
Lista de Exercícios de Recuperação do 2 Bimestre. Lista de exercícios de Recuperação de Matemática 3º E.M.
 Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
Lsta de Exercícos de Recuperação do Bmestre Instruções geras: Resolver os exercícos à caneta e em folha de papel almaço ou monobloco (folha de fcháro). Copar os enuncados das questões. Entregar a lsta
Estimativa dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro.
 Estmatva dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro. O. L. L. Moraes 1, H. R. da Rocha 2, M. A. Faus da Slva Das 2, O Cabral 3 1 Departamento
Estmatva dos fluxos turbulentos de calor sensível, calor latente e CO 2, sobre cana-de-açúcar, pelo método do coespectro. O. L. L. Moraes 1, H. R. da Rocha 2, M. A. Faus da Slva Das 2, O Cabral 3 1 Departamento
(note que não precisa de resolver a equação do movimento para responder a esta questão).
 Mestrado Integrado em Engenhara Aeroespacal Mecânca e Ondas 1º Ano -º Semestre 1º Teste 31/03/014 18:00h Duração do teste: 1:30h Lea o enuncado com atenção. Justfque todas as respostas. Identfque e numere
Mestrado Integrado em Engenhara Aeroespacal Mecânca e Ondas 1º Ano -º Semestre 1º Teste 31/03/014 18:00h Duração do teste: 1:30h Lea o enuncado com atenção. Justfque todas as respostas. Identfque e numere
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Capítulo 1. O plano complexo. 1.1. Introdução. Os números complexos começaram por ser introduzidos para dar sentido à 2
 Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Capítulo O plano compleo Introdução Os números compleos começaram por ser ntrodudos para dar sentdo à resolução de equações polnomas do tpo Como os quadrados de números reas são sempre maores ou guas a
Capítulo. Associação de resistores. Resoluções dos exercícios propostos. P.135 a) R s R 1 R 2 R s 4 6 R s 10 Ω. b) U R s i U 10 2 U 20 V
 apítulo 7 da físca Exercícos propostos Undade apítulo 7 ssocação de resstores ssocação de resstores esoluções dos exercícos propostos 1 P.15 a) s 1 s 6 s b) U s U 10 U 0 V c) U 1 1 U 1 U 1 8 V U U 6 U
apítulo 7 da físca Exercícos propostos Undade apítulo 7 ssocação de resstores ssocação de resstores esoluções dos exercícos propostos 1 P.15 a) s 1 s 6 s b) U s U 10 U 0 V c) U 1 1 U 1 U 1 8 V U U 6 U
Introdução à condução de calor estacionária
 Introdução à condução de calor estacionária Exercício 1 - O telhado de uma casa com aquecimento elétrico tem 6m de comprimento, 8m de largura e 0, 25m de espessura e é feito de uma camada plana de concreto
Introdução à condução de calor estacionária Exercício 1 - O telhado de uma casa com aquecimento elétrico tem 6m de comprimento, 8m de largura e 0, 25m de espessura e é feito de uma camada plana de concreto
REGRESSÃO LOGÍSTICA. Seja Y uma variável aleatória dummy definida como:
 REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
REGRESSÃO LOGÍSTCA. ntrodução Defnmos varáves categórcas como aquelas varáves que podem ser mensurados usando apenas um número lmtado de valores ou categoras. Esta defnção dstngue varáves categórcas de
Estimativa da Incerteza de Medição da Viscosidade Cinemática pelo Método Manual em Biodiesel
 Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
Material de apoio para as aulas de Física do terceiro ano
 COLÉGIO LUTERANO CONCÓRDIA Concórda, desenvolvendo conhecmento com sabedora Mantenedora: Comundade Evangélca Luterana Crsto- Nteró Materal de apoo para as aulas de Físca do tercero ano Professor Rafael
COLÉGIO LUTERANO CONCÓRDIA Concórda, desenvolvendo conhecmento com sabedora Mantenedora: Comundade Evangélca Luterana Crsto- Nteró Materal de apoo para as aulas de Físca do tercero ano Professor Rafael
Trabalho e Energia. Definimos o trabalho W realizado pela força sobre uma partícula como o produto escalar da força pelo deslocamento.
 Trabalho e Energa Podemos denr trabalho como a capacdade de produzr energa. Se uma orça eecutou um trabalho sobre um corpo ele aumentou a energa desse corpo de. 1 OBS: Quando estudamos vetores vmos que
Trabalho e Energa Podemos denr trabalho como a capacdade de produzr energa. Se uma orça eecutou um trabalho sobre um corpo ele aumentou a energa desse corpo de. 1 OBS: Quando estudamos vetores vmos que
Suporte Básico para Sistemas de Tempo Real
 Suporte Básco para Sstemas de Tempo Real Escalonamento e Comuncação Sldes elaborados por George Lma, com atualzações realzadas por Ramundo Macêdo Suporte Básco para Sstemas de Tempo-Real Escalonamento
Suporte Básco para Sstemas de Tempo Real Escalonamento e Comuncação Sldes elaborados por George Lma, com atualzações realzadas por Ramundo Macêdo Suporte Básco para Sstemas de Tempo-Real Escalonamento
ELETRICIDADE E MAGNETISMO
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Professor: Renato Mederos ELETRICIDADE E MAGNETISMO NOTA DE AULA III Goâna - 2014 CORRENTE ELÉTRICA Estudamos anterormente
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Professor: Renato Mederos ELETRICIDADE E MAGNETISMO NOTA DE AULA III Goâna - 2014 CORRENTE ELÉTRICA Estudamos anterormente
CQ110 : Princípios de FQ
 CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
Análise Econômica da Aplicação de Motores de Alto Rendimento
 Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Aula 03 Erros experimentais Incerteza. Aula 03 Prof. Valner Brusamarello
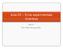 Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
ANEXO II METODOLOGIA E CÁLCULO DO FATOR X
 ANEXO II Nota Técnca nº 256/2009-SRE/ANEEL Brasíla, 29 de julho de 2009 METODOLOGIA E ÁLULO DO FATOR X ANEXO II Nota Técnca n o 256/2009 SRE/ANEEL Em 29 de julho de 2009. Processo nº 48500.004295/2006-48
ANEXO II Nota Técnca nº 256/2009-SRE/ANEEL Brasíla, 29 de julho de 2009 METODOLOGIA E ÁLULO DO FATOR X ANEXO II Nota Técnca n o 256/2009 SRE/ANEEL Em 29 de julho de 2009. Processo nº 48500.004295/2006-48
Ciências Física e química
 Dretos Exclusvos para o autor: rof. Gl Renato Rbero Gonçalves CMB- Colégo Mltar de Brasíla Reservados todos os dretos. É probda a duplcação ou reprodução desta aula, com ou sem modfcações (plágo) no todo
Dretos Exclusvos para o autor: rof. Gl Renato Rbero Gonçalves CMB- Colégo Mltar de Brasíla Reservados todos os dretos. É probda a duplcação ou reprodução desta aula, com ou sem modfcações (plágo) no todo
Associação de resistores em série
 Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
Assocação de resstores em sére Fg.... Na Fg.. está representada uma assocação de resstores. Chamemos de I, B, C e D. as correntes que, num mesmo nstante, passam, respectvamente pelos pontos A, B, C e D.
Experiência V (aulas 08 e 09) Curvas características
 Experênca (aulas 08 e 09) Curvas característcas 1. Objetvos 2. Introdução 3. Procedmento expermental 4. Análse de dados 5. Referêncas 1. Objetvos Como no expermento anteror, remos estudar a adequação de
Experênca (aulas 08 e 09) Curvas característcas 1. Objetvos 2. Introdução 3. Procedmento expermental 4. Análse de dados 5. Referêncas 1. Objetvos Como no expermento anteror, remos estudar a adequação de
INTRODUÇÃO AO CÁLCULO DE ERROS NAS MEDIDAS DE GRANDEZAS FÍSICAS
 Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
5.1 Seleção dos melhores regressores univariados (modelo de Índice de Difusão univariado)
 5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
MAE5778 - Teoria da Resposta ao Item
 MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
MAE5778 - Teora da Resposta ao Item Fernando Henrque Ferraz Perera da Rosa Robson Lunard 1 de feverero de 2005 Lsta 2 1. Na Tabela 1 estão apresentados os parâmetros de 6 tens, na escala (0,1). a b c 1
ÍNDICE NOTA INTRODUTÓRIA
 OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
Controle Estatístico de Qualidade. Capítulo 8 (montgomery)
 Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
Controle Estatístco de Qualdade Capítulo 8 (montgomery) Gráfco CUSUM e da Méda Móvel Exponencalmente Ponderada Introdução Cartas de Controle Shewhart Usa apenas a nformação contda no últmo ponto plotado
01. Em porcentagem das emissões totais de gases do efeito estufa, o Brasil é o quarto maior poluidor, conforme a tabela abaixo:
 PROCESSO SELETIVO 7 RESOLUÇÃO MATEMÁTICA Rosane Soares Morera Vana, Luz Cláudo Perera, Lucy Tem Takahash, Olímpo Hrosh Myagak QUESTÕES OBJETIVAS Em porcentagem das emssões totas de gases do efeto estufa,
PROCESSO SELETIVO 7 RESOLUÇÃO MATEMÁTICA Rosane Soares Morera Vana, Luz Cláudo Perera, Lucy Tem Takahash, Olímpo Hrosh Myagak QUESTÕES OBJETIVAS Em porcentagem das emssões totas de gases do efeto estufa,
Palavras-chaves detector infravermelho, transmissão atmosférica, atenuação. I. INTRODUÇÃO
 Atenuação atmosférca da Radação Infravermelha: Influênca de elevados níves hgrométrcos no desempenho operaconal de mísses ar-ar. André Gustavo de Souza Curtyba, Rcardo A. Tavares Santos, Fabo Durante P.
Atenuação atmosférca da Radação Infravermelha: Influênca de elevados níves hgrométrcos no desempenho operaconal de mísses ar-ar. André Gustavo de Souza Curtyba, Rcardo A. Tavares Santos, Fabo Durante P.
Despacho Econômico de. Sistemas Termoelétricos e. Hidrotérmicos
 Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Física. Setor A. Índice-controle de Estudo. Prof.: Aula 25 (pág. 86) AD TM TC. Aula 26 (pág. 86) AD TM TC. Aula 27 (pág.
 Físca Setor Prof.: Índce-controle de studo ula 25 (pág. 86) D TM TC ula 26 (pág. 86) D TM TC ula 27 (pág. 87) D TM TC ula 28 (pág. 87) D TM TC ula 29 (pág. 90) D TM TC ula 30 (pág. 90) D TM TC ula 31 (pág.
Físca Setor Prof.: Índce-controle de studo ula 25 (pág. 86) D TM TC ula 26 (pág. 86) D TM TC ula 27 (pág. 87) D TM TC ula 28 (pág. 87) D TM TC ula 29 (pág. 90) D TM TC ula 30 (pág. 90) D TM TC ula 31 (pág.
Consideraremos agora, uma de cada vez, as equivalentes angulares das grandezas de posição, deslocamento, velocidade e aceleração.
 CAPÍTULO 5 77 5.1 Introdução A cnemátca dos corpos rígdos trata dos movmentos de translação e rotação. No movmento de translação pura todas as partes de um corpo sofrem o mesmo deslocamento lnear. Por
CAPÍTULO 5 77 5.1 Introdução A cnemátca dos corpos rígdos trata dos movmentos de translação e rotação. No movmento de translação pura todas as partes de um corpo sofrem o mesmo deslocamento lnear. Por
Probabilidade e Estatística. Correlação e Regressão Linear
 Probabldade e Estatístca Correlação e Regressão Lnear Correlação Este uma correlação entre duas varáves quando uma delas está, de alguma forma, relaconada com a outra. Gráfco ou Dagrama de Dspersão é o
Probabldade e Estatístca Correlação e Regressão Lnear Correlação Este uma correlação entre duas varáves quando uma delas está, de alguma forma, relaconada com a outra. Gráfco ou Dagrama de Dspersão é o
Departamento de Informática. Modelagem Analítica. Modelagem Analítica do Desempenho de Sistemas de Computação. Disciplina: Medida de Probabilidade
 Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
Departaento de Inforátca Dscplna: do Desepenho de Ssteas de Coputação Medda de Probabldade Prof. Sérgo Colcher colcher@nf.puc-ro.br Teora da Probabldade Modelo ateátco que perte estudar, de fora abstrata,
MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE
 MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE R. L. S. CANEVESI 1, C. L. DIEL 2, K. A. SANTOS 1, C. E. BORBA 1, F. PALÚ 1, E. A. DA SILVA 1 1 Unversdade Estadual
MODELAGEM MATEMÁTICA DO PROCESSO DE EVAPORAÇÃO MULTI-EFEITO NA INDÚSTRIA DE PAPEL E CELULOSE R. L. S. CANEVESI 1, C. L. DIEL 2, K. A. SANTOS 1, C. E. BORBA 1, F. PALÚ 1, E. A. DA SILVA 1 1 Unversdade Estadual
O migrante de retorno na Região Norte do Brasil: Uma aplicação de Regressão Logística Multinomial
 O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
O mgrante de retorno na Regão Norte do Brasl: Uma aplcação de Regressão Logístca Multnomal 1. Introdução Olavo da Gama Santos 1 Marnalva Cardoso Macel 2 Obede Rodrgues Cardoso 3 Por mgrante de retorno,
Professor Mauricio Lutz CORRELAÇÃO
 Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
PROVA DE MATEMÁTICA DO VESTIBULAR 2013 DA UNICAMP-FASE 1. RESOLUÇÃO: PROFA. MARIA ANTÔNIA C. GOUVEIA
 PROVA DE MATEMÁTICA DO VESTIBULAR 03 DA UNICAMP-FASE. PROFA. MARIA ANTÔNIA C. GOUVEIA QUESTÃO 37 A fgura abaxo exbe, em porcentagem, a prevsão da oferta de energa no Brasl em 030, segundo o Plano Naconal
PROVA DE MATEMÁTICA DO VESTIBULAR 03 DA UNICAMP-FASE. PROFA. MARIA ANTÔNIA C. GOUVEIA QUESTÃO 37 A fgura abaxo exbe, em porcentagem, a prevsão da oferta de energa no Brasl em 030, segundo o Plano Naconal
Apostila de Estatística Curso de Matemática. Volume II 2008. Probabilidades, Distribuição Binomial, Distribuição Normal. Prof. Dr. Celso Eduardo Tuna
 Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Esta aula: Conceitos fundamentais: bipolos, tensão e corrente Geradores de tensão e de corrente Convenções Transferência de energia Resistores
 Esta aula: Concetos fundamentas: bpolos, tensão e corrente Geradores de tensão e de corrente Conenções Transferênca de energa Resstores TEORA DE CRCUTOS Crcuto elétrco: Coleção de dspostos elétrcos conectados
Esta aula: Concetos fundamentas: bpolos, tensão e corrente Geradores de tensão e de corrente Conenções Transferênca de energa Resstores TEORA DE CRCUTOS Crcuto elétrco: Coleção de dspostos elétrcos conectados
3.1. Conceitos de força e massa
 CAPÍTULO 3 Les de Newton 3.1. Concetos de força e massa Uma força representa a acção de um corpo sobre outro,.e. a nteracção físca entre dos corpos. Como grandeza vectoral que é, só fca caracterzada pelo
CAPÍTULO 3 Les de Newton 3.1. Concetos de força e massa Uma força representa a acção de um corpo sobre outro,.e. a nteracção físca entre dos corpos. Como grandeza vectoral que é, só fca caracterzada pelo
Controlo Metrológico de Contadores de Gás
 Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Prof. Antônio Carlos Fontes dos Santos. Aula 1: Divisores de tensão e Resistência interna de uma fonte de tensão
 IF-UFRJ Elementos de Eletrônca Analógca Prof. Antôno Carlos Fontes dos Santos FIW362 Mestrado Profssonal em Ensno de Físca Aula 1: Dvsores de tensão e Resstênca nterna de uma fonte de tensão Este materal
IF-UFRJ Elementos de Eletrônca Analógca Prof. Antôno Carlos Fontes dos Santos FIW362 Mestrado Profssonal em Ensno de Físca Aula 1: Dvsores de tensão e Resstênca nterna de uma fonte de tensão Este materal
Material de apoio para as aulas de Física do terceiro ano
 COLÉGIO LUTERANO CONCÓRDIA 67 Anos Educando com o Coração Mantenedora: Comundade Evangélca Luterana Crsto- Nteró Materal de apoo para as aulas de Físca do tercero ano Professor Rafael Frank de Rodrgues
COLÉGIO LUTERANO CONCÓRDIA 67 Anos Educando com o Coração Mantenedora: Comundade Evangélca Luterana Crsto- Nteró Materal de apoo para as aulas de Físca do tercero ano Professor Rafael Frank de Rodrgues
2 - Análise de circuitos em corrente contínua
 - Análse de crcutos em corrente contínua.-corrente eléctrca.-le de Ohm.3-Sentdos da corrente: real e convenconal.4-fontes ndependentes e fontes dependentes.5-assocação de resstêncas; Dvsores de tensão;
- Análse de crcutos em corrente contínua.-corrente eléctrca.-le de Ohm.3-Sentdos da corrente: real e convenconal.4-fontes ndependentes e fontes dependentes.5-assocação de resstêncas; Dvsores de tensão;
Sistemas de Filas: Aula 5. Amedeo R. Odoni 22 de outubro de 2001
 Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Análise de Regressão. Profa Alcione Miranda dos Santos Departamento de Saúde Pública UFMA
 Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Redução do consumo de energia de um equipamento de frio
 Faculdade de Engenhara da Unversdade do Porto Redução do consumo de energa de um equpamento de fro Nuno Mguel Rocha Mesquta VERSÃO PROVISÓRIA Dssertação/Relatóro de Projecto realzada(o) no âmbto do Mestrado
Faculdade de Engenhara da Unversdade do Porto Redução do consumo de energa de um equpamento de fro Nuno Mguel Rocha Mesquta VERSÃO PROVISÓRIA Dssertação/Relatóro de Projecto realzada(o) no âmbto do Mestrado
Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Cálculo do Conceito Preliminar de Cursos de Graduação
 Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Nesse circuito, os dados indicam que a diferença de potencial entre os pontos X e Y, em volts, é a) 3,3 c) 10 e) 18 b) 6,0 d) 12.
 Aprmorando os Conhecmentos de Eletrcdade Lsta 7 Assocação de esstores Prof.: Célo Normando. (UNIFO-97) O resstor, que tem a curva característca representada no gráfco abao, é componente do crcuto representado
Aprmorando os Conhecmentos de Eletrcdade Lsta 7 Assocação de esstores Prof.: Célo Normando. (UNIFO-97) O resstor, que tem a curva característca representada no gráfco abao, é componente do crcuto representado
Universidade do Estado do Rio de Janeiro Instituto de Matemática e Estatística Econometria
 Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
Unversdade do Estado do Ro de Janero Insttuto de Matemátca e Estatístca Econometra Revsão de modelos de regressão lnear Prof. José Francsco Morera Pessanha professorjfmp@hotmal.com Regressão Objetvo: Estabelecer
Y X Baixo Alto Total Baixo 1 (0,025) 7 (0,175) 8 (0,20) Alto 19 (0,475) 13 (0,325) 32 (0,80) Total 20 (0,50) 20 (0,50) 40 (1,00)
 Bussab&Morettn Estatístca Básca Capítulo 4 Problema. (b) Grau de Instrução Procedênca º grau º grau Superor Total Interor 3 (,83) 7 (,94) (,) (,33) Captal 4 (,) (,39) (,) (,3) Outra (,39) (,7) (,) 3 (,3)
Bussab&Morettn Estatístca Básca Capítulo 4 Problema. (b) Grau de Instrução Procedênca º grau º grau Superor Total Interor 3 (,83) 7 (,94) (,) (,33) Captal 4 (,) (,39) (,) (,3) Outra (,39) (,7) (,) 3 (,3)
PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA
 658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
658 Gaudo & Zandonade Qum. Nova Qum. Nova, Vol. 4, No. 5, 658-671, 001. Dvulgação PROPOSIÇÃO, VALIDAÇÃO E ANÁLISE DOS MODELOS QUE CORRELACIONAM ESTRUTURA QUÍMICA E ATIVIDADE BIOLÓGICA Anderson Coser Gaudo
Universidade Federal do Paraná
 Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Problema do fechamento
Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Problema do fechamento
OTIMIZAÇÃO DO SERVIÇO DE RESERVA GIRANTE EM SISTEMAS HIDROELÉTRICOS. Thales Sousa * José Antônio Jardini Mário Masuda Rodrigo Alves de Lima
 SNPEE SEMINÁRIO NACIONAL DE PRODUÇÃO E RANSMISSÃO DE ENERGIA ELÉRICA GGH - 33 6 a 2 Outubro de 2005 Curtba - Paraná GRUPO I GRUPO DE ESUDO DE GERAÇÃO HIDRÁULICA - GGH OIMIZAÇÃO DO SERVIÇO DE RESERVA GIRANE
SNPEE SEMINÁRIO NACIONAL DE PRODUÇÃO E RANSMISSÃO DE ENERGIA ELÉRICA GGH - 33 6 a 2 Outubro de 2005 Curtba - Paraná GRUPO I GRUPO DE ESUDO DE GERAÇÃO HIDRÁULICA - GGH OIMIZAÇÃO DO SERVIÇO DE RESERVA GIRANE
