RM 68 INCERTEZA DE MEDIÇÃO: GUIA PRÁTICO DO AVALIADOR DE LABORATÓRIOS SUMÁRIO 1 OBJETIVO E CAMPO DE APLICAÇÃO 2 REFERÊNCIAS 3 DEFINIÇÕES 4 METODOLOGIA
|
|
|
- Rosângela Fernanda Caires Carreira
- 8 Há anos
- Visualizações:
Transcrição
1 RM 68 INCERTEZA DE MEDIÇÃO: GUIA PRÁTICO DO AVALIADOR DE LABORATÓRIOS PROCEDIMENTO DO SISTEMA DE GESTÃO DA QUALIDADE REVISÃO: 05 ABR/013 SUMÁRIO 1 OBJETIVO E CAMPO DE APLICAÇÃO REFERÊNCIAS 3 DEFINIÇÕES 4 METODOLOGIA 1 OBJETIVO E CAMPO DE APLICAÇÃO O presente documento estabelece crtéros e orentações aos avaladores da Rede Metrológca RS quanto à avalação da ncerteza de medção em laboratóros reconhecdos ou postulantes ao reconhecmento de competênca pela Rede Metrológca RS segundo a NBR ISO/IEC Este documento não deve ser entenddo como um substtuto ao Gua para a Expressão da Incerteza de Medção (GUM), que é consderado o método nternaconal de referênca para a expressão da ncerteza de medção. O presente documento vsa a fornecer orentações complementares e a drmr eventuas dúvdas dos avaladores de laboratóros da Rede Metrológca RS, quando da realzação de avalações. REFERÊNCIAS ALA. G108 - Gudelnes for Estmatng Uncertanty for Mcrobologcal Countng Methods. 1ª edção, 007. Dsponível em: ABNT/INMETRO. Gua para a Expressão da Incerteza de Medção (GUM). Tercera edção braslera em língua portuguesa. Ro de Janero: ABNT, INMETRO, p. EURACHEM/CITAC. Quantfyng Uncertanty n Analytcal Measurement. ª ed., 000. Dsponível em: EURACHEM/CITAC. Measurement uncertanty arsng from samplng. EURACHEM, CITAC, EUROLAB, Nordtest, UK RSC AMC. 1ª ed., 007. Dsponível em: European Co-operaton for Acredtaton (EA). EA-4/0 Expresson of the Uncertanty of Measurement n Calbraton p. Dsponível em: European Co-operaton for Acredtaton (EA). EA-4/16 EA Gudelnes on the Expresson of the Uncertanty n Quanttatve Testng p. Dsponível em: INMETRO. Vocabuláro nternaconal de termos fundamentas e geras de metrologa (VIM): portara INMETRO nº 09 de INMETRO, SENAI/DN. 5ª edção. Ro de Janero: Ed. SENAI, 007. REDE METROLÓGICA RS Págna 1 de 3
2 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 INMETRO. DOQ-CGCRE Orentação sobre a valdação de métodos de ensaos químcos. INMETRO. DOQ-CGCRE Orentações para a expressão da melhor capacdade de medção nos escopos de acredtação de laboratóros de calbração. INMETRO. DOQ-CGCRE Orentação para realzação de calbração de meddores analógcos de pressão. INMETRO. NIT-DICLA-01 Expressão da Incerteza de Medção. IPAC. OGC005 - Gua para a Estmatva de Incertezas em Ensaos Mcrobológcos. Revsão de janero de 006. Dsponível em: IPAC. OGC007 - Gua para a Quantfcação de Incerteza em Ensaos Químcos. Revsão de janero de 007. Dsponível em: ISO. ISO Accuracy (trueness and precson) of measurement methods and results. ISO, NORDTEST. Uncertanty from Samplng: A Nordtest handbook for samplng planners on samplng qualty assurance and uncertanty estmaton. 1ª ed., 007. Dsponível em: UKAS. M The Expresson of Uncertanty and Confdence n Measurement. UKAS, ª Edção, 007. Dsponível em: RM 0 PROCEDIMENTO PARA RECONHECIMENTO DE COMPETÊNCIA DE LABORATÓRIOS RM 53 ORIENTAÇÕES SOBRE DECLARAÇÃO DA INCERTEZA DE MEDIÇÃO EM METROLOGIA DIMENSIONAL RM 55 ORIENTAÇÕES SOBRE DECLARAÇÃO DA INCERTEZA DE MEDIÇÃO NA ÁREA DE TORQUE RM 59 POLÍTICA PARA A IMPLEMENTAÇÃO DA INCERTEZA DE MEDIÇÃO EM LABORATÓRIOS DE ENSAIO FR 53 CHECK-LIST PARA AVALIAÇÃO DA INCERTEZA DE MEDIÇÃO 3 DEFINIÇÕES As defnções constantes no GUM e no VIM se aplcam, em especal: Incerteza de medção: parâmetro, assocado ao resultado da medção, que caracterza a dspersão dos valores que podem ser fundamentadamente atrbuídos a um mensurando (ABNT/INMETRO, 003). REDE METROLÓGICA RS Págna de 3
3 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev METODOLOGIA 4.1 O que é ncerteza? A defnção formal do GUM para ncerteza de medção traz város pontos a destacar. Prmeramente, ressalta-se que a ncerteza está relaconada a um valor de medção, que é o resultado da medção, e não ao valor verdadero do mensurando, o qual na prátca não é conhecdo. O resultado da medção é apenas a melhor estmatva de tal valor verdadero e, na ausênca de efetos sstemátcos, geralmente é obtdo pela méda artmétca de N medções repetdas do mesmo mensurando. O segundo ponto a destacar é que a ncerteza caracterza uma faxa de dspersão ou ntervalo, e não um valor pontual. Nesse sentdo, a ncerteza não deve ser confundda com erro, pos esse últmo é um valor pontual e não uma faxa e usualmente pode ser corrgdo, quando aplcado um fator de correção adequado. Já a ncerteza é a dúvda remanescente assocada ao resultado da medção. Ela mede o grau de desconhecmento sobre aqulo que está sendo meddo. Por fm, cabe ressaltar que a ncerteza corresponde a uma faxa de valores que podem ser atrbuídos fundamentadamente ao mensurando, sto é, de uma forma fundamentada e realsta, não devendo ser entendda como uma faxa de segurança. Ou seja, a ncerteza não deve, por um lado, ser subestmada e, por outro, tampouco deve ser sobreestmada. Exemplo 01: suponha que o dâmetro de uma peça medda por um laboratóro através de uma méda de observações repetdas seja de 10,3 mm, com ncerteza de 0,03 mm (dgamos que esse valor de ncerteza tenha sdo calculado pelo laboratóro), para uma probabldade de abrangênca de 95,45%. Ou seja, o dâmetro da peça será (10,3 ± 0,03) mm. Em outras palavras, sso quer dzer que, com 95,45% de probabldade, o ntervalo de ncerteza que va desde 10,9 mm até 10,35 mm compreenderá o valor do dâmetro da peça e que a melhor estmatva para esse dâmetro é de 10,3 mm. 4. Importânca e mpacto da ncerteza Como um resultado de medção nada mas é do que meramente uma estmatva do valor verdadero do mensurando, a ncerteza torna-se necessára para expressar o grau de dúvda assocado ao resultado da medção. Dessa forma, a ncerteza é fundamental em dversas stuações, tas como: a) na calbração de equpamentos, nstrumentos e padrões, para verfcar se os mesmos encontram-se dentro das tolerâncas defndas; b) na área de ensaos, para verfcar se o resultado do ensao pode ser aprovado ou não; c) na área legal, para verfcar conformdade de resultados de medções com lmtes de tolerâncas legas; d) no controle de rscos assocados à tomada de decsão de aprovar ou rejetar uma amostra. REDE METROLÓGICA RS Págna 3 de 3
4 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Adconalmente, a ncerteza de medção pode ser um dferencal compettvo, pos o clente tende a buscar aquele laboratóro que tenha melhor qualdade na sua medda e, portanto, a menor ncerteza. Assm, a ncerteza se consttu como um parâmetro fundamental que ndca a qualdade da medção. A ncerteza possblta a comparabldade das medções e é partcularmente útl ao clente na tomada de decsões. Quando há um lmte de tolerânca máxmo ou mínmo para o mensurando, seja ele estabelecdo por uma legslação ou de alguma outra forma, a ncerteza torna-se mprescndível para a nterpretação correta do resultado da medção. Exemplo 0: uma legslação estabelece que o teor máxmo de contamnantes em uma amostra de pescado é de 0,00 mg/g. Se o resultado de uma medção for próxmo a esse lmte, por exemplo, 0,197 mg/g, surge uma dúvda: o nível de contamnantes na amostra, de fato, atende à legslação, ou ele está acma do permtdo, uma vez que o resultado é apenas uma estmatva e esse apresenta uma ncerteza? A Fgura 1 lustra tal stuação. Lmte Máxmo Permtdo de 0,00 mg/g Probabldade de não atender à legslação Resultado da medção de 0,197 mg/g Fgura 1. Impacto da ncerteza na decsão de aprovar ou rejetar uma amostra Levando em consderação a ncerteza, o usuáro dessa medção pode avalar qual a probabldade do valor de contamnantes no pescado estar acma do lmte máxmo permtdo pela legslação. Por exemplo, se a ncerteza expandda da medção for de U = 0,004 mg/g, para uma probabldade de abrangênca de 95,45% de uma dstrbução normal, com fator de abrangênca k =, a probabldade do nível de contamnantes não atender à legslação será conforme segue: Prmero transforma-se a varável para o escore-z: Z X x 0,00 0,197 (1) 1,5 u ( y) 0,004 / c Onde X é o lmte superor da legslação, x é o resultado da medção e u c (y) é o valor da ncerteza padrão combnada da medção, equvalente a uma medda de dspersão de um desvo padrão, obtda por U / k. E em seguda, calcula-se a probabldade da varável assumr um valor padronzado maor do que o de escore-z calculado: REDE METROLÓGICA RS Págna 4 de 3
5 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 P(X > z) = 1 P(X z) = 1 P(X 1,5) = 1 0,933 = 0,067 () Ou seja, há uma chance de aproxmadamente 7% do pescado não atender ao lmte máxmo permtdo de contamnantes. Este tpo de nformação possblta ao usuáro dessa medção avalar e defnr um rsco acetável na sua tomada de decsão. Assm, se ele decdr consderar a amostra como aprovada, saberá que estará ncorrendo em um rsco de 7% de ter tomado uma decsão errada, ou seja, aprovar uma amostra quando na verdade devera reprová-la. Esse conceto de avalação de rsco se estende a váras stuações e só pode ser conhecdo caso a ncerteza também a seja. Dessa forma, se a ncerteza não tver sdo expressada de uma manera adequada, a nterpretação do resultado também será prejudcada, podendo acarretar em desperdícos e retrabalhos para o usuáro da medção. A ncerteza de medção também é uma ferramenta de valosa utldade para o laboratóro, no sentdo de possbltar a dentfcação dos fatores que mas nfluencam no resultado do ensao/calbração e, dessa forma, mplementar controles adequados para a garanta da qualdade e melhora contínua. Tendo em vsta o exposto, a cudadosa avalação da ncerteza de medção por parte do avalador da Rede Metrológca RS torna-se um fator fundamental na avalação da competênca técnca de laboratóros de calbração e ensao. 4.3 Breve revsão sobre o método de expressão de ncerteza de medção O objetvo desse tópco é realzar, de uma manera sucnta, uma revsão sobre o método de expressão da ncerteza 1 descrto pelo GUM, que é a referênca nternaconal na área. Maores detalhes podem ser consultados no referdo documento e nas demas publcações ndcadas nas referêncas. Os passos do método podem ser resumdos no fluxograma da Fgura. 1 O termo expressão da ncerteza, conforme utlzado pelo GUM, fo empregado neste documento no seu sentdo mas amplo, o qual compreende desde o estudo das componentes de ncerteza e a sua estmatva, até a sua apresentação. Optou-se por não utlzar o termo avalação da ncerteza porque esse podera ser confunddo com a atvdade de avalação realzada pelo avalador da Rede Metrológca RS. REDE METROLÓGICA RS Págna 5 de 3
6 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Passo 1: defnr modelo matemátco da medção Passo : defnr as componentes de ncerteza Todas as componentes de ncerteza estão representadas no modelo matemátco da medção? Não Sm Passo 3: estmar as ncertezas padrão Passo 4: calcular os coefcentes de sensbldade Passo 5: avalar possíves correlações Exstem correlações entre as componentes de ncerteza? Sm Não Passo 6: obter a ncerteza combnada Quantfcar os efetos de correlação Passo 7: obter a ncerteza expandda Passo 8: arredondar a ncerteza e resultado da medção Fgura. Fluxograma dos passos para a expressão da ncerteza de medção Ao fnal, convém apresentar todos os cálculos realzados por meo de uma planlha de ncerteza. Convém que tal planlha apresente, no mínmo, a descrção das componentes de ncerteza, o valor das ncertezas padrão, os coefcentes de sensbldade, as contrbuções para ncerteza, a ncerteza combnada, o valor do fator de abrangênca k e a ncerteza expandda. Um modelo, baseado no documento do Inmetro NIT-DICLA-01, é apresentado na Tabela 1. Tal modelo é apenas orentatvo, não sendo mandatóro. REDE METROLÓGICA RS Págna 6 de 3
7 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Tabela 1. Modelo de planlha de ncerteza A segur, estão detalhados os passos descrtos no fluxograma da Fgura. Passo 1: Estabelecer o Modelo Matemátco da Medção O GUM está baseado na le da propagação de ncertezas. A expressão da ncerteza de medção nca pelo estabelecmento de um modelo matemátco para a medção. Na maora dos casos, o mensurando Y não é meddo dretamente, mas é determnado a partr de N outras grandezas de entrada X 1, X,..., X N através de uma relação funconal f: Y = f(x 1, X,..., X N ) (3) Tas grandezas de entrada são as varáves do modelo matemátco da medção. Exemplo 03: se desejamos medr a tensão de ruptura,, de um corpo de prova em um ensao de tração, temos uma relação funconal que depende da força F aplcada para romper o corpo de prova e a área A de sua seção transversal: = f(f, A) = F / A (4) Em determnadas stuações, o modelo matemátco da medção pode ser tão smples quanto a expressão Y = X 1 X. Isso é o caso, por exemplo, de uma medção dreta, obtda por meo de uma comparação de duas grandezas. Exemplo 04: em calbrações, o mensurando geralmente é o erro de ndcação, defndo pelo VIM como a ndcação de um nstrumento de medção menos um valor verdadero (convenconal) da grandeza de entrada correspondente. Logo, o modelo matemátco para o erro de ndcação será: EI = VI VVC (5) Onde EI é o erro de ndcação, VI é o valor ndcado pelo nstrumento e VVC é o valor verdadero convenconal. Em alguns casos, pode ser dfícl explctar o modelo matemátco da medção. Veja a seção 4.4 deste documento para maores orentações quanto ao estabelecmento do modelo matemátco da medção. REDE METROLÓGICA RS Págna 7 de 3
8 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Passo : Defnr as Componentes de Incertezas A segur, deve-se realzar uma análse crítca a fm de dentfcar todas as componentes de ncerteza. Tas componentes podem estar atreladas a condções ambentas, operador, equpamentos e padrões utlzados, método de medção, amostragem e outros fatores. Uma vez defndas as componentes de ncerteza, deve-se verfcar se todas elas estão devdamente representadas como grandezas de entrada no modelo matemátco da medção. Em caso negatvo, deve-se complementar o modelo matemátco pela ntrodução de tas grandezas. Maores detalhes sobre modelos matemátcos de medção constam no tem 4.4. Para auxlar na defnção das componentes de ncerteza, o laboratóro pode fazer uso do dagrama de causa e efeto, porém sua utlzação não deve ser entendda como obrgatóra. Os tens 4.5. e deste documento apresentam uma relação de componentes de ncerteza comum em dversos tpos de calbrações e ensaos. Passo 3: Estmar as Incertezas Padrão As ncertezas assocadas às varáves do modelo matemátco da medção são avaladas de acordo com os métodos de avalação chamados pelo GUM de Tpo A e Tpo B. A avalação do Tpo A da ncerteza é o método que emprega uma análse estatístca de uma sére de observações repetdas no momento do ensao/calbração. A ncerteza padrão do Tpo A pode ser expressa pelo desvo padrão expermental da méda, obtdo conforme tem deste documento. A avalação do Tpo B é o método que emprega outros meos que não a análse estatístca de uma sére de observações repetdas no momento do ensao/calbração. Nesse caso, a avalação da ncerteza é baseada em outros conhecmentos, tas como: a) dados hstórcos de desempenho do método de medção; b) ncertezas herdadas da calbração dos equpamentos e padrões; c) especfcações dos equpamentos e padrões; d) faxa de condções ambentas, entre outros. Com os métodos de avalação do Tpo A e do Tpo B, estma-se a ncerteza padrão de cada grandeza de entrada do modelo matemátco da medção. A ncerteza padrão, u(x ), é uma medda de dspersão equvalente a um desvo padrão. As ncertezas padrão são dependentes do tpo de componente de ncerteza e da dstrbução de probabldade a ela assocada. A Fgura 3 exemplfca o caso de uma varável descrta por uma dstrbução de probabldade retangular, com largura ± a. Para transformar essa componente de ncerteza (±a) em uma ncerteza padrão, deve-se dvdr a por 3. O fator que é empregado para converter a componente de ncerteza em uma ncerteza padrão (no exemplo, o fator 3) é chamado de dvsor. Fgura 3. Varável aleatóra com dstrbução retangular REDE METROLÓGICA RS Págna 8 de 3 a
9 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Por exemplo, magne que o erro máxmo admssível de um equpamento seja de ±0,50 %. Então, a ncerteza padrão u(x ) correspondente, admtndo uma dstrbução de probabldade retangular, será de: 0,50 u( x ) 0,9% 3 (6) A dstrbução de probabldade para cada varável depende do tpo de nformação que se tem dsponível a respeto da respectva componente de ncerteza. A Fgura 4 fornece orentações quanto à atrbução de dstrbuções de probabldade, assm como o seu dvsor aproprado. Tpo de Componente de Incerteza Quando se conhecem apenas os valores máxmos e mínmos de varação (±a): por exemplo, o erro máxmo admssível para um determnado equpamento ou o efeto causado pela resolução fnta do equpamento utlzado Dstrbução de Dvsor Probabldade Retangular 3 Quando se conhecem os valores máxmos e mínmos de varação (±a) e o valor mas provável: por exemplo, o erro de posconamento de um nstrumento em uma marca de escala Trangular 6 Desvo padrão da méda de um conjunto de N medções repetdas t-student N Desvo padrão de dados hstórcos de repettvdade e/ou reprodutbldade, na stuação em que o resultado do ensao/calbração é obtdo por meo de uma únca medção e não por uma méda t-student 1 Incerteza herdada da calbração de equpamentos e padrões Normal ou t- Student, conforme certfcado de calbração Valor de k nformado no certfcado de calbração Desvo padrão de um processo de contagem de elementos dscretos, com méda m e desvo padrão m Posson 1 Fgura 4. Dstrbuções de probabldade e seus dvsores aproprados para o tpo de componente de ncerteza REDE METROLÓGICA RS Págna 9 de 3
10 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Passo 4: Coefcentes de Sensbldade Os coefcentes de sensbldade, c, são o quanto a estmatva de saída Y é nfluencada por varações da estmatva de entrada x. O produto entre a ncerteza padrão, u(x ), e seu respectvo coefcente de sensbldade, c, dá orgem a chamada contrbução de ncerteza, u (y), que corresponde a uma medda de dspersão equvalente a um desvo padrão, com a mesma undade de medda do mensurando. Os coefcentes de sensbldade são calculados através das dervadas parcas de Y em relação a cada varável X. Abaxo estão apresentadas duas regras de aplcação das dervadas para cálculo dos coefcentes de sensbldade em stuações corrqueras de laboratóro: Regra 1: se o modelo matemátco da medção for uma pura soma de N varáves, os coefcentes de sensbldade serão todos guas a um. Caso haja subtração, o snal do coefcente será negatvo. Exemplo 05: um laboratóro deseja realzar uma pesagem de uma amostra contda em um recpente. Para tanto, realza a pesagem do recpente vazo e, após colocada a amostra, realza nova pesagem, correspondendo à massa total do recpente com a amostra. A massa de amostra, M a, será gual à massa total, M t, menos a massa do recpente vazo M r (ou seja, M a = M t M r ). Os coefcentes de sensbldade c Mt e c Mr para as varáves massa total e massa do recpente vazo serão, respectvamente: c Mt = 1 c Mr = 1 Regra : se o modelo matemátco da medção for apenas um produto de N varáves, os coefcentes de sensbldade serão guas a ( y / x ), ou seja, eles serão guas ao resultado da medção dvddo pelo valor correspondente da varável que se quer calcular o coefcente. Note que aqu não é utlzado o valor de ncerteza da varável, mas sm, a melhor estmatva do valor da varável em s. Lembre-se que, para varáves que estão dvdndo em uma equação, pode-se também expressá-las na forma de produto. Isto é, se desejarmos passar 1 / X para o numerador, teremos então 1. X -. Exemplo 06: consderando o exemplo 03, do ensao de tensão de ruptura, se o valor de força aplcada para romper o corpo de prova for de 500 N e a área for de 50 mm, os coefcentes de sensbldade para a força, c F, e para a área, c A, serão: c F = ( F / A ) / F = 1 / A = 1 / 50 = 0,0 mm - c A = ( F. A -1 ) / A = - F. A - = - F / A = / 50 = - 1 N/mm 4 Observação: o snal negatvo no segundo coefcente é devdo ao expoente negatvo da varável área, quando essa está sendo dervada, na sua multplcação com a força. As dervadas também podem ser estmadas por smulação numérca. O resultado, neste caso, será aproxmado. O método da smulação de Kragten, descrto na Eurachem (000), pode ser consultado. REDE METROLÓGICA RS Págna 10 de 3
11 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Passo 5: Avalar e Quantfcar as Possíves Correlações A correlação exste quando duas grandezas de entrada, X e X j, apresentam uma relação de dependênca entre elas ou com uma tercera grandeza de entrada comum a ambas. Tal relação pode estar presente quando, por exemplo, as duas grandezas de entrada são meddas com um mesmo equpamento. Nesse caso, pode-se dzer que a correlação será forte. O coefcente de correlação, r(x,x j ), mede o grau de correlação lnear entre duas varáves. Ele pode varar desde 1 até 1. No caso de duas grandezas de entrada meddas com um mesmo equpamento, pode-se dzer, para efetos prátcos, que r(x,x j ) = 1. Efetos de correlação podem reduzr a ncerteza combnada quando, por exemplo, um nstrumento é utlzado como um comparador entre um padrão e um em calbração. Tal caso consste em uma correlação negatva. Em outras stuações, os erros das medções de varáves correlaconadas serão combnados em uma mesma dreção e sso acarretará um aumento da ncerteza combnada. Esse caso consste em uma correlação postva. O efeto da correlação será negatvo se r(x,x j ) < 0 e será postvo se r(x,x j ) > 0. Quando duas varáves x e x j são meddas smultaneamente em um processo de n medções repetdas, o coefcente de correlação r(x,x j ) é obtdo da segunte forma: s( x, x ) j r( x, x ) j s( x ) s( x ) j (7) Onde s(x ) é o desvo padrão assocado a x, s(x j ) é o desvo padrão assocado a x j e s(x,x j ) é a covarânca assocada a x e x j, obtdos através dos dados das n medções repetdas de x e x j. A relação de dependênca entre duas varáves também pode ser avalada matematcamente por meo da avalação das componentes de ncerteza que são comuns entre ambas as varáves. Isto pode ser feto através do cálculo da covarânca. Por exemplo, suponha que duas varáves X 1 e X dependam de um conjunto de varáves não-correlaconadas Q 1, Q,..., Q N. Assm: X 1 = f(q 1, Q,..., Q N ) e X = g(q 1, Q,..., Q N ) (8) Se u (q ) é o quadrado da ncerteza assocada à varável Q, então os quadrados das ncertezas assocadas à X 1 e com X serão: N f u ( x ) u ( q ) 1 1 q N g u ( x ) u ( q ) 1 q (9) (10) Então, a covarânca assocada com X 1 e X será: u( x f g u 1 q q N, x ) ( q ) 1 (11) REDE METROLÓGICA RS Págna 11 de 3
12 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Em razão de somente aqueles termos para os quas f q 0 e g q 0, para um dado, contrbuírem para o somatóro da Equação 10, a covarânca é zero se nenhuma varável é comum a ambos f e g. Exemplo 07: um laboratóro de análses químcas realza uma dlução de amostra, ppetando 1 ml de amostra em um balão volumétrco de 10 ml e avolumando com água destlada. O modelo matemátco para o fator de dlução, F, será: F = V f / V (1) Onde V f é o volume fnal de dlução de 10 ml, meddo com balão volumétrco, e V é o volume ncal ppetado de amostra a ser dluída, de 1 ml. A varação de temperatura, T, rá causar uma expansão volumétrca, V, tanto em V como em V f, de acordo com: V = V 0..T (13) Onde V 0 é o volume nomnal não expanddo e é o coefcente de expansão volumétrca do líqudo em dlução. Consdere nesse exemplo, o da água, que vale,1 x 10-4 ºC -1. Consdere também uma varação de temperatura no laboratóro, T, de ± 5 ºC. Com auxílo da Fgura 4, podemos atrbur uma dstrbução de probabldade retangular para a varação de temperatura e, dessa forma, a ncerteza padrão relaconada à varação de temperatura será: u( T) 5/ 3 ml (14) Assm, V e V f estarão correlaconadas devdo ao efeto da varação da temperatura, T, que ocorre em ambas as varáves. A covarânca entre V e V f pode ser calculada com base na Equação 11: u( V, V f V ) T V f u ( T ) V T V f u ( T ) (15) 4, / 3 0, u( V, V ) 1 ml (16) Passo 6: Obter a Incerteza Combnada f Uma vez obtdas todas as ncertezas padrão e os coefcentes de sensbldade, a le de propagação de ncertezas estabelece que as ncertezas padrão relaconadas a cada varável do modelo matemátco da medção devem ser propagadas para gerar uma ncerteza combnada u c (y) tal que: u c N N y c u x u y 1 (17) Tal ncerteza representa uma faxa de dspersão equvalente a um desvo padrão, avalado ao redor do resultado da medção. Quando exstrem correlações entre as componentes de ncerteza o efeto de tas correlações devem ser ncorporados à ncerteza combnada. A Equação 17 é então reescrta: 1 REDE METROLÓGICA RS Págna 1 de 3
13 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 u c N N j N y c u x c c ux ux rx, x 1 (18) 1 j1 Outra forma, alternatva à Equação 18, é através das covarâncas: u c N N j N y c u x c c ux, x 1 j 1 j 1 j j j (19) Exemplo 08: um metrologsta deseja medr, através de um cronômetro, o tempo que uma amostra leva para atngr determnado estado prevamente defndo. Ele repete seu expermento cnco vezes e o resultado fnal é a méda artmétca das cnco repetções. Consdere as seguntes componentes de ncerteza: a) desvo padrão expermental da méda das repetções; b) ncerteza advnda do erro máxmo admssível do cronômetro, especfcado pelo seu fabrcante; c) efeto da resolução fnta do cronômetro utlzado. Tal exemplo é apenas lustratvo, porém pode ser estenddo para dversas áreas da metrologa. O modelo matemátco da medção pode ser escrto como: Y = X + esp + res (0) Onde Y é o tempo médo que a amostra leva para atngr o estado, X é a melhor estmatva do tempo, obtdo pela méda artmétca das cnco repetções, esp é a ncerteza advnda do erro máxmo admssível do cronômetro, especfcado pelo seu fabrcante, e res é o efeto causado pela resolução fnta do cronômetro. Se o valor das cnco medções são 3,0 s, 3,1 s, 3,0 s, 3,07 s e 3,1 s, logo a méda será 3,07 s e o desvo padrão das observações repetdas será 0,05 s. Consdere que o erro máxmo admssível do cronômetro seja de ±0,0 s e que a resolução do cronômetro seja de 0,01 s. O erro máxmo admssível e o efeto da resolução fnta do cronômetro são tpcamente componentes de ncerteza com dstrbução de probabldade retangular, conforme ndcado na Fgura 4. Já o desvo padrão da méda das repetções está assocado a uma varável com dstrbução t-student. Assm sendo, as ncertezas padrão obtdas com o auxílo da Fgura 4 serão: u( Δ esp 0,0/ 3 0,0115 s (1) u( Δ res (0,01/ ) / 3) 0,009 s () u ( X ) 0, 05/ 5 0,04 s (3) Para o cálculo dos coefcentes de sensbldade, aplcamos a regra 1 descrta anterormente e sabemos, então, que todos eles serão guas a um. Portanto, a ncerteza combnada, consderando que não exstem correlações entre as componentes de ncerteza, é obtda por meo da Equação 17: j c N y c u x u X u u 0,053 s u (4) 1 esp res REDE METROLÓGICA RS Págna 13 de 3
14 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Passo 7: Obter a Incerteza Expandda Aplcando o Teorema do Lmte Central, pode-se dzer que a dstrbução de probabldade de Y será aproxmadamente normal, ou t-student para um determnado grau de lberdade eff. Tal aproxmação melhora na medda em que: a) há um número maor de contrbuções de ncerteza; b) os valores das contrbuções de ncerteza são próxmos um dos outros, sto é, não haja nenhuma contrbução de ncerteza domnante sobre as demas; c) as dstrbuções de probabldade assocadas às contrbuções de ncerteza se assemelhem da dstrbução normal. Assumndo-se uma dstrbução de probabldade normal para Y, o ntervalo de ± 1 desvo padrão ao redor da melhor estmatva do mensurando corresponde a uma probabldade de abrangênca de aproxmadamente 68%. Para aumentar tal probabldade de abrangênca, deve-se multplcar a ncerteza combnada pelo fator de abrangênca k. O resultado é a chamada ncerteza expandda, U, tal que: U = k u c (y) (5) Onde k é defndo para uma determnada probabldade de abrangênca (geralmente 95,45%). Para uma dstrbução normal e uma probabldade de abrangênca de 95,45%, k =. Quando uma componente de ncerteza do Tpo A é avalada por um número reduzdo de observações repetdas (N < 30), torna-se mas adequado atrbur uma dstrbução de probabldade t-student para Y do que a Normal. Na dstrbução t-student, o valor de k será dependente, além da probabldade de abrangênca, do grau de lberdade efetvo. Dessa forma, o valor de k nem sempre será gual a dos. Na estatístca, em geral, o grau de lberdade é N 1, ou seja, o número total de medções menos um. Em ncerteza, como exstem componentes de ncerteza que não necessaramente são avaladas por meo de uma análse estatístca, torna-se necessáro um conceto mas genérco para o grau de lberdade. Pode-se dzer que: O grau de lberdade na ncerteza quantfca a credbldade sobre cada componente de ncerteza. Assm, um alto grau de credbldade mplca em um alto grau de lberdade. Por exemplo, para uma varável com dstrbução retangular, pode-se atrbur nfntos graus de lberdade, pos temos alta credbldade na estmatva da sua ncerteza padrão, já que a dstrbução retangular é fechada dentro de um ntervalo (tem-se 100% de certeza de que o valor da varável estará contdo no ntervalo ± a). O mesmo se aplca a dstrbuções trangulares. O grau de lberdade assocado ao mensurando y, chamado grau de lberdade efetvo, eff, pode ser estmado por meo da fórmula de Welch-Satterthwate: REDE METROLÓGICA RS Págna 14 de 3
15 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 v eff N 1 y 4 uc c u( x ) v 4 y 4 uc 4 N u ( y) 1 v (6) A Tabela apresenta o valor de k em função do valor de eff calculado, consderando uma probabldade de abrangênca de 95,45 %. Para outros valores de k, recomenda-se consultar o GUM. Tabela. Valor de k em função do valor de eff calculado, consderando probabldade de abrangênca de 95,45 % eff k 1 13,97 4,53 3 3,31 4,87 5,65 6,5 7,43 8,37 9,3 10,8 15,18 0,13 5,11 30,09 35,07 40,06 50,05 100,03,00 Exemplo 09: consdere o resultado do exemplo 08. Para obter a ncerteza expandda, prmero deve-se calcular eff de acordo com a Equação 6. Como o efeto da resolução fnta e o erro máxmo admssível do cronômetro são componentes de ncerteza descrtas por dstrbução retangular, pode-se atrbur nfntos graus de lberdade para tas componentes. Assm, eff será: v eff y 4 uc N c u( x ) 1 v 4 0, ,053 0, , ,6 (7) O valor de eff deve ser nterpolado ou truncado para o valor mas baxo. Dessa forma, eff = 6. O valor de k, segundo a Tabela será, então,,5. Dessa forma, a ncerteza expandda pode obtda por meo da Equação 5, tal que: U = k u c (y) =,5 0,053 = 0,0637 s (8) REDE METROLÓGICA RS Págna 15 de 3
16 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Observação: no caso de componentes de ncerteza correlaconadas, a fórmula de Welch- Satterthwate da Equação 6 não pode ser utlzada, pos pode gerar resultados ncoerentes. Em tal stuação, recomenda-se utlzar a fórmula Generalzada de Wllnk. Se qualquer grupo de grandezas de entrada é estmada a partr de um conjunto de N medções repetdas, então eff será: Isso será váldo se u N y 1 c u ( x ) v eff N c u 1 N 1 c u( x ) v A Equação 9 dfere da 6 no smples fato de que na Equação 9 o numerador é calculado como se não houvesse correlações entre as componentes de ncerteza. Passo 8: Arredondar Incerteza e Resultado da Medção A ncerteza expandda deve ser arredondada para, no máxmo, dos algarsmos sgnfcatvos (não confundr com casas decmas). Algarsmos sgnfcatvos são todos aqueles contados, da esquerda para a dreta, a partr do prmero algarsmo dferente de zero. Exemplos: x 4 (9) 45,30 possu quatro algarsmos sgnfcatvos e duas casas decmas; 0,0595 possu três algarsmos sgnfcatvos e quatro casas decmas; 0,0450 possu três algarsmos sgnfcatvos e quatro casas decmas. O valor numérco do resultado da medção deve ser arredondado para o mesmo número de casas decmas do valor da ncerteza expandda. Para o processo de arredondamento, as regras usuas de arredondamento de números devem ser utlzadas (para mas detalhes ver ISO 31-0:199, anexo B). Entretanto, se o arredondamento dmnu o valor numérco da ncerteza de medção em mas de 5%, o arredondamento deve ser feto para cma. Exemplo 10: a ncerteza expandda no caso da medção do tempo descrta no exemplo 09, arredondada para dos algarsmos sgnfcatvos, será U = 0,064 s, pos o últmo algarsmo da Equação 8 é maor que cnco, logo arredonda-se para cma. Contudo, se o laboratóro desejar expressar a ncerteza com um algarsmo sgnfcatvo e, dessa forma, utlzar o mesmo número de casas decmas que o cronômetro dspõe, o erro de arredondamento para baxo será: 0,0637 0,06 Erro Arredondamento 100 5,8% 0,0637 (30) Como o erro de arredondamento nesse caso fo maor do que 5%, o arredondamento não pode ser feto para baxo e a ncerteza expandda será, então, 0,07 s. O resultado fnal da medção pode ser apresentado como (3,07 ± 0,07) s. WILLINK, R. A generalzaton of the Welch Satterthwate formula for use wth correlated uncertanty components. Metrologa 44, IOP: 007. REDE METROLÓGICA RS Págna 16 de 3
17 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 É mportante que tanto o resultado da medção, quanto a ncerteza sejam adequadamente apresentados e ndquem a undade de medda utlzada pelo laboratóro. Quando expressa a ncerteza expandda U, convém que o resultado Y seja apresentado da forma Y = y ± U, fornecendo tanto a undade de medda para y quanto para U. Na apresentação da ncerteza, o laboratóro deve, anda, ndcar o valor de k, a probabldade de abrangênca utlzada para obter U, a dstrbução de probabldade e os graus de lberdade efetvos, quando se tratar de uma dstrbução t-student. Vale lembrar que a apresentação, em relatóro de ensaos, da ncerteza de medção só é mandatóra quando solctada pelo clente ou quando essa afetar a conformdade com um lmte de especfcação. 4.4 Modelos matemátcos da medção A representação da medção através de um modelo matemátco é o passo ncal e fundamental para a ncerteza de medção. Tal modelo deve relaconar o mensurando Y com as N varáves das quas ele depende. A relação deve ser expressa através de uma função. Mutas vezes, o método de medção explcta um modelo matemátco, como no exemplo de tensão de ruptura, apresentado na Equação 4. Em geral, na área de calbração, quando se tratar de uma comparação dreta, o modelo matemátco será uma pura soma e/ou subtração de N varáves. Os documentos EA-4/0 e M3003 trazem uma sére de exemplos de tas casos. O prmero passo é redgr o modelo matemátco básco da medção e, em seguda, complementálo com as demas grandezas dentfcadas como componentes de ncerteza. Exemplo 11 (baseado no M3003): um resstor é calbrado frente a outro resstor padrão. A comparação é realzada pela conexão de ambos em sére e permtndo a passagem de uma corrente constante entre eles. A tensão ao redor de cada um deles é medda. Como a mesma corrente passa entre ambos, a razão entre as tensões V S e V X será a mesma razão dos valores das duas resstêncas, onde V S é a tensão no resstor padrão e V X é a tensão no resstor em calbração. O modelo matemátco básco da medção será então: R V (31) S S R V X X Se a resstênca padrão R S é conhecda, então a resstênca em calbração pode ser determnada se a Equação 31 for reescrta: V (3) X R R X S V O modelo matemátco da medção, como expresso na Equação 3, não ncorpora todas as varáves que afetam a ncerteza da medção. Há de se consderar, anda, os seguntes fatores: a) derva do padrão ao longo do tempo R D ; S REDE METROLÓGICA RS Págna 17 de 3
18 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 b) efeto da varação da temperatura T em função do coefcente de temperatura do resstor R TC ; tal coefcente pode ser determnado expermentalmente pelo laboratóro; c) repettvdade das leturas das razões das tensões s(v). Assm, o modelo matemátco da medção descrto na Equação 3 deve ser complementado, de tal forma que: V (33) X R R R R s(v ) X S D TC T V S Esse processo de ncar com um modelo matemátco básco da medção, sob forma smplfcada, e complementá-lo em seguda com todas as varáves que afetam a ncerteza é um fator fundamental para a adequada aplcação do método do GUM. Em outras stuações, partcularmente em áreas específcas de ensaos, como na químca, pode ser mpratcável explctar o modelo matemátco da medção sob forma detalhada. Nessas stuações, o laboratóro pode determnar expermentalmente os fatores ou, pelo menos, consderar a expressão genérca para o mensurando Y: Y X (34) rep exat outros Onde X é o resultado da medção, rep é o efeto devdo à repettvdade das medções, exat é o efeto devdo à exatdão e outros são os efetos causados por outros fatores eventualmente presentes na medda. Tas fatores são varáves com esperança gual a zero, de forma a não alterar o valor do resultado da medção, porém com um valor de ncerteza defndo. As ncertezas desses fatores podem ser obtdas expermentalmente, por exemplo, através de dados de valdação do método, controle de qualdade ou projetos fatoras. 4.5 Consderações sobre componentes de ncerteza Consderações geras As componentes de ncerteza devem ser explctadas, sob forma de varáves, no modelo matemátco da medção, conforme descrto anterormente no tem 4.4. Nesse sentdo, cabe ao avalador verfcar se nenhuma componente de ncerteza relevante é neglgencada pelo laboratóro. Por outro lado, também deve-se estar atento para eventual dupla contagem de componentes de ncerteza. O dagrama de causa e efeto pode ser utlzado pelo laboratóro, pos ajuda a evtar essa dupla contagem de componentes de ncerteza, ao mesmo tempo em que faclta o agrupamento de componentes cujo efeto combnado possa ser avalado. Um exemplo de dupla contagem de componentes de ncerteza é o caso em que o laboratóro estma as componentes de repettvdade assocadas a cada grandeza de entrada e, ao fnal, estma a componente de repettvdade do mensurando Y, através da repetção completa de medções. A componente de repettvdade do mensurando Y já ncorpora a repettvdade assocada a cada grandeza de entrada. Sendo assm, não sera necessáro consderar em separado as componentes de repettvdade assocadas a cada grandeza de entrada. REDE METROLÓGICA RS Págna 18 de 3
19 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 A segur, são apresentadas algumas componentes de ncerteza pertnentes nas áreas de calbração e de ensao. Outras componentes de ncerteza também poderão ser consderadas, dependendo de cada caso. Os avaladores devem observar os documentos pertnentes da Rede Metrológca RS quanto às componentes de ncerteza em áreas específcas, como metrologa dmensonal e torque, estabelecdas nos RM 53 e RM 55, respectvamente, e para ensaos, conforme polítca defnda no RM Componentes de ncerteza na área de calbração Usualmente, tem-se como componentes de ncerteza na área de calbração, dependendo do tpo de medção, o segunte: a) desvo padrão da méda de medções repetdas; b) ncerteza da calbração do padrão (ncerteza herdada), dada em seu certfcado de calbração; c) derva dos padrões, sto é, a varação do padrão no ntervalo entre suas duas últmas calbrações; quando o hstórco não está dsponível, uma regra útl é consderar como derva, pelo menos, a ncerteza da calbração do padrão; d) ncerteza do fator de correção para erros sstemátcos do padrão; o fator de correção deve ser estmado por meo de uma análse de regressão dos erros sstemátcos do padrão; e) erro máxmo admssível para o padrão, quando uma correção para os erros sstemátcos não é aplcada; em tal caso, é possível elmnar as componentes de ncerteza b, c e d lstadas anterormente, quando essas estão ncluídas na análse crítca do erro máxmo admssível do laboratóro; a correção para erros sstemátcos conhecdos é sempre uma stuação preferível do que nclur a componente de erro máxmo admssível na ncerteza da medção. f) efeto da resolução fnta de letura dos equpamentos; g) efeto das condções ambentas, por exemplo temperatura ou umdade; h) hsterese: a ndcação de alguns equpamentos pode varar quando as medções são realzadas no sentdo ascendente ou descendente com relação à faxa de medção; ) outros fatores, de acordo com o tpo de medção. A Fgura 5 traz uma relação de componentes de ncerteza específcas que podem ser relevantes em dversas áreas de calbração. A relação a segur fo elaborada baseada nos documentos ctados nas referêncas. A Fgura 5 deve ser entendda apenas como um gua orentatvo. Em últma análse, caberá ao avalador verfcar se as componentes descrtas a segur serão pertnentes em cada caso e se haverá outras componentes relevantes a serem consderadas. Maores detalhes podem ser consultados nas referêncas ctadas. REDE METROLÓGICA RS Págna 19 de 3
20 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 Área de Calbração Componentes de ncerteza específcas Eletrcdade a) ncerteza herdada da calbração b) derva do padrão c) condções ambentas d) ncerteza de correções para erros sstemátcos e) efetos das resoluções do padrão e do nstrumento em calbração f) desvo padrão da méda das medções Massa a) ncerteza herdada da calbração da massa de referênca b) derva do padrão c) desvo padrão da méda das medções d) efeto da resolução da balança e) condções ambentas f) empuxo do ar Temperatura a) ncerteza herdada da calbração do termômetro de referênca b) derva do padrão c) efetos das resoluções do padrão e do nstrumento em calbração d) nstabldade e heterogenedade do banho termostátco e) correção da coluna emergente, quando da calbração de termômetros de mersão parcal f) tensão parasta da chave comutadora, quando da calbração de termopares g) temperatura da junção de referênca, quando da calbração de termopares h) cabo de compensação, quando da calbração de termopares ) desvo padrão da méda das medções Dmensonal a) ncerteza herdada da calbração do padrão b) derva do padrão c) condções ambentas d) compressão elástca, relaconada à força de medção aplcada e) erro de cosseno f) erros geométrcos (planeza e paralelsmo) g) efetos das resoluções do padrão e do nstrumento em calbração h) desvo padrão da méda das medções Pressão a) ncerteza herdada da calbração do padrão b) derva do padrão c) ncerteza de correções para erros sstemátcos d) efetos das resoluções do padrão e do nstrumento em calbração e) desvo padrão da méda das medções f) ncerteza da dferença de altura entre o padrão e o nstrumento em calbração Torque a) ncerteza herdada da calbração do padrão b) derva do padrão c) ncerteza de correções para erros sstemátcos d) erro de posconamento do pontero do nstrumento em calbração e) efeto da resolução do padrão f) desvo padrão da méda das medções Fgura 5. Componentes de ncerteza específcas em áreas de calbração REDE METROLÓGICA RS Págna 0 de 3
21 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev Componentes de ncerteza na área de ensao A Fgura 6 traz uma relação de componentes de ncerteza específcas que podem ser relevantes em dversas áreas de ensao. Assm como na Fgura 5, a Fgura 6 deve ser entendda apenas como um gua orentatvo. Caberá ao avalador verfcar se as componentes descrtas na Fgura 6 serão pertnentes em cada caso e se haverá outras componentes relevantes a serem consderadas. Maores detalhes podem ser consultados nos documentos de referênca ctados. Área de Ensao Ensaos Químcos e Físco- Químcos Ensaos Mcrobológcos e Ecotoxcológcos Ensaos Mecâncos Componentes de ncerteza específcas Ensaos ttulométrcos: a) ncerteza do volume gasto na ttulação da amostra b) ncerteza do volume gasto na ttulação do branco c) ncerteza da massa molar d) ncerteza da pureza do ttulante e) ncerteza das dluções f) repettvdade e reprodutbldade ntralaboratoral Ensaos gravmétrcos: a) ncerteza da massa ncal b) ncerteza da massa fnal c) repettvdade Ensaos nstrumentas (espectrofotometra, cromatografa, etc.): a) ncerteza da curva de calbração b) repettvdade c) ncerteza do volume ou massa tomada de amostra d) ncerteza de dlução e) ncerteza da recuperação f) ncerteza dos padrões Reprodutbldade ntralaboratoral Ensaos de Tração/Compressão: a) ncerteza na medção da força aplcada b) ncerteza na medção das dmensões do corpo de prova c) condções ambentas d) repettvdade Ensaos de Dureza: a) ncerteza do padrão utlzado na verfcação nterna ndreta ou ncerteza da calbração externa dreta b) repettvdade c) efeto da resolução do durômetro d) condções ambentas Ensaos Impactos: a) ncerteza da máquna de ensao b) repettvdade c) efeto da resolução da máquna d) perdas por atrto e) condções ambentas Fgura 6. Componentes de ncerteza específcas em áreas de ensao REDE METROLÓGICA RS Págna 1 de 3
22 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev Consderações sobre a repettvdade O GUM cta que a melhor estmatva do valor do mensurando, na ausênca de efetos sstemátcos, é obtda através da méda artmétca de N observações repetdas do mesmo mesurando. O desvo padrão expermental da méda é, neste caso, uma medda de ncerteza assocada ao valor da méda, ndcando a repettvdade da medção, sendo calculado por: s s X (35) N Onde s é o desvo padrão expermental das observações repetdas da medção. Em alguns casos, as observações repetdas podem estar correlaconadas e, assm, a Equação 35 pode não ser o estmador mas adequado da repettvdade. Isso pode ocorrer, por exemplo, em medções na área de freqüênca e uma alternatva à Equação 35 é utlzar a varânca Allan 3. Em dversas stuações, sobretudo em ensaos, o resultado da medção é obtdo por meo de uma únca medção, pos a repetção pode não ser técnca ou economcamente vável. Dessa forma, não haverá como calcular o desvo padrão da méda de medções repetdas, pos a medção não é repetda. Essa mportante componente de ncerteza, contudo, ndca os efetos aleatóros de repettvdade da medção e necessta ser consderada de outra forma. Nas stuações em que uma únca medda é utlzada para expressar o resultado da medção, o laboratóro pode estmar a componente de repettvdade através de um estudo hstórco, realzado prevamente à medção. Por exemplo, a repettvdade pode ser estmada através de uma sére de, no mínmo, sete medções realzadas em duplcatas, totalzando catorze resultados de ensao/calbrações. Neste caso, o desvo padrão de repettvdade será gual à méda das dferenças entre as duplcatas, dvddo pelo coefcente 1,18 4 : D s 1,18 (36) No caso de meddas úncas utlzadas para expressar o resultado da medção (sto é, o resultado é um valor ndvdual e não uma méda), o desvo padrão calculado pela Equação 36 não deve ser dvdo pelo dvsor N apresentado na Equação 35. Exstem város métodos para estmar a repettvdade. Recomenda-se consultar os documentos DOQ-CGCRE-008 e a ISO 575 para maores nformações a respeto dos estudos de repettvdade. Outros documentos também podem ser utlzados como referêncas pelo laboratóro, desde que sejam reconhecdos naconal ou nternaconalmente. Em certas áreas da metrologa, pode ser necessáro um tratamento matemátco prévo nos dados, por exemplo, através da aplcação de logartmos. Esse é o caso na mcrobologa, devdo ao 3 ALLAN, D. W. (1987), IEEE Trans. Instrum. Meas. IM-36, O coefcente 1,18 é váldo para medções realzadas em duplcatas e para um número total de dados 30. Para um número dferente de repetções ou para um número total de dados menor, recomenda-se consultar: AIAG. MSA Measurement Systems Analyss. AIAG. Daymler Chrysler Corporaton, Ford Motor Company and General Motors Corporaton, 3.ed, 00. REDE METROLÓGICA RS Págna de 3
23 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev. 05 crescmento exponencal dos mcro-organsmos. Podem ser consultadas as referêncas do ALA (007) ou do IPAC (006) em tal stuação Consderações sobre a reprodutbldade A reprodutbldade é concetuada como o grau de concordânca entre os resultados das medções de um mesmo mensurando, efetuadas sob condções varadas de medção. A reprodutbldade nterna refere-se à avalação sobre a mesma amostra, amostras dêntcas ou padrões, utlzando o mesmo método, no mesmo laboratóro, mas defnndo as condções a varar, tas como analstas, equpamentos ou tempos. Exstem város métodos para determnar a reprodutbldade nterna, sendo dos dos prncpas deles através de (INMETRO, 008): a) cartas de controle de ampltude, que poderão ser aplcados através de replcatas de amostras/tens de calbração ou com padrões estáves ao longo do tempo; b) um estudo com t amostras/tens de calbração meddos n vezes cada um deles, tal que o desvo padrão de reprodutbldade nterna será obtdo através de: Onde: (37) Um método smplfcado, porém menos efcaz para estmar a reprodutbldade nterna basea-se na execução de n medções (n 15), em condções pré-defndas, tal que a sua estmatva será: S (j,k) é o desvo padrão de reprodutbldade nterna relatvo. Os símbolos relatvos às condções ntermedáras podem aparecer entre parêntess (por exemplo, varação dos fatores tempo e operadores ). Recomenda-se consultar os documentos DOQ-CGCRE-008 ou a ISO 575 para maores nformações a respeto dos estudos de reprodutbldade. Assm como ctado no tem 4.5.4, pode ser necessáro um tratamento matemátco prévo nos dados, por exemplo, através da aplcação de logartmos. Para tanto, podem ser consultadas as referêncas ctadas no tem em questão. Também vale lembrar que outras referêncas também podem ser utlzadas pelo laboratóro, desde que sejam reconhecdos naconal ou nternaconalmente. (38) REDE METROLÓGICA RS Págna 3 de 3
24 RM 68 Incerteza de Medção: Gua Prátco do Avalador de Laboratóros rev Consderações sobre a ncerteza de curvas de regressão Alguns equpamentos em químca analítca, tas como espectrofotômetros e cromatógrafos, produzem resultados dretamente proporconas à concentração do analto em amostras de acordo com uma letura de comprmento de onda ou ntensdade de resposta. Para a quantfcação dos resultados é, então, requerdo que se conheça a dependênca entre a resposta medda pelo equpamento e a concentração do analto. Tal relação de dependênca é determnada pela verfcação nterna do equpamento com padrões rastreáves com concentrações defndas. A partr de tas resultados, calcula-se a equação de regressão, determnada pelo método dos mínmos quadrados. Para uma curva de regressão de prmero grau, mutas vezes chamada na químca de curva de calbração, temos que: y = a + bx (39) onde y é a resposta observada pelo equpamento, x é o valor de concentração do padrão de referênca, a é o coefcente lnear da reta e b é o coefcente angular da reta. A partr da Equação 39, quantfca-se então a concentração prevsta em uma determnada amostra ensaada, x prev, a partr de uma resposta observada pelo equpamento, y obs, tal que: x prev = (y obs a)/b (40) Exstem váras formas par estmar a ncerteza padrão da curva de regressão no ponto x prev. A Equação 41, recomendada pela Eurachem (000) é uma forma delas, porém atenta-se para o fato que a Equação 41 é apenas uma forma smplfcada de estmar a ncerteza, pos não consdera os efetos de correlação entre os coefcentes da reta a e b. S 1 ( x x) (41) prev u( x ) 1 prev b n x ( x ) / n Onde x prev é o valor prevsto pela curva obtdo por uma letura ndvdual, n é o número de pontos na curva de regressão, S é o desvo padrão dos resíduos, calculado pelas dferenças quadrátcas entre o valor calculado pela curva, y calc, e o valor de referênca obtdo pela letura do padrão, y real : S n 1 ( y calc y n real ) (4) A ncerteza padrão da curva de regressão lnear de prmero grau, u(x prev ), será uma componente de ncerteza com n graus de lberdade. Uma forma mas adequada de estmar a ncerteza padrão da curva de regressão no ponto x prev é consderando a correlação entre os coefcente a e b da reta, conforme recomendação do GUM. Neste caso, u(x prev ) é estmado por: u( x prev ) c u ( a) c u ( b) c c u( a) u( b) r( a, b) (43) a b a b REDE METROLÓGICA RS Págna 4 de 3
METROLOGIA E ENSAIOS
 METROLOGIA E ENSAIOS Incerteza de Medção Prof. Aleandre Pedott pedott@producao.ufrgs.br Freqüênca de ocorrênca Incerteza da Medção Dstrbução de freqüênca das meddas Erro Sstemátco (Tendênca) Erro de Repettvdade
METROLOGIA E ENSAIOS Incerteza de Medção Prof. Aleandre Pedott pedott@producao.ufrgs.br Freqüênca de ocorrênca Incerteza da Medção Dstrbução de freqüênca das meddas Erro Sstemátco (Tendênca) Erro de Repettvdade
Introdução à Análise de Dados nas medidas de grandezas físicas
 Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
Introdução à Análse de Dados nas meddas de grandezas físcas www.chem.wts.ac.za/chem0/ http://uregna.ca/~peresnep/ www.ph.ed.ac.uk/~td/p3lab/analss/ otas baseadas nos apontamentos Análse de Dados do Prof.
NOTA II TABELAS E GRÁFICOS
 Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
Depto de Físca/UFMG Laboratóro de Fundamentos de Físca NOTA II TABELAS E GRÁFICOS II.1 - TABELAS A manera mas adequada na apresentação de uma sére de meddas de um certo epermento é através de tabelas.
TEORIA DE ERROS * ERRO é a diferença entre um valor obtido ao se medir uma grandeza e o valor real ou correto da mesma.
 UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
UNIVERSIDADE FEDERAL DO ESPÍRITO SANTO CENTRO DE CIÊNCIAS EXATAS DEPARTAMENTO DE FÍSICA AV. FERNANDO FERRARI, 514 - GOIABEIRAS 29075-910 VITÓRIA - ES PROF. ANDERSON COSER GAUDIO FONE: 4009.7820 FAX: 4009.2823
Expressão da Incerteza de Medição para a Grandeza Energia Elétrica
 1 a 5 de Agosto de 006 Belo Horzonte - MG Expressão da ncerteza de Medção para a Grandeza Energa Elétrca Eng. Carlos Alberto Montero Letão CEMG Dstrbução S.A caletao@cemg.com.br Eng. Sérgo Antôno dos Santos
1 a 5 de Agosto de 006 Belo Horzonte - MG Expressão da ncerteza de Medção para a Grandeza Energa Elétrca Eng. Carlos Alberto Montero Letão CEMG Dstrbução S.A caletao@cemg.com.br Eng. Sérgo Antôno dos Santos
Estimativa da Incerteza de Medição da Viscosidade Cinemática pelo Método Manual em Biodiesel
 Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
Estmatva da Incerteza de Medção da Vscosdade Cnemátca pelo Método Manual em Bodesel Roberta Quntno Frnhan Chmn 1, Gesamanda Pedrn Brandão 2, Eustáquo Vncus Rbero de Castro 3 1 LabPetro-DQUI-UFES, Vtóra-ES,
Introdução e Organização de Dados Estatísticos
 II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
II INTRODUÇÃO E ORGANIZAÇÃO DE DADOS ESTATÍSTICOS 2.1 Defnção de Estatístca Uma coleção de métodos para planejar expermentos, obter dados e organzá-los, resum-los, analsá-los, nterpretá-los e deles extrar
Aula Características dos sistemas de medição
 Aula - Característcas dos sstemas de medção O comportamento funconal de um sstema de medção é descrto pelas suas característcas (parâmetros) operaconas e metrológcas. Aqu é defnda e analsada uma sére destes
Aula - Característcas dos sstemas de medção O comportamento funconal de um sstema de medção é descrto pelas suas característcas (parâmetros) operaconas e metrológcas. Aqu é defnda e analsada uma sére destes
A ESTIMATIVA DA INCERTEZA DE MEDIÇÃO PELOS MÉTODOS DO ISO GUM 95 E DE SIMULAÇÃO DE MONTE CARLO
 A ESTIMATIVA DA INCERTEZA DE MEDIÇÃO PELOS MÉTODOS DO ISO GUM 95 E DE SIMULAÇÃO DE MONTE CARLO Paulo Roberto Gumarães Couto INMETRO-DIMCI-DIMEC-LAPRE prcouto@nmetro.gov.br INTRODUÇÃO 3 ISO GUM 95 4. Estmatva
A ESTIMATIVA DA INCERTEZA DE MEDIÇÃO PELOS MÉTODOS DO ISO GUM 95 E DE SIMULAÇÃO DE MONTE CARLO Paulo Roberto Gumarães Couto INMETRO-DIMCI-DIMEC-LAPRE prcouto@nmetro.gov.br INTRODUÇÃO 3 ISO GUM 95 4. Estmatva
Covariância e Correlação Linear
 TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
TLF 00/ Cap. X Covarânca e correlação lnear Capítulo X Covarânca e Correlação Lnear 0.. Valor médo da grandeza (,) 0 0.. Covarânca na propagação de erros 03 0.3. Coecente de correlação lnear 05 Departamento
7. Resolução Numérica de Equações Diferenciais Ordinárias
 7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
7. Resolução Numérca de Equações Dferencas Ordnáras Fenômenos físcos em dversas áreas, tas como: mecânca dos fludos, fluo de calor, vbrações, crcutos elétrcos, reações químcas, dentre váras outras, podem
Princípios do Cálculo de Incertezas O Método GUM
 Prncípos do Cálculo de Incertezas O Método GUM João Alves e Sousa Laboratóro Regonal de Engenhara Cvl - LREC Rua Agostnho Perera de Olvera, 9000-64 Funchal, Portugal. E-mal: jasousa@lrec.pt Resumo Em anos
Prncípos do Cálculo de Incertezas O Método GUM João Alves e Sousa Laboratóro Regonal de Engenhara Cvl - LREC Rua Agostnho Perera de Olvera, 9000-64 Funchal, Portugal. E-mal: jasousa@lrec.pt Resumo Em anos
Análise de Regressão. Profa Alcione Miranda dos Santos Departamento de Saúde Pública UFMA
 Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
Análse de Regressão Profa Alcone Mranda dos Santos Departamento de Saúde Públca UFMA Introdução Uma das preocupações estatístcas ao analsar dados, é a de crar modelos que explctem estruturas do fenômeno
2 Incerteza de medição
 2 Incerteza de medção Toda medção envolve ensaos, ajustes, condconamentos e a observação de ndcações em um nstrumento. Este conhecmento é utlzado para obter o valor de uma grandeza (mensurando) a partr
2 Incerteza de medção Toda medção envolve ensaos, ajustes, condconamentos e a observação de ndcações em um nstrumento. Este conhecmento é utlzado para obter o valor de uma grandeza (mensurando) a partr
ÍNDICE NOTA INTRODUTÓRIA
 OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
OGC00 05-0-06 ÍDICE. Introdução. Âmbto e defnções 3. Avalação da ncerteza de medção de estmatvas das grandezas de entrada 4. Cálculo da ncerteza-padrão da estmatva da grandeza 5 de saída 5. Incerteza de
Informação. Nota: Tradução feita por Cláudio Afonso Kock e Sérgio Pinheiro de Oliveira.
 Informação Esta publcação é uma tradução do Gua de Calbração EURAMET Gua para a Estmatva da Incerteza em Medções de Dureza (EURAMET/cg-16/v.01, July 007). Os dretos autoras do documento orgnal pertencem
Informação Esta publcação é uma tradução do Gua de Calbração EURAMET Gua para a Estmatva da Incerteza em Medções de Dureza (EURAMET/cg-16/v.01, July 007). Os dretos autoras do documento orgnal pertencem
Ministério da Educação. Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira. Cálculo do Conceito Preliminar de Cursos de Graduação
 Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
Mnstéro da Educação Insttuto Naconal de Estudos e Pesqusas Educaconas Aníso Texera Cálculo do Conceto Prelmnar de Cursos de Graduação Nota Técnca Nesta nota técnca são descrtos os procedmentos utlzados
LQA - LEFQ - EQ -Química Analítica Complemantos Teóricos 04-05
 LQA - LEFQ - EQ -Químca Analítca Complemantos Teórcos 04-05 CONCEITO DE ERRO ALGARISMOS SIGNIFICATIVOS Embora uma análse detalhada do erro em Químca Analítca esteja fora do âmbto desta cadera, sendo abordada
LQA - LEFQ - EQ -Químca Analítca Complemantos Teórcos 04-05 CONCEITO DE ERRO ALGARISMOS SIGNIFICATIVOS Embora uma análse detalhada do erro em Químca Analítca esteja fora do âmbto desta cadera, sendo abordada
Professor Mauricio Lutz CORRELAÇÃO
 Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Professor Maurco Lutz 1 CORRELAÇÃO Em mutas stuações, torna-se nteressante e útl estabelecer uma relação entre duas ou mas varáves. A matemátca estabelece város tpos de relações entre varáves, por eemplo,
Sistemas de Filas: Aula 5. Amedeo R. Odoni 22 de outubro de 2001
 Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Sstemas de Flas: Aula 5 Amedeo R. Odon 22 de outubro de 2001 Teste 1: 29 de outubro Com consulta, 85 mnutos (níco 10:30) Tópcos abordados: capítulo 4, tens 4.1 a 4.7; tem 4.9 (uma olhada rápda no tem 4.9.4)
Portaria Inmetro nº 248 de 17 de julho de 2008
 INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL - Portara Inmetro nº 248 de 17 de julho de 2008 O PRESIDENTE DO INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL,
INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL - Portara Inmetro nº 248 de 17 de julho de 2008 O PRESIDENTE DO INSTITUTO NACIONAL DE METROLOGIA, NORMALIZAÇÃO E QUALIDADE INDUSTRIAL,
Algarismos Significativos Propagação de Erros ou Desvios
 Algarsmos Sgnfcatvos Propagação de Erros ou Desvos L1 = 1,35 cm; L = 1,3 cm; L3 = 1,30 cm L4 = 1,4 cm; L5 = 1,7 cm. Qual destas meddas está correta? Qual apresenta algarsmos com sgnfcado? O nstrumento
Algarsmos Sgnfcatvos Propagação de Erros ou Desvos L1 = 1,35 cm; L = 1,3 cm; L3 = 1,30 cm L4 = 1,4 cm; L5 = 1,7 cm. Qual destas meddas está correta? Qual apresenta algarsmos com sgnfcado? O nstrumento
IV - Descrição e Apresentação dos Dados. Prof. Herondino
 IV - Descrção e Apresentação dos Dados Prof. Herondno Dados A palavra "dados" é um termo relatvo, tratamento de dados comumente ocorre por etapas, e os "dados processados" a partr de uma etapa podem ser
IV - Descrção e Apresentação dos Dados Prof. Herondno Dados A palavra "dados" é um termo relatvo, tratamento de dados comumente ocorre por etapas, e os "dados processados" a partr de uma etapa podem ser
Probabilidade e Estatística. Correlação e Regressão Linear
 Probabldade e Estatístca Correlação e Regressão Lnear Correlação Este uma correlação entre duas varáves quando uma delas está, de alguma forma, relaconada com a outra. Gráfco ou Dagrama de Dspersão é o
Probabldade e Estatístca Correlação e Regressão Lnear Correlação Este uma correlação entre duas varáves quando uma delas está, de alguma forma, relaconada com a outra. Gráfco ou Dagrama de Dspersão é o
Objetivos da aula. Essa aula objetiva fornecer algumas ferramentas descritivas úteis para
 Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Objetvos da aula Essa aula objetva fornecer algumas ferramentas descrtvas útes para escolha de uma forma funconal adequada. Por exemplo, qual sera a forma funconal adequada para estudar a relação entre
Regressão e Correlação Linear
 Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Probabldade e Estatístca I Antono Roque Aula 5 Regressão e Correlação Lnear Até o momento, vmos técncas estatístcas em que se estuda uma varável de cada vez, estabelecendo-se sua dstrbução de freqüêncas,
Despacho Econômico de. Sistemas Termoelétricos e. Hidrotérmicos
 Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
Despacho Econômco de Sstemas Termoelétrcos e Hdrotérmcos Apresentação Introdução Despacho econômco de sstemas termoelétrcos Despacho econômco de sstemas hdrotérmcos Despacho do sstema braslero Conclusões
5.1 Seleção dos melhores regressores univariados (modelo de Índice de Difusão univariado)
 5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
5 Aplcação Neste capítulo será apresentada a parte empírca do estudo no qual serão avalados os prncpas regressores, um Modelo de Índce de Dfusão com o resultado dos melhores regressores (aqu chamado de
PARTE 1. 1. Apresente as equações que descrevem o comportamento do preço de venda dos imóveis.
 EXERCICIOS AVALIATIVOS Dscplna: ECONOMETRIA Data lmte para entrega: da da 3ª prova Valor: 7 pontos INSTRUÇÕES: O trabalho é ndvdual. A dscussão das questões pode ser feta em grupo, mas cada aluno deve
EXERCICIOS AVALIATIVOS Dscplna: ECONOMETRIA Data lmte para entrega: da da 3ª prova Valor: 7 pontos INSTRUÇÕES: O trabalho é ndvdual. A dscussão das questões pode ser feta em grupo, mas cada aluno deve
Nota Técnica Médias do ENEM 2009 por Escola
 Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
Nota Técnca Médas do ENEM 2009 por Escola Crado em 1998, o Exame Naconal do Ensno Médo (ENEM) tem o objetvo de avalar o desempenho do estudante ao fm da escolardade básca. O Exame destna-se aos alunos
Universidade Federal da Bahia Instituto de Física Departamento de Física da Terra e do Meio Ambiente TEXTOS DE LABORATÓRIO T E O R I A D E E R R O S
 Unversdade Federal da Baha Insttuto de Físca Departamento de Físca da Terra e do Meo Ambente TEXTOS DE LABORATÓRIO T E O R I A D E E R R O S Físca I SALVADOR, BAHIA 013 1 Prefáco Esta apostla é destnada
Unversdade Federal da Baha Insttuto de Físca Departamento de Físca da Terra e do Meo Ambente TEXTOS DE LABORATÓRIO T E O R I A D E E R R O S Físca I SALVADOR, BAHIA 013 1 Prefáco Esta apostla é destnada
Aula 03 Erros experimentais Incerteza. Aula 03 Prof. Valner Brusamarello
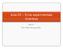 Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Aula 03 Erros epermentas Incerteza Aula 03 Prof. Valner Brusamarello Incerteza Combnada Efeto da Incerteza sobre = f ± u, ± u, L, ± u, L ( ) 1 1 Epansão em Sére de Talor: k k L f = f 1,, 3, + ± uk + L,,,
Coordenação Geral de Acreditação
 Coordenação Geral de Acredtação ORIENTAÇÕES PARA APLICAÇÃO DOS REQUISITOS TÉCNICOS DA ABNT NBR ISO/IEC 1705 NA ACREDITAÇÃO DE LABORATÓRIOS DE CALIBRAÇÃO PARA O GRUPO DE SERVIÇO DE FÍSICO-QUÍMICA Documento
Coordenação Geral de Acredtação ORIENTAÇÕES PARA APLICAÇÃO DOS REQUISITOS TÉCNICOS DA ABNT NBR ISO/IEC 1705 NA ACREDITAÇÃO DE LABORATÓRIOS DE CALIBRAÇÃO PARA O GRUPO DE SERVIÇO DE FÍSICO-QUÍMICA Documento
1 a Lei de Kirchhoff ou Lei dos Nós: Num nó, a soma das intensidades de correntes que chegam é igual à soma das intensidades de correntes que saem.
 Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
Les de Krchhoff Até aqu você aprendeu técncas para resolver crcutos não muto complexos. Bascamente todos os métodos foram baseados na 1 a Le de Ohm. Agora você va aprender as Les de Krchhoff. As Les de
3 Metodologia de Avaliação da Relação entre o Custo Operacional e o Preço do Óleo
 3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
CQ110 : Princípios de FQ
 CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
CQ110 : Prncípos de FQ CQ 110 Prncípos de Físco Químca Curso: Farmáca Prof. Dr. Marco Vdott mvdott@ufpr.br Potencal químco, m potencal químco CQ110 : Prncípos de FQ Propredades termodnâmcas das soluções
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Estatística stica Descritiva
 AULA1-AULA5 AULA5 Estatístca stca Descrtva Prof. Vctor Hugo Lachos Davla oo que é a estatístca? Para mutos, a estatístca não passa de conjuntos de tabelas de dados numércos. Os estatístcos são pessoas
AULA1-AULA5 AULA5 Estatístca stca Descrtva Prof. Vctor Hugo Lachos Davla oo que é a estatístca? Para mutos, a estatístca não passa de conjuntos de tabelas de dados numércos. Os estatístcos são pessoas
UNIVERSIDADE PRESBITERIANA MACKENZIE CCSA - Centro de Ciências Sociais e Aplicadas Curso de Economia
 CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
CCSA - Centro de Cêncas Socas e Aplcadas Curso de Economa ECONOMIA REGIONAL E URBANA Prof. ladmr Fernandes Macel LISTA DE ESTUDO. Explque a lógca da teora da base econômca. A déa que sustenta a teora da
INTRODUÇÃO AO CÁLCULO DE ERROS NAS MEDIDAS DE GRANDEZAS FÍSICAS
 Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO AO CÁLCULO DE ERROS AS MEDIDAS DE GRADEAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...3
Aula 7: Circuitos. Curso de Física Geral III F-328 1º semestre, 2014
 Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
Aula 7: Crcutos Curso de Físca Geral III F-38 º semestre, 04 Ponto essencal Para resolver um crcuto de corrente contínua, é precso entender se as cargas estão ganhando ou perdendo energa potencal elétrca
7 - Distribuição de Freqüências
 7 - Dstrbução de Freqüêncas 7.1 Introdução Em mutas áreas há uma grande quantdade de nformações numércas que precsam ser dvulgadas de forma resumda. O método mas comum de resumr estes dados numércos consste
7 - Dstrbução de Freqüêncas 7.1 Introdução Em mutas áreas há uma grande quantdade de nformações numércas que precsam ser dvulgadas de forma resumda. O método mas comum de resumr estes dados numércos consste
Escolha do Consumidor sob condições de Risco e de Incerteza
 9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
9/04/06 Escolha do Consumdor sob condções de Rsco e de Incerteza (Capítulo 7 Snyder/Ncholson e Capítulo Varan) Turma do Prof. Déco Kadota Dstnção entre Rsco e Incerteza Na lteratura econômca, a prmera
4 Critérios para Avaliação dos Cenários
 Crtéros para Avalação dos Cenáros É desejável que um modelo de geração de séres sntétcas preserve as prncpas característcas da sére hstórca. Isto quer dzer que a utldade de um modelo pode ser verfcada
Crtéros para Avalação dos Cenáros É desejável que um modelo de geração de séres sntétcas preserve as prncpas característcas da sére hstórca. Isto quer dzer que a utldade de um modelo pode ser verfcada
Influência dos Procedimentos de Ensaios e Tratamento de Dados em Análise Probabilística de Estrutura de Contenção
 Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Influênca dos Procedmentos de Ensaos e Tratamento de Dados em Análse Probablístca de Estrutura de Contenção Mara Fatma Mranda UENF, Campos dos Goytacazes, RJ, Brasl. Paulo César de Almeda Maa UENF, Campos
Sempre que surgir uma dúvida quanto à utilização de um instrumento ou componente, o aluno deverá consultar o professor para esclarecimentos.
 Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Insttuto de Físca de São Carlos Laboratóro de Eletrcdade e Magnetsmo: Transferênca de Potênca em Crcutos de Transferênca de Potênca em Crcutos de Nesse prátca, estudaremos a potênca dsspada numa resstênca
Variação ao acaso. É toda variação devida a fatores não controláveis, denominadas erro.
 Aplcação Por exemplo, se prepararmos uma área expermental com todo cudado possível e fzermos, manualmente, o planto de 100 sementes seleconadas de um mlho híbrdo, cudando para que as sementes fquem na
Aplcação Por exemplo, se prepararmos uma área expermental com todo cudado possível e fzermos, manualmente, o planto de 100 sementes seleconadas de um mlho híbrdo, cudando para que as sementes fquem na
Análise de Incertezas I.B De Paula
 Um bom expermentalsta deve fazer todo o esforço possível para mnmzar os erros de seu expermento. Cabe ao expermentalsta a responsabldade de apresentar uma medda da confabldade de seus dados. amos defnr
Um bom expermentalsta deve fazer todo o esforço possível para mnmzar os erros de seu expermento. Cabe ao expermentalsta a responsabldade de apresentar uma medda da confabldade de seus dados. amos defnr
Cap. IV Análise estatística de incertezas aleatórias
 TLF 010/11 Cap. IV Análse estatístca de ncertezas aleatóras Capítulo IV Análse estatístca de ncertezas aleatóras 4.1. Méda 43 4.. Desvo padrão 44 4.3. Sgnfcado do desvo padrão 46 4.4. Desvo padrão da méda
TLF 010/11 Cap. IV Análse estatístca de ncertezas aleatóras Capítulo IV Análse estatístca de ncertezas aleatóras 4.1. Méda 43 4.. Desvo padrão 44 4.3. Sgnfcado do desvo padrão 46 4.4. Desvo padrão da méda
CORRELAÇÃO E REGRESSÃO
 CORRELAÇÃO E REGRESSÃO Constata-se, freqüentemente, a estênca de uma relação entre duas (ou mas) varáves. Se tal relação é de natureza quanttatva, a correlação é o nstrumento adequado para descobrr e medr
CORRELAÇÃO E REGRESSÃO Constata-se, freqüentemente, a estênca de uma relação entre duas (ou mas) varáves. Se tal relação é de natureza quanttatva, a correlação é o nstrumento adequado para descobrr e medr
Análise Econômica da Aplicação de Motores de Alto Rendimento
 Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
Análse Econômca da Aplcação de Motores de Alto Rendmento 1. Introdução Nesta apostla são abordados os prncpas aspectos relaconados com a análse econômca da aplcação de motores de alto rendmento. Incalmente
CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnilesteMG
 1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
1 CENTRO UNIVERSITÁRIO DO LESTE DE MINAS GERAIS - UnlesteMG Dscplna: Introdução à Intelgênca Artfcal Professor: Luz Carlos Fgueredo GUIA DE LABORATÓRIO LF. 01 Assunto: Lógca Fuzzy Objetvo: Apresentar o
Prof. Antônio Carlos Fontes dos Santos. Aula 1: Divisores de tensão e Resistência interna de uma fonte de tensão
 IF-UFRJ Elementos de Eletrônca Analógca Prof. Antôno Carlos Fontes dos Santos FIW362 Mestrado Profssonal em Ensno de Físca Aula 1: Dvsores de tensão e Resstênca nterna de uma fonte de tensão Este materal
IF-UFRJ Elementos de Eletrônca Analógca Prof. Antôno Carlos Fontes dos Santos FIW362 Mestrado Profssonal em Ensno de Físca Aula 1: Dvsores de tensão e Resstênca nterna de uma fonte de tensão Este materal
Prof. Lorí Viali, Dr.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Prof. Lorí Val, Dr. UFRG Insttuto de Matemátca
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Prof. Lorí Val, Dr. UFRG Insttuto de Matemátca
Prof. Lorí Viali, Dr.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ 1 É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ 1 É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Cálculo do Conceito ENADE
 Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Insttuto aconal de Estudos e Pesqusas Educaconas Aníso Texera IEP Mnstéro da Educação ME álculo do onceto EADE Para descrever o cálculo do onceto Enade, prmeramente é mportante defnr a undade de observação
Sistemas Robóticos. Sumário. Introdução. Introdução. Navegação. Introdução Onde estou? Para onde vou? Como vou lá chegar?
 Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
Sumáro Sstemas Robótcos Navegação Introdução Onde estou? Para onde vou? Como vou lá chegar? Carlos Carreto Curso de Engenhara Informátca Ano lectvo 2003/2004 Escola Superor de Tecnologa e Gestão da Guarda
INTRODUÇÃO À ANÁLISE DE DADOS NAS MEDIDAS DE GRANDEZAS FÍSICAS
 Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO À AÁLISE DE DADOS AS MEDIDAS DE GRADEZAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...4
Físca Laboratoral Ano Lectvo 003/04 ITRODUÇÃO À AÁLISE DE DADOS AS MEDIDAS DE GRADEZAS FÍSICAS. Introdução.... Erros de observação: erros sstemátcos e erros fortutos ou acdentas... 3. Precsão e rgor...4
1. ANÁLISE EXPLORATÓRIA E ESTATÍSTICA DESCRITIVA
 1. ANÁLISE EXPLORATÓRIA E ESTATÍSTICA DESCRITIVA 014 Estatístca Descrtva e Análse Exploratóra Etapas ncas. Utlzadas para descrever e resumr os dados. A dsponbldade de uma grande quantdade de dados e de
1. ANÁLISE EXPLORATÓRIA E ESTATÍSTICA DESCRITIVA 014 Estatístca Descrtva e Análse Exploratóra Etapas ncas. Utlzadas para descrever e resumr os dados. A dsponbldade de uma grande quantdade de dados e de
Y X Baixo Alto Total Baixo 1 (0,025) 7 (0,175) 8 (0,20) Alto 19 (0,475) 13 (0,325) 32 (0,80) Total 20 (0,50) 20 (0,50) 40 (1,00)
 Bussab&Morettn Estatístca Básca Capítulo 4 Problema. (b) Grau de Instrução Procedênca º grau º grau Superor Total Interor 3 (,83) 7 (,94) (,) (,33) Captal 4 (,) (,39) (,) (,3) Outra (,39) (,7) (,) 3 (,3)
Bussab&Morettn Estatístca Básca Capítulo 4 Problema. (b) Grau de Instrução Procedênca º grau º grau Superor Total Interor 3 (,83) 7 (,94) (,) (,33) Captal 4 (,) (,39) (,) (,3) Outra (,39) (,7) (,) 3 (,3)
X = 1, se ocorre : VB ou BV (vermelha e branca ou branca e vermelha)
 Estatístca p/ Admnstração II - Profª Ana Cláuda Melo Undade : Probabldade Aula: 3 Varável Aleatóra. Varáves Aleatóras Ao descrever um espaço amostral de um expermento, não especfcamos que um resultado
Estatístca p/ Admnstração II - Profª Ana Cláuda Melo Undade : Probabldade Aula: 3 Varável Aleatóra. Varáves Aleatóras Ao descrever um espaço amostral de um expermento, não especfcamos que um resultado
CAPÍTULO VI Introdução ao Método de Elementos Finitos (MEF)
 PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
PMR 40 - Mecânca Computaconal CAPÍTULO VI Introdução ao Método de Elementos Fntos (MEF). Formulação Teórca - MEF em uma dmensão Consderemos a equação abao que representa a dstrbução de temperatura na barra
3 A técnica de computação intensiva Bootstrap
 A técnca de computação ntensva ootstrap O termo ootstrap tem orgem na expressão de língua nglesa lft oneself by pullng hs/her bootstrap, ou seja, alguém levantar-se puxando seu própro cadarço de bota.
A técnca de computação ntensva ootstrap O termo ootstrap tem orgem na expressão de língua nglesa lft oneself by pullng hs/her bootstrap, ou seja, alguém levantar-se puxando seu própro cadarço de bota.
Controlo Metrológico de Contadores de Gás
 Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Controlo Metrológco de Contadores de Gás José Mendonça Das (jad@fct.unl.pt), Zulema Lopes Perera (zlp@fct.unl.pt) Departamento de Engenhara Mecânca e Industral, Faculdade de Cêncas e Tecnologa da Unversdade
Variabilidade Espacial do Teor de Água de um Argissolo sob Plantio Convencional de Feijão Irrigado
 Varabldade Espacal do Teor de Água de um Argssolo sob Planto Convenconal de Fejão Irrgado Elder Sânzo Aguar Cerquera 1 Nerlson Terra Santos 2 Cásso Pnho dos Res 3 1 Introdução O uso da água na rrgação
Varabldade Espacal do Teor de Água de um Argssolo sob Planto Convenconal de Fejão Irrgado Elder Sânzo Aguar Cerquera 1 Nerlson Terra Santos 2 Cásso Pnho dos Res 3 1 Introdução O uso da água na rrgação
Universidade Salvador UNIFACS Cursos de Engenharia Cálculo IV Profa: Ilka Rebouças Freire. Integrais Múltiplas
 Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
Unversdade Salvador UNIFACS Cursos de Engenhara Cálculo IV Profa: Ilka ebouças Frere Integras Múltplas Texto 3: A Integral Dupla em Coordenadas Polares Coordenadas Polares Introduzremos agora um novo sstema
PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS DO CEARÁ
 GOVERNO DO ESTADO DO CEARÁ SECRETARIA DO PLANEJAMENTO E GESTÃO - SEPLAG INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE NOTA TÉCNICA Nº 29 PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS
GOVERNO DO ESTADO DO CEARÁ SECRETARIA DO PLANEJAMENTO E GESTÃO - SEPLAG INSTITUTO DE PESQUISA E ESTRATÉGIA ECONÔMICA DO CEARÁ - IPECE NOTA TÉCNICA Nº 29 PROJEÇÕES POPULACIONAIS PARA OS MUNICÍPIOS E DISTRITOS
UNIVERSIDADE DO ESTADO DA BAHIA - UNEB DEPARTAMENTO DE CIÊNCIAS EXATAS E DA TERRA COLEGIADO DO CURSO DE DESENHO INDUSTRIAL CAMPUS I - SALVADOR
 Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
Matéra / Dscplna: Introdução à Informátca Sstema de Numeração Defnção Um sstema de numeração pode ser defndo como o conjunto dos dígtos utlzados para representar quantdades e as regras que defnem a forma
REGRESSÃO NÃO LINEAR 27/06/2017
 7/06/07 REGRESSÃO NÃO LINEAR CUIABÁ, MT 07/ Os modelos de regressão não lnear dferencam-se dos modelos lneares, tanto smples como múltplos, pelo fato de suas varáves ndependentes não estarem separados
7/06/07 REGRESSÃO NÃO LINEAR CUIABÁ, MT 07/ Os modelos de regressão não lnear dferencam-se dos modelos lneares, tanto smples como múltplos, pelo fato de suas varáves ndependentes não estarem separados
NOÇÕES SOBRE CORRELAÇÃO E REGRESSÃO LINEAR SIMPLES
 NOÇÕES SOBRE CORRELAÇÃO E REGRESSÃO LINEAR SIMPLES 1 O nosso objetvo é estudar a relação entre duas varáves quanttatvas. Eemplos:. Idade e altura das cranças.. v. Tempo de prátca de esportes e rtmo cardíaco
NOÇÕES SOBRE CORRELAÇÃO E REGRESSÃO LINEAR SIMPLES 1 O nosso objetvo é estudar a relação entre duas varáves quanttatvas. Eemplos:. Idade e altura das cranças.. v. Tempo de prátca de esportes e rtmo cardíaco
Eletroquímica 2017/3. Professores: Renato Camargo Matos Hélio Ferreira dos Santos.
 Eletroquímca 2017/3 Professores: Renato Camargo Matos Hélo Ferrera dos Santos http://www.ufjf.br/nups/ Data Conteúdo 07/08 Estatístca aplcada à Químca Analítca Parte 2 14/08 Introdução à eletroquímca 21/08
Eletroquímca 2017/3 Professores: Renato Camargo Matos Hélo Ferrera dos Santos http://www.ufjf.br/nups/ Data Conteúdo 07/08 Estatístca aplcada à Químca Analítca Parte 2 14/08 Introdução à eletroquímca 21/08
MODELOS DE REGRESSÃO PARAMÉTRICOS
 MODELOS DE REGRESSÃO PARAMÉTRICOS Às vezes é de nteresse nclur na análse, característcas dos ndvíduos que podem estar relaconadas com o tempo de vda. Estudo de nsufcênca renal: verfcar qual o efeto da
MODELOS DE REGRESSÃO PARAMÉTRICOS Às vezes é de nteresse nclur na análse, característcas dos ndvíduos que podem estar relaconadas com o tempo de vda. Estudo de nsufcênca renal: verfcar qual o efeto da
UNIVERSIDADE DE PERNAMBUCO. Física Experimental. Prof o José Wilson Vieira
 UNIVERSIDADE DE PERNAMBUCO ESCOLA POLITÉCNICA DE PERNAMBUCO Físca Expermental Prof o José Wlson Vera wlson.vera@upe.br AULA 01: PROCESSOS DE ANÁLISE GRÁFICA E NUMÉRICA MODELO LINEAR Recfe, agosto de 2015
UNIVERSIDADE DE PERNAMBUCO ESCOLA POLITÉCNICA DE PERNAMBUCO Físca Expermental Prof o José Wlson Vera wlson.vera@upe.br AULA 01: PROCESSOS DE ANÁLISE GRÁFICA E NUMÉRICA MODELO LINEAR Recfe, agosto de 2015
3ª AULA: ESTATÍSTICA DESCRITIVA Medidas Numéricas
 PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA DE TRASPORTES E GESTÃO TERRITORIAL PPGTG DEPARTAMETO DE EGEHARIA CIVIL ECV DISCIPLIA: TGT41006 FUDAMETOS DE ESTATÍSTICA 3ª AULA: ESTATÍSTICA DESCRITIVA Meddas umércas
PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA DE TRASPORTES E GESTÃO TERRITORIAL PPGTG DEPARTAMETO DE EGEHARIA CIVIL ECV DISCIPLIA: TGT41006 FUDAMETOS DE ESTATÍSTICA 3ª AULA: ESTATÍSTICA DESCRITIVA Meddas umércas
RISCO. Investimento inicial $ $ Taxa de retorno anual Pessimista 13% 7% Mais provável 15% 15% Otimista 17% 23% Faixa 4% 16%
 Análse de Rsco 1 RISCO Rsco possbldade de perda. Quanto maor a possbldade, maor o rsco. Exemplo: Empresa X va receber $ 1.000 de uros em 30 das com títulos do governo. A empresa Y pode receber entre $
Análse de Rsco 1 RISCO Rsco possbldade de perda. Quanto maor a possbldade, maor o rsco. Exemplo: Empresa X va receber $ 1.000 de uros em 30 das com títulos do governo. A empresa Y pode receber entre $
Os modelos de regressão paramétricos vistos anteriormente exigem que se suponha uma distribuição estatística para o tempo de sobrevivência.
 MODELO DE REGRESSÃO DE COX Os modelos de regressão paramétrcos vstos anterormente exgem que se suponha uma dstrbução estatístca para o tempo de sobrevvênca. Contudo esta suposção, caso não sea adequada,
MODELO DE REGRESSÃO DE COX Os modelos de regressão paramétrcos vstos anterormente exgem que se suponha uma dstrbução estatístca para o tempo de sobrevvênca. Contudo esta suposção, caso não sea adequada,
Distribuição de Massa Molar
 Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
Químca de Polímeros Prof a. Dr a. Carla Dalmoln carla.dalmoln@udesc.br Dstrbução de Massa Molar Materas Polmércos Polímero = 1 macromolécula com undades químcas repetdas ou Materal composto por númeras
1. CORRELAÇÃO E REGRESSÃO LINEAR
 1 CORRELAÇÃO E REGREÃO LINEAR Quando deseja-se estudar se exste relação entre duas varáves quanttatvas, pode-se utlzar a ferramenta estatístca da Correlação Lnear mples de Pearson Quando essa correlação
1 CORRELAÇÃO E REGREÃO LINEAR Quando deseja-se estudar se exste relação entre duas varáves quanttatvas, pode-se utlzar a ferramenta estatístca da Correlação Lnear mples de Pearson Quando essa correlação
DESENVOLVIMENTO DE UM PROGRAMA COMPUTACIONAL PARA CONTROLE DE MEDIÇÕES DIMENSIONAIS COM ÊNFASE NA GARANTIA DA CONFORMIDADE DE PRODUTOS
 DESENVOLVIMENTO DE UM PROGRAMA COMPUTACIONAL PARA CONTROLE DE MEDIÇÕES DIMENSIONAIS COM ÊNFASE NA GARANTIA DA CONFORMIDADE DE PRODUTOS JOSÉ EDUARDO FERREIRA DE OLIVEIRA (CRFET-PE) jefocefetpe@yahoo.com.br
DESENVOLVIMENTO DE UM PROGRAMA COMPUTACIONAL PARA CONTROLE DE MEDIÇÕES DIMENSIONAIS COM ÊNFASE NA GARANTIA DA CONFORMIDADE DE PRODUTOS JOSÉ EDUARDO FERREIRA DE OLIVEIRA (CRFET-PE) jefocefetpe@yahoo.com.br
Programa de Certificação de Medidas de um laboratório
 Programa de Certfcação de Meddas de um laboratóro Tratamento de dados Elmnação de dervas Programa de calbração entre laboratóros Programa nterno de calbração justes de meddas a curvas Tratamento dos resultados
Programa de Certfcação de Meddas de um laboratóro Tratamento de dados Elmnação de dervas Programa de calbração entre laboratóros Programa nterno de calbração justes de meddas a curvas Tratamento dos resultados
Caderno de Exercícios Resolvidos
 Estatístca Descrtva Exercíco 1. Caderno de Exercícos Resolvdos A fgura segunte representa, através de um polígono ntegral, a dstrbução do rendmento nas famílas dos alunos de duas turmas. 1,,75 Turma B
Estatístca Descrtva Exercíco 1. Caderno de Exercícos Resolvdos A fgura segunte representa, através de um polígono ntegral, a dstrbução do rendmento nas famílas dos alunos de duas turmas. 1,,75 Turma B
Apostila de Estatística Curso de Matemática. Volume II 2008. Probabilidades, Distribuição Binomial, Distribuição Normal. Prof. Dr. Celso Eduardo Tuna
 Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Apostla de Estatístca Curso de Matemátca Volume II 008 Probabldades, Dstrbução Bnomal, Dstrbução Normal. Prof. Dr. Celso Eduardo Tuna 1 Capítulo 8 - Probabldade 8.1 Conceto Intutvamente pode-se defnr probabldade
Curso de extensão, MMQ IFUSP, fevereiro/2014. Alguns exercício básicos
 Curso de extensão, MMQ IFUSP, feverero/4 Alguns exercíco báscos I Exercícos (MMQ) Uma grandeza cujo valor verdadero x é desconhecdo, fo medda três vezes, com procedmentos expermentas dêntcos e, portanto,
Curso de extensão, MMQ IFUSP, feverero/4 Alguns exercíco báscos I Exercícos (MMQ) Uma grandeza cujo valor verdadero x é desconhecdo, fo medda três vezes, com procedmentos expermentas dêntcos e, portanto,
PLANILHAS EXCEL/VBA PARA PROBLEMAS ENVOLVENDO EQUILÍBRIO LÍQUIDO-VAPOR EM SISTEMAS BINÁRIOS
 PLANILHAS EXCEL/VBA PARA PROBLEMAS ENVOLVENDO EQUILÍBRIO LÍQUIDO-VAPOR EM SISTEMAS BINÁRIOS L. G. Olvera, J. K. S. Negreros, S. P. Nascmento, J. A. Cavalcante, N. A. Costa Unversdade Federal da Paraíba,
PLANILHAS EXCEL/VBA PARA PROBLEMAS ENVOLVENDO EQUILÍBRIO LÍQUIDO-VAPOR EM SISTEMAS BINÁRIOS L. G. Olvera, J. K. S. Negreros, S. P. Nascmento, J. A. Cavalcante, N. A. Costa Unversdade Federal da Paraíba,
Aplicando o método de mínimos quadrados ordinários, você encontrou o seguinte resultado: 1,2
 Econometra - Lsta 3 - Regressão Lnear Múltpla Professores: Hedbert Lopes, Prscla Rbero e Sérgo Martns Montores: Gustavo Amarante e João Marcos Nusdeo QUESTÃO 1. Você trabalha na consultora Fazemos Qualquer
Econometra - Lsta 3 - Regressão Lnear Múltpla Professores: Hedbert Lopes, Prscla Rbero e Sérgo Martns Montores: Gustavo Amarante e João Marcos Nusdeo QUESTÃO 1. Você trabalha na consultora Fazemos Qualquer
BALANÇO HÍDRICO: UMA FERRAMENTA PARA GESTÃO INDUSTRIAL E OTIMIZAÇÃO AMBIENTAL.
 BALANÇO HÍDRICO: UMA FERRAMENTA PARA GESTÃO INDUSTRIAL E OTIMIZAÇÃO AMBIENTAL. Leonardo Slva de Souza (1) Mestrando em Engenhara Químca(UFBA). Pesqusador da Rede Teclm. Bárbara Vrgína Damasceno Braga (1)
BALANÇO HÍDRICO: UMA FERRAMENTA PARA GESTÃO INDUSTRIAL E OTIMIZAÇÃO AMBIENTAL. Leonardo Slva de Souza (1) Mestrando em Engenhara Químca(UFBA). Pesqusador da Rede Teclm. Bárbara Vrgína Damasceno Braga (1)
ESTATÍSTICA MULTIVARIADA 2º SEMESTRE 2010 / 11. EXERCÍCIOS PRÁTICOS - CADERNO 1 Revisões de Estatística
 ESTATÍSTICA MULTIVARIADA º SEMESTRE 010 / 11 EXERCÍCIOS PRÁTICOS - CADERNO 1 Revsões de Estatístca -0-11 1.1 1.1. (Varáves aleatóras: função de densdade e de dstrbução; Méda e Varânca enquanto expectatvas
ESTATÍSTICA MULTIVARIADA º SEMESTRE 010 / 11 EXERCÍCIOS PRÁTICOS - CADERNO 1 Revsões de Estatístca -0-11 1.1 1.1. (Varáves aleatóras: função de densdade e de dstrbução; Méda e Varânca enquanto expectatvas
UTILIZAÇÃO DO MÉTODO DE TAGUCHI NA REDUÇÃO DOS CUSTOS DE PROJETOS. Uma equação simplificada para se determinar o lucro de uma empresa é:
 UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
UTILIZAÇÃO DO MÉTODO DE TAGUCHI A REDUÇÃO DOS CUSTOS DE PROJETOS Ademr José Petenate Departamento de Estatístca - Mestrado em Qualdade Unversdade Estadual de Campnas Brasl 1. Introdução Qualdade é hoje
Metodologia IHFA - Índice de Hedge Funds ANBIMA
 Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
Metodologa IHFA - Índce de Hedge Funds ANBIMA Versão Abrl 2011 Metodologa IHFA Índce de Hedge Funds ANBIMA 1. O Que é o IHFA Índce de Hedge Funds ANBIMA? O IHFA é um índce representatvo da ndústra de hedge
2 Metodologia de Medição de Riscos para Projetos
 2 Metodologa de Medção de Rscos para Projetos Neste capítulo remos aplcar os concetos apresentados na seção 1.1 ao ambente de projetos. Um projeto, por defnção, é um empreendmento com metas de prazo, margem
2 Metodologa de Medção de Rscos para Projetos Neste capítulo remos aplcar os concetos apresentados na seção 1.1 ao ambente de projetos. Um projeto, por defnção, é um empreendmento com metas de prazo, margem
CURSO ON-LINE PROFESSOR: VÍTOR MENEZES
 O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
O Danel Slvera pedu para eu resolver mas questões do concurso da CEF. Vou usar como base a numeração do caderno foxtrot Vamos lá: 9) Se, ao descontar uma promssóra com valor de face de R$ 5.000,00, seu
Física. Setor B. Índice-controle de Estudo. Prof.: Aula 23 (pág. 86) AD TM TC. Aula 24 (pág. 87) AD TM TC. Aula 25 (pág.
 Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Físca Setor Prof.: Índce-controle de studo ula 23 (pág. 86) D TM TC ula 24 (pág. 87) D TM TC ula 25 (pág. 88) D TM TC ula 26 (pág. 89) D TM TC ula 27 (pág. 91) D TM TC ula 28 (pág. 91) D TM TC evsanglo
Elaboração: Fevereiro/2008
 Elaboração: Feverero/2008 Últma atualzação: 19/02/2008 E ste Caderno de Fórmulas tem por objetvo esclarecer aos usuáros a metodologa de cálculo e os crtéros de precsão utlzados na atualzação das Letras
Elaboração: Feverero/2008 Últma atualzação: 19/02/2008 E ste Caderno de Fórmulas tem por objetvo esclarecer aos usuáros a metodologa de cálculo e os crtéros de precsão utlzados na atualzação das Letras
UNIVERSIDADE FEDERAL DO PARANÁ DEPARTAMENTO DE ESTATÍSTICA CE 071 ANÁLISE DE REGRESSÃO LINEAR. Cesar Augusto Taconeli
 UNIVERSIDADE FEDERAL DO PARANÁ DEPARTAMENTO DE ESTATÍSTICA CE 7 ANÁLISE DE REGRESSÃO LINEAR Cesar Augusto Taconel Curtba-PR . INTRODUÇÃO Taconel, C.A. Análse de Regressão Lnear Ao se tratar da relação
UNIVERSIDADE FEDERAL DO PARANÁ DEPARTAMENTO DE ESTATÍSTICA CE 7 ANÁLISE DE REGRESSÃO LINEAR Cesar Augusto Taconel Curtba-PR . INTRODUÇÃO Taconel, C.A. Análse de Regressão Lnear Ao se tratar da relação
As tabelas resumem as informações obtidas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de informações.
 1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
1. TABELA DE DISTRIBUIÇÃO DE FREQÜÊNCIA As tabelas resumem as normações obtdas da amostra ou da população. Essas tabelas podem ser construídas sem ou com perda de normações. As tabelas sem perda de normação
www.obconcursos.com.br/portal/v1/carreirafiscal
 www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
www.obconcursos.com.br/portal/v1/carrerafscal Moda Exercíco: Determne o valor modal em cada um dos conjuntos de dados a segur: X: { 3, 4,, 8, 8, 8, 9, 10, 11, 1, 13 } Mo 8 Y: { 10, 11, 11, 13, 13, 13,
MEDIÇÕES DE VIBRAÇÕES NO CORPO HUMANO ESTIMATIVA DA INCERTEZA
 Acústca 008 0 - de Outubro, Combra, Portugal Unversdade de Combra MEDIÇÕES DE VIBRAÇÕES NO CORPO HUMANO ESTIMATIVA DA INCERTEZA Jorge Fradque, Fátma Inglês Drecção Regonal da Economa de Lsboa e Vale do
Acústca 008 0 - de Outubro, Combra, Portugal Unversdade de Combra MEDIÇÕES DE VIBRAÇÕES NO CORPO HUMANO ESTIMATIVA DA INCERTEZA Jorge Fradque, Fátma Inglês Drecção Regonal da Economa de Lsboa e Vale do
Experiência V (aulas 08 e 09) Curvas características
 Experênca (aulas 08 e 09) Curvas característcas 1. Objetvos 2. Introdução 3. Procedmento expermental 4. Análse de dados 5. Referêncas 1. Objetvos Como no expermento anteror, remos estudar a adequação de
Experênca (aulas 08 e 09) Curvas característcas 1. Objetvos 2. Introdução 3. Procedmento expermental 4. Análse de dados 5. Referêncas 1. Objetvos Como no expermento anteror, remos estudar a adequação de
