Regressão Linear - Introdução
|
|
|
- Gonçalo Fortunato Natal
- 7 Há anos
- Visualizações:
Transcrição
1 Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo lear À varável Y chama-se varável depedete e à varável x varável depedete ou explcatva. Exemplos: º) O úmero de horas de estudo poderá está relacoado com a ota obtda pelo aluo. As horas de estudo é a varável depedete (x) e a ota obtda será a varável depedete (Y). º) A relação etre o º de fogos florestas (Y) e a temperatura máxma mesal (x).
2 Regressão Lear - Itrodução Na regressão lear múltpla pretede-se relacoar uma varável depedete Y com dversas varáves depedetes x, x,, x k através do modelo lear Y = β + β x + β x β 0 k x k Exemplos: º) O peso de uma pessoa depede da sua altura, mas certamete também depederá da sua dade, desdade dos ossos e perímetro da ctura. º) O cosumo de eerga depederá da temperatura mas também depede do preço da electrcdade.
3 Regressão Lear Smples - Correlação O poto de partda da aálse da regressão lear deve ser o estudo da exstêca (ou ão) de uma relação lear etre as varáves. Para estudar a relação etre duas varáves exstem métodos: - gráfcos: dagramas de dspersão - umércos: coefcete de correlação de pearso Método gráfco: Os dagramas de dspersão cosstem a represetação gráfca dos pares ordeados (x ;Y ) um sstema de exos cartesaos, de modo a observamos uma uvem de potos correspodetes à amostra obtda. Quato mas os potos represetados se ajustarem a uma recta, melhor será a relação lear etre as varáves. 3
4 Regressão Lear Smples - Correlação Exemplo: Num estudo realzado a 0 pessoas regstaram-se as suas dades e os íves de colesterol, tedo-se obtdo: Idade Colesterol 30,60 60,50 40,0 0,40 50,70 30,80 40,0 0,50 70,80 60,60 Dagrama de dspersão: colesterol,80,40,00, dade De uma forma tutva podemos coclur que parece exstr uma relação lear etre as varáves, que matematcamete 4 se traduzrá através de uma recta.
5 Regressão Lear Smples - Correlação Através dos segutes gráfcos pode-se coclur que: Y Y Y x x x Há uma forte correlação lear postva. Há uma forte correlação lear egatva. Há uma fraca correlação lear. 5
6 Regressão Lear Smples - Correlação Método umérco: O coefcete de correlação (amostral), ou coefcete de correlação lear de Pearso, é uma medda habtual do grau de assocação lear das varáves: ( x x)( y y) = R = = ( x x) ( y y) YY = = Y ode Y, e YY também podem ser defdos por: Y = = = = x y x y = = = YY = = x y ( ) x ( ) y = 6
7 Regressão Lear Smples - Correlação Iterpretação do coefcete de correlação (amostral): Este coefcete vara etre - e : R Quato maor for o valor absoluto de R, mas forte será a assocação lear etre as varáves. Se R estver próxmo de zero etão as varáves serão ão correlacoadas. Se R for postvo etão a relação lear é postva (x e Y varam o mesmo setdo) e se R for egatvo a relação lear é egatva (x e Y varam em setdos opostos). Se R for gual a ou - a relação lear será perfeta! - -0,8 0 0,8 Forte correlação lear egatva Fraca correlação lear Forte correlação lear postva 7
8 Regressão Lear Smples O modelo Objectvo: Quado exste uma forte correlação etre as varáves em estudo qual é a melhor relação lear etre as elas? Yˆ = ˆ β + ˆ β x ; ˆ β, ˆ β R 0 0 Método dos mímos quadrados: Um dos métodos mas utlzados para estmar a recta que melhor se ajusta aos valores observados é o método dos mímos quadrados. Este método cosste em determar os valores de e que mmzam a soma do quadrado dos erros (desvos dos valores observados Y dos valores obtdos pelo modelo ). Yˆ ˆβ 0 ˆβ 8
9 Regressão Lear Smples O modelo Y Ŷ Y e Yˆ = ˆ β + ˆ β x 0 ˆβ ˆβ Os valores de 0e que mmzam a soma do quadrado dos erros E = e = ( Y ˆ β β x ) = ˆ 0 = x x são dados por: ˆ β = Y e ˆ β 0 = Y ˆ β x 9
10 Regressão Lear Smples O modelo Exemplo: Pegado ovamete o exemplo das varáves Idade/Colesterol, verfca-se que: Idade Colesterol 30,60 60,50 40,0 0,40 50,70 30,80 40,0 0,50 70,80 60,60 0 x = 0 = x Model = = 40; 0400; (Costat) Idade 0 = y 0 = a. Depedet Varable: Colesterol = y. = Coeffcets a 47.4; 969 Ustadardzed Stadardzed Coeffcets Coeffcets B Std. Error Beta t Sg.,94,4 6,56,000,08,003,955 9,07,000 0 x = y = ^ 0 =, β 0 94 ^ =, β 0 08 ordeada a orgem declve da recta 0
11 Regressão Lear Smples O modelo Sedo a recta de regressão dada por: Colesterol = 0, , 08 * Idade
12 Regressão Lear Smples Avalação do modelo Estado o modelo de regressão lear estabelecdo tora-se ecessáro avalar a sua qualdade. Para sso exstem város métodos, gráfcos e umércos: Coefcete de determação Aálse de resíduos Teste ao declve da recta
13 Regressão Lear Smples Avalação do modelo Coefcete de determação R : É uma medda da proporção da varabldade de Y explcada pelo modelo de regressão lear, já que cosste a razão etre a soma dos quadrados dos resíduos e a soma dos quadrados total. Por defção, o coefcete de determação é: Y R = = YY ode já foram defdos aterormete e se tem: Y, e YY R T R = ( Yˆ Y ) e = ( Y Y ) = T = 3
14 Regressão Lear Smples Avalação do modelo O coefcete de determação é smplesmete o quadrado do coefcete de correlação amostral. R só pode assumr valores etre 0 e : 0 R Em geral, se a relação etre x e Y for fortemete lear R deve assumr um valor próxmo de (superor a 0.9). No etato, se R estver próxmo de zero deve-se ter cudado com as coclusões a trar. Pode ão sgfcar que o modelo de regressão lear esteja desajustado. 4
15 Regressão Lear Smples Avalação do modelo Exemplo: Cosderado ovamete o exemplo das varáves Idade/Colesterol, verfca-se que : = YY Y 769 ; =.456; = R = e R logo. = Model Summary No SPSS: Model Adjusted Std. Error of R R Square R Square the Estmate,955 a,9,900,6493 a. Predctors: (Costat), Idade Coefcete de correlação Coefcete de determação 5
16 Regressão Lear Smples Avalação do modelo Aálse dos resíduos: Este método de aálse da qualdade do modelo de regressão cosste em represetar grafcamete os valores predtos versus resíduos, Y ˆ;. ( ) e Se ajustameto for bom, os potos represetados ão devem apresetar qualquer correlação ou padrão: devem ser ormas, com varâca costate e depedetes. O dagrama de resíduos deve apresetar uma macha de potos aleatóros e com a mesma dspersão em toro do exo dos xx. 6
17 Regressão Lear Smples Avalação do modelo x Exemplo: No exemplo que tem sdo cosderado, efectuado as prevsões e calculado os erros correspodetes obtém-se: Y Yˆ 30,6,76-0,6 60,5,60-0,0 40,,04 0,6 0,4,48-0,08 50,7,3 0,38 30,8,76 0,04 40,,04 0,06 0,5,48 0,0 70,8,88-0,08 60,6,60 0,00 e = Y Yˆ 7
18 Regressão Lear Smples Avalação do modelo Teste ao declve da recta: Esta aálse da qualdade de ajustameto do modelo de regressão lear é o fudo a resposta à questão: Será que Y depede mesmo de x? Para respoder a esta perguta realza-se o teste de hpóteses: H : β = 0 vs H : β 0 0 A forma mas smples de se tomar uma decsão é usado a estatístca MQ F = MQ R E e o p-value que resultam da tabela ANOVA. Deve-se rejetar a hpótese ula, e portato assumr que x flueca Y, se o p-value for baxo (meor do que 0.05). 8
19 Regressão Lear Smples ANOVA ANOVA Aalyss of Varace A aálse da varâca, um modelo de regressão lear, cosste em separar a varabldade das observações em duas parcelas: varabldade devda à regressão e a varabldade resdual. = ( Y Y ) = ( Yˆ Y ) + ( Y Y ) ˆ = = = + T R E O sgfcado da regressão é tato maor quato maor for R e meor for E. Usualmete esta formação é agrupada uma tabela: tabela ANOVA. 9
20 Regressão Lear Smples ANOVA Tabela ANOVA Fotes de varação Varações (Somas dos desvos quadrátcos) Graus de Lberdade (Nº de varáves depedetes) Desvos Quadrátcos Médos Regressão R MQ R = R Resdual E MQ E E = Total T 0
21 Regressão Lear Smples ANOVA Exemplo: A tabela ANOVA do exemplo das varáves Idade/Colesterol é dada (o SPSS) por: Model Regresso Resdual Total a. Predctors: (Costat), Idade b. Depedet Varable: Colesterol ANOVA b Sum of Squares df Mea Square F Sg.,38,38 8,9,000 a,8 8,07,456 9 Coclusão: ( ) A estatístca F toma o valor 8,9,38/ 0,07 e o p-value do teste é ulo. Por assumr um valor baxo, pode-se coclur que faz setdo utlzar um modelo de regressão lear etre estas varáves.
22 Regressão Lear Múltpla O modelo Um modelo de regressão lear múltpla descreve a relação (lear) etre um cojuto de varáves depedetes,,,, k, e uma varável depedete Y: Y = β + β x + β x β 0 k x k Para estmar coefcetes do modelo,, pode-se aplcar ovamete o método dos mímos quadrados e mmzar a soma do quadrado dos erros: β 0, β,..., β k ( Y ˆ β ˆ β x +... ˆ β x ) E = + 0 = k k
23 3 Regressão Lear Múltpla O modelo Após a realzação dos cálculos adequados, os estmadores dos coefcetes são dados pelas soluções das gualdades: ode. k k Y k Y k x x Y k k k k k β β β β β β β ˆ... ˆ ˆ ˆ... ˆ... ˆ... ˆ 0 = = + + = + + ( ) = = q p q p q p q p
24 Regressão Lear Múltpla O modelo Exemplo: Supodo agora que o ível de colesterol uma pessoa depede da sua dade e também do seu peso, regstou-se o peso das 0 pessoas aalsadas aterormete. Idade Peso Colesterol 30 57, , ,0 0 67, , , ,0 0 64, , ,60 Model (Costat) dade peso Ustadardzed Coeffcets a. Depedet Varable: colesterol Coeffcets a Stadardzed Coeffcets B Std. Error Beta t Sg.,88,4,458,66,09,003,958 0,438,000,0,006,7,878,03 Cosderado x como sedo a varável Idade e x a varável Peso, o modelo é: Y ˆ = x x 4
25 Regressão Lear Múltpla Avalação do modelo Novamete exstem dversos métodos para aalsar a qualdade de ajustameto do modelo de regressão lear múltpla e a sua sgfcâca: Coefcete de determação (ajustado) Aálse gráfca das prevsões e dos resíduos Teste ao sgfcado da regressão 5
26 Regressão Lear Múltpla Avalação do modelo Coefcete de determação (ajustado): O coefcete de determação, para a regressão múltpla, é defdo de forma aáloga ao da regressão smples: Tal como aterormete se o ajustameto do modelo for bom, R estará próxmo de. R = R T No etato: Na regressão múltpla já ão se tem o quadrado de ehum coefcete de correlação. Ao troduzrmos ovas varáves depedetes o modelo o valor de R aumeta, o que pode duzr em erro uma vez que mutas varáves pode ão sgfcar um melhor modelo. Para cotorar o problema é usual cosderar o coefcete de determação ajustado. 6
27 Regressão Lear Múltpla Avalação do modelo O coefcete de determação ajustado defe-se pela expressão: R a = ( ) E ( k ) T ode k represeta o º de varáves depedetes o modelo. Exemplo: No exemplo ateror tem-se R = 0.94, o que represeta boas dcações quato à qualdade do modelo. Model Model Summary b Adjusted Std. Error of R R Square R Square the Estmate,970 a,94,94,4379 a. Predctors: (Costat), peso, dade b. Depedet Varable: colesterol 7
28 Regressão Lear Múltpla Avalação do modelo Aálse gráfca: Como o modelo de regressão múltpla é uma hpersuperfíce, em sempre é possível verfcar smultaeamete o comportameto de Y em fução das dversas varáves depedetes. Normalmete aalsa-se a relação etre Y e cada uma das varáves x dvdualmete, através dos respectvos dagramas de dspersão. Um outro método gráfco muto utlzado cosste em represetar grafcamete as observações versus os valores prevstos. Se o modelo for adequado, os valores prevstos devem estar próxmos dos observados e portato o dagrama de dspersão deve coter todos os Y = Y potos próxmos da recta. x Yˆ 8
29 Regressão Lear Múltpla Avalação do modelo Exemplo: No exemplo ateror verfca-se que os potos estão próxmos da recta, o que sugere que o modelo cosderado ão será desajustado. Y = x ( Y ; ˆ ) Y Colesterol Observado Prevsto Y Yˆ,60,66,50,6,0,7,40,48,70,40,80,73,0,4,50,45,80,83,60,64 9
30 Regressão Lear Múltpla Avalação do modelo A aálse dos resíduos é completamete aáloga à da regressão lear smples: quato mas aleatóra for a dsposção dos potos em toro do exo das abcssas melhor será a qualdade do modelo. ( Y ˆ; ) e Exemplo: Ao lado ecotra-se represetado o dagrama dos resíduos do exemplo ateror. 30
31 Regressão Lear Múltpla Avalação do modelo Teste ao sgfcado da regressão: Pretede-se com esta aálse testar se tem sgfcado cosderar o modelo de regressão todas as varáves depedetes x,,x k. As hpóteses a cosderar são: H : β =... = β = 0 vs H : Algumβ 0 k j 0 MQ F = MQ R Mas uma vez deve-se usar a estatístca e o p-value que decorre da tabela ANOVA para tomar uma decsão. Rejeta-se a hpótese ula, e assume-se que há varáves depedetes a fluecar Y, se o p-value for baxo ( 0.05). E 3
32 Regressão Lear Múltpla ANOVA A terpretação da tabela ANOVA é aáloga ao caso da regressão smples e o cotexto da regressão lear múltpla é dada por: Fotes de varação Regressão Resdual Varações (Somas dos desvos quadrátcos) R E Graus de Lberdade (Nº de varáves depedetes) k k Desvos Quadrátcos Médos MQ = R R k E MQ = E k Total T 3
33 Regressão Lear Múltpla ANOVA Exemplo: A tabela ANOVA do exemplo cosderado é dada por: Model Regresso Resdual Total ANOVA b Sum of Squares df Mea Square F Sg.,3,56 55,897,000 a,45 7,0,456 9 a. Predctors: (Costat), peso, dade b. Depedet Varable: colesterol Como o p-value do teste é zero, poderá fazer setdo utlzar um modelo de regressão lear com todas estas varáves depedetes. 33
Capítulo 5: Ajuste de curvas pelo método dos mínimos quadrados
 Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Regressão Linear e Multilinear
 Regressão Lear e Multlear Deleameto Expermetal Mestrado em Sstemas de Produção em Agrcultura Medterrâca Modelo de Regressão Lear Smples X Varável Idepedete Y Varável Depedete y =β +β x +ε β ordeada a orgem
Regressão Lear e Multlear Deleameto Expermetal Mestrado em Sstemas de Produção em Agrcultura Medterrâca Modelo de Regressão Lear Smples X Varável Idepedete Y Varável Depedete y =β +β x +ε β ordeada a orgem
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou expermetal. Numa relação expermetal os valores de uma das varáves
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou expermetal. Numa relação expermetal os valores de uma das varáves
Matemática Ficha de Trabalho
 Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
2-0,0041295**.C 2 + 0,0017052**.T.C
 14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
Probabilidade e Estatística. Correlação e Regressão Linear
 Probabldade e Estatístca Correlação e Regressão Lnear Varáves Varável: característcas ou tens de nteresse de cada elemento de uma população ou amostra Também chamada parâmetro, posconamento, condção...
Probabldade e Estatístca Correlação e Regressão Lnear Varáves Varável: característcas ou tens de nteresse de cada elemento de uma população ou amostra Também chamada parâmetro, posconamento, condção...
3 - ANÁLISE BIDIMENSIONAL
 INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
ANÁLISE DE REGRESSÃO E CORRELAÇÃO
 ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
ANÁLISE DE REGRESSÃO E CORRELAÇÃO
 ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves A aálse de regressão e correlação compreedem
ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves A aálse de regressão e correlação compreedem
Avaliação da qualidade do ajuste
 Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
Relatório 2ª Atividade Formativa UC ECS
 Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
CAPÍTULO 5. Ajuste de curvas pelo Método dos Mínimos Quadrados
 CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
REGESD Prolic Matemática e Realidade- Profª Suzi Samá Pinto e Profº Alessandro da Silva Saadi
 REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo IV, Iterolação Polomal, estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo IV, Iterolação Polomal, estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
Regressão e Correlação
 Regressão e Correlação Júlo Osóro Regressão & Correlação: geeraldades Em mutas stuações de pesqusa cetífca, dspomos de uma amostra aleatóra de pares de dados (x, ), resultates da medda cocomtate de duas
Regressão e Correlação Júlo Osóro Regressão & Correlação: geeraldades Em mutas stuações de pesqusa cetífca, dspomos de uma amostra aleatóra de pares de dados (x, ), resultates da medda cocomtate de duas
Tópicos Extras 2ª parte. Análise de Correlação e Regressão
 Tópcos Extras ª parte Aálse de Correlação e Regressão 1 Defções báscas ANÁLISE DE CORRELAÇÃO Mesurar a força da assocação etre as varáves (geralmete através do cálculo de algum coefcete). ANÁLISE DE REGRESSÃO
Tópcos Extras ª parte Aálse de Correlação e Regressão 1 Defções báscas ANÁLISE DE CORRELAÇÃO Mesurar a força da assocação etre as varáves (geralmete através do cálculo de algum coefcete). ANÁLISE DE REGRESSÃO
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Análise de Regressão
 Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
Regressao Simples. Parte II: Anova, Estimação Intervalar e Predição
 egressao Smples Parte II: Aova, Estmação Itervalar e Predção Aálse de Varâca Nem todos os valores das amostras estão cotdos a reta de regressão, e quato mas afastados estverem por, a reta represetará a
egressao Smples Parte II: Aova, Estmação Itervalar e Predção Aálse de Varâca Nem todos os valores das amostras estão cotdos a reta de regressão, e quato mas afastados estverem por, a reta represetará a
PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA
 UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
? Isso é, d i= ( x i. . Percebeu que
 Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Modelo de Regressão Simples
 Modelo de Regressão Smples Hstora Hstóra Termo regressão fo troduzdo por Fracs Galto (8-9). Estudo sobre altura de pas e flhos. Karl Pearso coletou mas de ml regstros e verfcou a le de regressão uversal
Modelo de Regressão Smples Hstora Hstóra Termo regressão fo troduzdo por Fracs Galto (8-9). Estudo sobre altura de pas e flhos. Karl Pearso coletou mas de ml regstros e verfcou a le de regressão uversal
Licenciatura em Ciências USP/ Univesp funções polinomiais 4
 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
REGRESSÃO LINEAR 05/10/2016 REPRESENTAÇAO MATRICIAL. Y i = X 1i + 2 X 2i k X ni + i Y = X + INTRODUÇÃO SIMPLES MÚLTIPLA
 REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
Estatística Descritiva
 Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
7 Análise de covariância (ANCOVA)
 Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Regressão Simples. Parte III: Coeficiente de determinação, regressão na origem e método de máxima verossimilhança
 Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: Prof. Lorí Val, Dr. val@pucrs.br http://www.pucrs.br/famat/val www.pucrs.br/famat/val/ correlacoal ou expermetal. Numa relação expermetal os valores
É o grau de assocação etre duas ou mas varáves. Pode ser: Prof. Lorí Val, Dr. val@pucrs.br http://www.pucrs.br/famat/val www.pucrs.br/famat/val/ correlacoal ou expermetal. Numa relação expermetal os valores
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
tica Professor Renato Tião
 Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO
 NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO ISABEL C. C. LEITE SALVADOR BA 007 Estatístca Prof.ª Isabel C. C. Lete TEORIA DA AMOSTRAGEM DISTRIBUIÇÃO AMOSTRAL DOS ESTIMADORES A teora da amostragem
NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO ISABEL C. C. LEITE SALVADOR BA 007 Estatístca Prof.ª Isabel C. C. Lete TEORIA DA AMOSTRAGEM DISTRIBUIÇÃO AMOSTRAL DOS ESTIMADORES A teora da amostragem
x n = n ESTATÍSTICA STICA DESCRITIVA Conjunto de dados: Organização; Amostra ou Resumo; Apresentação. População
 ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
MEDIDAS DE DISPERSÃO:
 MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
MEDID DE DIPERÃO: fução dessas meddas é avalar o quato estão dspersos os valores observados uma dstrbução de freqüêca ou de probabldades, ou seja, o grau de afastameto ou de cocetração etre os valores.
Gráfico de Controle de Regressão Aplicado ao Monitoramento de Características da Qualidade do Eletrodo de Carbono
 Gráfco de Cotrole de Regressão Aplcado ao Motorameto de Característcas da Qualdade do Eletrodo de Carboo Marcello Neva de Mello, evamarcello@gmal.com Wager Rogéro Ferrera Phero, wager35@gmal.com Edso Marcos
Gráfco de Cotrole de Regressão Aplcado ao Motorameto de Característcas da Qualdade do Eletrodo de Carboo Marcello Neva de Mello, evamarcello@gmal.com Wager Rogéro Ferrera Phero, wager35@gmal.com Edso Marcos
Modelos de regressão linear: abordagem clássica
 Modelos de regressão lear: abordagem clássca Prof. Marcelo Rubes mrubes@me.uerj.br Depto. Estatístca Aálse de Regressão Objetvo: Determar uma fução matemátca que descreva a relação etre uma varável cotíua
Modelos de regressão lear: abordagem clássca Prof. Marcelo Rubes mrubes@me.uerj.br Depto. Estatístca Aálse de Regressão Objetvo: Determar uma fução matemátca que descreva a relação etre uma varável cotíua
Estatística Básica - Continuação
 Professora Adraa Borsso http://www.cp.utfpr.edu.br/borsso adraaborsso@utfpr.edu.br COEME - Grupo de Matemátca Meddas de Varabldade ou Dspersão Estatístca Básca - Cotuação As meddas de tedêca cetral, descrtas
Professora Adraa Borsso http://www.cp.utfpr.edu.br/borsso adraaborsso@utfpr.edu.br COEME - Grupo de Matemátca Meddas de Varabldade ou Dspersão Estatístca Básca - Cotuação As meddas de tedêca cetral, descrtas
Construção e Análise de Gráficos
 Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
ESCOLA SUPERIOR DE TECNOLOGIA E GESTÃO
 Área Cetífca Matemátca Udade Curso Egehara do Ambete Ao º Semestre º Folha Nº 8: Aálse de Regressão e de Correlação Probabldades e Estatístca Ao 00/0. Pretede-se testar um strumeto que mede a cocetração
Área Cetífca Matemátca Udade Curso Egehara do Ambete Ao º Semestre º Folha Nº 8: Aálse de Regressão e de Correlação Probabldades e Estatístca Ao 00/0. Pretede-se testar um strumeto que mede a cocetração
( k) Tema 02 Risco e Retorno 1. Conceitos Básicos
 FEA -USP Graduação Cêcas Cotábes EAC05 04_0 Profa. Joaíla Ca. Rsco e Retoro. Cocetos Báscos Rotero BE-cap.6 Tema 0 Rsco e Retoro. Cocetos Báscos I. O que é Retoro? II. Qual é o Rsco de um Atvo Idvdual
FEA -USP Graduação Cêcas Cotábes EAC05 04_0 Profa. Joaíla Ca. Rsco e Retoro. Cocetos Báscos Rotero BE-cap.6 Tema 0 Rsco e Retoro. Cocetos Báscos I. O que é Retoro? II. Qual é o Rsco de um Atvo Idvdual
MÉTODO DOS MÍNIMOS QUADRADOS
 MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
Centro de massa, momento linear de sistemas de partículas e colisões
 Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Análise dos resíduos e Outlier, Alavancagem e Influência
 Análse dos resíduos e Outler, Alavancagem e Influênca Dagnóstco na análse de regressão Usadas para detectar problemas com o ajuste do modelo de regressão. Presença de observações mal ajustadas (pontos
Análse dos resíduos e Outler, Alavancagem e Influênca Dagnóstco na análse de regressão Usadas para detectar problemas com o ajuste do modelo de regressão. Presença de observações mal ajustadas (pontos
Análise Exploratória de Dados
 Aálse Eploratóra de Dados Objetvos Aálse bvarada: uma varável qualtatva e uma quattatva: represetar grafcamete as duas varáves combadas; defr e calcular uma medda de assocação etre as varáves. Eemplo 1
Aálse Eploratóra de Dados Objetvos Aálse bvarada: uma varável qualtatva e uma quattatva: represetar grafcamete as duas varáves combadas; defr e calcular uma medda de assocação etre as varáves. Eemplo 1
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Introdução à Correlação e Regressão Linear
 Itrodução à Correlação e Regressão Lear Ru Carvalho Olvera rolv@st.utl.pt Estatístca Descrtva amostras bvaradas Amostras bvaradas: cada etdade (dvíduo/objecto é caracterzado por um par de varáves (atrbutos
Itrodução à Correlação e Regressão Lear Ru Carvalho Olvera rolv@st.utl.pt Estatístca Descrtva amostras bvaradas Amostras bvaradas: cada etdade (dvíduo/objecto é caracterzado por um par de varáves (atrbutos
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA
 INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Sumário. Mecânica. Sistemas de partículas
 Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
MODELOS DE REGRESSÃO APLICADOS EM EPIDEMIOLOGIA I, II e III. (HEP- 5743, HEP-5763 e HEP-5764)
 FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
MÓDULO 8 REVISÃO REVISÃO MÓDULO 1
 MÓDULO 8 REVISÃO REVISÃO MÓDULO A Estatístca é uma técca que egloba os métodos cetícos para a coleta, orgazação, apresetação, tratameto e aálse de dados. O objetvo da Estatístca é azer com que dados dspersos
MÓDULO 8 REVISÃO REVISÃO MÓDULO A Estatístca é uma técca que egloba os métodos cetícos para a coleta, orgazação, apresetação, tratameto e aálse de dados. O objetvo da Estatístca é azer com que dados dspersos
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
MAE116 Noções de Estatística
 Grupo C - º semestre de 004 Exercíco 0 (3,5 potos) Uma pesqusa com usuáros de trasporte coletvo a cdade de São Paulo dagou sobre os dferetes tpos usados as suas locomoções dáras. Detre ôbus, metrô e trem,
Grupo C - º semestre de 004 Exercíco 0 (3,5 potos) Uma pesqusa com usuáros de trasporte coletvo a cdade de São Paulo dagou sobre os dferetes tpos usados as suas locomoções dáras. Detre ôbus, metrô e trem,
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Medidas Numéricas Descritivas:
 Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional. ou experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal Prof. Lorí Val, Dr. val@pucrs.br http://www.pucrs.br/famat/val/ ou expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal Prof. Lorí Val, Dr. val@pucrs.br http://www.pucrs.br/famat/val/ ou expermetal. Numa relação expermetal os valores de uma das varáves
MODELOS DE REGRESSÃO APLICADOS EM EPIDEMIOLOGIA I, II e III. (HEP- 5743, HEP-5763 e HEP-5764)
 FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
Estudo das relações entre peso e altura de estudantes de estatística através da análise de regressão simples.
 Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
Estudo das relações etre peso e altura de estudates de estatístca através da aálse de regressão smples. Waessa Luaa de Brto COSTA 1, Adraa de Souza COSTA 1. Tago Almeda de OLIVEIRA 1 1 Departameto de Estatístca,
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Vamos estudar o conceito de variabilidade absoluta considerando o conjunto de notas obtidas por cinco alunos:
 Medidas de Disperção Itrodução: - Observamos ateriormete que as medidas de tedêcia cetral são usadas para resumir, em um úico úmero, aquele parâmetro que será o represetate do cojuto de dados. Estas medidas
Medidas de Disperção Itrodução: - Observamos ateriormete que as medidas de tedêcia cetral são usadas para resumir, em um úico úmero, aquele parâmetro que será o represetate do cojuto de dados. Estas medidas
3 - ANÁLISE BIDIMENSIONAL
 INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
Revisão de Estatística X = X n
 Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
Luis Felipe Dias Lopes, Dr. lflopes@smail.ufsm.br, phil.zaz@zaz.com.br D E - UFSM 2 0 0 3
 APOSTILA ESTATÍSTICA Lus Felpe Das Lopes, Dr. lflopes@smal.ufsm.br, phl.zaz@zaz.com.br D E - UFSM 0 0 3 Sumáro Cocetos báscos. População x Amostra. Ceso x Amostragem.3 Dado x Varável.4 Parâmetros x estatístcas.5
APOSTILA ESTATÍSTICA Lus Felpe Das Lopes, Dr. lflopes@smal.ufsm.br, phl.zaz@zaz.com.br D E - UFSM 0 0 3 Sumáro Cocetos báscos. População x Amostra. Ceso x Amostragem.3 Dado x Varável.4 Parâmetros x estatístcas.5
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
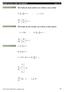 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
( ) ( ) ( ) ( ) ( ) 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Introdução.
 55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
55 3 - INTRODUÇÃO À RESOLUÇÃO DE SISTEMAS NÃO LINEARES. Itrodução. No processo de resolução de um problema prático é reqüete a ecessidade de se obter a solução de um sistema de equações ão lieares. Dada
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
2. MODELO DETALHADO: Relações de Recorrência. Exemplo: Algoritmo Recursivo para Cálculo do Fatorial Substituição Repetida
 . MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
. MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO
 ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal
ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal
Macroeconometria Aula 3 Revisão de estatística e teste de hipótese
 Macroecoometra 008. Aula 3 Revsão de estatístca e teste de hpótese 3.5. Estmação No estudo das probabldades, o objetvo é calcular a probabldade de evetos préespecfcados. De agora em date o objetvo muda.
Macroecoometra 008. Aula 3 Revsão de estatístca e teste de hpótese 3.5. Estmação No estudo das probabldades, o objetvo é calcular a probabldade de evetos préespecfcados. De agora em date o objetvo muda.
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Parte 3 - Regressão linear simples
 Parte 3 - Regressão lear smples Defção do modelo Modelo de regressão empregado para eplcar a relação lear etre duas varáves (ajuste de uma reta). O modelo de regressão lear smples pode ser epresso a forma:
Parte 3 - Regressão lear smples Defção do modelo Modelo de regressão empregado para eplcar a relação lear etre duas varáves (ajuste de uma reta). O modelo de regressão lear smples pode ser epresso a forma:
RACIOCÍNIO LÓGICO / ESTATÍSTICA LISTA 2 RESUMO TEÓRICO
 RACIOCÍIO LÓGICO - Zé Carlos RACIOCÍIO LÓGICO / ESTATÍSTICA LISTA RESUMO TEÓRICO I. Cocetos Icas. O desvo médo (DM), é a méda artmétca dos desvos de cada dado da amostra em toro do valor médo, sto é x
RACIOCÍIO LÓGICO - Zé Carlos RACIOCÍIO LÓGICO / ESTATÍSTICA LISTA RESUMO TEÓRICO I. Cocetos Icas. O desvo médo (DM), é a méda artmétca dos desvos de cada dado da amostra em toro do valor médo, sto é x
13 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL
 3 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL Como vto em amotragem o prmero bmetre, etem fatore que fazem com que a obervação de toda uma população em uma pequa eja mpratcável, muta veze em vrtude
3 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL Como vto em amotragem o prmero bmetre, etem fatore que fazem com que a obervação de toda uma população em uma pequa eja mpratcável, muta veze em vrtude
9 Medidas Descritivas
 1 9 Meddas Descrtvas Vmos aterormete que um cojuto de dados pode ser resumdo através de uma dstrbução de freqüêcas, e que esta pode ser represetada através de uma tabela ou de um gráfco. Se o cojuto refere-se
1 9 Meddas Descrtvas Vmos aterormete que um cojuto de dados pode ser resumdo através de uma dstrbução de freqüêcas, e que esta pode ser represetada através de uma tabela ou de um gráfco. Se o cojuto refere-se
CONHECIMENTOS ESPECÍFICOS
 CONHECIMENTOS ESPECÍFICOS Uma uversdade oferece um curso para capactação profssoal de joves caretes. Ao fal do curso, cada jovem partcpate será avalado por meo de uma prova teórca e de uma prova prátca,
CONHECIMENTOS ESPECÍFICOS Uma uversdade oferece um curso para capactação profssoal de joves caretes. Ao fal do curso, cada jovem partcpate será avalado por meo de uma prova teórca e de uma prova prátca,
Variáveis Indicadoras. Roteiro. Introdução
 Varáves Indcadoras Rotero 1. Introdução 2. Varável Bnára de Intercepto 3. Varável de Interação 4. Aplcação 5. Varáves Qualtatvas com Váras Categoras 6. Referêncas Introdução Varáves Bnáras Modelo estenddo
Varáves Indcadoras Rotero 1. Introdução 2. Varável Bnára de Intercepto 3. Varável de Interação 4. Aplcação 5. Varáves Qualtatvas com Váras Categoras 6. Referêncas Introdução Varáves Bnáras Modelo estenddo
Distribuições de Probabilidades
 Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
A esse tipo de tabela, cujos elementos não foram numericamente organizados, denominamos tabela primitiva.
 Dstrbução de Frequênca Tabela prmtva ROL Suponhamos termos feto uma coleta de dados relatvos à estaturas de quarenta alunos, que compõem uma amostra dos alunos de um colégo A, resultando a segunte tabela
Dstrbução de Frequênca Tabela prmtva ROL Suponhamos termos feto uma coleta de dados relatvos à estaturas de quarenta alunos, que compõem uma amostra dos alunos de um colégo A, resultando a segunte tabela
AVALIAÇÃO DE GANHOS E PERDAS EM FUNDOS DE INVESTIMENTOS UTILIZANDO REGRESSÃO LINEAR. José Antonio Stark Ferreira
 1 AVALIAÇÃO DE GANHOS E PERDAS EM FUNDOS DE INVESTIMENTOS UTILIZANDO REGRESSÃO LINEAR José Atoo Stark Ferrera I - INTRODUÇÃO O presete estudo fo desevolvdo objetvado mesurar os gahos e perdas patrmoas
1 AVALIAÇÃO DE GANHOS E PERDAS EM FUNDOS DE INVESTIMENTOS UTILIZANDO REGRESSÃO LINEAR José Atoo Stark Ferrera I - INTRODUÇÃO O presete estudo fo desevolvdo objetvado mesurar os gahos e perdas patrmoas
INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR
 INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR Hetor Achlles Dutra da Rosa - hetorachlles@yahoo.com.br Cetro Federal de Educação Tecológca Celso Suckow da Foseca CEFET/RJ
INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR Hetor Achlles Dutra da Rosa - hetorachlles@yahoo.com.br Cetro Federal de Educação Tecológca Celso Suckow da Foseca CEFET/RJ
Prof. Lorí Viali, Dr.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Prof. Lorí Val, Dr. UFRG Insttuto de Matemátca
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Prof. Lorí Val, Dr. UFRG Insttuto de Matemátca
