ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO
|
|
|
- Natan Bastos da Conceição
- 7 Há anos
- Visualizações:
Transcrição
1 ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal de Sata Catara, Cetro Tecológco. C.P CEP Floraópols, Brasl glso@eps.ufsc.br; rogero@se.ufsc.br; marts@eps.ufsc.br, pacheco@eps.ufsc.br ABSTRACT Ths work presets the use of a methodology proposed by Taaka, Uema & Asa (982). That approach gves to the decso maker a output preseted as a rage, the he ca pck some value from ths rage. Ths s the ma advatage of ths methodology. The correspodet results show that whe a fuzzfcato of the observed values s troduced, ad the parameter value H s equal to 0,5, the metoed methodology defte mproves ts performace. KEYWORDS Fuzzy Lear Programmg, Regresso, Lear Statstcal Models. RESUMO O presete estudo é a utlzação do método proposto por Taaka, Uema & Asa (982). A prcpal vatagem da metodologa apresetada é de que a saída estmada é um tervalo, ode o tomador de decsão pode optar por um úmero pertecete a esse tervalo. Os resultados alcaçados mostram que os dados são dfusos e o parâmetro H é gual a 0.5, a metodologa apresetada melhora a performace de maera sgfcatva.
2 . INTRODUÇÃO Modelos de Regressão Lear são amplamete usados hoe em egócos, admstração, ecooma, egehara (Loacga ad Church, 990), bem como em mutas outros campos tradcoalmete ão quattatvo tal como cêcas socas, saúde e bológca (Klebaum ad Kupper, 978; Neter et al., 985). O processo de detfcar e austar um modelo é de crucal mportâca para utlzação do mesmo com sucesso. Em termos geral, austar um modelo cosste em determar os valores dos seus parâmetros que satsfatoramete reproduz os coutos de observações dspoíves com cofaça. Problemas relacoado com a detfcação e o austameto de modelos leares podem ser classfcado em duas categoras:. É frequetemete dfícl ustfcar a suposção de leardade para o modelo partcular, e 2. Não exstem mutas vezes observações bastate para valdar a relação estatístca etre a varável depedete e depedete. Taaka, Uema & Asa (982) troduzram um modelo de regressão baseado em programação lear usado um modelo lear dfuso com os parâmetros tragular dfuso smétrco. Heshmaty & Kadel (985) utlzou essa abordagem para prevsão em ambetes de certeza. Nas téccas de regressão covecoal, a dfereça etre os valores observado e os valores estmados do modelo é assumdo ser devdo aos erros de observações e a dfereça é cosderada uma varável aleatóra. Mas em regressão dfusa, a dfereça etre os valores observado e estmado é assumdo ser devdo a ambgüdade eretemete presete o sstema. A saída para uma etrada especfcada é assumda estar um tervalo de valores possíves,.é., a saída pode escolher qualquer um desses valores possíves. Nesse trabalho será formulado dos tpos de problemas com programação lear para obtermos os modelos de regressão lear dfuso:. Descrevemos uma formulação de programação lear de aálse de regressão com um modelo de tervalo lear para dados com valor real ( x, y ), =, 2,..., m, ode x = ( x, x 2,..., x ) é o -ésmo vetor de etrada e y é o valor da saída correspodete. Um modelo de tervalo lear é represetado usado parâmetros de tervalo A como
3 Y (x ) = A 0 + A x A x () ode Y (x ) é o tervalo predto correspodete ao vetor de etrada x. Na formulação de programação lear troduzdo esse trabalho, um modelo de tervalo lear é obtdo como a soma míma das larguras dos tervalos predtos que clu o dado. Mas especfcamete, um problema de programação lear é formulado para obter o tervalo dos parâmetros A tal que a soma das larguras de Y (x ) é mmzada sueto a y Y (x ) para =, 2,..., m. 2. Extedemos a formulação de programação lear para o caso de dado com valor em tervalo ( x, y ), =, 2,..., m, ode o valor de saída Y é dado como tervalo. O parâmetro dfuso do modelo lear obtdo sgfca uma dstrbução de possbldade que correspode a fuzzfcação do sstema. Os parâmetros dfuso estudado esse trabalho correspode a restrta classe de fuções de pertêca tragular. Esse modelo de regressão dfuso pode ser muto útl para ecotrar uma estrutura dfusa em sstema de avalação. Utlzamos o software de Programação Lear - LINDO e o software STATISTIC para os demas cálculos. 2. FUNÇÃO DE REGRESSÃO DIFUSA COM PARÂMETROS DIFUSOS Aálse de regressão é usado para modelar a relação etre varáves depedetes e depedetes. Em aálse de regressão, a varável depedete, y, é uma fução das varáves depedetes; e o grau de cotrbução de cada varável para a saída é represetado pelos coefcetes das varáves. Um modelo de regressão lear crsp é mostrado a Eq. (2), Y = f (x, a) = a 0 + a x + a 2 x a x (2) A equação (3) mostra um modelo de regressão lear dfuso típco, Y = f ( x, A) = A 0 + A x + A 2 x A x (3) ode A é o -ésmo coefcete dfuso. Regressão dfusa estma um tervalo de valores possíves que são represetado por uma dstrbução de possbldade, cohecda como a fução de pertêca. Fuções de pertêca
4 são formadas por atrbur um valor de pertêca especfco (grau de pertêca) para cada um dos valores estmados (Fg. ). Tas fuções de pertêca são também defdas para os coefcetes das varáves depedetes. Fuções de pertêca tragular para os coefcetes dfusos, como aqueles mostrados a Fg., permt a solução ser crada va uma formulação de programação lear; outras fuções de pertêca para os coefcetes requer abordages alteratvas. A fução de pertêca µ A para cada um dos coefcetes é expressada como µ A = p a c 0 p c x caso cotráro p + c (4) A fução dfusa A é uma fução de dos parâmetros, p e c, cohecdo como o valor médo e a expasão (desvo padrão), respectvamete. A expasão deota a fuzzfcação da fução. A fgura mostra a fução de pertêca para um úmero dfuso "aproxmadamete p." Os parâmetros dfusos A = { A,...., A } pode ser deotado a forma de vetor como = {p, c}, ode p = (p,..., p ) e c = (c,..., c ). Portato, a saída é uma versão revsada da Eq. (3), Y = (p, c ) x + (p 2, c 2 ) x (p, c ) x A fução de pertêca para o parâmetro dfuso de saída, Y, é dado por A µ max(m[ µ y) = 0 A Y ( ( a )]) Substtudo a Eq. (4) a Eq. (5), obteremos { a y = f ( x, a)} Φ caso cotráro (5) µ Y y ( y) = = = p x c x x o x = o, y = 0 (6) As equações aterores são aplcadas para m coutos de dados que pode ser obtda por amostragem. Os dados de etrada e saída pode ser dfuso ou ão dfuso. A tabela mostra um
5 exemplos de coutos de dados ão dfuso. Na tabela, y é a saída da -ésma amostra e x é a -ésma varável de etrada para a -ésma amostra. TABELA : Um exemplo dos coutos de dados para dados ão dfuso Número da Amostra Saída y etradas x y x, x 2,...., x Μ Μ Μ m Y m x m, x 2m,...., x m 2.. O CASO DE DADOS NÃO DIFUSO Taaka et al. [982] tha determado a solução para o modelo de regressão por coverte-lo em um problema de programação lear. Para dados ão dfuso o obetvo do modelo de regressão é determar os parâmetros ótmo A * tal que o couto de saída dfuso, que cotém, estar assocado com um valor de pertêca maor do que h,.é., y µ ( ) h, =,...., m (7) Y y O grau h é especfcado pelo usuáro. A fgura 2 mostra a fução de pertêca para a saída dfusa. A equação (7) declara que a saída dfusa estará etre A e B da Fg. 2. Na fgura o valor do poto médo ( = p x cosderar a Eq. (6), ode h é especfcado pelo usuáro. ) e a expasão (dspersão) ( = c x ) são obtdo por Em regressão buscamos achar os coefcetes dfuso que mmze a expasão (dspersão) da saída dfuso para todos os coutos de dados. A equação (8) mostra a fução obetva que tem de ser mmzada.
6 O m m c x (8) = = = A fução obetva dada a Eq. (8) é mmzada, sueto as duas restrções. As restrções são obtdas por substtur a eq. (6) a Eq. (7); elas toram-se e y px h) = = y p x + h) ( c x (9) = = ( c x (0) Desde que cada couto de dados produz duas restrções, exste um total de 2m restrções para cada couto de dados O CASO DE DADOS DIFUSO
7 Quado o uízo (ulgameto) humao ou meddas mprecsas estão evolvdas em determar a saída, a saída é raramete um úmero crsp. A saída em tas stuações é melhor represetada por um úmero dfuso como Y = (y, e ), ode y é o valor do poto médo e e represeta a ambgüdade a saída, como vemos a Fg. 3. A fução de pertêca para a saída dfusa observada é dada como y y µ Y ( y) = () e Uma estmatva dessa saída dfusa pode ser obtdo da Eq. (6) como y = p x = µ * ( y) = Y para =, m (2) c x O grau de auste do modelo lear dfuso estmada Y * = * A + 0 Ax + * * Ax * A x para os dados h Y Y * h ode Y = (Y, e ) é determado por h, que maxmza h sueto a h Y = {y µ ( y) h } Y h Y * = {y µ ( y) h } (3) * Y
8 A fgura 4 lustra esses cocetos. O obetvo do modelo de regressão lear dfusa é determar os parâmetros dfusos A * que mmza a expasão (dspersão) sueto a restrção que h H para todo, ode H é escolhdo pelo usuáro como o grau de auste do modelo lear dfuso. O -ésmo parâmetro de auste, h, é computado da Fg. 4 como y p = x h = (4) c x e = Em resumo a fução obetva para ser mmzada é O m m c x (5) = = = Sueto as restrções y px H ) ( c x + ( H ) e (6) = = e y p x + H ) ( c x ( H ) e (7) = = para cada couto de dado ode =,..., m. Nas eqs. (6) e (7) otamos que e = y - y.
9 3. APLICAÇÃO Esse modelo de regressão lear dfuso é aplcado a um couto de dados ão dfuso sobre o tamaho de uma lctação em mlhão de dolares (X) e o custo para a frma preparar a lctação em ml dolares (Neter J. e Wasserma W., 974, pg. 33). Os dados de etrada e saída são mostrados a tabela 2. Tabela 2: Custo para Frma de Preparar Lctações CUSTO DA FIRMA ( Y ) TAMANHO LICITAÇÃO ( X )
10 O modelo aplcado a esses dados fo Y = A 0 + A X, ode A 0 = (p 0, c 0 ) e A = (p, c ). Das eqs. (8) - (0), o problema de programação lear para os dados acma é formulado como segue: Sueto a M 2c c p p -0.5c c 5.5 p 0 +.2p -0.5c c. p p -0.5c 0-2.8c 20 p 0 +8p -0.5c 0-4c 47.5 p p +0.5c c 5.5 p 0 +.2p +0.5c c. p p +0.5c c 20 p 0 +8p +0.5c 0 +4c 47.5 c 0, c 0 obtemos a segute estmatva da reta dfusa ^ Y = (5.4, 0.57) + (4.28,.90) X Se substturmos os valores de X a estmatva da reta dfusa vemos que 6 dos valores de Y dado ão estão cotdo a saída dfusa. Para cotorar esse problema de que 6 valores ão estão cotdo a saída da reta dfusa estmada, propomos os segutes tervalos para os valores Y dados, torado as saídas dfuso.
11 Tabela 3: Custo para Frma de Preparar Lctações CUSTO DA FIRMA ( Y ) TAMANHO LICITAÇÃO ( X ) SAÍDA DIFUSA Y = ( Y, e ) (5.5, 4.0)..2 (., 3.0) (62.6, 32.0) (35.4, 8.0) (24.9, 2.0) (28., 2.0) (5.0,.0) ( ) (42.0, 2.0) (0.,.0) (20.0,.0) (47.5, 30.0) Das eqs. (5) - (7), o problema de programação lear para os dados acma é formulado como segue: M 2c c Sueto a p p -0.5c c 3.5 p 0 +.2p -0.5c c 9.6 p p -0.5c 0-2.8c 9.5 p 0 +8p -0.5c 0-4c 32.5 p p +0.5c c 7.5 p 0 +.2p +0.5c c 2.6 p p +0.5c c 20.5 p 0 +8p +0.5c 0 +4c 62.5 c 0, c 0 A reta dfusa estmada agora é:
12 Y * = (6.4, 2.8) + (5., 3.6) X Substtudo todos os tervalos da saída dfusa essa reta dfusa estmada, vemos que a relação h Y Y * h * cotdo em Y = (4.6, 27.7). 6 é satsfeta para todos eles com H = 0.5, ou sea Y 6 = (28., 2.0) estar 4. DISCUSSÃO Aalsado o modelo proposto de regressão lear dfusa utlzado a programação lear para dados ão dfuso como também para a saída, podemos levatar as segute cosderações:. Se optasse pelo modelo de regressão clássca teríamos a segute reta estmada: ^ Y = X com R 2 = O modelo proposto (eq. 3) para aalsar os dados ão dfuso desse trabalho, ão se comportou bem, pos 50% dos valores observados quado substtuído a reta dfusa estmada ão estava cotdo o tervalo dfuso. 3. Em frete a esse problema, o autor optou pela fuzzfcação da saída em fução do erro de estmação dado pela reta estmada clássca ( ε = y y ). 4. Plotamos o gráfco dos valores estmados versos valores observados com a reta estmada e vmos que todos os potos que estava acma dessa reta a fuzzfcação sera bem maor do que aqueles potos que estavam abaxo da reta estmada (gráfco ). 5. Levado em cota todas a essas cosderações, propomos a segute fuzzfcação das saídas (tabela 3). ^
13 75 Gráfco : Valores Estmados versos Valores Observados Valores Observados Valores Estmados Regressão 95% de cofaça. 5. CONCLUSÕES Com base os resultados obtdos esse trabalho podemos colocar algumas sugestões do método proposto por Taaka et al. [982]:. É um método alteratvo em relação ao método de regressão lear clássca, com uma vatagem de que a saída estmada é um tervalo ode o tomador de decsão pode optar por um úmero pertecete a esse tervalo. 2. Como fo vsto o decorrer do trabalho quado os dados X e Y são valores reas quado se austa um modelo ode os parâmetros desse modelo é dfuso, para os dados do trabalho o modelo ão fucoou bem, dexado 50% dos valores observados fora dos tervalos dfuso. 3. Mas quado a saída é fuzzfcada o modelo se comportou bem. 4. A fuzzfcação dos valores de saída ão é um processo fácl, exgdo das pessoas que estão evolvda com o problema cohecmeto bastate profudo sobre o mesmo para propor uma boa fuzzfcação.
14 6. BIBLIOGRAFIA KACPRZYK J. AND FEDRIZZI M. (Edtores). Studes Fuzzess: Fuzzy Regresso Aalyss. Volume. Omtech Press Warsaw ad Physca-Verlag Hedelberg, 992. TANAKA, H., UEJIMA, S. AND ASAI, K. Lear Regresso Aalyss wth Fuzzy Model, IEEE Trasactos Systems Ma, ad Cyberetcs, vol. SMC - 2, , º 6, 982. HESHMATY, B. AND KANDEL, A. Fuzzy Lear Regresso ad ts Applcatos to Forecastg Ucerta Evromet, Fuzzy Sets ad Systems 5, 59-9, 985. NETER J. AND WASSERMAN W. Appled Lear Statstcal Models: Regresso, Aalyss of Varace, ad Expermetal Desgs. Rchard D. Irw, Ic., 974. * e também UNIVALI - Uversdade do Vale do Itaaí, Rodova SC 407 Km 4 - São José, SC CEP
Regressão Linear - Introdução
 Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
2-0,0041295**.C 2 + 0,0017052**.T.C
 14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO
 NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO ISABEL C. C. LEITE SALVADOR BA 007 Estatístca Prof.ª Isabel C. C. Lete TEORIA DA AMOSTRAGEM DISTRIBUIÇÃO AMOSTRAL DOS ESTIMADORES A teora da amostragem
NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO ISABEL C. C. LEITE SALVADOR BA 007 Estatístca Prof.ª Isabel C. C. Lete TEORIA DA AMOSTRAGEM DISTRIBUIÇÃO AMOSTRAL DOS ESTIMADORES A teora da amostragem
Licenciatura em Ciências USP/ Univesp funções polinomiais 4
 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Análise de Regressão
 Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
Aálse de Regressão Prof. Paulo Rcardo B. Gumarães. Itrodução Os modelos de regressão são largamete utlzados em dversas áreas do cohecmeto, tas como: computação, admstração, egeharas, bologa, agrooma, saúde,
6.1 - PROCEDIMENTO DE AVALIAÇÃO DE INCERTEZA EM MEDIÇÕES DIRETAS
 7 6 - PROCEDIMENTO DE AVALIAÇÃO DE INCERTEZA EM MEDIÇÕES DIRETAS A medção dreta é aquela cuja dcação resulta aturalmete da aplcação do sstema de medção sobre o mesurado Há apeas uma gradeza de etrada evolvda
7 6 - PROCEDIMENTO DE AVALIAÇÃO DE INCERTEZA EM MEDIÇÕES DIRETAS A medção dreta é aquela cuja dcação resulta aturalmete da aplcação do sstema de medção sobre o mesurado Há apeas uma gradeza de etrada evolvda
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
Matemática Ficha de Trabalho
 Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
Estudo do intervalo de confiança da regressão inversa utilizando o software R
 Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA
 UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
Gráfico de Controle de Regressão Aplicado ao Monitoramento de Características da Qualidade do Eletrodo de Carbono
 Gráfco de Cotrole de Regressão Aplcado ao Motorameto de Característcas da Qualdade do Eletrodo de Carboo Marcello Neva de Mello, evamarcello@gmal.com Wager Rogéro Ferrera Phero, wager35@gmal.com Edso Marcos
Gráfco de Cotrole de Regressão Aplcado ao Motorameto de Característcas da Qualdade do Eletrodo de Carboo Marcello Neva de Mello, evamarcello@gmal.com Wager Rogéro Ferrera Phero, wager35@gmal.com Edso Marcos
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
Análise dos resíduos e Outlier, Alavancagem e Influência
 Análse dos resíduos e Outler, Alavancagem e Influênca Dagnóstco na análse de regressão Usadas para detectar problemas com o ajuste do modelo de regressão. Presença de observações mal ajustadas (pontos
Análse dos resíduos e Outler, Alavancagem e Influênca Dagnóstco na análse de regressão Usadas para detectar problemas com o ajuste do modelo de regressão. Presença de observações mal ajustadas (pontos
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
Estatística Descritiva
 Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
Modelo de Regressão Simples
 Modelo de Regressão Smples Hstora Hstóra Termo regressão fo troduzdo por Fracs Galto (8-9). Estudo sobre altura de pas e flhos. Karl Pearso coletou mas de ml regstros e verfcou a le de regressão uversal
Modelo de Regressão Smples Hstora Hstóra Termo regressão fo troduzdo por Fracs Galto (8-9). Estudo sobre altura de pas e flhos. Karl Pearso coletou mas de ml regstros e verfcou a le de regressão uversal
CAPÍTULO 5. Ajuste de curvas pelo Método dos Mínimos Quadrados
 CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
CAPÍTULO Ajuste de curvas pelo Método dos Mímos Quadrados Ajuste Lear Smples (ou Regressão Lear); Ajuste Lear Múltplo (ou Regressão Lear Múltpla); Ajuste Polomal; Regressão Não Lear Iterpolação polomal
Regressao Simples. Parte II: Anova, Estimação Intervalar e Predição
 egressao Smples Parte II: Aova, Estmação Itervalar e Predção Aálse de Varâca Nem todos os valores das amostras estão cotdos a reta de regressão, e quato mas afastados estverem por, a reta represetará a
egressao Smples Parte II: Aova, Estmação Itervalar e Predção Aálse de Varâca Nem todos os valores das amostras estão cotdos a reta de regressão, e quato mas afastados estverem por, a reta represetará a
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
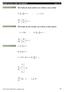 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
Capítulo V - Interpolação Polinomial
 Métodos Numércos C Balsa & A Satos Capítulo V - Iterpolação Polomal Iterpolação Cosdere o segute couto de dados: x : x0 x x y : y y y 0 m m Estes podem resultar de uma sequêca de meddas expermetas, ode
Métodos Numércos C Balsa & A Satos Capítulo V - Iterpolação Polomal Iterpolação Cosdere o segute couto de dados: x : x0 x x y : y y y 0 m m Estes podem resultar de uma sequêca de meddas expermetas, ode
A análise de variância de uma classificação (One-Way ANOVA) verifica se as médias de k amostras independentes (tratamentos) diferem entre si.
 Prof. Lorí Va, Dr. http://www. ufrgs.br/~va/ va@mat.ufrgs.br aáse de varâca de uma cassfcação (Oe-Way NOV) verfca se as médas de amostras depedetes (tratametos) dferem etre s. Um segudo tpo de aáse de
Prof. Lorí Va, Dr. http://www. ufrgs.br/~va/ va@mat.ufrgs.br aáse de varâca de uma cassfcação (Oe-Way NOV) verfca se as médas de amostras depedetes (tratametos) dferem etre s. Um segudo tpo de aáse de
3 - ANÁLISE BIDIMENSIONAL
 INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
A PROGRAMAÇÃO LINEAR FUZZY EM PROBLEMAS DE MISTURA
 Pesqusa Operacoal a Socedade: Educação, Meo Ambete e Desevolvmeto a 5/09/06 Goâa, GO A PROGRAMAÇÃO LINEAR FUZZY EM PROBLEMAS DE MISTURA Adre Gadolpho Uversdade Católca de Petrópols alvesga@gbl.com.br Rcardo
Pesqusa Operacoal a Socedade: Educação, Meo Ambete e Desevolvmeto a 5/09/06 Goâa, GO A PROGRAMAÇÃO LINEAR FUZZY EM PROBLEMAS DE MISTURA Adre Gadolpho Uversdade Católca de Petrópols alvesga@gbl.com.br Rcardo
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
Centro de Ciências Agrárias e Ambientais da UFBA Departamento de Engenharia Agrícola
 Cetro de Cêcas Agráras e Ambetas da UFBA Departameto de Egehara Agrícola Dscpla: AGR Boestatístca Professor: Celso Luz Borges de Olvera Assuto: Estatístca TEMA: Somatóro RESUMO E NOTAS DA AULA Nº 0 Seja
Cetro de Cêcas Agráras e Ambetas da UFBA Departameto de Egehara Agrícola Dscpla: AGR Boestatístca Professor: Celso Luz Borges de Olvera Assuto: Estatístca TEMA: Somatóro RESUMO E NOTAS DA AULA Nº 0 Seja
5 Critérios para Análise dos Resultados
 5 Crtéros para Aálse dos Resultados Este capítulo tem por objetvos forecer os crtéros utlzados para aálse dos dados ecotrados a pesqusa, bem como uma vsão geral dos custos ecotrados e a forma de sua evolução
5 Crtéros para Aálse dos Resultados Este capítulo tem por objetvos forecer os crtéros utlzados para aálse dos dados ecotrados a pesqusa, bem como uma vsão geral dos custos ecotrados e a forma de sua evolução
REGRESSÃO LINEAR 05/10/2016 REPRESENTAÇAO MATRICIAL. Y i = X 1i + 2 X 2i k X ni + i Y = X + INTRODUÇÃO SIMPLES MÚLTIPLA
 REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou expermetal. Numa relação expermetal os valores de uma das varáves
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou expermetal. Numa relação expermetal os valores de uma das varáves
MODELOS DE REGRESSÃO APLICADOS EM EPIDEMIOLOGIA I, II e III. (HEP- 5743, HEP-5763 e HEP-5764)
 FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR
 INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR Hetor Achlles Dutra da Rosa - hetorachlles@yahoo.com.br Cetro Federal de Educação Tecológca Celso Suckow da Foseca CEFET/RJ
INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR Hetor Achlles Dutra da Rosa - hetorachlles@yahoo.com.br Cetro Federal de Educação Tecológca Celso Suckow da Foseca CEFET/RJ
15/03/2012. Capítulo 2 Cálculo Financeiro e Aplicações. Capítulo 2 Cálculo Financeiro e Aplicações. Capítulo 2 Cálculo Financeiro e Aplicações
 Itrodução.1 Juros Smples Juro: recompesa pelo sacrfíco de poupar o presete, postergado o cosumo para o futuro Maora das taxas de uros aplcadas o mercado facero são referecadas pelo crtéro smples Determa
Itrodução.1 Juros Smples Juro: recompesa pelo sacrfíco de poupar o presete, postergado o cosumo para o futuro Maora das taxas de uros aplcadas o mercado facero são referecadas pelo crtéro smples Determa
3 Procedimento Experimental
 3 Procedmeto Expermetal 3. Sstema de medção de vazão com extesômetro A Fg. 9 mostra o sstema de medção de vazão com extesômetro, o qual fo motado o laboratóro da PUC-Ro. este sstema, duas tubulações com,5
3 Procedmeto Expermetal 3. Sstema de medção de vazão com extesômetro A Fg. 9 mostra o sstema de medção de vazão com extesômetro, o qual fo motado o laboratóro da PUC-Ro. este sstema, duas tubulações com,5
NOTAS DE AULA DA DISCIPLINA CE076. ], T 2 = conhecido como T 2 de Hotelling
![NOTAS DE AULA DA DISCIPLINA CE076. ], T 2 = conhecido como T 2 de Hotelling NOTAS DE AULA DA DISCIPLINA CE076. ], T 2 = conhecido como T 2 de Hotelling](/thumbs/97/134766993.jpg) 4 INFERÊNCIA SOBRE O VETOR DE MÉDIAS 4. TESTE PARA UM VETOR DE MÉDIAS µ Lembrado o caso uvarado: H : µ = µ H : µ µ Nível de sgfcâca: α Estatístca do teste: X µ t = s/ ~ t Decsão: se t > t - (α/) rejeta-se
4 INFERÊNCIA SOBRE O VETOR DE MÉDIAS 4. TESTE PARA UM VETOR DE MÉDIAS µ Lembrado o caso uvarado: H : µ = µ H : µ µ Nível de sgfcâca: α Estatístca do teste: X µ t = s/ ~ t Decsão: se t > t - (α/) rejeta-se
MODELOS DE REGRESSÃO APLICADOS EM EPIDEMIOLOGIA I, II e III. (HEP- 5743, HEP-5763 e HEP-5764)
 FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
FACULDADE DE AÚDE PÚBLICA - UP DEPARTAMENTO DE EPIDEMIOLOGIA MODELO DE REGREÃO APLICADO EM EPIDEMIOLOGIA I, II e III (HEP- 5743, HEP-5763 e HEP-5764) Profa. Dra. MARIA DO ROARIO DIA DE OLIVEIRA LATORRE
Avaliação da qualidade do ajuste
 Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Apostila de Introdução Aos Métodos Numéricos
 Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
Apostla de Itrodução Aos Métodos Numércos PARTE III o Semestre - Pro a. Salete Souza de Olvera Buo Ídce INTERPOAÇÃO POINOMIA...3 INTRODUÇÃO...3 FORMA DE AGRANGE... 4 Iterpolação para potos (+) - ajuste
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Construção e Análise de Gráficos
 Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
MÉTODO DOS MÍNIMOS QUADRADOS
 MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
Macroeconometria Aula 3 Revisão de estatística e teste de hipótese
 Macroecoometra 008. Aula 3 Revsão de estatístca e teste de hpótese 3.5. Estmação No estudo das probabldades, o objetvo é calcular a probabldade de evetos préespecfcados. De agora em date o objetvo muda.
Macroecoometra 008. Aula 3 Revsão de estatístca e teste de hpótese 3.5. Estmação No estudo das probabldades, o objetvo é calcular a probabldade de evetos préespecfcados. De agora em date o objetvo muda.
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Capítulo 5: Ajuste de curvas pelo método dos mínimos quadrados
 Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Cálculo Numérico. Ajuste de Curvas Método dos Mínimos Quadrados. Profa. Vanessa Rolnik 1º semestre 2015
 Cálculo Numérco Ajuste de Curvas Método dos Mímos Quadrados Profa. Vaessa Rolk º semestre 05 Ajuste de curvas Para apromar uma fução f por um outra fução de uma famíla prevamete escolhda (caso cotíuo)
Cálculo Numérco Ajuste de Curvas Método dos Mímos Quadrados Profa. Vaessa Rolk º semestre 05 Ajuste de curvas Para apromar uma fução f por um outra fução de uma famíla prevamete escolhda (caso cotíuo)
Relatório 2ª Atividade Formativa UC ECS
 Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Prof. Eugênio Carlos Stieler
 UNEMAT Uversdade do Estado de Mato Grosso Matemátca Facera http://www2.uemat.br/eugeo SÉRIE DE PAGAMENTOS 1. NOÇÕES SOBRE FLUXO DE CAIXA Prof. Eugêo Carlos Steler Estudar sem racocar é trabalho perddo
UNEMAT Uversdade do Estado de Mato Grosso Matemátca Facera http://www2.uemat.br/eugeo SÉRIE DE PAGAMENTOS 1. NOÇÕES SOBRE FLUXO DE CAIXA Prof. Eugêo Carlos Steler Estudar sem racocar é trabalho perddo
FINANCIAMENTOS UTILIZANDO O EXCEL
 rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
rofessores Ealdo Vergasta, Glóra Márca e Jodála Arlego ENCONTRO RM 0 FINANCIAMENTOS UTILIZANDO O EXCEL INTRODUÇÃO Numa operação de empréstmo, é comum o pagameto ser efetuado em parcelas peródcas, as quas
PROBLEMA DE INCERTEZA EM SISTEMAS DINÂMICOS UTILIZANDO DEFUZZIFICAÇÃO PELO CENTROIDE
 POSMEC 205 Smpóso do Programa de Pós-Graduação em Egehara Mecâca Faculdade de Egehara Mecâca Uversdade Federal de Uberlâda 8 e 9 de Novembro de 205, Uberlâda - MG PROBLEM DE INCERTEZ EM SISTEMS DINÂMICOS
POSMEC 205 Smpóso do Programa de Pós-Graduação em Egehara Mecâca Faculdade de Egehara Mecâca Uversdade Federal de Uberlâda 8 e 9 de Novembro de 205, Uberlâda - MG PROBLEM DE INCERTEZ EM SISTEMS DINÂMICOS
(1) no domínio : 0 x < 1, : constante não negativa. Sujeita às condições de contorno: (2-a) (2-b) CC2: 0
 EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são otdas com ase em
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Distribuições de Probabilidades
 Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Tabela 1 Números de acidentes /mês no Cruzamento X em CG/07. N de acidentes / mês fi f
 Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
Lsta de exercícos Gabarto e chave de respostas Estatístca Prof.: Nelse 1) Calcule 1, e para o segute cojuto de valores. A,1,8,0,11,,7,8,6,,9, 1 O úmero que correspode a 5% do rol é o valor. O úmero que
Confiabilidade Estrutural
 Professor Uversdade de Brasíla Departameto de Egehara Mecâca Programa de Pós graduação em Itegrdade Estrutural Algortmo para a Estmatva do Idce de Cofabldade de Hasofer-Ld Cofabldade Estrutural Jorge Luz
Professor Uversdade de Brasíla Departameto de Egehara Mecâca Programa de Pós graduação em Itegrdade Estrutural Algortmo para a Estmatva do Idce de Cofabldade de Hasofer-Ld Cofabldade Estrutural Jorge Luz
Probabilidades e Estatística
 Departameto de Matemátca robabldades e Estatístca LEAN, LEE, LEGI, LERC, LMAC, MEAer, MEAmb, MEBol, MEEC, MEMec 2 o semestre 20/202 2 o Teste B 08/06/202 :00 Duração: hora e 30 mutos Justfque coveetemete
Departameto de Matemátca robabldades e Estatístca LEAN, LEE, LEGI, LERC, LMAC, MEAer, MEAmb, MEBol, MEEC, MEMec 2 o semestre 20/202 2 o Teste B 08/06/202 :00 Duração: hora e 30 mutos Justfque coveetemete
A esse tipo de tabela, cujos elementos não foram numericamente organizados, denominamos tabela primitiva.
 Dstrbução de Frequênca Tabela prmtva ROL Suponhamos termos feto uma coleta de dados relatvos à estaturas de quarenta alunos, que compõem uma amostra dos alunos de um colégo A, resultando a segunte tabela
Dstrbução de Frequênca Tabela prmtva ROL Suponhamos termos feto uma coleta de dados relatvos à estaturas de quarenta alunos, que compõem uma amostra dos alunos de um colégo A, resultando a segunte tabela
II. Propriedades Termodinâmicas de Soluções
 II. Propredades Termodâmcas de Soluções 1 I. Propredades Termodâmcas de Fludos OBJETIVOS Eteder a dfereça etre propredade molar parcal e propredade de uma espéce pura Saber utlzar a equação de Gbbs-Duhem
II. Propredades Termodâmcas de Soluções 1 I. Propredades Termodâmcas de Fludos OBJETIVOS Eteder a dfereça etre propredade molar parcal e propredade de uma espéce pura Saber utlzar a equação de Gbbs-Duhem
A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: enchentes
 Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
Mostra Nacoal de Icação Cetífca e Tecológca Iterdscplar VI MICTI Isttuto Federal Catarese Câmpus Camború 30 a 3 de outubro de 03 A REGRESSÃO LINEAR EM EVENTOS HIDROLÓGICOS EXTREMOS: echetes Ester Hasse
ANÁLISE DE ERROS. Todas as medidas das grandezas físicas deverão estar sempre acompanhadas da sua dimensão (unidades)! ERROS
 ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
3 Experimento com Mistura com Respostas Não-Normais
 Modelagem em Epermetos Mstura-Processo para Otmzação de Processos Idustras 5 Epermeto com Mstura com Respostas Não-Normas Neste capítulo é apresetado o plaejameto e aálse de um EM com respostas ão ormas,
Modelagem em Epermetos Mstura-Processo para Otmzação de Processos Idustras 5 Epermeto com Mstura com Respostas Não-Normas Neste capítulo é apresetado o plaejameto e aálse de um EM com respostas ão ormas,
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS
 CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo IV, Iterolação Polomal, estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são
CAP. V AJUSTE DE CURVAS PELO MÉTODO DOS MÍNIMOS QUADRADOS No caítulo IV, Iterolação Polomal, estudamos uma forma de ldar com fuções matemátcas defdas or taelas de valores. Frequetemete, estas taelas são
Atividades Práticas Supervisionadas (APS)
 Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Uversdade Tecológca Federal do Paraá Prof: Lauro Cesar Galvão Campus Curtba Departameto Acadêmco de Matemátca Cálculo Numérco Etrega: juto com a a parcal DATA DE ENTREGA: da da a PROVA (em sala de aula
Capítulo 5 CINEMÁTICA DIRETA DE ROBÔS MANIPULADORES
 Cemátca da Posção de Robôs Mapuladores Capítulo 5 CINEMÁTICA DIRETA DE ROBÔS MANIPULADORES A cemátca de um robô mapulador é o estudo da posção e da velocdade do seu efetuador e dos seus lgametos. Quado
Cemátca da Posção de Robôs Mapuladores Capítulo 5 CINEMÁTICA DIRETA DE ROBÔS MANIPULADORES A cemátca de um robô mapulador é o estudo da posção e da velocdade do seu efetuador e dos seus lgametos. Quado
Medidas Numéricas Descritivas:
 Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
RESUMO E EXERCÍCIOS NÚMEROS COMPLEXOS ( )
 NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
Probabilidade e Estatística. Correlação e Regressão Linear
 Probabldade e Estatístca Correlação e Regressão Lnear Varáves Varável: característcas ou tens de nteresse de cada elemento de uma população ou amostra Também chamada parâmetro, posconamento, condção...
Probabldade e Estatístca Correlação e Regressão Lnear Varáves Varável: característcas ou tens de nteresse de cada elemento de uma população ou amostra Também chamada parâmetro, posconamento, condção...
7 Análise de covariância (ANCOVA)
 Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
Plejameto de Expermetos II - Adlso dos Ajos 74 7 Aálse de covarâca (ANCOVA) 7.1 Itrodução Em algus expermetos, pode ser muto dfícl e até mpossível obter udades expermetas semelhtes. Por exemplo, pode-se
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Estatística: Aplicação ao Sensoriamento Remoto SER ANO Estimação Pontual
 Estatístca: Aplcação ao Sesorameto Remoto SER 04 - ANO 08 Estmação Potual Camlo Daleles Reó camlo@dp.pe.br http://www.dp.pe.br/~camlo/estatstca/ Iferêca Estatístca Cosdere o expermeto: retram-se 3 bolas
Estatístca: Aplcação ao Sesorameto Remoto SER 04 - ANO 08 Estmação Potual Camlo Daleles Reó camlo@dp.pe.br http://www.dp.pe.br/~camlo/estatstca/ Iferêca Estatístca Cosdere o expermeto: retram-se 3 bolas
Regressão e Correlação
 Regressão e Correlação Júlo Osóro Regressão & Correlação: geeraldades Em mutas stuações de pesqusa cetífca, dspomos de uma amostra aleatóra de pares de dados (x, ), resultates da medda cocomtate de duas
Regressão e Correlação Júlo Osóro Regressão & Correlação: geeraldades Em mutas stuações de pesqusa cetífca, dspomos de uma amostra aleatóra de pares de dados (x, ), resultates da medda cocomtate de duas
8 Programação linear 78
 8 Programação lear 78 8 Programação lear A programação lear cosderou duas fuções objetvo: (a) maxmzação da comercalzação do gás e (b) mmzação das perdas (recetas e multas cotratuas). Foram dealzados dos
8 Programação lear 78 8 Programação lear A programação lear cosderou duas fuções objetvo: (a) maxmzação da comercalzação do gás e (b) mmzação das perdas (recetas e multas cotratuas). Foram dealzados dos
Prof. Janete Pereira Amador 1
 Prof. Jaete Perera Amador 1 1 Itrodução Mutas stuações cotdaas podem ser usadas como expermeto que dão resultados correspodetes a algum valor, e tas stuações podem ser descrtas por uma varável aleatóra.
Prof. Jaete Perera Amador 1 1 Itrodução Mutas stuações cotdaas podem ser usadas como expermeto que dão resultados correspodetes a algum valor, e tas stuações podem ser descrtas por uma varável aleatóra.
2. MODELO DETALHADO: Relações de Recorrência. Exemplo: Algoritmo Recursivo para Cálculo do Fatorial Substituição Repetida
 . MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
. MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto
 Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Apresenta-se em primeiro lugar um resumo da simbologia adoptada no estudo da quadratura de Gauss.
 CAÍTULO QUADRATURA DE GAUSS Mutos dos tegras que é eessáro alular o âmbto da aplação do Método dos Elemetos Ftos (MEF) ão são trvas,.e., ou a prmtva da ução tegrada ão exste expltamete, ou é demasado omplada
CAÍTULO QUADRATURA DE GAUSS Mutos dos tegras que é eessáro alular o âmbto da aplação do Método dos Elemetos Ftos (MEF) ão são trvas,.e., ou a prmtva da ução tegrada ão exste expltamete, ou é demasado omplada
Critérios de correção e orientações de resposta exame
 Mstéro da Cêca, Tecologa e Eso Superor U.C. 1037 Elemetos de Probabldade e Estatístca 1 de Juho de 011 Crtéros de correção e oretações de resposta eame Neste relatóro apresetam-se os crtéros e um eemplo
Mstéro da Cêca, Tecologa e Eso Superor U.C. 1037 Elemetos de Probabldade e Estatístca 1 de Juho de 011 Crtéros de correção e oretações de resposta eame Neste relatóro apresetam-se os crtéros e um eemplo
( ) ( IV ) n ( ) Escolha a alternativa correta: A. III, II, I, IV. B. II, III, I, IV. C. IV, III, I, II. D. IV, II, I, III. E. Nenhuma das anteriores.
 Prova de Estatístca Epermetal Istruções geras. Esta prova é composta de 0 questões de múltpla escolha a respeto dos cocetos báscos de estatístca epermetal, baseada os lvros BANZATTO, A.D. e KRONKA, S.N.
Prova de Estatístca Epermetal Istruções geras. Esta prova é composta de 0 questões de múltpla escolha a respeto dos cocetos báscos de estatístca epermetal, baseada os lvros BANZATTO, A.D. e KRONKA, S.N.
( k) Tema 02 Risco e Retorno 1. Conceitos Básicos
 FEA -USP Graduação Cêcas Cotábes EAC05 04_0 Profa. Joaíla Ca. Rsco e Retoro. Cocetos Báscos Rotero BE-cap.6 Tema 0 Rsco e Retoro. Cocetos Báscos I. O que é Retoro? II. Qual é o Rsco de um Atvo Idvdual
FEA -USP Graduação Cêcas Cotábes EAC05 04_0 Profa. Joaíla Ca. Rsco e Retoro. Cocetos Báscos Rotero BE-cap.6 Tema 0 Rsco e Retoro. Cocetos Báscos I. O que é Retoro? II. Qual é o Rsco de um Atvo Idvdual
Probabilidades e Estatística LEE, LEIC-A, LEIC-T, LEMat, LERC, MEBiol, MEBiom, MEEC, MEFT, MEMec, MEQ
 Duração: 90 mutos Grupo I Probabldades e Estatístca LEE, LEIC-A, LEIC-T, LEMat, LERC, MEBol, MEBom, MEEC, MEFT, MEMec, MEQ Justfque coveetemete todas as respostas 1 o semestre 018/019 10/01/019 09:00 o
Duração: 90 mutos Grupo I Probabldades e Estatístca LEE, LEIC-A, LEIC-T, LEMat, LERC, MEBol, MEBom, MEEC, MEFT, MEMec, MEQ Justfque coveetemete todas as respostas 1 o semestre 018/019 10/01/019 09:00 o
Universidade Federal de Alfenas - Unifal-MG Departamento de Ciências Exatas
 Uversdade Federal de Alfeas - Ufal-MG Departameto de Cêcas Exatas Apostla Laboratóro de Físca I Prof. Dr. Célo Wsewsk Alfeas 05. oções geras sobre meddas de gradezas e avalação de certezas.. Medção (measuremet).....
Uversdade Federal de Alfeas - Ufal-MG Departameto de Cêcas Exatas Apostla Laboratóro de Físca I Prof. Dr. Célo Wsewsk Alfeas 05. oções geras sobre meddas de gradezas e avalação de certezas.. Medção (measuremet).....
ESTATÍSTICA Exame Final 1ª Época 3 de Junho de 2002 às 14 horas Duração : 3 horas
 Faculdade de cooma Uversdade Nova de Lsboa STTÍSTIC xame Fal ª Época de Juho de 00 às horas Duração : horas teção:. Respoda a cada grupo em folhas separadas. Idetfque todas as folhas.. Todas as respostas
Faculdade de cooma Uversdade Nova de Lsboa STTÍSTIC xame Fal ª Época de Juho de 00 às horas Duração : horas teção:. Respoda a cada grupo em folhas separadas. Idetfque todas as folhas.. Todas as respostas
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
