INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR
|
|
|
- Lucas Malheiro Marroquim
- 7 Há anos
- Visualizações:
Transcrição
1 INTERPRETANDO ALGUNS CONCEITOS DE PROBABILIDADE ESTATÍSTICA VIA ÁLGEBRA LINEAR Hetor Achlles Dutra da Rosa - hetorachlles@yahoo.com.br Cetro Federal de Educação Tecológca Celso Suckow da Foseca CEFET/RJ Aveda Maracaã, 229 Maracaã CEP Ro de Jaero - RJ José Luz Ferades - jlferades@cefet-rj.br Marcos Olvera de Pho - dephogalos@aol.com Resumo: Este trabalho tem como objetvo ressaltar a mportâca da Matemátca, em especal da Álgebra Lear e da Probabldade e Estatístca para os cursos de graduação em Egehara. Dessa forma pretede-se desevolver determados cocetos de Probabldade e Estatístca a partr de um referecal pautado em cocetos de Álgebra Lear, promovedo dessa maera uma assocação etre essas duas áreas da Matemátca. O desevolvmeto desses cocetos ocorre a partr de problemas smples, característcos da área de Egehara. Cotudo, um dos objetvos desse trabalho é promover uma reflexão a respeto da forma com que os cocetos matemátcos em geral são levados aos cursos de graduação em Egehara. Palavras-chaves: Eso de Matemátca; Álgebra Lear, Probabldade e Estatístca. 1. INTRODUÇÃO Segudo BECKER (1997) etede-se que é de fudametal mportâca para aluos de graduação a área de Cêcas Exatas, em especal, as áreas relacoadas às Egeharas, o desevolvmeto de uma sólda formação matemátca que é resposável, detre outras cosas, pelo auxílo a resolução de problemas característcos de suas áreas. Nesse setdo faz-se ecessáro estmular os aluos e profssoas dessas áreas a compreeder e aplcar, com seguraça, os cohecmetos téccos adqurdos ao logo dos cursos de graduação. Date dsso, esse trabalho ressalta a mportâca da Estatístca e da Álgebra Lear a área de Egehara, servdo ambas, como elemetos sgfcatvos para a tomada de decsões e de suporte às aálses de problemas relacoados a essas áreas. É mportate destacar que o eso tato de Estatístca quato de Álgebra Lear devem estar relacoados etre s, e à questões que teham verdadero sgfcado para os estudates de egehara em geral. Segudo BROUSSEAU (1988) cabe às dscplas relacoadas à Probabldade e Estatístca, oferecdas aos cursos de graduação em Egehara, apresetar métodos e téccas que possam ser aplcados um cotexto própro e pecular dessas áreas, cotrbudo para o etedmeto de
2 feômeos e para o desevolvmeto terpretatvo dos mesmos, a fm de que possam ser estabelecdas aálses qualtatvas e quattatvas de tas feomeos. Stetcamete, estatístca é a cêca dos dados uma cêca para o produtor e o cosumdor de formações umércas. Ela evolve coleta, classfcação, sumarzação, orgazação, aálse e terpretação de dados. (MARTINS, 2002, p.19) Quato à Álgebra Lear temos que: A Álgebra Lear é o estudo dos espaços vetoras e das trasformações leares etre eles. Quado os espaços têm dmesões ftas, as trasformações leares possuem matrzes. Também possuem matrzes as formas bleares e, mas partcularmete, as formas quadrátcas. Assm a Álgebra Lear, além de vetores e trasformações leares, lda também com matrzes e formas quadrátcas. São umerosas e bastate varadas as stuações, em Matemátca e em suas aplcações, ode esses objetos ocorrem. Daí a mportâca da Álgebra Lear o eso da Matemátca. (LIMA, 1995 prefáco) Na prátca é comum observar que mutos cursos de Álgebra Lear correspodem a um cojuto de defções e teoremas descoexos com o uverso dos futuros egeheros, fazedo com que erroeamete, a terprete como mas uma dscpla sem sgfcado e sem relevâca para a sua formação. Esse trabalho tem como objetvo relacoar algus cocetos de Álgebra Lear aos cocetos de Probabldade e Estatístca, a fm de permtr a resolução de problemas e facltar a compreesão de cocetos que se apresetam terlgados. Assm, serão apresetadas algumas defções báscas de Álgebra Lear, como a oção de espaços vetoras, bem como a apresetação da defção de produto tero, que correspode a uma oção que erquece a estrutura de um espaço vetoral, permtdo o uso da lguagem geométrca. Date dos etes matemátcos tratados pela Álgebra lear será feta uma aplcação detro da Estatístca, ou seja, com o auxílo desses elemetos apresetados serão apresetados cocetos estatístcos. Acredta-se que a abordagem utlzada vablza uma assocação etre essas duas áreas da Matemátca, possbltado dar maor setdo à Álgebra Lear equato dscpla dos cursos de egehara e também mostrar aos estudates as suas aplcações detro da Estatístca. 2. UM POUCO DE ÁLGEBRA LINEAR Um espaço vetoral real é um cojuto V, ão vazo, com duas operações: soma, + V V V, e multplcação por escalar IR V V, tas que, para quasquer uvw,, V e α, β IR, as segutes propredades são satsfetas: ) ( u+ v) + w= u+ ( v+ w) ) u+ v= v+ u ) 0 V tal que u+ 0 = u v) u V tal que u+ ( u) = 0 v) α( u+ v) = αu+ αv v) ( α + β)u = αu+ βu v) ( αβ) u = α( βu) v) 1u = u
3 Dz-se que qualquer elemeto de um espaço vetoral é um vetor. Como exemplo de espaço vetoral tem-se o cojuto IR, sto é, o cojuto formado pelos vetores -uplas dos úmeros reas: IR = {( x1, x2,..., x ) x IR} tal que para quasquer u = ( x1, x2,..., x ) e v= ( y1, y2,..., y ) em IR e α IR estão defdas as operações u+ v= ( x1+ y1, x2 + y2,..., x + y) e αu = ( αx1, αx2,..., αx ). Tal fato pode ser mostrado pela smples verfcação dos axomas que caracterzam em espaço vetoral. Em partcular, segue que 2 3 IR e IR, sto é, o cojuto dos vetores o plao e o espaço, respectvamete em relação às operações defdas aalogamete, como em IR, também são espaços vetoras. Dado um espaço vetoral V, um subcojuto W, ão vazo, será um subespaço vetoral de V se: ) para quasquer uv, W tem-se u+ v W ) para quasquer α IR, tem-se αu W Num espaço vetoral com v1, v2,..., v V o cojuto { v1, v2,..., v } é learmete depedete (LI) se a equação α1v1+ α2v αv= 0 mplca em α1 = α2 =... = α = 0. Caso cotráro, dz-se que { v1, v2,..., v } é learmete depedete (LD). Pode-se ecotrar, detro de um espaço vetoral V, um cojuto fto de vetores, tas que outro vetor de V seja uma combação lear deles, esse cojuto é deomado base de V. Isto é, mas especfcamete, um cojuto { v, v,...,v } de vetores de V é uma base V se, e somete se, { v, v,..., v } é LI e se { v1, v2,..., v } gera V, ou seja, [ v1, v2,..., v ] = V. É teressate observar que um espaço vetoral pode ser estudado a partr de uma abordagem geométrca, sto é, um espaço vetoral é possível determar meddas que varam de espaço para espaço e que têm sgfcados própros em relação a atureza desses espaços. Sedo V um espaço vetoral real, um produto tero sobre V é uma fução que a cada par de vetores uv,, assoca um úmero real, deotado por < uv, >, satsfazedo as segutes propredades: ) < uv, >=< vu, >, u, v V ) < u+ v, w>=< u, v>+< v, w>, u, v, w V ) < αuv, >= α < uv, >, u, v V v) < u, u > 0 e < uu, >= 0 u= 0, u V Em IR defe-se o produto tero usual etre dos vetores u = ( x1, x2,..., x ) e v= ( y1, y2,..., y ) como sedo < uv, >= xy 1 1+ xy xy, uma vez que essa le verfca as quatro, propredades que caracterzam um produto tero. O produto tero serve, detre outras cosas, para caracterzar a oção de ortogoaldade etre vetores. Dado um espaço vetoral V com produto tero <, >, dz-se que dos vetores uv, Vsão ortogoas em relação ao <, > se < uv, >= 0 e deota-se esse fato por u v. Assm, prova-se que dado um cojuto de vetores, ão ulos, { v1, v2,..., v } dos a dos ortogoas tem-se que { v1, v2,..., v } é LI. Esse resultado permte caracterzar bases ortogoas, ou seja, { v, v,..., v } é base ortogoal de V se < v, v >= 0 para j. A defção de base ortogoal tora-se relevate porque permte estabelecer um procedmeto padrão para se ecotrar as coordeadas de um vetor qualquer em relação a base. j
4 Cosdere V um espaço vetoral com produto tero <, > e β = { u1, u2,..., u } uma base de V e w um vetor qualquer de V. Pode-se obter as coordeadas de w em relação a base β, ou seja, pela defção de base tem-se w= α v + α v + + α v. (1) Aplcado o produto tero <, >, os dos membros dessa gualdade por v obtém-se < v, w>= α < v, v > (2) que mplca em < wv, > α =, (3) < v, v > coordeada cohecda por coefcete de Fourrer de w em relação a v. Seja V um espaço vetoral com produto tero <, > defe-se orma de um vetor u em relação a esse produto tero, o úmero u = < u, u >. (4) Caso, u = 1 u é dto vetor utáro, ou dz-se que u está ormalzado. Para quasquer uv, V e α IR, a oção de orma apreseta as segutes propredades: u 0 e u = 0 u = 0; (5) αu = α u ; (6) < uv, > u v (desgualdade de Schwarz) e (7) u+ v u + v (desgualdade tragular). (8) A desgualdade de Schwarz permte defr âgulo etre dos vetores ão ulos, em um espaço vetoral V mudo de um produto tero, sto é, dados uv, V, vetores ão ulos, etão tem-se que < uv. > 1 (9) u v ou seja, < uv, > 1, (10) u v e, portato exste um âgulo θ etre 0 e π radaos tal que < uv, > cosθ =. (11) u v A defção de orma tora-se ecessára para a caracterzação de bases cohecdas como ortoormas, sto é, uma base β = { u1, u2,..., u } de V é ortoormal se for ortogoal e se cada um de seus vetor é utáro. Vale lembrar que a partr de qualquer base de um espaço vetoral pode-se obter uma base ortoormal utlzado-se o processo de ortogoalzação de Gram- Schmdt e em seguda ormalzado os vetores obtdos esse processo. A obteção de uma base ortoormal a partr de uma base qualquer de um espaço vetoral aparece descrto em LIMA, 2002.
5 de Dados um espaço vetoral V mudo de um produto tero <, > e um subcojuto S V, dz-se que S = { v V v é ortogoal a todos os vetores de S} é chamado complemeto ortogoal de S. 3. PROBABILIDADE ESTATÍSTICA E ÁLGEBRA LINEAR A partr de problemas propostos serão caracterzadas algumas oções de Probabldade Estatístca a fm de uma posteror assocação com as oções de Álgebra Lear descrtas a secção ateror desse trabalho. PROBLEMA 1: Uma dústra que produz determado produto eletrôco percebedo que esses produtos ão tem a mesma durabldade, devdo à varações a lha de produção, qualdade de materas, etc resolve fazer experêcas com relação ao úmero de horas de uso efetvo relacoado durabldade com a respectva probabldade. A partr dos dados cotdos a tabela abaxo, qual a probabldade méda dos compoetes? Tabela 1 Relação durabldade/h e probabldade Durabldade/h Probabldade 1/3 1/4 1/4 1/6 Sedo X uma varável aleatóra dscreta, com valores x 1, x 2,..., x k tem-se que a esperaça matemátca de X, ou méda de X é defda por k µ ( x) = Ex [ ] = xpx ( ). (12) No problema estudado durabldade/h correspode a uma varável aleatóra que assume os valores 4200, 5000, 5400 e 6000, daí: µ ( x) = E[ x] = = 4975 horas. (13) Sedo a varâca uma medda de dspersão que avala o grau de homogeedade dos valores da varável aleatóra em toro da méda, defe-se a varâca de uma varável aleatóra dscreta por = 1 k σ ( x) = VAR( x) = E[( x µ ( x)) ] = ( x µ ( x)) p. (14) Portato, o problema cosderado: σ ( x) = VAR( x) = ( ) + ( ) + ( ) + ( ) = (15) ,99 A partr do cálculo da raz quadrada da varâca obtém-se o desvo padrão, sto é: σ = σ 2 ( x). (16) No exemplo em questão, σ ( x) ,99 648,56. (17) Os cocetos de Probabldade Estatístca abordados estão relacoados à cocetos de Álgebra Lear. Na aálse de expermetos tem-se que um feômeo estudado possu = 1
6 possbldades dsttas S1, S2,..., S de se mafestar, ode cada uma dessas possbldades apreseta probabldades p1, p2,..., p respectvamete. O cojuto S = { S1, S2,..., S } correspode ao espaço amostral e o vetor p = ( p1, p2,..., p ) ao vetor de probabldades. Assm, date de um expermeto de espaço amostral S = { S1, S2,..., S } com vetor de probabldades aleatóro p = ( p1, p2,..., p ) é possível assocar, a cada elemeto S do espaço amostral, um valor X, ode X = ( x1, x2,..., x) correspode ao vetor varável aleatóra. 4 No problema 1, pode-se defr o segute produto tero o IR : < ( x, x, x, x ),( y, y, y, y ) >= p x y + p x y + p x y + p x y (18) ode o vetor X = ( x1, x2, x3, x4) correspode ao vetor durabldade, Y = ( y1, y2, y3, y4) assume em cada coordeada y o valor 1, sto é, Y = ( y1, y2, y3, y4) = (1,1,1,1) e p 1, p 2, p 3 e p 4 são as respectvas probabldades das varáves aleatóras x1, x2, x3 e x 4. Daí, X = µ ( x) = E[( x)] =< (4200,5000,5400,6000),(1,1,1,1) >= (19) = = VAR( x ) =< (4200,5000,5400, 6000) 4975(1,1,1,1),(4200,5000,5400,6000) 4975(1,1,1,1) >= (20) = ,99 σ ( x) = ((4200,5000,5400, 6000), 4975(1,1,1,1)) 648,56 (21) Date do exposto, de uma maera geral, pode-se cosderar em IR : < ( x, x,..., x ),(1,1,...,1) >= p x y + p x y p x y (22) Se uma gradeza assume valores x 1, x 2,..., x represetadas o vetor X = ( x1, x2,..., x ) com probabldades p1, p2,..., p respectvamete, etão o valor médo dessa gradeza (méda ou valor esperado) pode ser dado por X =< X,(1,1,...,1) >; (23) a varâca defe-se por VAR( x) =< X X (1,1,...,1), X X (1,1,...,1) > (24) e o desvo padrão por σ ( x) = X X(1,1,...,1). (25) A terpretação va Álgebra Lear pode-se esteder ada, a stuações em que a partr de um feômeo assocado a um espaço amostral S = { S1, S2,..., S }, com vetor probabldade p = ( p1, p2,..., p ) e dos feômeos represetados por duas varáves aleatóras X = ( x, x,..., x ) e Y = ( y, y,..., y ) deseja-se descobrr qual a relação exstete etre X e Y. Sedo X e Y os valores médos correspodetes a X e Y, respectvamete cosdera-se os vetores: X X(1,1,...,1) = ( x1 X, x2 X,..., x X) (26) e Y Y(1,1,...,1) = ( y1 Y, y2 Y,..., y Y) (27) Se exstr um λ tal que: ( y1 Y, y2 Y,..., y Y) = λ ( x1 X, x2 X,..., x X) (28)
7 pode-se coclur que a medda que X vara, Y também vara proporcoalmete, caracterzado dessa forma uma relação etre ambas. Para que λ exsta é ecessáro que os vetores teham a mesma dreção, sto é, que o âgulo etre eles seja 0 ou π, e portato cosθ = 1 ou 1. Logo, o cosseo do âgulo etre dos vetores X X(1,1,...,1) e Y Y(1,1,...,1) é uma medda da relação etre X e Y. Este valor é cohecdo como coefcete de correlação lear etre X e Y deotado, geralmete, pelos estatístcos por r( X, Y ). Assm, r( X, Y) é defdo por: < ( X X(1,1,...,1), Y Y(1,1,...,1)) > r( X, Y) = X X(1,1,...,1) Y Y(1,1,...,1) PROBLEMA 2: Cosdere um grupo de10 aluos da qual são cohecdas as otas de Álgebra Lear e Estatístca dadas pela tabela abaxo: Tabela 2: Notas dos aluos Aluo Álgebra Lear Estatístca Qual a correlação etre os resultados as duas matéras? Prmeramete tem-se que o espaço amostral correspode ao cojuto dos aluos, umerados de 1 a 10, S = {1,2,...,10}. Como a probabldade de se cosderar as otas de qualquer aluo é gual, o vetor probabldade é dado por p =,,...,, a varável aleatóra que dá as otas de Álgebra Lear é X = (2,8,5,7,7,5,3,1,9,9) e a que dá as otas de Estatístca é Y = (1,9,7,2,7,4,6,3,9,7). Daí, tem-se que X = 5,6 e Y = 5,5. Logo, e o coefcete de correlação é rxy (, ) 0, CONCLUSÃO (29) X X(1,1,...,1) = ( 3,6;2,4; 0,6;...; 4,6;3,4;3,4) (30) Y Y(1,1,...,1) = ( 4,5;3,5;1,5;...; 2,5;3,5;1,5) (31) < X X(1,1,...,1), Y Y(1,1,...,1) > 4,9 (32) 2 2 X X(1,1,...,1) 7,4 e Y Y(1,1,...,1) 7,2 (33) A maera em que foram expostos os cocetos de Álgebra Lear e de Probabldade estatístca sugere uma relação etre essas duas áreas da Matemátca que em cojuto são capazes de resolver problemas característcos das áreas de egehara. Cotudo, essa forma de expor tas cocetos rompe com uma vsão compartmetalzada do eso de matemátca e sem coexões com o mudo real. Etede-se que essa forma de eso baseada uma proposta terdscplar cotrbu para uma formação mas sólda de tas cocetos, além de dar sgfcado a cada uma das áreas da matemátca, revelado o quato, se fazem ecessáras e útl para a formação dos futuros egeheros. 5. REFERÊNCIAS BIBLIOGRÁFICAS BECKER, F. A Epstemologa do professor O Cotdao da Escola, 5ª Ed., Ed. Vozes, 1997
8 BROUSSEAU, G., Fodemets et méthodes de la ddactque dês máthématques. I: _Recherces e Ddactque dês Mathématques, Greoble: v.9,.3, p , LANG, S., Lear Álgebra, Ed. Addso-Wesley, LIMA. E. L. Álgebra Lear. Ro de Jaero: IMPA, LIPSCHUTZ, S. Probabldade. 4 ª ed. São Paulo: Makro books, MACHADO, S. (Org.), Educação matemátca: Uma Itrodução.São Paulo: EDUC, MARTINS, G. de A. Estatístca geral e aplcada. 2 ª ed. São Paulo: Atlas, MENDANHALL, W. Probabldade e estatístca. Ro de Jaero: Campus, 2 v INTERPRETING SOME CONCEPTS OF STATISTICAL PROBABILITY SAW LINEAR ALGEBRA Abstract: Ths work has as objectve emphaszes the mportace of the Mathematcs, especally of the Leal Algebra ad of the Probablty ad Statstcs for the degree courses Egeerg. I that way t teds to develop certa cocepts of Probablty ad Statstcs startg from a ruled referetal cocepts of Leal Algebra, promotg that way a assocato amog those two areas of the Mathematcs. The developmet of those cocepts, they happe startg from smple problems, characterstc of the area of Egeerg. However, t teds to promote a reflecto regardg the form wth that the mathematcal cocepts geeral are take to the degree courses Egeerg. Key-words: Mathematcs Teachgs; Lear Algebra, Probablty ad Statstcs.
Regressão Linear - Introdução
 Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
Regressão Lear - Itrodução Na aálse de regressão lear pretede-se estudar e modelar a relação (lear) etre duas ou mas varáves. Na regressão lear smples relacoam-se duas varáves, x e Y, através do modelo
2-Geometria da Programação Linear
 I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
I 88 Otmzação Lear -Geometra da Programação Lear ProfFeradoGomde DC-FEEC-Ucamp Coteúdo. Poledros e cojutos coveos. Potos etremos vértces soluções báscas factíves 3. Poledros a forma padrão 4. Degeeração
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 CAPES INTERPOLAÇÃO
 Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Uversdade Federal do Ro Grade FURG Isttuto de Matemátca, Estatístca e Físca IMEF Edtal CAPES INTERPOLAÇÃO Pro. Atôo Mauríco Mederos Alves Proª Dese Mara Varella Martez Matemátca Básca ara Cêcas Socas II
Capítulo 2 O conceito de Função de Regressão Populacional (FRP) e Função de Regressão Amostral (FRA)
 I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
I Metodologa da Ecoometra O MODELO CLÁSSICO DE REGRESSÃO LINEAR. Formulação da teora ou da hpótese.. Especfcação do modelo matemátco da teora. 3. Especfcação do modelo ecoométrco da teora. 4. Obteção de
Estatística Descritiva
 Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
Estatístca Descrtva Cocetos Báscos População ou Uverso Estatístco: coj. de elemetos sobre o qual cde o estudo estatístco; Característca Estatístca ou Atrbuto: a característca que se observa os elemetos
É o quociente da divisão da soma dos valores das variáveis pelos números deles:
 Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
Meddas de Posção. Itrodução Proª Ms. Mara Cytha O estudo das dstrbuções de requêcas, os permte localzar a maor cocetração de valores de uma dstrbução. Porém, para ressaltar as tedêcas característcas de
AULA Produto interno em espaços vectoriais reais ou complexos Produto Interno. Norma. Distância.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Introdução à Teoria dos Números Notas 1 Os Princípios da Boa Ordem e de Indução Finita Prof Carlos Alberto S Soares
 Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
AULA Os 4 espaços fundamentais Complemento ortogonal.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Construção e Análise de Gráficos
 Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
4 Capitalização e Amortização Compostas
 4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
4.1 Itrodução Quado queremos fazer um vestmeto, podemos depostar todos os meses uma certa quata em uma cadereta de poupaça; quado queremos comprar um bem qualquer, podemos fazê-lo em prestações, a serem
CURSO SOBRE MEDIDAS DESCRITIVA Adriano Mendonça Souza Departamento de Estatística - UFSM -
 CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
CURSO SOBRE MEDIDAS DESCRITIVA Adrao Medoça Souza Departameto de Estatístca - UFSM - O telecto faz pouco a estrada que leva à descoberta. Acotece um salto a coscêca, chame-o você de tução ou do que quser;
tica Professor Renato Tião
 Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Números complexos Algumas equações do segudo grau como x + 1 = 0 ão possuem solução o uverso real e o estudo destas soluções ão pareca ecessáro até o século XVI quado o matemátco aphael Bombell publcou
Derivada de uma matriz em ordem a um escalar. Derivada de um escalar em ordem a uma matriz DERIVAÇÃO COM MATRIZES. Y = y m. X = x m X = y = = b.
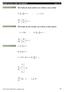 DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
DEFINIÇÃO Dervada de uma matrz em ordem a um escalar [ ] Y = y m : ; y = f() z Y z = y : m z DEFINIÇÃO 2 Dervada de um escalar em ordem a uma matrz h = f( X ) ; [ ]: X = x m EXEMPLO [ y] h h m X = x :
Módulo: Binômio de Newton e o Triângulo de Pascal. Binômio de Newton e o Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Trâgulo de Pascal Bômo de Newto e o Trâgulo de Pascal Exercícos Itrodutóros Exercíco Para
Matemática Ficha de Trabalho
 Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
Matemátca Fcha de Trabalho Meddas de tedêca cetral - 0º ao MEDIDAS DE LOCALIZAÇÃO Num estudo estatístco, depos de recolhdos e orgazados os dados, há a ase de trar coclusões através de meddas que possam,
INTRODUÇÃO A ESTATÍSTICA
 Hewlett-Packard INTRODUÇÃO A ESTATÍSTICA Aulas 01 e 06 Elso Rodrgues, Gabrel Carvalho e Paulo Luz Sumáro Defções... 1 EXERCÍCIOS FUNDAMENTAIS... 1 Meddas de tedêca cetral... 1 Méda artmétca smples... 1
Hewlett-Packard INTRODUÇÃO A ESTATÍSTICA Aulas 01 e 06 Elso Rodrgues, Gabrel Carvalho e Paulo Luz Sumáro Defções... 1 EXERCÍCIOS FUNDAMENTAIS... 1 Meddas de tedêca cetral... 1 Méda artmétca smples... 1
Licenciatura em Ciências USP/ Univesp funções polinomiais 4
 Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Lcecatura em Cêcas USP/Uvesp FUNÇÕES POLINOMIAIS 4 51 TÓPICO Gl da Costa Marques 4.1 Potecação 4. Fuções Polomas de grau 4.3 Fução Polomal do Segudo Grau ou Fução Quadrátca 4.4 Aálse da Forma Geral dos
Centro de Ciências Agrárias e Ambientais da UFBA Departamento de Engenharia Agrícola
 Cetro de Cêcas Agráras e Ambetas da UFBA Departameto de Egehara Agrícola Dscpla: AGR Boestatístca Professor: Celso Luz Borges de Olvera Assuto: Estatístca TEMA: Somatóro RESUMO E NOTAS DA AULA Nº 0 Seja
Cetro de Cêcas Agráras e Ambetas da UFBA Departameto de Egehara Agrícola Dscpla: AGR Boestatístca Professor: Celso Luz Borges de Olvera Assuto: Estatístca TEMA: Somatóro RESUMO E NOTAS DA AULA Nº 0 Seja
MEDIDAS DE POSIÇÃO: X = soma dos valores observados. Onde: i 72 X = 12
 MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
MEDIDAS DE POSIÇÃO: São meddas que possbltam represetar resumdamete um cojuto de dados relatvos à observação de um determado feômeo, pos oretam quato à posção da dstrbução o exo dos, permtdo a comparação
2-0,0041295**.C 2 + 0,0017052**.T.C
 14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
14. Itrodução ao estudo de regressão lear smples 14.1. Itrodução Itrodução ao estudo de regressão lear smples IS 78,9137 -,341836**.T +,78753**.C -,7154**.T -,4195**.C +,175**.T.C R 77,17% IS, % Fgura
Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística Prof. Lorí Viali, Dr. PUCRS FAMAT: Departamento de Estatística
 Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
Prof. Lorí Val, Dr. http://www.pucrs.br/famat/val/ val@pucrs.br Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Prof. Lorí Val, Dr. PUCRS FAMAT: Departameto de Estatístca Obetvos A Aálse de
NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO
 NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO ISABEL C. C. LEITE SALVADOR BA 007 Estatístca Prof.ª Isabel C. C. Lete TEORIA DA AMOSTRAGEM DISTRIBUIÇÃO AMOSTRAL DOS ESTIMADORES A teora da amostragem
NOTAS DE AULA - ESTATÍSTICA TEORIA DA AMOSTRAGEM ESTIMAÇÃO ISABEL C. C. LEITE SALVADOR BA 007 Estatístca Prof.ª Isabel C. C. Lete TEORIA DA AMOSTRAGEM DISTRIBUIÇÃO AMOSTRAL DOS ESTIMADORES A teora da amostragem
1) Escrever um programa que faça o calculo de transformação de horas em minuto onde às horas devem ser apenas número inteiros.
 Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
Dscpla POO-I 2º Aos(If) - (Lsta de Eercícos I - Bmestre) 23/02/2015 1) Escrever um programa que faça o calculo de trasformação de horas em muto ode às horas devem ser apeas úmero teros. Deverá haver uma
13 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL
 3 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL Como vto em amotragem o prmero bmetre, etem fatore que fazem com que a obervação de toda uma população em uma pequa eja mpratcável, muta veze em vrtude
3 ESTIMAÇÃO DE PARÂMETROS E DISTRIBUIÇÃO AMOSTRAL Como vto em amotragem o prmero bmetre, etem fatore que fazem com que a obervação de toda uma população em uma pequa eja mpratcável, muta veze em vrtude
Professor Mauricio Lutz REGRESSÃO LINEAR SIMPLES. Vamos, então, calcular os valores dos parâmetros a e b com a ajuda das formulas: ö ; ø.
 Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Professor Maurco Lutz 1 EGESSÃO LINEA SIMPLES A correlação lear é uma correlação etre duas varáves, cujo gráfco aproma-se de uma lha. O gráfco cartesao que represeta essa lha é deomado dagrama de dspersão.
Confiabilidade Estrutural
 Professor Uversdade de Brasíla Departameto de Egehara Mecâca Programa de Pós graduação em Itegrdade Estrutural Algortmo para a Estmatva do Idce de Cofabldade de Hasofer-Ld Cofabldade Estrutural Jorge Luz
Professor Uversdade de Brasíla Departameto de Egehara Mecâca Programa de Pós graduação em Itegrdade Estrutural Algortmo para a Estmatva do Idce de Cofabldade de Hasofer-Ld Cofabldade Estrutural Jorge Luz
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira INEP Ministério da Educação MEC. Índice Geral de Cursos (IGC)
 Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
Isttuto Nacoal de Estudos e Pesqusas Educacoas Aíso exera INEP stéro da Educação EC Ídce Geral de Cursos (IGC) O Ídce Geral de Cursos (IGC) é ua éda poderada dos cocetos dos cursos de graduação e pós-graduação
RESUMO E EXERCÍCIOS NÚMEROS COMPLEXOS ( )
 NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
NÚMEROS COMPLEXOS Forma algébrca e geométrca Um úmero complexo é um úmero da forma a + b, com a e b reas e = 1 (ou, = -1), chamaremos: a parte real; b parte magára; e udade magára. Fxado um sstema de coordeadas
Capítulo 5: Ajuste de curvas pelo método dos mínimos quadrados
 Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
1. Revisão Matemática
 1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
Prof. Janete Pereira Amador 1
 Prof. Jaete Perera Amador 1 1 Itrodução Mutas stuações cotdaas podem ser usadas como expermeto que dão resultados correspodetes a algum valor, e tas stuações podem ser descrtas por uma varável aleatóra.
Prof. Jaete Perera Amador 1 1 Itrodução Mutas stuações cotdaas podem ser usadas como expermeto que dão resultados correspodetes a algum valor, e tas stuações podem ser descrtas por uma varável aleatóra.
Teoria Elementar da Probabilidade. a) Cada experiência poderá ser repetida indefinidamente sob condições essencialmente inalteradas.
 Estatístca 47 Estatístca 48 Teora Elemetar da Probabldade SPECTOS PERTINENTES À CRCTERIZÇÃO DE UM EXPERIÊNCI LETÓRI MODELOS MTEMÁTICOS DETERMINÍSTICOS PROBBILÍSTICOS PROCESSO (FENÓMENO) LETÓRIO - Quado
Estatístca 47 Estatístca 48 Teora Elemetar da Probabldade SPECTOS PERTINENTES À CRCTERIZÇÃO DE UM EXPERIÊNCI LETÓRI MODELOS MTEMÁTICOS DETERMINÍSTICOS PROBBILÍSTICOS PROCESSO (FENÓMENO) LETÓRIO - Quado
Relatório 2ª Atividade Formativa UC ECS
 Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Relatóro 2ª Atvdade Formatva Eercíco I. Quado a dstrbução de dados é smétrca ou apromadamete smétrca, as meddas de localzação méda e medaa, cocdem ou são muto semelhates. O mesmo ão acotece quado a dstrbução
Estatística - exestatmeddisper.doc 25/02/09
 Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
Estatístca - exestatmeddsper.doc 5/0/09 Meddas de Dspersão Itrodução ão meddas estatístcas utlzadas para avalar o grau de varabldade, ou dspersão, dos valores em toro da méda. ervem para medr a represetatvdade
CAPÍTULO III. Aproximação de funções pelo método dos Mínimos Quadrados
 Métodos Nuércos CAPÍULO III C. Balsa & A. Satos Aproxação de fuções pelo étodo dos Míos Quadrados. Algus cocetos fudaetas de Álgebra Lear Relebraos esta secção algus cocetos portates da álgebra Lear que
Métodos Nuércos CAPÍULO III C. Balsa & A. Satos Aproxação de fuções pelo étodo dos Míos Quadrados. Algus cocetos fudaetas de Álgebra Lear Relebraos esta secção algus cocetos portates da álgebra Lear que
Medidas de Localização
 07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
07/08/013 Udade : Estatístca Descrtva Meddas de Localzação João Garbald Almeda Vaa Cojuto de dados utlzação de alguma medda de represetação resumo dos dados. E: Um cojuto com 400 observações como aalsar
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
MA12 - Unidade 4 Somatórios e Binômio de Newton Semana de 11/04 a 17/04
 MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
MA1 - Udade 4 Somatóros e Bômo de Newto Semaa de 11/04 a 17/04 Nesta udade troduzremos a otação de somatóro, mostrado como a sua mapulação pode sstematzar e facltar o cálculo de somas Dada a mportâca de
IND 1115 Inferência Estatística Aula 9
 Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
Coteúdo IND 5 Iferêca Estatístca Aula 9 Outubro 2004 Môca Barros Dfereça etre Probabldade e Estatístca Amostra Aleatóra Objetvos da Estatístca Dstrbução Amostral Estmação Potual Estmação Bayesaa Clássca
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
Estatística: Aplicação ao Sensoriamento Remoto SER ANO Estimação Pontual
 Estatístca: Aplcação ao Sesorameto Remoto SER 04 - ANO 08 Estmação Potual Camlo Daleles Reó camlo@dp.pe.br http://www.dp.pe.br/~camlo/estatstca/ Iferêca Estatístca Cosdere o expermeto: retram-se 3 bolas
Estatístca: Aplcação ao Sesorameto Remoto SER 04 - ANO 08 Estmação Potual Camlo Daleles Reó camlo@dp.pe.br http://www.dp.pe.br/~camlo/estatstca/ Iferêca Estatístca Cosdere o expermeto: retram-se 3 bolas
Cursos de Licenciatura em Ensino de Matemática e de EGI. Teoria de Probabilidade
 Celso Albo FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhaguee, Av. de Moçambque, km, Tel: +258 240078, Fax: +258 240082, Maputo Cursos de Lcecatura em Eso de Matemátca
Celso Albo FACULDADE DE CIÊNCIAS NATURAIS E MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA Campus de Lhaguee, Av. de Moçambque, km, Tel: +258 240078, Fax: +258 240082, Maputo Cursos de Lcecatura em Eso de Matemátca
ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO
 ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal
ANÁLISE DE REGRESSÃO LINEAR COM MODELO DIFUSO Slva, Glso Mederos e; Bastos, Rogéro Cd; Marts, Aleadro * ; Pacheco *, Roberto C. S.; Programa de Pós-Graduação em Egehara de Produção PPGEP Uversdade Federal
MÉTODO DOS MÍNIMOS QUADRADOS
 MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
MÉTODO DOS MÍNIMOS QUADRADOS I - INTRODUÇÃO O processo de medda costtu uma parte essecal a metodologa cetífca e também é fudametal para o desevolvmeto e aplcação da própra cêca. No decorrer do seu curso
2. NOÇÕES MATEMÁTICAS
 . NOÇÕES MATEMÁTICAS Este capítulo retoma algumas oções matemátcas ecessáras para uma boa compreesão de algus aspectos que serão mecoados e detalhados o presete trabalho. Algus destes aspectos podem abstrar
. NOÇÕES MATEMÁTICAS Este capítulo retoma algumas oções matemátcas ecessáras para uma boa compreesão de algus aspectos que serão mecoados e detalhados o presete trabalho. Algus destes aspectos podem abstrar
3- Autovalores e Autovetores.
 MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
MÉTODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 3- Autovalores e Autovetores. 3.- Autovetores e Autovalores de ua Matrz. 3.- Métodos para ecotrar os Autovalores e Autovetores de ua Matrz. 3.- Autovetores
CAPÍTULO III - POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA
 Polômos de Jacob e CAPÍTULO III - POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA III--)INTRODUÇÃO Para um melhor etedmeto do método da colocação ortogoal e sua relação com o método dos resíduos poderados (MRP),
Polômos de Jacob e CAPÍTULO III - POLINÔMIOS DE JACOBI E QUADRATURA NUMÉRICA III--)INTRODUÇÃO Para um melhor etedmeto do método da colocação ortogoal e sua relação com o método dos resíduos poderados (MRP),
Avaliação da qualidade do ajuste
 Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Avalação da qualdade do ajuste 1 Alguma termologa: Modelo ulo: é o modelo mas smples que pode ser defdo, cotedo um úco parâmetro ( µ) comum a todos os dados; Modelo saturado: é o modelo mas complexo a
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
Média. Mediana. Ponto Médio. Moda. Itabira MEDIDAS DE CENTRO. Prof. Msc. Emerson José de Paiva 1 BAC011 - ESTATÍSTICA. BAC Estatística
 BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
BAC 0 - Estatístca Uversdade Federal de Itajubá - Campus Itabra BAC0 - ESTATÍSTICA ESTATÍSTICA DESCRITIVA MEDIDAS DE CENTRO Méda Medda de cetro ecotrada pela somatóra de todos os valores de um cojuto,
Medidas Numéricas Descritivas:
 Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
Meddas Numércas Descrtvas: Meddas de dspersão Meddas de Varação Varação Ampltude Ampltude Iterquartl Varâca Desvo absoluto Coefcete de Varação Desvo Padrão Ampltude Medda de varação mas smples Dfereça
Distribuições de Probabilidades
 Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Estatístca - aulasestdstrnormal.doc 0/05/06 Dstrbuções de Probabldades Estudamos aterormete as dstrbuções de freqüêcas de amostras. Estudaremos, agora, as dstrbuções de probabldades de populações. A dstrbução
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
3 - ANÁLISE BIDIMENSIONAL
 INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
INE 7001 - Aálse Bdmesoal 1 3 - ANÁLISE BIDIMENSIONAL É comum haver teresse em saber se duas varáves quasquer estão relacoadas, e o quato estão relacoadas, seja a vda prátca, seja em trabalhos de pesqusa,
Centro de massa, momento linear de sistemas de partículas e colisões
 Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
Cetro de massa, mometo lear de sstemas de partículas e colsões Prof. Luís C. Pera stemas de partículas No estudo que temos vdo a fazer tratámos os objectos, como, por exemplo, blocos de madera, automóves,
MÓDULO 8 REVISÃO REVISÃO MÓDULO 1
 MÓDULO 8 REVISÃO REVISÃO MÓDULO A Estatístca é uma técca que egloba os métodos cetícos para a coleta, orgazação, apresetação, tratameto e aálse de dados. O objetvo da Estatístca é azer com que dados dspersos
MÓDULO 8 REVISÃO REVISÃO MÓDULO A Estatístca é uma técca que egloba os métodos cetícos para a coleta, orgazação, apresetação, tratameto e aálse de dados. O objetvo da Estatístca é azer com que dados dspersos
Faculdade de Economia, Administração e Contabilidade de Ribeirão Preto
 Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Faculdade de Ecooma, Admstração e Cotabldade de Rberão Preto Ecooma Moetára Curso de Ecooma / º. Semestre de 014 Profa. Dra. Rosel da Slva Nota de aula CAPM Itrodução Há dos modelos bastate utlzados para
Exercícios - Sequências de Números Reais (Solução) Prof Carlos Alberto S Soares
 Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
Exercícos - Sequêcas de Números Reas (Solução Prof Carlos Alberto S Soares 1 Dscuta a covergêca da sequẽca se(2. Calcule, se exstr, lm se(2. Solução 1 Observe que se( 2 é lmtada e 1/ 0, portato lm se(2
Números Complexos. 2. (IME) Seja z um número complexo de módulo unitário que satisfaz a condição z 2n 1, onde n é um número inteiro positivo.
 Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Requisitos metrológicos de instrumentos de pesagem de funcionamento não automático
 Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
Requstos metrológcos de strumetos de pesagem de fucoameto ão automátco 1. Geeraldades As balaças estão assocadas de uma forma drecta à produção do betão e ao cotrolo da qualdade do mesmo. Se são as balaças
DISTRIBUIÇÃO HIPERGEOMÉTRICA
 7 DISTRIBUIÇÃO HIPERGEOMÉTRICA Cosdere-se uma população fta costtuída por N elemetos dstrbuídos por duas categoras eclusvas e eaustvas de dmesões M e N M, respectvamete. Os elemetos da prmera categora
7 DISTRIBUIÇÃO HIPERGEOMÉTRICA Cosdere-se uma população fta costtuída por N elemetos dstrbuídos por duas categoras eclusvas e eaustvas de dmesões M e N M, respectvamete. Os elemetos da prmera categora
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
? Isso é, d i= ( x i. . Percebeu que
 Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
AULA Espaços Vectoriais Estruturas Algébricas.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resolvedo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resolvedo os problemas
UNICAMP - 2004. 2ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
 UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
UNICAMP - 004 ª Fase MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Em uma sala há uma lâmpada, uma televisão [TV] e um aparelho de ar codicioado [AC]. O cosumo da lâmpada equivale
Gráfico de Controle de Regressão Aplicado ao Monitoramento de Características da Qualidade do Eletrodo de Carbono
 Gráfco de Cotrole de Regressão Aplcado ao Motorameto de Característcas da Qualdade do Eletrodo de Carboo Marcello Neva de Mello, evamarcello@gmal.com Wager Rogéro Ferrera Phero, wager35@gmal.com Edso Marcos
Gráfco de Cotrole de Regressão Aplcado ao Motorameto de Característcas da Qualdade do Eletrodo de Carboo Marcello Neva de Mello, evamarcello@gmal.com Wager Rogéro Ferrera Phero, wager35@gmal.com Edso Marcos
Distribuições Amostrais. Estatística. 8 - Distribuições Amostrais UNESP FEG DPD
 Dstrbuções Amostras Estatístca 8 - Dstrbuções Amostras 08- Dstrbuções Amostras Dstrbução Amostral de Objetvo: Estudar a dstrbução da população costtuída de todos os valores que se pode obter para, em fução
Dstrbuções Amostras Estatístca 8 - Dstrbuções Amostras 08- Dstrbuções Amostras Dstrbução Amostral de Objetvo: Estudar a dstrbução da população costtuída de todos os valores que se pode obter para, em fução
Faculdade de Tecnologia de Catanduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL
 Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
Faculdade de Tecologa de Cataduva CURSO SUPERIOR DE TECNOLOGIA EM AUTOMAÇÃO INDUSTRIAL 5. Meddas de Posção cetral ou Meddas de Tedêca Cetral Meddas de posção cetral preocupam-se com a caracterzação e a
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA
 INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
INTRODUÇÃO ÀS PROBABILIDADES E ESTATÍSTICA 003 Iformações: relembra-se os aluos teressados que a realzação de acções presecas só é possível medate solctação vossa, por escrto, à assstete da cadera. A realzação
CAPÍTULO 9 - Regressão linear e correlação
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO 9 - Regressão lear e correlação Veremos esse capítulo os segutes assutos essa ordem: Correlação amostral Regressão Lear Smples Regressão Lear Múltpla Correlação
Representação dos padrões. Tipos de atributos. Etapas do processo de agrupamento. 7.1 Agrupamento clássico. 7. Agrupamento fuzzy (fuzzy clustering)
 7. Agrupaeto fuzzy (fuzzy clusterg) 7. Agrupaeto clássco Agrupaeto é a classfcação ão-supervsoada de padrões (observações, dados, objetos, eeplos) e grupos (clusters). Itutvaete, padrões seelhates deve
7. Agrupaeto fuzzy (fuzzy clusterg) 7. Agrupaeto clássco Agrupaeto é a classfcação ão-supervsoada de padrões (observações, dados, objetos, eeplos) e grupos (clusters). Itutvaete, padrões seelhates deve
REGESD Prolic Matemática e Realidade- Profª Suzi Samá Pinto e Profº Alessandro da Silva Saadi
 REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
REGESD Prolc Matemátca e Realdade- Profª Suz Samá Pto e Profº Alessadro da Slva Saad Meddas de Posção ou Tedêca Cetral As meddas de posção ou meddas de tedêca cetral dcam um valor que melhor represeta
PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA
 UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
UNIVERSIDADE DE ÉVORA DEPARTAMENTO DE ENGENHARIA RURAL PROBABILIDADE E ESTATÍSTICA APLICADA À HIDROLOGIA 0 ESTATÍSTICA E PROBABILIDADE APLICADA À HIDROLOGIA. Itrodução Nehum processo hdrológco é puramete
Métodos iterativos. Capítulo O Método de Jacobi
 Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Capítulo 4 Métodos teratvos 41 O Método de Jacob O Método de Jacob é um procedmeto teratvo para a resolução de sstemas leares Tem a vatagem de ser mas smples de se mplemetar o computador do que o Método
Como CD = DC CD + DC = 0
 (9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
(9-0 www.eltecampas.com.br O ELITE RESOLVE IME 008 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO Determe o cojuto-solução da equação se +cos = -se.cos se + cos = se cos ( se cos ( se se.cos cos + + = = (
Forma padrão do modelo de Programação Linear
 POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
POGAMAÇÃO LINEA. Forma Padrão do Modelo de Programação Lear 2. elações de Equvalêca 3. Suposções da Programação Lear 4. Eemplos de Modelos de PPL 5. Suposções da Programação Lear 6. Solução Gráfca e Iterpretação
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
x n = n ESTATÍSTICA STICA DESCRITIVA Conjunto de dados: Organização; Amostra ou Resumo; Apresentação. População
 ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
ESTATÍSTICA STICA DESCRITIVA Prof. Lorí Val, Dr. val@mat.ufrgs.br http://.ufrgs.br/~val/ Orgazação; Resumo; Apresetação. Cojuto de dados: Amostra ou População Um cojuto de dados é resumdo de acordo com
( ) ( IV ) n ( ) Escolha a alternativa correta: A. III, II, I, IV. B. II, III, I, IV. C. IV, III, I, II. D. IV, II, I, III. E. Nenhuma das anteriores.
 Prova de Estatístca Epermetal Istruções geras. Esta prova é composta de 0 questões de múltpla escolha a respeto dos cocetos báscos de estatístca epermetal, baseada os lvros BANZATTO, A.D. e KRONKA, S.N.
Prova de Estatístca Epermetal Istruções geras. Esta prova é composta de 0 questões de múltpla escolha a respeto dos cocetos báscos de estatístca epermetal, baseada os lvros BANZATTO, A.D. e KRONKA, S.N.
ANÁLISE DE ERROS. Todas as medidas das grandezas físicas deverão estar sempre acompanhadas da sua dimensão (unidades)! ERROS
 ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
ANÁLISE DE ERROS A oservação de um feómeo físco ão é completa se ão pudermos quatfcá-lo. Para é sso é ecessáro medr uma propredade físca. O processo de medda cosste em atrur um úmero a uma propredade físca;
Estudo do intervalo de confiança da regressão inversa utilizando o software R
 Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
Estudo do tervalo de cofaça da regressão versa utlzado o software R Llae Lopes Cordero João Domgos Scalo. Itrodução Na maora das aplcações evolvedo regressão, determa-se o valor de Y correspodete a um
A análise de variância de uma classificação (One-Way ANOVA) verifica se as médias de k amostras independentes (tratamentos) diferem entre si.
 Prof. Lorí Va, Dr. http://www. ufrgs.br/~va/ va@mat.ufrgs.br aáse de varâca de uma cassfcação (Oe-Way NOV) verfca se as médas de amostras depedetes (tratametos) dferem etre s. Um segudo tpo de aáse de
Prof. Lorí Va, Dr. http://www. ufrgs.br/~va/ va@mat.ufrgs.br aáse de varâca de uma cassfcação (Oe-Way NOV) verfca se as médas de amostras depedetes (tratametos) dferem etre s. Um segudo tpo de aáse de
ESTATÍSTICA MÓDULO 2 OS RAMOS DA ESTATÍSTICA
 ESTATÍSTICA MÓDULO OS RAMOS DA ESTATÍSTICA Ídce. Os Ramos da Estatístca...3.. Dados Estatístcos...3.. Formas Icas de Tratameto dos Dados....3. Notação por Ídces...5.. Notação Sgma ()...5 Estatístca Módulo
ESTATÍSTICA MÓDULO OS RAMOS DA ESTATÍSTICA Ídce. Os Ramos da Estatístca...3.. Dados Estatístcos...3.. Formas Icas de Tratameto dos Dados....3. Notação por Ídces...5.. Notação Sgma ()...5 Estatístca Módulo
Ivan G. Peyré Tartaruga. 1 Metodologia espacial
 RELATÓRIO DE PESQUISA 5 Procedmetos o software ArcGIS 9. para elaborar os mapas da Regão Metropoltaa de Porto Alegre RMPA com as elpses de dstrbução drecoal etre 99 e 000 Iva G. Peré Tartaruga Metodologa
RELATÓRIO DE PESQUISA 5 Procedmetos o software ArcGIS 9. para elaborar os mapas da Regão Metropoltaa de Porto Alegre RMPA com as elpses de dstrbução drecoal etre 99 e 000 Iva G. Peré Tartaruga Metodologa
Complexidade Computacional da Determinação da Correspondência entre Imagens
 Complexdade Computacoal da Determação da Correspodêca etre Images Adraa Karlstroem Laboratóro de Sstemas Embarcados Departameto de Egehara Mecatrôca Escola Poltécca da Uversdade de São Paulo adraa.karlstroem@pol.usp.br
Complexdade Computacoal da Determação da Correspodêca etre Images Adraa Karlstroem Laboratóro de Sstemas Embarcados Departameto de Egehara Mecatrôca Escola Poltécca da Uversdade de São Paulo adraa.karlstroem@pol.usp.br
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
Estatística Notas de Aulas ESTATÍSTICA. Notas de Aulas. Professor Inácio Andruski Guimarães, DSc. Professor Inácio Andruski Guimarães, DSc.
 Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Estatístca Notas de Aulas ESTATÍSTICA Notas de Aulas Professor Iáco Adrus Gumarães, DSc. Professor Iáco Adrus Gumarães, DSc. Estatístca Notas de Aulas SUMÁRIO CONCEITOS BÁSICOS 5. Estatístca. Estatístca
Sumário. Mecânica. Sistemas de partículas
 Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
Sumáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - Sstemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. -
6.1 - PROCEDIMENTO DE AVALIAÇÃO DE INCERTEZA EM MEDIÇÕES DIRETAS
 7 6 - PROCEDIMENTO DE AVALIAÇÃO DE INCERTEZA EM MEDIÇÕES DIRETAS A medção dreta é aquela cuja dcação resulta aturalmete da aplcação do sstema de medção sobre o mesurado Há apeas uma gradeza de etrada evolvda
7 6 - PROCEDIMENTO DE AVALIAÇÃO DE INCERTEZA EM MEDIÇÕES DIRETAS A medção dreta é aquela cuja dcação resulta aturalmete da aplcação do sstema de medção sobre o mesurado Há apeas uma gradeza de etrada evolvda
ANÁLISE DE REGRESSÃO E CORRELAÇÃO
 ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
ANÁLISE DE REGRESSÃO E CORRELAÇÃO Quado se cosderam oservações de ou mas varáves surge um poto ovo: O estudo das relações porvetura estetes etre as varáves. A aálse de regressão e correlação compreedem
II. Propriedades Termodinâmicas de Soluções
 II. Propredades Termodâmcas de Soluções 1 I. Propredades Termodâmcas de Fludos OBJETIVOS Eteder a dfereça etre propredade molar parcal e propredade de uma espéce pura Saber utlzar a equação de Gbbs-Duhem
II. Propredades Termodâmcas de Soluções 1 I. Propredades Termodâmcas de Fludos OBJETIVOS Eteder a dfereça etre propredade molar parcal e propredade de uma espéce pura Saber utlzar a equação de Gbbs-Duhem
Capítulo 2. Aproximações de Funções
 EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo Aproações de Fuções Há bascaete dos tpos de probleas de aproações: ) ecotrar ua fução as sples, coo u polôo, para aproar
EQE-358 MÉTODOS NUMÉRICOS EM ENGENHARIA QUÍMICA PROFS. EVARISTO E ARGIMIRO Capítulo Aproações de Fuções Há bascaete dos tpos de probleas de aproações: ) ecotrar ua fução as sples, coo u polôo, para aproar
REGRESSÃO LINEAR 05/10/2016 REPRESENTAÇAO MATRICIAL. Y i = X 1i + 2 X 2i k X ni + i Y = X + INTRODUÇÃO SIMPLES MÚLTIPLA
 REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
Probabilidade e Estatística. Correlação e Regressão Linear
 Probabldade e Estatístca Correlação e Regressão Lnear Varáves Varável: característcas ou tens de nteresse de cada elemento de uma população ou amostra Também chamada parâmetro, posconamento, condção...
Probabldade e Estatístca Correlação e Regressão Lnear Varáves Varável: característcas ou tens de nteresse de cada elemento de uma população ou amostra Também chamada parâmetro, posconamento, condção...
Probabilidade: Diagramas de Árvore
 Probabldade: Dagramas de Árvore Ana Mara Lma de Faras Departamento de Estatístca (GET/UFF) Introdução Nesse texto apresentaremos, de forma resumda, concetos e propredades báscas sobre probabldade condconal
Probabldade: Dagramas de Árvore Ana Mara Lma de Faras Departamento de Estatístca (GET/UFF) Introdução Nesse texto apresentaremos, de forma resumda, concetos e propredades báscas sobre probabldade condconal
CAPÍTULO 2 - Estatística Descritiva
 INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
INF 6 Prof. Luz Alexadre Peterell CAPÍTULO - Estatístca Descrtva Podemos dvdr a Estatístca em duas áreas: estatístca dutva (ferêca estatístca) e estatístca descrtva. Estatístca Idutva: (Iferêca Estatístca)
