Instituto Tecnológico de Aeronáutica VIBRAÇÕES MECÂNICAS MPD-42
|
|
|
- Paulo Cabreira Benke
- 5 Há anos
- Visualizações:
Transcrição
1 VIBRAÇÕES MECÂNICAS MPD-4 1
2 SISTEMAS CONTÍNUOS: SOUÇÃO EXATA MPD-4
3 Sstemas contínuos: solução eata Intoução Sstemas scetos e sstemas contínuos epesentam os tpos e sstemas feentes? Ambos são meas epesentações matemátcas e sstemas fscamente êntcos MPD-4 3
4 Sstemas contínuos: solução eata Intoução Dfeença básca: Sstemas scetos têm um númeo fnto e gaus e lbeae Sstemas contínuos têm nfntos gaus e lbeae MPD-4 4
5 Sstemas contínuos: solução eata Intoução O ínce é assocao a uma massa concentaa. Em contapata, uma cooenaa espacal entfca a posção e um elemento nfntesmal. Consstente com esse fato sstemas scetos são govenaos po equações feencas onáas e sstemas contínuos po equações feencas pacas. MPD-4 5
6 Sstemas contínuos: solução eata Intoução Tpos e sstemas contínuos Fos em vbação tansvesal a oem Baas em vbação aal a oem Eos em toção nâmca a oem Vgas em fleão nâmca 4 a oem Soluções eatas só são possíves em tpos especalmente smples e sstemas contínuos MPD-4 6
7 Sstemas contínuos: solução eata Sstema sceto sstema contínuo Este uma elação bastante esteta ente sstemas scetos e sstemas contínuos. Vbação tansvesal e um fo 1 Sstema sceto análse lmte Sstema contínuo MPD-4 7
8 Sstemas contínuos: solução eata Sstema sceto sstema contínuo F 1 F F +1 m 1 m m +1 MPD-4 8
9 Sstemas contínuos: solução eata Sstema sceto sstema contínuo F F +1 F 1 T 1 T T = tensão no fo F = foça etena v 1 v v +1 1 T v v v T 1 + F = 1 v m v t MPD-4 9
10 MPD-4 1 Sstemas contínuos: solução eata Sstema sceto sstema contínuo t v m F v v T v v T = + + Equações válas paa = 1,...,n quano v t = v n+1 t =. Outas conções e contono poem também se conseaas.
11 MPD-4 11 Sstemas contínuos: solução eata Sstema sceto sstema contínuo e + = = v v v v v v t v m F v T v T = + t v m F v T = + Equações ncementas nas componentes vetcas a foça e tação
12 Sstemas contínuos: solução eata Sstema sceto sstema contínuo Se o númeo e massas m cesce nefnamente n as massas m e as stâncas e v tenem a zeo. No lmte, v, t T + f, t = ρ v, t t one f, t é a foça etena stbuía po unae e compmento e ρ a ensae e massa po unae e compmento. MPD-4 1
13 Sstemas contínuos: solução eata Sstema sceto sstema contínuo f,t v,t MPD-4 13
14 Sstemas contínuos: solução eata Sstema sceto sstema contínuo f,t T + T θ T θ + θ v θ = MPD-4 14
15 MPD-4 15 Sstemas contínuos: solução eata Sstema sceto sstema contínuo,, t t v t f v T v v T T = ρ e e Newton paa a componente vetcal: Despezano temos e a oem:,,, t t v t f t v T = + ρ
16 Sstemas contínuos: solução eata Sstema sceto sstema contínuo Atavés e um pocesso lmte patu-se e um sstema sceto paa um contínuo. No entanto, o mas comum é segu o camnho nveso e tal foma que um sstema físco contínuo seja apomao matematcamente po um sstema sceto. Se os paâmetos foem não-unfomemente stbuíos o pocemento e apomação eve se capaz e leva sso em conta. MPD-4 16
17 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo v, t T = ρ Conção e valo ncal: v, = v v&, =& v Conção e contono: v, t = v, t = v, t t MPD-4 17
18 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo Investga-se a possblae e movmento síncono, sto é, a foma o fo não mua com o tempo, somente a ampltue o movmento. Matematcamente pocua-se um solução na foma sepaável: v, t = V Ft Se v, t epesenta uma osclação hamônca e estável então Ft eve se lmtaa paa qualque nstante e tempo. MPD-4 18
19 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo 1 ρ V V T = 1 F t F t t O lao esqueo epene somente o espaço enquanto o lao eto epene somente o tempo. Paa tanto, 1 ρ V V T = 1 F t F t t = ω MPD-4 19
20 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo V T = ω ρ V F t + ω F t = t O snal e ω fo seleconao e foma que Ft não apesentasse temos eponencas. MPD-4
21 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo A função Ft = C cosωt φ é síncona. Resta sabe se os paões e eslocamento V são também possíves. V T = ω ρ V V = V = MPD-4 1
22 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo A constante ω pemanece netemnaa. O poblema consste em se enconta os valoes e ω que levem a soluções não tvas e V. V T V = ω ρ Obsevação: se V fo solução então αv também seá solução. MPD-4
23 Sstemas contínuos: solução eata Vbação lve: o poblema e auto-valo Aplcação as conções e contono leva à equação caacteístca o poblema e autovalo cuja solução fonece um númeo nfnto e feqüêncas natuas ω e moos natuas V assocaos. Em geal, A V é solução o poblema. A poe se únca se a otogonalae os moos fo levaa em conta. MPD-4 3
24 Sstemas contínuos: solução eata Eemplo: o poblema e auto-valo Resolva o poblema e auto-valo assocao com a vbação e um fo unfome fo em = e = e esboce a foma os tês pmeos moos e vbação. A tensão T no fo é constante. V + β V = V = V = com β = ω ρ T MPD-4 4
25 Sstemas contínuos: solução eata Eemplo: o poblema e auto-valo V = Asn β + Bcos β V = B= V = Asn β V = sn β = β = Equação caacteístca π V = A π sn MPD-4 5
26 Sstemas contínuos: solução eata Eemplo: o poblema e auto-valo 1..5 y/a v/a moo 1 moo moo / / MPD-4 6
27 Sstemas contínuos: solução eata Eemplo: o poblema o cabo suspenso Fomule o poblema e auto-valo assocao à vbação lateal e um cabo unfome suspenso sob ação a gavae. g MPD-4 7
28 Sstemas contínuos: solução eata Baa em vbação aal A vbação aal lve e uma baa é escta pela mesma equação feencal que o poblema o fo em vbação tansvesal. Substtu: ρ po m = massa po unae e compmento T po EA = gez aal MPD-4 8
29 Sstemas contínuos: solução eata Baa em vbação aal u,t u, t = U F t U EA = ω m U U = U = MPD-4 9
30 MPD-4 3 Sstemas contínuos: solução eata Baa em vbação aal k k k k k k M M M M M = = ] [ ] [ m m EA k /1 /1 /5 /5 /5 /5
31 Sstemas contínuos: solução eata Baa em vbação aal 1.5 Moo Moo V 1 /A. V /A / / MPD-4 31
32 Sstemas contínuos: solução eata Baa em vbação aal 1.5 Moo Moo V 3 /A. V 4 /A / / MPD-4 3
33 V 5 /A Sstemas contínuos: solução eata Baa em vbação aal Moo 5 Moo Feqüêncas eato apo / m ω =ω EA MPD-4 33
34 Sstemas contínuos: solução eata Baa em vbação aal As feqüêncas o moelo apomao são mas baas que as o moelo eato evo à concentação e massa no cento a baa. Obvamente a utlzação e mas massas concentaas leva a melhoes esultaos o moelo apomao. MPD-4 34
35 Sstemas contínuos: solução eata Eecícos Consee uma baa unfome em vbação aal que possu os os etemos lves e ache os tês pmeos moos e vbação. u,t MPD-4 35
36 Sstemas contínuos: solução eata Eecícos Obte as equação o movmento e as conções e contono e uma baa faa em = e conectaa a uma mola em =. EA, m u,t k MPD-4 36
37 Sstemas contínuos: solução eata Eecícos Obte as equação o movmento e as conções e contono e uma baa faa em = e supotano uma massa concentaa em =. EA, m u,t M MPD-4 37
38 Sstemas contínuos: solução eata Eecícos Obte as equação o movmento e as conções e contono e uma baa unfome faa em = e supotano uma massa concentaa em um ponto nteno localzao em = a. EA 1, m 1 EA, m a M b MPD-4 38
39 Sstemas contínuos: solução eata Vga em fleão nâmca As equações nâmcas e fos em vbação tansvesal e baas em vbação aal são êntcas nas suas fomas. Ambas levam a equações e seguna oem. No caso e vbação e vgas em fleão as equações são e quata oem. MPD-4 39
40 Sstemas contínuos: solução eata Vga em fleão nâmca y f,t f,t M+M M Q Q+Q MPD-4 4
41 Sstemas contínuos: solução eata Vga em fleão nâmca Q, t v, t Q, t + Q, t + f, t = m t M, t Q, t M, t + M, t + Q, t + + Q, t + f, t = m M, t + Q, t = v, t t f, t = MPD-4 41
42 Sstemas contínuos: solução eata Vga em fleão nâmca M, t + f, t = m v, t t Teoa básca e fleão e vgas: M, t = EI v, t MPD-4 4
43 Sstemas contínuos: solução eata Vga em fleão nâmca EI v, t + f, t = m v, t t A equação contém evaas em elação a até quata oem. MPD-4 43
44 Sstemas contínuos: solução eata Vga em fleão nâmca Conções e contono: Engaste: v, t =, v, t = = v, t Apoo smples: v, t =, EI = v, t v, t ve: EI =, = EI MPD-4 44 = = =
45 Sstemas contínuos: solução eata Vga em fleão nâmca As conções e contono e engastamento e uma e apoo smples estão elaconaas à geometa o poblema e, po sso, são chamaas conções e contono geométcas. As conções e contono e etemo lve e uma e apoo smples estão elaconaas aos balanços e foça e momento e são chamaas conções e contono natuas. MPD-4 45
46 Sstemas contínuos: solução eata Vga em fleão nâmca f,t v, t = V F t V EI m V =ω MPD-4 46
47 Sstemas contínuos: solução eata Vga em fleão nâmca Conções e contono: v, t = v, t =,, v, t EI v, t EI = = = = MPD-4 47
48 Sstemas contínuos: solução eata Vga em fleão nâmca Vga unfome: EI=EI e m=m 4 V 4 β V = 4 V = V = V, V, = com = = = 4 β = m EI ω MPD-4 48
49 Solução geal: Sstemas contínuos: solução eata Vga em fleão nâmca V = C sn β + C cosβ + C3 snh β + C4 cosh 1 β V [ C cosβ C sn β + C cosh β C snh ] = β β V = β [ C sn β C cosβ + C snh β C cosh β ] 4 MPD-4 49
50 Sstemas contínuos: solução eata Vga em fleão nâmca Aplcação e conções e contono: V = e V = = C =C4 = Csn β + Csnh β = 1 Csn β + Csnh β = sn β = β = π MPD-4 5
51 Sstemas contínuos: solução eata Vga em fleão nâmca Feqüêncas natuas e moos e vbação ω = π EI m 4 V = A sn π MPD-4 51
52 Sstemas contínuos: solução eata Eecíco Consee uma vga unfome em balanço. Enconte a equação feencal e movmento e a equação caacteístca a fleão nâmca. EI, m V = A [ cosβ coshβ = 1 sn β snh β sn β snh β + cosβ + coshβ cosβ coshβ ] MPD-4 5
53 Sstemas contínuos: solução eata Eecíco Uma vga em fleão nâmca está apoaa numa funação elástca e gez stbuía k. Enconte a equação feencal e movmento e a equação caacteístca. EI, m k MPD-4 53
54 Sstemas contínuos: solução eata Otogonalae e moos Em sstemas scetos há otogonalae os moos e vbação em elação às matzes e massa e gez. No caso e sstemas contínuos também este um tpo e otogonalae os moos. MPD-4 54
55 Sstemas contínuos: solução eata Otogonalae e moos Sstema sceto com matz e massa agonal: T { u} [ m]{ u} s n = = 1 mu u s = com s Pocesso lmte fazeno n ρ u u = s com s MPD-4 55
56 Sstemas contínuos: solução eata Otogonalae e moos Otogonalae com elação à massa: V EI m V = ω V s EI ω m V s s = MPD-4 56
57 MPD-4 57 Sstemas contínuos: solução eata Otogonalae e moos = + = s s s s s V m V V V EI V EI V V EI V V EI V ω Multplcação po V s :
58 MPD-4 58 Sstemas contínuos: solução eata Otogonalae e moos = + = s s s s s s V m V V V EI V EI V V EI V V EI V ω Multplcação po V :
59 MPD-4 59 Sstemas contínuos: solução eata Otogonalae e moos s s s s s s V EI V V EI V V EI V V EI V V m V + = ω ω Subtação:
60 Sstemas contínuos: solução eata Otogonalae e moos Aplcação as conções e contono: ω ω m V V = s s s ω m V V = ω s s Auto-funções otogonas com elação a m MPD-4 6
61 Sstemas contínuos: solução eata Otogonalae e moos Otogonalae com elação à gez Vs V EI = ω m V V = s MPD-4 61
62 MPD-4 6 Sstemas contínuos: solução eata Otogonalae e moos Otogonalae com elação à gez = = + = s s s s s V V EI V V EI V EI V V EI V V EI V
63 Sstemas contínuos: solução eata Otogonalae e moos Otogonalae com elação à gez V EI Vs = com s MPD-4 63
64 Sstemas contínuos: solução eata Otogonalae e moos Nomalzação os moos m V V = δ s s 1 = se se = s s EI V V s =δ s ω MPD-4 64
65 Sstemas contínuos: solução eata Otogonalae e moos Sstema contínuo Ínces e s poem se tocaos m V > V EI Sstema sceto Matzes [m] e [k] smétcas Matz [m] postva efna Matz [k] postva sem-efna MPD-4 65
66 Sstemas contínuos: solução eata Eecíco Uma vga em fleão nâmca está engastaa em = e supotaa po uma mola lnea e gez k em =. Pove otogonalae os moos e vbação. EI, m k MPD-4 66
67 Sstemas contínuos: solução eata Quocente e Raylegh Assm como o quocente e Raylegh poe se efno paa sstemas scetos há uma efnção paa sstemas contínuos. Seja a baa em vbação aal com um etemo lve. u,t MPD-4 67
68 Sstemas contínuos: solução eata Quocente e Raylegh U EA = ω m U U U = EA = U U U EA EA λ= ω = = m U m U MPD-4 68
69 Sstemas contínuos: solução eata Quocente e Raylegh U = =1 cu U m U Uj = δ Uj j EA = λjδj RU = = 1 = 1 c λ c RU λ 1 MPD-4 69
70 MPD-4 7 Sstemas contínuos: solução eata A equação a ona,, t t v t v T = ρ Fo em vbação tansvesal lve Fo unfome sob tensão constante ρ T c t t v c t v = = com, 1,
71 Sstemas contínuos: solução eata A equação a ona A equação a ona em uma mensão v, t 1 = c v, t t c é a velocae e popagação. Solução geal: v, t = F1 ct + F + ct MPD-4 71
72 Sstemas contínuos: solução eata A equação a ona F 1 ct popagação na eção postva e F + ct popagação na eção negatva e Ona senoal: π v, t = Asn ct = Asn kπ ωt λ one λ é o compmento e ona, k = 1/λ é o númeo e ona e ω = π / λ é a feqüênca. MPD-4 7
73 Sstemas contínuos: solução eata A equação a ona Movmento geao pela supeposção e uas onas senoas êntcas popagano-se em eções contáas. v, t = Asn kπ ωt + Asn k π + ωt = Asn k π cos ωt As uas onas combnam-se paa foma uma únca ona estaconáa cujo paão e movmento oscla na feqüênca ω. MPD-4 73
74 Sstemas contínuos: solução eata A equação a ona A equação a ona conteno evaas e seguna oem no espaço vale paa as análses e fos, baas e eos mas não paa vgas. Poblemas e vbação lve sem amotecmento são caactezaos po soluções que epesentam onas estaconáas. MPD-4 74
ELECTROMAGNETISMO E ÓPTICA Cursos: MEBiom + MEFT + LMAC 1 o TESTE (16/4/2016) Grupo I
ELECTROMAGNETIMO E ÓPTICA Cusos: MEBom + MEFT + LMAC o TETE (6/4/06) Gupo I A fgua epesenta um conensao esféco e um conuto eteo 3 também esféco. O conensao é consttuío po um conuto nteo e ao R cm e po
F-328 Física Geral III
F-328 Físca Geal III Aula exploatóa Cap. 24 UNICAMP IFGW F328 1S2014 F328 1S2014 1 Pontos essencas Enega potencal elétca U Sstema de cagas Equvalente ao tabalho executado po um agente exteno paa taze as
Prof. Anderson Coser Gaudio Departamento de Física Centro de Ciências Exatas Universidade Federal do Espírito Santo
POBEMAS ESOVIDOS DE FÍSICA Pof. Aneson Cose Gauo Depatamento e Físca Cento e Cêncas Eatas Unvesae Feeal o Espíto Santo http://www.cce.ufes.b/aneson aneson@np.ufes.b Últma atualzação: 8/11/6 15: H 4 - e
MATEMÁTICA II - Engenharias/Itatiba SISTEMAS LINEARES
- Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
DE CONDUÇÃO, CORRENTE DE DESLOCAMENTO, EQUAÇÕES DE MAXWELL
EETROMAGNETIMO II 195 21 CORRENTE DE CONDUÇÃO, CORRENTE DE DEOCAMENTO, EQUAÇÕE DE MAXWE 21.1 - Coente e Conução e Coente e Deslocamento A coente elétca é um fenômeno conheco po toos e o seu compotamento
Física Geral. Força e Torque
ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
Curso de Análise Matricial de Estruturas 1 II.6 FORMULAÇÃO DAS MATRIZES DE FLEXIBILIDADE E RIGIDEZ EM TERMOS DE ENERGIA
Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
Uma sonda de exploração espacial prepara-se para colocar um satélite de comunicações numa órbita em redor do planeta Marte.
Lcencatua em Engenhaa Geológca e de Mnas Lcencatua em Matemátca Aplcada e Computação Mestado Integado em Engenhaa Bomédca Mecânca e Ondas 1º Ano -º Semeste º Teste/1º Exame 0/06/017 11:30h Duação do teste:
Dinâmica do Sistema Solar
Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
MECÂNICA DOS FLUIDOS: NOÇÕES, LABORATÓRIO E APLICAÇÕES (PME 3332) Gabarito Terceira Prova
MECÂNIC DOS LUIDOS: NOÇÕES, LBORTÓRIO E PLICÇÕES (PME 333) Gabato Tecea Pova - 06. (3,0 ontos) U oleouto consste e N conuntos e sée caa u eles foao o ua boba oulsoa (booste) e u techo e tubulação longo.
Vamos adotar que as cargas fixas (cargas 1 e 2 na figura 1) tem valor Q e +Q e a carga suspensa pelo fio tem carga +q (carga 3).
Duas cagas e mesmo móulo e sinais opostos estão fixas sobe uma linha hoizontal a uma istância uma a outa. Uma esfea, e massa m caegaa com uma caga elética, pesa a um fio é apoximaa, pimeio e uma as cagas
Dinâmica de Gases. Capítulo 10 Escoamento cônico
Dinâmica e Gases Capítulo 10 Escoamento cônico 1 10.1 Intoução Cones são fequentemente empegaos na aeoinâmica e mísseis supesônicos, ifusoes e aviões supesônicos e expeimentos e pesquisa sobe os escoamentos
Introdução. Introdução. Introdução Objetivos. Introdução Corpo rígido. Introdução Notação
Intodução Intodução à obótca Descção espacal e ansfomações (/2) of. Douglas G. Machaet douglas.machaet@dcc.ufmg.b Intodução à obótca - Descção espacal e ansfomações (/2) 2 Intodução osções e Oentações
PEF Projeto de Estruturas Marítimas ESFORÇOS NA PLATAFORMA FIXA
PEF 506 - Projeto e Estruturas Marítmas ESFORÇOS NA PLATAFORMA FIXA 1. Introução O prncpal esorço agente em uma plataorma xa é aquele avno o movmento o meo luo. evo à complexae o movmento as partículas
3 MÉTODOS DE EXTRAÇÃO DA CORRENTE DE SEQÜÊNCIA NEGATIVA
14 3 MÉTODOS DE EXTRAÇÃO DA CORRENTE DE SEQÜÊNCA NEGATVA Os métoos e extração as correntes e seüênca negatva sponíves na lteratura são agrupaos seguno suas característcas comuns e tem suas notações unformzaas.
Física I. Aula 9 Rotação, momento inércia e torque
Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO. Departamento de Engenharia Mecânica
PME 00 MECÂNIC P3 6 de unho de 009 Duação da Pova: 0 mnutos (não é pemtdo uso de calculadoas) ENÇÃ: a pova consta de 3 questões de aplcação da teoa estudada valendo 0 pontos e de 4 questões teócas, cua
FÍSICA III - FGE a Prova - Gabarito
FÍICA III - FGE211 1 a Pova - Gabaito 1) Consiee uas cagas +2Q e Q. Calcule o fluxo o campo elético esultante essas uas cagas sobe a supefície esféica e aio R a figua. Resposta: Pela lei e Gauss, o fluxo
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
ESCO POITÉCNIC D UNIESIDDE DE SÃO PUO venda Pofesso Mello Moaes, nº 31. cep 558-9, São Paulo, SP. Telefone: 11 391 5337 Fa: 11 3813 1886 Depatamento de Engenhaa Mecânca PME 3 MECÂNIC II Pmea Pova 9 de
ANÁLISE DINÂMICA DE SISTEMAS CONTÍNUOS
ANÁISE DINÂMICA DE SISTEMAS CONTÍNUOS INTRODUÇÃO Sstemas dscretos e sstemas contínuos representam modelos matemátcos dstntos de sstemas fsícos semelhantes, com característcas dnâmcas semelhantes Os sstemas
Plano de Aula Leitura obrigatória Mecânica Vetorial para Engenheiros, 5ª edição revisada, Ferdinand P. Beer, E. Russell Johnston, Jr.
UC - Goás Curso: Engenhara Cvl Dscplna: Mecânca Vetoral Corpo Docente: Gesa res lano e Aula Letura obrgatóra Mecânca Vetoral para Engenheros, 5ª eção revsaa, ernan. Beer, E. ussell Johnston, Jr. Etora
Ondas - 2EE 2003 / 04. Caracterização do canal de rádio
Ondas - EE 3 / 4 Pncpas modelos de popagação do canal de ádo. Modelo de atenuação Seja: () - p T a potênca tansmtda (W); () - l a atenuação do snal no canal de tansmssão, a potênca ecebda p R (W) é p R
A lei de Newton da gravitação é comumente expressa pela relação: F =
Gavitação GRAVITAÇÃO 11 15 11.1 Intoução A lei e Newton a gavitação é comumente epessa pela elação: F = M M 1 1 G ˆ 1 Esta lei efee-se à foça ente uas massas pontuais. Uma questão que poe se colocaa é
Física I IME. 2º Semestre de Instituto de Física Universidade de São Paulo. Professor: Luiz Nagamine Fone: 3091.
Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
Campo Magnético Gerado por Linhas Aéreas de Transmissão
Campo Magnétco Geao po Lnas éeas e Tansmssão Calos Henque Costa Gumaães Depatamento e Engenaa Elétca Unvesae Feeal Flumnense Nteó, Basl ccg@vm.uff.b esumo O campo magnétco geao po lnas aéeas e tansmssão
MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO
Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
Os fundamentos da Física Volume 3 1. Resumo do capítulo
Os fundamentos da Físca Volume 3 1 Capítulo 13 Campo magnétco Ímãs são copos que apesentam fenômenos notáves, denomnados fenômenos magnétcos, sendo os pncpas: I. ataem fagmentos de feo (lmalha). o caso
CÁLCULO VETORIAL E GEOMETRIA ANALÍTICA Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 6 PLANO. v r 1
Luiz Fancisco a Cuz Depatamento e Matemática Unesp/Bauu CAPÍTULO 6 PLANO Definição: Seja A um ponto qualque o plano e v e v ois vetoes LI (ou seja, não paalelos), mas ambos paalelos ao plano. Seja X um
EQUAÇÕES DINÂMICAS DE MOVIMENTO PARA CORPOS RÍGIDOS UTILIZANDO REFERENCIAL MÓVEL
NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
Exercício cálculo de irradiância
Uma cena ao a live é iluminada pela iadiância sola E s. Assume-se que todos os objectos da cena têm uma eflectância média ρ e compotam-se como eflectoes Lambetianos. Detemine a iadiância média no detecto
Aula 3 Trabalho e Energia - Bioenergética
Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
TICA MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
CAPÍTULO 2 Está MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA TICA Fedinand P. Bee E. Russell Johnston, J. Notas de Aula: J. Walt Ole Teas Tech Univesit das Patículas Mecânica Vetoial paa Engenheios: Está
CÁLCULO DIFERENCIAL E INTEGRAL II 014.2
CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
Capítulo 2 Galvanômetros
Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
Prof. Anderson Coser Gaudio Departamento de Física Centro de Ciências Exatas Universidade Federal do Espírito Santo
POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
Eletricidade e Magnetismo II Licenciatura: 1ª Aula (30/07/2012) Prof. Alvaro Vannucci. Revisão das Leis de Gauss, de Ampère e de Faraday
Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
TICA MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA. Nona Edição CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
CAPÍTULO 2 Está MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA TICA Fedinand P. Bee E. Russell Johnston, J. Notas de Aula: J. Walt Ole Teas Tech Univesit das Patículas Conteúdo Intodução Resultante de Duas
INTEGRAL DE LINHA E ROTACIONAL DE UM CAMPO VETORIAL
ISTITUTO DE FÍSICA DA UFBA DEPARTAMETO DE FÍSICA DO ESTADO SÓLIDO DISCIPLIA: FÍSICA ERAL E EXPERIMETAL IV FIS ITERAL DE LIHA E ROTACIOAL DE UM CAMPO VETORIAL Sea um campo de velocdades v não unfome em
CAPÍTULO 10 DINÂMICA DO MOVIMENTO ESPACIAL DE CORPOS RÍGIDOS
94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
PPNL. Conjuntos Convexos. Exemplos. Otimização e Conjuntos Convexos
PPNL Min (Max) f(x) s. a. g i (x) (,, =) b i, i =,,m one x = (x,,x n ) T é o veto n-imensional as vaiáveis e ecisão; f (x) é a função objetivo; g i (x) são as funções e estição e os b i são constantes
Análise Multivariada
Análse Multvaada Aula 8: Análse de Coespondêna (AC) Pof. Adm Antono Betaell Juno Juz de Foa AC Téna exploatóa que busa dentfa assoações ente vaáves ategóas (ao nvés de ontínuas). Repesentação geométa das
Potencial Elétrico. Prof. Cláudio Graça 2012
Potencal Elétco Po. Cláudo Gaça Campo elétco e de potencal Campo e Potencal Elétcos E Potencal gavtaconal Potencal Elétco O potencal elétco é a quantdade de tabalho necessáo paa move uma caga untáa de
APÊNDICE. Revisão de Trigonometria
E APÊNDICE Revisão de Tigonometia FUNÇÕES E IDENTIDADES TRIGONOMÉTRICAS ÂNGULOS Os ângulos em um plano podem se geados pela otação de um aio (semi-eta) em tono de sua etemidade. A posição inicial do aio
PROVA COMENTADA. Figura 1 Diagrama de corpo livre: sistema de um grau de liberdade (1gdl) F F F P 0. k c i t
? Equilíbio da estutua PROVA COMENTADA a) Diagama de copo live (DCL): Paa monta o diagama de copo live deve-se inclui todas as foças atuando no bloco de massa m. Obseve que o bloco pode movimenta-se somente
1. Obtenha o modelo de ½ carro:
Lsta Aulas Prátcas de Sclab 1 Suspensão vecular Modelo de ½ de carro 1. Obtenha o modelo de ½ carro: v H A v A l A l M, J v M = 200 kg; J = 512 kgm 2 ; l A = 0,8 m; l = 0,8 m; k A = 10.000 N/m; k = 10.000
4.4 Mais da geometria analítica de retas e planos
07 4.4 Mais da geometia analítica de etas e planos Equações da eta na foma simética Lembemos que uma eta, no planos casos acima, a foma simética é um caso paticula da equação na eta na foma geal ou no
O perímetro da circunferência
Univesidade de Basília Depatamento de Matemática Cálculo 1 O peímeto da cicunfeência O peímeto de um polígono de n lados é a soma do compimento dos seus lados. Dado um polígono qualque, você pode sempe
Projeto 3. 8 de abril de y max y min. Figura 1: Diagrama de um cabo suspenso.
Cabos suspensos Projeto 3 8 e abril e 009 A curva escrita por um cabo suspenso pelas suas etremiaes é enominaa curva catenária. y ma y min 0 Figura 1: Diagrama e um cabo suspenso. A equação que escreve
Física Geral I - F Aula 13 Conservação do Momento Angular e Rolamento. 2 0 semestre, 2010
Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
TICA. Sistemas Equivalentes de Forças MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA. Nona Edição CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
CPÍTULO 3 Copos ECÂNIC VETORIL PR ENGENHEIROS: ESTÁTIC TIC Fednand P. Bee E. Russell Johnston, J. Notas de ula: J. Walt Ole Teas Tech Unvest Rígdos: Sstemas Equvalentes de Foças 2010 The cgaw-hll Companes,
Algumas observações com relação ao conjunto de apostilas do curso de Fundamentos de Física Clássica ministrado pelo professor Ricardo (DF/CCT/UFCG).
undamentos de isica Classica Pof Ricado OBS: ESTAS APOSTILAS ORAM ESCRITAS, INICIALMENTE, NUM PC CUJO TECLADO NÃO POSSUIA ACENTUAÇÃO GRÁICA (TECLADO INGLES) PORTANTO, MUITAS PALAVRAS PODEM ESTAR SEM ACENTOS
.FL COMPLEMENTOS DE MECÂNICA. Mecânica. Recuperação de doentes com dificuldades motoras. Desempenho de atletas
COMPLEMENTOS DE MECÂNICA Recuperação e oentes com fculaes motoras Mecânca Desempenho e atletas Construção e prótese e outros spostvos CORPOS EM EQUILÍBRIO A prmera conção e equlíbro e um corpo correspone
Versão 2 RESOLUÇÃO GRUPO I. = 0. Tal permite excluir a opção C.
Teste Intemédo de Matemátca A Vesão Teste Intemédo Matemátca A Vesão Duação do Teste: 90 mnutos.05.0.º Ano de Escoladade Deceto-Le n.º 7/00, de 6 de maço RESOLUÇÃO GRUPO I. Resposta (C) Tem-se: a b log
Consideremos uma distribuição localizada de carga elétrica, de densidade ρ(x), sob a ação de um potencial eletrostático externo ϕ E (x).
pansão Multpola da nega de uma Dstbução de Caga sob a Ação de Potencal letostátco teno. Físca Nuclea e de Patículas Cesa Augusto Zen Vasconcellos Consdeemos uma dstbução localzada de caga elétca, de densdade
ELETROTÉCNICA (ENE078)
UNIVERSIDADE FEDERAL DE JUIZ DE FORA Graduação em Engenhara Cvl ELETROTÉCNICA (ENE078) PROF. RICARDO MOTA HENRIQUES E-mal: rcardo.henrques@ufjf.edu.br Aula Número: 19 Importante... Crcutos com a corrente
1ªAula do cap. 10 Rotação
1ªAula do cap. 10 Rotação Conteúdo: Copos ígidos em otação; Vaiáveis angulaes; Equações Cinemáticas paa aceleação angula constante; Relação ente Vaiáveis Lineaes e Angulaes; Enegia Cinética de Rotação
Mecânica Técnica. Aula 5 Vetor Posição, Aplicações do Produto Escalar. Prof. MSc. Luiz Eduardo Miranda J. Rodrigues
ula 5 Veto Posição, plicações do Poduto Escala Pof. MSc. Luiz Eduado Mianda J. Rodigues Pof. MSc. Luiz Eduado Mianda J. Rodigues Tópicos bodados Nesta ula Vetoes Posição. Veto Foça Oientado ao Longo de
VETORES GRANDEZAS VETORIAIS
VETORES GRANDEZAS VETORIAIS Gandezas físicas que não ficam totalmente deteminadas com um valo e uma unidade são denominadas gandezas vetoiais. As gandezas que ficam totalmente expessas po um valo e uma
Curso de Engenharia Física Tecnológica 2014/2015. sin 2 θ ϕ 2. 3x 2 1 ), P 3 = 1 2
Mecânca Quântca Sére 7 Curso e Engenhara Físca Tecnológca 2014/2015 Vers~ao e 12 e Novembro e 2014) 7.1 Mostre que, em coorenaas esfércas, se tem L ± = e ±ϕ ± θ +cotθ ) ϕ e L 2 = 2 2 θ +cotθ 2 θ + 1 )
Aula 4: Campo Elétrico de um Sistema de Cargas Puntiformes
Univesiae Feeal o Paaná Seto e Ciências xatas Depatamento e Física Física III Pof. D. Ricao Lui Viana Refeências bibliogáficas: H. 4-4, 4-5, 4-6, 4-9 S. -7, -9 T. 8-6, 8-7, 9- Aula 4: Campo lético e um
Aula Prática 5: Preparação para o teste
Aula Pática 5: Pepaação paa o teste Tipo I: Equação Newton Foças não estauadoas & Enegia Tipo II: Equação Newton Foças estauadoas & Enegia Tipo III: Cicula & Gavidade & Enegia Poblema tipo 1: Equação Newton
Eletrônica II PSI3322
Eletônca II PSI33 Pogamação paa a Tecea Poa 8 3/0 04/ O amplfcado dfeencal MOS com caga ata Eecíco 7. Seda, Cap. 7 p. 45 456 9 6/0 6/0 O amplfcado cascode MOS: análse de pequenos snas Seda, Cap. 6 p. 385
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Funções de base nebulosas e modelagem de dinâmica não-linear
Unvesdade Fedeal de Mnas Geas Fom the SelectedWoks of 2004 Funções de base nebulosas e modelagem de dnâmca não-lnea, Unvesdade Fedeal de Mnas Geas Avalable at: https://woks.bepess.com/gladstone/7/ Cento
a) A energia potencial em função da posição pode ser representada graficamente como
Solução da questão de Mecânica uântica Mestado a) A enegia potencial em função da posição pode se epesentada gaficamente como V(x) I II III L x paa x < (egião I) V (x) = paa < x < L (egião II) paa x >
FGE0270 Eletricidade e Magnetismo I
FGE7 Eleticidade e Magnetismo I Lista de eecícios 1 9 1. As cagas q 1 = q = µc na Fig. 1a estão fias e sepaadas po d = 1,5m. (a) Qual é a foça elética que age sobe q 1? (b) Colocando-se uma teceia caga
4/10/2015. Física Geral III
Físca Geal III Aula Teóca 9 (Cap. 6 pate 3/3): ) Cálculo do campo a pat do potencal. ) Enega potencal elétca de um sstema de cagas. 3) Um conduto solado. Po. Maco R. Loos Cálculo do campo a pat do potencal
Física C Superintensivo
ísca C Superntensvo Exercícos 01) C 1) Contato entre e Depos o equlíbro Q = Q = + e 5 e = 1e. ) Contato entre e C Depos o equlíbro Q = Q C = + e 1 e = +1e. 05) q 1 Q resultante 1 0) 4 01. Incorreta. Se
QUESTÃO 1. r z = b. a) y
QUESTÃO 1 Uma longa baa cilíndica condutoa, de aio R, está centada ao longo do eixo z. A baa possui um cote muito fino em z = b. A baa conduz em toda sua extensão e no sentido de z positivo, uma coente
Resposta: A dimensão b deve ser de b=133,3 mm e uma força P = 10,66 kn.
Uc Engenhara Cvl e ESA Resstênca os ateras Eame oelo A vga e maera tem seção transversal retangular e ase e altura. Supono = m, etermnar a mensão, e moo que ela atnja smultaneamente sua tensão e fleão
Capítulo 4 CONSERVAÇÃO DA MASSA E DA ENERGIA
Capítulo 4 COSERAÇÃO DA MASSA E DA EERGIA 4.1. Equações para um Sstema Fechao 4.1.1. Defnções Consere o volume materal e uma aa substânca composta por espéces químcas lustrao na Fgura 4.1, one caa espéce
Seção 8: EDO s de 2 a ordem redutíveis à 1 a ordem
Seção 8: EDO s de a odem edutíveis à a odem Caso : Equações Autônomas Definição Uma EDO s de a odem é dita autônoma se não envolve explicitamente a vaiável independente, isto é, se fo da foma F y, y, y
Breve Revisão de Cálculo Vetorial
Beve Revsão de Cálculo Vetoal 1 1. Opeações com vetoes Dados os vetoes A = A + A j + A k e B = B + B j + B k, dene-se: Poduto escala ente os vetoes A e B A B A B Daí, cos A AB cos A B B A A B B AB A B
UFRJ COPPE PEB COB /01 Nome:
UFJ OPPE PEB OB 78 7/ Nome: ) Um polo apresenta a característca e corrente e tensão a fgura abaxo. Mostre, caso ocorra, o(s) nteralo(s) e tempo one o polo fornece energa ao sstema. Utlzano os sentos e
UFSCar Cálculo 2. Quinta lista de exercícios. Prof. João C.V. Sampaio e Yolanda K. S. Furuya
UFSCa Cálculo 2. Quinta lista de eecícios. Pof. João C.V. Sampaio e Yolanda K. S. Fuua Rega da cadeia, difeenciais e aplicações. Calcule (a 4 w (0,, π/6, se w = 4 4 + 2 u (b (c 2 +2 (, 3,, se u =. Resposta.
Fundamentos da Eletrostática Aula 14 Expansão Multipolar I
Funamentos a Eletostática Aula 14 Expansão Multipola I Pof. Alex G. Dias Pof. Alysson F. Feai O Campo Elético istante e uma istibuição e caga Em váias ocasiões este cuso, após calcula o campo e/ou o potencial
n θ E Lei de Gauss Fluxo Eletrico e Lei de Gauss
Fundamentos de Fisica Clasica Pof icado Lei de Gauss A Lei de Gauss utiliza o conceito de linhas de foça paa calcula o campo elético onde existe um alto gau de simetia Po exemplo: caga elética pontual,
Aula 6: Aplicações da Lei de Gauss
Univesidade Fedeal do Paaná eto de Ciências xatas Depatamento de Física Física III Pof. D. Ricado Luiz Viana Refeências bibliogáficas: H. 25-7, 25-9, 25-1, 25-11. 2-5 T. 19- Aula 6: Aplicações da Lei de
CAPÍTULO 04 CINEMÁTICA INVERSA DE POSIÇÃO
Capítulo 4 - Cinemática Invesa de Posição 4 CAPÍTULO 04 CINEMÁTICA INVERSA DE POSIÇÃO 4.1 INTRODUÇÃO No capítulo anteio foi visto como detemina a posição e a oientação do ógão teminal em temos das vaiáveis
Aula 16. Nesta aula, iniciaremos o capítulo 6 do livro texto, onde vamos estudar a estabilidade e o equilíbrio do plasma como um fluido.
Aula 16 Nesta aula, iniciaemos o capítulo 6 do livo texto, onde vamos estuda a estabilidade e o equilíbio do plasma como um fluido. 6.1 Equilíbio e Estabilidade Do ponto de vista das patículas individuais,
9. Lei de Ampère (baseado no Halliday, 4 a edição)
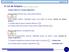9. Le de Ampèe Capítulo 9 9. Le de Ampèe (baseado no Hallday, 4 a edção) Campo Elétco e Campo Magnétco Vmos (anteomente) que, paa campo elétco: q 1 E q. Duas cagas elétca, execem foças uma sobe as outas,
CAPÍTULO V CÁLCULO DOS ESFORÇOS INTERNOS RESISTENTES DADOS a, 1/R a E e O
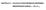CAPÍTULO V CÁLCULO DOS ESFOÇOS ITEOS ESISTETES DADOS a / a E e O Cálculo os Esforços Internos esstentes Daos /r e εo 5 Cálculo os Esforços Internos esstentes Daos a /r a e e o 5 Introução A etermnação
Asas Finitas Escoamento permamente e incompressível
Escoamento pemamente e incompessível Caacteização geomética da asa - Espessua finita muito meno do que a envegadua e a coda - Foma geomética deteminada po: a) Planta (vaiação de coda e ângulo de flecha)
Aula 4: O Potencial Elétrico
Aula 4: O Potencal létco Cuso de Físca Geal III F-38 º semeste, 4 F38 S4 Potencal elétco Como podemos elacona a noção de oça elétca com os concetos de enega e tabalho? Denndo a enega potencal elétca (Foça
2ªAula do cap. 11. Quantidade de Movimento Angular L. Conservação do Momento Angular: L i = L f
2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
2 Equações Governantes e Formalismo Básico dos Métodos de Partículas
Equações Goenantes e Fomalismo Básico os Métoos e Patículas Equações Goenantes e Fomalismo Básico os Métoos e Patículas Neste capítulo são apesentaas as equações goenantes que moelam o moimento os luios
Credenciamento Portaria MEC 3.613, de D.O.U
edenciamento Potaia ME 3.63, de 8..4 - D.O.U. 9..4. MATEMÁTIA, LIENIATURA / Geometia Analítica Unidade de apendizagem Geometia Analítica em meio digital Pof. Lucas Nunes Ogliai Quest(iii) - [8/9/4] onteúdos
Energia no movimento de uma carga em campo elétrico
O potencial elético Imagine dois objetos eletizados, com cagas de mesmo sinal, inicialmente afastados. Paa apoximá-los, é necessáia a ação de uma foça extena, capaz de vence a epulsão elética ente eles.
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
PME MEÂNI Pova Substitutiva de junho de 9 uação da Pova: minutos (não é pemitido uso de calculadoas) ª Questão (,5 pontos) ω No disco de cento e massa 4m, há uma uia tansvesal po onde desliza sem atito
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
Fenômenos de Transporte I
Prof. Carlos Ruberto Fragoso Jr. Fenômenos e Transporte I 1. Funamentos e Cnemátca os Fluos 1.1 Defnções Escoamento é a eformação contínua e um fluo que sofre a ação e uma força tangencal, por menor que
( ) 10 2 = = 505. = n3 + n P1 - MA Questão 1. Considere a sequência (a n ) n 1 definida como indicado abaixo:
P1 - MA 1-011 Questão 1 Considee a sequência (a n ) n 1 definida como indicado abaixo: a 1 = 1 a = + 3 a 3 = + 5 + 6 a = 7 + 8 + 9 + 10 (05) (a) O temo a 10 é a soma de 10 inteios consecutivos Qual é o
Física Experimental: Mecânica. Aula 1. Introdução ao laboratório
Física Expeimental: Mecânica Aula 1 Intodução ao laboatóio 1 Conteúdo desta aula: -Objetivos... slides 3 6 -Divisão de gupos... slides 6 8 -Uso de equipamentos... slides 9 11 -Unidades Intenacionais...
Campo Gravítico da Terra
Campo Gavítico da Tea 3. otencial Gavítico O campo gavítico é um campo vectoial (gandeza com 3 componentes) Seá mais fácil tabalha com uma gandeza escala, que assume apenas um valo em cada ponto Seá possível
3 Formulação Matemática
3 Fomulação Matemática 3. Descição do poblema O poblema a se analisado é mostado na fig. 3.. O fluido escoa atavés de um duto cicula de diâmeto d, passa atavés de um duto maio ( diâmeto D ) e sofe uma
CAPÍTULO 3 DEPENDÊNCIA LINEAR
Luiz Fancisco da Cuz Depatamento de Matemática Unesp/Bauu CAPÍTULO 3 DEPENDÊNCIA LINEAR Combinação Linea 2 n Definição: Seja {,,..., } um conjunto com n etoes. Dizemos que um eto u é combinação linea desses