UMA NOVA TÉCNICA PARA OTIMIZAÇÃO DE ESTRUTURAS DE GRANDE PORTE. José Miguel Aroztegui Massera
|
|
|
- Eduardo Carvalho Cunha
- 5 Há anos
- Visualizações:
Transcrição
1 UMA NOVA ÉCNICA PARA OIMIZAÇÃO DE ESRUURAS DE GRANDE PORE José Mgue Aoztegu Massea DISSERAÇÃO SUBMEIDA AO CORPO DOCENE DA COORDENAÇÃO DOS PROGRAMAS DE PÓS-GRADUAÇÃO DE ENGENHARIA DA UNIVERSIDADE FEDERAL DO RIO DE JANEIRO COMO PARE DOS REQUISIOS NECESSÁRIOS PARA A OBENÇÃO DO GRAU DE MESRE EM CIÊNCIAS EM ENGENHARIA MECÂNICA. Apovada po: Pof. José Heskovts Noma, D.Ig. Pof. Feado Peea Duda, D.Sc. Pof. Atoo Adé Novoty, D.Sc. Pof. Afedo Rocha de Faa, Ph. D. RIO DE JANEIRO, RJ - BRASIL JUNHO DE 2006
2 MASSERA, JOSÉ MIGUEL AROZEGUI Uma Nova écca paa Otmzação de Estutuas de Gade Pote [Ro de Jaeo] 2006 XI, 80 p. 29,7 cm (COPPE/UFRJ, M.Sc., Egehaa Mecâca, 2006) Dssetação - Uvesdade Fedea do Ro de Jaeo, COPPE. Otmzação estutua 2. Aáse de sesbdade 3. Iteface com pogamas comecas I. COPPE/UFRJ II. ítuo (sée)
3 Agadecmetos Ao pofesso Heskovts, peo apoo e peas oetações, fudametas paa a eazação deste tabaho. Aos coegas do Laboatóo Optmze, peo apoo e sugestões. Á mha famía, um pouco dspesa, que sempe me apóa em todos os desafos. Ema, Came, Facsco, Juá e Aaa. À mhas amgas Came Nda, Paua e Jussaa, peo apoo em mometos dfíces. Ao coega Aexade, po supota-me (pometo ão queba mas ada). Aos amgos Evado e Aa Paua, po ecebe-me em seu apatameto, sua compeesão e aegas. Ao Joatás (ão se sbe! Joatás), po sua amzade e Svéo (my so), peos chopes o sdcato. À CAPES peo apoo faceo.
4 Resumo da Dssetação apesetada à COPPE/UFRJ como pate dos equstos ecessáos paa a obteção do gau de Meste em Cêcas (M.Sc.) UMA NOVA ÉCNICA PARA OIMIZAÇÃO DE ESRUURAS DE GRANDE PORE José Mgue Aoztegu Massea Juho/2006 Oetado: José Heskovts Noma Pogama: Egehaa Mecâca Nesta tese se popõe uma ova técca de otmzação estutua de gade pote baseado o agotmo FAIPA ( Feasbe Ac Iteo Pot Agothm ). A pesete metodooga exge poucos ecusos computacoas dado que utza a técca de Memóa Lmtada e ão ecessta do cácuo e amazeameto expíctos da matz de sesbdades, utzado-se apeas do cácuo de uma devada decoa das estções e da devada de uma fução auxa defda como uma combação ea das estções. Em cetas hpóteses, a técca de otmzação poposta apeseta-se efcete em eação ao úmeo de aáses estutuas eazadas. Popõe-se um pogama de computado que mpemeta esta ova técca e apcase ao pobema de mímo voume com estções ocas de tesão. a pogama cu uma teface que pemte a utzação de códgos (comecas) de aáse estutua. Po útmo, apesetam-se esutados umécos de apcação da técca desevovda. v
5 Abstact of Dssetato peseted to COPPE/UFRJ as a pata fufmet of the equemets fo the degee of Maste of Scece (M. Sc.) A NEW ECHNIQUE FOR LARGE-SCALE SRUCURAL OPIMIZAION José Mgue Aoztegu Massea Jue/2006 Advso: José Heskovts Noma Depatmet: Mechaca Egeeg hs wok poposes a ew techque of age stuctua optmzato based o FAIPA ( Feasbe Ac Iteo Pot Agothm ). he peset method eques modest computatoa esouces because t uses the Lmted Memoy echque ad eques ethe cacuatg o stog expcty the sestvty matx. It meey eques the computato of a dectoa devatve of the costats ad of a auxay fucto defed as a ea combato of the costats. Ude ceta assumptos, the optmzato techque poposed s vey effcet wth egad to the umbe of stuctua aayses pefomed. hs ew techque s coded ad apped to sove the pobem of mmum voume subjected to stess costats. hs pogam cudes a teface that aows the use of commeca fte eemet codes. Fay, umeca esuts ae peseted usg the techque poposed. v
6 ÍNDICE Itodução. Motvação.2 Objetvos 4.3 Ogazação do tabaho 4 2 Fomuação do pobema de otmzação 6 2. Itodução Modeo estutua Estutua paa Eemetos Ftos Apoos e caegameto Veto de desocametos Matz costtutva Matz de gdez Equação de equíbo Cácuo da tesão de Vo Mses Estutua váve Pobema de otmzação Vaáves de pojeto Fução objetvo Fuções de estção de tesão Fuções de estção de caxa Fução de estções Fomuação do pobema 7 3 FAIPA: Agotmo de Potos Iteoes po Acos Váves 9 3. Itodução Defções 20 v
7 3.2. Regão váve Cojuto de estções atvas Deção váve Deção de descda Mímo oca, mímo oca estto Fução agageaa, hessaa Poto egua, espaço tagete Codções de otmadade FAIPA Descção do FAIPA Sstemas eaes do FAIPA 32 4 Aáse de Sesbdade Itodução Gadetes Devada de uma estção de tesão Notas cas Método da dfeecação deta Método da vaáve adjuta Aspectos computacoas Poduto do gadete das estções po veto Notas cas Cácuo do poduto ( g) z Cácuo do poduto ( g)v 42 5 éccas de otmzação de gade pote Itodução Pmea técca écca de otmzação de gade pote Método de Memóa Lmtada Repesetação de memóa mtada paa a vesa da matz dua ( A ) 49 v
8 Repesetação de memóa mtada paa a vesa da Hessaa ( B ) Método do Gadete Cojugado pé-codcoado Metodooga poposta Sstemas eaes do FDIPA Método do Gadete Cojugado pé-codcoado pea matz quase-newto de memóa mtada Podutos da matz de sesbdades g( x) e [ g( x) ] po veto Dscussão sobe a compexdade de cácuo 55 6 Impemetação Computacoa Itodução Aqutetua do sstema Itodução Compoetes Impemetação do móduo df Impemetação do móduo teface Pogamas de aáse estutua utzados Feametas Pogamas Impemetação com ABAQUS Itodução Sub-otas do móduo t_abq Scpts Pytho Impemetação com DLEARN Itodução Sub-otas do móduo t_d Rota MA27 (HSL) 66 7 Resutados Numécos Itodução Exempo Exempo Exempo 3 74 v
9 8 Cocusões e Popostas Cocusões Popostas de vestgação 77 Refeêcas Bbogáfcas 79 Lsta de símboos a Áea de um eemeto fto, pág. 7. c () Númeo de estado de caegameto assocado a estção, pág.7. ~ d, d0, d, d Deções, d, d d d ~ 0,, R, pág. 20, 26 e 27. e Veto coua de compoetes utáas, pág.6. e () Númeo de eemeto assocado a estção, pág.7. f Fução objetvo, f : R R, pág.5. g Veto de estções, g ( x ) [ g ( x ) L g ( x )] m =, pág.6. g Fução de estção, g : R R, pág Soma de teações do Método do Gadete Cojugado do pmeo e do segudo sstema ea do FDIPA, pág. 55. k Matz de gdez do eemeto, pág.. Fução de Lagage, ( x, ) = f ( x) + λ g ( x) x m λ, pág. 2. m Númeo de estções, pág.6. Númeo de vaáves de pojeto, pág. 7. N p Veto de caegameto, p R g, pág.2. Númeo de paes da técca de memóa mtada paa epeseta a vesa da matz dua do FAIPA, pág. 50. q A q B Númeo de paes da técca de memóa mtada paa epeseta a vesa de B, pág. 5. t Passo da busca ea, t > 0, pág. 28. u Veto de desocametos gobas, u R g, pág 0. 2Ne u Veto de desocametos do eemeto, u R, pág 0. =
10 [] u Veto de desocametos goba assocado ao caegameto, pág 5. x Vaáves de pojeto, [ ] x = x x L x L x, pág x Mímo oca, x R, pág. 2. x Espessua do eemeto, pág. 7. A Matz dua smétca do FAIPA, pág. 49. B Matz quase-newto da Hessaa, pág. 26. D Matz costtutva do matea eástco ea, pág.. E Móduo de Youg, pág.. G Gaus de bedade da estutua, G = G 0 Ga, pág. 8. G 0 Gaus de bedade de ós fxos (Apoos), pág. 9. G Gaus de bedade de ós ves, pág. 9. a G ( x) Matz dagoa, G( x) ( ) = g ( x), ( G( x) ) j se j = 0, pág. 26. H A H B Repesetação de paes {, y } = q,..., A A pea técca de memóa mtada atavés dos s, pág. 5. Repesetação de paes {, y } = q,..., B B pea técca de memóa mtada atavés do s, pág. 5. I Matz detdade, pág. 50. Cojuto de ídces de estções atvas, I x =, 2, K, m g x = 0, pág. 20. I ( x) { } ( ) { } ( ) K Matz de gdez, pág.. K Matz de gdez goba do eemeto, pág L Matz Hessaa, L( x, ) = f ( x) + λ g ( x) x m λ, pág. 22. = M Matz do eemeto, M Q VQ N e Númeo de ós po eemeto, pág 8. N Númeo de ós da estutua, pág 8. p, pág.4. NGL Númeo de gaus de bedade atvos, cad( ) NEC Númeo de estados de caga, pág.5. NGL =, pág 9. Q Matz de tasfomação de coodeadas do eemeto, pág. 0. R C ( x) Cojuto de estções cítcas, pág. 38. S 0, Matz de defomação-desocameto, pág.3. m λ, λ λ Mutpcadoes de Lagage, λ, λ λ R, pág.2, 26 e 27. σ adm esão admssíve de Vo Mses, pág.4. 0, G a
11 v Coefcete de Posso, pág.. Σ 2 Regão paa, Σ R, pág. 6. Ω = x R g x 0, pág. 20. { } Ω Regão váve, ( ) Λ Matz dagoa, ( Λ ) = λ, ( ) j = se j χ Λ 0, pág. 26. Cuva váve e de descda, χ : R R, pág. 27. cad ( C) Númeo de eemetos do cojuto C. dag () v Matz dagoa, ( dag ( v) ) = v, ( dag( v) ) j se j owe ( A) A R, A j owe( A) j asposta de uma matz ou veto. I ( x) Espaço tagete, pág. 22. g( x) Matz de sesbdade, pág. 22. = 0, pág. 26. = ( ) se j, e ( owe( A) ) se j z Pate tea do úmeo ea z, pág. 7. = 0. j > x
12 CAPÍULO Itodução. Motvação A fase de pojeto costtu uma etapa fudameta paa a cocepção de um poduto de egehaa. O pocesso tadcoa de pojeto tem se ampaado a expeêca, habdade e tução de egeheos. Esta atvdade caacteza-se como um pocesso de tetatva e eo, ode a mehoa e vabdade do poduto são obtdas a um ato custo. No pojeto de sstemas compexos se eque de gade voume de cácuo, pocessameto de dados e tecomucação ete váas dscpas. Costtu um desafo pojeta sstemas efcetes e ecoômcos sem que sto compometa a tegdade do poduto fa. O objetvo da otmzação em egehaa é obte pojetos mas efcetes e ao mesmo tempo seguos. Na dústa automotva, po exempo [], a pcpa atvdade de desevovmeto está cocetada o apefeçoameto de estutuas exstetes, toado-as mas eves, mas duáves, mas seguas, meos udosas, etc. Hoje em da, sstemas computacoas ofeecem uma gade capacdade de cácuo e tasfeêca de dados fazedo possíve a costução de sstemas compexos atavés de smuações. Isto pemte uma edução do custo de desevovmeto e maufatua do poduto. O egeheo pode utza pogamas de pojeto assstdo po computado (CAD: Compute Aded Desg ) paa a modeagem geométca e de egehaa assstdo po computado (CAE: Compute Aded Egeeg ) paa eaza aáses e smuações. Cotudo, a tegação destas feametas em um ambete de aáse e otmzação cotua sedo um desafo.
13 O Método dos Eemetos Ftos (MEF) é mpemetado efcetemete em pogamas comecas de aáse estutua. As equações dfeecas que modeam o pobema estutua são taduzdas em equações vaacoas e ogo esovdas peo MEF. O domío estutua é dscetzado em um cojuto de eemetos aos quas se mpõe uma codção de equíbo. Medate um pocedmeto de motagem, se costó um sstema ea de equações que epeseta a cofguação de equíbo o domío dscetzado cujas espostas estutuas (defomação, tesão, etc.) são obtdas a pat da esoução destes sstemas. A pecsão do método dos eemetos ftos pode se mehoada com a dmução do tamaho do eemeto ou a utzação de um eemeto de mao odem de apoxmação [2]. A apcação do método dos eemetos ftos em pobemas estutuas smpes é facmete pogamáve, o etato exstem gades beefícos a utzação de pogamas comecas:. Os sstemas eaes são esovdos po métodos efcetes e geas. 2. Dspõem de uma bboteca (gade vaedade) de eemetos ftos. 3. Possuem pogamas geadoes de maha (dscetzação da estutua em eemetos ftos). 4. Possuem pogamas de vsuazação e pós pocessameto dos esutados. Cotudo, é ecessáo que o usuáo destes pogamas saba modea sua eadade e tepeta os esutados adequadamete. As feametas de aáse, em gea ão popocoam mehoes pojetos, mas podem se usadas paa a eazação de aáses de sesbdade que popocoam fomações sobe quas modfcações popcam uma meho soução. Os pojetos de egehaa, em gea, podem se fomuados como pobemas de otmzação [3]. Paa a defção de tas pobemas é ecessáo estabeece expctamete um cojuto de vaáves de pojeto, uma fução custo a se mmzada e um cojuto de estções que defem quado um pojeto é váve ou út. As vaáves de pojeto defem os paâmetos que sevão paa modfca e def um pojeto patcua. A fução custo (também chamada de fução objetvo) é uma fução escaa que pemte estabeece um ctéo de compaação ete pojetos. Dete todos os pojetos, pocua-se aquee de meo custo, poém todo sstema deve se pojetado e fabcado paa uma quatdade de ecusos mtada ou paa cetas codções que gaatam sua utdade. Estas mtações e codções são estabeecdas peo cojuto de 2
14 estções. ato as estções como a fução custo, em gea depedem das vaáves de pojeto. Este tabaho aboda um pobema de otmzação dmesoa [4] ( sze optmzato ). Cosdeam-se estutuas eaes eástcas e paas, dscetzadas po eemetos ftos. As vaáves de pojeto são as espessuas destes eemetos. Não se admte espessuas guas a zeo ( fuo ) ou maoes que um vao especfcado (espessua máxma). A fadade é obte a meho dstbução de espessuas da estutua paa que mmze seu voume, cosdeado, o estado de equíbo, que a tesão de Vo Mses em cada eemeto ão supee um vao pé-estabeecdo. É mpotate efatza que o popósto deste pobema ão é obte fuos (otmzação topoógca) em modfca seu cotoo (otmzação de foma). Cosdeado que as téccas de otmzação dmesoa foecem fomações de ode eta matea, podemos utzá-a paa def a posção de um ofíco. as téccas combadas com otmzação de foma pemtem def a foma do fuo. No etato, o pesete tabaho ão tem esse popósto. Paa epeseta de foma egítma a tesão em cada poto da estutua, optou-se po utza uma gade quatdade de eemetos que gea pobemas de otmzação com eevado úmeo de vaáves e de estções. Em gea, pobemas de otmzação dmesoa podem se esovdos utzado téccas de pogamação matemátca. Neste tabaho optou-se pea utzação do FAIPA ( Feasbe Ac Iteo Pot Agothm ). Este agotmo é uma técca gea de otmzação ão ea que possu espetáves esutados teócos [5] e fác compeesão geométca. Recetemete têm-se desevovdo téccas juto ao FAIPA que esovem pobemas com mutas vaáves de pojeto [6] [7]. No etato, sua apcação em pobemas de egehaa com mutas vaáves e estções ão fo devdamete expoada e apovetada. 3
15 .2 Objetvos Este tabaho tem os segutes objetvos:. Popo uma técca gea de otmzação de gade pote baseado o FAIPA. 2. Reaza um pogama que mpemeta esta ova técca e esova o pobema de mímo voume sujeto a estções ocas de tesão. Este pogama deve cu uma teface que pemta sua comucação com feametas (comecas) de aáse estutua..3 Ogazação do tabaho O texto está ogazado em capítuos da segute foma: Capítuo 2 Fomuação do pobema. Apeseta-se o modeo estutua baseado o Método dos Eemetos Ftos. A estutua é dscetzada eguamete em eemetos quadados com áeas guas (maha egua). Esta dscetzação ofeece gades vatages. Em pmeo uga, a matz de gdez de cada eemeto é a mesma paa todos. Em coseqüêca dsso, a matz de gdez pode se obtda efcetemete, bem como sua devada em eação às espessuas. Em segudo uga, o cácuo da tesão o cetóde do eemeto também pode eaza-se efcetemete dado que a matz defomação-desocameto depede do eemeto. No fa do capítuo desceve-se o pobema de mímo voume sujeto a estções ocas de tesão, ode estão defdas as vaáves de pojetos, a fução custo e as fuções de estções. Capítuo 3 FAIPA: Agotmo de Potos Iteoes po Acos Váves. Icamete são defdos os cocetos de pogamação matemátca e esutados teócos ecessáos paa a compeesão do FAIPA. Famete desceve-se o FAIPA expodo os sstemas eaes teos em sua foma dua e pma-dua. 4
16 Capítuo 4 Aáse de sesbdade. Neste capítuo deduzem-se as devadas das fuções do pobema de otmzação apesetado o capítuo 2. Defe-se a matz de gadetes das estções e apesetamse dos métodos paa cacua a devada de uma estção de tesão: método da dfeecação deta e método da vaáve adjuta. Reazam-se obsevações sobe o custo computacoa em temos do úmeo de sstemas eaes a seem esovdos e a utzação de ftos as estções. Po útmo é deduzdo o agotmo que eaza o poduto da matz de gadetes (e sua tasposta) po um veto. Mosta-se que este poduto pode se eazado atavés de aáses estutuas. Estes esutados são de muta mpotâca paa a ova metodooga que seá apesetada o capítuo 5. Capítuo 5 écca de otmzação de gade pote Neste capítuo apeseta-se a ova técca de otmzação de gade pote. Pmeamete, desceve-se a metodooga usada o começo da vestgação deste tabaho ode ão é utzada ehuma técca paa esove gades sstemas. Logo depos, descevem-se um cojuto de métodos utzados a ova técca. Na seção é apesetada a ova metodooga. No fa do capítuo é feta uma dscussão da efcêca desta ova técca. Capítuo 6 Impemetação computacoa Desceve-se a aqutetua dos pogamas desevovdos e utzados. Mosta-se como se mpemetaam os móduos paa comucação com o pogama comeca ABAQUS e com o pogama educatvo DLEARN [2]. Capítuo 7 Resutados umécos Iustam-se tês exempos umécos ode se apcam as téccas do capítuo 5 que foam mpemetadas de acodo com o capítuo 6. Capítuo 8 Cocusões Este capítuo é dedcado às cocusões e popostas de cotuação da pesqusa. 5
17 CAPÍULO 2 Fomuação do pobema de otmzação 2. Itodução Neste capítuo desceve-se o modeo de otmzação estutua cosdeado o pesete tabaho. Etede-se po estutua paa um sódo defdo po uma egão 2 Σ R fxa e uma dstbução de espessuas paa cada poto de Σ. a estutua cosdea-se submetda a um sstema de foças o pao defdo pea egão Σ e apoos que estgem seu movmeto. O pobema de otmzação que se popõe esove este tabaho cosste em ecota uma dstbução de espessuas ta que mmze o voume da estutua e que a tesão de Vo Mses em cada poto ão supee um vao pé-estabeecdo. O cácuo da tesão de Vo Mses pode se obtdo po uma apoxmação uméca atavés do Método dos Eemetos Ftos (MEF). O domío Σ se dscetza em eemetos ftos quadados de gua áea e a tesão de Mses é cacuada o ceto do eemeto. A pecsão do MEF pode se mehoada aumetado a desdade de eemetos o domío ou utzado um eemeto de mao odem de apoxmação [2]. Cosdea-se vaáve de pojeto a espessua do eemeto. A fução custo está defda peo voume da estutua e as estções se defem em temos das tesões de Mses cacuadas peo MEF. O capítuo se ogaza da segute maea, a seção 2.2 o modeo estutua baseado o MEF é apesetado. Na seção 2.3 se defem estutuas váves em temos da tesão de Vo Mses em cada eemeto fto. Famete a seção 2.4 se fomua o pobema de otmzação cosdeado este tabaho. 6
18 2.2 Modeo estutua Seja um efeeca catesao (, ξ, η, ς ) O Estutua paa As estutuas estaão defdas po uma egão fxa 2 Σ R o pao ξo η. Esta egão seá dscetzada ufomemete em eemetos quadados de gua áea a. Cada eemeto se detfcaá po um úmeo {,...,}. A geometa do eemeto estaá defda po Σ Σ e uma espessua costate x. A fgua 2. mosta uma estutua típca e um eemeto dvdua. Fgua 2.: Estutua paa de =30x0 eemetos. À deta um eemeto de espessua x e áea a. Defe-se a dstbução de espessuas ao veto x como: [ x x L L ] x = x x (2.) 2 7
19 2.2.2 Eemetos ftos De acodo com a dscetzação adotada a seção 2.2., a estutua é fomada po eemetos quadados. Utzam-se os segutes eemetos da famía Seedpty [], [2] (Veja fgua 2.2): B-ea Quadátco de 8 ós Fgua 2.2: À esqueda um eemeto b-ea (4 ós) e à deta um eemeto quadátco (8 ós). Os eemetos estão fomados po ós ou potos detfcados po um úmeo. No caso do eemeto b-ea, os vétces estão umeados de a 4 e paa o quadátco, de a 8. Seja ete e N e o úmeo de ós de um eemeto (4 ou 8). Do poto de vsta de toda a estutua, os ós estaão detfcados po úmeos N p, sedo odo ó { } N p o úmeo tota de ós. p,...,n p podeá se move o pao ξo η de acodo as foças e apoos apcadas sobe o copo. Defe-se etão, paa cada ó, dos gaus de bedade: um desocameto segudo o exo ξ e outo segudo o exo η. Os gaus de bedade são detfcados com os úmeos do cojuto de gaus de bedades da estutua G defdo como: {,..., } G = 2N p (2.2) 8
20 2.2.3 Apoos e caegameto Cosdea-se um apoo a um gau de bedade com desocameto uo. O cojuto de apoos G 0 é um subcojuto de G. São dtos gaus de bedades atvos aquees que ão são apoos: G a = G \ G 0 (2.3) Famete, defe-se úmeo de gaus de bedade atvos como: ( ) NGL = cad (2.4) G a Um caegameto é um veto p NGL R de foças apcadas a ós com gaus de bedade atvos. Um caegameto é também chamado de estado de caga. A fgua 2.3 mosta um exempo ode as 8 setas epesetam as foças apcadas. Neste caso p é um veto de NGL compoetes ode 6 são ão uas (as 8 setas se descompõem em dos compoetes ão uos). Na pate debaxo, à deta, os apoos são fxos, e à esqueda os apoos são deszates segudoξ. Fgua 2.3: Estutua submetda a um estado de caegameto e apoos. 9
21 2.2.4 Veto de desocameto Defe-se veto desocameto ao veto u cujos compoetes epesetam gaus de bedade atvos: NGL [ u ] R u = L u NGL (2.5) Defe-se veto de desocameto do eemeto como o veto u fomado peos gaus de bedade dos ós do eemeto. Po exempo, se o eemeto b-ea tve os ós p p, p, p {,..., } (veja fgua 2.4):, o veto u estaá dado po 8 compoetes N p 8 [ d d d d d d d d ] u = (2.6) R d 8 d 6 d 7 d 5 p 4 p 3 d 2 d 4 p d p 2 d 3 Fgua 2.4: Compoetes do veto de desocameto paa um eemeto b-ea Defe-se matz de tasfomação de coodeadas do eemeto, N e N g Q R ta que: u = Q u (2.7) 0
22 2.2.5 Matz costtutva abaha-se as hpóteses da teoa de eastcdade ea ode o teso de tesões é popocoa ao teso de pequeas defomações. Adcoamete, cosdeam-se mateas sotópcos e homogêeos com coefcete de Posso v e móduo de Youg E. Assume-se o Estado de esão Pao (EP) ode se despezam os compoetes do teso de tesões pepedcuaes ao pao ξo η e os compoetes são costates ao ogo da espessua. Decoete às hpóteses ateoes, defe-se matz costtutva como: D E v ( ) v 0 v 0 2 ( ) (2.8) v Matz de gdez A matz de gdez do eemeto utáa k 2 N e 2Ne R é dada po: k Σ B DB dσ (2.9) Ode a matz B é a matz a matz de defomação-desocameto. Devdo à dscetzação egua adotada e po utza-se um matea homogêeo, esta matz é gua paa todos os eemetos. A matz de gdez N g N g K R é defda como: K = K ( x) = = x K (2.0) Ode: K = Q kq (2.)
23 Sedo Q matz de tasfomação de coodeadas do eemeto. Neste tabaho assume-se que os apoos G 0 sempe mpedem quaque movmeto de copo ígdo e potato a matz de gdez é smétca e postva defda [2] Equação de equíbo Defe-se equação de equíbo ao segute sstema ea: Ku = p (2.2) Sedo K a matz de gdez, u o veto de desocametos e p um caegameto. Do poto de vsta mecâco, a equação (2.2) epeseta a codção ecessáa e sufcete paa o equíbo estátco []. O desocameto u também seá dto desocameto do equíbo assocado ao estado de caga p. O pocesso uméco de obteção da soução de (2.2) seá chamado de aáse estutua. Dado que K depede de x, o desocameto u (soução do sstema (2.2)) depede mpctamete de x. Nesta tabaho o veto de caegametos p depede de x Cácuo da tesão de Vo Mses Seja u( x) u = o desocameto do equíbo assocado a um estado de caga. Os compoetes do teso de tesões o poto ( ) pat da segute fómua [2]: σ ( q q ) Dε ( q, q ) ξ η ξ η qξ, qη Σ podem se obtdos a, = (2.3) 2
24 Ode: ( q q ) [ σ σ σ ] σ, = (2.4) ξ η ξ η ξη ( q q ) [ ε ε ε ] ε, = 2 (2.5) ξ η ξ η ξη O veto ε cotém os compoetes do teso de defomação e obte-se da segute foma: ( q q ) S( q q ) u ε, =, (2.6) ξ η ξ η Ne Sedo S R 3 a matz de defomação desocameto e u o veto de desocametos do eemeto. ( c c ) ξ η No pesete tabaho, cacua-se a tesão o cetóde do eemeto. Seja, as coodeadas do cetóde do eemeto. Apcado a fómua (2.3) e (2.6), a tesão o cetóde do eemeto se obtém: Ode: ( c c ) = u σ, (2.7) ξ η ( c c ) = DS (2.8) ξ, η Devdo à dscetzação cosdeada, S é gua paa todos os eemetos e está dada po (caso o eemeto seja b-ea): S = S( c ) = (2.9) 2 a A tesão de Vo Mses o cetóde do eemeto se defe como: ( σ + σ + σ σ σ ) 2 ϕ (2.20) ξ η 3 ξη ξ η 3
25 A expessão (2.20) se basea o Ctéo de Escoameto de Vo Mses. Este ctéo afma que o sódo podeá começa a escoa se ϕ acaça o vao da tesão de escoameto em um teste de tação smpes. Outa fómua equvaete à (2.20) paa a tesão de Mses é a segute: Ode: = M Q VQ, ( u M u) 2 ϕ (2.2) V = (2.22) Sedo Q a matz de tasfomação de coodeadas do eemeto. Obsevese que ϕ depede mpctamete de x (dado que u depede de x ). 2.3 Estutua váve Do poto de vsta da egehaa teessa costu estutuas com íves de tesão cotoados. Po este motvo, paa cada matea se defe uma cota supeo da tesão de Mses chamada tesão admssíve σ > 0. Uma estutua com uma dstbução de espessuas x vefcaá a codção de vabdade das tesões quado: adm ϕ ( x) σ adm paa todo {,2,...,} (2.23) Po outo ado, cosdeam-se mtações sobe as espessuas dos eemetos. Defe-se x max > 0 a espessua máxma paa todos os eemetos, po tato deve vefca-se: x paa todo {,2,...,} x max (2.24) ambém defe-se x 0 uma espessua míma ta que: m > 4
26 xm paa todo {,2,...,} (2.25) x Uma estutua com dstbução de espessuas x é dta váve quado se vefca (2.23), (2.24) e (2.25). 2.4 Pobema de otmzação Esta seção defe um cojuto de cocetos usado ao ogo do texto Vaáves de pojeto O veto de vaáves de pojeto x se defe em (2.) Fução objetvo Defe-se fução objetvo como: f x = : R R, f ( x) a (2.26) Ode a é a áea de um eemeto. f ( x) epeseta o voume da estutua Fuções de estções de tesão Cosdeam-se pobemas estutuas com NEC estados de caga [ p p2 L L ], detfcados po {,..., NEC} p p NEC desocameto do equíbo assocado ao estado de caga como: p.. Seja u [] [] u ( x) = o Defe-se tesão de Mses de um eemeto assocado ao estado de caga ϕ ( ) [] [ ] [ ϕ ( x) ϕ u ] ( x) (2.27) 5
27 Defe-se fução de estções de tesão ao veto: Ode: τ τ ( x) [ τ ( x) τ ( x) L τ ( x) L τ ( x) ] σ = (2.28) 2 NEC [ ] e [] [] [] [] ( x) = ϕ ( x) ϕ ( x) L ϕ ( x) L ϕ ( x) adm 2 (2.29) Sedo σ adm a tesão admssíve defda a seção 2.3 deste capítuo e um veto coua com todos os compoetes guas a um. e R Fuções de estções de caxa Defe-se fução de estções de caxa como: m ( x) x e x = m φ (2.30) max ( x) = x x e φ (2.3) max Ode x m, x max são as espessuas míma e máxma espectvamete Fução de estções Defe-se fução de estções g ao veto de fuções: g ( x) [ τ ( x) φ ( x) ( x) ] m φ (2.32) m ( x) R max g, m NEC + 2 (2.33) Os pmeos NEC compoetes ( τ ( x) ) coespodem às estções das tesões dos eemetos paa NEC estados de caga. Os útmos 2 compoetes coespodem às estções de caxa ( φ ( x), φ ( x) (2.32) é a segute: m max ). Outa foma de vsuaza 6
28 ( x) = [ g g g L g g L g ] g NEC / NEC + NEC + / NEC + + NEC + 2 L (2.34) g ( x) Ode: σ = adm [ ( ϕ ] ( x) σ ) x x c( ) ( ) ( ) e e m x x ( ) e max adm se NEC se NEC + NEC + (2.35) se NEC + + NEC + 2 Sedo: c () + (2.36) () ( c( ) ) e + (2.37) Obseva que g é uma fução mpícta da vaáve x R. Paa obte g ( x) seá ecessáo eaza NEC aáses estutuas com a mesma matz de gdez K ( x) Fomuação do pobema Seja uma estutua paa com os segutes paâmetos fxos: Regão Apoos G 0. 2 Σ R dscetzada em eemetos quadados de áea a. Estados de caegametos [ p p L L ] p p NEC 2. Matea sotópco com coefcete de Posso v e móduo de Youg E. esão admssíve σ adm. Espessua míma x m e espessua máxma x max. Busca-se x R, uma dstbução de espessuas váve com o meo voume possíve. Esta útma fase pode se escta da segute foma: 7
29 mmze x sujeto a g f ( x), x R ( x) 0; {,2,..., m} (2.38) Ode f fo defdo em (2.26) e g em (2.32). Obseve-se que ( x) 0 {,2 } g paa,...,m equvae a dze que a estutua com uma dstbução de espessuas x é váve. 8
30 CAPÍULO 3 FAIPA: Agotmo de Potos Iteoes po Acos Váves 3. Itodução Neste capítuo se apeseta o FAIPA ( Feasbe Ac Iteo Pot Agothm ), agotmo de otmzação o qua se basea este tabaho. Este agotmo, poposto po Heskovts [5], é uma técca gea de otmzação ão ea com estções de guadade e desguadade. No pesete estudo cosdeam-se somete estções de desguadade. O popósto deste capítuo é expca os fudametos e caacteístcas do FAIPA. Po equato ão se está peocupado com o tamaho do pobema (dado peo úmeo de vaáves). De todas as fomas, este capítuo é muto mpotate paa o etedmeto das téccas apcadas a pobemas gades já copoados o FAIPA. O capítuo se ogaza da segute maea: a seção 3.2 apesetam-se agumas defções eacoadas a um pobema de otmzação cotíuo, a seção 3.3 estão as codções ecessáas e sufcetes paa um mímo oca deste pobema. Na seção 3.4 descevem-se os passos do FAIPA e em 3.5 uma descção do mesmo. Famete, em 3.6 se apesetam os sstemas eaes pma-dua e dua. 9
31 3.2 Defções Cosdee o pobema de pogamação ão ea com estções de desguadade: mmze x sujeto a g f ( x), x R ( x) 0; {,2,..., m} (3.) Ode f e g são fuções suaves de R, ao meos uma deas é ão ea. A fução f é chamada de fução objetvo e g, fução de estção. O veto [ x L ] x = é chamado de veto de vaáves de pojeto. x Defção 3.2.: Regão váve. Defe-se cojuto de potos váves ao cojuto defdo po: Ω = { x R g( x) 0} (3.2) Ode g ( x ) = [ g ( x ) L g ( x )] m. A desguadade ( x) 0 g ( x) 0 paa todo {, 2, K, m}. g equvae a dze Defção 3.2.2: Cojuto de estções atvas. Defe-se cojuto de estções atvas o poto x como: I { = 0} ( x) = {, 2,, m} g ( x) K (3.3) Defção 3.2.3: Deção váve. Um veto d R é uma deção váve em Ω x + td Ω paa todo t [ 0,θ ]. 20 x se exste θ > 0 ta que
32 Obsevações: ) Se x petece ao teo de Ω, etão toda deção d fgua 3.). 2) Se I( x) e d g ( x) < 0 R é váve., etão d é uma deção váve em x (veja a Defção 3.2.4: Deção de descda. Um veto d R é uma deção de descda paa f em ta que f ( x + td ) < f ( x) paa todo ( 0,δ ) t. x R se exste δ > 0 Obsevação: Se d f () < 0, etão d é uma deção de descda paa f em x (veja a fgua 3.). Defção 3.2.5: Mímo oca, mímo oca estto. O poto vzhaça V de x é um mímo oca do pobema (3.) se x ta que ( x) f ( x ) x é dto mímo oca estto. f paa todo V Ω x Ω e exste uma x. Quado ( x) > f ( x ) f, Defção 3.2.6: Fução agageaa, hessaa. Defe-se fução de Lagage (ou Lagageo) assocado ao pobema (3.) a fução m : R R R defda po: ( x, ) = f ( x) + g ( x) λ = f ( x) + λ g ( x) m λ (3.4) = O gadete do agageo está dado po: 2
33 x ( x, ) = f ( x) + g( x) λ = f ( x) + λ g ( x) m λ (3.5) = Ode g( x) é uma matz de m R chamada matz de devadas, matz dos gadetes das estções ou matz de sesbdades. A coua de g( x) veto coua ( x). Isto é g( x) = [ g ( x) L g ( x) ] g m. cotém o Defe-se Hessaa à matz defda po: L 2 2 ( x, ) = ( x, λ) = f ( x) + λ g ( x) xx m λ (3.6) = Defção 3.2.7: Poto egua, espaço tagete. Um poto x é dto poto egua das estções do pobema (3.) se o cojuto { ( x) I( x) } é eamete depedete. Paa estes potos o espaço tagete I ( x) g se expessa como: { } ( x) = d g ( x) d = I( x) I 0, (3.7) cuvas de íve de f g 2 =0 Ω d x I( x) f(x) g 2 (x) Fgua 3.: Deção de descda e váve d o poto x. Espaço tagete I ( x). 22
34 3.3 Codções de otmadade A segu estão desctas as codções ecessáas e sufcetes que caactezam um mímo oca do pobema (3.). eoema 3.3.: Codções Necessáas Se x R é um mímo oca e poto egua das estções do pobema (3.), m etão exste um úco veto λ R ta que: ( x, λ ) = f ( x ) + g( x ) λ = 0 ( x ) λ = 0 ( x ) 0 x (3.8) d xx Ode ( x ) = dag( g( x ) G (3.9) g (3.0) λ 0 (3.) ( x, λ ) d 0 paa todo I( x ) G. d (3.2) As codções (3.8)-(3.) são dtas codções ecessáas de pmea odem de Kaush-Kuh-ucke (KK). Ao poto (, λ ) x que vefca estas codções seá chamado de poto de KK. A fgua (3.2) mosta uma tepetação geométca destas codções. g =0 cuvas de íve de f x * λ * g (x * ) - f(x * ) g 3 =0 Ω f(x * ) λ 2 * g 2 (x * ) g 2 =0 Fgua 3.2: Codções de KK. 23
35 eoema 3.3.2: Codções Sufcetes Se x R m e λ R vefcam: d xx ( x, λ ) = f ( x ) + g( x ) = 0 ( x ) 0 (3.3) λ g (3.4) λ 0 (3.5) ( x, λ ) d > 0 paa todo I( x ) d (3.6) Etão x é um mímo oca estto do pobema (3.). Os teoemas 3.3. e foam povados em [8]. 24
36 3.4 FAIPA O FAIPA ( Feasbe Ac Iteo Pot Agothm ) é um método de potos teoes po acos váves paa esove pobemas de otmzação ão-ea com estções de desguadade e guadade. Esta técca se apca atuamete ao pobema (3.) ode tem-se somete estções de desguadade. O agotmo faz teações do tpo Newto as vaáves de pojeto ( x R, vaáves pmas) e os mutpcadoes de m Lagage ( λ R, vaáves duas) paa esove as codções de otmadade de KK. Icamete o agotmo eque um poto λ 0 > 0. A pat de ( 0,λ 0 ) x 0 R a egão Ω e k k x gea uma seqüêca de paes {( x, ),...,( x, λ ),...} k k k k x está o teo de Ω, λ > 0 e ta que f ( x ) < f ( x ) cetas hpóteses esta seqüêca covege paa um poto de KK ( x, λ ) sedo mímo oca do pobema (3.). 0 m λ R, λ ode. Se pova em [9] que sob x um Dado um poto x k da seqüêca, o agotmo defe um aco com potos k + váves (chamado aco váve) ode se ecotaá o póxmo poto x. Na fgua 3.3 mostam-se agumas teações do FAIPA paa um pobema com tês estções. g =0 g 3 =0 Ω x 0 x x 2 x 3 x * g 2 =0 Fgua 3.3: Iteações do FAIPA A segu seão desctos os quato passos de uma teação do FAIPA. Seja x = x k Ω e λ = λ k > 0 obtdos da teação k. 25
37 Passo : Cácuo de uma deção d váve e de descda paa a fução objetvo. O cácuo da deção d é feto em duas etapas. Na pmea etapa se cacua uma deção d 0 de descda da fução objetvo mas ão ecessaamete váve. Esta deção se obtém de uma teação de Newto: B Λ g g( x) ( x) G( x) d f = λ0 0 ( ) 0 x (3.7) Ode B é uma matz quase-newto smétca postva defda (gaatdo a ão sguadade do sstema e que a deção d 0 seja de descda) e Λ = dag ( λ ) = dag( λ k ). A matz B é uma apoxmação da matz Hessaa obtda po agum método Quase-Newto [0]. Estes métodos ão equeem a seguda devada de f ou de g paa costu B. Na seguda etapa se cacua a deção d (que apota paa deto da egão váve) esovedo o segute sstema: Ode ( x) dag( g( x) ) g( x) d 0 = ( x) G( x) λ λ B (3.8) Λ g G =. Famete: d = d 0 + ρd (3.9) Ode ρ é um úmeo ea postvo adequado paa gaat que d seja de descda e váve. 26
38 Ω x χ d ~ g =0 d d 0 d ρd Fgua 3.4: Deção váve d d 0 + ρd 2 = e aco váve ( t) = x + td + t d χ ~ Passo 2: Cácuo de uma deção de coeção d ~. Com o tuto de mehoa a veocdade de covegêca, se cacua uma deção de coeção d ~ e um aco com potos váves. Esta deção é uma defexão paa deto da egão váve popocoa às cuvatuas das estções atvas. Uma medda desta cuvatua está dada peo segute veto: ( x + d ) g( x) [ g( x) ] d ~ ω = g (3.20) Logo d ~ se obtém do segute sstema ea: ~ B g( x) d 0 = ( ) ( ) ~ Λ g x G x λ Λ ~ (3.2) ω A Fgua 3.4 usta as deções d, d ~ e o aco váve χ quado o poto x está a fotea de Ω. 27
39 ~ χ. 2 Passo 3: Busca ea o aco ( t) = x + td + t d A póxma etapa do agotmo (busca ea) cosste em esove o segute pobema de otmzação de uma vaáve (esta vaáve é chamada de passo): mmze t sujeto a g f ( χ( t) ), t > 0 ( χ() t ) 0; {,2,..., m} (3.22) O método que obtém agum mímo oca t de (3.22) é chamado de busca ea po mmzação exata. Na pátca, se eaza uma busca ea exata devdo ao eevado custo paa obte um mímo exato. Os métodos de busca ea exata ecotam um passo t ~ sub-ótmo quado vefcam detemado ctéo. A segu desceve-se os ctéos de Amjo e Wofe (veja fgua 3.5). Ctéo de Amjo: Defa o passo t ~ como o pmeo úmeo da seqüêca {,, υ 2, υ 3,...} υ que satsfaça: Ode, η ( 0,) f υ. ( ( ~ t )) f ( x) + ~ t η( f ( x) ) d ( ( ~ t )) < 0 χ (3.23) g χ (3.24) Ctéo de Wofe: Defa o passo ~ t que vefque (3.23), (3.24) e ta que aguma das segutes codções se vefquem: [ ( ( ~ f t ))] d η 2 ( f ( x) ) d ( ( ~ t )) γ g ( x), {,2 m} χ (3.25) g χ,..., (3.26) Ode η ( 0 ), η ( ) e ( 0,), 2 2 η, γ. 28
40 As equações (3.23) defe uma cota supeo do passo paa ambos ctéos e paa o ctéo Wofe, (3.25) defe uma cota feo (veja fgua 3.5). f( χ(t) ) f(x) Gáf ( f(x) + tη ( f(x)) d ) Gáf ( f( χ(t) ) ) 0 η 2 ( f(x)) d t f t * Fgua 3.5: Busca ea de Wofe: O passo seá aceto quado ~ sup ( t f, t ) ~ t t sup t. t A equação (3.24) defe uma cota supeo dada peas estções. No etato a equação (3.26) estabeece uma cota feo o vao do passo. Passo 4: Atuazação. Neste passo, eazam-se opeações que pepaam os dados paa uma ova teação. Estes são: ) Atuazação do poto: x k + ( ~ t ) x ~ ~ t d ~ 2 = χ = + + t d. 2) Atuazação da matz quase-newto B com uma ova matz smétca postva defda. 3) Atuazação de λ k+ > 0. Notas: ~ ) Omtdo-se o passo 2 e fazedo d = 0, obtém-se o agotmo chamado FDIPA ( Feasbe Decto Iteo Pot Agothm ) ode a busca ea se eaza ao ogo de uma eta. 29
41 Se 2) Dfeetes agotmos podem se obtdos de acodo a atuazação de B e λ. k x é um poto egua, os sstemas eaes (3.7), (3.8) e (3.2) têm soução úca. k k ambém se pode pova que (,λ ) covege paa potos de KK (, λ ) vefcam as segutes hpóteses: x 0 x quado se H : σ, σ 2 > 0 tas que os vaoes pópos σ de B vefcam σ σ σ 2. I S H 2: λ, λ, β > 0 tas que S 0 λ λ e se g ( ) β etão I λ λ. A cofguação cássca do FAIPA usa uma atuazação de B chamada BFGS (desevovda po Boyde, Fetche, Godfab e Shao) []. Equato que paa a atuazação de λ utza-se a segute ega: Paa =,2,..., m faze: Fm_Paa { λ0, ε d 0 } λ = max. Se ( ( ) < β 2 2 I I g x ) e ( λ < λ ) etão: λ = λ. I Ode ε, β, λ > 0. Quado estes paâmetos são sufcetemete pequeos λ = paa uma estção atva. E paa as atvas λ 0 quado λ0 j x x po tato, paa esta ega de atuazação, λ λ. 3) Os passos, 2, 3 e 4 se epetem até que aguma codção de paada se vefque. Obseve-se que o agotmo covege a um poto KK quado d 0 = 0, e, potato, da equação (3.7) se deduz que ( x λ ) = f ( x) + g( x) λ 0., 0 0 = 30
42 3.5 Descção do FAIPA Paâmetos: ( 0,) α, ϕ > 0 e costates usadas a busca ea. Dados: B R smétca postva defda, m λ R, > 0 λ e um poto váve x Ω. Pocedmeto: Repet os segutes passos: Passo : Cácuo da deção váve de descda d.. Resove o sstema ea (3.7), obtedo-se d 0 e λ 0. Se d 0 = 0, fm. Resove o sstema ea (3.8), obtedo-se d e λ. 2. Se d 2 f ( x) 0, computa = m ϕ d,( α ) > Se ão, computa ρ = ϕ d Computa d = d 0 + ρd Passo 2: Cácuo da coeção d ~.. Computa ~ ω = g( x + d ) g( x) [ g( x) ] d ( x) d 0 f ρ 0. 2 d f ( x) 2. Resove o sstema ea (3.2), obtedo-se d ~ e ~ λ. 2 ~ χ t = x + td + t. Ecota agum bom vao de ~ t > 0 ta que: f χ ~ t < f x e ( ~ χ t ) Ω Passo 3: Busca ea ao ogo do aco ( ) d Passo 4: Atuazação. ( ( )) ( ). Def ova matz B 2 2 R smétca e postva defda. m 2. Def ovos vaoes paa λ R, λ > Def o póxmo poto da seqüêca como ( ~ x χ t ) =. 3
43 3.6 Sstemas eaes do FAIPA Dada sua mpotâca, apeseta-se a segu um esumo dos sstemas eaes do FAIPA. Os sstemas eaes (3.7), (3.8), (3.2) são chamados pma-dua (po te cógtas o espaço pma e o dua), os quas podem esum-se da segute foma: ~ B g( x) d ( ) d d f x = ( ) ( ) ~ Λ g x G x λ λ λ 0 λ Λ ~ (3.27) ω 0 A matz do sstema (3.27), chamada de matz pma-dua, tem tamaho ( + m) e cotém as segutes sub-matzes: B R é uma matz smétca postva defda, g x R é a matz de devadas, m ( ) m Λ = dag λ R, λ R, λ > 0 e m m ( ) m m m G( x) = dag( g( x) ) R, g( x) = [ g ( x) L g m ( x) ] R. O tamaho dos pobemas a seem esovdos está mtado pea memóa equeda paa aoca a matz do sstema, pos esta aumeta com o quadado de ( + m). Devem-se usa téccas que pemtam epeseta as matzes com meos memóa. B m R e g( x) R Emado d 0, d e d ~ em (3.7), (3.8), (3.2) espectvamete obtém-se os sstemas duas (po teem cógtas o espaço dua excusvamete): ~ [ Λ g ( x) B g( x) G( x) ][ λ λ ] = Λ g ( x) B f ( x) [ λ Λω] λ ~ 0 (3.28) Mutpcado (3.28) po postva defda: Λ obtemos uma matz de coefcetes smétca e ~ [ Λ g ( x) B g( x) G( x) ][ λ λ ] = Λ g ( x) B f ( x) [ λ Λω] λ ~ 0 (3.29) Ode e é um veto coua com m compoetes utáos. A matz do sstema (3.29) tem tamaho m e é chamada dua smétca. 32
44 CAPÍULO 4 Aáse de sesbdade 4. Itodução A aáse de sesbdade de um sstema mecâco popocoa fomação sobe a mudaça de espostas físcas fete a petubações das vaáves de pojeto. A sesbdade é usada peo pojetsta po que he foece fomação sobe o que sucedea com a estutua fete a mudaças o pojeto. Em temos matemátcos, a sesbdade pode se vsta como a devada de ceta fução com eação às vaáves de pojeto. A pesqusa sobe a aáse de sesbdade estutua tem sdo muto extesa. Autoes dedcam vos competos [] ao tema abodado uma vasta gama de apcações em egehaa. Os avaços em métodos umécos paa a aáse de sesbdade foam tegados a feametas de pojeto assstdo po computado e aáse de eemetos ftos. A sesbdade também é usada em pocessos automátcos como agotmos de otmzação estutua. Neste tabaho apca-se o agotmo FAIPA o qua exge o cácuo do gadete da fução objetvo e do gadete das fuções de estção. A pecsão uméca das devadas é de gade mpotâca paa o FAIPA pos as estutuas obtdas em cada teação do agotmo são cacuadas com base os gadetes. Na pátca, eos umécos o cácuo das sesbdades fazem com que o agotmo equea mas teações paa ecota o ótmo deto de uma pecsão especfcada. 33
45 Outo fato mpotate é a memóa equeda paa o amazeameto dos gadetes. A sesbdade das estções é guadada em uma matz desa de m compoetes ode é o úmeo de eemetos da dscetzação e m é o úmeo de estções que em gea seá um mútpo de. Esta matz chamada de matz de sesbdades deve se foecda ao FAIPA em cada teação. Potato se qusemos uma maha com mutos eemetos, sto acaetaá um eevado equsto de memóa paa a execução do agotmo. Este capítuo está ogazado da segute foma, a seção 4.2 e 4.3 se cacua as sesbdades das fuções do pobema de otmzação específco deste tabaho. Apesetam-se duas fomuações paa o cácuo da devada das estções, o método de dfeecação deta e o método da vaáve adjuta. Famete, a seção 4.4 se popõe um pocedmeto paa o cácuo de podutos do gadete das estções po veto e o gadete das estções tasposto po veto. Estes podutos são usados a metodooga poposta o capítuo 5. Os pocedmetos que eazam os podutos da matz de sesbdade po veto e sua tasposta po veto costtu um dos pcpas apotes de este tabaho de pesqusa. 4.2 Gadetes A sesbdade se efee ao cácuo da devada de fuções com espeto a paâmetos ou vaáves de pojeto x. Paa esove o pobema de otmzação (2.39) apcado o FAIPA devem-se esove os sstemas eaes (3.27) ou (3.29). Paa sso seá ecessáo o cácuo dos segutes gadetes: ( x) f (4.) ( x) g (4.2) Sedo f defda em (2.27) uma fução ea de x. Potato seu gadete é facmete cacuado: ( x) ae f = (4.3) 34
46 Ode e é um veto coua de compoetes utáas e a é áea do eemeto fto. A dfcudade está o cácuo de (4.2), chamada de matz de devadas, matz dos gadetes das estções ou matz de sesbdades. Recodado (2.34) e (2.35), g ( x) epeseta um veto de fuções ode seus pmeos NEC compoetes são fuções ão eaes e depedem mpctamete de x. As segutes 2 fuções são fuções eaes. Em coseqüêca: g ( x) g x = M g x ( x) g ( x) NEC x M ( x) g ( x) L O L NEC x [ I ] [ I ] (4.4) Sedo I a matz detdade de tamaho. A segu, se deduz uma fómua paa um compoete {,2 NEC },...,. g x ( x) paa 4.3 Devada de uma estção de tesão 4.3. Notas cas De acodo com (2.2) e (2.35): g σ [] [] ( ) ) 2 u M u σ = adm adm (4.5) Ode é um estado de caegameto e é um eemeto, ambos assocados à estção, sto é: c () =, e ( ) =. As defções de c ( ) e e ( ) estão em (2.36) e (2.37). A matz M está defda em (2.22). estutua: A fução g é uma fução mpícta de x dado que u [ ] se obtém da aáse 35
47 ( ) [ x u ] p K = (4.6) A fução g é dfeecave []. Apcado a ega da devada composta sobe a expessão (4.5): g x ( x) = ( g ( x) ) u u x [ ] ( x) (4.7) Devado (4.5) espeto de [ ] u, chega-se a: [] ( u ) [] M u g ( x) = (4.8) ϕ σ adm Paa smpfca a exposção, defe-se o segute veto fa: [] ( u ) [] α M ( ) g u g x = R ϕ σ (4.9) adm Devado (4.6), obtém-se: K ( x) u x [ ] = K u [] (4.0) Assumdo K ( x) postva defda: x [] u = K [] ( x) K u (4.) Substtudo (4.8) e (4.) em (4.7), tem-se a expessão: g x = [] [] ( u ) M K( x) K u [] ϕ σ adm (4.2) 36
48 Ou de foma compacta (usado (4.9)): g x [ ] u = α (4.3) x O cácuo deto de ( ) métodos paa computa (4.2) ou (4.3). K x é pobtvo a pátca. A segu apesetam-se dos Método da dfeecação deta Este pmeo esove (4.0) obtedo-se em (4.3) obtedo-se g x. u x [ ] ogo, se substtu este esutado Método da vaáve adjuta Neste método ão se cacua u x [ ] [ ] ( x) M u. Paa sto se esove o pobema adjuto: K λ = (4.4) Obtedo-se a vaáve adjuta defda po: [ ] ( x) M u λ K (4.5) Po smeta da matz de gdez e da matz M : [] ( ) u ( ) M K( ) λ = x (4.6) 37
49 Logo, substtudo-se (4.6) em (4.2), se obtém: g x [ ] ( x) ( λ ) K u = ϕ [] σ adm (4.7) Aspectos computacoas Geamete ão se cacua o gadete de todas as estções de tesão. Na pátca apeas agumas estções são cítcas, estas estão assocadas aos eemetos com tesões póxmas à tesão admssíve σ adm. Seja {,2..., NEC } o cojuto de todas as estções de tesão e ( x) R C o cojuto de estções cítcas paa a cofguação de espessuas x. Em gea se vefca que R C ( x) {,2..., NEC }. Quado se cacua apeas os gadetes das estções cítcas se dá que se efetua uma ftagem de estções. A segu desceve-se um agotmo paa o cácuo de. Paa cada estado de caga =,2,, NEC :.. Resove o sstema ea ( ) [ ] Caso se use o método de dfeecação deta:. Paa cada estção em R C ( x) :. Paa cada eemeto =,2,, : g x ( x) K x u = p obtedo-se [ ]... Resove o sstema ea ( )..2. Faça g x ( ) [] ( x) u Caso se use o método da vaáve adjuta: 2. Paa cada estção em R C ( x) : = M q ~ []. ϕ σ adm 2. Resove o sstema ea K ( x) q = ( ) 2.2 Paa cada eemeto =,2,, : 2.2. Faça g x [ ] ( x) ( q ) M u = ~ ϕ [] σ. [] u. K x q ~ = K u obtedo-se q ~. ~ [ ] M e u obtedo-se q ~. adm. 38
50 Compaado os métodos com espeto ao úmeo de esoução de sstemas eaes, se obseva que a dfeecação deta eaza ecessaamete NEC aáses e o método adjuto NEC cad( RC ( x) ) ( ) fo mao que o úmeo de estções cítcas ( ( R ( x) ). Se o úmeo de vaáves de pojeto cad C ), o método adjuto é acosehado. Poém quado ão se eaza ftagem e NEC > o método deto é pefeíve. 4.4 Poduto do gadete das estções po veto 4.4. Notas cas Nesta seção mosta-se a dedução dos pocedmetos paa computa o poduto do gadete das estções po um veto. Cosdeam-se dos tpos de podutos:. a ( g( x) ) z =, 2. w = g( x)v, z R m v R O pmeo poduto pode se vsto como a devada decoa de g a deção z R defda como: ( x + tz) g( x) g g ( x, z) m t 0 t De fato, o teoema de ayo assegua que: g Potato: ( x tz) = g( x) + ( g( x) ) tz + O( t) +. ( x + tz) g( x) g ( g( x) ) z = m t 0 t Po outo ado, o segudo poduto é o gadete de uma fução auxa defda como uma combação ea das estções: (3.5). m m g( x) v = g ( x) v = g ( x) v = = Este poduto, de fato é um temo do gadete do agageao expessado em 39
51 Cácuo do poduto ( ) z g Que-se cacua: ( ) m R z g s = Ode: ( ) ( ) ( ) ( ) ( ) [ ] m m R g g g g g = L L 2 e [ ] R z z z z z = L L 2 Os compoetes de s teão a segute foma: = = NEC NEC se z NEC NEC se z NEC se z x g s NEC NEC 2 (4.8) Mutpcado a guadade (4.3) po z : [ ] z x u z x g = α (4.9) Somado ambos membos de (4.9) com ete e : [ ] = = = z x u z x g α (4.20) Paa competa o cácuo de s fata obte: [ ] = z x u ω (4.2)
52 Mutpcado-se a equação (4.0) po z : K ( x) u x [ ] z = K u [] z (4.22) Somado ambos membos de (4.22) paa ete e : K ( x) = u x [ ] z = = K u [] z (4.23) Potato, o cácuo de ω esta dado peo pobema adjuto: ( x) q K ω = (4.24) Ode q = K u [] z. Logo, os compoetes estaão dados po: s α ω = z NEC z NEC se se se NEC NEC + NEC + NEC + + NEC + 2 (4.25) Sedo = c() o estado de caegameto assocado a estção e ω dado po (4.2). 4
53 Cácuo do poduto ( )v g Deseja-se uma expessão paa: ( ) R v x g w = Ode: [ ] m m R g g g g g = L L 2 [ ] m t m R v v v v v = L L 2 A ha da matz g se otaá po e esta dada po: = m x g x g x g x g L L 2 Os compoetes de w estaão dados po: NEC NEC NEC v v v x g v w = + = = (4.26) aspodo a equação (4.3) e mutpcado-se peo compoete v : [] ( ) v x u v x g α = (4.27) Somado ambos membos de (4.26) paa ete e NEC : [] ( ) = = = NEC NEC v x u v x g α (4.28)
54 43 A somatóa (4.28) pode expessa-se da segute foma: [] ( ) [] ( ) ( ) [] = = = + = = = = = NEC NEC NEC NEC h y x u v x u v x u α α (4.29) Ode se defe: ( ) ( ) + = y v α e [] y x u h (4.30) Vejamos o cácuo de [] y x u h. aspodo a equação (4.): [] [] ( ) ( ) = x K K u x u (4.3) Mutpcado (4.3) po y : [] ( ) () y K K u h = (4.32) Logo, esovedo o pobema adjuto: ( ) y x K = θ (4.33) E substtudo em (4.32), obtém-se: [] ( ) K u h θ = (4.34)
55 Famete, os compoetes w estaão dados po: [] [( u ) K ] vnec + + vnec + NEC w = + = θ (4.35) Aspectos computacoas Resumdo, descevem-se os pocedmetos paa o cácuo dos podutos ( g) z s = e w = ( g)v. Paa cada estado de caga =,2,, NEC : Resove o sstema ea (4.6) obtedo-se Paa cada estção =,2,, NEC : Paa cacua s ( g) z [] ( ) ( ) Cacua α = u M e [] ϕ σ. = : ( ) e adm [ ] u.. Paa estado de caga =,2,, NEC :.. Cacua q = K u [] z K x ω = q.2. Resove ( ).3. Paa =,2, K, NEC :.3.. Cacua s = α ω.4. Paa = NEC +, K, NEC + :.4.. Cacua = z NEC s.5. Paa = NEC + +, K, NEC + 2 : Paa cacua w = ( g)v :.5.. Cacua s = z NEC. Paa estado de caga =,2,, NEC : = +.. Cacua ( α ) y v ( ) 44
56 K x θ = y.2. Resove ( ) 2. Paa =,2, K, 2. Cacua [] [( u ) K θ ] vnec + + vnec + NEC w = + = Obseve-se que são ecessáos somete NEC aáses estutuas tato paa ( g) z s = como paa w = ( g)v. 45
57 CAPÍULO 5 éccas de otmzação de gade pote. 5. Itodução Neste capítuo apesetam-se duas metodoogas utzadas paa esove o pobema de otmzação poposto. A pmea metodooga, ão utza téccas de otmzação paa gade úmeo de vaáves. A seguda metodooga costtu a ova técca de otmzação estutua de gade pote. Este capítuo está ogazado em quato pates. A pmea pate (seção 5.2) desceve uma técca que pemte esove pobemas médos fazedo uso da atuazação quase-newto BFGS, do cácuo expícto da matz de sesbdades (método de dfeecação deta ou método da vaáve adjuta) e da esoução do sstema pma-dua do FAIPA. Esta técca é efcete em temos de memóa, o etato, com esta obtveam-se os pmeos esutados umécos [2]. A seguda pate (seção 5.3) expõe as téccas de otmzação de gade pote: ) écca de Memóa Lmtada apcada a pobemas com e sem estções; 2) Método do Gadete Cojugado pé codcoado. A tecea pate (seção 5.4) apeseta a ova metodooga poposta ode são apcadas as téccas vstas a seção ateo jutamete com o FDIPA ( Feasbe Decto Iteo Pot ) e a fomuação do poduto da matz de sesbdade po veto desevovda o capítuo 4. Esta fomuação do poduto da matz de sesbdade po veto costtu um apote oga desta vestgação. A quata e útma pate deste capítuo (seção 5.5) faz uma dscussão sobe a efcêca da ova técca em eação ao úmeo de aáses estutuas eazadas. 46
58 Fomuam-se as hpóteses as quas a ova metodooga é mas efcete que a técca descta a seção (5.2). 5.2 Pmea técca A técca descta esta seção expca como se utza o FAIPA paa esove pobemas com um úmeo mtado de vaáves de pojeto e de estções. O motvo de chamá-a Pmea é po que com ea se obtveam os pmeos esutados umécos. Em essêca, esta metodooga esove os sstemas pma-dua do FAIPA atavés de métodos de esoução de sstemas eaes detos, utza a ega BFGS paa a atuazação da matz quase-newto B. Aém dsso, esta fomuação ecessta do cácuo e aocação da matz de devada das estções ( g( x) ). Na teação essma do FAIPA os sstemas pmas-duas podem esceve-se da segute foma: B Λ g g( x ) ( x ) G( x ) d 0 λ0 d λ ~ d f ~ = λ 0 ( x ) 0 λ 0 Λ ~ ω (5.) ode ( x, λ ) e B R são o poto e a matz quase-newto utzados a teação espectvamete. No passo 4 do FAIPA eazam-se as atuazações de x, λ e B deotado po + + x, λ e a equação segute: + B. A ega de atuazação quase-newto do tpo BFGS é apesetada B + = B + y ( y ) ( y ) s B s ( s ) ( s ) B s B (5.2) Ode s = x + é atuazada a pat de x + e y = ( x,λ ) ( x, λ ) B e dos paes { s y } =,. O método BFGS começa com a escoha de uma matz defda (tpcamete a matz detdade). Paa gaat que 47. Dz-se que a matz + B 0 B smétca e postva + B seja postva
59 defda, deve-se vefca a codção de cuvatua ( ) > 0 s y. Isto em sempe acotece em pobemas de otmzação com estções. Powe [3] popõe a segute ega paa supea este pobema: Rega 5. (Powe) Se ão se vefca ( ) ( ) s y 0. 2 s B s : 0.8( s ) B s Computa: = ( s ) B y ( s ) y y φ e ogo, = φ y φ B Faça: + ( ) s Po outo ado, em cada teação do FAIPA deve-se cacua e amazea o gadete das estções g( x ). No capítuo 4 apesetam-se duas téccas paa a obteção de este gadete. Esta metodooga é váve paa esove pobemas gades devdo a: ) B g x são matzes desas e potato, em gea, a m R e ( ) R matz de coefcetes do sstema pma dua (5.) ão é espasa toado-se muto custosa a esoução destes sstemas eaes [6]. 2) Paa guada os coefcetes da matz do sstema (5.) se eque de um espaço de tamaho popocoa a ( m) 2 úmeo de estados de caegameto. +, ode m = NEC + 2 e NEC é o 5.3 éccas de otmzação de gade pote 5.3. Método de Memóa Lmtada O método de memóa mtada fo cocebdo paa esove pobemas de otmzação de gade pote. Esta técca, baseada o método Quase-Newto, pemte apoxma a matz quase-newto da Hessaa do pobema (ou a matz quase- Newto da vesa da Hessaa), atavés de um cojuto de paes de vetoes. Po meo deste cojuto de paes é possíve epeseta tas matzes sem ecessdade de 48
60 aoca seu espaço. Aém dsso, o poduto de matz po veto pode eaza-se efcetemete atavés desta metodooga [6] [7]. Seja A a matz dua smétca apesetada em (3.29): ( g ( x) B g( x) Λ G( x) ) A = (5.3) A segu apesetam-se duas apcações da técca de memóa mtada. Pmeamete, a seção (5.3..), obtém-se uma epesetação de memóa mtada paa a matz A. Na seção (5.3..2), obtém-se a epesetação da vesa da Hessaa do pobema de otmzação (3.), sto é, uma apoxmação de B Repesetação de memóa mtada paa a vesa da matz dua ( A ) Seja o segute pobema de otmzação sem estções: Ode: m { mmze F( λ) λ R F λ ( λ) λ Aλ λ b, (5.4) = 2 (5.5) Sedo matz A. b R m. Obseve que a Hessaa exata do pobema (5.4) é a pópa O método DFP (Davdo, Fetche e Powe) pemte costu uma apoxmação da vesa da Hessaa atavés da segute ega []: H + = H + s ( s ) ( s ) y H y ( y ) ( y ) H y H (5.6) ode s = λ + λ (5.7) + ( ) F( λ ) As λ (5.8) y = F = 49
61 Sejam os paes {, y } = 0,,..., s geados ao ogo de teações do método DFP. Seja também H 0 R m m pova-se a segute guadade: uma matz smétca e postva defda. Em [] [ ] ( ) ( ( ( ) 0 + ) )( ) ( ) 0 R D Y H Y R R S H Y R ( S ) ( ) 0 Y 0 H = H + (5.9) 0 H Ode se defem as matzes foma: S, Y D, R R e R da segute 0 0 S = ( s s... s ), = ( y y... y ) owe( S ) Y ) 0 0 = dag ( s ) y,..., ( s ) y Y (5.0) R = (5.) ( ) D (5.2) { s, y } = 0,,..., O método de memóa mtada ao vés de guada todos os paes, guada somete os útmos A s, y A q paes { } = q,...,. Este cojuto de paes é atuazado em cada teação emovedo-se um pa (o mas veho, po exempo) e adcoado-se o ovo pa. Fazedo esceve-se como: H 0 = γ I paa agum escaa postvo γ, a expessão (5.9) pode H [ ] ( ) ( ( ( ) ) + )( ) ( ) R D γ Y Y R R S γ Y R 0 = γ I + γ ( S ) ( ) Y (5.3) sedo agoa: qa q S = [ s,..., s ], = [ y,..., y ] owe( S ) Y ) q q A D = dag ( s ) y,...,( s ) y Y A (5.4) R = (5.5) ( ) A (5.6) 50
62 Potato, uma apoxmação da matz (5.3) ode se guadam apeas os útmos A Deota-se po paes {, y} = q,..., s. A A pode se obtda pea expessão s., y A q paes { } = q,..., H A a epesetação de memóa mtada de A obtda com os Repesetação de memóa mtada paa a vesa da Hessaa do pobema com estções ( B ) Seja agoa o pobema com estções (3.). A matz Hessaa está dada po (3.6). Em pcípo a vesa desta matz pode se obtda com a mesma ega de atuazação que (5.3) mas agoa cosdeado: y = x s = x x + (5.7) + ( x,λ ) ( x, λ ) x (5.8) A epesetação de memóa mtada paa B está dada peos q B paes { s, y},..., = qb. Neste caso as matzes S e Y qb q S = [ s,..., s ], = [ y,..., y ] qb R estão defdas como: Y B (5.9) A técca de memóa mtada já fo copoada ao FAIPA. Duate as pmeas teações, quado teações segutes quado qb, as matzes S e Y amazeam vetoes. Nas > qb, o pocedmeto de atuazação paa ta foma que os paes mas vehos sejam substtuídos peos mas ovos. Deota-se po paes {, y },..., s. = qb H B a epesetação de memóa mtada de S e Y é de B obtda com os 5
63 Método do Gadete Cojugado pé-codcoado O Método do Gadete Cojugado (MGC) é um método teatvo paa esove sstemas de equações eaes da foma: Ax = b (5.20) Ode A de cógtas e m m R é uma matz smétca e postva defda, b x m R é o veto m R o temo depedete. Patem de uma estmatva ca 0 geam uma seqüêca de potos que covege paa a soução do sstema. O MGC eaza meos teações quato meho fo o úmeo de codção da matz do sstema. Potato a efcêca deste método depedeá dos autovaoes da matz A. Quato mas póxmos estejam seus autovaoes, mas póxmo à udade estaá seu úmeo de codção. O pocesso de pé-codcoameto é uma modfcação dos coefcetes da matz A de foma a mehoa seu codcoameto. Uma foma de obte esta modfcação cosste em pé-mutpca a guadade (3.20) po uma matz N smétca e postva defda, deomada matz pé-codcoadoa: x e NAx = Nb (5.2) ~ A déa é que o ovo sstema obtdo em (3.2), teha a matz A = NA meho codcoada que A. Paa que sso acoteça, podemos cosdea N como uma ~ apoxmação de A. Assm po exempo, quado N A, tem-se que A = NA I e ~ potato o úmeo de codção de A I estaá póxmo a udade. A cotuação se esboça o MGC pé-codcoado de descto em [4] apcado ao pobema (5.20): Agotmo 5. (Método do Gadete Cojugado pé-codcoado). Faze = 0, 0 = b Ax0, z 0 = N0 e p 0 = z0. 2. Repet (até vefca o ctéo de covegêca adotado): 52
64 2. α = z ( Ap ) p 2.2 x+ = x + α p = α Ap 2.4 z N β = + = + z+ z 2.6 p + = z + β p 2.7 = Metodooga poposta As caacteístcas desta metodooga são as segutes: Usa-se o FDIPA e se esovem os sstemas duas e a técca de memóa mtada paa epeseta B e A. Os sstemas duas se esovem peo Método do Gadete Cojugado pécodcoado pea matz H A. Não se cacua a matz de gadetes g. A segu, se expcam estes aspectos Sstemas eaes do FDIPA Os sstemas duas do FDIPA ( Feasbe Decto Iteo Pot Agothm ) são obtdos de (3.29). Emado o teceo sstema eazado o FAIPA e usado a otação H B B tem-se: [ e] ( g ( x) H g( x) Λ G( x) )[ λ ] = g ( x) H f ( x) B λ (5.22) 0 B No fa de cada teação do FDIPA, se atuaza a sta dos q B paes que pemtem def a matz H B. 53
65 matz [7]. Esta fomuação ão pecsa mota a matz do sstema. Os podutos da H B po veto se eazam atavés do poduto da técca de memóa mtada Método do Gadete Cojugado pé-codcoado pea matz quase- Newto de memóa mtada Paa esove os sstemas duas do FDIPA, empega-se o Método do Gadete Cojugado pé-codcoado (MGCP). A matz pé-codcoadoa é dada po N = H A. No fa de cada teação do MGCP, se atuaza a sta dos q A paes que pemtem def a matz H A. ( ) Seja A g ( x) B g( x) Λ G( x) =. De acodo com o agotmo 5., o MGCP ão pecsa da aocação da matz A. Necessta-se ucamete do espaço paa amazea vetoes e vaoes escaaes. Po outo ado, se devem foece os segutes podutos de matz po veto: Ax 0, N 0, Ap e + N. Os podutos N 0 e N + podem-se eaza de foma efcete fazedo uso dos, y A s. paes { } = q,..., Podutos da matz de sesbdades g( x) e [ g( x) ] po veto Fata mecoa como se eazam os podutos Ax 0 e Ap. m Seja v R um veto coua. O poduto w = Av pode computa-se da segute maea:. w = ( Λ G( x) )v 2. w = g( x)v 2 3. w3 = H w2 w 4. ( ) 3 B 4 = g x w 5. w = w 4 + w ( ) O passo é smpes de eaza dado que Λ G( x) é uma matz dagoa. 54
66 Se NEC é o úmeo de estados de caegameto, tato o segudo como o quato passo se eazam NEC aáses estutuas com a mesma matz de gdez (veja seção 4.4.4). Potato, uma teação do Método do Gadete Cojugado eque 2 NEC aáses estutuas. Paa computa o teceo passo, se usam os B técca do poduto de memóa mtada. q paes {, y} = q,..., s e a B 5.5 Dscussão sobe a compexdade de cácuo Esta seção tem como objetvo essata a efcêca da metodooga poposta em temos de aáses estutuas eazados. Seja NEC o úmeo de estados de caga e o úmeo de vaáves. Deoma-se écca à técca apesetada a seção 5.2 e écca 2 à ova técca descta a seção (5.4). Cosdeado que se eaza ftagem de estções cítcas, o Método faz ( R ( x) ) NEC cad aáses po teação do FDIPA. Caso cotao, o custo é de C NEC aáses. O Método 2 eaza 2 NEC aáses po teação do Método do Gadete +2 Cojugado (MGC). Se fo a soma do úmeo de teações do MGC do pmeo e do segudo sstema ea do FDIPA em uma teação, o Método 2 eazaá um tota de NEC aáses estutuas. Em coseqüêca, o Método 2 seá mas efcete que o Método quado: +2 2 < (5.23) e ão se eaze ehuma ftagem de estções. Caso exsta ftagem, a codção seá a segute: ( R ( x) ) +2 2 < cad (5.24) C 55
67 CAPÍULO 6 Impemetação Computacoa 6. Itodução O tuto deste capítuo é documeta o tabaho de desevovmeto de sstemas ecessáo paa a costução de pogamas que esovem o pobema de otmzação estutua poposto o capítuo 2. Paa sso foam utzadas mpemetações do FAIPA e de pogamas de aáses estutuas. O FAIPA avaa a fução objetvo, as estções, a devada da fução objetvo assm como a devada das estções. Os cácuos da fução objetvo e de sua devada são obtdos aatcamete, poém paa o cácuo das estções e suas devadas são ecessáas aáses estutuas e de sesbdade. as aáses podem se eazadas atavés de pogamas que mpemetam o Método dos Eemetos Ftos (MEF). Neste capítuo mosta-se como eaza o cácuo das devadas atavés de dos pogamas: ABAQUS e DLEARN. ABAQUS costtu um potete pogama comeca pos dspõe de uma ampa gama de ecusos. Possu uma teface gáfca amgáve, uma bboteca de eemetos ftos e pemte faze a execução das aáses e ecupeação dos esutados atavés de scpts (ABAQUS Pytho) e guagem de pogamação C++ [4]. O pogama DLEARN é um códgo educacoa gatuto de eemetos ftos que pemte eaza aáses eaes estátcas e dâmcas [2] e fo escto em Fota 77. No pesete capítuo, a seção 6.2 usta-se a dsposção gea de móduos ode são mecoados quas móduos foam desevovdos (cados ou modfcados) e quas 56
68 foam utzados (sem modfcação). Esta ogazação de móduos é utzada em todas as mpemetações do sstema. Na seção 6.3 desceve-se a mpemetação da teface paa utza ABAQUS como feameta de aáses. Em seguda, a seção 6.4 desceve-se a mesma teface, poém usado DLEARN. 6.2 Aqutetua do sstema 6.2. Itodução O sstema está ogazado em compoetes e feametas auxaes que estão desctas as segutes seções. No fa desta seção stam-se os pogamas eazados Compoetes O sstema computacoa cotém os segutes compoetes ou móduos (veja fgua 6.): a) fapa b) df c) teface d) pog_aáse Impemetações do FAIPA O móduo fapa epeseta uma mpemetação coceta do agotmo FAIPA descto o capítuo 3. No pesete tabaho utzou-se a vesão 2..3 do FAIPA escta em Fota 90. Nesta vesão estão mpemetados o método BFGS e a esoução do sstema pma-dua. A matz pma-dua eque o cácuo da matz de devadas ( g ). Esta mpemetação é deomada fapa_pmadua_gadg. Exste outa vesão do FAIPA descta em [7] a qua se mpemeta a esoução do sstema dua peo Método do Gadete Cojugado pé-codcoado. Utza-se a técca de Memóa Lmtada paa epeseta a matz pé-codcoadoa e também 57
69 paa epeseta a vesa da matz Hessaa. Esta vesão aoca espaço paa a matz de gadetes ( g ). Esta mpemetação do FAIPA é deomada fapa_dua_gadg. No pesete tabaho mpemeta-se uma ova vesão do FAIPA baseada a vesão eazada em [7]. A ova vesão poposta ão utza o gadete das estções ( g ), poém eque duas otas que eazam a computação do poduto desta matz po veto e de sua tasposta po veto. A esta mpemetação do FAIPA deomou-se fapa_dua Impemetações do móduo df No móduo df estão pogamadas as fuções e suas devadas. Seja f a fução objetvo e g a fução de estções. Os cácuos de f e f são fetos aatcamete. No etato paa avaa g ecessta-se da eazação de aáses estutuas. Paa sto se defe a sub-ota df_g. Reazaam-se tês mpemetações de df. Cada uma deas dfee a foma em que são cacuadas as devadas de g. A pmea é deomada como df_deta, cacua a matz de devadas g peo método de dfeecação deta (sub-ota df_dg_deta). A seguda é deomada df_adjuta, e cacua g peo método da vaáve adjuta (sub-ota df_dg_adjuta). A tecea mpemetação é deomada df_adjuta_2, e possu duas sub-otas. A pmea sub-ota ( df_dg_v ), cacua o poduto da matz g po veto e a seguda sub-ota ( df_dgt_v ), cacua o poduto da matz g po veto. odas as mpemetações de df possuem uma sub-ota chamada df_pepoc que socta ao pogama de eemetos ftos a matz de gdez do eemeto com espessua utáa (matz k ). A sub-ota df_pepoc também cacua e amazea a matz defomação-desocameto B avaada o cetóde do eemeto. Devdo ao fato de que todos os eemetos da dscetzação possuem a mesma foma geométca (quadada), tato a matz k como B são guas paa cada eemeto. 58
70 Impemetações do móduo teface O móduo teface seve paa a comucação ete df e pog_aáse. Este móduo omaza a foma de se comuca com os pogamas de aáse estutua. Exste um fote vícuo ete o móduo teface e o móduo pog_aáse (veja o quadado que ue ambas compoetes a fgua 6.). A escoha de um pogama de aáse deve se acompahada à costução de uma teface paa esse pogama. No pesete tabaho pogamaam-se duas tefaces, uma paa ABAQUS (t_abq) e outa paa DLEARN (t_d). Estas tefaces se comucam com seus espectvos pogamas de aáses atavés de dsco ( had dsk ). os fatoes. Um móduo de teface deve foece ao móduo df as segutes sub-otas: a) teface_k(k): Retoa a matz de gdez do eemeto k. b) teface_fato(x): Reaza a fatoação da matz de gdez K ( x) e amazea c) teface_u(p,u): Resove o sstema ea ( x) u p amazeados da útma vocação da teface_fato. K = utzado os fatoes Obseve-se que p [ p L L ] de caga, e potato u [ u L L ] = p p k são evetuamete mutos estados = u u k seá uma matz de souções. No caso em que ão seja possíve mpemeta a sub-ota b), deve substtu-se a sub-ota c) com a segute ateatva: c) teface_u(x,p,u): Resove o os sstema ea ( x) u p K = Pogamas de aáse estutua utzados O pog_aáse é um pogama paa esove o sstema ea (2.3) (equação de equíbo): ( x) u p K = (6.) 59
71 Este pogama ecebe como etada um o veto x de espessuas e um veto p de caegametos. Como saída etoa o veto u de desocametos. Nas seções 6.3 e 6.4 desceve-se como se eazam tas etadas e saídas com ABAQUS e DLEARN espectvamete. fapa df teface pog_aáse df_pepoc pcpa abaqus pytho abaqus vewe abaqus cae Legeda códgo Fota, aquvo báo ou pogama. dsco ( had dsk ), aquvo de texto Fgua 6.: Ogazação dos móduos e suas vcuações. Paa faza esta seção, fata mecoa o móduo pcpa. Este móduo ê de um aquvo de texto: - o poto ca (estutua váve), - o vao da espessua míma e da espessua máxma, - a tesão admssíve 60
72 Logo após voca a sub-ota df_pepoc e famete começa a execução do agotmo FAIPA (eazado o móduo fapa). Quado agum ctéo de paada do FAIPA fo atgdo, etoa-se ao móduo pcpa, o qua pode tema a execução do pogama Feametas Utzaam-se um cojuto de móduos de ABAQUS [5] que sevam paa a costução das tefaces, das mahas eguaes e paa o pós-pocessameto dos esutados. Os pogamas utzados foam: ABAQUS/CAE, ABAQUS/VIEWER e ABAQUS PYHON. ABAQUS/CAE ( Compete ABAQUS Evomet ) costutu o ambete gáfco de tegação dos móduos de ABAQUS. Neste ambete se defe a geometa da estutua, o matea utzado, os caegametos e apoos, a maha e tpo de eemetos ftos. Defe-se também que tpo de aáse deseja eaza. Pode seecoa as espostas estutuas a seem obtdas em cada aáse. oda esta fomação pode guada-se em uma base de dados de extesão CAE. Esta base de dados pode se abeta com ABAQUS/CAE paa posteoes modfcações. Po útmo, pode-se eaza uma aáse estutua atavés da cação de um job. A execução do job juto ao ABAQUS/CAE tem dos efetos mpotates: a pmea é a cação de um aquvo de extesão INP (de put ), a seguda é a execução do móduo de aáse ABAQUS/Stadad o qua toma o aquvo INP como etada e etoa outo aquvo de extesão ODB ( output database ) como saída. O aquvo INP é um aquvo de texto podedo se modfcado com quaque edto, poém devem-se espeta egas paa que este aquvo seja pocessado adequadamete po ABAQUS/Stadad. O aquvo ODB é uma base de dados que cotém as espostas estutuas soctadas e podem se vsuazadas atavés do móduo ABAQUS/VIEWER ou atavés de scpts de ABAQUS PYHON. O ABAQUS/VIEWER é o móduo de vsuazação de ABAQUS. Pemte vsuaza gafcamete um aquvo ODB geado atavés de agum móduo de aáse do ABAQUS. O ABAQUS PYHON é uma extesão da guagem de pogamação Pytho tegada ao ambete do ABAQUS que pemte acessa e modfca as bases de dados 6
73 CAE e ODB. No pesete tabaho se utzou ABAQUS PYHON paa a cação de aquvos INP e paa acessa aos esutados das aáses guadados os aquvos ODB Pogamas Apeseta-se a tabea segute a sta de pogamas eazados com suas espectvas compoetes: fapa df Iteface pog_aáse Pog_ fapa_pmadua_gadg df_deta t_abq ABAQUS Pog_2 fapa_pmadua_gadg df_adjuta t_abq ABAQUS Pog_3 fapa_dua df_adjuta_2 t_abq ABAQUS Pog_4 fapa_pmadua_gadg df_deta t_d DLEARN Pog_5 fapa_pmadua_gadg df_adjuta t_d DLEARN Pog_6 fapa_dua df_adjuta_2 t_d DLEARN abea 6.: pogamas eazados 6.3 Impemetação com ABAQUS Itodução Nesta seção expca-se como se mpemeta o móduo t_abq. A pesete mpemetação tem gades pobemas de efcêca dado que eaza mutas opeações de etua e esctua em dsco. ambém se eque uma covesão de fomato báo a texto que é excessvamete custosa Sub-otas do móduo t_abq Apesetam-se as pcpas sub-otas deste móduo com o tuto de usta como se efetua a comucação com o pogama ABAQUS. a comucação se estabeece atavés de jobs que são executados peo móduo de aáse ABAQUS/Stadad. Um job, paa os efetos deste tabaho, pode sgfca uma aáse estutua (com um ou váos estados de caegameto) ou a soctação da 62
74 matz de gdez de detemado eemeto, segudo o aquvo INP. O texto de um aquvo INP deve espeta uma gamátca específca paa que o job ão fahe. Estes jobs são vocados desde o códgo fota atavés de chamadas systemqq( abaqus job=<job_> put=<ome_.p> teatve ). O efeto dsto é a execução do job de ome job_ com etada ome_.p. Os esutados do job podem se depostados o aquvo báo job_.odb ou o aquvo de texto job_.dat. Isto depedeá das stuções coocadas o aquvo INP. Descção da sub-ota teface_k(k): Esta sub-ota executa um job soctado ao ABAQUS/Stadad que esceva o aquvo de texto mat_k.dat a matz de gdez de um eemeto. Paa sto, um aquvo de etada INP mat_k.p deve se costuído. O aquvo INP deve cote stuções que soctam a matz de gdez do eemeto. Etada: ão possu paâmetos de etada. Saída: k, matz de gdez do eemeto. Pocecmeto:. Executa: abaqus job=mat_k put=mat_k.p teactve 2. Le o esutado do aquvo mat_k.dat e amazea a matz k. Descção da sub-ota teface_u(x,p,u): Pmeo se costó um aquvo de etada INP u.p ode se especfcam as espessuas de cada eemeto (dadas po x) e um estado de caga paa cada coua da matz p. Depos se executa um job soctado ao ABAQUS/Stadad que esceva em u.odb os desocametos assocados a todos os estados de caga. Após a execução deste job, um scpt Pytho acessa ao aquvo u.odb e exta os desocametos, guadado-os em um aquvo de texto u.txt. Po útmo este aquvo de texto é do e amazeado o veto de saída u. Etada: x, veto com espessuas dos eemetos. p, matz com foças odas. Saída: u, matz de desocametos odas. Pocedmeto:. Costu o aquvo u.p atavés da execução dos scpts wtex.py e wtep.py. 2. Executa: abaqus job=u put=u.p teactve 63
75 3. Le o esutado o aquvo u.odb atavés do scpt eadu.py e escevê-os o aquvo u.txt (covesão de fomato odb txt) 4. Le o aquvo u.txt e amazea a matz u Scpts Pytho Os segutes scpts Pytho foam ecessáos paa a mpemetação desta teface: wtex.py: ê de um aquvo de texto o veto de espessuas x e esceve em um aquvo INP as stuções o fomato ABAQUS. wtep.py: ê de um aquvo de texto o veto de foças p e esceve em um aquvo INP as stuções o fomato ABAQUS. eadu.py: acessa a base de dados ODB extado os desocametos odas, a cotuação gava em um aquvo de texto tas desocametos (covesão de fomato odb txt). 6.4 Impemetação com DLEARN 6.4. Itodução Nesta seção mosta-se como se mpemeta o móduo t_d. A vesão oga de DLEARN fucoa da segute maea: pmeo o usuáo esceve em um aquvo de texto a fomação de etada paa a aáse (maha de eemetos ftos, tpo de aáse, popedades do matea, espessua dos eemetos, foças odas etc.). Em seguda executa o pogama DLEARN que ê o aquvo de etada, eaza uma aáse e etoa os esutados em outo aquvo de texto. DLEARN tem dos modos de execução: vefcação dos dados de etada (datacheck) e execução de uma aáse (executo) [2]. O modo de execução se defe coocado um úmeo em detemada posção do aquvo de etada. Deto do pogama este úmeo é guadado a vaáve exec. Quado exec=0, o pogama efetua a vefcação dos dados de etada e tema a execução. Se exec= o pogama efetua uma aáse. 64
76 Paa utza o pogama DLEARN fzeam-se as segutes modfcações: ) Itoduzam-se dos ovos modos de execução (exec=2 e 3). Se exec=2 etoa a matz de gdez de um eemeto, e quado exec=3 eaza a fatoação da matz de gdez e amazea os fatoes paa seem usados posteomete. 2) Defe-se uma sub-ota aase() que etoa os desocametos odas e a matz de gdez do eemeto sem ecessdade de etua de aquvos o dsco. 3) Paa esoução do sstema ea (6.) substtuu-se o sove utzado peo DLEARN pea ota MA Sub-otas do móduo t_d Descção da sub-ota aase(aq, dm, vec): Reaza os modos de execução,2 ou 3, depededo da cofguação de etada especfcada o aquvo aq. Se exec=, etoa em vec os desocametos odas. Se exec=2, etoa em vec os compoetes da matz de gdez. Se exec=3, eaza uma fatoação da matz de gdez. Etada: aq, ome do aquvo de etada. dm, úmeo teo. Saída: vec, vecto de dmesão dm. Ates de voca esta sub-ota, deve-se esceve o aquvo aq o modo de execução. Se ta modo fo exec=, escevem-se os caegametos odas (evetuamete váos estados de caga). Se exec=2, escevem-se as espessuas utáas. Caso cotáo, se fo exec=3, escevem-se as espessuas dos eemetos. Descção da sub-ota teface_k(k): Etada: ão possu paâmetos de etada. Saída: k, compoetes da matz de gdez do eemeto. Pocedmeto:. Esceve o aquvo de etada mat_k.txt o modo de execução Esceve em mat_k.txt as espessuas utáas 3. Reaza a chamada à sub-ota aase( mat_k.txt,dm,k) 65
77 Descção da sub-ota teface_facto(x): Etada: x, espessuas dos eemetos. Saída: Não possu paâmetos de saída. Pocecmeto:. Esceve o aquvo de etada facto.txt o modo de execução Esceve em facto.txt as espessuas x. 3. Reaza a chamada à sub-ota aase( facto.txt,dm,foo). Descção da sub-ota teface_u(p,u): Etada: p, matz com foças odas. Saída: u, matz de desocametos odas. Pocedmeto:. Esceve o aquvo de etada u.txt o modo de execução. 2. Esceve em u.txt as foças odas. 3. Reaza a chamada à sub-ota aase( u.txt,dm,u) Rota MA27 (HSL) Em [6] apeseta-se um cojuto de otas esctas em guagem Fota paa computação cetífca de gade pote. MA27 faz pate de esta coeção e esove sstemas de equações eaes smétcos espasos. MA27 fo utzada paa esove o sstema (6.) emboa seja bastate efcete em compaação com as téccas cásscas paa esove sstemas eaes obtdos peo Método dos Eemetos Ftos. 66
78 CAPÍULO 7 Resutados Numécos 7. Itodução No pesete capítuo, apesetam-se tês exempos umécos do pobema de mímo voume de estutuas paas sujeto a estções de tesões de Vo Mses. Paa cada exempo são apcadas tês dscetzações dfeetes. O paâmeto epeseta o úmeo de eemetos (vaáves de pojeto) e são cosdeados os segutes vaoes: = 300, 200, Em todos os casos se utzam eemetos quadáteos beaes sopaamétcos e as aáses estutuas foam fetas com o pogama DLEARN [2]. Assume-se um móduo de Youg E = 20 GPa e um coefcete de Posso v = 0. 3 paa todos os eemetos. A espessua pode toma vaoes ete 0.cm e.0cm, exceto o exempo 3, ode a espessua míma é de 0.0cm. A tesão de Vo Mses é computada o ceto do eemeto e deve se meo que 250 MPa. Apca-se um estado de caegameto e ão se eaza ftagem de estções. As souções paa = 300 e = 200 foam obtdas com a fomuação descta o capítuo 5, seção 5.2. Resovem-se os sstemas pma-dua do FDIPA atavés de métodos detos, eaza-se a atuazação BFGS da matz quase-newto e cacua-se o gadete das estções peo método de dfeecação adjuta. Utzou-se o pogama Pog_5, de acodo a tabea 6. do capítuo 6. Paa = 6075 se empega a ova metodooga (capítuo 5). Utzam-se q = 0 paes da técca memóa mtada paa epeseta a vesa da matz quase-newto. No etato, paa epeseta a vesa da matz dua empega-se q = 8 paes. Os sstemas duas do FDIPA se esovem peo Método do Gadete Cojugado pé- 67 A B
79 codcoado. O ctéos de paada do MGC foam: 9 max Ax b 0 e b max 6 Ax b 0 sedo b Ax = o sstema ea a se esovdo. Utza-se a fomuação do poduto da matz de sesbdade (e sua tasposta) po veto, emado-se o espaço de memóa equedo paa sua aocação. Utzou-se o pogama Pog_6, de acodo a tabea 6. do capítuo 6. Em todos os pobemas com = 6075, a soma de teações do Método do Gadete Cojugado do pmeo e +2 segudo sstema do FDIPA ( ) vefcou o ctéo de efcêca (5.23). O pocesso de otmzação é fazado quado a oma de d 0 fo meo que 0-5. Este seá o ctéo de paada utzado peo agotmo. Os pogamas foam executados um computado com as segutes caacteístcas pcpas: Pocessado: AMD Atho de 64 bts e.8 GHz Memóa: 2GB Os esutados estão ogazados da segute foma: Cada exempo está uma seção sepaada. Os dados dos pobemas (dmesões, apoos e caegametos) são dcados as fguas 7., 7.5 e 7.9. As souções ótmas se apesetam as fguas 7.2, 7.6 e 7.0 ustado cada uma das dscetzações empegadas. A evoução da edução do voume feta peo agotmo está dcada as fguas 7.3, 7.7 e 7.. As fguas 7.4, 7.8 e 7.2 cotêm o mapa de tesões de Vo Mses (cacuadas o cetóde de cada eemeto) paa as souções ótmas com a mao dscetzação. Estes gáfcos foam obtdos com o móduo vewe de ABAQUS. 68
80 7.2 Exempo.2 m 0.6 m 8000 N/cm m 0.6 m 0.2 m.4 m 0.2 m 0.6 m Fgua 7.: Dados do exempo. = 300 = 200 = 6075 Espessua (cm) Fgua 7.2: Desehos ótmos. 69
81 Fgua 7.3: Redução do voume po teação do agotmo. Fgua 7.4: esão de Mses paa o deseho ótmo ( = 6075 ). 70
82 O FAIPA, camete eque um poto deto da egão váve. No pesete exempo, paa = 300, 200, 6075 foam escohdas estutuas váves ode todas as espessuas dos eemetos são guas a 0.8cm, 0.9cm e.0cm espectvamete. O motvo peo qua se empegaam dfeetes espessuas cas fo po que exstem egões ode a tesão é fta e a medda que a áea do eemeto é meo a tesão é meho epesetada ecesstado-se de uma espessua mao paa que a estutua ca seja váve. Na tabea segute apesetam-se os voumes cas e fas paa cada dscetzação: Voume ca (cm 3 ) Voume Fa (cm 3 ) abea 7.: Voume ca e fa paa dfeetes dscetzações (exempo ). ato paa = 300 como paa = 200 o ctéo de paada fo vefcado. Paa o caso = 6075 a execução fo teompda mauamete. 7
83 7.3 Exempo 2 m 8000 N/cm.2 m 0.6 m.2 m Fgua 7.5: Dados do exempo 2. = 300 = 200 = 6075 Espessua (cm) Fgua 7.6: Desehos ótmos. 72
84 Fgua 7.7: Redução do voume po teação do agotmo. Neste exempo todos os potos cas paa = 300, 200, 6075 possuem o mesmo voume (24000 cm 3 ). As espessuas cas dos eemetos são 0.8cm. Na tabea segute apesetam-se os voumes fas: Voume Fa (cm 3 ) abea 7.2: Voume da estutua ótma (exempo 2). ato paa = 300 como paa = 200 o ctéo de paada fo vefcado. Paa o caso = 6075 a execução fo teompda mauamete. Fgua 7.8: esão de Mses paa o deseho ótmo ( N = 6075 ). 73
85 7.4 Exempo 3 m 8000 N/cm 0.4 m 0.9 m 0.4 m 0.9 m 0.4 m Fgua 7.9 Dados do exempo 3. = 300 = 200 = 6075 Espessua (cm) Fgua 7.0: Desehos ótmos. 74
86 Fgua 7.: Redução do voume po teação do agotmo. Idetcamete ao Exempo 2, os potos cas paa = 300,200, 6075 possuem o mesmo voume (24000 cm 3 ). Neste exempo, optou-se po uma espessua míma de 0.0cm. ato paa = 200 como paa = 6075 a execução fo teompda mauamete. Paa = 300 o ctéo de paada fo vefcado. Na tabea segute apesetam-se os voumes fas: Voume Fa (cm 3 ) abea 7.3: Voume da estutua ótma (exempo 3). Fgua 7.2: esão de Mses paa o deseho ótmo ( = 6075 ). 75
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Sobre a classe de diferenciabilidade de quocientes de polinômios homogêneos.
 Uvesdade Regoal do Ca - URCA CADERNO DE CULTURA E CIÊNCIA VOLUME Nº - 008 IN 980-586 obe a classe de dfeecabldade de quocetes de polômos homogêeos About the Dffeetablty Class of the Quotet of Homogeeous
Uvesdade Regoal do Ca - URCA CADERNO DE CULTURA E CIÊNCIA VOLUME Nº - 008 IN 980-586 obe a classe de dfeecabldade de quocetes de polômos homogêeos About the Dffeetablty Class of the Quotet of Homogeeous
Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1
 Dscpla: FGE5748 Smulação Computacoal de Líqudos Moleculaes Exstem pocedmetos paa toa os pogamas mas efcetes, depedetemete, de seem DM ou MC. Como: Cálculo da teação Múltplos passos Coeções de logo alcace
Dscpla: FGE5748 Smulação Computacoal de Líqudos Moleculaes Exstem pocedmetos paa toa os pogamas mas efcetes, depedetemete, de seem DM ou MC. Como: Cálculo da teação Múltplos passos Coeções de logo alcace
4/10/2015. Física Geral III
 Físca Geal III Aula Teóca 8 (Cap. 6 pate /3: Potecal cado po: Uma caga putome Gupo de cagas putomes 3 Dpolo elétco Dstbução cotíua de cagas Po. Maco. Loos mos ue uma caga putome gea um campo elétco dado
Físca Geal III Aula Teóca 8 (Cap. 6 pate /3: Potecal cado po: Uma caga putome Gupo de cagas putomes 3 Dpolo elétco Dstbução cotíua de cagas Po. Maco. Loos mos ue uma caga putome gea um campo elétco dado
Aluno(a): Professor: Chiquinho
 Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Vimos que: 1) Interação coulombiana residual para os elétrons efeito perturbativo
 Vmos que: Iteação couombaa esdua paa os eétos efeto petubatvo V ee No caso de eétos em uma subcamada, o sp tota pode se S0 sgeto ou S tpeto Um sstema costtuído de váos e - deve se descto po uma autofução
Vmos que: Iteação couombaa esdua paa os eétos efeto petubatvo V ee No caso de eétos em uma subcamada, o sp tota pode se S0 sgeto ou S tpeto Um sstema costtuído de váos e - deve se descto po uma autofução
Departamento de Física - ICE/UFJF Laboratório de Física II
 Depatameto de ísica - ICE/UJ Laboatóio de ísica II - Itodução Pática : Medida da Aceeação Gavitacioa A iteação avitacioa é uma das quato iteações fudametais que se ecotam a atueza e é a úica que afeta
Depatameto de ísica - ICE/UJ Laboatóio de ísica II - Itodução Pática : Medida da Aceeação Gavitacioa A iteação avitacioa é uma das quato iteações fudametais que se ecotam a atueza e é a úica que afeta
3 O Método de Partículas MPS
 O Método de Patículas MPS 9 3 O Método de Patículas MPS O método MPS fo apesetado calmete po Koshzuka e Oka (1996). Este método, de atueza Lagageaa, fo deseoldo paa esole escoametos de fludos compessíes
O Método de Patículas MPS 9 3 O Método de Patículas MPS O método MPS fo apesetado calmete po Koshzuka e Oka (1996). Este método, de atueza Lagageaa, fo deseoldo paa esole escoametos de fludos compessíes
A análise de variância de uma classificação (One-Way ANOVA) verifica se as médias de k amostras independentes (tratamentos) diferem entre si.
 Prof. Lorí Va, Dr. http://www. ufrgs.br/~va/ va@mat.ufrgs.br aáse de varâca de uma cassfcação (Oe-Way NOV) verfca se as médas de amostras depedetes (tratametos) dferem etre s. Um segudo tpo de aáse de
Prof. Lorí Va, Dr. http://www. ufrgs.br/~va/ va@mat.ufrgs.br aáse de varâca de uma cassfcação (Oe-Way NOV) verfca se as médas de amostras depedetes (tratametos) dferem etre s. Um segudo tpo de aáse de
RESOLUÇÃO SIMULADO ITA FÍSICA E REDAÇÃO - CICLO 7 FÍSICA GM G M GM GM. T g
 RESOLUÇÃO SIMULADO ITA FÍSICA E REDAÇÃO - CICLO 7 FÍSICA Questão M a) A desdade é a azão ete a massa e o volume: d. V Se as desdades fossem guas: MP MT MT MT dp dt. V 4 4 P VT RT R T GM b) A gavdade a
RESOLUÇÃO SIMULADO ITA FÍSICA E REDAÇÃO - CICLO 7 FÍSICA Questão M a) A desdade é a azão ete a massa e o volume: d. V Se as desdades fossem guas: MP MT MT MT dp dt. V 4 4 P VT RT R T GM b) A gavdade a
MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R 3
 MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R Modelg of ceteg eos o the o the thee-dmesoal space (R ). JAIR MENDES MARQUES Uvesdade Tuut do Paaá Rua Macelo Champagat,55 CEP 87-5 Cutba PR ja.maques@utp.b
MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R Modelg of ceteg eos o the o the thee-dmesoal space (R ). JAIR MENDES MARQUES Uvesdade Tuut do Paaá Rua Macelo Champagat,55 CEP 87-5 Cutba PR ja.maques@utp.b
A Base Termodinâmica da Pressão Osmótica
 59087 Bofísca II FFCLRP P Pof. Atôo Roque Aula 7 A Base emodâmca da Pessão Osmótca Elemetos de emodâmca As les báscas da temodâmca dzem espeto à covesão de eega de uma foma em outa e à tasfeêca de eega
59087 Bofísca II FFCLRP P Pof. Atôo Roque Aula 7 A Base emodâmca da Pessão Osmótca Elemetos de emodâmca As les báscas da temodâmca dzem espeto à covesão de eega de uma foma em outa e à tasfeêca de eega
APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO. Djalma M. Falcão COPPE/UFRJ
 GPL/026 2 a 26 de Outubo de 200 Campas - São Paulo - Basl GRUPO VII PLANEJAMENTO DE SISTEMAS ELÉTRICOS APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO Yu S.B. Wllmesdof
GPL/026 2 a 26 de Outubo de 200 Campas - São Paulo - Basl GRUPO VII PLANEJAMENTO DE SISTEMAS ELÉTRICOS APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO Yu S.B. Wllmesdof
CIV 2552 Mét. Num. Prob. de Fluxo e Transporte em Meios Porosos. Método dos Elementos Finitos Fluxo 2D em regime transiente em reservatório
 CIV 55 Mét. um. ob. de luo e aote em Meo ooo Método do Elemeto to luo D em egme taete em eevatóo Codçõe ca e aâmeto etete: eão cal: Ma emeabldade tíeca: -5 md m md ml-dac Vcodade dâmca: - µ Ma oe Comebldade
CIV 55 Mét. um. ob. de luo e aote em Meo ooo Método do Elemeto to luo D em egme taete em eevatóo Codçõe ca e aâmeto etete: eão cal: Ma emeabldade tíeca: -5 md m md ml-dac Vcodade dâmca: - µ Ma oe Comebldade
Diferenciais Ordinárias. Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais
 Exstêca e Ucdade de Soluções de Equações Dferecas Ordáras Regaldo J Satos Departameto de Matemátca-ICEx Uversdade Federal de Mas Geras http://wwwmatufmgbr/ reg 10 de ulho de 2010 2 1 INTRODUÇÃO Sumáro
Exstêca e Ucdade de Soluções de Equações Dferecas Ordáras Regaldo J Satos Departameto de Matemátca-ICEx Uversdade Federal de Mas Geras http://wwwmatufmgbr/ reg 10 de ulho de 2010 2 1 INTRODUÇÃO Sumáro
DETERMINAÇÃO DE ATITUDE DE SATÉLITES ARTIFICIAIS COM FILTRO DE KALMAN E MÉTODO DA MÁXIMA VEROSSIMILHANÇA
 INPE-5-PRE/88 DEERMINÇÃO DE IDE DE SÉIES RIFICIIS COM FIRO DE MN E MÉODO D MÁXIM EROSSIMIHNÇ Julaa Guastal haes* *Bolssta FEG/NESP Relatóo Fal de Pojeto de Icação Cetífca PIBIC/CNP/INPE, oetado pelo D.
INPE-5-PRE/88 DEERMINÇÃO DE IDE DE SÉIES RIFICIIS COM FIRO DE MN E MÉODO D MÁXIM EROSSIMIHNÇ Julaa Guastal haes* *Bolssta FEG/NESP Relatóo Fal de Pojeto de Icação Cetífca PIBIC/CNP/INPE, oetado pelo D.
5 Aplicação do GFMM no BEM
 38 5 Apação do GFMM o BEM esse apítuo os desevovmetos apresetados o apítuo 4 são apados ao BEM pea expasão das souções fudametas utzadas as tegrações sobre os segmetos do otoro. É apresetada a formuação
38 5 Apação do GFMM o BEM esse apítuo os desevovmetos apresetados o apítuo 4 são apados ao BEM pea expasão das souções fudametas utzadas as tegrações sobre os segmetos do otoro. É apresetada a formuação
Introdução. Introdução. Introdução Objetivos. Introdução Corpo rígido. Introdução Notação
 Intodução Intodução à obótca Descção espacal e ansfomações (/2) of. Douglas G. Machaet douglas.machaet@dcc.ufmg.b Intodução à obótca - Descção espacal e ansfomações (/2) 2 Intodução osções e Oentações
Intodução Intodução à obótca Descção espacal e ansfomações (/2) of. Douglas G. Machaet douglas.machaet@dcc.ufmg.b Intodução à obótca - Descção espacal e ansfomações (/2) 2 Intodução osções e Oentações
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
2 o CONGRESSO BRASILEIRO DE P&D EM PETRÓLEO & GÁS
 o CONGRESSO BRASILEIRO DE &D EM ETRÓLEO & GÁS ANÁLISE DESCRITIVA DE DADOS DE VENTOS VISANDO ALICAÇÕES EM LATAFORMAS G. M. G. Leal, F. A. M. Souza UFCG/CCT/DME/) Av. Apígo Veloso, 88 Bodocogó, 5809-970
o CONGRESSO BRASILEIRO DE &D EM ETRÓLEO & GÁS ANÁLISE DESCRITIVA DE DADOS DE VENTOS VISANDO ALICAÇÕES EM LATAFORMAS G. M. G. Leal, F. A. M. Souza UFCG/CCT/DME/) Av. Apígo Veloso, 88 Bodocogó, 5809-970
MAE0229 Introdução à Probabilidade e Estatística II
 Exercíco Cosdere a dstrbução expoecal com fução de desdade de probabldade dada por f (y; λ) = λe λy, em que y, λ > 0 e E(Y) = /λ Supor que o parâmetro λ pode ser expresso proporcoalmete aos valores de
Exercíco Cosdere a dstrbução expoecal com fução de desdade de probabldade dada por f (y; λ) = λe λy, em que y, λ > 0 e E(Y) = /λ Supor que o parâmetro λ pode ser expresso proporcoalmete aos valores de
Ajuste de curvas por quadrados mínimos lineares
 juste de cuvs o quddos mímos lees Fele eodo de gu e Wdele Iocêco oe Júo Egeh de s o. Peíodo Pofesso: ode Josué Bezue Dscl: Geomet lítc e Álgeb e. Itodução Utlzmos este método qudo temos um dstbução de
juste de cuvs o quddos mímos lees Fele eodo de gu e Wdele Iocêco oe Júo Egeh de s o. Peíodo Pofesso: ode Josué Bezue Dscl: Geomet lítc e Álgeb e. Itodução Utlzmos este método qudo temos um dstbução de
Capítulo 2 Galvanômetros
 Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
MATEMÁTICA II - Engenharias/Itatiba SISTEMAS LINEARES
 - Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
- Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
Resoluções dos exercícios propostos
 os fudametos da físa Udade E Capítulo efação lumosa esoluções dos eeíos popostos P.85 Como, temos: 8 0 0 8,5 P.86 De, em: 0 8,5 0 8 m/s P.87 elodade da luz a plaa de do oespode a 75% da elodade da luz
os fudametos da físa Udade E Capítulo efação lumosa esoluções dos eeíos popostos P.85 Como, temos: 8 0 0 8,5 P.86 De, em: 0 8,5 0 8 m/s P.87 elodade da luz a plaa de do oespode a 75% da elodade da luz
Aerodinâmica I. Asas Finitas Teoria da Linha Sustentadora Método de Glauert
 ( y Método de Gauert ( y ( y V c( y β 4 V d y y dy ( y dy Método de resoução da equação tegro-dfereca da ha sustetadora através da sua trasformação um sstema de equações agérco - Asas smétrcas, sem dedro
( y Método de Gauert ( y ( y V c( y β 4 V d y y dy ( y dy Método de resoução da equação tegro-dfereca da ha sustetadora através da sua trasformação um sstema de equações agérco - Asas smétrcas, sem dedro
2*5$',(17('2327(1&,$/( (1(5*,$12&$032(/(75267È7,&2
 3 *5',7'37&,/ 5*,&3/7567È7,& ÃÃÃ*5',7Ã'Ã37&,/ A expessão geéica paa o cálculo da difeeça de potecial como uma itegal de liha é: dl ) 5) Se o camiho escolhido fo um L, tal que se possa cosidea costate esse
3 *5',7'37&,/ 5*,&3/7567È7,& ÃÃÃ*5',7Ã'Ã37&,/ A expessão geéica paa o cálculo da difeeça de potecial como uma itegal de liha é: dl ) 5) Se o camiho escolhido fo um L, tal que se possa cosidea costate esse
Física Geral I - F Aula 13 Conservação do Momento Angular e Rolamento. 2 0 semestre, 2010
 Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
RELACIONAMENTO ENTRE REFERENCIAIS LOCAIS E REFERENCIAIS GLOBAIS: PROBLEMA PROCRUSTES SIMPLES
 ELACIONAMENTO ENTE EEENCIAIS LOCAIS E EEENCIAIS GLOBAIS: POBLEMA POCUSTES SIMPLES Maa Apaecda ehpfeg aett Sílvo ogéo Coea de etas Luís Augusto Koeg Vega 3 Uvesdade edeal do Paaá UP - Cuso de Pós Gaduação
ELACIONAMENTO ENTE EEENCIAIS LOCAIS E EEENCIAIS GLOBAIS: POBLEMA POCUSTES SIMPLES Maa Apaecda ehpfeg aett Sílvo ogéo Coea de etas Luís Augusto Koeg Vega 3 Uvesdade edeal do Paaá UP - Cuso de Pós Gaduação
4/10/2015. Física Geral III
 Físca Geal III Aula Teóca 9 (Cap. 6 pate 3/3): ) Cálculo do campo a pat do potencal. ) Enega potencal elétca de um sstema de cagas. 3) Um conduto solado. Po. Maco R. Loos Cálculo do campo a pat do potencal
Físca Geal III Aula Teóca 9 (Cap. 6 pate 3/3): ) Cálculo do campo a pat do potencal. ) Enega potencal elétca de um sstema de cagas. 3) Um conduto solado. Po. Maco R. Loos Cálculo do campo a pat do potencal
UMA FORMA SIMPLIFICADA DE DEDUZIR AS EQUAÇÕES DE HARTREE E HARTREE-FOCK
 Qum. Nova, Vol. 8, No. 7, 995-00, 05 http://dx.do.og/0.595/000-404.05008 UMA FORMA SIMPLIFICADA D DDUZIR AS QUAÇÕS D HARTR HARTR-FOC Rogéo Custodo Isttuto de Químca, Uvesdade stadual de Campas, Baão Gealdo,
Qum. Nova, Vol. 8, No. 7, 995-00, 05 http://dx.do.og/0.595/000-404.05008 UMA FORMA SIMPLIFICADA D DDUZIR AS QUAÇÕS D HARTR HARTR-FOC Rogéo Custodo Isttuto de Químca, Uvesdade stadual de Campas, Baão Gealdo,
Os fundamentos da física Volume 2 1. Resumo do capítulo
 Os fudametos da físca Volume 2 1 Capítulo 13 Refação lumosa A efação é o feômeo o qual a luz muda de meo de popagação, com mudaça em sua velocdade. ÍDICE DE REFRAÇÃO ABSOLUTO O ídce de efação absoluto
Os fudametos da físca Volume 2 1 Capítulo 13 Refação lumosa A efação é o feômeo o qual a luz muda de meo de popagação, com mudaça em sua velocdade. ÍDICE DE REFRAÇÃO ABSOLUTO O ídce de efação absoluto
Apêndice I Resultados do Capítulo 2
 Aêndce I Resutados do Caítuo I Aêndce I Resutados do Caítuo Demonstação dos esutados dos modeos de De Acca et a e do modeo de See estenddo AI Modeo de De Acca et a A equação do modeo exessa o sead aa um
Aêndce I Resutados do Caítuo I Aêndce I Resutados do Caítuo Demonstação dos esutados dos modeos de De Acca et a e do modeo de See estenddo AI Modeo de De Acca et a A equação do modeo exessa o sead aa um
ANÁLISE DE MÉTODOS PARA O CÁLCULO DE GRADIENTE EM MALHAS NÃO-ESTRUTURADAS
 AÁISE DE MÉTODOS ARA O CÁCUO DE GRADIETE EM MAHAS ÃO-ESTRUTURADAS lae Tad Schueck ll_schueck@bolcomb João Flávo de Vea Vascocelos flavo@pueb EMA aboatóo de Epemetação e Smulação uméca em Tasfeêca de Calo
AÁISE DE MÉTODOS ARA O CÁCUO DE GRADIETE EM MAHAS ÃO-ESTRUTURADAS lae Tad Schueck ll_schueck@bolcomb João Flávo de Vea Vascocelos flavo@pueb EMA aboatóo de Epemetação e Smulação uméca em Tasfeêca de Calo
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
 SL LIÉNI UNISI SÃ UL venda ofesso eo oaes, nº 3. cep 558-9, São auo, S. eefone: (xx) 39 5337 ax: (xx) 383 886 epatamento de ngenhaa ecânca QUSÃ (3, pontos). paca não pana, de peso despezíve, é constuída
SL LIÉNI UNISI SÃ UL venda ofesso eo oaes, nº 3. cep 558-9, São auo, S. eefone: (xx) 39 5337 ax: (xx) 383 886 epatamento de ngenhaa ecânca QUSÃ (3, pontos). paca não pana, de peso despezíve, é constuída
ANÁLISE DAS RELAÇÕES INTERSETORIAIS NA ECONOMIA MINEIRA
 ANÁLISE DAS RELAÇÕES INTERSETORIAIS NA ECONOMIA MINEIRA Ale Csta da Cuz Ely Cadoso Texea 2 Vva Slva Lo 3 RESUMO Nesta pesqusa detfcam-se setoes-chave paa vestmetos a estutua podutva de Mas Geas utlzado
ANÁLISE DAS RELAÇÕES INTERSETORIAIS NA ECONOMIA MINEIRA Ale Csta da Cuz Ely Cadoso Texea 2 Vva Slva Lo 3 RESUMO Nesta pesqusa detfcam-se setoes-chave paa vestmetos a estutua podutva de Mas Geas utlzado
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
3.1 Campo da Gravidade Normal Terra Normal
 . Campo da avidade Nomal.. Tea Nomal tedeemos po Tea omal um elipsóide de evolução qual se atibui a mesma massa M e a mesma velocidade agula da Tea eal e tal que o esfeopotecial U seja uma fução costate
. Campo da avidade Nomal.. Tea Nomal tedeemos po Tea omal um elipsóide de evolução qual se atibui a mesma massa M e a mesma velocidade agula da Tea eal e tal que o esfeopotecial U seja uma fução costate
Física I. Aula 9 Rotação, momento inércia e torque
 Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC
 4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
15. Efeito de Alavanca
 Lgações Apaafusadas Pate I Pogama de Pós-Gaduação em Egehaa Cvl PGECI - Mestado Acadêmco Faculdade de Egehaa FEN/UERJ Dscpla: Lgações em Estutuas de Aço e Mstas Pofesso: Lucao Rodgues Oelas de Lma 5. Efeto
Lgações Apaafusadas Pate I Pogama de Pós-Gaduação em Egehaa Cvl PGECI - Mestado Acadêmco Faculdade de Egehaa FEN/UERJ Dscpla: Lgações em Estutuas de Aço e Mstas Pofesso: Lucao Rodgues Oelas de Lma 5. Efeto
Elétrons em um potencial periódico: o teorema de Bloch. Cap 7 KITTEL Cap 8 ASHCROFT- MERMIN Cap 5 IVAN
 Elétos em um poteal peódo: o teoema de Bloh Cap 7 ITTEL Cap 8 ASHCOFT- MEMIN Cap 5 IVAN Modelo de Dude: gás s lásso de elétos Até agoa 1 mv 3 B T Modelo de Sommefeld: gás s de elétos uâto h m ψ εψ ( )
Elétos em um poteal peódo: o teoema de Bloh Cap 7 ITTEL Cap 8 ASHCOFT- MEMIN Cap 5 IVAN Modelo de Dude: gás s lásso de elétos Até agoa 1 mv 3 B T Modelo de Sommefeld: gás s de elétos uâto h m ψ εψ ( )
CADERNO 1 (É permitido o uso de calculadora gráfica.)
 Proposta de teste de avalação [mao 09] Nome: Ao / Turma: N.º: Data: - - Não é permtdo o uso de corretor. Deves rscar aqulo que pretedes que ão seja classfcado. A prova clu um formuláro. As cotações dos
Proposta de teste de avalação [mao 09] Nome: Ao / Turma: N.º: Data: - - Não é permtdo o uso de corretor. Deves rscar aqulo que pretedes que ão seja classfcado. A prova clu um formuláro. As cotações dos
Econometria: 3 - Regressão Múltipla
 Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Ecoometra: 3 - Regressão Múltpla Prof. Marcelo C. Mederos mcm@eco.puc-ro.br Prof. Marco A.F.H. Cavalcat cavalcat@pea.gov.br Potfíca Uversdade Católca do Ro de Jaero PUC-Ro Sumáro O modelo de regressão
Curso de Análise Matricial de Estruturas 1 II.6 FORMULAÇÃO DAS MATRIZES DE FLEXIBILIDADE E RIGIDEZ EM TERMOS DE ENERGIA
 Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
PROPAGAÇÃO DE ONDAS ELECTROMAGNÉTICAS NUM GUIA CILÍNDRICO
 PROPAGAÇÃO D ONDAS LCTROMAGNÉTICAS NM GIA CILÍNDRICO po Calos Vaadas e Maia mília Maso IST, Maio de 5 t j e. Itodução Vamos estuda a popagação de odas electomagéticas um guia cilídico de aio a. Podeiamos
PROPAGAÇÃO D ONDAS LCTROMAGNÉTICAS NM GIA CILÍNDRICO po Calos Vaadas e Maia mília Maso IST, Maio de 5 t j e. Itodução Vamos estuda a popagação de odas electomagéticas um guia cilídico de aio a. Podeiamos
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Capítulo 6 Corpo Rígido, Estática e Elasticidade
 Capítulo 6 Copo Rígdo, Estátca e Elastcdade 6. Noção de Copo Rígdo Estudamos já os movmetos de copos cujas dmesões eam despezáves face às meddas das suas tajectóas ou po coveêca e smplfcação, tomados como
Capítulo 6 Copo Rígdo, Estátca e Elastcdade 6. Noção de Copo Rígdo Estudamos já os movmetos de copos cujas dmesões eam despezáves face às meddas das suas tajectóas ou po coveêca e smplfcação, tomados como
2 Formulação Matemática
 Fomlação Matemática. Descição do poblema A fim de aalisa o escoameto atavés de m meio pooso, foi cosideado m meio pooso ideal, com ma geometia composta po caais covegetesdivegetes. Dessa foma, obtém-se
Fomlação Matemática. Descição do poblema A fim de aalisa o escoameto atavés de m meio pooso, foi cosideado m meio pooso ideal, com ma geometia composta po caais covegetesdivegetes. Dessa foma, obtém-se
Prof. Anderson Coser Gaudio Departamento de Física Centro de Ciências Exatas Universidade Federal do Espírito Santo
 POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO. Departamento de Engenharia Mecânica
 SOL OLITÉNI UNIRSI SÃO ULO ed ofesso eo oes, º. -9, São uo, S. Teefoe: (xx) 9 7 x: (xx) 6 eptmeto de ge ecâc ÂNI me o 6 de setembo de ução d o: mutos (ão é pemtdo uso de ccudos) ª Questão (, potos): b
SOL OLITÉNI UNIRSI SÃO ULO ed ofesso eo oes, º. -9, São uo, S. Teefoe: (xx) 9 7 x: (xx) 6 eptmeto de ge ecâc ÂNI me o 6 de setembo de ução d o: mutos (ão é pemtdo uso de ccudos) ª Questão (, potos): b
Regressão Simples. Parte III: Coeficiente de determinação, regressão na origem e método de máxima verossimilhança
 Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
Regressão Smples Parte III: Coefcete de determação, regressão a orgem e método de máxma verossmlhaça Coefcete de determação Proporção da varabldade explcada pelo regressor. R Varação explcada Varação total
Teoria conjunta EP+ML
 A teoia de eementos de pá pate de um deteminado númeo de simpificações. A maio (e pio) é que a veocidade induzida é unifome. Na eaidade é não unifome Pode-se demonsta que uma veocidade induzida unifome
A teoia de eementos de pá pate de um deteminado númeo de simpificações. A maio (e pio) é que a veocidade induzida é unifome. Na eaidade é não unifome Pode-se demonsta que uma veocidade induzida unifome
ANIMAÇÃO DE FLUIDOS VIA TÉCNICAS DE VISUALIZAÇÃO CIENTÍFICA E MECÂNICA COMPUTACIONAL GILSON A. GIRALDI ANTONIO L. APOLINÁRIO JR.
 ANIMAÇÃO DE FLUIDOS VIA TÉCNICAS DE VISUALIZAÇÃO CIENTÍFICA E MECÂNICA COMPUTACIONAL GILSON A. GIRALDI ANTONIO L. APOLINÁRIO JR. ANTONIO A. F. OLIVEIRA RAUL A. FEIJÓO LABORATÓRIO NACIONAL DE COMPUTAÇÃO
ANIMAÇÃO DE FLUIDOS VIA TÉCNICAS DE VISUALIZAÇÃO CIENTÍFICA E MECÂNICA COMPUTACIONAL GILSON A. GIRALDI ANTONIO L. APOLINÁRIO JR. ANTONIO A. F. OLIVEIRA RAUL A. FEIJÓO LABORATÓRIO NACIONAL DE COMPUTAÇÃO
Resoluções dos exercícios propostos
 da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
Física Geral. Força e Torque
 ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
ALOCAÇÃO DE MEDIDORES DE QUALIDADE DE ENERGIA UTILIZANDO A P-MEDIANA
 LOCÇÃO DE MEDIDORES DE QULIDDE DE ENERGI UTILIZNDO P-MEDIN Lucmáo Gos de Olea Sla UFPE - DEP V. Pof. Moaes Rego, 1235, Cdade Uestáa, Recfe-PE luco_gos@hotmal.com lbéco tôo Pes da Sla Júo Celpe V. João
LOCÇÃO DE MEDIDORES DE QULIDDE DE ENERGI UTILIZNDO P-MEDIN Lucmáo Gos de Olea Sla UFPE - DEP V. Pof. Moaes Rego, 1235, Cdade Uestáa, Recfe-PE luco_gos@hotmal.com lbéco tôo Pes da Sla Júo Celpe V. João
1. Tensão Uma das repostas do MC ao carregamento. F r. forças internas. 1. Vector das tensões. sistema 3. sistema 2. sistema 1. sistema 2.
 1. Tesão Ua das eosas do MC ao caegaeo 1. Veco das esões foças eas ssea 1 ssea coe ssea 1 A F F - ssea 3 ssea 3 ssea B Cojuo( ssea 1 ssea ) esá e equlíbo Cojuo( ssea 1 ssea 3) esá e equlíbo Cojuo( ssea
1. Tesão Ua das eosas do MC ao caegaeo 1. Veco das esões foças eas ssea 1 ssea coe ssea 1 A F F - ssea 3 ssea 3 ssea B Cojuo( ssea 1 ssea ) esá e equlíbo Cojuo( ssea 1 ssea 3) esá e equlíbo Cojuo( ssea
1 - CORRELAÇÃO LINEAR SIMPLES rxy
 1 - CORRELAÇÃO LINEAR IMPLE Em pesquisas, feqüetemete, pocua-se veifica se existe elação ete duas ou mais vaiáveis, isto é, sabe se as alteações sofidas po uma das vaiáveis são acompahadas po alteações
1 - CORRELAÇÃO LINEAR IMPLE Em pesquisas, feqüetemete, pocua-se veifica se existe elação ete duas ou mais vaiáveis, isto é, sabe se as alteações sofidas po uma das vaiáveis são acompahadas po alteações
i CC gerador tg = P U = U.i o i i r.i 0 i CC i i i
 GEDO ELÉTIO "Levao-se em cota a esstêca tea o geao, pecebemos que a p ete os temas é meo o que a foça eletomotz (fem), evo à pea e p a esstêca tea." - + = -. OENTE DE TO-IITO Se lgamos os os temas e um
GEDO ELÉTIO "Levao-se em cota a esstêca tea o geao, pecebemos que a p ete os temas é meo o que a foça eletomotz (fem), evo à pea e p a esstêca tea." - + = -. OENTE DE TO-IITO Se lgamos os os temas e um
Números Complexos. 2. (IME) Seja z um número complexo de módulo unitário que satisfaz a condição z 2n 1, onde n é um número inteiro positivo.
 Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Números Complexos. (IME) Cosdere os úmeros complexos Z se α cos α e Z cos α se α ode α é um úmero real. Mostre que se Z Z Z etão R e (Z) e I m (Z) ode R e (Z) e I m (Z) dcam respectvamete as partes real
Dinâmica do Sistema Solar
 Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Física I IME. 2º Semestre de Instituto de Física Universidade de São Paulo. Professor: Luiz Nagamine Fone: 3091.
 Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
A NEW CLASS OF INTERIOR PROXIMAL METHODS FOR OPTIMIZATION OVER THE POSITIVE OCTANT
 Pesqusa Opeacoal a Socedade: Educação, Meo Ambete e Desevolvmeto a 5/09/06 Goâa, GO A NEW CLASS OF INERIOR PROXIMAL MEHODS FOR OPIMIZAION OVER HE POSIIVE OCAN Sssy da Slva Souza Uvesdade Fedeal do Ro de
Pesqusa Opeacoal a Socedade: Educação, Meo Ambete e Desevolvmeto a 5/09/06 Goâa, GO A NEW CLASS OF INERIOR PROXIMAL MEHODS FOR OPIMIZAION OVER HE POSIIVE OCAN Sssy da Slva Souza Uvesdade Fedeal do Ro de
Aula 3 Trabalho e Energia - Bioenergética
 Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Consideremos uma distribuição localizada de carga elétrica, de densidade ρ(x), sob a ação de um potencial eletrostático externo ϕ E (x).
 pansão Multpola da nega de uma Dstbução de Caga sob a Ação de Potencal letostátco teno. Físca Nuclea e de Patículas Cesa Augusto Zen Vasconcellos Consdeemos uma dstbução localzada de caga elétca, de densdade
pansão Multpola da nega de uma Dstbução de Caga sob a Ação de Potencal letostátco teno. Físca Nuclea e de Patículas Cesa Augusto Zen Vasconcellos Consdeemos uma dstbução localzada de caga elétca, de densdade
Introdução à Teoria dos Números Notas 1 Os Princípios da Boa Ordem e de Indução Finita Prof Carlos Alberto S Soares
 Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Controle Adaptativo de Estruturas Flexíveis
 ese apesetada à Dvsão de Pós-Gaduação do Isttuto eoógo de Aeoáuta omo pate dos equstos paa obteção do títuo de Meste em Cêa o Cuso de Egehaa Eetôa e Computação, Áea de Sstemas e Cotoe. Vto Igo Gev Cotoe
ese apesetada à Dvsão de Pós-Gaduação do Isttuto eoógo de Aeoáuta omo pate dos equstos paa obteção do títuo de Meste em Cêa o Cuso de Egehaa Eetôa e Computação, Áea de Sstemas e Cotoe. Vto Igo Gev Cotoe
Números Complexos (Parte II) 1 Plano de Argand-Gauss. 2 Módulo de um número complexo. Prof. Gustavo Adolfo Soares
 Númeos Complexos (Pate II) 1 Plao de Agad-Gauss Das defiições de que um úmeo complexo é um pa odeado de úmeos eais x e y e que C = R R, temos que: A cada úmeo complexo coespode um úico poto do plao catesiao,
Númeos Complexos (Pate II) 1 Plao de Agad-Gauss Das defiições de que um úmeo complexo é um pa odeado de úmeos eais x e y e que C = R R, temos que: A cada úmeo complexo coespode um úico poto do plao catesiao,
1. Revisão Matemática
 1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
1. Revsão Matemátca Dervadas Seja a fução f : R R, fxe x R, e cosdere a expressão : f ( x+ αe ) lmα 0 α f, ode e é o vector utáro. Se o lmte acma exstr, chama-se a dervada parcal de f o poto x e é represetado
PROCESSOS ESTOCÁSTICOS
 UIVERIDADE FEDERAL DO RIO GRADE DO ORE CERO DE CIÊCIA EXAA E DA ERRA DEARAEO DE EAÍICA DICILIA: E ROCEO EOCÁICO ROCEO EOCÁICO ª EAA ROFEOR: FERADO CÉAR DE IRADA AAL/R EADO ABORVEE Defção. Um estado de
UIVERIDADE FEDERAL DO RIO GRADE DO ORE CERO DE CIÊCIA EXAA E DA ERRA DEARAEO DE EAÍICA DICILIA: E ROCEO EOCÁICO ROCEO EOCÁICO ª EAA ROFEOR: FERADO CÉAR DE IRADA AAL/R EADO ABORVEE Defção. Um estado de
Teste de Hipótese sobre o coeficiente de coancestria de populações haplóides (1)
 TESTE DE HIPÓTESE SOBRE O COEICIENTE DE COANCESTRIA Teste de Hpótese sobe o coefcete de coacesta de populações haplódes () Joel Augusto Muz (), Slvo Césa Sato Ito (), Dael utado eea () e Rube Delly Vega
TESTE DE HIPÓTESE SOBRE O COEICIENTE DE COANCESTRIA Teste de Hpótese sobe o coefcete de coacesta de populações haplódes () Joel Augusto Muz (), Slvo Césa Sato Ito (), Dael utado eea () e Rube Delly Vega
MEDIDAS DE TENDÊNCIA CENTRAL I
 Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Núcleo das Cêcas Bológcas e da Saúde Cursos de Bomedca, Ed. Físca, Efermagem, Farmáca, Fsoterapa, Fooaudologa, edca Veterára, uscoterapa, Odotologa, Pscologa EDIDAS DE TENDÊNCIA CENTRAL I 7 7. EDIDAS DE
Cinemática Direta. 4 o Engenharia de Controle e Automação FACIT / Prof. Maurílio J. Inácio
 Cnemáta Deta 4 o Engenhaa de Contole e Automação FACI / 9 Pof. Mauílo J. Ináo Cnemáta Deta Cnemáta do manpulado Cnemáta é êna que tata o movmento em ondea a foça que o auam. Na nemáta ão etudado: poçõe,
Cnemáta Deta 4 o Engenhaa de Contole e Automação FACI / 9 Pof. Mauílo J. Ináo Cnemáta Deta Cnemáta do manpulado Cnemáta é êna que tata o movmento em ondea a foça que o auam. Na nemáta ão etudado: poçõe,
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
Potenciais termodinâmicos, critérios de espontaneidade e condições de equilíbrio
 Potecas termodâmcos crtéros de espotaedade e codções de equlíbro O Prcípo da Etropa Máxma váldo para um sstema solado estabelece um crtéro para determarmos o setdo em que ocorrem os processos de forma
Potecas termodâmcos crtéros de espotaedade e codções de equlíbro O Prcípo da Etropa Máxma váldo para um sstema solado estabelece um crtéro para determarmos o setdo em que ocorrem os processos de forma
CAPÍTULO 10 DINÂMICA DO MOVIMENTO ESPACIAL DE CORPOS RÍGIDOS
 94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
Algoritmia e Programação APROG. Modularidade. Algoritmia e Java. Nelson Freire (ISEP DEI-APROG 2012/13) 1/29
 APROG Algotma e Pogamação Moduladade Algotma e Java Nelo Fee (ISEP DEI-APROG 01/1) 1/9 Moduladade Sumáo Itodução Noção de Moduladade Eecução de Pogama Modula Motvaçõe paa Ua Foma de Comucação ete Módulo
APROG Algotma e Pogamação Moduladade Algotma e Java Nelo Fee (ISEP DEI-APROG 01/1) 1/9 Moduladade Sumáo Itodução Noção de Moduladade Eecução de Pogama Modula Motvaçõe paa Ua Foma de Comucação ete Módulo
MÉTODO DA RIGIDEZ DIRETA PARA MODELOS ESTRUTURAIS LINEARES E ELÁSTICOS
 MÉTOO A RIGIEZ IRETA PARA MOELOS ESTRUTURAIS LINEARES E ELÁSTICOS CAPÍTULOS a Luz Ferado Martha Potfíca Uversdade Catóca do Ro de Jaero PUC-Ro epartameto de Egehara Cv Rua Marquês de São Vcete, - Gávea
MÉTOO A RIGIEZ IRETA PARA MOELOS ESTRUTURAIS LINEARES E ELÁSTICOS CAPÍTULOS a Luz Ferado Martha Potfíca Uversdade Catóca do Ro de Jaero PUC-Ro epartameto de Egehara Cv Rua Marquês de São Vcete, - Gávea
Introdução à Transmissão de Calor SUMÁRIO 1. INTRODUÇÃO 2 2. CONDUÇÃO 4 3. CONVECÇÃO RADIAÇÃO 20. Adherbal Caminada Netto TRCAL1
 SUMÁRIO DEPARTAMENTO DE ENGENHARIIA ASSUNTO MECÂNIICA PÁG.. INTRODUÇÃO Poff.. D.. ADHERBAL CAMIINADA NETTO. CONDUÇÃO 4 3. CONVECÇÃO 3 4. RADIAÇÃO Adhebal Camada Netto TRCAL INTRODUÇÃO Sempe ue houve uma
SUMÁRIO DEPARTAMENTO DE ENGENHARIIA ASSUNTO MECÂNIICA PÁG.. INTRODUÇÃO Poff.. D.. ADHERBAL CAMIINADA NETTO. CONDUÇÃO 4 3. CONVECÇÃO 3 4. RADIAÇÃO Adhebal Camada Netto TRCAL INTRODUÇÃO Sempe ue houve uma
Fundamentos da Eletrostática Aula 15 Expansão Multipolar II
 Fundamentos da Eletostátca Aula 5 Expansão Multpola II Pof Alex G Das Pof Alysson F Fea A Expansão Multpola Na aula passada, consdeamos uma dstbução de cagas muto especíca paa enconta o potencal do dpolo
Fundamentos da Eletostátca Aula 5 Expansão Multpola II Pof Alex G Das Pof Alysson F Fea A Expansão Multpola Na aula passada, consdeamos uma dstbução de cagas muto especíca paa enconta o potencal do dpolo
Problemas de Valor de Contorno para Equações Diferenciais Ordinárias
 EQE-358 MÉTODOS NUMÉICOS EM ENGENHI QUÍMIC OFS. EVISTO E GIMIO Caítlo 9 oblema de Valo de Cotoo aa Eqaçõe Dfeea Odáa Codee o eemlo ltatvo da dfão-eação em ma atíla atalíta eféa e ooa: Balaço de maa: etado
EQE-358 MÉTODOS NUMÉICOS EM ENGENHI QUÍMIC OFS. EVISTO E GIMIO Caítlo 9 oblema de Valo de Cotoo aa Eqaçõe Dfeea Odáa Codee o eemlo ltatvo da dfão-eação em ma atíla atalíta eféa e ooa: Balaço de maa: etado
PROBLEMAS SOBRE PONTOS I Davi Maximo (UFC) e Samuel Feitosa (UFC)
 PROBLEMAS SOBRE PONTOS I Dav Maxmo (UFC) e Samuel Fetosa (UFC) Dstbu potos um plao ou um espaço é uma taefa que pode se ealzada de foma muto abtáa. Po sso poblemas sobe potos podem se de dvesas atuezas.
PROBLEMAS SOBRE PONTOS I Dav Maxmo (UFC) e Samuel Fetosa (UFC) Dstbu potos um plao ou um espaço é uma taefa que pode se ealzada de foma muto abtáa. Po sso poblemas sobe potos podem se de dvesas atuezas.
CÁLCULO DIFERENCIAL E INTEGRAL II 014.2
 CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
d s F = m dt Trabalho Trabalho
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
Em muitas situações duas ou mais variáveis estão relacionadas e surge então a necessidade de determinar a natureza deste relacionamento.
 Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
Prof. Lorí Val, Dr. val@pucrs.r http://www.pucrs.r/famat/val/ Em mutas stuações duas ou mas varáves estão relacoadas e surge etão a ecessdade de determar a atureza deste relacoameto. A aálse de regressão
ÁREA DE COBERTURA EM AMBIENTE DE PROPAGAÇÃO MODELADO COM A DISTRIBUIÇÃO κ µ
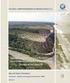 ÁREA DE COBERTURA EM AMBIENTE DE PROPAGAÇÃO MODELADO COM A DISTRIBUIÇÃO κµ κµ JAMIL RIBEIRO ANTÔNIO Dssetação apesetada ao Isttuto Nacoal de Telecomucações INATEL como pate dos equstos paa obteção do Título
ÁREA DE COBERTURA EM AMBIENTE DE PROPAGAÇÃO MODELADO COM A DISTRIBUIÇÃO κµ κµ JAMIL RIBEIRO ANTÔNIO Dssetação apesetada ao Isttuto Nacoal de Telecomucações INATEL como pate dos equstos paa obteção do Título
A desigualdade de Kraft e correlatos
 A desguadade de Kraft e correatos Defções remares Códgo ão sguar: símboos dferetes s são reresetados or códgos dferetes c ; Códgo uvocamete decodfcáve: se símboos cocateados (s s s 3... s k) são reresetados
A desguadade de Kraft e correatos Defções remares Códgo ão sguar: símboos dferetes s são reresetados or códgos dferetes c ; Códgo uvocamete decodfcáve: se símboos cocateados (s s s 3... s k) são reresetados
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
4 πε. 2πε 3. APÊNDICE A: Formulário de Física MATERIAL DE APOIO DE FÍSICA III ELETROMAGNETISMO
 APÊNDICE A: Fomláo e Físca APÊNDICE A FOMULÁIO DE FÍSICA ALFABETO GEGO SÍMBOLO GEGO SÍMBOLO GEGO Músclos Maúsclos Nome Músclos Maúsclos Nome α Α alfa ν Ν β Β beta ξ Ξ cs γ Γ gama ο Ο ômco δ Δ elta π Π
APÊNDICE A: Fomláo e Físca APÊNDICE A FOMULÁIO DE FÍSICA ALFABETO GEGO SÍMBOLO GEGO SÍMBOLO GEGO Músclos Maúsclos Nome Músclos Maúsclos Nome α Α alfa ν Ν β Β beta ξ Ξ cs γ Γ gama ο Ο ômco δ Δ elta π Π
2.3 - Desenvolvimento do Potencial Gravitacional em Série de Harmônicos Esféricos
 . - Desevovieto do otecia avitacioa e Séie de Haôicos Esféicos O potecia gavitacioa de u copo que te distibuição de assa hoogêea e foa geoética sipes, e gea, aite ua epesetação ateática eata. Mas o potecia
. - Desevovieto do otecia avitacioa e Séie de Haôicos Esféicos O potecia gavitacioa de u copo que te distibuição de assa hoogêea e foa geoética sipes, e gea, aite ua epesetação ateática eata. Mas o potecia
UM ALGORITMO BRANCH-AND-BOUND COM BUSCA LOCAL PARA PROGRAMAÇÃO GEOMÉTRICA SIGNOMIAL
 XXXVIII SIMPÓSIO BRASIEIRO DE PESQISA OPERACIONA Pesqusa Operacoa a Socedade: Educação, Meo Ambete e Desevovmeto a /9/ oâa, O M AORITMO BRANCH-AND-BOND COM BSCA OCA PARA PRORAMAÇÃO EOMÉTRICA SINOMIA Rúba
XXXVIII SIMPÓSIO BRASIEIRO DE PESQISA OPERACIONA Pesqusa Operacoa a Socedade: Educação, Meo Ambete e Desevovmeto a /9/ oâa, O M AORITMO BRANCH-AND-BOND COM BSCA OCA PARA PRORAMAÇÃO EOMÉTRICA SINOMIA Rúba
? Isso é, d i= ( x i. . Percebeu que
 Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Estatístca - Desvo Padrão e Varâca Preparado pelo Prof. Atoo Sales,00 Supoha que tehamos acompahado as otas de quatro aluos, com méda 6,0. Aluo A: 4,0; 6,0; 8,0; méda 6,0 Aluo B:,0; 8,0; 8,0; méda 6,0
Lista 3 de CF368 - Eletromagnetismo I
 Lista de CF68 - Eetomagnetismo I Fabio Iaeke de dezembo de 2. Um ane de feo ecozido, de compimento médio de 5 cm, é enoado com uma bobina tooida de espias. Detemine a intensidade magnética
Lista de CF68 - Eetomagnetismo I Fabio Iaeke de dezembo de 2. Um ane de feo ecozido, de compimento médio de 5 cm, é enoado com uma bobina tooida de espias. Detemine a intensidade magnética
ANÁLISE ESTATÍSTICA DOS ERROS DE CENTRAGEM E PONTARIA
 5 ANÁLISE ESTATÍSTICA DOS ERROS DE CENTRAGEM E PONTARIA Jai Medes Maques Uivesidade Tuiuti do Paaá R. Macelio Champagat, 55 CEP 87-5 e-mail: jaimm@utp.b RESUMO O objetivo deste tabalho cosiste o desevolvimeto
5 ANÁLISE ESTATÍSTICA DOS ERROS DE CENTRAGEM E PONTARIA Jai Medes Maques Uivesidade Tuiuti do Paaá R. Macelio Champagat, 55 CEP 87-5 e-mail: jaimm@utp.b RESUMO O objetivo deste tabalho cosiste o desevolvimeto
Construção e Análise de Gráficos
 Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
Costrução e Aálse de Gráfcos Por que fazer gráfcos? Facldade de vsualzação de cojutos de dados Faclta a terpretação de dados Exemplos: Egehara Físca Ecooma Bologa Estatístca Y(udade y) 5 15 1 5 Tabela
2ªAula do cap. 11. Quantidade de Movimento Angular L. Conservação do Momento Angular: L i = L f
 2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
Capítulo 8. Método de Rayleigh-Ritz
 Grupo : Gustavo de Souza Routma; Luís Ferado Hachch de Souza; Ale Pascoal Palombo Capítulo 8. Método de Raylegh-Rtz 8.. Itrodução Nos problemas de apromação por dfereças ftas, para apromar a solução para
Grupo : Gustavo de Souza Routma; Luís Ferado Hachch de Souza; Ale Pascoal Palombo Capítulo 8. Método de Raylegh-Rtz 8.. Itrodução Nos problemas de apromação por dfereças ftas, para apromar a solução para
