Introdução à Transmissão de Calor SUMÁRIO 1. INTRODUÇÃO 2 2. CONDUÇÃO 4 3. CONVECÇÃO RADIAÇÃO 20. Adherbal Caminada Netto TRCAL1
|
|
|
- Lídia Lobo
- 5 Há anos
- Visualizações:
Transcrição
1 SUMÁRIO DEPARTAMENTO DE ENGENHARIIA ASSUNTO MECÂNIICA PÁG.. INTRODUÇÃO Poff.. D.. ADHERBAL CAMIINADA NETTO. CONDUÇÃO 4 3. CONVECÇÃO 3 4. RADIAÇÃO Adhebal Camada Netto TRCAL
2 INTRODUÇÃO Sempe ue houve uma dfeeça de tempeatua ete dos sstemas uasue, haveá um fluxo de eega ete eles. Ao pocesso pelo ual a eega é tasmtda, em decoêca da dfeeça de tempeatua, dá-se o ome de tasmssão de calo. O setdo em ue se dá esta tasfeêca de eega é estabelecdo pelo Segudo Pcípo da Temodâmca, ue dz: Nehum pocesso é possível, se o seu úco esultado fo uma tasfeêca líuda de calo de um sstema com uma detemada tempeatua, paa outo sstema com tempeatua mas elevada. Isto ue dze, po exemplo, ue ão se pode auece ada mas uma chalea com água uete, smplesmete colocado-a sobe uma chapa fa. Obvamete, esse caso, a chapa é ue se aueceá, à medda ue a água e a chalea esfam, cessado o pocesso de tasmssão de calo uado a água, a chalea e a chapa estveem todas a mesma tempeatua. Este exemplo, a sua smplcdade cotdaa, demosta bem os pcípos báscos ue devemos te em mete: a) a tasfeêca de eega ete os copos como coseüêca da dfeeça de tempeatua; b) o setdo em ue se pocessam os feômeos atuas. De uma maea geal, costuma-se faze a dstção ete tês mecasmos ou modos báscos de tasmssão de calo: codução, covecção e adação. Na ealdade, Do poto de vsta da teoa cétca, o calo ada mas é do ue eega molecula. Adhebal Camada Netto TRCAL
3 o ue gealmete ocoe é te-se dos ou mas deles atuado smultaeamete, sedo ecessáo leva em cota a combação de seus efetos. Cotudo, ão é ao ue um deles pedome uattatvamete de tal foma, ue os efetos coespodetes aos outos dos possam se despezados a pátca. De ualue maea, é sempe ecessáo aalsa cudadosamete o poblema ue se teha em mãos, paa ue ão seja dexado de lado um mecasmo cujos efetos sejam sgfcatvos, ou veham a se toa sgfcatvos pela alteação das codções ue fluem o poblema. Nos capítulos ue se seguem abodaemos os tês modos ou mecasmos báscos de tasmssão de calo. Adhebal Camada Netto TRCAL3
4 CONDUÇÃO É a tasmssão de calo, sem gade deslocameto de massa, ete pates de um sstema ou ete dos sstemas em cotato físco deto, devdo à dfeeça de tempeatua exstete ete as dtas pates ou ete os dtos sstemas. No exemplo mecoado ateomete, a chalea tasmte tpcamete calo à chapa fa, ue esta em cotato físco deto com ela, po codução. A dx x Fg.. - Tasmssão de calo po codução Adhebal Camada Netto TRCAL4
5 O cetsta facês J.B.J. Foue fo uem, em 8, eucou a elação básca paa a tasmssão de calo po codução. Ele vefcou, expemetalmete, ue a uatdade de calo tasmtda, a udade de tempo, atavés de uma paede plaa (fg..) ea popocoal a: A - áea da seção pepedcula ao setdo de tasmssão de calo; dt dx - gadete de tempeatua atavés da seção A; ou seja, dt A. dx Esta elação de popocoaldade pode se covetda em uma euação, toduzdo-se uma costate de popocoaldade, cujo valo depede do mateal. dt. A. dx (.) O sal egatvo fo toduzdo a euação, em vtude de o aumeto de tempeatua se da o setdo veso da tasmssão de calo, ou seja, pelo fato de o gadete de tempeatua se egatvo. A costate é chamada de codutbldade ou codutvdade témca, e é uma popedade de cada mateal. Ela expessa a uatdade de calo tasmtda, a udade de tempo, atavés de uma seção com áea utáa, em decoêca de um gadete de tempeatua utáo. A euação (.) é bastate smplfcada, pos, ao escevê-la cosdeou-se a tasmssão de calo apeas a deção geéca x. Além dsso, admtu-se o chamado egme pemaete, ou seja, ue o gadete de tempeatua ão vae com o tempo, e ada mas, ue o gadete de tempeatua seja o mesmo em todos os potos da áea A e ue a codutvdade témca ão vae com a tempeatua. Em mutos casos pode-se smplfca mas uma vez a euação (.), admtdo ue a vaação de tempeatua seja lea ao logo do mateal. Em outas palavas, pode-se admt ue o gadete de tempeatua seja gual a (T o T ) / x, como mostado a fgua.. Tal é o caso de uma baa metálca evestda po um mateal solate, ue tem suas extemdades expostas às tempeatuas costates T o e T, sedo T o > T. Chegamos, potato, a: Adhebal Camada Netto TRCAL5
6 A. ( T T ) x ( T T. A. x. ) T. A. (.) x T T x Tempeatua costate T Isolate Tempeatua costate T Fg.. - Codução de calo em uma baa solada Obsevado a euação (.), podemos, po aaloga com um ccuto elétco de coete cotíua, cosdea T como uma dfeeça de potecal de tempeatua, ue foça, a uatdade de calo a udade de tempo, aáloga à coete elétca, atavés da esstêca ofeecda pelo mateal da paede. Dessa maea, toduzmos o coceto de esstêca témca, R, e de seu veso, a codutâca témca, C: Adhebal Camada Netto TRCAL6
7 x R (.3) C. A E podemos esceve ada: V ccuto elétco R T R ccuto témco A aaloga com o ccuto elétco os pemte deduz apdamete, tedo-se em mete as mesmas smplfcações fetas paa se chega à euação (.), as segutes expessões paa a codução de calo atavés de paedes de cofguação smples: a) Codução de calo atavés de uma paede plaa composta T T T T 3 3 T x x x 3 x Fg..3 Codução de calo atavés de uma paede plaa composta Obseve-se ue os dvesos mateas ue compõem a paede ofeecem esstêcas em sée à codução de calo. Assm, podemos esceve paa a esstêca total: Adhebal Camada Netto TRCAL7
8 Adhebal Camada Netto TRCAL8 R R R R 3... R x x x x A L 3 3 (.4) Como R T, temos: x x x A T T L (.5) ou x T A. (.6) Obseve-se, ue a euação (.5) só apaecem as tempeatuas T o e T das faces exteas da paede. b) Codução de.calo atavés de uma paede clídca composta Icalmete, vamos detema a esstêca témca (R) paa este tpo de cofguação, cosdeado o cldo da fgua.4. Fg..4 - Paede clídca e T T L
9 Paa o cldo, a euação (.) pode se escta da segute maea: dt ( πl) d Sepaado as vaáves e tegado ete os lmtes dcados a fgua.4, temos: e d π L T T dt π ( T T ) L e l (.7) Cosdeado-se a codução de calo po udade de compmeto (L) da paede clídca, temos a segute expessão paa a esstêca témca: R e l (.8) πk T T T T Fg..5 - Codução de calo atavés de paedes clídcas e esfécas compostas Da mesma maea ue o caso ateo da paede plaa, os dvesos mateas ue compõem a paede clídca composta mostada a fgua.5 ofeecem esstêca Adhebal Camada Netto TRCAL9
10 Adhebal Camada Netto TRCAL em sée à codução de calo. Assm, utlzado-se a expessão (.8) paa cada camada de mateal, pode-se esceve paa a esstêca total: ( ) Κ Κ Κ o R... l l l π Lembado ue R T, temos: ( ) l l l T T L π ou ( ) ( ) l T T π ode é o calo tasmtdo po udade de compmeto. Paa uma paede clídca, mutas vezes também é coveete expessa o calo tasmtdo po udade de áea, a exemplo do ue fo feto paa as paedes plaas. No caso de um cldo, como a áea vaa com o ao, é comum foece-se o fluxo de calo em fução da áea extea do solameto (A e πl ): ( ) l T
11 Adhebal Camada Netto TRCAL ode ( ). l é a espessua euvalete de cada camada. c) Codução de calo atavés de uma paede esféca A expessão paa o fluxo de calo coduzdo atavés de uma paede esféca é obtda de maea aáloga à das paedes clídcas. Neste caso, pode-se supo ue a fgua.5 epesete uma seção ue passa pelo ceto de uma esfea solada. Paa uma esfea de paede smples teemos: ( ) d d Τ 4π 4 T T dt d e π ( ) e e Τ Τ 4π E obtém-se a segute expessão paa a esstêca témca: e e e e R Α Α 4π No caso de uma paede esféca composta, temos paa a esstêca: ( ) ( ) R π E paa o calo tasmtdo po codução: ( ) ( ) ( ) Τ Τ π
12 ou ( Τ Τ ) 4π ( ) ( ).. Gostaíamos de esum o ue fo dto até esta altua as segutes déas báscas:. Paa ue haja tasmssão de calo, é ecessáo have uma dfeeça de tempeatua ( T), e uato mao esta dfeeça, mao a uatdade de calo tasmtda;. Quato mao a áea supefcal (A), mao a tasmssão de calo; 3. Uma mao espessua de paede ( x) sgfca uma meo tasmssão de calo po codução; 4. A codutvdade témca () é uma caacteístca de cada mateal. Quado o valo de é elevado, o mateal é omalmete chamado coduto de calo. No caso cotáo, o mateal é chamado solate. Adhebal Camada Netto TRCAL
13 CONVECÇÃO É um mecasmo ue tem especal mpotâca a tasmssão de calo os meos líudos e gasosos, ou ete estes e uma supefíce sólda. Como ão depede exclusvamete da dfeeça de tempeatuas, mas também de um cosdeável deslocameto de massa, a covecção foge da defção pecsa de tasmssão de calo. As coetes maítmas e os vetos costtuem mpotates agetes atuas da tasmssão de calo po covecção de uma egão paa outa do Globo. O a uete (meos deso) sobe T T T > T O a mas fo (mas deso) desce Fg. 3. Coete elemeta de covecção A covecção costuma se classfcada como lve ou atual e foçada. Na covecção lve, as dfeeças de desdade decoetes das dfeeças de tempeatua o teo do líudo ou do gás geam as chamadas coetes de covecção (fgua 3.). Se o escoameto das patículas do líudo ou gás fo estabelecdo po meos mecâcos, temos a chamada covecção foçada. Toda vez ue sopamos o café ates Adhebal Camada Netto TRCAL3
14 de bebê-lo, tesfcamos a tasmssão de calo ete o líudo cotdo a xícaa e o a po um pocesso de covecção foçada. Paede sólda T T Fludo T Fg. 3. Tasmssão de calo ete um fludo e uma paede sóda O celebe físco glês Isaac Newto popôs, em 7, a segute euação paa a tasmssão de calo ete uma supefíce sólda e um fludo (líudo ou gás): ode (fg. 3.): h. A. T (3.) uatdade de calo tasmtda a udade de tempo; A áea de tasmssão de calo; Camada lmte T T T, sedo T o a tempeatua do fludo a coete pcpal e T a tempeatua a supefíce da paede sólda; h coefcete de película médo, ue depede de úmeos fatoes. Po aaloga com o ue fo feto paa a codução, podemos def a esstêca témca a covecção como: Mas goosamete, sea a tempeatua a uma dstâca da supefíce em ue o gadete de tempeatua, a deção omal à supefíce, seja despezível. Adhebal Camada Netto TRCAL4
15 R h. A (3.) A euação (3.), ue é uma defção de h e ão a expessão de uma le ue desceva o feômeo da covecção, apaeta uma falsa smplcdade, uma vez ue a detemação de h paa os poblemas ecotados a pátca é, va de ega, uma taefa complexa. A detemação do coefcete de película h pode se feta pelos segutes métodos: a) método puamete expemetal; b) aálse dmesoal combada com dados expemetas; c) esolução das euações dfeecas ue defem a toca de calo po covecção (solução exata e solução apoxmada). A aálse dmesoal, emboa ão foeça fomações pecsas sobe a atueza do feômeo da covecção, é matematcamete smples e tem sdo amplamete utlzada em cojuto com dados expemetas a detemação do coefcete de película, uma vez ue pemte ampla o campo de aplcação das expeêcas ealzadas coelacoado os esultados obtdos em temos de gupos admesoas. Fo W. Nusselt uem, pela pmea vez, aplcou o método da aálse dmesoal ao estudo da tasmssão de calo po covecção. Em 99 ele desevolveu as euações báscas paa a covecção foçada e mas tade, em 95, as euações paa a covecção atual. A título de exemplo, examaemos a aplcação do método ao caso da covecção foçada de um fludo em escoameto atavés de um tubo. O pmeo-passo cosste em selecoa as vaáves sgfcatvas, ou seja, auelas ue devem se levadas em cota uado se pocua tepeta o feômeo em estudo, e expm-las dmesoalmete em um sstema de dmesões pmáas. A escolha das dmesões pmáas é abtáa e utlzaemos o compmeto, L, a massa, M, a tempeatua, θ, e o tempo, T. Adhebal Camada Netto TRCAL5
16 VARIÁVEL SÍMBOLO DIMENSÃO Coefcete de película h [ Μ θ ] Τ 3 Codutvdade témca do fludo 3 [ Μ L θ ] Τ Desdade do fludo ρ 3 [ Μ L ] Vscosdade do fludo µ [ Μ L ] Τ Calo específco do fludo c p [ L θ ] Τ Velocdade do fludo V [ L Τ ] Dâmeto do tubo D [ L ] Tabela 3. Vaáves sgfcatvas O segudo passo cosste a detemação do úmeo de gupos admesoas depedetes ecessáos paa expm a elação ue desceve o feômeo em estudo. Paa tato, utlzaemos o segute teoema: Teoema dos π de Bucgham - o úmeo de gupos admesoas depedetes ecessáos, ue se pode obte ao se comba as vaáves sgfcatvas de um poblema, é gual ao úmeo dessas vaáves físcas meos o úmeo de dmesões pmáas utlzadas paa descevê-las dmesoalmete. Chamado-se π, π, etc., a esses gupos, a expessão ue elacoa as vaáves evolvdas o poblema é da foma: f (π, π, π 3,...,) Assm, como temos 7 vaáves sgfcatvas e 4 dmesões pmáas, pecsaemos de tês gupos admesoas depedetes paa obte uma elação ue desceva o feômeo. Paa cada π podemos esceve: π h a b ρ c µ d c p e V f D g ou π [M θ - T -3 ] a. [ML θ - T -3 ] b. [M L - 3 ] c. [M L - T -l ] d. [L θ - T - ] e. [L T -l ] f. [L] g Adhebal Camada Netto TRCAL6
17 Como π é um gupo admesoal, a soma dos expoetes de cada dmesão pmáa deve se ula. M : a b c d L : b - 3c - d e f g θ : - a - b - e T : - 3a - 3b - d - e - f Como há mas cógtas do ue euações, devemos atbu valoes a tês dos expoetes, desde ue os expoetes escolhdos sejam depedetes, sto é, desde ue o detemate fomado com os coefcetes dos demas expoetes ão seja ulo. Como estamos teessados o coefcete de película, vamos guala o seu coefcete à udade, ou seja, a e, paa smplfca a mapulação algébca, vamos faze d f. Resolvedo as euações, chegamos ao segute esultado: a b - c d e f g Assm, o pmeo gupo admesoal obtdo, π, seá h D π Os outos dos gupos admesoas seam obtdos de foma aáloga ao ue fo feto paa π, e teíamos falmete: h D π N Nu (Númeo de Nusselt) V D ρ π N Re (Númeo de Reyolds) µ c π 3 N P (Númeo de Padtl) p µ Adhebal Camada Netto TRCAL7
18 e f (N Nu, N Re, N P ) ou N Nu f (N Re, N P ) ou ada, N Nu C (N Re ) m. (N P ) (3.3) ode as costates C, m e devem se detemadas expemetalmete. A gade vatagem da utlzação dos gupos admesoas é ue os esultados de expeêcas dvduas, ealzadas paa um fludo patcula, em cotato com uma paede de dmesões específcas, podem se utlzados paa outos fludos, outas dmesões de paede de mesma cofguação e outas velocdades de escoameto, desde ue seja obsevada a gualdade dos gupos admesoas. De maea aáloga ao ue fo feto ateomete, chegaíamos à segute expessão paa a covecção atual de um fludo em cotato com um copo clídco: N Nu C (N G. N P ) m (3.4) ode: N G 3 D ρ β g T (Númeo de Gashof); µ β coefcete de expasão volumétca do fludo; g aceleação da gavdade; e T dfeeça de tempeatua ete a supefíce da paede e o fludo. Também esse caso, as costates C e m são detemadas expemetalmete. Adhebal Camada Netto TRCAL8
19 Costuma-se chama o poduto do úmeo de Gashof e do úmeo de Padtl de úmeo de Raylegh, N Ra, e a elação (3.4) pode se eescta da segute foma: N Nu C (N Ra ) m (3.5) E o valo de h pode se falmete obtdo da segute foma: h N Nu (3.6) D Adhebal Camada Netto TRCAL9
20 RADIAÇÃO É o mecasmo de tasmssão de calo pelo ual a eega emtda po um copo, a uma dada tempeatua, é absovda po outo copo, a uma tempeatua mas baxa, sedo covetda em eega tea deste últmo. A emssão de eega po um copo se faz em lha eta, em todas as deções e com a velocdade da luz. Além dsso, ão é ecessáo ue haja um meo temedáo paa ue ocoa a tasfeêca de eega a foma de calo adate ete dos copos com tempeatuas dfeetes. Assm, o Sol tasmte calo à Tea atavés do vazo teplaetáo, ode ão há sóldos, líudos ou gases paa ue a tasfeêca de eega se faça po codução ou covecção. Na ealdade, as adações témcas e lumosa são fomas de eega adate, popagado-se po odas eletomagétcas, ue dfeem apeas os espectvos compmetos de oda. A adação eletomagétca emtda po um copo sódo, auecdo até ceca de 7 o C, é costtuída po odas com compmeto mao do ue auelas pecebdas pelo olho humao. Acma de 7 o C, o etato, a adação emtda passa a se, em pate, costtuída po luz vsível, como acotece com o flameto das lâmpadas cadescetes. Todos os copos absovem eega e a eega adate total emtda po um copo, a udade de tempo, é popocoal à áea da supefíce emssoa e à uata potêca da tempeatua absoluta desta supefíce, ou seja: 4 σ A T (4.) ode: σ 5,7 x -8 W/m. K 4, chamada costate de Stefa-Boltzma; Adhebal Camada Netto TRCAL
21 A áea da supefíce emssoa (m ); e T tempeatua absoluta da supefíce emssoa (K o C 73). A go, esta expessão se aplca apeas a um copo ego deal, ue sea um absovedo e um adado pefeto de eega. As supefíces dos copos eas absovem e emtem, a udade de tempo, uma uatdade de eega meo do ue a supefíce do copo ego de mesma tempeatua. Temos, potato, paa um copo eal: 4 ε σ A T (4. ) ode ε emssvdade. Paa o copo ego, ε.... a. t Fg. 4. Dstbução da eega cdete Qualue copo está cotuamete emtdo eega adate e absovedo pate da eega adate ue sobe ele cde poveete do meo ue o ceca. Nos copos eas, em toda a eega adate cdete é absovda a, podedo have uma pacela desta eega ue é efletda e outa ue é tasmtda atavés do copo t. Assm sedo, podemos esceve (fg. 4.): a t Adhebal Camada Netto TRCAL
22 ou a t % ode: a absotvdade, pocetagem da eega cdete absovda pelo copo; efletvdade, pocetagem efletda a supefíce do copo; e t tasmssvdade, pocetagem ue atavessa o copo sem se absovda. Ao se atgdo o eulíbo témco com o meo ue o ceca, ualue copo deve absove e emt uatdades guas de eega paa ue sua tempeatua se mateha costate. Neste caso, a absotvdade é gual à emssvdade (a ε), sedo ambas % paa o copo ego e tedo um valo pecetual meo paa os copos eas, ue depedeá dos valoes pecetuas de e t). Quado dos copos ão estão em eulíbo témco, ou seja, uado exste uma dfeeça de tempeatua ete eles, e uado ão exste algo ue blouee ou tecepte a toca de adação, haveá uma tasfeêca de calo do copo com tempeatua mas elevada paa o de tempeatua feo, pos esse caso, este últmo ecebe mas eega do ue emte. Como esultado dsto, há uma ttocca líl íuda de eega adate ete os dos copos, ue povoca a elevação da tempeatua dauele ue se ecota à tempeatua mas baxa. Cofome já mecoado ateomete, ao se atgda a gualdade de tempeatuas, cada copo passa a absove e emt a mesma uatdade de eega, sem ue ocoa uma toca líuda de eega adate, matedo-se costate a tempeatua de eulíbo. Paa dos copos matdos a tempeatuas dfeetes e costates (egme pemaete), a toca líuda de calo po adação ete eles é dada pela segute expessão geal: 4 4 T T 5,7 A F G. F E (4.3) ode: uatdade de calo adate tasmtdo; Adhebal Camada Netto TRCAL
23 A áea do copo cosdeado; F G fato de cofguação, ue leva em cota a geometa e a dsposção elatva dos copos; e F E fato de emssvdade, ue leva em cota o fato de ão seem dos copos egos. A título de exemplo de aplcação da fómula (4.3) a um caso patcula, C.Chstase deduzu em 883 a segute expessão paa o calo tasmtdo po adação ete um copo evolvete (supefíce côcava) e um copo evolvdo (supefíce covexa): A ε A σ A. ε 4 4 ( T T ) (4.4) ode: A áea do copo evolvdo; A áea do copo evolvete; ε emssvdade do copo evolvdo; e ε emssvdade do copo evolvete. A fómula (4.4) se aplca a esfeas cocêtcas e a cldos coaxas. Se supusemos ue a áea do vóluco é tão mao ue a áea do copo evolvdo, ue o segudo temo do deomado da euação (4.4) possa se despezado, obtemos a segute expessão: 4 4 ( T ) ε σ A T (4.5) Cofome ateomete mecoado, supõe-se ue o vóuco se mateha sempe côcavo e o copo evolvdo sempe covexo. Adhebal Camada Netto TRCAL3
24 CONDUÇÃO, CONVECÇÃO E RADIAÇÃO COMBINADAS Se voltamos a cosdea o cldo da fgua.4 cecado de a à tempeatua T, vemos ue, em egme pemaete, a mesma uatdade de calo tasmtda adalmete po codução atavés das paedes sóldas é cedda ao meo ambete po covecção e adação. Em outas palavas, a uatdade de calo c tasmtda po codução é gual à soma de duas uatdades de calo, cv e tasmtdas espectvamete po covecção e adação, ou seja: π c ( T T ) L e l cv h. Ae T ( T ) ε σ Ae 4 4 ( T T ) e c cv ( T T ) πl e l. A ( T T ) 4 4 h e σ ( T T ) ε (5.) A e Às vezes, é coveete expessa a euação da adação da segute foma: Adhebal Camada Netto TRCAL4
25 h ( T ). A T (5.) ode h é defdo como um coefcete de adação. No caso do cldo da fgua.4, vemos ue: ( T T ) ( T ) h ε σ (5.3) T Substtudo a expessão (5.) paa a euação (5.), temos: ( T T ) πl e l ( h h ) Ae ( T T ) hc Ae ( T T ) (5.4) Na elação (5.4) o coefcete h c (h h ) costtu uma combação dos coefcetes de covecção e de adação. Se voltamos a cosdea o caso da paede composta da fgua.3, levado agoa em cota o calo tasmtdo po covecção e adação em ambas as faces, em cotato, espectvamete, com fludos as tempeatuas T A e T B, podemos esceve, po aaloga com um ccuto elétco de esstêcas em sée e utlzado a elação (.6):. T TB x (5.5) h h A A ca cb ode h c e h A c B são os coefcetes combados de covecção e adação paa o escoameto as faces da paede, espectvamete, mas auecda e meos auecda. A elação (5.5) pode se escta de maea mas smples, medate a defção de um ccoeeff cc eettee globall dee ttassm ssssão dee ccal lo, U, com udades dêtcas às de h: U. A. T (5.6) ode: Adhebal Camada Netto TRCAL5
26 U h c A x h c B O coefcete global de tasmssão de calo pode se obtdo de foma aáloga paa paedes com outas cofguações. Adhebal Camada Netto TRCAL6
27 EXERCÍÍCIIO Uma paede plaa de um foo é composta po duas camadas: a pmea de tjolos solates com 5 mm de espessua, e a seguda de tjolos de costução com 38 mm de espessua. A tempeatua a face tea é T. o C, e a tempeatua a face extea é T 6 o C. A codutvdade témca dos tjolos solates é dada po, T cal/m.h. o C e a dos tjolos de costução po c, T cal/m.h. o C. Calcule a fluxo de calo atavés da paede. EXERCÍÍCIIO A paede de um foo é composta de uma camada tea de tjolos efatáos (,5 W/m.K) com 76 mm de espessua e de uma camada extea de aço comum ( 4,53 W/m.K) com 6,35 mm de espessua. A tempeatua a face tea é de 649 o C. Calcule a fluxo de calo atavés da paede e a tempeatua a face extea da paede do foo. A tempeatua do a ambete é 7 o C e pode-se utlza o valo de 68,4 W/m.K paa o coefcete combado de covecção e adação. Adhebal Camada Netto TRCAL7
28 EXERCÍÍCIIO 3 Uma tubulação clídca de aço tem ao exteo gual a 76, mm. Paa solá-la, dspõe-se o almoxafado de telhas de um mateal solate com,865 W/m.K a 5 o C. A tempeatua do fludo a ede é 48 o C. Calcule a espessua de solate ecessáa paa lmta a uatdade de calo pedda po meto de caalzação a 95 W/m. A tempeatua do a ambete é o C e pode-se utlza o valo de W/m.K paa o coefcete combado de covecção e adação. EXERCÍÍCIIO 4 Uma tubulação clídca de aço tem dâmeto exteo gual a,68 m, va se solada com um sstema solate composto po um mateal solate cuja codutvdade témca pode se cosdeada apoxmadamete costate e gual a,37 W/m.K a faxa de tempeatuas de a 4 o C, e po um mateal de evestmeto com emssvdade,. Essa tubulação coduz um fludo a tempeatua de - o C. A tempeatua ambete é gual a 38 o C, a umdade elatva do a é 75% e a velocdade do veto, m/s. Calcule a espessua de solate ecessáa paa evta a codesação a supefíce do evestmeto. Adhebal Camada Netto TRCAL8
RESOLUÇÃO SIMULADO ITA FÍSICA E REDAÇÃO - CICLO 7 FÍSICA GM G M GM GM. T g
 RESOLUÇÃO SIMULADO ITA FÍSICA E REDAÇÃO - CICLO 7 FÍSICA Questão M a) A desdade é a azão ete a massa e o volume: d. V Se as desdades fossem guas: MP MT MT MT dp dt. V 4 4 P VT RT R T GM b) A gavdade a
RESOLUÇÃO SIMULADO ITA FÍSICA E REDAÇÃO - CICLO 7 FÍSICA Questão M a) A desdade é a azão ete a massa e o volume: d. V Se as desdades fossem guas: MP MT MT MT dp dt. V 4 4 P VT RT R T GM b) A gavdade a
4/10/2015. Física Geral III
 Físca Geal III Aula Teóca 8 (Cap. 6 pate /3: Potecal cado po: Uma caga putome Gupo de cagas putomes 3 Dpolo elétco Dstbução cotíua de cagas Po. Maco. Loos mos ue uma caga putome gea um campo elétco dado
Físca Geal III Aula Teóca 8 (Cap. 6 pate /3: Potecal cado po: Uma caga putome Gupo de cagas putomes 3 Dpolo elétco Dstbução cotíua de cagas Po. Maco. Loos mos ue uma caga putome gea um campo elétco dado
Aluno(a): Professor: Chiquinho
 Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Aluo(a): Pofesso: Chquho Estatístca Básca É a cêca que tem po objetvo oeta a coleta, o esumo, a apesetação, a aálse e a tepetação de dados. População e amosta - População é um cojuto de sees com uma dada
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Binômio de Newton e o Triângulo de Pascal. Somas de elementos em Linhas, Colunas e Diagonais do Triângulo de Pascal. 2 ano do E.M.
 Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas do Tâgulo de Pascal ao do EM Módulo: Bômo de Newto e o Tâgulo de Pascal Somas de elemetos em Lhas, Coluas e Dagoas
A Base Termodinâmica da Pressão Osmótica
 59087 Bofísca II FFCLRP P Pof. Atôo Roque Aula 7 A Base emodâmca da Pessão Osmótca Elemetos de emodâmca As les báscas da temodâmca dzem espeto à covesão de eega de uma foma em outa e à tasfeêca de eega
59087 Bofísca II FFCLRP P Pof. Atôo Roque Aula 7 A Base emodâmca da Pessão Osmótca Elemetos de emodâmca As les báscas da temodâmca dzem espeto à covesão de eega de uma foma em outa e à tasfeêca de eega
Sobre a classe de diferenciabilidade de quocientes de polinômios homogêneos.
 Uvesdade Regoal do Ca - URCA CADERNO DE CULTURA E CIÊNCIA VOLUME Nº - 008 IN 980-586 obe a classe de dfeecabldade de quocetes de polômos homogêeos About the Dffeetablty Class of the Quotet of Homogeeous
Uvesdade Regoal do Ca - URCA CADERNO DE CULTURA E CIÊNCIA VOLUME Nº - 008 IN 980-586 obe a classe de dfeecabldade de quocetes de polômos homogêeos About the Dffeetablty Class of the Quotet of Homogeeous
Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1
 Dscpla: FGE5748 Smulação Computacoal de Líqudos Moleculaes Exstem pocedmetos paa toa os pogamas mas efcetes, depedetemete, de seem DM ou MC. Como: Cálculo da teação Múltplos passos Coeções de logo alcace
Dscpla: FGE5748 Smulação Computacoal de Líqudos Moleculaes Exstem pocedmetos paa toa os pogamas mas efcetes, depedetemete, de seem DM ou MC. Como: Cálculo da teação Múltplos passos Coeções de logo alcace
Os fundamentos da física Volume 2 1. Resumo do capítulo
 Os fudametos da físca Volume 2 1 Capítulo 13 Refação lumosa A efação é o feômeo o qual a luz muda de meo de popagação, com mudaça em sua velocdade. ÍDICE DE REFRAÇÃO ABSOLUTO O ídce de efação absoluto
Os fudametos da físca Volume 2 1 Capítulo 13 Refação lumosa A efação é o feômeo o qual a luz muda de meo de popagação, com mudaça em sua velocdade. ÍDICE DE REFRAÇÃO ABSOLUTO O ídce de efação absoluto
3 O Método de Partículas MPS
 O Método de Patículas MPS 9 3 O Método de Patículas MPS O método MPS fo apesetado calmete po Koshzuka e Oka (1996). Este método, de atueza Lagageaa, fo deseoldo paa esole escoametos de fludos compessíes
O Método de Patículas MPS 9 3 O Método de Patículas MPS O método MPS fo apesetado calmete po Koshzuka e Oka (1996). Este método, de atueza Lagageaa, fo deseoldo paa esole escoametos de fludos compessíes
Resoluções dos exercícios propostos
 os fudametos da físa Udade E Capítulo efação lumosa esoluções dos eeíos popostos P.85 Como, temos: 8 0 0 8,5 P.86 De, em: 0 8,5 0 8 m/s P.87 elodade da luz a plaa de do oespode a 75% da elodade da luz
os fudametos da físa Udade E Capítulo efação lumosa esoluções dos eeíos popostos P.85 Como, temos: 8 0 0 8,5 P.86 De, em: 0 8,5 0 8 m/s P.87 elodade da luz a plaa de do oespode a 75% da elodade da luz
Elétrons em um potencial periódico: o teorema de Bloch. Cap 7 KITTEL Cap 8 ASHCROFT- MERMIN Cap 5 IVAN
 Elétos em um poteal peódo: o teoema de Bloh Cap 7 ITTEL Cap 8 ASHCOFT- MEMIN Cap 5 IVAN Modelo de Dude: gás s lásso de elétos Até agoa 1 mv 3 B T Modelo de Sommefeld: gás s de elétos uâto h m ψ εψ ( )
Elétos em um poteal peódo: o teoema de Bloh Cap 7 ITTEL Cap 8 ASHCOFT- MEMIN Cap 5 IVAN Modelo de Dude: gás s lásso de elétos Até agoa 1 mv 3 B T Modelo de Sommefeld: gás s de elétos uâto h m ψ εψ ( )
APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO. Djalma M. Falcão COPPE/UFRJ
 GPL/026 2 a 26 de Outubo de 200 Campas - São Paulo - Basl GRUPO VII PLANEJAMENTO DE SISTEMAS ELÉTRICOS APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO Yu S.B. Wllmesdof
GPL/026 2 a 26 de Outubo de 200 Campas - São Paulo - Basl GRUPO VII PLANEJAMENTO DE SISTEMAS ELÉTRICOS APLICAÇÃO DE TÉCNICAS PROBABILÍSTICAS ÀS TARIFAS DE USO DO SISTEMA DE TRANSMISSÃO Yu S.B. Wllmesdof
CIV 2552 Mét. Num. Prob. de Fluxo e Transporte em Meios Porosos. Método dos Elementos Finitos Fluxo 2D em regime transiente em reservatório
 CIV 55 Mét. um. ob. de luo e aote em Meo ooo Método do Elemeto to luo D em egme taete em eevatóo Codçõe ca e aâmeto etete: eão cal: Ma emeabldade tíeca: -5 md m md ml-dac Vcodade dâmca: - µ Ma oe Comebldade
CIV 55 Mét. um. ob. de luo e aote em Meo ooo Método do Elemeto to luo D em egme taete em eevatóo Codçõe ca e aâmeto etete: eão cal: Ma emeabldade tíeca: -5 md m md ml-dac Vcodade dâmca: - µ Ma oe Comebldade
Capítulo 6 Corpo Rígido, Estática e Elasticidade
 Capítulo 6 Copo Rígdo, Estátca e Elastcdade 6. Noção de Copo Rígdo Estudamos já os movmetos de copos cujas dmesões eam despezáves face às meddas das suas tajectóas ou po coveêca e smplfcação, tomados como
Capítulo 6 Copo Rígdo, Estátca e Elastcdade 6. Noção de Copo Rígdo Estudamos já os movmetos de copos cujas dmesões eam despezáves face às meddas das suas tajectóas ou po coveêca e smplfcação, tomados como
i CC gerador tg = P U = U.i o i i r.i 0 i CC i i i
 GEDO ELÉTIO "Levao-se em cota a esstêca tea o geao, pecebemos que a p ete os temas é meo o que a foça eletomotz (fem), evo à pea e p a esstêca tea." - + = -. OENTE DE TO-IITO Se lgamos os os temas e um
GEDO ELÉTIO "Levao-se em cota a esstêca tea o geao, pecebemos que a p ete os temas é meo o que a foça eletomotz (fem), evo à pea e p a esstêca tea." - + = -. OENTE DE TO-IITO Se lgamos os os temas e um
AULA 23 FATORES DE FORMA DE RADIAÇÃO TÉRMICA
 Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
Notas de aula de PME 336 Pocessos de Tasfeêcia de Calo e Massa 98 AULA 3 ATORES DE ORMA DE RADIAÇÃO TÉRMICA Cosidee o caso de duas supefícies egas quaisque que tocam calo po adiação témica ete si. Supoha
Prof. Anderson Coser Gaudio Departamento de Física Centro de Ciências Exatas Universidade Federal do Espírito Santo
 POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
PROPAGAÇÃO E RADIAÇÃO DE ONDAS ELECTROMAGNÉTICAS (PROE) CONCEITOS FUNDAMENTAIS
 MC Ao Lectvo 6/7 º Semeste PROPAGAÇÃO RADIAÇÃO D ONDAS LCTROMAGNÉTICAS (PRO) CONCITOS FUNDAMNTAIS Custódo Pexeo Setembo 6 ste documeto fo cocebdo paa sev de gua as aulas teócas e apeas como tal deveá se
MC Ao Lectvo 6/7 º Semeste PROPAGAÇÃO RADIAÇÃO D ONDAS LCTROMAGNÉTICAS (PRO) CONCITOS FUNDAMNTAIS Custódo Pexeo Setembo 6 ste documeto fo cocebdo paa sev de gua as aulas teócas e apeas como tal deveá se
Eletricidade e Magnetismo II Licenciatura: 1ª Aula (30/07/2012) Prof. Alvaro Vannucci. Revisão das Leis de Gauss, de Ampère e de Faraday
 Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
Dinâmica do Sistema Solar
 Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Física I IME. 2º Semestre de Instituto de Física Universidade de São Paulo. Professor: Luiz Nagamine Fone: 3091.
 Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
Física I. Aula 9 Rotação, momento inércia e torque
 Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
ELECTROMAGNETISMO E ÓPTICA Cursos: MEBiom + MEFT + LMAC 1 o TESTE (16/4/2016) Grupo I
 ELECTROMAGNETIMO E ÓPTICA Cusos: MEBom + MEFT + LMAC o TETE (6/4/06) Gupo I A fgua epesenta um conensao esféco e um conuto eteo 3 também esféco. O conensao é consttuío po um conuto nteo e ao R cm e po
ELECTROMAGNETIMO E ÓPTICA Cusos: MEBom + MEFT + LMAC o TETE (6/4/06) Gupo I A fgua epesenta um conensao esféco e um conuto eteo 3 também esféco. O conensao é consttuío po um conuto nteo e ao R cm e po
MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO
 Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
Existem várias aplicações onde a medição do fluxo de calor é desejada: análise de cargas térmicas, isolamento de tubulações, etc.
 MEDIDORES DE FLUXO DE CALOR Exstem váas aplcações onde a medção do fluxo de calo é desejada: análse de cagas témcas, solamento de tubulações, etc. Meddo tpo Plug Quando o fluxo de calo é mposto na supefíce
MEDIDORES DE FLUXO DE CALOR Exstem váas aplcações onde a medção do fluxo de calo é desejada: análse de cagas témcas, solamento de tubulações, etc. Meddo tpo Plug Quando o fluxo de calo é mposto na supefíce
3.1 Campo da Gravidade Normal Terra Normal
 . Campo da avidade Nomal.. Tea Nomal tedeemos po Tea omal um elipsóide de evolução qual se atibui a mesma massa M e a mesma velocidade agula da Tea eal e tal que o esfeopotecial U seja uma fução costate
. Campo da avidade Nomal.. Tea Nomal tedeemos po Tea omal um elipsóide de evolução qual se atibui a mesma massa M e a mesma velocidade agula da Tea eal e tal que o esfeopotecial U seja uma fução costate
DINÂMICA DOS SISTEMAS DE PARTÍCULAS E DOS CORPOS RÍGIDOS
 DNÂCA DS SSTEAS DE ARTÍCUAS E DS CRS RÍDS. Cabta Neves Setembo de 005 Ídce ometo lea de um sstema de atículas... 3 Teoema do movmeto do ceto de massa... 3 3 cío da Cosevação do ometo ea... 6 4 cío do Tabalho-Eega
DNÂCA DS SSTEAS DE ARTÍCUAS E DS CRS RÍDS. Cabta Neves Setembo de 005 Ídce ometo lea de um sstema de atículas... 3 Teoema do movmeto do ceto de massa... 3 3 cío da Cosevação do ometo ea... 6 4 cío do Tabalho-Eega
A ab = 1 pol 2 A bd = 2 pol 2. L AB = 2,0 pés = 24 pol L BC = 1,5 pés = 18 pol L CD = 1,0 pés = 12 pol
 Resstêca dos Mateas ecícos de Foças as emplo - baa composta de -3 (=9 ks) mostada a fgua abao está composta po dos segmetos, B e BD, com áeas da seção tasvesal B = pol e BD = pol. Detema o deslocameto
Resstêca dos Mateas ecícos de Foças as emplo - baa composta de -3 (=9 ks) mostada a fgua abao está composta po dos segmetos, B e BD, com áeas da seção tasvesal B = pol e BD = pol. Detema o deslocameto
Aula 3 Trabalho e Energia - Bioenergética
 Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Eletromagnetismo Licenciatura. 18 a aula. Professor Alvaro Vannucci
 leomagesmo Lcecaua 8 a aula Pofesso Alvao Vaucc Na úlma aula vmos... Poêca adada po um Dpolo léco que Oscla: P dpolo p 0 4 c quao que a Poêca adada po uma aea mea-oda: P aea q 0 4 c Agoa, em emos do valo
leomagesmo Lcecaua 8 a aula Pofesso Alvao Vaucc Na úlma aula vmos... Poêca adada po um Dpolo léco que Oscla: P dpolo p 0 4 c quao que a Poêca adada po uma aea mea-oda: P aea q 0 4 c Agoa, em emos do valo
FLUXO E DIVERGENTE DE UM CAMPO VETORIAL
 ISTITUTO DE FÍSIC D UFB DEPRTMETO DE FÍSIC DO ESTDO SÓLIDO DISCIPLI: FÍSIC ERL E EXPERIMETL I FIS 4 FLUXO E DIERETE DE UM CMPO ETORIL Os concetos de dvegente e otaconal estão elaconados aos de fluo e de
ISTITUTO DE FÍSIC D UFB DEPRTMETO DE FÍSIC DO ESTDO SÓLIDO DISCIPLI: FÍSIC ERL E EXPERIMETL I FIS 4 FLUXO E DIERETE DE UM CMPO ETORIL Os concetos de dvegente e otaconal estão elaconados aos de fluo e de
Eletromagnetismo II 1 o Semestre de 2007 Noturno - Prof. Alvaro Vannucci
 leomagesmo II o Semese de 7 Nouo - Pof. Alvao Vaucc 3 a aula /ab/7 Vmos: Odas sfécas (vácuo: = Ψ (modo T e B = ( ψ ω c ' = ω B ' = ψ c ( ψ (modo TM ; ω Ψ + Ψ = sedo que ψ sasfaz: c (equação scala de Helmholz
leomagesmo II o Semese de 7 Nouo - Pof. Alvao Vaucc 3 a aula /ab/7 Vmos: Odas sfécas (vácuo: = Ψ (modo T e B = ( ψ ω c ' = ω B ' = ψ c ( ψ (modo TM ; ω Ψ + Ψ = sedo que ψ sasfaz: c (equação scala de Helmholz
UM MÉTODO PARA CONDUÇÃO DE INVENTÁRIOS FLORESTAIS SEM O USO DE EQUAÇÕES VOLUMÉTRICAS 1
 Um Método paa Codução de Ivetáos Floestas sem 3 UM MÉTODO PARA CONDUÇÃO DE INVENTÁRIOS FLORESTAIS SEM O USO DE EQUAÇÕES VOLUMÉTRICAS Helo Gaca Lete e Vald Calos Lma de Adade 3 RESUMO - Neste tabalho foam
Um Método paa Codução de Ivetáos Floestas sem 3 UM MÉTODO PARA CONDUÇÃO DE INVENTÁRIOS FLORESTAIS SEM O USO DE EQUAÇÕES VOLUMÉTRICAS Helo Gaca Lete e Vald Calos Lma de Adade 3 RESUMO - Neste tabalho foam
Difusão entre Dois Compartimentos
 59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
59087 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 4 Dfusão etre Dos Compartmetos A le de Fck para membraas (equação 4 da aula passada) mplca que a permeabldade de uma membraa a um soluto é dada pela razão
1 - CORRELAÇÃO LINEAR SIMPLES rxy
 1 - CORRELAÇÃO LINEAR IMPLE Em pesquisas, feqüetemete, pocua-se veifica se existe elação ete duas ou mais vaiáveis, isto é, sabe se as alteações sofidas po uma das vaiáveis são acompahadas po alteações
1 - CORRELAÇÃO LINEAR IMPLE Em pesquisas, feqüetemete, pocua-se veifica se existe elação ete duas ou mais vaiáveis, isto é, sabe se as alteações sofidas po uma das vaiáveis são acompahadas po alteações
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou. experimental.
 É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
É o grau de assocação etre duas ou mas varáves. Pode ser: correlacoal ou Prof. Lorí Val, Dr. val@mat.ufrgs.r http://www.mat.ufrgs.r/~val/ expermetal. Numa relação expermetal os valores de uma das varáves
(1) no domínio : 0 x < 1, : constante não negativa. Sujeita às condições de contorno: (2-a) (2-b) CC2: 0
 EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
EXEMPLO MOTIVADO II EXEMPLO MOTIVADO II Método da Apromação Polomal Aplcado a Problemas Udrecoas sem Smetra. Equações Dferecas Ordáras Problemas de Valores o otoro Estrutura Geral do Problema: dy() d y()
2*5$',(17('2327(1&,$/( (1(5*,$12&$032(/(75267È7,&2
 3 *5',7'37&,/ 5*,&3/7567È7,& ÃÃÃ*5',7Ã'Ã37&,/ A expessão geéica paa o cálculo da difeeça de potecial como uma itegal de liha é: dl ) 5) Se o camiho escolhido fo um L, tal que se possa cosidea costate esse
3 *5',7'37&,/ 5*,&3/7567È7,& ÃÃÃ*5',7Ã'Ã37&,/ A expessão geéica paa o cálculo da difeeça de potecial como uma itegal de liha é: dl ) 5) Se o camiho escolhido fo um L, tal que se possa cosidea costate esse
UMA FORMA SIMPLIFICADA DE DEDUZIR AS EQUAÇÕES DE HARTREE E HARTREE-FOCK
 Qum. Nova, Vol. 8, No. 7, 995-00, 05 http://dx.do.og/0.595/000-404.05008 UMA FORMA SIMPLIFICADA D DDUZIR AS QUAÇÕS D HARTR HARTR-FOC Rogéo Custodo Isttuto de Químca, Uvesdade stadual de Campas, Baão Gealdo,
Qum. Nova, Vol. 8, No. 7, 995-00, 05 http://dx.do.og/0.595/000-404.05008 UMA FORMA SIMPLIFICADA D DDUZIR AS QUAÇÕS D HARTR HARTR-FOC Rogéo Custodo Isttuto de Químca, Uvesdade stadual de Campas, Baão Gealdo,
Física Geral I - F Aula 13 Conservação do Momento Angular e Rolamento. 2 0 semestre, 2010
 Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO. Departamento de Engenharia Mecânica
 PME 00 MECÂNIC P3 6 de unho de 009 Duação da Pova: 0 mnutos (não é pemtdo uso de calculadoas) ENÇÃ: a pova consta de 3 questões de aplcação da teoa estudada valendo 0 pontos e de 4 questões teócas, cua
PME 00 MECÂNIC P3 6 de unho de 009 Duação da Pova: 0 mnutos (não é pemtdo uso de calculadoas) ENÇÃ: a pova consta de 3 questões de aplcação da teoa estudada valendo 0 pontos e de 4 questões teócas, cua
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Equlíbro e o Potecal de Nerst 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 11 Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
2ªAula do cap. 11. Quantidade de Movimento Angular L. Conservação do Momento Angular: L i = L f
 2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
Cap. 5. Testes de Hipóteses
 Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
Cap. 5. Testes de Hpóteses Neste capítulo será estudado o segudo problema da ferêca estatístca: o teste de hpóteses. Um teste de hpóteses cosste em verfcar, a partr das observações de uma amostra, se uma
2 o CONGRESSO BRASILEIRO DE P&D EM PETRÓLEO & GÁS
 o CONGRESSO BRASILEIRO DE &D EM ETRÓLEO & GÁS ANÁLISE DESCRITIVA DE DADOS DE VENTOS VISANDO ALICAÇÕES EM LATAFORMAS G. M. G. Leal, F. A. M. Souza UFCG/CCT/DME/) Av. Apígo Veloso, 88 Bodocogó, 5809-970
o CONGRESSO BRASILEIRO DE &D EM ETRÓLEO & GÁS ANÁLISE DESCRITIVA DE DADOS DE VENTOS VISANDO ALICAÇÕES EM LATAFORMAS G. M. G. Leal, F. A. M. Souza UFCG/CCT/DME/) Av. Apígo Veloso, 88 Bodocogó, 5809-970
Capítulo 2 Galvanômetros
 Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
AULA Produto interno em espaços vectoriais reais ou complexos Produto Interno. Norma. Distância.
 Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Note bem: a letura destes apotametos ão dspesa de modo algum a letura ateta da bblografa prcpal da cadera Chama-se a ateção para a mportâca do trabalho pessoal a realzar pelo aluo resoledo os problemas
Fundamentos da Eletrostática Aula 15 Expansão Multipolar II
 Fundamentos da Eletostátca Aula 5 Expansão Multpola II Pof Alex G Das Pof Alysson F Fea A Expansão Multpola Na aula passada, consdeamos uma dstbução de cagas muto especíca paa enconta o potencal do dpolo
Fundamentos da Eletostátca Aula 5 Expansão Multpola II Pof Alex G Das Pof Alysson F Fea A Expansão Multpola Na aula passada, consdeamos uma dstbução de cagas muto especíca paa enconta o potencal do dpolo
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC
 4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
3.3 Potencial e campo elétrico para dadas configurações de carga.
 . Potencial e campo elético paa dadas configuações de caga. Emboa a maio utilidade do potencial se evele em situações em ue a pópia configuação de caga é uma incógnita, nas situações com distibuições conhecidas
. Potencial e campo elético paa dadas configuações de caga. Emboa a maio utilidade do potencial se evele em situações em ue a pópia configuação de caga é uma incógnita, nas situações com distibuições conhecidas
Radiosidade. Claudio Esperança Paulo Roma Cavalcanti
 Radosdade Claudo Esperaça Paulo Roma Cavalcat Radosdade Resumo Modelo de lumação global Lumosdade aparete de um poto de uma superfíce depede de todos os potos de todas as superfíces Cada obeto da cea é
Radosdade Claudo Esperaça Paulo Roma Cavalcat Radosdade Resumo Modelo de lumação global Lumosdade aparete de um poto de uma superfíce depede de todos os potos de todas as superfíces Cada obeto da cea é
CAPÍTULO 10 DINÂMICA DO MOVIMENTO ESPACIAL DE CORPOS RÍGIDOS
 94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
Capítulo V - Interpolação Polinomial
 Métodos Numércos C Balsa & A Satos Capítulo V - Iterpolação Polomal Iterpolação Cosdere o segute couto de dados: x : x0 x x y : y y y 0 m m Estes podem resultar de uma sequêca de meddas expermetas, ode
Métodos Numércos C Balsa & A Satos Capítulo V - Iterpolação Polomal Iterpolação Cosdere o segute couto de dados: x : x0 x x y : y y y 0 m m Estes podem resultar de uma sequêca de meddas expermetas, ode
Sumário. Mecânica. Sistemas de partículas
 umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
umáro Udade I MECÂNICA 2- Cetro de massa e mometo lear de um sstema de partículas - stemas de partículas e corpo rígdo. - Cetro de massa. - Como determar o cetro de massa dum sstema de partículas. - Vetor
Matemática do Ensino Médio vol.2
 Matemática do Ensino Médio vol.2 Cap.11 Soluções 1) a) = 10 1, = 9m = 9000 litos. b) A áea do fundo é 10 = 0m 2 e a áea das paedes é (10 + + 10 + ) 1, = 51,2m 2. Como a áea que seá ladilhada é 0 + 51,2
Matemática do Ensino Médio vol.2 Cap.11 Soluções 1) a) = 10 1, = 9m = 9000 litos. b) A áea do fundo é 10 = 0m 2 e a áea das paedes é (10 + + 10 + ) 1, = 51,2m 2. Como a áea que seá ladilhada é 0 + 51,2
F-328 Física Geral III
 F-328 Físca Geal III Aula exploatóa Cap. 24 UNICAMP IFGW F328 1S2014 F328 1S2014 1 Pontos essencas Enega potencal elétca U Sstema de cagas Equvalente ao tabalho executado po um agente exteno paa taze as
F-328 Físca Geal III Aula exploatóa Cap. 24 UNICAMP IFGW F328 1S2014 F328 1S2014 1 Pontos essencas Enega potencal elétca U Sstema de cagas Equvalente ao tabalho executado po um agente exteno paa taze as
INTEGRAL DE LINHA E ROTACIONAL DE UM CAMPO VETORIAL
 ISTITUTO DE FÍSICA DA UFBA DEPARTAMETO DE FÍSICA DO ESTADO SÓLIDO DISCIPLIA: FÍSICA ERAL E EXPERIMETAL IV FIS ITERAL DE LIHA E ROTACIOAL DE UM CAMPO VETORIAL Sea um campo de velocdades v não unfome em
ISTITUTO DE FÍSICA DA UFBA DEPARTAMETO DE FÍSICA DO ESTADO SÓLIDO DISCIPLIA: FÍSICA ERAL E EXPERIMETAL IV FIS ITERAL DE LIHA E ROTACIOAL DE UM CAMPO VETORIAL Sea um campo de velocdades v não unfome em
RELACIONAMENTO ENTRE REFERENCIAIS LOCAIS E REFERENCIAIS GLOBAIS: PROBLEMA PROCRUSTES SIMPLES
 ELACIONAMENTO ENTE EEENCIAIS LOCAIS E EEENCIAIS GLOBAIS: POBLEMA POCUSTES SIMPLES Maa Apaecda ehpfeg aett Sílvo ogéo Coea de etas Luís Augusto Koeg Vega 3 Uvesdade edeal do Paaá UP - Cuso de Pós Gaduação
ELACIONAMENTO ENTE EEENCIAIS LOCAIS E EEENCIAIS GLOBAIS: POBLEMA POCUSTES SIMPLES Maa Apaecda ehpfeg aett Sílvo ogéo Coea de etas Luís Augusto Koeg Vega 3 Uvesdade edeal do Paaá UP - Cuso de Pós Gaduação
Forma Integral das Equações Básicas para Volume de Controle (cont.)
 EOLA DE ENGENHARIA DE SÃO CARLOS Núcleo de Egehaia Témica e Fluidos Foma Itegal das Equações Básicas paa Volume de Cotole (cot.) Teoema do Taspote de Reyolds: elação geal ete a taxa de vaiação de qq. popiedade
EOLA DE ENGENHARIA DE SÃO CARLOS Núcleo de Egehaia Témica e Fluidos Foma Itegal das Equações Básicas paa Volume de Cotole (cot.) Teoema do Taspote de Reyolds: elação geal ete a taxa de vaiação de qq. popiedade
Resoluções dos exercícios propostos
 da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
Luiz Facisco da Cuz Depatameto de Matática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas b defiidas a que se pudesse
d s F = m dt Trabalho Trabalho
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Trabalho 1. Itrodução
DETERMINAÇÃO DE ATITUDE DE SATÉLITES ARTIFICIAIS COM FILTRO DE KALMAN E MÉTODO DA MÁXIMA VEROSSIMILHANÇA
 INPE-5-PRE/88 DEERMINÇÃO DE IDE DE SÉIES RIFICIIS COM FIRO DE MN E MÉODO D MÁXIM EROSSIMIHNÇ Julaa Guastal haes* *Bolssta FEG/NESP Relatóo Fal de Pojeto de Icação Cetífca PIBIC/CNP/INPE, oetado pelo D.
INPE-5-PRE/88 DEERMINÇÃO DE IDE DE SÉIES RIFICIIS COM FIRO DE MN E MÉODO D MÁXIM EROSSIMIHNÇ Julaa Guastal haes* *Bolssta FEG/NESP Relatóo Fal de Pojeto de Icação Cetífca PIBIC/CNP/INPE, oetado pelo D.
Vimos que: 1) Interação coulombiana residual para os elétrons efeito perturbativo
 Vmos que: Iteação couombaa esdua paa os eétos efeto petubatvo V ee No caso de eétos em uma subcamada, o sp tota pode se S0 sgeto ou S tpeto Um sstema costtuído de váos e - deve se descto po uma autofução
Vmos que: Iteação couombaa esdua paa os eétos efeto petubatvo V ee No caso de eétos em uma subcamada, o sp tota pode se S0 sgeto ou S tpeto Um sstema costtuído de váos e - deve se descto po uma autofução
ANIMAÇÃO DE FLUIDOS VIA TÉCNICAS DE VISUALIZAÇÃO CIENTÍFICA E MECÂNICA COMPUTACIONAL GILSON A. GIRALDI ANTONIO L. APOLINÁRIO JR.
 ANIMAÇÃO DE FLUIDOS VIA TÉCNICAS DE VISUALIZAÇÃO CIENTÍFICA E MECÂNICA COMPUTACIONAL GILSON A. GIRALDI ANTONIO L. APOLINÁRIO JR. ANTONIO A. F. OLIVEIRA RAUL A. FEIJÓO LABORATÓRIO NACIONAL DE COMPUTAÇÃO
ANIMAÇÃO DE FLUIDOS VIA TÉCNICAS DE VISUALIZAÇÃO CIENTÍFICA E MECÂNICA COMPUTACIONAL GILSON A. GIRALDI ANTONIO L. APOLINÁRIO JR. ANTONIO A. F. OLIVEIRA RAUL A. FEIJÓO LABORATÓRIO NACIONAL DE COMPUTAÇÃO
CIRCUITOS ELÉTRICOS CONCEITOS BÁSICOS
 CCUTOS ELÉTCOS CONCETOS BÁSCOS Prof. Marcos Fergütz jul/07 - Carga Elétrca (Q, q) [ Udade: Coulomb C ] e - Quado se forece ou retra eerga do elétro (e - ), pode-se movmetá-lo por etre as camadas (K, L,
CCUTOS ELÉTCOS CONCETOS BÁSCOS Prof. Marcos Fergütz jul/07 - Carga Elétrca (Q, q) [ Udade: Coulomb C ] e - Quado se forece ou retra eerga do elétro (e - ), pode-se movmetá-lo por etre as camadas (K, L,
6. MÉTODOS APROXIMADOS DE ANÁLISE DE SISTEMAS CONTÍNUOS
 6. ÉOOS APROXAOS ANÁS SSAS CONÍNUOS Nos dos capítulos aterores, estudaram-se métodos exactos de aálse de sstemas dscretos e de sstemas cotíuos. Agora, serão aalsados algus métodos aproxmados da solução
6. ÉOOS APROXAOS ANÁS SSAS CONÍNUOS Nos dos capítulos aterores, estudaram-se métodos exactos de aálse de sstemas dscretos e de sstemas cotíuos. Agora, serão aalsados algus métodos aproxmados da solução
CAPÍTULO 2 DINÂMICA DA PARTÍCULA: FORÇA E ACELERAÇÃO
 13 CAPÍTULO 2 DINÂMICA DA PATÍCULA: OÇA E ACELEAÇÃO Nese capíulo seá aalsada a le de Newo a sua foma dfeecal, aplcada ao movmeo de paículas. Nesa foma a foça esulae das foças aplcadas uma paícula esá elacoada
13 CAPÍTULO 2 DINÂMICA DA PATÍCULA: OÇA E ACELEAÇÃO Nese capíulo seá aalsada a le de Newo a sua foma dfeecal, aplcada ao movmeo de paículas. Nesa foma a foça esulae das foças aplcadas uma paícula esá elacoada
Os fundamentos da Física Volume 3 1. Resumo do capítulo
 Os fundamentos da Físca Volume 3 1 Capítulo 13 Campo magnétco Ímãs são copos que apesentam fenômenos notáves, denomnados fenômenos magnétcos, sendo os pncpas: I. ataem fagmentos de feo (lmalha). o caso
Os fundamentos da Físca Volume 3 1 Capítulo 13 Campo magnétco Ímãs são copos que apesentam fenômenos notáves, denomnados fenômenos magnétcos, sendo os pncpas: I. ataem fagmentos de feo (lmalha). o caso
n. A densidade de corrente associada a esta espécie iônica é J n. O modelo está ilustrado na figura abaixo.
 5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
5910187 Bofísca II FFCLRP USP Prof. Atôo Roque Aula 6 Equlíbro e o Potecal de Nerst Nesta aula, vamos utlzar a equação para o modelo de eletrodfusão o equlíbro obtda a aula passada para estudar o trasporte
Aula 7: Potencial Elétrico
 Unvesdade Fedeal do Paaná Seto de Cêncas Exatas Depatamento de Físca Físca III Po. D. Rcado Luz Vana Reeêncas bblogácas: H. 6-, 6-, 6-3, 6-4, 6-5, 6-6, 6-, 6- S. 4-, 4-3, 4-4, 4-5 T. -, -, -3, -6 Aula
Unvesdade Fedeal do Paaná Seto de Cêncas Exatas Depatamento de Físca Físca III Po. D. Rcado Luz Vana Reeêncas bblogácas: H. 6-, 6-, 6-3, 6-4, 6-5, 6-6, 6-, 6- S. 4-, 4-3, 4-4, 4-5 T. -, -, -3, -6 Aula
Disciplina: FGE5748 Simulação Computacional de Líquidos Moleculares 1
 Dscplna: FGE5748 Smulação Computaconal de Líudos Moleculaes 1 Dnâmca Molecula F v f v a t s f s v t(1/)a t () Método Monte Calo P e ( / kt ) Z no ensemble NVT σ ε Dscplna: FGE5748 Smulação Computaconal
Dscplna: FGE5748 Smulação Computaconal de Líudos Moleculaes 1 Dnâmca Molecula F v f v a t s f s v t(1/)a t () Método Monte Calo P e ( / kt ) Z no ensemble NVT σ ε Dscplna: FGE5748 Smulação Computaconal
CAPÍTULO 3 MEDIDAS DE TENDÊNCIA CENTRAL E VARIABILIDADE PPGEP Medidas de Tendência Central Média Aritmética para Dados Agrupados
 3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
3.1. Meddas de Tedêca Cetral CAPÍTULO 3 MEDIDA DE TENDÊNCIA CENTRAL E VARIABILIDADE UFRG 1 Há váras meddas de tedêca cetral. Etre elas ctamos a méda artmétca, a medaa, a méda harmôca, etc. Cada uma dessas
Seção 24: Laplaciano em Coordenadas Esféricas
 Seção 4: Laplaciano em Coodenadas Esféicas Paa o leito inteessado, na pimeia seção deduimos a expessão do laplaciano em coodenadas esféicas. O leito ue estive disposto a aceita sem demonstação pode dietamente
Seção 4: Laplaciano em Coodenadas Esféicas Paa o leito inteessado, na pimeia seção deduimos a expessão do laplaciano em coodenadas esféicas. O leito ue estive disposto a aceita sem demonstação pode dietamente
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
 PME 3100 MECÂNIC I Teceia Pova 6 de uho de 015 Duação da Pova: 110 miutos (ão é pemitido uso de calculadoas) 1ª Questão (4,0 potos) fiua mosta um disco de ceto, massa m e aio, que pate do epouso e ola
PME 3100 MECÂNIC I Teceia Pova 6 de uho de 015 Duação da Pova: 110 miutos (ão é pemitido uso de calculadoas) 1ª Questão (4,0 potos) fiua mosta um disco de ceto, massa m e aio, que pate do epouso e ola
MATEMÁTICA II - Engenharias/Itatiba SISTEMAS LINEARES
 - Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
- Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
Universidade de São Paulo Instituto de Física. Física Moderna II. Profa. Márcia de Almeida Rizzutto 2 o Semestre de Física Moderna 2 Aula 20
 Uivesidade de São Paulo Istituto de Física Física Modea II Pofa. Mácia de Almeida Rizzutto o Semeste de 14 Física Modea 1 Todos os tipos de ligação molecula se devem ao fato de a eegia total da molécula
Uivesidade de São Paulo Istituto de Física Física Modea II Pofa. Mácia de Almeida Rizzutto o Semeste de 14 Física Modea 1 Todos os tipos de ligação molecula se devem ao fato de a eegia total da molécula
ELETRICIDADE CAPÍTULO 3 LEIS DE CIRCUITOS ELÉTRICOS
 ELETICIDADE CAPÍTULO 3 LEIS DE CICUITOS ELÉTICOS - CONSIDEE A SEGUINTE ELAÇÃO: 3. LEI DE OHM - QUALQUE POCESSO DE CONVESÃO DE ENEGIA PODE SE ELACIONADO A ESTA EQUAÇÃO. - EM CICUITOS ELÉTICOS : - POTANTO,
ELETICIDADE CAPÍTULO 3 LEIS DE CICUITOS ELÉTICOS - CONSIDEE A SEGUINTE ELAÇÃO: 3. LEI DE OHM - QUALQUE POCESSO DE CONVESÃO DE ENEGIA PODE SE ELACIONADO A ESTA EQUAÇÃO. - EM CICUITOS ELÉTICOS : - POTANTO,
Para duas variáveis aleatórias X e Y define-se Função Distribuição Cumulativa CDF F XY (x,y)
 Vaáves Aleatóas (contnuação) Po. Waldec Peella Dstbução Conunta: po: Paa duas vaáves aleatóas e dene-se Função Dstbução Cuulatva CDF F (,y) P ( e y ) = F (,y ) e a Função Densdade de Pobabldade de Pobabldade
Vaáves Aleatóas (contnuação) Po. Waldec Peella Dstbução Conunta: po: Paa duas vaáves aleatóas e dene-se Função Dstbução Cuulatva CDF F (,y) P ( e y ) = F (,y ) e a Função Densdade de Pobabldade de Pobabldade
MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R 3
 MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R Modelg of ceteg eos o the o the thee-dmesoal space (R ). JAIR MENDES MARQUES Uvesdade Tuut do Paaá Rua Macelo Champagat,55 CEP 87-5 Cutba PR ja.maques@utp.b
MODELAGEM DO ERRO DE CENTRAGEM NO ESPAÇO TRIDIMENSIONAL R Modelg of ceteg eos o the o the thee-dmesoal space (R ). JAIR MENDES MARQUES Uvesdade Tuut do Paaá Rua Macelo Champagat,55 CEP 87-5 Cutba PR ja.maques@utp.b
Números Complexos (Parte II) 1 Plano de Argand-Gauss. 2 Módulo de um número complexo. Prof. Gustavo Adolfo Soares
 Númeos Complexos (Pate II) 1 Plao de Agad-Gauss Das defiições de que um úmeo complexo é um pa odeado de úmeos eais x e y e que C = R R, temos que: A cada úmeo complexo coespode um úico poto do plao catesiao,
Númeos Complexos (Pate II) 1 Plao de Agad-Gauss Das defiições de que um úmeo complexo é um pa odeado de úmeos eais x e y e que C = R R, temos que: A cada úmeo complexo coespode um úico poto do plao catesiao,
EQUAÇÕES DINÂMICAS DE MOVIMENTO PARA CORPOS RÍGIDOS UTILIZANDO REFERENCIAL MÓVEL
 NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
Credenciada e Autorizada pelo MEC, Portaria n. o. 644 de 28 de março de 2001 Publicado no D.O.U. em 02/04/2001
 Ceecaa e Autozaa pelo MEC, Potaa. o. 644 e 8 e maço e 00 Publcao o D.O.U. em 0/04/00 ESTATÍSTICA Pelo Poesso Gealo Pacheco A Estatístca é uma pate a Matemátca Aplcaa que oece métoos paa coleta, ogazação,
Ceecaa e Autozaa pelo MEC, Potaa. o. 644 e 8 e maço e 00 Publcao o D.O.U. em 0/04/00 ESTATÍSTICA Pelo Poesso Gealo Pacheco A Estatístca é uma pate a Matemátca Aplcaa que oece métoos paa coleta, ogazação,
Capítulo 5: Ajuste de curvas pelo método dos mínimos quadrados
 Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Capítulo : Ajuste de curvas pelo método dos mímos quadrados. agrama de dspersão No capítulo ateror estudamos uma forma de ldar com fuções matemátcas defdas por uma taela de valores. Frequetemete o etato
Física Geral. Força e Torque
 ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
PROBLEMAS SOBRE PONTOS I Davi Maximo (UFC) e Samuel Feitosa (UFC)
 PROBLEMAS SOBRE PONTOS I Dav Maxmo (UFC) e Samuel Fetosa (UFC) Dstbu potos um plao ou um espaço é uma taefa que pode se ealzada de foma muto abtáa. Po sso poblemas sobe potos podem se de dvesas atuezas.
PROBLEMAS SOBRE PONTOS I Dav Maxmo (UFC) e Samuel Fetosa (UFC) Dstbu potos um plao ou um espaço é uma taefa que pode se ealzada de foma muto abtáa. Po sso poblemas sobe potos podem se de dvesas atuezas.
REGRESSÃO LINEAR 05/10/2016 REPRESENTAÇAO MATRICIAL. Y i = X 1i + 2 X 2i k X ni + i Y = X + INTRODUÇÃO SIMPLES MÚLTIPLA
 REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
REGRESSÃO LINEAR CUIABÁ, MT 6/ INTRODUÇÃO Relação dos valores da varável depedete (varável resposta) aos valores de regressoras ou exógeas). SIMPLES MÚLTIPLA (varáves depedetes,... =,,, K=,,, k em que:
Condução Unidimensional em Regime Permanente
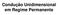 Condução Unidimensional em Regime Pemanente Num sistema unidimensional os gadientes de tempeatua existem somente ao longo de uma única coodenada, e a tansfeência de calo ocoe exclusivamente nesta dieção.
Condução Unidimensional em Regime Pemanente Num sistema unidimensional os gadientes de tempeatua existem somente ao longo de uma única coodenada, e a tansfeência de calo ocoe exclusivamente nesta dieção.
Interpolação. Exemplo de Interpolação Linear. Exemplo de Interpolação Polinomial de grau superior a 1.
 Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Iterpolação Iterpolação é um método que permte costrur um ovo cojuto de dados a partr de um cojuto dscreto de dados potuas cohecdos. Em egehara e cêcas, dspõese habtualmete de dados potuas, obtdos a partr
Capítulo 4 Variáveis Aleatórias Discretas. Prof. Fabrício Maciel Gomes
 Capítulo 4 Vaiáveis Aleatóias Discetas Pof. Fabício Maciel Gomes Picipais Distibuições de Pobabilidade Discetas Equipovável Beoulli Biomial Poisso Geomética Pascal Hipegeomética Distibuição Equipovável
Capítulo 4 Vaiáveis Aleatóias Discetas Pof. Fabício Maciel Gomes Picipais Distibuições de Pobabilidade Discetas Equipovável Beoulli Biomial Poisso Geomética Pascal Hipegeomética Distibuição Equipovável
2. MODELO DETALHADO: Relações de Recorrência. Exemplo: Algoritmo Recursivo para Cálculo do Fatorial Substituição Repetida
 . MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
. MODELO DETALHADO: Relações de Recorrêca Exemplo: Algortmo Recursvo para Cálculo do Fatoral Substtução Repetda T T ( ) ( ) t 1, T ( + t, > T ( ) T ( + t T ( ) ( T( ) + t + t ) + t T ( ) T ( ) T ( ) +
Revisão de Estatística X = X n
 Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Revsão de Estatístca MÉDIA É medda de tedêca cetral mas comumete usada ara descrever resumdamete uma dstrbução de freqüêca. MÉDIA ARIMÉTICA SIMPLES São utlzados os valores do cojuto com esos guas. + +...
Introdução à Teoria dos Números Notas 1 Os Princípios da Boa Ordem e de Indução Finita Prof Carlos Alberto S Soares
 Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
Itrodução à Teora dos Números 018 - Notas 1 Os Prcípos da Boa Ordem e de Idução Fta Prof Carlos Alberto S Soares 1 Prelmares Neste curso, prortaramete, estaremos trabalhado com úmeros teros mas, quado
q(x) = x 4 6x x² - 18x + 10 * z+ z + w + w = 6 ** z z + zw + z w + z w + w w = 15
 MATEMÁTICA Sejam a i, a + si e a + ( s) + ( + s) i ( > ) temos de uma seqüêcia. Detemie, em fução de, os valoes de e s que toam esta seqüêcia uma pogessão aitmética, sabedo que e s são úmeos eais e i -.
MATEMÁTICA Sejam a i, a + si e a + ( s) + ( + s) i ( > ) temos de uma seqüêcia. Detemie, em fução de, os valoes de e s que toam esta seqüêcia uma pogessão aitmética, sabedo que e s são úmeos eais e i -.
MAE0229 Introdução à Probabilidade e Estatística II
 Exercíco Cosdere a dstrbução expoecal com fução de desdade de probabldade dada por f (y; λ) = λe λy, em que y, λ > 0 e E(Y) = /λ Supor que o parâmetro λ pode ser expresso proporcoalmete aos valores de
Exercíco Cosdere a dstrbução expoecal com fução de desdade de probabldade dada por f (y; λ) = λe λy, em que y, λ > 0 e E(Y) = /λ Supor que o parâmetro λ pode ser expresso proporcoalmete aos valores de
O perímetro da circunferência
 Univesidade de Basília Depatamento de Matemática Cálculo 1 O peímeto da cicunfeência O peímeto de um polígono de n lados é a soma do compimento dos seus lados. Dado um polígono qualque, você pode sempe
Univesidade de Basília Depatamento de Matemática Cálculo 1 O peímeto da cicunfeência O peímeto de um polígono de n lados é a soma do compimento dos seus lados. Dado um polígono qualque, você pode sempe
Cinemática Direta. 4 o Engenharia de Controle e Automação FACIT / Prof. Maurílio J. Inácio
 Cnemáta Deta 4 o Engenhaa de Contole e Automação FACI / 9 Pof. Mauílo J. Ináo Cnemáta Deta Cnemáta do manpulado Cnemáta é êna que tata o movmento em ondea a foça que o auam. Na nemáta ão etudado: poçõe,
Cnemáta Deta 4 o Engenhaa de Contole e Automação FACI / 9 Pof. Mauílo J. Ináo Cnemáta Deta Cnemáta do manpulado Cnemáta é êna que tata o movmento em ondea a foça que o auam. Na nemáta ão etudado: poçõe,
INTRODUÇÃO AO ESTUDO DA ÁLGEBRA LINERAR Luiz Francisco da Cruz Departamento de Matemática Unesp/Bauru CAPÍTULO 2 ESPAÇOS VETORIAIS
 Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
Luiz Facisco da Cuz Depatameto de Matemática Uesp/Bauu CAPÍTULO ESPAÇOS VETORIAIS 1 Históico Sabe-se que, até pelo meos o fial do século XIX, ão havia ehuma teoia ou cojuto de egas bem defiidas a que se
