F U N Ç Ã O. Obs.: Noção prática de uma função é quando o valor de uma quantidade depende do valor de outra.

Transcrição

1 Definição: F U N Ç Ã O Uma função f definida em um conjunto de números reais A, é uma regra ou lei (equação ou algoritmo) de correspondência, que atribui um único número real a cada número do conjunto A. O conjunto A dos valores permitidos para chama-se Domínio da função e o conjunto dos valores correspondentes de chamase Imagem da função. Representação: ou f (), pois f ( ) Salário R$, Horas trabalhadas ou. ou f ( ). Variável Dependente () Variável Independente () Obs.: Noção prática de uma função é quando o valor de uma quantidade depende do valor de outra. Eemplos: Salário (variável dependente ) depende do nº de horas trabalhadas (variável independente ); Produção de uma fábrica () depende do número de máquinas utilizadas (); Resistência de um fio elétrico () depende do diâmetro do fio com comprimento fio (); Volume de um gás com pressão constante () depende da temperatura (); etc. Aplicações: ) Um vendedor recebe mensalmente um salário composto de duas partes: uma parte fia, no valor de R$ 6,, e uma parte variável, que corresponde a uma comissão de 8% do total de vendas que ele fez durante o mês. a) Epressar a função que representa seu salário mensal. b) Calcular o salário do vendedor sabendo que durante um mês ele vendeu R$., em produtos. ) O preço a pagar por uma corrida de tái depende da distância percorrida. A tarifa é composta de duas partes: uma fia denominada bandeirada e uma parte variável que depende do número de quilômetros rodados. Suponha que a bandeirada esteja custando R$, e o quilômetro rodado, R$,68. a) Epresse a função que representa a tarifa. b) Quanto se pagará por uma corrida em que o tái rodou km? ) Uma Cia de energia elétrica cobra pela fatura mensal uma tarifa fia de R$, mais R$,4 por kwh consumido. a) Escreva uma função que permita calcular o valor pago mensalmente em função da quantidade de kwh consumidos. b) De acordo com a função escrita, calcule a quantia a ser paga pelo consumo de: 8 kwh, 7 kwh e kwh. c) Quantos kwh uma família consumiu em um mês cujo valor pago foi de R$,? 4) O preço de venda de um livro é de R$ 4, a unidade. Sabendo que o custo de cada livro corresponde a um valor fio de R$, mais R$, por unidade, construa uma função capaz de determinar o lucro líquido (valor descontado das despesas) na venda de livros, e o lucro obtido na venda de 6 livros. ) Um motorista de tái cobra R$, de bandeirada (valor fio) mais R$,7 por quilômetro rodado (valor variável). Determine o valor a ser pago por uma corrida relativa a um percurso de 8 quilômetros. 6) Uma pessoa vai escolher um plano de saúde entre duas opções A e B. Condições dos planos: Plano A cobra um valor fio mensal de R$ 8, e R$, por consulta num certo período e o Plano B cobra um valor fio mensal de R$, e R$, por consulta num certo período. Temos que o gasto total de cada plano é dado em função do número de consultas dentro do período pré estabelecido. Determinar: a) a função correspondente a cada plano. b) Em qual situação o plano A é mais econômico; o plano B é mais econômico; os dois se equivalem. Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br

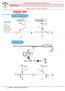
2 Função do º Grau: A. + B ou f() A. + B É a função f dada por A. + B, com Є R e A e B números reais não nulos (zero). A representação gráfica da função do º grau é uma reta pelo ponto (, B), ou seja, o valor do número real B, sempre será um ponto, que deverá ser marcado em cima da reta do. Sendo assim, necessitamos de mais um ponto para a construção da reta. Eemplo : (,) (,) (,). + D(f) < < + ou R Im(f) < < + ou R A > Função Crescente Eemplo : 4. +, se 4. + (,) (,) (,) 4. + se D(f) Im(f) A < Função Decrescente Resumo (esboço gráfico): A > Coeficiente Angular Positivo (+) + A + B A < Coeficiente Angular Negativo ( ) A + B Função Crescente Função Decrescente Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br

3 Coeficiente Angular e Coeficiente Linear A. + B A é a variação em para cada aumento unitário em, é chamado Coeficiente Angular da reta. B identifica o ponto de intersecção da reta com o eio, é chamado Coeficiente Linear. Eemplo: (,) (,) 8 (,8) A 6 -- Coeficiente Angular Coeficiente Linear Ponto de intersecção com o eio B um aumento unitário em acarreta um aumento de unidades em. -- Eercícios: Construa o gráfico de cada uma das funções e determine o domínio D(f) e o conjunto imagem Im(f): a) + e) f ( ) i) + m) f ( ) + b) f ( ). + 4 f) f ( ) + 4 j) f ( ) n) f ( ),6 c) f ( ) + g) f ( ) + k) f ( ) 4 o) f ( ) d) f ( ) h) + l) f ( ) 6 p) Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br

4 Função Constante: k ou f() k Seja k um número real qualquer. A função f definida em R e tal que f() k, recebe o nome de função constante, portanto, o valor de não varia com o aumento de. A representação gráfica de uma função constante é sempre uma reta paralela ou coincidente com o eio (abscissas), passando pelo ponto (, ). Eemplo : ou f() D(f) < < + ou R Im(f) - Eemplo :,, se se Nota: É importante observarmos nesse eemplo que temos (funções) constantes e cada uma delas é delimitada em cima do eio de acordo com seu Domínio, ou seja, a primeira função, está em cima do eio sobre o intervalo de (zero) até (dois) e a segunda função, está em cima do eio sobre o intervalo de (dois) até (cinco). Esses intervalos que delimitam as funções, estabelecendo fronteiras, são chamados de Domínio da função. Eercícios: Construa o gráfico de cada uma das funções e determine o domínio D(f) e o conjunto imagem Im(f): a) f ( ) + d) f ( ) g), se b) e) f ( ) h), se, se 7 c) f ( ) 7 f) i), se < 6, se > 4 Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br

5 Funções Definidas por Várias Sentenças: Construa o gráfico de cada uma das funções e determine o domínio D(f) e o conjunto imagem Im(f): a) 4, se f ( ) d) + 7, se >, se f ( ) +, se < g), se > f ( ), se, se > b) +, se f ( ) e) +, se >, se < f ( ), se h), se > f ( ) + +, se +, se > c) +, se f ( ) f), se >, se < f ( ), se < i) 4, se f +, se < ) ( ), se ( Estudo do Sinal de uma Função do º Grau: O estudo do sinal de uma função do º grau consiste em determinar os valores reais de para os quais é zero, menor que zero ou maior do que zero, ou seja: f(), f() > e f() <. Eemplo: f(). 4 Primeiro, calculamos o zero da função, ou seja, fazemos f() / (zero da função) f(). 4 (, ) 4 (, 4) (, ) f() f() < f() f() 4 + f() > Resumindo: A função f() 4 se anula [f() ] quando. A função f() 4 é positiva [f() > crescente ] quando >. A função f() 4 é negativa [f() < decrescente ] quando <. 4 Eercícios: ) Estude a variação do sinal das seguintes funções do º grau: a) f ( ) + c) f ( ) e) + 6 g) b) + 9 d) f ( ) + f) f ( ) h) Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br f ( ) + ) O lucro de uma Indústria que vende um único produto é dado pela fórmula matemática L() 4 ; L representa o lucro e, a quantidade de produto vendido. Determine a quantidade mínima desse produto que deve ser vendida para que há lucro.

6 Eercícios complementares com funções: ) Escrever a equação da reta A + B, que contém os pontos: P (, ) P (, ) P (, ) a) b) c) P (, ) P (8,) P (, ) ) Obtenha a função f() a. + b, de acordo com cada um dos gráficos a seguir: a) (, ) b) c) (, ) d) P d) P (, ) (8, ) (, ) Resp: f ()/. + Resp: f() ½. Resp: f(). + Resp: f(). ) Uma barra de ferro foi aquecida até uma temperatura de C e a seguir foi resfriada até a temperatura de 6 C. O gráfico mostra a temperatura da barra em função do tempo. a) Depois de quanto tempo, após o início do resfriamento, a temperatura da barra atingiu C. Resp: f ( ) 6. + b) De a 6 minutos, em que intervalo de tempo à temperatura da barra esteve positiva? Resp: a min c) De a 6 minutos, em que intervalo de tempo à temperatura da barra esteve negativa? Resp: a 6 min 6 Temperatura ( C ) 6 Tempo (min) 4) Dada a função do º grau f ( ), calcule: a) f ( ) Resp: b) f ( ) Resp: 7/ c) f ( ) Resp: 4 d) f Resp: ½ ) Se f ( ). +, calcule os valores reais de para que se tenha: a) f ( ) Resp: / b) f ( ) Resp: c) f ( ) - ½ Resp: /6 6) Dada à função f ( ) a. + b, sabe-se que f ( ) 4 e f ( ). Escrever a função f e calcular f ( ). Resp: f ( ). + 6 e f ( ) 7) A função f é definida por f ( ) a. + b. Sabe-se que f ( ) e f ( ). Obter o valor de f ( ). Resp: f ( ) 8) Dada a função f ( ) a. + b e sabendo que f ( ) e f ( ), calcule f. Resp: 9) Obter os valores dos coeficientes linear e angular da função do º grau tal que f ( ) e f ( ). Resp: a e b ) Dada à função f ( ) a. +, determine o valor de a para se tenha f ( 4 ). Resp: a ) O tempo t (em minutos) de desembarque de passageiros de um navio usado para cruzeiros marítimos é n dado ela lei: t ( n ) 7 +, sendo n o número de passageiros. Classifique como verdadeira ( V ) ou falsa ( F ) cada uma das afirmações seguintes: a) Em horas desembarcam 7 passageiros. Resp: ( V ) b) O tempo necessário para o desembarque de 6 passageiros é o dobro do tempo gasto por passageiros. Resp: ( F ) Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br 6

7 Gráficos (RESUMO): Domínio e Imagem ) ) ² Função Par ³ Função Ímpar D(f) < < + ou R Im(f) < + ou [,+ [ D(f) < < + ou R Im(f) < < + ou R ) 4) Função Racional Função Racional D(f) ou R* Im(f) ou R* D(f) ou R* Im(f) < < + ou R + * ) 6) Função Irracional Função Irracional D(f) < + ou [,+ [ Im(f) < + ou [,+ [ D(f) - < < + ou R Im(f) - < < + ou R Atividades Práticas com Domínio de Funções: A) Determine o domínio de cada função definida por: ) f ( ) ) f ( ), com ) f ( ) 4) f ( ) ) f ( ) 6) f ( ) 6 7 Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br

8 7) f ( ) 4 + 8) f ( ) + 9) f ( ) + ) f ( ) ln( ) ) f ( ) 4 ) f ( ) B) Determine o domínio de cada função definida por: ) 4) 7) + f ( ) ) f ( ) ) ( ) f ) f ( ) 9 + 6) ( + f ) + 8) f ( ) 9) 9 f ( ) 4 f ( ) + + f ( ) ) f ( ) + ) + C) Determine o domínio de cada função definida por: ) ) ( ) f { R/ e 4} f ( ) + ) + 4 D ) f ( ) + D { R/,, } 4) 4 ) ( ) ln ( ) f { R/ >} 7) f ( ) ln (6. + ) { R/ < ou > 8} D) Determine o domínio de cada função definida por: f ( ) 9 D R f ( ) f ( ) + 4 D R / < D 6) f ( ) ln ( ) D { R / < < } D 8) f ( ) ln D { R / 4 < < ou > 4} 6 + ) f ( ) + ) f ( ) ) f ( ) + 4) f ( ) ) f ( ) 6) f ( ) ) f ( ) + 8) f ( ) + 9) f ( ) + ) f ( ) + ) f 4 + ( ) ) f ( ) + ) f ( ) 4) f ( ) + 4 BIBLIOGRAFIA: BOULOS, P. Cálculo Diferencial e Integral, Volume. São Paulo, Pearson 6. DEMANA, F. D. Pré cálculo. São Paulo: Pearson, 9. GIOVANNI, J. R. Matemática Fundamental: º Grau: Volume Único. São Paulo: FTD, 994. LEITHOLD, L. Matemática Aplicada a Economia e Administração. São Paulo: Harbra,. MACHADO, A.S. Matemática Temas e Metas: 6 Funções e Derivadas. São Paulo: Atual, 988. SILVA, S.M. Matemática Básica para Cursos Superiores. São Paulo: Atlas,. 8 Prof.Ms.Carlos Henrique carloshjc@ahoo.com.br