Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes
|
|
|
- Raquel Lagos Martins
- 8 Há anos
- Visualizações:
Transcrição
1 Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44
2 Análise do Lugar da Raízes A resposta transitória depende da localização dos pólos de malha fechada Como os pólos de malhada fechada se movem no plano-s à medida que o ganho de malha varia? Dornellas (UNIVASF) Juazeiro - BA 2 / 44
3 Análise do Lugar da Raízes Os pólos de malha fechada são as raízes da equação característica Método do Lugar das Raízes: permite que as raízes da equação característica sejam representados graficamente para todos os valores de um parâmetro do sistema Dornellas (UNIVASF) Juazeiro - BA 3 / 44
4 Método do Lugar da Raízes C(s) R(s) = G(s) 1+G(s)H(s) Equação característica: Condição angular 1+G(s)H(s) = 0 G(s)H(s) = 1 (G(s)H(s)) = ±180 (2k+1) (k = 0,1,2,...) Condição de módulo G(s)H(s) = 1 Dornellas (UNIVASF) Juazeiro - BA 4 / 44
5 Método do Lugar da Raízes Lugar das raízes Lugar dos pontos no plano-s que satisfaz a condição angular Considere G(s)H(s) G(s)H(s)= K(s+z 1)(s+z 2 )...(s+z m ) (s+ p 1 )(s+ p 2 )...(s+ p n ) onde k > 0 é o ganho Dornellas (UNIVASF) Juazeiro - BA 5 / 44
6 Passos para obtenção do Lugar das Raízes e Exemplo 1 Localizar os pólos e zeros de G(s)H(s) no plano-s 2 Determinar os trechos do lugar das raízes no eixo real 3 Determinar as assíntotas do lugar das raízes 4 Determinar os pontos de partida e os de chegada do eixo real 5 Determinar o ângulo de partida de um pólo complexo (ou de chegada a um zero complexo) do lugar das raízes 6 Determinar os pontos onde o lugar das raízes pode cruzar o eixo imaginário 7 Obter uma série de pontos de teste na região próxima à origem do plano-s e esboçar o lugar das raízes 8 Determinar os pólos de malha fechada Dornellas (UNIVASF) Juazeiro - BA 6 / 44
7 1. Localizar os pólos e zeros de G(s)H(s) no plano-s Os ramos se iniciam nos pólos de malha aberta e terminam nos zeros de malha aberta (finitos ou infinitos) O lugar das raízes é sempre simétrico em relação ao eixo real Dornellas (UNIVASF) Juazeiro - BA 7 / 44
8 Exemplo Considere o sistema G(s)H(s) = K s(s+1)(s+2) -2-1 Dornellas (UNIVASF) Juazeiro - BA 8 / 44
9 2. Determinar os trechos do lugar das raízes no eixo real Os pólos e zeros complexos de malha aberta não influenciam os trechos do lugar das raízes no eixo real Se o número de pólos reais e zeros reais à direita do ponto de teste for ímpar, então o ponto de testes pertence ao lugar das raízes Dornellas (UNIVASF) Juazeiro - BA 9 / 44
10 Exemplo -2-1 s (s)+ (s+1)+ (s+2) = 0 Dornellas (UNIVASF) Juazeiro - BA 10 / 44
11 Exemplo -2-1 s (s)+ (s+1)+ (s+2) = 180 Dornellas (UNIVASF) Juazeiro - BA 11 / 44
12 Exemplo -2 s -1 (s)+ (s+1)+ (s+2) = 360 Dornellas (UNIVASF) Juazeiro - BA 12 / 44
13 Exemplo s -2-1 (s)+ (s+1)+ (s+2) = = 180 Dornellas (UNIVASF) Juazeiro - BA 13 / 44
14 Exemplo -2-1 Dornellas (UNIVASF) Juazeiro - BA 14 / 44
15 3. Determinar as assíntotas do lugar das raízes Ângulo das assíntotas G(s)H(s) = K(s+z 1)(s+z 2 )...(s+z m ) (s+ p 1 )(s+ p 2 )...(s+ p n ) ±180 (2k+1) n m (k = 0,1,2,...) Ponto de interseção das abscissas no eixo real (p 1 + p p n ) (z 1 + z z m ) n m Dornellas (UNIVASF) Juazeiro - BA 15 / 44
16 Exemplo Ângulo das assíntotas G(s)H(s) = K s(s+1)(s+2) ±180 (2k+1) 3 0 = ±60 (2k+1) (k = 0,1,2,...) Ponto de interseção das abscissas no eixo real (0+1+2) (0) = Dornellas (UNIVASF) Juazeiro - BA 16 / 44
17 Exemplo Assíntotas Dornellas (UNIVASF) Juazeiro - BA 17 / 44
18 4. Determinar os pontos de partida e os de chegada do eixo real -2-1 Ponto de partida Dornellas (UNIVASF) Juazeiro - BA 18 / 44
19 4. Determinar os pontos de partida e os de chegada do eixo real Exprimir K em função de s na equação característica Os pontos de partida e os de chegada do eixo real são raízes de Observação: dk ds = 0 Nem todas as raízes serão pontos de partida e chegada É necessário que pertençam ao lugar das raízes no eixo real Dornellas (UNIVASF) Juazeiro - BA 19 / 44
20 Exemplo Equação característica: G(s)H(s) = K s(s+1)(s+2) K s(s+1)(s+2) = 1 k = s3 3s 2 2s dk ds = 0 3s2 6s 2 = 0 s = 1 ± 3 3 Dornellas (UNIVASF) Juazeiro - BA 20 / 44
21 Exemplo 3 s= 1± Somente pertence ao lugar das raízes no eixo real Dornellas (UNIVASF) Juazeiro - BA 21 / 44
22 5. Determinar o ângulo de partida de um pólo complexo (ou de chegada a um zero complexo) do lugar das raízes Tomar um ponto de teste nas proximidades de um pólo complexo (ou zero complexo) As contribuições angulares de todos os pólos e zeros devem satisfazer a condição angular Dornellas (UNIVASF) Juazeiro - BA 22 / 44
23 Exemplo φ 1 ( θ 1 + θ 2) = ±180 (2k+1) ou θ 1 = 180 θ 2 +φ 1 = 180 θ 2 +φ 1 Dornellas (UNIVASF) Juazeiro - BA 23 / 44
24 6. Determinar os pontos onde o lugar das raízes pode cruzar o eixo imaginário Duas maneiras: Critério da estabilidade de Routh k? Fazendo s = jω na equação característica, e resolver para ω e k Dornellas (UNIVASF) Juazeiro - BA 24 / 44
25 Exemplo Equação característica K s(s+1)(s+2) + 1 = 0 s3 + 3s 2 + 2s+k = 0 Critério de Routh: s s 2 3 K s 1 2 K 3 0 s 0 K O lugar das raízes pode cruzar o eixo imaginário para Usando a equação auxiliar da linha s 2 3s 2 + K = 0 3s = 0 s = ± j 2 2 K 3 = 0 K = 6 Dornellas (UNIVASF) Juazeiro - BA 25 / 44
26 Exemplo Fazendo s = jω na equação característica ( jω) 3 + 3( jω) 2 + 2( jω)+k = 0 jω 3 3ω jω+k = 0 { ω 3 { + 2ω = 0 ω = 0,± 2 3ω 2 + K = 0 K = 3ω 2 Para ω = 0, K = 0 é inadmissível Para ω = ± 2, K = 6 Dornellas (UNIVASF) Juazeiro - BA 26 / 44
27 Exemplo j 2 j 2 Dornellas (UNIVASF) Juazeiro - BA 27 / 44
28 7. Obter uma série de pontos de teste na região próxima à origem do plano-s e esboçar o lugar das raízes Duas maneiras: Manualmente, observando-se a condição angular Através do MatLab (função rlocus) Dornellas (UNIVASF) Juazeiro - BA 28 / 44
29 Exemplo Gráfico do lugar das raízes de G(s) = k/[s(s+1)(s+2)] j 2 1 Eixo imaginário j Eixo real Dornellas (UNIVASF) Juazeiro - BA 29 / 44
30 8. Determinar os pólos de malha fechada A condição de módulo permite encontrar o valor de K relativo a qualquer ponto específico do lugar das raízes Dornellas (UNIVASF) Juazeiro - BA 30 / 44
31 Exemplo Gráfico do lugar das raízes de G(s) = k/[s(s+1)(s+2)] k = 6 1 Eixo imaginário k = k = Eixo real Dornellas (UNIVASF) Juazeiro - BA 31 / 44
32 Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Requisitos dos sistemas de controle Requisitos da resposta transitória Requisitos em regime permanente Projeto pelo Lugar das raízes Alterar o lugar das raízes pela adição de pólos e zeros na função de transferência de malha aberta O novo lugar das raízes deve passar pelos pólos de malha fechada desejados Dornellas (UNIVASF) Juazeiro - BA 32 / 44
33 Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Ajustar o ganho Nem sempre permite o desempenho desejado Melhora o regime permanente, mas torna o sistema pouco estável, ou até mesmo instável Reprojetar o sistema Modificação de sua estrutura Adição de um compensador Dornellas (UNIVASF) Juazeiro - BA 33 / 44
34 Esquemas de compensação Compensação em série Compensação em paralelo Dornellas (UNIVASF) Juazeiro - BA 34 / 44
35 Efeitos da adição de pólos Dornellas (UNIVASF) Juazeiro - BA 35 / 44
36 Efeitos da adição de zeros Dornellas (UNIVASF) Juazeiro - BA 36 / 44
37 Compensador avanço de fase s+ 1 T G c (s) = K c s+ 1 αt onde α < 1 e consequentemente p > z Técnica: Considere um sistema = K c s+z s+ p instável ou estável, mas com resposta transitória insatisfatória Modificar o lugar das raízes para que um par de pólos dominantes de malha fechada passe pela posição desejada no plano-s Dornellas (UNIVASF) Juazeiro - BA 37 / 44
38 Compensador atraso de fase onde β > 1 Técnica: Considere um sistema G c (s) = ˆK c s+ 1 T s+ 1 βt com resposta transitória satisfatória e com resposta em regime permanente insatisfatória Aumentar o ganho de malha aberta sem alterar sensivelmente as características da resposta transitória Dornellas (UNIVASF) Juazeiro - BA 38 / 44
39 Compensador atraso de fase Para evitar uma alteração significativa do lugar das raízes A contribuição angular do compensador atraso de fase deve ser pequena ( ) s+ 5 1 T < s+ 1 < 0 βt É possível alocar o pólo e o zero próximos um do outro e da origem do plano-s. Para um pólo dominante de malha fechada s = s 1, G c (s 1 ) = ˆK c s T s βt = ˆK c s T s βt = ˆK c s T s βt = ˆK c Dornellas (UNIVASF) Juazeiro - BA 39 / 44
40 Compensador atraso de fase Fazendo ˆK c = 1 As características da resposta transitória não serão alteradas O ganho resultante da função de transferência de malha aberta pode ser aumentado por um fator β > 1 Sistema não compensado Sistema compensado K v = lim s 0 sg(s) ˆK v = lim s 0 sg c (s)g(s) = lim s 0 G c (s)k v = ˆK c βk v Dornellas (UNIVASF) Juazeiro - BA 40 / 44
41 Compensador atraso e avanço de fase onde γ > 1 e β > 1 G c (s) = K c ( s+ 1 T 1 s+ γ T 1 )( ) s+ 1 T 2 s+ 1 βt 1 Consideramos K c pertencente à porção de avanço de fase Técnica: Melhorar tanto a resposta transitória quanto a resposta em regime permanente Dornellas (UNIVASF) Juazeiro - BA 41 / 44
42 Compensação em paralelo Na compensação em série C(s) R(s) = G c (s)g(s) 1+G c (s)g(s)h(s) Equação característica 1+G c (s)g(s)h(s) = 0 Dados G(s) e H(s), o problema de projeto é a determinação de G c (s) Dornellas (UNIVASF) Juazeiro - BA 42 / 44
43 Compensação em paralelo Na compensação em paralelo C(s) R(s) = G 2 (s) 1+G 2 (s)g c (s) G 2 (s) G 1 (s) 1+G 1 (s) 1+G 2 (s)g c (s) H(s) = G 1 (s)g 2 (s) 1+G 2 (s)g c (s)+g 1 (s)g 2 (s)h(s) Dornellas (UNIVASF) Juazeiro - BA 43 / 44
44 Compensação em paralelo Equação característica G 2 (s) 1+G 2 (s)g c (s)+g 1 (s)g 2 (s)h(s) = 0 1+G c (s) G 1 (s)g 2 (s)h(s) = 0 Fazendo Temos 1+G c (s)g f (s) = 0 G f (s) = G 2 (s) G 1 (s)g 2 (s)h(s) O projeto de G c (s) é o mesmo que no caso da compensação em série Dornellas (UNIVASF) Juazeiro - BA 44 / 44
Root Locus (Método do Lugar das Raízes)
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 13 Análise no domínio da frequência
Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Estabilidade. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
VI. MÉTODO DO LUGAR GEOMÉTRICO DAS RAÍZES
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE VI. MÉTODO DO LUGAR GEOMÉTRICO DAS RAÍZES Prof. Davi Antônio dos Santos (davists@ita.br) Departamento
O lugar das raízes p. 1/54. O lugar das raízes. Newton Maruyama
O lugar das raízes p. 1/54 O lugar das raízes Newton Maruyama O lugar das raízes p. 2/54 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização
ANÁLISE LINEAR DE SISTEMAS
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
AULA 8 COMPENSAÇÃO POR ATRASO DE FASE. Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I PROF. DR. ALFREDO DEL SOLE LORDELO
Universidade Federal do ABC UFABC ESTA003-17: SISTEMAS DE CONTROLE I AULA 8 COMPENSAÇÃO POR ATRASO DE FASE PROF. DR. ALFREDO DEL SOLE LORDELO TELA CHEIA A configuração do compensador eletrônico por atraso
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech cassiano@ieee.org
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
AULA #12. Estabilidade de Sistemas de Controle por
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Estabilidade no Domínio da Freqüência
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Desempenho de Sistemas de Controle Realimentados
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE ELETRÔNICA LUGAR DAS RAÍZES
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE ELETRÔNICA LUGAR DAS RAÍZES A função de transferência do circuito abaixo em malha fechada é: F(s) = C(s) = G(s)
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE ELETRÔNICA Prof. Paulo Roberto Brero de Campos
MINISTÉRIO DA EDUCAÇÃO UNIVERSIDADE TECNOLÓGICA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMICO DE ELETRÔNICA Prof. Paulo Roberto Brero de Campos LUGAR DAS RAÍZES INTRODUÇÃO O método do Lugar das Raízes é uma
Aula 11. Cristiano Quevedo Andrea 1. Curitiba, Outubro de DAELT - Departamento Acadêmico de Eletrotécnica
Aula 11 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Outubro de 2011. Resumo 1 Introdução - Lugar das Raízes
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
O método do lugar das raízes
4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada em função
Sistemas de Controle 2
Pontifícia Universidade Católica de Goiás Escola de Engenharia Sistemas de Controle 2 Cap.8 - Técnicas do Lugar das Raízes Prof. Dr. Marcos Lajovic Carneiro Sistemas de Controle 2 Prof. Dr. Marcos Lajovic
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
EXERCÍCIOS RESOLVIDOS
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
PROJETO DE CONTROLADORES A PARTIR DO PLANO S. critério Routh-Hurwitz análise de estabilidade análise de desempenho
PROJETO DE CONTROLADORES A PARTIR DO PLANO S critério Routh-Hurwitz análise de estabilidade análise de desempenho Critério Routh-Hurwitz: análise da estabilidade Sistemas de primeira ordem: 1 x o (t)=
Método do lugar das Raízes
Guilherme Luiz Moritz 1 1 DAELT - Universidade Tecnológica Federal do Paraná 03 de 2013 Objetivos Entender os objetivos do método do lugar das raízes Aprender a traçar o lugar das raízes Interpretar o
O método do lugar das raízes
Capítulo 4 O método do lugar das raízes 4.1 Introdução Neste capítulo é apresentado o método do lugar das raízes, que consiste basicamente em levantar a localização dos pólos de um sistema em malha fechada
Aula 12 Root Locus LGR (Lugar Geométrico das Raízes) parte II
Aula 12 Root Locus LGR (Lugar Geométrico das Raízes) parte II Recapitulando (da parte I): Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada, quando K varia.
Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros
Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Sistema de excitação
Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
SISTEMAS DE CONTROLE II
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
SC1 Sistemas de Controle 1. Cap. 5 Método do Lugar das Raízes Abordagem de Projetos Prof. Tiago S Vítor
SC1 Sistemas de Controle 1 Cap. 5 Método do Lugar das Raízes Abordagem de Projetos Prof. Tiago S Vítor Sumário 1. Introdução 2. Definições 3. Alguns detalhes construtivos sobre LR 4. Condições para um
2 a PROVA CONTROLE DINÂMICO Turma B 2 /2015
ENE/FT/UnB Departamento de Engenharia Elétrica Prova individual, sem consulta. Faculdade de Tecnologia É permitido usar calculadora. Universidade de Brasília Prof. Adolfo Bauchspiess Auditório SG11, 21/1/215,
MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES
MAT1154 ANÁLISE QUALITATIVA DE PONTOS DE EQUILÍBRIO DE SISTEMAS NÃO-LINEARES VERSÃO 1.0.2 Resumo. Este texto resume e complementa alguns assuntos dos Capítulo 9 do Boyce DiPrima. 1. Sistemas autônomos
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional. n=1
Sociedade Brasileira de Matemática Mestrado Profissional em Matemática em Rede Nacional MA Números e Funções Reais Avaliação - GABARITO 3 de abril de 203. Determine se as afirmações a seguir são verdadeiras
Sessão Prática: Simulação e Controle com LabVIEW
Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
SCS Sistemas de Controle / Servomecanismos. Aula 04 Diagrama do lugar geométrico das raízes
Aula 04 Diagrama do lugar geométrico das raízes Definição: O lugar das raízes de um sistema é um gráfico que representa a trajetória das raízes de sua equação característica pólos da função de transferência
Técnicas de Lugar das Raízes. Carlos Alexandre Mello. Carlos Alexandre Mello 1
Técnicas de Lugar das Raízes Carlos Alexandre Mello 1 Introdução Lugar das raízes é um método de análise e projeto para estabilidade e resposta de transiente É uma representação gráfica dos polos de um
Resposta Transitória de Circuitos com Elementos Armazenadores de Energia
ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
Capítulo 3 Sistemas de Controle com Realimentação
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 1. x > y ou x < y ou x = y
Capítulo Funções, Plano Cartesiano e Gráfico de Função Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
Lugar Geométrico das Raízes (Root Locus)
Lugar Geométrico das Raízes (Root Locus) ENGC4: Sistemas de Controle I Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 18 de janeiro de 016 Prof. Tito Luís Maia Santos 1/
SISTEMAS DE CONTROLO. Objectivos Pedagógicos
SISTEMAS DE CONTROLO Responsável: Prof. Doutor João Miguel Gago Pontes de Brito Lima Atendimento (Gab. 2.63): Terça e Quarta das 11:00 à 13:00 Objectivos Pedagógicos Pretende-se com esta disciplina fornecer
FUNÇÃO DO 1º GRAU. Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência:
FUNÇÃO DO 1º GRAU Vamos iniciar o estudo da função do 1º grau, lembrando o que é uma correspondência: Correspondência: é qualquer conjunto de pares ordenados onde o primeiro elemento pertence ao primeiro
Análise de Erro Estacionário
Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
Um resumo das regras gerais para a construção do lugar das raízes p. 1/43. Newton Maruyama
Um resumo das regras gerais para a construção do lugar das raízes p. 1/43 Um resumo das regras gerais para a construção do lugar das raízes Newton Maruyama Um resumo das regras gerais para a construção
RESUMO 2 - FÍSICA III
RESUMO 2 - FÍSICA III CAMPO ELÉTRICO Assim como a Terra tem um campo gravitacional, uma carga Q também tem um campo que pode influenciar as cargas de prova q nele colocadas. E usando esta analogia, podemos
EA616B Análise Linear de Sistemas Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br
Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período.
Período : exp( j α) α/2π = N/K (irredutível) em que se N,K Z então K é o período. sin(t) = sin (t + T), ou exp(t) = exp(t+t) em que T é o período. [sin(a) e/ou cos(a) ]+[ sin(b) e/ou cos(b)] = o periodo
CONTROLO DE SISTEMAS
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
2 - Modelos em Controlo por Computador
Modelação, Identificação e Controlo Digital 2-Modelos em Controlo por Computador 1 2 - Modelos em Controlo por Computador Objectivo: Introduzir a classe de modelos digitais que são empregues nesta disciplina
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Introdução Diagramas de Bode Gráficos Polares Gráfico de Amplitude em db Versus Fase. Aula 14. Cristiano Quevedo Andrea 1
Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Outubro 2012. 1 / 48 Resumo 1 Introdução 2 Diagramas de Bode 3
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
UNIVERSIDADE FEDERAL FLUMINENSE
UNIVERSIDADE FEDERAL FLUMINENSE Escola de Engenharia Industrial Metalúrgica de Volta Redonda PROVAS RESOLVIDAS DE CÁLCULO VETORIAL Professora Salete Souza de Oliveira Aluna Thais Silva de Araujo P1 Turma
Circuitos Osciladores
Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Tópico 3. Limites e continuidade de uma função (Parte 2)
Tópico 3. Limites e continuidade de uma função (Parte 2) Nessa aula continuaremos nosso estudo sobre limites de funções. Analisaremos o limite de funções quando o x ± (infinito). Utilizaremos o conceito
Método do Lugar das Raízes
Método do Lugar das Raízes 1. Esboçando o Lugar das Raízes (LR) pag.1 Controle de Sistemas Lineares Aula 9 O procedimento para esboçar o gráfico do Lugar das Raízes é realizado em 12 passos ordenados a
Cap. 7 - Fontes de Campo Magnético
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
PONTIFÍCIA UNIVERSIDADE CATÓLICA DO PARANÁ CURSO DE ENGENHARIA CIVIL DISCIPLINA DE CÁLCULO DIFERENCIAL E INTEGRAL I
1) Considerações gerais sobre os conjuntos numéricos. Ao iniciar o estudo de qualquer tipo de matemática não podemos provar tudo. Cada vez que introduzimos um novo conceito precisamos defini-lo em termos
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
Erros de Estado Estacionário. Carlos Alexandre Mello. Carlos Alexandre Mello 1
Erros de Estado Estacionário Carlos Alexandre Mello 1 Introdução Projeto e análise de sistemas de controle: Resposta de Transiente Estabilidade Erros de Estado Estacionário (ou Permanente) Diferença entre
Departamento de Engenharia Química e de Petróleo UFF. Disciplina: TEQ102- CONTROLE DE PROCESSOS. Diagrama de Bode. Outros Processos de Separação
Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ102- CONTROLE DE PROCESSOS custo Diagrama de Bode Outros Processos de Separação Prof a Ninoska Bojorge 5.A. Traçado das Assíntotas Traçado
Exemplos de aplicação das leis de Newton e Conservação do Momento Linear
Exemplos de aplicação das leis de Newton e Conservação do Momento Linear Cálculo de resultante I Considere um corpo sobre o qual atual três forças distintas. Calcule a força resultante. F 1 = 10 N 30 F
Pólos, Zeros e Estabilidade
Pólos, Zeros e Estabilidade Definindo Estabilidade A condição para estabilidade pode também ser expressa da seguinte maneira: se um sistema é estável quando sujeito a um impulso, a saída retoma a zero.
Somatórias e produtórias
Capítulo 8 Somatórias e produtórias 8. Introdução Muitas quantidades importantes em matemática são definidas como a soma de uma quantidade variável de parcelas também variáveis, por exemplo a soma + +
Amplificadores lineares e filtros
Instrumentação de Controle - 167347 Departamento de Engenharia Elétrica (ENE) Universidade de Brasília (UnB) Amplificadores lineares e filtros Tópicos Características de amplificadores operacionais Amplificadores
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
2. Função polinomial do 2 o grau
2. Função polinomial do 2 o grau Uma função f: IR IR que associa a cada IR o número y=f()=a 2 +b+c com a,b,c IR e a0 é denominada função polinomial do 2 o grau ou função quadrática. Forma fatorada: a(-r
Funções algébricas do 1º grau. Maurício Bezerra Bandeira Junior
Maurício Bezerra Bandeira Junior Definição Chama-se função polinomial do 1º grau, ou função afim, a qualquer função f de IR em IR dada por uma lei da forma f(x) = ax + b, onde a e b são números reais dados
IV. ESTABILIDADE DE SISTEMAS LIT
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE IV. ESTABILIDADE DE SISTEMAS LIT Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros
107484 Controle de Processos Aula: Função de transferência, diagrama de blocos, polos e zeros Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 2 o Semestre
AV1 - MA 12-2012. (b) Se o comprador preferir efetuar o pagamento à vista, qual deverá ser o valor desse pagamento único? 1 1, 02 1 1 0, 788 1 0, 980
Questão 1. Uma venda imobiliária envolve o pagamento de 12 prestações mensais iguais a R$ 10.000,00, a primeira no ato da venda, acrescidas de uma parcela final de R$ 100.000,00, 12 meses após a venda.
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO
SESSÃO 5: DECLINAÇÃO SOLAR AO LONGO DO ANO Respostas breves: 1.1) 9,063 N 1.2) norte, pois é positiva. 1.3) São José (Costa Rica). 2) Não, porque Santa Maria não está localizada sobre ou entre os dois
Capítulo 4 Resposta em frequência
Capítulo 4 Resposta em frequência 4.1 Noção do domínio da frequência 4.2 Séries de Fourier e propriedades 4.3 Resposta em frequência dos SLITs 1 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da
Análise do Lugar das Raízes
Análise do Lugar das Raízes A característica básica da resposta transitória de um sistema de malha fechada, depende essencialmente da localização dos pólos de malha fechada. É importante, então, que o
Modelo Matemático e Controle de um Robô Móvel. 2.1. Modelo do motor que aciona cada roda do robô
1. Introdução Modelo Matemático e Controle de um Robô Móvel Nesta aula serão apresentadas leis de controle que permitem a um robô móvel nãoholonômico navegar de maneira coordenada desde uma localização
1 P r o j e t o F u t u r o M i l i t a r w w w. f u t u r o m i l i t a r. c o m. b r
Exercícios Potencial Elétrico 01. O gráfico que melhor descreve a relação entre potencial elétrico V, originado por uma carga elétrica Q < 0, e a distância d de um ponto qualquer à carga, é: 05. Duas cargas
Projetos de Controle
Projetos de Cotrole EA7 - Prof. Vo Zube Cotrole do Pêdulo Ivertido com Carro.... Modelo matemático (pg. 7 das Notas de Aula).... Cotrole por realimetação de estados supodo acesso a todos os estados (CASO
Função. Definição formal: Considere dois conjuntos: o conjunto X com elementos x e o conjunto Y com elementos y. Isto é:
Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
Métodos de Sintonização de Controladores PID
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
6. Geometria, Primitivas e Transformações 3D
6. Geometria, Primitivas e Transformações 3D Até agora estudamos e implementamos um conjunto de ferramentas básicas que nos permitem modelar, ou representar objetos bi-dimensionais em um sistema também
Melhoramos a resposta temporal associando um compensador de avanço de fase que contribui com
Compensador por Avanço / Atraso de fase A compensação de avanço / atraso de fase, é a composição das duas técnicas vistas anteriormente em um único compensador. Melhoramos a resposta temporal associando
Newton Maruyama. Projeto de Controladores No Domínio Da Freqüência p. 1/4
Projeto de Controladores No Domínio Da Freqüência Newton Maruyama Projeto de Controladores No Domínio Da Freqüência p. 1/4 Compensação por avanço de fase Função de Transferência: H(s)=K c α Ts+ 1 αts+
SC1 Sistemas de Controle 1. Cap. 4 Técnicas do Lugar Geométrico das Raízes Prof. Tiago S Vítor
SC1 Sistemas de Controle 1 Cap. 4 Técnicas do Lugar Geométrico das Raízes Prof. Tiago S Vítor Sumário 1. Introdução 2. Definição do Lugar Geométrico das Raízes 3. Propriedades do Lugar Geométrico das Raízes
EES-49/2012 Prova 2. Individual Duração: 100 minutos. Consulta permitida a uma página A4 com anotações pessoais e fórmulas.
EES-49/2012 Prova 2 Individual Duração: 100 minutos Consulta permitida a uma página A4 com anotações pessoais e fórmulas. Permitido o uso de calculadora para a realização de operações básicas, incluindo
Função de Transferência de Malha Fechada
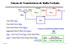Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Prova 2 - Sistemas de Controle Projetos
Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional
CIRCUITOS ELÉTRICOS II
CIRCUITOS ELÉTRICOS II Prof.: Helder Roberto de O. Rocha Engenheiro Eletricista Doutorado em Computação Corrente Elétrica Quantidade de carga elétrica deslocada por unidade de tempo As correntes elétricas
Fundamentos de Controle
Fundamentos de Controle Modelagem matemática de sistemas de controle Prof. Juliano G. Iossaqui Engenharia Mecânica Universidade Tecnológica Federal do Paraná (UTFPR) Londrina, 2017 Prof. Juliano G. Iossaqui
Só Matemática O seu portal matemático http://www.somatematica.com.br FUNÇÕES
FUNÇÕES O conceito de função é um dos mais importantes em toda a matemática. O conceito básico de função é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
ANÁLISE DO LUGAR DAS RAÍZES
VII- &$3Ì78/ 9,, ANÁLISE DO LUGAR DAS RAÍZES 7.- INTRODUÇÃO O étodo de localização e análise do lugar das raízes é ua fora de se representar graficaente os pólos da função de transferência de u sistea
a 1 x 1 +... + a n x n = b,
Sistemas Lineares Equações Lineares Vários problemas nas áreas científica, tecnológica e econômica são modelados por sistemas de equações lineares e requerem a solução destes no menor tempo possível Definição
APLICAÇÕES DA DERIVADA
Notas de Aula: Aplicações das Derivadas APLICAÇÕES DA DERIVADA Vimos, na seção anterior, que a derivada de uma função pode ser interpretada como o coeficiente angular da reta tangente ao seu gráfico. Nesta,
Estabilidade no Domínio da Freqüência
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
LABORATÓRIO DE CONTROLE I ESTUDO DE COMPENSADORES DE FASE
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 4: ESTUDO DE COMPENSADORES DE FASE COLEGIADO DE ENGENHARIA ELÉTRICA DISCENTES: Lucas