Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
|
|
|
- Sérgio Garrau Gonçalves
- 8 Há anos
- Visualizações:
Transcrição
1 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
2 Sistema de malha fechada G(s) G(s) G(s)
3 Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada, quando K varia. Aqui vamos fazer sempre para K >, mas também é possível construir o Root Locus para K < ou para - < K <.
4 Root Locus (RL) Lugar Geométrico das Raízes (LGR) Mas o Root Locus é na verdade o lugar geométrico dos polos, ou seja, das raízes da equação característica, do sistema de malha fechada Plano Complexo jω eixo imaginário eixo real Logo, o Root Locus é traçado no plano complexo É fácil de observar que o Root Locus é SIMÉTRICO em relação ao eixo real Ou seja, a parte de cima é um espelho da parte de baixo
5 Como já sabemos, a função de transferência de malha fechada (FTMF) do sistema é dada por F.T. 1+ G(s) G(s)H(s) e os polos de malha fechada deste sistema são as raízes da equação característica da FTMF É fácil de mostrar que estas raízes da equação característica da FTMF são as mesmas raízes que 1 + G(s) H(s)
6 Ou seja, calcula-se a expressão 1 + G(s) H(s) e depois calcula-se as raízes do numerador. Estas serão raízes da equação característica da FTMF sem a necessidade de calcular a FTMF Na verdade, a equação característica desta FTMF é justamente o numerador de 1 + G(s) H(s)
7 Exemplo 1: K (s + 1) (s 4) 1 s Observe que: 1 + G(s)H(s) 1 + K (s + 1) (s 4)s
8 Exemplo 1 (continuação) logo, 1 + G(s)H(s) s + (K 4)s + (s 4)s e portanto, a equação característica da FTMF é dada por: K s + (K 4)s + K que poderia igualmente ser obtida (embora com um pouco mais de contas) através do denominador da FTMF, que é dada por: FTMF s K (s + 1)s + (K 4)s + K
9 Exemplo : Vamos fazer o Root Locus do sistema M.F. K (s ) (s + 5) Observe que: 1 + G(s)H(s) K (s ) 1 + (s + 5) (K + 1)s + (5 (s + 5) K)
10 Exemplo (continuação) K (s ) (s + 5) Logo, a equação característica do sistema M.F. é: ( K + 1) s + (5 K) e o único polo de M.F. é: s (K 5) (K + 1)
11 Exemplo (continuação) K (s ) (s + 5) Portanto, o Root Locus deste sistema é o lugar geométrico de s s (K 5) (K + 1) no plano complexo, quando varia-se o K, para K >.
12 Exemplo (continuação) Observe que: se K se K s 5 s + Portanto, é fácil de observar que o Root Locus deste sistema é o segmento de reta no eixo real entre 5 e +, isto é [ 5,+]. eixo imaginário x 5 o eixo real
13 Exemplo (continuação) Na verdade, o segmento de reta que vai de 5 para, quando K vai de a. e note que K,5 quando s. K K,5 K eixo imaginário x 5 o eixo real
14 Exemplo (continuação) Como este sistema de M.F. é de 1ª ordem, e portanto, o único polo de M.F. é real, este Root Locus fica inteiramente localizado no eixo real. K K,5 eixo imaginário K x 5 o eixo real
15 Exemplo (continuação) O Root Locus permite-nos ver que para K <,5 o sistema M.F. é estável, pois neste caso o único polo M.F. estará no SPE, enquanto que para K,5 o sistema M.F. não é estável. K K,5 eixo imaginário K x 5 o eixo real
16 Exemplo 3: s K + s 3 Observe que: 1 + G(s)H(s) 1 + (s K 1)(s + 3) s + s s + + (K s 3 3)
17 Exemplo 3 (continuação) K s + s 3 Logo, a equação característica do sistema M.F. é: s + s + (K 3) e os polos de M.F. são: s 1 ± 4 K
18 Exemplo 3 (continuação) K s + s 3 Portanto, o Root Locus deste sistema é o lugar geométrico de s s 1 ± 4 K no plano complexo, quando varia-se o K, para K >.
19 Exemplo 3 (continuação) Observe que: se K s 3 e s 1 eixo imaginário K K x 3 x 1 eixo real
20 Exemplo 3 (continuação) além disso: se K < 4 se K 4 s 1 ± s 1 4 K polos reais polos reais e duplos eixo imaginário K K 4 K x 3 1 x 1 eixo real
21 Exemplo 3 (continuação) e ainda: se K 3 s o Root Locus passa pela origem eixo imaginário K K 4 K 3 K x 3 1 x 1 eixo real
22 Exemplo 3 (continuação) Mas este Root Locus não fica restrito ao eixo real, pois se K > 4 s K K K 4 1 ± j K eixo imaginário K 3 4 complexos conjugados com parte real 1 e a parte imaginária variando de a. K x 3 1 x 1 eixo real K
23 Exemplo 3 (continuação) Resumindo, Este Root Locus tem ramos E mostrando os ramos deste Root Locus com cores diferentes, como faz o Matlab K eixo imaginário K K 4 K 3 K x 3 1 x 1 eixo real K
24 Exemplo 3 (continuação) E mostrando os ramos deste Root Locus com cores diferentes, como faz o Matlab K eixo imaginário K K 4 K 3 K x 3 1 x 1 eixo real K
25 Exemplo 3 (continuação) O Root Locus permite-nos ver que para K 3 o sistema M.F. não é estável, enquanto que para K > 3 o sistema M.F. é estável, pois neste caso os polos M.F. estarão no SPE. K eixo imaginário K K 4 K 3 K x 3 1 x 1 eixo real K
26 Note que o Root Locus depende apenas do produto G(s) H(s) e não de G(s) ou de H(s) separadamente. Portanto, se os sistemas de malha fechada abaixo satisfazem G 1 (s) H 1 (s) G (s) H (s) então os Root Locus destes dois sistemas serão o mesmo
27 A expressão G(s) H(s) é chamada de função de transferência do sistema em malha aberta (FTMA). G(s) H(s) (FTMA) é como malha fosse aberta aqui tornando-se aberta
28 Portanto, os polos e zeros de G(s) H(s) são chamados de polos e zeros de malha aberta. Vamos chamar de n e m o número de polos e zeros de G(s) H(s), respectivamente ou seja: n número de polos de malha aberta m número de zeros de malha aberta
29 Regras para a construção do Root Locus A seguir vamos apresentar 8 regras que auxiliarão na elaboração do esboço do Root Locus para um sistema de malha fechada com FTMA dada por G(s) H(s).
30 Regra #1 Número de ramos
31 Regra #1 Número de ramos O número de ramos n de um Root Locus é o número de polos de malha aberta, ou seja, o número de polos de G(s) H(s). n nº ramos nº polos de G(s) H(s)
32 Regra # Intervalos com e sem Root Locus no eixo real
33 Regra # Intervalos com e sem Root Locus no eixo real Um ponto s no eixo real pertencerá ao Root Locus se houver um número ímpar de polos e zeros reais de malha aberta a direita de s. ou seja, se houver um número ímpar de polos e zeros reais de G(s) H(s) a direita de s.
34 Exemplo 4: Aplicação da Regra # Intervalos com e sem Root Locus no eixo real x x o x x o x o x o eixo real x x o o o x x eixo real
35 Exemplo 4 (continuação) Aplicação da Regra # x x o x o x o eixo real x x o x o o x o o x x eixo real
36 Exemplo 5: Aplicação da Regra # Intervalos com e sem Root Locus no eixo real Considere o sistema de M.F. no qual G(s)H(s) K (s + 1)(s + )(s + 3) x x x 3 1 eixo real
37 Regra #3 Pontos de início e término dos ramos do Root Locus
38 Regra #3 Pontos de início e término dos ramos do Root Locus Os n ramos do Root Locus começam nos n polos de malha aberta ou seja, começam nos n polos de G(s) H(s) m dos n ramos do Root Locus terminam nos m zeros de malha aberta ou seja, terminam nos m zeros de G(s) H(s) e os restantes: (n m) ramos do Root Locus terminam no infinito ( )
39 Regra #3 Pontos de início e término dos ramos do Root Locus (continuação) Note que (n m) é a diferença entre o número de polos de malha aberta n e o número de zeros de malha aberta m i.e., a diferença entre o número de polos e zeros de G(s) H(s) Se n m então (n m), e portanto nenhum ramo termina no infinito ( ) Logo, se o número de polos de malha aberta for igual ao número de zeros de malha aberta, então nenhum ramo termina no infinito ( )
40 Regra #4 Assíntotas no infinito
41 Regra #4 Assíntotas no infinito Para os (n m) ramos do Root Locus que não terminam nos m zeros de malha aberta, isto é, os m zeros finitos de G(s) H(s), pode-se determinar a direção que eles vão para o infinito no plano complexo. γ ângulo da assíntota com o eixo real γ 18º (i + 1) (n m) i,1,, L
42 Regra #4 Assíntotas no infinito (continuação) Aplicando-se a fórmula obtém-se a tabela abaixo: n m γ ângulo da assíntota com o eixo real 1 18º 9º e 9º 3 6º, 6º e 18º 4 45º, 45º, 135º e 135º 5 36º, 36º, 18º, 18º e 18º 6 3º, 3º, 9º, 9º, 15º e 15º : : : : : :
43 Regra #5 Pontos de interseção das assíntotas com o eixo real
44 Regra #5 Pontos de interseção das assíntotas com o eixo real As (n m) assíntotas no infinito ficam determinadas pelas suas direções (ângulos γ) e pelo ponto onde eles se encontram no eixo real, σ o dado pela expressão: σ o n Re(p ) i i 1 j 1 (n m) m Re(z j )
45 Regra #6 Pontos do eixo real onde há encontro de ramos
46 Regra #6 Pontos do eixo real onde há encontro de ramos Primeiro constrói-se a equação 1 + G(s) H(s), e daí obtém-se uma expressão para K em função de s: K(s) então calcula-se a derivada de Kem relação a s, dk/ds Agora, através da equação abaixo em s dk ds obtém-se os pontos s do eixo real onde há encontro de ramos
47 Regra #6 Pontos do eixo real onde há encontro de ramos (continuação) A equação em s dk ds em geral tem um número de soluções s s 1 s s s s 3 s s 4 s s 5 maior que o número de pontos de encontro de ramos no eixo real É necessário cancelar as soluções que não sejam pontos pertencentes ao Root Locus s s 1 s s s s 3 s s 4 s s 5
48 Regra #6 Pontos do eixo real onde há encontro de ramos (continuação) eixo real Quando há encontro de ramos no eixo real pode ser ramos que se encontram e ENTRAM no eixo real ou ramos que se encontram e PARTEM do eixo real.
49 Regra #6 Pontos do eixo real onde há encontro de ramos (continuação) Para um ponto s s onde há encontro de ramos no eixo real, calculamos a segunda derivada de K(s) em s s d K ds s s'
50 Regra #6 Pontos do eixo real onde há encontro de ramos (continuação) Se d K ds s s' < s eixo real ramos que se encontram e PARTEM do eixo real
51 Regra #6 Pontos do eixo real onde há encontro de ramos (continuação) Se d K ds s s' > s eixo real ramos que se encontram e ENTRAM no eixo real
52 Regra #6 Pontos do eixo real onde há encontro de ramos (continuação) Se d K ds s s' s eixo real mais de ramos que se encontram neste ponto prosseguir para Regra #7 Encontro de mais de dois ramos
53 Exemplo 6: Aplicação da Regra #6 Pontos do eixo real onde há encontro de ramos Retornando ao Exemplo 1, fazendo tem-se que: e portanto: K (s + 1) 1 + G(s)H(s) 1 + (s 4)s dk ds K (s + s ) (s + 1) (s 4)s (s + 1) s 1 s Logo, s 1 e s são os pontos onde há encontro de ramos
54 Exemplo 6 (continuação) Aplicação da Regra #6 Para se saber o valor de K em cada um destes pontos é necessário substituí-los (s 1 e s ) na expressão de K Logo, os pontos onde há encontro de ramos são K (s 4)s (s + 1) s 1 1 s 1 (K 1) e K (s 4)s (s + 1) s 4 s (K 4)
55 Exemplo 6 (continuação) Aplicação da Regra #6 os pontos onde há encontro de ramos são s 1 (K 1) e s (K 4) K 4 K 1 s s 1 eixo real
56 Exemplo 6 (continuação) Aplicação da Regra #6 Agora para se saber se cada um destes encontro de ramos são de ramos que CHEGAM ou de ramos que PARTEM, é necessário calcular a segunda derivada d K ds 18 (s + 1) 3 substituindo-se pelos pontos onde há encontro de ramos: s 1 e s d K ds s 1 18 (s + 1) 3 s 1 3 < ramos que PARTEM do eixo real d K ds s 18 (s + 1) 3 s + 3 > ramos que ENTRAM no eixo real
57 Exemplo 6 (continuação) Aplicação da Regra #6 Logo, os pontos onde há encontro de ramos são: s 1 (K 1) ramos que PARTEM do eixo real s (K 4) ramos que ENTRAM no eixo real K 4 K 1 s s 1 eixo real
58 Exemplo 7: Aplicação da Regra #6 Pontos do eixo real onde há encontro de ramos Retornando ao Exemplo 5 então G(s)H(s) K (s + 1)(s + )(s + 3) K 1 + G(s)H(s) 1+ (s + 1) (s + ) (s + 3) K (s + 1)(s + )(s s 3 6s 11s + 6 3) dk 3s ds 1s 11
59 Exemplo 7 (continuação) Aplicação da Regra #6 logo, fazendo dk ds 3s 1s 11 s,58 s 1,43 agora, observando os intervalos com e sem Root Locus no eixo real (exemplo 5) x x x 3 1 concluímos que somente uma das soluções, s 1,43 está num intervalo com Root Locus eixo real
60 Regra #7 Encontro de mais de dois ramos
61 Regra #7 Encontro de mais de dois ramos Na aplicação da regra anterior se d K ds s s' isto significa que há encontro de mais de dois ramos e tem que se continuar a derivar K(s) para derivadas de ordem mais altas até que k d K k ds η d K η ds s s' k 3, 4,5,L para algumη
62 Regra #7 Encontro de mais de dois ramos Se η d K η ds s s' e k d K k ds s s' isto significa que há encontro de η ramos em s ou seja, η ramos CHEGAM e η ramos PARTEM em s (continuação) para k < η O encontro de 3 ramos ou mais não é muito comum Certamente ocorre com menos frequência que o encontro de ramos (Regra #6) Portanto esta Regra #7 não é sempre utilizada. Somente naqueles casos em que, ao aplicar a Regra #6, nós encontrarmos d K ds s s'
63 Regra #7 Encontro de mais de dois ramos (continuação) Um encontro de 3 ramos em s pode ter o seguinte aspeto 3 ramos CHEGAM e 3 ramos PARTEM em s s eixo real
64 Regra #7 Encontro de mais de dois ramos (continuação) Um encontro de 4 ramos em s pode ter o seguinte aspeto 4 ramos CHEGAM e 4 ramos PARTEM em s s eixo real
65 Exemplo 8: Aplicação da Regra #7 Encontro de mais de dois ramos G(s)H(s) (s K 3 1) 1 + G(s)H(s) K s dk 3s ds s d K ds s 6s s aplicar Regra #7 (a começar pela derivada de 3ª ordem)
66 Exemplo 8 (continuação) Aplicação da Regra #7 3 d K 3 ds s 6 3 ramos CHEGAM e 3 ramos PARTEM em s K Este exemplo apenas ilustra a aplicação da Regra #7 Para fazer o esboço deste Root Locus completo é necessário aplicar todas as regras encontro de 3 ramos em s,5 +,866j K x K 1 K x s 1 K x,5,866j K K eixo real
67 Obrigado! Felippe de Souza
Root Locus (Método do Lugar das Raízes)
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
EA616B Análise Linear de Sistemas Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
Aula 12 Root Locus LGR (Lugar Geométrico das Raízes) parte II
Aula 12 Root Locus LGR (Lugar Geométrico das Raízes) parte II Recapitulando (da parte I): Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada, quando K varia.
Função do 2º Grau. Alex Oliveira
Função do 2º Grau Alex Oliveira Apresentação A função do 2º grau, também chamada de função quadrática é definida pela expressão do tipo: y = f(x) = ax² + bx + c onde a, b e c são números reais e a 0. Exemplos:
Potenciação no Conjunto dos Números Inteiros - Z
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Universidade Presbiteriana Mackenzie. Controle II
Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica Controle II Notas de Aula Prof. Marcio Eisencraft Segundo semestre de 004 Universidade Presbiteriana Mackenzie Curso de Engenharia Elétrica
Truques e Dicas. = 7 30 Para multiplicar fracções basta multiplicar os numeradores e os denominadores: 2 30 = 12 5
Truques e Dicas O que se segue serve para esclarecer alguma questão que possa surgir ao resolver um exercício de matemática. Espero que lhe seja útil! Cap. I Fracções. Soma e Produto de Fracções Para somar
Sistemas a Tempo Discreto - Projeto
Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
CONTROLO DE SISTEMAS
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
Aula 9 ESCALA GRÁFICA. Antônio Carlos Campos
Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
Eduardo Camponogara. DAS-5103: Cálculo Numérico para Controle e Automação. Departamento de Automação e Sistemas Universidade Federal de Santa Catarina
Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle e Automação 1/48 Sumário Arredondamentos Erros 2/48 Sumário Arredondamentos
24/Abril/2013 Aula 19. Equação de Schrödinger. Aplicações: 1º partícula numa caixa de potencial. 22/Abr/2013 Aula 18
/Abr/013 Aula 18 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda e níveis
Curvas em coordenadas polares
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Apresentação de Dados em Tabelas e Gráficos
Apresentação de Dados em Tabelas e Gráficos Os dados devem ser apresentados em tabelas construídas de acordo com as normas técnicas ditadas pela Fundação Instituto Brasileiro de Geografia e Estatística
Exercícios 1. Determinar x de modo que a matriz
setor 08 080509 080509-SP Aula 35 MATRIZ INVERSA Uma matriz quadrada A de ordem n diz-se invertível, ou não singular, se, e somente se, existir uma matriz que indicamos por A, tal que: A A = A A = I n
Prova 2 - Sistemas de Controle Projetos
Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional
Gráficos de funções em calculadoras e com lápis e papel (*)
Rafael Domingos G Luís Universidade da Madeira/Escola Básica /3 São Roque Departamento de Matemática Gráficos de funções em calculadoras e com lápis e papel (*) A difusão de calculadoras gráficas tem levado
Nome: N.º: endereço: data: Telefone: E-mail: PARA QUEM CURSA O 9 Ọ ANO EM 2014. Disciplina: MaTeMÁTiCa
Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSA O 9 Ọ ANO EM 04 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 6 A soma das medidas dos catetos de um triângulo retângulo é 8cm
Os gráficos estão na vida
Os gráficos estão na vida A UUL AL A Nas Aulas 8, 9 e 28 deste curso você já se familiarizou com o estudo de gráficos. A Aula 8 introduziu essa importante ferramenta da Matemática. A Aula 9 foi dedicada
Texto 07 - Sistemas de Partículas. A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica.
Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Análise de Erro Estacionário
Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
ITA - 2004 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR
ITA - 2004 3º DIA MATEMÁTICA BERNOULLI COLÉGIO E PRÉ-VESTIBULAR Matemática Questão 01 Considere as seguintes afirmações sobre o conjunto U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} I. U e n(u) = 10 III. 5 U e {5}
Notas sobre a Fórmula de Taylor e o estudo de extremos
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Capítulo 5: Aplicações da Derivada
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
0,999... OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel
Nível Intermediário 0,999... OU COMO COLOCAR UM BLOCO QUADRADO EM UM BURACO REDONDO Pablo Emanuel Quando um jovem estudante de matemática começa a estudar os números reais, é difícil não sentir certo desconforto
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Aula 2 - Cálculo Numérico
Aula 2 - Cálculo Numérico Erros Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 2 - Cálculo Numérico 1 / 41 Sumário Sumário 1 Sumário 2 Erros Modelagem Truncamento Representação
APOSTILA TECNOLOGIA MECANICA
FACULDADE DE TECNOLOGIA DE POMPEIA CURSO TECNOLOGIA EM MECANIZAÇÃO EM AGRICULTURA DE PRECISÃO APOSTILA TECNOLOGIA MECANICA Autor: Carlos Safreire Daniel Ramos Leandro Ferneta Lorival Panuto Patrícia de
Propriedades das Funções Deriváveis. Prof. Doherty Andrade
Propriedades das Funções Deriváveis Prof Doerty Andrade 2005 Sumário Funções Deriváveis 2 Introdução 2 2 Propriedades 3 3 Teste da derivada segunda para máimos e mínimos 7 2 Formas indeterminadas 8 2 Introdução
Notação. Quantidades Económicas de Encomenda. 1.1 Quantidade Económica de Wilson. 1.1 Quantidade Económica de Wilson
Notação uantidades Económicas de Encomenda. Taxa de Constante taxa de procura (unidades de produto / unidade de ) A custo de encomenda ( / encomenda) C custo unitário do produto ( / unidade de produto)
Capítulo 7. Topologia Digital. 7.1 Conexidade
Capítulo 7 Topologia Digital A Topologia Digital estuda a aplicação das noções definidas em Topologia sobre imagens binárias. Neste capítulo vamos introduzir algumas noções básicas de Topologia Digital,
4. A FUNÇÃO AFIM. Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares
38 4. A FUNÇÃO AFIM Uma função f: R R chama-se afim quando existem números reais a e b tais que f(x) = ax + b para todo x R. Casos particulares 1) A função identidade fr : Rdefinida por f(x) = x para todo
INSTITUTO TECNOLÓGICO
PAC - PROGRAMA DE APRIMORAMENTO DE CONTEÚDOS. ATIVIDADES DE NIVELAMENTO BÁSICO. DISCIPLINAS: MATEMÁTICA & ESTATÍSTICA. PROFº.: PROF. DR. AUSTER RUZANTE 1ª SEMANA DE ATIVIDADES DOS CURSOS DE TECNOLOGIA
MÉDIA ARITMÉTICA MÉDIA PONDERADA MODA MEDIANA
MÉDIA ARITMÉTICA MÉDIA PONDERADA MODA MEDIANA Em um amostra, quando se têm os valores de uma certa característica, é fácil constatar que os dados normalmente não se distribuem uniformemente, havendo uma
b) a 0 e 0 d) a 0 e 0
IFRN - INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO RN PROFESSOR: MARCELO SILVA MATEMÁTICA FUNÇÃO DO º GRAU 1. Um grupo de pessoas gastou R$ 10,00 em uma lanchonete. Quando foram pagar a conta,
Matemática para Engenharia
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Circuitos de 2 ª ordem: RLC. Parte 1
Circuitos de 2 ª ordem: RLC Parte 1 Resposta natural de um circuito RLC paralelo Veja circuito RLC paralelo abaixo: A tensão é a mesma e aplicando a soma de correntes que saem do nó superior temos: v R
Faculdade de Computação
UNIVERSIDADE FEDERAL DE UBERLÂNDIA Faculdade de Computação Disciplina : Teoria da Computação Professora : Sandra Aparecida de Amo Lista de Exercícios n o 2 Exercícios sobre Modelos de Máquinas de Turing
ESPAÇOS MUNIDOS DE PRODUTO INTERNO
ESPAÇOS MUNIDOS DE PRODUTO INTERNO Angelo Fernando Fiori 1 Bruna Larissa Cecco 2 Grazielli Vassoler 3 Resumo: O presente trabalho apresenta um estudo sobre os espaços vetoriais munidos de produto interno.
Construção dos números racionais, Números fracionários e operações com frações
Construção dos números racionais, Números fracionários e operações com frações O número racional pode ser definido a partir da aritmética fechamento da operação de divisão entre inteiros ou partir da geometria
Modelo Matemático e Controle de um Robô Móvel. 2.1. Modelo do motor que aciona cada roda do robô
1. Introdução Modelo Matemático e Controle de um Robô Móvel Nesta aula serão apresentadas leis de controle que permitem a um robô móvel nãoholonômico navegar de maneira coordenada desde uma localização
Aula 13 Análise no domínio da frequência
Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIAS
MÓDULO 4 DISTRIBUIÇÃO DE FREQÜÊNCIS Como vimos no módulo 1, para que nós possamos extrair dos dados estatísticos de que dispomos a correta análise e interpretação, o primeiro passo deverá ser a correta
Cap. 7 - Fontes de Campo Magnético
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
Resoluções comentadas de Raciocínio Lógico e Estatística - SEPLAG-2010 - APO
Resoluções comentadas de Raciocínio Lógico e Estatística - SEPLAG-010 - APO 11. O Dia do Trabalho, dia 1º de maio, é o 11º dia do ano quando o ano não é bissexto. No ano de 1958, ano em que o Brasil ganhou,
CCI-22 CCI-22. 2) Erros de arredondamento. Matemática Computacional
Matemática Computacional 2) Erros de arredondamento Carlos Alberto Alonso Sanches Erros de representação e de cálculo Tipos de erros Erro inerente: sempre presente na incerteza das medidas experimentais
AGES FACULDADE DE CIÊNCIAS HUMANAS E SOCIAIS DIRETORIA DE ENSINO CÁLCULOS PARA 100%
AGES FACULDADE DE CIÊNCIAS HUMANAS E SOCIAIS DIRETORIA DE ENSINO CÁLCULOS PARA 100% 1. CÁLCULO PARA SABER A MÉDIA FINAL DO ALUNO 1.1. DISCIPLINAS EMINENTEMENTE TEÓRICAS São consideradas disciplinas eminentemente
Apresentação Caule e Folha. Exemplo
Análise Exploratória de Dados As técnicas de análise exploratória de dados consistem em gráficos simples de desenhar que podem ser utilizados para resumir rapidamente um conjunto de dados. Uma destas técnicas
Estruturas de Repetição
Estruturas de Repetição Lista de Exercícios - 04 Algoritmos e Linguagens de Programação Professor: Edwar Saliba Júnior Estruturas de Repetição O que são e para que servem? São comandos que são utilizados
Notas de Cálculo Numérico
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Capítulo 3 Modelos Estatísticos
Capítulo 3 Modelos Estatísticos Slide 1 Resenha Variáveis Aleatórias Distribuição Binomial Distribuição de Poisson Distribuição Normal Distribuição t de Student Distribuição Qui-quadrado Resenha Slide
Desenhando perspectiva isométrica
Desenhando perspectiva isométrica A UU L AL A Quando olhamos para um objeto, temos a sensação de profundidade e relevo. As partes que estão mais próximas de nós parecem maiores e as partes mais distantes
QUANTIFICADORES. Existem frases declarativas que não há como decidir se são verdadeiras ou falsas. Por exemplo: (a) Ele é um campeão da Fórmula 1.
LIÇÃO 4 QUANTIFICADORES Existem frases declarativas que não há como decidir se são verdadeiras ou falsas. Por exemplo: (a) Ele é um campeão da Fórmula 1. (b) x 2 2x + 1 = 0. (c) x é um país. (d) Ele e
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
13 a Aula 2004.10.13 AMIV LEAN, LEC Apontamentos
3 a Aula 2004.0.3 AMIV LEAN, LEC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 3. Singularidades isoladas Para na prática podermos aplicar o teorema dos resíduos com eficiência, precisamos de conhecer
Lista de Exercícios 03
Lista de Exercícios 03 Aplicações das relações e funções no cotidiano Ao lermos um jornal ou uma revista, diariamente nos deparamos com gráficos, tabelas e ilustrações. Estes, são instrumentos muito utilizados
Este procedimento gera contribuições não só a φ 2 e φ 4, mas também a ordens superiores. O termo por exemplo:
Teoria Quântica de Campos II 168 Este procedimento gera contribuições não só a φ 2 e φ 4, mas também a ordens superiores. O termo por exemplo: Obtemos acoplamentos com derivadas também. Para o diagrama
29/Abril/2015 Aula 17
4/Abril/015 Aula 16 Princípio de Incerteza de Heisenberg. Probabilidade de encontrar uma partícula numa certa região. Posição média de uma partícula. Partícula numa caixa de potencial: funções de onda
ATENÇÃO: A partir da amostra da aula, terá uma idéia de onde o treinamento de eletroeletrônica poderá lhe levar.
ATENÇÃO: O material a seguir é parte de uma das aulas da apostila de MÓDULO 1 que por sua vez, faz parte do CURSO de ELETRO ANALÓGICA -DIGITAL que vai do MÓDULO 1 ao 4. A partir da amostra da aula, terá
TEORIA UNIDIMENSIONAL DAS
Universidade Federal do Paraná Curso de Engenharia Industrial Madeireira MÁQUINAS HIDRÁULICAS AT-087 Dr. Alan Sulato de Andrade alansulato@ufpr.br INTRODUÇÃO: O conhecimento das velocidades do fluxo de
QUIMICA ORGÂNICA BÁSICA
QUIMICA ORGÂNICA BÁSICA Hibridização Revisão - Química Orgânica Básica 1 Tabela Periódica 2 Moléculas Diatômicas 3 Moléculas Poliatômicas 4 Eletronegatividade 5 A interação da luz e a matéria 6 Hibridização
MATEMÁTICA I AULA 07: TESTES PARA EXTREMOS LOCAIS, CONVEXIDADE, CONCAVIDADE E GRÁFICO TÓPICO 02: CONVEXIDADE, CONCAVIDADE E GRÁFICO Este tópico tem o objetivo de mostrar como a derivada pode ser usada
4Distribuição de. freqüência
4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
Unidade III: Movimento Uniformemente Variado (M.U.V.)
Colégio Santa Catarina Unidade III: Movimento Uniformemente Variado (M.U.V.) 17 Unidade III: Movimento Uniformemente Variado (M.U.V.) 3.1- Aceleração Escalar (a): Em movimentos nos quais as velocidades
Resolvendo problemas com logaritmos
A UA UL LA Resolvendo problemas com logaritmos Introdução Na aula anterior descobrimos as propriedades dos logaritmos e tivemos um primeiro contato com a tábua de logarítmos. Agora você deverá aplicar
Ricardo Bento Afonso Nº51571 Rubén Ruiz Holgado Nº64643
Ricardo Bento Afonso Nº51571 Rubén Ruiz Holgado Nº64643 Programação não linear para que serve? A programação linear tem a função objectivo e os constrangimentos lineares. O que nem sempre acontece na realidade,
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
Singularidades de Funções de Variáveis Complexas
Singularidades de Funções de Variáveis Complexas AULA 11 META: Introduzir o conceito de singularidades de funções de variáveis complexas. OBJETIVOS: Ao fim da aula os alunos deverão ser capazes de: Definir
I CAPÍTULO 19 RETA PASSANDO POR UM PONTO DADO
Matemática Frente I CAPÍTULO 19 RETA PASSANDO POR UM PONTO DADO 1 - RECORDANDO Na última aula, nós vimos duas condições bem importantes: Logo, se uma reta passa por um ponto e tem um coeficiente angular,
DISTRIBUIÇÃO DE FREQÜÊNCIAS
DISTRIBUIÇÃO DE FREQÜÊNCIAS 1 Dados Brutos: são os dados tomados como eles são, de forma desorganizada. Indica-se por x i Rol: são os dados organizados em ordem crescente ou decrescente. Tamanho da amostra:
Geometria Analítica Plana.
Geometria Analítica Plana. Resumo teórico e eercícios. 3º Colegial / Curso Etensivo. Autor - Lucas Octavio de Souza (Jeca) Estudo de Geometria Analítica Plana. Considerações gerais. Este estudo de Geometria
ESTATÍSTICA ORGANIZAÇÃO E REPRESENTAÇÃO DE DADOS. Tabelas. Frequência absoluta. Frequência relativa
Tabelas. Frequência absoluta. Frequência relativa Com a análise de uma turma, elaborou as seguintes Tabelas: Tabelas. Frequência absoluta. Frequência relativa Perguntou-se a cada aluno a altura e obteve-se
Projeto de sistemas de controle
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Sistemas Lineares. Módulo 3 Unidade 10. Para início de conversa... Matemática e suas Tecnologias Matemática
Módulo 3 Unidade 10 Sistemas Lineares Para início de conversa... Diversos problemas interessantes em matemática são resolvidos utilizando sistemas lineares. A seguir, encontraremos exemplos de alguns desses
Estabilidade. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Experimento 3 # Professor: Data: / / Nome: RA:
BC-0209 Fenômenos Eletromagnéticos Experimento 3 # Campo Magnético de Correntes Elétricas Professor: Data: / / Introdução e Objetivos Relatos históricos indicam que a bússola já era um instrumento utilizado
É usual representar uma função f de uma variável real a valores reais e com domínio A, simplesmente por y=f(x), x A
4. Função O objeto fundamental do cálculo são as funções. Assim, num curso de Pré-Cálculo é importante estudar as idéias básicas concernentes às funções e seus gráficos, bem como as formas de combiná-los
Unidade 3 Função Logarítmica. Definição de logaritmos de um número Propriedades operatórias Mudança de base Logaritmos decimais Função Logarítmica
Unidade 3 Função Logarítmica Definição de aritmos de um número Propriedades operatórias Mudança de base Logaritmos decimais Função Logarítmica Definição de Logaritmo de um número Suponha que certo medicamento,
Resolução dos Exercícios sobre Derivadas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Tabelas vista de estrutura
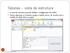Tabelas vista de estrutura A vista de estrutura permite definir a configuração dos dados Vamos adicionar os restantes campos à tabela carros, de acordo com o modelo de dados feito no papel 47 Tabelas vista
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocaba.unesp.
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocaba.unesp.br Transformações Lineares 1 Definição e Exemplos 2 Núcleo e Imagem
VESTIBULAR 2004 - MATEMÁTICA
01. Dividir um número real não-nulo por 0,065 é equivalente a multiplicá-lo por: VESTIBULAR 004 - MATEMÁTICA a) 4 c) 16 e) 1 b) 8 d) 0. Se k é um número inteiro positivo, então o conjunto A formado pelos
Variáveis aleatórias contínuas e distribuiçao Normal. Henrique Dantas Neder
Variáveis aleatórias contínuas e distribuiçao Normal Henrique Dantas Neder Definições gerais Até o momento discutimos o caso das variáveis aleatórias discretas. Agora vamos tratar das variáveis aleatórias
Plano de Aula. 1 - Como abrir o programa KmPlot
Plano de Aula Aluno(a):PIBID MATEMÁTICA Escola: Escola Estadual de Ensino Médio Mestre Santa Bárbara Disciplina: Matemática Conteúdo: Função quadrática Assunto: Gráficos, coeficientes da função Público
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
Função de Transferência de Malha Fechada
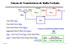Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Capítulo SETE Números em Ponto Fixo e Ponto Flutuante
Capítulo SETE Números em Ponto Fixo e Ponto Flutuante 7.1 Números em ponto fixo Observação inicial: os termos ponto fixo e ponto flutuante são traduções diretas dos termos ingleses fixed point e floating
Além do Modelo de Bohr
Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
Aritmética de Ponto Flutuante
Aritmética de Ponto Flutuante Entre 1970 e 1980 um grupo formado por cientistas e engenheiros de diferentes empresas de computação realizou um trabalho intenso na tentativa de encontrar um padrão de representação
XXVI Olimpíada de Matemática da Unicamp. Instituto de Matemática, Estatística e Computação Científica Universidade Estadual de Campinas
Gabarito da Prova da Primeira Fase 15 de Maio de 010 1 Questão 1 Um tanque de combustível, cuja capacidade é de 000 litros, tinha 600 litros de uma mistura homogênea formada por 5 % de álcool e 75 % de
A B C F G H I. Apresente todas as soluções possíveis. Solução
19a Olimpíada de Matemática do Estado do Rio Grande do Norte - 008 Segunda Etapa Em 7/09/008 Prova do Nível I (6 o ou 7 o Séries) (antigas 5ª ou 6ª séries) 1 a Questão: Substitua as nove letras da figura
Faculdades Anhanguera
2º Aula de Física 2.1 Posição A posição de uma partícula sobre um eixo x localiza a partícula em relação á origem, ou ponto zero do eixo. A posição é positiva ou negativa, dependendo do lado da origem
Análise de Arredondamento em Ponto Flutuante
Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
MATEMÁTICA 3. Resposta: 29
MATEMÁTICA 3 17. Uma ponte deve ser construída sobre um rio, unindo os pontos A e, como ilustrado na figura abaixo. Para calcular o comprimento A, escolhe-se um ponto C, na mesma margem em que está, e
por séries de potências
Seção 23: Resolução de equações diferenciais por séries de potências Até este ponto, quando resolvemos equações diferenciais ordinárias, nosso objetivo foi sempre encontrar as soluções expressas por meio
Distribuição de probabilidades
Luiz Carlos Terra Para que você possa compreender a parte da estatística que trata de estimação de valores, é necessário que tenha uma boa noção sobre o conceito de distribuição de probabilidades e curva