SISTEMAS DE CONTROLE II
|
|
|
- Ana Júlia Barata Meneses
- 8 Há anos
- Visualizações:
Transcrição
1 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta
2 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações 5) Resposta muito susceptível a ruídos de medição Exemplo: ε.sen(ω.t) Sinal Ondulado Utilizando um controlador PID (parte Derivativa), a resposta fica: ε. ω.cos(ω.t) isso mostra que os ruídos são amplificados.
3 A resposta adequada é aquela resposta sem oscilações (ou poucas oscilações), rápida, sem erro em regime permanente (ou com erro em regime permanente nulo), robusta a perturbações e pouco susceptível a ruídos de medição. - Regulação x Rastreamento Regulação Regulação consiste no problema de levar o sistema de volta ao ponto de operação x 1 = x 1 -x 10 x 2 = x 2 -x 20 Regulação (no novo sistema de coordenadas) consiste em levar o sistema para a origem.
4 Rastreamento O rastreamento consiste em levar o sistema a acompanhar um sinal de referência qualquer. - Sequência de projeto 1) Escolha do controlador 2) Sintonia inicial a) Métodos de Ziegler-Nichols b) Método polinomial c) Método do lugar das raízes (roots-locus) d) Método frequencial (Diagrama de Bode) e) Método por variáveis de estado 3) Sintonia fina (ajuste intuitivo)
5 - Índice de desempenho r Referência y Saída da planta y final lim t y t P.O. (Porcentagem de Overshoot) ym áx yfinal P.O. =.100% yfinal Ts (Tempo de acomodação ou tempo de estabilização) é o tempo necessário para a resposta ficar dentro de um percentual em relação ao valor final. - Critérios para o percentual Ts 5% (Tolerância de 5%) Ts 2% (Tolerância de 2%) Erro e = r y Erro em regime permanente e. r. = lim t e(t) - Controlador Proporcional (P) U(s) = Kc.E(s) => u(t) = Kc.e(t) Em geral, o erro em regime não é nulo e o ganho é proporcional ao erro.
6 Em geral: Kc pequeno P.O. baixo Tempo de acomodação alto Erro em regime alto Kc intermediário Essa é a situação mais adequada para porcentagem de overshoot, tempo de acomodação e erro em regime. Nos projetos utilizamos o Kc intermediário.
7 Kc grande P.O. alto Tempo de acomodação alto Erro em regime baixo - Controlador Proporcional-Integrativo (PI) U(s) = Kc + Ki s ). E(s) => u(t) = Kc. e t + Ki t 0 e t. dt Veja que em u(t), temos uma parte proporcional e outra parte integrativa.
8 A parte proporcional age no início e a parte integrativa age no final. Vamos mostrar porque a saída y não pode ficar abaixo nem acima da referência em regime permanente.
9
10 Agora vamos ver um exemplo acima do nível da referência em regime permanente.
11 - Conclusão geral: Com o controlador PI consegue-se um e. r. = 0 para r(t) tipo degrau.
12 Ki pequeno Porcentagem de overshoot baixa Tempo de acomodação alto Ki grande Porcentagem de overshoot alto Tempo de acomodação alto Ki intermediário Respostas adequadas para porcentagem de overshoot e tempo de acomodação. - Controlador Proporcional Integrativo Derivativo (PID) U(s) = Kc + Ki s + Kd. s. E(s) => u(t) = Kc. e t + Ki e t. dt + Kd. d dt e(t)
13 Conclusão: a parte derivativa se opõe as outras duas componentes e faz isso com mais intensidade quando o módulo da variação do erro é maior. Como o Kd é mais relacionado a porcentagem de overshoot, vamos analisá-lo com Kc e Ki constante. Kd grande Porcentagem de Overshoot baixo Kd pequeno Porcentagem de Overshoot alto Kd intermediário Resposta adequada para a porcentagem de overshoot Conclusão final: Com um controlador PID é possível obter um desempenho transitório adequado.
14 - Controlador PID Efeito de cada componente As componentes proporcionais, derivativa e integrativa atuam em momentos distintos. A parte proporcional P mais importante no início do transitório. A parte proporcional I mais importante em regime permanente. A parte proporcional D mais importante quando a saída da planta está variando mais rapidamente. Parametrizações do PID G c (s) = U(s) E(s) G c (s) função de transferência do controlador G c (s) = Kc + Ki. 1 + Kd. s s (mais intuição) G c (s) = Kc(1 + Ki = Kc τi Kd = Kc. τd 1 τi.s + τd. s) (melhor para projeto)
15 - Sistemas de 1ª Ordem qi vazão de entrada qi > 0 bomba está colocando líquido no reservatório qi < 0 bomba está retirando líquido do reservatório qi = Ki.u u tensão aplicada na bomba q0 vazão de saída q0 = R h nível R resistência de restrição V = A.h V volume A área da seção reta u entrada y = h saída d dt = 1 R. A A. d dt = qi q0 A. d dt = Ki. u R Ki. +. u Descrição por variáveis de estado A - Aplicando a transformada de Laplace (C. I. nulas)
16 s + 1 R. A s. H s = 1 R. A Ki. H s +. U s A Ki H(s). H s =. U s A U(s) = Y(s) = G s = U(s) Ki. R R. A. s + 1 = K τs + 1 K = Ki.R ganho estático Τ = R.A constante de tempo G(s) = K τs+1 função de transferência Para u(t) = C1, C1 0, U(s) = C1 (u é um degrau) Y s = G s. U s = s K τs + 1. C1 K s s = s + 1. C1 s = K1 τ s K2 s τ K. C1 τ K1 = = K. C1 1 τ K2 = K. C1 τ 1 τ = K. C1 y(t) = -1 {Y(s)} = K. C1. e t τ + K. C1 = K. C1(1 e t τ) t Y erro(%) τ 0,63.K.C τ 0,86.K.C τ 0,95.K.C 1 5 4τ 0,98.K.C 1 2 5τ > 0,99.K.C 1 < 1 T s5% = 3 τ (tempo necessário para y ficar dentro de uma tolerância de 5% em relação ao valor final)
17 T s2% = 4 τ (tempo necessário para y ficar dentro de uma tolerância de 2% em relação ao valor final) Regime permanente na pratica: t 5 τ Ex. K G s = τ Pólo(s): 1 τ < 0 Sistema estável Zero(s): -x- τ 1 Grande 1 τ 1 pequeno, pólo próximo do eixo imaginário sistema lento τ 2 Pequeno 1 τ 2 grande, pólo afastado do eixo imaginário sistema rápido -Planta de 2ª Ordem
18 f=u Força x=y Deslocamento K Constante da mola B Coeficiente de atrito viscoso M. x = f K. x B. x M. x + K. +B. x = f Descrição por variáveis de estado x 1 = x x 1 = x 2 x 2 =x x 2= K M. x 1 B M. x 2+ 1 M. f y = x 1 x = x 1 x 2 x 1 x 2 = 0 1 K B M M. x 1 x M.u y = 1 0. x 1 x 2 x = A. x + B. u y = C. x + D. u (B é uma matriz) D só aparece quando a saída influencia diretamente na entrada A = 0 1 K B M M ; B = 0 1 M ; C = 1 0 Aplicando a Transformada de Laplace e considerando Condições Iniciais nulas, temos: M. s 2. X s + B. s. X s + K. X s = F s M. s 2 + B. s + K. X s = F s X s F s = Y s U s = G s = 1 M. s 2 + B. s + K = 1 M s 2 + B M + K M
19 G s = K s ξ. ω n. s + ω n 2 Onde: K = 1 M 2. ξ. ω n = B M ω n 2 = K M ω n Frequência natural ξ Fator de amortecimento G s = K s ξ. ω n. s + ω n 2 Zeros: -x- Pólos: s ξ. ω n. s + ω n 2 = 0 s = 2. ξ. ω n 2 ± 4. ξ 2. ω n 2 4. ω n 2 2 s = ξ. ω n ± ω n. ξ 2 1 1º Caso: ξ > 1 Pólos reais, distintos e negativos s 1 = ξ. ω n + ω n. ξ 2 1 s 2 = ξ. ω n ω n. ξ 2 1 O efeito de s 1 é muito lento, o efeito de s 2 é muito rápido.
20 Para u t = 1 U s = 1 s Y s = G s. U s = K (s + ξ. ω n ω n. ξ 2 1). s + ξ. ω n + ω n. ξ 2 1. s K1 s + ξ. ω n ω n. ξ 2 1) + K2 s + ξ. ω n + ω n. ξ 2 1) + K3 s y t = L 1 Y s = K1. e ( ξ.ω n + ω n. ξ 2 1)t + K2. e ( ξ.ω n ω n. ξ 2 1)t + K3, t 0. Coeficiente de atrito grande deixa o ξ > 0 lim t y(t) = lim s. Y(s) = lim s 0 Caso Sobre-Amortecido s 0 s. K s 2 + 2ξ. ω n. s + ω n 2. 1 s = K ω n 2 2º caso: ξ=1 pólos reais iguais e negativos s 1 = s 2 = -ω n Y s = G s. U s = k s + ω 2. 1 n s = k 1 s + ω 2 + k 2 n s + ω + k 3 n s
21 y t = L 1 Y(s) = K 1. e ω n.t + K 2. e ω n.t + K 3 3º caso: 0 < ξ < 1 s 1,2 = ξ. ω n ± j. ω n 1 ξ 2 a 2 = ξ. ω n 2 + ω n 2. 1 ξ 2 a = ω n cos Θ = ξ. ω n ω n ξ = cos Θ Para u t = 1, U s = 1 s Y s = G s. U s = K s + ξ. ω n j. ω n. 1 ξ 2. s + ξ. ω n + j. ω n. 1 ξ 2. s
22 K1 s + ξ. ω n j. ω n. 1 ξ 2 + K2 s + ξ. ω n + j. ω n. 1 ξ + K3 2 s y t = L 1 Y s = K1. e ( ξ.ω n + j.ω n. 1 ξ 2 )t + K2. e ( ξ.ω n j.ω n. 1 ξ 2 )t + K3, t 0. y t = K ω n 2. [1 e ξ.ω n.t 1 ξ 2. sen(ω n. 1 ξ 2. t + arcos ξ ] P.O. (Porcentagem de Overshoot) P.O. = y m áx K ω n 2 K ωn = 100. e π.ξ 1 ξ 2 Para: ξ = 0,7 P. O. = 5% θ = 45º Para: Ts 5% = 3.τ = Ts 2% = 4.τ = ξ = 0,5 P. O. = 16,3% θ = 60º 3 ξ.ω n, τ valor para a exponencial ficar ξ.ω n
23 Regime permanente na prática t Ex.: Deseja-se P.O. 5% Ts 2% 4s P.O. = 5% ξ = 0,7 θ = 45º Ts 2% = 4 = 4 ξ.ω n ξ. ω n = 1 5 ξ.ω n Pólos: -1 + j, -1 j. Obs: para ξ = 0, temos: y t = K ω n 2. 1 sin ω n. t + 90 o = K ω n 2. 1 cos ω n. t 0,1,-1 P.O=100% Ts2% Ts5%
24 -Sistemas de ordem maior Aproxima-se por um sistema de 1ª ordem Aproxima-se por um sistema de 2ª ordem Real de um pólo dominado 5*. Real de um pólo dominante * boa aproximação Sistema aproximadamente de 1ª ordem - Estabilidade Ex.: u t = 1 Degrau unitário U s = 1 s
25 Y s = G s. U s = 1 s 2. 1 s = K1 s 2 + K2 s K1 = 1 s s=2 = 1 2 K2 = 1 s 2 s=0 = y t = 1 2. e2.t 1 2 t 0 y h (t) = 1 2. e2.t Componente homogênea y p (t) = 1 Componente particular 2 lim t y (t) Sistema instável Pólo: 2 Pólo com parte real positiva, sistema instável. Ex.: u t = 1 Degrau unitário U s = 1 s Y s = G s. U s = 1 s s = K1 s K2 s
26 K1 = 1 s s=-2 = K2 = 1 s+2 s=0 = 1 2 y t = 1 2. e 2.t t 0 y h (t) = 1 2. e 2.t Componente homogênea y p (t) = + 1 Componente particular 2 Pólo: -2 Pólo real negativo, sistema estável. -Critério algébrico para a estabilidade (critério de Routh-Hurwitg) N s G s = a 3 s 3 + a 2 s 2 + a 2 s + a 0 1º passo: a 0, a 1, a 2,e a 3 com mesmo sinal (nenhum pode se anular)\ 2º passo: s 3 a 3 a 1 s 2 a 2 a 0 b 0 = a 2.a 1 a 3.a 0 a 2 s 1 b 0 0 s 0 a 0 Coeficientes da 1ª coluna com o mesmo sinal (nenhum pode se anular) 1º passo + 2º passo sistema estável
27 -Zeros e pólos G s = s + a s + 2 (s + 3) Zero: -a Pólos: -2,-3 u t = 1 t U s = 1 s Y s = G s. U s = s + a s + 2 s + 3 s = K 1 s K 2 s K 3 s K 1 = s + a s + 3 s= 2 = a 2 2 = 2 a 2 K2 = K3 = s+a s+2 s s= 3 = a 3 3 s+a s+2. s+3 s=0 = a 6 y t = 2 a 2. e 2.t + a 3 3. e 3.t + a 6, t 0. y h (t) = 2 a 2. e 2.t + a 3 3. e 3.t y p (t) = a 6 e 2.t Modos do sistema (Determinado pelos pólos) e 3t Pólo em -2 modo e 2.t Pólo em -3 modo e 3.t O efeito do pólo pode ser atenuado pelo zero reduz o efeito do pólo com o zero próximo a ele. Zero em a pondera os modos do sistema.
28 - Desempenho em regime permanente Supor o sistema em malha fechada estável r Referência (Comportamento desejado para y). y Saída da planta. e.r. erro em regime permanente e.r. = lim t e t = lim s 0 s. E s e.r. = lim t e t = lim s 0 1º caso: r t = C 1, t 0 (degrau) K p constate de erro ao degrau K p = lim s 0 G s E s = R s Y s = R s G s. E s E s = s 1+G s. R(s) e.r. = lim s 0 2º caso: r t = C 2. t, t 0 (rampa) G s. R(s) R(s) = C 1 s s 1+G s. C 1 s = C 1 1+K P R s = C 2 s 2 e.r. = lim s 0 s 1+G s. C 2 s 2 = C 2 K v
29 K v = lim s 0 s. G s constante de erro à rampa -Planta tipo 0 G s = K 1. s+z 1 s+z 2 s+p 1 s+p 2 s+p 3 Kp = lim s 0 G(s) = K 1. Z 1. Z 2 P 1. P 2. P 3 0 e.r 0 K v = lim s 0 s. G s = 0 e.r. Planta tipo 1 G s = K 1 s + Z 1 (s + Z 2 ) s s + P 1 s + P 2 s + P 3
30 Kp = lim s 0 G(s) e. r. = 0 Kv = lim sg s = Z 1. Z 2. Z 3 0 e. r. 0 s 0 P 1. P 2. P 3 Efeito de perturbações r Referência p Perturbação Se G 1 (s) = 1, perturbação na entrada da planta Se G 2 (s) = 1, perturbação na saída da planta
31 Se G 1 (s) 1 e G 2 (s) 1, perturbação em um ponto intermediário da planta - Efeito de R(s) Considera-se P(s) 0 Y(s) R(s) = G 1 s. G 2 (s) 1 + G 1 s. G 2 (s) = G TC s Função de Transferência de Comando Efeito de P(s) Considera-se R(s) 0 Y(s) P(s) = G 2 (s) 1+G 1 (s).g 2 (s) = G tp s função de transferência de perturbação Y s = G tc s. R s + G tp s. P s Influência da referência Influência da perturbação Teorema do valor inicial e valor final Teorema do valor inicial lim f t = lim s. F s t 0 s Teorema do valor final (função estável)
32 lim t f t = lim s. F s s 0 -Efeito de ruídos oscilações. Supor r = constante = c r referência Na prática, a medida de y vem contaminada por ruídos, em geral, na forma de y medido = y teórico + ε. sin ωt Se houver necessidade de uti lização da componente derivativa (D) nos controladores do tipo PID (controlador PD e controlador PID), ocorrerá uma amplificação do ruído.
33 e = r y = r y teórico + ε. sin ωt d dt e t = d dt { r y teórico + ε. sin ωt } Em regime permanente, lim t y teórico = C (supor e.r. = 0) d lim t e t = ε. ω. sin ωt, há uma amplificação de ω vezes dt Obs.: no caso de ruídos causados pela fonte de alimentação, temos: f = 60 Hz ω = 2.π.f = 377 rad/s Um sistema com grande ruído não usamos controladores. - Introdução de um filtro Ex: Filtro passivo de 1ª Ordem Análise em aberto: V i = R. i + V o i = C. d dt V o V i = R. C. d dt V o + V o Aplicando a transformada de Laplace V i s = R. C. s. V o s + V o (s)
34 V o (s) V i (s) = 1 R. C. s + 1 = 1 filtro passa baixa τ. s + 1 τ = R. C - Introdução de um filtro na parte derivativa dos controladores PID Teoria τ d. s Pratica τ d.s introdução de um filtro 1+τ d.s Projeto sem filtro o Projeto mais simples o Sintonia fina mais trabalhosa Projeto com filtro o Projeto mais complexo o Sintonia fina menos trabalhosa No caso do projeto sem filtro, como a implementação sempre é feita com filtro, calcula-se a constante do filtro como: τ d = τ d N, 3 N 10 constante N sempre é números inteiros N=10 o Comportamento próximo do caso teórico o Amplificação significativa dos ruídos N=3 o Comportamento distante do caso teórico o Amplificação pequena dos ruídos Valor mais usado na pratica: N=5 *Na parte integrativa, atenua-se o ruído, pois ε. sen(ω. t) ε. cos ω. t atenua ω - Projeto de controladores Controlador tipo relé
35 Seja r = c u=m, para e 0 u=-m, para e 0 Supor: G s = K s+a.(s+b), K,a,b > 0 Para u=m U s = M s Para Y s = K s+a.(s+b). M s lim t y t = lim s. Y s = lim s. s 0 s 0 K s + a. (s + b). M s = K. M a. b Se K.M a.b < c, temos: Se K.M a.b = c, temos:
36 Para u = M U s = M s lim t K. M y t = lim Y s = s 0 a. b Se K.M a.b > c, temos:
37 M o Resposta atinge a referência mais rapidamente o Oscilações maiores amplitude das oscilações maiores o Tempo de estabilização maior M o Resposta atinge a referência mais lentamente o Oscilações menores o Tempo de estabilização menor Problema: alta freqüência de chaveamento
38 Solução: introdução de histerese u = M, para : e < e < e d dx e t < 0 u = -M, para : e - < e < e d dx e > 0 largura da histerese KM ab > c
39 Resposta oscilatória com pequena freqüência de chaveamento o Oscilações o Freqüência de chaveamento o Oscilações o Freqüência de chaveamento Obs: PI melhora o erro a parte integrativa ajuda a proporcional PID melhora o transitório a parte derivativa se opõem as partes P e I Ex: G s = r=1 1 s+2 s+3 - Controlador PID Método de sintonia inicial o Ziegler-Nichols o Polinomial o Lugar das raízes o Frequencial Método da sensibilidade malha fechada Método da curva de reação malha aberta - Método de Ziegler-Nichols 1) Sintonia inicial pelo método da sensibilidade 2) Sintonia inicial pelo método da curva de reação G s = K c τ i. s + τ d. s K τ i. τ d. s 2 + τ i. s + 1 c τ i. s K 1 c. τ i. τ s2 + d τ. s + 1 d τ i. τ d K τ i s c. τ d s τ d. s + 1 τ i. τ d s
40 s τ d. s + 1 τ i.τ d = 0 s = 1 τ d ± 1 τ τ d i.τ d 2 s = 1 τ d ± τ i 4τ d τ i. τ d 2 2 Caso mais simples: zeros reais iguais Zeros reais e iguais são: - 1 2τ d τ i 4τ d = 0 τ i = 4τ d - Método polinomial o Oferece a melhor sintonia inicial o Método que faz mais cálculos controladores mais sofisticado. 4 = b(s) s(s+1) a(s) n p = 0 n a = 2 Projetar o controlador mais simples de forma que o sistema em malha fechada apresente: P.O 5% T s2% 4s e.r 0,01 para r(t) = 2 Projete o controlador mais simples
41 Planta tipo 1 e.r = 0, para r(t) = 1 P.O 5% ξ = 0,7 θ = 45º T s2% = 4 ξ.ω n = 4 ξ. ω n = 1 Pólos de malha fechada: a s = s + 1 j s j = s = s 2 + 2s + 2 grau de a = 2 Grau a tem que ser maior ou igual ao grau da planta. G s = p(s) l s Se p(s) e l(s) forem coprimos; podemos escrever da seguinte forma: n p < n a n p < 2 n p = 0 p s = p 0 primeira tentativa n p = 1 p s = p 1 segunda tentativa n l max(n a n a, n b 1) n l max (0, 1) n l 0 l s = l 0
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA. Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva
 UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
 Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
5. Diagramas de blocos
 5. Diagramas de blocos Um sistema de controlo pode ser constituído por vários componentes. O diagrama de blocos é uma representação por meio de símbolos das funções desempenhadas por cada componente e
5. Diagramas de blocos Um sistema de controlo pode ser constituído por vários componentes. O diagrama de blocos é uma representação por meio de símbolos das funções desempenhadas por cada componente e
Estabilidade. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Desempenho de Sistemas de Controle Realimentados
 Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
5 Transformadas de Laplace
 5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
5 Transformadas de Laplace 5.1 Introdução às Transformadas de Laplace 4 5.2 Transformadas de Laplace definição 5 5.2 Transformadas de Laplace de sinais conhecidos 6 Sinal exponencial 6 Exemplo 5.1 7 Sinal
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
AULA #12. Estabilidade de Sistemas de Controle por
 AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
AULA #12 Estabilidade de Sistemas de Controle por Realimentação Estabilidade de Sistemas de Controle por Realimentação A presença de medidores, controladores e elementos finais de controle afetam as características
Modelagem no Domínio da Frequência. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
Modelagem no Domínio da Frequência Carlos Alexandre Mello 1 Transformada de Laplace O que são Transformadas? Quais as mais comuns: Laplace Fourier Cosseno Wavelet... 2 Transformada de Laplace A transf.
11/07/2012. Professor Leonardo Gonsioroski FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA.
 FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
FUNDAÇÃO EDSON QUEIROZ UNIVERSIDADE DE FORTALEZA DEPARTAMENTO DE ENGENHARIA ELÉTRICA Aulas anteriores Tipos de Sinais (degrau, rampa, exponencial, contínuos, discretos) Transformadas de Fourier e suas
Resposta Transitória de Circuitos com Elementos Armazenadores de Energia
 ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
ENG 1403 Circuitos Elétricos e Eletrônicos Resposta Transitória de Circuitos com Elementos Armazenadores de Energia Guilherme P. Temporão 1. Introdução Nas últimas duas aulas, vimos como circuitos com
Departamento de Engenharia Química e de Petróleo UFF. Disciplina: TEQ102- CONTROLE DE PROCESSOS. Diagrama de Bode. Outros Processos de Separação
 Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ102- CONTROLE DE PROCESSOS custo Diagrama de Bode Outros Processos de Separação Prof a Ninoska Bojorge 5.A. Traçado das Assíntotas Traçado
Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ102- CONTROLE DE PROCESSOS custo Diagrama de Bode Outros Processos de Separação Prof a Ninoska Bojorge 5.A. Traçado das Assíntotas Traçado
Projeto de sistemas de controle
 Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
V. ANÁLISE NO DOMÍNIO DO TEMPO
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE V. ANÁLISE NO DOMÍNIO DO TEMPO Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO
 PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
PMR3404 Controle I Aula 3
 PMR3404 Controle I Aula 3 Resposta estática Ações de controle PID Newton Maruyama 23 de março de 2017 PMR-EPUSP Classificação de sistemas de acordo com o seu desempenho em regime estático Seja o seguinte
PMR3404 Controle I Aula 3 Resposta estática Ações de controle PID Newton Maruyama 23 de março de 2017 PMR-EPUSP Classificação de sistemas de acordo com o seu desempenho em regime estático Seja o seguinte
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica
 UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
Ações de controle básicas: uma análise do desempenho em regime
 Capítulo 3 Ações de controle básicas: uma análise do desempenho em regime estático 3. Introdução Neste capítulo, as ações de controle básicas utilizadas em controladores industriais e o seu desempenho
Capítulo 3 Ações de controle básicas: uma análise do desempenho em regime estático 3. Introdução Neste capítulo, as ações de controle básicas utilizadas em controladores industriais e o seu desempenho
MICROMASTER MM4. Usando o Controle de Malha Fechada (PID) Edição 08.2002. IND 1 Drives technology Suporte Técnico Drives Hotline
 s MICROMASTER MM4 Usando o Controle de Malha Fechada (PID) Edição 08.2002 IND 1 Drives technology Suporte Técnico Drives Hotline USANDO O CONTROLE DE MALHA FECHADA NO MM4 O que é controle de malha fechada
s MICROMASTER MM4 Usando o Controle de Malha Fechada (PID) Edição 08.2002 IND 1 Drives technology Suporte Técnico Drives Hotline USANDO O CONTROLE DE MALHA FECHADA NO MM4 O que é controle de malha fechada
Função de Transferência de Malha Fechada
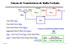 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Sistemas Embarcados. Controladores PI, PD e PID
 Sistemas Embarcados Controladores PI, PD e PID Controladores PI, PD e PID O que são os controladores PI, PD e PID? Aplicações dos controladores Implementação analógica dos controladores Implementação digital
Sistemas Embarcados Controladores PI, PD e PID Controladores PI, PD e PID O que são os controladores PI, PD e PID? Aplicações dos controladores Implementação analógica dos controladores Implementação digital
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Análise de Erro Estacionário
 Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 15
 Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Ondas (continuação) Ondas propagando-se em uma dimensão Vamos agora estudar propagação de ondas. Vamos considerar o caso simples de ondas transversais propagando-se ao longo da direção x, como o caso de
Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros
 Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Capítulo Cálculo da resposta no domínio do tempo: o papel dos pólos e zeros. Introdução O cálculo da resposta no domínio do tempoy(t) de um sistemag(t) pode ser calculado através da integral de convolução:
Resumo. Sinais e Sistemas Transformada de Laplace. Resposta ao Sinal Exponencial. Transformada de Laplace
 Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
Resumo Sinais e Sistemas Transformada de aplace lco@ist.utl.pt Instituto Superior Técnico Definição da transformada de aplace. Região de convergência. Propriedades da transformada de aplace. Sistemas caracterizados
ANÁLISE LINEAR DE SISTEMAS
 ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
ANÁLISE LINEAR DE SISTEMAS JOSÉ C. GEROMEL DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br Campinas, Janeiro de 2007
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Controlador PID: algoritmo, estrutura e sintonia
 Controlador PID: algoritmo, estrutura e sintonia Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 05 de setembro de 2018. Sumário 1 Introdução
Controlador PID: algoritmo, estrutura e sintonia Prof. Marcus V. Americano da Costa F o Departamento de Engenharia Química Universidade Federal da Bahia Salvador-BA, 05 de setembro de 2018. Sumário 1 Introdução
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes
 Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Métodos de Sintonização de Controladores PID
 3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech cassiano@ieee.org
 Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES
 1 INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES 1.1 - Instrumentação Importância Medições experimentais ou de laboratório. Medições em produtos comerciais com outra finalidade principal. 1.2 - Transdutores
1 INSTRUMENTAÇÃO INDUSTRIAL 1. INTRODUÇÃO / DEFINIÇÕES 1.1 - Instrumentação Importância Medições experimentais ou de laboratório. Medições em produtos comerciais com outra finalidade principal. 1.2 - Transdutores
Curso de Instrumentista de Sistemas. Fundamentos de Controle. Prof. Msc. Jean Carlos
 Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Modelagem no Domínio do Tempo. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Carlos Alexandre Mello 1 Modelagem no Domínio da Frequência A equação diferencial de um sistema é convertida em função de transferência, gerando um modelo matemático de um sistema que algebricamente relaciona
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação
 Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 1
 597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
597 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Movimentos Periódicos Para estudar movimentos oscilatórios periódicos é conveniente ter algum modelo físico em mente. Por exemplo, um
Circuitos Osciladores
 Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Circuitos Osciladores Em virtude da realimentação do sinal, a estabilidade do circuito deve ser analisada pois quando a freqüência aumenta, o deslocamento de fase varia e como parte deste sinal é adicionado
Sistema de excitação
 Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Sistema de excitação Introdução Introdução A função do sistema de excitação é estabelecer a tensão interna do gerador síncrono; Em consequência,o sistema de excitação é responsável não somente pela tensão
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial
 Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Transformada de Laplace. Parte 3
 Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Transformada de Laplace Parte 3 Elementos de circuito no domínio da frequência O resistor no domínio da frequência Pela lei de OHM : v= Ri A transformada da equação acima é V(s) = R I(s) O indutor no domínio
Filtros de sinais. Conhecendo os filtros de sinais.
 Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
Filtros de sinais Nas aulas anteriores estudamos alguns conceitos importantes sobre a produção e propagação das ondas eletromagnéticas, além de analisarmos a constituição de um sistema básico de comunicações.
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem
 p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
p. 1/2 Resumo Especificação de Filtros Filtro de Butterworth Filtro de Chebyshev Filtros de Primeira Ordem Filtros de Segunda Ordem Introdução Os primeiros filtros construídos eram circuitos LC passivos.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace
 Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Sinais e Sistemas Unidade 5 Representação em domínio da frequência para sinais contínuos: Transformada de Laplace Prof. Cassiano Rech, Dr. Eng. rech.cassiano@gmail.com Prof. Rafael Concatto Beltrame, Me.
Exercícios resolvidos P2
 Exercícios resolvidos P Questão 1 Dena as funções seno hiperbólico e cosseno hiperbólico, respectivamente, por sinh(t) = et e t e cosh(t) = et + e t. (1) 1. Verique que estas funções satisfazem a seguinte
Exercícios resolvidos P Questão 1 Dena as funções seno hiperbólico e cosseno hiperbólico, respectivamente, por sinh(t) = et e t e cosh(t) = et + e t. (1) 1. Verique que estas funções satisfazem a seguinte
Aula 13 Análise no domínio da frequência
 Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
Aula 13 Análise no domínio da frequência A resposta em frequência é a resposta do sistema em estado estacionário (ou em regime permanente) quando a entrada do sistema é sinusoidal. Métodos de análise de
1. Sinais de teste. 2. Sistemas de primeira ordem. 3. Sistemas de segunda ordem. Especificações para a resposta
 Desempenho de Sistemas de Controle Realimentados 1. Sinais de teste. Sistemas de primeira ordem 3. Sistemas de segunda ordem Especificações para a resposta Fernando de Oliveira Souza pag.1 Engenharia de
Desempenho de Sistemas de Controle Realimentados 1. Sinais de teste. Sistemas de primeira ordem 3. Sistemas de segunda ordem Especificações para a resposta Fernando de Oliveira Souza pag.1 Engenharia de
Circuitos Elétricos Senoides e Fasores
 Circuitos Elétricos Senoides e Fasores Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Corrente contínua x corrente alternada. Ver War of Currentes
Circuitos Elétricos Senoides e Fasores Alessandro L. Koerich Engenharia de Computação Pontifícia Universidade Católica do Paraná (PUCPR) Introdução Corrente contínua x corrente alternada. Ver War of Currentes
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG04037 Sistemas de Controle Digitais
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade
 Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Sessão Prática: Simulação e Controle com LabVIEW
 Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Universidade Federal do Rio de Janeiro. Princípios de Instrumentação Biomédica. Módulo 4
 Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
Universidade Federal do Rio de Janeiro Princípios de Instrumentação Biomédica Módulo 4 Faraday Lenz Henry Weber Maxwell Oersted Conteúdo 4 - Capacitores e Indutores...1 4.1 - Capacitores...1 4.2 - Capacitor
Ações Básicas de Controle
 Ações Básicas de Controle ENGA71: Análise e Projeto de Sistemas de Controle Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 18 de julho de 2016 Sumário 1 Introdução 2 Ações
Ações Básicas de Controle ENGA71: Análise e Projeto de Sistemas de Controle Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 18 de julho de 2016 Sumário 1 Introdução 2 Ações
Compensadores. Controle 1 - DAELN - UTFPR. Os compensadores são utilizados para alterar alguma característica do sistema em malha fechada.
 Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Processos industriais INSTRUMENTAÇÃO E CONTROLE. Pirâmide da automação 29/1/2012. Controle automático de processo
 Processos industriais INSTRUMENTAÇÃO E CONTROLE Controle automático de processo Processos Contínuos: são aqueles que possuem saídas contínuas como, por exemplo, processos de geração de energia. Processos
Processos industriais INSTRUMENTAÇÃO E CONTROLE Controle automático de processo Processos Contínuos: são aqueles que possuem saídas contínuas como, por exemplo, processos de geração de energia. Processos
Figura 2.1: Carro-mola
 Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
Capítulo 2 EDO de Segunda Ordem com Coeficientes Constantes 2.1 Introdução - O Problema Carro-Mola Considere um carro de massa m preso a uma parede por uma mola e imerso em um fluido. Colocase o carro
PARTE 2 FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL
 PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
PARTE FUNÇÕES VETORIAIS DE UMA VARIÁVEL REAL.1 Funções Vetoriais de Uma Variável Real Vamos agora tratar de um caso particular de funções vetoriais F : Dom(f R n R m, que são as funções vetoriais de uma
2.1 - Análise de Sistemas Realimentado pelo Lugar das Raízes- G 4 (s) = G 2 5 (s) = (s+5) G 6 (s) =
 ENG04035 - Sistemas de Controle I Prof. João Manoel e Prof. Romeu LISTA DE EXERCÍCIOS 2.1 - Análise de Sistemas Realimentado pelo Lugar das Raízes- 1. Considere os seguintes processos: 5 1 G 1 (s) = (s2)(s10)
ENG04035 - Sistemas de Controle I Prof. João Manoel e Prof. Romeu LISTA DE EXERCÍCIOS 2.1 - Análise de Sistemas Realimentado pelo Lugar das Raízes- 1. Considere os seguintes processos: 5 1 G 1 (s) = (s2)(s10)
Caracterização temporal de circuitos: análise de transientes e regime permanente. Condições iniciais e finais e resolução de exercícios.
 Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
Conteúdo programático: Elementos armazenadores de energia: capacitores e indutores. Revisão de características técnicas e relações V x I. Caracterização de regime permanente. Caracterização temporal de
RELATÓRIO FINAL: PROJETO DESAFIO CONTROLE DE POSIÇÃO DE UMA VÁLVULA
 RELATÓRIO FINAL: PROJETO DESAFIO CONTROLE DE POSIÇÃO DE UMA VÁLVULA Laboratório de Controle e Automação 1 ( LECI 1 ) Professor: Reinaldo Martinez Palhares Integrantes: Henrique Goseling Araújo, Hugo Montalvão
RELATÓRIO FINAL: PROJETO DESAFIO CONTROLE DE POSIÇÃO DE UMA VÁLVULA Laboratório de Controle e Automação 1 ( LECI 1 ) Professor: Reinaldo Martinez Palhares Integrantes: Henrique Goseling Araújo, Hugo Montalvão
Geração de Energia Elétrica
 Geração de Energia Elétrica Aspectos Dinâmicos da Geração Hidroelétrica Joinville, 21 de Março de 2012 Escopo dos Tópicos Abordados Controle de Carga-Frequência Regulação Primária Modelo do Sistema de
Geração de Energia Elétrica Aspectos Dinâmicos da Geração Hidroelétrica Joinville, 21 de Março de 2012 Escopo dos Tópicos Abordados Controle de Carga-Frequência Regulação Primária Modelo do Sistema de
Processos em Engenharia: Introdução a Servomecanismos
 Processos em Engenharia: Introdução a Servomecanismos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101 - Aula 7 p.1/47
Processos em Engenharia: Introdução a Servomecanismos Prof. Daniel Coutinho coutinho@das.ufsc.br Departamento de Automação e Sistemas DAS Universidade Federal de Santa Catarina UFSC DAS 5101 - Aula 7 p.1/47
Eletrônica Analógica
 UNIVERSIDADE FEDERAL DO PARÁ FACULDADE DE ENGENHARIA DE COMPUTAÇÃO E TELECOMUNICAÇÕES Eletrônica Analógica Transistores de Efeito de Campo Professor Dr. Lamartine Vilar de Souza lvsouza@ufpa.br www.lvsouza.ufpa.br
UNIVERSIDADE FEDERAL DO PARÁ FACULDADE DE ENGENHARIA DE COMPUTAÇÃO E TELECOMUNICAÇÕES Eletrônica Analógica Transistores de Efeito de Campo Professor Dr. Lamartine Vilar de Souza lvsouza@ufpa.br www.lvsouza.ufpa.br
ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04
 ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 15 Sumário Trabalho e EP Energia potencial Forças conservativas Calculando
ENERGIA POTENCIAL E CONSERVAÇÃO DE ENERGIA Física Geral I (1108030) - Capítulo 04 I. Paulino* *UAF/CCT/UFCG - Brasil 2012.2 1 / 15 Sumário Trabalho e EP Energia potencial Forças conservativas Calculando
Tipos de controladores e funcionamento
 Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ141- INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS custo Malhas Outros Processos de controle: de Separação Tipos de controladores e funcionamento
Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ141- INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS custo Malhas Outros Processos de controle: de Separação Tipos de controladores e funcionamento
Tal como no caso dos filtros passivos, os filtros ativos de 1 a ordem só produzem resposta passa-baixa ou passa-alta, com apenas um capacitor.
 FILTOS ATIVOS FILTOS ATIVOS DE a ODEM Tal como no caso dos filtros passivos, os filtros ativos de a ordem só produzem resposta passa-baixa ou passa-alta, com apenas um capacitor. Filtros passa-banda ou
FILTOS ATIVOS FILTOS ATIVOS DE a ODEM Tal como no caso dos filtros passivos, os filtros ativos de a ordem só produzem resposta passa-baixa ou passa-alta, com apenas um capacitor. Filtros passa-banda ou
Capítulo 4 Resposta em frequência
 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da frequência 4.2 Séries de Fourier e propriedades 4.3 Resposta em frequência dos SLITs 1 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da
Capítulo 4 Resposta em frequência 4.1 Noção do domínio da frequência 4.2 Séries de Fourier e propriedades 4.3 Resposta em frequência dos SLITs 1 Capítulo 4 Resposta em frequência 4.1 Noção do domínio da
Utilização de Gás. Módulo: Válvulas e Sistemas de Controle
 Utilização de Gás Módulo: Válvulas e Sistemas de Controle PROCESSO INDUSTRIAL Variável Controlada: Temperatura Meio Controlado: Fluido Variável Manipulada: Vazão Agente de Controle: Vapor Malha de Controle
Utilização de Gás Módulo: Válvulas e Sistemas de Controle PROCESSO INDUSTRIAL Variável Controlada: Temperatura Meio Controlado: Fluido Variável Manipulada: Vazão Agente de Controle: Vapor Malha de Controle
Objetivos de Controle
 Objetivos de Controle ENGC42: Sistemas de Controle I Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 13 de janeiro de 2016 Prof. Tito Luís Maia Santos 1/ 30 Sumário 1 Introdução
Objetivos de Controle ENGC42: Sistemas de Controle I Departamento de Engenharia Elétrica - DEE Universidade Federal da Bahia - UFBA 13 de janeiro de 2016 Prof. Tito Luís Maia Santos 1/ 30 Sumário 1 Introdução
Campos Vetoriais e Integrais de Linha
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
 Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Fundamentos de Automação. Hidráulica 01/06/2015. Hidráulica. Hidráulica. Hidráulica. Considerações Iniciais CURSO DE AUTOMAÇÃO INDUSTRIAL
 Ministério da educação - MEC Secretaria de Educação Profissional e Técnica SETEC Instituto Federal de Educação Ciência e Tecnologia do Rio Grande do Sul Campus Rio Grande Fundamentos de Automação CURSO
Ministério da educação - MEC Secretaria de Educação Profissional e Técnica SETEC Instituto Federal de Educação Ciência e Tecnologia do Rio Grande do Sul Campus Rio Grande Fundamentos de Automação CURSO
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE CONTROLADORES A SISTEMAS DE 1ªORDEM E 2º ORDEM
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 3: APLICAÇÃO DE CONTROLADORES A SISTEMAS DE 1ªORDEM E 2º ORDEM COLEGIADO DE ENGENHARIA
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 3: APLICAÇÃO DE CONTROLADORES A SISTEMAS DE 1ªORDEM E 2º ORDEM COLEGIADO DE ENGENHARIA
IBM1018 Física Básica II FFCLRP USP Prof. Antônio Roque Aula 6. O trabalho feito pela força para deslocar o corpo de a para b é dado por: = =
 Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Energia Potencial Elétrica Física I revisitada 1 Seja um corpo de massa m que se move em linha reta sob ação de uma força F que atua ao longo da linha. O trabalho feito pela força para deslocar o corpo
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
CINÉTICA QUÍMICA CINÉTICA QUÍMICA EQUAÇÃO DE ARRHENIUS
 CINÉTICA QUÍMICA CINÉTICA QUÍMICA EQUAÇÃO DE ARRHENIUS A DEPENDÊNCIA DA VELOCIDADE DE REAÇÃO COM A TEMPERATURA A velocidade da maioria das reações químicas aumenta à medida que a temperatura também aumenta.
CINÉTICA QUÍMICA CINÉTICA QUÍMICA EQUAÇÃO DE ARRHENIUS A DEPENDÊNCIA DA VELOCIDADE DE REAÇÃO COM A TEMPERATURA A velocidade da maioria das reações químicas aumenta à medida que a temperatura também aumenta.
Função. Definição formal: Considere dois conjuntos: o conjunto X com elementos x e o conjunto Y com elementos y. Isto é:
 Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
Função Toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função. Definição formal:
Razão de Rejeição a Fonte de Potência (PSRR)
 215 Outra unidade que expressa de forma direta o efeito da CMRR. Pode ser obtida observando que a tensão de offset V CM é expressa por: V CM = V C. 1/CMRR = V C.CMRR -1 Agora como CMRR -1 expressa-lo em
215 Outra unidade que expressa de forma direta o efeito da CMRR. Pode ser obtida observando que a tensão de offset V CM é expressa por: V CM = V C. 1/CMRR = V C.CMRR -1 Agora como CMRR -1 expressa-lo em
IFBA. CELET Coordenação do Curso Técnico em Eletrônica Professor: Edvaldo Moraes Ruas, EE. Vitória da Conquista, 2010
 IFBA CELET Coordenação do Curso Técnico em Eletrônica Professor: Edvaldo Moraes Ruas, EE Vitória da Conquista, 2010 A realimentação Negativa estabiliza o ganho de tensão, diminui a distorção e aumenta
IFBA CELET Coordenação do Curso Técnico em Eletrônica Professor: Edvaldo Moraes Ruas, EE Vitória da Conquista, 2010 A realimentação Negativa estabiliza o ganho de tensão, diminui a distorção e aumenta
Modelo Matemático e Controle de um Robô Móvel. 2.1. Modelo do motor que aciona cada roda do robô
 1. Introdução Modelo Matemático e Controle de um Robô Móvel Nesta aula serão apresentadas leis de controle que permitem a um robô móvel nãoholonômico navegar de maneira coordenada desde uma localização
1. Introdução Modelo Matemático e Controle de um Robô Móvel Nesta aula serão apresentadas leis de controle que permitem a um robô móvel nãoholonômico navegar de maneira coordenada desde uma localização
4. Curvas planas. T = κn, N = κt, B = 0.
 4. CURVAS PLANAS 35 4. Curvas planas Nesta secção veremos que no caso planar é possível refinar a definição de curvatura, de modo a dar-lhe uma interpretação geométrica interessante. Provaremos ainda o
4. CURVAS PLANAS 35 4. Curvas planas Nesta secção veremos que no caso planar é possível refinar a definição de curvatura, de modo a dar-lhe uma interpretação geométrica interessante. Provaremos ainda o
UNIVERSIDADE CATÓLICA DE GOIÁS. DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201) Prof.
 01 UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201) Prof. EDSON VAZ NOTA DE AULA III (Capítulo 7 e 8) CAPÍTULO 7 ENERGIA CINÉTICA
01 UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Disciplina: FÍSICA GERAL E EXPERIMENTAL I (MAF 2201) Prof. EDSON VAZ NOTA DE AULA III (Capítulo 7 e 8) CAPÍTULO 7 ENERGIA CINÉTICA
Circuitos Elétricos III
 Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
Circuitos Elétricos III Prof. Danilo Melges (danilomelges@cpdee.ufmg.br) Depto. de Engenharia Elétrica Universidade Federal de Minas Gerais A Transformada de Laplace em análise de circuitos parte 2 Equivalente
Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP. Prof. Cassiano Rech cassiano@ieee.org
 Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP cassiano@ieee.org 1 Operação como PFP Como a freqüência de comutação do interruptor S é muito maior que a freqüência
Controle de Conversores Estáticos Controle de um conversor boost CCM para correção do FP cassiano@ieee.org 1 Operação como PFP Como a freqüência de comutação do interruptor S é muito maior que a freqüência
LABORATÓRIO DE CONTROLE I ESTUDO DE COMPENSADORES DE FASE
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 4: ESTUDO DE COMPENSADORES DE FASE COLEGIADO DE ENGENHARIA ELÉTRICA DISCENTES: Lucas
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 4: ESTUDO DE COMPENSADORES DE FASE COLEGIADO DE ENGENHARIA ELÉTRICA DISCENTES: Lucas
Automação Industrial
 Automação Industrial Unidade 2 Respostas de um Sistema de Controle Prof. Rodrigo Cardoso Fuentes diretor.ctism@gmail.com Prof. Rafael Concatto Beltrame beltrame@mail.ufsm.br Objetivos da Aula 1. Definir
Automação Industrial Unidade 2 Respostas de um Sistema de Controle Prof. Rodrigo Cardoso Fuentes diretor.ctism@gmail.com Prof. Rafael Concatto Beltrame beltrame@mail.ufsm.br Objetivos da Aula 1. Definir
Introdução AVALIAÇÃO DE DESEMPENHO. No domínio do tempo. No domínio da freqüência. Função de transferência. Módulo e fase da função de transferência
 AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
AVALIAÇÃO DE DESEMPENHO Introdução Introdução Análise no domínio do tempo Resposta ao degrau Resposta à rampa Aula anterior Resposta à parábola Análise no domínio da freqüência Diagramas de Bode Diagrama
EQE-594 Controle e Instrumentação de Processos Profa. Ofélia de Q.F. Araújo EQ/UFRJ CONTROLE SELETIVO e OVERRIDE
 CONTROLE SELETIVO e OVERRIDE Nas estratégias de controle, pode surgir a necessidade de aplicar lógica seletora de sinais. Define-se, para tal, chaves seletoras de sinais: (1) Chave Seletora de Valor Alto
CONTROLE SELETIVO e OVERRIDE Nas estratégias de controle, pode surgir a necessidade de aplicar lógica seletora de sinais. Define-se, para tal, chaves seletoras de sinais: (1) Chave Seletora de Valor Alto
Departamento de Matemática - UEL - 2010. Ulysses Sodré. http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
 Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Matemática Essencial Extremos de funções reais Departamento de Matemática - UEL - 2010 Conteúdo Ulysses Sodré http://www.mat.uel.br/matessencial/ Arquivo: minimaxi.tex - Londrina-PR, 29 de Junho de 2010.
Circuitos CA I. 1 Resumo da aula anterior. Aula 6. 5 de abril de 2011
 Circuitos CA I Aula 6 5 de abril de 20 Resumo da aula anterior Estudamos a teoria formulada por Lammor que permite explicar a existência de diamagnetismo em algumas substancia. Basicamente a teoria supõe
Circuitos CA I Aula 6 5 de abril de 20 Resumo da aula anterior Estudamos a teoria formulada por Lammor que permite explicar a existência de diamagnetismo em algumas substancia. Basicamente a teoria supõe
2.3- DIAGRAMAS DE BLOCOS E DE FLUXO DE SINAL. FÓRMULA DE MASON DIAGRAMA DE BLOCOS DB
 2.3 DIRMS DE BLOOS E DE FLUXO DE SINL. FÓRMUL DE MSON DIRM DE BLOOS DB Os sistemas de controle, geralmente, são constituídos por vários componentes ou partes interligadas. Para mostrar estas interconexões
2.3 DIRMS DE BLOOS E DE FLUXO DE SINL. FÓRMUL DE MSON DIRM DE BLOOS DB Os sistemas de controle, geralmente, são constituídos por vários componentes ou partes interligadas. Para mostrar estas interconexões
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Sintonia de Controladores PID
 Sintonia de Controladores PID Objetivo: Determinar K p, K i e K d de modo a satisfazer especificações de projeto. Os efeitos independentes dos ganhos K p, K i e K d na resposta de malha fechada do sistema
Sintonia de Controladores PID Objetivo: Determinar K p, K i e K d de modo a satisfazer especificações de projeto. Os efeitos independentes dos ganhos K p, K i e K d na resposta de malha fechada do sistema
