Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG04037 Sistemas de Controle Digitais
|
|
|
- Ágata Mangueira Tavares
- 8 Há anos
- Visualizações:
Transcrição
1 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio de 2 Por definição, a expressão do controlador PID contínuo é u(t) e(t) + K i t e(τ)dτ + K d d dt e(t) onde K p, K i e K d são os ganhos proporcional, integral e derivativo, respectivamente. Para que os parâmetros do controlador PID possam ser mais facilmente associados aos polos e eros da função de transferência, é mais conveniente que os ganhos sejam parametriados da seguinte forma: ( u(t) e(t) + t T i e(τ)dτ + T d d dt e(t) onde T i e T d são os tempos integral e derivativo, respectivamente, tais que K i = K p T i e K d T d. 2 Controlador PID Digital Na sua versão digital, o controlador PID tem uma estrutura como mostrado na Fig.. Ou seja, tem-se C() + C i () + C d () )
2 K p E() C i () + + U() + C d () Figura : Estrutura do controlador PID digital. Dependendo da aproximação utiliada para a integral e a derivada, C i () e C d () podem assumir várias formas diferentes. Forward differences: T C i () = K i = K T p T i ( ) = K p τ i ( ) com τ i = T i T C d () = K d T T d T τ d ( ) com τ d = T d T C() + K p τ i ( ) + K pτ d ( ) τ i ( ) + + τ i τ d ( ) 2 τ i ( ) τ i ( ) + + τ i τ d ( ) τ i ( ) τ i τ d 2 + (τ i 2τ i τ d ) + + τ i τ d τ i τ i ( ) ( ) 2 + τ d 2 + τ i τ d + τ d τ d ( ) 2 + τ d 2 + τ iτ d τ i + τ i τ d C() τ d () 2
3 A função de transferência possui dois eros reais ou complexos e um polo em =. Como a função de transferência possui mais eros finitos do que polos finitos a sua implementação é problemática. Assim, é preferível utiliar as outras aproximações que não apresentam esse problema. Backward differences: T C i () = K i = K T p T i ( ) = K p τ i ( ) C d () = K d T T d T τ d C() + K p τ i ( ) + K pτ d τ i ( ) τ i τ d ( ) 2 τ i ( ) τ i ( 2 ) τ i τ d ( ) τ i ( ) (τ i + + τ i τ d ) 2 (τ i + 2τ i τ d ) + τ i τ d τ i ( ) τ i + + τ i τ d 2 τi+2τiτd τ = K i ++τ i τ d + p τ i ( ) τ iτ d τ i ++τ i τ d C() ( + τ i + τ d ) 2 +2τd + τ i +τ d + τ d + τ i +τ d ( ) A função de transferência possui dois eros reais ou complexos, um polo em = e um polo em =. Aproximação bilinear: T + C i () = K i 2 = K T + p 2T i = K + p 2τ i 2 C d () = K d T + = K 2 pt d T + τ d 2 + 3
4 + C() + K p 2τ i + K pτ d 2 + 2τ i ( + )( ) + ( + ) 2 + 4τ i τ d ( ) 2 2τ i ( + )( ) 2τ i ( 2 ) + ( ) + 4τ i τ d ( ) 2τ i ( + )( ) (2τ i + + 4τ i τ d ) 2 + (2 8τ i τ d ) + + 4τ i τ d 2τ i 2τ i ( + )( ) 2τ i + + 4τ i τ d τiτd 2τ = K i ++4τ i τ d + +4τ iτ d 2τ i 2τ i ++4τ i τ d p 2τ i ( + )( ) ( C() + ) τ d 2τ i τ i 4τ d τ 2τ d i ( + )( ) 2τ i +2τ d + 2τ i +2τ d A função de transferência possui dois eros reais ou complexos, um polo em = e um polo em =. Assim, o controlador PID apresenta dois polos e dois eros. As posições dos polos são determinadas pela aproximação utiliada, para backward differences tem-se polos em = e = e para aproximação bilinear tem-se polos em = e =. As posições dos dois eros são determinadas pelos parâmetros do controlador. 3 Controlador PD Digital Para um controlador PD tem-se C() + C d () Dependendo da aproximação utiliada para a derivada, C d () pode assumir várias formas diferentes. Forward differences: C() + K p τ d ( ) ( + τ d ( )) (τ d + τ d ) ( C() τ d + τ ) d τ d 4
5 A função de transferência possui apenas um ero real dentro do círculo unitário em = τ d τ d. Como a função de transferência possui mais eros finitos do que polos finitos a sua implementação é problemática. Assim, é preferível utiliar as outras aproximações que não apresentam esse problema. Backward differences: C() + K p τ d + τ d ( ) ( + τ d ) τ d C() ( + τ d ) τ d +τ d (2) A função de transferência possui um ero real dentro do círculo unitário em = τ d +τ d e um polo em =. Aproximação bilinear: C() + K p τ d 2 + ( + ) + 2τ d ( ) + ( + 2τ d ) + 2τ d + C() ( + 2τ d ) + 2τ d +2τ d + A função de transferência possui um ero real dentro do círculo unitário em = 2τ d +2τ d e um polo em =. Assim, o controlador PD apresenta um polo e um ero. A posição do polo é determinadas pela aproximação utiliada, para backward differences tem-se polo em = e para aproximação bilinear tem-se polo em =. A posição do ero é determinada pelos parâmetros do controlador. 4 Controlador PI Digital Para um controlador PI tem-se 5
6 C() + C i () Dependendo da aproximação utiliada para a integral C i () pode assumir várias formas diferentes. Forward differences: C() + K p τ i ( ) τ i ( ) + τ i ( ) τ i τ i + τ i ( ) τ i τ C() = K i p A função de transferência possui um ero real dentro do círculo unitário em = τ i τ i e um polo em =. Ao contrário dos controladores PID e PD, essa função de transferência não apresenta problemas de implementação. Backward differences: C() + K p τ i ( ) τ i ( ) + τ i ( ) (τ i + ) τ i τ i ( ) τ i + τi C() τ i τ i + A função de transferência possui um eros real dentro do círculo unitário em = τ i τ i e um polo em =. + Aproximação bilinear: T + C i () = K i 2 = K T + p 2T i = K + p 2τ i 6
7 C() + K p 2τ i + 2τ i ( ) + ( + ) 2τ i ( ) (2τ i + ) + 2τ i 2τ i ( ) C() 2τ i + 2τ i + 2τi 2τ i + A função de transferência possui um ero real dentro do círculo unitário em = 2τ i 2τ i e um polo em =. + Assim, o controlador PI apresenta um polo e um ero. A posição do polo é a mesma para todas as aproximações, =. A posição do ero é determinada pelos parâmetros do controlador. Ou seja, para um controlador PI, a flexibilidade de projeto é a mesma seja qual for a aproximação utiliado. No entanto, os valores dos parâmetros variam dependendo da aproximação escolhida. 5 Projeto de Controlador PID O projeto de um controlador PID digital é um caso particular de projeto de controladores no domínio, onde a posição dos polos é determinada pela aproximação utiliada e apenas os eros e o ganho DC do controlador podem ser livremente determinados para atingir-se as especificações do projeto. Para controladores PI ou PD, a situação é análoga, tendo-se porém apenas um ero para ser determinado em função das especificações. Exemplo Seja o sistema descrito por G() = (, 8) 2 (3) Projetar um controlador para obter o menor tempo de acomodação possível. A Figura 2 mostra o lugar das raíes para o sistema sem compensador. Como o objetivo é ter o menor tempo de acomodação possível, deve-se ter os polos de malha fechada com o menor raio possível. Como o lugar das raíes é uma circunferência de raio,8, qualquer ganho menor do que 3,2 posiciona os polos sobre a circunferência e portanto tem o mesmo tempo de acomodação. Para reduir-se o tempo de acomodação é necessário introduir um compensador 7
8 Eixo Imaginário Eixo Real Figura 2: Lugar da raíes para o sistema (3) sem compensador. que faça com que o lugar das raíes seja tal que possibilite localiar todos os polos mais próximo da origem do plano, de preferência localia-los na origem do plano. Utiliando-se um controlador PI não há como reduir a circunferência, pois esse controlador possui um polo em = e independentemente da posição do ero, não há como reduir o raio da circunferência, como mostra a Fig. 3. Um compensador PD obtido com a aproximação bilinear também não permite obter-se o desempenho desejado, pois não é possível sequer garantir que todos os polos em malha fechada fiquem dentro do círculo unitário, como mostra a Fig. 4. Utiliando-se um compensador PD obtido com a aproximação backward differences resulta no lugar das raíes mostrado na Fig. 5. Note que ocorre um cancelamento do ero da planta com o polo do controlador e através do ade- 8
9 Eixo Imaginário Eixo Real Figura 3: Lugar da raíes para o sistema (3) com compensador PI. quado posicionamento do ero do controlador é possível faer com que o lugar das raíes passe pela origem do plano. Isso ocorre quando o ero do controlador é posicionado em =, 4. Com essa disposição de polos e eros e malha aberta, o ganho em malha fechada para posicionar os polos de malha fechada na origem do plano é K = distância dos polos distância dos eros = Assim, o controlador é dado por =.6 Assim, de (2) tem-se C() =, 6, 4 9 (4)
10 Eixo Imaginário Eixo Real Figura 4: Lugar da raíes para o sistema (3) com compensador PD obtido com aproximação bilinear. de onde C() ( + τ d ) τ d +τ d =, 6, 4 K p ( + τ d ) =, 6 τ d + τ d =, 4 Portanto τ d =, 6667 e K p =, 96, que leva a K d τ d T =, 64T. A Fig. 6 mostra a resposta do sistema ao degrau unitário.
11 Eixo Imaginário Eixo Real Figura 5: Lugar da raíes para o sistema (3) com compensador PD obtido com aproximação backward differences. Outra possibilidade seria utiliar um controlador PID. No entanto, se for utiliada a aproximação bilinear, obtém-se uma situação semelhante à resultante com o controlador PID, como mostra o diagrama do lugar das raíes mostrado na Fig. 7. Obviamente os eros em =, 4 e =, 4 podem ser livremente localiados, mas qualquer localiação não fará com que o lugar das raíes seja tal que permita que todos os polos de malha fechada sejam localiados na origem. Porém, utiliando-se um compensador PID obtido com a aproximação backward differences resulta no lugar das raíes mostrado na Fig. 8. Note que ocorre um cancelamento do ero da planta com o polo na origem do controlador. Os dois eros do controlador podem ser livremente localiados. Uma escolha conveniente é utiliar um dos eros para cancelar um dos polos da planta em =, 8 e loca-
12 2.5 Saída, Controle Tempo (sec) Figura 6: Resposta ao degrau do sistema (3) com o compensador (4). liar o outro ero de forma que o diagrama do lugar das raíes passe pela origem do plano. Isso ocorre quando o ero é posicionado em =, Com essa disposição de polos e eros e malha aberta, o ganho em malha fechada para posicionar os polos de malha fechada na origem do plano é distância dos polos K = =.8 distância dos eros.4444 =.82 Assim, o controlador é dado por Assim, de (2) tem-se (, 8)(, 4444) C() =, 82 ( ) (5) 2
13 Eixo Imaginário Eixo Real Figura 7: Lugar da raíes para o sistema (3) com compensador PID obtido com aproximação bilinear. ( C() + ) 2 +2τd + τ + d +τ τ d + +τ + τ i τ d i d τ i ( ) de onde =, 82 (, 8)(, 4444) ( ) =, 82 2, , 3555 ( ) 3
14 Eixo Imaginário Eixo Real Figura 8: Lugar da raíes para o sistema (3) com compensador PID obtido com aproximação backward differences. ou K p ( + τ i + τ d ) =, τ d + τ i + τ d =, 2444 τ d + τ i + τ d =,
15 K p ( + τ i + τ d ) =, 82 τ i + 2τ i τ d τ i + + τ i τ d =, 2444 τ i τ d τ i + + τ i τ d =, 3555 que é equivalente a K p ( + τ i + τ d ) =, 82 τ i τ d, 3235τ i =, 6469 τ i τ d, 556τ i =, 556 Portanto τ i = 4.88, τ d =, 6665 e K p =, 962, que leva a K i = Kp τ i T =, 2T e K d τ d T =, 64T. A Fig. 9 mostra a resposta do sistema ao degrau unitário. 6 Controlador PID Ótimo Utiliando a aproximação backward differences, a sua expressão do controlador PID na forma discreta é: u(k) e(k) + K i T k i= e(i) + K d T (e(k) e(k )) (6) E considerando (6) atrasado de um período de amostragem tem-se: e k u(k ) e(k ) + K i T e(i) + K d T i= (e(k ) e(k 2)) u(k) u(k ) (e(k) e(k ))+K i Te(k)+K d T ou 5 (e(k) 2e(k ) + e(k 2))
16 2.5 Saída, Controle Tempo (sec) Figura 9: Resposta ao degrau do sistema (3) com o compensador (5). u(k) = u(k )+K p (e(k) e(k ))+K i Te(k)+K d T (e(k) 2e(k ) + e(k 2)) que é uma forma mais conveniente de ser utiliada por evitar problemas de overflow devido ao somatório. Adicionalmente, na presença de saturação, basta corrigir o valor de u(k ) para o valor saturado para evitar o problema de windup. O problema de controle PID ótimo consiste em obter-se os valores de K p, K i e K d de forma que o desempenho do sistema seja o melhor possível. Ou seja, um controlador ótimo é um controlador que fa com que o desempenho do sistema seja, no mínimo, tão bom quanto o possível de ser obtido com qualquer outro controlador 2. Outro aspecto do problema é o que significa melhor desempenho. Obviamente, o que é desempenho melhor depende de como se mede o desempenho. Em Obviamente, existem técnicas mais sofisticadas de anti-windup, mas estão fora do escopo do problema tratado aqui. 2 Em sistemas de controle, otimiar significa obter comprovadamente o melhor possível e não apenas melhorar o desempenho. 6
17 controle ótimo é usual definir um índice de desempenho, usualmente denominado de custo, cujo valor é um escalar. Os custos mais utiliados são: Integral of Squared Error (ISE): o desempenho do sistema é avaliado pela expressão (7). A característica deste índice de desempenho é que ele dá grande peso para erros grandes e pequeno peso para erros pequenos. Um sistema que minimia este critério tende a apresentar uma rápida diminuição em um erro inicial grande. Portanto, a resposta é rápida e oscilatória. Assim, o sistema tem baixa estabilidade relativa. J(K p,k i,k d ) = n e 2 (k) (7) k= Integral of Absolute Error (IAE): o desempenho do sistema é avaliado pela expressão (8). Um sistema ótimo baseado neste critério é um sistema que tem um amortecimento raoável e uma característica de resposta transitória satisfatória. J(K p,k i,k d ) = n e(k) (8) k= Integral of Time Squared Error (ITSE): o desempenho do sistema é avaliada pela expressão (9). Uma característica é que, na resposta ao degrau unitário, um erro inicial grande é ponderado com peso baixo, enquanto que erros que ocorrem mais tarde na resposta transitória são bastante penaliados. J(K p,k i,k d ) = n ke 2 (k) (9) k= Critério ITAE: o desempenho do sistema é avaliado pela expressão (). Assim como no critério apresentado anteriormente, um erro inicial grande em uma resposta a degrau unitário é ponderado com peso pequeno e erros que ocorrem mais tarde na resposta transitória são bastante penaliados. A característica de um sistema que minimia este critério é que o overshoot é pequeno e oscilações são bem amortecidas J(K p,k i,k d ) = n k e(k) () k= 7
18 Assim, na abordagem de controle ótimo, os ganhos do controlador PID podem ser obtidos através de K p,k i,k d = arg min K p,k i,k d J(K p,k i,k d ) Embora em alguns casos seja possível realiar a minimiação de forma algébrica, em geral a obtenção da solução requer o uso do modelo do sistema no espaço de estados. Por outro lado, tendo-se apenas o modelo entrada-saída do sistema é possível computar o custo J(K p,k i,k d ) conhecendo-se os valores dos ganhos. Dessa forma é possível utiliar procedimentos numéricos para realiar a minimiação. Uma vantagem da otimiação numérica é que o método de sintonia do controlador aplica-se também a plantas não lineares. 6. Método de Hooke-Jeeves O método de Hooke-Jeeves é um método simples para realiar uma minimiação numérica multidimensional. O método consiste basicamente em determinar uma direção de decremento do custo e faer uma minimiação unidimensional nessa direção. Dados o vetor de ganhos K, de dimensão n, o passo do algoritmo de otimiação h, a precisão de parada ǫ e um valor inicial para os ganhos K(), o algoritmo é. Achar a direção de busca Para i = até n faça K (k) K (k).. Se J K i (k) + h J K i (k) faça H i = h.. K n (k) K n (k) Senão K (k) K (k).. Se J K i (k) h J K i (k) faça H i = h.. K n (k) K n (k) Senão faça H i = 8
19 2. Busca unidimensional (Algoritmo de Davies-Swan-Campey) K(k + ) = K(k) + λ H Onde λ = arg minj (K(k) + λh) λ 3. Critério de parada Se J (K(k + )) J (K(k)) ǫ ou k > número máximo de iterações K = K(k + ) e fim Senão k = k + e vá para O método de Davies-Swam-Campey, dada um valor inicial λ (), passo inicial δ(k), a tolerância ǫ, e K [, ] 3 é:. λ (k) = λ (k) δ(k) λ (k) = λ (k) + δ(k) J (k) = J (λ (k)) J (k) = J (λ (k)) 2. Se J (k) > J (k) faça p = e vá para 3 senão calcule J (k) = J (λ (k)) Se J (k) < J (k) faça p = e vá para 3 senão vá para 6 3. Para n =, 2, calcule J n (k) = f (λ n (k) + 2 n pδ(k)) até J n (k) > J n (k) 4. Calcule J m (k) = J (λ n (k) + 2 n 2 pδ(k)) 5. Se J m (k) J n (k), calcule Senão calcule λ (k + ) = λ n (k) + 2n 2pδ(k) (J n 2 (k) J m (k)) 2 (J n 2 (k) 2J n (k) + J m (k)) λ (k + ) = λ m (k) + 2n 2pδ(k) (J n (k) J n (k)) 2 (J n (k) 2J m (k) + J n (k)) Se 2 n 2 δ(k) ǫ vá para 7 senão faça δ(k + ) = Kδ(k) e vá para 3 Um valor típico é K =.. 9
20 6. Calcule λ (k + ) = λ (k) + δ(k) (J (k) J (k)) 2 (J (k) 2J (k) + J (k)) Se δ(k) ǫ vá para 7 senão faça δ(k + ) = Kδ(k) e vá para 7. λ = λ (k + ) Utiliando os algoritmos acima para o sistema descrito por 4.25 G(s) = s s s e utiliando o critério ISE, resulta nos ganhos K p =, 754, K i =, 35, K d = 4,, com um J(2) = 5, 389, e a figura mostra o sinal de saída, o sinal de controle, o sinal erro e a evolução do custo. 8 6 u(t) y(t) e(t) J(t) Figura : Resposta do PID ótimo segundo o critério ISE. Pode-se perceber que a amplitude do sinal de controle pode tornar-se bastante elevada, eventualmente tornando a implementação do controlador impossível na prática. Uma alternativa para contornar esse problema é incluir no custo uma ponderação para a energia de controle, substituindo os critérios por 2
21 ISE : IAE : J(K p,k i,k d ) = J(K p,k i,k d ) = n ( e 2 (k) + ρu 2 (k) ) () k= n ( e(k) + ρu 2 (k) ) (2) Repetindo a otimiação para a mesma planta, porém utiliando critério ISE com ρ =., resulta nos ganhos K p =, 759, K i =, 9, K d = 2, 346, com um J(2) = 38, 64, e a figura mostra o sinal de saída, o sinal de controle, o sinal erro e a evolução do custo/. k= u(t) y(t) e(t) J(t) Figura : Resposta do PID ótimo segundo o critério ISE com ρ =.. Note-se que não é intuitivo o ajuste do parâmetro ρ e que não existe uma correspondência direta do valor desse parâmetro com especificações típicas da resposta desejada para o sistema, como tempo de acomodação e overshoot. Uma abordagem alternativa, para se recuperar intuição na especificação dos parâmetros é utiliar um critério semelhante ao ISE, mas utiliando (para efeitos de cálculo do critério) o erro em relação à um modelo de referência e não em relação a referência em sí. Ou seja, calculado o custo por 2
22 J(K p,k i,k d ) = n e 2 m(k) onde e m (k) = y(k) y m (k), sendo y m (k) a saída de um modelo de referência escolhido para ter o desempenho desejado para o sistema. Nesse caso, utiliou-se o modelo k= Y ( s) U(s) = s 2 + s + A otimiação para a mesma planta, porém utiliando o modelo de referência resulta nos ganhos K p =, 755, K i =, 2, K d =, 294, com um J(2) =, 437, e a figura 2 mostra o sinal de saída, o sinal de controle, o sinal erro e a evolução do custo..6.4 u(t) y(t) ym(t) e(t) J(t) Figura 2: Resposta do PID ótimo em relação ao modelo de referência. 22
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica
 UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
CONTROLO DE SISTEMAS
 UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA. Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva
 UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
EXERCÍCIOS RESOLVIDOS
 ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
ENG JR ELETRON 2005 29 O gráfico mostrado na figura acima ilustra o diagrama do Lugar das Raízes de um sistema de 3ª ordem, com três pólos, nenhum zero finito e com realimentação de saída. Com base nas
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Projeto de sistemas de controle
 Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte:
 Processo A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte: K=26.4 Ganho L=203 Atraso em ms τ=334 Constante de tempo em ms.
Processo A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte: K=26.4 Ganho L=203 Atraso em ms τ=334 Constante de tempo em ms.
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Eduardo Camponogara. DAS-5103: Cálculo Numérico para Controle e Automação. Departamento de Automação e Sistemas Universidade Federal de Santa Catarina
 Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle e Automação 1/48 Sumário Arredondamentos Erros 2/48 Sumário Arredondamentos
Eduardo Camponogara Departamento de Automação e Sistemas Universidade Federal de Santa Catarina DAS-5103: Cálculo Numérico para Controle e Automação 1/48 Sumário Arredondamentos Erros 2/48 Sumário Arredondamentos
Curso de Instrumentista de Sistemas. Fundamentos de Controle. Prof. Msc. Jean Carlos
 Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Curso de Instrumentista de Sistemas Fundamentos de Controle Prof. Msc. Jean Carlos Ações de controle em malha fechada Controle automático contínuo em malha fechada Ação proporcional A característica da
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
 Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Faculdade Sagrada Família
 AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
AULA 12 - AJUSTAMENTO DE CURVAS E O MÉTODO DOS MÍNIMOS QUADRADOS Ajustamento de Curvas Sempre que desejamos estudar determinada variável em função de outra, fazemos uma análise de regressão. Podemos dizer
Equações Diferenciais Ordinárias
 Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Capítulo 8 Equações Diferenciais Ordinárias Vários modelos utilizados nas ciências naturais e exatas envolvem equações diferenciais. Essas equações descrevem a relação entre uma função, o seu argumento
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos. Prof. Cassiano Rech cassiano@ieee.org
 Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Controle de Conversores Estáticos Retroação de estados: Projeto por alocação de pólos cassiano@ieee.org 1 Projeto por alocação de pólos Na abordagem convencional, usando por exemplo o método do lugar das
Tipos de malha de Controle
 Tipos de malha de Controle SUMÁRIO 1 - TIPOS DE MALHA DE CONTROLE...60 1.1. CONTROLE CASCATA...60 1.1.1. Regras para Selecionar a Variável Secundária...62 1.1.2. Seleção das Ações do Controle Cascata e
Tipos de malha de Controle SUMÁRIO 1 - TIPOS DE MALHA DE CONTROLE...60 1.1. CONTROLE CASCATA...60 1.1.1. Regras para Selecionar a Variável Secundária...62 1.1.2. Seleção das Ações do Controle Cascata e
Métodos de Sintonização de Controladores PID
 3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace
 Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Análise de Sistemas em Tempo Contínuo usando a Transformada de Laplace Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do
Medição tridimensional
 A U A UL LA Medição tridimensional Um problema O controle de qualidade dimensional é tão antigo quanto a própria indústria, mas somente nas últimas décadas vem ocupando a importante posição que lhe cabe.
A U A UL LA Medição tridimensional Um problema O controle de qualidade dimensional é tão antigo quanto a própria indústria, mas somente nas últimas décadas vem ocupando a importante posição que lhe cabe.
Texto 07 - Sistemas de Partículas. A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica.
 Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Controlabilidade e Observabilidade
 IA536 - Teoria de Sistemas Lineares - FEEC/UNICAMP contr 1/18 Controlabilidade e Observabilidade Sfrag replacements R 1 R 2 + u C 1 C 2 R 3 y A tensão no capacitor C 2 não pode ser controlada pela entrada
IA536 - Teoria de Sistemas Lineares - FEEC/UNICAMP contr 1/18 Controlabilidade e Observabilidade Sfrag replacements R 1 R 2 + u C 1 C 2 R 3 y A tensão no capacitor C 2 não pode ser controlada pela entrada
Figura 5.1.Modelo não linear de um neurônio j da camada k+1. Fonte: HAYKIN, 2001
 47 5 Redes Neurais O trabalho em redes neurais artificiais, usualmente denominadas redes neurais ou RNA, tem sido motivado desde o começo pelo reconhecimento de que o cérebro humano processa informações
47 5 Redes Neurais O trabalho em redes neurais artificiais, usualmente denominadas redes neurais ou RNA, tem sido motivado desde o começo pelo reconhecimento de que o cérebro humano processa informações
Problemas de Valor Inicial para Equações Diferenciais Ordinárias
 Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Problemas de Valor Inicial para Equações Diferenciais Ordinárias Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática Aplicada - Mestrados
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
MD Sequências e Indução Matemática 1
 Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Sequências Indução Matemática Renato Martins Assunção assuncao@dcc.ufmg.br Antonio Alfredo Ferreira Loureiro loureiro@dcc.ufmg.br MD Sequências e Indução Matemática 1 Introdução Uma das tarefas mais importantes
Função de Transferência de Malha Fechada
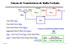 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional
 Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO
 TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
Universidade Federal do Paraná
 Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Problema do fechamento
Universidade Federal do Paraná Programa de pós-graduação em engenharia de recursos hídricos e ambiental TH705 Mecânica dos fluidos ambiental II Prof. Fernando Oliveira de Andrade Problema do fechamento
3 Matemática financeira e atuarial
 3 Matemática financeira e atuarial A teoria dos juros compostos em conjunto com a teoria da probabilidade associada à questão da sobrevivência e morte de um indivíduo são os fundamentos do presente trabalho.
3 Matemática financeira e atuarial A teoria dos juros compostos em conjunto com a teoria da probabilidade associada à questão da sobrevivência e morte de um indivíduo são os fundamentos do presente trabalho.
Instituto Superior Técnico Departamento de Matemática Última actualização: 11/Dez/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 11/Dez/2003 ÁLGEBRA LINEAR A FICHA 8 APLICAÇÕES E COMPLEMENTOS Sistemas Dinâmicos Discretos (1) (Problema
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 11/Dez/2003 ÁLGEBRA LINEAR A FICHA 8 APLICAÇÕES E COMPLEMENTOS Sistemas Dinâmicos Discretos (1) (Problema
Sistemas Embarcados. Controladores PI, PD e PID
 Sistemas Embarcados Controladores PI, PD e PID Controladores PI, PD e PID O que são os controladores PI, PD e PID? Aplicações dos controladores Implementação analógica dos controladores Implementação digital
Sistemas Embarcados Controladores PI, PD e PID Controladores PI, PD e PID O que são os controladores PI, PD e PID? Aplicações dos controladores Implementação analógica dos controladores Implementação digital
Modelo Matemático e Controle de um Robô Móvel. 2.1. Modelo do motor que aciona cada roda do robô
 1. Introdução Modelo Matemático e Controle de um Robô Móvel Nesta aula serão apresentadas leis de controle que permitem a um robô móvel nãoholonômico navegar de maneira coordenada desde uma localização
1. Introdução Modelo Matemático e Controle de um Robô Móvel Nesta aula serão apresentadas leis de controle que permitem a um robô móvel nãoholonômico navegar de maneira coordenada desde uma localização
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 2 - Cálculo Numérico
 Aula 2 - Cálculo Numérico Erros Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 2 - Cálculo Numérico 1 / 41 Sumário Sumário 1 Sumário 2 Erros Modelagem Truncamento Representação
Aula 2 - Cálculo Numérico Erros Prof. Phelipe Fabres Anhanguera Prof. Phelipe Fabres (Anhanguera) Aula 2 - Cálculo Numérico 1 / 41 Sumário Sumário 1 Sumário 2 Erros Modelagem Truncamento Representação
Universidade Federal de São João Del Rei - UFSJ
 Universidade Federal de São João Del Rei - UFSJ Instituída pela Lei 0.45, de 9/04/00 - D.O.U. de /04/00 Pró-Reitoria de Ensino de Graduação - PROEN Disciplina: Cálculo Numérico Ano: 03 Prof: Natã Goulart
Universidade Federal de São João Del Rei - UFSJ Instituída pela Lei 0.45, de 9/04/00 - D.O.U. de /04/00 Pró-Reitoria de Ensino de Graduação - PROEN Disciplina: Cálculo Numérico Ano: 03 Prof: Natã Goulart
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial
 Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Aula 8 Controladores do tipo Proporcional, Integral e Diferencial Introdução Estrutura do Controlador PID Efeito da Ação Proporcional Efeito da Ação Integral Efeito da Ação Derivativa Sintonia de Controladores
Potenciação no Conjunto dos Números Inteiros - Z
 Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Rua Oto de Alencar nº 5-9, Maracanã/RJ - tel. 04-98/4-98 Potenciação no Conjunto dos Números Inteiros - Z Podemos epressar o produto de quatro fatores iguais a.... por meio de uma potência de base e epoente
Análise e Processamento de Bio-Sinais. Mestrado Integrado em Engenharia Biomédica. Sinais e Sistemas. Licenciatura em Engenharia Física
 Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Análise e Processamento de Bio-Sinais Mestrado Integrado em Engenharia Biomédica Licenciatura em Engenharia Física Faculdade de Ciências e Tecnologia Slide Slide 1 1 Tópicos: Representação de Sinais por
Realimentação. Engº Sun Hsien Ming
 NT 204/98 Realimentação Engº Sun Hsien Ming 1. Introdução Dando continuidade à divulgação dos conceitos e recursos do sistema SCOOT, o presente trabalho pretende abordar o processo de realimentação. A
NT 204/98 Realimentação Engº Sun Hsien Ming 1. Introdução Dando continuidade à divulgação dos conceitos e recursos do sistema SCOOT, o presente trabalho pretende abordar o processo de realimentação. A
8- Controlador PID. PID = Proporcional + Integral + Derivativo
 Controlaor PID 154 8- Controlaor PID PID = Proporcional + Integral + Derivativo É interessante assinalar que mais a metae os controlaores inustriais em uso nos ias atuais utiliza estratégias e controle
Controlaor PID 154 8- Controlaor PID PID = Proporcional + Integral + Derivativo É interessante assinalar que mais a metae os controlaores inustriais em uso nos ias atuais utiliza estratégias e controle
Matemática para Engenharia
 Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Matemática para Engenharia Profa. Grace S. Deaecto Faculdade de Engenharia Mecânica / UNICAMP 13083-860, Campinas, SP, Brasil. grace@fem.unicamp.br Segundo Semestre de 2013 Profa. Grace S. Deaecto ES401
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Dist. da linha saída à 1ª barreira
 TÉCNICA DAS CORRIDAS COM BARREIRAS Antes de mais nada podemos dizer que as corridas com barreiras são provas de velocidade rasa porque, muito embora o barreiristas se depare com uma série de barreiras
TÉCNICA DAS CORRIDAS COM BARREIRAS Antes de mais nada podemos dizer que as corridas com barreiras são provas de velocidade rasa porque, muito embora o barreiristas se depare com uma série de barreiras
Flambagem de Colunas Introdução
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Flambagem de Colunas Introdução Os sistemas
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Flambagem de Colunas Introdução Os sistemas
LABORATÓRIO DE CONTROLE I APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM
 UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
UNIVERSIDADE FEDERAL DO VALE DO SÃO FRANCISCO COLEGIADO DE ENGENHARIA ELÉTRICA LABORATÓRIO DE CONTROLE I Experimento 5: APLICAÇÃO DE COMPENSADORES DE FASE DE 1ª ORDEM E DE 2ª ORDEM COLEGIADO DE ENGENHARIA
Tipos de controladores e funcionamento
 Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ141- INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS custo Malhas Outros Processos de controle: de Separação Tipos de controladores e funcionamento
Departamento de Engenharia Química e de Petróleo UFF Disciplina: TEQ141- INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS custo Malhas Outros Processos de controle: de Separação Tipos de controladores e funcionamento
Campos Vetoriais e Integrais de Linha
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Testedegeradoresde. Parte X. 38 Testes de Ajuste à Distribuição. 38.1 Teste Chi-Quadrado
 Parte X Testedegeradoresde números aleatórios Os usuários de uma simulação devem se certificar de que os números fornecidos pelo gerador de números aleatórios são suficientemente aleatórios. O primeiro
Parte X Testedegeradoresde números aleatórios Os usuários de uma simulação devem se certificar de que os números fornecidos pelo gerador de números aleatórios são suficientemente aleatórios. O primeiro
Eletrônica Analógica
 UNIVERSIDADE FEDERAL DO PARÁ FACULDADE DE ENGENHARIA DE COMPUTAÇÃO E TELECOMUNICAÇÕES Eletrônica Analógica Transistores de Efeito de Campo Professor Dr. Lamartine Vilar de Souza lvsouza@ufpa.br www.lvsouza.ufpa.br
UNIVERSIDADE FEDERAL DO PARÁ FACULDADE DE ENGENHARIA DE COMPUTAÇÃO E TELECOMUNICAÇÕES Eletrônica Analógica Transistores de Efeito de Campo Professor Dr. Lamartine Vilar de Souza lvsouza@ufpa.br www.lvsouza.ufpa.br
Notas sobre a Fórmula de Taylor e o estudo de extremos
 Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
Notas sobre a Fórmula de Taylor e o estudo de etremos O Teorema de Taylor estabelece que sob certas condições) uma função pode ser aproimada na proimidade de algum ponto dado) por um polinómio, de modo
APLICAÇÕES DA CURVA s NO GERENCIAMENTO DE PROJETOS
 CONCEITOS GERAIS : A curva S representa graficamente o resultado da acumulação das distribuições percentuais, parciais, relativas à alocação de determinado fator de produção (mão de obra, equipamentos
CONCEITOS GERAIS : A curva S representa graficamente o resultado da acumulação das distribuições percentuais, parciais, relativas à alocação de determinado fator de produção (mão de obra, equipamentos
Compensadores. Controle 1 - DAELN - UTFPR. Os compensadores são utilizados para alterar alguma característica do sistema em malha fechada.
 Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
CAPÍTULO 3. Sistemas com Vários Componentes (Multicomponentes) em Modelos Markovianos de Decisão
 CAPÍTULO 3 Sistemas com Vários Componentes (Multicomponentes) em Modelos Markovianos de Decisão 3.1 - Multicomponentes Conceitos Básicos: O conceito de multicomponente é utilizado em diversas áreas de
CAPÍTULO 3 Sistemas com Vários Componentes (Multicomponentes) em Modelos Markovianos de Decisão 3.1 - Multicomponentes Conceitos Básicos: O conceito de multicomponente é utilizado em diversas áreas de
Instituto Tecnológico de Aeronáutica Divisão de Engenharia Eletrônica Departamento de Sistemas e Controle
 Instituto Tecnológico de Aeronáutica Divisão de Engenharia Eletrônica Departamento de Sistemas e ontrole EES-5/ ELE/AES Engenharia de ontrole LAB : rojeto e Simulação de ontrolador com ealimentação de
Instituto Tecnológico de Aeronáutica Divisão de Engenharia Eletrônica Departamento de Sistemas e ontrole EES-5/ ELE/AES Engenharia de ontrole LAB : rojeto e Simulação de ontrolador com ealimentação de
Aula 9 ESCALA GRÁFICA. Antônio Carlos Campos
 Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
Aula 9 ESCALA GRÁFICA META Apresentar as formas de medição da proporcionalidade entre o mundo real e os mapas através das escalas gráficas. OBJETIVOS Ao final desta aula, o aluno deverá: estabelecer formas
DESENVOLVIMENTO DE UM ROBÔ MANIPULADOR INDUSTRIAL
 1 DESENVOLVIMENTO DE UM ROBÔ MANIPULADOR INDUSTRIAL Carlos Henrique Gonçalves Campbell Camila Lobo Coutinho Jediael Pinto Júnior Associação Educacional Dom Bosco 1. Objetivo do Trabalho Desenvolvimento
1 DESENVOLVIMENTO DE UM ROBÔ MANIPULADOR INDUSTRIAL Carlos Henrique Gonçalves Campbell Camila Lobo Coutinho Jediael Pinto Júnior Associação Educacional Dom Bosco 1. Objetivo do Trabalho Desenvolvimento
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva nos pontos onde e Vamos determinar a reta tangente à curva nos pontos de abscissas
Vibrações Mecânicas. Vibração Livre Sistemas com 1 GL. Ramiro Brito Willmersdorf ramiro@willmersdorf.net
 Vibrações Mecânicas Vibração Livre Sistemas com 1 GL Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2015.1 Introdução Modelo 1
Vibrações Mecânicas Vibração Livre Sistemas com 1 GL Ramiro Brito Willmersdorf ramiro@willmersdorf.net Departamento de Engenharia Mecânica Universidade Federal de Pernambuco 2015.1 Introdução Modelo 1
A otimização é o processo de
 A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Eiste um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento de otimização.
A otimização é o processo de encontrar a melhor solução (ou solução ótima) para um problema. Eiste um conjunto particular de problemas nos quais é decisivo a aplicação de um procedimento de otimização.
CAPÍTULO I. UNIVERSIDADE FEDERAL DE UBERLÂNDIA FACULDADE DE ENGENHARIA ELÉTRICA Apostila de Eletrônica Digital. Sistemas de Numeração. 1.
 CAPÍTULO I Sistemas de Numeração. Introdução O decimal é o mais importante dos sistemas numéricos. Ele está fundamentado em certas regras que são a base de formação para qualquer outro sistema. Além do
CAPÍTULO I Sistemas de Numeração. Introdução O decimal é o mais importante dos sistemas numéricos. Ele está fundamentado em certas regras que são a base de formação para qualquer outro sistema. Além do
Além do Modelo de Bohr
 Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
Análise de Erro Estacionário
 Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
x As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas.
 Å 6pULHV GH SRWrQFLDV As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas. Um eemplo típico é a série, O cálculo do valor
Å 6pULHV GH SRWrQFLDV As VpULHVGHSRWrQFLDV são um caso particularmente importante das séries de funções, com inúmeras aplicações tanto teóricas como práticas. Um eemplo típico é a série, O cálculo do valor
O mercado de bens CAPÍTULO 3. Olivier Blanchard Pearson Education. 2006 Pearson Education Macroeconomia, 4/e Olivier Blanchard
 O mercado de bens Olivier Blanchard Pearson Education CAPÍTULO 3 3.1 A composição do PIB A composição do PIB Consumo (C) são os bens e serviços adquiridos pelos consumidores. Investimento (I), às vezes
O mercado de bens Olivier Blanchard Pearson Education CAPÍTULO 3 3.1 A composição do PIB A composição do PIB Consumo (C) são os bens e serviços adquiridos pelos consumidores. Investimento (I), às vezes
Análise de Arredondamento em Ponto Flutuante
 Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
Capítulo 2 Análise de Arredondamento em Ponto Flutuante 2.1 Introdução Neste capítulo, chamamos atenção para o fato de que o conjunto dos números representáveis em qualquer máquina é finito, e portanto
OANAFAS é um programa computacional
 ANAFAS Análise de Faltas Simultâneas OANAFAS é um programa computacional para cálculo de curtos-circuitos. Permite a execução automática de grande variedade de faltas e possui facilidades, como estudo
ANAFAS Análise de Faltas Simultâneas OANAFAS é um programa computacional para cálculo de curtos-circuitos. Permite a execução automática de grande variedade de faltas e possui facilidades, como estudo
GABARITO - DEF30. Questão 1
 GABARITO - DEF30 Questão 1 a) Ensaio em aberto: Um dos lados do transformador é deixado em aberto, normalmente o lado de alta tensão. Instrumentos de medição são conectados para medir a corrente I 1, V
GABARITO - DEF30 Questão 1 a) Ensaio em aberto: Um dos lados do transformador é deixado em aberto, normalmente o lado de alta tensão. Instrumentos de medição são conectados para medir a corrente I 1, V
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE DEPARTAMENTO DE ENGENHARIA MECÂNICA DESENHO MECÂNICO CORTES. Prof. Márcio Valério de Araújo
 UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE DEPARTAMENTO DE ENGENHARIA MECÂNICA DESENHO MECÂNICO CORTES Prof. Márcio Valério de Araújo INTRODUÇÃO IMPORTÂNCIA DA REPRESENTAÇÃO EM CORTE NO DESENHO TÉCNICO
UNIVERSIDADE FEDERAL DO RIO GRANDE DO NORTE DEPARTAMENTO DE ENGENHARIA MECÂNICA DESENHO MECÂNICO CORTES Prof. Márcio Valério de Araújo INTRODUÇÃO IMPORTÂNCIA DA REPRESENTAÇÃO EM CORTE NO DESENHO TÉCNICO
[ \ x Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \.
 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar
&DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV1 &DStWXOR±6LVWHPDVGH(TXDo}HV/LQHDUHV Å 1Ro}HV *HUDLV Recordemos o caso mais simples de um VLVWHPD de duas HTXDo}HVOLQHDUHV nas duas LQFyJQLWDV [ e \. [\ [\ É fácil verificar
UNIVERSIDADE FEDERAL DA PARAÍBA UFPB CENTRO DE CIÊNCIAS AGRÁRIAS - CCA Departamento de Solos e Engenharia Rural - DSER. Aula 02
 UNIVERSIDADE FEDERAL DA PARAÍBA UFPB CENTRO DE CIÊNCIAS AGRÁRIAS - CCA Departamento de Solos e Engenharia Rural - DSER Aula 02 Prof. Dr. Guttemberg da Silva Silvino Introdução Topografia Definição de Topografia
UNIVERSIDADE FEDERAL DA PARAÍBA UFPB CENTRO DE CIÊNCIAS AGRÁRIAS - CCA Departamento de Solos e Engenharia Rural - DSER Aula 02 Prof. Dr. Guttemberg da Silva Silvino Introdução Topografia Definição de Topografia
Aritmética de Ponto Flutuante e Noções de Erro. Ana Paula
 Aritmética de Ponto Flutuante e Noções de Erro Sumário 1 Introdução 2 Sistemas de Numeração 3 Representação de Números Inteiros no Computador 4 Representação de Números Reais no Computador 5 Operações
Aritmética de Ponto Flutuante e Noções de Erro Sumário 1 Introdução 2 Sistemas de Numeração 3 Representação de Números Inteiros no Computador 4 Representação de Números Reais no Computador 5 Operações
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores. Controlo 2005/2006. Controlo de velocidade de um motor D.C.
 Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
ESPAÇOS MUNIDOS DE PRODUTO INTERNO
 ESPAÇOS MUNIDOS DE PRODUTO INTERNO Angelo Fernando Fiori 1 Bruna Larissa Cecco 2 Grazielli Vassoler 3 Resumo: O presente trabalho apresenta um estudo sobre os espaços vetoriais munidos de produto interno.
ESPAÇOS MUNIDOS DE PRODUTO INTERNO Angelo Fernando Fiori 1 Bruna Larissa Cecco 2 Grazielli Vassoler 3 Resumo: O presente trabalho apresenta um estudo sobre os espaços vetoriais munidos de produto interno.
Controle de Veículos Aéreos
 12, 13 e 14/11/2014, Parnaíba-PI Controle de Veículos Aéreos Prof. Dr. Mário Sarcinelli Filho Universidade Federal do Espírito Santo UFES Bolsista de Produtividade em Pesquisa PQ-2 do CNPq Orientador de
12, 13 e 14/11/2014, Parnaíba-PI Controle de Veículos Aéreos Prof. Dr. Mário Sarcinelli Filho Universidade Federal do Espírito Santo UFES Bolsista de Produtividade em Pesquisa PQ-2 do CNPq Orientador de
Análise no Domínio do Tempo de Sistemas em Tempo Discreto
 Análise no Domínio do Tempo de Sistemas em Tempo Discreto Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Análise no Domínio do Tempo de Sistemas em Tempo Discreto Edmar José do Nascimento (Análise de Sinais e Sistemas) http://www.univasf.edu.br/ edmar.nascimento Universidade Federal do Vale do São Francisco
Sistemas supervisórios
 Sistemas supervisórios O software supervisório utiliza a representação de objetos estáticos e animados para representar todo o processo de uma planta, assim como uma interface IHM. Ela opera em dois modos:
Sistemas supervisórios O software supervisório utiliza a representação de objetos estáticos e animados para representar todo o processo de uma planta, assim como uma interface IHM. Ela opera em dois modos:
NT 204/98. Realimentação. Engºs: Sun Hsien Ming. 1. Introdução
 NT 204/98 Realimentação Engºs: Sun Hsien Ming 1. Introdução Dando continuidade à divulgação dos conceitos e recursos do sistema SCOOT, o presente trabalho pretende abordar o processo de realimentação.
NT 204/98 Realimentação Engºs: Sun Hsien Ming 1. Introdução Dando continuidade à divulgação dos conceitos e recursos do sistema SCOOT, o presente trabalho pretende abordar o processo de realimentação.
MDF: Conceitos Básicos e algumas Aplicações na Engenharia Estrutural
 Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 00 Associação Brasileira de Métodos Computacionais em Engenharia MDF: Conceitos Básicos e algumas Aplicações na Engenharia Estrutural L. R.
Universidade Federal de São João Del-Rei MG 6 a 8 de maio de 00 Associação Brasileira de Métodos Computacionais em Engenharia MDF: Conceitos Básicos e algumas Aplicações na Engenharia Estrutural L. R.
4Distribuição de. freqüência
 4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
4Distribuição de freqüência O objetivo desta Unidade é partir dos dados brutos, isto é, desorganizados, para uma apresentação formal. Nesse percurso, seção 1, destacaremos a diferença entre tabela primitiva
Notas de Cálculo Numérico
 Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Notas de Cálculo Numérico Túlio Carvalho 6 de novembro de 2002 2 Cálculo Numérico Capítulo 1 Elementos sobre erros numéricos Neste primeiro capítulo, vamos falar de uma limitação importante do cálculo
Sistemas Operacionais. Prof. André Y. Kusumoto andrekusumoto.unip@gmail.com
 Sistemas Operacionais Prof. André Y. Kusumoto andrekusumoto.unip@gmail.com Estruturas de Sistemas Operacionais Um sistema operacional fornece o ambiente no qual os programas são executados. Internamente,
Sistemas Operacionais Prof. André Y. Kusumoto andrekusumoto.unip@gmail.com Estruturas de Sistemas Operacionais Um sistema operacional fornece o ambiente no qual os programas são executados. Internamente,
Falso: F = Low voltage: L = 0
 Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 PORTAS LOGICAS 1.1 INTRODUÇÃO Em 1854, George Boole introduziu o formalismo que até hoje se usa para
Curso Técnico em Eletrotécnica Disciplina: Automação Predial e Industrial Professor: Ronimack Trajano 1 PORTAS LOGICAS 1.1 INTRODUÇÃO Em 1854, George Boole introduziu o formalismo que até hoje se usa para
Projecto de Programação por Objectos 2007/08 Escalonamento em Multi-processador por Programação Evolutiva MEBiom/MEEC 1 Problema
 Projecto de Programação por Objectos 2007/08 Escalonamento em Multi-processador por Programação Evolutiva MEBiom/MEEC 1 Problema Considere-se um sistema com um conjunto finito de processadores P = {p1,...,
Projecto de Programação por Objectos 2007/08 Escalonamento em Multi-processador por Programação Evolutiva MEBiom/MEEC 1 Problema Considere-se um sistema com um conjunto finito de processadores P = {p1,...,
Notação. Quantidades Económicas de Encomenda. 1.1 Quantidade Económica de Wilson. 1.1 Quantidade Económica de Wilson
 Notação uantidades Económicas de Encomenda. Taxa de Constante taxa de procura (unidades de produto / unidade de ) A custo de encomenda ( / encomenda) C custo unitário do produto ( / unidade de produto)
Notação uantidades Económicas de Encomenda. Taxa de Constante taxa de procura (unidades de produto / unidade de ) A custo de encomenda ( / encomenda) C custo unitário do produto ( / unidade de produto)
Eng Civil Washington Peres Núñez Dr. em Engenharia Civil pela Universidade Federal do Rio Grande do Sul
 PESQUISA ANÁLISE DE CARACTERÍSTICAS DE QUALIDADE DE MISTURAS ASFÁLTICAS PRODUZIDAS NA ATUALIDADE NO SUL DO BRASIL E IMPACTOS NO DESEMPENHO DE PAVIMENTOS FLEXÍVEIS. MANUAL DE OPERAÇÃO DO BANCO DE DADOS
PESQUISA ANÁLISE DE CARACTERÍSTICAS DE QUALIDADE DE MISTURAS ASFÁLTICAS PRODUZIDAS NA ATUALIDADE NO SUL DO BRASIL E IMPACTOS NO DESEMPENHO DE PAVIMENTOS FLEXÍVEIS. MANUAL DE OPERAÇÃO DO BANCO DE DADOS
CONTROLE DE NÍVEL UTILIZANDO ALGORITMO PID IMPLEMENTADO NO CLP
 CONTROLE DE NÍVEL UTILIZANDO ALGORITMO PID IMPLEMENTADO NO CLP Felipe Martins Guimarães felipem.guimaraes@hotmail.com Instituto Nacional de Telecomunicações Inatel Nataniele Thaís do Nascimento na.niele@tai.inatel.br
CONTROLE DE NÍVEL UTILIZANDO ALGORITMO PID IMPLEMENTADO NO CLP Felipe Martins Guimarães felipem.guimaraes@hotmail.com Instituto Nacional de Telecomunicações Inatel Nataniele Thaís do Nascimento na.niele@tai.inatel.br
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade
 Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Considerações sobre redimensionamento de motores elétricos de indução
 Considerações sobre redimensionamento de motores elétricos de indução Artigo publicado na revista Lumiere Electric edição nº 166 Aplicações de investimentos dentro das empresas sempre são questionadas
Considerações sobre redimensionamento de motores elétricos de indução Artigo publicado na revista Lumiere Electric edição nº 166 Aplicações de investimentos dentro das empresas sempre são questionadas
Sistemas de Controle Digital
 ADL 24 Cap 13 Sistemas de Controle Digital Vantagens dos Computadores Digitais O uso de computadores digitais na malha leva às seguintes vantagens sobre os sistemas analógicos: (1) custo, (2) flexibilidade
ADL 24 Cap 13 Sistemas de Controle Digital Vantagens dos Computadores Digitais O uso de computadores digitais na malha leva às seguintes vantagens sobre os sistemas analógicos: (1) custo, (2) flexibilidade
Desenvolvimento de Estratégia para Programação do Futebol de Robôs da Mauá
 Desenvolvimento de Estratégia para Programação do Futebol de Robôs da Mauá Wânderson O. Assis, Alessandra D. Coelho, Marcelo M. Gomes, Cláudio G. Labate, Daniel F. Calasso, João Carlos G. C. Filho Escola
Desenvolvimento de Estratégia para Programação do Futebol de Robôs da Mauá Wânderson O. Assis, Alessandra D. Coelho, Marcelo M. Gomes, Cláudio G. Labate, Daniel F. Calasso, João Carlos G. C. Filho Escola
O Gerenciamento de Documentos Analógico/Digital
 Tipos de GED: Document imaging Document management Document Imaging / Document Management O Gerenciamento de Documentos Analógico/Digital Mundo analógico Criação Revisão Processamento Arquivo Mundo digital
Tipos de GED: Document imaging Document management Document Imaging / Document Management O Gerenciamento de Documentos Analógico/Digital Mundo analógico Criação Revisão Processamento Arquivo Mundo digital
Máximos, mínimos e pontos de sela Multiplicadores de Lagrange
 Máximos, mínimos e pontos de sela Multiplicadores de Lagrange Anderson Luiz B. de Souza Livro texto - Capítulo 14 - Seção 14.7 Encontrando extremos absolutos Determine o máximo e mínimo absolutos das funções
Máximos, mínimos e pontos de sela Multiplicadores de Lagrange Anderson Luiz B. de Souza Livro texto - Capítulo 14 - Seção 14.7 Encontrando extremos absolutos Determine o máximo e mínimo absolutos das funções
EE531 - Turma S. Diodos. Laboratório de Eletrônica Básica I - Segundo Semestre de 2010
 EE531 - Turma S Diodos Laboratório de Eletrônica Básica I - Segundo Semestre de 2010 Professor: José Cândido Silveira Santos Filho Daniel Lins Mattos RA: 059915 Raquel Mayumi Kawamoto RA: 086003 Tiago
EE531 - Turma S Diodos Laboratório de Eletrônica Básica I - Segundo Semestre de 2010 Professor: José Cândido Silveira Santos Filho Daniel Lins Mattos RA: 059915 Raquel Mayumi Kawamoto RA: 086003 Tiago
Desenvolvimento de Amperímetro Alicate Baseado em Magnetômetros GMR para Medição de Correntes Elétricas Contínuas
 Desenvolvimento de Amperímetro Alicate Baseado em Magnetômetros GMR para Medição de Correntes Elétricas Contínuas Alunos: Marcos Civiletti de Carvalho e Camila Schuina Orientador: Carlos Roberto Hall Barbosa
Desenvolvimento de Amperímetro Alicate Baseado em Magnetômetros GMR para Medição de Correntes Elétricas Contínuas Alunos: Marcos Civiletti de Carvalho e Camila Schuina Orientador: Carlos Roberto Hall Barbosa
P. P. G. em Agricultura de Precisão DPADP0803: Geoestatística (Prof. Dr. Elódio Sebem)
 Considerações Iniciais É impossível saber, antes de amostrar, de que maneira os valores das variáveis irão se comportar: se dependente ou independente uma da outra. Devido as limitações da estatística
Considerações Iniciais É impossível saber, antes de amostrar, de que maneira os valores das variáveis irão se comportar: se dependente ou independente uma da outra. Devido as limitações da estatística
