Prova 2 - Sistemas de Controle Projetos
|
|
|
- Ângelo Barbosa Brunelli
- 8 Há anos
- Visualizações:
Transcrição
1 Prova - Sistemas de Controle Projetos Pedro Batista (887) - pedro@ufpa.br Paulo Victor Mocbel (887) - pvmocbel@gmail.com December 4, Projeto de Controlador PI ideal Desejamos adicionar um controlador proporcional integral, no sistema da Equação para levar a zero seu erro de regime, em resposta ao degrau unitário. Como foi dado do problema o sistema opera com coeficiente de amortecimento igual a.74. G(s) = () (s+)(s+)(s+) Para levar o erro de regime a zero, adicionamos um polo em zero, para que esse polo não influencie na resposta trasitória do sistema, adicionamos também um zero próximo a este., o ganho K também é adicionado ao o sistema, e esse se torna o mostrado na Equação. Para este plotamos o LGR e o coeficiente de amortecimento na Figura, podemos então definir o ganho do sistema. Simulamos o sistema sem o controlador, e o sistema controlado na Figura onde podemos observar que o erro de regime será levado a zero. K(s+.) G(s) = () s(s+)(s+)(s+) Para gerar o LGR o código utilizado no matlab é mostrado na Figura 3, onde utilizamosozpk pararepresentarosistema, eosgridparaplotarocoeficientede amortecimento. Já para simulação dos sitemas usamos o esquema do simulink mostrado na Figura 4. Projeto de Compensador por Atraso de Fase Devemos compensar o sistema da Equação 3, com um compensador por atraso de fase. Para isso desenvolvemos os códigos das Figuras 8, 9 e 7, onde calculamos primeiramente o ganho do sistema não controlado K = 6(Figura a). Simulamos e encontramos seu erro de regime (V r =.889) e dividimo-os por, para encontrar K pc = 89., com esse definimos que nosso novo polo deve estar em p c =.3, a partir do qual calculamos o novo zero z c =.443 e ganho K = (Figura b). Simulamos então o novo sistema, o resultado é mostrado na Figura 6, e a saída de execução do programa na Figura. G(s) = K s(s+)(s+)(s+) (3)
2 Root Locus.7 System: p_zpk Gain: 6 Pole: i Damping:.7 Overshoot (%): 7.8 Frequency (rad/sec): Figure : LGR para o sistema da Equação, com coeficiente de amortecimento igual a Projeto de um Controlador por Atraso de Fase Nosso objetivo aqui é projetar um compensador por atraso de fase que resulte em um k p =, com função de transferência da equação 4 sem alterar de forma brusca a localização o pólo dominante que produz um M p de %. Para isso primeiramente devemos encontrar o valor de ξ para podermos encontrar no k do sistema não compensado. Portanto usando a equação chegamos ao valor de ξ =.9. A partir desse valor podemos traçar o lgr do nosso sistema não compensado, como mostrado na figura, assim podendo encontra o valor de k = 4. Com o valor de k em mãos podemos calcular o valor de K p através da formula mostrada na equação 6. A parti desse valor usamos agora a equação 7, dela chegamos a equação 8 que é o valor de a relação entre zc e pc, para K pc =. Coloncando o valor pc =., encontramos zc =.34. Assim nosso compensador fica como mostrado na equação 9. Agora devemos saber qual é o valor do novo k para o sistema com o compensador, para tanto plotamos o seu lgr, como na figura e visualizamos k = 4.4. Observando a resposta sem e com o compensador, mostrada na figura 3 vemos que houve uma modificação considerável na resposta transitória do sistema com relação ao adicionamento do compensador. Isso ocorre pelo fato de termo adicionado um pólo que influênciou nosso pólo dominante,não obdecendo o critério de vezes afastado (o novo encontrasse em -7.9 e o outro em -). G(s) = k (s+)(s+4)(s+6) (4) M p = e πξ (πξ) ()
3 .4. com controlador pi sistema original Figure : Simulação para o sistema da Equação, e sua versão controlada (Equação com ganho K = 6. p_zpk=zpk([-.], [ - - -], ) rlocus(p_zpk) sgrid(.7, xi ) Figure 3: Código do MATLAB utilizado para plotar o LGR da Equação K p = 4 = (6) zc K pc = K p pc (7) zc pc = K pc K p =.3447 (8) G c (s) = k(s+.34) (s+.) (9) 4 Projeto de um Controlador PD Dada a função de transferência de ramo direto dada pela equação, queremos projetar um controlador PD reduzindo o tempo de estabilização a um fator de. Primeiramente vamos encontrar o valor de K correspondente a ξ =.77. Para isso plotamos o lgr do sistema não compensado, como mostrado na figura 4, de onde encontramos k = 6.3. Como queremos que o tempo de resposta 3
4 (a) Esquema utilizado para o sistema não con-(btrolado (Equação ). lado (Equação Esquema utilizado para o sistema contro- ). Figure 4: Esquemas montados no simulink para simular os sistemas do Problema seja reduzido temos que encontrar primeiramente o tempo de estabilização do sistema através da equação. Reduzindo o mesmo a metade como descrito na equação. Agora podemos calcular as partes real e imaginária do polo dominante. Fazemos isso nas equações 3, 4 e. Feito isso devemos projetar a localização o zero do nosso compensador através da equação 6, assim encontraremos os valores dos ângulos como na equação 7. De posse desse valores e usando a relação descrita em 8 encontramos θ = Agora podemos calcular o valor exato do zero do nosso compensador como descrito na equação 9. Com esse valor em mãos podemos finalmente plotar nosso lgr do sistema compensado, mostrado na figura, de onde encontramos k =. As reposta sem e com o compensador estão na figura 6 G(s) = k (s+)(s+)(s+3)(s+6) () T s = 4 ρ = 4 = 3.89 ().4 T s = 3.89 =.94 () ρ = 4 =.8.94 (3) ρ = ξ W n W n =.8 = (4) W d = w n ξ =. () G c = s+zc (6) θ = 7.43,θ 3 = 9.4,θ 4 = 67,θ 4 = 7.96 (7) θ θ θ3 θ4 θ = 8 (8) tan(8 3.73) =.8 zc =.693 (9).8 zc 4
5 Projeto de um Controlador PID Para a função de transferência da Equação, desejas-se para o degrau unitário um instante de pico T p em.47 segundos e um coeficiente de amortecimento ξ =.8. G(s) = O roteiro do laboratório mostra que: K (s+)(s+4) π T p = w n ξ Podemos então definir w n como segue w n = π T = π p ξ.47.8 =.9 A partir das notas de aula encontramos: () w d = w n q ξ = 3. σ = w n ξ =.9.8 = 4.7 s = σ ±w d = 4.7±3. Usamos então a condição de ângulo para calcular a posição requerida do zero do compensador, os cálculos são mostrados na Figura 7 onde foi definido que o novo zero deve estar em Com esses dados calculamos o ganho do sistema k = 3. (Figura 8). A nova função de transferência de malha aberta do sistema é: G(s) = 3.(s ) (s+)(s+4) Podemos encontrar a função de transferência de malha fechada de acordo com fórmula: G f (s) = G(s) +G(s) = (s+7)(s+4)(s+) (s+)(s+4)(s +6s+) Desta forma observamos que os polos desta equação são.±.88, e 4. Observamos então que dentro do intervalo de. = 7. ( vezes o polo dominante) temos dois polos, caracterizando um sistema de terceira ordem que não pode ser aproximado por um sistema de segunda ordem.
6 Root Locus.74 System: q Gain: 6 Pole: i Damping:.74 Overshoot (%): 7.4 Frequency (rad/sec): (a) LGR para o sistema da Equação 3 não controlado. Root Locus.74 System: q Gain: Pole: i Damping:.74 Overshoot (%): 7.4 Frequency (rad/sec): (b) LGR para o sistema da Equação 3 controlado, com zero em.443 e polo em.3. Figure : LGR para solução do Problema 6
7 .4. sistema sem controlador sistema controlado X: 6.6 Y:.889 X: 9.7 Y: Figure 6: Resultado da simulação do sistema da Equação 3 original e controlado conforme Problema. Figure 7: Sistema do simulink utilizado no programa da Figura 9 function [newgain] = lgrgain(zeros, poles, gain, q, figureid); figure(figureid); q = zpk(zeros, poles, gain) rlocus(q); sgrid(q, ); k = input( ganho? ); newgain = k; end Figure 8: Função para gerar o LGR e solicitar o ganho para o usuário o ganho do sistema. 7
8 simname= q_sim figureini = ; desiredvalue = ; q=.74; k=; poles = [- - -]; zeros = []; k = lgrgain(zeros, poles, k, q, figureini + ); sim(simname); figure(figureini); plot(scopedata.time, ScopeData.signals.values(:,)); legend( sistema sem controlador ); simlen = length(scopedata.time); finalvalue = ScopeData.signals.values(simLen,); userfinalvalue = input([ regime " numstr(finalvalue) "? [New] ]); if not(isempty(userfinalvalue)) finalvalue = userfinalvalue; end err = desiredvalue - finalvalue; newerr = err / ; %equaç~oes da apostila pg 76 kp = (-err) / err; kpc = (-newerr) / newerr polevalue = input( Valor do novo polo? ); %equaç~ao apostila pg 77 zerovalue = (kpc/kp)*polevalue; disp([ Novo zero " numstr(zerovalue) " ]); zeros = horzcat(zeros, zerovalue); poles = horzcat(poles, polevalue); k = lgrgain(zeros, poles,, q, figureini+); sim(simname) figure(figureini); hold; plot(scopedata.time, ScopeData.signals.values(:,), r ); hold; %legend( sistema sem controlador ); 8 Figure 9: Função para resolver o problema da Seção
9 simname = q_sim Zero/pole/gain: (s+) (s+) (s+) ganho? 6 regime ".889"? [New] Valor do novo polo? -.3 Novo zero "-.443" Zero/pole/gain: (s+.44) (s+) (s+) (s+) (s+.3) ganho? Current plot held Current plot released Figure : Saída da execução do programa da Figura. Root Locus System: a Gain: 4 Pole:.3 +.7i Damping:.94 Overshoot (%): 9.8 Frequency (rad/sec): Figure : lgr do sistema não compensado da Seção 3. 9
10 Root Locus.9 System: a Gain: 4.4 Pole: i Damping:.93 Overshoot (%): 9.9 Frequency (rad/sec): Figure : lgr do sistema compensado da Seção 3..9 sem com o controlador.8 resposta ao degrau unitã rio tempo(s) Figure 3: Resposta do sistema compensado Seção 3.
11 Root Locus System: a Gain: 6.3 Pole:. +.3i Damping:.7 Overshoot (%): 4.8 Frequency (rad/sec): Figure 4: lgr do sistema não compensado da Seção 4. Root Locus.77 System: a Gain: Pole:.6 +.9i Damping:.73 Overshoot (%): 4.48 Frequency (rad/sec): Figure : lgr do sistema compensado Seção 4.
12 .3.3 sem com o controlador resposta ao degrau unitã rio tempo(s) Figure 6: Resposta do sistema com e sem compensador Seção 4. Figure 7: Calculo da condição de ângulo para projetar o compensador para o problema da Seção.
13 Root Locus System: g Gain: 3. Pole: 4 + 3i Damping:.8 Overshoot (%):. Frequency (rad/sec): Figure 8: LGR para o sistema da Equação, com um novo zero em
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA. Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva
 UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
UNIVERSIDADE GAMA FILHO PROCET DEPARTAMENTO DE ENGENHARIA ELÉTRICA Disciplina de Controle II Prof. MC. Leonardo Gonsioroski da Silva Controlador Proporcional Controlador PI A Relação entre a saída e o
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I
 Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Aula 11 Root Locus LGR (Lugar Geométrico das Raízes) parte I Sistema de malha fechada G(s) G(s) G(s) Sistema de malha fechada K O Root Locus é o lugar geométrico dos polos do sistema de malha fechada,
Root Locus (Método do Lugar das Raízes)
 Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Root Locus (Método do Lugar das Raízes) Ambos a estabilidade e o comportamento da resposta transitória em um sistema de controle em malha fechada estão diretamente relacionadas com a localização das raízes
Sistemas a Tempo Discreto - Projeto
 Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Sistemas a Tempo Discreto - Projeto 1. Especificações de Projeto no domínio discreto 2. Projeto via Emulação 2.1 Controladores Equivalentes Discretos 2.2 Mapeamento pólo-zero 2.3 Avaliação do projeto pag.1
Controle de Sistemas. O Método do Lugar das Raízes. Renato Dourado Maia. Universidade Estadual de Montes Claros. Engenharia de Sistemas
 Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Controle de Sistemas O Método do Lugar das Raízes Renato Dourado Maia Universidade Estadual de Montes Claros Engenharia de Sistemas Introdução No projeto de um sistema de controle, é fundamental se determinar
Função de Transferência de Malha Fechada
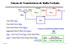 Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
Função de Transferência de Malha Fechada R(s) B(s) + - E(s) Controlador Gc(S) U(s) Sensor G(S) Planta C(s) C(s)=G(s)*U(s) H(S) C(s)=G(s)*Gc(s)*E(s) C(s)=G(s)*Gc(s)*[ R(s)-B(s) ] C(s)=G(s)*Gc(s)*[ R(s)-H(s)*C(s)
CONTROLO DE SISTEMAS
 UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
UNIVERSIDADE DA BEIRA INTERIOR DEPARTAMENTO DE ENGENHARIA ELECTROMECÂNICA CONTROLO DE SISTEMAS Lugar Geométrico das Raízes PROJECTO E ANÁLISE DA RESPOSTA TRANSITÓRIA E ESTABILIDADE Parte 1/3 - Compensação
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO
 TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
TRABALHO: CONTROLE DE UM SISTEMA PÊNDULO-CARRO Professor: Tiago Dezuo 1 Objetivos Desenvolver técnicas de controle por variáveis de estado clássicas e ótimas, realizando comparações de desempenho entre
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO. Professor Leonardo Gonsioroski
 ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
ESCOLA NAVAL DIRETORIA DE ENSINO DA MARINHA DEPARTAMENTO DE ENGENHARIA CONTROLE E AUTOMAÇÃO Na aula passada vimos Compensação de sistemas Efeitos da Adição de pólos e zeros Compensadores de Avanço de Fase
Me todos de Ajuste de Controladores
 Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Me todos de Ajuste de Controladores Recapitulando aulas passadas Vimos algumas indicações para a escolha do tipo de controlador feedback dependendo da malha de controle que está sendo projetada. Vimos
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade
 Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Laboratórios de CONTROLO (LEE) 2 o Trabalho Motor DC Controlo de Velocidade Baseado no trabalho Controlo de Velocidade de um motor DC de E. Morgado, F. Garcia e J. Gaspar João Miguel Raposo Sanches 1 o
Métodos de Sintonização de Controladores PID
 3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
3ª Aula de Controlo Inteligente Controlo PI iscreto Métodos de Sintonização de Controladores PI Os controladores PI são muito utilizados em aplicações industrias. A função de transferência que define o
RELATÓRIO FINAL PROJETO DESAFIO CONTROLE DE POSIÇÃO ATRAVÉS DE MOTOR DE CORRENTE CONTÍNUA
 RELATÓRIO FINAL PROJETO DESAFIO CONTROLE DE POSIÇÃO ATRAVÉS DE MOTOR DE CORRENTE CONTÍNUA Laboratório De Controle I (LECI) Professor: Reinaldo Martinez Palhares Integrantes : Antônio J. R. Chaves, Marcelo
RELATÓRIO FINAL PROJETO DESAFIO CONTROLE DE POSIÇÃO ATRAVÉS DE MOTOR DE CORRENTE CONTÍNUA Laboratório De Controle I (LECI) Professor: Reinaldo Martinez Palhares Integrantes : Antônio J. R. Chaves, Marcelo
Laboratório de Projeto por Intermédio do Root Locus
 Laboratório de Projeto por Intermédio do Root Locus Revisão Revisão Entrada Expressão do erro estacionário Degrau, Rampa, Parábola, Dado o sistema: Método do Lugar das Raízes Exercício 1 - Controlador
Laboratório de Projeto por Intermédio do Root Locus Revisão Revisão Entrada Expressão do erro estacionário Degrau, Rampa, Parábola, Dado o sistema: Método do Lugar das Raízes Exercício 1 - Controlador
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle
 Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
Laboratórios 9, 10 e 11: Projeto de Controladores pelo Lugar das Raízes DAS5317 Sistemas de Controle Hector Bessa Silveira e Daniel Coutinho 2012/2 1 Objetivos Neste próximos laboratórios, utilizar-se-á
1 A Integral por Partes
 Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Métodos de Integração Notas de aula relativas aos dias 14 e 16/01/2004 Já conhecemos as regras de derivação e o Teorema Fundamental do Cálculo. Este diz essencialmente que se f for uma função bem comportada,
Estabilidade no Domínio da Freqüência
 Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Estabilidade no Domínio da Freqüência Introdução; Mapeamento de Contornos no Plano s; Critério de Nyquist; Estabilidade Relativa; Critério de Desempenho no Domínio do Tempo Especificado no Domínio da Freqüência;
Controle II. Estudo e sintonia de controladores industriais
 Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Controle II Estudo e sintonia de controladores industriais Introdução A introdução de controladores visa modificar o comportamento de um dado sistema, o objetivo é, normalmente, fazer com que a resposta
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores. Controlo 2005/2006. Controlo de velocidade de um motor D.C.
 Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
Instituto Superior Técnico Licenciatura em Engenharia Electrotécnica e de Computadores Controlo 2005/2006 Controlo de velocidade de um motor D.C. Elaborado por E. Morgado 1 e F. M. Garcia 2 Reformulado
Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional
 Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Universidade do Estado de Santa Catarina UDESC Centro de Ciências Tecnológicas CCT Departamento de Engenharia Mecânica DEM Sistemas de Controle (CON) Ações Básicas de Controle e Controle Proporcional Aula
Sessão Prática: Simulação e Controle com LabVIEW
 Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
Sessão Prática: Simulação e Controle com LabVIEW 1 Visão geral Este tutorial mostra as características dos controles proporcional (P), integral (I) e derivativo (D), e como utilizálos para obter a resposta
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE
 INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
INSTRUMENTAÇÃO E CONTROLE DE PROCESSOS TRANSFORMADAS DE LAPLACE Preliminares No estudo de sistemas de controle, e comum usar-se diagramas de blocos, como o da figura 1. Diagramas de blocos podem ser utilizados
Curvas em coordenadas polares
 1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
1 Curvas em coordenadas polares As coordenadas polares nos dão uma maneira alternativa de localizar pontos no plano e são especialmente adequadas para expressar certas situações, como veremos a seguir.
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG04037 Sistemas de Controle Digitais
 Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Engenharia Elétrica ENG437 Sistemas de Controle Digitais Introdução Controladores PID Prof. Walter Fetter Lages 2 de maio
Toolbox de Sistemas de Controle MATLAB
 Toolbox de Sistemas de Controle MATLAB Control System Toolbox Grupo PET Engenharia Elétrica UFMS Campo Grande MS Junho - 2003 2 Índice Índice 3 1. Introdução 4 2. Representação dos Sistemas 5 2.1. Representação
Toolbox de Sistemas de Controle MATLAB Control System Toolbox Grupo PET Engenharia Elétrica UFMS Campo Grande MS Junho - 2003 2 Índice Índice 3 1. Introdução 4 2. Representação dos Sistemas 5 2.1. Representação
Aula 11. Cristiano Quevedo Andrea 1. Curitiba, Outubro de DAELT - Departamento Acadêmico de Eletrotécnica
 Aula 11 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Outubro de 2011. Resumo 1 Introdução - Lugar das Raízes
Aula 11 Cristiano Quevedo Andrea 1 1 UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Outubro de 2011. Resumo 1 Introdução - Lugar das Raízes
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica
 UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
UNIVERSIDADE FEDERAL DE SANTA MARIA COLÉGIO TÉCNICO INDUSTRIAL DE SANTA MARIA Curso de Eletrotécnica Apostila de Automação Industrial Elaborada pelo Professor M.Eng. Rodrigo Cardozo Fuentes Prof. Rodrigo
Campos Vetoriais e Integrais de Linha
 Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Cálculo III Departamento de Matemática - ICEx - UFMG Marcelo Terra Cunha Campos Vetoriais e Integrais de Linha Um segundo objeto de interesse do Cálculo Vetorial são os campos de vetores, que surgem principalmente
Projeto de sistemas de controle
 Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Projeto de sistemas de controle Os controladores clássicos encontrados na literatura podem ser classificados como: Controladores de duas posições (ou on-off). Controladores proporcionais. Controladores
Laboratório de Projeto de Avanço e Atraso
 Laboratório de Projeto de Avanço e Atraso Revisão Entrada Expressão do erro estacionário Degrau, Rampa, Parábola, Dado o sistema: Exercício 1 - Controlador de Atraso No Matlab projete um compensador P
Laboratório de Projeto de Avanço e Atraso Revisão Entrada Expressão do erro estacionário Degrau, Rampa, Parábola, Dado o sistema: Exercício 1 - Controlador de Atraso No Matlab projete um compensador P
Capítulo 3 Sistemas de Controle com Realimentação
 Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
Capítulo 3 Sistemas de Controle com Realimentação Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Sistemas de Controle com
TG-01-2012-EL. e-mail 1 : diego190103@gmail.com; e-mail 2 : ffpuccia@uol.com.br; e-mail 3 : peleggi@ig.com.br;
 Controle de ângulos de azimute e de elevação num sistema Aeroestabilizador Diego Amorim 1 ; Filipe Puccia 2 & Regis Peleggi 3. Orientador: Alexandre Brincalepe Campo. TG-01-2012-EL 1, 2,3 Graduandos do
Controle de ângulos de azimute e de elevação num sistema Aeroestabilizador Diego Amorim 1 ; Filipe Puccia 2 & Regis Peleggi 3. Orientador: Alexandre Brincalepe Campo. TG-01-2012-EL 1, 2,3 Graduandos do
Estabilidade. Carlos Alexandre Mello. Carlos Alexandre Mello cabm@cin.ufpe.br 1
 Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
Estabilidade Carlos Alexandre Mello 1 Introdução Já vimos que existem três requisitos fundamentais para projetar um sistema de controle: Resposta Transiente Estabilidade Erros de Estado Estacionário Estabilidade
A lei de Gauss é uma lei geral. Ela vale para qualquer distribuição de cargas e qualquer superfície fechada.
 Aplicações da lei de Gauss A lei de Gauss é uma lei geral. Ela vale para qualquer distribuição de cargas e qualquer superfície fechada. De maneira genérica, a lei de Gauss diz que: Fluxo elétrico sobre
Aplicações da lei de Gauss A lei de Gauss é uma lei geral. Ela vale para qualquer distribuição de cargas e qualquer superfície fechada. De maneira genérica, a lei de Gauss diz que: Fluxo elétrico sobre
Resolvendo problemas com logaritmos
 A UA UL LA Resolvendo problemas com logaritmos Introdução Na aula anterior descobrimos as propriedades dos logaritmos e tivemos um primeiro contato com a tábua de logarítmos. Agora você deverá aplicar
A UA UL LA Resolvendo problemas com logaritmos Introdução Na aula anterior descobrimos as propriedades dos logaritmos e tivemos um primeiro contato com a tábua de logarítmos. Agora você deverá aplicar
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE AVANÇO Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1 EM COMPUTADOR DE UM PROJETO...1
UNIVERSIDADE DE MOGI DAS CRUZES - ENGENHARIA ELÉTRICA Prof. José Roberto Marques CURSO DE ENGENHARIA ELÉTRICA ELETRÔNICA DE POTÊNCIA
 CURSO DE ENGENHARIA ELÉTRICA ELETRÔNICA DE POTÊNCIA Exp. 1 (Simulação) LABORATÓRIO DE SIMULAÇÂO DE FONTES CHAVEADAS O objetivo deste laboratório é simular fontes chaveadas Buck (abaixadora de potencial)
CURSO DE ENGENHARIA ELÉTRICA ELETRÔNICA DE POTÊNCIA Exp. 1 (Simulação) LABORATÓRIO DE SIMULAÇÂO DE FONTES CHAVEADAS O objetivo deste laboratório é simular fontes chaveadas Buck (abaixadora de potencial)
Laboratório 7 Circuito RC *
 Laboratório 7 Circuito RC * Objetivo Observar o comportamento de um capacitor associado em série com um resistor e determinar a constante de tempo do circuito. Material utilizado Gerador de função Osciloscópio
Laboratório 7 Circuito RC * Objetivo Observar o comportamento de um capacitor associado em série com um resistor e determinar a constante de tempo do circuito. Material utilizado Gerador de função Osciloscópio
Ajuste de Controle PID utilizando Algoritmo Genético
 Centro Universitário de Brasília UniCEUB FACULDADE DE TECNOLOGIA E CIÊNCIAS SOCIAIS APLICADAS - FATECS Curso de Engenharia da Computação Hugo de Souza Santos Ajuste de Controle PID utilizando Algoritmo
Centro Universitário de Brasília UniCEUB FACULDADE DE TECNOLOGIA E CIÊNCIAS SOCIAIS APLICADAS - FATECS Curso de Engenharia da Computação Hugo de Souza Santos Ajuste de Controle PID utilizando Algoritmo
SISTEMAS DE CONTROLE II
 SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
SISTEMAS DE CONTROLE II - Algumas situações com desempenho problemático 1) Resposta muito oscilatória 2) Resposta muito lenta 3) Resposta com erro em regime permanente 4) Resposta pouco robusta a perturbações
Aula 3 OS TRANSITÒRIOS DAS REDES ELÉTRICAS
 Aula 3 OS TRANSITÒRIOS DAS REDES ELÉTRICAS Prof. José Roberto Marques (direitos reservados) A ENERGIA DAS REDES ELÉTRICAS A transformação da energia de um sistema de uma forma para outra, dificilmente
Aula 3 OS TRANSITÒRIOS DAS REDES ELÉTRICAS Prof. José Roberto Marques (direitos reservados) A ENERGIA DAS REDES ELÉTRICAS A transformação da energia de um sistema de uma forma para outra, dificilmente
Função do 2º Grau. Alex Oliveira
 Função do 2º Grau Alex Oliveira Apresentação A função do 2º grau, também chamada de função quadrática é definida pela expressão do tipo: y = f(x) = ax² + bx + c onde a, b e c são números reais e a 0. Exemplos:
Função do 2º Grau Alex Oliveira Apresentação A função do 2º grau, também chamada de função quadrática é definida pela expressão do tipo: y = f(x) = ax² + bx + c onde a, b e c são números reais e a 0. Exemplos:
Estrutura geral de um sistema com realimentação unitária negativa, com um compensador (G c (s) em série com a planta G p (s).
 2 CONTROLADORES PID Introdução Etrutura geral de um itema com realimentação unitária negativa, com um compenador (G c () em érie com a planta G p (). 2 Controladore PID 2. Acção proporcional (P) G c ()
2 CONTROLADORES PID Introdução Etrutura geral de um itema com realimentação unitária negativa, com um compenador (G c () em érie com a planta G p (). 2 Controladore PID 2. Acção proporcional (P) G c ()
5910170 Física II Ondas, Fluidos e Termodinâmica USP Prof. Antônio Roque Aula 21
 Aula 1 Ondas sonoras harmônicas Na aula passada deduzimos a equação de onda para ondas sonoras propagando-se em uma dimensão. Vimos que ela pode ser escrita em termos de três variáveis medidas em relação
Aula 1 Ondas sonoras harmônicas Na aula passada deduzimos a equação de onda para ondas sonoras propagando-se em uma dimensão. Vimos que ela pode ser escrita em termos de três variáveis medidas em relação
Cálculo em Computadores - 2007 - trajectórias 1. Trajectórias Planas. 1 Trajectórias. 4.3 exercícios... 6. 4 Coordenadas polares 5
 Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Cálculo em Computadores - 2007 - trajectórias Trajectórias Planas Índice Trajectórias. exercícios............................................... 2 2 Velocidade, pontos regulares e singulares 2 2. exercícios...............................................
Controle de elevador
 Controle de elevador Aluno...: Leonardo Rafael Coordenador: Prof. Eng Luiz Antonio Vargas Pinto vargasp@uol.com.br Escola Técnica Rubens de Faria e Souza 1 Dedicatória e Agradecimentos Dedico aos meus
Controle de elevador Aluno...: Leonardo Rafael Coordenador: Prof. Eng Luiz Antonio Vargas Pinto vargasp@uol.com.br Escola Técnica Rubens de Faria e Souza 1 Dedicatória e Agradecimentos Dedico aos meus
USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO
 João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
João Baptista Bayão Ribeiro USO DO SCILAB PARA REALIZAÇÃO EM COMPUTADOR DE UM PROJETO DE UM COMPENSADOR DE ATRASO-AVANÇO EXEMPLO 7.04 DO OGATA Rio de Janeiro 2014 2 ÍNDICE USO DO SCILAB PARA REALIZAÇÃO...1
Álgebra. SeM MiSTéRio
 Álgebra SeM MiSTéRio Série SeM MiSTéRio Alemão Sem Mistério Álgebra Sem Mistério Cálculo Sem Mistério Conversação em Alemão Sem Mistério Conversação em Espanhol Sem Mistério Conversação em Francês Sem
Álgebra SeM MiSTéRio Série SeM MiSTéRio Alemão Sem Mistério Álgebra Sem Mistério Cálculo Sem Mistério Conversação em Alemão Sem Mistério Conversação em Espanhol Sem Mistério Conversação em Francês Sem
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade
 REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
REPRESENTAÇÃO DE DADOS EM SISTEMAS DE COMPUTAÇÃO AULA 03 Arquitetura de Computadores Gil Eduardo de Andrade O conteúdo deste documento é baseado no livro Princípios Básicos de Arquitetura e Organização
AULA DE REPOSIÇÃO 001 / 3º ANO
 UL DE REPOSIÇÃO 00 / 3º NO Introdução Inicialmente, para a primeira aula, será feita uma retomada de todo o assunto já estudado, uma vez que não é nada fácil simplesmente retomar o conteúdo sem que sejam
UL DE REPOSIÇÃO 00 / 3º NO Introdução Inicialmente, para a primeira aula, será feita uma retomada de todo o assunto já estudado, uma vez que não é nada fácil simplesmente retomar o conteúdo sem que sejam
Projeto "Aqui Tem Cultura"
 Projeto "Aqui Tem Cultura" Objetivo Informar jovens e adultos brasileiros a respeito das seguintes expressões culturais: cinema, teatro, artes plásticas, música e dança no Brasil Requisitos 1. Exibir uma
Projeto "Aqui Tem Cultura" Objetivo Informar jovens e adultos brasileiros a respeito das seguintes expressões culturais: cinema, teatro, artes plásticas, música e dança no Brasil Requisitos 1. Exibir uma
AÇÕES DE CONTROLE. Ações de Controle Relação Controlador/Planta Controlador proporcional Efeito integral Efeito derivativo Controlador PID
 AÇÕES E CONTROLE Açõe de Controle Relação Controlador/Planta Controlador roorcional Efeito integral Efeito derivativo Controlador PI Controle de Sitema Mecânico - MC - UNICAMP Açõe comun de controle Ação
AÇÕES E CONTROLE Açõe de Controle Relação Controlador/Planta Controlador roorcional Efeito integral Efeito derivativo Controlador PI Controle de Sitema Mecânico - MC - UNICAMP Açõe comun de controle Ação
ELEMENTOS DE MÁQUINAS I
 UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA MECÂNICA ELEMENTOS DE MÁQUINAS I APOSTILA PARA O CURSO 2 o Semestre de 2001 Molas Helicoidais e Planas AUTOR: P ROF. DR. AUTELIANO A NTUNES DOS
UNIVERSIDADE ESTADUAL DE CAMPINAS FACULDADE DE ENGENHARIA MECÂNICA ELEMENTOS DE MÁQUINAS I APOSTILA PARA O CURSO 2 o Semestre de 2001 Molas Helicoidais e Planas AUTOR: P ROF. DR. AUTELIANO A NTUNES DOS
fx-82ms fx-83ms fx-85ms fx-270ms fx-300ms fx-350ms
 O uso da Calculadora Científica (Casio fx) fx-82ms fx-83ms fx-85ms fx-270ms fx-300ms fx-350ms Prof. Ms. Renato Francisco Merli 2013 1 Sumário 1. Antes de Começar... 2 2. Cálculos Básicos... 8 3. Cálculos
O uso da Calculadora Científica (Casio fx) fx-82ms fx-83ms fx-85ms fx-270ms fx-300ms fx-350ms Prof. Ms. Renato Francisco Merli 2013 1 Sumário 1. Antes de Começar... 2 2. Cálculos Básicos... 8 3. Cálculos
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa
 1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
1) Eficiência e Equilíbrio Walrasiano: Uma Empresa Suponha que há dois consumidores, Roberto e Tomás, dois bens abóbora (bem 1) e bananas (bem ), e uma empresa. Suponha que a empresa 1 transforme 1 abóbora
Implantação do sistema Condominium
 Implantação do sistema Condominium Nesse manual iremos acompanhar o passo a passo para a implantação do sistema, portanto iremos pular algumas telas do cadastro, que deverão ser preenchidas após a implantação
Implantação do sistema Condominium Nesse manual iremos acompanhar o passo a passo para a implantação do sistema, portanto iremos pular algumas telas do cadastro, que deverão ser preenchidas após a implantação
07/03/07 1ª aula de Matlab 10:30 12:00
 07/03/07 1ª aula de Matlab 10:30 12:00 Apresentação do Matlab (interfaces, help) Exercícios: matrizes/vetores, operações aritméticas, comandos básicos, células. Funções: zeros, ones, length, clear, help,
07/03/07 1ª aula de Matlab 10:30 12:00 Apresentação do Matlab (interfaces, help) Exercícios: matrizes/vetores, operações aritméticas, comandos básicos, células. Funções: zeros, ones, length, clear, help,
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação
 Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
Universidade Gama Filho Campus Piedade Departamento de Engenharia de Controle e Automação Laboratório da Disciplina CTA-147 Controle I Análise da Resposta Transitória (Este laboratório foi uma adaptação
CAPÍTULO 4 - BALANÇOS MATERIAIS. Existem dois tipos fundamentais de entidade em termodinâmica, estados de um sistema, e os processos de um sistema.
 Existem dois tipos fundamentais de entidade em termodinâmica, estados de um sistema, e os processos de um sistema. Sempre que duas ou mais propriedades de um sistema variam, diz-se que ocorreu um processo.
Existem dois tipos fundamentais de entidade em termodinâmica, estados de um sistema, e os processos de um sistema. Sempre que duas ou mais propriedades de um sistema variam, diz-se que ocorreu um processo.
Estudaremos métodos numéricos para resolução de sistemas lineares com n equações e n incógnitas. Estes podem ser:
 1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
1 UNIVERSIDADE FEDERAL DE VIÇOSA Departamento de Matemática - CCE Cálculo Numérico - MAT 271 Prof.: Valéria Mattos da Rosa As notas de aula que se seguem são uma compilação dos textos relacionados na bibliografia
7 AULA. Curvas Polares LIVRO. META Estudar as curvas planas em coordenadas polares (Curvas Polares).
 1 LIVRO Curvas Polares 7 AULA META Estudar as curvas planas em coordenadas polares (Curvas Polares). OBJETIVOS Estudar movimentos de partículas no plano. Cálculos com curvas planas em coordenadas polares.
1 LIVRO Curvas Polares 7 AULA META Estudar as curvas planas em coordenadas polares (Curvas Polares). OBJETIVOS Estudar movimentos de partículas no plano. Cálculos com curvas planas em coordenadas polares.
Aula 4 Conceitos Básicos de Estatística. Aula 4 Conceitos básicos de estatística
 Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Aula 4 Conceitos Básicos de Estatística Aula 4 Conceitos básicos de estatística A Estatística é a ciência de aprendizagem a partir de dados. Trata-se de uma disciplina estratégica, que coleta, analisa
Transformada z. ADL 25 Cap 13. A Transformada z Inversa
 ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
ADL 25 Cap 13 Transformada z A Transformada z Inversa Qualquer que seja o método utilizado a transformada z inversa produzirá somente os valores da função do tempo nos instantes de amostragem. Portanto,
EA616B Análise Linear de Sistemas Resposta em Frequência
 EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
EA616B Análise Linear de Sistemas Resposta em Frequência Prof. Pedro L. D. Peres Faculdade de Engenharia Elétrica e de Computação Universidade Estadual de Campinas 2 o Semestre 2013 Resposta em Frequência
Guião do Trabalho Laboratorial Nº 3 Análise do Comportamento de uma Suspensão de Automóvel
 SISEL Sistemas Electromecânicos Guião do Trabalho Laboratorial Nº 3 Análise do Comportamento de uma Suspensão de Automóvel GRIS Group of Robotics and Intelligent Systems Homepage: http://www.dee.isep.ipp.pt/~gris
SISEL Sistemas Electromecânicos Guião do Trabalho Laboratorial Nº 3 Análise do Comportamento de uma Suspensão de Automóvel GRIS Group of Robotics and Intelligent Systems Homepage: http://www.dee.isep.ipp.pt/~gris
Análise de Erro Estacionário
 Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
Análise de Erro Estacionário Sistema de controle pode apresentar erro estacionário devido a certos tipos de entrada. Um sistema pode não apresentar erro estacionário a uma determinada entrada, mas apresentar
APOSTILA DE EXEMPLO (Esta é só uma reprodução parcial do conteúdo)
 APOSTILA DE EXEMPLO (Esta é só uma reprodução parcial do conteúdo) 1 Índice Aula 1...3 Introdução... 3 Formatações de tabela... 4 Função HOJE... 6 Função SE... 6 Exercícios... 7 Exercício de Fixação...
APOSTILA DE EXEMPLO (Esta é só uma reprodução parcial do conteúdo) 1 Índice Aula 1...3 Introdução... 3 Formatações de tabela... 4 Função HOJE... 6 Função SE... 6 Exercícios... 7 Exercício de Fixação...
Texto 07 - Sistemas de Partículas. A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica.
 Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
Texto 07 - Sistemas de Partículas Um ponto especial A figura ao lado mostra uma bola lançada por um malabarista, descrevendo uma trajetória parabólica. Porém objetos que apresentam uma geometria, diferenciada,
A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte:
 Processo A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte: K=26.4 Ganho L=203 Atraso em ms τ=334 Constante de tempo em ms.
Processo A função de transferência do processo, considerando um sistema de primeira ordem com atraso e invariante no tempo, é a seguinte: K=26.4 Ganho L=203 Atraso em ms τ=334 Constante de tempo em ms.
Processamento Digital de Sinais Aula 05 Professor Marcio Eisencraft fevereiro 2012
 Aula 05 - Sistemas de tempo discreto Classificação Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044. Páginas 25-36. HAYKIN, S. S.; VAN VEEN,
Aula 05 - Sistemas de tempo discreto Classificação Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044. Páginas 25-36. HAYKIN, S. S.; VAN VEEN,
Conhecendo o Decoder
 Conhecendo o Decoder O Decoder da sua ion TV, ou receptor, também é chamado de STB, sigla em inglês para Set Top Box, que é o aparelho responsável por receber o sinal de TV, decodificá-lo e enviá-lo para
Conhecendo o Decoder O Decoder da sua ion TV, ou receptor, também é chamado de STB, sigla em inglês para Set Top Box, que é o aparelho responsável por receber o sinal de TV, decodificá-lo e enviá-lo para
A metodologia ARIMA (Auto-regressivo-Integrado-Média-Móvel),
 nfelizmente, o uso de ferramentas tornais de previsão é muito pouco adotado por empresas no Brasil. A opinião geral é que no Brasil é impossível fazer previsão. O ambiente econômico é muito instável, a
nfelizmente, o uso de ferramentas tornais de previsão é muito pouco adotado por empresas no Brasil. A opinião geral é que no Brasil é impossível fazer previsão. O ambiente econômico é muito instável, a
Mercados financeiros CAPÍTULO 4. Olivier Blanchard Pearson Education. 2006 Pearson Education Macroeconomia, 4/e Olivier Blanchard
 Mercados Olivier Blanchard Pearson Education CAPÍTULO 4 4.1 Demanda por moeda O Fed (apelido do Federal Reserve Bank) é o Banco Central dos Estados Unidos. A moeda, que você pode usar para transações,
Mercados Olivier Blanchard Pearson Education CAPÍTULO 4 4.1 Demanda por moeda O Fed (apelido do Federal Reserve Bank) é o Banco Central dos Estados Unidos. A moeda, que você pode usar para transações,
Compensadores. Controle 1 - DAELN - UTFPR. Os compensadores são utilizados para alterar alguma característica do sistema em malha fechada.
 Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Compenadore 0.1 Introdução Controle 1 - DAELN - UTFPR Prof. Paulo Roberto Brero de Campo O compenadore ão utilizado para alterar alguma caracterítica do itema em malha fechada. 1. Avanço de fae (lead):
Cap. 7 - Fontes de Campo Magnético
 Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
Universidade Federal do Rio de Janeiro Instituto de Física Física III 2014/2 Cap. 7 - Fontes de Campo Magnético Prof. Elvis Soares Nesse capítulo, exploramos a origem do campo magnético - cargas em movimento.
COMO PROGRAMAR SEU TIME
 COMO PROGRAMAR SEU TIME 1) INSTALAÇÃO: Instale o simulador da categoria SIMUROSOT da FIRA. O simulador é gratuito e está disponível para download no site da FIRA (www.fira.net) ou no site da competição
COMO PROGRAMAR SEU TIME 1) INSTALAÇÃO: Instale o simulador da categoria SIMUROSOT da FIRA. O simulador é gratuito e está disponível para download no site da FIRA (www.fira.net) ou no site da competição
Gráficos de funções em calculadoras e com lápis e papel (*)
 Rafael Domingos G Luís Universidade da Madeira/Escola Básica /3 São Roque Departamento de Matemática Gráficos de funções em calculadoras e com lápis e papel (*) A difusão de calculadoras gráficas tem levado
Rafael Domingos G Luís Universidade da Madeira/Escola Básica /3 São Roque Departamento de Matemática Gráficos de funções em calculadoras e com lápis e papel (*) A difusão de calculadoras gráficas tem levado
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes
 Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
Análise e Projeto de Sistemas de Controle pelo Método do Lugar das Raízes Saulo Dornellas Universidade Federal do Vale do São Francisco Juazeiro - BA Dornellas (UNIVASF) Juazeiro - BA 1 / 44 Análise do
3º Bimestre. Física I. Autor: Geraldo Velazquez
 3º Bimestre Autor: Geraldo Velazquez SUMÁRIO UNIDADE III... 4 Capítulo 3: Eletromagnetismo... 4 3.1 Introdução... 4 3.2 Campo Magnético (B)... 6 3.3 Campo Magnético Gerado Por Corrente... 7 3.4 Campo
3º Bimestre Autor: Geraldo Velazquez SUMÁRIO UNIDADE III... 4 Capítulo 3: Eletromagnetismo... 4 3.1 Introdução... 4 3.2 Campo Magnético (B)... 6 3.3 Campo Magnético Gerado Por Corrente... 7 3.4 Campo
Introdução às equações diferenciais
 Introdução às equações diferenciais Professor Leonardo Crochik Notas de aula 1 O que é 1. é uma equação:... =... 2. a incógnita não é um número x R, mas uma função x(t) : R R 3. na equação estão presentes,
Introdução às equações diferenciais Professor Leonardo Crochik Notas de aula 1 O que é 1. é uma equação:... =... 2. a incógnita não é um número x R, mas uma função x(t) : R R 3. na equação estão presentes,
Manual das planilhas de Obras v2.5
 Manual das planilhas de Obras v2.5 Detalhamento dos principais tópicos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Gerando previsão de custos da obra (Módulo
Manual das planilhas de Obras v2.5 Detalhamento dos principais tópicos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Gerando previsão de custos da obra (Módulo
Lista de Exercícios - Potenciação
 Nota: Os exercícios desta aula são referentes ao seguinte vídeo Matemática Zero 2.0 - Aula 14 - Potenciação ou Exponenciação - (parte 1 de 2) Endereço: https://www.youtube.com/watch?v=20lm2lx6r0g Gabaritos
Nota: Os exercícios desta aula são referentes ao seguinte vídeo Matemática Zero 2.0 - Aula 14 - Potenciação ou Exponenciação - (parte 1 de 2) Endereço: https://www.youtube.com/watch?v=20lm2lx6r0g Gabaritos
Aula 4 Estatística Conceitos básicos
 Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
Aula 4 Estatística Conceitos básicos Plano de Aula Amostra e universo Média Variância / desvio-padrão / erro-padrão Intervalo de confiança Teste de hipótese Amostra e Universo A estatística nos ajuda a
CADERNO DE ATIVIDADES UMA PROPOSTA METODOLÓGICA PARA O ESTUDO DAS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS POR MÉTODOS NUMÉRICOS.
 1 CADERNO DE ATIVIDADES UMA PROPOSTA METODOLÓGICA PARA O ESTUDO DAS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS POR MÉTODOS NUMÉRICOS. PONTIFÍCIA UNIVERSIDADE CATÓLICA DE MINAS GERAIS MESTRADO EM ENSINO DE CIÊNCIAS
1 CADERNO DE ATIVIDADES UMA PROPOSTA METODOLÓGICA PARA O ESTUDO DAS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS POR MÉTODOS NUMÉRICOS. PONTIFÍCIA UNIVERSIDADE CATÓLICA DE MINAS GERAIS MESTRADO EM ENSINO DE CIÊNCIAS
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica
 O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
O Princípio da Complementaridade e o papel do observador na Mecânica Quântica A U L A 3 Metas da aula Descrever a experiência de interferência por uma fenda dupla com elétrons, na qual a trajetória destes
Além do Modelo de Bohr
 Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
Além do Modelo de Bor Como conseqüência do princípio de incerteza de Heisenberg, o conceito de órbita não pode ser mantido numa descrição quântica do átomo. O que podemos calcular é apenas a probabilidade
HandsOn Session. Especificação, Modelação e Projecto de Sistemas Embutidos. Simulink - introdução. Paulo Pedreiras, Luís Almeida {pbrp,lda}@ua.
 Especificação, Modelação e Projecto de Sistemas Embutidos Simulink - introdução HandsOn Session Paulo Pedreiras, Luís Almeida {pbrp,lda}@ua.pt Departamento de Electrónica, Telecomunicações e Informática
Especificação, Modelação e Projecto de Sistemas Embutidos Simulink - introdução HandsOn Session Paulo Pedreiras, Luís Almeida {pbrp,lda}@ua.pt Departamento de Electrónica, Telecomunicações e Informática
Primeiros passos das Planilhas de Obra v2.6
 Primeiros passos das Planilhas de Obra v2.6 Instalação, configuração e primeiros passos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Preparar inicialização das
Primeiros passos das Planilhas de Obra v2.6 Instalação, configuração e primeiros passos para uso das planilhas de obra Elaborado pela Equipe Planilhas de Obra.com Conteúdo 1. Preparar inicialização das
Investigando números consecutivos no 3º ano do Ensino Fundamental
 Home Índice Autores deste número Investigando números consecutivos no 3º ano do Ensino Fundamental Adriana Freire Resumo Na Escola Vera Cruz adota-se como norteador da prática pedagógica na área de matemática
Home Índice Autores deste número Investigando números consecutivos no 3º ano do Ensino Fundamental Adriana Freire Resumo Na Escola Vera Cruz adota-se como norteador da prática pedagógica na área de matemática
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) III Resolução de sistemas lineares por métodos numéricos. Objetivos: Veremos
Variáveis aleatórias contínuas e distribuiçao Normal. Henrique Dantas Neder
 Variáveis aleatórias contínuas e distribuiçao Normal Henrique Dantas Neder Definições gerais Até o momento discutimos o caso das variáveis aleatórias discretas. Agora vamos tratar das variáveis aleatórias
Variáveis aleatórias contínuas e distribuiçao Normal Henrique Dantas Neder Definições gerais Até o momento discutimos o caso das variáveis aleatórias discretas. Agora vamos tratar das variáveis aleatórias
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A22 (1) O circuito a seguir amplifica a diferença de
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA SÉRIE DE EXERCÍCIO #A22 (1) O circuito a seguir amplifica a diferença de
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO
 PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br
PRINCÍPIOS DE CONTROLE E SERVOMECANISMO JOSÉ C. GEROMEL e RUBENS H. KOROGUI DSCE / Faculdade de Engenharia Elétrica e de Computação UNICAMP, CP 6101, 13083-970, Campinas, SP, Brasil, geromel@dsce.fee.unicamp.br
Processos Estocásticos
 Processos Estocásticos Terceira Lista de Exercícios 22 de julho de 20 Seja X uma VA contínua com função densidade de probabilidade f dada por Calcule P ( < X < 2. f(x = 2 e x x R. A fdp dada tem o seguinte
Processos Estocásticos Terceira Lista de Exercícios 22 de julho de 20 Seja X uma VA contínua com função densidade de probabilidade f dada por Calcule P ( < X < 2. f(x = 2 e x x R. A fdp dada tem o seguinte
Capítulo 5: Aplicações da Derivada
 Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Instituto de Ciências Exatas - Departamento de Matemática Cálculo I Profª Maria Julieta Ventura Carvalho de Araujo Capítulo 5: Aplicações da Derivada 5- Acréscimos e Diferenciais - Acréscimos Seja y f
Sistema topograph 98. Tutorial Módulo Fundiário
 Sistema topograph 98 Tutorial Módulo Fundiário Preparando o desenho para o Módulo Fundiário _ 1. Na área de trabalho do Windows, procure o ícone do topograph e dê um duplo clique sobre ele para carregar
Sistema topograph 98 Tutorial Módulo Fundiário Preparando o desenho para o Módulo Fundiário _ 1. Na área de trabalho do Windows, procure o ícone do topograph e dê um duplo clique sobre ele para carregar
1. A corrida de vetores numa folha de papel.
 1. A corrida de vetores numa folha de papel. desenhando a pista. o movimento dos carros. o início da corrida. as regras do jogo. 2. A corrida no computador. o número de jogadores. o teclado numérico. escolhendo
1. A corrida de vetores numa folha de papel. desenhando a pista. o movimento dos carros. o início da corrida. as regras do jogo. 2. A corrida no computador. o número de jogadores. o teclado numérico. escolhendo
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU
 Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Cálculo Numérico Faculdade de Engenharia, Arquiteturas e Urbanismo FEAU Prof. Dr. Sergio Pilling (IPD/ Física e Astronomia) II Métodos numéricos para encontrar raízes (zeros) de funções reais. Objetivos:
Esquema: Representação da força de atração gravitacional entre dois corpos de massas M 1 e M 2
 As Forças de Marés As marés são conhecidas de todos, principalmente por aqueles que moram próximo ao mar e dele vivem. Muitos deles sabem prever a maré em função da Lua e do Sol, sem sequer saber qual
As Forças de Marés As marés são conhecidas de todos, principalmente por aqueles que moram próximo ao mar e dele vivem. Muitos deles sabem prever a maré em função da Lua e do Sol, sem sequer saber qual
Desempenho de Sistemas de Controle Realimentados
 Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
Desempenho de Sistemas de Controle Realimentados. Erro em estado estacionário de sistemas de controle realimentados 2. Erro em estado estacionário de sistemas com realimentação não-unitária 3. Índice de
