DINÂMICA CAÓTICA E SINCRONIZAÇÃO DE FASE EM MAPAS ACOPLADOS
|
|
|
- Raul Filipe Lagos
- 5 Há anos
- Visualizações:
Transcrição
1 Istituto de Geociêcias e Ciêcias Exatas Campus de Rio Claro DINÂMICA CAÓTICA E SINCRONIZAÇÃO DE FASE EM MAPAS ACOPLADOS Alie Pereira da Silva Orietador Prof. Dr. Ricardo Egydio de Carvalho Dissertação de Mestrado apresetada ao Istituto de Geociêcias e Ciêcias Exatas do Campus de Rio Claro, da Uiversidade Estadual Paulista Júlio de Mesquita Filho, como parte dos requisitos para obteção do título de Mestre em Física. Rio Claro (SP) 0
2 i Comissão Examiadora Prof. Dr. Ricardo Egydio de Carvalho (orietador) UNESP Rio Claro (SP) Prof. Dr. Elbert Eistei Nehrer Macau INPE São José dos Campos (SP) Prof. Dr. José Maoel Balthazar UNESP Rio Claro (SP) Alie Pereira da Silva CANDIDATA Rio Claro, de fevereiro de 0. Resultado: APROVADA
3 ii À miha família
4 iii Agradecimetos Ao Professor Ricardo Egydio de Carvalho pela orietação, esiametos, sugestões, ateção e paciêcia. sesibilidade. À Professora Aa Paula Mijolaro pela cotribuição, auxílio, icetivo, coselhos e Ao Professor Edso Deis Leoel pelo auxílio e esiametos. À CAPES Coordeação de Aperfeiçoameto de Pessoal de Nível Superior pelo apoio fiaceiro. Aos meus colegas de laboratório pelo auxílio e amizade. Aos meus sogros João e Salete pelo acolhimeto, ateção e cariho. Aos meus pais e irmãos Luiz, Yeda, Samuel e Nádia pelo apoio das mais diversas formas, icetivo, cariho, compreesão e tudo o que fizeram por mim. Ao meu amorado Viícius pela paciêcia, amor, dedicação e por me suportar em mometos difíceis.
5 iv Resumo Silva, A. P., Dissertação de Mestrado, Istituto de Geociêcias e Ciêcias Exatas, UNESP, Rio Claro, 0. Este trabalho tem como objetivo eteder e desevolver estudos relacioados à sicroização de fase em sistemas diâmicos discretos. Foi utilizado um modelo simples de osciladores ão-lieares deomiado mapa circular. Iicialmete é apresetado um estudo extesivo do mapa circular e suas propriedades diâmicas. É apresetado também a trasição de movimeto quase-periódico para movimeto caótico em uma rota quase-periódica para o caos do mapa circular. Em seguida, foram acoplados dois mapas circulares através de um acoplameto bidirecioal ão liear. O efeito de trasição para o estado sícroo é iduzido por uma crise iterior, através do surgimeto de um atrator caótico, o qual iduz periodicidade oscilatória o sistema. É mostrado que a sicroização de dois mapas circulares acoplados é iflueciada pela difereça do úmero de rotação e a itesidade do parâmetro de ão liearidade. A trasição para o estado ão sícroo é iduzida por uma crise iterior, através da expasão do atrator caótico até perder sua periodicidade. Posteriormete, foi itroduzido um ruído braco gaussiao o acoplameto e um ruído aditivo em dois sistemas diferetes de dois mapas circulares acoplados. Os resultados obtidos para o primeiro sistema mostraram que o espaço de fases, a ação de um ruído braco gaussiao o acoplameto e aditivo destroem o atrator caótico, e o sistema perde sicroização de fase perfeita e imperfeita. Os resultados obtidos para o segudo sistema mostraram que o espaço de fases, a ação de um ruído braco gaussiao o acoplameto destrói o atrator caótico, e o sistema perde sicroização de fase perfeita e imperfeita. No etato, a ação de um ruído braco gaussiao aditivo iduz um efeito de seguda ordem, o qual ocorre a dessicroização de fase imperfeita, e permaece a sicroização de fase perfeita o sistema, isto é, o sistema matém apeas sicroização de fase perfeita a preseça de ruído. Palavras chave: travameto de freqüêcia, caos, quase-periodicidade, sicroização de fase, mapa circular, crise iterior, ruído braco gaussiao, deslizametos de fase.
6 v Abstract Silva, A. P., Master Dissertatio, Istituto de Geociêcias e Ciêcias Exatas, UNESP, Rio Claro, 0. This reach has as objective to uderstad ad to develop studies related to the phase sychroizatio i discreet dyamical systems. A simple model of oscillators o-liear deomiated circle map was studied. Iitially a extesive study of the chaotic dyamics of the circle map is preseted. It is also preseted the trasitio of quasi-periodic behavior for chaotic behavior i a quasi-periodic route to chaos i the circle map. Soo after, was itroduced a o-liear bidirectioal couplig i two circle maps, ad studied the trasitio effects to phase sychroizatio, iduced by iterior crisis, through appearace of a chaotic attractor, which iduce oscillatory periodicity i the system. It is show that the phase sychroizatio of two coupled circle maps is iflueced by the differece of the widig umber ad the itesity of the o-liear parameter. The trasitio for the osychroizatio is iduced by iterior crisis, through of expasio of chaotic attractor. Later o, a gaussia white oise was itroduced i the couplig ad a addictive oise i two differet systems of two coupled circle maps. The results for the first system show that a additive ad couplig gaussia white oise iduce the expasio of the chaotic attractor, ad cosequetly, iduce a loss of perfect ad imperfect phase sychroizatio. The results for the secod system show that a couplig gaussia white oise iduce the loss of perfect ad imperfect phase sychroizatio. However, the additive gaussia white oise iduce a effect of secod order, i which occur the loss of imperfect phase sychroizatio, but the perfect phase sychroizatio stay i system. Keywords: frequecy lockig, phase lockig, chaos, quasi-periodicity, phase sychroizatio, circle map, iterior crisis, gaussia white oise, phase slips, periodically drive chaotic oscillators.
7 Sumário Itrodução... Mapa Circular e Caos Sistemas Diâmicos Mapas e Seção de Poicaré Mapa Circular Estabilidade Caos Expoetes de Lyapuov Atratores Atrator Caótico em Crise Mapa Circular e Quase-Periodicidade Quase-periodicidade e seções de Poicaré Número de Rotação Travameto de Freqüêcia Líguas de Arold Escada do Diabo Árvore de Farey Uiversalidade a rota quase-periódica para o caos Uiversalidade local Uiversalidade Global Sicroização de fase em mapas circulares acoplados Mapas circulares acoplados Expoetes de Lyapuov Sicroização de Fase Trasição para sicroização de fase Iterpretação do movimeto oscilatório Sicroização de fase em dois mapas circulares acoplados Diagramas para regiões de sicroização Trasição para ão sicroização Efeitos de ruído sobre sicroização de fase em mapas circulares acoplados Iterpretação da diâmica de fase... 69
8 vii 5. Efeitos de ruído braco gaussiao sobre o primeiro sistema de dois mapas circulares acoplados Dessicroização de fase iduzida por ruído gaussiao o acoplameto Dessicroização de fase iduzida por ruído gaussiao aditivo Efeitos de ruído braco gaussiao sobre o segudo sistema de dois mapas circulares acoplados Dessicroização de fase iduzida por ruído gaussiao o acoplameto Efeito de seguda ordem iduzido por ruído gaussiao aditivo Coclusões e perspectivas A Cometários Itrodutórios sobre Processos Radômicos A. Desidade de probabilidade uidimesioal, média e variâcia A. Desidade de probabilidade bidimesioal, correlação e covariâcia A.3 Processo estacioário A.4 O processo ruído braco B Algoritmo para gerar úmeros aleatórios distribuídos de acordo com a distribuição gaussiaa Referêcias Bibliográficas... 06
9 Capítulo Itrodução A palavra sicroização é de origem grega, σύγ χρόνος, a qual sigifica compartilhar o tempo comum. Pode-se eteder etão que, dois elemetos sicroizados apresetam comportameto idêtico ou ocorrem ao mesmo tempo. No século XVII, o astrôomo, físico e matemático holadês C. Huyghes, pateteou o primeiro relógio de pêdulo, buscado aumetar a precisão dos istrumetos de medida utilizados em estudos de astroomia. O cietista otou que dois relógios de pêdulo colocados cotíguos em uma mesma parede tedem a sicroizar seus pêdulos em fase ou em oposição de fase. Mesmo quado alguma perturbação era aplicada aos relógios, depois de algus miutos a sicroização se restabelecia. A partir de etão, iiciou-se a aálise dos estudos de sicroização. Este feômeo é cohecido como travameto de freqüêcia (mode lockig ou equivaletemete, phase lockig ou frequecy lockig) e geralmete está presete em sistemas dissipativos com freqüêcias competido etre si []. As freqüêcias podem surgir diamicamete detro do sistema ão liear ou através do acoplameto de um movimeto oscilate com uma força periódica extera. O travameto de freqüêcia ocorre quado a razão etre as duas freqüêcias fica travada em uma razão de dois úmeros iteiros para um itervalo fiito de valores dos parâmetros. Na atureza, o exemplo mais cohecido de travameto de freqüêcia é o movimeto da Terra e da Lua. A freqüêcia de rotação da Lua em toro de seu eixo é travada (ou sicroizada) com seu período de revolução em toro da Terra, de tal maeira que a Lua mostra sempre a mesma face para a Terra. Matematicamete, essa é a razão mais simples de travameto de freqüêcia /, uma vez que os dois osciladores têm a mesma freqüêcia []. Um sistema pode possui duas freqüêcias que caracterizam sua diâmica e competem etre si. Quado a razão etre tais freqüêcias é racioal, o comportameto do sistema é deomiado periódico, por outro lado, quado a razão etre as freqüêcias é irracioal, o comportameto do sistema é deomiado quase-periódico [3]. No regime de quaseperiodicidade, o comportameto do sistema uca se repete exatamete igual, parecedo bastate irregular. Existe uma rota para o comportameto torar-se caótico, deomiada por rota quase-periódica para o caos [4], que ocorre quado bifurcações de período ocorrem o
10 sistema levado o comportameto regular (periódico) para um comportameto caótico. Em 965, o matemático russo V. I. Arold propôs um modelo ão liear que esboça um círculo sobre ele mesmo, deomiado mapa circular (circle map) [5]. Tal sistema, apesar de simples, possibilita a compreesão teórica e a aálise de diversos comportametos diâmicos complexos evolvedo iteração ão liear etre osciladores periódicos, e osciladores sob ação de uma força periódica. O mapa circular é cosiderado uma ferrameta padrão de estudo a rota quase-periódica para o caos. Algus exemplos de sistemas físicos, cujo comportameto diâmico pode ser modelado por mapas circulares são: a covecção forçada de Rayleigh-Béard [6,7], células cardíacas perturbadas periodicamete [8,9], osciladores guiados periodicamete [0,] e codutividade elétrica em Niobato de Sódio e Bário []. Quado as freqüêcias do mapa circular se toram periódicas, para determiados itervalos dos valores dos parâmetros, o sistema está em um regime de travameto de freqüêcia. As regiões para esses itervalos de travameto, costituem estruturas complexas o espaço dos parâmetros, chamadas líguas de Arold. Cada lígua correspode a uma região de travameto de freqüêcia, associada a cada úmero racioal da razão etre as freqüêcias [3]. As regiões de travameto de freqüêcia se apresetam em patamares bem defiidos e orgaizados, e são regidos pela chamada série de Farey. Esses patamares formam uma estrutura fractal deomiada Escada do Diabo, ode cada degrau está associado a uma cada lígua de Arold. Recetemete, pesquisas sobre sicroização vêm sedo voltadas para sistemas caóticos [4]. Um sistema diâmico é chamado caótico sempre que sua evolução depede sesitivamete de suas codições iiciais, isto é, duas trajetórias emergido de codições iiciais próximas, se separam expoecialmete o curso do tempo [5]. Como resultado, sistemas caóticos desafiam itrisecamete a sicroização. Quado um sistema diâmico dissipativo evolui para um comportameto caótico, tal estado pode estar associado a um atrator estraho. Diversas iformações podem ser extraídas do estudo de atratores. A caracterização das propriedades de atratores, com a utilização de teorias recetes de diâmica ão-liear permite a aálise de siais experimetais com comportameto caótico []. Cotudo, verificou-se que existe uma certa ordem subjacete ao caos. Sistemas diâmicos caóticos são determiísticos, isto é, sua evolução é descrita por uma regra bem defiida. É possível mostrar que, acoplado de forma adequada dois ou mais sistemas
11 3 caóticos, existe a possibilidade de sicroizá-los de forma que seus comportametos sejam semelhates. Isto causou um forte crescimeto em pesquisas sobre a teoria de oscilações caóticas e suas aplicações em biologia, física, química, comuicação e muitas outras áreas da ciêcia e egeharia [6], devido ao grade iteresse em sicroização de osciladores caóticos acoplados [7,8]. Algus exemplos de aplicações são: piscar de luzes de um cojuto de uma espécie de vaga-lumes [9,0], células de marca-passo o coração [,], atividade rítmica o cérebro devido a disparos sicroizados de um eorme úmero de eurôios [3-5], células secretoras de isulia do pâcreas [6], costrução de maipuladores de robô [7], em rádio-física, rádio-egeharia e rádio-comuicação sicroização é aplicada para estabilização de geradores, para sitetizar freqüêcias e modulação de siais em sistemas Doppler [8]. Além disso, esquemas de comuicação eficiete são baseados em comuicação caótica [9-3] e questões de sicroização são também cruciais para desig de computadores com arquitetura paralela [3]. Em sistemas caóticos, podem haver vários tipos diferetes de sicroização, a saber [33]: () Sicroização completa (ou idêtica) () Sicroização geeralizada (3) Sicroização de fase (4) Sicroização de fase imperfeita (5) Sicroização em atraso (6) Sicroização em atraso itermitete (7) Quase sicroização Sicroização completa de osciladores idêticos cosiste a perfeita igualdade etre as trajetórias dos dois osciladores, obtida devido ao acoplameto etre eles, de tal maeira que eles se matém sicroizados um com o outro o curso do tempo. Sicroização geeralizada ocorre quado os osciladores acoplados são completamete diferetes, e o comportameto diâmico de um dos osciladores é determiado pelo outro. Sicroização de fase pode ser cosiderada como um regime itermediário de sicroização, ode as fases dos osciladores evoluem de forma sicroizadas, equato suas amplitudes permaecem diferetes. Sicroização de fase imperfeita é uma situação ode ocorrem deslizametos de fase, isto é, saltos o valor da difereça de fase, detro de um regime de sicroização de fase.
12 4 Sicroização em atraso é um ível etre sicroização de fase e sicroização completa. Neste caso, os osciladores sicroizam suas fases e amplitudes com um atraso o tempo, isto é, um oscilador se atrasa o tempo em relação ao outro. Sicroização em atraso itermitete implica que os dois osciladores estão a maior parte do tempo em regime de sicroização em atraso, mas podem ocorrer itervalos de comportameto ão sicroizado quado as trajetórias do sistema possuem expoetes de Lyapuov positivos. Fialmete, quase sicroização resulta em um limite assitótico da difereça etre um subcojuto das variáveis de um oscilador e o correspodete subcojuto das variáveis do outro oscilador. Esta dissertação é focada o estudo de sicroização de fase em mapas circulares discretos. Em particular, a trasição para a sicroização de fase em dois mapas circulares acoplados, correspode a uma mudaça a estrutura topológica do atrator caótico. No mapa circular, a variável diâmica é uma variável agular [34]. Se essa variável é caótica, a diâmica do sistema pode ser geralmete represetada como um camiho parcialmete radômico. A sicroização de fase em sistemas de mapas circulares acoplados ocorre para valores de expoetes de Lyapuov positivos, cotrariamete à sicroização de fase de osciladores caóticos em geral. Atualmete, efeitos ão ituitivos de ruídos em sistemas ão lieares tem sido assuto de grade iteresse, pois é ievitável a preseça de ruído em sistemas aturais e experimetais [35,36]. No processo de sicroização, ruídos podem iflueciar de diferetes maeiras. Geralmete ele faz a difereça de fase oscilar ao redor do míimo do poço, cosiderado o comportameto da difereça de fase como uma partícula em um potecial icliado [37]. Assim, o ruído faz a difereça de fase escalar sobre a barreira de eergia ocasioalmete se deslocado para o míimo viziho, resultado em um efeito degradate, por exemplo, iduzido deslizametos de sicroização de fase em mapas circulares acoplados. Este trabalho está estruturado da seguite forma: o capítulo apreseta a descrição do mapa circular e suas propriedades diâmicas. O capítulo 3 trata do ceário de quaseperiodicidade, ode é mostrado que o mapa circular exibe o feômeo de travameto de freqüêcia em uma rota quase-periódica para o caos. No capítulo 4 é apresetada a sicroização de fase de dois mapas circulares acoplados ão liearmete, os efeitos de trasição para o comportameto sícroo, sob quais codições esse comportameto é possível, e os efeitos de trasição para o comportameto ão sícroo. O capítulo 5 apreseta a cotribuição cietifica deste trabalho, o aspecto de estudo dos efeitos de ruído sobre a
13 5 sicroização de fase em dois sistemas diferetes de dois mapas circulares acoplados. O estudo é feito itroduzido um ruído o acoplameto e posteriormete um ruído aditivo, isto é, adicioado ao sistema. Fialmete, o capítulo 6, são apresetadas as coclusões e perspectivas de trabalho futuro.
14 Capítulo Mapa Circular e Caos Neste capítulo será apresetado o modelo feomeológico deomiado mapa circular, o qual possibilita a compreesão teórica e a aálise do comportameto de osciladores periódicos iteragido ão liearmete e comportameto de um oscilador sob ação de uma força periódica. O mapa circular possui uma estrutura diâmica caótica, isto é, possui sesibilidade ás codições iiciais. A preseça de atratores o espaço de fases caracteriza a diâmica do sistema como dissipativa.. Sistemas Diâmicos Um sistema diâmico é chamado determiístico quado a sua evolução é descrita por uma regra bem defiida. Ele será etão, caracterizado pelo estado do sistema, que cotém toda iformação essecial acerca dele e pela sua diâmica, que forece a regra segudo a qual um estado evolui com o passar do tempo. Uma classe de regras importate para a descrição de feômeos aturais são as equações difereciais. Mais especificamete, utiliza-se como regra um sistema de equações difereciais ordiárias de primeira ordem, da seguite forma dx = F( x( t), μ) x ΙR ; μ ΙR dt, (.) ode μ é um parâmetro de cotrole do sistema. Se F ( x, μ) é ão liear, o sistema é caótico [38]. O sistema (.) é chamado autôomo, devido ao fato de o tempo ão aparecer explicitamete o sistema. A solução desse sistema com a codição iicial x ( t = 0) = x0, é chamada trajetória ou órbita do sistema. O cojuto de todas as trajetórias do sistema é chamado de fluxo. Quado o parâmetro μ é variado, podem ocorrer mudaças qualitativas a estrutura do sistema. Para cada codição iicial, x 0, existe uma órbita o espaço que é origiado pelo cojuto de variáveis x (t) e é chamado de espaço de fases.
15 7. Mapas e Seção de Poicaré Deomia-se mapa um sistema diâmico que evolui o tempo de uma forma discreta. Existem várias razões para se estudar mapas do poto de vista do seu comportameto diâmico. Com efeito, há iúmeros modelos cujas soluções aparecem sob a forma de relações de recorrêcia e portato por uma diâmica descrita por mapas []. Mapas são em geral mais simples para se aalisar do que os sistemas de equações diferecias que lhe deram origem. Um fluxo cotíuo pode dar origem a um mapa discreto costruido uma superfície com dimesão (N ), que itercepta trasversalmete o fluxo, deomiada seção de Poicaré. Uma vez escolhida a seção, observam-se os potos de cosecutivas itersecções da trajetória com esta, sedo que a seqüêcia discreta de potos resultates origia um mapa, chamado mapa de Poicaré. Portato, a seção de Poicaré associa ao fluxo de um sistema diâmico cotíuo o tempo um mapa discreto. Dado um poto sobre a seção de Poicaré, pode-se pergutar qual será o próximo poto sobre a mesma que a trajetória irá origiar a cada vez que ela itercepta a seção o mesmo setido. Dessa forma, a aálise da estabilidade de uma órbita periódica se reduz à aálise da estabilidade de um poto fixo do mapa gerado por essa órbita. Uma seção de Poicaré para o sistema (.) gera o seguite mapa: x i+ = P( xi ), (.) ode i represeta os passos temporais fixos e discretos, x i represeta a i-ésima iterseção da trajetória com a seção de Poicaré. A órbita do mapa será etão a seqüêcia de potos + ( x i ) defiida pela equação (.), que é geericamete deomiada uma equação de difereças. Uma órbita periódica correspode a um poto fixo o mapa de Poicaré. Uma órbita quaseperiódica é represetada a seção de Poicaré por potos radomicamete distribuídos, semelhate a uma órbita caótica..3 Mapa Circular Uma classe importate de sistemas diâmicos são os sistemas de fase, também chamados de osciladores, os quais possuem uma variável de fase ou uma variável agular como variável. A fase é a variável que correspode ao movimeto de rotação ao logo de uma
16 8 projeção circular. Um poto em um círculo é chamado freqüetemete de um âgulo ou fase de um oscilador. O oscilador mais simples de todos é aquele o qual a fase muda uiformemete, isto é, um movimeto uiforme ao redor do círculo a uma certa freqüêcia agular. Sistemas com oscilações auto-sustetadas oscilam sem a ecessidade de uma força periódica extera. O tempo decorrido para uma oscilação recebe o ome de período. A freqüêcia é o iverso do período. Um exemplo de um oscilador é o mapa circular (ou mapa de círculo), o qual trata-se de um mapa uidimesioal discreto, cuja iteração da variável é iterpretada como a medida de um âgulo que especifica ode a trajetória está sobre um círculo [3,5,]. Esta idéia é motivada pela cosideração do estado de um sistema que pode ser sempre represetado por um poto a superfície de um toróide tridimesioal, coforme a figura. (a). A represetação do movimeto pode ser simplificada tomado-se a seção de Poicaré do toróide. Se as variáveis do espaço de fases são propriamete escaladas, etão os potos de itersecção estarão sobre um círculo o plao de Poicaré, sedo possível usar um âgulo para especificar ode a trajetória ficará sobre a seção de cruzameto, coforme a figura. (b). (a) (b) Figura.: Represetação gráfica da idéia do mapa circular. Em (a) movimeto de uma trajetória sobre a superfície de um toróide tridimesioal. Em (a) seção de Poicaré para toro, ode a variável θ especifica ode o poto da trajetória está sobre a seção de cruzameto. Em geral, um mapa desse tipo pode ser escrito como θ + = f ( θ) (.3) ode a fução f(θ) é periódica o âgulo θ. A trajetória (ou órbita) é defiida como a
17 9 seqüêcia de âgulos θ 0, θ, θ,... Por coveiêcia, será cosiderada a medida do âgulo θ em uidades tal que θ = correspoda a uma revolução completa ao redor do círculo. A variável θ a equação (.3) é defiida em módulo. Com esta coveção, os âgulos θ = 0,7 e θ =,7 referem-se ao mesmo poto o círculo. Ates de itroduzir o mapa circular propriamete dito, é feita uma aálise de um caso simples, o qual a fução f(θ) é liear [3]: θ + = f ( θ ) = θ + ω mod [] (.4) Neste caso, a iteração de f(θ) cosiste simplesmete em adicioar o úmero ω ao valor aterior do âgulo. Assim, a iteração desloca a trajetória ao redor do círculo em passos de tamaho ω. A figura. mostra dois exemplos do mapa liear (.4), com valores diferetes de ω. (a) (b) Figura.: Dois gráficos da fução de mapa liear da equação (.4). θ + foi plotado como uma fução de θ. Em (a) ω = 0,4; em (b) a ω = 0,9. O salto súbito de f(θ) = até 0 é resultado de θ mod []. Não há ehum salto físico a localização de potos da trajetória. O mapa circular seo, muitas vezes mecioado simplesmete como mapa circular, é um sistema ão liear com a ão liearidade tomado a forma especifica de uma fução seo: κ θ+ = θ + ω se(πθ) mod [] (.5) π
18 0 O parâmetro κ é a itesidade de ão liearidade. Quado κ = 0, o mapa circular se reduz ao simples mapa liear da equação (.4). ω é o parâmetro de relação de freqüêcia e o termo π o deomiador é somete uma coveção ligada com uso [0,] como a extesão dos valores dos âgulos. Na figura.3 é possível otar uma mudaça iteressate o comportameto do mapa circular em κ =. Para κ >, algus valores de θ + tem mais do que um possível precursor θ. Dessa forma, diz-se que para κ >, o mapa circular é ão iversível. Por isso, as iteradas do mapa irão itroduzir um dobrameto das trajetórias, o que pode levar a um comportameto caótico. A descotiuidade do mapa as figuras.3 (a) e (b) é somete aparete. Quado o valor do âgulo excede, subtrai-se do valor e retora-se ao poto mais baixo da fução, como mostrado a figura. (a) (b) Figura.3: Dois gráficos da fução de mapa circular da equação (.5). Em (a) mapa circular seo para k = 0,7. Em (b) mapa circular seo para κ =,8. θ + foi plotado como uma fução de θ + com ω = 0,6. Note que para κ >, há algus valores f(θ) que tem dois possíveis θs como precursores. Etão, diz-se que para κ >, o mapa circular seo é ão iversível..3. Estabilidade Seja θ pertecete ao domíio de f(θ). A seqüêcia de úmeros θ, f(θ), f(f(θ)), f(f(f(θ))),..., cohecida como as iteradas de θ, costituem o que se chama de órbita do poto θ. Desta forma, se todos os potos θ, f(θ), f () (θ), f (3) (θ),..., f (k-) (θ), são distitos, eles formam a órbita periódica de período k de θ. Sedo assim, os potos que se repetem a cada iterada são ditos serem de período e, geralmete são deomiados de potos fixos ou potos de equilíbrio, os potos que se repetem a cada duas iteradas são de
19 período e assim sucessivamete []. Os potos fixos do mapa circular correspodem aos valores que satisfazem a equação θ κ = θ + ω se(πθ) (.6) π ou equivaletemete πω se ( πθ) =. (.7) κ Dessa forma, se κ πω (.8) etão haverá pelo meos um poto fixo para o mapa circular que possa ser calculado aaliticamete. Vale a pea ressaltar que quado a equação (.8) ão é satisfeita, os potos fixos existetes ão podem ser calculados aaliticamete. Se a trajetória se aproxima de θ coforme se itera o mapa, diz-se que θ é um poto fixo atrator ou (equivaletemete) um poto fixo estável. Se a trajetória se move para loge de θ, etão diz-se que θ é um poto fixo repulsor ou (equivaletemete) um poto fixo istável. O estudo da estabilidade reduz-se à ivestigação do valor de df/dθ calculado o poto de equilíbrio: df dθ = κ cos( πθ). (.9) Se df/dθ <, θ é um poto fixo estável. Se df/dθ >, etão θ é um poto fixo istável. Dessa forma, um poto fixo do mapa circular seo será estável se 0 < κ cos(πθ) <. Caso cotrário, o poto fixo será istável. Foram calculados aaliticamete os potos fixos do mapa circular seo (.5) para os valores dos parâmetros κ = 0,9 e ω = 0,. Foram ecotrados dois potos fixos, cujas estabilidades foram aalisadas através da equação (.9). A tabela. apresetada esses potos fixos ecotrados, suas localizações, seus valores das derivadas, suas classificações e
20 estabilidade. A figura.4 (a) mostra a evolução das iterações para o sistema cohecido como diagrama da teia, ode a reta icliada de 45º é a fução idetidade e a liha curva é f(θ). Os potos ode ocorrem cruzametos etre f(θ) e a fução idetidade são os potos fixos. Nessa figura a codição iicial foi θ 0 = 0,4, é possível otar que as trajetórias se afastam do poto fixo istável θ = 0,965 e se aproximam do poto fixo estável θ = 0, Poto Fixo Localização Valor da equação (.9) o poto Classificação Estabilidade A θ = 0,38035 df/dθ =,6703 repulsor istável B θ = 0,965 df/dθ = 0,3796 atrator estável Tabela.: Potos fixos e suas classificações do mapa (.5) com valores dos parâmetros κ = 0,9 e ω = 0,. Uma seguda situação para valores dos parâmetros κ = 0,9 e ω = 0,9 foi aalisada. Nesta situação, a equação (.8) ão é satisfeita, etão, os potos fixos para este valor ão podem ser calculados aaliticamete. A figura.4 (b) mostra a evolução das iterações para o sistema com esses valores dos parâmetros e codição iicial de θ 0 = 0,55. É possível otar que há dois cruzametos etre a fução idetidade e f(θ), havedo etão dois potos fixos, cujas localizações são aproximadamete θ = 0,6 e θ = 0,89. É possível otar que as trajetórias se afastam do poto θ = 0,6, o qual é istável, e se aproximam do poto θ = 0,88, o qual é estável. Ressalte-se que, embora ão seja possível calcular aaliticamete os potos fixos para determiados valores dos parâmetros, ão sigifica que esses potos ão existam. Eles apeas devem ser calculados umericamete. (a) (b) Figura.4: Evolução das iterações do mapa circular seo, os potos fixos estão ilustrados em vermelho. Em (a) κ = 0,9 e ω = 0,. O gráfico mostra que as trajetórias se afastam do poto fixo θ = 0,38035 e se aproximam do poto fixo θ = 0,965. A codição iicial foi θ 0 = 0,4. Em (b), κ = 0,9 e ω = 0,9. O mapa agora tem um poto fixo estável próximo de θ = 0,88 e um poto fixo istável próximo de θ = 0,6. A codição iicial foi θ 0 = 0,55.
21 3.3. Caos O termo caos é usado para referir-se à ão previsibilidade. A istabilidade diâmica que coduz a ão previsibilidade deve ser mais expoecial do que liear o tempo, porque o caso liear a previsibilidade é possível, equato o caso caótico ão há previsibilidade alguma. Esta istabilidade é puramete determiística e istrísica à diâmica [,5,38]. Isto é, sistemas caóticos são sesíveis às codições iiciais. Iterações do mapa circular são apresetadas a figura.5. A trasição para o caos ocorre quado f(θ) perde sua iversilidade. Em.5 (a) κ = 0,8, os potos a órbita quase ão passam pelo mesmo poto, isto mostra que ão há caos e este caso o movimeto é quaseperiódico. Em.5 (b) as iterações mostram uma oscilação auto-sustetada isolada, ode os potos a órbita retoram ao poto de partida depois de um certo úmero de iterações, este movimeto é cohecido como ciclo limite, e este caso o movimeto é periódico. Sistemas com oscilações auto-sustetadas oscilam sem a ecessidade de uma força periódica extera. Em.5 (c) as iterações mostram que os potos a órbita uca passam exatamete pelo mesmo poto, e este caso o movimeto é caótico. Ao variar-se os parâmetros do mapa (.5), ocorrem mudaças tato a posição como as características qualitativas dos potos de equilíbrio. Uma mudaça qualitativa a diâmica do sistema é deomiada bifurcação. Em uma bifurcação ovos potos de equilíbrio podem aparecer e outros ateriormete estáveis se torar istáveis e vice-versa. (a) (b)
22 4 (c) Figura.5: Evolução de iterações do mapa circular seo para ω = 0. e (a) κ = 0,8 a órbita é quase periódica, (b) κ =,0 a órbita é um ciclo limite, (c) κ =, a órbita é caótica. Uma das pricipais formas de caracterizar a diâmica de um sistema caótico é o diagrama de bifurcações, uma represetação gráfica do comportameto qualitativo das órbitas para cada valor do parâmetro de cotrole []. Quado ocorre uma bifurcação o diagrama de fases muda qualitativamete, ovos potos fixos podem aparecer e outros ateriormete estáveis podem ser torar istáveis e vice-versa. A maeira de costruir o diagrama de bifurcações é simples. Costrói-se um gráfico em que o eixo horizotal correspode aos valores do parâmetro de cotrole e o eixo vertical aos valores de θ. Para cada valor do parâmetro de cotrole, itera-se a variável de fase para uma codição iicial e gera-se a órbita correspodete. Um certo úmero dos primeiros potos da órbita é descartado, para dar tempo a que a órbita evolua para o seu comportameto fial, quer este seja uma órbita periódica ou caótica - chama-se a isto elimiar o trasiete. Em seguida marca-se o gráfico, para esse valor do parâmetro de cotrole, os valores de θ assumidos pela órbita ao logo de um úmero bastate grade de iterações. Acima de κ =, o diagrama de bifurcações para o mapa circular seo tora-se bastate complicado. A cada bifurcação ocorre uma duplicação de período até o sistema etrar em regime caótico. Por isso a rota para o caos ficou cohecida como rota de duplicação de período. As figuras.6 (a) e (b) mostram os diagramas de bifurcação para uma extesão de valores de κ e dois valores de ω, 0,50000 e 0,75. Deve-se tomar muito cuidado ao distiguir quase-periodicidade de caos, para isto, basta otar a estrutura atada do comportameto quase-periódico e comparar com a difusão radômica das áreas caóticas. Observa-se também que estes diagramas depedem sigificatemete do valor de ω.
23 5 (a) (b) Figura.6: Diagramas de bifurcação para o mapa circular seo. Os valores de κ são dados ao logo do eixo horizotal. O valor das codições iiciais é zero. Em (a) ω = 0, Note que o comportameto caótico ocorre bem acima de κ =. Em (b) ω = 0, Note que para κ < o comportameto é quase-periódico e periódico. Imediatamete acima de κ = há comportameto caótico, e logo em seguida surgem jaelas de periodicidade. Para κ > há duplicação de período e mais caos..3.3 Expoetes de Lyapuov Para medir a taxa de divergêcia expoecial de trajetórias vizihas e portato quatificar a depedêcia sesitiva às codições iiciais, isto é, a istabilidade expoecial, utilizam-se os expoetes de Lyapuov []. Uma das características do caos é a divergêcia de trajetórias vizihas. Para um sistema caótico esta divergêcia é expoecial o tempo (ou para um mapa iterado, expoecial o úmero de iterações da fução). Dessa forma, a propriedade do estado caótico é uma característica de um grupo de trajetórias. Cotudo, uma trajetória sobre um atrator caótico para um sistema limitado, freqüetemete retora para qualquer poto aterior ifiitamete próximo da trajetória. Etão, pode-se examiar a divergêcia desses potos vizihos (correspodete a tempos bastate diferetes) sobre uma trajetória. Para isto, cosidera-se um poto θ 0 e outro poto viziho θ 0 + ε, ambos o atrator. Etão itera-se o mapa vezes para cada valor e cosidera-se o valor absoluto da difereça etre os resultados [3]: d ( ) ( ) f θ + ε ) f ( θ ). (.0) ( 0 0 Se o comportameto é caótico, espera-se que esta distâcia cresça expoecialmete
24 6 com, etão escreve-se d ε f θ + ε ( ) ( ) ( 0 ) ( 0 ε f θ ) e λ (.) ou ( ) ( ) f ( θ0 + ε) f ( θ0) λ = l, (.) ε esta última equação defie o expoete de Lyapuov λ para a trajetória. Cosiderado agora ε 0, é possível recohecer dos cálculos que a razão sobre o lado direito da equação (.) é a defiição do valor absoluto da derivada de f () com respeito a θ 0. Pela aplicação da regra da cadeia por difereciação, a derivada de f () pode ser escrita como um produto de derivadas de f(θ) evoluída os potos sucessivos da trajetória θ 0, θ,..., θ. Etão, pode-se escrever a defiição do expoete de Lyapuov também como λ = l( f ( θ0) f ( θ)... f ( θ ) ) (.3) ode f (θ i ) = df/dθ. Pode-se escrever a equação (.3) como λ = (l f ( θ0) + l f ( θ) l f ( θ ) ) (.4) A equação (.4) mostra que o expoete de Lyapuov é somete a média do logaritmo atural do valor absoluto dos potos a trajetória e costitui uma medida da divergêcia expoecial (λ > 0) ou da cotração (λ < 0). Este é o cálculo do expoete de Lyapuov para uma úica codição iicial [3]. No limite o expoete de Lyapuov ão deve mais depeder da codição iicial θ i. Com efeito, quado se itera um mapa ifiitas vezes acaba-se por visitar todo o atrator, ão importado qual o poto de partida. No etato, a pratica trabalha-se sempre com fiito. É portato ecessário calcular-se o expoete de Lyapuov médio, o qual é calculado para algumas codições iiciais e em seguida a média etre eles. Em mapas p-dimesioais tem-se
25 7 p expoetes de Lyapuov que correspodem às p direções liearmete idepedetes do espaço de fases as quais o elemeto de volume iicial pode se expadir ou cotrair. Para verificar que o mapa circular as regiões acima de κ = sobre a difusão dos potos da trajetória são realmete caóticas, deve-se calcular o expoete de Lyapuov para a trajetória. Coforme a equação (.4), o cálculo do expoete de Lyapuov para o mapa circular (uidimesioal) é imediato λ = lim l f ( θi). (.5) i= 0 A figura.7 (a) mostra o expoete de Lyapuov para o mapa circular, calculado em fução de κ correspodete ao diagrama da figura.6 (a) e valor de ω = 0, Note que o valor do expoete é positivo em algumas regiões acima de κ =, as quais são caóticas. A figura.7 (b) mostra o expoete de Lyapuov para o diagrama da figura.6 (b), ode as regiões quase-periódicas geram um expoete igual a zero. Assim, pode-se usar o expoete de Lyapuov para distiguir comportameto quase-periódico de comportameto caótico, mostrado que ambos comportametos parecem muito similares o diagrama de bifurcação. (a) (b) Figura.7: O expoete de Lyapuov é represetado graficamete como fução de κ. Em (a) ω = 0,5. Pela comparação desta figura com a Figura.5-(a), percebe-se que o expoete de Lyapuov é egativo para comportameto periódico e positivo para o comportameto caótico. Em (b) ω = 0, Pela comparação desta figura com a Figura.5-(b)percebe-se que o expoete de Lyapuov é zero para o comportameto quaseperiódico. Nas regiões em que λ > i 0, o mapa circular possui uma istabilidade orbital as
26 8 direções associadas, e a solução é caótica associada a um atrator estraho, em razão da depedêcia sesitiva às codições iiciais. Neste caso, após algum tempo, a distâcia etre dois estados iiciais diferetes aumeta. Para uma solução periódica ou quase-periódica os deslocametos ao logo da trajetória ão devem se alterar, correspodedo a um simples deslocameto do poto iicial. Nestes casos, após algum tempo, a distâcia etre dois estados iiciais diferetes permaece costate. Segue portato que o caso de solução periódica ou quase-periódica λ < i 0 as direções perpediculares ao movimeto e λ = i 0 ao logo da trajetória..3.4 Atratores Na mecâica clássica os sistemas diâmicos são separados em duas grades classes: sistemas coservativos e sistemas dissipativos. Os sistemas coservativos são aqueles para o qual o teorema de Liouville é aplicável [39], f f ( θ ) = = 0 (.6) θ i = i A equação (.6) iforma que o volume do espaço de fases ão se cotrai e em se expade, ou aida, a eergia do sistema se coserva. Por outro lado, sistemas dissipativos são aqueles que apresetam atritos iteros que dissipam a eergia de forma a ão coservá-la. Portato a esses sistemas o teorema de Liouville ão é aplicável. Em sistemas diâmicos dissipativos, um cojuto de codições iiciais de órbitas o espaço de fases irá covergir um cojuto ivariate através da evolução o tempo. Tal cojuto trasiete pode ser um poto, curva, área e assim por diate, e é deomiado atrator [,5,38]. O cojuto de codições iicias que são atraídas para o atrator é deomiado bacia de atração. Geericamete, cada atrator é iteiramete rodeado o espaço de fases por sua própria bacia de atração. Coseqüetemete todos os movimetos trasietes iiciados em uma pequea vizihaça ao redor do atrator move-se assitoticamete de volta para ele, torado-se assitoticamete estável o setido de Lyapuov. Um atrator estraho pode ser visto como resultado da combiação de dobras com um úmero ifiito de expasões em pelo meos uma direção e cotrações em outras direções. Como coseqüêcia, é extremamete difícil, seão impossível a prática, seguir a evolução de um fluxo caótico quado a
27 9 divergêcia das trajetórias sobre o atrator tora-se rápida. (a) (b) (c) Figura.8: Atratores do mapa circular para ω = 0,75 e diferetes valores de κ (a) κ =,63 atrator tipo poto fixo, (b) κ =,65 atrator tipo duplo ciclo e (c) κ = 3,9, atrator tipo estraho. Atratores só são possíveis em sistemas dissipativos. Foram calculados umericamete atratores do mapa circular para ω = 0,75 e diferetes valores de κ, mostrados a figura.8. Na figura.8 (a) κ =,63, é possível otar que os valores de θ covergem para um úico poto, caracterizado o atrator como poto fixo. Na figura.8 (b) κ =,67, os valores de θ covergem para dois potos, caracterizado o atrator como duplo ciclo. Na figura.8 (c) κ = 3,94, os valores de θ ão possuem padrões de repetição, caracterizado o atrator como estraho. Um atrator é chamado caótico quado as trajetórias depedem sesitivamete das codições iiciais. Essa depedêcia sesitiva às codições iiciais tem coseqüêcias práticas. Com efeito, um atrator estraho potos iicialmete próximos estarão expoecialmete separados depois de um itervalo de tempo suficietemete logo.
28 0 Por outro lado, um sistema diâmico dissipativo as soluções geram elemetos de volume que se cotraem de maeira que a diâmica tede a uma região limitada do espaço de fases. Sistemas que exibem atratores estrahos podem apresetar oscilações irregulares ou caóticas..3.5 Atrator Caótico em Crise Crise é um eveto de bifurcação o qual o atrator caótico e sua bacia de atração desaparecem ou repetiamete expadem seu tamaho [40,4,4]. Quado o atrator caótico é destruído, o tipo de crise é chamada crise de froteira. A repetia expasão do atrator caótico é chamada crise iterior. Em ambos os casos a crise ocorre porque um poto fixo istável colide com o atrator caótico quado algum parâmetro de cotrole é mudado. Na crise de froteira, o poto fixo istável está a froteira da bacia de atração do atrator caótico, e a colisão marca a destruição do atrator e sua bacia para valores do parâmetro imediatamete acima do valor crítico da colisão. As órbitas que perteciam ao atrator habitam caoticamete ao redor da velha região do atrator durate um certo tempo trasiete, e em seguida divergem para o ifiito. Na crise iterior, a colisão do poto fixo istável com o atrator caótico ocorre o iterior da bacia de atração do atrator, e uma expasão do atrator caótico ocorre devido às órbitas sobre ele serem repelidas pelo poto fixo istável, e passam a habitar regiões do espaço de fases que aida ão eram habitadas. (a) (b) Figura.9: Em (a) diagrama de bifurcação para o mapa circular seo. Os valores de κ são dados ao logo do eixo horizotal e ω =,. O valor das codições iiciais é zero. Note que uma bifurcação pouco ates de κ = dá origem a dois ramos istáveis (vermelho) e um ramo estável (azul). Em (b) colisão do atrator caótico com um dos ramos istáveis, ele repetiamete expade seu tamaho, em um eveto de crise iterior.
29 No diagrama de bifurcações.9 para o mapa circular, é possível otar que para os valores iiciais de κ o movimeto é quase-periódico. O movimeto se tora periódico devido a uma bifurcação pouco ates de κ =, que dá origem a dois ramos istáveis ilustrados em vermelho, e um ramo estável ilustrado em azul. Coforme o valor de κ aumeta, ocorrem mais bifurcações, origiado um atrator caótico. Quado um dos ramos istáveis se choca com o atrator caótico, este repetiamete expade seu tamaho. Note que, devido ao mapa circular ser cosiderado mod [], o atrator caótico possui duas badas. O ramo istável que se choca com o atrator caótico, se localiza etre as duas badas do atrator. Dessa forma, a colisão do poto fixo istável com o atrator caótico ocorre detro da bacia de atração do atrator, e o eveto ocorrido foi uma crise iterior.
30 Capítulo 3 Mapa Circular e Quase-Periodicidade O ceário de quase-periodicidade apreseta uma competição etre duas ou mais freqüêcias idepedetes que caracterizam as diâmicas do sistema. Se a razão etre as freqüêcias é um úmero racioal tem-se travameto de freqüêcia o sistema, por outro lado, se a razão é um úmero irracioal, o comportameto do sistema é quase-periódico. Neste capítulo será visto o feômeo de travameto de freqüêcia para o mapa circular, o qual é cosiderado uma ferrameta padrão para a ivestigação de rota quase-periódica para o caos. 3. Quase-periodicidade e seções de Poicaré A competição etre duas ou mais freqüêcias pode ocorrer em dois tipos de sistemas, a saber. Primeiro, em um sistema ão liear com uma freqüêcia de oscilação atural, guiado por uma força periódica extera. Devido à ão liearidade, a freqüêcia de oscilação atural geralmete depede da amplitude das oscilações. Neste caso, a competição é etre a freqüêcia exteramete aplicada e a freqüêcia de oscilação atural. Segudo, em sistemas ão lieares que espotaeamete desevolvem oscilações em duas (ou mais) freqüêcias quado algum parâmetro do sistema é variado. Neste caso, há uma competição etre as diferetes freqüêcias do próprio sistema [43]. O comportameto de um sistema com duas freqüêcias pode ser descrito por trajetórias cofiadas a a superfície de um toro [3]. Uma freqüêcia, chamada F, é associada com o movimeto de trajetórias ao redor da grade circuferêcia do toro, a outra freqüêcia, F, é associada com o movimeto ao redor de pequeas seções de cruzametos do toro. Se uma seção de Poicaré é escolhida, tal que corte através do toro, etão chega-se à seguite descrição dos potos de itersecção de Poicaré para diferetes valores da razão de freqüêcia p/q: Deixe T = /F ser o período de tempo para uma volta ao redor da circuferêcia exterior do toro, e T = /F ser o período para uma volta ao redor da pequea seção de cruzameto. Desde que a razão da freqüêcia é p/q, a razão dos períodos é
31 3 T = T p q (3.). Por exemplo, se p/q = /3, etão o tempo para girar ao redor da pequea seção de cruzameto é 3, e o tempo para girar ao redor da grade circuferêcia é. (a) (b) (c) p/q = /3 p/q = 3/5 p/q = irracioal Figura 3.: Em (a) seção de Poicaré para uma trajetória com razão de freqüêcia igual a :3. A trajetória periódica começa em poto 0, etão bate o poto, e fialmete chega o poto 3 ode começou. Em (b) seção de Poicaré para uma trajetória periódica com razão de freqüêcia igual a 3:5. Em (c) seção de Poicaré para uma trajetória quase-periódica com razão de freqüêcia irracioal. A Figura 3. mostra os potos de itersecção de Poicaré para três razões de freqüêcias diferetes. Na figura 3. (a) As trajetórias começam o poto do marco 0. Depois de um tempo ao redor da grade circuferêcia do toro, o poto da trajetória regressa ao plao de Poicaré, seguido o setido horário da figura, a trajetória tem viajado /3 do camiho ao redor da pequea seção de cruzameto durate este tempo. Por isso, ela chega ao poto marcado o diagrama. Depois de mais uma viagem ao redor do lado de fora do toro, o poto da trajetória é 4/3 do camiho ao redor e chega o poto. Fialmete, depois de três vezes ao redor de outra circuferêcia, o poto da trajetória é 6/3 do camiho e chega o seu poto de iício. Dessa forma, a trajetória completou voltas ao redor da grade circuferêcia do toro, e itersectou a pequea seção de cruzameto em três potos diferetes, daí a razão :3. A seqüêcia dos potos de itersecção de Poicaré para uma razão de freqüêcia de 3:5 é mostrada a figura 3. (b), e para uma razão irracioal é mostrada a figura 3. (c). Se a razão de freqüêcia for F /F = p/q, a trajetória sobre o toro fecha-se depois de q ciclos, e a seção de Poicaré cosistirá de q potos. Se a razão p/q for um úmero
32 4 irracioal, os potos a seção de Poicaré uca irão repetir, e os potos evetualmete se acumulam ao redor da curva, cobrido o plao de Poicaré. 3. Número de Rotação Em um oscilador ão liear com duas freqüêcias de oscilação F e F, a razão etre essas freqüêcias é chamada úmero de rotação [3]: F F ρ = (3.). O termo úmero de rotação vem da geometria do espaço de estados das trajetórias girado ao redor de um toro. O úmero de rotação ρ diz quato tempo a trajetória gira ao redor da pequea seção de cruzameto do toro cada vez ao redor da grade circuferêcia do toro. Se o úmero de rotação é racioal o comportameto do sistema é periódico. Se o úmero de rotação é irracioal o comportameto do sistema é quase-periódico. O úmero de rotação para o mapa circular da equação (.5) é defiido por [3]: f ( ) ( θ0) θ0 ρ = lim (3.3) ode f () (θ) é a -ésima iterada da variável θ do mapa circular. O cálculo de (3.3) é idepedete do valor da codição iicial θ 0 e é efetuado sem admitir θ mod []. Este cálculo represeta o limite da razão etre a distâcia agular percorrida e o úmero de iterações, ou seja, o úmero de rotação correspode ao aumeto médio da fase por uidade de tempo. O limite é icluído para elimiar qualquer comportameto trasiete. O úmero de rotação para o mapa liear da equação (.4) é defiido por: ω + θ0 θ0 ρ = lim = ω. (3.4) Dessa forma, para o mapa liear da equação (.4) ρ = ω. No etato, para fuções ão lieares, ρ e ω serão geralmete diferetes.
33 5 3.3 Travameto de Freqüêcia Travameto de freqüêcia (ou sicroização de freqüêcia) é um feômeo comum sempre que dois ou mais osciladores iteragem ão liearmete. Se o úmero de rotação é racioal sobre algum itervalo de valores do parâmetro de cotrole, etão os dois osciladores estão um estado de travameto de freqüêcia. Uma freqüêcia é travada como sedo um úmero racioal vezes a outra freqüêcia [3]. Aalisado o mapa circular em κ <, há potos fixos com travameto de freqüêcia 0:, :, :, e assim por diate, os quais ocorrem para algum itervalo de valores do parâmetro ω. Quado ρ é igual à razão 0:, sigifica que a trajetória sobre o toro possui período e completa 0 ciclos por período, isto é, a trajetória ão gira ao redor de toda a seção de cruzameto do toro, e correspode ao úico poto a seção de Poicaré. Dessa forma, de acordo com a equação (.8), para um valor específico de κ haverá um poto fixo para um itervalo de valores de ω em 0 ω κ/π, ode o úmero de rotação defiido pela equação (3.3) é igual a 0: [3]. Quado ρ é igual à razão :, sigifica que a trajetória sobre o toro possui período e completa ciclo por período, isto é, a cada volta completa o toro a trajetória passa pelo mesmo poto úico a seção de Poicaré. Deste modo, para determiar o itervalo de valores do parâmetro ω ode ocorre travameto de freqüêcia a razão de :, é ecessário levarse em cota que está sedo medido âgulos de modulo. Assim, um poto fixo pode ocorrer se [3]: κ θ + = θ + ω se(πθ). (3.5) π isto é, π se (πθ) = ( ω ). (3.6) κ Isto leva à codição κ ω. (3.7) π
34 6 Portato, de acordo com a equação (3.7), para um valor específico de κ haverá um poto fixo para um itervalo de valores de ω em κ/π ω, ode o úmero de rotação defiido pela equação (3.3) é igual a :. Em ambos os itervalos de travameto de freqüêcia 0: e :, coforme κ se aproxima de, o itervalo de valores de ω sobre o qual ocorre travameto de freqüêcia aumeta. A figura 3. (a) mostra a evolução das iterações do mapa circular com κ = 0,79 e ω = 0,5. Note que a órbita habita em um ciclo de dois valores correspodete a sicroização de freqüêcia :, isto é, a órbita é periódica com período. A figura 3. (b) mostra que esses dois valores do ciclo correspodem aos potos fixos estáveis da seguda iterada do mapa circular ilustrados em vermelho, os quais ocorrem quado θ + cruza com a fução idetidade (reta icliada de 45 ). Coforme κ aumeta, a extesão dos valores de ω para o qual ocorre a sicroização de freqüêcia : também aumeta. Embora ão seja possível ecotrar a extesão de sicroização de freqüêcia : aaliticamete, é fácil de se ecotrar umericamete para um dado valor de κ. Para isso, é ecessário apeas ecotrar a extesão dos valores de ω que dão os potos fixos para f (). (a) (b) Figura 3.: Em (a) o mapa circular seo é mostrado com κ = 0,79 e ω = 0,5. O gráfico uma órbita correspodete à sicroização de freqüêcia :. Em (b), a seguda iterada do mapa circular é mostrada e os potos em vermelho idicam que os dois valores do ciclo correspodem aos dois potos fixos estáveis da seguda iterada da fução localizados próximos de 0,06 e 0,55. A figura 3.3 mostra a evolução das iterações do mapa circular com κ = 0,95 e ω = 0,34. Note que a órbita habita em um ciclo de três valores correspodete a sicroização de freqüêcia :3, isto é, a órbita é periódica com período 3. A figura 3.3 (b) mostra que esses três valores do ciclo correspodem aos potos fixos estáveis da terceira iterada do mapa circular ilustrados em vermelho, os quais ocorrem quado θ +3 cruza com a fução
35 7 idetidade (reta icliada de 45 ). Coforme κ aumeta, a extesão dos valores de ω para o qual ocorre a sicroização de freqüêcia :3 também aumeta. (a) (b) Figura 3.3: Em (a) o mapa circular seo é mostrado com κ = 0,95 e ω = 0,34. O gráfico uma órbita correspodete à sicroização de freqüêcia :3. Em (b), a terceira iterada do mapa circular é mostrada e os potos em vermelho idicam que os três valores do ciclo correspodem aos três potos fixos estáveis da terceira iterada da fução localizados próximos de 0,33, 0,54, 0,9. (a) (b) Figura 3.4: Em (a) o mapa circular seo é mostrado com κ = 0,87 e ω = 0,8. O gráfico uma órbita correspodete à sicroização de freqüêcia :4. Em (b), a quarta iterada do mapa circular é mostrada e os potos em vermelho idicam que os quatro valores do ciclo correspodem aos quatro potos fixos estáveis da quarta iterada da fução localizados próximos de 0,05, 0,9, 0,43, 0,66. A figura 3.4 mostra a evolução das iterações do mapa circular com κ = 0,87 e ω = 0,8. Note que a órbita habita em um ciclo de quatro valores correspodete a sicroização de freqüêcia :4, isto é, a órbita é periódica com período 4. A figura 3.3 (b) mostra que esses quatro valores do ciclo correspodem aos potos fixos estáveis da quarta iterada do mapa circular ilustrados em vermelho, os quais ocorrem quado θ +4 cruza com a fução
36 8 idetidade (reta icliada de 45 ). Coforme κ aumeta, a extesão dos valores de ω para o qual ocorre a sicroização de freqüêcia :4 também aumeta. A sicroização de freqüêcia p:q ocorre quado a q-ésima iterada do mapa cruza a liha de 45º. Para maiores valores de q, a amplitude da parte oscilatória da fução dimiui; por isso, a extesão dos valores de ω para o qual a sicroização de freqüêcia p:q ocorre fica meor coforme q aumeta. 3.3 Líguas de Arold A largura dos itervalos em que ocorre travameto de freqüêcia pode ser estudada como fução do parâmetro de ão liearidade κ. O diagrama esboçado o plao κ-ω desses itervalos formam algumas séries de triâgulos estreitos levemete distorcidos, cohecidos como líguas de Arold []. Cada lígua represeta a região o espaço dos parâmetros associado a um particular úmero de rotação; a lígua associada ao úmero de rotação p/q deomia-se lígua-p/q. Detro das líguas o comportameto é periódico. Nas regiões fora das líguas o comportameto é quase-periódico. As líguas de Arold foram calculadas para o mapa circular da seguite maeira. Primeiro, foram determiados os valores dos úmeros de rotação p/q a serem esboçados o plao κ-ω. Em seguida, foram iterados 3,4 0 8 cojutos diferetes de valores dos parâmetros κ e ω, e calculado o úmero de rotação dado pela equação (3.3) para cada cojuto. Foram plotados os valores dos cojutos que geram úmeros de rotação, cujos valores possuem uma difereça meor ou igual a 0 5 com relação aos valores dos úmeros de rotação p/q escolhidos. Esses cojutos formam as líguas de Arold mostradas a figura 3.5. Para um oscilador ão liear, em geral, a freqüêcia de oscilação depede da amplitude do oscilador de movimeto. Etão, sob codições ormais, esperara-se que a freqüêcia de um oscilador ão liear mude se algum parâmetro do sistema mudar, porque esta mudaça o parâmetro irá mudar a amplitude de oscilação. Sobre esta cosideração, é ecessário um cojuto muito preciso de valores dos parâmetros para coseguir uma razão de freqüêcia particular, dita p/q. Porém, o mapa circular o travameto de freqüêcia em uma mesma razão p/q acotece sobre alguma extesão de valores dos parâmetros. Para o mapa circular cada ρ irracioal correspode a um úico ω. Etretato, existem itervalos fiitos do parâmetro ω os quais o mapa iterado se matém com o mesmo úmero de rotação ρ = p/q racioal e {θ i (κ,ω)} é periódico com período p. Diz-se que a equação se
37 9 trava ou se sicroiza com o úmero de rotação ao logo do itervalo [3]. Figura 3.5: Algumas regiões de travameto de freqüêcia para o mapa circular, chamadas Líguas de Arold. Em κ = 0, a maior parte o eixo ω cosiste de comportameto quase-periódico. Coforme κ aumeta, as regiões de sicroização de freqüêcia se alargam. Acima da liha κ =, as regiões de sicroização de freqüêcia se sobrepõem gerado caos. Coforme κ se aproxima de, o mapa circular possui maiores itervalos dos valores de ω sobre o qual os potos fixos existem, coforme a equação (.8), ou seja, há itervalos maiores de valores de ω para o qual as órbitas cruzam a liha icliada de 45º o gráfico do mapa. Isto sigifica que há um maior úmero de oscilações, e coseqüetemete, maiores itervalos dos valores do parâmetro ω sobre o qual o travameto de freqüêcia ocorre, e as regiões de travameto de freqüêcia se expadem para echer itervalos fiitos ao logo do eixo ω. Em κ = costitui uma liha crítica, ode as líguas de Arold se toram largas o suficiete para se sobreporem. Para κ > a sobreposição das líguas gera mais do que uma freqüêcia possível de oscilação, gerado um comportameto caótico. Fora das líguas as órbitas quase-periódicas remaescetes desaparecem abruptamete, dado origem a órbitas caóticas, e os valores de ω para os quais o sistema apreseta comportameto quaseperiódico toram-se um cojuto de medida ula.
38 Escada do Diabo A fução ρ(ω) forma um diagrama deomiado escada do Diabo: uma fução mootoicamete crescete com patamares de largura fiita para cada racioal ω []. A escada do Diabo foi calculada para o mapa circular da seguite maeira. Primeiro, foram determiados os valores dos úmeros de rotação p/q a serem esboçados o diagrama. Em seguida, foi fixado o valor de κ = e iterados 0 5 valores diferetes de ω e calculado o úmero de rotação dado pela equação (3.3) para cada ω. Foram plotados os valores de p/q como uma fução de ω, para os valores de ω que geram úmeros de rotação, cujos valores possuem uma difereça meor ou igual a 0 5 com relação aos valores dos úmeros de rotação p/q escolhidos. A figura 3.6 mostra a escada do Diabo, ode as frações p/q, idicam o úmero de rotação detro de cada lígua a altura de κ =. Como se pode observar, a estrutura da escada do diabo é auto-similar, isto é, ao ampliar-se cada patamar vê-se uma estrutura similar à aterior. Pode-se, portato, compreeder a desigação escada do diabo : existe um úmero ifiito de degraus etre cada dois degraus. Mas, aturalmete, a maioria dos degraus tem largura ifiitesimal, uma vez que existe uma ifiidade (cotável) deles um itervalo fiito [3]. Figura 3.6: O úmero de rotação ρ = p/q esboçado como fução do parâmetro de freqüêcia ω para o mapa circular seo com κ =. Note que os platôs de travameto de freqüêcia p/q ão mudam para uma substacial extesão de ω. Esses platôs formam a chama Escada do Diabo. Essa estrutura é auto-similar. Do poto de vista da estabilidade estrutural os regimes de quase-periodicidade (p/q
39 3 irracioal) são estruturalmete istáveis; com efeito, uma modificação ifiitesimal o parâmetro de cotrole trasforma-o um regime periódico, ou seja, o sistema etra um dos itervalos com estado travado. Por outro lado, os regimes de travameto (p/q racioal) são estruturalmete estáveis. Para valores de ω que ão correspodem a um platô de travameto, os valores da trajetória devem evetualmete cobrir uma curva completa sobre o diagrama θ + - θ. A fig. 3.7 mostra os resultados da iteração gráfica do mapa circular para parâmetros que geram comportameto quase-periódico. Figura 3.7: Evolução das iterações do mapa circular seo com κ = 0,6 e ω = 0, A codição iicial é 0,5. O comportameto é quase-periódico (sem travameto de freqüêcia). A trajetória evetualmete cobre uma completa extesão dos valores de θ. 3.5 Árvore de Farey Uma observação a figura 3.6 é que os platôs de sicroização de freqüêcia dimiuem em largura (ao logo do eixo ω) quado o deomiador a fração p/q aumeta. Por exemplo, o platô ρ = /4 é meor do que o platô para ρ = /3. No mapa circular seo, diferetes p s, tem a mesma largura para um dado q. Dessa forma, para duas frações racioais p/q e p /q, a fração racioal que está etre elas e tem o meor deomiador é a fração [3,44]: p q + + p. q
40 3 É possível ordear as frações racioais que estão etre 0 e de acordo com o aumeto dos deomiadores pela costrução da árvore de Farey, mostrada a figura 3.8. Para costruir a árvore de Farey, cada ova fração é formada adicioado umeradores e deomiadores de frações racioais, gerado as correspodetes ramificações. Em cada liha horizotal todas as frações tem o mesmo deomiador e correspodem a degraus de sicroização com mesmo tamaho para o mapa circular. A largura dos platôs dimiuem coforme se move para baixo a árvore. A árvore de Farey mostra a ordem e os tamahos relativos dos platôs de sicroização mas ão mostra a duração dos degraus, os quais depedem do valor de κ, a itesidade de ão liearidade. Cotudo, a árvore de Farey sugere uma uiversalidade o comportameto de sicroização de freqüêcia. Figura 3.8: A costrução da árvore de Farey a qual ordea úmeros racioais etre 0 e. Para um determiado valor de ω ρ = p/q, pode-se expressar o travameto de freqüêcia observado que depois de q iterações do mapa circular valor atual mais p, isto é [3,44] f ω, o valor do âgulo é o ( f q ) ω ( θ ) = p + θ. (3.8) Dessa forma, para um valor de ω um pouco maior, o sistema pode possuir travameto de freqüêcia com ρ = p /q, isto é
41 33 ( ) f q ( θ ) = p θ. (3.9) ω + escrever Assim, combiado as duas iterações dadas pelas equações (3.8) e (3.9), pode-se f ( θ )) = p + p ( q) ( q ) ω ( fω + θ. (3.0) Coforme ω aumeta, as iterações do mapa atigem um valor maior do que p + p + θ, devido ao aumeto de f(θ) com ω. O excesso do resultado pode ser compesado dimiuido o valor de ω. Portato, aumetado ω equato ω dimiui simultaeamete, a equação (3.0) que é escrita em termos de ω e ω, pode ser escrita para um úico valor de ω = ω 3, como ( q+ q ) fω ( θ) = p + p + θ. (3.) 3 A equação (3.) diz que existe em um itervalo de valores de ω 3 localizado etre dois itervalos ω e ω (com úmeros de rotação racioais p/q e p /q respectivamete), o qual possui um ovo úmero de rotação (p + p )/(q + q ), coforme ilustrado o diagrama da árvore de Farey. 3.6 Uiversalidade a rota quase-periódica para o caos O mapa circular apreseta comportameto quase-periódico para valores de κ <, quado as razões das freqüêcias são irracioais. O aumeto da itesidade de κ coduz do comportameto quase-periódico ao comportameto caótico [45]. Este tipo de trasição para o caos é caracterizado por dois tipos de uiversalidade a seguir Uiversalidade local Este tipo de uiversalidade está associada com a trasição de quase-periodicidade para o caos para um úmero de rotação irracioal específico, isto é, local. Uma maeira de aproximar um determiado úmero irracioal como uma seqüêcia
42 34 de úmeros racioais é pelo método de frações cotíuas. O úmero irracioal cohecido como média dourada G = ( 5 ) / = 0, pode ser escrito como [3]: G = (3.) Acrescetado frações o deomiador, tem-se a -ésima ordem de aproximação para G, gerado uma seqüêcia de aproximações racioais, chamada seqüêcia trucada, a qual coverge para um úmero irracioal quado. G é chamada a -ésima covergete para G. Uma outra relação de costrução usa a chamada seqüêcia de Fiboacci. A seqüêcia de Fiboacci é defiida usado dois úmeros base F 0 = 0 e F = e a relação de recursão [3,44] + = F + F F, (3.3) isto é, o -ésimo úmero a seqüêcia é igual à soma de dois úmeros ateriores a seqüêcia. Etão, o úmero irracioal média dourada é aproximado pela seqüêcia de Fiboacci por F G = lim. (3.4) F + A trasição de quase-periodicidade para o caos foi observada para o úmero de rotação média dourada, o qual é a base de ivestigação de uiversalidade local para o mapa circular. Na figura 3.5, é possível otar que as larguras das líguas dimiuem para deomiadores grades. A característica uiversal local a ser estudada, evolve valores de ω que dão lugar à seqüêcia de úmeros de rotação (para κ ) que se aproximam da média dourada seguido a seqüêcia de razões de úmeros de Fiboacci dada pela equação (3.4). Para defiir esta uiversalidade, basta itroduzir um valor particular de ω (κ), o qual através
43 35 da equação (3.9) coverge para um úmero de rotação igual à -ésima aproximação da média dourada : F ρ = lim. (3.5) F + Os valores dos parâmetros ω (κ) os quais geram os úmeros de rotação ρ em (3.5) e possuem θ = 0 como um poto a trajetória, tedem para uma costate δ [3,44] ω δ ( κ ) = lim ω ( κ ) ω ( κ ) ω + ( κ ). (3.6) ( κ ) ode, δ ( κ ) =, para κ < δ ( κ ) =, para κ = (3.7-a) (3.7-b) A costate δ forece a razão de difereças sucessivas os valores de ω quado é permitido o úmero de rotação se aproximar do valor média dourada. A figura 3.9 foi calculada para o mapa circular da seguite maeira. Primeiro, foi determiado o valor do úmero de rotação média dourada a ser esboçado o plao κ-ω. Em seguida, foram iterados,8 0 7 cojutos diferetes de valores dos parâmetros κ e ω, e calculado o úmero de rotação dado pela equação (3.3) para cada cojuto. Foram plotados os valores dos cojutos que geram úmeros de rotação, cujos valores possuem uma difereça meor ou igual a 0 6 com relação ao valor do úmero de rotação média dourada. Esses cojutos formam um diagrama mostrado a figura 3.9. Dessa forma, a figura 3.9 mostra os cojutos de valores dos parâmetros κ e ω, os quais geram úmero de rotação irracioal média dourara, ode o limite quado, ω = 0, Coforme o parâmetro de ão liearidade aumeta, o parâmetro ω deve ser balaceado para mater o úmero de rotação ρ fixo para o valor irracioal média dourada, para garatir a quase-periodicidade.
44 36 Figura 3.9: Espaço dos parâmetros para úmeros de rotação irracioal média dourada. dadas por: As distacias d de θ = 0 até o próximo elemeto de um ciclo pertecete a ω (κ) são d F = f ( 0) F ω. (3.8) Essas distâcias são escaladas como d α( κ ) = lim d ( κ ). (3.9) ( ) κ + ode, α ( κ ) =,68... para κ < α ( κ ) =, para κ = (3.0-a) (3.0-b) Os valores de δ(κ) e α(κ) para κ < foram calculados através da equação (3.9), e para κ = foram tirados da literatura [3,44]. Os fatores de escala δ(κ) e α(κ) são costates uiversais para sistemas que apresetam trasição para o caos via quase-periodicidade, e represetam para o mapa circular o mesmo papel que as costates de Feigebaum represetam para o mapa logístico [46].
45 Uiversalidade Global Este tipo de uiversalidade está associada com propriedades uiversais globais para um cojuto de valores de ω que são complemetares às líguas de Arold e correspodem a úmeros de rotação irracioais, descrevedo o comportameto de escala desse cojuto [44]. Dimesão Fractal Fractais são formas geométricas com padrões complexos que se repetem ifiitamete, mesmo limitados a uma região fiita (idepedêcia da escala), e possuem estrutura geométrica auto-similar []. O coceito de dimesão fractal pode ser visto da seguite maeira: seja um cojuto de potos A um espaço de dimesão r. Recobre-se esses potos com hiper-cubos de lado ε. Defie-se dimesão de Hausdorff-Besecovitch ou dimesão fractal como [] log N( ε ) D = lim (3.) ε 0 log(/ ε ) ode N(ε) é o úmero míimo de hiper-cubos de lado ε ecessário para cobrir todo o cojuto de potos A, ou seja, N(ε) varia segudo D ε para ε 0. A dimesão fractal (ou dimesão de Hausdorff), recupera o coceito euclidiao de dimesão iteira e permite a sua geeralização para cojutos mais complexos. No caso de objetos fractais, a dimesão apreseta-se fracioária []. Um dos algoritmos uméricos dispoíveis para o cálculo da dimesão fractal é o algoritmo da cotagem de caixas, o qual faz o uso direto da defiição de dimesão fractal. Neste algoritmo divide-se a região do espaço de fases ocupada pelo atrator em caixas de dimesão ε; itera-se o mapa vezes ( grade) e cotam-se quatas destas caixas, N(ε), têm pelo meos um poto do atrator, repetido o cálculo para diversos valores de ε. D é dada pela icliação do gráfico log N(ε) log /ε. Voltado o assuto para o mapa circular, em κ = devido à sobreposição das líguas de Arold, o cojuto dos valores de ω correspodetes a úmeros de rotação irracioais é um fractal de medida igual a zero. A seguir será descrito o cálculo da dimesão do cojuto dos úmeros de rotação irracioais em κ =.
46 38 Figura 3.0: Largura dos itervalos Δω(p/q) em κ =. Este diagrama é auto-similar. Primeiro foi calculado a largura Δω(p/q) dos itervalos dos valores de ω com travameto de freqüêcia p/q, dos degraus da escada da figura 3.6 o poto crítico κ =, mostrado a figura 3.0. Note que este diagrama é auto-similar. Presume-se que evetualmete Δω(p/q) > 0 para todo p e todo q. Ao icluir mais e mais degraus a escada o eixo ω tora-se mais e mais cheio [,47]. Para ivestigar se os itervalos de sicroização irão ou ão evetualmete cobrir todo o eixo ω, é calculada a largura total S(ε) de todos os degraus que são maiores do que uma escala ε escolhida arbitrariamete. O iteresse é o espaço etre os degraus, S(ε) e sua medida sobre a escala ε para ecotrar o úmero de buracos etre os degraus N(ε) = [ S(ε)]/ε. N(ε) foi calculado para 5 valores de ε escolhidos aleatoriamete e decrescedo sucessivamete o itervalo [0,00; 0,0004]. A figura 3. mostra o gráfico de log N(ε) log (/ε). Os potos formam uma liha reta idicado comportameto de uma lei de potêcia: D N( ε ). (3.) ε
47 39 Figura 3.: Gráfico de log N(ε) log (/ ε) em κ =. A icliação da liha reta forece o valor de D 0,9. Através da icliação da liha reta a Figura 3. foi ecotrado o valor de D 0 = 0,9 ± 0,0048, com um erro percetual de 5,7% do resultado umérico de D = 0,87 ecotrado em [43]. Sabedo que N(ε) = [ S(ε)]/ε, a equação (3.) mostra que quado em ε 0, o espaço etre dois degraus desaparece da seguite forma: S( ε D ε ). (3.3) Neste caso, ão haverá úmeros de rotação irracioais, e coseqüetemete, ão haverá movimeto quase-periódico em κ =, e a escada será chamada completa, ou seja, o espaço etre dois degraus possuirá medida zero. Dessa forma, em κ = o cojuto complemetar dos itervalos dos valores de ω com platô de travameo de freqüêcia (espaço etre os degraus), é etão um cojuto de Cator [,47]. O expoete D represeta a dimesão fractal para esse cojuto de Cator. A dimesão pode ser cosiderada uma maeira útil de caracterizar as propriedades de escada o poto crítico, pois D é o expoete característico para o sistema a trasição de quase-periodicidade para o caos, é uiversal para uma grade classe de fuções. Espectro de estrutura multifractal Muitos fractais ão são homogêeos em sua ivariaça de escala, sedo mais complexos e com medida associada bastate irregular, são os chamados multifractais. O
48 40 coceito de dimesão fractal é isuficiete para caracterizar toda a riqueza da estrutura de um cojuto multifractal. A caracterização completa dos multifractais exige um cojuto ifiito de dimesões: as dimesões geeralizadas de Reyi defiidas como [] N ( ε ) q log pi i= D q = lim. q ε 0 log ε (3.4) ode q pertece ao cojuto de úmeros reais e varia de a +, p i é a fração de potos que estão a i-ésima caixa após iterações do mapa, equato N(ε) é o úmero de caixas ecessárias para cobrir todo o atrator. A difereça etre as ifiitas dimesões D q mede o grau de ão-homogeeidade do atrator. Quado D q D q, q q, diz-se que o atrator é um multifractal. O ídice q faz o papel de uma lete com a qual observa-se o cojuto. Quado q as regiões mais desas do atrator são realçadas. Iversamete, quado q são as regiões mais rarefeitas que se destacam. Dessa forma, o úmero real q serve para caracterizar o subcojuto de sigularidades que determia D q. Os multifractais são estatisticamete auto-similares e obedecem a uma lei de escala múltipla, ode os expoetes são fuções que variam cotiuamete []. Uma dessas fuções é o chamado espectro de sigularidades f(α), defiido a seguir. A descrição dos multifractais em termos do espectro de sigularidades, permite-se falar em termos de uma uiversalidade global os sistemas diâmicos caóticos, sigificado que uma órbita o espaço de fases tem uma uiversalidade métrica como um todo. Ou seja, atratores estrahos multifractais devem ser caracterizados por um cojuto de medidas fractais, sigulares em cada poto, que por sua vez são caracterizadas pelas suas sigularidades. A fução f(α) caracteriza a distribuição estática de potos o atrator e é uiversal para atratores gerados por sistemas diâmicos caóticos semelhates. Multifractais podem ser etedidos como a iterligação de diferetes cojutos cada um caracterizado por uma sigularidade α diferete, e portato, por uma dimesão de Hausdorff f(α) diferete []. Na literatura é mostrado que a fução f(α) se relacioa com as dimesões geeralizadas de Reyi por meio de uma trasformação de Legedre []: f ( α ) = qα ( q ) (3.5) D q
49 4 e portato α ( q) = [( q ) Dq ]. (3.6) q A fução f(α) foi calculada para o mapa circular segudo as seguites etapas: foi ajustada uma curva aos potos previamete calculados de D q (q). Em seguida foi determiado o grau do poliômio da curva D q (q). Foi calculada a derivada da equação (3.6) resultado a expressão para α(q), e os valores de α(q) ecotrados para cada q foram substituídos a equação (3.5), para fialmete obter a curva f(α). No mapa circular, em κ = e úmero de rotação irracioal média dourada o parâmetro ω coverge para ω = 0, A fução D q (q) associada ao mapa circular para estes valores dos parâmetros, foi calculada através do método da cotagem de caixas, ode recobriu-se o espaço de fases com caixas de tamaho ε, cada uma com ídice i. Foram etão calculadas as probabilidades Ni pi (ε ) =, (3.7) N ode N i é o úmero de potos detro da caixa i, para = 0 5 iterações. O cálculo foi repetido para 0 valores de ε variado o itervalo [0,; 0,00], e costruído o gráfico log i [ p ( ε )] i q log ε para cada q. Os potos desse gráfico formaram uma reta cuja icliação é igual a (q ) D q. O cálculo foi repetido para 60 valores de q, resultado a curva D q (q) mostrada a figura 3.. Na figura 3. é possível otar que a curva D q (q) é uma fução sigmoidal, se ecaixado o modelo de Boltzma. Os cálculos uméricos realizados foreceram A A D ( q) = A +. q + e q q0 dq (3.8) ode A =,87993, A = 0,63837, q 0 =,908 e dq =,884.
50 4 Figura 3.: Gráfico das dimesões geeralizadas D q como uma fução de q para o mapa circular, com κ = e úmero de rotação igual à média dourada. Cohecedo-se a fução D q (q), foi calculada umericamete a derivada da equação (3.6), resultado a fução α(q): q q 0 dq ( A A)e ( q) = q q0 dq ( q ) A A α + A +. + e dq + e q q 0 dq (3.9) Figura 3.3: Gráfico da distribuição f(α) para o mapa circular, com κ = e úmero de rotação igual à média dourada.
51 43 Através da equação (3.9), foram calculados os valores de α(q), os quais foram substituídos a equação (3.5). O cálculo foi repetido para cada valor de q mostrado a figura 3., gerado a curva f(α) mostrada a figura 3.3. No espectro f(α), o maior valor de α correspodete à região meos desa de forma que o lado de pequeos valores de α a curva f(α) correspodem a valores de q positivo e altos valores de α correspodem a valores de q egativo. Coforme já mecioado, as distacias ao redor de θ = 0 escalam por um fator uiversal dado pela equação (3.0-b). Dessa forma, a região mais rarefeita pode ser expressada aaliticamete como: α l G l β = max =, (3.30) ode β =,885, o fator de escala a vizihaça de θ = 0 para o mapa circular seo [3]. Na outra extremidade, o meor valor de α correspode à região mais desa é expressada como: α l G l β = mi = 3 0, (3.3) O pico da distribuição ocorre em f(α) =, e correspode ao valor de q = 0. Sistemas diâmicos que obedecem uma rota para o caos através de quaseperiodicidade podem ser represetados por uma mesma fução uiversal f(α).
52 Capítulo 4 Sicroização de fase em mapas circulares acoplados Ivestigações teóricas a diâmica de sistemas ão-lieares revelaram a existêcia do feômeo de sicroização de fase em osciladores caóticos acoplados. Neste feômeo os osciladores oscilam em fase quado o acoplameto supera a difereça das freqüêcias aturais, ajustado os ritmos das oscilações e os osciladores mutuamete etram em uma freqüêcia travada (ou sicroizada). Neste capítulo serão apresetados a sicroização de fase de dois mapas circulares acoplados ão liearmete, os efeitos de trasição para o comportameto sícroo, sob quais codições esse comportameto é possível e os efeitos de trasição para o comportameto ão sícroo. 4. Mapas circulares acoplados Coforme já mecioado, a variável θ o mapa circular pode ser defiida por um âgulo que especifica ode a trajetória está a seção de Poicaré de um movimeto o espaço de fases sobre um toro. Quado há sobre um toro duas trajetórias ão idêticas, elas se toram ão idepedetes quado iteragem fracamete etre si. Para isso, basta acoplar as duas trajetórias. Pode haver diferetes formas de iteração, ou acoplameto etre dois osciladores. Basicamete pode-se dividir as formas de acoplameto em duas classes: acoplameto uidirecioal e acoplameto bidirecioal [33,36]. No acoplameto uidirecioal somete um dos sistemas recebe a ifluêcia do outro, um sistema com este tipo de acoplameto é chamado mestre-escravo. Isto implica que o sistema escravo segue a diâmica do sistema mestre, e a diâmica do sistema escravo é alterada pela ifluêcia do sistema mestre, porém, o iverso ão ocorre, isto é, o sistema mestre evolui de forma isolada. Já o acoplameto bidirecioal ambos os sistemas são acoplados um com o outro, de forma a ocorrer um itercâmbio de iformações etre eles, e a costate de acoplameto iduz um ajustameto dos ritmos, gerado um mútuo comportameto sícroo.
53 45 como: Um sistema de dois mapas circulares acoplados bidirecioalmete pode ser descrito θ θ + + = θ = θ κ ε ε + ω se(πθ ) se(πθ ) + se(πθ ) π π π. (4.) κ ε ε + ω se(πθ ) se(πθ) + se(πθ ) π π π ode há duas variáveis de fase θ e θ, ω e ω são as freqüêcias ão perturbadas, κ é o parâmetro de cotrole ão liear do sistema possuido o mesmo valor em ambas as equações e ε é o parâmetro de acoplameto. Quado o acoplameto é zero, o sistema se tora dois mapas circulares idepedetes. Um sistema de dois mapas circulares acoplados é geralmete imagiado como um simples paradigma para dois pêdulos caóticos acoplados ou dois osciladores acoplados. Os potos fixos para o sistema (4.) correspodem aos valores que satisfazem a equação θ θ κ ε ε = θ + ω se(πθ ) se(πθ ) + se(πθ ) π π π κ ε ε = θ + ω se(πθ ) se(πθ ) + se(πθ ) π π π (4.) equivalete a se(πθ se(πθ π ( ωε ωκ + ωε ) ) = κ ( κ ε ). (4.3) π ( ωκ ωε ωε ) ) = κ ( κ ε ) Dessa forma, se κ ( κ ε ) π ( ω ε ωκ + ω e κ κ ε ) π ( ω κ ω ε ω ε ( ε ) ) (4.4-a) (4.4-b)
54 46 etão haverá pelo meos um poto fixo para o sistema, que pode ser calculado aaliticamete. De modo aálogo ao mapa idividual, os potos fixos que podem ser calculados aaliticamete ocorrem somete para certas combiações de κ, ω, ω e ε. Se houver potos fixos, etão pode-se examiar sua estabilidade através dos autovalores λ e λ da matriz jacobiaa utilizado a equação de autovalores [] J λ I = 0, (4.5) ode I é a matriz idetidade e J é a matriz jacobiaa do sistema dada por []: J = κ cos(πθ ) + ε cos(πθ ) ε cos(πθ ) κ cos(πθ ε cos(πθ ) ) + ε cos(πθ. (4.6) ) 4. Expoetes de Lyapuov Coforme foi visto o capitulo deste trabalho, os expoetes de Lyapuov forecem uma medida de depedêcia sesitiva às codições iiciais, ou seja, a taxa média de divergêcia das trajetórias. Em um mapa bidimesioal tem-se dois expoetes de Lyapuov que correspodem às duas direções liearmete idepedetes do espaço de fases as quais o elemeto de volume iicial pode se expadir ou cotrair. Os expoetes de Lyapuov para o sistema (4.) são defiidos por [] λ, = lim l Λ,, (4.7) ode os Λ, são os módulos dos autovalores da matriz M defiida por M = i= J (θ r ), (4.8) i e os J ( θ r i ) são as matrizes Jacobiaas defiidas pela equação (4.6), calculadas o poto θ r i da trajetória. O cálculo dos expoetes de Lyapov λ, a partir de (4.7) e (4.8) apreseta algus problemas. Em geral, mesmo para um úmero pequeo de iterações, os elemetos da matriz
55 47 M toram-se muito grades, causado problemas de overflow que iviabilizam o cálculo umérico. O algoritmo descrito a seguir cotora tais problemas e, de modo aálogo ao caso uidimesioal, o calculo os expoetes λ, é reduzido a uma média simples. O maior problema é calcular o produtório M r r r r = J ( θ ) = J ( θ ) J ( θ )... J ( θ ) J J... J, (4.9) i= i e os autovalores associados. Coforme demostrado a literatura [], é possível trasformar M um produto de matrizes triagulares. Como o produto de matrizes triagulares é também uma matriz triagular e os autovalores de uma matriz triagular são seus elemetos diagoais, pode-se, dessa maeira, cotorar as dificuldades que o cálculo direto do produtório que (4.9) apreseta. Coforme também demostrado a literatura [], uma matriz J qualquer pode ser escrita como o produto de uma matriz ortogoal O e uma matriz triagular T: J = OT, J O = OT i i i i, (4.0) o que é equivalete a J = OT, i = OT i ioi J. (4.) O produtório (4.9) pode etão ser escrito como J( θ r i ) = OTO O T O... OT = OTT... T. (4.) i= Na literatura [] é demostrado que a matriz ortogoal O ão participa do cálculo. Como o produto de matrizes triagulares é uma matriz triagular e seus autovalores são os próprios elemetos de sua diagoal, tem-se para grade i= r J ( θ i ) = Ti = i= e λ 0 e... λ (4.3)
56 48 ou seja, λ = lim l Λ λ = lim l Λ = lim = lim i= i= l T l T (4.4) ode T e T são os elemetos diagoais e da matriz triagular T i. Uma matriz geérica ortogoal em duas dimesões é cosθ seθ O =. seθ cosθ Sabe-se que J = OT. Como O é ortogoal, O = O T, etão T T = O J (4.5) Dessa forma, T pode ser obtido a partir de (4.5). Escreve-se a matriz triagular T que se quer determiar como a c T =. (4.6) 0 b Substituido as equações (4.6) e (4.6) a (4.5), o elemeto ulo da matriz T forece 0 = [ κ cos(πθ ) + ε cos(πθ )] se θ + [ ε cos(πθ )] cosθ, (4.7) ou seja, ε cos(πθ ) tg θ =. (4.8) + κ cos(πθ ) ε cos(πθ ) Uma vez obtido θ, e portato a matriz O, a matriz T = O T J fica completamete determiada, e calcula-se a, b e c. O produto T T -... T pode ser escrito como
57 49 a ( ) a ( )... a() = 0 etc., (4.9) b ( ) b ( )... b () e coseqüetemete Λ = a ) a ( )... (), ( a = b ( ) b ( )... b Λ (), (4.0) são os autovalores de J ( θ r ) e os expoetes de Lyapuov coforme a equação (4.7). i= i 4.3 Sicroização de Fase A sicroização de siais periódicos é um feômeo bem cohecido a física, egeharia e outras áreas. Sistemas caóticos também podem ser coectados de uma forma que suas oscilações sejam sicroizadas [7,8,33]. A sicroização completa é a forma mais simples de sicroização em sistemas caóticos. Ela cosiste de uma superposição perfeita de trajetórias caóticas de dois ou mais sistemas acoplados, de tal maeira que as trajetórias se matém iguais uma com a outra o trajeto ao logo do tempo, ou seja, há uma completa coicidêcia dos estados idividuais dos sistemas. Neste caso, as fases e as amplitudes são as mesmas. Este mecaismo foi primeiramete mostrado para ocorrer quado dois sistemas caóticos idêticos acoplados possuem expoetes de Lyapuov todos egativos. Sistemas oscilatórios caóticos ão idêticos podem atigir um regime itermediário de sicroização, o qual as fases são sicroizadas equato as amplitudes permaecem diferetes. Esse feômeo é chamado sicroização de fase, a qual pode ser cosiderada como sedo uma forma mais fraca de sicroização do que a sicroização completa. Na sicroização de fase os sistemas acoplados oscilam em fase. No movimeto de sicroização de fase a difereça das fases é limitada em um itervalo fiito, equato o movimeto ão sícroo correspode a um crescimeto ilimitado da difereça de fase. Dessa forma, sicroização de fase de dois osciladores caóticos fracamete acoplados pode ser descrita como a diâmica da difereça de fase [33] φ = m θ m θ, (4.)
58 50 ode m e m são iteiros, θ e θ são as fases dos sistemas iteragido e m : m é a razão do travameto das fases, ou a ordem de sicroização. Isto sigifica que m períodos de θ correspodem a m períodos de θ, isto é, equato θ realiza m oscilações, θ realiza m oscilações. A codição de sicroização de fase é a existêcia de um platô de φ suficietemete logo. Como um resultado de sicroização de fase, oscilações caóticas ão idêticas possuem as fases travadas uma com a outra através de um fraco acoplameto. Quado m e m são diferetes de, diz-se que tem uma sicroização de fase imperfeita. Para ivestigar este tipo de sicroização, uma variável de fase, bem defiida, deve ser idetificada em ambos os sistemas acoplados. A sicroização m : m pode ser também caracterizada pela razão das fases de cada oscilador, isto é, pela razão dos úmeros de rotação idividuais: ρ ρ w =, (4.) ode ρ, correspodem aos úmeros de rotação calculados através da equação (3.). 4.4 Trasição para sicroização de fase Na trasição para o regime de sicroização de fase, os osciladores acoplados que oscilavam com fases diferetes mutuamete passarão a oscilar com as fases travadas, devido à superação da divergêcia das trajetórias pelo acoplameto [48]. A figura 4. (a) mostra os expoetes de Lyapuov em fução do parâmetro de acoplameto ε, para o sistema (4.) com os valores dos parâmetros ω = 0,, ω = 0, e κ =,5. A figura 4. (b) mostra a razão dos úmeros de rotação w dada pela equação (4.) pela itesidade do acoplameto ε para o sistema (4.) com os mesmos valores de (b). Equato os expoetes de Lyapuov são egativos, o úmero de rotação cresce idefiidamete. Quado um dos expoetes se tora positivo, o úmero de rotação decai bruscamete. Quado o segudo expoete também se tora positivo, são observadas pequeas regiões de sicroização de fase imperfeita. Coforme ε aumeta, uma cosiderável região de sicroização de fase perfeita : é observada. Note que os platôs de sicroização de fase existem apeas quado os dois expoetes de Lyapov são positivos, isto é, quado o sistema é hipercaótico.
59 5 (a) (b) Figura 4.: (a) Expoetes de Lyapuov e (b) úmero de rotação w em fução do coeficiete de acoplameto ε para o sistema (4.) com ω = 0,, ω = 0, e κ =,5. Pequeas regiões de sicroização de fase imperfeita e uma cosiderável região de sicroização : são observadas. A figura 4. (a) mostra o diagrama de bifurcações e a figura 4. (b) mostra o expoete de Lyapuov, ambos em fução do coeficiete de ão liearidade κ para o mapa circular idividual dado pela equação (.5) com ω = 0,. Em (a) é possível otar que para κ =,5 o sistema está em regime regular. Em (b) é possível otar que para κ =,5 o expoete de Lyapuov é egativo, assim como a figura 4. (a) para ε = 0. (a) (b) Figura 4.: (a) Diagrama de bifurcação e (b) expoete de Lyapuov em fução do coeficiete da ão liearidade κ para o mapa (.5) com ω = 0,. É possível otar que para κ =,5 o expoete de Lyapuov é egativo, assim como a figura 4. (a) para ε = 0.
60 5 A figura 4.3 (a) mostra o diagrama de bifurcações e a figura 4.3 (b) mostra o expoete de Lyapuov, ambos em fução do coeficiete de ão liearidade κ para o mapa circular idividual dado pela equação (.5) com ω = 0,. Em (a) é possível otar que para κ =,5 o sistema está em regime regular. Em (b) é possível otar que para κ =,5 o expoete de Lyapuov é egativo, assim como a figura 4. (a) para ε = 0. (a) (b) Figura 4.3: (a) Diagrama de bifurcação e (b) expoete de Lyapuov em fução do coeficiete da ão liearidade κ para o mapa (.5) com ω = 0,. É possível otar que para κ =,5 o expoete de Lyapuov é egativo, assim como a figura 4. (a). Para aalisar o mecaismo de trasição para a sicroização mais precisamete, através da equação (4.3) foram calculados os potos fixos para o sistema (4.) com valores dos parâmetros ω = 0,, ω = 0,, κ =,5 e ε = 0,4, valor do acoplameto um pouco ates de surgir os platôs de sicroização de fase. Foram ecotrados quatro potos fixos, cujas estabilidades foram aalisadas através dos autovalores ecotrados pela equação (4.5). A tabela 4. mostra os potos fixos ecotrados, suas localizações o espaço de fases, seus autovalores, suas classificações e estabilidade de acordo com os autovalores. Uma variedade sobre um espaço de fases pode ser visualizada como uma curva suave formado um cojuto do espaço de fases. Uma variedade ivariate é uma variedade com a codição adicioal de que órbitas iiciado sobre ela permaecem a variedade através do curso de sua evolução diâmica. Em sistemas dissipativos, para um poto fixo tipo sela hiperbólica existem pelo meos duas variedades, sedo dois ramos estáveis e dois ramos istáveis. As variedades estáveis são formadas pelo cojuto de órbitas que se aproximam do poto de sela ao logo da evolução diâmica do sistema [5]. As variedades istáveis são formadas pelo cojuto de órbitas que se afastam do poto de sela, evoluido para o atrator. Um ó hiperbólico istável, por sua vez, possui apeas variedades istáveis.
61 53 Poto Fixo A Localização o espaço de fases θ = 0,4493; θ = 0,8947 Autovalores Classificação Estabilidade λ =,438; λ = 0,3565 poto de sela hiperbólico Istável B θ = 0,35507; θ = 0,053 λ =,6484; λ = 0,756 poto de sela hiperbólico Istável C θ = 0,4493; θ = 0,053 λ = 0,786; λ = 0,775 atrator tipo odo hiperbólico Assitoticamete Estável D θ = 0,35507; θ = 0,8947 λ =,773; λ =,73 repulsor tipo odo hiperbólico Istável Tabela 4.: Potos fixos e suas classificações para o sistema (4.) e os valores dos parâmetros ω = 0,, ω = 0,, κ =,5 e ε = 0,4. O cojuto de coordeadas cartesiaas que defie a cofiguração do sistema, ou seja, as posições das órbitas um dado istate, é chamado de espaço de fases ou espaço de fase. As variedades podem ser obtidas através do mapeameto do sistema o espaço de fases. Primeiro foi calculado aaliticamete a localização do poto fixo o espaço de fases, coforme a tabela 4.. Depois foram calculados os auto-valores e auto-vetores para cada poto hiperbólico. As variedades istáveis foram obtidas a partir da iteração do mapa com pequeos icremetos as compoetes dos auto-vetores, seguido o procedimeto: foi distribuída uma grade com um úmero N de codições iiciais em toro do poto hiperbólico. As dimesões da grade foram da ordem de 0 5. Após 0 iterações os potos já se distribuíam aproximadamete ao logo de duas curvas, as quais são a aproximação para as variedades istáveis do poto hiperbólico. A variedade estável foi obtida seguido o procedimeto: as compoetes do espaço de fases foram divididas em 0 5 partes, resultado em 0 0 codições iiciais diferetes ao logo de todo o espaço de fases, que foram iteradas. Após 0 iterações, foram plotadas as codições iicias que camiham para o poto hiperbólico, as quais são a aproximação para as variedades estáveis do poto hiperbólico. Esse método se chama método do chuveiro. Quado as variedades se ecotram, há classificações dos potos ode há o ecotro. Um poto pertecete à variedade estável de um poto hiperbólico e à variedade istável do mesmo poto hiperbólico, é deomiado poto homoclíico. Um poto pertecete à variedade estável de um poto hiperbólico e à variedade istável de um poto hiperbólico distito, é deomiado poto heteroclíico [5].
62 54 A figura 4.4 mostra o espaço de fases para o sistema de dois mapas circulares acoplados, dado por (4.), para ω = 0,, ω = 0,, κ =,5 e ε = 0,4, com os potos fixos da tabela 4. e suas variedades. O quadrado preto é um repulsor, o círculo é um atrator e as duas cruzes são potos de sela. As lihas verdes são as variedades istáveis do repulsor ó hiperbólico, as lihas em viho são as variedades estáveis do poto de sela A, as lihas vermelhas são as variedades istáveis do poto de sela A, as lihas violetas são as variedades estáveis do poto de sela B e as lihas azuis são as variedades istáveis do poto de sela B. Todas as órbitas que ão se iiciam em alguma das variedades, camiham em direção ao ó hiperbólico estável. As variedades istáveis do ó hiperbólico istável camiham em direção ao atrator, à sela A e à sela B. As trajetórias iiciadas ao logo das variedades istáveis das selas A e B camiham em direção ao ó estável. Figura 4.4: Espaço de fases para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e d = 0,4. O quadrado preto é um repulsor, o círculo é um atrator e as duas cruzes são potos de sela. As lihas verdes são as variedades istáveis do repulsor, as lihas em viho são as variedades estáveis do poto de sela A, as lihas vermelhas são as variedades istáveis do poto de sela A, as lihas violetas são as variedades estáveis do poto de sela B e as lihas azuis são as variedades istáveis do poto de sela B. Coforme o parâmetro de acoplameto ε aumeta, as selas A e B se aproximam do ó estável e do ó istável respectivamete, e em ε = 0,49 eles se ecotram. Apesar de sobrepostos o espaço de fases, as coordeadas dos potos que eram potos fixos, são agora complexas tal como descrito a tabela 4.. A figura 4.5 (a) mostra o espaço de fases próximo
63 55 aos potos fixos em ε = 0,4. A figura 4.5 (b) mostra a sobreposição dos potos que eram fixos em ε = 0,49. No etato, a figura 4.5 merece um estudo mais detalhado. Poto Fixo Localização o espaço de fases θ = 0,37; θ = 0,5 4, ³i θ = 0,37; θ = 0,5 4, ³i 3 θ = 0,3689; θ = 0,5 4, ³i 4 θ = 0,3689; θ = 0,5 4, ³i Tabela 4.: Potos fixos para o sistema (4.) e os valores dos parâmetros ω = 0,, ω = 0,, κ =,5 e ε = 0,49. (a) (b) Figura 4.5: Espaço de fases próximo aos potos fixos para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e (a) ε = 0,4; (b) ε = 0,49. O círculo azul é o atrator, o quadrado verde é o repulsor e as cruzes pretas são as selas A e B. Em (a) os potos fixos matém uma distâcia etre si. Em (b) é possível otar que as selas A e B se sobrepõem com o atrator e o repulsor respectivamete. Após a sobreposição dos potos fixos, imediatamete o sistema passa de regular para caótico, como mostrado a figura 4.6. Em 4.6 (a) o sistema com ε = 0,485 é regular, existido um atrator tipo poto fixo. Após um feômeo de bifurcação sela-ó, o eveto passa a comportar-se caoticamete e perde a estabilidade estrutural, coforme mostrado em 4.6 (b) o sistema com ε = 0,49 é caótico. O sistema permaece caótico para valores de ε > 0,49.
64 56 (a) (b) Figura 4.6: Espaço de fases para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e (a) ε = 0,485; (b) ε = 0,49. Em (a) o sistema é regular com um atrator tipo poto fixo. Em (b) o sistema é caótico. A sicroização de fase para um sistema de dois mapas circulares acoplados ocorre quado ambas as trajetórias do sistema possuem úmeros de rotação racioais. Neste caso, as trajetórias são periódicas. A sicroização de fase represeta a relação etre os períodos das trajetórias. Isto pode ocorrer mesmo quado o sistema é caótico ou hipercaótico. Coforme mostrado a figura 4. (b), quado ε = 0,6 o sistema apreseta um platô de sicroização de fase imperfeita 5:4. A figura 4.7 (a) mostra o espaço de fases para ε = 0,55, quado aida ão há sicroização. Neste caso, o sistema ão possui periodicidade oscilatória. A figura 4.7 (b) mostra o espaço de fases para ε = 0,6, quado há um atrator caótico de ove badas, e coseqüetemete, sicroização de fase imperfeita 5:4. Neste caso, o atrator caótico iduz uma estabilidade para as trajetórias dos dois sistemas acoplados de forma que os sistemas seguem as mesmas trajetórias ao logo das badas do atrator caótico, oscilado sicroizados com uma relação de fase 5:4. Dessa forma, apesar de caótico, o sistema possui periodicidade oscilatória a preseça de um atrator caótico e coseqüetemete, possui sicroização de fase. Coforme o parâmetro de acoplameto ε aumeta, o sistema perde a sicroização de fase 5:4. A figura 4.7 (c) mostra o espaço de fases para ε = 0,69, quado ão há sicroização. A figura 4.7 (d) mostra o espaço de fases para ε = 0,74, quado surge um atrator caótico de oze badas, e coseqüetemete, sicroização de fase imperfeita 6:5. Neste caso, os sistemas seguem as mesmas trajetórias ao logo das badas do atrator caótico, oscilado agora com uma relação de fase 6:5. Aumetado aida mais o parâmetro de acoplameto ε, o sistema perde a sicroização de fase 6:5. A figura 4.7 (e) mostra o espaço de fases para ε = 0,9, quado ão
65 57 há sicroização. A figura 4.7 (f) mostra o espaço de fases para ε = 0,95, quado surge um atrator caótico de duas badas, e coseqüetemete, sicroização de fase perfeita :. Neste caso, os sistemas seguem as mesmas trajetórias ao logo das badas do atrator caótico, oscilado agora com uma relação de fase :. Do poto de vista de sicroização, as lacuas etre as badas do atrator caótico correspodem a deslizametos de difereça de fase θ θ, coforme a figura 4.7 [33,49]. A liha (a) da figura 4.8 correspode à sicroização de fase 5:4, mostrado a figura 4.7 (b). A liha (b) da figura 4.8 correspode à sicroização de fase 6:5, mostrado a figura 4.7 (d). A liha (c) da figura 4.8 correspode à sicroização de fase :, mostrado a figura 4.7 (f). Coforme se pode otar, a dimiuição do úmero de deslizametos exibe uma tedêcia do sistema para sicroização de fase perfeita ode ão há deslizametos. Cotrariamete, o aumeto do úmero de deslizametos exibe uma tedêcia do sistema para perder sicroização. No movimeto sícroo, a órbita caótica está em poucas badas o espaço de fases. (a) (b) (c) (d)
66 58 (e) (f) Figura 4.7: Espaços de fase para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e diferetes valores do acoplameto: (a) ε = 0,55, ode aida ão há sicroização; (b) ε = 0,6, ode surge um atrator caótico de 9 badas, resultado em sicroização 5:4. (c) ε = 0,69, ode ão há mais sicroização 5:4; (d) ε = 0,74, ode surge um atrator caótico de badas, resultado em sicroização 6:5; (e) ε = 0,90, ode ão há mais sicroização de fase 6:5 e (f) ε = 0,95, ode surge um atrator caótico de duas badas, resultado em sicroização :. Figura 4.8: Evolução da difereça de fase θ θ para o sistema (4.). Em (a) e (b) o sistema possui sicroização de fase imperfeita. Em (c) o sistema possui sicroização de fase perfeita. Em 98 C. Grebogi, E. Ott e J. A. Yorke [40] itroduziram o termo crise para descrever certas mudaças qualitativas a diâmica caótica que ocorrem coforme se varia o parâmetro de cotrole. Tais mudaças, correspodem ao aparecimeto ou desaparecimeto de atrator caótico, ou uma variação descotiua o seu tamaho, coforme já mecioado. Dessa forma, a crise ocorre quado um atrator caótico é destruído, ou criado ou altera seu tamaho. Coforme se pode otar a figura 4.7, a sicroização de fase ocorre quado surge um atrator caótico. Pode-se afirmar portato, que a trasição do comportameto ão sícroo para o comportameto sícroo em dois mapas circulares acoplados ocorre através de
67 59 crise iterior [48], gerado um atrator caótico o qual iduz periodicidade oscilatória o sistema. 4.5 Iterpretação do movimeto oscilatório Coforme já mecioado, um sistema de dois mapas circulares acoplados pode ser iterpretado como a seção de Poicaré do movimeto de duas trajetórias ão idêticas sobre um toro. Se o sistema possui sicroização de fase com úmero de rotação w = m : m, sigifica que m períodos de θ correspode a m períodos de θ, isto é, equato θ marca m potos a seção de Poicaré, θ marca m potos. A figura 4.9 mostra a represetação da seção de Poicaré para um sistema de dois mapas circulares acoplados. Na figura 4.9 (a), o sistema possui sicroização de fase 5:4. Neste caso, equato a trajetória θ possui período 5 (5 potos a seção de Poicaré), a trajetória θ possui período 4 (4 potos a seção de Poicaré), resultado em um total de 9 potos a seção de Poicaré e o atrator caótico correspode possui um total de 9 badas, coforme mostra a figura 4.7 (b). Na figura 4.9 (b), o sistema possui sicroização de fase 6:5. Neste caso, equato a trajetória θ possui período 6 (6 potos a seção de Poicaré), a trajetória θ possui período 4 (4 potos a seção de Poicaré), resultado em um total de potos a seção de Poicaré e o atrator caótico correspode possui um total de badas, coforme mostra a figura 4.7 (d). Na figura 4.9 (c), o sistema possui sicroização de fase :. Neste caso, equato a trajetória θ possui período ( poto a seção de Poicaré), a trajetória θ possui período ( poto a seção de Poicaré), resultado em potos a seção de Poicaré e o atrator caótico correspodete possui um total de badas, coforme a figura 4.7 (f). (a) (b) (c) w = 5/4 w = 6/5 w = / Figura 4.9: Seções de Poicaré para duas trajetórias com razão de freqüêcia igual a (a) w = 5:4; (b) w = 6:5 e (c) w = :.
68 Sicroização de fase em dois mapas circulares acoplados Coforme já mecioado, a sicroização de fase ocorre quado os sistemas acoplados oscilam em fase, porém com amplitudes diferetes. A figura 4.0 foi costruída iterado o sistema (4.) para uma codição iicial, e plotadas as iterações. A figura 4.0 (a) mostra a evolução das fases em ε =,47, quado o sistema possui sicroização de fase :. Neste caso, embora o movimeto seja hipercaótico, o acoplameto ajusta os ritmos de oscilação e os sistemas oscilam em fase, porém as amplitudes são diferetes. A figura 4.0 (b) mostra a evolução das fases em ε =,8, ode ão há sicroização e os sistemas ão oscilam em fase. (a) (b) Figura 4.0: Evolução das fases para sistema (4.). (a) Estado sicroizado com ε =,47, ode o movimeto possui periodicidade oscilatória. (b) Estado ão sicroizado com ε =,8, ode ão há periodicidade oscilatória o movimeto. Foram aalisadas as propriedades de sicroização em diferetes valores do parâmetro de cotrole κ. Como pode ser visto as líguas de Arold dadas pela figura 3.5, para um valor fixo de ω, com o aumeto do parâmetro κ, os úmeros de rotação idividuais ρ podem ser variados. Dessa forma, será apresetado o estudo de dois casos diferetes de distribuição de freqüêcia. No primeiro caso, foram escolhidos úmeros de rotação idividuais ρ e ρ de tal maeira que, para todos os valores de κ simulados, os úmeros de rotação para o mapa circular idepedete, ou seja, sem acoplameto, são idêticos e, coseqüetemete, pertecem à mesma lígua de Arold a figura 3.5. No segudo caso, foram escolhidos úmeros de rotação idividuais ρ e ρ de tal maeira que, para todos os valores de κ
69 6 simulados, os úmeros de rotação para o mapa circular idepedete, são diferetes e, coseqüetemete, pertecem à líguas de Arold diferetes. Para costruir a figura 4.0, foram calculados os úmeros de rotação da equação (4.) em fução do acoplameto ε, para diferetes valores de κ. O primeiro caso de distribuição de freqüêcia é mostrado a figura 4.0 (a), para ω = 0,95, ω = 0,99. A depedêcia de w o parâmetro de acoplameto ε, demostra claramete a existêcia de regiões de sicroização de fase : para κ 0, para pequeos valores do acoplameto. Isto era de se esperar, pois se os sistemas acoplados possuem freqüêcias pertecetes à mesma lígua de Arold (o mapa idividual), etão para ε = 0, o sistema composto se tora dois sistemas idepedetes, os quais possuem o mesmo úmero de rotação, ou seja, suas freqüêcias são travadas, e portato, possuem sicroização de fase :. Porém, com o aumeto do acoplameto ão liear, o sistema perde a sicroização. Dessa forma, o fato das freqüêcias dos mapas acoplados pertecerem à mesma lígua de travameto de freqüêcia o mapa idividual, ão garate a ocorrêcia de sicroização para todos os valores de acoplameto. As larguras dessas regiões de sicroização aumetam com o aumeto de κ. (a) (b) Figura 4.: O úmero de rotação w em fução do coeficiete de acoplameto ε para o sistema (4.) em diferetes de κ e (a) ω = 0,95, ω = 0,99 e (b) ω = 0,4, ω = 0,5. O segudo caso é mostrado a figura 4.0 (b), para ω = 0,4, ω = 0,5. A depedêcia de w o parâmetro de acoplameto ε demostra claramete a existêcia de regiões de sicroização de fase : para κ 0. Porém, este caso, o sistema ão sicroiza para baixos valores de acoplameto. Quado ε, = 0 ão há sicroização, aumetado sua itesidade surgem as regiões de sicroização m : m e sicroização :. Aumetado mais aida o
70 6 acoplameto, o sistema perde sicroização. Quato maior o valor de κ, maior será o valor do itervalo de ε para o sistema etrar em sicroização de fase e maior o valor de ε a perder a sicroização. 4.7 Diagramas para regiões de sicroização Em sistemas de dois mapas circulares acoplados são observadas diferetes propriedades de sicroização. Foram executadas simulações uméricas, iterado cojutos diferetes de valores dos parâmetros ε e κ, e calculado o úmero de rotação dado pela equação (4.) para cada cojuto. Foram plotados os valores dos cojutos que correspodiam ao valor do úmero de rotação ρ /. O cálculo foi repetido para diferetes valores de ω. A figura 4. idica que a estrutura geométrica e os tamahos das regiões de sicroização depedem fortemete do parâmetro κ, o qual defie a itesidade de ão liearidade do comportameto do sistema. Certamete que os processos de travameto de freqüêcia para mapas circulares idividuais (ão acoplados) ão pode ser exatamete progosticado para o movimeto de mapas circulares acoplados. Porém, algumas regras comus do aparecimeto e desaparecimeto de sicroização podem ser obtidas e explicadas pelo cohecimeto das propriedades do comportameto de mapas idividuais [48]. O valor do acoplameto o qual ocorre a trasição para a sicroização depede da difereça etre os úmeros de rotação de ambos sistemas acoplados. Coforme mostra a figura 4., para maiores difereças etre as freqüêcias dos sistemas acoplados, e coseqüetemete maiores difereças etre os úmeros de rotação, são ecessários maiores valores do acoplameto para haver sicroização. Com o aumeto de κ, os tamahos das regiões de sicroização toram-se maiores até um certo valor de κ, coforme já mecioado sobre a figura 4.. A partir de um certo valor de κ, o tamaho das regiões toram-se meores. Isto acotece devido à sobreposição das líguas de Arold os mapas idividuais para valores de κ >, e coseqüetemete movimeto caótico sem estabilidade estrutural.
71 63 (a) (b) (c) (d) (e) (f) Figura 4.: Diagrama para sicroização de fase : de κ em fução do acoplameto ε para o sistema (4.) com ω = 0, e diferetes valores de ω : (a) 0,; (b) 0,; (c) 0,3; (d) 0,5; e) 0,6 e f) 0,7. A figura 4.3 mostra a região de sicroização para o sistema de dois mapas circulares acoplados o diagrama de ε em fução a difereça das freqüêcias ω ω. Coforme as difereças etre as freqüêcias aumetam, são ecessários maiores valores de acoplameto para haver sicroização, coforme já mecioado sobre a figura 4.. Aumetado o acoplameto, a região de sicroização desaparece, restado apeas pequeas ilhas de sicroização. Isto ocorre porque o acoplameto é ão liear, e quado chega a um certo valor crítico, ele passa a ão superar mais a divergêcia etre as trajetórias, e o sistema perde a sicroização. Dessa forma, mesmo para freqüêcias idêticas os dois sistemas acoplados (Δω = 0), há um valor limite (crítico) de acoplameto para haver sicroização. Note que essa estrutura é muito similar às líguas de Arold.
72 64 Figura 4.3: Diagrama para sicroização de fase : de ε em fução da difereça das freqüêcias ω ω para o sistema (4.) com κ = 0,4 e ω = 0,5. A estrutura dessa região é similar às líguas de Arold. 4.8 Trasição para ão sicroização Na figura 4. (b) pode-se observar que o sistema perde sicroização de fase : perto de ε =,75, o valor crítico de acoplameto para a perda de sicroização, equato os expoetes de Lyapuov ão mudam seus siais durate a trasição. Para aalisar o mecaismo de perda de sicroização mais precisamete, através da equação (4.3) foram calculados os potos fixos do sistema (4.) para valores dos parâmetros ω = 0,, ω = 0,, κ =,5 e ε =,47, valor do acoplameto pouco ates da perda de sicroização. Foram ecotrados quatro potos fixos, cujas estabilidades foram aalisadas através do cálculo da equação (4.5). A tabela 4.3 apresetada os potos fixos ecotrados, suas localizações o espaço de fases, seus autovalores, suas classificações e estabilidade de acordo com os autovalores. A figura 4.4 apreseta o espaço de fases para o sistema (4.) para os valores dos parâmetros ω = 0,, ω = 0,, κ =,5 e ε =,47. Os dois quadrados em preto são focos istáveis e as duas cruzes são potos de sela. As lihas em viho são as variedades estáveis do poto de sela A, as lihas vermelhas são as variedades istáveis do poto de sela A, as lihas violetas são as variedades estáveis do poto de sela B, as lihas azuis são as variedades istáveis do poto de sela B e a parte em ciza é o atrator caótico. As trajetórias iiciadas ao
73 65 logo da variedade do foco C camiham em direção às selas A e B, e as iiciadas ao logo da variedade do foco D camiham em direção à sela B. As trajetórias iiciadas ao logo das variedades istáveis das selas A e B camiham em direção do atrator caótico. Note que a estrutura das variedades estáveis de ambos os potos de sela são formadas por regiões simétricas o espaço de fases. Poto Fixo A Localização o espaço de fases θ = 0,875; θ = 0,5756 Autovalores Classificação Estabilidade λ =,6609; λ = 0,3 poto de sela hiperbólico istável B θ = 0,375; θ = 0,3444 λ =,6889; λ = 0,339 poto de sela hiperbólico istável C θ = 0,375; θ = 0,5756 λ = 0, ,67474i; λ = 0,9975 0,67474i repulsor tipo foco hiperbólico istável D θ = 0,875; θ = 0,3444 λ =, ,67474i; λ =,005 0,67474i repulsor tipo foco hiperbólico istável Tabela 4.3: Potos fixos e suas classificações para o sistema (4.) e os valores dos parâmetros ω = 0,, ω = 0,, κ =,5 e ε =,47. Figura 4.4: Espaço de fases para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e ε =,47. Os dois quadrados em preto são focos istáveis e as duas cruzes são potos de sela. As lihas em viho são as variedades estáveis do poto de sela A, as lihas vermelhas são as variedades istáveis do poto de sela A, as lihas violetas são as variedades estáveis do poto de sela B, as lihas azuis são as variedades istáveis do poto de sela B e a parte em ciza é o atrator caótico.
74 66 (a) (b) Figura 4.5: Espaço de fases para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e ε =,47. Em (a) estão as variedades estáveis e istáveis do poto de sela A. Em (b) estão as variedades estáveis e istáveis do poto de sela B. Para melhor visualizar as variedades de cada poto de sela, a figura 4.5 (a) apreseta as variedades estáveis e istáveis do poto de sela A, e 4.5 (b) as variedades estáveis e istáveis do poto de sela B. O sistema está o regime de sicroização de fase : devido ao atrator caótico iduzir periodicidade ao sistema, fazedo as trajetórias seguirem o mesmo camiho ao logo das badas do atrator [50]. A variedade estável da sela A represeta o papel de bacia limite o qual previe que as órbitas o iterior do atrator caótico sejam repelidas para todo o espaço de fases. A bacia de atração correspode ao cojuto de todas as codições iiciais que levam ao atrator. No sistema (4.), todas as codições iiciais sobre o espaço de fases camiham em direção ao atrator. Dessa forma, todo o espaço de fases correspode à bacia de atração do atrator, e ambos os potos de sela e ambos os focos estão o iterior da bacia de atração do atrator caótico. A figura 4.6 (a) mostra o espaço de fases, com o atrator caótico e os potos fixos em ε =,47. Note a figura 4.6 (c) que o poto de sela A está bastate próximo do atrator caótico. Para que o atrator caótico permaeça sicroizado, as trajetórias detro dele ão podem cruzar com a variedade estável da sela A. Ao aumetar o acoplameto até ε =,495, as órbitas periódicas o iterior do atrator caótico colidem com a sela A, coforme mostrado as figuras 4.6 (b) e (d). Após essa colisão, as órbitas periódicas passam a seguir ao logo da variedade istável da sela. Esse feômeo é cohecido como crise iterior. Na crise iterior, um poto fixo istável existete detro da bacia de atração do atrator caótico, colide com o atrator caótico quado algum parâmetro de cotrole é variado. Quado a colisão ocorre, o atrator caótico expade seu tamaho. Esta expasão ocorre porque as
75 67 trajetórias sobre o atrator caótico evetualmete se aproximam do poto fixo istável e são repelidas pela variedade istável do poto fixo para regiões do espaço de fases que aida ão haviam sido visitadas ates da colisão ocorrer. O efeito é a expasão das órbitas do atrator caótico sobre o espaço de fases. Como coseqüêcia da expasão do atrator caótico devido à crise iterior, as órbitas que seguiam as trajetórias ao logo das badas do atrator caótico, agora habitam todo o espaço de fases, isto é, ão há mais periodicidade oscilatória e o sistema perde sicroização. Dessa forma, a trasição para o estado ão sicroizado é realizada com alguma mudaça a estrutura diâmica do sistema caótico. (a) (b) (c) (d) Figura 4.6: Espaço de fases para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e (a) ε =,47, ode o atrator caótico iduz periodicidade oscilatória o sistema; (b) ε =,495, ode diferetes direções de rotação das órbitas se toram possíveis destruido a sicroização. (c) Zoom de (a) próximo do poto de sela. A sela e sua variedade estável ão cruzam com o atrator. (d) Cruzameto da sela com o atrator, ode as órbitas do atrator caótico passam a seguir a variedade estável da sela.
76 68 Etede-se por tempo trasiete o tempo ecessário para que o sistema evolua para um comportameto assitótico. Para verificar a evolução das órbitas até o seu comportameto fial, uma certa quatidade das primeiras iterações foi descartada, para elimiar o trasiete. A figura 4.7 mostra as mudaças da estrutura do atrator caótico. Em 4.7 (a) a crise iterior aida ão ocorreu, e as órbitas o atrator são periódicas. Em 4.7 (b) a crise já ocorreu o sistema, e as órbitas periódicas o iterior do atrator caótico começaram a ser repelidas pelo poto de sela hiperbólico. Em 4.7 (c) o atrator caótico expadiu seu tamaho, habitado uma região maior o espaço de fases. Em 4.7 (d) o atrator caótico expadiu até habitar todo o espaço de fases, e coseqüetemete, o sistema perdeu a periodicidade oscilatória e perdeu a sicroização de fase. (a) (b) (c) (d) Figura 4.7: Retratos de fase para o sistema (4.) com ω = 0,, ω = 0,, κ =,5 e diferetes valores do acoplameto (a) ε =,47; (b) ε =,5, (c) ε =,58 e (d) ε =,9. Em (a) aida existe sicroização de fase :. Em (b) e (c) o atrator caótico está aumetado seu tamaho. Em (d) o atrator foi expadido até habitar todo o espaço de fases e o sistema perdeu a periodicidade oscilatória e dessicroizou o sistema.
77 Capítulo 5 Efeitos de ruído sobre sicroização de fase em mapas circulares acoplados Em geral sicroização de fase perfeita e imperfeita são destruídas quado osciladores estão a preseça de ruído, o que é ievitável em sistemas reais. Este capítulo traz uma cotribuição cietífica para o cohecimeto dos efeitos de ruído sobre a sicroização de fase em sistemas de dois mapas circulares acoplados. O estudo foi realizado itroduzido um ruído o acoplameto e posteriormete um ruído aditivo. Foram estudados dois sistemas de mapas circulares acoplados. No primeiro sistema, o ruído o acoplameto e o ruído aditivo iduzem dessicroização de fase perfeita e imperfeita. No segudo sistema, o ruído o acoplameto iduz dessicroização de fase perfeita e imperfeita, e o ruído aditivo iduz um efeito de seguda ordem, dessicroizado apeas a sicroização de fase imperfeita. 5. Iterpretação da diâmica de fase Ates de apresetar os resultados uméricos, será apresetado um etedimeto ituitivo do efeito de um ruído a sicroização de dois osciladores acoplados, através da iterpretação da diâmica da difereça de fase. Seja um sistema composto por dois mapas circulares dado por ) ( ) ( ) ( ) ( x x dse x F b x x x x dse x F b x x + + = + + = + + (5.) ode F(x) é uma fução seccioalmete liear π-periódica da forma F(x) = cx/π defiida o itervalo [ π, π], e c é o parâmetro de cotrole. Itroduzido um ruído aditivo o sistema (5.), ele fica modificado para ξ ξ = = + + ) ( ) ( ) ( ) ( x x dse x F b x x x x dse x F b x x (5.) ode ξ é um ruído braco gaussiao (veja apêdice A).
78 70 Seja a difereça de fase do sistema (5.) dada por ϕ. (5.3) + = x+ x+ É feito o uso do fato de que a variação da difereça de fase a cada iterada, pode ser descrita por c Δ ϕ = ϕ+ ϕ = Δb ϕ dseϕ, (5.4) π ode Δ b = b b. É feito também o uso do fato de que a evolução de ϕ + pode ser descrita em termos de um potecial V(φ ) d Δϕ = V ( ϕ ) ϕ (5.5) com c V ( ϕ ) = Δbϕ dϕ ϕ dseϕ (5.6) π o qual pode facilmete ser calculado V ( ϕ ϕ c ) = Δbϕ + d cosϕ. (5.7) π A diâmica da difereça de fase pode ser represetada como a de uma partícula superamortecida em um potecial icliado. Neste quadro, o efeito do ruído é a idução de saltos de fase etre míimos vizihos o potecial. Um valor ão ulo de ϕ correspode a um trasporte dirigido o potecial [37]. O potecial (5.7) é ilustrado a figura 5.. Em (a), (b) e (c) a ausêcia de ruído o sistema está detro da região de sicroização, sigificado que a itesidade do acoplameto é grade o suficiete para iduzir sicroização. Três valores de Δb são ilustrados: (a) Δb > 0, (b) Δb = 0 e (c) Δb < 0. Quado Δb > 0 (figura 5. (a)), se a partícula estiver sob a ifluêcia
79 7 de ruído ela oscilará ao redor do míimo local do poço de potecial. Se o ruído aplicado tem uma distribuição gaussiaa, etão para qualquer altura da barreira, cedo ou tarde a perturbação irá alcaçar um valor que seja suficiete para arremessar a partícula sobre a barreira. A partícula salta para o poço viziho de vez em quado, e esses saltos, ou deslizametos de fase, represetam um processo radômico. Com cada salto para a direita, ϕ aumeta em π, e com cada salto para a esquerda dimiui em π. É muito mais fácil para a partícula superar as mais baixas barreiras à direita que à esquerda, assim, a direção preferida da partícula flutuar é para direita, embora os saltos a direção oposta ão sejam impossíveis. A difereça de fase ϕ irá em média aumetar ilimitadamete com o tempo. A 5. (b) ilustra o comportameto de ϕ o meio da região de sicroização (Δb = 0). Para qualquer itesidade do acoplameto a partícula tem a mesma probabilidade de salto para a esquerda que para a direita, e em média ϕ ão muda. A figura 5. (c) ilustra o caso em que ϕ flutua preferivelmete para a esquerda. Geralmete, detro da região de sicroização a difereça de fase exibe platôs de certa duração que correspode ao estado de sicroização de fase, iterrompido por saltos de π. A duração de permaêcia detro de cada poço potecial é proporcioal à itesidade de sicroização. Nas figuras 5. (d) e (e) a situação é ilustrada esquematicamete para o caso quado o acoplameto ão é grade o suficiete para iduzir sicroização, e o sistema está fora da região de sicroização. Nesse caso ão há ehum poço potecial para ϕ, e ela desliza para baixo, esta ou aquela direção depededo do sial da difereça Δb.
80 7 (a) (d) (b) (c) (e) Figura 5.: Ilustração esquemática do comportameto da difereça de fase φ como uma partícula em um potecial icliado V(φ ). (a), (b) e (c) mostra a partícula detro da região de sicroização; (d) e (e) mostra a partícula fora da região de sicroização. 5. Efeitos de ruído braco gaussiao sobre o primeiro sistema de dois mapas circulares acoplados No capítulo aterior, foi demostrado o feômeo de sicroização de fase em um sistema de dois mapas circulares acoplados. Porém, é ievitável a preseça de ruído em
81 73 sistemas aturais e experimetais. Portato, é relevate explorar os efeitos de ruído sobre a robustez do processo de sicroização [5]. Ruídos podem iflueciar a sicroização de fase de diferetes maeiras. Coforme já mecioado, geralmete ele faz a difereça de fase flutuar ao redor do míimo do poço de potecial, e escala sobre a barreira de eergia ocasioalmete se deslocado para o míimo viziho, resultado em um efeito degradate, por exemplo, iduzido deslizametos de sicroização de fase em osciladores. 5.. Dessicroização de fase iduzida por ruído gaussiao o acoplameto Para ivestigar os efeitos de ruído sobre um sistema de dois mapas circulares acoplados, foi itroduzido um ruído gaussiao o acoplameto do sistema (4.), o qual passa a ser descrito como: θ θ + + = θ = θ κ ε ( + ξ ) ε ( + ξ ) + ω se(πθ) se(πθ ) + se(πθ) π π π κ ε ( + ξ ) ε( + ξ ) + ω se(πθ ) se(πθ) + se(πθ ) π π π (5.8) ode ξ é um ruído braco gaussiao (veja apêdices A e B). O sistema (5.8) pode ser iterpretado como a seção de Poicaré de duas trajetórias sobre a superfície de um toro ão idêticas e acopladas. Essas trajetórias estão sob a ifluêcia de uma perturbação o acoplameto do sistema. A figura 5. mostra o úmero de rotação calculado através da equação (4.) em fução do acoplameto para o sistema (5.8), com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4. É possível otar que, coforme a variâcia do ruído aumeta, uma dessicroização é iduzida ao sistema. Em 5. (a) o sistema está livre de ruído. Note que há pequeos platôs de sicroização de fase imperfeita m : m e um cosiderável platô de sicroização de fase perfeita :. Em 5. (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3. O ruído iduz uma dessicroização de fase imperfeita m : m, porém o sistema aida matém a sicroização de fase perfeita :. Em 5. (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -. O ruído, agora com variâcia maior, iduziu uma dessicroização de fase :, e o sistema ão possui sicroização de fase perfeita ou imperfeita.
82 74 (a) (b) (c) Figura 5.: Número de rotação w pelo coeficiete de acoplameto ε para o sistema (5.8) com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4. O úmero de rotação é plotado como uma fução do acoplameto. Em (a) o sistema está livre de ruído. O sistema está sob a ifluêcia de um ruído com variâcia (b) σ = 0-3 e (c) σ = 0 -. Para uma melhor iterpretação do comportameto diâmico de um sistema de dois mapas circulares acoplados sob a ifluêcia de ruído gaussiao o parâmetro de acoplameto, a figura 5.3 apreseta o espaço de fases para o sistema (5.8) com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε = 0,6 e diferetes variâcias de ruído. Em 5.3 (a) o sistema está livre de ruído. A preseça de um atrator caótico de 9 badas faz com que o sistema possua sicroização de fase imperfeita 5:4. Em 5.3 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-5, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase imperfeita. Em 5.3 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4, este caso o atrator caótico expadiu aida mais. Em 5.3 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até que ele ocupe todo o espaço de fases, e o sistema perdeu a periodicidade, resultado a
83 75 perda de sicroização de fase imperfeita. (a) (b) (c) (d) Figura 5.3: Espaço de fases para o sistema (5.8) e valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε = 0,6. Em (a) o sistema possui sicroização de fase imperfeita 5:4 e está livre de ruído. Note a preseça de um atrator periódico de ove badas. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-5. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3, o qual destruiu o atrator, dessicroizado o sistema. Para aalisar o mecaismo de perda de sicroização mais precisamete, foram calculados os potos fixos do sistema (5.8) para valores dos parâmetros ω = 0,9, ω = 0,, κ =,4 e ε =,35, valor do acoplameto pouco ates da perda de sicroização. Foram ecotrados quatro potos fixos, cujas estabilidades foram aalisadas através dos autovalores da matriz jacobiaa. A tabela 5. apresetada os potos fixos ecotrados, suas localizações o espaço de fases, seus autovalores, suas classificações e estabilidade de acordo com os autovalores.
84 76 Poto Fixo A Localização o espaço de fases θ = 0,3057; θ = 0,3385 Autovalores Classificação Estabilidade λ =,58; λ = 0,4664 poto de sela hiperbólico istável B θ = 0,9743; θ = 0,648 λ =,5373; λ = 0,4003 poto de sela hiperbólico istável C θ = 0,3057; θ = 0,648 λ = 0,9949 0,5583i; λ = 0, ,5583i repulsor tipo foco hiperbólico istável θ = 0,9743; λ D =,005 0,5583i; repulsor tipo foco istável θ = 0,3385 λ =, ,5583i hiperbólico Tabela 5.: Potos fixos e suas classificações para o sistema (5.8) com ω = 0,9, ω = 0,, κ =,4 e ε =,35. A figura 5.4 apreseta o espaço de fases para o sistema (5.8) para os valores dos parâmetros ω = 0,9, ω = 0,, κ =,4 e ε =,35. Os dois quadrados em preto são focos istáveis e as duas cruzes são potos de sela. As lihas em viho são as variedades estáveis do poto de sela A, as lihas vermelhas são as variedades istáveis do poto de sela A, as lihas violetas são as variedades estáveis do poto de sela B, as lihas azuis são as variedades istáveis do poto de sela B e a parte em ciza escuro é o atrator caótico. As trajetórias iiciadas ao logo da variedade do foco C camiham em direção às selas A e B, e as iiciadas ao logo da variedade do foco istável D camiham em direção à sela B. As trajetórias iiciadas ao logo das variedades istáveis das selas A e B camiham em direção do atrator caótico. Note que a estrutura das variedades estáveis de ambos os potos de sela são formadas por regiões simétricas o espaço de fases. Para uma melhor iterpretação do comportameto diâmico de um sistema de dois mapas circulares acoplados sob a ifluêcia de ruído gaussiao o parâmetro de acoplameto, a figura 5.5 apreseta o espaço de fases para o sistema (5.8) com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε =,35 e diferetes variâcias de ruído. Em 5.5 (a) o sistema está livre de ruído. A preseça de um atrator caótico faz com que o sistema possua sicroização de fase perfeita :. Em 5.5 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase perfeita. Em 5.5 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso o atrator caótico expadiu aida mais, e é possível otar que as órbitas do atrator estão seguido as variedades istáveis dos potos de sela A e B. Em 5.5 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até que ele ocupe todo o
85 77 espaço de fases, e portato perder a periodicidade, resultado a perda de sicroização de fase. Figura 5.4: Espaço de fases de dois mapas circulares acoplados do sistema (5.8) para ω = 0,9, ω = 0,, κ =,4 e ε =,35. Os dois quadrados em preto são focos istáveis e as duas cruzes são potos de sela. As lihas em viho são as variedades estáveis do poto de sela A, as lihas vermelhas são as variedades istáveis do poto de sela A, as lihas violetas são as variedades estáveis do poto de sela B, as lihas azuis são as variedades istáveis do poto de sela B e a parte em ciza é o atrator caótico. Coforme já mecioado, a crise iterior um poto fixo istável existete detro da bacia de atração do atrator caótico, colide com o atrator caótico quado algum parâmetro de cotrole é variado. Quado a colisão ocorre, o atrator caótico expade seu tamaho. Esta expasão ocorre porque as trajetórias sobre o atrator caótico evetualmete se aproximam do poto fixo istável e são repelidas pelo poto fixo para regiões do espaço de fases que aida ão haviam sido visitadas ates da colisão ocorrer. O efeito é a expasão das órbitas do atrator caótico sobre o espaço de fases. Dessa forma, coforme mostra as figuras 5.4 e 5.5, cojectura-se que o ruído gaussiao o acoplameto iduziu uma crise iterior e dessicroizou o sistema [5].
86 78 (a) (b) (c) (d) Figura 5.5: Espaço de fases para o sistema (5.8) e valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε =,35. Em (a) o sistema possui sicroização de fase perfeita : e está livre de ruído. Note a preseça de um atrator caótico. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, e o atrator caótico passou a seguir as variedades istáveis dos potos de sela A e B. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual destruiu o atrator, dessicroizado o sistema. A figura 5.6 mostra a evolução da difereça de fase do sistema (5.8) para ω = 0,9, ω = 0,, κ =,4 e ε =,35. A liha (a) da figura 5.6 represeta o sistema com sicroização de fase : livre de ruído, cuja diâmica é mostrada a figura 5.5 (a). Neste caso a evolução da difereça de fase permaece costate. A liha (b) da figura 5.6 represeta o sistema sob a ifluêcia de ruído com variâcia σ = 0 -, cuja diâmica é mostrada a figura 5.5 (d). Neste caso a evolução da difereça de fase é composta por uma sucessão de saltos discretos. Isto é uma idicação de que ruído o parâmetro de acoplameto iduz deslizametos de fase o sistema. Devido a estes deslizametos em média a difereça de fase θ θ é uma fução crescete o tempo. Esses deslizametos de fase correspodem aos de saltos de fase etre míimos
87 79 vizihos o potecial represetados a ilustração esquemática do comportameto da difereça de fase φ como uma partícula em um potecial icliado, mostrados a figura 5.. Figura 5.6: Evolução da difereça de fase do sistema (5.8) para ω = 0,9, ω = 0,, κ =,4 e ε =,35. A liha (a) represeta o sistema livre de ruído com sicroização de fase :, resultado em uma difereça de fase costate. A liha (b) represeta o sistema sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual iduziu deslizametos de fase. 5.. Dessicroização de fase iduzida por ruído gaussiao aditivo Para ivestigar os efeitos de ruído sobre um sistema de dois mapas circulares acoplados, foi itroduzido um ruído gaussiao aditivo ao sistema (4.), o qual passa a ser descrito como: θ θ + + = θ = θ κ ε ε + ω se(πθ) se(πθ ) + se(πθ) + ξ π π π κ ε ε + ω se(πθ ) se(πθ) + se(πθ ) + ξ π π π (5.9) ode ξ é um ruído braco gaussiao. A figura 5.7 mostra o úmero de rotação calculado através da equação (4.) em fução do acoplameto para o sistema (5.9), para os valores dos parâmetros ω = 0,3, ω = 0,4, κ =,3. É possível otar que, coforme a variâcia do ruído aumeta, uma dessicroização é iduzida ao sistema. Em 5.7 (a) o sistema está livre de ruído. Note que há pequeos platôs de sicroização de fase imperfeita m : m e um cosiderável platô de
88 80 sicroização de fase perfeita :. Em 5.7 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4. O ruído iduz uma dessicroização de fase imperfeita m : m, porém o sistema aida matém a sicroização de fase perfeita :. Em 5.7 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -. O ruído, agora com variâcia maior, iduziu uma dessicroização de fase :, e o sistema agora ão possui sicroização de fase perfeita ou imperfeita. (a) (b) (c) Figura 5.7: Número de rotação w pelo coeficiete de acoplameto ε para o sistema (5.9) e valores dos parâmetros ω = 0,3, ω = 0,4, κ =,3. O úmero de rotação é plotado como uma fução do acoplameto. Em (a) o sistema está livre de ruído. O sistema está sob a ifluêcia de um ruído com variâcia (b) σ = 0-4 e (c) σ = 0 -. Para uma melhor iterpretação do comportameto diâmico de um sistema de dois mapas circulares acoplados sob a ifluêcia de ruído gaussiao o parâmetro de acoplameto, a figura 5.8 apreseta o espaço de fases para o sistema (5.9) com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε = 0,6 e diferetes variâcias de ruído. Em 5.8 (a) o sistema está livre de ruído. A preseça de um atrator caótico faz com que o sistema possua sicroização de fase imperfeita 3:. Em 5.8 (b) o sistema está sob a ifluêcia de um ruído
89 8 com variâcia σ = 0-6, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase imperfeita. Em 5.8 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-5, este caso o atrator caótico expadiu aida mais. Em 5.8 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até que ele ocupe todo o espaço de fases e o sistema perdeu a periodicidade, resultado a perda de sicroização de fase imperfeita. (a) (b) (c) (d) Figura 5.8: Espaço de fases para o sistema (5.9) com valores dos parâmetros ω = 0,3, ω = 0,4, κ =,3, ε = 0,. Em (a) o sistema possui sicroização de fase imperfeita 3: e está livre de ruído. Note a preseça de um atrator periódico. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-6. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-5. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4, o qual destruiu o atrator, dessicroizado o sistema. Para uma melhor iterpretação da diâmica de um sistema de dois mapas circulares acoplados sob a ifluêcia de ruído gaussiao aditivo, a figura 5.9 mostra o espaço de fases para o sistema (5.9) e valores dos parâmetros ω = 0,3, ω = 0,4, κ =,3, ε =,88 e diferetes
90 8 variâcias de ruído. Em 5.9 (a) o sistema está livre de ruído. A preseça de um atrator caótico de várias badas faz com que o sistema possua sicroização de fase perfeita :. Em 5.9 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4, este caso, o ruído iduziu uma expasão de cada uma das badas do atrator caótico, porém o sistema aida possui sicroização de fase perfeita. Em 5.9 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3 e o atrator aida mais expadido habita quase todo o espaço de fases. Em 5.9 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até ocupar todo o espaço de fases e o sistema perdeu a periodicidade, resultado a dessicroização de fase. (a) (b) (c) (d) Figura 5.9: Espaço de fases para o sistema (5.9) e valores dos parâmetros ω = 0,3, ω = 0,4, κ =,3, ε =,88. Em (a) o sistema possui sicroização de fase : e está livre de ruído. Note a preseça de um atrator caótico de várias badas. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4, o qual expadiu as badas do atrator, mas o sistema aida está sicroizado. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3, e o atrator caótico expadiu aida mais. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual destruiu o atrator, dessicroizado o sistema.
91 83 A figura 5.0 mostra a evolução da difereça de fase do sistema (5.9) para ω = 0,3, ω = 0,4, κ =,3 e ε =,88. A liha (a) da figura 5.0 represeta o sistema com sicroização de fase : livre de ruído, este caso a evolução da difereça de fase permaece costate. A liha (b) da figura 5.0 represeta o sistema sob a ifluêcia de ruído com variâcia σ = 0 -, este caso a evolução da difereça de fase é composta por uma sucessão de saltos discretos. Isto é uma idicação de que ruído aditivo iduz deslizametos de fase o sistema [35]. Devido a estes deslizametos em média a difereça de fase θ θ é uma fução crescete o tempo. Figura 5.0: Evolução da difereça de fase do sistema (5.9) com ω = 0,3, ω = 0,4, κ =,3 e ε =,88. A liha (a) represeta o sistema livre de ruído com sicroização de fase :, resultado em uma difereça de fase costate. A liha (b) represeta o sistema sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual iduziu deslizametos de fase. Comparado os resultados, o sistema (5.8) com ruído o acoplameto, dessicroiza com uma variâcia meor de ruído do que o sistema (5.9) com ruído aditivo, ou seja, para que um ruído possa iduzir dessicroização ao sistema, é ecessário uma variâcia maior para ruído o acoplameto do que para ruído aditivo. 5.3 Efeitos de ruído braco gaussiao sobre o segudo sistema de dois mapas circulares acoplados Um sistema composto por dois mapas circulares acoplados pode ser descrito como:
92 84 θ θ + + = θ = θ κ ε + ω se(πθ) + se(πθ πθ) π π. (5.0) κ ε + ω se(πθ ) + se(πθ πθ ) π π ode ε é o parâmetro de acoplameto. O sistema (5.0) possui apeas um termo de acoplameto bidirecioal ão liear em cada equação, equato o sistema (4.) possui dois termos de acoplameto bidirecioal ão liear em cada equação Dessicroização de fase iduzida por ruído gaussiao o acoplameto Para ivestigar os efeitos de ruído sobre um sistema de dois mapas circulares acoplados, foi itroduzido um ruído gaussiao o acoplameto do sistema (5.0), o qual passa a ser descrito como: θ θ + + = θ = θ κ ε( + ξ) + ω se(πθ) + se(πθ πθ) π π. (5.) κ ε ( + ξ ) + ω se(πθ ) + se(πθ πθ ) π π ode ξ é um ruído braco gaussiao. A figura 5. mostra o úmero de rotação calculado através da equação (4.) em fução do acoplameto para o sistema (5.), para os valores dos parâmetros ω = 0,, ω = 0,, κ = 0,4. É possível otar que, coforme a variâcia do ruído aumeta, uma dessicroização é iduzida ao sistema. Em 5. (a) o sistema está livre de ruído. Note que há pequeos platôs de sicroização de fase imperfeita m : m e um cosiderável platô de sicroização de fase perfeita :. Em 5. (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -. O ruído iduz uma dessicroização de fase imperfeita m : m, porém o sistema aida matém a sicroização de fase perfeita :. Em 5. (c) o sistema está sob a ifluêcia de um ruído com variâcia σ =. O ruído, agora com variâcia maior, iduziu uma dessicroização de fase :, e o sistema ão possui sicroização de fase perfeita ou imperfeita.
93 85 (a) (b) (c) Figura 5.: Número de rotação w pelo coeficiete de acoplameto ε para o sistema (5.) e valores dos parâmetros ω = 0,, ω = 0,, κ = 0,4. O úmero de rotação é plotado como uma fução do acoplameto. Em (a) o sistema está livre de ruído. O sistema está sob a ifluêcia de um ruído com variâcia (b) σ = 0 - e (c) σ =. Um sistema é estruturalmete estável se trajetórias suficietemete próximas têm retratos de fases equivaletes. Assim, a estabilidade estrutural sigifica a robustez de um poto ou uma região o espaço das trajetórias, etededo-se robustez como a propriedade que o sistema apreseta de reter as características qualitativas da sua diâmica, relativamete a pequeas perturbações ou mudaças as fuções evolvidas a sua defiição. Assim, a alta itesidade da variâcia do ruído a figura 5. (c) é um artifício para mostrar a robustez da sicroização de fase do sistema. Para uma melhor iterpretação do comportameto diâmico de um sistema de dois mapas circulares acoplados sob a ifluêcia de ruído gaussiao o parâmetro de acoplameto, a figura 5. apreseta o espaço de fases para o sistema (5.) com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε = 0,6 e diferetes variâcias de ruído. Em 5. (a) o sistema está livre de ruído. A preseça de um atrator caótico de 3 badas faz com que o
94 86 sistema possua sicroização de fase imperfeita :. Em 5. (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase imperfeita. Em 5. (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso o atrator caótico expadiu aida mais. Em 5. (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até que ele ocupe todo o espaço de fases e o sistema perdeu a periodicidade, resultado a perda de sicroização de fase imperfeita. (a) (b) (c) (d) Figura 5.: Espaço de fases para o sistema (5.8) e valores dos parâmetros ω = 0,, ω = 0,, κ = 0,4, ε = 0,3. Em (a) o sistema possui sicroização de fase imperfeita : e está livre de ruído. Note a preseça de um atrator periódico de três badas. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual destruiu o atrator, dessicroizado o sistema. Para visualizar melhor a diâmica desse segudo sistema de dois mapas circulares acoplados sob a ifluêcia de ruído braco gaussiao aditivo, a figura 5.3 apreseta o
95 87 espaço de fases para o sistema (5.) e valores dos parâmetros ω = 0,, ω = 0,, κ = 0,4 e ε = 0,75. Em 5.3 (a) o sistema está livre de ruído. A preseça de um atrator caótico de badas faz com que o sistema possua sicroização de fase perfeita :. Em 5.3 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase perfeita. Em 5.3(c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, e o atrator caótico expadiu aida mais. Em 5.3 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ =, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até ele ocupar todo o espaço de fases e perder a periodicidade, resultado a perda de sicroização de fase. (a) (b) (c) (d) Figura 5.3: Espaço de fases para o sistema (5.) e valores dos parâmetros ω = 0,, ω = 0,, κ = 0,4, ε = 0,75. Em (a) o sistema possui sicroização de fase : e está livre de ruído. Note a preseça de um atrator caótico. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual expadiu o atrator, mas aida há sicroização de fase :. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ =, o qual expadiu o atrator caótico até ocupar todo o espaço de fases e perder a periodicidade, dessicroizado o sistema.
96 88 A figura 5.4 mostra a evolução da difereça de fase do sistema (5.) para ω = 0,, ω = 0,, κ = 0,4 e ε = 0,75. A liha (a) da figura 5.4 represeta o sistema com sicroização de fase : livre de ruído, cuja diâmica é mostrada a figura 5.3 (a). Neste caso a evolução da difereça de fase permaece costate. A liha (b) da figura 5.3 represeta o sistema sob a ifluêcia de ruído com variâcia σ =, cuja diâmica é represetada a figura 5.3 (d). Neste caso a evolução da difereça de fase é composta por uma sucessão de saltos discretos. Isto é uma idicação de que ruído o parâmetro de acoplameto iduz deslizametos de fase o tempo. Figura 5.4: Evolução da difereça de fase do sistema (5.) para ω = 0,, ω = 0,, κ = 0,4, ε = 0,75. A liha (a) represeta o sistema livre de ruído com sicroização de fase :, resultado em uma difereça de fase costate. A liha (b) represeta o sistema sob a ifluêcia de um ruído com variâcia σ =, o qual iduziu deslizametos de fase Efeito de seguda ordem iduzido por ruído gaussiao aditivo Para ivestigar os efeitos de ruído sobre um sistema de dois mapas circulares acoplados, foi itroduzido um ruído gaussiao aditivo ao sistema (5.0), o qual passa a ser descrito como: θ θ + + = θ = θ κ ε + ω se(πθ) + se(πθ πθ) + ξ π π. (5.) κ ε + ω se(πθ ) + se(πθ πθ ) + ξ π π
97 89 ode ξ é um ruído braco gaussiao. A figura 5.5 mostra o úmero de rotação calculado através da equação (4.) em fução do acoplameto para o sistema (5.), para os valores dos parâmetros ω = 0,, ω = 0,38, κ = 0,5. Em 5.5 (a) o sistema está livre de ruído. Note que há pequeos platôs de sicroização de fase imperfeita m : m e um cosiderável platô de sicroização de fase perfeita :. Em 5.5 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -. O ruído iduz uma dessicroização de fase imperfeita m : m, porém o sistema aida matém a sicroização de fase perfeita :. Em 5.5 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 3. Neste caso, o sistema mateve a sicroização de fase perfeita, mesmo sob ifluêcia de ruído com alta variâcia. Assim, esse segudo sistema de dois mapas circulares acoplados sob a ifluêcia de um ruído braco gaussiao aditivo, perde sicroização de fase imperfeita mas matém a sicroização de fase perfeita. (a) (b) (c) Figura 5.5: Número de rotação w pelo coeficiete de acoplameto ε para o sistema (5.) com ω = 0,, ω = 0,38, κ = 0,5. O úmero de rotação é plotado como uma fução do acoplameto. Em (a) o sistema está livre de ruído. O sistema está sob a ifluêcia de um ruído com variâcia (b) σ = 0 - e (c) σ = 0 3.
98 90 Para uma melhor iterpretação do comportameto diâmico de um sistema de dois mapas circulares acoplados sob a ifluêcia de ruído gaussiao o parâmetro de acoplameto, a figura 5.6 apreseta o espaço de fases para o sistema (5.) com valores dos parâmetros ω = 0,9, ω = 0,, κ =,4, ε = 0,6 e diferetes valores da variâcia σ do ruído. Em 5.6 (a) o sistema está livre de ruído. A preseça de um atrator caótico de 3 badas faz com que o sistema possua sicroização de fase imperfeita :. Em 5.6 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase imperfeita. Em 5.6 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3, este caso o atrator caótico expadiu aida mais. Em 5.6 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso a ação do ruído sobre o sistema expadiu o atrator caótico até que ele ocupe todo o espaço de fases e o sistema perdeu a periodicidade, resultado a perda de sicroização de fase imperfeita. Para visualizar melhor a diâmica desse segudo sistema de dois mapas circulares acoplados sob a ifluêcia de ruído braco gaussiao aditivo, a figura 5.7 apreseta o espaço de fases para o sistema (5.) e valores dos parâmetros ω = 0,, ω = 0,38, κ = 0,5 e ε =, e diferetes valores da variâcia σ do ruído. Em 5.7 (a) o sistema está livre de ruído. A preseça de um atrator caótico faz com que o sistema possua sicroização de fase perfeita :. Em 5.7 (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, este caso, o ruído iduziu uma expasão do atrator caótico, porém o sistema aida possui sicroização de fase perfeita. Em 5.7 (c) o sistema está sob a ifluêcia de um ruído com variâcia σ =, e o atrator expadiu um pouco mais. Em 5.7 (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 3, este caso a ação do ruído sobre o sistema ão expadiu o atrator até ele habitar todo o espaço de fases, e o atrator cotiua periódico, isto é, há um certo limite de expasão que o atrator caótico pode atigir, e esse segudo sistema de dois mapas circulares acoplados possui sicroização de fase perfeita a preseça de ruído gaussiao aditivo.
99 9 (a) (b) Figura 5.6: Espaço de fases para o sistema (5.8) e valores dos parâmetros ω = 0,, ω = 0,38, κ = 0,5, ε = 0,7. Em (a) o sistema possui sicroização de fase imperfeita : e está livre de ruído. Note a preseça de um atrator periódico de três badas. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-4. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0-3. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual destruiu o atrator, dessicroizado o sistema. Dessa forma, a itrodução de um ruído braco gaussiao aditivo este segudo sistema de dois mapas circulares acoplados, iduz um efeito de seguda ordem, o qual ocorre a dessicroização de fase imperfeita e permaece a sicroização de fase perfeita o sistema, isto é, o sistema matém sicroização de fase perfeita a preseça de ruído.
100 9 (a) (b) (a) (b) Figura 5.7: Espaço de fases para o sistema (5.) e valores dos parâmetros ω = 0,, ω = 0,38, κ = 0,5 ε =,. Em (a) o sistema possui sicroização de fase : e está livre de ruído. Note a preseça um atrator caótico. Em (b) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 -, o qual expadiu o atrator, mas aida há sicroização de fase :. Em (c) o sistema está sob a ifluêcia de um ruído com variâcia σ =, e o atrator caótico expadiu aida mais. Em (d) o sistema está sob a ifluêcia de um ruído com variâcia σ = 0 3, o qual ão expadiu o atrator caótico até habitar todo o espaço de fases, matedo a periodicidade e a sicroização de fase perfeita.
101 Capítulo 6 Coclusões e perspectivas Nesta dissertação, foram estudadas as propriedades da diâmica caótica de um oscilador de fase discreto o tempo, chamado mapa circular. Foi ivestigada a trasição para o caos através da sobreposição de regiões de órbitas periódicas que formam um regime o espaço de parâmetros do mapa circular, chamado líguas de Arold. A partir do poto crítico, ode κ =, as regiões começam a iteragir e se sobrepõem origiado caos. Abaixo do poto crítico se ecotram órbitas quase-periódicas, as quais desaparecem quado as líguas de Arold começam a se sobreporem. Através do mapa circular pode-se ivestigar a sicroização de freqüêcia em osciladores caóticos. Essa sicroização pode ser vista a estrutura da Escada do Diabo, que apreseta os períodos de sicroização, a repetição dos padrões. Esses períodos de sicroização são úmeros de rotação racioais, ode o movimeto é periódico. Quado o úmero de rotação é irracioal, o movimeto é quase-periódico, e ão há sicroização. Na liha crítica, as órbitas periódicas formam uma escada do Diabo completa, cuja complemetaridade é um cojuto de Cator de dimesão fractal D = 0,9. Foi estudada também a sicroização de fase em osciladores caóticos, através de um sistema de dois mapas circulares acoplados ão liearmete. A trasição para o estado sicroizado ocorre com alguma mudaça a estrutura do espaço de fases. Quado ambos os expoetes de Lyapuov são egativos o sistema ão está sicroizado. A ocorrêcia de uma bifurcação gera a mudaça do sial de um dos expoetes de Lyapuov, e em seguida o outro sial também se tora positivo. O sistema se tora etão hipercaótico. A trasição para o regime sicroizado é realizada através de uma crise iterior, gerado um atrator caótico que iduz periodicidade oscilatória o sistema, de forma que os dois mapas acoplados seguem a mesma trajetória ao logo das badas do atrator caótico, oscilado em fase. Coforme a difereça etre as freqüêcias de cada mapa aumeta, são ecessários maiores valores de acoplameto para haver sicroização. A estrutura da região de sicroização o espaço dos parâmetros do acoplameto pela difereça de freqüêcias, é muito similar às líguas de Arold. Aumetado a itesidade do acoplameto, a região de sicroização desaparece, devido ao fato de o acoplameto ão superar mais a divergêcia
102 94 etre as trajetórias, e o sistema perde a sicroização. Dessa forma, há um certo valor crítico de acoplameto para haver sicroização, mesmo o caso em que a difereça etre as freqüêcias é igual a zero. Os cálculos uméricos mostraram que, o fato de as freqüêcias dos mapas acoplados pertecerem à mesma lígua de rotação o mapa idividual, ão é garatia de sicroização para o sistema, pois este caso, somete há sicroização para pequeos valores do acoplameto. A trasição para o regime ão sicroizado é realizada com alguma mudaça a estrutura do cojuto caótico. Quado o sistema está sicroizado sob a preseça de um atrator caótico, a mudaça os valores dos parâmetros pode gerar uma crise iterior o sistema. Como coseqüêcia dessa crise, as órbitas o iterior do atrator caótico são repelidas pela variedade istável de um poto sela hiperbólico, o que faz o atrator expadir o espaço de fases, suscitado mais áreas a serem visitadas pelas órbitas periódicas do atrator. Dessa forma, as órbitas o atrator caótico deixam de ser periódicas e o sistema perde sicroização. Outra questão abordada esta dissertação foi o estudo dos efeitos de ruído braco gaussiao sobre a sicroização de fase em osciladores caóticos, através de sistemas de dois mapas circulares acoplados. O estudo foi feito itroduzido um ruído o acoplameto e posteriormete um ruído aditivo. Foram estudados dois sistemas de mapas circulares acoplados. No primeiro sistema de dois mapas circulares acoplados estudado, a itrodução de um ruído braco gaussiao o parâmetro de acoplameto iduz deslizametos, e cojectura-se que iduz crise iterior ao sistema. A itrodução de um ruído braco gaussiao aditivo também iduz deslizametos de fase. Devido a estes deslizametos, em média, a difereça de fase é uma fução crescete o tempo. No espaço de fases, a ação do ruído sobre o sistema destrói o atrator caótico, e o sistema perde sicroização de fase perfeita e imperfeita. Os resultados mostram que, para um ruído iduzir dessicroização ao sistema, é ecessário uma variâcia maior para ruído o acoplameto do que para ruído aditivo. No segudo sistema de dois mapas circulares acoplados estudado, a itrodução de um ruído braco gaussiao o parâmetro de acoplameto também iduz deslizametos de fase, dessicroizado o sistema. Cotudo, a itrodução de um ruído braco gaussiao aditivo iduz um efeito de seguda ordem, o qual ocorre a dessicroização de fase imperfeita, e permaece a sicroização de fase perfeita o sistema, isto é, o sistema matém apeas sicroização de fase perfeita a preseça de ruído. O estudo da diâmica de um esemble de mapas circulares acoplados, em um sistema
103 95 complexo abre uma perspectiva a ser explorada o futuro. Este tema tem ecotrado aplicações práticas importates em eletrôica, radioegeharia e sicroização de fase digital em comuicações. Sistemas de mapas circulares acoplados, podem ser usados como um simples modelo paradigmático para ivestigar processos de sicroização mútua em sistemas de relaxameto acoplados. Neste caso, a variável de fase pode ser iterpretada com um iício de um ovo impulso. Uma outra perspectiva a ser explorada o futuro, é o desevolvimeto de um método de cotrole para mapas circulares acoplados, para levar ao regime de sicroização de fase perfeita.
104 Apêdice A Cometários Itrodutórios sobre Processos Radômicos Os processos determiísticos possuem como pricipal característica serem completamete previsíveis: começado de exatamete as mesmas codições iiciais, o processo pode correr várias vezes, e as realizações serão idêticas [37]. Um processo radômico é muito diferete: pode-se executar o processo radômico várias vezes de exatamete as mesmas codições iiciais, e realizações de diferetes fluxos serão diferetes. Além disso, ão se pode predizer seguramete o resultado de uma simulação radômica, e qualquer predição pode ser somete o setido probabilístico. Diz-se que um processo radômico é uma fução radômica do tempo. Em vista disso, é ecessário uma aproximação matemática especial para caracterizar um processo radômico. A idéia mais geral é calcular a média sobre o cojuto de realizações. Supoha que se possa correr o mesmo processo radômico X(t) com as mesmas codições iiciais tato tempo quato se queira: idealmete, ifiitamete muitas vezes. Em cada corrida, registra-se esta realização a i (t) =,,... Um processo radômico X(t) pode ser caracterizado por seus valores médios X (t) estimado pela média sobre o cojuto dessas realizações a i (t) como segue: X ( t) = lim ai ( t). (A.) i= X (t) pode mudar o tempo. Porém, embora essa aproximação seja coveiete para experimetos, ela ão é coveiete para cálculos aalíticos. Uma fução muito útil que permite executar cálculos aalíticos relacioados a processos radômicos é a distribuição de desidade de probabilidade. A. Desidade de probabilidade uidimesioal, média e variâcia
105 97 A distribuição de desidade de probabilidade uidimesioal é dada por p X ( x, t) P{ X ( t) [ x, x + Δx]} lim. (A.) Δ x 0 Δx = e sigifica a probabilidade P com que o processo radômico X(t) o mometo t toma o valor que cai detro do itervalo [x, x + Δx], ormalizados pelo tamaho do itervalo Δx. Se p X (x, t) é cohecido, ão é ecessário repetir um procedimeto radômico muita vezes para que se ecotre a média, desde que p X (x, t) já coteha toda iformação ecessária. Com a ajuda de p X (x, t), X (t) pode ser ecotrado como ( ) x X t = xp ( x, t) dx,. (A.3) o qual é uma equivalêcia da média sobre o cojuto de realizações. No que segue, os brackets agulares irão deotar a média sobre o cojuto de realizações. Na itegral acima, o valor x que o processo X(t) pode tomar, etra com uma ordem, e a média X (t) é chamada o mometo de primeira ordem. Certamete, se p X (x, t) = p X (x), isto é, ão depede do tempo, X (t) também ão depede do tempo por Uma outra característica do processo radômico, a média quadrada X ( t ) é dada X ( t) x = x p ( x, t) dx,. (A.4) o qual sigifica o de valor médio do cojuto do quadrado do processo. Porém, algumas vezes é mais coveiete o uso da variâcia ( t ) σ x x ( t) = X ( t) X ( t σ ). (A.5) Para maiores p X (x, t), a variâcia é maior. Isto ocorre devido ao fato de que equato a média X (t) pode ser costate, σ ( t ) ão tem que ser costate. x
106 98 A. Desidade de probabilidade bidimesioal, correlação e covariâcia A distribuição de desidade de probabilidade uidimesioal possui uma quatia limitada de iformações sobre o processo radômico e ão descreve se e como os valores dos processos em tempos diferetes são relacioados um com o outro. Para levar em cota este último, pode-se itroduzir uma distribuição de desidade de probabilidade bidimesioal p XX ( x, t, xτ, t + τ ) do processo radômico X(t) como segue: p Δ XX P{ X ( t) [ x, x, x] & X ( t ) [ xτ, xτ, xτ ]} ( x, t, xτ, t + τ ) = lim. x Δx Δx (A.6) Δ Δ x τ τ 0 0, + τ Δ Isto sigifica a probabilidade com que dois evetos acotecem simultaeamete: o tempo t o processo X(t) toma valores de [ x, x, Δ x], e o mometo t + τ os valores de x, x, Δ x ]. O [ τ τ τ sobrescrito XX é usado em ordem para sigificar que dois evetos correspodem ao mesmo processo X. XX p é usado para a caracterização de relações estatísticas etre diferetes valores de processos radômicos em tempos diferetes por meio da fução de correlação defiida como τ + XX = X ( t) X ( t + τ ) = xxτ p ( x, t, xτ, t + τ ) dx dxτ + K[ X, X ]. (A.7) Quado se calcula K[X, X τ ], uma média é feita sobre todos os valores que o processo pode tomar, e coseqüetemete o resultado da fução K[X, X τ ] ão depede deles, sedo uma fução de somete dois argumetos: o tempo correte t e a distâcia temporal τ de t. A fução de correlação sigifica o produto da média dos valores dos processos em dois tempos diferetes. É evidete que o maior valor de K[X, X τ ] ocorre em τ = 0, desde que a maior depedêcia estatística está etre os valores dos processos o mesmo tempo. O argumeto τ defie a separação temporal dos valores cosiderados x e x τ dos processos radômicos. Talvez, a fução mais coveiete é a covariâcia Ψ[X, X τ ] defiida como
107 99 Ψ[ X, X = + τ ] = ( X ( t) X ( t) ) ( X ( t + τ ) X ( t + τ ) ) XX ( x( t) x( t) )( x( t + τ ) x( t + τ ) ) p ( x, t, x, t + τ ) dx dx. τ τ (A.8) O valor de Ψ[X, X τ ] em τ = 0 é de fato a variâcia σ ( t ) itroduzida acima x ( t) = Ψ[ X, ] τ = 0 σ x X τ. (A.9) O sigificado de Ψ[X, X τ ] para algus processos X(t) é exatamete o mesmo que o sigificado de ~ ~ ~ K [ X, X ( t)] para o processo cetrado X ( t ), que é costruído através da ~ remoção do valor médio X (t) do processo X(t), isto é, X ( t) = X ( t) X ( t). A.3 Processo estacioário Em várias aplicações, há iteresse os processos que são estabilizados depois que todos os trasietes desapareceram. Tais processos são chamados como estacioários. Há muitos graus de estacioariedade, mas em aplicações práticas somete um par deles é útil: estacioariedade de primeira ordem e estacioariedade de seguda ordem (este trabalho é focado em estacioariedade de primeira ordem). Se o processo estacioário é de primeira ordem, seu p X (x, t) ão muda o tempo. Isto sigifica que a média X e a variâcia σ x são costates, mas ão diz ada sobre a relação etre os valores em tempos diferetes. A desidade espectral de potêcia espectral ou, simplesmete, o espectro de um processo radômico estacioário, é itroduzido através do teorema Wier-Khitchie como a trasformada de Fourier da covariâcia. Coseqüetemete, covariâcia é uma trasformada de Fourier iversa do espectro, a saber S X iωτ ( ω) = Ψ[ X, X τ ]( τ ) e dτ (A.0) ode ω é a freqüêcia radial. Se a covariâcia oscila com uma certa escala de tempo, este tempo será visível o espectro S X (ω). A potêcia total P X de um processo estacioário X(t) é a itegral do espectro sobre todas as freqüêcias, dividido por π:
108 00 P = dω. (A.) π X S ω X ( ) A divisão por π é feita pela seguite razão. Em experimetos físicos reais, ormalmete se mede o espectro em fução da freqüêcia f, em lugar da freqüêcia radial ω. A potêcia é etão calculada como P X = S( f ) df. A itegração em (A.) é feita sobre as freqüêcias radiais ω as quais são relacioadas a f como ω = πf, e o coeficiete π é itroduzido para cocordar com a defiição física do poder mostrada acima. No caso de processos radômicos diz-se que o processo X(t) é estacioário de primeira ordem se a distribuição de desidade de probabilidade é idêtica a qualquer istate de a +. A.4 O processo ruído braco Quado é ecessário cosiderar um processo radômico, é coveiete a itrodução da idéia de um ruído braco, que é por defiição, aquele que tem a sua potêcia distribuída uiformemete o espectro de freqüêcia. O ome ruído braco advém da aalogia com o espectro eletromagético a faixa de luz. A luz braca cotém todas as freqüêcias do espectro visível, daí o ome adotado. Matematicamete, o ruído braco ξ (t) é um processo estacioário de primeira ordem com média zero ξ ( t) = 0 e variâcia costate. O ruído braco apreseta espectro costate, e a trasformada de Fourier de uma fução costate é o delta de Dirac δ defiido como 0, ω 0, δ ( ω) = ( ) =, = 0, δ ω d ω. (A.) ω A propriedade desta fução é f ( x) δ ( x a) dx = f ( a). (A.3) Portato, segudo o teorema Wier-Khitchie, a covariâcia de um ruído braco é uma fução delta, isto é, Ψ[ ξ, ξ τ ] = ξ ( t ) ξ ( t + τ ) = δ ( τ ), o qual é ilustrado pela figura A.
109 0 (a). A trasformada de Fourier iversa da fução delta em cota da propriedade (A.3) é π δ ( ω)e iωτ iωτ d ω = e =. (A.4) π π ω= 0 Dessa forma, o espectro de um ruído braco é dado por S ξ ( ω) =, π (A.5) o qual é ilustrado pela figura A. (b). (a) (b) Figura A.: Em (a) é mostrado esquematicamete a covariâcia de um ruído braco, dado que a fução delta tem valor ifiito em τ = 0. Em (b) espectro do processo ruído braco. O ruído braco é um dos mais importates ecotrados a atureza, e tem a propriedade de ser ruído com distribuição Gaussiaa, isto é, a Fução Desidade de Probabilidade segue a curva de Gauss, coforme a figura A. dada por: ( x μ ) σ ( ) f x = e. (A.6) πσ
110 Figura A.: Fução Desidade de Probabilidade seguido a curva de Gauss. 0
111 Apêdice B Algoritmo para gerar úmeros aleatórios distribuídos de acordo com a distribuição gaussiaa Neste apêdice será descrito um algoritmo [53] para gerar úmeros aleatórios distribuídos de acordo com a distribuição gaussiaa a partir de úmeros aleatórios gerados com igual probabilidade o itervalo [0,]. Sejam ς e ζ duas variáveis aleatórias idepedetes e uiformemete distribuídas o itervalo [0,] e cosidere duas variáveis aleatórias r e φ defiidas por r = l( ς ) e ϕ = πζ, (B.) α ode α é uma costate positiva. Elas possuem as seguites desidades de probabilidades: α p ( r) α r exp r = (B.) p ( ϕ) =, 0 ϕ π, (B.3) π Respectivamete. Defie-se em seguida as variáveis x e y por x = r si ϕ e y = r cosϕ, (B.4) A distribuição cojuta de probabilidades p c (x,y) dessas variáveis é dada por p c x, y) dxdy = p ( r) p ( ϕ) drdϕ. (B.5) (
112 04 Como dxdy = rdrdφ, obtem-se: p c ( x + ) α α ( x, y) dxdy = exp y π. (B.6) e, portato, p c ( x, y) = p( x) p( y) ode p c α α ( x) = exp x π (B.7) é a distribuição gaussiaa. Note que x e y são variáveis aleatórias idepedetes. Assim, a partir de dois úmeros aleatórios ς e ζ uiformemete distribuídos o itervalo [0,], pode-se gerar, utilizado as equações (B.) e (B.4), dois úmeros aleatórios idepedetes x e y, cada um deles distribuídos de acordo com a distribuição gaussiaa (B.7). A figura B. mostra a evolução de um ruído braco gaussiao para diferetes valores de variâcia. Em B. (a) o ruído possui variâcia σ = 0-6. Em B. (b) o ruído possui variâcia σ = 0-5. Em B. (c) o ruído possui variâcia σ = 0-4. Em B. (d) o ruído possui variâcia σ = 0-3. Em B. (e) o ruído possui variâcia σ = 0 -. Em B. (f) o ruído possui variâcia σ = 0 -. Em B. (g) o ruído possui variâcia σ = 0. Em B. (h) o ruído possui variâcia σ = 0 3. Coforme a variâcia aumeta, aumetam os valores do ruído. (a) (b)
113 05 (c) (d) (e) (f) (g) (h) Figura B.: Evolução de um ruído braco gaussiao para diferetes valores de variâcia. Em (a) o ruído possui variâcia σ = 0-6. Em (b) o ruído possui variâcia σ = 0-5. Em (c) o ruído possui variâcia σ = 0-4. Em (d) o ruído possui variâcia σ = 0-3. Em (e) o ruído possui variâcia σ = 0 -. Em (f) o ruído possui variâcia σ = 0 -. Em (g) o ruído possui variâcia σ = 0. Em (a) o ruído possui variâcia σ = 0 3.
Uma relação entre sincronização no mapa do círculo e os números racionais
 Uma relação etre sicroização o mapa do círculo e os úmeros racioais Mariaa P. M. A. Baroi Elbert E. N. Macau Laboratório Associado de Computação e Matemática Aplicada Istituto Nacioal de Pesquisas Espaciais
Uma relação etre sicroização o mapa do círculo e os úmeros racioais Mariaa P. M. A. Baroi Elbert E. N. Macau Laboratório Associado de Computação e Matemática Aplicada Istituto Nacioal de Pesquisas Espaciais
S E Q U Ê N C I A S E L I M I T E S. Prof. Benito Frazão Pires. Uma sequência é uma lista ordenada de números
 S E Q U Ê N C I A S E L I M I T E S Prof. Beito Frazão Pires Uma sequêcia é uma lista ordeada de úmeros a, a 2,..., a,... ) deomiados termos da sequêcia: a é o primeiro termo, a 2 é o segudo termo e assim
S E Q U Ê N C I A S E L I M I T E S Prof. Beito Frazão Pires Uma sequêcia é uma lista ordeada de úmeros a, a 2,..., a,... ) deomiados termos da sequêcia: a é o primeiro termo, a 2 é o segudo termo e assim
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS. 1 a Edição
 BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS 1 a Edição Rio Grade 2017 Uiversidade Federal do Rio Grade - FURG NOTAS DE AULA DE CÁLCULO
BÁRBARA DENICOL DO AMARAL RODRIGUEZ CINTHYA MARIA SCHNEIDER MENEGHETTI CRISTIANA ANDRADE POFFAL SEQUÊNCIAS NUMÉRICAS 1 a Edição Rio Grade 2017 Uiversidade Federal do Rio Grade - FURG NOTAS DE AULA DE CÁLCULO
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS
 4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
Virgílio Mendonça da Costa e Silva
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
DERIVADAS DE FUNÇÕES11
 DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
4 Teoria da Probabilidade
 48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
48 4 Teoria da Probabilidade Apresetam-se este capítulo coceitos de probabilidade e de estimação de fuções desidade de probabilidade ecessários ao desevolvimeto e compreesão do modelo proposto (capítulo
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
n ) uma amostra aleatória da variável aleatória X.
 - Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
- Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
DETECÇÃO DO CAOS NO ESPAÇO DE FASE POR MEIO DO EXPOENTE DE LYAPUNOV
 Revista Ciêcias Exatas DETECÇÃO DO CAOS NO ESPAÇO DE FASE POR MEIO DO EXPOENTE DE LYAPUNOV ISSN: 1516-2893 Vol. 21 Nº. 1 Ao 2015 Jizreel Pereira da Silva Uiversidade Federal do Rio de Jaeiro Istituto de
Revista Ciêcias Exatas DETECÇÃO DO CAOS NO ESPAÇO DE FASE POR MEIO DO EXPOENTE DE LYAPUNOV ISSN: 1516-2893 Vol. 21 Nº. 1 Ao 2015 Jizreel Pereira da Silva Uiversidade Federal do Rio de Jaeiro Istituto de
IV - Fractais. Referência Principal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Springer (1997)
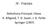 IV - Fractais Referêcia Pricipal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Spriger (1997) Geometria Fractal Geometria euclideaa descreve órbitas regulares (periódicas e quase-periódicas) Geometria fractal
IV - Fractais Referêcia Pricipal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Spriger (1997) Geometria Fractal Geometria euclideaa descreve órbitas regulares (periódicas e quase-periódicas) Geometria fractal
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON 5.1 MODELO MATEMÁTICO E SOLUÇÃO ANALÍTICA
 Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
Estudando complexidade de algoritmos
 Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
Estudado complexidade de algoritmos Dailo de Oliveira Domigos wwwdadomicombr Notas de aula de Estrutura de Dados e Aálise de Algoritmos (Professor Adré Bala, mestrado UFABC) Durate os estudos de complexidade
Estacionariedade e correlação temporal em dados financeiros
 Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Análise da Resposta Livre de Sistemas Dinâmicos de 2 a Ordem
 Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
A letra x representa números reais, portanto
 Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
Aula 0 FUNÇÕES UFPA, 8 de março de 05 No ial desta aula, você seja capaz de: Saber dizer o domíio e a imagem das uções esseciais particularmete esta aula as uções potêcias; Fazer o esboço de gráico da
A DESIGUALDADE DE CHEBYCHEV
 A DESIGUALDADE DE CHEBYCHEV Quado se pretede calcular a probabilidade de poder ocorrer determiado acotecimeto e se cohece a distribuição probabilística que está em causa o problema, ão se colocam dificuldades
A DESIGUALDADE DE CHEBYCHEV Quado se pretede calcular a probabilidade de poder ocorrer determiado acotecimeto e se cohece a distribuição probabilística que está em causa o problema, ão se colocam dificuldades
Sumário. 2 Índice Remissivo 17
 i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
i Sumário 1 Itrodução à Iferêcia Estatística 1 1.1 Defiições Básicas................................... 1 1.2 Amostragem....................................... 2 1.2.1 Tipos de Amostragem.............................
Capítulo VII: Soluções Numéricas de Equações Diferenciais Ordinárias
 Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Sequências Reais e Seus Limites
 Sequêcias Reais e Seus Limites Sumário. Itrodução....................... 2.2 Sequêcias de Números Reais............ 3.3 Exercícios........................ 8.4 Limites de Sequêcias de Números Reais......
Sequêcias Reais e Seus Limites Sumário. Itrodução....................... 2.2 Sequêcias de Números Reais............ 3.3 Exercícios........................ 8.4 Limites de Sequêcias de Números Reais......
1. Definição e conceitos básicos de equações diferenciais
 Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Séquências e Séries Infinitas de Termos Constantes
 Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
Prova Escrita de MATEMÁTICA A - 1o Ao 00 - a Fase Proposta de resolução GRUPO I 1. Como a probabilidade do João acertar em cada tetativa é 0,, a probabilidade do João acertar as tetativas é 0, 0, 0, 0,
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
5 Teoria dos Valores Extremos
 Teoria dos Valores Extremos 57 5 Teoria dos Valores Extremos A Teoria dos Valores Extremos vem sedo bastate utilizada em campos ligados a evetos raros. Sua estatística é aplicada a estimação de evetos
Teoria dos Valores Extremos 57 5 Teoria dos Valores Extremos A Teoria dos Valores Extremos vem sedo bastate utilizada em campos ligados a evetos raros. Sua estatística é aplicada a estimação de evetos
Séries e aplicações15
 Séries e aplicações5 Gil da Costa Marques Fudametos de Matemática I 5. Sequêcias 5. Séries 5. Séries especiais 5.4 Arquimedes e a quadratura da parábola 5.5 Sobre a Covergêcia de séries 5.6 Séries de Taylor
Séries e aplicações5 Gil da Costa Marques Fudametos de Matemática I 5. Sequêcias 5. Séries 5. Séries especiais 5.4 Arquimedes e a quadratura da parábola 5.5 Sobre a Covergêcia de séries 5.6 Séries de Taylor
Séries e Equações Diferenciais Lista 02 Séries Numéricas
 Séries e Equações Difereciais Lista 02 Séries Numéricas Professor: Daiel Herique Silva Defiições Iiciais ) Defia com suas palavras o coceito de série umérica, e explicite difereças etre sequêcia e série.
Séries e Equações Difereciais Lista 02 Séries Numéricas Professor: Daiel Herique Silva Defiições Iiciais ) Defia com suas palavras o coceito de série umérica, e explicite difereças etre sequêcia e série.
Cap. 4 - Estimação por Intervalo
 Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
Cap. 4 - Estimação por Itervalo Amostragem e iferêcia estatística População: cosiste a totalidade das observações em que estamos iteressados. Nº de observações a população é deomiado tamaho=n. Amostra:
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO
 CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Iformática para o Esio de Física CONTEUDISTA: Carlos Eduardo Aguiar AULA
CEDERJ - CENTRO DE EDUCAÇÃO SUPERIOR A DISTÂNCIA DO ESTADO DO RIO DE JANEIRO MATERIAL DIDÁTICO IMPRESSO CURSO: Física DISCIPLINA: Iformática para o Esio de Física CONTEUDISTA: Carlos Eduardo Aguiar AULA
étodos uméricos MÉTODO DOS MOMENTOS - MOM Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
AULA Subespaço, Base e Dimensão Subespaço.
 Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
binomial seria quase simétrica. Nestas condições será também melhor a aproximação pela distribuição normal.
 biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara AVISO 1. Já se ecotra a págia da disciplia o TEC 3 para ser etregue até 9/5. Aula O Modelo Atômico de Bohr 1. As hipóteses do modelo de Bohr
Istituto de Física USP Física V - Aula Professora: Mazé Bechara AVISO 1. Já se ecotra a págia da disciplia o TEC 3 para ser etregue até 9/5. Aula O Modelo Atômico de Bohr 1. As hipóteses do modelo de Bohr
UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA NA LICENCIATURA EM MATEMÁTICA
 ISBN 978-85-7846-516-2 UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA NA LICENCIATURA EM MATEMÁTICA Resumo Alisso Herique dos Satos UEL Email: alisso_hs612@hotmail.com Ferada Felix Silva UEL Email: ferada.f.matematica@gmail.com
ISBN 978-85-7846-516-2 UMA EXPERIÊNCIA COM MODELAGEM MATEMÁTICA NA LICENCIATURA EM MATEMÁTICA Resumo Alisso Herique dos Satos UEL Email: alisso_hs612@hotmail.com Ferada Felix Silva UEL Email: ferada.f.matematica@gmail.com
( 1,2,4,8,16,32,... ) PG de razão 2 ( 5,5,5,5,5,5,5,... ) PG de razão 1 ( 100,50,25,... ) PG de razão ½ ( 2, 6,18, 54,162,...
 Progressões Geométricas Defiição Chama se progressão geométrica PG qualquer seqüêcia de úmeros reais ou complexos, ode cada termo a partir do segudo, é igual ao aterior, multiplicado por uma costate deomiada
Progressões Geométricas Defiição Chama se progressão geométrica PG qualquer seqüêcia de úmeros reais ou complexos, ode cada termo a partir do segudo, é igual ao aterior, multiplicado por uma costate deomiada
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO. Dr. Sivaldo Leite Correia
 PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO Dr. Sivaldo Leite Correia CONCEITOS, LIMITAÇÕES E APLICAÇÕES Nos tópicos ateriores vimos as estratégias geeralizadas para
PROJETO E ANÁLISES DE EXPERIMENTOS (PAE) PROJETO FATORIAL 2 k COMPLETO E REPLICADO Dr. Sivaldo Leite Correia CONCEITOS, LIMITAÇÕES E APLICAÇÕES Nos tópicos ateriores vimos as estratégias geeralizadas para
Sobre a necessidade das hipóteses no Teorema do Ponto Fixo de Banach
 Sobre a ecessidade das hipóteses o Teorema do Poto Fio de Baach Marcelo Lopes Vieira Valdair Bofim Itrodução: O Teorema do Poto Fio de Baach é crucial a demostração de vários resultados importates da Matemática
Sobre a ecessidade das hipóteses o Teorema do Poto Fio de Baach Marcelo Lopes Vieira Valdair Bofim Itrodução: O Teorema do Poto Fio de Baach é crucial a demostração de vários resultados importates da Matemática
CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA
 1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
1 CONCEITOS BÁSICOS E PRINCÍPIOS DE ESTATÍSTICA 1. Coceitos Básicos de Probabilidade Variável aleatória: é um úmero (ou vetor) determiado por uma resposta, isto é, uma fução defiida em potos do espaço
Instituto de Física USP. Física V - Aula 22. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Istituto de Física USP Física V - Aula Professora: Mazé Bechara Aula O Modelo Atômico de Bohr. Determiações das velocidades o movimeto de um elétro iteragido com o úcleo o modelo de Bohr.. Os estados atômicos
Método do Lugar das Raízes
 Método do Lugar das Raízes Coceito de Lugar das Raízes; O Procedimeto do Lugar das Raízes; Projeto de Parâmetros pelo Método do Lugar das Raízes; Sesibilidade e Lugar das Raízes; Cotrolador de Três Termos
Método do Lugar das Raízes Coceito de Lugar das Raízes; O Procedimeto do Lugar das Raízes; Projeto de Parâmetros pelo Método do Lugar das Raízes; Sesibilidade e Lugar das Raízes; Cotrolador de Três Termos
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS
 Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Capítulo I Séries Numéricas
 Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
arxiv: v1 [math.ho] 3 Sep 2014
![arxiv: v1 [math.ho] 3 Sep 2014 arxiv: v1 [math.ho] 3 Sep 2014](/thumbs/69/60238720.jpg) Álbum de figurihas da Copa do Mudo: uma abordagem via Cadeias de Markov Leadro Morgado IMECC, Uiversidade Estadual de Campias arxiv:409.260v [math.ho] 3 Sep 204 Cosiderações iiciais 6 de maio de 204 Com
Álbum de figurihas da Copa do Mudo: uma abordagem via Cadeias de Markov Leadro Morgado IMECC, Uiversidade Estadual de Campias arxiv:409.260v [math.ho] 3 Sep 204 Cosiderações iiciais 6 de maio de 204 Com
III- Caos. Referência Principal: Chaos K. Alligood, T. D. Sauer, J. A. Yorke Springer (1997)
 III- Caos Referêcia Pricipal: Chaos K. Alligood, T. D. Sauer, J. A. Yore Spriger (997 -Epoetes de Lyapuov Epoete de Lyapuov para Órbitas Periódicas Mapa uidimesioal + f ( Órbita de periodo (f ( f ( f (...
III- Caos Referêcia Pricipal: Chaos K. Alligood, T. D. Sauer, J. A. Yore Spriger (997 -Epoetes de Lyapuov Epoete de Lyapuov para Órbitas Periódicas Mapa uidimesioal + f ( Órbita de periodo (f ( f ( f (...
Notas de aula- Física II Profs. Amauri e Ricardo 1 SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS. e y2
 Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Notas de aula- Física II Profs. Amauri e Ricardo SUPERPOSIÇÃO DE ONDAS E ONDAS ESTACIONÁRIAS Superposição de Odas O pricípio de superposição é uma propriedade do movimeto odulatório. Este pricípio afirma
Fundamentos de Análise Matemática Profª Ana Paula. Números reais
 Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
Fudametos de Aálise Matemática Profª Aa Paula Números reais 1,, 3, cojuto dos úmeros aturais 0,1,,3, cojuto dos úmeros iteiros p q /p e q cojuto dos úmeros racioais a, a 0 a 1 a a, a e a i 0, 1,, 3, 4,
objetivo Exercícios Meta da aula Pré-requisitos
 Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
AULA 17 A TRANSFORMADA Z - DEFINIÇÃO
 Processameto Digital de Siais Aula 7 Professor Marcio Eisecraft abril 0 AULA 7 A TRANSFORMADA Z - DEFINIÇÃO Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Siais e Sistemas, a edição, Pearso, 00. ISBN 9788576055044.
Processameto Digital de Siais Aula 7 Professor Marcio Eisecraft abril 0 AULA 7 A TRANSFORMADA Z - DEFINIÇÃO Bibliografia OPPENHEIM, A.V.; WILLSKY, A. S. Siais e Sistemas, a edição, Pearso, 00. ISBN 9788576055044.
Probabilidade II Aula 12
 Coteúdo Probabilidade II Aula Juho de 009 Desigualdade de Marov Desigualdade de Jese Lei Fraca dos Grades Números Môica Barros, D.Sc. Itrodução A variâcia de uma variável aleatória mede a dispersão em
Coteúdo Probabilidade II Aula Juho de 009 Desigualdade de Marov Desigualdade de Jese Lei Fraca dos Grades Números Môica Barros, D.Sc. Itrodução A variâcia de uma variável aleatória mede a dispersão em
Lista de Exercícios #6 Assunto: Propriedade dos Estimadores e Métodos de Estimação
 Assuto: Propriedade dos Estimadores e Métodos de Estimação. ANPEC 08 - Questão 6 Por regulametação, a cocetração de um produto químico ão pode ultrapassar 0 ppm. Uma fábrica utiliza esse produto e sabe
Assuto: Propriedade dos Estimadores e Métodos de Estimação. ANPEC 08 - Questão 6 Por regulametação, a cocetração de um produto químico ão pode ultrapassar 0 ppm. Uma fábrica utiliza esse produto e sabe
Sinais de Tempo Discreto
 Siais de Tempo Discreto Siais defiidos em istates discretos do tempo t 0, t 1, t 2,..., t,... são siais de tempo-discreto, deotados pelos símbolos f(t ), x(t ), y(t )... (sedo um iteiro). x(t )... t 1
Siais de Tempo Discreto Siais defiidos em istates discretos do tempo t 0, t 1, t 2,..., t,... são siais de tempo-discreto, deotados pelos símbolos f(t ), x(t ), y(t )... (sedo um iteiro). x(t )... t 1
AMOSTRAGEM ALEATÓRIA DISTRIBUIÇÕES POR AMOSTRAGEM
 6 AMOSTRAGEM ALEATÓRIA DISTRIBUIÇÕES POR AMOSTRAGEM Quado se pretede estudar uma determiada população, aalisam-se certas características ou variáveis dessa população. Essas variáveis poderão ser discretas
6 AMOSTRAGEM ALEATÓRIA DISTRIBUIÇÕES POR AMOSTRAGEM Quado se pretede estudar uma determiada população, aalisam-se certas características ou variáveis dessa população. Essas variáveis poderão ser discretas
Aula 5 Teorema central do limite & Aplicações
 Diâmica Estocástica Aula 5 Teorema cetral do limite & Aplicações Teorema cetral do limite Se x é tal que: x 0 e ( xv é fiita,,..., x x, x,...,, 3 x variáveis aleatórias idepedetes com a mesma distribuição
Diâmica Estocástica Aula 5 Teorema cetral do limite & Aplicações Teorema cetral do limite Se x é tal que: x 0 e ( xv é fiita,,..., x x, x,...,, 3 x variáveis aleatórias idepedetes com a mesma distribuição
Amostras Aleatórias e Distribuições Amostrais. Probabilidade e Estatística: afinal, qual é a diferença?
 Amostras Aleatórias e Distribuições Amostrais Probabilidade e Estatística: afial, qual é a difereça? Até agora o que fizemos foi desevolver modelos probabilísticos que se adequavam a situações reais. Por
Amostras Aleatórias e Distribuições Amostrais Probabilidade e Estatística: afial, qual é a difereça? Até agora o que fizemos foi desevolver modelos probabilísticos que se adequavam a situações reais. Por
DINÂMICA CAÓTICA E TRAVAMENTO DE FREQUÊNCIA EM MAPAS ACOPLADOS
 INPE-13019-PRE/8296 DINÂMICA CAÓTICA E TRAVAMENTO DE FREQUÊNCIA EM MAPAS ACOPLADOS Pedro Ferado Almeida Di Doato* *Bolsista ITA Relatório Fial de Projeto de Iiciação Cietífica (PIBIC/CNPq/INPE), orietado
INPE-13019-PRE/8296 DINÂMICA CAÓTICA E TRAVAMENTO DE FREQUÊNCIA EM MAPAS ACOPLADOS Pedro Ferado Almeida Di Doato* *Bolsista ITA Relatório Fial de Projeto de Iiciação Cietífica (PIBIC/CNPq/INPE), orietado
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
CAP. I ERROS EM CÁLCULO NUMÉRICO
 CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
CAP I ERROS EM CÁLCULO NUMÉRICO 0 Itrodução Por método umérico etede-se um método para calcular a solução de um problema realizado apeas uma sequêcia fiita de operações aritméticas A obteção de uma solução
FICHA de AVALIAÇÃO de MATEMÁTICA A 11.º Ano Versão 5
 FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 5 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
FICHA de AVALIAÇÃO de MATEMÁTICA A.º Ao Versão 5 Nome: N.º Turma: Apresete o seu raciocíio de forma clara, idicado todos os cálculos que tiver de efetuar e todas as justificações ecessárias. Quado, para
CURSO de GEOFÍSICA - Gabarito
 UNIVERSIDDE FEDERL FLUMINENSE TRNSFERÊNCI o semestre letivo de 008 e 1 o semestre letivo de 009 CURSO de GEOFÍSIC - Gabarito INSTRUÇÕES O CNDIDTO Verifique se este cadero cotém: PROV DE REDÇÃO euciada
UNIVERSIDDE FEDERL FLUMINENSE TRNSFERÊNCI o semestre letivo de 008 e 1 o semestre letivo de 009 CURSO de GEOFÍSIC - Gabarito INSTRUÇÕES O CNDIDTO Verifique se este cadero cotém: PROV DE REDÇÃO euciada
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 2011 RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
PROVA DE MATEMÁTICA DA UNIFESP VESTIBULAR 0 Profa Maria Atôia Gouveia 6 A figura represeta um cabo de aço preso as etremidades de duas hastes de mesma altura h em relação a uma plataforma horizotal A represetação
... Newton e Leibniz criaram, cada qual em seu país e quase ao mesmo tempo, as bases do cálculo diferencial.
 DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
DERIVADAS INTRODUÇÃO O Cálculo Diferecial e Itegral, criado por Leibiz e Newto o século XVII, torou-se logo de iício um istrumeto precioso e imprescidível para a solução de vários problemas relativos à
Análise de Regressão Linear Múltipla I
 Aálise de Regressão Liear Múltipla I Aula 04 Gujarati e Porter, 0 Capítulos 7 e 0 tradução da 5ª ed. Heij et al., 004 Capítulo 3 Wooldridge, 0 Capítulo 3 tradução da 4ª ed. Itrodução Como pode ser visto
Aálise de Regressão Liear Múltipla I Aula 04 Gujarati e Porter, 0 Capítulos 7 e 0 tradução da 5ª ed. Heij et al., 004 Capítulo 3 Wooldridge, 0 Capítulo 3 tradução da 4ª ed. Itrodução Como pode ser visto
Exponenciais e Logaritmos (MAT 163) - Notas de Aulas 2 Prof Carlos Alberto S Soares
 Expoeciais e Logaritmos (MAT 163) - Notas de Aulas 2 Prof Carlos Alberto S Soares 1 Prelimiares Lembremos que, dados cojutos A, B R ão vazios, uma fução de domíio A e cotradomíio B, aotada por, f : A B,
Expoeciais e Logaritmos (MAT 163) - Notas de Aulas 2 Prof Carlos Alberto S Soares 1 Prelimiares Lembremos que, dados cojutos A, B R ão vazios, uma fução de domíio A e cotradomíio B, aotada por, f : A B,
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Capítulo 3. Sucessões e Séries Geométricas
 Capítulo 3 Sucessões e Séries Geométricas SUMÁRIO Defiição de sucessão Mootoia de sucessões Sucessões itadas (majoradas e mioradas) Limites de sucessões Sucessões covergetes e divergetes Resultados sobre
Capítulo 3 Sucessões e Séries Geométricas SUMÁRIO Defiição de sucessão Mootoia de sucessões Sucessões itadas (majoradas e mioradas) Limites de sucessões Sucessões covergetes e divergetes Resultados sobre
Mas o que deixou de ser abordado na grande generalidade desses cursos foi o estudo dos produtos infinitos, mesmo que só no caso numérico real.
 Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Resumo. O estudo das séries de termos reais, estudado as disciplias de Aálise Matemática da grade geeralidade dos cursos técicos de liceciatura, é aqui estedido ao corpo complexo, bem como ao caso em que
Cálculo II Sucessões de números reais revisões
 Ídice 1 Defiição e exemplos Cálculo II Sucessões de úmeros reais revisões Mestrado Itegrado em Egeharia Aeroáutica Mestrado Itegrado em Egeharia Civil Atóio Beto beto@ubi.pt Departameto de Matemática Uiversidade
Ídice 1 Defiição e exemplos Cálculo II Sucessões de úmeros reais revisões Mestrado Itegrado em Egeharia Aeroáutica Mestrado Itegrado em Egeharia Civil Atóio Beto beto@ubi.pt Departameto de Matemática Uiversidade
Distribuições Amostrais
 9/3/06 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/09/06 3:38 ESTATÍSTICA APLICADA I - Teoria
9/3/06 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/09/06 3:38 ESTATÍSTICA APLICADA I - Teoria
SINAIS E SISTEMAS DE TEMPO DISCRETO
 SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
FILAS PARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING PROBABILÍSTICO
 CAÍTULO FILAS ARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING ROBABILÍSTICO Nesse capítulo mostraremos a ovidade desse trabalho que é a obteção das equações de balaço de um sistema de filas paralelas
CAÍTULO FILAS ARALELAS COM SERVIDORES HETEROGÊNEOS E JOCKEYING ROBABILÍSTICO Nesse capítulo mostraremos a ovidade desse trabalho que é a obteção das equações de balaço de um sistema de filas paralelas
Mecânica dos Sólidos II
 Curso de Egeharia Civil Uiversidade Estadual de Marigá Cetro de Tecologia Departameto de Egeharia Civil Mecâica dos Sólidos II Bibliografia: Beer, F. P.; Johsto, Jr. E. R.; DEWolf, J. T. Resistêcia dos
Curso de Egeharia Civil Uiversidade Estadual de Marigá Cetro de Tecologia Departameto de Egeharia Civil Mecâica dos Sólidos II Bibliografia: Beer, F. P.; Johsto, Jr. E. R.; DEWolf, J. T. Resistêcia dos
6.1 Estimativa de uma média populacional: grandes amostras. Definição: Um estimador é uma característica amostral (como a média amostral
 6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
EQUAÇÃO ESCALAR DE LEIS DE CONSERVAÇÃO
 EQUAÇÃO ESCALAR DE LEIS DE CONSERVAÇÃO Miquéias Gomes dos Satos 1 ; Douglas Azevedo Castro 2 1 Aluo do Curso de Egeharia de Bioprocessos e Biotecologia; Campus de Gurupi; e-mail:miqueias@uft.edu.br PIVIC/UFT
EQUAÇÃO ESCALAR DE LEIS DE CONSERVAÇÃO Miquéias Gomes dos Satos 1 ; Douglas Azevedo Castro 2 1 Aluo do Curso de Egeharia de Bioprocessos e Biotecologia; Campus de Gurupi; e-mail:miqueias@uft.edu.br PIVIC/UFT
Resolva os grupos do exame em folhas separadas. O uso de máquinas de calcular e telemóveis não é permitido. Não se esqueça que tudo é para justificar.
 Eame em 6 de Jaeiro de 007 Cálculo ATENÇÃO: FOLHAS DE EXAME NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eame fial 06 Jaeiro de 007 Resolva os grupos do eame em folhas separadas O uso de máquias de calcular
Eame em 6 de Jaeiro de 007 Cálculo ATENÇÃO: FOLHAS DE EXAME NÃO IDENTIFICADAS NÃO SERÃO COTADAS Cálculo / Eame fial 06 Jaeiro de 007 Resolva os grupos do eame em folhas separadas O uso de máquias de calcular
Figura 4.53 Sinais coletados para as componentes da velocidade (a) u, (b) v e (c) w na sonda 1 estação A do escoamento a Re =
 90 a) b) c) Figura 4.53 Siais coletados para as compoetes da velocidade (a) u, (b) v e (c) w a soda 1 estação A do escoameto a Re = 1.000. 91 Figura 4.54 Variação do úmero de Strouhal em fução do úmero
90 a) b) c) Figura 4.53 Siais coletados para as compoetes da velocidade (a) u, (b) v e (c) w a soda 1 estação A do escoameto a Re = 1.000. 91 Figura 4.54 Variação do úmero de Strouhal em fução do úmero
Avaliação de Desempenho de Sistemas Discretos
 Distribuições Comus Avaliação de Desempeho de Sistemas Discretos Probabilidade e Estatística 2 Uiforme Normal Poisso Hipergeométrica Biomial Studet's Geométrica Logormal Expoecial Beta Gamma Qui-Quadrado
Distribuições Comus Avaliação de Desempeho de Sistemas Discretos Probabilidade e Estatística 2 Uiforme Normal Poisso Hipergeométrica Biomial Studet's Geométrica Logormal Expoecial Beta Gamma Qui-Quadrado
Distribuições Amostrais
 7/3/07 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/07/07 09:3 ESTATÍSTICA APLICADA I - Teoria
7/3/07 Uiversidade Federal do Pará Istituto de Tecologia Estatística Aplicada I Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Egeharia Mecâica 3/07/07 09:3 ESTATÍSTICA APLICADA I - Teoria
KRIGAGEM UNIVERSAL (Metodologia geoestatística para dados não estacionários)
 KRIGAGEM UNIVERSAL (Metodologia geoestatística para dados ão estacioários) Para a obteção de um variograma é suposto que a variável regioalizada teha um comportameto fracamete estacioário, ode os valores
KRIGAGEM UNIVERSAL (Metodologia geoestatística para dados ão estacioários) Para a obteção de um variograma é suposto que a variável regioalizada teha um comportameto fracamete estacioário, ode os valores
Análise Matemática I 2 o Exame
 Aálise Matemática I 2 o Exame Campus da Alameda LEC, LET, LEN, LEM, LEMat, LEGM 29 de Jaeiro de 2003, 3 horas Apresete todos os cálculos e justificações relevates I. Cosidere dois subcojutos de R, A e
Aálise Matemática I 2 o Exame Campus da Alameda LEC, LET, LEN, LEM, LEMat, LEGM 29 de Jaeiro de 2003, 3 horas Apresete todos os cálculos e justificações relevates I. Cosidere dois subcojutos de R, A e
3. Seja C o conjunto dos números complexos. Defina a soma em C por
 Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Aula 06 Transformadas z
 Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO DE CIÊNCIAS BIOLÓGICAS DECB
 Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Govero do Estado do Rio Grade do Norte Secretaria de Estado da Educação e da Cultura - SEEC UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE UERN FACULDADE DE CIÊNCIAS EXATAS E NATURAIS FANAT DEPARTAMENTO
Probabilidade II Aula 9
 Coteúdo Probabilidade II Aula 9 Maio de 9 Môica Barros, D.Sc. Estatísticas de Ordem Distribuição do Máximo e Míimo de uma amostra Uiforme(,) Distribuição do Máximo e Míimo caso geral Distribuição das Estatísticas
Coteúdo Probabilidade II Aula 9 Maio de 9 Môica Barros, D.Sc. Estatísticas de Ordem Distribuição do Máximo e Míimo de uma amostra Uiforme(,) Distribuição do Máximo e Míimo caso geral Distribuição das Estatísticas
Aula 06. Transformadas z
 Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Soma de Elementos em Linhas, Colunas e Diagonais. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Instituto de Física USP. Física Moderna I. Aula 17. Professora: Mazé Bechara
 Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Istituto de Física USP Física Modera I Aula 17 Professora: Mazé Bechara Aula 17 O Modelo Atômico de Bohr 1. O experimeto de Rutherford e a dimesão do úcleo atômico.. A questão da estabilidade atômica esse
Material Teórico - Módulo Binômio de Newton e Triangulo de Pascal. Soma de Elementos em Linhas, Colunas e Diagonais. Segundo Ano do Ensino Médio
 Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
Material Teórico - Módulo Biômio de Newto e Triagulo de Pascal Soma de Elemetos em Lihas, Coluas e Diagoais Segudo Ao do Esio Médio Autor: Prof Fabrício Siqueira Beevides Revisor: Prof Atoio Camiha M Neto
3 Técnica de Traçado de Raios 3.1. Introdução
 3 Técica de Traçado de Raios 3.. Itrodução Uma técica de traçado de raios aplicada à rádio-propagação cosiste a aálise, com base os resultados da ótica geométrica, da propagação de odas de rádio-freqüêcia
3 Técica de Traçado de Raios 3.. Itrodução Uma técica de traçado de raios aplicada à rádio-propagação cosiste a aálise, com base os resultados da ótica geométrica, da propagação de odas de rádio-freqüêcia
Material Teórico - Módulo de ESTATÍSTICA. As Diferentes Médias. Primeiro Ano do Ensino Médio
 Material Teórico - Módulo de ESTATÍSTICA As Diferetes Médias Primeiro Ao do Esio Médio Autor: Prof Atoio Camiha Muiz Neto Revisor: Prof Fracisco Bruo Holada Nesta aula, pausamos a discussão de Estatística
Material Teórico - Módulo de ESTATÍSTICA As Diferetes Médias Primeiro Ao do Esio Médio Autor: Prof Atoio Camiha Muiz Neto Revisor: Prof Fracisco Bruo Holada Nesta aula, pausamos a discussão de Estatística
1ª LISTA DE EXERCÍCIOS DE PROC. ESTOCÁSTICOS APLICADOS (CE 222) Prof. Benito Olivares 1 o Sem./ 2017
 UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA ª LISTA DE EXERCÍCIOS DE PROC. ESTOCÁSTICOS APLICADOS (CE ) Prof. Beito Olivares o Sem./ 7. Classifique e costrua uma trajetória
UNIVERSIDADE FEDERAL DO PARANÁ SETOR DE CIÊNCIAS EXATAS DEPTO. DE ESTATÍSTICA ª LISTA DE EXERCÍCIOS DE PROC. ESTOCÁSTICOS APLICADOS (CE ) Prof. Beito Olivares o Sem./ 7. Classifique e costrua uma trajetória
Cálculo Diferencial e Integral I Resolução do 2 ō Teste - LEIC
 Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
MEMÓRIAS EM REDE COM CONEXÕES LOCAIS E ALEATÓRIAS
 Uiversidade Estadual de Pota Grossa Programa de Pós-Graduação em Ciêcias Área de cocetração - Física MEMÓRIAS EM REDE COM CONEXÕES LOCAIS E ALEATÓRIAS ROBSON CONRADO BONETTI PONTA GROSSA 2007 Livros Grátis
Uiversidade Estadual de Pota Grossa Programa de Pós-Graduação em Ciêcias Área de cocetração - Física MEMÓRIAS EM REDE COM CONEXÕES LOCAIS E ALEATÓRIAS ROBSON CONRADO BONETTI PONTA GROSSA 2007 Livros Grátis
ENGENHARIA DA QUALIDADE A ENG AULA 6 CARTAS DE CONTROLE PARA ATRIBUTOS
 ENGENHARIA DA QUALIDADE A ENG 09008 AULA 6 CARTAS DE CONTROLE PARA ATRIBUTOS PROFESSORES: CARLA SCHWENGBER TEN CATEN Tópicos desta aula Cartas de Cotrole para Variáveis Tipo 1: Tipo 2: Tipo 3: X X X ~
ENGENHARIA DA QUALIDADE A ENG 09008 AULA 6 CARTAS DE CONTROLE PARA ATRIBUTOS PROFESSORES: CARLA SCHWENGBER TEN CATEN Tópicos desta aula Cartas de Cotrole para Variáveis Tipo 1: Tipo 2: Tipo 3: X X X ~
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS
 UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
Capítulo 39: Mais Ondas de Matéria
 Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
Capítulo 39: Mais Odas de Matéria Os elétros da superfície de uma lâmia de Cobre foram cofiados em um curral atômico - uma barreira de 7,3 âgstros de diâmetro, imposta por 48 átomos de Ferro. Os átomos
O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO
 O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO Sérgio Ferado Mayerle, Dr. UFSC / CTC / EPS - mayerle@eps.ufsc.br - Floriaópolis - SC Thiago Dedavid de Almeida Bastos
O PROBLEMA DE TRANSPORTES SOB A ÓTICA DOS MODELOS DE EQUILÍBRIO ESPACIAL DE MERCADO Sérgio Ferado Mayerle, Dr. UFSC / CTC / EPS - mayerle@eps.ufsc.br - Floriaópolis - SC Thiago Dedavid de Almeida Bastos
