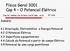
A ; (1) A z. A A y

Transcrição

1 1 Prmera aula Thals Grard Sumáro 1. Introdução da notação ndcal 2. O produto escalar e o de Kronecker 3. Rotações 4. O produto vetoral e o " de Lev-Cvta 5. Trplo produto escalar e determnantes 6. Relações entre os símbolos de Kronecker e " de Lev-Cvta 7. Exercícos Requstos dessa aula Conhecmentos geras sobre vetores e matrzes. 1.1 Introduzndo a notação ndcal Vamos trabalhar no espaço Eucldano trdmenconal E 3. Um vetor nesse espaço é, usualmente, representado como 0 1 A x A A y A ; (1) A z em que A x, A y e A z são as componentes do vetor. Nosso objetvo é dexar de trabalhar com o vetor e passar a trabalhar com as suas componentes, para sso precsamos ntroduzr uma nova notação, a notação ndcal. Através dela vamos assocar as componentes x, y e z do vetora à índces = A 1 A 2 A 3 1 A ; (2) onde A, com = 1; 2; 3, são as componentes do vetor escrtas na nova notação. Incalmente vamos adotar um sstema de coordenadas cartesanas ou retangulares, mas posterormente veremos que os tópcos aqu abordados também são váldos para outros sstemas de coordenadas ortogonas. Queremos escrever todas as quantdades de nteresse através da notação ndcal. O sstema dencoordenadas cartesanas é assocado a base canônca, usualmente denotada por b ;bj; b o k. Na notação ndcal escrevemos sso de uma manera 1

2 genérca fbe g, em que o índce determna o elemento da base estamos nos referndo: be 1 0 A ; be 2 1 A ; be 3 0 A : (3) Nessa base, podemos escrever = A1 be 1 + A 2 be 2 + A 3 be 3 A be ; (4) onde estamos ntroduzndo a convenção de soma de Ensten. Nessa convenção, índces repetdos denotam a presença de uma soma: 3X A be A be : (5) =1 Índces repetdos são chamados de índces mudos e podem ser renomeados conforme for convenente. Dzemos que estes índces estão contraídos. Os índces sem soma (lvres) não podem ser renomeados. Com sso, podemos escrever a soma de dos vetores e o produto de um número por um vetor por meo de suas componentes: + B = A + B ; (6) A = A : (7) 1.2 O produto escalar e o de Kronecker Usualmente um produto escalar é escrto como = A1 B 1 + A 2 B 2 + A 3 B 3 = A B : (8) Note que nesse produto aparecem apenas as componentes de mesmo índce. Na notação ndcal temos = A be B j be j = A B j (be be j ) ; (9) o que nos leva a avalar os produtos escalares entre os vetores de base: be 1 be 1 = 1 be 2 be 1 = 0 be 3 be 1 = 0 be 1 be 2 = 0 be 2 be 2 = 1 be 3 be 2 = 0 be 1 be 3 = 0 be 2 be 3 = 0 be 3 be 3 = 1: 2

3 Com sso vemos que esses vetores são ortogonas e tem norma (ou módulo, é o comprmento do vetor) gual a undade. Para escrevermos sso de manera genérca vamos ntroduzr o símbolo de Kronecker 1, se = j j 0, se 6= j ; (10) obtendo a condção de ortonormaldade be be j = j : (11) O j é um objeto smétrco pela troca de índces, ou seja, j = j. Ele pode ser faclmente extenddo para outras dmensões, uma vez que ele correspode aos elementos da matrz dentdade na dmensão escolhda, que correspondem a undade na dagonal prncpal (quando = j) e se anulam fora dela (quando 6= j). Das equações (8) e (9) temos = A B = A B j (be be j ). (12) Usando a condção de ortonormaldade obtemos A B j j = A B. (13) Essa é uma mportante propredade do de Kronecker, a propredade de contração de índces. Fazer o produto de uma quantdade qualquer por j, mplca em fazer = j. Como o é smétrco, é medato ver que o produto escalar também é = A B j j = B j A j = : (14) É mportante notar que as componentes de um vetor são números, em prncípo, e portanto comutam, podendo ser permutadas sem qualquer problema. Sempre que tvermos índces somados podemos renomeá-los. Desse modo, pode-se renomear os índces se sso facltar no reconhecmento de alguma quantdade (por exemplo, temos que B j A j = B A j j ). Vamos ver um exemplo do emprego da notação ndcal para o cálculo de uma dentdade: B + B = B + B = (A B ) (A + B ) = A A + A B B A B B = A A B B = = A 2 + B 2 : (15) 3

4 Nós denotamos o módulo de um vetor como p A = A = A. É nteressante dar uma nterpretação geométrca ao produto escalar. Em um caso bem especí co temos be1 = A be be 1 = A 1 = A 1 ; (16) ou seja, o produto escalar de um vetor com o vetor untáro be 1 ltra a componente x ( = 1) de, que é a únca componente de paralela ao vetor be 1. O produto escalar be 1 dá o que chamamos de projeção de na dreção be 1. Esse padrão é váldo para qualquer produto escalar. Quando temos dos vetores arbtráros e, o produto escalar leva em conta apenas a parte paralela dos dos vetores, a projeção de um vetor na dreção do outro. Escrevendo = k +? ; (17) em que k é a parte de paralela a e? é a parte perpendcular, temos = k : (18) Seja o ângulo entre os dos vetores, então temos que = AB cos ; (19) onde A é o comprmento de e B cos é o comprmento de k. Projetar na dreção de, ou vce-versa, é equvalente, a nal o produto escalar é smétrco. 1.3 Rotações Vamos supor que um corpo descreve uma trajetóra r = (x; y; z) = (x 1 ; x 2 ; x 3 ) no espaço. O ntervalo percorrdo entre dos pontos dessa trajetóra s é dado através da equação s 2 = x x x 2 3: (20) Essa quantdade é uma medda de comprmento e pode ser encarada como um produto escalar. Sendo assm, se qusermos que uma medda de comprmento seja nvarante, também teremos que o produto escalar é nvarante frente um certo tpo de tranformação (exemplos de transformações são: translação, rotação, boost, dlatação,...). Podemos nos perguntar nesse ponto qual é a transformação mas genérca que dexa o produto escalar nvarante. 4

5 Na forma vetoral, a condção de nvarânca pode ser escrta como 0 0 = ; (21) onde a "lnha" ndca o vetor transformado. Mas o produto escalar é avalado exatamente da mesma forma que o produto de uma matrz lnha por uma matrz coluna. Pensando assm, podemos escrever a condção de nvarânca na forma matrcal A 0T B 0 = A T B: (22) Podemos escrever as transformações A 7 0 = RA B 7 0 = RB ; (23) em que R é uma matrz quadrada n n que representa a transformação no espaço Eucldano n-dmensonal. Usando essas transformações obtemos a condação que é satsfeta quando ou seja, A T B = A 0T B 0 = (RA) T (RB) = A T R T RB; (24) R T R = 1; (25) R 1 = R T : (26) Aqu escrevemos a matrz dentdade smplsmente como 1. Uma matrz que satsfaz essa condção é dta ortogonal. Para o determnante temos det R T R = det R T det (R) = (det R) 2 = det (1) = 1 det R = 1: (27) O conjunto de matrzes ortogonas n n recebe o nome de grupo O (n), onde o O vem de ortogonal e o n é a dmensão do espaço Eucldano. Se xarmos o determnante como sendo a undade temos o chamado grupo SO (n), onde o S vem de specal. Não entraremos em detalhes sobre grupos aqu. Neste momento, basta magnar que estamos tratando com um conjunto de matrzes (ortogonas e com determnante gual a undade) que satsfazem uma sére de propredades bem de ndas. Com sso, mostramos que a transformação mas genérca que mantém o produto escalar nvarante no espaço Eucldano é uma transformação ortogonal. 5

6 Vamos examnar o caso bdmensonal com mas detalhe. Podemos escrever para a matrz R de modo genérco R = : (28) A nversa dessa matrz vale R 1 = 1 det R : (29) Usando a condção de ortoganaldade e o determnante gual a undade podemos estabelecer relações entre as componentes da matrz: R 1 = = = R T ; (30) portanto obedece a condção R = (31) det R = = 1: (32) Uma parametrzação possível, que satsfaz essas condções é cos sn R = ; (33) sn cos que é uma matrz de rotação genérca para o caso bdmensonal. Na próxma aula entenderemos melhor porque essa á uma matrz de rotação. No caso trdmensonal teríamos três rotações possíves, uma em torno de cada exo. Sendo assm, no espaço Eucldano, a transformação mas genérca que dexa o produto escalar nvarante é a rotação. Lembrando que, por enquanto, estamos nos restrngndo ao caso em que o determnante é postvo. 1.4 O produto vetoral e o " de Lev-Cvta Usualmente o produto vetoral é escrto sobre a forma de um determnante be 1 be 2 be 3 A B = A 1 A 2 A 3 B 1 B 2 B 3 : (34) 6

7 Isso é exclusvo para o caso trdmensonal, que é o caso em questão. O produto vetoral é um produto cruzado, que mstura as componentes de índces dferentes como em A B j A j B. Em outras dmensões ele não é um vetor e não pode ser expresso em termos de um determnante. Como exemplo, no caso bdmensonal, ele vale smplesmente = A 1 B 2 A 2 B 1. Na notação ndcal o produto vetoral ca = A be B j be j = A B j (be be j ) ; (35) o que nos leva a avalar os produtos vetoras entre os vetores de base: be 1 be 1 = 0 be 2 be 1 = be 3 be 3 be 1 = be 2 be 1 be 2 = be 3 be 2 be 2 = 0 be 3 be 2 = be 1 be 1 be 3 = be 2 be 2 be 3 = be 1 be 3 be 3 = 0: Daqu tramos que: para índces guas o produto se anula, para índces dferentes obtemos como resultado o vetor untáro perpendcular ao plano formado por be be j. O snal desse vetor é postvo para permutações pares dos índces 123 e negatvo para permutações ímpares. Para escrevermos sso de manera genérca vamos ntroduzr o " de Lev-Cvta 8 < " jk : 1, para permutações pares de " 123 1, para permutações ímpares de " 123 0, quando há repetção de índces : (36) Ele é um objeto totalmente antssmétrco na troca dos índces, sto é, se permutarmos um índce uma únca vez há uma mudança de snal (" jk = " jk ), se permutarmos duas vezes o snal permanece gual (" jk = " kj ), e assm por dante. Dferentemente do de Kronecker, o " não tem um formato geral para uma dmensão arbtrára D. Nesse caso, ele deve ser de ndo como um objeto totalmente antssmétrco com D índces. Com essa de nção, temos para o produto vetoral entre vetores untáros e para um produto vetoral genérco be be j = " jk be k (37) = A B j " jk be k ; (38) que também pode ser expresso em termos de suas componentes B = " kj A B j : (39) k 7

8 Pela antssmetra do " é medato que = "jk A B j = " jk B j A = : (40) Dferentemente dos casos em que estamos acostumados, o produto vetoral não comuta. Não podemos trocar os vetores de posção sem pagar um preço por sso. Para exempl car, podemos olhar para o produto B + B, cujas componentes são h B + B = " jk B + B = " jk (A j B j ) (A k + B k ) j = " jk A j A k " jk B j B k + " jk A j B k " jk B j A k Aqu os termos do tpo " jk A j A k e " jk B j B k se anulam por serem o produto de uma quantdade smétrca na troca de índces por uma quantdade antssmétrca = "jk A j A k = " jk A k A j = " kj A k A j = = 0: k Reconhecer esse tpo de produto em equações pode smpl car sgn catvamente as contas. Voltando para o produto, temos h B + B = " jk A j B k " jk A k B j Voltando para a notação vetoral B + B = " jk A j B k " kj A k B j = 2" jk A j B k = 2 B : = 2 B : (41) De manera análoga ao produto escalar, queremos nterpretar geometrcamente o produto vetoral. Esse produto ltra apenas as componentes perpendculares dos vetores. Se escrevermos o vetor como (17), então temos que =? : (42) Como o comprmento de? é B sn, temos = AB sn : (43) 8

9 Essa é exatamente a área de um paralelolgramo de ndo pelos vetores e. Imagne que temos o vetor formando a base e o topo do paralelogramo, enquanto o vetor forma as lateras. Este paralelogramo tem base de comprmento A e as lateras de comprmento B sn. Com sso, a área é dada por AB sn. É nteressante notar que estamos falando de um vetor, o que sugere que a área também seja vsta como um vetor. A dreção desse vetor é perpendcular a superfíce e deve ser espec cada para que se conheça exatamente qual é a área. 1.5 Trplo produto escalar e determnantes Olhando para as componentes do trplo produto escalar B = A B = A (" jk B j C k ) = (" jk A B j ) C k = A C ; (44) vemos que podemos trocar os produtos escalar e vetoral de posção. Além dsso, de acordo com as propredades do símbolo de Lev-Cvta, obtemos as relações entre as permutações pares de ABC = = (45) e entre as ímpares = = ; (46) sendo que elas se assocam entre s através da troca de snal = : (47) É nteressante notar também que, na notação usual be 1 be 2 be 3 A C = (A 1 be 1 + A 2 be 2 + A 3 be 3 ) B 1 B 2 B 3 C 1 D 2 E 3 : (48) Se abrrmos o determnante temos algo do tpo h (A 1 be 1 + A 2 be 2 + A 3 be 3 ) C be 1 + C be 2 + C 3 be 3 ;

10 entretanto, no produto escalar, apenas componentes de mesmo índce são não nulas, temos A 1 be 1 C be 1 + A 2 be 2 C be 2 + A 3 be 3 C be 3 ; 1 mas sso é equvalente a colocar as componentes do vetor na prmera lnha do determnante: A 1 A 2 A 3 A C = B 1 B 2 B 3 C 1 D 2 E 3 : (49) De nndo a 1 A, a 2 B e a 3 C, temos a 11 a 12 a 13 A C = a 21 a 22 a 23 a 31 a 32 a 33 ; (50) o que nos sugere que o determnante de uma matrz arbtrára M possa ser escrto em termos do " de Lev-Cvta a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 = " jka 1 a 2j a 3k : (51) Daqu tramos propredades como a de que a troca de duas lnhas do determnante produz uma mudança de snal. Se zermos os índces que estão xos vararem também, vemos que eles também são assocados ao " por causa de suas propredades: " lmn a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 2 = " jka l a mj a nk : (52) Se de nrmos um palelepípedo, cuja base é o paralelogramo descrto por e e cuja lateral é dada por, então o produto A C resulta em seu volume. No caso dos vetores de base podemos escrever be (be j be k ) = be " jkl be l = " jkl l = " jk : (53) Isso de ne o que chamamos de regra da mão dreta, portanto o sstema de coordenadas é dto dextrógro. Se o resultado fosse negatvo teríamos a regra da mão esquerda e o sstema de coordenadas sera levógro. Os vetores untáros são 10 3

11 de ndos de forma que sgam a regra da mão dreta, pos assm o volume nesse sstema de coordenadas é postvo: be 1 (be 2 be 3 ) = 1: (54) 1.6 Relações entre os símbolos de Kronecker e " de Lev- Cvta Vamos olhar para as componentes do produto A C : h A B = " jk A j B = " jk A j " klm B l C m = " kj " klm A j B l C m : É possível escrevermos o produto de dos " s de Lev-Cvta em termos de s de Kronecker. Para essa dentdade usamos " kj " klm = l jm m jl : (55) Vamos tomar ela como sendo verdade por enquanto, posterormente entraremos em detalhes sobre essa relação e outras do tpo. Temos h A C = ( l jm m jl ) A j B l C m = A j B C j A j B j C = B A C A : (56) k Voltando para a forma vetoral A C = B B A : (57) Quando falamos de vetores, essa é uma das dentdades mas utlzadas e por sso serve como uma "propaganda" postva para a notação. Uma pessoa, com certo domíno no uso da notação ndcal, pode encontrar esse resultado em três ou quatro lnhas. Tradconalmente, esse resultado é obtdo pela multplcação explcta dos vetores, sto é, prmero calculamos o determnante be 1 be 2 be 3 B 1 B 2 B 3 C 1 C 2 C 3 11

12 e usamos o resultado nesse segundo determnante be 1 be 2 be 3 A 1 A 2 A 3 B 2 C 3 B 3 C 2 B 3 C 1 B 1 C 3 B 1 C 2 B 2 C 1 : Comparando os dos casos ca evdente a smpl cação obtda quando se trabalha com a notação ndcal. Vamos voltar para as relações entre os " s e s. Vamos deduzr essas relações para o caso do espaço Eucldano bdmensonal E 2, em que o símbolo de Lev- Cvta possu apenas dos índces, " j. Vamos começar pelo produto " j " kl. Pelas propredades do ", sabemos que 6= j e k 6= l. Levando em conta todas as permutações possíves de índces temos a combnação " j " kl = a k jl + b l jk : (58) É necessáro que tenhamos os mesmos índces em todos os termos da equação, sso garante que temos o mesmo tpo de objeto em todos os termos (por exemplo, podemos gualar vetores apenas a vetores). Fazendo = j, temos 0 = a k l + b l k = (a + b) k l ; de onde tramos a condção de que b = a, portanto " j " kl = a ( k jl l jk ) : (59) Fazendo k = l chegaríamos na mesma conclusão. Olhando para uma das possbldades não nulas podemos xar o parâmetro a " 12 " 12 = 1 = a: (60) Usando as outras possbldades não nulas (" 12 " 21, " 21 " 12 e " 21 " 21 ) chegamos ao mesmo resultado. Por m, temos a prmera propredade, que pode ser ent cada a um determnante " j " kl = k jl l jk = k l : (61) Agora se contrarmos os índces e k, temos " j " l = S jl = jl: (62) 12 jk jl

13 Usamos um fator de smetra S, que vem da soma em. Imagne que j e l são índces xos, nesse caso há uma únca possbldade para o índce. Se contrarmos j com l, temos " j " j = S = 2: (63) O fator de smetra é dos porque temos dos índces repetdos. Exstem dos valores acessíves para o índce, mas após ele ser xado exste uma únca possbldade para j, com sso o fator de smetra é S = 2:1 = 2. Agora vamos voltar para o E 3. A dea é escrevermos o produto " jk " lmn em termos de todas as combnações possíves entre os s. Deve-se lembrar que ambos os lados da equação contém, obrgatoramente, a mesma estrutura de índces. Váras possbldades se anulam devdo as propredades de smetra do " e do. Por m, usando as condções necessáras, obtem-se o determnante " jk " lmn = l m n jl jm jn kl km kn : (64) Outras dentdades são obtdas através da contração de índces. Para todos os índces contrados, temos " jk " jk = S = 3: (65) Aqu podemos ver melhor a orgem do fator de smetra. Temos três possbldades para o índce, quando ele está xo restam duas para o j e então resta só uma para o k: S = 3:2:1 = 3. No exercíco 4 vamos encontrar essas dentdades para os casos tr e quadrdmensonal e então vamos generalzar esse resultado para o espaço Eucldano n- dmensonal. 1.7 Exercícos 1. Calcule as seguntes dentdades = (66) A B + B = A 2 B 2 (67) 13

14 A B + B = 2 (68) B C = B C A = C A B = B A (69) B A = B A C = A C B (70) B C = A B C (71) A C = B C C B (72) A B B = A 2 B 2 2 B (73) A C + C B A + C B = 0 (74) C B D = C D D C (75) C B D = a + b + c + d D (76) 2. O momento angular de uma partícula é dado por L = r p = m r v, onde p é o momento lnear. Com velocdades lnear e angular relaconadas por v = r, mostre que L = mr 2 [ ( ^r 0 ) ^r 0 ] (77) Aqu, ^r 0 é um vetor untáro na dreção radal. Para ^r = 0 sso se reduz a L = mr 2 = I, onde I é o momento de nérca. 3. A energa cnétca de uma únca partícula é dada por T = 1 2 mv2. Para o movmento de rotação, essa expressão se transforma em 1 2 m ( r ) 2. Mostre que T = 1 2 m hr 2 2 ( r ) 2 : (78) Para r = 0 essa expressão se reduz a T = 1 2 I2, com o momento de nérca I dado por mr Encontre as relações entre os símbolos " de Lev-Cvta e de Kronecker para três e quatro dmensões. Generalze para o caso D-dmensonal. Os exercícos 2 e 3 foram trados do lvro do Arfken, cuja referênca fo passada. 14