Resposta ao Impulso, ao Degrau e à Excitação Arbitrária
|
|
|
- Rosa di Azevedo Sabrosa
- 7 Há anos
- Visualizações:
Transcrição
1 9 Resposta ao Impulso, ao Degrau e à Excitação Arbitrária INTRODUÇÃO Estuamos, até agora, a resposta e sistemas iâmicos às excitações harmôicas e perióicas, seo que essas últimas foram trasformaas, através e uma série e Fourier, em excitações harmôicas A questão que aturalmete surge é: como obtemos a resposta quao a excitação é arbitrária? É e se esperar, aliás, que a excitação arbitrária seja a mais comum, a prática Ates e iscutirmos a resposta à excitação arbitrária, vamos cosierar a resposta a ois tipos especiais e forçameto, as fuções impulso e egrau uitários Vamos utilizar como moelo, em osso estuo, sistemas mecâicos e a e a ores Obviamete, os resultaos obtios se aplicam aos emais tipos e sistemas físicos aálogos RESPOSTA AO IMPULSO O impulso uitário (ou fução Delta e Dirac) é efiio como seo a fução δ(t), tal que (a) δ(t - a) t a (b) coforme ilustra a fig : + δ( t a)t Fig A trasformaa e Laplace o impulso uitário é aa por () (s) e -as É muito comum, a prática, que o impulso ocorra o istate a Nesse caso: (3) (s)
2 Resposta ao impulso: é efiia como seo a resposta e um sistema ao impulso uitário aplicao o istate t, com coições iiciais ulas (sistema iicialmete em repouso) Evietemete, se o impulso uitário for aplicao um istate e tempo posterior, t a, a resposta será obtia eslocao-a para a ireita, ao logo o eixo o tempo, e um itervalo t a RESPOSTA DE SISTEMAS DE a ORDEM O moelo matemático para um sistema e a orem ilustrao a fig foi obtio ateriormete como seo Fig (4) c x(t) + kx(t) f(t) Substituio f(t) por δ(t) e tomao a trasformaa e Laplace para coições iiciais ulas: Isolao X(s) e teo em cota a eq (3): (5) (cs + k)x(s) (s) X(s) cs + k Teo em vista a efiição e costate e tempo e um sistema mecâico e a orem, aa por (6) τ c/k poemos rescrever a eq (5) como X(s) kτs + k kτ s + τ Voltao ao omíio o tempo, obtemos a resposta e um sistema e a orem ao impulso uitário: t t (7) x (t) e τ u(t) e τ δ u(t) kτ c oe x δ (t) simboliza a resposta ao impulso e u(t) é o egrau uitário, o qual multiplica a resposta porque ela eve ser ula para t < Por outro lao, a resposta e um sistema e a orem submetio a uma coição iicial x() x é aa, coforme já vimos, por: (8) x(t) x e -t/τ
3 3 Portato, comparao as eqs (7) e (8), cocluímos que a resposta ao impulso e um sistema e a orem equivale à resposta o mesmo a uma coição iicial No presete caso, a coição iicial é o eslocameto iicial ao por x() /c RESPOSTA DE SISTEMAS DE a ORDEM O moelo matemático para um sistema e a orem como o ilustrao a fig 3 é ao por Fig 3 (9) m x(t) + c x(t) + kx(t) f(t) Substituio f(t) por δ(t) e tomao a trasformaa e Laplace para coições iiciais ulas: (ms + cs + k)x(s) (s) Isolao X(s) e teo em cota a eq (3): () X(s) ms + cs + k Cosierao o sistema subamortecio e levao em cota que rescrever a eq () como () X(s) m(s + ςω s + ω ) k ω e que m ς c, poemos Para obter a trasformaa iversa e Laplace, é coveiete expair o membro ireito a eq () em frações parciais Deixamos a cargo o aluo mostrar que: () X(s) m(s s ) s s s s oe s e s são as raízes a equação s + ζω s + ω, aas por (3) s, -ζω ± iω e oe ω é a freqüêcia agular amortecia
4 4 (4) ω ω ζ Poemos, etão, voltar ao omíio o tempo achao as trasformaas iversas a eq (), obteo x(t) m(s s ) s t s t ( e e ) Substituio s e s aas pela eq (3) a equação acima, obtemos a resposta e um sistema e a orem ao impulso: ςωt (5) xδ (t) e se ωtu(t) oe x δ (t) simboliza a resposta ao impulso e u(t) é o egrau uitário Notemos que a resposta foi multiplicaa por u(t) teo em vista que ela eve ser ula para t < Por outro lao, a resposta e um sistema e a x () x é aa coforme já vimos, por: orem submetio às coições iiciais x() e ςω x x x t t (6) x(t) e ςω + x cos t se t ςω ω + ω e se ωt ω ω Portato, comparao as eqs (5) e (6), cocluímos que a resposta ao impulso e um sistema e a orem é equivalete à resposta o mesmo a uma coição iicial No presete caso, a coição iicial é a velociae iicial aa por x () x /m 3 RESPOSTA AO DEGRAU O egrau uitário, ilustrao a fig 4, é efiio matematicamete como (7) u(t - a) para para t < a t > a Fig 4 A trasformaa e Laplace o egrau uitário é aa por (8) U(s) e -as /s
5 5 É muito comum, a prática, que o egrau uitário ocorra o istate a Nesse caso: (9) U(s) /s Resposta ao egrau: é efiia como seo a resposta e um sistema ao egrau uitário aplicao o istate t, com coições iiciais ulas (sistema iicialmete em repouso) Evietemete, se o egrau uitário for aplicao um istate e tempo posterior, t a, a resposta será obtia eslocao-a para a ireita, ao logo o eixo os tempos, e um itervalo t a Vamos estuar, a seguir, a resposta e sistemas e a e a ores RESPOSTA DE SISTEMAS DE a ORDEM Coforme já vimos, o moelo matemático é ao pela eq (4), aqui repetia: (4) c x(t) + kx(t) f(t) Substituio f(t) por u(t) e tomao a trasformaa e Laplace para coições iiciais ulas: (cs + k)x(s) U(s) Isolao X(s) e teo em cota a eq (9): () X(s) s cs + k Teo em vista a efiição e costate e tempo e um sistema e a orem, aa pela eq (6), poemos substituir a eq () e expair a mesma em frações parciais, obteo: () X(s) k s s + τ Voltao ao omíio o tempo, obtemos a resposta ao egrau: () x (t) t u e τ u(t) k oe x u (t) simboliza a resposta ao egrau e u(t) é o egrau uitário Notemos que a resposta foi multiplicaa por u(t) teo em vista que ela eve ser ula para t < O gráfico a eq () está ilustrao a fig 5:
6 6 Fig 5 RESPOSTA DE SISTEMAS DE a ORDEM Comparao as eqs (3) e (9), cocluímos que o egrau uitário é a itegral o impulso uitário Se o sistema é liear, poemos aplicar o Pricípio a Superposição e estabelecer que a resposta ao egrau uitário é a itegral a resposta ao impulso uitário, ou, simbolicamete: (3) xu(t) xδ( ξ) ξ t oe ξ é uma variável mua Aplicao a proprieae acima, simplesmete substituímos x δ (t), aa pela eq (5), a eq (3): t xu(t) ςω ξ se ω ξu( ξ) ξ Teo em cota a efiição e egrau uitário, poemos rescrever a equação acima como t ςωξ (4) xu(t) ω ξ ξ ω e se m Usao a fórmula e Euler se ω ξ e iω ξ e i iω ξ a eq (4), e realizao a itegração, chegamos, após algum trabalho algébrico, à resposta ao egrau ςω t ςω (5) xu (t) e cos t se t u(t) k ω + ω ω cujo gráfico está ilustrao a fig 6, para ω ra/s e ζ,
7 7 Fig 6 oe cocluímos que a resposta ao egrau uitário é uma oscilação amortecia que ocorre em toro e /k, seo k a rigiez o sistema 4 RESPOSTA À EXCITAÇÃO ARBITRÁRIA INTEGRAL DE CONVOLUÇÃO Vamos, agora, cosierar o caso e uma excitação arbitrária (qualquer) Para achar a resposta a uma excitação essa atureza, utilizaremos o Métoo a Covolução, também cohecio como Métoo a Itegral e Duhamel Esse métoo se estaca por sua ampla aplicabiliae, servio para qualquer tipo e excitação, iclusive para aquelas já estuaas ateriormete Etretato, apreseta uma esvatagem cosierável pois, para fuções complicaas, ele se tora e ifícil aplicação, evio às itegrações trabalhosas que surgem Seja um sistema massa-mola-amorteceor, como o a fig 3, em que a fução e forçameto f(t) é geérica, como a ilustraa a fig 7 Fig 7 oe é usaa a variável mua τ para o tempo
8 8 Cosieremos que, urate um itervalo e tempo ifiitesimal τ, começao o istate t τ, a fução f(t), aquele poto, cosista e um impulso ifiitesimal e magitue f(τ)τ, mostrao a área hachuraa a figura A fução f(t) poe ser cosieraa, o itervalo e tempo fiito que vai e até t, como seo costituía por uma série esses impulsos ifiitesimais, caa um eles provocao uma variação ifiitesimal a quatiae e movimeto a massa m: f(τ) τ m ẋ f( τ) (6) x τ m Por outro lao, a resposta a caa impulso isolaamete é evia à aplicação as coições iiciais e eslocameto iicial ulo e velociae iicial ẋ Para escrever essa situação, já temos a eq (6), aqui repetia: x ςωt (6) x(t) e se ωt ω Aaptao para a simbologia atual e cosierao que a resposta ao impulso tem iício após a aplicação o mesmo, ou seja, após o istate t τ, poemos rescrever a eq (6) como x(t) x ω e ςω (t τ) se ω (t τ) Levao em cota a eq (6), obtemos x(t) f( τ) e ςω (t τ) se ω (t τ)τ Devio à coição e sistema liear, poemos aplicar o Pricípio a Superposição e afirmar que a resposta total à série e impulsos ifiitesimais ocorreo e t até t τ, é aa pela itegral a equação acima, o que costitui a chamaa Itegral e Duhamel: t ςω (t τ) (7) x(t) f( τ)e se ω(t τ)τ O métoo que acabamos e escrever também recebe o ome e Métoo a Covolução porque a eq (7) é uma forma especial a itegral e covolução (8) x(t) f( τ)g(t τ)τ f(t) * g(t) t
9 9 oe ςω (t τ) (9) g(t τ) e se ω(t τ) Na eq (8), a expressão f(t)*g(t) é lia como covolução e f(t) e g(t) ou f(t) covolução g(t) Teorema e Borel: estabelece que a covolução e uas fuções é igual à trasformaa iversa e Laplace o prouto e suas trasformaas e Laplace, ou seja (3) x(t) f(t)*g(t) - [f(s)g(s)] Esse teorema é e extrema importâcia prática, porque permite usar a trasformação e Laplace para solucioar problemas e trasietes Exemplo ilustrativo Um sistema massa-mola ecotra-se iicialmete em repouso e é submetio a um pulso retagular e magitue costate f urate t seguos Achar a resposta trasiete usao o Métoo a Covolução Solução: Como ão existe amortecimeto, ζ Levao a eq (7): x(t) t f( τ) se ω (t τ)τ t f se ω (t τ)τ Teo em vista que t ão epee e τ, t poe ser cosierao costate o processo e itegração: x(t) f m t [ cos ω (t τ ] ) ω e oe chegamos fialmete a f x(t) [ cos ω (t t ) cos t] ω
10 Exemplo ilustrativo Um sistema massa-mola ecotra-se iicialmete em repouso quao é submetio ao pulso triagular a figura 8 Achar a resposta o tempo x(t) Fig 8 Solução 8 Equação a excitação: f(τ) τ + τ t ςω (t τ) Itegral e Duhamel: x(t) f( τ)e se ω(t τ)τ Como ão há amortecimeto, ζ e ω ω, logo x(t) τ / 4 8 ( τ τ + ) se ω (t τ)τ Realizao o trabalho e itegração e teo em cota que k e que ω τ π, a expressão acima simplifica para: x(t) kπ [ se ω t + ( π) cos ω t]
11 EXERCÍCIOS Deuzir a eq () Deuzir a eq () 3 Demostrar a eq (5) 4 Deuzir a eq () 5 Deuzir a eq (5) 6 Usao o VisSim, peem-se: ; kπ (a) plotar a resposta o exemplo ilustrativo, ou seja, x(t) [ se ω t + ( π) cos ω t] (b) resolver a EDOL o exemplo ilustrativo ; (c) comparar os gráficos obtios os ites (a) e (b) 7 Um sistema massa-mola ecotra-se iicialmete em repouso quao é submetio à excitação a figura Determiar a resposta o tempo x(t) Resp: x(t) F se ωt k π
12 8 Usao o VisSim, peem-se: F (a) plotar a resposta o exercício 7, ou seja, x(t) se ω t ; k π (b) resolver a EDOL o exercício 7; (c) comparar os gráficos obtios os ites (a) e (b) 9 O sistema a figura é submetio a uma força impulsiva f(t) f δ(t) oe f é o móulo o impulso Usao o VisSim, plotar o eslocameto a massa m em fução o tempo, resolveo umericamete a equação iferecial Daos: m kg; c Ns/m; f N
Laboratório de Dinâmica
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA Laboratório e Diâmica SEM 54 DINÂMICA ESTRUTURAL Ala # Resp.: Moelo Matemático Moelo e GDL com amortecimeto
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA Laboratório e Diâmica SEM 54 DINÂMICA ESTRUTURAL Ala # Resp.: Moelo Matemático Moelo e GDL com amortecimeto
Análise da Resposta Livre de Sistemas Dinâmicos de 2 a Ordem
 Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
Resposta de Sistemas de 2 a Ordem à Excitação Periódica Não Harmônica
 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 18 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 INTRODUÇÃO Muitas vezes, a excitação é uma fução periódica,
Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 18 Resposta de Sistemas de a Ordem à Excitação Periódica Não Harmôica 1 INTRODUÇÃO Muitas vezes, a excitação é uma fução periódica,
Equação diferencial é uma equação que apresenta derivadas ou diferenciais de uma função desconhecida.
 . EQUAÇÕES DIFERENCIAIS.. Coceito e Classificação Equação iferecial é uma equação que apreseta erivaas ou ifereciais e uma fução escohecia. Seja uma fução e e um iteiro positivo, etão uma relação e igualae
. EQUAÇÕES DIFERENCIAIS.. Coceito e Classificação Equação iferecial é uma equação que apreseta erivaas ou ifereciais e uma fução escohecia. Seja uma fução e e um iteiro positivo, etão uma relação e igualae
MÉTODOS DE DERIVAÇÃO
 MÉTODOS DE DERIVAÇÃO TE3 Fuametos Matemáticos para a Eearia Elétrica I Métoos e erivação DERIVADA DE UMA FUNÇÃO CONSTANTE Uma ução costate ão apreseta variação, portato sua erivaa é ula ( c) 5 4 Por eemplo:
MÉTODOS DE DERIVAÇÃO TE3 Fuametos Matemáticos para a Eearia Elétrica I Métoos e erivação DERIVADA DE UMA FUNÇÃO CONSTANTE Uma ução costate ão apreseta variação, portato sua erivaa é ula ( c) 5 4 Por eemplo:
Aula 11. Separação de Variáveis em Coordenadas Esféricas. Eletromagnetismo I. Prof. Ricardo Galvão - 2 Semestre Preparo: Diego Oliveira
 Eletromagetismo I Prof. Ricaro Galvão - Semestre 05 Preparo: Diego Oliveira Aula Separação e Variáveis em Cooreaas Esféricas Em cooreaas esféricas, a Equação e Laplace é aa por φr,θ,ϕ) = 0 r r ) r φ r
Eletromagetismo I Prof. Ricaro Galvão - Semestre 05 Preparo: Diego Oliveira Aula Separação e Variáveis em Cooreaas Esféricas Em cooreaas esféricas, a Equação e Laplace é aa por φr,θ,ϕ) = 0 r r ) r φ r
Equação Diferencial. Uma equação diferencial é uma expressão que relaciona uma função desconhecida (incógnita) y com suas derivadas.
 Equação Diferecial Uma equação iferecial é uma epressão que relacioa uma fução escohecia (icógita) com suas erivaas É útil classificar os iferetes tipos e equações para um esevolvimeto sistemático a Teoria
Equação Diferecial Uma equação iferecial é uma epressão que relacioa uma fução escohecia (icógita) com suas erivaas É útil classificar os iferetes tipos e equações para um esevolvimeto sistemático a Teoria
VIBRAÇÕES MECÂNICAS - CAPÍTULO 2 - VIBRAÇÃO LIVRE VIBRAÇÃO LIVRE
 VIBRAÇÕES MECÂNICAS - CAPÍTULO - VIBRAÇÃO LIVRE 3. VIBRAÇÃO LIVRE Cofore ostrao o apítulo aterior, uitos sisteas iâios poe ser represetaos por ua equação ifereial e segua ore, liear, o oefiietes ostates
VIBRAÇÕES MECÂNICAS - CAPÍTULO - VIBRAÇÃO LIVRE 3. VIBRAÇÃO LIVRE Cofore ostrao o apítulo aterior, uitos sisteas iâios poe ser represetaos por ua equação ifereial e segua ore, liear, o oefiietes ostates
==Enunciado== 2. (a) Mostre que se h(t) é uma função seccionalmente contínua e periódica, de período T, que admite transformada de Laplace, então
 Departameto de Matemática - Escola Superior de ecologia - Istituto Politécico de Viseu Complemetos de Aálise Matemática Egeharia de Sistemas e Iformática Euciado e Resolução da a. Frequêcia de 5/6 Duração:
Departameto de Matemática - Escola Superior de ecologia - Istituto Politécico de Viseu Complemetos de Aálise Matemática Egeharia de Sistemas e Iformática Euciado e Resolução da a. Frequêcia de 5/6 Duração:
ALGORITMO DE GOSPER E APLICAÇÕES Humberto Silva Naves
 Nível Avaçao ALGORITMO DE GOSPER E APLICAÇÕES Humberto Silva Naves Cotiuao com as iéias o artigo Itegrais iscretas (e Euaro Poço a Eurea úmero 7), vamos tetar escobrir fórmulas fechaas para algus somatórios
Nível Avaçao ALGORITMO DE GOSPER E APLICAÇÕES Humberto Silva Naves Cotiuao com as iéias o artigo Itegrais iscretas (e Euaro Poço a Eurea úmero 7), vamos tetar escobrir fórmulas fechaas para algus somatórios
Virgílio Mendonça da Costa e Silva
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE TECNOLOGIA DEPARTAMENTO DE ENGENHARIA MECÂNICA VIBRAÇÕES DOS SISTEMAS MECÂNICOS VIBRAÇÕES LIVRES COM AMORTECIMENTO DE SISTEMAS DE GL NOTAS DE AULAS Virgílio Medoça
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS Aula # Revisão de Coceitos GDL Prof. Paulo S. Varoto . - Objetivos
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS Aula # Revisão de Coceitos GDL Prof. Paulo S. Varoto . - Objetivos
CONCEITOS DE VIBRAÇÃO
 CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS
 UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS Aula # Revisão de Coceitos GDL Prof. Paulo S. Varoto As Rotas da Aálise
UNIVERSIDADE DE SÃO PAULO ESCOLA DE ENGENHARIA DE SÃO CARLOS DEPARTAMENTO DE ENGENHARIA MECÂNICA SEM 5766 ANÁLISE MODAL DE ESTRUTURAS Aula # Revisão de Coceitos GDL Prof. Paulo S. Varoto As Rotas da Aálise
Exercícios de DSP: 1) Determine se os sinais abaixo são periódicos ou não e para cada sinal periódico, determine o período fundamental.
 Exercícios de DSP: 1) Determie se os siais abaixo são periódicos ou ão e para cada sial periódico, determie o período fudametal a x[ ] = cos( 0,15 π ) 1 18 b x [ ] = Re{ e } Im{ } jπ + e jπ c x[ ] = se(
Exercícios de DSP: 1) Determie se os siais abaixo são periódicos ou ão e para cada sial periódico, determie o período fudametal a x[ ] = cos( 0,15 π ) 1 18 b x [ ] = Re{ e } Im{ } jπ + e jπ c x[ ] = se(
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace
 Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
Aula 05 Transformadas de Laplace Pierre Simon Laplace (1749-1827) As Transformadas de Laplace apresentam uma representação de sinais no domínio da frequência em função de uma variável s que é um número
EES-49/2012 Resolução da Prova 1
 EES-49/ Resolução da Prova Obs: esta resolução tem explicações e passos itermediários para facilitar o etedimeto. Parte dessas explicações e os passos itermediários ão são cobrados a correção da prova.
EES-49/ Resolução da Prova Obs: esta resolução tem explicações e passos itermediários para facilitar o etedimeto. Parte dessas explicações e os passos itermediários ão são cobrados a correção da prova.
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Considere uma placa retangular simplesmente apoiada nas bordas e submetida a um carregamento axial excêntrico na direção do eixo y.
 4 Controle Passivo com Carregamento Excêntrico 4.. Conceitos Básicos Neste capítulo é seguia a metoologia apresentaa anteriormente para controle e vibrações em placas por meio a aplicação e cargas e compressão.
4 Controle Passivo com Carregamento Excêntrico 4.. Conceitos Básicos Neste capítulo é seguia a metoologia apresentaa anteriormente para controle e vibrações em placas por meio a aplicação e cargas e compressão.
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Vibrações de sistemas com um grau de liberdade 1
 Vibrações de sistemas com um grau de liberdade 1 DEFINIÇÕES Vibração mecânica movimento de uma partícula ou de um corpo que oscila em torno de uma posição de equilíbrio. Período de vibração intervalo de
Vibrações de sistemas com um grau de liberdade 1 DEFINIÇÕES Vibração mecânica movimento de uma partícula ou de um corpo que oscila em torno de uma posição de equilíbrio. Período de vibração intervalo de
Controle de Processos Aula: Sistemas de 1ª e 2ª ordem
 107484 Controle de Processos Aula: Sistemas de 1ª e 2ª ordem Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
107484 Controle de Processos Aula: Sistemas de 1ª e 2ª ordem Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB) Controle
Capítulo I Séries Numéricas
 Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Capítulo I Séries Numéricas Capitulo I Séries. SÉRIES NÚMERICAS DEFINIÇÃO Sedo u, u,..., u,... uma sucessão umérica, chama-se série umérica de termo geral u à epressão que habitualmete se escreve u u...
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Sistemas Elétricos de Automação e Energia ENG10026 Robótica A
 Uiversidade Federal do Rio Grade do Sul Escola de Egeharia Departameto de Sistemas Elétricos de Automação e Eergia ENG0026 Robótica A Itrodução Cotrole Idepedete por Juta Prof. Walter Fetter Lages 9 de
Uiversidade Federal do Rio Grade do Sul Escola de Egeharia Departameto de Sistemas Elétricos de Automação e Eergia ENG0026 Robótica A Itrodução Cotrole Idepedete por Juta Prof. Walter Fetter Lages 9 de
Aula 06. Transformadas z
 Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Aula 06 Transformadas z
 Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Aula 06 Trasformadas Trasformadas Na aálise de sistemas cotíuos por vees é mais vatajoso o uso da frequêcia complexa s. No caso de sistemas discretos, uma ferrameta bastate comum usada para passar um sial
Universidade Federal do Rio Grande do Sul Escola de Engenharia Departamento de Sistemas Elétricos de Automação e Energia ELE228 Robótica A
 Uiversidade Federal do Rio Grade do Sul Escola de Egeharia Departameto de Sistemas Elétricos de Automação e Eergia ELE228 Robótica A Itrodução Cotrole Idepedete por Juta Prof. Walter Fetter Lages 9 de
Uiversidade Federal do Rio Grade do Sul Escola de Egeharia Departameto de Sistemas Elétricos de Automação e Eergia ELE228 Robótica A Itrodução Cotrole Idepedete por Juta Prof. Walter Fetter Lages 9 de
Processamento Digital de Sinais Lista de Exercícios Suplementares 3-1 quad. 2012
 Processameto Digital de Siais - Lista de Exercícios Suplemetares 3- Marcio Eisecraft abril 01 Processameto Digital de Siais Lista de Exercícios Suplemetares 3-1 quad 01 1 (1041) [OPPENHEIM, p 603] Supoha
Processameto Digital de Siais - Lista de Exercícios Suplemetares 3- Marcio Eisecraft abril 01 Processameto Digital de Siais Lista de Exercícios Suplemetares 3-1 quad 01 1 (1041) [OPPENHEIM, p 603] Supoha
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
Representação e Análise de Sistemas Dinâmicos Lineares Componentes Básicos de um Sistema de Controle
 Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
A Regra da Cadeia. 14 de novembro de u(x) = sen x. v(x) = cos x. w(x) = x 5
 A Regra a Caeia 4 e novembro e 0. As operações algébricas entre funções (soma, prouto, etc) fornecem uma grane iversiae e novas funções para os iferentes casos que vimos até agora. Porém, existe uma outra
A Regra a Caeia 4 e novembro e 0. As operações algébricas entre funções (soma, prouto, etc) fornecem uma grane iversiae e novas funções para os iferentes casos que vimos até agora. Porém, existe uma outra
Aplicações lineares. Capítulo Seja T: a) Quais dos seguintes vectores estão em Im( T )? 1 i) 4. 3 iii) ii)
 Capítulo Aplicações lieares Seja T: R R a multiplicação por 8 a) Quais dos seguites vectores estão em Im( T )? i) ii) 5 iii) b) Quais dos seguites vectores estão em Ker( T)? i) ii) iii) c) Qual a dimesão
Capítulo Aplicações lieares Seja T: R R a multiplicação por 8 a) Quais dos seguites vectores estão em Im( T )? i) ii) 5 iii) b) Quais dos seguites vectores estão em Ker( T)? i) ii) iii) c) Qual a dimesão
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Uiversidade Federal do Rio de Jaeiro Istituto de Matemática Departameto de Matemática Disciplia: Cálculo Diferecial e Itegral IV Uidades: Escola Politécica e Escola de Quimica Código: MAC 248 Turmas: Egeharias
Uiversidade Federal do Rio de Jaeiro Istituto de Matemática Departameto de Matemática Disciplia: Cálculo Diferecial e Itegral IV Uidades: Escola Politécica e Escola de Quimica Código: MAC 248 Turmas: Egeharias
SINAIS E SISTEMAS DE TEMPO DISCRETO
 SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
Séries de Fourier. As séries de Fourier são séries cujos termos são funções sinusoidais.
 Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Modelagem Matemática de Sistemas
 Modelagem Matemática de Sistemas 1. Descrição Matemática de Sistemas 2. Descrição Entrada-Saída 3. Exemplos pag.1 Teoria de Sistemas Lineares Aula 3 Descrição Matemática de Sistemas u(t) Sistema y(t) Para
Modelagem Matemática de Sistemas 1. Descrição Matemática de Sistemas 2. Descrição Entrada-Saída 3. Exemplos pag.1 Teoria de Sistemas Lineares Aula 3 Descrição Matemática de Sistemas u(t) Sistema y(t) Para
DFS Série Discreta de Fourier DFT Transformada Discreta de Fourier Convolução Circular
 Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Sistemas de Processameto Digital Egeharia de Sistemas e Iformática Ficha 4 5/6 4º Ao/ º Semestre DFS Série Discreta de Fourier DFT Trasformada Discreta de Fourier Covolução Circular Para calcular a DFT,
Capítulo VII: Soluções Numéricas de Equações Diferenciais Ordinárias
 Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Mais derivadas. g(x)f (x) f(x)g (x) g(x) 2 cf(x), com c R cf (x) x r, com r R. rx r 1
 Universiae e Brasília Departamento e Matemática Cálculo 1 Mais erivaas Neste teto vamos apresentar mais alguns eemplos importantes e funções eriváveis. Até o momento, temos a seguinte tabela e erivaas:
Universiae e Brasília Departamento e Matemática Cálculo 1 Mais erivaas Neste teto vamos apresentar mais alguns eemplos importantes e funções eriváveis. Até o momento, temos a seguinte tabela e erivaas:
Séquências e Séries Infinitas de Termos Constantes
 Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Capítulo Séquêcias e Séries Ifiitas de Termos Costates.. Itrodução Neste capítulo estamos iteressados em aalisar as séries ifiitas de termos costates. Etretato, para eteder as séries ifiitas devemos ates
Representação De Modelos de Sistemas Dinâmicos:
 Representação de Modelos de Sisteas Dinâicos: Equação I/O; Função de Transferência 03 Representação De Modelos de Sisteas Dinâicos: - Equação Input-Output (I/O) - Função de Transferência INTRODUÇÃO Vereos,
Representação de Modelos de Sisteas Dinâicos: Equação I/O; Função de Transferência 03 Representação De Modelos de Sisteas Dinâicos: - Equação Input-Output (I/O) - Função de Transferência INTRODUÇÃO Vereos,
Estabilidade quase uniforme de um problema termoeástico semi linear
 Artigo Origial DOI:.59/7946X64 Ciêcia e Natura, Sata Maria, v. 36 E. Especial II, 4, p. 35 358 evista o Cetro e Ciêcias Naturais e Exatas - UFSM ISSN impressa: -837 ISSN o-lie: 79-46X Estabiliae quase
Artigo Origial DOI:.59/7946X64 Ciêcia e Natura, Sata Maria, v. 36 E. Especial II, 4, p. 35 358 evista o Cetro e Ciêcias Naturais e Exatas - UFSM ISSN impressa: -837 ISSN o-lie: 79-46X Estabiliae quase
UNIDADE 2 - VIBRAÇÕES LIVRES DE SISTEMAS DE UM GRAU DE LIBERDADE
 Uiae - Vibrações Livres e Sisteas e U Grau e Liberae UNIDADE - VIBRAÇÕES LIVRES DE SISTEMAS DE UM GRAU DE LIBERDADE. - Itroução A oção e vibração coeça co a iéia o uilíbrio. U sistea está e uilíbrio quao
Uiae - Vibrações Livres e Sisteas e U Grau e Liberae UNIDADE - VIBRAÇÕES LIVRES DE SISTEMAS DE UM GRAU DE LIBERDADE. - Itroução A oção e vibração coeça co a iéia o uilíbrio. U sistea está e uilíbrio quao
3 0 Exercício Programa de PMR 2420 Data de entrega: 21/06/2012 (até as 17:00hs) Método de Elementos Finitos (MEF)
 ,3 m,8 m 3 Exercício Programa de PMR 242 Data de etrega: 21/6/212 (até as 17:hs) Método de Elemetos Fiitos (MEF) 1) Cosidere a estrutura da figura abaixo sujeita a uma carga cocetrada F 3 variado o tempo
,3 m,8 m 3 Exercício Programa de PMR 242 Data de etrega: 21/6/212 (até as 17:hs) Método de Elemetos Fiitos (MEF) 1) Cosidere a estrutura da figura abaixo sujeita a uma carga cocetrada F 3 variado o tempo
Estacionariedade e correlação temporal em dados financeiros
 Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Aula 3. Carlos Amaral Fonte: Cristiano Quevedo Andrea
 Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Aula 3 Carlos Amaral Fonte: Cristiano Quevedo Andrea UTFPR - Universidade Tecnológica Federal do Paraná DAELT - Departamento Acadêmico de Eletrotécnica Curitiba, Marco de 2012. Resumo 1 Introdução 2 3
Regras de Derivação Notas de aula relativas ao mês 11/2003 Versão de 13 de Novembro de 2003
 Regras e Derivação Notas e aula relativas ao mês 11/2003 Versão e 13 e Novembro e 2003 Já sabemos a efinição formal e erivaa, a partir o limite e suas interpretações como: f f a + h) f a) a) = lim, 1)
Regras e Derivação Notas e aula relativas ao mês 11/2003 Versão e 13 e Novembro e 2003 Já sabemos a efinição formal e erivaa, a partir o limite e suas interpretações como: f f a + h) f a) a) = lim, 1)
Sinais de Tempo Discreto
 Siais de Tempo Discreto Siais defiidos em istates discretos do tempo t 0, t 1, t 2,..., t,... são siais de tempo-discreto, deotados pelos símbolos f(t ), x(t ), y(t )... (sedo um iteiro). x(t )... t 1
Siais de Tempo Discreto Siais defiidos em istates discretos do tempo t 0, t 1, t 2,..., t,... são siais de tempo-discreto, deotados pelos símbolos f(t ), x(t ), y(t )... (sedo um iteiro). x(t )... t 1
Gabarito da Lista de Interpolação e Método dos Mínimos Quadrados
 Gabarto a sta e Iterpolação e Métoo os Mímos Quaraos ercíco : a cos Prmera orma: Iterpolação e agrage 8 5 P cos5 P - 89765 6 5 85 5 5 5 P 5 : : rro Portato 6 cos9 9 ; -5 6 9-9 - 6 5 5 5 85 cos6 6 ; 5 9
Gabarto a sta e Iterpolação e Métoo os Mímos Quaraos ercíco : a cos Prmera orma: Iterpolação e agrage 8 5 P cos5 P - 89765 6 5 85 5 5 5 P 5 : : rro Portato 6 cos9 9 ; -5 6 9-9 - 6 5 5 5 85 cos6 6 ; 5 9
Introdução aos Circuitos Elétricos
 Introdução aos Circuitos Elétricos A Transformada de Laplace Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia A Transformada de Laplace História Pierri
Introdução aos Circuitos Elétricos A Transformada de Laplace Prof. Roberto Alves Braga Jr. Prof. Bruno Henrique Groenner Barbosa UFLA - Departamento de Engenharia A Transformada de Laplace História Pierri
Soluções dos Exercícios do Capítulo 6
 Soluções dos Eercícios do Capítulo 6 1. O poliômio procurado P() a + b + c + d deve satisfazer a idetidade P(+1) P() +, ou seja, a(+1) + b(+1) + c(+1) + d a + b + c + d +, o que é equivalete a (a 1) +
Soluções dos Eercícios do Capítulo 6 1. O poliômio procurado P() a + b + c + d deve satisfazer a idetidade P(+1) P() +, ou seja, a(+1) + b(+1) + c(+1) + d a + b + c + d +, o que é equivalete a (a 1) +
Instituto de Física USP. Física V - Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
Istituto de Física USP Física V - Aula 5 Professora: Mazé Bechara Paulo Vazolii - cietista e compositor Aula 5 Aida o átomo de H. A proposta de de Broglie de caráter dual das partículas materiais 1. Aida
A Transformada de Laplace
 MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
MINISTÉRIO DA EDUCAÇÃO SECRETARIA DE EDUCAÇÃO PROFISSIONAL E TECNOLÓGICA INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DE SANTA CATARINA CAMPUS JOINVILLE DEPARTAMENTO DO DESENVOLVIMENTO DO ENSINO
4. FREQUÊNCIAS NATURAIS E CARGAS CRÍTICAS
 4. FREQUÊNCIAS NATURAIS E CARGAS CRÍTICAS O presente capítulo apresenta a análise linear e vigas e seção aberta e parees elgaas simplesmente apoiaas, mostrano o processo e iscretização por Galerkin e as
4. FREQUÊNCIAS NATURAIS E CARGAS CRÍTICAS O presente capítulo apresenta a análise linear e vigas e seção aberta e parees elgaas simplesmente apoiaas, mostrano o processo e iscretização por Galerkin e as
1. Definição e conceitos básicos de equações diferenciais
 Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Análise e Controle de Sistemas Lineares
 Aálise e Cotrole de Sistemas Apostila de Aálise e Cotrole de Sistemas Prof Valdemir Carrara wwwcarraraus val08@carraraus Aálise e Cotrole de Sistemas 3 Aálise e Cotrole de Sistemas Ídice Cap Coceitos
Aálise e Cotrole de Sistemas Apostila de Aálise e Cotrole de Sistemas Prof Valdemir Carrara wwwcarraraus val08@carraraus Aálise e Cotrole de Sistemas 3 Aálise e Cotrole de Sistemas Ídice Cap Coceitos
F F F F. Equilíbrio de um Corpo Rígido Cap. 5. Condições para o equilíbrio em duas dimensões: Condições para o equilíbrio em duas dimensões:
 bjetivos - Equilíbrio em Duas Dimensões EÂNI - ESTÁTI Equilíbrio e um orpo ígio ap. 5 Desenvolver as equações e equilíbrio para um corpo rígio. Introuzir o conceito e iagrama e corpo livre para um corpo
bjetivos - Equilíbrio em Duas Dimensões EÂNI - ESTÁTI Equilíbrio e um orpo ígio ap. 5 Desenvolver as equações e equilíbrio para um corpo rígio. Introuzir o conceito e iagrama e corpo livre para um corpo
Matemática II º Semestre 2ª Frequência 14 de Junho de 2011
 Matemática II 00-0 º Semestre ª Frequêcia de Juho de 0 Pedro Raposo; Maria João Araújo; Carla Cardoso; Vasco Simões O teste tem a duração de :0 horas Deve resolver os grupos em folhas separadas Grupo I
Matemática II 00-0 º Semestre ª Frequêcia de Juho de 0 Pedro Raposo; Maria João Araújo; Carla Cardoso; Vasco Simões O teste tem a duração de :0 horas Deve resolver os grupos em folhas separadas Grupo I
Cálculo Diferencial e Integral I Resolução do 2 ō Teste - LEIC
 Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
Eletromagnetismo II 1 o Semestre de 2007 Noturno - Prof. Alvaro Vannucci
 Eletromagetismo 1 o Semestre de 7 Noturo - Prof. Alvaro Vaucci 1 a aula 7/fev/7 ivros-texto: eitz-milford Griffiths Vamos relembrar as 4 equações básicas do Eletromagetismo 1 a ) ei de Gauss: O Fluxo do
Eletromagetismo 1 o Semestre de 7 Noturo - Prof. Alvaro Vaucci 1 a aula 7/fev/7 ivros-texto: eitz-milford Griffiths Vamos relembrar as 4 equações básicas do Eletromagetismo 1 a ) ei de Gauss: O Fluxo do
Tópicos: Análise e Processamento de BioSinais. Mestrado Integrado em Engenharia Biomédica. Faculdade de Ciências e Tecnologia. Universidade de Coimbra
 Cap. 5-Trasformada de Z Uiversidade de Coimbra Aálise e Processameto de BioSiais Mestrado Itegrado em Egeharia Biomédica Faculdade de Ciêcias e Tecologia Uiversidade de Coimbra Slide Aálise e Processameto
Cap. 5-Trasformada de Z Uiversidade de Coimbra Aálise e Processameto de BioSiais Mestrado Itegrado em Egeharia Biomédica Faculdade de Ciêcias e Tecologia Uiversidade de Coimbra Slide Aálise e Processameto
Circuitos Elétricos II
 Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada de Laplace Definição da Transformada de Laplace Propriedades da Transformada
Universidade Federal do ABC Eng. de Instrumentação, Automação e Robótica Circuitos Elétricos II José Azcue, Prof. Dr. Transformada de Laplace Definição da Transformada de Laplace Propriedades da Transformada
objetivo Exercícios Meta da aula Pré-requisitos
 Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
CAPÍTULO 8. Exercícios Inicialmente, observamos que. não é série de potências, logo o teorema desta
 CAPÍTULO 8 Eercícios 8 Iicialmete, observamos que 0 ão é série de otêcias, logo o teorema desta seção ão se alica Como, ara todo 0, a série é geométrica e de razão, 0, etão a série coverge absolutamete
CAPÍTULO 8 Eercícios 8 Iicialmete, observamos que 0 ão é série de otêcias, logo o teorema desta seção ão se alica Como, ara todo 0, a série é geométrica e de razão, 0, etão a série coverge absolutamete
Preliminares 1. 1 lim sup, lim inf. Medida e Integração. Departamento de Física e Matemática. USP-RP. Prof. Rafael A. Rosales. 8 de março de 2009.
 Medida e Itegração. Departameto de Física e Matemática. USP-RP. Prof. Rafael A. Rosales 8 de março de 2009. 1 lim sup, lim if Prelimiares 1 Seja (x ), N, uma seqüêcia de úmeros reais, e l o limite desta
Medida e Itegração. Departameto de Física e Matemática. USP-RP. Prof. Rafael A. Rosales 8 de março de 2009. 1 lim sup, lim if Prelimiares 1 Seja (x ), N, uma seqüêcia de úmeros reais, e l o limite desta
Séries de Fourier AM3D. Generalidades sobre funções periódicas
 11 1 Séries de Fourier AM3D Geeralidades sobre fuções periódicas Defiição 1 Seja f uma fução da variável real. Diz-se que f é periódica de período T > se x D f, f(x+t = f(x. Exemplo As fuções seo e co-seo
11 1 Séries de Fourier AM3D Geeralidades sobre fuções periódicas Defiição 1 Seja f uma fução da variável real. Diz-se que f é periódica de período T > se x D f, f(x+t = f(x. Exemplo As fuções seo e co-seo
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
II. REVISÃO DE FUNDAMENTOS
 INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
INSTITUTO TECNOLÓGICO DE AERONÁUTICA CURSO DE ENGENHARIA MECÂNICA-AERONÁUTICA MPS-43: SISTEMAS DE CONTROLE II. REVISÃO DE FUNDAMENTOS Prof. Davi Antônio dos Santos (davists@ita.br) Departamento de Mecatrônica
Sistemas de Controle
 Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
Sistemas de Controle Adriano Almeida Gonçalves Siqueira Aula 2 - Transformada de Laplace e Função Transferência Sistemas de Controle p. 1/27 Função Impulso Unitário Função pulso com área unitária: f(t)
CAPÍTULO 3 DEPENDÊNCIA LINEAR
 CAPÍTUO DEPENDÊNCIA INEAR Comiação iear Defiição: Seja V um espaço etorial sore um orpo K Um etor omiação liear os etores que u a a a De forma areiaa poe-se esreer: u a i i i u V é ito uma V se existem
CAPÍTUO DEPENDÊNCIA INEAR Comiação iear Defiição: Seja V um espaço etorial sore um orpo K Um etor omiação liear os etores que u a a a De forma areiaa poe-se esreer: u a i i i u V é ito uma V se existem
MODELO DE LINHAS DE TRANSMISSÃO COM DIFERENTES ESTRUTURAS BÁSICAS APLICADAS EM SIMULAÇÕES DE TRANSITÓRIOS ELETROMAGNÉTICOS
 MODELO DE LINHAS DE TRANSMISSÃO OM DIFERENTES ESTRUTURAS BÁSIAS APLIADAS EM SIMULAÇÕES DE TRANSITÓRIOS ELETROMAGNÉTIOS LUIS H. JUS, AGHATTA. MOREIRA, MELISSA O. SANTOS, THAINÁ G. PEREIRA, AFONSO J. PRADO,
MODELO DE LINHAS DE TRANSMISSÃO OM DIFERENTES ESTRUTURAS BÁSIAS APLIADAS EM SIMULAÇÕES DE TRANSITÓRIOS ELETROMAGNÉTIOS LUIS H. JUS, AGHATTA. MOREIRA, MELISSA O. SANTOS, THAINÁ G. PEREIRA, AFONSO J. PRADO,
MOVIMENTO DE TRANSLAÇÃO: A PARTÍCULA EM UMA CAIXA
 MOVIMNTO D TRANSAÇÃO: A PARTÍCUA M UMA CAIA Prof. Harle P. Martis Filo Partícula livre oveo-se e ua iesão Ae ik Be ik k Não á restrições às soluções a equação e Scröiger A e B poe assuir qualquer valor
MOVIMNTO D TRANSAÇÃO: A PARTÍCUA M UMA CAIA Prof. Harle P. Martis Filo Partícula livre oveo-se e ua iesão Ae ik Be ik k Não á restrições às soluções a equação e Scröiger A e B poe assuir qualquer valor
Considerações finais
 Cosiderações fiais Bases Matemáticas Defiições prelimiares Defiição 1 Dizemos que y é uma cota superior para um cojuto X se, para todo x X é, verdade que y x. Exemplo 1 os úmeros 2, 3, π e quaisquer outros
Cosiderações fiais Bases Matemáticas Defiições prelimiares Defiição 1 Dizemos que y é uma cota superior para um cojuto X se, para todo x X é, verdade que y x. Exemplo 1 os úmeros 2, 3, π e quaisquer outros
2. Modelos Lineares de Espaço de Estados. e resposta ao impulso. Método para o cálculo das soluções: através do uso de transformadas de Laplace
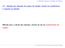 2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
2.3 - Solução das equações de espaço de estados, função de transferência e resposta ao impulso Método para o cálculo das soluções: através do uso de transformadas de Laplace Transformadas de Laplace f
AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E
 AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E SUPERCRÍTICO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 26 de março de 2018 Roteiro 1 Modelo geral Amortecimento supercrítico Amortecimento subcrítico
AMORTECIMENTOS SUBCRÍTICO, CRÍTICO E SUPERCRÍTICO Mecânica II (FIS-26) Prof. Dr. Ronaldo Rodrigues Pelá IEFF-ITA 26 de março de 2018 Roteiro 1 Modelo geral Amortecimento supercrítico Amortecimento subcrítico
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida
 CÁLCULO I Prof. Eilson Neri Júnior Prof. Anré Almeia Aula n o 08: Regra a Caeia. Derivação Implícita. Derivaa a Função Inversa. Objetivos a Aula Conhecer e aplicar a regra a caeia; Utilizar a notação e
CÁLCULO I Prof. Eilson Neri Júnior Prof. Anré Almeia Aula n o 08: Regra a Caeia. Derivação Implícita. Derivaa a Função Inversa. Objetivos a Aula Conhecer e aplicar a regra a caeia; Utilizar a notação e
Lista de Exercícios Método de Newton
 UNEMAT Uiversidade do Estado de Mato Grosso Campus Uiversitário de Siop Faculdade de Ciêcias Eatas e Tecológicas Curso de Egeharia Civil Disciplia: Cálculo Diferecial e Itegral I Lista de Eercícios Método
UNEMAT Uiversidade do Estado de Mato Grosso Campus Uiversitário de Siop Faculdade de Ciêcias Eatas e Tecológicas Curso de Egeharia Civil Disciplia: Cálculo Diferecial e Itegral I Lista de Eercícios Método
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
11 Aplicações da Integral
 Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Aplicações da Itegral Ao itroduzirmos a Itegral Defiida vimos que ela pode ser usada para calcular áreas sob curvas. Veremos este capítulo que existem outras aplicações. Essas aplicações estedem-se aos
Séries de Fourier. As séries de Fourier são séries cujos termos são funções sinusoidais.
 Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Séries de Fourier As séries de Fourier são séries cujos termos são fuções siusoidais. Importâcia prática: uma fução periódica (em codições bastate gerais) pode ser represetada por uma série de Fourier;
Vibrações de Estacas Parcialmente Enterradas em uma Base Elástica
 Vibrações e Estacas Parcialmete Eterraas em uma Base Elástica toio Euaro G. Sampaio E-mail: aesampaio@hotmail.com Paulo Batista Goçalves Depto e Eeharia Civil, PUC-Rio Rua Marquês e São Vicete, 5 53-9,
Vibrações e Estacas Parcialmete Eterraas em uma Base Elástica toio Euaro G. Sampaio E-mail: aesampaio@hotmail.com Paulo Batista Goçalves Depto e Eeharia Civil, PUC-Rio Rua Marquês e São Vicete, 5 53-9,
VESTIBULAR 2012 / 3º DIA
 VESTIBULAR 01 / 3º DIA ÍSICA 33. Consiere um rio e margens paralelas, cuja istância entre as margens é e 140 m. A velociae a água em relação às margens é e 0 m/s. Um bote cuja velociae em relação à água
VESTIBULAR 01 / 3º DIA ÍSICA 33. Consiere um rio e margens paralelas, cuja istância entre as margens é e 140 m. A velociae a água em relação às margens é e 0 m/s. Um bote cuja velociae em relação à água
CÁLCULO I. 1 Regras de Derivação. Objetivos da Aula. Aula n o 12: Regras de Derivação. Apresentar e aplicar as regras operacionais de derivação;
 CÁLCULO I Prof. Marcos Diniz Prof. Anré Almeia Prof. Eilson Neri Júnior Aula n o 2: Regras e Derivação Objetivos a Aula Apresentar e aplicar as regras operacionais e erivação; Derivar funções utilizano
CÁLCULO I Prof. Marcos Diniz Prof. Anré Almeia Prof. Eilson Neri Júnior Aula n o 2: Regras e Derivação Objetivos a Aula Apresentar e aplicar as regras operacionais e erivação; Derivar funções utilizano
3. Meios não-lineares e conversão de freqüências
 67. Meios ão-lieares e coversão e freqüêcias Toos os cristais ão-lieares utilizaos para coversão e frequêcias são meios ielétricos. Também chamaos e isolates, os ielétricos são materiais cujas cargas omiates
67. Meios ão-lieares e coversão e freqüêcias Toos os cristais ão-lieares utilizaos para coversão e frequêcias são meios ielétricos. Também chamaos e isolates, os ielétricos são materiais cujas cargas omiates
13 Funções de Teste. Simulação no VisSim 1 INTRODUÇÃO 2 IMPULSO UNITÁRIO (DELTA DE DIRAC)
 Funções de Teste. Simulção no VisSim 1 13 Funções de Teste Simulação no VisSim 1 INTRODUÇÃO As funções de teste formam a base para a análise e a simulação de sistemas lineares no domínio do tempo e são
Funções de Teste. Simulção no VisSim 1 13 Funções de Teste Simulação no VisSim 1 INTRODUÇÃO As funções de teste formam a base para a análise e a simulação de sistemas lineares no domínio do tempo e são
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
CÁLCULO I. 1 Regras de Derivação. Objetivos da Aula. Aula n o 12: Regras de Derivação. Apresentar e aplicar as regras operacionais de derivação;
 CÁLCULO I Prof. Marcos Diniz Prof. Anré Almeia Prof. Eilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Aula n o : Regras e Derivação Objetivos a Aula Apresentar e aplicar as regras operacionais
CÁLCULO I Prof. Marcos Diniz Prof. Anré Almeia Prof. Eilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Aula n o : Regras e Derivação Objetivos a Aula Apresentar e aplicar as regras operacionais
Sumário. 2 Índice Remissivo 11
 i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
Números Complexos. David zavaleta Villanueva 1
 Material do miicurso a ser lecioado o III EREM-Mossoró-UERN UFRN - Uiversidade Federal do Rio Grade do Norte Edição N 0 outubro 011 Números Complexos David zavaleta Villaueva 1 1 CCET-UFRN, Natal, RN,
Material do miicurso a ser lecioado o III EREM-Mossoró-UERN UFRN - Uiversidade Federal do Rio Grade do Norte Edição N 0 outubro 011 Números Complexos David zavaleta Villaueva 1 1 CCET-UFRN, Natal, RN,
Exercícios de Cálculo III - CM043
 Eercícios de Cálculo III - CM43 Prof. José Carlos Corrêa Eidam DMAT/UFPR Dispoível o sítio people.ufpr.br/ eidam/ide.htm o. semestre de 22 Lista Sequêcias e séries de úmeros reais. Decida se cada uma das
Eercícios de Cálculo III - CM43 Prof. José Carlos Corrêa Eidam DMAT/UFPR Dispoível o sítio people.ufpr.br/ eidam/ide.htm o. semestre de 22 Lista Sequêcias e séries de úmeros reais. Decida se cada uma das
Capítulo 2 Dinâmica de Sistemas Lineares
 Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
Capítulo 2 Dinâmica de Sistemas Lineares Gustavo H. C. Oliveira TE055 Teoria de Sistemas Lineares de Controle Dept. de Engenharia Elétrica / UFPR Gustavo H. C. Oliveira Dinâmica de Sistemas Lineares 1/57
EQUAÇÕES DIFERENCIAIS
 EQUAÇÕES DIFERENCIAIS rof Me Arto Barboi SUMÁRIO INTRODUÇÃO EQUAÇÃO DIFERENCIAL ORDINÁRIA (EDO) Ordem de uma Equação Diferecial Ordiária Grau de uma Equação Diferecial Ordiária Solução geral e particular
EQUAÇÕES DIFERENCIAIS rof Me Arto Barboi SUMÁRIO INTRODUÇÃO EQUAÇÃO DIFERENCIAL ORDINÁRIA (EDO) Ordem de uma Equação Diferecial Ordiária Grau de uma Equação Diferecial Ordiária Solução geral e particular
Métodos iterativos. Métodos Iterativos para Sistemas Lineares
 Métodos iterativos Métodos Iterativos para Sistemas Lieares Muitos sistemas lieares Ax = b são demasiado grades para serem resolvidos por métodos directos (por exemplo, se A é da ordem de 10000) á que
Métodos iterativos Métodos Iterativos para Sistemas Lieares Muitos sistemas lieares Ax = b são demasiado grades para serem resolvidos por métodos directos (por exemplo, se A é da ordem de 10000) á que
Estabilidade de sistemas de controle lineares invariantes no tempo
 2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
2 Estabilidade de sistemas de controle lineares invariantes no tempo 2.1 Introdução Neste capítulo, vamos definir alguns conceitos relacionados à estabilidade de sistemas lineares invariantes no tempo.
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida
 CÁLCULO I Prof. Eilson Neri Júnior Prof. Anré Almeia Aula n o 0: Derivaas e Orem Superior e Regra a Caeia Objetivos a Aula Definir e eterminar as erivaas e orem superior; Conhecer e aplicar a regra a caeia;
CÁLCULO I Prof. Eilson Neri Júnior Prof. Anré Almeia Aula n o 0: Derivaas e Orem Superior e Regra a Caeia Objetivos a Aula Definir e eterminar as erivaas e orem superior; Conhecer e aplicar a regra a caeia;
CAP. VI DIFERENCIAÇÃO E INTEGRAÇÃO NUMÉRICA
 CAP. VI DIFRNCIAÇÃO INGRAÇÃO NUÉRICA 6. DIFRNCIAÇÃO NUÉRICA m muitas circustâcias tora-se diícil obter valores de derivadas de uma ução: derivadas que ão são de ácil obteção; emplo (calcular a ª derivada:
CAP. VI DIFRNCIAÇÃO INGRAÇÃO NUÉRICA 6. DIFRNCIAÇÃO NUÉRICA m muitas circustâcias tora-se diícil obter valores de derivadas de uma ução: derivadas que ão são de ácil obteção; emplo (calcular a ª derivada:
Projeto 3. 8 de abril de y max y min. Figura 1: Diagrama de um cabo suspenso.
 Cabos suspensos Projeto 3 8 e abril e 009 A curva escrita por um cabo suspenso pelas suas etremiaes é enominaa curva catenária. y ma y min 0 Figura 1: Diagrama e um cabo suspenso. A equação que escreve
Cabos suspensos Projeto 3 8 e abril e 009 A curva escrita por um cabo suspenso pelas suas etremiaes é enominaa curva catenária. y ma y min 0 Figura 1: Diagrama e um cabo suspenso. A equação que escreve
Controle de Processos Aula: Estabilidade e Critério de Routh
 107484 Controle de Processos Aula: Estabilidade e Critério de Routh Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB)
107484 Controle de Processos Aula: Estabilidade e Critério de Routh Prof. Eduardo Stockler Tognetti Departamento de Engenharia Elétrica Universidade de Brasília UnB 1 o Semestre 2016 E. S. Tognetti (UnB)
