Circuitos de Corrente Alternada I

Transcrição

1 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems a ntaçã cmplexa para análise ds mesms. Em particular, estudarems as curvas de tensã versus crrente para resistres, indutres e capacitres submetids a tensões alternadas. Estudarems também s circuits C e L e sua utilizaçã cm filtrs de freqüências. Sempre que surgir uma dúvida quant à utilizaçã de um instrument u cmpnente, alun deverá cnsultar prfessr para esclareciments. I. Definições gerais Ns circuits de crrente cntínua, a resistência elétrica é a única grandeza que expressa impediment a passagem da crrente elétrica. Em crrente alternada, existem utrs efeits além d resistiv que influenciam a passagem de crrente n circuit; pr exempl, a indutância quand circuit cntém bbinas, u a capacitância quand circuit cntém capacitres. Deste md, a razã tensã/crrente em um circuit de crrente alternada nã depende apenas das resistências elétricas d mesm. Pr esse mtiv, a razã entre tensã e crrente em um circuit de crrente alternada recebe um utr nme: impedância, um term que fi prpst pr Oliver Heaviside em Heaviside deu grandes cntribuições à teria eletrmagnética, tend refrmulad as equações de Maxwell na ntaçã vetrial mderna. As cntribuições de Heaviside também incluem cálcul vetrial, métds de resluçã de equações diferenciais e teria de circuits elétrics e linhas de transmissã, além de ter intrduzid utrs terms cm indutância, cndutância e eletrets. A impedância de um circuit é cmpsta de três cmpnentes: Z : cmpnente resistiva da impedância u simplesmente resistência (); Z C : cmpnente capacitiva da impedância u reatância capacitiva (X C ); Z L : cmpnente indutiva da impedância u reatância indutiva (X L ); Uma utra grandeza imprtante na descriçã de circuits de crrente alterna é a freqüência das tensões e crrentes d circuit. A freqüência linear é medida em Hertz 1

2 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I (Hz) e é igual a númer de cicls pr segund; seu símbl é usualmente f. A freqüência angular é medida em rad / s e é igual a taxa de variaçã da fase da crrente; seu símbl é nrmalmente ω. A relaçã entre as duas é: ω π f (1) II. Circuits esistivs, Capacitivs u Indutivs Na prática, é impssível bter circuits de crrente alternada cm características puramente resistivas, indutivas u capacitivas. Mesm assim é didátic tratar esses cass ideais, para se ter uma idéia de seu cmprtament. Neste cas, tratament pde ser feit através de equações diferenciais simples. As características previstas individualmente sã mantidas quand tratarms de circuits que cntenham cmbinações desses elements. a) Circuit Puramente esistiv Anterirmente, estudams s efeits da tensã e da crrente cntínua em resistres. Agra vams estudar um resistr submetid a uma fnte de tensã alternada da frma cs( ω t + δ ), cm na figura 1. Figura 1 Esquema elétric de um circuit puramente resistiv. Ohm: A crrente que flui através d resistr pde ser calculada utilizand-se a lei de I cs( ωt + δ ) I cs( ωt + δ ) ()

3 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Neste cas, bservams que tensã e crrente variam cssenidalmente n temp, e nã existe diferença de fase entre ambas. A amplitude da crrente, I, é dada simplesmente pr /. A ptência instantânea dissipada n resistr é dada pr: P I ωt + δ cs ( ) (3) pr: O valr médi da ptência dissipada em um u mais períds cmplets é dad P med T 1 1 t dt T cs ( ω + δ ) (4) Na equaçã 4, T representa um u mais períds cmplets. ems dessa equaçã que a ptência média é diferente de zer para qualquer valr ω, ist é, independentemente da freqüência um resistr sempre dissipa a mesma ptência elétrica em um circuit nde tensã e crrente variam n temp. A impedância d circuit, em módul, é dada pela razã entres s valres de pic da tensã ( ) e da crrente (I ): Z I (5) Prtant, neste cas a impedância é simplesmente a resistência d circuit. b) Circuit Puramente Capacitiv: Na figura mstrams um capacitr submetid a uma diferença de ptencial da frma cs( ωt + δ ). A carga acumulada n capacitr é Q Q cs( ωt + δ ), nde Q C. 3

4 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I I δ ~ + - C + - Q Figura Esquema elétric de um circuit puramente capacitiv. A crrente I que flui através d circuit pde ser calculada da seguinte frma: dq I ωc sin( ωt + δ ) I cs( ωt + δ + π / ) dt (6) Neste cas, bservams que tensã e crrente variam n temp, mas estã fra de fase pr um ângul de 90 (π/ rad). Em um circuit puramente capacitiv a crrente é adiantada em relaçã à tensã (u seja, pic de crrente crre antes d pic de tensã) e tem amplitude dada pr I ωc. Nte que esse cmprtament é de fat esperad, pis assim que capacitr descarregad é ligad n circuit a crrente é máxima e a tensã é mínima (pis capacitr está descarregad) e à medida que temp passa a crrente diminui e a tensã aumenta (a carga vai se acumuland nas placas d capacitr) e depis de um cert temp a crrente é zer e a tensã é máxima (capacitr carregad). A ptência dissipada neste circuit é dada pr: P I C cs( ωt + δ ).sin( ωt + δ ) (7) A ptência média é: P med T C sin( ) cs( ) ω t + δ ωt + δ dt C sin( + ) 0 ωt δ dt T T T (8) A ptência média dissipada em um circuit puramente capacitiv é sempre nula, para qualquer valr de ω. Em utras palavras, um capacitr nã dissipa ptência; ele 4

5 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I armazena energia (em frma de energia eletrstática) durante uma parte d cicl para frnecê-la durante a utra parte, de md que flux médi é nul. A impedância d circuit, em módul, é dada pela razã entre s valres máxims de tensã ( ) e de crrente (I ), u seja: Z X C I 1 ωc (8) A impedância capacitiva (u reatância capacitiva) é inversamente prprcinal à freqüência da tensã alternada. N limite de tensã cntínua, vai a infinit, que significa que nã há crrente. De fat, quand um capacitr é ligad a uma fnte de tensã cntínua, ele se carrega (usualmente de frma rápida) até a tensã da fnte e a crrente deixa de circular. c) Circuit Puramente Indutiv: Na figura 3 mstrams um indutr submetid a uma frça eletrmtriz da frma cs( ω t + δ ). A diferença de ptencial sbre um indutr pde ser escrita cm: di L cs( ω t + δ ) dt (9) I + δ ~ L Figura 3 Esquema elétric de um circuit puramente indutiv. A crrente I que flui através d circuit pde ser calculada da seguinte frma: I π t + dt t + + C I t + + C L cs( ω δ ) sin( ω δ ) cs( ω δ ) ωl (10) 5

6 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I A tensã e a crrente variam peridicamente n temp, e estã fra de fase pr um ângul de 90. Entretant, n cas d circuit puramente indutiv a crrente é atrasada em relaçã à tensã. Esse resultad pde ser cmpreendid qualitativamente se lembrarms que a frça cntra eletrmtriz n indutr é prprcinal a taxa de variaçã da crrente n temp (lei de Faraday-Lenz). Quand indutr é ligad a circuit ele se cmprta cm um curt-circuit (estams desprezand efeit resistiv) e a crrente tende a aumentar rapidamente (máxima taxa de variaçã) e imediatamente aparece uma tensã ns terminais d indutr (frça cntra-eletrmmtriz) de md a impedir que a crrente se estabeleça. À medida que temp passa a frma eletrmtriz da fnte faz cm que a crrente vai se estabelecend de frma mais lenta e a tensã n indutr vai diminuind até que a crrente atinja um valr que equilíbri e a tensã ns terminais d indutr seja nula. O pic de máxima tensã n indutr crre antes da máxima crrente e, prtant, a tensã está adiantada em relaçã a crrente. Cm n cas d circuit puramente capacitiv, a ptência média dissipada n circuit é nula para qualquer valr de ω. O indutr armazena energia (em frma magnética) durante uma parte d cicl e frnece essa energia na utra parte d cicl. A impedância d circuit é, em módul, a razã entre e I, u seja: Z X L I ωl (11) A impedância de um circuit puramente indutiv cresce cm a freqüência, e vai a zer em circuits de crrente cntínua. De fat, cm nesses circuits a crrente nã varia, a tensã sbre indutr é nula. Um indutr real (bbina) é cmpst pr muitas vltas de fis enrlads e pssui, além da indutância, uma resistência. Assim, cstuma-se dizer que na prática tda indutância vem sempre acmpanhada de uma resistência. Prém essa afirmaçã nã é ttalmente verdadeira, já que hje existem materiais que em baixa temperaturas pdem atingir estad supercndutr e ter resistência elétrica nula. Em utras palavras uma bbina feita de um material supercndutr é um indutr pur, u seja, cnverte energia elétrica em energia magnética da frma mais eficiente pssível. Iss pde 6

7 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I parecer a princípi uma idealizaçã sem muita aplicaçã, mas, de fat, ns equipaments de ressnância magnética nuclear, cmuns em hspitais hje em dia, a geraçã d alt camp magnétic necessári a experiment (u exame clínic, n cas) é feita através de um slenóide feit de material supercndutr, justamente para aprveitar essa máxima eficiência na cnversã de energia elétrica em energia magnética. III. A ntaçã cmplexa Na análise de circuits de crrente alternada, é bastante útil usar frmalism da impedância cmplexa, que usa as prpriedades das expnenciais imaginárias para simplificar a análise de prblemas que envlvem valres (tensões e crrentes) que variam senidalmente. A grande vantagem é que as equações diferenciais lineares transfrmam-se facilmente em equações rdinárias. Em tds s cass, valr de fat das tensões e crrentes (valr que pde ser medid em um experiment) é a parte real d númer cmplex. Na ntaçã cmplexa, tensã e crrente alternadas senidais sã expressas cm: i t ( t) e ω (1a) i t I( t) I e ω (1b) e I pdem assumir valres cmplexs. O cnceit de impedância também pde ser generalizad na ntaçã cmplexa, cm send a razã entre s valres cmplexs da tensã e da crrente. O resultad é em geral um númer cmplex, cuj módul é igual à impedância real (razã entre s valres de pic) e argument é igual à diferença de fase entre a crrente e a tensã (psitiv se a tensã fr adiantada cm relaçã à crrente). N cas de um resistr, a tensã e a crrente estã em fase, lg a impedância cmplexa é um númer real, igual à impedância real: 7

8 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Z (13) N cas d capacitr, a crrente é adiantada de 90º em relaçã à tensã, lg a impedância cmplexa está n eix imaginári negativ. Seu módul é dad pela equaçã 8. Prtant: Z C i ix C ωc (14) N cas d indutr, a crrente é atrasada de 90º em relaçã à tensã, lg a impedância cmplexa está n eix imaginári psitiv, cm módul dad pela equaçã 11. Prtant: Z ix iω L (15) L L I. Circuits C e L série Na análise ds circuits esquematizads na figura 4a e 4b, utilizarems frmalism da impedância cmplexa. ams assumir que s circuits sã alimentads pr uma fnte de tensã senidal da frma ( t) cs( ωt), que na ntaçã cmplexa i t se escreve ( t) e ω. A crrente que atravessa circuit é também senidal, e dada i t pr I ( t) Ke ω. (a) (b) (t) (t) (t) ~ ~ C C (t) (t) (t) L Figura 4: Circuits de crrente alternada. (a) C; (b) L 8

9 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Para circuit C, utilizand a lei de Kirchhff, pdems escrever: ( t) + C (16) As tensões n resistr e n capacitr sã dadas pr: i t I( t) Ke ω (17) C Q I( t). dt e C C iωc 1 K i ω. t (18) Substituind na equaçã 16 e canceland a expnencial que é cmum a tds s terms, btems: K. K + i ω C (19) Iss permite determinar K: K 1 i ωc (0) crrente: A impedância cmplexa é a razã entre s valres cmplexs da tensã e da Z I K 1 i ωc (1) O módul da impedância, que é a razã entre s valres de pic da tensã e da crrente, é módul desse valr: 9

10 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Z 1 + ωc () N circuit L, figura 4b, a tensã sbre indutr é dada pr: di L L ωlke dt iωt (3) A tensã ttal é dada pr ( t) +. Lg: L K + iωlk (4) Lg: K + iωl (5) A impedância cmplexa e seu módul sã, prtant: Z + iω. L (6) Z + ( ωl) (7) Cm frmalism de impedâncias cmplexas a análise ds circuits de crrente alternada fica muit parecida cm tratament dads as circuits de crrente cntínua. D mesm md que uma cmbinaçã de resistres em série e em paralel pde ser representada pr um únic resistr equivalente, um circuit cntend uma cmbinaçã arbitrária de resistres, indutres e capacitres pde ser representad pr uma impedância ttal Z. As equações 1 e 6 mstram que a impedância cmplexa equivalente de cmpnentes ligads em série é a sma das impedâncias cmplexas individuais, cm acntece cm as resistências em circuits de crrente cntínua. Da 10

11 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I mesma frma, a regra de assciaçã de impedâncias cmplexas em paralel é idêntica à das resistências. N entant, devems ressaltar que: O frmalism de impedância cmplexa é útil para tratar relações lineares, cm, pr exempl, uma equaçã de malha, mas nã pde ser usad quand as relações nã sã lineares, cm n cálcul de ptência. O frmalism de impedância cmplexa pde ser aplicad diretamente a circuits cm geradres de nda senidal, mas nã a circuits cm geradres de utr tip de nda.. Filtrs C ( passa-alta ) e L ( passa-baixa ) Os circuits L e C pssuem prpriedades muit interessante quant analisad cm funçã da freqüência. Esses circuits funcinam cm filtrs elétrics e sã utilizads em instalações elétricas e equipaments eletrônics para rejeitar ruíd e para prtegê-ls, pr exempl, cntra transientes induzids pela queda de rais durante as trmentas. De md geral um filtr pde ser representad cm um circuit cm dis terminais de entrada e dis de saída, cm na figura 5. Filtr s Figura 5 epresentaçã de um Filtr elétric Td filtr é caracterizad pr uma funçã de transferência, T(ω), definida cm send quciente entre a tensã (cmplexa) ns terminais de saída pela tensã (cmplexa) ns terminais da entrada: s ( s ) T( ω) ( ) max max e iφ (8) 11

12 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I O módul da funçã de transferência é a razã entre s valres de pic da tensã ns terminais de saída e entrada; argument é a diferença de fase entre eles (psitiv se a saída estiver adiantada em relaçã à entrada). a) Filtr C (u passa-alta ) A assciaçã em série de um resistr e um capacitr (mstrad na figura 4a) frma um circuit simples, prém de muita utilidade. Neste circuit, bserva-se um cmprtament característic da tensã n resistr ( ) em funçã da freqüência. Cnsiderand que a saída d filtr está ns terminais d resistr, a funçã de transferência pde ser escrita da seguinte frma: T ( ω) Z i ωc (9) O módul da funçã de transferência é: T ( ω) ωc (30) Para altas freqüências ( ω >> 1/ C ), a tensã de é aprximadamente igual à tensã de entrada d geradr ( ). Em baixas freqüências, é menr que a tensã de entrada. Lg este circuit privilegia a passagem de crrentes alternadas cm altas freqüências, send pr iss cnhecid cm filtr passa-alta. Na freqüência ω 1/ C, metade da ptência frnecida é atenuada pel circuit, e pr iss esse valr é denminad freqüência de meia-ptência. A funçã de transferência pde ser escrita em terms dessa freqüência: T ( ω) 1+ 1 ( ω / ω) (31) 1

13 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I A funçã de transferência é definida em term das tensões. Em algumas aplicações, é mais interessante pensar em terms de ptência. Para uma dada carga que será alimentada pela saída d filtr, a ptência é prprcinal a quadrad da tensã. Prtant, a razã entre as ptências é igual a quadrad da funçã de transferência. b) Filtr L (u passa-baixa ) Da mesma frma, a assciaçã em série de um resistr e um indutr, figura 4b, frma um utr circuit de grande utilidade. Neste cas a funçã de transferência pde ser escrita cm: T ( ω) Z 1 ωl 1+ i (3) O módul da funçã de transferência é: T ( ω) 1 ωl 1+ (33) Neste circuit, a tensã é aprximadamente igual a tensã a baixas freqüências ( ω << / L ). Em altas freqüências a tensã sbre a resistência (u seja, a crrente) é atenuada e pr iss filtr é denminad filtr passa-baixa. A freqüência ω L é a freqüência de meia-ptência, cm n filtr C. Esta freqüência pde ser / adtada cm a freqüência de crte d filtr. A funçã de transferência pde ser escrita em terms dessa freqüência: T ( ω) 1+ 1 ( ω / ω ) (34) 13

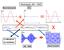
14 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Na figura 6a, há gráfic da funçã de transferência para s filtrs C e L. Na figura 6b, há um gráfic de ptência, que é igual a quadrad da funçã de transferência. Nte n gráfic d quadrad da funçã de transferência que, quand T(ω) 0.5 ω ω 0, justificand a denminaçã freqüência de meia ptência. (a) (b) T(ω) 0.4 T(ω) 0.4 Filtr L (passa-baixas) Filtr C (passa-altas) 0. Filtr L (passa-baixas) Filtr C (passa-altas) ω /ω 0 ω/ω 0 Figura 6 espsta de filtrs C e L em funçã da freqüência. (a) Funçã de transferência. (b) elaçã entre ptência de saída e ptência de entrada. Os filtrs C e L sã muit usads cm filtrs de freqüência em várias aplicações; um exempl é ns sistemas de sm cm várias caixas. A caixa mair, chamada de wfer, executa melhr s sns graves (de baixa freqüência), e a caixa menr ( twitter) executa melhr s aguds (de alta freqüência). O sinal que vai para wfer passa pr um filtr passa-baixas (L), e sinal que vai para twitter passa pr um filtr passa-altas (C). O resultad é que cada caixa reprduz apenas a faixa de freqüências para a qual seu desempenh é melhr, que melhra a qualidade d sm. 14

15 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Experiments Para quantificar cmprtament instantâne de tensões e crrentes que variam n temp, utilizarems um scilscópi. Prtant, preste muita atençã na ligaçã d scilscópi para que s cabs terra estejam sempre ligads n mesm pnt d circuit. 1. Curva xi de resistres, capacitres e indutres Nesta parte da prática estarems interessads em caracterizar cmprtament instantâne das curvas de tensões cm funçã da crrente (curvas xi) para resistres, indutres e capacitres. a) Utilizarems um scilscópi e um geradr de funções para medir a curva xi de resistres, capacitres e indutres em regime de crrente alternada. Para iss, use a mntagem da figura 7, cm scilscópi n md X-Y. N canal 1 (eix hrizntal), vcê deverá medir a crrente, a mens de um fatr de escala (lembre-se que, em um resistr, I / ); n canal (eix vertical), vcê deverá medir a tensã sbre cmpnente. Oscilscópi ~ X Canal 1 Canal (x) (y) Figura 7 Circuit utilizad para medir a curva -I característica de cmpnentes eletrônics. b) Clque um resistr de 1 kω e ajuste geradr de sinais para um sinal senidal de máxima amplitude e freqüência de cerca de 1 khz. c) Cnfigure scilscópi n md X-Y, ambs s canais em 5 /div e acplament DC e canal invertid (justifique prquê em seu relatóri). d) Clque um resistr n lugar d cmpnente X e bserve a curva xi na tela d scilscópi. arie a freqüência da fnte (de alguns Hz até dezenas de khz) e descreva que acntece cm a curva. cê deverá bservar uma reta cm mesm ceficiente angular em qualquer freqüência. Determine ceficiente angular e explique esse resultad. 15

16 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I e) Clque um capacitr de 0, µf n lugar d cmpnente X e bserve a curva xi na tela d scilscópi. arie a freqüência da fnte (desde alguns Hz até dezenas de khz) e descreva cm é a curva bservada e seu cmprtament cm funçã da freqüência. Frmule matematicamente prblema de md a prever tip de curva bservada e cmprtament cm funçã da freqüência. f) Clque um indutr de 44 mh n lugar d cmpnente X e bserve a curva xi na tela d scilscópi. arie a freqüência da fnte (desde alguns Hz até dezenas de khz) e descreva que acntece cm a curva. Frmule matematicamente prblema de md a prever tip de curva bservada e cmprtament cm funçã da freqüência.. Filtr C (passa-alta) Nesta parte da prática estarems interessads em verificar cmprtament das curva de transferência de filtrs passa-alta. a) Mnte circuit C mstrad na figura 8, cm 1 kω e C 0, µf. Ajuste geradr de funções para bter um sinal senidal de freqüência 1 khz cm amplitude máxima. ~ CH 1 CH Filtr C Figura 8 Circuit para determinar a curva característica de um filtr C b) Utilizand s dis canais d scilscópi, levante a curva da funçã de transferência d circuit, u seja, meça valr da tensã n geradr ( ) e na resistência ( ), em funçã da freqüência e faça um gráfic de / em funçã da 16

17 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I freqüência. Meça também valr da tensã n capacitr ( C ) Obs: durante tda a medida verifique valr da tensã (nã assuma que ele será mesm sempre). Certifique-se que s cabs de terra ds dis canais d scilscópi estejam cnectad n mesm pnt d circuit. Para medir a tensã sbre capacitr e resistr, ajuste scilscópi para visualizaçã de um canal, cm acplament DC. Para medir a tensã fnte, vcê pde usar md Add cm canal invertid (prque a fnte está ligada entre s terminais psitivs de cada canal); Utilize a mesma escala vertical para ambs s canais d scilscópi. c) Faça um gráfic de / e C / em funçã da freqüência. Uma sugestã é variar de 50 Hz até khz. d) Faça um gráfic da ptencia dissipada em cm funçã da freqüência e,cm esses dads, determine a freqüência de crte d filtr e cmpare cm valr esperad ω 0 1 C. 3. Filtr L (passa-baixas) Nesta parte da prática estarems interessads em verificar cmprtament das curva de transferência de filtrs passa-baixa. a) Mnte circuit L, utilizand 1 kω e L 44 mh. O circuit está mstrad na figura 9. ~ CH 1 CH L Filtr L Figura 9 Circuit para determinar a curva característica de um filtr L 17

18 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I b) Prceda da mesma maneira que n experiment anterir. Faça um gráfic de / e L / em funçã da freqüência. Uma sugestã é variar de 100 Hz até 0 khz. c) Faça um gráfic da ptencia dissipada em cm funçã da freqüência e, cm esses dads, determine a freqüência de crte d filtr, e cmpare cm valr esperad ω / L. Funçã de transferência de um filtr C ω/π (Hz) () () C () Funçã de transferência de um filtr L 18

19 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I ω/π (Hz) () () L () 19

20 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Apêndice Frmulaçã d Mdel de Drude para crrentes alternadas O mdel de Drude é um mdel teóric permite prever e calcular as prpriedades elétricas de materiais. Há várias maneiras de frmular mdel; em uma delas, faz-se a hipótese de que sbre s elétrns age, além da frça elétrica, uma frça de arrast prprcinal a sua velcidade. Iss nã entra em cntradiçã cm a hipótese de elétrn só interagir cm a rede de íns de fund durante as clisões prque que cnta é cmprtament médi ttal ds elétrns. Cm essa hipótese, a equaçã de mviment é: dv m dt m ee γv m (A1) Essa é uma equaçã diferencial de primeira rdem, linear e nã-hmgênea na variável v m, que é a velcidade média ds elétrns. Ela admite uma sluçã estacinária (v m cnstante n temp) se E fr cnstante também: v m ee γ (A) A crrente que atravessa um fi de seçã transversal A e cmpriment L é: I neav m ne AE γ (A3) Lembrand que E / L, escrevems: I ne A (A4) γ L ems entã que a hipótese da frça de arrast prprcinal à velcidade tem cm cnseqüência que a crrente é prprcinal a diferença de ptencial, à área e 0

21 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I inversamente prprcinal a cmpriment d fi, que fi demnstrad experimentalmente pr Ohm. A resistência desse cndutr é: γ I ne L A (A5) A resistividade d material é: γ ρ ne (A6) A grande vantagem dessa frmulaçã é que ela permite também cnsiderar cas de crrente alternada, quand camp elétric varia senidalmente n temp. Nesses cass, a equaçã A1 deve ser reslvida assumind um camp elétric da frma: E E cs( ωt) (A8) Para facilitar a resluçã, vams utilizar a ntaçã cmplexa e permitir que camp elétric e a velcidade ds elétrns assumam valres cmplexs. O camp elétric é escrit entã cm uma expnencial imaginária: E E exp( iωt) (A9) A sluçã particular a ser prcurada deve ter a mesma dependência tempral d camp elétric: v m v exp( iωt) (A10) Substituíms A1 em A1 e reslvems para v : 1

22 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I v ee γ + imω (A11) A diferença entre essa expressã e a A é que denminadr γ fi substituíd pr γ + imω (que vale γ n cas de crrente cntínua). Seguind s passs que levaram da A até a A6, resultad é: I ne A ( γ + imω). L (A1) A impedância d fi cndutr vale: Z γ I ne L mω L + i A ne A (A13) ems entã que a impedância de um cndutr tem uma parte real cnstante e uma parte imaginária prprcinal à freqüência. O primeir term tem a frma da impedância de uma resistência, enquant segund tem a frma da impedância de uma indutância. Em utras palavras, td cndutr é igual à assciaçã de um resistr cm um indutr. A resistência e indutância características sã: γ ne L A (A15) L m ne L A (A16) Cm era esperad, valr da resistência é mesm que fi calculad n cas de crrente cntínua. Da mesma frma que fi definida a resistividade, também definims a indutividade e a impeditividade de um material. Para pder ter uma idéia d efeit indutiv d fi retilíne, vams calcular a razã entre a reatância indutiva e a resistência d fi:

23 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I X L ω L ω (A16) γ / m Na freqüência ω γ / m, a reatância indutiva e a resistência tem mesm valr. Ns cndutres metálics, valr típic de γ / m é da rdem de s -1. Assim, mesm a freqüências relativamente altas de 100 MHz, a reatância indutiva é várias rdens de grandeza menr que a resistência, e pde certamente ser desprezada. 3