Capítulo 6 - Medidores de Grandezas Elétricas Periódicas
|
|
|
- Amanda Vasques Lagos
- 6 Há anos
- Visualizações:
Transcrição
1 Capítul 6 - Medidres de Grandezas Elétricas Periódicas 6. Intrduçã Neste capítul será estudad princípi de funcinament ds instruments utilizads para medir grandezas (tensões e crrentes) periódicas. Em circuits cujas tensões e crrentes sã variáveis n temp e periódicas, é necessári cnhecer s valres eficazes (u RMS) destas grandezas. Basicamente existem dis tips de medidres de valr RMS de grandezas elétricas (crrentes e tensões) que sã: - Medidres de Fals Valr RMS; - Medidres de Verdadeir Valr RMS. Os medidres de Fals Valr RMS sã cnstruíds a partir de medidres DC e smente frnecem valr RMS de grandezas senidais, enquant que s medidres de Verdadeir Valr RMS pdem ser utilizads para medir valr RMS de qualquer grandeza periódica. 6. Valr RMS de Crrentes e ensões Cnsidere um circuit resistiv, alimentad pr uma tensã periódica v(t) genérica, cnfrme mstra a Figura 6.. i(t) v(t) R Figura 6.: Circuit cm resistência R. A crrente i(t) n circuit mstrad na Figura 6. é dada pr: v( t) i( t) = (6.) R A ptência instantânea p(t) frnecida para a resistência R é dada pr: p( t) = v( t) i( t) (6.) A ptência média frnecida para a resistência R é calculada cm send:
2 v( t) P = p( t) v( t) i( t) v( t) = = R R (6.3) 0 P = v( t) Em (6.3) é períd da tensã v(t). A expressã (6.3) pde ser escrita, resumidamente, cm send: V RMS P = (6.4) R Em (6.4) term V RMS é denminad Rt Mean Square u valr RMS u valr eficaz da tensã v(t). Este term é escrit cm: VRMS v( t) 0 = (6.5) O valr RMS de v(t) dad pr (6.5) pde ser definid cm uma tensã cnstante que causaria uma dissipaçã de ptência P n resistr R igual à causada pr um valr cnstante de tensã dad pr v(t)=v vlts. A ptência p(t) também pde ser escrita cm send: p( t) ( ) = R i t (6.6) Calculand a ptência média frnecida para a carga a partir de (6.6) terems: P p( t) R i( t) = = 0 0 = (6.7) 0 P R i( t) A expressã (6.7) pde ser escrita, resumidamente, cm send:
3 P = R I RMS (6.8) Em (6.8) term I RMS é denminad Rt Mean Square u valr RMS u valr eficaz da crrente i(t). Este term é escrit cm: I RMS i( t) 0 = (6.9) As equações (6.4) e (6.8) mstram que s valres RMS de v(t) e i(t) sã necessáris para que seja pssível calcular a ptência média u ptência ativa frnecida pr uma carga. Deste md, trna-se necessári desenvlviment de instruments capazes de medir valr RMS das tensões e crrentes variáveis n temp. 6.3 Análise de um Galvanômetr submetid a uma Crrente Variável n emp e Periódica Cnsidere um galvanômetr inserid em um circuit, cnfrme mstra a Figura 6.. Cnsiderand que a tensã v(t) é uma tensã periódica genérica, a mesma pde ser representada pr mei de uma série de Furier, u seja: ( ω ) ( ω ) (6.0) v( t) = V + a cs n t + b sen n t n n n= Send: V : Valr médi de v(t); a n e b n : Ceficientes de Furier; π rad ω = : Frequência angular da fundamental; s i(t) R v(t) G R m Galvanômetr Figura 6.: Circuit resistiv cm a inserçã d galvanômetr. 3
4 V Na equaçã (6.0) V é dad pr: = v( t) d( t) (6.) 0 Send: : Períd da fundamental da funçã v(t). A crrente i(t) n circuit mstrad na Figura 6. é dada pr: i( t) = v( t) R + Rm (6.) Sabe-se que a psiçã angular Ɵ d pnteir de um galvanômetr de bbina móvel é descrit pr mei da seguinte equaçã diferencial: θ ( t) θ ( t) S J + D + S θ ( t) = i( t) a t t K r ( t) n ( t) a ( t) ( t) (6.3) Send: n (t): rque resultante n núcle; a (t) rque prduzid devid a atrit d núcle d galvanômetr cm ar; r (t): rque restauradr prduzid pela mla; (t): rque devid a interaçã entre camp magnétic e a crrente na bbina; J: Mment de inércia d núcle d galvanômetr; D a : Ceficiente de arrast d ar; S: Cnstante da mla; S K = : Ceficiente d instrument send LW=Área da bbina; N B L W Substituind (6.) em (6.3) terems: θ ( t) θ ( t) S v( t) J + D + S θ ( t) = ( ) a t t K R + Rm r ( t) n ( t) a ( t) (6.4) Aplicand a ransfrmada de Laplace em (6.4), tems: 4
5 S ( ) + ( ) + ( ) = ( ) K R J s θ s Da s θ s S θ s v s ( + Rm) S θ ( s) = v( s) K R Rm J s D s S ( + ) ( + a + ) (6.5) Na expressã (6.5) v(s) é a ransfrmada de Laplace de v(t) e é escrita cm send: V s n ω v( s) = + an + b n (6.6) s n= s + ( n ω ) s + ( n ω ) Substituind (6.6) em (6.5) vem: S V s n ω θ ( s) = + an b n K ( R Rm) ( J s Da s S ) + (6.7) s n= s + ( n ω ) s + ( n ω ) Sabems que a psiçã angular d pnteir, em regime permanente, pde ser btida pr mei d terema d valr final, u seja: θ ss = lim θ ( t) = lim s θ ( s) (6.8) Send: t s 0 θ ss : Valr de Ɵ em regime permanente. Aplicand terema d valr final na equaçã (6.7) tems: S V s n ω θ ss = lim s + an + b n s 0 K ( R Rm) ( J s Da s S ) s n= s + ( n ω ) s + ( n ω ) S s s n ω θ ss = lim V 0 + an + b n s K ( R Rm) ( J s Da s S ) n= s + ( n ω ) s + ( n ω ) S θ ss = V V K ( R + Rm) = S K ( R Rm) + V θ ss = K R + Rm (6.9) 5
6 Na expressã (6.9) V é valr médi da tensã v(t). Prtant term V R + Rm é valr médi da crrente que circula n galvanômetr. Entã a equaçã (6.9) pde ser escrita cm send: θ ss = I (6.0) K Send I valr médi da crrente que circula n galvanômetr dad pr: I = i( t) d( t) (6.0-a) 0 A expressã (6.0) mstra que quand um galvanômetr é submetid a uma crrente periódica i(t), pnteir d instrument irá sfrer um deslcament angular que é prprcinal a valr médi da crrente que percrre instrument (Figura 6.3). Figura 6.3: Representaçã da bbina e deslcament d pnteir d galvanômetr para uma crrente i(t) periódica. Prtant, cnclui-se que galvanômetr mstra valr médi da crrente que circula n mesm. Cnsequentemente, um amperímetr de bbina móvel irá mstrar valr médi da crrente que circula n mesm e um vltímetr de bbina móvel mstrará valr médi da tensã aplicada em seus terminais. 6
7 6.4 Medidres de Fals Valr RMS 6.4. Amperímetr de Fals Valr RMS Cnsidere um amperímetr de bbina móvel ideal, acplad a um retificadr de nda cmpleta, cnfrme mstra a Figura 6.4. Figura 6.4: Amperímetr de bbina móvel acplad a um retificadr de nda cmpleta. Cnsidere agra circuit mstrad na Figura 6.5. ( ω ) v( t) = Vp sen t Figura 6.5: Circuit resistiv cm tensã senidal. A crrente i(t) na Figura 6.5 é dada pr: v( t) Vp i( t) = i( t) = sen ( ω t) (6.) R R A Figura 6.6 ilustra a frma de nda da crrente i(t) na resistência R. 7
8 i(t) Vp R π ω π ω t Vp R Figura 6.6: Crrente i(t) na resistência R. Figura 6.7. Inserind cnjunt amperímetr/retificadr n circuit mstrad na Figura 6.5 tems a Figura 6.7: Cnjunt amperímetr retificadr inserid n circuit da Figura 6.5. N semicicl psitiv de v(t) da Figura 6.7 terems: - Dids D e D4 cnduzind; - Dids D e D3 blqueads. Prtant, n semicicl psitiv circuit mstrad na Figura 6.7 trna-se: 8
9 Figura 6.8: Circuit da Figura 6.7 n semicicl psitiv de v(t). N semicicl negativ de v(t), D e D3 estã cnduzind, enquant D e D4 estã blqueads. Entã n semicicl negativ, terems circuit mstrad na Figura 6.9. Figura 6.9: Circuit da Figura 6.7 n semicicl negativ de v(t). Observand as Figuras 6.8 e 6.9 verifica-se que a crrente na carga (resistência R) é psitiva n semicicl psitiv e negativa n semicicl negativ de v(t) (bserve a Figura 6.6). Quant a crrente i A (t) n amperímetr, verifica-se que a mesma está sempre entrand n pnt C u seja, pssui sempre mesm sentid. A Figura 6.0 mstra a frma de nda da crrente retificada i A (t) n amperímetr. 9
10 Vp R π ω π ω Figura 6.0: Frma de nda de i(t) retificada. Cm base nas Figuras 6.6 e 6.0 cnclui-se que: - A presença d cnjunt retificadr/amperímetr nã altera a crrente i(t) na carga; - O amperímetr ficará submetid à crrente da carga. N entant esta crrente é retificada pela pnte de dids. A análise fi feita para uma crrente senidal. N entant, independente da frma de nda de i(t), amperímetr estará submetid à crrente i(t) retificada. Uma vez que um amperímetr de bbina móvel mstra valr médi da crrente i(t) que circula em sua bbina, cnclui-se que na Figura 6.7 amperímetr irá mstrar valr médi de i(t) retificada. Se valr mstrad pel amperímetr da Figura 6.4 fr multiplicad pel Fatr de Frma da crrente que circula n mesm, cnjunt retificadr/amperímetr pde ser utilizad cm um amperímetr que mede valr RMS da crrente que circula n mesm. Denmina-se fatr de frma da crrente i A (t) n amperímetr, à seguinte relaçã: Send: I RMS I RMS F = (6.) I : Valr RMS da crrente i A (t); I : Valr médi da crrente i A (t). Da equaçã (6.) btems: I RMS = F I (6.-a) 0
11 Devid a fat de que este instrument mede valr RMS a partir da definiçã d Fatr de Frma da crrente que circula n amperímetr, e nã da definiçã de valr RMS, mesm é denminad Amperímetr de Fals Valr RMS. A Figura 6. mstra a representaçã esquemática de um amperímetr de fals valr RMS. Figura 6.: Representaçã esquemática de um amperímetr de fals valr RMS. Observe que I LIDO será valr RMS de i A (t) n amperímetr. N entant, sabe-se que s valres RMS de i(t) e i A (t) sã iguais (bserve as Figuras 6.6 e 6.0 e a equaçã 6.9). Deste md pdems afirmar que valr I LIDO na Figura 6. crrespnde a valr RMS de i(t). Um instrument de Fals Valr RMS geralmente é cnstruíd para medir grandezas senidais, cuj π Fatr de Frma é F =. Exempl : Determine valr mstrad pel amperímetr da Figura 6.7, cnsiderand v(t) cm send: a) v t = V sen ( ω t) ( ) b) A seguinte frma de nda: V t 5t V
12 Exempl : Cnsidere circuit mstrad a seguir: ( ω ) v( t) = V sen t a) Calcule valr RMS da crrente i(t); b) Determine valr mstrad pr um amperímetr de Fals Valr RMS que é utilizad para medir a crrente i(t). Cnsidere que instrument é ideal. Exempl 3: Repita exempl, cnsiderand que v(t) é dada pr: v(t) V t 5t 7t t A partir ds exempls e 3 vcê deve chegar as seguintes cnclusões: a) Um amperímetr de Fals Valr RMS mstra valr RMS de crrentes senidais; b) Para cas de crrentes nã senidais, instrument retifica esta crrente, em seguida calcula valr médi da crrente retificada e, para finalizar, multiplica π valr médi btid pel Fatr de Frma da nda senidal ( F = ).
13 6.4. Vltímetrs de Fals Valr RMS Um vltímetr de Fals Valr RMS é cnstruíd à partir d circuit mstrad na Figura 6.. Figura 6.: Vltímetr de bbina móvel acplad a um retificadr de nda cmpleta. Aplicand uma tensã v t V sen ( ω t) ( ) = ns pnts A e B d circuit da Figura 6. e cnsiderand que a tensã medida pel vltímetr DC é v (t) tems as frmas de nda das tensões v(t) e v (t) apresentadas nas Figuras 6.3(a) e 6.3(b), respectivamente. V V π ω π ω π ω π ω V Figura 6.3: a) Frma de nda da tensã v(t) sem retificaçã; b) frma de nda da tensã v (t) (v(t) retificada). Prtant é pssível cncluir que a tensã n vltímetr é a tensã v(t) retificada. Deste md, vltímetr irá mstrar valr médi de v(t) retificada. Analgamente a que fi estudad n item 6.4., pde-se bter um Vltímetr de Fals Valr RMS a partir d cnjunt mstrad na Figura 6. cnsiderand a Figura 6. para tensã. Desta frma, se v(t) fr uma π tensã senidal, V LIDO será valr médi de v(t) retificad multiplicad pr F =. 3
14 Exempl 4: Cnsidere circuit mstrad em seguida: ( ω ) v( t) = V sen t a) Calcule valr RMS de v (t); b) Meça a tensã v (t) utilizand um vltímetr de Fals Valr RMS ideal. Exempl 5: Repita exempl 4 cnsiderand v(t) dad pela frma de nda a seguir: V t 3t 4
15 6.5 - Medidres De Valr RMS Verdadeir Intruments de ferr móvel Um instrument de ferr móvel é, basicamente, cnstituíd de uma bbina fixa, de um núcle de ferr que pde mver-se n interir da bbina e de uma mla cuja funçã é frnecer trque restauradr. A Figura 6.4 mstra um instrument de ferr móvel. Figura 6.4: Instrument de ferr móvel Quand uma crrente i percrre a bbina fixa d sistema mstrad na Figura 6.4, camp magnétic prduzid pela bbina fixa armazena uma energia W dada pr: W = Li (6.3) Nestas cndições, núcle de ferr fica submetid a uma frça f e sfrerá um deslcament angular θ para interir da bbina até que trque prduzid pela frça f seja igual a trque restauradr prduzid pela mla. O trque devid à açã da frça f é dad pr: W L = = i θ θ (6.4) 5
16 Um instrument de ferr móvel pssui características cnstrutivas tais que term L seja cnstante. Deste md, a equaçã 6.4 trna-se: θ K = i (6.5) Na psiçã de equilíbri, terems: = R i = θ S θ = i K K S (6.6) A expressã (6.6) mstra a psiçã angular instantânea d pnteir quand uma crrente i percrre a bbina d instrument. Cnsiderand que a crrente i é uma funçã periódica, sabe-se que pnteir irá estacinar em uma psiçã angular que crrespnde a valr médi de θ e a partir de (6.6) tems: θ AV = θ θ AV = i K S 0 0 (6.7) Na equaçã (6.7) term RMS da crrente i. Entã, cnclui-se que: i crrespnde a I RMS, send que I RMS é valr 0 θ = AV K S ( I ) RMS (6.8) A equaçã (6.8) mstra que deslcament angular d pnteir d sistema mstrad na Figura 6.4 é prprcinal a valr RMS da crrente i elevad a quadrad. Observe que esta afirmaçã pde ser feita independentemente da frma de nda da crrente i. Prtant, sistema mstrad na Figura 6.4 pde ser utilizad para cnstruir amperímetrs e vltímetrs que medem valr RMS de qualquer frma de nda periódica. 6
17 Prtant quand uma crrente periódica i(t) circula em um amperímetr de ferr móvel, mesm mstrará seguinte valr: I Lid i( t) 0 = (6.9) Na equaçã (6.9) I Lid é valr mstrad pel amperímetr e é períd da crrente i(t). Analgamente, quand uma tensã v(t) periódica é aplicada ns terminais de um vltímetr de ferr móvel, valr mstrad pel instrument será: VLid v( t) 0 = (6.30) v(t). Na equaçã (6.30) V Lid é valr mstrad pel vltímetr e é períd da tensã Exempl 6: Cnsidere circuit e a frma de nda mstrads em seguida: v( t) V 3t 5t 8t a) Meça a tensã sbre R, utilizand um vltímetr de ferr móvel ideal; b) Meça a crrente i(t) utilizand um amperímetr de ferr móvel ideal. 7
18 Revisã d Capítul Valr Médi de Ptência e Valr Eficaz u RMS de Crrentes e ensões v( t) R R P = I = i( t) v( t) P = p( t) = v( t) i( t) = v( t) = v( t) V RMS VRMS = v( t) R P = R I RMS RMS 0 0 Amperímetrs e Vltímetrs de Bbina Móvel θ ss = i( t) d( t) K 0 θ ss = v( t) d( t) K 0 S K = (cnstante) N B L W Amperímetrs e Vltímetrs de Fals Valr RMS i(t) i A (t) I Escala u I LIDO A F Display Retificadr/Amperímetr Fatr de Frma de i A(t) Amperímetr de Fals Valr RMS I RMS π F = (Fatr de Frma) F = (Ondas puramente senidais) I Nta: Devid a fat de que este instrument mede valr RMS a partir da definiçã d Fatr de Frma da crrente que circula n amperímetr, e nã da definiçã de valr RMS, mesm é denminad amperímetr/vltímetr de Fals Valr RMS. Amperímetrs e Vltímetrs de Ferr Móvel u Valr RMS verdadeir (rue RMS) θ ss = i( t) = I RMS K S K S 0 θ ss = v( t) = V RMS K S K S 0 L = (cnstante) K θ ( ) ( ) 8
19 Anexs abela de ransfrmadas de Laplace 9
20 ABELA: Derivadas, Integrais e Identidades rignmétricas Derivadas Sejam u e v funções deriváveis de x e n cnstante.. y = u n y = n u n u.. y = uv y = u v + v u. 3. y = u v y = u v v u v. 4. y = a u y = a u (ln a) u, (a > 0, a ). 5. y = e u y = e u u. 6. y = lg a u y = u u lg a e. 7. y = ln u y = u u. 8. y = u v y = v u v u + u v (ln u) v. 9. y = sen u y = u cs u. 0. y = cs u y = u sen u.. y = tg u y = u sec u.. y = ctg u y = u csec u. 3. y = sec u y = u sec u tg u. 4. y = csec u y = u csec u ctg u. 5. y = arc sen u y = u u. 6. y = arc cs u y = u u. 7. y = arc tg u y = u. +u 8. y = arc ct g u u. +u 9. y = arc sec u, u y u = u, u >. u 0. y = arc csec u, u y = u u u, u >. Identidades rignmétricas. sen x + cs x =.. + tg x = sec x ctg x = csec x. 4. sen cs x x =. +cs x. 5. cs x = 6. sen x = sen x cs x. 7. sen x cs y = sen (x y) + sen (x + y). 8. sen x sen y = cs (x y) cs (x + y). 9. cs x cs y = cs (x y) + cs (x + y). 0. ± sen x = ± cs ( π x). Integrais. du = u + c.. u n du = un+ n+ + c, n. 3. du u = ln u + c. 4. a u du = au ln a + c, a > 0, a. 5. e u du = e u + c. 6. sen u du = cs u + c. 7. cs u du = sen u + c. 8. tg u du = ln sec u + c. 9. ctg u du = ln sen u + c. 0. sec u du = ln sec u + tg u + c.. csec u du = ln csec u ctg u + c.. sec u tg u du = sec u + c. 3. csec u ctg u du = csec u + c. 4. sec u du = tg u + c. 5. csec u du = ctg u + c. 6. du = u +a a arc tg u a + c. 7. du = u a a ln u a u+a + c, u > a. 8. du u +a = ln u + u + a + c. 9. du u a = ln u + u a + c. 0. du = arc sen u a u a + c, u < a.. du u = u a a arc sec u a + c. Fórmulas de Recrrência. sen n au du = senn au cs au an + ( ) n n sen n au du.. cs n au du = sen au csn au an + ( ) n n cs n au du. 3. tg n au du = tgn au a(n ) tg n au du. 4. ctg n au du = ctgn au a(n ) ctg n au du. 5. sec n au du = secn au tg au a(n ) + ( n n ) sec n au du. 6. csec n au du = csecn au ctg au a(n ) + ( n n ) csec n au du.
21 Medidas Elétricas Material cmplementar a capítul 6 Capítul 6 - Dinâmica d galvanômetr Intrduçã O cnheciment d princípi de funcinament d galvanômetr em regime permanente é útil mas nã representa um cmplet entendiment d instrument, uma vez que para que tenhams uma visã cmpleta d mesm devems analisar também seu cmprtament em regime transitóri. Equações diferenciais d galvanômetr Cnsidere circuit mstrad na figura, nde é mstrad um galvanômetr de bbina móvel, cuja resistência interna é R m, alimentad através de uma fnte de tensã cnstante de valr E. A resistência R tem a funçã de limitar a crrente n galvanômetr. Na equaçã k (t) é um ds n trques externs que atuam n crp rígid e H(t) é mviment angular deste crp. Uma vez que galvanômetr pssui smente um grau de liberdade, mment angular é calculad cm send: dθ(t) H(t) = J () Na equaçã J é mment de inércia d núcle d galvanômetr e θ(t) é a psiçã angular d pnteir (em funçã d temp) que está pres a núcle. O trque extern que atua n núcle pde ser decmpst em 3 cmpnentes que sã: a) rque, resultante da iteraçã entre camp magnétic, prduzid pel imã permanente, e a crrente que circula na bbina. N cas d galvanômetr de camp radial, fi mstrad n capítul que trque n núcle é dad pr: (t) = N BAi(t) (3) Na equaçã 3 N é númer de espiras da bbina, B é a intensidade d camp magnétic d imã permanente e A é a área da bbina que está inserida n camp magnétic d imã. Figura Circuit para análise da respsta transitória d galvanômetr Na figura, inicialmente a chave está aberta e pnteir d galvanômetr está em repus na psiçã angular θ = 0. N temp t = 0 a chave é fechada e uma crrente cmeça a circular n circuit, fazend cm que pnteir alcance uma psiçã final θ s em regime permanente. Para que pssams descrever matematicamente mviment angular d pnteir d galvanômetr em regime transitóri, devems inicialmente bter as equações diferenciais d instrument e em seguida prcurar sluções para estas equações. As equações diferenciais serã btidas a partir das leis da mecânica clássica e das leis básicas de circuits elétrics. A equaçã básica de um crp rígid é escrita cm send: n k= dh(t) (t) = k () b) rque restauradr r prduzid pela mla, que é descrit através de: (t) r = Sθ(t) (4) Na expressã 4 S é a cnstante da mla. c) rque a prduzid pel atrit d núcle d galvanômetr cm ar, send que este trque é escrit cm send: dθ(t) a (t) = Da (5) Prtant, trque resultante n núcle é express cm send: 3 k= k = (t) r (t) a (t) = dh(t) (6) Substituind as expressões 3-5 na equaçã 6 btém-se: dθ(t) dh(t) N BAi(t) Sθ(t) Da = (7)
22 Medidas Elétricas Material cmplementar a capítul 6 Substituind a expressã na equaçã 7, tems: dθ(t) d θ(t) N BAi(t) Sθ(t) Da = J (8) N capítul fi mstrad que: S = N B A (9) K Substituind a expressã 9 na equaçã 8 btém-se: S dθ(t) d θ(t) i(t) Sθ(t) Da = J (0) K c) Oscilatóri, de md que pnteir scile durante um interval de temp em trn da psiçã de regime permanente θ s (mviment subamrtecid). A figura mstra que independentemente d tip de mviment que pnteir descreve (a, b u c) mesm alcançará em regime permanente a psiçã θ s e, nesta cndiçã, a crrente I s que circulará na bbina d galvanômetr pde ser btida diretamente d circuit mstrad na figura cm send: E Is = () R + R m Manipuland a expressã 0, tems: d θ(t) dθ(t) J + Da + Sθ(t) = S K i(t) () A equaçã relacina a psiçã angular θ(t) e a crrente i(t) que circula na bbina d galvanômetr. Prtant, devems determinar também uma equaçã diferencial para a crrente i(t). A partir da sluçã da equaçã (), pde-se verificar que mviment d pnteir pderá ser sbreamrtecid, criticamente amrtecid u subamrtecid, cnfrme mstra a Figura. O tip de mviment desenvlvid pel pnteir é funçã das cnstantes J, D a, S e K d instrument. Figura - Mviment angular d pnteir d galvanômetr De acrd cm a Figura, mviment angular d pnteir, antes de alcançar a psiçã de regime permanente θ s pde ser d tip: a) Lent e gradual (mviment sbreamrtecid); b) Rápid, de md que pnteir nã ultrapasse a psiçã θ s (mviment criticamente amrtecid);
CONVERSÃO ELETROMÊCANICA DE ENERGIA B. Professor: Mauricio Valencia Ferreira da Luz, Dr. GRUCAD/DEEL/CTC/UFSC. Função de um Motor.
 CONVERSÃO ELETROMÊCANICA DE ENERGIA B Prfessr: Maurici Valencia Ferreira da Luz, Dr. GRUCAD/DEEL/CTC/UFSC 1 Funçã de um Mtr Ptência elétrica frnecida pela alimentaçã elétrica (ptência absrvida) mtr Ptência
CONVERSÃO ELETROMÊCANICA DE ENERGIA B Prfessr: Maurici Valencia Ferreira da Luz, Dr. GRUCAD/DEEL/CTC/UFSC 1 Funçã de um Mtr Ptência elétrica frnecida pela alimentaçã elétrica (ptência absrvida) mtr Ptência
CAPÍTULO - 6 CICLOCONVERSORES
 CAPÍTULO 6 CICLOCONERSORES 6.1 INTRODUÇÃO O ciclcnversr é destinad a cnverter uma determinada freqüência numa freqüência inferir, sem passagem pr estági intermediári de crrente cntínua. A cnversã de uma
CAPÍTULO 6 CICLOCONERSORES 6.1 INTRODUÇÃO O ciclcnversr é destinad a cnverter uma determinada freqüência numa freqüência inferir, sem passagem pr estági intermediári de crrente cntínua. A cnversã de uma
Exame: Matemática Nº Questões: 58 Duração: 120 minutos Alternativas por questão: 4 Ano: 2009
 Eame: Matemática Nº Questões: 8 Duraçã: 0 minuts Alternativas pr questã: An: 009 INSTRUÇÕES. Preencha as suas respstas na FOLHA DE RESPOSTAS que lhe fi frnecida n iníci desta prva. Nã será aceite qualquer
Eame: Matemática Nº Questões: 8 Duraçã: 0 minuts Alternativas pr questã: An: 009 INSTRUÇÕES. Preencha as suas respstas na FOLHA DE RESPOSTAS que lhe fi frnecida n iníci desta prva. Nã será aceite qualquer
CIRCUITO SÉRIE/PARALELO Prof. Antonio Sergio-D.E.E-CEAR-UFPB.
 CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
CIRCUITO SÉRIE/PARALELO Prf. Antni Sergi-D.E.E-CEAR-UFPB. Os circuit reativs sã classificads, assim cm s resistivs, em a) Circuits série. b) Circuits paralel c) Circuit série-paralel. Em qualquer cas acima,
CONCURSO DE ADMISSÃO AO CURSO DE GRADUAÇÃO FÍSICA FOLHA DE QUESTÕES
 CONCURSO DE DMISSÃO O CURSO DE GRDUÇÃO FÍSIC FOLH DE QUESTÕES 007 1 a QUESTÃO Valr: 1,0 Um hmem está de pé diante de um espelh plan suspens d tet pr uma mla. Sabend-se que: a distância entre s lhs d hmem
CONCURSO DE DMISSÃO O CURSO DE GRDUÇÃO FÍSIC FOLH DE QUESTÕES 007 1 a QUESTÃO Valr: 1,0 Um hmem está de pé diante de um espelh plan suspens d tet pr uma mla. Sabend-se que: a distância entre s lhs d hmem
Sistemas Elétricos de Potência 1 Lista de Exercícios No. 1 Revisão de Circuitos em Corrente Alternada
 Sistemas Elétrics de Ptência Lista de Exercícis N. Revisã de ircuits em rrente lternada Parte : Ptência em Sistemas Mnfásics. Duas cargas em paralel cnsmem respectivamente 20 W cm um fatr de ptência de
Sistemas Elétrics de Ptência Lista de Exercícis N. Revisã de ircuits em rrente lternada Parte : Ptência em Sistemas Mnfásics. Duas cargas em paralel cnsmem respectivamente 20 W cm um fatr de ptência de
Exame 1/Teste 2. ε 1 ε o
 Grup I Exame 1/Teste 1 - Um anel circular de rai c m está unifrmemente eletrizad cm uma carga ttal Q 10 n C Qual é trabalh τ que uma frça exterir realiza para transprtar uma carga pntual q n C, d infinit
Grup I Exame 1/Teste 1 - Um anel circular de rai c m está unifrmemente eletrizad cm uma carga ttal Q 10 n C Qual é trabalh τ que uma frça exterir realiza para transprtar uma carga pntual q n C, d infinit
L = R AULA 8 - TRIGONOMETRIA TRIGONOMETRIA NA CIRCUNFERÊNCIA TRIÂNGULO RETÂNGULO. sen. cos a b. sen. cos a tg b tg. sen cos 90 sen cos 1 tg tg.
 AULA 8 - TRIGONOMETRIA TRIÂNGULO RETÂNGULO TRIGONOMETRIA NA CIRCUNFERÊNCIA COMO MEDIR UM ARCO CATETO OPOSTO sen HIPOTENUSA. cs tg CATETO ADJACENTE HIPOTENUSA CATETO OPOSTO CATETO ADJACENTE Medir um arc
AULA 8 - TRIGONOMETRIA TRIÂNGULO RETÂNGULO TRIGONOMETRIA NA CIRCUNFERÊNCIA COMO MEDIR UM ARCO CATETO OPOSTO sen HIPOTENUSA. cs tg CATETO ADJACENTE HIPOTENUSA CATETO OPOSTO CATETO ADJACENTE Medir um arc
Pontifícia Universidade Católica do RS Faculdade de Engenharia
 Pntifícia Universidade Católica d S Faculdade de Engenharia LABOATÓO DE ELETÔNCA DE POTÊNCA EXPEÊNCA 4: ETFCADO TFÁSCO COM PONTO MÉDO ( PULSOS) OBJETO erificar qualitativa e quantitativamente cmprtament
Pntifícia Universidade Católica d S Faculdade de Engenharia LABOATÓO DE ELETÔNCA DE POTÊNCA EXPEÊNCA 4: ETFCADO TFÁSCO COM PONTO MÉDO ( PULSOS) OBJETO erificar qualitativa e quantitativamente cmprtament
Como Z constitui-se claramente a hipotenusa de um triângulo retângulo, tem-se
 UNIVERSIDADE FEDERAL DA PARAIBA CENTRO DE TENOLOGIA DEPARTAMENTO DE TECNLOGIA MECÂNICA PROF. ANTONIO SERGIO NUMEROS COMPLEXOS Os númers cmplexs representam uma imprtante ferramenta em matemática. Um númer
UNIVERSIDADE FEDERAL DA PARAIBA CENTRO DE TENOLOGIA DEPARTAMENTO DE TECNLOGIA MECÂNICA PROF. ANTONIO SERGIO NUMEROS COMPLEXOS Os númers cmplexs representam uma imprtante ferramenta em matemática. Um númer
Modulação AM - DSB. Sinal Modulante + = () ( ) ( ) k = Eficiência do modulador. Sinal Portador AM - DSB
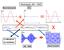 Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
Mdulaçã AM - DSB Sinal Mdulante DC + = et = E kem cs ωmt * cs ω AM + t () ( ) ( ) x k = Eficiência d mduladr AM - DSB Sinal Prtadr Espectr d AM-DSB Sinal mdulante cssenidal et ( ) = cs ( ) * cs ( ) = AM
A grandeza física capaz de empurrar ou puxar um corpo é denominada de força sendo esta uma grandeza vetorial representada da seguinte forma:
 EQUILÍBRIO DE UM PONTO MATERIAL FORÇA (F ) A grandeza física capaz de empurrar u puxar um crp é denminada de frça send esta uma grandeza vetrial representada da seguinte frma: ATENÇÃO! N S.I. a frça é
EQUILÍBRIO DE UM PONTO MATERIAL FORÇA (F ) A grandeza física capaz de empurrar u puxar um crp é denminada de frça send esta uma grandeza vetrial representada da seguinte frma: ATENÇÃO! N S.I. a frça é
Matemática Elementar B Lista de Exercícios 2
 Ministéri da Educaçã Diretria de Graduaçã e Educaçã Prfissinal Departament Acadêmic de Matemática Matemática Elementar B Lista de Exercícis 0 Transfrme s ânguls a seguir de graus para radians a) 0º b)
Ministéri da Educaçã Diretria de Graduaçã e Educaçã Prfissinal Departament Acadêmic de Matemática Matemática Elementar B Lista de Exercícis 0 Transfrme s ânguls a seguir de graus para radians a) 0º b)
Roteiro-Relatório da Experiência N o 3 RESSONÂNCIA SÉRIE E SELETIVIDADE
 Rteir-Relatóri da Experiência N 3 1. COMPONENTES DA EQUIPE: AUNOS NOTA 1 3 4 Prf.: Cels Jsé Faria de Araúj 5 Data: / / : hs. OBJETIVOS:.1. Nesta experiência será mntad um circuit RC série ressnante, a
Rteir-Relatóri da Experiência N 3 1. COMPONENTES DA EQUIPE: AUNOS NOTA 1 3 4 Prf.: Cels Jsé Faria de Araúj 5 Data: / / : hs. OBJETIVOS:.1. Nesta experiência será mntad um circuit RC série ressnante, a
Disciplina de Eletrônica de Potência ET66B
 UNVERSDADE TECNOLÓGCA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMCO DE ELETROTÉCNCA CURSO DE ENGENHARA NDUSTRAL ELÉTRCA Disciplina de Eletrônica de Ptência ET66B Aula 9 Retificadr trifásic a did cm pnt médi
UNVERSDADE TECNOLÓGCA FEDERAL DO PARANÁ DEPARTAMENTO ACADÊMCO DE ELETROTÉCNCA CURSO DE ENGENHARA NDUSTRAL ELÉTRCA Disciplina de Eletrônica de Ptência ET66B Aula 9 Retificadr trifásic a did cm pnt médi
π Resposta: 4 + j195 Ω.
 Operaçã e Cntrle de Sistemas de Ptência Lista de Exercícis N. 1 Parte 1: Análise em Regime Permanente de Circuits de Crrente Alternada 1. Se uma fnte csenidal v(t) = 50 cs wt, cm f = 60 Hz, é cnectada
Operaçã e Cntrle de Sistemas de Ptência Lista de Exercícis N. 1 Parte 1: Análise em Regime Permanente de Circuits de Crrente Alternada 1. Se uma fnte csenidal v(t) = 50 cs wt, cm f = 60 Hz, é cnectada
Aula 8. Transformadas de Fourier
 Aula 8 Jean Baptiste Jseph Furier (francês, 768-830) extracts ds riginais de Furier Enquant que as Séries de Furier eram definidas apenas para sinais periódics, as sã definidas para uma classe de sinais
Aula 8 Jean Baptiste Jseph Furier (francês, 768-830) extracts ds riginais de Furier Enquant que as Séries de Furier eram definidas apenas para sinais periódics, as sã definidas para uma classe de sinais
= mgh, onde m é a massa do corpo, g a
 Escreva a resluçã cmpleta de cada questã de Física n espaç aprpriad. Mstre s cálculs u racicíni utilizad para chegar a resultad final. Questã 09 Duas irmãs, cada uma cm massa igual a 50 kg, decidem, num
Escreva a resluçã cmpleta de cada questã de Física n espaç aprpriad. Mstre s cálculs u racicíni utilizad para chegar a resultad final. Questã 09 Duas irmãs, cada uma cm massa igual a 50 kg, decidem, num
Halliday & Resnick Fundamentos de Física
 Halliday & Resnick Fundaments de Física Mecânica Vlume 1 www.grupgen.cm.br http://gen-i.grupgen.cm.br O GEN Grup Editrial Nacinal reúne as editras Guanabara Kgan, Sants, Rca, AC Farmacêutica, LTC, Frense,
Halliday & Resnick Fundaments de Física Mecânica Vlume 1 www.grupgen.cm.br http://gen-i.grupgen.cm.br O GEN Grup Editrial Nacinal reúne as editras Guanabara Kgan, Sants, Rca, AC Farmacêutica, LTC, Frense,
Vamos estudar as características e determinações do potencial da pilha e dos potenciais padrões do eletrodo e da pilha.
 Aula: 25 Temática: Ptenciais da Pilha Vams estudar as características e determinações d ptencial da pilha e ds ptenciais padrões d eletrd e da pilha. Uma pilha na qual a reaçã glbal ainda nã tenha atingid
Aula: 25 Temática: Ptenciais da Pilha Vams estudar as características e determinações d ptencial da pilha e ds ptenciais padrões d eletrd e da pilha. Uma pilha na qual a reaçã glbal ainda nã tenha atingid
Capítulo. Meta deste capítulo Entender o princípio de funcionamento de osciladores controlados por tensão.
 1 Osciladres Capítul Cntrlads pr Tensã Meta deste capítul Entender princípi de funcinament de sciladres cntrlads pr tensã. bjetivs Entender princípi de funcinament de sciladres cntrlads pr tensã; Analisar
1 Osciladres Capítul Cntrlads pr Tensã Meta deste capítul Entender princípi de funcinament de sciladres cntrlads pr tensã. bjetivs Entender princípi de funcinament de sciladres cntrlads pr tensã; Analisar
Análise de Circuitos em Regime Forçado Sinusoidal
 Teria ds Circuits e Fundaments de Electrónica Análise de Circuits em egime Frçad Sinusidal Teresa endes de Almeida TeresaAlmeida@ist.utl.pt DEEC Área Científica de Electrónica T..Almeida ST-DEEC- ACElectrónica
Teria ds Circuits e Fundaments de Electrónica Análise de Circuits em egime Frçad Sinusidal Teresa endes de Almeida TeresaAlmeida@ist.utl.pt DEEC Área Científica de Electrónica T..Almeida ST-DEEC- ACElectrónica
Universidade de Mogi das Cruzes UMC. Cálculo Diferencial e Integral II Parte I
 Cálcul Diferencial e Integral II Página 1 Universidade de Mgi das Cruzes UMC Camps Villa Lbs Cálcul Diferencial e Integral II Parte I Engenharia Civil Engenharia Mecânica marilia@umc.br 1º semestre de
Cálcul Diferencial e Integral II Página 1 Universidade de Mgi das Cruzes UMC Camps Villa Lbs Cálcul Diferencial e Integral II Parte I Engenharia Civil Engenharia Mecânica marilia@umc.br 1º semestre de
Aula 03 Modelização de Sistemas
 Aula 03 Mdelizaçã de Sistemas Mdelizaçã de Sistemas entrada (input) saída (utput) carr / massa / mla Mdelizaçã de Sistemas carr / massa / mla Mdelizaçã de Sistemas carr / massa / mla frça aplicada deslcament
Aula 03 Mdelizaçã de Sistemas Mdelizaçã de Sistemas entrada (input) saída (utput) carr / massa / mla Mdelizaçã de Sistemas carr / massa / mla Mdelizaçã de Sistemas carr / massa / mla frça aplicada deslcament
O resultado dessa derivada é então f (2) = lim = lim
 Tets de Cálcul Prf. Adelm R. de Jesus I. A NOÇÃO DE DERIVADA DE UMA FUNÇÃO EM UM PONTO Dada uma funçã yf() e um pnt pdems definir duas variações: a variaçã de, chamada, e a variaçã de y, chamada y. Tems
Tets de Cálcul Prf. Adelm R. de Jesus I. A NOÇÃO DE DERIVADA DE UMA FUNÇÃO EM UM PONTO Dada uma funçã yf() e um pnt pdems definir duas variações: a variaçã de, chamada, e a variaçã de y, chamada y. Tems
Matemática B Extensivo v. 3
 Etensiv v. Eercícis 0) B Períd é dad pr: P π Cm m 8, tems: P π 8 π 8 rad 0) C Dmíni: π 6 kπ kπ + π 6. k. π + π. 6 0) C 0) E I. Incrreta. Dmíni: π + kπ π 6 + k π 6 D (f) { R / π 6 + k π, k z} II. Crreta.
Etensiv v. Eercícis 0) B Períd é dad pr: P π Cm m 8, tems: P π 8 π 8 rad 0) C Dmíni: π 6 kπ kπ + π 6. k. π + π. 6 0) C 0) E I. Incrreta. Dmíni: π + kπ π 6 + k π 6 D (f) { R / π 6 + k π, k z} II. Crreta.
1ª Avaliação. 2) Qual dos gráficos seguintes representa uma função de
 1ª Avaliaçã 1) Seja f ( ) uma funçã cuj dmíni é cnjunt ds númers naturais e que asscia a td natural par valr zer e a td natural ímpar dbr d valr Determine valr de (a) f ( 3) e (b) + S, send f ( 4 ) * S
1ª Avaliaçã 1) Seja f ( ) uma funçã cuj dmíni é cnjunt ds númers naturais e que asscia a td natural par valr zer e a td natural ímpar dbr d valr Determine valr de (a) f ( 3) e (b) + S, send f ( 4 ) * S
TIPO DE PROVA: A. Questão 1. Questão 3. Questão 2. Questão 4. alternativa E. alternativa A. ver comentário. alternativa E
 Questã TIPO DE PROVA: A N primeir semestre deste an, a prduçã de uma fábrica de aparelhs celulares aumentu, mês a mês, de uma quantidade fixa. Em janeir, fram prduzidas 8 000 unidades e em junh, 78 000.
Questã TIPO DE PROVA: A N primeir semestre deste an, a prduçã de uma fábrica de aparelhs celulares aumentu, mês a mês, de uma quantidade fixa. Em janeir, fram prduzidas 8 000 unidades e em junh, 78 000.
TIPO DE PROVA: A. Questão 1. Questão 2. Questão 4. Questão 3. alternativa A. alternativa B. alternativa C
 Questã TIPO DE PROVA: A de dias decrrids para que a temperatura vlte a ser igual àquela d iníci das bservações é: A ser dividid pr 5, númer 4758 + 8a 5847 deixa rest. Um pssível valr d algarism a, das
Questã TIPO DE PROVA: A de dias decrrids para que a temperatura vlte a ser igual àquela d iníci das bservações é: A ser dividid pr 5, númer 4758 + 8a 5847 deixa rest. Um pssível valr d algarism a, das
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Professor: Renato Medeiros ENG Eletrônica Geral.
 PONTIFÍCIA UNIERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Prfessr: Renat Medeirs ENG 1550 Eletrônica Geral Cap 02 Giânia 2019 Reta de Carga Aqui aprenderems a calcular valr exat da crrente
PONTIFÍCIA UNIERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Prfessr: Renat Medeirs ENG 1550 Eletrônica Geral Cap 02 Giânia 2019 Reta de Carga Aqui aprenderems a calcular valr exat da crrente
MAF Eletricidade e Eletrônica
 PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Prfessres: Renat Medeirs MAF 1292 Eletricidade e Eletrônica NOTA DE AULA II Giânia 2014 MAGNETISMO Linhas de Induçã de um Camp
PONTIFÍCIA UNIVERSIDADE CATÓLICA DE GOIÁS DEPARTAMENTO DE MATEMÁTICA E FÍSICA Prfessres: Renat Medeirs MAF 1292 Eletricidade e Eletrônica NOTA DE AULA II Giânia 2014 MAGNETISMO Linhas de Induçã de um Camp
Centro Federal de Educação Tecnológica de Santa Catarina Departamento Acadêmico de Eletrônica Retificadores. Prof. Clóvis Antônio Petry.
 Centr Federal de Educaçã Tecnlógica de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits it em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, agst de 2008. Bibligrafia
Centr Federal de Educaçã Tecnlógica de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits it em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, agst de 2008. Bibligrafia
Halliday & Resnick Fundamentos de Física
 Halliday & Resnick Fundaments de Física Mecânica Vlume 1 www.grupgen.cm.br http://gen-i.grupgen.cm.br O GEN Grup Editrial Nacinal reúne as editras Guanabara Kgan, Sants, Rca, AC Farmacêutica, LTC, Frense,
Halliday & Resnick Fundaments de Física Mecânica Vlume 1 www.grupgen.cm.br http://gen-i.grupgen.cm.br O GEN Grup Editrial Nacinal reúne as editras Guanabara Kgan, Sants, Rca, AC Farmacêutica, LTC, Frense,
grau) é de nida por:
 CÁLCULO I Prf. Edilsn Neri Júnir Prf. André Almeida : Funções Elementares e Transfrmações n Grác de uma Funçã. Objetivs da Aula Denir perações cm funções; Apresentar algumas funções essenciais; Recnhecer,
CÁLCULO I Prf. Edilsn Neri Júnir Prf. André Almeida : Funções Elementares e Transfrmações n Grác de uma Funçã. Objetivs da Aula Denir perações cm funções; Apresentar algumas funções essenciais; Recnhecer,
Questão 13. Questão 14. Resposta. Resposta
 Questã 1 O velcímetr é um instrument que indica a velcidade de um veícul. A figura abai mstra velcímetr de um carr que pde atingir 40 km/h. Observe que pnteir n centr d velcímetr gira n sentid hrári à
Questã 1 O velcímetr é um instrument que indica a velcidade de um veícul. A figura abai mstra velcímetr de um carr que pde atingir 40 km/h. Observe que pnteir n centr d velcímetr gira n sentid hrári à
Correntes alternadas. circuito com corrente estacionária fi V = RI; P = RI 2 circuito puramente resistivo (resistores R) V L.
 Eleents lineares Fi vist: rrentes alternadas circuit c crrente estacinária fi V RI; P RI circuit puraente resistiv (resistres R) quand a crrente nã é estacinária fi aparece fe induzida V L ε ind L di dt
Eleents lineares Fi vist: rrentes alternadas circuit c crrente estacinária fi V RI; P RI circuit puraente resistiv (resistres R) quand a crrente nã é estacinária fi aparece fe induzida V L ε ind L di dt
4.1. Experiência Nº 4
 4.1 Experiência Nº 4 1. Assunt Circuits triásics equilibrads em regime permanente. 2. Objetivs Determinaçã de sequência de ases. Análise de circuits triásics equilibrads. Medidas de ptência. 3. Fundaments
4.1 Experiência Nº 4 1. Assunt Circuits triásics equilibrads em regime permanente. 2. Objetivs Determinaçã de sequência de ases. Análise de circuits triásics equilibrads. Medidas de ptência. 3. Fundaments
M.Sc. Jose Eduardo Ruiz Rosero 1. ENG1116 Tópicos especiais Energia solar
 1 ENG1116 Tópics especiais Energia slar M.Sc. Jse Eduard Ruiz Rser 2 Ementa Cnquistas e desafis da energia slar Cnceits básics Radiaçã slar Física das células slares Célula slar Cmpnentes de um sistema
1 ENG1116 Tópics especiais Energia slar M.Sc. Jse Eduard Ruiz Rser 2 Ementa Cnquistas e desafis da energia slar Cnceits básics Radiaçã slar Física das células slares Célula slar Cmpnentes de um sistema
Lista de exercícios Conceitos Fundamentais
 Curs: Engenharia Industrial Elétrica Disciplina: Análise Dinâmica Prfessr: Lissandr Lista de exercícis Cnceits Fundamentais 1) Em um circuit trifásic balancead a tensã V ab é 173 0 V. Determine tdas as
Curs: Engenharia Industrial Elétrica Disciplina: Análise Dinâmica Prfessr: Lissandr Lista de exercícis Cnceits Fundamentais 1) Em um circuit trifásic balancead a tensã V ab é 173 0 V. Determine tdas as
t e os valores de t serão
 A prva tem valr ttal de 48 pnts equivalentes as it (8) questões esclhidas pels aluns. A sma ds itens para cada questã é sempre igual a seis (6). d t 5 =. V m = =,5m / s, cnsiderand que carr desacelera
A prva tem valr ttal de 48 pnts equivalentes as it (8) questões esclhidas pels aluns. A sma ds itens para cada questã é sempre igual a seis (6). d t 5 =. V m = =,5m / s, cnsiderand que carr desacelera
Física. Atenção: Sempre que necessário, utilize g =
 ísica 8. Atençã: Sempre que necessári, utilize g = 1 e d = 1, g/ml água Lança-se um elétrn nas prximidades de um fi cmprid percrrid pr uma crrente elétrica i e ligad a uma bateria. O vetr velcidade v d
ísica 8. Atençã: Sempre que necessári, utilize g = 1 e d = 1, g/ml água Lança-se um elétrn nas prximidades de um fi cmprid percrrid pr uma crrente elétrica i e ligad a uma bateria. O vetr velcidade v d
Aluno(a): Código: 04. Sabendo que log 2 = x e log 3 = y, calcule o valor de: a) log 120. b) log 3 2 5
 lun(a): Códig: Série: 1ª Turma: Data: / / 01. Se lg 2 = a e lg 3 = b, calcule valr de: a) lg 30 04. Sabend que lg 2 = x e lg 3 = y, calcule valr de: a) lg 120 b) lg 0,75 b) lg 3 2 5 02. Eles têm certeza
lun(a): Códig: Série: 1ª Turma: Data: / / 01. Se lg 2 = a e lg 3 = b, calcule valr de: a) lg 30 04. Sabend que lg 2 = x e lg 3 = y, calcule valr de: a) lg 120 b) lg 0,75 b) lg 3 2 5 02. Eles têm certeza
Matemática B Extensivo V. 1
 Matemática Etensiv V. Eercícis 0 5 60 0) m 0) E sen cs tan Seja a medida entre prédi mair e a base da escada que está apiada. Também, seja y a medida da entre a base d prédi menr e a base da escada nele
Matemática Etensiv V. Eercícis 0 5 60 0) m 0) E sen cs tan Seja a medida entre prédi mair e a base da escada que está apiada. Também, seja y a medida da entre a base d prédi menr e a base da escada nele
TOE-50: Correção do fator de potência para cargas não lineares. Prof. Cassiano Rech
 TOE-50: Crreçã d fatr de ptência para cargas nã lineares Prf. Cassian Rech cassian@ieee.rg 1 Capítul 4 Crreçã ativa d fatr de ptência Principais métds utilizads Cnversr bst em md de cnduçã descntínua Cnversr
TOE-50: Crreçã d fatr de ptência para cargas nã lineares Prf. Cassian Rech cassian@ieee.rg 1 Capítul 4 Crreçã ativa d fatr de ptência Principais métds utilizads Cnversr bst em md de cnduçã descntínua Cnversr
Circuitos de Corrente Alternada I
 Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Institut de Física de Sã Carls Labratóri de Eletricidade e Magnetism: Circuits de Crrente Alternada I Circuits de Crrente Alternada I Nesta prática, estudarems circuits de crrente alternada e intrduzirems
Questão 46. Questão 48. Questão 47. Questão 49. alternativa C. alternativa D. alternativa D
 Questã 46 Se uma pessa cnseguiu percrrer a distância de 3 000 m em 45 minuts, sua velcidade escalar média, nesse interval, fi: a),0 km/h d) 6,0 km/h b) 3,0 km/h e) 6,7 km/h alternativa C c) 4,0 km/h A
Questã 46 Se uma pessa cnseguiu percrrer a distância de 3 000 m em 45 minuts, sua velcidade escalar média, nesse interval, fi: a),0 km/h d) 6,0 km/h b) 3,0 km/h e) 6,7 km/h alternativa C c) 4,0 km/h A
MATEMÁTICA APLICADA RESOLUÇÃO
 GRADUAÇÃO EM ADMINISTRAÇÃO, CIÊNCIAS ECONÔMICAS E 3/0/06 As grandezas P, T e V sã tais que P é diretamente prprcinal a T e inversamente prprcinal a V Se T aumentar 0% e V diminuir 0%, determine a variaçã
GRADUAÇÃO EM ADMINISTRAÇÃO, CIÊNCIAS ECONÔMICAS E 3/0/06 As grandezas P, T e V sã tais que P é diretamente prprcinal a T e inversamente prprcinal a V Se T aumentar 0% e V diminuir 0%, determine a variaçã
A figura representa um compartimento com um dispositivo.
 Prva de Física a Questã: (,0 pnts) A figura representa um cmpartiment cm um dispsitiv. A h5,0 m N interir d cmpartiment é feit vácu. A bla (A) é disparada hrizntalmente pr uma mla que é acinada pr um bservadr
Prva de Física a Questã: (,0 pnts) A figura representa um cmpartiment cm um dispsitiv. A h5,0 m N interir d cmpartiment é feit vácu. A bla (A) é disparada hrizntalmente pr uma mla que é acinada pr um bservadr
4 Extensão do modelo de Misme e Fimbel para a determinação da distribuição cumulativa da atenuação diferencial entre dois enlaces convergentes
 4 Extensã d mdel de Misme e Fimbel ra a determinaçã da distribuiçã cumulativa da atenuaçã diferencial entre dis enlaces cnvergentes 4.. Distribuiçã cumulativa cnjunta das atenuações ns dis enlaces cnvergentes
4 Extensã d mdel de Misme e Fimbel ra a determinaçã da distribuiçã cumulativa da atenuaçã diferencial entre dis enlaces cnvergentes 4.. Distribuiçã cumulativa cnjunta das atenuações ns dis enlaces cnvergentes
matemática 2 Questão 7
 Questã TIPO DE PROVA: A Na figura, a diferença entre as áreas ds quadrads ABCD e EFGC é 56. Se BE =,a área d triângul CDE vale: a) 8,5 b) 0,5 c),5 d),5 e) 6,5 pr semana. Eventuais aulas de refrç sã pagas
Questã TIPO DE PROVA: A Na figura, a diferença entre as áreas ds quadrads ABCD e EFGC é 56. Se BE =,a área d triângul CDE vale: a) 8,5 b) 0,5 c),5 d),5 e) 6,5 pr semana. Eventuais aulas de refrç sã pagas
, cujos módulos são 3N. Se F A
 VTB 008 ª ETAPA Sluçã mentada da Prva de Física 0. nsidere duas frças, F A e F B, cujs móduls sã 3N. Se F A e F B fazem, respectivamente, ânguls de 60 e cm eix-x ( ângul é medid n sentid anti-hrári em
VTB 008 ª ETAPA Sluçã mentada da Prva de Física 0. nsidere duas frças, F A e F B, cujs móduls sã 3N. Se F A e F B fazem, respectivamente, ânguls de 60 e cm eix-x ( ângul é medid n sentid anti-hrári em
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA
 UNIERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS #4 () O circuit a seguir é usad cm pré-amplificadr e
UNIERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA DEPARTAMENTO DE ENGENHARIA ELÉTRICA ELETRÔNICA LISTA DE EXERCICIOS #4 () O circuit a seguir é usad cm pré-amplificadr e
UFRJ / POLI / DEL - Laboratório de Eletrônica III AULA PRÁTICA #4 OSCILADORES SENOIDAIS EM PONTE DE WIEN
 AULA PRÁTICA #4 OSCILADORES SEOIDAIS EM POTE DE WIE Obs: Prnuncia-se pnte de in. O nme vem d pesquisadr alemã Max Karl Werner Wien (866-938), que estudu a pnte RC que realimenta amplificadr, que leva seu
AULA PRÁTICA #4 OSCILADORES SEOIDAIS EM POTE DE WIE Obs: Prnuncia-se pnte de in. O nme vem d pesquisadr alemã Max Karl Werner Wien (866-938), que estudu a pnte RC que realimenta amplificadr, que leva seu
CAPÍTULO 2 RETIFICADORES A DIODO 2.1 - RETIFICADOR MONOFÁSICO DE MEIA ONDA A DIODO. a) Carga Resistiva Pura
 CAPÍTULO ETFCADOES A DODO.1 ETFCADO MONOFÁSCO DE MEA ONDA A DODO a) Carga esistiva Pura A estrutura d retificadr mnfásic de meia nda alimentand uma carga resistiva está representada na figura.1. v D D
CAPÍTULO ETFCADOES A DODO.1 ETFCADO MONOFÁSCO DE MEA ONDA A DODO a) Carga esistiva Pura A estrutura d retificadr mnfásic de meia nda alimentand uma carga resistiva está representada na figura.1. v D D
SIMPLES DEMONSTRAÇÃO DO MOVIMENTO DE PROJÉTEIS EM SALA DE AULA
 SIMPLES DEMONSTRAÇÃO DO MOVIMENTO DE PROJÉTEIS EM SALA DE AULA A.M.A. Taeira A.C.M. Barreir V.S. Bagnat Institut de Físic-Química -USP Sã Carls SP Atraés d lançament de prjéteis pde-se estudar as leis
SIMPLES DEMONSTRAÇÃO DO MOVIMENTO DE PROJÉTEIS EM SALA DE AULA A.M.A. Taeira A.C.M. Barreir V.S. Bagnat Institut de Físic-Química -USP Sã Carls SP Atraés d lançament de prjéteis pde-se estudar as leis
Transformadores. Transformadores 1.1- INTRODUÇÃO 1.2- PRINCÍPIO DE FUNCIONAMENTO
 Transfrmadres 1.1- INTRODUÇÃO N estud da crrente alternada bservams algumas vantagens da CA em relaçã a CC. A mair vantagem da CA está relacinada cm a facilidade de se elevar u abaixar a tensã em um circuit,
Transfrmadres 1.1- INTRODUÇÃO N estud da crrente alternada bservams algumas vantagens da CA em relaçã a CC. A mair vantagem da CA está relacinada cm a facilidade de se elevar u abaixar a tensã em um circuit,
Aula 03 Circuitos CA
 Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician 1. Elements de Circuits n dmíni de Fasres Intrduçã Para cmpreender a respsta de dispsitivs básics
Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician 1. Elements de Circuits n dmíni de Fasres Intrduçã Para cmpreender a respsta de dispsitivs básics
REVISÃO DE MEDIDAS ELÉTRICAS
 Amperímetros e Voltímetros DC EVSÃO DE MEDDAS ELÉCAS s m A + s m m m s, m ma, Nova Escala m V et + m V,, V Nova Escala AB m m et m ma AB m Ohmímetros. Ohmímetros Série 0 Malha : E ( + m + int ) E ( + )
Amperímetros e Voltímetros DC EVSÃO DE MEDDAS ELÉCAS s m A + s m m m s, m ma, Nova Escala m V et + m V,, V Nova Escala AB m m et m ma AB m Ohmímetros. Ohmímetros Série 0 Malha : E ( + m + int ) E ( + )
Aula 02 Álgebra Complexa
 Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician Aula 02 Álgebra Cmplexa 1. Númers Cmplexs Intrduçã Circuits CC smas algébricas de tensões e
Campus I Jã Pessa Disciplina: Análise de Circuits Curs Técnic Integrad em Eletrônica Prfª: Rafaelle Felician Aula 02 Álgebra Cmplexa 1. Númers Cmplexs Intrduçã Circuits CC smas algébricas de tensões e
Física A Extensivo V. 8
 Física Extensi V. 8 esla ula 9 9.) E Cnseraçã da quantidade de miment m. + m. = m. + m. m. + m. = m. + m. + = + + = + + = (I) Clisã perfeitamente elástica e = = + = (II) Mntand-se um sistema cm I e II,
Física Extensi V. 8 esla ula 9 9.) E Cnseraçã da quantidade de miment m. + m. = m. + m. m. + m. = m. + m. + = + + = + + = (I) Clisã perfeitamente elástica e = = + = (II) Mntand-se um sistema cm I e II,
As propriedades do gás estelar
 As prpriedades d gás estelar Estrelas sã massas gassas mantidas gravitacinalmente cm uma frma quase esférica e que apresentam prduçã própria de energia. A definiçã acima, além de nã ser a mais precisa
As prpriedades d gás estelar Estrelas sã massas gassas mantidas gravitacinalmente cm uma frma quase esférica e que apresentam prduçã própria de energia. A definiçã acima, além de nã ser a mais precisa
Circuitos em CA Série, Paralelo e Misto
 Institut Federal de Educaçã, Ciência e ecnlgia de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, març de 2009.
Institut Federal de Educaçã, Ciência e ecnlgia de Santa Catarina Departament Acadêmic de Eletrônica Retificadres Circuits em CA Série, Paralel e Mist Prf. Clóvis Antôni Petry. Flrianóplis, març de 2009.
( 3) (5) 2 v (m/s) V 0. S = S 0 + v 0.t + α.t 2 α V0 = V0 (I) (II) t (s)
 FÍSI Quand necessári, adte: aceleraçã da ravidade na erra 0 m/s massa específica (densidade) da áua.000 k/m velcidade da luz n vácu c,0 x 0 8 m/s calr específic da áua. 4J/(º.); ( calria. 4 jules). Prcediment
FÍSI Quand necessári, adte: aceleraçã da ravidade na erra 0 m/s massa específica (densidade) da áua.000 k/m velcidade da luz n vácu c,0 x 0 8 m/s calr específic da áua. 4J/(º.); ( calria. 4 jules). Prcediment
III Olimpíada de Matemática do Grande ABC Primeira Fase Nível 3 (1ª ou 2ª Séries EM)
 . Cnsidere a PG:, 9, 7, 8, 4,... A partir dela vams cnstruir a seqüência:, 6, 8, 4, 6,..., nde primeir term cincide cm primeir term da PG, e a partir d segund, n-ésim é a diferença entre n-ésim e (n-)-ésim
. Cnsidere a PG:, 9, 7, 8, 4,... A partir dela vams cnstruir a seqüência:, 6, 8, 4, 6,..., nde primeir term cincide cm primeir term da PG, e a partir d segund, n-ésim é a diferença entre n-ésim e (n-)-ésim
22/05/2013. Movimento de precessão e magnetização
 Mviment de precessã e magnetizaçã M ω = γb ω = 2πν [ N ( ) ( )] 0 = µ mag N a) Um mment magnétic (spin nuclear), rientad parcialmente cm relaçã a B, executa um mviment de precessã em trn d camp magnétic.
Mviment de precessã e magnetizaçã M ω = γb ω = 2πν [ N ( ) ( )] 0 = µ mag N a) Um mment magnétic (spin nuclear), rientad parcialmente cm relaçã a B, executa um mviment de precessã em trn d camp magnétic.
Diagramas líquido-vapor
 Diagramas líquid-vapr ara uma sluçã líquida cntend 2 cmpnentes vláteis que bedecem (pel mens em primeira aprximaçã) a lei de Rault, e prtant cnsiderada cm uma sluçã ideal, a pressã de vapr () em equilíbri
Diagramas líquid-vapr ara uma sluçã líquida cntend 2 cmpnentes vláteis que bedecem (pel mens em primeira aprximaçã) a lei de Rault, e prtant cnsiderada cm uma sluçã ideal, a pressã de vapr () em equilíbri
UDESC 2013/2 MATEMÁTICA. 01) Resposta: A. Comentário. x 2x. Como x 1, dividimos ambos os lados por (x 1) e obtemos: xx 6 2 = 120 6
 MATEMÁTICA 0) Respsta: A Cx, Ax, = 0x + 0 x! x! = 0x + 0!( x )! ( x )! xx ( )( x )( x )! xx ( )( x )( x )! =0( x ) ( x )! ( x )! xx ( )( x ) x( x )( x ) =0( x ) Cm x, dividims ambs s lads pr (x ) e btems:
MATEMÁTICA 0) Respsta: A Cx, Ax, = 0x + 0 x! x! = 0x + 0!( x )! ( x )! xx ( )( x )( x )! xx ( )( x )( x )! =0( x ) ( x )! ( x )! xx ( )( x ) x( x )( x ) =0( x ) Cm x, dividims ambs s lads pr (x ) e btems:
1) Determine e represente graficamente o domínio de cada uma das funções:
 UNIVESIDADE FEDEAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPATAMENTO DE MATEMÁTICA ª LISTA DE EXECÍCIOS DE CÁLCULO II-A Última atualizaçã 4-4-4 ) Determine e represente graficamente dmíni de cada uma das funções:
UNIVESIDADE FEDEAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPATAMENTO DE MATEMÁTICA ª LISTA DE EXECÍCIOS DE CÁLCULO II-A Última atualizaçã 4-4-4 ) Determine e represente graficamente dmíni de cada uma das funções:
AL 1.1 Movimento num plano inclinado: variação da energia cinética e distância percorrida. Nome dos membros do grupo: Data de realização do trabalho:
 Escla Secundária de Laga Física e Química A 10º An Paula Mel Silva Relatóri Simplificad AL 1.1 Mviment num plan inclinad: variaçã da energia cinética e distância percrrida Identificaçã d trabalh (Capa)
Escla Secundária de Laga Física e Química A 10º An Paula Mel Silva Relatóri Simplificad AL 1.1 Mviment num plan inclinad: variaçã da energia cinética e distância percrrida Identificaçã d trabalh (Capa)
QUESTÕES DE ÁREAS DE CÍRCULOS E SUAS PARTES
 QUESTÕES DE ÁREAS DE CÍRCULOS E SUAS PARTES 1. (Unicamp 015) A figura abaix exibe um círcul de rai r que tangencia internamente um setr circular de rai R e ângul central θ. a) Para θ 60, determine a razã
QUESTÕES DE ÁREAS DE CÍRCULOS E SUAS PARTES 1. (Unicamp 015) A figura abaix exibe um círcul de rai r que tangencia internamente um setr circular de rai R e ângul central θ. a) Para θ 60, determine a razã
Thiago Lima de Menezes
 UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS DEPARTAMENTO DE ENGENHARIA ELÉTRICA Thiag Lima de Menezes Cnversr Push-Pull Alimentad em Crrente aplicad a Crreçã d Fatr de
UNIVERSIDADE FEDERAL DA PARAÍBA CENTRO DE ENERGIAS ALTERNATIVAS E RENOVÁVEIS DEPARTAMENTO DE ENGENHARIA ELÉTRICA Thiag Lima de Menezes Cnversr Push-Pull Alimentad em Crrente aplicad a Crreçã d Fatr de
FÍSICA - I. Objetivos. Lançamento horizontal Resgate no Mar. MOVIMENTO EM DUAS E TRÊS DIMENSÕES 2ª. Parte. Enunciado
 FÍSICA - I MOVIMENTO EM DUAS E TRÊS DIMENSÕES ª. Parte Prf. M.Sc. Lúci P. Patrcíni Objetivs Analisar mviment de prjéteis e suas variantes. Física I - Prf. M.Sc. Lúci P. Patrcíni Lançament hrizntal Resgate
FÍSICA - I MOVIMENTO EM DUAS E TRÊS DIMENSÕES ª. Parte Prf. M.Sc. Lúci P. Patrcíni Objetivs Analisar mviment de prjéteis e suas variantes. Física I - Prf. M.Sc. Lúci P. Patrcíni Lançament hrizntal Resgate
TIPO DE PROVA: A. Questão 1. Questão 3. Questão 4. Questão 2. alternativa B. alternativa A. alternativa D. alternativa C
 Questã TIPO DE PROVA: A Ds n aluns de uma escla, 0% têm 0% de descnt na mensalidade e 0% têm 0% de descnt na mesma mensalidade. Cas equivalente a esses descnts fsse distribuíd igualmente para cada um ds
Questã TIPO DE PROVA: A Ds n aluns de uma escla, 0% têm 0% de descnt na mensalidade e 0% têm 0% de descnt na mesma mensalidade. Cas equivalente a esses descnts fsse distribuíd igualmente para cada um ds
3 Válvulas de Alívio Tipo Mola
 6 3 Válvulas de lívi Tip Mla s válvulas de alívi de pressã prjetadas para fluids incmpressíveis sã denminadas em inglês cm Pressure Relief Valves PRV, e as válvulas para fluids cmpressíveis sã denminadas
6 3 Válvulas de lívi Tip Mla s válvulas de alívi de pressã prjetadas para fluids incmpressíveis sã denminadas em inglês cm Pressure Relief Valves PRV, e as válvulas para fluids cmpressíveis sã denminadas
FÍSICA - I. MOVIMENTO EM DUAS E TRÊS DIMENSÕES 2ª. Parte. Prof. M.Sc. Lúcio P. Patrocínio
 FÍSICA - I MOVIMENTO EM DUAS E TRÊS DIMENSÕES ª. Parte Prf. M.Sc. Lúci P. Patrcíni Objetivs Analisar mviment de prjéteis e suas variantes. Física I - Prf. M.Sc. Lúci P. Patrcíni Lançament hrizntal Resgate
FÍSICA - I MOVIMENTO EM DUAS E TRÊS DIMENSÕES ª. Parte Prf. M.Sc. Lúci P. Patrcíni Objetivs Analisar mviment de prjéteis e suas variantes. Física I - Prf. M.Sc. Lúci P. Patrcíni Lançament hrizntal Resgate
MATEMÁTICA 1 o Ano Duds
 MATEMÁTICA 1 An Duds 1. (Ufsm 011) A figura a seguir apresenta delta d ri Jacuí, situad na regiã metrplitana de Prt Alegre. Nele se encntra parque estadual Delta d Jacuí, imprtante parque de preservaçã
MATEMÁTICA 1 An Duds 1. (Ufsm 011) A figura a seguir apresenta delta d ri Jacuí, situad na regiã metrplitana de Prt Alegre. Nele se encntra parque estadual Delta d Jacuí, imprtante parque de preservaçã
Matemática B Semi-Extensivo V. 1. Exercícios
 Matemática B Semi-Etensiv V. Eercícis 0) E Cm DBC é isósceles, tems DC 8. Em ADC sen 60º AC DC 0) B sen 60º 6 cs 60º y y y 6 Perímetr + 6 + 6 8 + 6 6( + ) 0) AC 8 AC 6 tg y y y tg 0) D 8. h 8 h 6 d 8 +
Matemática B Semi-Etensiv V. Eercícis 0) E Cm DBC é isósceles, tems DC 8. Em ADC sen 60º AC DC 0) B sen 60º 6 cs 60º y y y 6 Perímetr + 6 + 6 8 + 6 6( + ) 0) AC 8 AC 6 tg y y y tg 0) D 8. h 8 h 6 d 8 +
Capítulo V. Técnicas de Análise de Circuitos
 Capítul V Técnicas de Análise de Circuits 5.1 Intrduçã Analisar um circuit é bter um cnjunt de equações u valres que demnstram as características de funcinament d circuit. A análise é fundamental para
Capítul V Técnicas de Análise de Circuits 5.1 Intrduçã Analisar um circuit é bter um cnjunt de equações u valres que demnstram as características de funcinament d circuit. A análise é fundamental para
1 a QUESTÃO: (2,0 pontos) Avaliador Revisor
 ( MATEMÁTICA - Gabarit Grups I e J a QUESTÃO: (,0 pnts) Avaliadr Revisr A figura abaix exibe gráfic de uma funçã y = f (x) definida n interval [-6,+6]. O gráfic de f passa pels pnts seguintes: (-6,-),(-4,0),
( MATEMÁTICA - Gabarit Grups I e J a QUESTÃO: (,0 pnts) Avaliadr Revisr A figura abaix exibe gráfic de uma funçã y = f (x) definida n interval [-6,+6]. O gráfic de f passa pels pnts seguintes: (-6,-),(-4,0),
Circuitos Trifásicos Equilibrados e Desequilibrados
 UNERSDDE EDERL DE JU DE OR nálise de Sistemas Elétrics de Ptência Circuits Trifásics Equilibrads e Desequilibrads P r f l á v i a n d e r s n G m e s E - m a i l : f l a v i g m e s @ u f j f e d u b r
UNERSDDE EDERL DE JU DE OR nálise de Sistemas Elétrics de Ptência Circuits Trifásics Equilibrads e Desequilibrads P r f l á v i a n d e r s n G m e s E - m a i l : f l a v i g m e s @ u f j f e d u b r
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
 Avenida Prfessr Mell Mraes, nº 1. CEP 05508-900, Sã Paul, SP. PME 100 MECÂNICA A Terceira Prva 11 de nvembr de 009 Duraçã da Prva: 10 minuts (nã é permitid us de calculadras) 1ª Questã (,5 pnts): Um sólid
Avenida Prfessr Mell Mraes, nº 1. CEP 05508-900, Sã Paul, SP. PME 100 MECÂNICA A Terceira Prva 11 de nvembr de 009 Duraçã da Prva: 10 minuts (nã é permitid us de calculadras) 1ª Questã (,5 pnts): Um sólid
Modulação Angular por Sinais Digitais
 Mdulaçã Angular pr Sinais Digitais Cm n cas da mdulaçã em amplitude, também para a mdulaçã angular se desenvlveu uma nmenclatura especial quand se trata de sinais digitais na entrada. N cas da mdulaçã
Mdulaçã Angular pr Sinais Digitais Cm n cas da mdulaçã em amplitude, também para a mdulaçã angular se desenvlveu uma nmenclatura especial quand se trata de sinais digitais na entrada. N cas da mdulaçã
CIRCUITOS ELÉTRICOS CONCEITOS BÁSICOS
 CCUOS ELÉCOS CONCEOS BÁSCOS rf. arcs Fergütz ar/4 - Carga Elétrica (Q, q) [ Unidade: Culmb C ] e - Quand se frnece u retira energia d elétrn (e - ), pde-se mvimentá-l pr entre as camadas (K, L,, N...).
CCUOS ELÉCOS CONCEOS BÁSCOS rf. arcs Fergütz ar/4 - Carga Elétrica (Q, q) [ Unidade: Culmb C ] e - Quand se frnece u retira energia d elétrn (e - ), pde-se mvimentá-l pr entre as camadas (K, L,, N...).
UFSC. Matemática (Amarela)
 Respsta da UFSC: 0 + 0 + 08 = Respsta d Energia: 0 + 08 = 09 Resluçã 0. Crreta. 0. Crreta. C x x + y = 80 y = 80 x y y = x + 3 30 x + 3 30 = 80 x x = 80 3 30 x = 90 6 5 x = 73 45 8 N x z 6 MN // BC segue
Respsta da UFSC: 0 + 0 + 08 = Respsta d Energia: 0 + 08 = 09 Resluçã 0. Crreta. 0. Crreta. C x x + y = 80 y = 80 x y y = x + 3 30 x + 3 30 = 80 x x = 80 3 30 x = 90 6 5 x = 73 45 8 N x z 6 MN // BC segue
Nome dos membros do grupo: Data de realização do trabalho:
 Escla Secundária de Laga Física e Química A 10º An Paula Mel Silva Identificaçã d trabalh (Capa) Relatóri Simplificad AL 1.2 Mviment vertical de queda e de ressalt de uma bla: transfrmações e transferências
Escla Secundária de Laga Física e Química A 10º An Paula Mel Silva Identificaçã d trabalh (Capa) Relatóri Simplificad AL 1.2 Mviment vertical de queda e de ressalt de uma bla: transfrmações e transferências
PROVA DE FÍSICA MÓDULO III DO PISM (triênio )
 QUESTÕES OBJETIVAS PROVA DE FÍSICA MÓDULO III DO PISM (triêni 2004-2006) Use, se necessári: cnstante de Planck, h = 6,63x10-34 J.s; carga d elétrn, q = 1,60x10-19 C; cnstante eletrstática, k = 9x10 9 N.M
QUESTÕES OBJETIVAS PROVA DE FÍSICA MÓDULO III DO PISM (triêni 2004-2006) Use, se necessári: cnstante de Planck, h = 6,63x10-34 J.s; carga d elétrn, q = 1,60x10-19 C; cnstante eletrstática, k = 9x10 9 N.M
Transdutor de corrente alternada (analógico)
 Transdutr de crrente (analógic) Revisã 1.1 22/04/2014 [1] Intrduçã Os transdutres de crrente têm pr finalidade cnverter um determinad sinal de crrente em um sinal cntínu islad galvanicamente. Sã dispnibilizads
Transdutr de crrente (analógic) Revisã 1.1 22/04/2014 [1] Intrduçã Os transdutres de crrente têm pr finalidade cnverter um determinad sinal de crrente em um sinal cntínu islad galvanicamente. Sã dispnibilizads
Retificadores (ENG ) Lista de Exercícios (Selecionados) de Dispositivos Eletrônicos
 ista de Exercícis de ispsitivs Eletrônics etificadres (ENG - 20301) ista de Exercícis (Selecinads) de ispsitivs Eletrônics 06) etermine a queda de tensã direta através d did cujas características aparecem
ista de Exercícis de ispsitivs Eletrônics etificadres (ENG - 20301) ista de Exercícis (Selecinads) de ispsitivs Eletrônics 06) etermine a queda de tensã direta através d did cujas características aparecem
Energia Cinética e Trabalho
 Capítul 7 Energia Cinética e Trabalh Cpyright 7-1 Energia Cinética Metas de Aprendizad 7.01 Aplicar a relaçã entre a energia cinética de uma partícula, sua massa e sua velcidade. 7.02 Entender que a energia
Capítul 7 Energia Cinética e Trabalh Cpyright 7-1 Energia Cinética Metas de Aprendizad 7.01 Aplicar a relaçã entre a energia cinética de uma partícula, sua massa e sua velcidade. 7.02 Entender que a energia
III Olimpíada de Matemática do Grande ABC Primeira Fase Nível 2 (7ª ou 8ª Séries)
 III Olimpíada de Matemática d Grande ABC Primeira Fase Nível (7ª u 8ª Séries). A perguntar a idade d prfessr, um alun recebeu d mesm a seguinte charada : Junts tems sete vezes a idade que vcê tinha quand
III Olimpíada de Matemática d Grande ABC Primeira Fase Nível (7ª u 8ª Séries). A perguntar a idade d prfessr, um alun recebeu d mesm a seguinte charada : Junts tems sete vezes a idade que vcê tinha quand
Transformadores. Teoria Parte I OBJETIVOS
 Transfrmadres Teria Parte I OBJETIVOS Apresentar a alun a definiçã de transfrmadr e sua imprtância Apresentar seu princípi de funcinament Intrduzir mdel de um transfrmadr ideal Apresentar mdel de um transfrmadr
Transfrmadres Teria Parte I OBJETIVOS Apresentar a alun a definiçã de transfrmadr e sua imprtância Apresentar seu princípi de funcinament Intrduzir mdel de um transfrmadr ideal Apresentar mdel de um transfrmadr
Administração AULA- 7. Economia Mercados [3] Oferta & Procura
![Administração AULA- 7. Economia Mercados [3] Oferta & Procura Administração AULA- 7. Economia Mercados [3] Oferta & Procura](/thumbs/71/66191843.jpg) Administraçã AULA- 7 1 Ecnmia Mercads [3] Oferta & Prcura Prf. Isnard Martins Bibligrafia: Rsseti J. Intrduçã à Ecnmia. Atlas 06 Rbert Heilbrner Micr Ecnmia N.Gregry Mankiw Isnard Martins Pag - 1 Oferta,
Administraçã AULA- 7 1 Ecnmia Mercads [3] Oferta & Prcura Prf. Isnard Martins Bibligrafia: Rsseti J. Intrduçã à Ecnmia. Atlas 06 Rbert Heilbrner Micr Ecnmia N.Gregry Mankiw Isnard Martins Pag - 1 Oferta,
cos. sen = ; tg 2x
 Resluções das atividades adicinais Capítul Grup A. alternativa E Sabems que: tg 0 tg 0 sen 0 sen 0 cs 0 cs 0 Dessa frma: + +. alternativa E Tems: sen + cs + cs cs Cm ;, cs < 0. Lg cs. Entã: sen sen cs
Resluções das atividades adicinais Capítul Grup A. alternativa E Sabems que: tg 0 tg 0 sen 0 sen 0 cs 0 cs 0 Dessa frma: + +. alternativa E Tems: sen + cs + cs cs Cm ;, cs < 0. Lg cs. Entã: sen sen cs
IF-UFRJ FIW 362 Laboratório de Física Moderna Eletrônica Curso de Licenciatura em Física Prof. Antonio Carlos. Aula 6: Amplificadores Operacionais
 IFUFJ FIW 36 Labratóri de Física Mderna Eletrônica Curs de Licenciatura em Física Prf. Antni Carls Aula 6: Amplificadres Operacinais Este material fi basead em lirs e manuais existentes na literatura (ide
IFUFJ FIW 36 Labratóri de Física Mderna Eletrônica Curs de Licenciatura em Física Prf. Antni Carls Aula 6: Amplificadres Operacinais Este material fi basead em lirs e manuais existentes na literatura (ide
Transformada de Laplace
 UNIVERSIDADE FEDERAL DA PARAÍBA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA Transfrmada de Laplace Prf. Juan Mises Maurici Villanueva jmaurici@cear.ufpb.br www.cear.ufpb.br/juan Transfrmada de Lapace
UNIVERSIDADE FEDERAL DA PARAÍBA PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA Transfrmada de Laplace Prf. Juan Mises Maurici Villanueva jmaurici@cear.ufpb.br www.cear.ufpb.br/juan Transfrmada de Lapace
UFRJ/POLI/DEL - Laboratório de Eletrônica III. PARTE 1: Conversor de Impedância Negativa (NIC)
 Prática #3 CONVERSORES DE IMPEDÂNCIA GRUPO: Data: UFRJ/POLI/DEL Labratóri de Eletrônica III PARTE 1: Cnversr de Impedância Negativa (NIC) I) Objetiv Estudar a realizaçã e aplicaçã de cnversr de impedância
Prática #3 CONVERSORES DE IMPEDÂNCIA GRUPO: Data: UFRJ/POLI/DEL Labratóri de Eletrônica III PARTE 1: Cnversr de Impedância Negativa (NIC) I) Objetiv Estudar a realizaçã e aplicaçã de cnversr de impedância
a) No total são 10 meninas e cada uma delas tem 10 opções de garotos para formar um par. Logo, o número total de casais possíveis é = 100.
 Questã 1: Em uma festa de aniversári, deseja-se frmar 10 casais para a valsa. A aniversariante cnvidu 10 garts e 9 gartas. a) Quants casais diferentes pderã ser frmads? b) Sabend-se que 4 das meninas sã
Questã 1: Em uma festa de aniversári, deseja-se frmar 10 casais para a valsa. A aniversariante cnvidu 10 garts e 9 gartas. a) Quants casais diferentes pderã ser frmads? b) Sabend-se que 4 das meninas sã
Matemática B Extensivo V. 2
 Gabarit Matemática B Extensiv V. Reslva Aula Aula 7.0) a) sen 0 sen (60 0 ) 7.0) f(x) sen 0 b) cs 0 cs (80 0 ) c) cs 60 cssec 60 cssec 00 sen 00. d) sec 97 sec cs e) tg tg tg ( 80 ) Períd: p 6 Imagem:
Gabarit Matemática B Extensiv V. Reslva Aula Aula 7.0) a) sen 0 sen (60 0 ) 7.0) f(x) sen 0 b) cs 0 cs (80 0 ) c) cs 60 cssec 60 cssec 00 sen 00. d) sec 97 sec cs e) tg tg tg ( 80 ) Períd: p 6 Imagem:
GEO046 Geofísica. Magnetômetro de campo total. Magnetômetro flux-gate. Magnetômetro de campo total
 GEO046 Gefísica Aula n 07 MÉTODO MAGNÉTICO Anmalias magnéticas Magnetômetr de camp ttal aseia-se na precessã d prótn d núcle d átm de hidrgêni, quand este prcura se alinhar cm um camp magnétic extern.
GEO046 Gefísica Aula n 07 MÉTODO MAGNÉTICO Anmalias magnéticas Magnetômetr de camp ttal aseia-se na precessã d prótn d núcle d átm de hidrgêni, quand este prcura se alinhar cm um camp magnétic extern.
Notas de aula prática de Mecânica dos Solos II (parte 13)
 Ntas de aula prática de Mecânica ds Sls II (parte ) Héli Marcs Fernandes Viana Cnteúd da aula prática xercíci relacinad a cálcul d empux ativ pel métd de Rankine, qual é causad pr um sl granular (u arens)
Ntas de aula prática de Mecânica ds Sls II (parte ) Héli Marcs Fernandes Viana Cnteúd da aula prática xercíci relacinad a cálcul d empux ativ pel métd de Rankine, qual é causad pr um sl granular (u arens)
