SOLUÇÃO NUMÉRICA DA EQUAÇÃO DE BURGERS PELO MÉTODO DAS DIFERENÇAS CENTRAIS DE SEXTA-ORDEM
|
|
|
- Júlio César Belmonte Carrilho
- 5 Há anos
- Visualizações:
Transcrição
1 Rvs Iromr d Irí Má. Vol. 7, N.º, pp. 7-, SLUÇÃ NUMÉRICA DA EQUAÇÃ DE BURGERS PEL MÉTD DAS DIERENÇAS CENTRAIS DE SEXTA-RDEM ESTANER CLAR RMÃ, JAIR APARECID MARTINS, LUIZ ELIPE MENDES DE MURA Uvrsdd drl d Ijá Cmps d Ir R Irmã Ivo Drmod,, Dsro Idsrl II, CEP 5-7, Ir MG Brsl Dprmo d Ehr d Prodo, Mso Mrls Av. Idpdê, 5, Ipor, CEP 7- Soro SP Brsl Uvrsdd Esdl d Cmps ldd d Ehr Mâ, Dprmo d Térm ldos R Mdlyv,, Cdd Uvrsár "Zro Vz", CEP:-6 Cmps SP Brsl Rdo d jlo d, pr pló 5 d or d Rsmo Es rlho m omo ojvo prsr plção d m sqm d drçs rs d 6 solção d qção d Brrs, dmosrdo s ê ldd d mplmção. A prr d omprçõs om oros méodos proposos por oros ors, dmosr-s q s méodo é ão qo város oros, porém, d ál ormlção mplmção lém d prsr m o so ompol. Plvrs-hv Méodo ds Drçs s, qção d Brrs, Méodo d Crk-Nolso Mhod, Sérs d Tylor.. INTRDUÇÃ Pr lsr ê mér do méodo ds drçs rs d 6, s rlho srá propos omo plção m smplção d qção d Nvr-Soks, mém ohd omo qção d Brrs. Ns osdr-s m rd d prssão lo, m ods s drçõs, q o somo é rdo ps drção, o q rsl s prssão: om,,, A, L, B,, sdo q é vsosdd má o domío ompol ddo omo L. ojvo prpl ds rlho é dmosrr q plção do méodo ds drçs rs d 6 pr dsrzção dos rmos sps jm om o méodo d Crk-Nolso pr o rmo rs é ão qo város oros méodos proposos lor r, r ls pod-s r [-5] r oros, porém, om vm d sr d ál mplmção d o so ompol.. INITE DIERENCE METHD Pr prolms ísos ovrdos por qçõs drs prs, pr smlção mér d s prolms é ssáro m méodo méro pr promr lms dss drvds. Ns rlho, o Méodo ds Drçs s srá lzdo. Cosdrdo m ção s drvd o poo,
2 E.C. Romão, J.A. Mrs, L..M. d Mor lm S é pddo m sérs d Tylor m oro d, m-s! Ssdo, rsl q é m promção d prmr ordm, so é, o rro d rmo é. Esrvdo m sérs d Tylor pr +, m-s [6],!! 5!! 6 Rorzdo 5, oém-s drç pr r, 7 Smlrm, pr 6, m-s drç pr rás, lm, somdo-s s 5 6, oém-s prssão ohd omo drç rl d sd ordm d, Pr drç rl d, Ch prs s órml, 6 6 Um orção spl ds rlho é osrção d m promção d 6 pr drçs rs pls sérs d Tylor. Ulzdo msm dé d 5 6 pr,, + + m-s,!!
3 Solção mér d qção d rrs plo méodo ds drçs rs d s-ordm!!!! Pls 5, 6,,, srv-s prssão, d d 6 6! 7 7! ! 5! Pl 5, sl-s m prssão pr drvd sd d prr do s ssm lr, d / 5 / / / / 5 / / d. Rsldo, ssm prssão, RMULAÇÃ NUMÉRICA Cosdrdo E, m oros plvrs, E lzdo o méodo d Crk-Nolso, oém-s, E od E
4 E.C. Romão, J.A. Mrs, L..M. d Mor Pr dsrzção spl srá lzdo o méodo ds drçs rs. ssm lr srá osrído omo s: Nó Nó NNós Codção d ooro m = =, rspvm. s.: Nós: qdd ol d ós mlh. Nó Nó NNós Drç Crl : od,, Nó Nó NNós Drç Crl : 5 od 6 6,, ros Nós Drç Crl 6 : 6 od ,,,,,,. APLICAÇÕES NUMÉRICAS Pr solção do ssm lr q rprs o prolm proposo, lz-s m ro hmd DLSLRG d lo orr. Dvdo à pdd d mmór ompol do ompdor lzdo, o possívl s prolm rlho, rmzr os os m m mrz h. Pr áls do rro omdo solção mér m omprção om solção lí, o lzd orm L, sdo s dd orm: m m, o sj, mor drç m módlo, dr odos os ós d mlh ompol, omprção d solção lí om mér. Pr dmosrr ê ds propos, sr prsm-s o plçõs mérs. Aplção Ns plção osdr-s qção om s ss odçõs d ooro l:,,. s,
5 Solção mér d qção d rrs plo méodo ds drçs rs d s-ordm Tl. Rsldos méros pr ls poos = =.. D [7] Kly Zh [] X [5] Prs E [] [5] =. =.5 =. = Tl. Comprção d rsldos méros d város ors solção. Al [] D [7] Do ] X [5] Prs E [5] =. = / =.5 =.5 =.5 =. = Aq, lzm-s os rlhos [,5,7,]. Arvés d l, o-s q os rsldos do prs rlho prs os mlhors rsldos, ssm omo o rlho [5] q lz m mlh mos rd m, porém lz m psso o mpo dz vzs mor, o sj, qo o prs rlho lz-s d pssos o mpo, [5] lz-s d pssos pssos o mpo ms, osodo ssm m so ompol osdrvlm mor. Aplção Ns plção osdr-s. om odçõs d ooro,,. m odção l do po,. /, od.5. Ns plção, os rlhos [5,7,,] srvrm d omprção dos rsldos méros ds rlho, jm om solção lí. Um rrís mpor q pod sr vdd l, é q o prs rlho [5] ssrm d m dsrzção mporl ms rd pr or os rsldos, qo q os oros rlhos, om m rmo mor o mpo, os rsldos prsm o prsão, porém ão ompv om [5] o prs rlho. Um rrís mpor d ão do méodo d drçs rs d 6 om o méodo d Crk-Nolso d é
6 E.C. Romão, J.A. Mrs, L..M. d Mor Tl. Comprção dos rsldos pr. zs Hss Prs = / = / = /6 E =. =. = Tl. Comprção dos rsldos pr zs [] Hss [] Prs = / = / = /6 E [] =. =. = ssdd d m psso d mpo ms m rdo, m orprd, rçs l ordm d prsão do méodo d dsrzção spl, sso m smpr é ssáro. Aplção Aq, srá lzdos os vlors l. l pr vsosdd má qção. Com rlção às odçõs d ooro l m-s,,,, Como rlhos pr omprção, s plção lzo-s [,]. A l mosr q o prs rlho lç os rsldos qdo omprdos om os oros dos rlhos om solção. É mpor rsslr q o psso d mpo lzdo o rmdáro qdo omprdo om os oros, od [] já oém os rsldos om m =. qo q [] ss d m psso d mpo =.. Ns rlho o lzdo m psso d mpo =.. Aplção Pr, s plção s odçõs d ooro l são d ordo om s solção lí, s, os jo domío ompol é.
7 Solção mér d qção d rrs plo méodo ds drçs rs d s-ordm Tl 5. Norm L pr = /. / / / /6 / /6 W d Lyo [] Prs Tl 6. Norm L pr = /. /5 / / / / W d Lyo [] Prs Ns plção m omprção om os rsldos méros prsdos por [] é rlzd. N l 5 -s = / vrm-s vlors d dmosrdo q o prs rlho o rmo do psso d mpo mlhor osm os rsldos, qo q m [] o msmo ão oorr. A- or l 6, = / vrm-s vlors d os rsldos méros dos dos rlhos mosrm rsldos q mlhorm pr d msm ordm d prsão. Applo 5 Pr s plção qção ovr é d orm, pr áls d rro srá lzd s solção lí pr omprçõs,, jo domío ompol é om s odçõs d ooro l sdo d ordo om solção lí []. s rsldos méros prsdos l 7 dmosrm pr m so od s odçõs d ooro dpdm do mpo do spço, o méodo proposo prs ls rsldos, ordo o mor rmo d m ordm d prsão m oro d CNCLUSÕES As d qlqr os, é mpor mor q o ojvo ds rlho ão o d prsr m méodo q oss mlhor o por q qlqr oro dr os rlhos q dos. Aq, prso-s m sqm d l ordm d drçs rs pr dsrzção spl do om m méodo d Crk-Nolso d sd-ordm d ál ormlção mplmção. A lzção do méodo d Crk-Nolso d mr q o lzdo prs ldd d ps ssr d odção l pr o ío dos állos, lmrdo q ls méodos d l ordm ssrm d ms d m psso d mpo, o q dlr m poo os állos. A lzção d m sqm d drçs rs d s-ordm possl lzção d m mlh spl poo rd, rdo ssm m ssm mrl d pq ordm lrdo ssm os állos, rssldo q s rlho lzo-s m rmzmo m mrz h por s rr d m prolm D, m prolms D o D, o or prpl ds rlho ormlm lz-s d rmzmo m vors q ohm ps os os ão los [] do ssm mrl possldo ssm m rd rmo d mlh ompol. Como propos pr rlhos ros, srá pldo s sqm qção d Brrs D pr lsr ê do méodo m domíos ms omplos s promdo ssm d prolms práos d hr d ís.
8 E.C. Romão, J.A. Mrs, L..M. d Mor AGRADECIMENTS Es rlho é podo plo Coslho Nol d Dsvolvmo Cío Tolóo CNPq Brsl Pro. 5/-5. REERÊNCIAS [] Hss, I.A., Slm, A.A., Hoshm, H.A., orh-ordr dr mhod or solv Brs qo, Appl. Mh. Comp. 7, 7-5 [] Lo, W., A mpl orh-ordr omp dr shm or o-dmsol Brrs qo, Appl. Mh. Comp., 6, [] Zh, C.C., W, R.H., Nmrl solo o Brrs qo y B-spl qs-rpolo, Appl. Mh. Comp.,, 6-7 [] W, J., Lyo, A., Nw mrl mhods or Brrs qo sd o sm-lr d modd qo pprohs, Appl. Nm. Mh., 6, [5] X, M., W, R.H., Zh, J.H.,, Q., A ovl mrl shm or solv Brrs s qo, Appl. Mh. Comp., 7, 7- [6] Ch, T.J., Compol ld Dyms, Cmrd Uvrsy Prss [7] D, I., Irk, D., Sk, B., A mrl solo o h Brrs qo s B-Spls, Appl. Mh. Comp., 6, 5 [] Kly, S., Bhdır, A.R., Özds, A., Nmrl solo o o-dmsol Brrs qo: pl d -pl dr mhod, J. Comp. Appl. Mh.,, 5 6 [] Al, A.H.A., Grdr, L.R.T., Grdr, G.A., A olloo mhod o Brrs s qo s spls, Comp. Mh. Appl. Mh. E., 5-7 [] Do, A., A Glrk lm pproh o Brrs qo, Appl. Mh. Comp., 57, -6 [] zs, T., Aks, E.N., zds, A., A lm pproh or solo o Brrs s qo, Appl. Mh. Comp.,, 7- [] Gors, A., A omprso w Col Hop rsormo d h domposo mhod or solv Brrs qos, Appl. Mh. Comp., 7, [] Romão, E.C., Cmpos, M.D., Mor, L..M., Applo o h Glrk d Ls-Sqrs Elm Mhods h solo o D Posso d Hlmholz qos, Comp. Mh. Appl., 6, - A NUMERICAL SLUTIN THE BURGERS EQUATIN USING SIXTH- RDER CENTRAL INITE DIERENCE Asr Ths ppr ms o prs h pplo o shm o rl drs D6 o solv h Brrs qo, show s y d sss or pplo. Th ppr srs wh h omprsos wh ohr mhods proposd y ohr hors, d rvls h h mhod proposd s sh s h ohrs; howvr, r dvs o sy mplmo d rdd ompol oss. Kywords Crl Dr Mhod, Brrs qo, Crk-Nolso Mhod, Tylor srs.
ALGUMAS PROPRIEDADES DAS CURVAS CONVEXAS DO PLANO
 Dprmo d Mmá ALGUMAS PROPRIEDADES DAS CURVAS CONVEXAS DO PLANO Aluo: Pul Muro Nus Ordor: Hr Nols Aux Irodução Nos ds us mmá fz-s prs m odos os lugrs. Ao olor um mod pr lfor ou osgur ls guém pr pr psr m
Dprmo d Mmá ALGUMAS PROPRIEDADES DAS CURVAS CONVEXAS DO PLANO Aluo: Pul Muro Nus Ordor: Hr Nols Aux Irodução Nos ds us mmá fz-s prs m odos os lugrs. Ao olor um mod pr lfor ou osgur ls guém pr pr psr m
Espaço de Estados. Modelo de Estado: y(t) = saída u(t) = entrada. função de transferência em cadeia fechada (f.t.c.f) :
 Epço Eo Eqo or corolo covcol - rlção r í-r, o fção rfrêc, o corolo moro - crção qçõ o m m rmo qçõ frc ªorm q pom r com m qção frcl ª orm form mrcl. O o oção mrcl mplfc m mo rprção mmác m qçõ. O mo úmro
Epço Eo Eqo or corolo covcol - rlção r í-r, o fção rfrêc, o corolo moro - crção qçõ o m m rmo qçõ frc ªorm q pom r com m qção frcl ª orm form mrcl. O o oção mrcl mplfc m mo rprção mmác m qçõ. O mo úmro
Módulo 03. Determinantes. [Poole 262 a 282]
![Módulo 03. Determinantes. [Poole 262 a 282] Módulo 03. Determinantes. [Poole 262 a 282]](/thumbs/74/70829060.jpg) Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
Móulo Not m, ltur sts potmtos ão sps moo lum ltur tt lor prpl r Cm-s à tção pr mportâ o trlo pssol rlzr plo luo rsolvo os prolms prstos lor, sm osult prév s soluçõs proposts, áls omprtv tr s sus rspost
Capítulo 4: Derivada A Reta Tangente. y = uma curva definida no intervalo ( a, ) e sejam ( x, y ) e Q( x y ) P dois pontos
 Isio d Ciêcis Es - Dprmo d Mmáic Cálclo I Proª Mri Jli Vr Crlo d Arjo Cpílo : Drid - A R T Sj b disios d cr Sj s r sc q pss plos poos P Q Cosidrdo o riâlo râlo PMQ, ir o ldo, mos q iclição d r s, o coici
Isio d Ciêcis Es - Dprmo d Mmáic Cálclo I Proª Mri Jli Vr Crlo d Arjo Cpílo : Drid - A R T Sj b disios d cr Sj s r sc q pss plos poos P Q Cosidrdo o riâlo râlo PMQ, ir o ldo, mos q iclição d r s, o coici
Matrizes - Teoria ...
 Mrzs - Tor Mrz Rgulr Mrz Rgulr d ord por é u qudro fordo por los dsposos lhs olus ou s Rprsros u rz d lhs olus por Os los d rz srão dfdos por u lr o dos íds o prro íd d lh o sgudo íd olu à qu pr o lo Iguldd
Mrzs - Tor Mrz Rgulr Mrz Rgulr d ord por é u qudro fordo por los dsposos lhs olus ou s Rprsros u rz d lhs olus por Os los d rz srão dfdos por u lr o dos íds o prro íd d lh o sgudo íd olu à qu pr o lo Iguldd
A formulação representada pelas equações (4.1)-(4.3) no método de elementos finitos é denominada de formulação forte (strong formulation).
 4. Fomlção Mcl o Méoo Elmos Fos s cpílo sá ps fomlção mcl o méoo lmos fos pos plcção o méoo lv ssms lgécos q pom s ogzos fom mcl p poso solção po éccs mécs pops p c po qção fcl: lípc pólc o hpólc. O poo
4. Fomlção Mcl o Méoo Elmos Fos s cpílo sá ps fomlção mcl o méoo lmos fos pos plcção o méoo lv ssms lgécos q pom s ogzos fom mcl p poso solção po éccs mécs pops p c po qção fcl: lípc pólc o hpólc. O poo
= n + 1. a n. n 1 =,,,,,, K,,K. K descreve uma sequência finita.
 DICIPINA: CÁCUO A CONTEÚDO: EQUÊNCIA PROFEORA: NEYVA ROMEIRO PERÍODO: BIMETRE EQUÊNCIA Um squêc um fução f cujo domío o cojuo dos ros posvos su gráfco o plo y do po, ou d, squêc um cojuo d prs orddos do
DICIPINA: CÁCUO A CONTEÚDO: EQUÊNCIA PROFEORA: NEYVA ROMEIRO PERÍODO: BIMETRE EQUÊNCIA Um squêc um fução f cujo domío o cojuo dos ros posvos su gráfco o plo y do po, ou d, squêc um cojuo d prs orddos do
OPÇÕES EXÓTICAS MSc MATEMÁTICA FINANCEIRA 2008/09 EXAME - Resolução 29/07/09 Duração: 2.5 horas
 OPÇÕE EÓICA AEÁICA FINANCEIRA 8/9 EAE - Rsolção 9/7/9 Drção:.5 hors CAO Consir m Eroi sor o ivo om srik om vnimno no momno om m rémio igl K. Ao onrário o q é hil o rémio k não é liqio hoj n rnsção (momno.
OPÇÕE EÓICA AEÁICA FINANCEIRA 8/9 EAE - Rsolção 9/7/9 Drção:.5 hors CAO Consir m Eroi sor o ivo om srik om vnimno no momno om m rémio igl K. Ao onrário o q é hil o rémio k não é liqio hoj n rnsção (momno.
RESOLUÇÃO DE EQUAÇÕES POR MEIO DE DETERMINANTES
 RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.
RESOLUÇÃO DE EQUAÇÕES POR EIO DE DETERINANTES Dtrmt um mtrz su orm Sj mtrz: O trmt st mtrz é: Emlo: Vmos suor o sstm us quçõs om us óts y: y y Est sstm quçõs o sr srto orm mtrl: y Est qução r três mtrzs:.
# D - D - D - - -
 1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
1 [ \ 2 3 4 5 Tl Como um Fcho 6 7 8 # Willim W Phlps (Ltr) nónimo / Erik Sti (Músic) rrnj por J shly Hll, 2007 9 10 11 12 [ \ [ \ # (Sopr) # (lto) # # Q Q [ \ # # # # # # # # # # # # 13 14 15 16# 17 18
TÓPICOS. Integração complexa. Integral de linha. Teorema de Cauchy. Fórmulas integrais de Cauchy.
 No m, liur dss pomos ão disps d modo lgum liur d iliogri pricipl d cdir hm-s à ção pr imporâci do rlho pssol rlir plo luo rsolvdo os prolms prsdos iliogri, sm ul prévi ds soluçõs proposs, ális compriv
No m, liur dss pomos ão disps d modo lgum liur d iliogri pricipl d cdir hm-s à ção pr imporâci do rlho pssol rlir plo luo rsolvdo os prolms prsdos iliogri, sm ul prévi ds soluçõs proposs, ális compriv
+ = x + 3y = x 1. x + 2y z = Sistemas de equações Lineares
 Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn
Sisms d quçõs Linrs Equção Linr Tod qução do ipo:.. n n Ond:,,., n são os ofiins;,,, n são s inógnis; é o rmo indpndn. E.: d - Equção Linr homogên qundo o rmo indpndn é nulo ( ) - Um qução linr não prsn
Messinki PUSERRUSLIITIN EM 10 MM PUSERRUSLIITIN EM 12 MM PUSERRUSLIITIN EM 15 MM PUSERRUSLIITIN EM 18 MM PUSERRUSLIITIN EM 22 MM
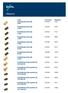 Messinki Tuote LVI-numero Pikakoodi PUSERRUSLIITIN EM 1551002 XV87 PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM 2 PUSERRUSLIITIN EM 35 MM
Messinki Tuote LVI-numero Pikakoodi PUSERRUSLIITIN EM 1551002 XV87 PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM 2 PUSERRUSLIITIN EM 35 MM
1 Sm ª 13. Então, se dispôs Davi com os seus homens, uns seiscentos, saíram de Queila e se foram sem rumo certo. Ziclague
 1 Sm. 23.13ª 13 Então, s dspôs Dv om os ss homns, ns ssntos, sírm d Q s form sm rmo rto. Z 1 Sm 27.1-3 1 Dss, porém, Dv onso msmo: Pod sr q m d vnh prr ns mãos d S; nd há, pos, mhor pr mm do q fr pr trr
1 Sm. 23.13ª 13 Então, s dspôs Dv om os ss homns, ns ssntos, sírm d Q s form sm rmo rto. Z 1 Sm 27.1-3 1 Dss, porém, Dv onso msmo: Pod sr q m d vnh prr ns mãos d S; nd há, pos, mhor pr mm do q fr pr trr
( ) 2. Eletromagnetismo I Prof. Dr. Cláudio S. Sartori - CAPÍTULO VIII Exercícios 1 ˆ ˆ ( ) Idl a R. Chamando de: x y du. tg θ
 Elromgnismo Prof. Dr. Cláudio S. Srori - CPÍTUO V Ercícios Emplo Cálculo do cmpo mgnéico d um fio d comprimno prcorrido por um corrn léric num pono P(,,. dl - r + + r dl d P(,, r r + + ( ( r r + + r r
Elromgnismo Prof. Dr. Cláudio S. Srori - CPÍTUO V Ercícios Emplo Cálculo do cmpo mgnéico d um fio d comprimno prcorrido por um corrn léric num pono P(,,. dl - r + + r dl d P(,, r r + + ( ( r r + + r r
Dualidade. Fernando Nogueira Dualidade 1
 Dldd Frnndo Nogr Dldd Todo prolm d P.L. pod sr ssttído por m modlo qvlnt dnomndo Dl. O modlo orgnl é chmdo Prml. Prolm Prml M Sjto j n j n c j j j j j j {... n} {... m} Prolm Dl Sjto W m m j c {... m}
Dldd Frnndo Nogr Dldd Todo prolm d P.L. pod sr ssttído por m modlo qvlnt dnomndo Dl. O modlo orgnl é chmdo Prml. Prolm Prml M Sjto j n j n c j j j j j j {... n} {... m} Prolm Dl Sjto W m m j c {... m}
Universidade Federal do Rio de Janeiro COPPE Programa de Engenharia Química 2014/1 1
 Univrsidd Fdrl do Rio d Jniro COPPE Progrm d Engnhri Químic COQ 79 ANÁLISE DE SISEMAS DA ENGENHARIA QUÍMICA AULA : Rprsnção m Espço d Esdos 4/ Rprsnção m Espço d Esdos Esdo: O sdo d um sism no mpo é o
Univrsidd Fdrl do Rio d Jniro COPPE Progrm d Engnhri Químic COQ 79 ANÁLISE DE SISEMAS DA ENGENHARIA QUÍMICA AULA : Rprsnção m Espço d Esdos 4/ Rprsnção m Espço d Esdos Esdo: O sdo d um sism no mpo é o
O Uso da Álgebra Linear nas Equações Diferenciais
 Uso d Álgr ir s Equçõs ifriis íi Gri ol úi Rsd rir Bofim Fuldd d mái FT Uivrsidd Fdrl d Urlâdi UFU 88 - Urlâdi ril d 8 Rsumo Álgr ir é um supor mmáio pr muis árs d iêi Vrmos omo lgus d sus rsuldos podm
Uso d Álgr ir s Equçõs ifriis íi Gri ol úi Rsd rir Bofim Fuldd d mái FT Uivrsidd Fdrl d Urlâdi UFU 88 - Urlâdi ril d 8 Rsumo Álgr ir é um supor mmáio pr muis árs d iêi Vrmos omo lgus d sus rsuldos podm
8 = 1 GRUPO II. = x. 1 ln x
 Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim
Tst Itrmédio Mtmátic A Rsolução (Vrsão ) Durção do Tst: 90 miutos 0.04.04.º Ao d Escolridd RESOLUÇÃO GRUPO I. Rspost (A) Tm-s: log^00h log00 + log + 04 06. Rspost (B) S c + m ou s +, tm-s lim. Como lim
Messinki PUSERRUSLIITIN EM 10 MM PUSERRUSLIITIN EM 12 MM PUSERRUSLIITIN EM 15 MM PUSERRUSLIITIN EM 18 MM PUSERRUSLIITIN EM 22 MM
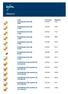 Messinki Tuote LVI-numero Pikakoodi PUSERRUSLIITIN EM 1551002 XV87 PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM 35 MM 10X
Messinki Tuote LVI-numero Pikakoodi PUSERRUSLIITIN EM 1551002 XV87 PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM PUSERRUSLIITIN EM 35 MM 10X
MESTRADO INTEGRADO EM ENGENHARIA INFORMÁTICA E COMPUTAÇÃO EIC0011 MATEMÁTICA DISCRETA
 1. Tm 40 livros irnts qu vi gurr m 4 ixs ors irnts, olono 10 livros m ix.. Qunts possiilis tm istriuir os livros pls ixs irnts? Justiiqu.. Suponh gor qu tinh 60 livros. Qunts possiilis pr os olor ns 4
1. Tm 40 livros irnts qu vi gurr m 4 ixs ors irnts, olono 10 livros m ix.. Qunts possiilis tm istriuir os livros pls ixs irnts? Justiiqu.. Suponh gor qu tinh 60 livros. Qunts possiilis pr os olor ns 4
MONTAGEM DO SISTEMA GLOBAL
 PMR 0 Mân Comptonl MOGEM DO SISEM GLOBL nts do sstm glol sr montdo dv-s stlr m sqm d nmrção glol pr spr topolog do sstm. tl o dn ontvdd dos lmntos d mlh d gr d págn 55. Como trt-s d m so ndmnsonl o sqm
PMR 0 Mân Comptonl MOGEM DO SISEM GLOBL nts do sstm glol sr montdo dv-s stlr m sqm d nmrção glol pr spr topolog do sstm. tl o dn ontvdd dos lmntos d mlh d gr d págn 55. Como trt-s d m so ndmnsonl o sqm
Hans Staden Luiz Antonio Aguiar PROJETO DE LEITURA. O autor. Romance histórico. Ficha Autor: Quadro sinóptico
 Hs S Lz r J L r Lz r s 9, Jr. sr Lrr rslr, l -J, s sr lr lr sss, é rss rs lrárs, rr, rr, só Lr slr rl r fs rçã rçã lrár. rl r rrs sórs qrs ár l rk. s íls ls vrss rês ss lvrs, lsv J lr íl f- l Jvl, 99,
Hs S Lz r J L r Lz r s 9, Jr. sr Lrr rslr, l -J, s sr lr lr sss, é rss rs lrárs, rr, rr, só Lr slr rl r fs rçã rçã lrár. rl r rrs sórs qrs ár l rk. s íls ls vrss rês ss lvrs, lsv J lr íl f- l Jvl, 99,
DIAGRAMA DE INTERLIGAÇÃO DE AUTOMAÇÃO NESS P2 COM SENSORES NESS P2 SEM SENSORES
 0 QUIPMTOS OTROLOS OMPRSSOR PRUSO IRM ITRLIÇÃO UTOMÇÃO 0.0.. SS P OM SSORS 0.0..0 SS P SM SSORS /0/ ILUSÃO O MOLO SM SSORS 0/0/ LTRÇÃO MR O TRSUTOR ORRT URO URO /0/ RVISÃO S IMSÕS O LYOUT /0/ LTRÇÃO O
0 QUIPMTOS OTROLOS OMPRSSOR PRUSO IRM ITRLIÇÃO UTOMÇÃO 0.0.. SS P OM SSORS 0.0..0 SS P SM SSORS /0/ ILUSÃO O MOLO SM SSORS 0/0/ LTRÇÃO MR O TRSUTOR ORRT URO URO /0/ RVISÃO S IMSÕS O LYOUT /0/ LTRÇÃO O
Integrais. A integral indefinida de uma função f(t) é representada como. Por outro lado, a integral definida, representada como
 J. A. M. Flipp d Soz Igris (rsmo l) Igris A igrl idfiid d m fção f() é rprsd como f ( τ) Por oro ldo, igrl dfiid, rprsd como f ( τ), f ( τ) τ o f ( τ) dτ 3 d fz Som d Rim q clcl ár so crv m m irvlo m dfiido
J. A. M. Flipp d Soz Igris (rsmo l) Igris A igrl idfiid d m fção f() é rprsd como f ( τ) Por oro ldo, igrl dfiid, rprsd como f ( τ), f ( τ) τ o f ( τ) dτ 3 d fz Som d Rim q clcl ár so crv m m irvlo m dfiido
Sobre a obra: Sobre nós:
 Sobre a obra: A presente obra é disponibilizada pela equipe do ebook espírita com o objetivo de oferecer conteúdo para uso parcial em pesquisas e estudos, bem como o simples teste da qualidade da obra,
Sobre a obra: A presente obra é disponibilizada pela equipe do ebook espírita com o objetivo de oferecer conteúdo para uso parcial em pesquisas e estudos, bem como o simples teste da qualidade da obra,
MOVIMENTOS SOB A AÇÃO DE UMA FORÇA RESULTANTE DE INTENSIDADE CONSTANTE
 MOVIMENTOS SOB A AÇÃO DE UMA ORÇA RESULTANTE DE INTENSIDADE CONSTANTE Trjóris Tmos os sguins csos: 1º) S forç rsuln ivr dirção d vlocidd só vrirá o módulo ds rjóri srá rilín. v R Ou R v º) S forç rsuln
MOVIMENTOS SOB A AÇÃO DE UMA ORÇA RESULTANTE DE INTENSIDADE CONSTANTE Trjóris Tmos os sguins csos: 1º) S forç rsuln ivr dirção d vlocidd só vrirá o módulo ds rjóri srá rilín. v R Ou R v º) S forç rsuln
Laplace para Problemas Setorialmente Homogêneos
 Trbho prdo o XXXVII CNMAC, S.J. do Cmpo - SP, 20 Prodg Sr of h Brz Soy of Compuo d Appd Mhm Té d Prção do Domío Apd Equção d Lp pr Probm Sorm Homogêo Cro Frdrh Loffr Progrm d Pó Grdução m Eghr M, PPGEM/UFES,
Trbho prdo o XXXVII CNMAC, S.J. do Cmpo - SP, 20 Prodg Sr of h Brz Soy of Compuo d Appd Mhm Té d Prção do Domío Apd Equção d Lp pr Probm Sorm Homogêo Cro Frdrh Loffr Progrm d Pó Grdução m Eghr M, PPGEM/UFES,
Revista Bioética ISSN: Conselho Federal de Medicina Brasil
 Revista Bioética ISSN: 1983-8042 bioetica@portalmedico.org.br Conselho Federal de Medicina Brasil de Pontes Regis, Arthur Henrique; Cornelli, Gabriele Situação jurídica dos animais e propostas de alterações
Revista Bioética ISSN: 1983-8042 bioetica@portalmedico.org.br Conselho Federal de Medicina Brasil de Pontes Regis, Arthur Henrique; Cornelli, Gabriele Situação jurídica dos animais e propostas de alterações
Adição dos antecedentes com os consequentes das duas razões
 Adição dos ntcdnts com os consqunts ds dus rzõs Osrv: 0 0 0 0, ou sj,, ou sj, 0 Otnh s trnsformds por mio d dição dos ntcdnts com os consqünts: ) ) ) 0 0 0 0 0 0 0 0 ) 0 0 0 0 ) 0 0 0 0 ) Osrv gor como
Adição dos ntcdnts com os consqunts ds dus rzõs Osrv: 0 0 0 0, ou sj,, ou sj, 0 Otnh s trnsformds por mio d dição dos ntcdnts com os consqünts: ) ) ) 0 0 0 0 0 0 0 0 ) 0 0 0 0 ) 0 0 0 0 ) Osrv gor como
CAPÍTULO 3. Exercícios é contínua, decrescente e k 2 positiva no intervalo [ 3, [. De ln x 1 para x 3, temos. dx 3.
 CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)
CAPÍTULO Exrcícios.. b) Sj séri. A fução f( x) é cotíu, dcrsct l x l x positiv o itrvlo [, [. D l x pr x, tmos dx dx. x l x x dx x covrgt Þ l x covrgt. l d) Sj séri 0 m [ 0, [. Tmos: x 4. A fução f( x)
EQUAÇÕES DIFERENCIAIS DE 2ª ORDEM:
 EQUÇÕES DIFERENCIIS DE ª ORDEM: Cofom dfção v m EDO d odm é m qção d fom F E fom é mo gl o o m ávl D modo q o gmo EDO om d odm f Com ê obd EDO d odm odmo q d odm m bm m dfí d olv Eo m d bl d EDO om d odm
EQUÇÕES DIFERENCIIS DE ª ORDEM: Cofom dfção v m EDO d odm é m qção d fom F E fom é mo gl o o m ávl D modo q o gmo EDO om d odm f Com ê obd EDO d odm odmo q d odm m bm m dfí d olv Eo m d bl d EDO om d odm
ESTE FORMULÁRIO É SOMENTE PARA CONSULTA. NÃO O UTILIZE COMO RASCUNHO.
 Uvrdd Tcológc drl do Prá DAMAT Dprmo Acdêmco d Mmác Dcpl: álculo Drcl grl 4 Proor: Rudmr u Nó ORMUÁRO ETE ORMUÁRO É OMENTE PARA ONUTA. NÃO O UTZE OMO RAUNHO.. ér d ourr/oc d ourr b co d b d co d. A orm
Uvrdd Tcológc drl do Prá DAMAT Dprmo Acdêmco d Mmác Dcpl: álculo Drcl grl 4 Proor: Rudmr u Nó ORMUÁRO ETE ORMUÁRO É OMENTE PARA ONUTA. NÃO O UTZE OMO RAUNHO.. ér d ourr/oc d ourr b co d b d co d. A orm
conjunto dos números inteiros. conjunto dos números que podem ser representados como quociente de números inteiros.
 Cpítulo I Noçõs Eltrs d Mtátic. Oprçõs co frcçõs, Equçõs Iquçõs Tipos d úros {,,,,,6, } cojuto dos úros turis. 0 { 0} {,,,, 0,,,, } cojuto dos úros itiros., 0 0 p : p, q q cojuto dos úros rciois ou frccioários,
Cpítulo I Noçõs Eltrs d Mtátic. Oprçõs co frcçõs, Equçõs Iquçõs Tipos d úros {,,,,,6, } cojuto dos úros turis. 0 { 0} {,,,, 0,,,, } cojuto dos úros itiros., 0 0 p : p, q q cojuto dos úros rciois ou frccioários,
VAGA VIVA 3 ESTRATÉGIA. GARAGEM (1º e 2ºpav) LUCAS PICCOLI WEINMANN. parking loft em Porto Alegre. Avenida Mauá. Rua General Câmara 02.
 Trss rso Loro Tr R rl âmr R sso o Nsmto R Sqr mpos 1:250 STUÇÃO TUL 20m PLNTÇÃO prk lot m Porto lr LOLZÇÃO 1 LUS POL WNNN Urs rl o Ro r o Sl Trlho olsão rso 2014.1 Ortor rt Pxoto Púlo pês Sls rm Lojs r
Trss rso Loro Tr R rl âmr R sso o Nsmto R Sqr mpos 1:250 STUÇÃO TUL 20m PLNTÇÃO prk lot m Porto lr LOLZÇÃO 1 LUS POL WNNN Urs rl o Ro r o Sl Trlho olsão rso 2014.1 Ortor rt Pxoto Púlo pês Sls rm Lojs r
Associação de Resistores e Resistência Equivalente
 Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos
Associção d sistors sistêci Equivlt. Itrodução A ális projto d circuitos rqurm m muitos csos dtrmição d rsistêci quivlt prtir d dois trmiis quisqur do circuito. Além disso, pod-s um séri d csos práticos
a x Solução a) Usando a Equação de Schrödinger h m
 www.fsc.com.br Consdr m rtícl d mss m confnd ntr os ontos / /, q od s movr lvrmnt nst rgão o longo do o. Son q s rds q lmtm st rgão sjm comltmnt mntrávs (oço d otncl nfnto ndmnsonl) rtícl stá sbmtd m otncl
www.fsc.com.br Consdr m rtícl d mss m confnd ntr os ontos / /, q od s movr lvrmnt nst rgão o longo do o. Son q s rds q lmtm st rgão sjm comltmnt mntrávs (oço d otncl nfnto ndmnsonl) rtícl stá sbmtd m otncl
Fernando Nogueira Dualidade 1
 Dldd Frnndo Nogr Dldd Todo problm d P.L. pod sr sbsttído por m modlo qvlnt dnomndo Dl. O modlo orgnl é chmdo Prml. Problm Prml j n j n c j j j j j j b {... n} {...m} Problm Dl Mn W m m b j c {... m} j
Dldd Frnndo Nogr Dldd Todo problm d P.L. pod sr sbsttído por m modlo qvlnt dnomndo Dl. O modlo orgnl é chmdo Prml. Problm Prml j n j n c j j j j j j b {... n} {...m} Problm Dl Mn W m m b j c {... m} j
ERROS ESTACIONÁRIOS. Controle em malha aberta. Controle em malha fechada. Diagrama completo. Análise de Erro Estacionário CONSTANTES DE ERRO
 ERROS ESTACIONÁRIOS Control Mlh Abrt Fhd Constnts d rro Tios d sistms Erros unitários Exmlo Control m mlh brt Ação bási, sm rlimntção A ntrd do ontroldor é um sinl d rrêni A síd do ontroldor é o sinl d
ERROS ESTACIONÁRIOS Control Mlh Abrt Fhd Constnts d rro Tios d sistms Erros unitários Exmlo Control m mlh brt Ação bási, sm rlimntção A ntrd do ontroldor é um sinl d rrêni A síd do ontroldor é o sinl d
Métodos Computacionais em Engenharia DCA0304 Capítulo 4
 Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d
Métodos Computciois m Eghri DCA34 Cpítulo 4 4 Solução d Equçõs Não-lirs 4 Técic d isolmto d rízs ris m poliômios Cosidrdo um poliômio d orm: P L Dsj-s cotrr os limits ds rízs ris dst poliômio Chmrmos d
TÉCNICAS DE INTEGRAÇÃO. 1.1 Integrais por Substituição Mudança de Variáveis
 UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis
UFP VIRTUL Liccitr m Mtmátic Distâci Discipli: álclo Difrcil Irl II Prof Jorg ost Drt Filho Ttor: Moisés Vi F d Olivir TÉNIS DE INTEGRÇÃO Técics d Irção Iris por Sbstitição Mdç d Vriávis Sjm f g fçõs tis
que indica que, através do operador H, pode-se determinar y(t) para qualquer u(t).
 8. REPRESENÇÃO NO ESPÇO DE ESDOS 8. Coco so ( prsção srá f o omío o mpo coío; s frçs com o cso scro são pqs srão prss posrorm). rprsção r/sí m ssm lr só é ál qo, o mpo cl, o ssm sá o so scoáro. ssm é ál
8. REPRESENÇÃO NO ESPÇO DE ESDOS 8. Coco so ( prsção srá f o omío o mpo coío; s frçs com o cso scro são pqs srão prss posrorm). rprsção r/sí m ssm lr só é ál qo, o mpo cl, o ssm sá o so scoáro. ssm é ál
BANCO DE FÓRMULAS PROF. FRED MOURA. Movimento Circular 1 T. a cp. = velocidade angular. = espaço angular. Unidades de medida
 O D ÓMUL O. D MOU MU & MU Moo ul Lço Oblíuo p = lo ul * opo l - MU y y y y y s y y y = lo é = ção spço = spço ul = o H s = Ilo po = üê * opo hozol - MU = spço (l) = píoo x os = spço Il = lo = lo l = lção
O D ÓMUL O. D MOU MU & MU Moo ul Lço Oblíuo p = lo ul * opo l - MU y y y y y s y y y = lo é = ção spço = spço ul = o H s = Ilo po = üê * opo hozol - MU = spço (l) = píoo x os = spço Il = lo = lo l = lção
!" # $$ " " '# " *+,!$%!-"( "%&'%"($ )%" !" #$% " &"% '(%&!" ) '%" *+( $&"% +"", -$. &) $% /.")" /
 !" # $$ "!" #$% " &"% '(%&!" ) '%" *+( $&"% +"", -$. &) $% /.")" #%"0&"#"1$!"%"2&% 3 "%&'%"($ )%" " '# " *+,!$%!-"( /4 56673 Livros Grátis http://www.livrosgratis.com.br Milhares de livros grátis para
!" # $$ "!" #$% " &"% '(%&!" ) '%" *+( $&"% +"", -$. &) $% /.")" #%"0&"#"1$!"%"2&% 3 "%&'%"($ )%" " '# " *+,!$%!-"( /4 56673 Livros Grátis http://www.livrosgratis.com.br Milhares de livros grátis para
09. Se. 10. Se. 12. Efetue: 13. Calcule C. a é:, determine a matriz X
 LIST DE EER MTRIZES E DETERMINNTES PROF ROGERINHO º ENSINO MÉDIO NOME Nº TURM Rrsn n for d l rz, co s, s, Dd rz, co, scrv rz (M O rço d u rz qudrd é so dos lnos d su dgonl rncl O rço d rz ) (, l qu é:
LIST DE EER MTRIZES E DETERMINNTES PROF ROGERINHO º ENSINO MÉDIO NOME Nº TURM Rrsn n for d l rz, co s, s, Dd rz, co, scrv rz (M O rço d u rz qudrd é so dos lnos d su dgonl rncl O rço d rz ) (, l qu é:
= 1, independente do valor de x, logo seria uma função afim e não exponencial.
 6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0
6. Função Eponncil É todo função qu pod sr scrit n form: f: R R + = Em qu é um númro rl tl qu 0
Problema do Caixeiro Viajante. Solução força bruta. Problema do Caixeiro Viajante. Projeto e Análise de Algoritmos. Problema do Caixeiro Viajante
 Projto Anális Aloritmos Prolm o Cixiro Vijnt Altirn Sors Silv Univrsi Frl o Amzons Instituto Computção Prolm o Cixiro Vijnt Um vim (tour) m um ro é um ilo qu pss por toos os vértis. Um vim é simpls quno
Projto Anális Aloritmos Prolm o Cixiro Vijnt Altirn Sors Silv Univrsi Frl o Amzons Instituto Computção Prolm o Cixiro Vijnt Um vim (tour) m um ro é um ilo qu pss por toos os vértis. Um vim é simpls quno
TÓPICOS. Melhor aproximação. Projecção num subespaço. Mínimo erro quadrático.
 Not m: litur dsts pontmntos não dispns d modo lgum litur tnt d iliogrfi principl d cdir Chm-s tnção pr importânci do trlho pssol rlizr plo luno rsolvndo os prolms prsntdos n iliogrfi, sm consult prévi
Not m: litur dsts pontmntos não dispns d modo lgum litur tnt d iliogrfi principl d cdir Chm-s tnção pr importânci do trlho pssol rlizr plo luno rsolvndo os prolms prsntdos n iliogrfi, sm consult prévi
1 Capítulo 2 Cálc l u c lo l I ntegra r l l em m R
 píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos
píulo álculo Ingrl m R píulo - álculo Ingrl SUMÁRIO rimiivs imdis ou qus-imdis rimiivção por prs por subsiuição rimiivção d unçõs rcionis Ingris órmul d Brrow ropridds do ingrl dinido Ingris prméricos
Abertura Celebração Coletiva Local: Pátio Central Oficina de Culinária Regiões do Brasil
 C ês I S C v ªF L D 12 Sb Púbc-Av C Esc T 51 6 EM EF EM Lv M-I 4 5 6 9 I M - I N3 N4 6 9 I T 71 7 EM 8 EM T 72 8 9 I 7 EM T 51 Ecçã If A 5 EF 2 Av/Pj Ab Cbçã Cv Lc: Pá C Ofic Cá Rõs Bs P Rflxõs - Rcs: c
C ês I S C v ªF L D 12 Sb Púbc-Av C Esc T 51 6 EM EF EM Lv M-I 4 5 6 9 I M - I N3 N4 6 9 I T 71 7 EM 8 EM T 72 8 9 I 7 EM T 51 Ecçã If A 5 EF 2 Av/Pj Ab Cbçã Cv Lc: Pá C Ofic Cá Rõs Bs P Rflxõs - Rcs: c
k 0 4 n NOTAS DE AULA A Integral Definida
 NOTS DE UL Itegrl Defd Som de Rem Teorem Fudmetl do Cálulo: Itegrl Defd Áre so um Curv [Eemplos e plções] Comprmeto de um Curv Pl Ls [ou Suve] Teorem do Vlor Médo pr Itegrs SOM DE RIEMNN Notção: k k Eemplos:
NOTS DE UL Itegrl Defd Som de Rem Teorem Fudmetl do Cálulo: Itegrl Defd Áre so um Curv [Eemplos e plções] Comprmeto de um Curv Pl Ls [ou Suve] Teorem do Vlor Médo pr Itegrs SOM DE RIEMNN Notção: k k Eemplos:
Formulação de Problemas 2D e 3D
 Formlção d Problms D D Mcâc Estrtrl (07/09/4) 0 Pdro V. Gmbo Dprtmto d Cêcs Arospcs . Itrodção A áls d lmtos ftos d problms bdmsos volv os msmos pssos báscos dos problms dmsos. A áls é m poco ms complcd
Formlção d Problms D D Mcâc Estrtrl (07/09/4) 0 Pdro V. Gmbo Dprtmto d Cêcs Arospcs . Itrodção A áls d lmtos ftos d problms bdmsos volv os msmos pssos báscos dos problms dmsos. A áls é m poco ms complcd
P PÓ P. P r r P P Ú P P. r ó s
 P PÓ P P r r P P Ú P P r ó s P r r P P Ú P P ss rt çã s t à rs r t t r rt s r q s t s r t çã r str ê t çã r t r r P r r Pr r r ó s Ficha de identificação da obra elaborada pelo autor, através do Programa
P PÓ P P r r P P Ú P P r ó s P r r P P Ú P P ss rt çã s t à rs r t t r rt s r q s t s r t çã r str ê t çã r t r r P r r Pr r r ó s Ficha de identificação da obra elaborada pelo autor, através do Programa
CARGA E DESCARGA DE CAPACITORES
 ARGA E DESARGA DE APAITORES O assuno dscudo ns argo, a carga a dscarga d capacors, aparcu dos anos conscuvos m vsbulars do Insuo Mlar d Engnhara ( 3). Ns sudo, srão mosradas as dduçõs das uaçõs d carga
ARGA E DESARGA DE APAITORES O assuno dscudo ns argo, a carga a dscarga d capacors, aparcu dos anos conscuvos m vsbulars do Insuo Mlar d Engnhara ( 3). Ns sudo, srão mosradas as dduçõs das uaçõs d carga
Primeira Prova de CTC-20 Estruturas Discretas 24/09/2009 Prof. Carlos Henrique Q. Forster
 Primir Prov CTC-0 Estruturs Disrts 4/09/009 Pro Crlos nriqu Q Forstr om: GABARITO 40 pontos Consir Z n { 0 n } Z é um grupo on é oprção ou-xlusivo Mostr qu oprção ou-xlusivo it--it m plvrs 3 its orm um
Primir Prov CTC-0 Estruturs Disrts 4/09/009 Pro Crlos nriqu Q Forstr om: GABARITO 40 pontos Consir Z n { 0 n } Z é um grupo on é oprção ou-xlusivo Mostr qu oprção ou-xlusivo it--it m plvrs 3 its orm um
tr EU H."i Ed <Ft En ,-t;dt.'j oa 5 F.> ?-.ES >.= ii EN -</9Fl _FU ca pla a- c)-e a-t- .Pi ce* ir. F. FT* te l^' ooo\ Q.a tr o^q Et C) slb Ca rr vti
 ?/ :; : 5 G VJ. iiu'. \..c G 3.;i.. f) \J + '= il 'i rl c pl _ ii >.= h:,;.'j e < n."i r r. 1! ' nr 9 ^^, r.!. l k J J l = r*r ( r f = 9 >,i r!.?. b r r &'= b 9 c l f l^' T*.i ir.. Gr
?/ :; : 5 G VJ. iiu'. \..c G 3.;i.. f) \J + '= il 'i rl c pl _ ii >.= h:,;.'j e < n."i r r. 1! ' nr 9 ^^, r.!. l k J J l = r*r ( r f = 9 >,i r!.?. b r r &'= b 9 c l f l^' T*.i ir.. Gr
Conceitos básicos População É constutuida por todos os elementos que são passíveis de ser analisados de tamanho N
 sísc Coceos áscos opulção É cosuud por odos os elemeos que são pssíves de ser lsdos de mho mosrgem Sucojuo d populção que é eecvmee lsdo com um ddo mho mosr leór mosr ode cd elemeo d populção êm hpóeses
sísc Coceos áscos opulção É cosuud por odos os elemeos que são pssíves de ser lsdos de mho mosrgem Sucojuo d populção que é eecvmee lsdo com um ddo mho mosr leór mosr ode cd elemeo d populção êm hpóeses
MECANISMOS DE REAÇÕES
 /4/7 MECSMS DE REÇÕES rof. Hrly. Mrins Filho Rçõs lmnrs Rçõs qu concm m pns um p são rçõs lmnrs. molculri rção lmnr é o númro moléculs qu rgm. Rção lmnr unimolculr: C molécul m um proili inrínsc s compor
/4/7 MECSMS DE REÇÕES rof. Hrly. Mrins Filho Rçõs lmnrs Rçõs qu concm m pns um p são rçõs lmnrs. molculri rção lmnr é o númro moléculs qu rgm. Rção lmnr unimolculr: C molécul m um proili inrínsc s compor
ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã str Pr ss t át r t çã tít st r t
 P P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã str Pr ss t át r t çã tít st r t Ficha catalográfica preparada pela Biblioteca Central da Universidade Federal de Viçosa - Câmpus Viçosa T B591e 2015
P P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã str Pr ss t át r t çã tít st r t Ficha catalográfica preparada pela Biblioteca Central da Universidade Federal de Viçosa - Câmpus Viçosa T B591e 2015
INTEGRAÇÃO NUMÉRICA. Em situações práticas, a função a ser integrada não é fornecida analiticamente, e sim por meio de pares (x, f(x)).
 NTEGRAÇÃ NUMÉRCA trodução Em stuçõs prátcs, ução sr tgrd ão é orcd ltcmt, sm por mo d prs,. Nsts csos tor-s cssár utlção d métodos umércos pr o cálculo do vlor d tgrl d. grupos: s métodos ms utldos podm
NTEGRAÇÃ NUMÉRCA trodução Em stuçõs prátcs, ução sr tgrd ão é orcd ltcmt, sm por mo d prs,. Nsts csos tor-s cssár utlção d métodos umércos pr o cálculo do vlor d tgrl d. grupos: s métodos ms utldos podm
Grafos. Luís Antunes. Grafos dirigidos. Grafos não dirigidos. Definição: Um grafo em que os ramos não são direccionados.
 Luís Antuns Grfos Grfo: G=(V,E): onjunto vértis/nós V um onjunto rmos/ros E VxV. Rprsntção visul: Grfos não irigios Dfinição: Um grfo m qu os rmos não são irionos. Grfos irigios Dfinição: Um grfo m qu
Luís Antuns Grfos Grfo: G=(V,E): onjunto vértis/nós V um onjunto rmos/ros E VxV. Rprsntção visul: Grfos não irigios Dfinição: Um grfo m qu os rmos não são irionos. Grfos irigios Dfinição: Um grfo m qu
O ESTADO DA ARTE DO MÉTODO DA DECOMPOSIÇÃO NA SOLUÇÃO DE PROBLEMAS DE CONDUÇÃO E RADIAÇÃO EM UMA PLACA
 5 Iol l Al Cof - IAC 5 So, S, Bzl, Ag 8 o S, 5 ASSOCIAÇÃO BRASILEIRA DE EERGIA UCLEAR - ABE ISB: 85-99--5 O ESADO DA ARE DO MÉODO DA DECOMOSIÇÃO A SOLUÇÃO DE ROBLEMAS DE CODUÇÃO E RADIAÇÃO EM UMA LACA
5 Iol l Al Cof - IAC 5 So, S, Bzl, Ag 8 o S, 5 ASSOCIAÇÃO BRASILEIRA DE EERGIA UCLEAR - ABE ISB: 85-99--5 O ESADO DA ARE DO MÉODO DA DECOMOSIÇÃO A SOLUÇÃO DE ROBLEMAS DE CODUÇÃO E RADIAÇÃO EM UMA LACA
CÁLCULO I 2º Semestre 2011/2012. Duração: 1 hora e 30 minutos
 NOVA SCHOOL OF BSINESS AND ECONOMICS CÁLCLO I º Smsr / TESTE INTERMÉDIO Tópi d rsolução Abril Duração: ora miuos Não é prmiido o uso d calculadoras. Não pod dsagraar as olas do uciado. Rspoda d orma jusiicada
NOVA SCHOOL OF BSINESS AND ECONOMICS CÁLCLO I º Smsr / TESTE INTERMÉDIO Tópi d rsolução Abril Duração: ora miuos Não é prmiido o uso d calculadoras. Não pod dsagraar as olas do uciado. Rspoda d orma jusiicada
4. Análise de Sistemas de Controle por Espaço de Estados
 Sisma para vrificação Lógica do Corolo Dzmro 3 4. ális d Sismas d Corol por Espaço d Esados No capiulo arior, vimos qu a formulação d um Prolma Básico d Corolo Ópimo Liar, ra cosidrado um sisma diâmico
Sisma para vrificação Lógica do Corolo Dzmro 3 4. ális d Sismas d Corol por Espaço d Esados No capiulo arior, vimos qu a formulação d um Prolma Básico d Corolo Ópimo Liar, ra cosidrado um sisma diâmico
Código PE-ACSH-2. Título:
 CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu
CISI Ctro Itrção Srvços Iformtc rão Excução Atv Itr o CISI Cóo Emto por: Grêc o Stor 1. Objtvo cmpo plcção Est ocumto tm como fl fr o prão brtur chmos suport o CISI. A brtur chmos é rlz o sstm hlpsk, qu
Sistemas Lineares Aplicações Veja a resolução no final
 Sstems Lneres Aplções Vej resolução no fnl (Fuvest-SP) Crlos e su rmã André form om seu horro Bdu à frmá de seu vô Lá enontrrm um velh lnç om defeto que só ndv orretmente pesos superores kg Assm eles se
Sstems Lneres Aplções Vej resolução no fnl (Fuvest-SP) Crlos e su rmã André form om seu horro Bdu à frmá de seu vô Lá enontrrm um velh lnç om defeto que só ndv orretmente pesos superores kg Assm eles se
Algumas considerações iniciais:
 Progrm d álulo d otmzção do n d ntrd íd do oltor olr trvé d orrlçõ r rd d rg m lnh lzd. lgum ondrçõ n: Condçõ d orção do fludo: t modlção não v lvr m ont vrçõ d tmrtur ud lo trto l borção do lor rovnnt
Progrm d álulo d otmzção do n d ntrd íd do oltor olr trvé d orrlçõ r rd d rg m lnh lzd. lgum ondrçõ n: Condçõ d orção do fludo: t modlção não v lvr m ont vrçõ d tmrtur ud lo trto l borção do lor rovnnt
c=mr cloj=klk=ttmjntov^
 c=mr cloj=klk=ttmjntov^ bهضنلëـ cê~ه ~لë aةىيëإـ kةاةêن~هاë fي~نل~هç bëé~ çن pîةهëâ~ a~هëâ kçêëâ pىçمل mçêيىضىئë إëëçيéêـ Magyar Polski esky Slovensky Românete Slovensko Hrvatski Srpski P cc ه¼ ½و apc
c=mr cloj=klk=ttmjntov^ bهضنلëـ cê~ه ~لë aةىيëإـ kةاةêن~هاë fي~نل~هç bëé~ çن pîةهëâ~ a~هëâ kçêëâ pىçمل mçêيىضىئë إëëçيéêـ Magyar Polski esky Slovensky Românete Slovensko Hrvatski Srpski P cc ه¼ ½و apc
c.c. É a função que associa a cada x X(S) um número f(x) que deve satisfazer as seguintes propriedades:
 Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj um vriávl ltóri com conjunto d vlors (S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. É função qu ssoci
Prof. Lorí Vili, Dr. vili@mt.ufrgs.r http://www.mt.ufrgs.r/~vili/ Sj um vriávl ltóri com conjunto d vlors (S). S o conjunto d vlors for infinito não numrávl ntão vriávl é dit contínu. É função qu ssoci
Lista de Exercícios 9 Grafos
 UFMG/ICEx/DCC DCC111 Mtmáti Disrt List Exríios 9 Gros Ciênis Exts & Engnhris 1 o Smstr 2018 1. O gro intrsção um olção onjuntos A 1, A 2,..., A n é o gro qu tm um vérti pr um os onjuntos olção tm um rst
UFMG/ICEx/DCC DCC111 Mtmáti Disrt List Exríios 9 Gros Ciênis Exts & Engnhris 1 o Smstr 2018 1. O gro intrsção um olção onjuntos A 1, A 2,..., A n é o gro qu tm um vérti pr um os onjuntos olção tm um rst
4.21 EXERCÍCIOS pg. 176
 78 EXERCÍCIOS pg 7 Nos rcícios d clculr s drivds sucssivs t ordm idicd, 5 7 IV V 7 c d c, 5, 8 IV V VI 8 8 ( 7) ( 8), ( ) ( ) '' ( ) ( ) ( ) ( ) 79 5, 5 8 IV, 8 7, IV 8 l, 9 s, 7 8 cos IV V VI VII 5 s
78 EXERCÍCIOS pg 7 Nos rcícios d clculr s drivds sucssivs t ordm idicd, 5 7 IV V 7 c d c, 5, 8 IV V VI 8 8 ( 7) ( 8), ( ) ( ) '' ( ) ( ) ( ) ( ) 79 5, 5 8 IV, 8 7, IV 8 l, 9 s, 7 8 cos IV V VI VII 5 s
Ô P Ó P P. ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã str Pr ss t át r t çã tít st r t
 Ô P Ó P P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã str Pr ss t át r t çã tít st r t 11/6/2015 FichaCatalografica :: Fichacatalografica Ficha catalográfica preparada pela Biblioteca Central da
Ô P Ó P P ss rt çã r s t à rs r ç s rt s 1 ê s Pr r Pós r çã str Pr ss t át r t çã tít st r t 11/6/2015 FichaCatalografica :: Fichacatalografica Ficha catalográfica preparada pela Biblioteca Central da
ESTIMATIVA: é o valor numérico obtido para o estimador numa certa amostra.
 I- STIMAÇÃO D PARÂMTROS 9 INTRODUÇÃO: Sj,,, um mostr ltór com fução (dsdd d proldd cohcd, sj d θ um vtor dos prâmtros dst vrávl ltór Assm θ {θ, θ,, θ k } os k prâmtros qu chmmos d spço d prâmtros dotdo
I- STIMAÇÃO D PARÂMTROS 9 INTRODUÇÃO: Sj,,, um mostr ltór com fução (dsdd d proldd cohcd, sj d θ um vtor dos prâmtros dst vrávl ltór Assm θ {θ, θ,, θ k } os k prâmtros qu chmmos d spço d prâmtros dotdo
ELECTROMAGNETISMO. TESTE 1 17 de Abril de 2010 RESOLUÇÕES. campo eléctrico apontam ambas para a esquerda, logo E 0.
 LTROMAGNTIMO TT 7 d Ail d 00 ROLUÇÕ Ao longo do io dos yy, o vcto cmpo léctico é pllo o io dos pont p squd Isto dv-s o fcto qu qulqu ponto no io dos yy stá quidistnt d dus ptículs cujs cgs são iguis m
LTROMAGNTIMO TT 7 d Ail d 00 ROLUÇÕ Ao longo do io dos yy, o vcto cmpo léctico é pllo o io dos pont p squd Isto dv-s o fcto qu qulqu ponto no io dos yy stá quidistnt d dus ptículs cujs cgs são iguis m
Uniforme Exponencial Normal Gama Weibull Lognormal. t (Student) χ 2 (Qui-quadrado) F (Snedekor)
 Prof. Lorí Vili, Dr. vili@pucrs.br vili@m.ufrgs.br hp://www.pucrs.br/fm/vili/ hp://www.m.ufrgs.br/~vili/ Uniform Exponncil Norml Gm Wibull Lognorml (Sudn) χ (Qui-qudrdo) F (Sndkor) Um VAC X é uniform no
Prof. Lorí Vili, Dr. vili@pucrs.br vili@m.ufrgs.br hp://www.pucrs.br/fm/vili/ hp://www.m.ufrgs.br/~vili/ Uniform Exponncil Norml Gm Wibull Lognorml (Sudn) χ (Qui-qudrdo) F (Sndkor) Um VAC X é uniform no
Hymnarium von Mestre Irineu. O Cruzeirinho
 Hymnrium von O ruzeirinho Prtituren RINH O MR - 2009 iretion: Mrco rcie Imperil Prtituren: isele rcie Imperil irigenten: Mestro nés Romno e isele rcie Imperil www.ceflupedrmr.org 117. ou Viv À eus Ns lturs
Hymnrium von O ruzeirinho Prtituren RINH O MR - 2009 iretion: Mrco rcie Imperil Prtituren: isele rcie Imperil irigenten: Mestro nés Romno e isele rcie Imperil www.ceflupedrmr.org 117. ou Viv À eus Ns lturs
Mackenzie Voluntario. Caro apoiador, Redes sociais: 8668 de 30/11/1981), que atua em solo brasileiro há 141 anos.
 C, O Mkz Vlá é m j sl Mkz, sm fs lvs (D º 8668 3/11/1981), q m sl bsl há 141 s. Iml m 24, m m l fl ssblz, mblz g s s ss gs, gss, lbs, fsss, ls, gs ls, fs, s, mgs fmls m mvm xmçã s ms q bgm s ss m, lém
C, O Mkz Vlá é m j sl Mkz, sm fs lvs (D º 8668 3/11/1981), q m sl bsl há 141 s. Iml m 24, m m l fl ssblz, mblz g s s ss gs, gss, lbs, fsss, ls, gs ls, fs, s, mgs fmls m mvm xmçã s ms q bgm s ss m, lém
Análise de Sistemas no Espaço de Estados
 MEE Mrdo m Engnhr Elcroécnc d ompdor MSD Modlção onrolo d Sm Dnâmco Ercíco d nál d Sm no Epço d Edo onjno d rcíco lordo plo docn Joé Tnrro Mchdo JTM, Mnl Sno Sl MSS, Víor odrg d nh V Jorg Erl d Sl JES.
MEE Mrdo m Engnhr Elcroécnc d ompdor MSD Modlção onrolo d Sm Dnâmco Ercíco d nál d Sm no Epço d Edo onjno d rcíco lordo plo docn Joé Tnrro Mchdo JTM, Mnl Sno Sl MSS, Víor odrg d nh V Jorg Erl d Sl JES.
Eu sou feliz, tu és feliz CD Liturgia II (Caderno de partituras) Coordenação: Ir. Miria T. Kolling
 Eu su iz, s iz Lirgi II (drn d prtirs) rdnçã: Ir. Miri T. King 1) Eu su iz, s iz (brr) & # #2 4. _ k.... k. 1 Eu su "Eu su iz, s iz!" ( "Lirgi II" Puus) iz, s _ iz, & # º #.. b... _ k _. Em cm Pi n cn
Eu su iz, s iz Lirgi II (drn d prtirs) rdnçã: Ir. Miri T. King 1) Eu su iz, s iz (brr) & # #2 4. _ k.... k. 1 Eu su "Eu su iz, s iz!" ( "Lirgi II" Puus) iz, s _ iz, & # º #.. b... _ k _. Em cm Pi n cn
PMR Mecânica Computacional para Mecatrônica. Elemento Isoparamétrico de 4 nós
 PMR3 - Mcâca opacoal para Mcarôca Elo Isoparaérco d ós osdros cal a fção rpoladora para lo raglar osrado a fgra: 3 sdo a arál d sado os cofcs as arás dpds. osdrado os alors dssa fção os ós do râglo os:
PMR3 - Mcâca opacoal para Mcarôca Elo Isoparaérco d ós osdros cal a fção rpoladora para lo raglar osrado a fgra: 3 sdo a arál d sado os cofcs as arás dpds. osdrado os alors dssa fção os ós do râglo os:
Folhas de Cálculo. O EXCEL como Folha de Cálculo
 Flh d Clul O qu é: U Flh d Clul é, dç, u ju d élul qu u glh u bl qu d l- vé d xõ lóg /u O qu : Ogzç ç d bl l d vl; F, í,, qu jud xu lul lx; Auzç d, vé d gç u d ódg d lul u d uld; Rç g d ç; d bl ulzd çõ
Flh d Clul O qu é: U Flh d Clul é, dç, u ju d élul qu u glh u bl qu d l- vé d xõ lóg /u O qu : Ogzç ç d bl l d vl; F, í,, qu jud xu lul lx; Auzç d, vé d gç u d ódg d lul u d uld; Rç g d ç; d bl ulzd çõ
9. MODELAGEM DE CONVERSORES: MODELO DA CHAVE PWM
 Fns Chs C. 9 Mlgm nrsrs: ml h PWM J. A. Pml 9. MOEAGEM E CONERSORES: MOEO A CHAE PWM As lgs báss nrsrs CCCC ssum um h nrl ur nãnrl sss lmns lnrs nrns n m. A njun ss us hs r nm h PWM [9.]. O bj ns íul é
Fns Chs C. 9 Mlgm nrsrs: ml h PWM J. A. Pml 9. MOEAGEM E CONERSORES: MOEO A CHAE PWM As lgs báss nrsrs CCCC ssum um h nrl ur nãnrl sss lmns lnrs nrns n m. A njun ss us hs r nm h PWM [9.]. O bj ns íul é
Aulas práticas: Introdução à álgebra geométrica
 Auls prátics: Introdução à álgr gométric Prolm Mostr qu ár A do prllogrmo d figur nx é dd por A= = αβ αβ y β α α β β A = αβ αβ α x α β = α + α, = β + β = = αβ + αβ = = ( αβ αβ)( ) = + = = 0 = = = 0 = Prolm
Auls prátics: Introdução à álgr gométric Prolm Mostr qu ár A do prllogrmo d figur nx é dd por A= = αβ αβ y β α α β β A = αβ αβ α x α β = α + α, = β + β = = αβ + αβ = = ( αβ αβ)( ) = + = = 0 = = = 0 = Prolm
Correção da fuvest ª fase - Matemática feita pelo Intergraus
 da fuvest 009 ª fase - Matemática 08.0.009 MATEMÁTIA Q.0 Na figura ao lado, a reta r tem equação y x no plano cartesiano Oxy. Além dis so, os pontos 0,,, estão na reta r, sendo 0 = (0,). Os pontos A 0,
da fuvest 009 ª fase - Matemática 08.0.009 MATEMÁTIA Q.0 Na figura ao lado, a reta r tem equação y x no plano cartesiano Oxy. Além dis so, os pontos 0,,, estão na reta r, sendo 0 = (0,). Os pontos A 0,
1 3Centrs e PP esq is II DD C n MM n Astr l i Astri C h i n Re. C h e H n g K n g F i n l n i I n i F rn 0 4 C n I n n si Al e m n h E st s U n i s I
 1 3Mr P e re s, R e s e r h D i re t r I D C B rs i l Br 0 0metr Cis e Bn L rg n Brsil, 2005-201 0 R e s l t s P ri m e i r T ri m e s t re e 2 0 0 7 Prer r Prer r Met e Bn Lrg em 2 0 1 0 n Brs i l : 10
1 3Mr P e re s, R e s e r h D i re t r I D C B rs i l Br 0 0metr Cis e Bn L rg n Brsil, 2005-201 0 R e s l t s P ri m e i r T ri m e s t re e 2 0 0 7 Prer r Prer r Met e Bn Lrg em 2 0 1 0 n Brs i l : 10
FACULDADES UNIFICADAS DA. Curso de Direito Escritório de Assistência Jurídica Registro OAB 6614 DA F UNDAÇ Ã O EDUCACIONAL DE B ARRETOS
 FACULDADES UNIFICADAS DA FUNDAÇÃO EDUCACIONAL DE BARRETOS Curso de Direito Escritório de Assistência Jurídica Registro OAB 6614 REGULAMENTO DO NÚ CLEO DE PRÁ TICA JURÍ DICA DA F UNDAÇ Ã O EDUCACIONAL DE
FACULDADES UNIFICADAS DA FUNDAÇÃO EDUCACIONAL DE BARRETOS Curso de Direito Escritório de Assistência Jurídica Registro OAB 6614 REGULAMENTO DO NÚ CLEO DE PRÁ TICA JURÍ DICA DA F UNDAÇ Ã O EDUCACIONAL DE
14º LEILÃO RR AGROPECUARIA
 14º LLÃO GOPCU 1 Z 3068 780 14/10/2014 32 20,35 2 38,5 MNDN M. VO D FO.V 2 Z 3792 652 15/12/2014 30 35,5 DONO D NV GKUS.DN N D V D U S 3 Z 3292 667 28/12/2014 30 18,02 4 35 DO S.MN LO D SS 4 Z 3302 699
14º LLÃO GOPCU 1 Z 3068 780 14/10/2014 32 20,35 2 38,5 MNDN M. VO D FO.V 2 Z 3792 652 15/12/2014 30 35,5 DONO D NV GKUS.DN N D V D U S 3 Z 3292 667 28/12/2014 30 18,02 4 35 DO S.MN LO D SS 4 Z 3302 699
Mecânica & Ondas. Módulo 10: O Oscilador harmónico. J. Seixas
 Mcânc & Onds Oscldor hrónco Spls Co ro Forçdo Oscldors copldos qução ds onds Módulo : O Oscldor hrónco J. Ss Prlnr: Poncs U forç dz - s consrv v s s u l qu du F d Por plo, grvdd é consrv v dgz F g F -
Mcânc & Onds Oscldor hrónco Spls Co ro Forçdo Oscldors copldos qução ds onds Módulo : O Oscldor hrónco J. Ss Prlnr: Poncs U forç dz - s consrv v s s u l qu du F d Por plo, grvdd é consrv v dgz F g F -
Como a x > 0 para todo x real, segue que: a x = y y 1. Sendo f -1 a inversa de f, tem-se que f -1 (y)= log a ( y y 1 )
 .(TA - 99 osidere s firmções: - Se f: é um fução pr e g: um fução qulquer, eão composição gof é um fução pr. - Se f: é um fução pr e g: um fução ímpr, eão composição fog é um fução pr. - Se f: é um fução
.(TA - 99 osidere s firmções: - Se f: é um fução pr e g: um fução qulquer, eão composição gof é um fução pr. - Se f: é um fução pr e g: um fução ímpr, eão composição fog é um fução pr. - Se f: é um fução
Princípios de Telecomunicações
 UNVERSDADE FEDERAL DE PERNAMBUO ro d cologi Gociêcis urso d Eghri Eléric Elrôic ODE Grupo d Psquis m omuicçõs Pricípios d lcomuicçõs élio MAGALÃES DE OLVERA, BEE, MEE, Docur, MEEE Lis d Exrcício 9 d Novmbro
UNVERSDADE FEDERAL DE PERNAMBUO ro d cologi Gociêcis urso d Eghri Eléric Elrôic ODE Grupo d Psquis m omuicçõs Pricípios d lcomuicçõs élio MAGALÃES DE OLVERA, BEE, MEE, Docur, MEEE Lis d Exrcício 9 d Novmbro
InBook. book. The. The inspiration by EGGER. n 01
 IBk Th Th p by EGGER bk 01 1 2 Th IBk by EGGER Bm-vd pm úm d IBk d Egg Dd mp, ddm- mph-v, vê, pf d çã, uv px vd d dg O mud ub fvlh d gd, d xpõ, d l: um lv d dg p db Avé d pm dçã, vhm p bv, mgulhm vgm,
IBk Th Th p by EGGER bk 01 1 2 Th IBk by EGGER Bm-vd pm úm d IBk d Egg Dd mp, ddm- mph-v, vê, pf d çã, uv px vd d dg O mud ub fvlh d gd, d xpõ, d l: um lv d dg p db Avé d pm dçã, vhm p bv, mgulhm vgm,
ANEXO II MODELO DE PROPOSTA
 Plnih01 ANEXO II MODELO DE PROPOSTA Lot Itm Dsrição Uni 1 2 3 4 5 Imprssão CARTAZ: Formto A4, 21x29,7 m, Ppl rilo, 120 g/m² Nº ors: 4/0 ors. Qunti Rgistrr: 6.000 Imprssão CARTAZ: Formto A4, 21x29,7 m Ppl
Plnih01 ANEXO II MODELO DE PROPOSTA Lot Itm Dsrição Uni 1 2 3 4 5 Imprssão CARTAZ: Formto A4, 21x29,7 m, Ppl rilo, 120 g/m² Nº ors: 4/0 ors. Qunti Rgistrr: 6.000 Imprssão CARTAZ: Formto A4, 21x29,7 m Ppl
Procedimento do U.S.HCM2010
 Eh Táo Poo o U.S.HM1 ál oo o, l (oo l o HM/1). íl ço o ção o ool zão /. íl ço /l ção o j (LoS So) V Tl 18-4,5 (HM1 ão l oo íl l ço o j é l ço lo áo) ál oção xl o oolo o EUA. o ção EMA, l à çõ áoo. oo o
Eh Táo Poo o U.S.HM1 ál oo o, l (oo l o HM/1). íl ço o ção o ool zão /. íl ço /l ção o j (LoS So) V Tl 18-4,5 (HM1 ão l oo íl l ço o j é l ço lo áo) ál oção xl o oolo o EUA. o ção EMA, l à çõ áoo. oo o
0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:
![0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é: 0, não há reação!), sendo. =, a concentração de A em um tempo t [A] t é:](/thumbs/95/123353134.jpg) - Rção orm zro: Es ipo rção ão po sr lmr (., ão há rção!), so poro ipo ν, logo, mos qu, i Igrção, pr 4 ) (, cocrção m um mpo é: 5 6 7 Eq. () 8 (Nos mplos i supori qu ). 9 - Rçõs orm : S loci rção é rmi
- Rção orm zro: Es ipo rção ão po sr lmr (., ão há rção!), so poro ipo ν, logo, mos qu, i Igrção, pr 4 ) (, cocrção m um mpo é: 5 6 7 Eq. () 8 (Nos mplos i supori qu ). 9 - Rçõs orm : S loci rção é rmi
Problemas de Electromagnetismo e Óptica LEAN + MEAer
 Pobls d logniso Ópi AN MA 7 Ópi P 7 (Pobl 3 do píulo do livo nodução à Físi d Dis d Dus l) O spo d opinos d ond p luz visívl vi n d 4x -9 (viol) 75x -9 (vlho) n qu vlos vi fquêni d luz visívl? n 75x 4
Pobls d logniso Ópi AN MA 7 Ópi P 7 (Pobl 3 do píulo do livo nodução à Físi d Dis d Dus l) O spo d opinos d ond p luz visívl vi n d 4x -9 (viol) 75x -9 (vlho) n qu vlos vi fquêni d luz visívl? n 75x 4
MATEMÁTICA A - 12o Ano Funções - Teorema de Bolzano Propostas de resolução
 MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos
MATEMÁTICA A - o Ano Funçõs - Torm d Bolzno Proposts d rsolução Exrcícios d xms tsts intrmédios. Dtrminndo s coordnds dos pontos P Q, m função d são, rsptivmnt P (,h() ) = P Q (,h() ) ( = Q, ln() ), tmos
121,8 127,6 126,9 131,3. Sb Te I Xe 27,0 28,1 31,0 32,1 35,5 39,9 69,7 72,6 74,9 79,0 79,9 83, Ga Ge As Se Br Kr. In Sn 114,8 118,7.
 PRVA DE QUÍMICA º 2º 3º 4º 5º 6º 7º TABELA PERIÓDICA DS ELEMENTS (IA),0 3 Li 6,9 Na 23,0 9 K 39, 2 (IIA) 4 Be 9,0 2 Mg 24,3 3 (III B) 4 5 6 7 8 9 0 2 20 2 22 23 24 25 26 27 28 29 30 Ca Sc Ti V Cr Mn Fe
PRVA DE QUÍMICA º 2º 3º 4º 5º 6º 7º TABELA PERIÓDICA DS ELEMENTS (IA),0 3 Li 6,9 Na 23,0 9 K 39, 2 (IIA) 4 Be 9,0 2 Mg 24,3 3 (III B) 4 5 6 7 8 9 0 2 20 2 22 23 24 25 26 27 28 29 30 Ca Sc Ti V Cr Mn Fe
4.1 Definição e interpretação geométrica de integral definido. Somas de Darboux.
 Aálse Memá I - Ao Levo 006/007 4- Cálulo Iegrl emr 4. Defção e erpreção geomér de egrl defdo. Soms de Drou. Def.4.- Sej f() um fução oíu o ervlo [, ]. M e m o mámo e o mímo vlor d fução, respevmee. Se
Aálse Memá I - Ao Levo 006/007 4- Cálulo Iegrl emr 4. Defção e erpreção geomér de egrl defdo. Soms de Drou. Def.4.- Sej f() um fução oíu o ervlo [, ]. M e m o mámo e o mímo vlor d fução, respevmee. Se
Agrupamento de Escolas Drª Laura Ayres
 cár rª r yrs, Qrtr, lé tífc-místc êcs clgs 11º 1 r fs Vz 15 X X X X X X X 9405 2 r s más 16 X X X X X X X 11481 3 r chz rt 16 X X X X X X X 11596 4 árbr f mrl rrã 15 X X X X X X X 11597 5 c f ckhm rrs
cár rª r yrs, Qrtr, lé tífc-místc êcs clgs 11º 1 r fs Vz 15 X X X X X X X 9405 2 r s más 16 X X X X X X X 11481 3 r chz rt 16 X X X X X X X 11596 4 árbr f mrl rrã 15 X X X X X X X 11597 5 c f ckhm rrs
