Biofísica II FFCLRP USP Prof. Antônio Roque Aula 3
|
|
|
- Vitorino Maranhão Lima
- 6 Há anos
- Visualizações:
Transcrição
1 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Proessos de Difusão Vamos agora disutir algus proessos de difusão que são diretamete relevates para a difusão em élulas e através de membraas elulares. Proessos de Difusão Ivariates o Tempo Equilíbrio Por defiição, o equilíbrio o fluxo é zero e a oetração é idepedete do tempo: φ = 0 e (x,t) = (x). Neste aso, a lei de Fik os dá que: φ = D d ( x ) dx = 0 d ( x ) dt = 0 = ostate. (1) No equilíbrio a oetração é ostate, idepedete do tempo e do espaço. Note que dizer que o fluxo é zero ão implia que ão haja movimeto de partíulas. O importate aqui é que o fluxo total ou líquido seja zero. 1
2 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Estado Estaioário Em um regime estaioário, tato o fluxo omo a oetração são idepedetes do tempo, mas o fluxo (o fluxo líquido) ão é ulo. Nesta situação, a equação da otiuidade, dá: φ x = t, os φ x = 0 φ = ostate. (2) O fluxo líquido é ostate, idepedete do espaço e do tempo (mas ote que ão é ulo omo o aso do item aterior!). Neste aso, a lei de Fik pode ser esrita troado-se a derivada parial de em relação a x por uma derivada total, φ = D x = D d dx. (3) Esta equação pode ser itegrada e sua solução geral é φ ( x) = ( x0 ) ( x x0 ), D (4) 2
3 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 ode x 0 é uma ostate de itegração que dá o valor da oetração em algum poto de referêia defiido pelas odições de otoro do problema. Portato, em um regime estaioário o fluxo é ostate e a oetração é uma fução liear da distâia x, omo mostrado a figura abaixo. Um regime estaioário de difusão pode oorrer quado houver um grade reservatório de partíulas iteragido difusivamete om um sistema otedo pouas partíulas. 3
4 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Porém, um aso mais realista, tato o fluxo omo a oetração depedem do tempo e do espaço e somete a solução da equação de difusão pode os revelar omo eles se omportam. Proessos de Difusão Depedetes do Tempo O estudo das soluções da equação de difusão para situações depedetes do tempo está além do esopo deste urso. Porém, vamos apresetar a solução para um aso importate, a saber, o de uma fote potual de partíulas. Este aso orrespode a uma situação físia em que se oloam 0 moles/m 2 de partíulas a posição x = 0 em t = 0 (pese um pigo de tita aido sobre uma tigela om água). A solução da equação de difusão (equação 9 da aula 1) para este aso partiular e para t > 0 pode ser obtida pelo método de separação de variáveis (isto ão será feito aqui) dado: ( x, t) = 0 4πDt e x 2 4Dt, para t > 0. (5) Esta solução tem a forma espaial de uma distribuição gaussiaa etrada a origem (ompare om a equação 8 da aula 2). À medida 4
5 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 que o tempo aumeta, a distribuição fia mais e mais espalhada e a sua altura dimiui. A largura (medida pelo desvio padrão) da distribuição aumeta o tempo omo 2 Dt, mas a área abaixo da urva permaee ostate (pois o úmero de partíulas se oserva). Isto está ilustrado a figura abaixo à esquerda. Na figura da direita, vemos omo o valor de (x,t) se omporta o tempo para três posições fixas (diferetes da origem). Para ada posição o omportameto é qualitativamete o mesmo: a oetração omeça omo (x,0) = 0, aumeta para um valor máximo e etão deai se aproximado assitotiamete de um valor de equilíbrio (este deaimeto vai om t -1/2 ). 5
6 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Difusão através de Membraas Membraas Homogêeas Estado Estaioário Vamos omeçar estudado o regime estaioário de difusão de um soluto através de uma membraa homogêea. Vamos osiderar uma membraa que separa duas regiões, hamadas de iterior e exterior. A membraa tem espessura d e separa duas soluções que otém o soluto as oetrações i o iterior e e o exterior (veja a figura aima). 6
7 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 A oetração do soluto detro da membraa é (x) (ote que estamos supodo estado estaioário, portato ão há depedêia om t). Vamos supor que a membraa é homogêea e que o oefiiete de difusão do soluto através da membraa é D. O fluxo por difusão das partíulas do soluto através da membraa será idiado por φ. Como estamos supodo um regime estaioário, o fluxo φ das partíulas do soluto através da membraa é ostate e (x) obedee à equação (4), φ ( x) = ( x0 ) ( x x0 ). D (6) Fazedo x 0 = 0, temos: Apliado esta equação para x = d, φ ( x) = (0) x. D φ D ( d) (0) = d φ = d D d ( (0) ( )) (7). (8) Substituido este valor de φ em (7) obtemos, 7
8 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 ( x) x = (0) [ (0) ( d) ]. (9) d Esta equação expressa o omportameto da oetração de soluto o iterior da membraa em fução de dois parâmetros, (0) e (d). Estes são os valores da oetração as iterfaes etre a membraa e as soluções do lado iterior e do lado exterior, respetivamete (iterfaes membraa-solução). Numa iterfae membraa-solução, o soluto está distribuído de aordo om a sua solubilidade a membraa e o solvete. Vamos supor que o solvete é o mesmo dos dois lados da membraa, por exemplo, água. Neste aso, defie-se o oefiiete de partição membraa-solução para o soluto omo: (0) k = = i ( d). e (10) Este oefiiete mede a razão etre a oetração do soluto a membraa e a solução, uma situação de equilíbrio. Se k > 1, o soluto é mais solúvel a membraa do que a solução; se k < 1, o soluto é mais solúvel a solução do que a membraa. 8
9 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Por exemplo, omo se mede o oefiiete de partição para um dado soluto a iterfae água-óleo? Joga-se água, óleo e o soluto em um reipiete e agita-se. Depois de algum tempo, omo a água e o óleo são imisíveis, o óleo estará flutuado sobre a água (figura abaixo). O soluto estará distribuído pelos dois meios oforme seu oefiiete de partição água-óleo k. Se ele for mais solúvel o óleo, sua oetração o óleo será maior do que a água (figura da esquerda abaixo). Se ele for mais solúvel a água, sua oetração a água será maior do que o óleo (figura da direita abaixo). Em termos de k, a equação (9) pode ser reesrita omo ( x) [ ] i i e x = k k. (11) d Note que esta equação só exige o oheimeto das oetrações do soluto as soluções exterior e iterior ( i e e ) e do oefiiete de partição k. 9
10 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 A equação (11) permite uma aálise gráfia do omportameto de (x) através da membraa. O gráfio da figura abaixo foi ostruído i supodo que > e, de maeira que a oetração dimiui liearmete à medida que ruzamos a membraa do iterior para o exterior (se i < e, a oetração aumetaria liearmete). Se k = 1, a oetração é uma fução otíua de x para qualquer poto. Se k 1, a oetração é uma fução desotíua as iterfaes etre a membraa e a solução. Em termos do oefiiete de partição k, o fluxo (equação 8) pode ser esrito omo: φ = D k d i e ( ). (12) 10
11 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Defie-se a permeabilidade da membraa ao soluto, P, omo: P D d k =. (13) A permeabilidade é proporioal ao oefiiete de difusão e ao oefiiete de partição e iversamete proporioal à espessura da membraa. As dimesões de P são: [ P ] = [ D] [ d] = [ área] [ tempo] [ omprimeto ] = [ omprimeto ] [ tempo] ou seja, P tem dimesões de veloidade (por exemplo, m/s)., Em termos da permeabilidade P o fluxo estaioário através de uma membraa homogêea é desrito pela equação φ = P ( i e ). (14) Segudo esta equação, a direção do fluxo de soluto é para fora da membraa (φ > 0) se a oetração do soluto o iterior for maior do que a oetração o exterior. Na situação oposta, o fluxo é para detro da membraa (φ < 0). A equação (14) é algumas vezes hamada de lei de Fik para membraas, pois mostra que o fluxo por difusão através da 11
12 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 membraa oorre o setido otrário ao do gradiete de oetração. Um tipo de trasporte de partíulas ujo setido de movimeto é otrário ao do gradiete de oetração das partíulas é hamado de trasporte passivo. Portato, o fluxo por difusão através de uma membraa é passivo. Note que o fluxo de soluto é proporioal ao produto da difereça de oetração pela permeabilidade. Se P for grade, dizemos que a membraa é altamete permeável ao soluto. Se P for pequea, dizemos que a membraa é pouo permeável ao soluto. Já se P = 0, dizemos que a membraa é impermeável ao soluto. O aso P = 0 é possível quado k = 0 (o soluto ão é solúvel a membraa), ou quado D = 0 (o soluto ão pode se difudir pela membraa), ou quado ambos são ulos. 12
13 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Trasiete 1 Em geral, quado um soluto se difude através de uma membraa existe um período trasiete ates que o regime estaioário se estabeleça. No regime estaioário, sabemos que a oetração varia liearmete através da membraa, mas omo é o seu omportameto durate o período trasiete? Nesta seção, vamos prourar estimar o tempo de duração do período trasiete até que o estado estaioário seja atigido. Vamos supor que os valores da oetração o iterior e o exterior da membraa, i e e, permaeem ostates durate todo o proesso e que a forma iiial da fução (x,t) é arbitrária omo mostrado a figura abaixo. 1 Esta seção pode ser omitida uma primeira leitura. 13
14 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 O valor iiial de (x,t) é (x,0) e o valor estaioário, atigido após um logo tempo, é (x, ). As odições de otoro são: ( 0, t) = k em x = 0 e i ( d, t) = k em x = d (para t > 0). e Para obter a solução geral (x,t) para este problema, devemos resolver a equação de difusão sujeita às odições iiiais e de otoro impostas. Como a solução estaioária é uma fução liear em x, podemos esrever a solução geral a forma: t ( x, t) = ( x, ) ( x, t), + ode (x, ) é a ompoete estaioária, dada por (11), e t (x,t) é a ompoete trasiete da solução. Note que a solução estaioária já satisfaz as odições de otoro para x = 0 e x = d. Isto implia que a solução trasiete deve satisfazer as seguites odições de otoro: t t ( 0, t) = ( d, t) = 0 para t > 0. Portato, para resolver o problema preisamos eotrar uma fução t (x,t) que satisfaça: (i) a equação de difusão; (ii) as odições de otoro aima; e (iii) teha um valor iiial arbitrário dado por t (x,0) = (x) - (x, ). 14
15 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 Os métodos de solução da equação de difusão estão além dos propósitos deste urso (eles serão tratados os ursos de Físia Matemátia). Para ossos objetivos aqui, basta saber que uma solução da equação de difusão que satisfaça as odições de otoro impostas sobre t (x,t) é dada pelo produto de uma fução do tipo se px, p = lπ/d (l iteiro) om uma fução do tipo p D e 2 t. Isto é, uma solução geral da equação de difusão para este aso é dada por uma superposição de termos do tipo se 2 p Dt ( l x d) e π : ode t ( x, t) t τ l = al se( lπx d ) e, (15) l= d τ l = = p D l π D (16) Os oefiietes a l podem ser obtidos pela odição iiial t (,0) = x al se( lπ x d ), (17) l =1 15
16 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 que é a expasão em série de Fourier de t (x,0). A ompoete trasiete da oetração ao logo da membraa é dada por uma superposição de termos seoidais om amplitudes deaido expoeialmete o tempo (equação 15). As ompoetes om valores grades de l orrespodem a osilações om grades frequêias espaiais e ostates temporais τ l pequeas (que deaem rapidamete). Já as ompoetes om valores pequeos de l orrespodem a osilações de baixa frequêia espaial e deaimeto temporal leto (τ l grade). A ompoete de deaimeto mais leto é a de maior τ l, que oorre para l = 1. Ela é defiida omo, τ ee = d 2. π 2 D (18) Esta ompoete é hamada de ostate temporal (ou ostate de tempo) do estado estaioário, pois é ela que limita o tempo que a oetração leva para atigir o regime estaioário. Para uma membraa de espessura d = 10 m (típia de uma membraa elular) e para uma difusão om D = 10-5 m 2 /s (difusão de uma moléula pequea a água), τ ee 10 s. Este é um tempo muito urto, idiado que o trasiete que preede o regime de 16
17 Biofísia II FFCLRP USP Prof. Atôio Roque Aula 3 difusão de estado estaioário em uma membraa eleular é muito rápido, podedo ser desprezado a maioria das vezes. Mesmo que o valor de D fosse várias ordes de gradeza maior, aida assim o valor de τ ee seria pequeo para uma membraa de espessura da ordem de gradeza da membraa elular. 17
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br O PROBLEMA DA ÁREA O PROBLEMA DA ÁREA Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b,
ANÁLISE DE ONDAS ESTÁTICAS SOBRE UMA MOLA ESPIRAL TENSIONADA E UMA CORDA TENSIONADA.
 Meâia Osilações e odas Odas meâias ANÁLISE DE ONDAS ESTÁTICAS SOBRE UMA MOLA ESPIRAL TENSIONADA E UMA CORDA TENSIONADA. Geração de odas logitudiais estátias em uma mola espiral e de odas trasversais estátias
Meâia Osilações e odas Odas meâias ANÁLISE DE ONDAS ESTÁTICAS SOBRE UMA MOLA ESPIRAL TENSIONADA E UMA CORDA TENSIONADA. Geração de odas logitudiais estátias em uma mola espiral e de odas trasversais estátias
MATEMÁTICA QUESTÃO 1. Resolução. Resolução Primeira solução:
 (9) 35-0 www.eliteampias.om.br O ELITE RESOLVE IME 007 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO 3 0 Cosidere as matrizes A= e B =, e seja P uma matriz 3 0 iversível tal que B = P - AP. Sedo um úmero
(9) 35-0 www.eliteampias.om.br O ELITE RESOLVE IME 007 MATEMÁTICA - DISCURSIVAS MATEMÁTICA QUESTÃO 3 0 Cosidere as matrizes A= e B =, e seja P uma matriz 3 0 iversível tal que B = P - AP. Sedo um úmero
Guiamento da luz Guias de ondas metálicos
 Guiameto de luz 81 Guiameto da luz 15 15.1 Guias de odas metálios Neste apítulo vamos abordar, de maeira bastate breve, um dos mais importates ompoetes óptios existetes, o guia de odas eletromagétias.
Guiameto de luz 81 Guiameto da luz 15 15.1 Guias de odas metálios Neste apítulo vamos abordar, de maeira bastate breve, um dos mais importates ompoetes óptios existetes, o guia de odas eletromagétias.
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS
 4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
4. MEDIDAS DINÂMICAS CONCEITOS BÁSICOS Muitas vezes os experimetos requerem medidas de gradezas físicas que variam com o tempo. Para a correta medição destas gradezas, é ecessário cohecer as propriedades
objetivo Exercícios Meta da aula Pré-requisitos
 Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Exercícios A U L A 6 Meta da aula Aplicar o formalismo quâtico estudado as Aulas a 5 deste módulo à resolução de um cojuto de exercícios. objetivo Esperamos que, após o térmio desta aula, você teha cosolidado
Análise da Resposta de Sistemas à Excitação Harmônica. Resposta em Freqüência
 Aálise da Resposta de Sistemas à Exitação Harmôia. Resposta em Freqüêia 6 Aálise da Resposta de Sistemas à Exitação Harmôia. Resposta em Freqüêia INTRODUÇÃO Estudamos, até agora (Apostilas 4 e 5), a resposta
Aálise da Resposta de Sistemas à Exitação Harmôia. Resposta em Freqüêia 6 Aálise da Resposta de Sistemas à Exitação Harmôia. Resposta em Freqüêia INTRODUÇÃO Estudamos, até agora (Apostilas 4 e 5), a resposta
e seja P uma matriz invisível tal que B = P -1 AP. Sendo n um número natural,
 3 Cosidere as matrizes A 3 alule o determiate da matriz A e 0 B, e seja P uma matriz ivisível tal que B P - AP Sedo um úmero atural, 0 det A det A, tem-se: Como ( ) ( ) ( ) det A 3 3 Cosidere uma seqüêia
3 Cosidere as matrizes A 3 alule o determiate da matriz A e 0 B, e seja P uma matriz ivisível tal que B P - AP Sedo um úmero atural, 0 det A det A, tem-se: Como ( ) ( ) ( ) det A 3 3 Cosidere uma seqüêia
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
MATEMÁTICA II Profa. Dra. Amada Liz Pacífico Mafrim Perticarrari amada@fcav.uesp.br Ecotre a área da região que está sob a curva y = f x de a até b. S = x, y a x b, 0 y f x Isso sigifica que S, ilustrada
2.2. Séries de potências
 Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Capítulo 2 Séries de Potêcias 2.. Itrodução Série de potêcias é uma série ifiita de termos variáveis. Assim, a teoria desevolvida para séries ifiitas de termos costates pode ser estedida para a aálise
Sumário. 2 Índice Remissivo 11
 i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
i Sumário 1 Esperaça de uma Variável Aleatória 1 1.1 Variáveis aleatórias idepedetes........................... 1 1.2 Esperaça matemática................................. 1 1.3 Esperaça de uma Fução de
Lista de Exercícios #4 Assunto: Variáveis Aleatórias Contínuas
 . ANPEC 8 - Questão Seja x uma variável aleatória com fução desidade de probabilidade dada por: f(x) = x, para x f(x) =, caso cotrário. Podemos afirmar que: () E[x]=; () A mediaa de x é ; () A variâcia
. ANPEC 8 - Questão Seja x uma variável aleatória com fução desidade de probabilidade dada por: f(x) = x, para x f(x) =, caso cotrário. Podemos afirmar que: () E[x]=; () A mediaa de x é ; () A variâcia
FICHA DE TRABALHO DE FÍSICA E QUÍMICA A JANEIRO 2010
 FICHA DE TRABALHO DE FÍSICA E QUÍMICA A JANEIRO 00 APSA Nº4 º Ao de Esolaridade. Na figura está represetado o omportameto de um feixe lumioso ao iidir sobre três superfíies distitas, A, B e C... Idetifique
FICHA DE TRABALHO DE FÍSICA E QUÍMICA A JANEIRO 00 APSA Nº4 º Ao de Esolaridade. Na figura está represetado o omportameto de um feixe lumioso ao iidir sobre três superfíies distitas, A, B e C... Idetifique
PROVA DE FÍSICA 2º ANO - 1ª MENSAL - 3º TRIMESTRE TIPO A
 PROVA DE FÍSICA º ANO - ª MENSAL - º TRIMESTRE TIPO A 0) Aalise o esquema abaio e assiale V pa a(s) verdadeira(s) e F pa a(s) falsa(s) as afirmativas que o seguem. (V) O âgulo de iidêia é 45 ; o de refração,
PROVA DE FÍSICA º ANO - ª MENSAL - º TRIMESTRE TIPO A 0) Aalise o esquema abaio e assiale V pa a(s) verdadeira(s) e F pa a(s) falsa(s) as afirmativas que o seguem. (V) O âgulo de iidêia é 45 ; o de refração,
Secção 1. Introdução às equações diferenciais
 Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Secção. Itrodução às equações difereciais (Farlow: Sec..,.) Cosideremos um exemplo simples de um feómeo que pode ser descrito por uma equação diferecial. A velocidade de um corpo é defiida como o espaço
Equação Diferencial. Uma equação diferencial é uma expressão que relaciona uma função desconhecida (incógnita) y com suas derivadas.
 Equação Difereial Uma equação difereial é uma epressão que relaioa uma fução desoheida (iógita) om suas derivadas É útil lassifiar os diferetes tipos de equações para um desevolvimeto sistemátio da Teoria
Equação Difereial Uma equação difereial é uma epressão que relaioa uma fução desoheida (iógita) om suas derivadas É útil lassifiar os diferetes tipos de equações para um desevolvimeto sistemátio da Teoria
1ª Lista de Exercícios. 1. São dados 2n números distintos distribuídos em dois vetores com n elementos A e B ordenados de maneira tal que
 Uiversidade Federal de Mias Gerais Departameto de Ciêia da Computação Algoritmos e Estruturas de Dados II (Turmas M, N, W, F) 1º Semestre de 01 Profs. Camilo Oliveira, Gisele Pappa, Ítalo Cuha, Loï Cerf,
Uiversidade Federal de Mias Gerais Departameto de Ciêia da Computação Algoritmos e Estruturas de Dados II (Turmas M, N, W, F) 1º Semestre de 01 Profs. Camilo Oliveira, Gisele Pappa, Ítalo Cuha, Loï Cerf,
Transporte Iônico e o Potencial de Membrana
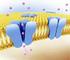 Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Trasporte Iôico e o Potecial de Membraa Até o mometo, cosideramos apeas o trasporte de solutos eutros (sem carga elétrica) através da membraa celular. A partir de agora, vamos passar a estudar o trasporte
Medidas, integração, Teorema da Convergência Monótona e o teorema de Riesz-Markov
 Medidas, itegração, Teorema da Covergêcia Moótoa e o teorema de Riesz-Markov 28 de Agosto de 2012 1 Defiições de Teoria da Medida Seja (Ω, F, ν) um espaço de medida: isto é, F é σ-álgebra sobre o cojuto
Medidas, itegração, Teorema da Covergêcia Moótoa e o teorema de Riesz-Markov 28 de Agosto de 2012 1 Defiições de Teoria da Medida Seja (Ω, F, ν) um espaço de medida: isto é, F é σ-álgebra sobre o cojuto
2 ESPECIFICAÇÃO DE MOTORES ELÉTRICOS 2.1 POTÊNCIA NOMINAL
 Módulo omado e roteção ESEIFIAÇÃO DE MOTORES ELÉTRIOS. OTÊIA OMIAL Quado deseja-se esolher um motor para aioar uma determiada arga, é preiso oheer o ojugado requerido pela arga e a rotação que esta arga
Módulo omado e roteção ESEIFIAÇÃO DE MOTORES ELÉTRIOS. OTÊIA OMIAL Quado deseja-se esolher um motor para aioar uma determiada arga, é preiso oheer o ojugado requerido pela arga e a rotação que esta arga
CÁLCULO I. Exibir o cálculo de algumas integrais utilizando a denição;
 CÁLCULO I Prof Edilso Neri Júior Prof Adré Almeida Aula o 9: A Itegral de Riema Objetivos da Aula Deir a itegral de Riema; Exibir o cálculo de algumas itegrais utilizado a deição; Apresetar fuções que
CÁLCULO I Prof Edilso Neri Júior Prof Adré Almeida Aula o 9: A Itegral de Riema Objetivos da Aula Deir a itegral de Riema; Exibir o cálculo de algumas itegrais utilizado a deição; Apresetar fuções que
Aula 5 Teorema central do limite & Aplicações
 Diâmica Estocástica Aula 5 Teorema cetral do limite & Aplicações Teorema cetral do limite Se x é tal que: x 0 e ( xv é fiita,,..., x x, x,...,, 3 x variáveis aleatórias idepedetes com a mesma distribuição
Diâmica Estocástica Aula 5 Teorema cetral do limite & Aplicações Teorema cetral do limite Se x é tal que: x 0 e ( xv é fiita,,..., x x, x,...,, 3 x variáveis aleatórias idepedetes com a mesma distribuição
binomial seria quase simétrica. Nestas condições será também melhor a aproximação pela distribuição normal.
 biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
biomial seria quase simétrica. Nestas codições será também melhor a aproximação pela distribuição ormal. Na prática, quado e p > 7, a distribuição ormal com parâmetros: µ p 99 σ p ( p) costitui uma boa
Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos. Análise de Algoritmos
 Aálise de Algoritmos Aálise de Algoritmos Prof Dr José Augusto Baraauskas DFM-FFCLRP-USP A Aálise de Algoritmos é um campo da Ciêcia da Computação que tem como objetivo o etedimeto da complexidade dos
Aálise de Algoritmos Aálise de Algoritmos Prof Dr José Augusto Baraauskas DFM-FFCLRP-USP A Aálise de Algoritmos é um campo da Ciêcia da Computação que tem como objetivo o etedimeto da complexidade dos
2. COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES
 CAPITULO II COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES Acreditamos que os coceitos de Combiação Liear (CL) e de Depedêcia Liear serão melhor etedidos se forem apresetados a partir de dois vetores
CAPITULO II COMBINAÇÃO LINEAR E DEPENDÊNCIA LINEAR DE VETORES Acreditamos que os coceitos de Combiação Liear (CL) e de Depedêcia Liear serão melhor etedidos se forem apresetados a partir de dois vetores
Universidade Federal Fluminense ICEx Volta Redonda Introdução a Matemática Superior Professora: Marina Sequeiros
 3. Poliômios Defiição: Um poliômio ou fução poliomial P, a variável x, é toda expressão do tipo: P(x)=a x + a x +... a x + ax + a0, ode IN, a i, i = 0,,..., são úmeros reais chamados coeficietes e as parcelas
3. Poliômios Defiição: Um poliômio ou fução poliomial P, a variável x, é toda expressão do tipo: P(x)=a x + a x +... a x + ax + a0, ode IN, a i, i = 0,,..., são úmeros reais chamados coeficietes e as parcelas
6.1 Estimativa de uma média populacional: grandes amostras. Definição: Um estimador é uma característica amostral (como a média amostral
 6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
6 ESTIMAÇÃO 6.1 Estimativa de uma média populacioal: grades amostras Defiição: Um estimador é uma característica amostral (como a média amostral x ) utilizada para obter uma aproximação de um parâmetro
DERIVADAS DE FUNÇÕES11
 DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
DERIVADAS DE FUNÇÕES11 Gil da Costa Marques Fudametos de Matemática I 11.1 O cálculo diferecial 11. Difereças 11.3 Taxa de variação média 11.4 Taxa de variação istatâea e potual 11.5 Primeiros exemplos
Universidade do Estado do Amazonas
 Uiversidade do Estado do Amazoas Professor Alessadro Moteiro 6 de Julho de 08 PROJETO DE EXTENSÃO Resoluções de Problemas de Aálise Real I 5º Ecotro/Parte I: Limites de Fuções 5. O Limite de uma Fução
Uiversidade do Estado do Amazoas Professor Alessadro Moteiro 6 de Julho de 08 PROJETO DE EXTENSÃO Resoluções de Problemas de Aálise Real I 5º Ecotro/Parte I: Limites de Fuções 5. O Limite de uma Fução
2- Resolução de Sistemas Não-lineares.
 MÉODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 2- Resolução de Sistemas Não-lieares. 2.- Método de Newto. 2.2- Método da Iteração. 2.3- Método do Gradiete. 2- Sistemas Não Lieares de Equações Cosidere
MÉODOS NUMÉRICOS PARA EQUAÇÕES DIFERENCIAIS PARCIAIS 2- Resolução de Sistemas Não-lieares. 2.- Método de Newto. 2.2- Método da Iteração. 2.3- Método do Gradiete. 2- Sistemas Não Lieares de Equações Cosidere
INFERÊNCIA ESTATÍSTICA: TESTE DE HIPÓTESES
 INFERÊNCIA ESTATÍSTICA: TESTE DE IPÓTESES 2 Teste de hipóteses Exemplo. Uma idústria adquire de um erto fabriate pios uja resistêia média à ruptura é espeifiada em 6 uid. (valor omial da espeifiação).
INFERÊNCIA ESTATÍSTICA: TESTE DE IPÓTESES 2 Teste de hipóteses Exemplo. Uma idústria adquire de um erto fabriate pios uja resistêia média à ruptura é espeifiada em 6 uid. (valor omial da espeifiação).
DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL. todas as repetições). Então, para todo o número positivo ξ, teremos:
 48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
48 DESIGUALDADES, LEIS LIMITE E TEOREMA DO LIMITE CENTRAL LEI DOS GRANDES NÚMEROS Pretede-se estudar o seguite problema: À medida que o úmero de repetições de uma experiêcia cresce, a frequêcia relativa
Análise Infinitesimal II LIMITES DE SUCESSÕES
 -. Calcule os seguites limites Aálise Ifiitesimal II LIMITES DE SUCESSÕES a) lim + ) b) lim 3 + 4 5 + 7 + c) lim + + ) d) lim 3 + 4 5 + 7 + e) lim + ) + 3 f) lim + 3 + ) g) lim + ) h) lim + 3 i) lim +
-. Calcule os seguites limites Aálise Ifiitesimal II LIMITES DE SUCESSÕES a) lim + ) b) lim 3 + 4 5 + 7 + c) lim + + ) d) lim 3 + 4 5 + 7 + e) lim + ) + 3 f) lim + 3 + ) g) lim + ) h) lim + 3 i) lim +
CCI-22 CCI-22. 5) Interpolação. Matemática Computacional
 CCI- CCI- atemátia Computaioal 5 Iterpolação Carlos Alerto Aloso Saes Poliômios iterpoladores, Formas de Lagrage, de Newto e de Newto-Gregory Itrodução Forma de Lagrage Forma de Newto CCI- Forma de Newto-Gregory
CCI- CCI- atemátia Computaioal 5 Iterpolação Carlos Alerto Aloso Saes Poliômios iterpoladores, Formas de Lagrage, de Newto e de Newto-Gregory Itrodução Forma de Lagrage Forma de Newto CCI- Forma de Newto-Gregory
Estacionariedade e correlação temporal em dados financeiros
 Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Estacioariedade e correlação temporal em dados fiaceiros Hoje em dia há uma quatidade imesa de dados fiaceiros sedo armazeados, egócio a egócio, pelo mudo afora. Gratuitamete, é possível coseguir facilmete
Capítulo VII: Soluções Numéricas de Equações Diferenciais Ordinárias
 Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo VII: Soluções Numéricas de Equações Difereciais Ordiárias 0. Itrodução Muitos feómeos as áreas das ciêcias egearias ecoomia etc. são modelados por equações difereciais. Supoa-se que se quer determiar
Métodos iterativos. Métodos Iterativos para Sistemas Lineares
 Métodos iterativos Métodos Iterativos para Sistemas Lieares Muitos sistemas lieares Ax = b são demasiado grades para serem resolvidos por métodos directos (por exemplo, se A é da ordem de 10000) á que
Métodos iterativos Métodos Iterativos para Sistemas Lieares Muitos sistemas lieares Ax = b são demasiado grades para serem resolvidos por métodos directos (por exemplo, se A é da ordem de 10000) á que
3. Seja C o conjunto dos números complexos. Defina a soma em C por
 Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Eercícios Espaços vetoriais. Cosidere os vetores = (8 ) e = ( -) em. (a) Ecotre o comprimeto de cada vetor. (b) Seja = +. Determie o comprimeto de. Qual a relação etre seu comprimeto e a soma dos comprimetos
Mestrado Integrado em Engenharia Civil. Disciplina: TRANSPORTES. Sessão Prática 4: Amostragem
 Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
Mestrado Itegrado em Egeharia Civil Disciplia: TRNSPORTES Prof. Resposável: José Mauel Viegas Sessão Prática 4: mostragem Istituto Superior Técico / Mestrado Itegrado Egª Civil Trasportes ulas Práticas
Distribuição Amostral da Média: Exemplos
 Distribuição Amostral da Média: Eemplos Talvez a aplicação mais simples da distribuição amostral da média seja o cálculo da probabilidade de uma amostra ter média detro de certa faia de valores. Vamos
Distribuição Amostral da Média: Eemplos Talvez a aplicação mais simples da distribuição amostral da média seja o cálculo da probabilidade de uma amostra ter média detro de certa faia de valores. Vamos
a = b n Vejamos alguns exemplos que nos permitem observar essas relações. = 4 4² = 16 radical radicando
 Caro aluo, Com o objetivo de esclarecer as dúvidas sobre a raiz quadrada, apresetamos este material a defiição de radiciação, o cálculo da raiz quadrada e algumas propriedades de radiciação. Além disso,
Caro aluo, Com o objetivo de esclarecer as dúvidas sobre a raiz quadrada, apresetamos este material a defiição de radiciação, o cálculo da raiz quadrada e algumas propriedades de radiciação. Além disso,
DETERMINANDO A SIGNIFICÂNCIA ESTATÍSTICA PARA AS DIFERENÇAS ENTRE MÉDIAS
 DTRMINANDO A SIGNIFIÂNIA STATÍSTIA PARA AS DIFRNÇAS NTR MÉDIAS Ferado Lag da Silveira Istituto de Física - UFRGS lag@if.ufrgs.br O objetivo desse texto é apresetar através de exemplos uméricos como se
DTRMINANDO A SIGNIFIÂNIA STATÍSTIA PARA AS DIFRNÇAS NTR MÉDIAS Ferado Lag da Silveira Istituto de Física - UFRGS lag@if.ufrgs.br O objetivo desse texto é apresetar através de exemplos uméricos como se
. Mas m 1 e Ftv (, ) , ou seja, ln v ln(1 t) ln c, com c 0 e
 CAPÍTULO 3 Eercícios 3 3 Seja a equação y y 0 B Como o Eercício ( item (e, yabl B y( Bl A 0 B B B B y(! y(! B 4 4 4 l A0! A( l A solução procurada é y ( l 4 l $ % 4 Pela ª Lei de Newto, m dv dt dv v dt
CAPÍTULO 3 Eercícios 3 3 Seja a equação y y 0 B Como o Eercício ( item (e, yabl B y( Bl A 0 B B B B y(! y(! B 4 4 4 l A0! A( l A solução procurada é y ( l 4 l $ % 4 Pela ª Lei de Newto, m dv dt dv v dt
S E Q U Ê N C I A S E L I M I T E S. Prof. Benito Frazão Pires. Uma sequência é uma lista ordenada de números
 S E Q U Ê N C I A S E L I M I T E S Prof. Beito Frazão Pires Uma sequêcia é uma lista ordeada de úmeros a, a 2,..., a,... ) deomiados termos da sequêcia: a é o primeiro termo, a 2 é o segudo termo e assim
S E Q U Ê N C I A S E L I M I T E S Prof. Beito Frazão Pires Uma sequêcia é uma lista ordeada de úmeros a, a 2,..., a,... ) deomiados termos da sequêcia: a é o primeiro termo, a 2 é o segudo termo e assim
Matemática. B) Determine a equação da reta que contém a diagonal BD. C) Encontre as coordenadas do ponto de interseção das diagonais AC e BD.
 Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
Matemática 0. Um losago do plao cartesiao oxy tem vértices A(0,0), B(,0), C(,) e D(,). A) Determie a equação da reta que cotém a diagoal AC. B) Determie a equação da reta que cotém a diagoal BD. C) Ecotre
1. Definição e conceitos básicos de equações diferenciais
 Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
Capítulo 7: Soluções Numéricas de Equações Difereciais Ordiárias. Itrodução Muitos feómeos as áreas das ciêcias, egearias, ecoomia, etc., são modelados por equações difereciais. Supoa-se que se quer determiar
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS
 UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
UMA INTRODUÇÃO À TEORIA DE PONTOS CRÍTICOS INTRODUÇÃO Carlos Herique Togo e Atôio Carlos Nogueira Hoje em dia, um dos mais produtivos e atraetes ramos da Matemática é a Teoria de Sigularidades A Teoria
Análise de Regressão Linear Múltipla I
 Aálise de Regressão Liear Múltipla I Aula 04 Gujarati e Porter, 0 Capítulos 7 e 0 tradução da 5ª ed. Heij et al., 004 Capítulo 3 Wooldridge, 0 Capítulo 3 tradução da 4ª ed. Itrodução Como pode ser visto
Aálise de Regressão Liear Múltipla I Aula 04 Gujarati e Porter, 0 Capítulos 7 e 0 tradução da 5ª ed. Heij et al., 004 Capítulo 3 Wooldridge, 0 Capítulo 3 tradução da 4ª ed. Itrodução Como pode ser visto
1- Resolução de Sistemas Lineares.
 MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
MÉTODOS NUMÉRICOS PR EQUÇÕES DIFERENCIIS PRCIIS 1- Resolução de Sistemas Lieares. 1.1- Matrizes e Vetores. 1.2- Resolução de Sistemas Lieares de Equações lgébricas por Métodos Exatos (Diretos). 1.3- Resolução
Eletromagnetismo II 1 o Semestre de 2007 Noturno - Prof. Alvaro Vannucci
 Eletromagetismo 1 o Semestre de 7 Noturo - Prof. Alvaro Vaucci 1 a aula 7/fev/7 ivros-texto: eitz-milford Griffiths Vamos relembrar as 4 equações básicas do Eletromagetismo 1 a ) ei de Gauss: O Fluxo do
Eletromagetismo 1 o Semestre de 7 Noturo - Prof. Alvaro Vaucci 1 a aula 7/fev/7 ivros-texto: eitz-milford Griffiths Vamos relembrar as 4 equações básicas do Eletromagetismo 1 a ) ei de Gauss: O Fluxo do
. Dessa forma, quanto menor o MSE, mais a imagem
 Uiversidade Federal de Perambuco CI / CCEN - Área II 1 o Exercício de Cálculo Numérico ( 18 / 06 / 2014 ) Aluo(a) 1- Questão 1 (2,5 potos) Cosidere uma imagem digital como uma matriz bidimesioal de dimesões
Uiversidade Federal de Perambuco CI / CCEN - Área II 1 o Exercício de Cálculo Numérico ( 18 / 06 / 2014 ) Aluo(a) 1- Questão 1 (2,5 potos) Cosidere uma imagem digital como uma matriz bidimesioal de dimesões
Dentro, a/2 < x < a/2: com: Ondas com a mesma amplitude nos 2 sentidos. Elas se combinam formando uma onda estacionária. Então podemos fazer A = B:
 Poços de potecial: E < V Detro a/ < < a/: ψ com: i i Ae + Be me p Odas com a mesma amplitude os setidos. Elas se combiam formado uma oda estacioária. Etão podemos fazer A B: ψ ψ i i + e B e Bʹ cos e Bʹ
Poços de potecial: E < V Detro a/ < < a/: ψ com: i i Ae + Be me p Odas com a mesma amplitude os setidos. Elas se combiam formado uma oda estacioária. Etão podemos fazer A B: ψ ψ i i + e B e Bʹ cos e Bʹ
Cap. VI Histogramas e Curvas de Distribuição
 TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
TLF /11 Capítulo VI Histogramas e curvas de distribuição 6.1. Distribuições e histogramas. 6 6.. Distribuição limite 63 6.3. Sigificado da distribuição limite: frequêcia esperada e probabilidade de um
Notas do Curso Inferência em Processos Estocásticos. 1 Estimação de máxima verossimilhança para cadeias de Markov de ordem k
 Notas do Curso Iferêcia em Processos Estocásticos Prof. Atoio Galves Trascrita por Karia Yuriko Yagiuma 1 Estimação de máxima verossimilhaça para cadeias de Markov de ordem k Seja (X ) =0,1,,... uma cadeia
Notas do Curso Iferêcia em Processos Estocásticos Prof. Atoio Galves Trascrita por Karia Yuriko Yagiuma 1 Estimação de máxima verossimilhaça para cadeias de Markov de ordem k Seja (X ) =0,1,,... uma cadeia
AULA Subespaço, Base e Dimensão Subespaço.
 Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Note bem: a leitura destes apotametos ão dispesa de modo algum a leitura ateta da bibliografia pricipal da cadeira TÓPICOS Subespaço. ALA Chama-se a ateção para a importâcia do trabalho pessoal a realizar
Cálculo II Sucessões de números reais revisões
 Ídice 1 Defiição e exemplos Cálculo II Sucessões de úmeros reais revisões Mestrado Itegrado em Egeharia Aeroáutica Mestrado Itegrado em Egeharia Civil Atóio Beto beto@ubi.pt Departameto de Matemática Uiversidade
Ídice 1 Defiição e exemplos Cálculo II Sucessões de úmeros reais revisões Mestrado Itegrado em Egeharia Aeroáutica Mestrado Itegrado em Egeharia Civil Atóio Beto beto@ubi.pt Departameto de Matemática Uiversidade
Matemática A Extensivo V. 6
 Matemática A Etesivo V. 6 Eercícios 0) B Reescrevedo a equação: 88 00 8 0 8 8 0 6 0 0 A raiz do umerador é e do deomiador é zero. Fazedo um quadro de siais: + + + Q + + O que os dá como solução R 0
Matemática A Etesivo V. 6 Eercícios 0) B Reescrevedo a equação: 88 00 8 0 8 8 0 6 0 0 A raiz do umerador é e do deomiador é zero. Fazedo um quadro de siais: + + + Q + + O que os dá como solução R 0
n ) uma amostra aleatória da variável aleatória X.
 - Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
- Distribuições amostrais Cosidere uma população de objetos dos quais estamos iteressados em estudar uma determiada característica. Quado dizemos que a população tem distribuição FX ( x ), queremos dizer
TRANSPORTES. Sessão Prática 4 Amostragem de escalares
 Mestrado Itegrado em Egeharia Civil TRNPORTE Prof. Resposável: Luis Picado atos essão Prática 4 mostragem de escalares Istituto uperior Técico / Mestrado Itegrado Egeharia Civil Trasportes ulas Práticas
Mestrado Itegrado em Egeharia Civil TRNPORTE Prof. Resposável: Luis Picado atos essão Prática 4 mostragem de escalares Istituto uperior Técico / Mestrado Itegrado Egeharia Civil Trasportes ulas Práticas
Avaliação da Rotação de Constelações 4-QAM e 16-QAM em Canais com Desvanecimento Rice 1
 Avaliação da Rotação de Costelações 4-QAM e 16-QAM em Caais om Desvaeimeto Rie 1 Mariaa F. Mota, Carlos D. M. Regis 3, Rafael F. Lopes 4 e Marelo. Alear 5 1 Parte do projeto de pesquisa PIBICT. Istituto
Avaliação da Rotação de Costelações 4-QAM e 16-QAM em Caais om Desvaeimeto Rie 1 Mariaa F. Mota, Carlos D. M. Regis 3, Rafael F. Lopes 4 e Marelo. Alear 5 1 Parte do projeto de pesquisa PIBICT. Istituto
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p
 ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma amostra.
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma amostra.
AULA 24 FATORES DE FORMA DE RADIAÇÃO TÉRMICA- cont...
 Notas de aula de PM 6 Processos de Trasferêcia de Calor e Massa 08 UL FTOS D FOM D DIÇÃO TÉMIC- cot... Na aula aterior estudamos o caso de fatores de forma e como se pode calcular a troca líquida de calor
Notas de aula de PM 6 Processos de Trasferêcia de Calor e Massa 08 UL FTOS D FOM D DIÇÃO TÉMIC- cot... Na aula aterior estudamos o caso de fatores de forma e como se pode calcular a troca líquida de calor
F- MÉTODO DE NEWTON-RAPHSON
 Colégio de S. Goçalo - Amarate - F- MÉTODO DE NEWTON-RAPHSON Este método, sob determiadas codições, apreseta vatages sobre os método ateriores: é de covergêcia mais rápida e, para ecotrar as raízes, ão
Colégio de S. Goçalo - Amarate - F- MÉTODO DE NEWTON-RAPHSON Este método, sob determiadas codições, apreseta vatages sobre os método ateriores: é de covergêcia mais rápida e, para ecotrar as raízes, ão
CAPÍTULO IV DESENVOLVIMENTOS EM SÉRIE
 CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
CAPÍTUO IV DESENVOVIMENTOS EM SÉRIE Série de Taylor e de Mac-auri Seja f ) uma fução real de variável real com domíio A e seja a um poto iterior desse domíio Supoha-se que a fução admite derivadas fiitas
MAE Introdução à Probabilidade e Estatística II Resolução Lista 1
 MAE 229 - Itrodução à Probabilidade e Estatística II Resolução Lista 1 Professor: Pedro Moretti Exercício 1 (a) Fazer histograma usado os seguites dados: Distribuição de probabilidade da variável X: X
MAE 229 - Itrodução à Probabilidade e Estatística II Resolução Lista 1 Professor: Pedro Moretti Exercício 1 (a) Fazer histograma usado os seguites dados: Distribuição de probabilidade da variável X: X
Aplicações lineares. Capítulo Seja T: a) Quais dos seguintes vectores estão em Im( T )? 1 i) 4. 3 iii) ii)
 Capítulo Aplicações lieares Seja T: R R a multiplicação por 8 a) Quais dos seguites vectores estão em Im( T )? i) ii) 5 iii) b) Quais dos seguites vectores estão em Ker( T)? i) ii) iii) c) Qual a dimesão
Capítulo Aplicações lieares Seja T: R R a multiplicação por 8 a) Quais dos seguites vectores estão em Im( T )? i) ii) 5 iii) b) Quais dos seguites vectores estão em Ker( T)? i) ii) iii) c) Qual a dimesão
( 1,2,4,8,16,32,... ) PG de razão 2 ( 5,5,5,5,5,5,5,... ) PG de razão 1 ( 100,50,25,... ) PG de razão ½ ( 2, 6,18, 54,162,...
 Progressões Geométricas Defiição Chama se progressão geométrica PG qualquer seqüêcia de úmeros reais ou complexos, ode cada termo a partir do segudo, é igual ao aterior, multiplicado por uma costate deomiada
Progressões Geométricas Defiição Chama se progressão geométrica PG qualquer seqüêcia de úmeros reais ou complexos, ode cada termo a partir do segudo, é igual ao aterior, multiplicado por uma costate deomiada
EXERCÍCIO: ONDAS INTERMITENTES
 EXERCÍCIO: ONDAS INTERMITENTES Egeharia de Tráfego 1 Cosidere ua aproxiação de u ruzaeto seaforizado o apaidade igual a 1750/h, e adita ua situação e ue a deada a hora-pio as aproxiações da ia priipal
EXERCÍCIO: ONDAS INTERMITENTES Egeharia de Tráfego 1 Cosidere ua aproxiação de u ruzaeto seaforizado o apaidade igual a 1750/h, e adita ua situação e ue a deada a hora-pio as aproxiações da ia priipal
FORMAS QUADRÁTICAS. Esta forma quadrada pode ser reescrita em forma matricial, segundo:
 PROGRAA DE ENGENHARIA QUÍICA/COPPE/UFRJ COQ 897- OIIZAÇÃO DE PROCESSOS- II/ FORAS QUADRÁICAS Em a epressão geral das formas quadráticas é: a a f (, ) cbb a, cujas derivadas parciais são: f(, ) b a a f(,
PROGRAA DE ENGENHARIA QUÍICA/COPPE/UFRJ COQ 897- OIIZAÇÃO DE PROCESSOS- II/ FORAS QUADRÁICAS Em a epressão geral das formas quadráticas é: a a f (, ) cbb a, cujas derivadas parciais são: f(, ) b a a f(,
XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução do treinamento 5 Nível 3
 UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução do treiameto 5
UNIVERSIDADE FEDERAL DE SANTA CATARINA CENTRO DE CIÊNCIAS FÍSICAS E MATEMÁTICAS DEPARTAMENTO DE MATEMÁTICA PET MATEMÁTICA XX OLIMPÍADA REGIONAL DE MATEMÁTICA DE SANTA CATARINA Resolução do treiameto 5
CORRELAÇÃO Aqui me tens de regresso
 CORRELAÇÃO Aqui me tes de regresso O assuto Correlação fez parte, acompahado de Regressão, do programa de Auditor Fiscal, até 998, desaparecedo a partir do cocurso do ao 000 para agora retorar soziho.
CORRELAÇÃO Aqui me tes de regresso O assuto Correlação fez parte, acompahado de Regressão, do programa de Auditor Fiscal, até 998, desaparecedo a partir do cocurso do ao 000 para agora retorar soziho.
Raízes de equações. O Problema. Equações. Algébricas Transcendentes
 Raízes de equações Algébrias Trasedetes O roblema É frequete em problemas ietífios e de egeharia a eessidade de se determiar o valor para que satisfaça uma dada fução f isto é f. O úmero é hamado de zero
Raízes de equações Algébrias Trasedetes O roblema É frequete em problemas ietífios e de egeharia a eessidade de se determiar o valor para que satisfaça uma dada fução f isto é f. O úmero é hamado de zero
Soluções dos Exercícios do Capítulo 6
 Soluções dos Eercícios do Capítulo 6 1. O poliômio procurado P() a + b + c + d deve satisfazer a idetidade P(+1) P() +, ou seja, a(+1) + b(+1) + c(+1) + d a + b + c + d +, o que é equivalete a (a 1) +
Soluções dos Eercícios do Capítulo 6 1. O poliômio procurado P() a + b + c + d deve satisfazer a idetidade P(+1) P() +, ou seja, a(+1) + b(+1) + c(+1) + d a + b + c + d +, o que é equivalete a (a 1) +
Cifra Aleatória P. Quaresma. Cifra Aleatorizada P. Quaresma
 às Cifra Aleatória Fieiras Defiição ( ) Uma -bit ifra por bloos é uma fução : V K V, tal que para ada -bit K K, (P, K) é uma fução ivertível (a fução de eriptação para K) de V para V, deotada por K (P).
às Cifra Aleatória Fieiras Defiição ( ) Uma -bit ifra por bloos é uma fução : V K V, tal que para ada -bit K K, (P, K) é uma fução ivertível (a fução de eriptação para K) de V para V, deotada por K (P).
Exponenciais e Logaritmos (MAT 163) - Notas de Aulas 2 Prof Carlos Alberto S Soares
 Expoeciais e Logaritmos (MAT 163) - Notas de Aulas 2 Prof Carlos Alberto S Soares 1 Prelimiares Lembremos que, dados cojutos A, B R ão vazios, uma fução de domíio A e cotradomíio B, aotada por, f : A B,
Expoeciais e Logaritmos (MAT 163) - Notas de Aulas 2 Prof Carlos Alberto S Soares 1 Prelimiares Lembremos que, dados cojutos A, B R ão vazios, uma fução de domíio A e cotradomíio B, aotada por, f : A B,
Distribuições de Estatísticas Amostrais e Teorema Central do Limite
 Distribuições de Estatísticas Amostrais e Teorema Cetral do Limite Vamos começar com um exemplo: A mega-sea de 996 a N 894 úmeros de a 6: Média: m 588 Desvio padrão: 756 49 amostras de 6 elemetos Frequêcia
Distribuições de Estatísticas Amostrais e Teorema Cetral do Limite Vamos começar com um exemplo: A mega-sea de 996 a N 894 úmeros de a 6: Média: m 588 Desvio padrão: 756 49 amostras de 6 elemetos Frequêcia
Teorema do limite central e es/mação da proporção populacional p
 Teorema do limite cetral e es/mação da proporção populacioal p 1 RESULTADO 1: Relembrado resultados importates Seja uma amostra aleatória de tamaho de uma variável aleatória X, com média µ e variâcia σ.temos
Teorema do limite cetral e es/mação da proporção populacioal p 1 RESULTADO 1: Relembrado resultados importates Seja uma amostra aleatória de tamaho de uma variável aleatória X, com média µ e variâcia σ.temos
Cálculo Diferencial e Integral I Resolução do 2 ō Teste - LEIC
 Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
Cálculo Diferecial e Itegral I Resolução do ō Teste - LEIC Departameto de Matemática Secção de Àlgebra e Aálise I.. Determie o valor dos seguites itegrais (i) e x se x dx x + (ii) x (x + ) dx (i) Visto
2 Modelo Log-periódico
 2 Modelo Log-periódio Neste apítulo serão apresetados o desevolvimeto feomeológio do modelo log-periódio e a dedução da equação fudametal que desreve o resimeto dos preços o tempo a fase pré-rash. 2.1.
2 Modelo Log-periódio Neste apítulo serão apresetados o desevolvimeto feomeológio do modelo log-periódio e a dedução da equação fudametal que desreve o resimeto dos preços o tempo a fase pré-rash. 2.1.
Análise da Resposta Livre de Sistemas Dinâmicos de 2 a Ordem
 Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
Aálise da Resposta Livre de Sistemas Diâmicos de Seguda Ordem 5 Aálise da Resposta Livre de Sistemas Diâmicos de a Ordem INTRODUÇÃO Estudaremos, agora, a resposta livre de sistemas diâmicos de a ordem
Fundamentos de Análise Matemática Profª Ana Paula. Sequência Infinitas
 Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
Fudametos de Aálise Matemática Profª Aa Paula Sequêcia Ifiitas Defiição 1: Uma sequêcia umérica a 1, a 2, a 3,,a,é uma fução, defiida o cojuto dos úmeros aturais : f : f a Notação: O úmero é chamado de
ANALYTICAL METHODS IN VIBRATION. Leonard Meirovitch Capitulo 1
 ANALYTICAL METHODS IN VIBRATION Leonard Meirovith Capitulo Comportamento de sistemas Um sistema é definido omo uma montagem de omponentes atuando omo um todo. Os omponentes são lassifiados e definidos
ANALYTICAL METHODS IN VIBRATION Leonard Meirovith Capitulo Comportamento de sistemas Um sistema é definido omo uma montagem de omponentes atuando omo um todo. Os omponentes são lassifiados e definidos
Testes de Hipóteses sobre uma Proporção Populacional
 Estatística II Atoio Roque Aula Testes de Hipóteses sobre uma Proporção Populacioal Seja o seguite problema: Estamos iteressados em saber que proporção de motoristas da população usa cito de seguraça regularmete.
Estatística II Atoio Roque Aula Testes de Hipóteses sobre uma Proporção Populacioal Seja o seguite problema: Estamos iteressados em saber que proporção de motoristas da população usa cito de seguraça regularmete.
MAE Introdução à Probabilidade e Estatística II Resolução Lista 2
 MAE 9 - Itrodução à Probabilidade e Estatística II Resolução Lista Professor: Pedro Moretti Exercício 1 Deotado por Y a variável aleatória que represeta o comprimeto dos cilidros de aço, temos que Y N3,
MAE 9 - Itrodução à Probabilidade e Estatística II Resolução Lista Professor: Pedro Moretti Exercício 1 Deotado por Y a variável aleatória que represeta o comprimeto dos cilidros de aço, temos que Y N3,
SINAIS E SISTEMAS DE TEMPO DISCRETO
 SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
SINAIS E SISTEMAS DE TEMPO DISCRETO SINAIS DE TEMPO DISCRETO Fução de uma variável idepedete iteira. Não é defiido em istates etre duas amostras sucessivas. É icorreto pesar que é igual a zero se ão é
Estimar uma proporção p (desconhecida) de elementos em uma população, apresentando certa característica de interesse, a partir da informação
 ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p 1 Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma
ESTIMAÇÃO DA PROPORÇÃO POPULACIONAL p 1 Objetivo Estimar uma proporção p (descohecida) de elemetos em uma população, apresetado certa característica de iteresse, a partir da iformação forecida por uma
CONCEITOS DE VIBRAÇÃO
 CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
CONCEITOS DE VIBRAÇÃO Paulo S. Varoto 55 3.1 - Itrodução O objetivo pricipal desta secção é o de apresetar coceitos básicos da teoria de vibrações bem como iterpretá-los sob o poto de vista dos esaios
Inicialmente consideremos um controlador PID analógico ideal (contínuo). de t τ. d 1
 CONROLAOR P GAL P EAL iialmete oideremo um otrolador P aalógio ideal (otíuo). 1 t de t ut () = u0 + k et () + et ( ) dt + d 0 1 dt u(t) - Ação de otrole o itate atual u 0 (t) - Bia ou valor da variável
CONROLAOR P GAL P EAL iialmete oideremo um otrolador P aalógio ideal (otíuo). 1 t de t ut () = u0 + k et () + et ( ) dt + d 0 1 dt u(t) - Ação de otrole o itate atual u 0 (t) - Bia ou valor da variável
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 11º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema III Sucessões Reais
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema III Sucessões Reais Tarefa º. Desta figura, do trabalho da Olívia e da Susaa, retire duas sequêcias e imagie o processo
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS º ANO DE ESCOLARIDADE DE MATEMÁTICA A Tema III Sucessões Reais Tarefa º. Desta figura, do trabalho da Olívia e da Susaa, retire duas sequêcias e imagie o processo
O Princípio da Substituição e o Teorema Central do Limite
 O Pricípio da Substituição e o Teorema Cetral do Limite Roberto Imbuzeiro M. F. de Oliveira 6 de Maio de 009 Resumo 1 Prelimiares são variáveis aleatórias idepedetes sat- No que segue {X i } {Y i} isfazedo
O Pricípio da Substituição e o Teorema Cetral do Limite Roberto Imbuzeiro M. F. de Oliveira 6 de Maio de 009 Resumo 1 Prelimiares são variáveis aleatórias idepedetes sat- No que segue {X i } {Y i} isfazedo
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON 5.1 MODELO MATEMÁTICO E SOLUÇÃO ANALÍTICA
 Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Capítulo 5. CASO 5: EQUAÇÃO DE POISSON No presete capítulo, é abordado um problema difusivo uidimesioal com absorção de calor (Icropera e DeWitt, 199, o que resulta uma equação de Poisso, que é uma equação
Cálculo Numérico Lista 02
 Cálculo Numérico Lista 02 Professor: Daiel Herique Silva Essa lista abrage iterpolação poliomial e método dos míimos quadrados, e cobre a matéria da seguda prova. Istruções gerais para etrega Nem todos
Cálculo Numérico Lista 02 Professor: Daiel Herique Silva Essa lista abrage iterpolação poliomial e método dos míimos quadrados, e cobre a matéria da seguda prova. Istruções gerais para etrega Nem todos
5. O algoritmo dos mínimos quadrados
 Apotametos de Processameto Adaptativo de Siais 5. O algoritmo dos míimos quadrados Método dos míimos quadrados Os algoritmos de míimos quadrados são uma alterativa aos algoritmos de gradiete. Estrutura
Apotametos de Processameto Adaptativo de Siais 5. O algoritmo dos míimos quadrados Método dos míimos quadrados Os algoritmos de míimos quadrados são uma alterativa aos algoritmos de gradiete. Estrutura
Instituto de Física USP. Física Moderna. Aula 25. Professora: Mazé Bechara
 Istituto de Física USP Física Modera Aula 5 Professora: Mazé Bechara Aula 5 A equação de Schroediger para estados estacioários ligados. Aplicação o movimeto uidimesioal. 1. Aplicação : os auto estados
Istituto de Física USP Física Modera Aula 5 Professora: Mazé Bechara Aula 5 A equação de Schroediger para estados estacioários ligados. Aplicação o movimeto uidimesioal. 1. Aplicação : os auto estados
Bases e dimensão. Roberto Imbuzeiro Oliveira. 22 de Março de 2012
 Bases e dimesão Roberto Imbuzeiro Oliveira 22 de Março de 2012 1 Defiições básicas Nestas otas X é espaço vetorial com mais de um elemeto sobre o corpo F {R, C}. Uma base (ão ecessariamete LI) de X é um
Bases e dimesão Roberto Imbuzeiro Oliveira 22 de Março de 2012 1 Defiições básicas Nestas otas X é espaço vetorial com mais de um elemeto sobre o corpo F {R, C}. Uma base (ão ecessariamete LI) de X é um
CAPÍTULO 3 DEPENDÊNCIA LINEAR
 CAPÍTUO DEPENDÊNCIA INEAR Comiação iear Defiição: Seja V um espaço etorial sore um orpo K Um etor omiação liear os etores que u a a a De forma areiaa poe-se esreer: u a i i i u V é ito uma V se existem
CAPÍTUO DEPENDÊNCIA INEAR Comiação iear Defiição: Seja V um espaço etorial sore um orpo K Um etor omiação liear os etores que u a a a De forma areiaa poe-se esreer: u a i i i u V é ito uma V se existem
a = b n Vejamos alguns exemplos que nos permitem observar essas relações. = 4 4² = 16 radical radicando
 RADICIAÇÃO CONTEÚDOS Radiciação Propriedades dos radicais Extração de fatores do radicado AMPLIANDO SEUS CONHECIMENTOS Radiciação A radiciação é defiida como a operação em que dado um úmero a e um úmero,
RADICIAÇÃO CONTEÚDOS Radiciação Propriedades dos radicais Extração de fatores do radicado AMPLIANDO SEUS CONHECIMENTOS Radiciação A radiciação é defiida como a operação em que dado um úmero a e um úmero,
étodos uméricos MÉTODO DOS MOMENTOS - MOM Prof. Erivelton Geraldo Nepomuceno PROGRAMA DE PÓS-GRADUAÇÃO EM ENGENHARIA ELÉTRICA
 étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
étodos uméricos MÉTODO DOS MOMETOS - MOM Prof. Erivelto Geraldo epomuceo PROGRAMA DE PÓS-GRADUAÇÃO EM EGEHARIA ELÉTRICA UIVERSIDADE DE JOÃO DEL-REI PRÓ-REITORIA DE PESQUISA CETRO FEDERAL DE EDUCAÇÃO TECOLÓGICA
Sociedade Portuguesa de Física, Divisão de Educação, 17 de Julho de 2008.
 Resolução da prova Físia e Químia 11.º/1.º ao (715), Fase ersão I, 008. Soiedade Portuguesa de Físia, Divisão de Eduação, 17 de Julho de 008. 1. 1.1. O silêio é total pois as odas sooras, que são odas
Resolução da prova Físia e Químia 11.º/1.º ao (715), Fase ersão I, 008. Soiedade Portuguesa de Físia, Divisão de Eduação, 17 de Julho de 008. 1. 1.1. O silêio é total pois as odas sooras, que são odas
Conversores Analógico/Digital (A/D)
 Coversores Aalógico/Digital (A/D) Um coversor A/D é um circuito ue coverte um ível de tesão (ou correte) em um valor umérico (digital) correspodete. São a base de ualuer istrumeto de medição digital. Existem
Coversores Aalógico/Digital (A/D) Um coversor A/D é um circuito ue coverte um ível de tesão (ou correte) em um valor umérico (digital) correspodete. São a base de ualuer istrumeto de medição digital. Existem
