Procedimento Para Solução de Problemas de Condução de Calor Com Condutividade Térmica Dependente da Temperatura
|
|
|
- Renato Alencastre Peixoto
- 7 Há anos
- Visualizações:
Transcrição
1 UNVERSDADE DO ESADO DO RO DE ANERO CENRO DE ECNOLOGA E CÊNCA FACULDADE DE ENGENHARA DEPARAMENO DE ENGENHARA MECÂNCA Pocedmento Paa Solução de Poblemas de Condução de Calo Com Condutvdade émca Dependente da empeatua 4 7 ulho/8
2 REOR Rcado Vealves de Casto VCE-REOR Maa Chstna Paão Maol SUB-REORA DE GRADUAÇÃO Lená Medeos de Menezes DREOR DO CENRO DE ECNOLOGA E CËNCAS Maa Geogna Munz Washngton DREOR DA FACULDADE DE ENGENHARA Pofª. Maa Eugêna Gouvêa CHEFE DO DEPARAMENO DE ENGENHARA MECÄNCA Pof. Fancsco osé da Cunha Pes Soeo COORDENADOR DE PROEO DE GRADUAÇÃO Pof. Calos Albeto Peea Coea ORENADOR Pof. Rogéo Matns Saldanha da Gama CO-ORENADOR Pof. Nobeto Mangavacch AUOR Leon Matos Rbeo de Lma BANCA EXAMNADORA Pof. Rogéo Matns Saldanha da Gama Pof. Calos Albeto Peea Coea Pof. Nobeto Mangavacch - -
3 Leon Matos Rbeo de Lma Oentado: Rogéo Matns Saldanha da Gama Co-oentado: Nobeto Mangavacch Pocedmento Paa Solução de Poblemas de Condução de Calo Com Condutvdade émca Dependente da empeatua Objetvo: A poposta deste tabalho é um pocedmento sstemátco que povê a solução eata de poblemas de tansfeênca de calo não-lnea em copos com condutvdade témca em função da tempeatua, atavés de uma seqüênca de poblemas lneaes, onde a solução é dada pelo lmte da seqüênca. - -
4 RESUMO Na gande maoa dos pojetos de engenhaa, poblemas de condução de calo sofem váas smplfcações paa que o sstema de equações pemta solução eata. No entanto, tas apomações possuem um custo, que se taduz em detupações do fenômeno físco eal, o que pode nos leva a esultados muto mpecsos. Um dos atfícos mas utlzados na modelagem de poblemas de condução de calo é assum a condutvdade témca nvaante com a tempeatua, fazendo com que o temo dfusvo da equação da condução fque lnea. Entetanto, a go, todo mateal, sem eceção, possu condutvdade témca dependente da tempeatua. Os pocedmentos analítcos conhecdos que levam em conta tal dependênca se estngem, anda, a um númeo lmtado poblemas. A poposta deste tabalho é um pocedmento sstemátco que povê a solução eata de poblemas de tansfeênca de calo em copos com condutvdade témca em função da tempeatua, atavés de uma seqüênca de poblemas lneaes, onde a solução é dada pelo lmte da seqüênca. O método empega a tansfomada de choff, a qual é a ncógnta em cada elemento da seqüênca e possu elação bunívoca com a tempeatua. Esta últma condção pemte que, esolvendo o sstema de equações em temos da tansfomada, obtenhamos o campo de tempeatua do copo. Neste tabalho, váos poblemas são esolvdos po meo do pocedmento poposto e os esultados são mostados e analsados. Nos casos de geometas mas compleas, empegamos o Método de Elementos Fntos (MEF ou o Método de Dfeenças Fntas (MDF. O MEF e o MDF são métodos numécos de solução de EDP s bastante dfunddos, amplamente utlzados em engenhaa, e pouco dscutdos nos cusos de gaduação da UER. Po sso este tabalho conta também com alguns eemplos de esolução de poblemas de tansmssão de calo lnea po meo destas feamentas, com detalhes de cada passo de sua fomulação, no ntuto de pove uma fonte de consulta nas aplcações do MEF e do MDF em casos clásscos de tansmssão de calo
5 ABSRAC n most pat of engneeng pojects, heat conducton poblems ae smplfed n the ntent that the equatons sstem allows eact soluton. Nevetheless, such smplfcatons ae, n fact, dstotons of the eal phscal phenomenon, whch can nduce us to ve mpecse esults. One of the most utlzed atfces n heat tansfe modelng s to assume themal conductvt nvaant wth tempeatue, whch maes the dffusve tem n the conducton equaton to be lnea. Stll, eve mateal, wth no eceptons, has tempeatue dependent themal conductvt. he analtcal pocedues that tae n account such dependence ae estcted to a lmted set of poblems. hs wo pesents a sstematc pocedue fo eact soluton of heat tansfe poblems n bodes wth tempeatue dependent themal conductvt, b means of a sequence of lnea poblems, whee the soluton s gven b the lmt of the sequence. he method emplos the choff tansfom, whch s the unnown n each sequence element, and has a bunvocal elaton wth tempeatue. hs last condton allows that, b solvng the sstem n tems of the tansfom, we obtan the tempeatue feld of the bod. n ths wo, the method s emploed to seveal poblems and esults ae shown and analzed. n cases of moe comple geometes the Fnte Element Method (FEM o the Fnte Dffeences Method (FDM s appled. hese methods ae numecal pocedues well dffused n PDE s soluton, wdel used n engneeng, and lttle dscussed n undegaduate couses n UER. Fo ths eason, ths wo also counts wth some esoluton eamples of lnea heat tansfe poblems b means of such technques, wth detals of each step of the numecal fomulatons, n ode to povde a souce of consultaton on FEM and FDM applcatons n classcal cases of heat tansmsson
6 ÍNDCE - ntodução 8. - Fomas de ansmssão de Calo 9. - Modelo de Resolução Poposto 9 - Concetos Báscos. - Condução. - Convecção. - Radação - Calculando a Dstbução de empeatuas de um Copo Pocedmento Lnea 4. - Equações Govenantes 4. - ansfomada de choff 4. - Constundo a Solução a Pat da Seqüênca de Poblemas Lneaes Convegênca Eemplos Eemplo Eemplo Eemplo Métodos Numécos em Poblemas de ansmssão de Calo Dfeenças Fntas Eemplo Eemplo Eemplo Elementos Fntos Em Busca da Foma Faca das Equações Govenantes Dscetzação do Domíno em Elementos Fntos Fomulação do Elemento Fnto angula Lnea Fomulação de Foma do Elemento Devada das Funções de Foma do Elemento Foma Faca po Elemento com as empeatuas Nodas Atbução das empeatuas Nodas aos Elementos da Malha Eemplo Eemplo Smulações Numécas Eemplo Eemplo Eemplo Eemplo 4 8 Conclusão 85 Refeêncas 86 Publcações
7 SÍMBOLOS c Φ g h L n ω Ω Ω q q q& R ρ σ u v calo específco tansfomada de choff do elemento da seqüênca veto aceleação da gavdade coefcente de toca de calo po convecção condutvdade témca tenso condutvdade témca compmento veto untáo nomal eteo tansfomada de choff egão do espaço ocupada pelo copo que conduz calo fontea do domíno Ω taa de tansfeênca de calo veto fluo de calo po undade de áea geação ntena de enega po undade de volume ao densdade constante de stefan-boltzmann tempeatua tenso tensão tempeatua de efeênca enega ntena veto velocdade - 7 -
8 NRODUÇÃO Estudos na áea de tansfeênca de calo são de fundamental mpotânca em váos amos de engenhaa. Engenheos eletcstas, po eemplo, estão sempe peocupados em evta danos mateas devdos a pontos de supeaquecmento, causados po desgn mpópo das tocas de calo em motoes elétcos, geadoes e tansfomadoes. Um engenheo eletônco está nteessado em conhece métodos efcentes de dsspação de calo em chp s e outos semcondutoes de manea que possam opea dento de faas seguas de tempeatua. Engenheos químcos estão nteessados em pocessos de tansfeênca de calo neentes a dvesas eações químcas. Um engenheo metalúgco estaa nteessado em conhece a taa de tansfeênca de calo necessáa paa um pocesso de tatamento témco patcula, como, po eemplo, numa fundção, onde a qualdade fnal do poduto está ntmamente lgada à taa de esfamento do pocesso. Engenheos agopecuáos estão nteessados na secagem de gãos, pocessamento de almentos e consevação. Um engenheo cvl deve te contole sobe o estesse témco desenvolvdo em cetos tpos de conceto, bem como o efeto da tansfeênca de massa e calo na constução e em mateas de constução. Um engenheo ambental está peocupado com o efeto da tempeatua na dspesão de poluentes no a, dfusão de poluentes em solos, polução témca em lagos e maes e seus mpactos na vda teeste e aquátca. O engenheo mecânco é o mas envolvdo com fenômenos de tansmssão de calo e conhece os pocessos témcos assocados à opeação de equpamentos como boles, condensadoes, pé-aquecedoes de a, ente mutos outos, sempe buscando ganho de desempenho. Usnas nucleaes equeem nfomação pecsa aceca dos pocessos de tansfeênca de calo, tendo em vsta que condções seguas de opeação são um fato fundamental em seu pojeto. Refgeação e sstemas de condconamento de a também envolvem dspostvos de toca de calo, egndo desgn cudadoso (e.g.: satéltes atfcas. anto a pesqusa fundamental quanto a pesqusa opeaconal em fenômenos de tansfeênca de calo são essencas paa a obtenção de soluções econômcas e efcentes paa poblemas cítcos encontados em mutos pojetos de engenhaa. Mas do que sso, se devemos potege o ambente, então é mpescndível entende os pocessos de tansfeênca de enega envolvdos e, se necessáo, toma as povdêncas devdas
9 . Fomas de tansmssão de calo Há tês modos báscos de tansmssão de calo: condução, adação e convecção. A go, somente a condução e a adação devem se classfcadas como pocessos de tansfeênca de calo, pos podem est ndependentes um do outo, enquanto que a convecção não ocoe sem a condção físca fundamental, que é a condução témca. Ela depende do tanspote mecânco de massa, sendo uma foma de tansmssão que combna movmento com condução de calo. Anda assm, a convecção é um meo de tansmssão de enega podeoso e muto utlzado em engenhaa, e po sso meece atenção especal. A maoa dos poblemas de tansfeênca de calo po condução é descta sob a hpótese de condutvdade témca ndependente da tempeatua. al suposção é matematcamente convenente poque, em geal, esulta em equações dfeencas pacas lneaes. No entanto, a condutvdade témca é sempe uma função dependente da tempeatua, e, mutas vezes, neglgenca tal dependênca (supondo condutvdade témca constante nos leva a uma descção matemátca mpecsa do pocesso de condução de calo.. Modelo de esolução poposto O objetvo pncpal deste tabalho é pove um pocedmento sstemátco e confável paa descção da tansfeênca de calo po condução em um sóldo ígdo, homogêneo e em epouso com condutvdade témca dependente da tempeatua. O pocedmento fonece solução eata e empega apenas o feamental utlzado em poblemas de condutvdade témca constante. O método consste na obtenção da solução de poblemas não-lneaes de tansfeênca de calo (condutvdade témca vaando com a tempeatua atavés de uma seqüênca de poblemas lneaes. A passagem do modelo matemátco ognal paa esta seqüênca é feta pelo empego da tansfomada de choff e a convegênca é gaantda, desde que atendda uma smples condção, confome seá vsto
10 CONCEOS BÁSCOS. Condução Sempe que est um gadente de tempeatua dento de um sstema ou ente sstemas em contato témco, haveá tansfeênca de calo po condução. Desta foma, em um copo com dfeenças ntenas de tempeatua, este um fluo de calo po condução dos pontos de mao tempeatua paa os de meno tempeatua, seja ele copo ígdo ou fludo. Este fluo seá tanto mao ou meno dependendo da condutvdade (ou condutbldade, como alguns autoes pefeem témca do mateal, que epesenta, em poucas palavas, a facldade com que o calo é conduzdo, e é sempe uma função da tempeatua, seja qual fo o mateal. A Le de Foue elacona o fluo de calo po condução com o gadente de tempeatuas e é epessa po: q gad( (. onde: q é o veto fluo de calo (enega po undade de tempo e áea; ˆ (, sendo o tenso condutvdade témca, smétco e postvo defndo, e é a tempeatua. No caso de mateas sotópcos,, onde é um escala postvo. Paa estes casos o fluo de calo passa a se apenas: q gad( (. Esta equação nos pemte conhece a taa de tansfeênca de enega témca, mas não nos pemte detemna o campo de tempeatuas, ou seja, a dstbução de tempeatuas, num dado copo. A equação da consevação da enega (Pmea Le da emodnâmca, tomada paa copos opacos, ígdos e em epouso, nos daá meos paa tanto. Em sua foma ntegal, a Equação da Consevação da Enega completa é dada po - -
11 d dt Ωt ρ u v v dv Ωt ρg vdv Ωt v nds Ωt qdv & Ωt q nds (. onde: ρ epesenta a densdade; u é a enega ntena; v é o veto velocdade; g é o veto aceleação da gavdade; é o tenso tensão; n é o veto nomal untáo eteo; q epesenta a geação ntena de enega po undade tempo e volume; & q é veto fluo de enega po undade de tempo e áea Ω é uma egão no espaço no nstante t t Ω é a fontea deω t t Levando em conta a consevação da massa e da quantdade de movmento, a equação fca, na foma local Du ρ dv( q gad ( v q& (.4 Dt gad ( v gad ( v. Logo, como Pela condção de copo ígdo temos que [ ], gad ( v (.5 A condção de copo em epouso esulta em v, ou seja, Du Dt u t [ gad u ] u ( v (.6 t Consdeando que a enega ntena é tal que u uˆ ( e du c (.7 d - -
12 onde c epesenta o calo específco do mateal, e as condções de copo ígdo, opaco e em epouso, a equação da enega passa e se, então, dada pela equação (sem mudança de fase ρ c dv( q q& (.8 t que também pode se chamada equação da condução de calo. Neste tabalho seá levada em conta a equação da condução em egme estaconáo, paa copos homogêneos com sotopa témca: [ gad ( ] q dv & (.9. Convecção A convecção é uma foma de tansmssão de calo que combna condução témca e movmento. De acodo com o que povoca o tanspote mecânco de massa a convecção é classfcada em natual ou foçada. Na convecção natual o deslocamento de massa ocoe apenas devdo à alteação na densdade da poção que ecebeu ou cedeu alguma pacela de calo. Na convecção foçada o movmento é povocado po algum fato eteno. Po eemplo, a convecção pomovda po um ventlado é foçada, enquanto que a convecção témca utlzada em geladeas caseas é natual. As coentes de convecção natual tansfeem a enega ntena amazenada no fludo essencalmente da mesma manea que as coentes de convecção foçada. Entetanto, a ntensdade do movmento de mstua é gealmente meno na convecção natual e, potanto, as taas de tansmssão de calo são menoes do que na convecção foçada. Anda assm mutos dspostvos em engenhaa dependem bascamente de convecção natual paa aefecmento. Neste tabalho a convecção seá consdeada apenas paa fns de condção de contono dos poblemas abodados. A Le de Newton do Resfamento (devda de fato a Foue epesenta o fluo de calo tansfedo po convecção natual pela equação ( q h (. - -
13 onde: q é um escala que epesenta o fluo nomal de calo po undade de tempo e áea; h é o coefcente de tansfeênca de calo po convecção; é uma tempeatua efeente a um ponto no fludo sufcentemente afastado da fontea de modo que a tempeatua do fludo não seja afetada pela pesença de uma fonte de aquecmento (ou esfamento.. Radação A adação témca pode se encaada como o fluo de adação eletomagnétca emtdo po uma entdade mateal (copo sóldo, banho de líqudo, mstua de gases devdo a uma tempeatua absoluta não nula (Bejan, 99, []. Ou seja, todo copo com tempeatua absoluta dfeente de zeo (consdeando a mpossbldade de tempeatua absoluta negatva emte enega témca po adação, atavés de ondas eletomagnétcas. Ao contáo da condução e da convecção, a adação não necessta de meo paa tansfe calo, emboa ele seja nfluente no pocesso. Dependendo do meo, o estudo da toca de calo po adação é dvddo em duas gandes áeas: adação em meo patcpante e adação em meo não patcpante. O meo é dto patcpante quando absove e/ou emte adação témca, ntefendo no pocesso de tansmssão de calo. Nos casos de adação témca em meo não-patcpante consdea-se vácuo o meo onde se popagam as ondas eletomagnétcas. A taa de enega emtda po adação témca po um copo é chamada pode emssvo. A Le de Stefan-Boltzmann fonece o pode emssvo paa copos negos pela equação q σ 4 (. onde q epesenta a enega adante emtda po undade de tempo e áea, é a 8 4 tempeatua absoluta e σ é a constante de Stefan-Boltzmann ( σ 5,67 W/m. Seja G o fluo total de adação que atnge uma dada supefíce. ês pocessos podem ocoe com G : - -
14 - uma poção α G é absovda; - uma outa poção ρ G é efletda pela supefíce; - uma tecea poção τ G atavessa o copo, devdo a tanspaênca. α, ρ e τ são coefcentes tas que (consevação de enega α ρ τ (. e são denomnados absovdade total (α, eflevdade total (ρ e tansmssvdade total (τ da supefíce. O conceto de copo nego, dealzado po Gustav choff, epesenta um copo capaz de absove toda adação ncdente sobe ele, sto é, ρ τ, paa qualque compmento de onda, e que emte enega po adação numa taa (po undade de áea 4 gual a σ. Paa copos eas usa-se, mutas vezes, o modelo de copo cnzento, que absove enega eletomagnétca em qualque compmento de onda e a emte popoconalmente a um paâmeto chamado emssvdade (ε, com < ε <, tal que a taa de enega q emtda po undade de áea de um copo cnzento po adação é dada po q εσ 4 (. Na equação segunte, a quantdade q epesenta o fluo de enega tocada po adação atavés de uma supefíce: 4 qεσ αg (.4 sendo α a absovdade (ou absotânca elatva à supefíce e G a enega ncdente. Obs.: paa poblemas com toca de calo po adação ente mas de dos copos é necessáo consdea as pacelas de adação efletda e tansmtda (que passou atavés do copo po tanspaênca. Neste tabalho não seá levada em conta tal stuação
15 CALCULANDO A DSRBUÇÃO DE EMPERAURAS DE UM CORPO A dstbução de tempeatua num detemnado copo contínuo, ígdo, opaco e em epouso, sujeto a toca de calo po convecção e adação na supefíce, em egme pemanente, é obtda a pat da solução do sstema de equações dfeencas pacas segunte (assumndo que o copo ocupe a egão Ω com fontea Ω : dv[ gad( ] q& em Ω 4 [ gad( ] n h( εσ αg sobe Ω (. Mutas vezes o efeto da adação é despezível em elação à convecção, e a condutvdade témca pode se apomada paa uma constante. Com sso, o sstema anteo passa a se dv [ gad ( ] q& em Ω [ gad ( ] n h( sobe Ω (. que é uma equação dfeencal pacal lnea sujeta a condção de contono lnea. Este é um poblema clássco de engenhaa, e conta com amplo feamental de esolução. Po eemplo, consdeemos um copo clíndco de ao R e compmento L, que gea enega unfomemente a uma taa q& (W/m³. Se L fo muto mao do que R (L>>R, é azoável supo que as duas etemdades estejam soladas temcamente. O copo toca calo po convecção com o ambente, que está a uma tempeatua, que não é afetada pela tempeatua do copo. Assumndo condutvdade témca constante, a equação da enega paa este poblema (em egme pemanente e os balanços de fluo de calo na supefíce, em coodenadas clíndcas, são desctos po q& em z h( em R em z e z L z < R (
16 cuja solução é únca e epesentada po qr & ( R q& 4 h (.4 magnando agoa um caso mas pátco, consdee um cabo elétco, muto compdo, de cobe, com mm de dâmeto, pelo qual passa uma coente elétca, sujeto a condução apenas na deção adal, tocando calo po convecção com o ambente, que está a uma tempeatua méda de 5 C (98. Assumndo condutvdade témca constante e gual a 99 W/m (paa tempeatua de 9, e coefcente de toca de calo po convecção (ou coefcente de flme h gual a W/m², se o fo conduz uma coente de 5 A submetda a uma tensão de volts, o campo de tempeatuas em qualque seção tansvesal do fo seá apomadamente como mosta a fgua segunte: Fgua. campo de tempeatua em cabo elétco
17 Note que a tempeatua é patcamente gual em toda a áea, como podemos compova pela dfeença ente as tempeatuas máma e mínma: 98,849 ma 98,8 mn ma mn,566 No entanto, se analsamos a dstbução de tempeatua de um outo copo clíndco, com cnco metos de dâmeto, de fba de vdo (suponhamos que seja sotópco, com condutvdade témca a 9 gual a,5w/m, fonte de enega ntena gual a W/m³, veemos que há gadentes de tempeatua consdeáves: Fgua. campo de tempeatua em copo clíndco com,5m de ao. 744,8458 ma 98, mn - 7 -
18 ma mn 446,48574 A campo da dstbução de tempeatuas paa o cabo elétco talvez não seja necessáa duante o pojeto, mas no caso da fba de vdo ela nos pemtu detecta um gadente de tempeatuas acentuado. Ao contáo deste poblema, em que a geometa é smples e tona fácl sabe a po onde estão as maoes tempeatuas, bem como as menoes, há poblemas com geometas compleas, que tonam sso muto dfícl sem o cálculo da dstbução de tempeatua. ambém com elação aos dos poblemas anteoes, vmos que a condutvdade témca fo apomada paa uma constante. Há mateas, entetanto, cuja condutvdade témca possu fote dependênca da tempeatua, como mosta a tabela segunte. condutvdade témca (W/m Beílo, 8, 6, 6, 7, 89, 7, Boo 5,5,7 8,7, 8, 6, 5, Gemâno 96,8 66,7 4, 7, 9,8 7,4 7,4 Feo 94, 8,5 69,4 54,7 4,,6 8, Slíco 64, 68, 98,9 6,9 4,, 5,7 abela. condutvdade témca de elementos metálcos
19 Fgua. cuvas de condutvdade témca De fato, a condutvdade témca, paa mutos mateas, vaa eponencalmente com a tempeatua: ( α ep( β (.5 sendo α e β constantes postvas. Paa estes mateas (e mutos outos, esolve o sstema (. com constante pode conduz a esultados etemamente longe da ealdade físca do poblema. Compaemos agoa dos poblemas guas, a não se po uma dfeença: no pmeo a condutvdade témca é uma função da tempeatua, e, no segundo, ela é apomada paa uma constante (méda da utlzada no pmeo. º poblema - 9 -
20 Copo clíndco de ao R m com fluo apenas na deção adal, tocando calo po convecção com o ambente, com condutvdade témca vaável e dada po 7 ep(, (.6 A tempeatua ambente é 98, o coefcente de flme h é W/m² e a geação ntena de calo unfome e gual a W/m³. O campo de tempeatua é dado po ( 6 ep ln ( e gafcamente epesentado po Fgua.4 cuvas de tempeatua paa copo com condutvdade témca vaável poblema - -
21 gual ao anteo eceto pela condutvdade témca, que seá a méda da utlzada acma, ou seja, ~ W/m. A solução do poblema e o gáfco do campo de tempeatua são apesentados a segu. ( (.8 Fgua.5 campo de tempeatua paa copo com condutvdade témca constante As dfeenças ente os esultados são evdentes. Po eemplo, no pmeo poblema, a tempeatua em 5 m é 4, enquanto que no segundo, também paa 5 m, a tempeatua é 458. Há pojetos de engenhaa onde essa dfeença de 46 C (que não é pequena é detemnante, podendo decd se o pojeto é factível ou não. O poblema em que levamos em conta a dependênca da tempeatua paa a condutvdade témca é smples, pemtndo a obtenção da solução analítca com facldade. No entanto, a maoa dos casos envolve geometas mas compleas. Nomalmente, em stuações nas quas os métodos analítcos de solução não são patcáves e a condutvdade témca não pode se tomada como constante, devdo a - -
22 estções de desgn que egem mao pecsão na detemnação do campo de tempeatua, utlza-se métodos numécos, que fonecem uma solução apomada. Uma aplcação de metodologa numéca de esolução pode se vsta em De Andade e Zapaol [], onde, a cada teação, a condutvdade témca é calculada a pat do campo de tempeatua do passo anteo. Este tpo de pocedmento possu sempe um eo assocado, poém, há poblemas de engenhaa que não abem muto espaço paa apomações. - -
23 4 PROCEDMENO LNEAR 4. Equações Govenantes Consdeemos um copo ígdo, opaco e sotópco em epouso, cuja confguação é epesentada pelo conjunto abeto Ω com contono Ω. O pocesso estaconáo de tansfeênca de calo dento do copo é matematcamente descto pela segunte equação dfeencal pacal elíptca: [ gad ( ] q em Ω dv & (4. onde, q& e denotam, espectvamente, o campo de tempeatua, a taa de geação ntena de calo (po undade de volume e a condutvdade témca. O foco deste tabalho são os poblemas de condução de calo com condutvdade témca dependente da tempeatua, ou seja, tomada como uma função da tempeatua local. Em outas palavas, ˆ( (4. Supondo que as faces do copo tocam calo com o ambente de acodo com a le de Newton do esfamento, as condções de contono assocadas à equação (4. são dadas po [ gad ( ] n h( sobe Ω (4. onde n é o veto nomal eteno untáo (defndo sobe Ω, h é o coefcente de tansfeênca de calo po convecção e é a tempeatua de efeênca (ambente. O poblema esultante (não-lnea é dado po [ gad ( ] q em Ω & [ gad ( ] n h( sobe Ω dv ( ansfomada de choff - -
24 - 4 - Como a condutvdade témca é sempe um valo postvo, uma nova vaável ω (tansfomada de choff pode se defnda po ˆ( ˆ( f d ξ ξ ω (4.5 sendo ω uma função nvesível de. Calculemos o gadente da ntegal acma: d gad gad ( ˆ ξ ξ ω (4.6 Se epesentamos o gadente em coodenadas catesanas etangulaes z j gad (, teemos, paa cada componente, d ( ˆ ξ ξ ω (4.7 d ( ˆ ξ ξ ω (4.8 d z z ( ˆ ξ ξ ω (4.9 Se analsamos apenas a componente teemos, po analoga, a esposta paa as componentes e z. Sabendo que,, ˆ (,, ˆ(,, ˆ (,, ˆ (,, ˆ( ( lm ( ( lm ( d d d d z z z z z ξ ξ ξ ξ ξ ξ ξ ξ (4. Podemos ntoduz a função ( ˆ G tal que ( ( ˆ ' G, de manea que
25 - 5 - ( ( d dg G z G z G (,, ˆ( ˆ,, ˆ( ˆ lm (4. Note que ( (,, ˆ(,, ˆ ( (,, ˆ( ˆ,, ˆ( ˆ z z d z G z G ξ ξ (4. logo d z ( (,, ˆ( ξ ξ (4. Dessa foma, as equações 4.7 a 4.9 esultam em, espectvamente, ( ω (4.4 ( ω (4.5 z z ( ω (4.6 ou seja, ( ( gad gad ω (4.7 A elação acma ndepende de sstema de coodenadas. Desta foma, o poblema ognal pode se eescto como segue: [ ] [ ] ( Ω Ω sobe ( ˆ ( em ( f h n gad q gad dv ω ω ω & (4.8
26 onde ˆ f ( ω. O poblema acma pemanece não-lnea, mas esta não-lneadade está assocada apenas ao contono, não à equação dfeencal pacal escta paa o nteo do copo. Como a condutvdade témca é postva paa todo domíno (do contáo estaíamos volando a ª Le da emodnâmca, com fluo de calo no sentdo da meno paa a mao tempeatua é possível nota que dω d > > e > paa todo o domíno (4.9 d dω ou seja, a tempeatua é uma função esttamente cescente de ω este uma elação bunívoca ente ω e. A conseqüênca dsso é muto mpotante, pos gaante que, em se conhecendo ω, seja possível obte, e vce-vesa. Em outas palavas, a pat da solução em ω do sstema (4.8 tem-se a solução de (4.4. Mas anda, podemos conclu que a tansfomada de choff sempe teá nvesa. Po eemplo, se tvemos paa < (4. paa sendo e constantes, a tansfomada é dada po dξ paa < ω (4. dξ paa ou anda ( ( paa < ω (4. paa cuja nvesa é - 6 -
27 - 7 - < paa paa ω ω (4. Somemos, agoa, as nvesas defndas nos ntevalos < e. Paa que esta soma valha paa todo (, ntoduzmos uma função F da segunte foma: < paa paa F F ω ω (4.4 Somando, temos F ω (4.5 F ω (4.6 F deve se uma função tal que, em <, / ω, e em, / ω, mantendo a equação (4.. Desta foma, F é detemnada a pat de: paa <, F F ω ω ω (4.7 paa, F F ω ω ω ω (4.8
28 É fácl ve que F pode se escta como F ω (4.9 e a nvesa de (4. é dada po ˆ ω ω ω (4. f ( Ou anda, se a condutvdade témca fo uma função eponencal da tempeatua: α ep( β (4. sendo α e β constantes postvas, a nvesa da tansfomada de choff α ω α ep( βξ dξ [ ep( β ep( β ] (4. β é faclmente calculada: βω lnep( β β α (4. Obs.: nem sempe a nvesa podeá se detemnada analtcamente. A altenatva é uma nvesão numéca. 4. Constundo a solução a pat de uma seqüênca de poblemas lneaes A solução de dv [ gad ( ω ] q& em Ω [ ] ( ˆ gad ( ω n h f ( ω sobe Ω (
29 pode se epesentada pelo lmte da seqüênca não-decescente [ Φ, Φ, Φ,...] elementos são obtdos a pat da solução dos poblemas lneaes abao:, cujos [ gad ( Φ ] [ gad ( Φ ] h fˆ ( Φ dv β q & n αφ [ ] αφ em Ω β sobe Ω (4.5 onde α é uma constante (sufcentemente gande paa que a seqüênca seja nãodecescente e Φ. É mpotante nota que, paa cada, a função Φ é a ncógnta e a função Φ é conhecda. Então, ˆ f ( Φ é sempe conhecda em (4.5, sendo estmada a pat da segunte equação: Φ fˆ ( Φ ˆ( ξ dξ (4.6 Paa cada posção espacal, a az da equação acma é únca. Esta uncdade é gaantda pela equação (4.9. Mas uma vez, a constante α deve se gande o sufcente paa gaant que, em qualque ponto de Ω, Φ Φ. Em Gama [] tal esultado é povado, assm como é fonecdo um lmte supeo paa o valo de α, Gama, [4]. Paa o poblema consdeado neste tabalho é sufcente escolhe α tal que h α (4.7 mn onde mn é o meno valo da condutvdade témca. 4.4 Convegênca - 9 -
30 O lmte da seqüênca[ Φ, Φ, Φ,...], denotada aqu po Φ este e é, de fato, uma solução do poblema. Paa pova esta assetva, comecemos mostando que uma solução de (4.4. Em outas palavas Φ é dv [ gad ( Φ ] q& em Ω [ Φ ] ( ˆ gad ( n h f ( Φ sobe Ω (4.8 Desde que β seja dado po β [ f ˆ ] ( Φ Φ h α (4.9 temos que (4.5 e (4.8 concdem. Então, Φ é uma solução. Agoa, levando em conta que a seqüênca é não-decescente e tem um lmte supeo, gaantmos a convegênca, uma vez que a solução de (4.8 petence ao mesmo espaço de soluções de (4.5 paa cada, Helmbeg, 974 [5], ohn, 98 [6]. Vejamos agoa tês eemplos de aplcação do pocedmento apesentado. 4.5 Eemplos 4.5. Eemplo Seja uma egão ocupada po um copo esféco com geação de calo unfome, nseda num únco meo, com h e, em um ceto sstema de undades. d d d d d d sobe em < (4.4 Assume-se que epesenta uma tempeatua absoluta e. A solução é faclmente alcançada e dada po - -
31 - - ( / 9 (4.4 Agoa, empeguemos o pocedmento poposto. Com a tansfomada de choff, o poblema esulta em sobe 9 4 ( ˆ em / < f d d d d d d ω ω ω ω (4.4 O pocedmento lnea paa obte os elementos da seqüênca é epesentado como segue: d d d d d d Φ Φ Φ Φ < Φ α β β α / 9 4 sobe em (4.4 ou, smplesmente po sobe 9 4 em / Φ Φ Φ Φ < Φ d d d d d d α α (4.44 Como o poblema só tem sentdo físco paa >, temos que mn >. Desta foma, podemos tabalha com qualque α /. Usemos α! A solução geal da equação paa < Φ d d d d (4.45
32 - - é paa 6 < Φ C (4.46 onde a constante C, paa >, é obtda das condções de contono. Em outas palavas / C C C (4.47 Então, C C C (4.48 A constante C é obtda a pat de C C (4.49 Se usássemos α, teíamos C C C (4.5 e a constante C sea obtda de 6 6 C C (4.5 A tabela 4. apesenta uma compaação ente os valoes obtdos paa C com os dos valoes dstntos de α.
33 α α C, ,8, , , ,549576,584, , , , , , , , , , , , , ,999998, , , , , , , ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, ,, abela 4. compaação ente esultados obtdos com α e α. É fácl mosta que C. Potanto, o lmte da seqüênca é dado po Φ 6 paa < (4.5 A solução é eatamente o lmte da seqüênca. Levando em conta que / ˆ 4 ω f ( (4.5 ω 9 temos o segunte esultado (concdente com a solução eata, pevamente obtda - -
34 - 4 - / ( Eemplo Pensemos em outo caso, epesentado po ( Ω Ω sobe em h d d q d d d d & (4.55 onde q&, e h são constantes postvas conhecdas e é uma função da tempeatua dada po (4.56 sendo uma constante postva e conhecda. Este modelo desceve um poblema de condução de calo num copo clíndco de ao R, que ocupa uma egão Ω com fontea Ω, e cujas faces cculaes são soladas temcamente. Aplquemos então o pocedmento poposto. A tansfomada de choff paa este poblema, bem como sua nvesa, são epesentadas po / 4 ( ˆ f d ω ω ω ψ ψ ω (4.57 A tansfomada nos pemte eesceve o poblema na foma
35 - 5 - ( Ω Ω sobe ( ˆ em f h d d q d d d d ω ω ω & (4.58 omemos a solução como sendo o lmte da seqüênca de poblemas lneaes cujas soluções são Φ, Φ, Φ,..., Φ e onde cada elemento da seqüênca é dado po [ ] f h d d q d d d d Φ Φ Ω Φ Φ Ω Φ α β β α ( ˆ sobe em & (4.59 onde / 4 ( ˆ f Φ Φ Φ (4.6 Resolvendo a equação que caega o temo dfusvo temos que 4 Φ C q& (4.6 com 4 R q C & Φ em R. A constante C pode se detemnada a pat da condção de contono ( R: Φ Φ Φ R q R q d d β α β α & & (4.6
36 Reescevendo C apenas em função de Φ temos C q& α [ ˆ q& f ( Φ ] Φ R R h α 4 (4.6 Lembando que ˆ f ( Φ é calculada a pat de (4.6. Fnalmente, a solução geal de (4.58 seá Φ & q 4 C (4.64 A pat da tansfomada equação (4.57 podemos detemna a solução de (4.55, utlzando a solução encontada paa Φ : Φ Φ 4 / (4.65 Utlzemos os seguntes valoes paa os paâmetos físcos e geométcos paa enconta o valo da constante C: W/m; h W/m²; 98 ; q& W/m³; R m. h Levando em conta a condção de convegênca da seqüênca α temos que α. Analsemos tês valoes paa α:, e. mn - 6 -
37 α α α C 9, 566, ,5-697, , , , , , ,66 567, , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , ,47 567, , , , , , , , , , , , , , , , , , , , , , , , , , abela 4. compaação ente esultados obtdos com α, α e α. Resolvendo o sstema (4.55 po métodos clásscos chegamos à solução: q& 4 M q& M 4 4 (4.66 onde a constante de ntegação M é calculada a pat de - 7 -
38 M qr & h qr & 4 qr & h h (4.67 que, nsendo os valoes das constantes do poblema é gual a 5646,665 W/m. Paa que as duas soluções sejam guas é necessáo que M C (4.68 Paa dos valoes de α e a constante C convegu paa (567,665, que atende à condção estabelecda em (4.68, com a dfeença que, paa α, C atngu o lmte muto mas apdamente do que paa α. Note anda que paa α, que vola a estção α, a sée smplesmente não convege. A conclusão fnal é que ambos os métodos esultam na mesma solução: ( 5646, ,665 4 ( Eemplo Como fo dto na seção 4., a seqüênca de funções Φ, que epesenta a tansfomada de choff paa cada teação, é não-decescente, desde que seja escolhdo um α adequado. Os dos eemplos anteoes já confmam esta popedade. Anda assm, consdeemos um outo poblema, no qual seá possível obseva gafcamente o cescmento da seqüênca e a convegênca das soluções obtdas em cada passo do pocesso teatvo paa a solução fnal. O poblema é matematcamente epesentado pelo sstema h h q& ( em < < L em L ( em (4.7 onde a condutvdade témca é dada po - 8 -
39 (4.7 A solução analítca deste poblema é epesentada mplctamente pela equação q & ( h h (4.7 onde é a tempeatua em e é dada po ql & ql ql hl ( hl h h ql ql hl h h (4.7 Usando os seguntes valoes paa as constantes: h W/m²; ; q& W/m³; L m. obtemos o campo de tempeatua mostado na póma fgua: - 9 -
40 Fgua 4. cuva de tempeatua epesentando solução do sstema (4.7. Empeguemos o pocedmento teatvo poposto paa o mesmo poblema. Plotando as soluções obtdas a pat da centésma teação em dante (plota os esultados desde o pmeo elemento da seqüênca pejudcaa a vsualzação podemos ve claamente o pocesso de convegênca paa a solução mostada pela fgua anteo, obtda po métodos clásscos de esolução de sstema de EDP s o campo de tempeatua do centésmo elemento da seqüênca é o mas nfeo da fgua
41 Fgua 4. seqüênca de soluções obtdas pelo método teatvo (cuvas em azul compaada com a solução dada po (4.7 e (4.7 (cuva em vemelho. Fgua 4. compaação do esultado fnal obtdo pelo pocedmento teatvo com a solução dada po (4.7 e (4.7. É fácl nota o compotamento cescente da seqüênca de poblemas lneaes e o pocesso de convegênca paa a solução eata do sstema (
42 5 MÉODOS NUMÉRCOS EM PROBLEMAS DE RANSMSSÃO DE CALOR Consdee o segunte poblema: dv[ gad ( ] q& em Ω 4 [ gad ( ] n h( εσ αg sobe Ω (5. Este modelo desceve a dstbução de tempeatuas de um ceto copo que ocupa uma egão Ω. Paa que conheçamos o valo da tempeatua em cada ponto do domíno Ω é pecso esolve a EDP sujeta às condções de contono defndas sobe Ω. Os métodos analítcos de solução, quando patcáves, povêem solução eata do sstema (5.. No entanto, o númeo de poblemas de engenhaa que podem se esolvdos analtcamente é etemamente lmtado, seja devdo à pesença de temos não-lneaes ou em conseqüênca de geometas compleas. Os métodos numécos são uma altenatva paa mutos dos casos não alcançados pelo feamental analítco conhecdo, poém fonecem sempe soluções que caegam algum eo assocado. Nos pocedmentos numécos o domíno, antes contínuo, é dscetzado, bem como a EDP defnda nele, que pode anda se dscetzada no tempo (o que não é necessáo paa poblema (5., que não possu dependênca do tempo. Os métodos de análse numéca, ao tata a solução em um númeo fnto de pontos dscetos, smplfcam a esolução do sstema de equações dfeencas tansfomando-o num sstema de equações algébcas. Dente os métodos numécos clásscos de esolução de EDP s estão o Método das Dfeenças Fntas (MDF, o Método de Volumes Fntos (MVF e o Método de e Elementos Fntos (MEF. Neste tabalho seão empegados o MDF e o MEF. 5. Dfeenças Fntas O MDF consste em eesceve equações dfeencas de foma que as devadas sejam tomadas em ntevalos fntos, ao nvés de nfntesmas. Ou seja, a devada da função f f ˆ (, defnda po - 4 -
43 df d ( f( f lm (5. sea, em dfeenças fntas, escta como segue: df d ( f( f (5. onde é uma vaação fnta (postva. Vejamos uma aplcação do MDF paa o segunte poblema de tansmssão de calo dv [ gad ( ] q& em Ω [ gad( ] n h( sobe Ω (5.4 Se as equações acma estveem em um sstema de coodenadas catesanas etangulaes e o domíno Ω fo uma placa etangula de lagua L e altua H, o sstema (5.4 pode se eescto na segunte foma: h h h h q& ( ( ( em < < L paa paa L paa ( paa H e < < H (5.5 Dscetzemos o domíno Ω. Devemos estpula um númeo de nós nc paa a deção e nl paa a deção. Desta foma camos uma malha de dfeenças fntas, lustada na fgua 5.. Dgamos que nc 7 e nl
44 H L Fgua 5. malha de dfeenças fntas Os valoes de e são calculados a pat de L nc H nl (5.6 A pat do domíno dsceto o sstema de equações dfeencas (5.5 pode se apomado paa o segunte sstema de equações lneaes algébcas: m, m, h m, m, ncm, nc h, n, n h, n nl, n nl, n ( ( h ( m, nc m, n m, n m, n m, n m, n m, n & q paa < m< nl paa < m< nl paa < n< nc ( paa < n< nc nl, n em < m< nl e < n< nc (5.7 Em eth e Bohn [7] há mas detalhes de como se chega às equações acma. A cada nó da malha há uma equação assocada. No caso de placas etangulaes, os nós das
45 qunas,,,nc, nl,, nl,nc não fazem pate do sstema lnea, podendo se calculados pela méda atmétca dos dos nós vznhos. Desta foma, paa este eemplo, a solução apomada do poblema (5.5 sea obtda da solução de um sstema de 8 equações lneaes (genealzando, paa placas etangulaes, são nl nc 4 equações. Quanto à esolução do sstema lnea há dvesas metodologas, sejam apomadas (e.g. métodos teatvos de Gauss-Sedel ou acob ou eatas (po meo de decomposção LU, nvesão deta da matz dos coefcentes, ente outos camnhos. 5.. Eemplo Vejamos uma aplcação do MDF paa o poblema -D epesentado po (5.5, com os seguntes valoes paa as popedades físcas: h 5 W/m²; 5 W/m; ; q& 5 W/m³; A placa tem 5m de lagua e m de altua. É utlzada uma malha 4 4, e paa esolve o sstema de equações lneaes empegamos o método teatvo Gauss-Sedel. O esultado é apesentado na fgua
46 Fgua 5. campo de tempeatuas em placa etangula. odas popedades físcas são constantes. Como espeado, a dstbução de tempeatuas apesenta váas smetas. 5.. Eemplo Consdeemos o mesmo poblema do eemplo anteo poém com geação ntena de enega dependente da posção q & qˆ (,. Utlzemos q & (5.8 O campo de tempeatuas calculado é gafcamente epesentado a segu
47 Fgua 5. campo de tempeatuas em placa com geação de enega dependente da posção. 5.. Eemplo Anda fazendo pequenas mudanças no mesmo poblema, consdeemos o coefcente de toca de calo po convecção h vaável com a posção, mantendo a elação paa q& dada pela equação (5.8. Utlzemos as seguntes funções paa h (absolutamente abtáas e sem compometmento físco: h h h h, h W/m, π (5.9 h hsen, h W/m, paa L h h 4, h W/m, paa paa L (, h W/m, paa H 4 4 Resultado:
48 Fgua 5.4 campo de tempeatuas em placa com geação de enega e coefcente de flme dependentes da posção. 5. Elementos Fntos Fomulemos a solução em elementos fntos paa a equação q& em Ω (5. sujeta às seguntes condções de contono: j n h ( sobe Γ (5. Este é um poblema bdmensonal de condução de calo num copo sujeto à le de Newton do esfamento. Os paâmetos físcos (condutvdade témca, q& (geação
49 ntena de calo e h (coefcente de toca de calo po convecção seão consdeados constantes. 5.. Em busca da foma faca das equações govenantes A foma faca das equações que govenam o poblema consste no estabelecmento de equações ntegas sobe o domíno Ω e o contono Γ do copo, efeentes à satsfação destas equações em um sentdo médo, em oposção ao sentdo estto pontual da foma fote da equação (5.. Obs.: Nesta seção utlzaemos letas em negto, maúsculas e mnúsculas, paa ndca matzes. Multplcando a EDP defnda em Ω po uma função abtáa w ˆ (,, denomnada função teste ou função peso, obtemos a equação w ˆ (, q& (5. a qual, se ntegada sobe o domíno Ω, esulta em Ω w ˆ (, q& dω (5. Note que, caso seja detemnado o campo de tempeatua paa o qual a equação (5. seja satsfeta, então a equação (5. também é satsfeta paa qualque que seja a função w ˆ (,. Po outo lado, caso se detemne uma solução ˆ(, que satsfaça a equação (5. paa qualque função w ˆ (,, então ˆ(, também é solução de (5.. Utlzando o conceto de devada do poduto, é fácl ve que
50 - 5 - Ω Ω Ω Ω d wq w w w w d q w & & (5.4 Agoa, pelo teoema de Gauss ou da dvegênca, temos que Γ Ω Γ Ω nd j w d w w (5.5 Fazendo q j (5.6 a equação (5. pode se eescta como ( Γ Ω Γ Ω d n w q d wq w w & (5.7 O fluo de calo n q que cuza a fontea Γ é gual a ( h, o qual, nsedo na segunda ntegal de (5.7, esulta em ( ( Γ Γ Γ Γ d h w h d n w q (5.8 e a equação (5.7 passa a se dada po ( Γ Ω Γ Ω d h w h d wq w w & ( Dscetzação do domíno em elementos fntos
51 O solução pelo MEF consste em dscetza o domíno do poblema em uma malha de elementos fntos ntelgados atavés de nós. Os elementos podem se de váos tpos, seja com elação ao númeo de gaus de lbedade, seja com o fomato do elemento. Em malhas -d são muto utlzados os elementos tangulaes, que podem se lneaes (nós apenas nos vétces, mn (nós nos vétces e no centóde, ou quadátcos (nós nos vétces e no meo de cada lado do tângulo. Neste poblema utlzaemos elementos tangulaes lneaes. No poblema dsceto de condução de calo as ncógntas passam a se as tempeatuas nodas, ou seja, os valoes do campo de tempeatua avalados nos nós da malha. Paa uma malha de N nós, as tempeatuas nodas seão amazenadas numa únca matz, da segunte foma: (5. M N onde é a tempeatua coespondente ao nó, é a tempeatuas coespondente ao nó, e assm po dante, até o númeo total de nós da malha N. O Método de Elementos Fntos tansfoma a equação dfeencal govenante do poblema em um sstema de equações algébcas que podemos epesenta po F (5. onde é a matz dos coefcentes, em geal denomnada matz de gdez, de odem N N, e F é a matz coluna de temos ndependentes, em geal denomnada veto de foças, de odem N. é a matz (5.. A essênca do MEF basea-se na déa, comum na engenhaa, de esolve um poblema compleo dvdndo-o em poblemas menoes e smples. Veemos agoa, na fomulação do elemento fnto, que a equação (5.9 é esolvda soladamente paa cada elemento, de manea a compo uma apomação paa a solução do poblema ognal dado po (5. e ( fomulação do elemento fnto tangula lnea - 5 -
52 O elemento fnto tangula lnea é um dos mas smples e caacteza-se, como já fo dto, po possu nós apenas nos vétces. A pat dos valoes das tempeatuas nos vétces do tângulo pode-se calcula a tempeatua em qualque ponto do elemento po ntepolação lnea. (, (, (, Fgua 5.5 elemento tangula lnea, com efeênca ao sstema de eos catesanos. No elemento tangula, a matz de ncógntas é oganzada da segunte foma: e (5. onde, e são as tempeatuas nos nós, e, espectvamente Funções de foma do elemento: O MEF povê uma solução apomada paa cada nó da malha. Como já dssemos, a tempeatua no nteo de cada elemento, numa malha de elementos tangulaes lneaes, pode se faclmente obtda po ntepolação lnea. A segunte elação pemte o cálculo da tempeatua ntepolada em qualque ponto do tângulo: a (
53 - 5 - onde [ ] (5.4 a a a a (5.5 a, a e a são constantes a seem detemnadas. A matz a pode se calculada atavés da mposção do valo da tempeatua em cada nó, ou seja ( ( ( a a a a a a a a a,,, (5.6 ou, em foma matcal, a a a (5.7 Numa notação mas compacta temos e Ga (5.8 onde G (5.9 que é a matz que contém as coodenadas dos nós do elemento. A matz de constantes a é, potanto, calculada po
54 e G a (5. sendo det( G G (5. Substtundo a equação (5. na equação (5. chegamos a e G (5. ou anda e N (5. onde G N (5.4 Consdeando a equação (5. e desenvolvendo o poduto acma, temos [ ] N N N N (5.5 onde ( ( ( [ ] ( ( ( [ ] ( ( ( [ ] A N A N A N t t t (5.6
55 N é a matz que contém as funções de ntepolação dos gaus de lbedade nodas, sto é, as tempeatuas nodas, e. Esta matz é usualmente denomnada matz de funções de foma Devada das funções de foma do elemento As devadas do campo de tempeatua, na fomulação do elemento fnto, podem se faclmente detemnadas a pat da equação (5. e epesentadas po e e ( N B gad ( gad (5.7 De manea análoga ao campo de tempeatua, a função de teste w ˆ (, é calculada, dento do elemento, po w Nw e (5.8 sendo w e w w (5.9 w E o gadente de w é calculado po e e ( N w Bw gad ( w gad (5.4 anto paa a tempeatua quanto paa a função teste, a matz B é tal que N N N B gad( N N N N (
56 Calculando as devadas das funções de foma em elação às coodenadas catesanas, chega-se a B (5.4 At 5..6 Foma faca po elemento com as tempeatuas nodas A equação (5.9, foma faca do poblema ognal, tomada paa cada elemento é epesentada po Ω e w w wq& dω w( h h dγ (5.4 e Γ ou po Ω e ( gad dω whdγ wh dγ wqdω Γ e gadw & (5.44 Γ e Ω e Agoa, nsendo em (5.44 as equações (5., (5.7, (5.8 e (5.4, chegamos a e e e e e e ( ( B dω ( Nw h( N dγ ( Nw hdγ ( Nw qd & Ω e Ω Bw (5.45 e Γ e Γ e Ω Levando em conta que e e w e são constantes em Ω e e Γ e, podemos eesceve a equação (5.45 da segunte foma: w (5.46 e e e e Ω Γ Γ Ω e e e ( B BdΩ N NhdΓ N hdγ N qd & Ω Como w e é completamente abtáo, a equação acma esulta em e Ω e e B BdΩ N NhdΓ N h dγ N qd & Ω (5.47 e Γ e Γ e Ω
57 Utlzando a foma compacta apesentada em (5. tomada po elemento temos e e e F (5.49 onde e Ω e B BdA N NhdL (5.5 e Ω e Ω e Ω e F N qda & N h dl (5.5 A segu esolveemos cada uma das ntegas. Depos de calculadas o sstema de equações algébcas estaá ponto paa se esolvdo. Cálculo de B BdA: Ω e Como B depende apenas das coodenadas dos vétces, que são constantes po elemento, a ntegal acma pode se calculada po e Ω B BdA B BA (5.5 t Vale lemba que a matz B é faclmente calculada pela equação (5.4. Note que, tendo em vsta que B é uma matz de odem, a odem do poduto B BAt seá, evdentemente,. Cálculo de N NhdL : Ω e Vamos enomea alguns elementos, apenas paa faclta o desenvolvmento. [ N N ] N (5.5 N
58 Pmeo elemento (N : c b a N (5.54 onde ( ( ( t t t A c A b A a (5.55 Segundo elemento (N : c b a N (5.56 onde ( ( ( t t t A c A b A a (5.57 eceo elemento (N : c b a N (5.58 onde
59 ( ( ( t t t A c A b A a (5.59 A matz esultante da multplcação N N é dada po [ ] N N N N N N N N N N N N N N N N N N N N N N N N N N (5.6 Genealzando cada elemento do poduto acma paa j N N, teemos, paa cada posção da matz N N, epessões da segunte foma: ( ( ( ( ( c c b b b c c b c a a c b a a b a a c b a c b a j j j j j j j j j j j j (5.6 O domíno da ntegal Ω e hdl N N (5.6 seá sempe um segmento de eta um lado de elemento tangula que compõe o contono da malha. As fguas a segu mostam uma malha de elementos tangulaes e um elemento em destaque.
60 Fgua 5.6 malha tangula. Os lados em azul e o lado em vemelho destacam o contono da malha. O tângulo com lado gfado em vemelho é mostado com detalhes na póma fgua. (, Lado petencente ao contono da malha (, (, Fgua 5.7 elemento tangula com lado compondo o contono, mostando as coodenadas dos vétces. A ntegal de lnha (5.6 é calculada sobe o lado em vemelho, que possu um compmento S. Substtundo (5.6 em (5.6, fcamos com a segunte ntegal: [ a a ( a b a b ( a c a c ( b c b c b b c c ] S j j j j j j j j j hdl (5.6 h ( com S aa jdl (
61 S ( a b a b dl j j (5.65 S ( a c a c dl j j (5.66 S ( b c b c dl 4 j j (5.67 S 5 b b dl (5.68 j S 6 cc j dl (5.69 Fazendo e, e paametzando as coodenadas e da segunte foma: s S s S (5.7 as soluções das ntegas acma são dadas po aa j S (5.7 ( a b a b S j j (5.7 ( a c a c S j j (5.7 ( b c b c S 4 j j (
62 bb j 5 S (5.75 cc j 6 S (5.76 Cálculo de N hdl : e Ω Utlzando a mesma epesentação po índces utlzada na ntegal (5.6, esta ntegal epesenta tês ntegas da segunte foma: ( a b c h dl S (5.77 com,,. Os índces coespondem aos elementos da matz [ N N ] A solução paa cada N é, então, dada po N. N S b c ( a b c h dl h S b c a (5.78 Cálculo de N q& da: Ω e Esta ntegal está defnda sobe toda a áea do elemento tangula. A ntegal sobe o tângulo pode se calculada a pat da soma das ntegas sob cada lado do tângulo. A póma fgua lusta a déa
63 Fgua 5.8 elemento tangula, com as ndcações dos sentdos de ntegação. A áea compeendda dento do tângulo é gual a soma das áeas sob cada um dos lados dele, se mantdo o sentdo de ntegação. Com sso, podemos esceve N q& da Ω e como sendo qda ˆ ( ˆ ( ˆ ( N & N qdd & N qdd & N qdd & (5.79 e Ω Lembando que cada ntegal, na pátca, são tês ntegas, cada uma efeente a um elemento N da matz N. A função que atua como lmte supeo da ntegal ntena da pmea pacela de (5.79, denotada po (, é detemnada po, levando em conta que os pontos ncal e fnal da eta são (, e ( ˆ,, ( ˆ (5.8 ou, numa foma mas compacta, - 6 -
64 ( ˆ β α (5.8 onde α e β epesentam os coefcentes angula e lnea da eta, espectvamente. As funções ( ˆ e ( ˆ são obtdas de manea análoga. Então, paa cada elemento N, teemos ( ( ( Ω e qdd c b a qdd c b a qdd c b a N qda ( ˆ ( ˆ ( ˆ & & & & (5.8 Fnalmente, chegamos à solução de cada pacela acma: ( ( ( ( ( ( ( ( c q b q a q qdd c b a ( ˆ β αβ α β α β α & & & & (5.8 ( ( ( ( ( ( ( ( q c b q a q qdd c b a ( ˆ β αβ α β α β α & & & & (5.84 ( ( ( ( ( ( ( ( c q b q a q qdd c b a ( ˆ β αβ α β α β α & & & & ( Atbução das tempeatuas nodas aos elementos da malha Em Souza [8] é apesentada a foma de atbu (5.5 e (5.5 aos elementos coetos na malha atavés da matz de ncdênca, que consttu uma etapa fundamental do método de elementos fntos. Agoa vejamos alguns poblemas de condução de calo esolvdos pelo MEF.
65 5..8 Eemplo físcos: Consdeemos o poblema de condução de calo com os seguntes paâmetos,5 q& 5 h 5 5 em algum sstema de undades. A placa possu lagua e altua guas a. O poblema é matematcamente descto pela equação 5 em < < L e < < H (5.86 sujeta às seguntes condções de contono: ( 5 ( 5 ( 5 paa paa L paa ( 5 paa H (5.87 O domíno fo dscetzado numa malha de elementos tangulaes, confome a fgua
66 Fgua 5.9 Malha de elementos fntos. Os lados pntados de peto são os que compõem o contono. Os nós da malha estão epesentados pelos pontos petos. Note que há apenas tês nós po tângulo, caacteístca do elemento lnea. O campo de tempeatua encontado pelo MEF como solução apomada é epesentado pela fgua a segu
67 Fgua 5. Solução obtda pelo MEF. Compaando a solução obtda po elementos fntos com a solução obtda po dfeenças fntas, a qual é mostada na fgua 5., é fácl pecebe que ambos pocedmentos chegaam a espostas patcamente guas
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC
 4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
4. TÉCNICA APLICADA A ANÁLISE BIDIMENSIONAL COM MEC Este capítulo sevá como base de compaação paa entende os eas objetvos deste tabalho e, a pat dsto, pecebe que alguns concetos aplcados pela técnca desenvolvda
MATEMÁTICA II - Engenharias/Itatiba SISTEMAS LINEARES
 - Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
- Mauco Fabb MATEMÁTICA II - Engenhaas/Itatba o Semeste de Pof Mauíco Fabb a Sée de Eecícos SISTEMAS IEARES IVERSÃO DE MATRIZES (I) Uma mat quadada A é nvetível se est a mat A - tal que AA - I Eecíco Pove
Aula 3 Trabalho e Energia - Bioenergética
 Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Aula 3 Tabalho e Enega - Boenegétca Cálculo deencal Taa de vaação nstantânea de uma unção: lm ( ) ( ) (Função devada) Notação: lm ( ) ( ) d d Cálculo ntegal Áea sob o gáco de uma unção: ( 1 ) ) ( 2 Áea
Eletricidade e Magnetismo II Licenciatura: 1ª Aula (30/07/2012) Prof. Alvaro Vannucci. Revisão das Leis de Gauss, de Ampère e de Faraday
 Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
Eletcdade e Magnetsmo II Lcencatua: ª Aula (3/7/) Pof. Alvao Vannucc evsão das Les de Gauss, de Ampèe e de Faaday Eletzação: as pmeas obsevações sobe eletzação ocoeam apomadamente em apomadamente 6 a.c.
FLUXO E DIVERGENTE DE UM CAMPO VETORIAL
 ISTITUTO DE FÍSIC D UFB DEPRTMETO DE FÍSIC DO ESTDO SÓLIDO DISCIPLI: FÍSIC ERL E EXPERIMETL I FIS 4 FLUXO E DIERETE DE UM CMPO ETORIL Os concetos de dvegente e otaconal estão elaconados aos de fluo e de
ISTITUTO DE FÍSIC D UFB DEPRTMETO DE FÍSIC DO ESTDO SÓLIDO DISCIPLI: FÍSIC ERL E EXPERIMETL I FIS 4 FLUXO E DIERETE DE UM CMPO ETORIL Os concetos de dvegente e otaconal estão elaconados aos de fluo e de
Introdução. Introdução. Introdução Objetivos. Introdução Corpo rígido. Introdução Notação
 Intodução Intodução à obótca Descção espacal e ansfomações (/2) of. Douglas G. Machaet douglas.machaet@dcc.ufmg.b Intodução à obótca - Descção espacal e ansfomações (/2) 2 Intodução osções e Oentações
Intodução Intodução à obótca Descção espacal e ansfomações (/2) of. Douglas G. Machaet douglas.machaet@dcc.ufmg.b Intodução à obótca - Descção espacal e ansfomações (/2) 2 Intodução osções e Oentações
5. TÉCNICA PROPOSTA PARA ANÁLISE 3D
 5. TÉCNICA PROPOSTA PARA ANÁLISE 3D Neste capítulo seá tatado de foma defntva o objetvo pncpal deste tabalho que é desenvolve uma técnca unfcada paa avala ntegas bdmensonas, tal como fo feto paa o caso
5. TÉCNICA PROPOSTA PARA ANÁLISE 3D Neste capítulo seá tatado de foma defntva o objetvo pncpal deste tabalho que é desenvolve uma técnca unfcada paa avala ntegas bdmensonas, tal como fo feto paa o caso
F-328 Física Geral III
 F-328 Físca Geal III Aula exploatóa Cap. 24 UNICAMP IFGW F328 1S2014 F328 1S2014 1 Pontos essencas Enega potencal elétca U Sstema de cagas Equvalente ao tabalho executado po um agente exteno paa taze as
F-328 Físca Geal III Aula exploatóa Cap. 24 UNICAMP IFGW F328 1S2014 F328 1S2014 1 Pontos essencas Enega potencal elétca U Sstema de cagas Equvalente ao tabalho executado po um agente exteno paa taze as
Prof. Anderson Coser Gaudio Departamento de Física Centro de Ciências Exatas Universidade Federal do Espírito Santo
 POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
POLEMAS ESOLVIDOS DE FÍSICA Pof. Andeson Cose Gaudo Depatamento de Físca Cento de Cêncas Eatas Unvesdade Fedeal do Espíto Santo http://www.cce.ufes.b/andeson andeson@npd.ufes.b Últma atualzação: 3/8/5
MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO
 Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
Depatamento de Físca da Faculdade de Cêncas da Unvesdade de Lsboa Mecânca A 008/09 1. Objectvo MOMENTO DE INÉRCIA DE UM CORPO RÍGIDO Estudo do movmento de otação de um copo ígdo. Detemnação do momento
Curso de Análise Matricial de Estruturas 1 II.6 FORMULAÇÃO DAS MATRIZES DE FLEXIBILIDADE E RIGIDEZ EM TERMOS DE ENERGIA
 Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
Cso de nálse Matcal de sttas II. FOMÇÃO DS MTIZS D FXIBIIDD IGIDZ M TMOS D NGI II.. Tabalho, nega de Defomação e nega Complementa de Defomação Defnções: dτ d tabalho o enega de defomação; dτ d tabalho
INTEGRAL DE LINHA E ROTACIONAL DE UM CAMPO VETORIAL
 ISTITUTO DE FÍSICA DA UFBA DEPARTAMETO DE FÍSICA DO ESTADO SÓLIDO DISCIPLIA: FÍSICA ERAL E EXPERIMETAL IV FIS ITERAL DE LIHA E ROTACIOAL DE UM CAMPO VETORIAL Sea um campo de velocdades v não unfome em
ISTITUTO DE FÍSICA DA UFBA DEPARTAMETO DE FÍSICA DO ESTADO SÓLIDO DISCIPLIA: FÍSICA ERAL E EXPERIMETAL IV FIS ITERAL DE LIHA E ROTACIOAL DE UM CAMPO VETORIAL Sea um campo de velocdades v não unfome em
Física Geral. Força e Torque
 ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
ísca Geal oça e Toqe oças Se há nteação ente dos objetos, então este ma foça atando sobe os dos objetos. Se a nteação temna, os copos deam de epementa a ação de foças. oças estem somente como esltado de
Resoluções dos exercícios propostos
 da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
da físca ndade Capítulo 9 Geadoes elétcos esoluções dos execícos popostos 1 P.19 Dados: 4 ; 1 Ω; 0 a) 0 4 1 4 b) Pot g Pot g 4 4 Pot g 96 W Pot º Pot º 0 4 Pot º 80 W Pot d Pot g Pot º Pot d 96 80 Pot
Física I. Aula 9 Rotação, momento inércia e torque
 Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
Físca º Semeste de 01 nsttuto de Físca- Unvesdade de São Paulo Aula 9 Rotação, momento néca e toque Pofesso: Vald Gumaães E-mal: valdg@f.usp.b Fone: 091.7104 Vaáves da otação Neste tópco, tataemos da otação
ELECTROMAGNETISMO E ÓPTICA Cursos: MEBiom + MEFT + LMAC 1 o TESTE (16/4/2016) Grupo I
 ELECTROMAGNETIMO E ÓPTICA Cusos: MEBom + MEFT + LMAC o TETE (6/4/06) Gupo I A fgua epesenta um conensao esféco e um conuto eteo 3 também esféco. O conensao é consttuío po um conuto nteo e ao R cm e po
ELECTROMAGNETIMO E ÓPTICA Cusos: MEBom + MEFT + LMAC o TETE (6/4/06) Gupo I A fgua epesenta um conensao esféco e um conuto eteo 3 também esféco. O conensao é consttuío po um conuto nteo e ao R cm e po
Capítulo 2 Galvanômetros
 Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
Capítulo 2 Galvanômetos 2.. Intodução O galvanômeto é um nstumento eletomecânco que é, bascamente, um meddo de coente elétca de pequena ntensdade. Exstem bascamente dos tpos de galvanômetos, que são os
EQUAÇÕES DINÂMICAS DE MOVIMENTO PARA CORPOS RÍGIDOS UTILIZANDO REFERENCIAL MÓVEL
 NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
NTAS DE AULA EQUAÇÕES DINÂICAS DE IENT PARA CRPS RÍIDS UTILIZAND REFERENCIAL ÓEL RBERT SPINLA BARBSA RSB PLI USP LDS TIAÇÃ Paa a obtenção das equações dnâmcas de um copo ígdo pode se convenente epessa
Existem várias aplicações onde a medição do fluxo de calor é desejada: análise de cargas térmicas, isolamento de tubulações, etc.
 MEDIDORES DE FLUXO DE CALOR Exstem váas aplcações onde a medção do fluxo de calo é desejada: análse de cagas témcas, solamento de tubulações, etc. Meddo tpo Plug Quando o fluxo de calo é mposto na supefíce
MEDIDORES DE FLUXO DE CALOR Exstem váas aplcações onde a medção do fluxo de calo é desejada: análse de cagas témcas, solamento de tubulações, etc. Meddo tpo Plug Quando o fluxo de calo é mposto na supefíce
TICA. Sistemas Equivalentes de Forças MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA. Nona Edição CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
 CPÍTULO 3 Copos ECÂNIC VETORIL PR ENGENHEIROS: ESTÁTIC TIC Fednand P. Bee E. Russell Johnston, J. Notas de ula: J. Walt Ole Teas Tech Unvest Rígdos: Sstemas Equvalentes de Foças 2010 The cgaw-hll Companes,
CPÍTULO 3 Copos ECÂNIC VETORIL PR ENGENHEIROS: ESTÁTIC TIC Fednand P. Bee E. Russell Johnston, J. Notas de ula: J. Walt Ole Teas Tech Unvest Rígdos: Sstemas Equvalentes de Foças 2010 The cgaw-hll Companes,
Fundamentos da Eletrostática Aula 15 Expansão Multipolar II
 Fundamentos da Eletostátca Aula 5 Expansão Multpola II Pof Alex G Das Pof Alysson F Fea A Expansão Multpola Na aula passada, consdeamos uma dstbução de cagas muto especíca paa enconta o potencal do dpolo
Fundamentos da Eletostátca Aula 5 Expansão Multpola II Pof Alex G Das Pof Alysson F Fea A Expansão Multpola Na aula passada, consdeamos uma dstbução de cagas muto especíca paa enconta o potencal do dpolo
Física I IME. 2º Semestre de Instituto de Física Universidade de São Paulo. Professor: Luiz Nagamine Fone: 3091.
 Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
Físca E º Semeste de 015 nsttuto de Físca Unvesdade de São Paulo Pofesso: uz Nagamne E-mal: nagamne@f.usp.b Fone: 091.6877 0, 04 e 09 de novembo otação º Semeste de 015 Cnemátca otaconal Neste tópco, tataemos
Para duas variáveis aleatórias X e Y define-se Função Distribuição Cumulativa CDF F XY (x,y)
 Vaáves Aleatóas (contnuação) Po. Waldec Peella Dstbução Conunta: po: Paa duas vaáves aleatóas e dene-se Função Dstbução Cuulatva CDF F (,y) P ( e y ) = F (,y ) e a Função Densdade de Pobabldade de Pobabldade
Vaáves Aleatóas (contnuação) Po. Waldec Peella Dstbução Conunta: po: Paa duas vaáves aleatóas e dene-se Função Dstbução Cuulatva CDF F (,y) P ( e y ) = F (,y ) e a Função Densdade de Pobabldade de Pobabldade
CAPÍTULO 10 DINÂMICA DO MOVIMENTO ESPACIAL DE CORPOS RÍGIDOS
 94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
94 CAPÍTUL 10 DNÂCA D VENT ESPACAL DE CPS ÍDS As equações geas que desceve o ovento de u copo ígdo no espaço pode se dvddas e dos gupos: as equações que desceve o ovento do cento de assa, equações de Newton
Breve Revisão de Cálculo Vetorial
 Beve Revsão de Cálculo Vetoal 1 1. Opeações com vetoes Dados os vetoes A = A + A j + A k e B = B + B j + B k, dene-se: Poduto escala ente os vetoes A e B A B A B Daí, cos A AB cos A B B A A B B AB A B
Beve Revsão de Cálculo Vetoal 1 1. Opeações com vetoes Dados os vetoes A = A + A j + A k e B = B + B j + B k, dene-se: Poduto escala ente os vetoes A e B A B A B Daí, cos A AB cos A B B A A B B AB A B
Uma sonda de exploração espacial prepara-se para colocar um satélite de comunicações numa órbita em redor do planeta Marte.
 Lcencatua em Engenhaa Geológca e de Mnas Lcencatua em Matemátca Aplcada e Computação Mestado Integado em Engenhaa Bomédca Mecânca e Ondas 1º Ano -º Semeste º Teste/1º Exame 0/06/017 11:30h Duação do teste:
Lcencatua em Engenhaa Geológca e de Mnas Lcencatua em Matemátca Aplcada e Computação Mestado Integado em Engenhaa Bomédca Mecânca e Ondas 1º Ano -º Semeste º Teste/1º Exame 0/06/017 11:30h Duação do teste:
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO. Departamento de Engenharia Mecânica
 PME 00 MECÂNIC P3 6 de unho de 009 Duação da Pova: 0 mnutos (não é pemtdo uso de calculadoas) ENÇÃ: a pova consta de 3 questões de aplcação da teoa estudada valendo 0 pontos e de 4 questões teócas, cua
PME 00 MECÂNIC P3 6 de unho de 009 Duação da Pova: 0 mnutos (não é pemtdo uso de calculadoas) ENÇÃ: a pova consta de 3 questões de aplcação da teoa estudada valendo 0 pontos e de 4 questões teócas, cua
4 O Método de Partículas SPH
 O Método de Patículas SPH 46 4 O Método de Patículas SPH O método SPH fo apesentado tanto po Lucy 1977, quanto po Gngold e Monaghan 1977 paa esolve, num pmeo momento, poblemas astofíscos em espaço tdmensonal.
O Método de Patículas SPH 46 4 O Método de Patículas SPH O método SPH fo apesentado tanto po Lucy 1977, quanto po Gngold e Monaghan 1977 paa esolve, num pmeo momento, poblemas astofíscos em espaço tdmensonal.
Física Geral I - F Aula 13 Conservação do Momento Angular e Rolamento. 2 0 semestre, 2010
 Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
Físca Geal - F -18 Aula 13 Consevação do Momento Angula e Rolamento 0 semeste, 010 Consevação do momento angula No sstema homem - haltees só há foças ntenas e, potanto: f f z constante ) ( f f Com a apoxmação
2 Teoria Geométrica da Difração - Teoria Uniforme da Difração.
 Teoa Geométca da fação - Teoa Unfome da fação. A análse do espalhamento e adação das ondas eletomagnétcas sobe os objetos utlzando soluções modas é estta a objetos cujas supefíces são desctas faclmente
Teoa Geométca da fação - Teoa Unfome da fação. A análse do espalhamento e adação das ondas eletomagnétcas sobe os objetos utlzando soluções modas é estta a objetos cujas supefíces são desctas faclmente
Os fundamentos da Física Volume 3 1. Resumo do capítulo
 Os fundamentos da Físca Volume 3 1 Capítulo 13 Campo magnétco Ímãs são copos que apesentam fenômenos notáves, denomnados fenômenos magnétcos, sendo os pncpas: I. ataem fagmentos de feo (lmalha). o caso
Os fundamentos da Físca Volume 3 1 Capítulo 13 Campo magnétco Ímãs são copos que apesentam fenômenos notáves, denomnados fenômenos magnétcos, sendo os pncpas: I. ataem fagmentos de feo (lmalha). o caso
Aula 7: Potencial Elétrico
 Unvesdade Fedeal do Paaná Seto de Cêncas Exatas Depatamento de Físca Físca III Po. D. Rcado Luz Vana Reeêncas bblogácas: H. 6-, 6-, 6-3, 6-4, 6-5, 6-6, 6-, 6- S. 4-, 4-3, 4-4, 4-5 T. -, -, -3, -6 Aula
Unvesdade Fedeal do Paaná Seto de Cêncas Exatas Depatamento de Físca Físca III Po. D. Rcado Luz Vana Reeêncas bblogácas: H. 6-, 6-, 6-3, 6-4, 6-5, 6-6, 6-, 6- S. 4-, 4-3, 4-4, 4-5 T. -, -, -3, -6 Aula
Volnei Borges*, Laci Maria Francio** e Justina Inês Fronza Brigoni**
 O USO DO MÉTODO LTS N NA OBTENÇÃO DE PARÂMETROS DE BLINDAGENS MÚLTIPLAS PARA NÊUTRONS E FÓTONS Volne Boges*, Lac Maa Fanco** e Justna Inês Fonza Bgon** *Depatamento de Engenhaa Nuclea da Unvesdade Fedeal
O USO DO MÉTODO LTS N NA OBTENÇÃO DE PARÂMETROS DE BLINDAGENS MÚLTIPLAS PARA NÊUTRONS E FÓTONS Volne Boges*, Lac Maa Fanco** e Justna Inês Fonza Bgon** *Depatamento de Engenhaa Nuclea da Unvesdade Fedeal
Consideremos uma distribuição localizada de carga elétrica, de densidade ρ(x), sob a ação de um potencial eletrostático externo ϕ E (x).
 pansão Multpola da nega de uma Dstbução de Caga sob a Ação de Potencal letostátco teno. Físca Nuclea e de Patículas Cesa Augusto Zen Vasconcellos Consdeemos uma dstbução localzada de caga elétca, de densdade
pansão Multpola da nega de uma Dstbução de Caga sob a Ação de Potencal letostátco teno. Físca Nuclea e de Patículas Cesa Augusto Zen Vasconcellos Consdeemos uma dstbução localzada de caga elétca, de densdade
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO
 ESCO POITÉCNIC D UNIESIDDE DE SÃO PUO venda Pofesso Mello Moaes, nº 31. cep 558-9, São Paulo, SP. Telefone: 11 391 5337 Fa: 11 3813 1886 Depatamento de Engenhaa Mecânca PME 3 MECÂNIC II Pmea Pova 9 de
ESCO POITÉCNIC D UNIESIDDE DE SÃO PUO venda Pofesso Mello Moaes, nº 31. cep 558-9, São Paulo, SP. Telefone: 11 391 5337 Fa: 11 3813 1886 Depatamento de Engenhaa Mecânca PME 3 MECÂNIC II Pmea Pova 9 de
Versão 2 RESOLUÇÃO GRUPO I. = 0. Tal permite excluir a opção C.
 Teste Intemédo de Matemátca A Vesão Teste Intemédo Matemátca A Vesão Duação do Teste: 90 mnutos.05.0.º Ano de Escoladade Deceto-Le n.º 7/00, de 6 de maço RESOLUÇÃO GRUPO I. Resposta (C) Tem-se: a b log
Teste Intemédo de Matemátca A Vesão Teste Intemédo Matemátca A Vesão Duação do Teste: 90 mnutos.05.0.º Ano de Escoladade Deceto-Le n.º 7/00, de 6 de maço RESOLUÇÃO GRUPO I. Resposta (C) Tem-se: a b log
Estudo da Propagação de Chorumes em Aquíferos
 Estudo da opagação de houmes em Aquífeos Macele Jaques nto Insttuto oltécnco, Unvesdade do Estado do Ro de Janeo, ova Fbugo-RJ Macus acheco e João Flávo Vasconcellos Insttuto oltécnco, Unvesdade do Estado
Estudo da opagação de houmes em Aquífeos Macele Jaques nto Insttuto oltécnco, Unvesdade do Estado do Ro de Janeo, ova Fbugo-RJ Macus acheco e João Flávo Vasconcellos Insttuto oltécnco, Unvesdade do Estado
CÁLCULO DIFERENCIAL E INTEGRAL II 014.2
 CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
CÁLCULO IFERENCIAL E INTEGRAL II Obsevações: ) Todos os eecícios popostos devem se esolvidos e entegue no dia de feveeio de 5 Integais uplas Integais uplas Seja z f( uma função definida em uma egião do
4/10/2015. Física Geral III
 Físca Geal III Aula Teóca 9 (Cap. 6 pate 3/3): ) Cálculo do campo a pat do potencal. ) Enega potencal elétca de um sstema de cagas. 3) Um conduto solado. Po. Maco R. Loos Cálculo do campo a pat do potencal
Físca Geal III Aula Teóca 9 (Cap. 6 pate 3/3): ) Cálculo do campo a pat do potencal. ) Enega potencal elétca de um sstema de cagas. 3) Um conduto solado. Po. Maco R. Loos Cálculo do campo a pat do potencal
2ªAula do cap. 11. Quantidade de Movimento Angular L. Conservação do Momento Angular: L i = L f
 2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
2ªAula do cap. 11 Quantdade de Movmento Angula. Consevação do Momento Angula: f Refeênca: Hallday, Davd; Resnck, Robet & Walke, Jeal. Fundamentos de Físca, vol.. 1 cap. 11 da 7 a. ed. Ro de Janeo: TC.
CONHECIMENTOS ESPECÍFICOS ENGENHEIRO / ÁREA ELETRICISTA
 CONHECIMENTOS ESPECÍFICOS ENGENHEIRO / ÁREA ELETRICISTA 26. Obseve a fgua abaxo. Consdeando que a fgua lusta uma ponte esstva, na qual fo nseda uma esstênca R = 8 Ω ente os nós C e D, a coente desse ccuto
CONHECIMENTOS ESPECÍFICOS ENGENHEIRO / ÁREA ELETRICISTA 26. Obseve a fgua abaxo. Consdeando que a fgua lusta uma ponte esstva, na qual fo nseda uma esstênca R = 8 Ω ente os nós C e D, a coente desse ccuto
Potencial Elétrico. Prof. Cláudio Graça 2012
 Potencal Elétco Po. Cláudo Gaça Campo elétco e de potencal Campo e Potencal Elétcos E Potencal gavtaconal Potencal Elétco O potencal elétco é a quantdade de tabalho necessáo paa move uma caga untáa de
Potencal Elétco Po. Cláudo Gaça Campo elétco e de potencal Campo e Potencal Elétcos E Potencal gavtaconal Potencal Elétco O potencal elétco é a quantdade de tabalho necessáo paa move uma caga untáa de
Distribuições Discretas. Estatística. 6 - Distribuição de Probabilidade de Variáveis Aleatórias Discretas UNESP FEG DPD
 Estatístca 6 - Dstbução de Pobabldade de Vaáves Aleatóas Dscetas 06-1 Como ocoe na modelagem de fenômenos detemnístcos em que algumas funções têm papel mpotante tas como: função lnea, quadátca exponencal,
Estatístca 6 - Dstbução de Pobabldade de Vaáves Aleatóas Dscetas 06-1 Como ocoe na modelagem de fenômenos detemnístcos em que algumas funções têm papel mpotante tas como: função lnea, quadátca exponencal,
Instituto Tecnológico de Aeronáutica VIBRAÇÕES MECÂNICAS MPD-42
 VIBRAÇÕES MECÂNICAS MPD-4 1 SISTEMAS CONTÍNUOS: SOUÇÃO EXATA MPD-4 Sstemas contínuos: solução eata Intoução Sstemas scetos e sstemas contínuos epesentam os tpos e sstemas feentes? Ambos são meas epesentações
VIBRAÇÕES MECÂNICAS MPD-4 1 SISTEMAS CONTÍNUOS: SOUÇÃO EXATA MPD-4 Sstemas contínuos: solução eata Intoução Sstemas scetos e sstemas contínuos epesentam os tpos e sstemas feentes? Ambos são meas epesentações
Dinâmica do Sistema Solar
 Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
Dnâmca do Sstema Sola Intodução Poblema de dos copos Poblema de N copos e movmento planetáo Dnâmca de pequenos copos Poblema de 3 copos Movmento essonante Caos Intodução Segunda le de Newton F = Le da
O perímetro da circunferência
 Univesidade de Basília Depatamento de Matemática Cálculo 1 O peímeto da cicunfeência O peímeto de um polígono de n lados é a soma do compimento dos seus lados. Dado um polígono qualque, você pode sempe
Univesidade de Basília Depatamento de Matemática Cálculo 1 O peímeto da cicunfeência O peímeto de um polígono de n lados é a soma do compimento dos seus lados. Dado um polígono qualque, você pode sempe
Geradores elétricos. Antes de estudar o capítulo PARTE I
 PART I ndade B 9 Capítulo Geadoes elétcos Seções: 91 Geado Foça eletomotz 92 Ccuto smples Le de Poullet 93 Assocação de geadoes 94 studo gáfco da potênca elétca lançada po um geado em um ccuto Antes de
PART I ndade B 9 Capítulo Geadoes elétcos Seções: 91 Geado Foça eletomotz 92 Ccuto smples Le de Poullet 93 Assocação de geadoes 94 studo gáfco da potênca elétca lançada po um geado em um ccuto Antes de
Energética Industrial
 Escola de Engenhaa Depatamento de Engenhaa Mecânca Enegétca Industal José Calos Fenandes exea 3 Escola de Engenhaa Depatamento de Engenhaa Mecânca pate A José Calos Fenandes exea ÍNDICE INRODUÇÃO. REVISÃO
Escola de Engenhaa Depatamento de Engenhaa Mecânca Enegétca Industal José Calos Fenandes exea 3 Escola de Engenhaa Depatamento de Engenhaa Mecânca pate A José Calos Fenandes exea ÍNDICE INRODUÇÃO. REVISÃO
ELETRICIDADE CAPÍTULO 3 LEIS DE CIRCUITOS ELÉTRICOS
 ELETICIDADE CAPÍTULO 3 LEIS DE CICUITOS ELÉTICOS - CONSIDEE A SEGUINTE ELAÇÃO: 3. LEI DE OHM - QUALQUE POCESSO DE CONVESÃO DE ENEGIA PODE SE ELACIONADO A ESTA EQUAÇÃO. - EM CICUITOS ELÉTICOS : - POTANTO,
ELETICIDADE CAPÍTULO 3 LEIS DE CICUITOS ELÉTICOS - CONSIDEE A SEGUINTE ELAÇÃO: 3. LEI DE OHM - QUALQUE POCESSO DE CONVESÃO DE ENEGIA PODE SE ELACIONADO A ESTA EQUAÇÃO. - EM CICUITOS ELÉTICOS : - POTANTO,
Óptica não Linear Introdução
 Óptca não lnea 95 Óptca não Lnea 6 6. Intodução A óptca não lnea tata do estudo da nteação da luz com a matéa no egme em que suas popedades óptcas são modfcadas pela pesença da luz. Muto emboa as popedades
Óptca não lnea 95 Óptca não Lnea 6 6. Intodução A óptca não lnea tata do estudo da nteação da luz com a matéa no egme em que suas popedades óptcas são modfcadas pela pesença da luz. Muto emboa as popedades
DINÂMICA DO CORPO RÍGIDO
 Dnâmca do copo ígdo 3 DNÂCA DO COPO ÍGDO 8 8. ntodução Um copo ígdo consttu-se de um conjunto de patículas (massas pontuas) dspostas de tal foma que as dstâncas elatvas ente elas são fxas. As les da mecânca
Dnâmca do copo ígdo 3 DNÂCA DO COPO ÍGDO 8 8. ntodução Um copo ígdo consttu-se de um conjunto de patículas (massas pontuas) dspostas de tal foma que as dstâncas elatvas ente elas são fxas. As les da mecânca
Concurso Professor Substituto Universidade Federal Fluminense
 Concuso Pofesso Substtuto Unvesdade Fedeal Flumnense Pova Aula Tema: Contole de Máqunas Elétcas Canddato:Lus Osca de Aaujo Poto Henques Intodução Os aconamentos eletôncos de máqunas elétcas são muto mpotantes
Concuso Pofesso Substtuto Unvesdade Fedeal Flumnense Pova Aula Tema: Contole de Máqunas Elétcas Canddato:Lus Osca de Aaujo Poto Henques Intodução Os aconamentos eletôncos de máqunas elétcas são muto mpotantes
UNIVERSIDADE DE TAUBATE HENRIQUE DE CAMARGO KOTTKE UMA VISÃO GLOBAL DA DINÂMICA DE NEWTON-EULER APLICADA A ROBÔS MANIPULADORES
 UNIVERSIDADE DE TAUBATE HENRIQUE DE CAMARGO KOTTKE UMA VISÃO GLOBAL DA DINÂMICA DE NEWTON-EULER APLICADA A ROBÔS MANIPULADORES Taubaté SP 2005 Lvos Gáts http://www.lvosgats.com.b Mlhaes de lvos gáts paa
UNIVERSIDADE DE TAUBATE HENRIQUE DE CAMARGO KOTTKE UMA VISÃO GLOBAL DA DINÂMICA DE NEWTON-EULER APLICADA A ROBÔS MANIPULADORES Taubaté SP 2005 Lvos Gáts http://www.lvosgats.com.b Mlhaes de lvos gáts paa
Ondas - 2EE 2003 / 04. Caracterização do canal de rádio
 Ondas - EE 3 / 4 Pncpas modelos de popagação do canal de ádo. Modelo de atenuação Seja: () - p T a potênca tansmtda (W); () - l a atenuação do snal no canal de tansmssão, a potênca ecebda p R (W) é p R
Ondas - EE 3 / 4 Pncpas modelos de popagação do canal de ádo. Modelo de atenuação Seja: () - p T a potênca tansmtda (W); () - l a atenuação do snal no canal de tansmssão, a potênca ecebda p R (W) é p R
Uma derivação simples da Lei de Gauss
 Uma deivação simples da Lei de Gauss C. E. I. Caneio de maço de 009 Resumo Apesentamos uma deivação da lei de Gauss (LG) no contexto da eletostática. Mesmo paa cagas em epouso, uma deivação igoosa da LG
Uma deivação simples da Lei de Gauss C. E. I. Caneio de maço de 009 Resumo Apesentamos uma deivação da lei de Gauss (LG) no contexto da eletostática. Mesmo paa cagas em epouso, uma deivação igoosa da LG
TRANSMISSÃO DE PRESSÃO EM FLUIDO DE PERFURAÇÃO CONFINADO EM POÇO FECHADO
 RANSMISSÃO DE PRESSÃO EM FLUIDO DE PERFURAÇÃO CONFINADO EM POÇO FECHADO anan G. M. Santos, Gabel M. Olvea e 3 Ceza O. R. Negão Bolssta de mestado da CAPES/PPGEM/UFPR Bolssta de doutoado da CAPES/PPGEM/UFPR
RANSMISSÃO DE PRESSÃO EM FLUIDO DE PERFURAÇÃO CONFINADO EM POÇO FECHADO anan G. M. Santos, Gabel M. Olvea e 3 Ceza O. R. Negão Bolssta de mestado da CAPES/PPGEM/UFPR Bolssta de doutoado da CAPES/PPGEM/UFPR
UFSCar Cálculo 2. Quinta lista de exercícios. Prof. João C.V. Sampaio e Yolanda K. S. Furuya
 UFSCa Cálculo 2. Quinta lista de eecícios. Pof. João C.V. Sampaio e Yolanda K. S. Fuua Rega da cadeia, difeenciais e aplicações. Calcule (a 4 w (0,, π/6, se w = 4 4 + 2 u (b (c 2 +2 (, 3,, se u =. Resposta.
UFSCa Cálculo 2. Quinta lista de eecícios. Pof. João C.V. Sampaio e Yolanda K. S. Fuua Rega da cadeia, difeenciais e aplicações. Calcule (a 4 w (0,, π/6, se w = 4 4 + 2 u (b (c 2 +2 (, 3,, se u =. Resposta.
MATEMÁTICA - 16/12/2010
 GGE RESPONDE - VESTIBULAR ITA (MATEMÁTICA) MATEMÁTICA - //. Dado Z a) b) - c) d) e) Z, então n e Z e Mas, Z = e (*) =e 8 = n z é gual a ; podemos esceve Z na foma pola: Z x y + xy + x + y + x y = (x -
GGE RESPONDE - VESTIBULAR ITA (MATEMÁTICA) MATEMÁTICA - //. Dado Z a) b) - c) d) e) Z, então n e Z e Mas, Z = e (*) =e 8 = n z é gual a ; podemos esceve Z na foma pola: Z x y + xy + x + y + x y = (x -
SÍNTESE DE MECANISMOS DE 4 BARRAS PARA GERAR TRAJETÓRIA CURVA ACOPLADORA
 SÍNTESE DE MECANISMOS DE BARRAS PARA GERAR TRAJETÓRIA CURVA ACOPLADORA Calos Sego Pvetta calos.pvetta@etep.edu.b Osvaldo Pado de Rezende osvaldo.ezende@etep.edu.b Eule Babosa eule.babosa@etep.edu.b Ana
SÍNTESE DE MECANISMOS DE BARRAS PARA GERAR TRAJETÓRIA CURVA ACOPLADORA Calos Sego Pvetta calos.pvetta@etep.edu.b Osvaldo Pado de Rezende osvaldo.ezende@etep.edu.b Eule Babosa eule.babosa@etep.edu.b Ana
0RGHODJHPGR&DQDOGH5iGLR3URSDJDomR0yYHO
 0GHODJHPG&DQDOGH5GL3USDJDom0yYHO Este tabalho se concenta no canal de ádo popagação móvel, no qual o ecepto se desloca em elação ao tansmsso. Neste meo de popagação o snal é susceptível a ntefeêncas po
0GHODJHPG&DQDOGH5GL3USDJDom0yYHO Este tabalho se concenta no canal de ádo popagação móvel, no qual o ecepto se desloca em elação ao tansmsso. Neste meo de popagação o snal é susceptível a ntefeêncas po
Funções de base nebulosas e modelagem de dinâmica não-linear
 Unvesdade Fedeal de Mnas Geas Fom the SelectedWoks of 2004 Funções de base nebulosas e modelagem de dnâmca não-lnea, Unvesdade Fedeal de Mnas Geas Avalable at: https://woks.bepess.com/gladstone/7/ Cento
Unvesdade Fedeal de Mnas Geas Fom the SelectedWoks of 2004 Funções de base nebulosas e modelagem de dnâmca não-lnea, Unvesdade Fedeal de Mnas Geas Avalable at: https://woks.bepess.com/gladstone/7/ Cento
PME5325-Fundamentos da Turbulência 2017
 46 CAPÍTULO. ALGUMAS CONSIDERAÇÕES SOBRE A CINEMÁTICA E A DINÂMICA DOS FLUIDOS.. Teoa do Movmento Elementa da Patícula Fluda.... Movmento de uma Patícula Fluda O movmento elementa de uma patícula, do ponto
46 CAPÍTULO. ALGUMAS CONSIDERAÇÕES SOBRE A CINEMÁTICA E A DINÂMICA DOS FLUIDOS.. Teoa do Movmento Elementa da Patícula Fluda.... Movmento de uma Patícula Fluda O movmento elementa de uma patícula, do ponto
Planejamento e Pesquisa 1 - Análise de variância
 Planejamento e Pesqusa - Análse de vaânca Um Fato Lane Alenca - Planejamento e Pesqusa - 0 Duabldade de 4 tpos de capetes: exh_aov.mtw Eu tnha 4 tpos de capetes e coloque cada tpo em quato casas (um tpo
Planejamento e Pesqusa - Análse de vaânca Um Fato Lane Alenca - Planejamento e Pesqusa - 0 Duabldade de 4 tpos de capetes: exh_aov.mtw Eu tnha 4 tpos de capetes e coloque cada tpo em quato casas (um tpo
TRATAMENTO DE SINGULARIDADES EM ESTRUTURAS CONDUTORAS PARA O MÉTODO FETD
 WAKEY CHMDKE TRATAMENTO DE NGUARDADE EM ETRUTURA CONDUTORA PARA O MÉTODO FETD Dssetação apesentada como equsto pacal paa a obtenção do gau de Meste, no Pogama de Pós- Gaduação em Engenhaa Elétca - PPGEE,
WAKEY CHMDKE TRATAMENTO DE NGUARDADE EM ETRUTURA CONDUTORA PARA O MÉTODO FETD Dssetação apesentada como equsto pacal paa a obtenção do gau de Meste, no Pogama de Pós- Gaduação em Engenhaa Elétca - PPGEE,
Cálculo Numérico BCC760 Interpolação Polinomial
 Cálculo Numérco BCC76 Interpolação Polnomal Departamento de Computação Págna da dscplna http://www.decom.ufop.br/bcc76/ 1 Interpolação Polnomal Conteúdo 1. Introdução 2. Objetvo 3. Estênca e uncdade 4.
Cálculo Numérco BCC76 Interpolação Polnomal Departamento de Computação Págna da dscplna http://www.decom.ufop.br/bcc76/ 1 Interpolação Polnomal Conteúdo 1. Introdução 2. Objetvo 3. Estênca e uncdade 4.
4 Discretização e Linearização
 4 Dscretzação e Lnearzação Uma vez defndas as equações dferencas do problema, o passo segunte consste no processo de dscretzação e lnearzação das mesmas para que seja montado um sstema de equações algébrcas
4 Dscretzação e Lnearzação Uma vez defndas as equações dferencas do problema, o passo segunte consste no processo de dscretzação e lnearzação das mesmas para que seja montado um sstema de equações algébrcas
MALHA ADAPTATIVA APLICADA AO MÉTODO DA FRONTEIRA IMERSA COM MODELO FÍSICO VIRTUAL
 3 o POSMEC - Smpóso do Pogama de Pós-Gaduação em Engenhaa Mecânca Unvesdade Fedeal de Ubelânda Faculdade de Engenhaa Mecânca MALHA ADAPTATIVA APLICADA AO MÉTODO DA FRONTEIRA IMERSA COM MODELO FÍSICO VIRTUAL
3 o POSMEC - Smpóso do Pogama de Pós-Gaduação em Engenhaa Mecânca Unvesdade Fedeal de Ubelânda Faculdade de Engenhaa Mecânca MALHA ADAPTATIVA APLICADA AO MÉTODO DA FRONTEIRA IMERSA COM MODELO FÍSICO VIRTUAL
Aula 4: O Potencial Elétrico
 Aula 4: O Potencal létco Cuso de Físca Geal III F-38 º semeste, 4 F38 S4 Potencal elétco Como podemos elacona a noção de oça elétca com os concetos de enega e tabalho? Denndo a enega potencal elétca (Foça
Aula 4: O Potencal létco Cuso de Físca Geal III F-38 º semeste, 4 F38 S4 Potencal elétco Como podemos elacona a noção de oça elétca com os concetos de enega e tabalho? Denndo a enega potencal elétca (Foça
JONY LAUREANO SILVEIRA MODELAGEM NUMÉRICA 3D DE PROBLEMAS DE COMPATIBILIDADE ELETROMAGNÉTICA UTILIZANDO O MÉTODO TLM-TD
 JONY LAUREANO SILEIRA MODELAGEM NUMÉRICA 3D DE PROBLEMAS DE COMPATIBILIDADE ELETROMAGNÉTICA UTILIZANDO O MÉTODO TLM-TD FLORIANÓPOLIS 00 UNIERSIDADE FEDERAL DE SANTA CATARINA PROGRAMA DE PÓS-GRADUAÇÃO EM
JONY LAUREANO SILEIRA MODELAGEM NUMÉRICA 3D DE PROBLEMAS DE COMPATIBILIDADE ELETROMAGNÉTICA UTILIZANDO O MÉTODO TLM-TD FLORIANÓPOLIS 00 UNIERSIDADE FEDERAL DE SANTA CATARINA PROGRAMA DE PÓS-GRADUAÇÃO EM
ANÁLISE DA PROPAGAÇÃO DE PRESSÃO EM FLUIDOS DE PERFURAÇÃO DURANTE KICK DE GÁS
 ANÁLISE DA PROPAGAÇÃO DE PRESSÃO EM FLUIDOS DE PERFURAÇÃO DURANTE KICK DE GÁS Jonathan F. Galdno, Gabel M. de Olvea, 3 Admlson T. Fanco, 3 Ceza O. R. Neão Mestando, dscente do cuso do Poama de Pós-Gaduação
ANÁLISE DA PROPAGAÇÃO DE PRESSÃO EM FLUIDOS DE PERFURAÇÃO DURANTE KICK DE GÁS Jonathan F. Galdno, Gabel M. de Olvea, 3 Admlson T. Fanco, 3 Ceza O. R. Neão Mestando, dscente do cuso do Poama de Pós-Gaduação
VETORES GRANDEZAS VETORIAIS
 VETORES GRANDEZAS VETORIAIS Gandezas físicas que não ficam totalmente deteminadas com um valo e uma unidade são denominadas gandezas vetoiais. As gandezas que ficam totalmente expessas po um valo e uma
VETORES GRANDEZAS VETORIAIS Gandezas físicas que não ficam totalmente deteminadas com um valo e uma unidade são denominadas gandezas vetoiais. As gandezas que ficam totalmente expessas po um valo e uma
8º CONGRESO IBEROAMERICANO DE ENGENHARIA MECANICA Cusco, 23 a 25 de Outubro de 2007
 8º CONGRESO IBEROAMERICANO DE ENGENHARIA MECANICA Cusco, 3 a 5 de Outubo de 7 INFLUÊNCIA DAS TOLERÂNCIAS DE MAQUINAGEM NO DESEMENHO CINEMÁTICO DE MECANISMOS aulo Floes*, J.C. menta Clao* * Depatamento
8º CONGRESO IBEROAMERICANO DE ENGENHARIA MECANICA Cusco, 3 a 5 de Outubo de 7 INFLUÊNCIA DAS TOLERÂNCIAS DE MAQUINAGEM NO DESEMENHO CINEMÁTICO DE MECANISMOS aulo Floes*, J.C. menta Clao* * Depatamento
Radiação Térmica Processos, Propriedades e Troca de Radiação entre Superfícies (Parte 2)
 Radação Térmca Processos, Propredades e Troca de Radação entre Superfíces (Parte ) Obetvo: calcular a troca por radação entre duas ou mas superfíces. Essa troca depende das geometras e orentações das superfíces,
Radação Térmca Processos, Propredades e Troca de Radação entre Superfíces (Parte ) Obetvo: calcular a troca por radação entre duas ou mas superfíces. Essa troca depende das geometras e orentações das superfíces,
Introdução aos Tensores pág.
 INTRODUÇÃO AOS TENSORES Intodução aos Tensoes pág.. Concetos pelmnaes... 3. Vetoes e tensoes contavaantes. Invaantes.... 4 3. Vetoes e tensoes covaantes. Tensoes mstos.... 5 4. Opeações fundamentas com
INTRODUÇÃO AOS TENSORES Intodução aos Tensoes pág.. Concetos pelmnaes... 3. Vetoes e tensoes contavaantes. Invaantes.... 4 3. Vetoes e tensoes covaantes. Tensoes mstos.... 5 4. Opeações fundamentas com
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO Departamento de Engenharia Mecânica
 ESCOL POLITÉCNIC D UNIVESIDDE DE SÃO PULO Depatamento de Engenhaia ecânica PE 100 ecânica Pova de ecupeação - Duação 100 minutos 05 de feveeio de 013 1 - Não é pemitido o uso de calculadoas, celulaes,
ESCOL POLITÉCNIC D UNIVESIDDE DE SÃO PULO Depatamento de Engenhaia ecânica PE 100 ecânica Pova de ecupeação - Duação 100 minutos 05 de feveeio de 013 1 - Não é pemitido o uso de calculadoas, celulaes,
9. Lei de Ampère (baseado no Halliday, 4 a edição)
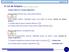 9. Le de Ampèe Capítulo 9 9. Le de Ampèe (baseado no Hallday, 4 a edção) Campo Elétco e Campo Magnétco Vmos (anteomente) que, paa campo elétco: q 1 E q. Duas cagas elétca, execem foças uma sobe as outas,
9. Le de Ampèe Capítulo 9 9. Le de Ampèe (baseado no Hallday, 4 a edção) Campo Elétco e Campo Magnétco Vmos (anteomente) que, paa campo elétco: q 1 E q. Duas cagas elétca, execem foças uma sobe as outas,
PROJETO ASTER: ESTRATÉGIA PARA MANOBRAS DE RENDEZVOUS DA SONDA ESPACIAL BRASILEIRA COM O ASTERÓIDE 2001 SN263
 839 PROJETO ASTER: ESTRATÉGIA PARA MANOBRAS DE RENDEZOUS DA SONDA ESPACIAL BRASILEIRA COM O ASTERÓIDE 2001 SN263 Abeuçon Atanáso Alves 1 ;AntonoDelson Conceção de Jesus 2 1. Bolssta voluntáo, Gaduando
839 PROJETO ASTER: ESTRATÉGIA PARA MANOBRAS DE RENDEZOUS DA SONDA ESPACIAL BRASILEIRA COM O ASTERÓIDE 2001 SN263 Abeuçon Atanáso Alves 1 ;AntonoDelson Conceção de Jesus 2 1. Bolssta voluntáo, Gaduando
SIMULAÇÃO DE ESCOAMENTOS DE FLUIDOS IMISCÍVEIS USANDO LATTICE BOLTZMANN
 UNIVERSIDADE FEDERAL DE SANTA CATARINA PRÓ-REITORIA DE PESQUISA E PÓS-GRADUAÇÃO DEPARTAMENTO DE APOIO À PESQUISA SIMULAÇÃO DE ESCOAMENTOS DE FLUIDOS IMISCÍVEIS USANDO LATTICE BOLTZMANN ASSINATURA PROFESSOR
UNIVERSIDADE FEDERAL DE SANTA CATARINA PRÓ-REITORIA DE PESQUISA E PÓS-GRADUAÇÃO DEPARTAMENTO DE APOIO À PESQUISA SIMULAÇÃO DE ESCOAMENTOS DE FLUIDOS IMISCÍVEIS USANDO LATTICE BOLTZMANN ASSINATURA PROFESSOR
SISTEMA DE COORDENADAS
 ELETROMAGNETISMO I 1 0 ANÁLISE VETORIAL Este capítulo ofeece uma ecapitulação aos conhecimentos de álgeba vetoial, já vistos em outos cusos. Estando po isto numeado com o eo, não fa pate de fato dos nossos
ELETROMAGNETISMO I 1 0 ANÁLISE VETORIAL Este capítulo ofeece uma ecapitulação aos conhecimentos de álgeba vetoial, já vistos em outos cusos. Estando po isto numeado com o eo, não fa pate de fato dos nossos
É o grau de associação entre duas ou mais variáveis. Pode ser: correlacional ou experimental.
 Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
Prof. Lorí Val, Dr. val@mat.ufrgs.br http://www.mat.ufrgs.br/~val/ É o grau de assocação entre duas ou mas varáves. Pode ser: correlaconal ou expermental. Numa relação expermental os valores de uma das
MONITORAÇÃO DA REATIVIDADE ATRAVÉS DO HISTÓRICO DA POTÊNCIA NUCLEAR. Alessandro da Cruz Gonçalves
 MONITORAÇÃO DA REATIVIDADE ATRAVÉS DO HISTÓRICO DA POTÊNCIA NUCLEAR Alessando da Cuz Gonçalves DISSERTAÇÃO SUBMETIDA AO CORPO DOCENTE DA COORDENAÇÃO DOS PROGRAMAS DE PÓS-GRADUAÇÃO DE ENGENHARIA DA UNIVERSIDADE
MONITORAÇÃO DA REATIVIDADE ATRAVÉS DO HISTÓRICO DA POTÊNCIA NUCLEAR Alessando da Cuz Gonçalves DISSERTAÇÃO SUBMETIDA AO CORPO DOCENTE DA COORDENAÇÃO DOS PROGRAMAS DE PÓS-GRADUAÇÃO DE ENGENHARIA DA UNIVERSIDADE
Análise de Processos ENG 514
 Pof. D. Édle Lns de lbuqueque, Eng. uímca I nálse de Pocessos - ENG 514, 2013.2 nálse de Pocessos ENG 514 aítulo 2 Modelagem enomenológca de Pocessos da Engenhaa uímca Pof. Édle Lns de lbuqueque Outubo
Pof. D. Édle Lns de lbuqueque, Eng. uímca I nálse de Pocessos - ENG 514, 2013.2 nálse de Pocessos ENG 514 aítulo 2 Modelagem enomenológca de Pocessos da Engenhaa uímca Pof. Édle Lns de lbuqueque Outubo
MODELAGEM DO ACOPLAMENTO ROTOR-GERADOR ELÉTRICO EM TURBINAS EÓLICAS DE EIXO HORIZONTAL
 MODELAGEM DO ACOPLAMENTO ROTOR-GERADOR ELÉTRICO EM TURBINAS EÓLICAS DE EIXO HORIZONTAL Sego Andés James Rueda, seanjau@hotmal.com 1 Jeson Rogéo Pnheo Vaz, jeson@ufpa.b 1 Andé Luz Amaante Mesquta, andeam@ufpa.b
MODELAGEM DO ACOPLAMENTO ROTOR-GERADOR ELÉTRICO EM TURBINAS EÓLICAS DE EIXO HORIZONTAL Sego Andés James Rueda, seanjau@hotmal.com 1 Jeson Rogéo Pnheo Vaz, jeson@ufpa.b 1 Andé Luz Amaante Mesquta, andeam@ufpa.b
Cap.10 Energia. Do professor para o aluno ajudando na avaliação de compreensão do capítulo.
 Cap.10 Enega Do poesso paa o aluno ajudando na avalação de compeensão do capítulo. É undamental que o aluno tenha ldo o capítulo. Poduto Escala Dene-se o poduto escala ente dos vetoes como sendo o poduto
Cap.10 Enega Do poesso paa o aluno ajudando na avalação de compeensão do capítulo. É undamental que o aluno tenha ldo o capítulo. Poduto Escala Dene-se o poduto escala ente dos vetoes como sendo o poduto
Aula18 (RG4) Desenvolvimento formal da Relatividade Geral
 Popto Alege, 7 de janeo de 3. Relatvdade e Cosmologa Hoaco Dotto Aula18 (RG4 Desenvolvmento fomal da Relatvdade Geal 18-1 Intodução No expemento elatado na aula passada, um obsevado em queda lve, odeado
Popto Alege, 7 de janeo de 3. Relatvdade e Cosmologa Hoaco Dotto Aula18 (RG4 Desenvolvmento fomal da Relatvdade Geal 18-1 Intodução No expemento elatado na aula passada, um obsevado em queda lve, odeado
3 Metodologia de Avaliação da Relação entre o Custo Operacional e o Preço do Óleo
 3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
3 Metodologa de Avalação da Relação entre o Custo Operaconal e o Preço do Óleo Este capítulo tem como objetvo apresentar a metodologa que será empregada nesta pesqusa para avalar a dependênca entre duas
Análise de Rotações Críticas em Discos Rotativos Montados sob Interferência
 NIVERSIDADE FEDERAL DE ITAJBÁ NIFEI INSTITTO DE ENGENHARIA MEÂNIA ROGRAMA DE ÓS-GRADAÇÃO EM ENGENHARIA MEÂNIA DISSERTAÇÃO DE MESTRADO Análse de Rotações ítcas em Dscos Rotatvos Montados so Intefeênca Auto:
NIVERSIDADE FEDERAL DE ITAJBÁ NIFEI INSTITTO DE ENGENHARIA MEÂNIA ROGRAMA DE ÓS-GRADAÇÃO EM ENGENHARIA MEÂNIA DISSERTAÇÃO DE MESTRADO Análse de Rotações ítcas em Dscos Rotatvos Montados so Intefeênca Auto:
Eletrotécnica AULA Nº 1 Introdução
 Eletrotécnca UL Nº Introdução INTRODUÇÃO PRODUÇÃO DE ENERGI ELÉTRIC GERDOR ESTÇÃO ELEVDOR Lnha de Transmssão ESTÇÃO IXDOR Equpamentos Elétrcos Crcuto Elétrco: camnho percorrdo por uma corrente elétrca
Eletrotécnca UL Nº Introdução INTRODUÇÃO PRODUÇÃO DE ENERGI ELÉTRIC GERDOR ESTÇÃO ELEVDOR Lnha de Transmssão ESTÇÃO IXDOR Equpamentos Elétrcos Crcuto Elétrco: camnho percorrdo por uma corrente elétrca
LIMITADOR DE CORRENTE ELÉTRICA SUPERCONDUTOR RESISTIVO MONOFÁSICO
 LIMITADOR DE CORRENTE ELÉTRICA SUPERCONDUTOR RESISTIVO MONOFÁSICO RAFAEL C. FREITAS, ERNESTO RUPPERT FILHO, ROBERTO P. HOMRICH, CARLOS A. BALDAN *, CARLOS Y. SHIGUE *, DALTRO G. PINATTI * Unvesdade Estadual
LIMITADOR DE CORRENTE ELÉTRICA SUPERCONDUTOR RESISTIVO MONOFÁSICO RAFAEL C. FREITAS, ERNESTO RUPPERT FILHO, ROBERTO P. HOMRICH, CARLOS A. BALDAN *, CARLOS Y. SHIGUE *, DALTRO G. PINATTI * Unvesdade Estadual
Resolução: a) ε = 12 V = ε r = 12 0,1 i cc = 120 A. b) i = ε R + r = 12. Respostas: a) Resolução: a) ε = R eq. b) U = R i 5,5 2,0 U = 11 V
 Tópco cutos elétcos 7 Tópco E Temos, a segu, a cuva caacteístca de um geado e um ccuto smples, em que esse geado almenta um essto de esstênca a) cc 0, cc 0 U () U () 0 0 0 () U b),0 6,0 0 0 () Detemne:
Tópco cutos elétcos 7 Tópco E Temos, a segu, a cuva caacteístca de um geado e um ccuto smples, em que esse geado almenta um essto de esstênca a) cc 0, cc 0 U () U () 0 0 0 () U b),0 6,0 0 0 () Detemne:
Análise Multivariada
 Análse Multvaada Aula 8: Análse de Coespondêna (AC) Pof. Adm Antono Betaell Juno Juz de Foa AC Téna exploatóa que busa dentfa assoações ente vaáves ategóas (ao nvés de ontínuas). Repesentação geométa das
Análse Multvaada Aula 8: Análse de Coespondêna (AC) Pof. Adm Antono Betaell Juno Juz de Foa AC Téna exploatóa que busa dentfa assoações ente vaáves ategóas (ao nvés de ontínuas). Repesentação geométa das
TICA MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA. Nona Edição CAPÍTULO. Ferdinand P. Beer E. Russell Johnston, Jr.
 CAPÍTULO 2 Está MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA TICA Fedinand P. Bee E. Russell Johnston, J. Notas de Aula: J. Walt Ole Teas Tech Univesit das Patículas Conteúdo Intodução Resultante de Duas
CAPÍTULO 2 Está MECÂNICA VETORIAL PARA ENGENHEIROS: ESTÁTICA TICA Fedinand P. Bee E. Russell Johnston, J. Notas de Aula: J. Walt Ole Teas Tech Univesit das Patículas Conteúdo Intodução Resultante de Duas
5.Força Eléctrica e Campo Eléctrico
 5.Foça Eléctca e Campo Eléctco Tópcos do Capítulo 5.1. Popedades das Cagas Eléctcas 5.2. Isolantes e Condutoes 5.3. Le de Coulomb 5.4. Campo Eléctco 5.5. Lnhas do Campo Eléctco 5.6. Movmento de Patículas
5.Foça Eléctca e Campo Eléctco Tópcos do Capítulo 5.1. Popedades das Cagas Eléctcas 5.2. Isolantes e Condutoes 5.3. Le de Coulomb 5.4. Campo Eléctco 5.5. Lnhas do Campo Eléctco 5.6. Movmento de Patículas
DIVERGÊNCIA DO FLUXO ELÉTRICO E TEOREMA DA DIVERGÊNCIA
 ELETROMAGNETIMO I 18 DIVERGÊNCIA DO FLUXO ELÉTRICO E TEOREMA DA DIVERGÊNCIA.1 - A LEI DE GAU APLICADA A UM ELEMENTO DIFERENCIAL DE VOLUME Vimos que a Lei de Gauss pemite estuda o compotamento do campo
ELETROMAGNETIMO I 18 DIVERGÊNCIA DO FLUXO ELÉTRICO E TEOREMA DA DIVERGÊNCIA.1 - A LEI DE GAU APLICADA A UM ELEMENTO DIFERENCIAL DE VOLUME Vimos que a Lei de Gauss pemite estuda o compotamento do campo
SEL Controle Não Linear Profa. Vilma A. Oliveira Natache S. D. Arrifano Renato Nascimento Rosa Junho 2008
 SEL 364 - Contole Não Lnea Pofa. Vlma A. Olvea Natache S. D. Afano Renato Nascmento Rosa Junho 008 Contolado fuzzy baseado no modelo akag-sugeno Sumáo. Intodução.... Modelo akag-sugeno.... Constução de
SEL 364 - Contole Não Lnea Pofa. Vlma A. Olvea Natache S. D. Afano Renato Nascmento Rosa Junho 008 Contolado fuzzy baseado no modelo akag-sugeno Sumáo. Intodução.... Modelo akag-sugeno.... Constução de
Sombreamento. Apontamentos CG + Edward Angel, Cap 6. Instituto Superior Técnico Computação Gráfica 2009/2010
 Sombeamento Apontamentos CG + Edwad Angel, Cap 6 Insttuto Supeo Técnco Computação Gáfca 2009/2010 1 Na últmas aulas Rastezação Dscetzação de lnhas Peenchmento de polígonos Alasng e Antalasng Sumáo Rastezação
Sombeamento Apontamentos CG + Edwad Angel, Cap 6 Insttuto Supeo Técnco Computação Gáfca 2009/2010 1 Na últmas aulas Rastezação Dscetzação de lnhas Peenchmento de polígonos Alasng e Antalasng Sumáo Rastezação
4. Potencial Elétrico (baseado no Halliday, 4a edição)
 4. Potencal létco 4. Potencal létco (baseado no Hallday, 4a edção) Gavtação, letostátca e nega Potencal Mutos poblemas podem se tatados atavés de semelhanças. x.: a Le de Coulomb e a Le da Gavtação de
4. Potencal létco 4. Potencal létco (baseado no Hallday, 4a edção) Gavtação, letostátca e nega Potencal Mutos poblemas podem se tatados atavés de semelhanças. x.: a Le de Coulomb e a Le da Gavtação de
PROFUNDIDADE DE MISTURA ATINGIDA PELA ONDA SOB VENTOS SEVEROS NO RESERVATÓRIO DE SALTO CAXIAS
 PROFUNDIDADE DE MISTURA ATINGIDA PELA ONDA SOB VENTOS SEVEROS NO RESERVATÓRIO DE SALTO CAXIAS Macelo Maques 1 *; Fenando O. de Andade 2 ; Elane P. Aantes 3 ; Csthane M. P. Okawa 4 1 Unvesdade Estadual
PROFUNDIDADE DE MISTURA ATINGIDA PELA ONDA SOB VENTOS SEVEROS NO RESERVATÓRIO DE SALTO CAXIAS Macelo Maques 1 *; Fenando O. de Andade 2 ; Elane P. Aantes 3 ; Csthane M. P. Okawa 4 1 Unvesdade Estadual
',9(5*Ç1&,$'2)/8;2(/e75,&2 (7(25(0$'$',9(5*Ç1&,$
 Ã Ã $Ã /(,Ã '(Ã *$866Ã $/,&$'$Ã $Ã 8Ã (/((17 ',)(5(1&,$/Ã'(Ã9/8( 17 ',9(5*Ç1&,$')/8;(/e75,& (7(5($'$',9(5*Ç1&,$ Ao final deste capítulo você deveá se capa de: ½ Entende o que é a Divegência de um veto
à à $à /(,à '(à *$866à $/,&$'$à $à 8à (/((17 ',)(5(1&,$/Ã'(Ã9/8( 17 ',9(5*Ç1&,$')/8;(/e75,& (7(5($'$',9(5*Ç1&,$ Ao final deste capítulo você deveá se capa de: ½ Entende o que é a Divegência de um veto
