A seqüência correta do ciclo de vida de uma angiosperma, desde o início da formação da flor, é a) gametófito gametas zigoto esporófito esporos
|
|
|
- Lídia Santana Bergmann
- 8 Há anos
- Visualizações:
Transcrição
1 21 e BIOLOGIA A btt-ingles (bttinh) é muito ric em mido. O órgão vegetl que rmzen ess substânci corresponde, e o mido é encontrdo nos, loclizdos no ds céluls. Os espços devem ser preenchidos, corret e respectivmente, por ) à riz; leucoplstos; vcúolo b) à riz; cloroplstos; citoplsm c) à riz; cloroplstos; vcúolo d) o cule; leucoplstos; vcúolo e) o cule; leucoplstos; citoplsm A btt-ingles (bttinh) rmzen no cule subterrâneo (tubérculo) grndes quntiddes de mido. Ess substânci é encontrd em orgnóides citoplsmáticos chmdos leucoplstos ou miloplstos. 22 d A seqüênci corret do ciclo de vid de um ngiosperm, desde o início d formção d flor, é ) gmetófito gmets zigoto esporófito esporos b) gmetófito gmets esporófito esporos zigoto c) gmetófito gmets zigoto esporos esporófito d) esporófito esporos gmetófito gmets zigoto e) esporófito esporos zigoto gmetófito gmets A flor é o prelho reprodutor ds ngiosperms formd prtir do esporófito. A seqüênci do ciclo de vid será: Esporófito Esporo Gmetófito Gmets Zigoto.
2 23 e A florest ou mt de rucáris situ-se nos estdos do Rio Grnde do Sul, Snt Ctrin, Prná e São Pulo. O pinheiro-do-prná (Arucri ngustifoli) é árvore mis crcterístic dess mt, chegndo tingir 25 m de ltur, com troncos de té 1,5 m de diâmetro. A respeito dess espécie vegetl, é correto firmr que ) é monóic, isto é, que mesm plnt present flores msculin e feminin. b) possui flores feminins trentes, fvorecendo polinizção por insetos e ves. c) possui fruto, o pinhão, que contém um semente em seu interior. d) tem folhs lrgs, permitindo lt tx de trnspirção. e) sus flores feminins possuem óvulos, ms não ovários. As plnts gimnosperms, entre els rucári, produzem flores msculins produtors de pólen e feminins formdors de óvulos. Nesss flores não se formm ovários. 24 Há um grupo de invertebrdos que present lgums crcterístics encontrds tmbém em corddos, evidencindo que mbos tiverm ncestris comuns. O grupo de invertebrdos e s crcterístics referids são ) b) c) d) e) Grupo Equinodermos Equinodermos Anelídeos Artrópodos Moluscos Crcterístics Esqueleto interno, deuterostomi e simetri bilterl n lrv Esqueleto interno, protostomi e simetri rdil n lrv Esqueleto interno, deuterostomi e simetri bilterl n lrv Esqueleto externo, protostomi e simetri rdil n lrv Esqueleto externo, deuterostomi e simetri bilterl n lrv Os equinodermos presentm lgums semelhnçs com os corddos, entre els: esqueleto interno de nturez clcári deuterostomi lrv com simetri bilterl
3 25 A Embrp desenvolveu um bioinseticid que tem em su composição um bctéri, o Bcillus sphericus, cpz de controlr s lrvs de pernilongos. Qundo ingerids pels lrvs, s bctéris liberm um substânci de nturez protéic que dnific o tubo digestório, cusndo morte ds lrvs por innição. Assim, lrvs de Anopheles, de Culex e de Aedes têm sido eliminds. Tl eliminção combte, respectivmente, s seguintes doençs: ) mlári, elefntíse e dengue. b) mlári, Chgs e leishmniose. c) febre mrel, leishmniose e dengue. d) mlári, febre mrel e toxoplsmose. e) toxoplsmose, mlári e dengue. Anopheles, Culex e Aedes são os vetores, respectivmente, d mlári, elefntíse e dengue. 26 A respeito do código genético, é correto firmr que ) é considerdo degenerdo, porque há códons diferentes pr um mesmo minoácido. b) present códons diferentes em cd espécie de ser vivo, o que explic diversidde biológic. c) é ddo pel seqüênci de minoácidos em um proteín. d) result em dus cópis idêntics, sem possibilidde de erro no processo, sempre que é copido. e) todos os seus tipos de bses nitrogends podem ser encontrdos tnto no DNA qunto no RNA. O código genético é dito degenerdo porque cd minoácido pode ser codificdo por dois ou mis códons diferentes.
4 27 O gráfico bixo represent o processo de digestão de mido. Anlisndo o gráfico cim, e considerndo o processo nele representdo, é correto firmr que ) II represent concentrção de milse, que, por ser um enzim, não é consumid durnte reção. b) III represent concentrção de glicose, que é produzid nesse processo. c) o ph ótimo pr ocorrênci dess reção é em torno de 2,0. d) I represent vrição n concentrção do substrto sobre o qul ge milse. e) esse processo ocorre exclusivmente no intestino delgdo. Enzims são ctlizdores biológicos. Acelerm reções sem serem consumids ns mesms.
5 28 c ncestrl equinodermos peixes nfíbios répteis mmíferos O esquem cim represent evolução dos nimis prtir de um ncestrl comum. Sbendo-se que o critério utilizdo pr seprr cd grupo se refere crcterístics do sistem circultório, é correto firmr que ) o ncestrl já possuí sistem circultório fechdo. b) 3 indic o surgimento de pigmentos respirtórios. c) todos possuem circulção dupl, prtir de 2. d) 4 indic o surgimento de 2 átrios. e) 5 indic seprção totl dos ventrículos. A circulção é simples nos peixes e dupl prtir dos nfíbios. 29 b ves Existe um tipo de rquitismo denomindo hipofosftemi, cusdo por um gene dominnte não letl situdo no cromossomo X. Se um homem fetdo cs-se com um mulher tmbém fetd, ms filh de pi norml, probbilidde de nscer um crinç norml é de ) 0% b) 25% c) 50% d) 75% e) 100% Alelos: H (hipofosftemi) e h (norml) (P) X H Y x X H X h (F 1 ) X H X H X H X h X H Y X h Y % fetdos 25% normis 30 d Os indivíduos 1, 3, 5 e 6 pertencem o grupo sngüíneo A; o indivíduo 2 pertence o tipo O e o indivíduo 4 pertence o tipo B. Sbendo se que polidctili é devid um gene utossômico dominnte, probbilidde de o csl 5X6 ter um crinç pertencente o tipo sngüíneo A e norml pr polidctili é de ) 1/4 b) 3/4 c) 1/2 d) 3/16 e) 1/16 Genótipos prentis: (5) I A i Pp x (6) I A i Pp P (crinç I A I A ou I A i e pp) = 3/4. 1/4 = 1/16
6 Comentário de Biologi Prov simples, com questões bordndo ssuntos básicos d mtéri.
04.01. O alto grau de exigência nos testes feitos em organismos transgênicos minimizam ao máximo os riscos para a saúde e para o ambiente.
 BIO 2E ul 04 04.01. O lto gru de exigênci nos testes feitos em orgnismos trnsgênicos minimizm o máximo os riscos pr súde e pr o mbiente. 04.02. Como o código genético é universl, é possível fzer trnsferênci
BIO 2E ul 04 04.01. O lto gru de exigênci nos testes feitos em orgnismos trnsgênicos minimizm o máximo os riscos pr súde e pr o mbiente. 04.02. Como o código genético é universl, é possível fzer trnsferênci
CRUZAMENTO Indivíduo 12 Indivíduo 18 aa X Aa
 BIO 3E ul 07 07.01. Pr determinr se um crcterístic genétic é dominnte ou recessiv trvés d interpretção de um genelogi, deve-se procurr um cruzmento entre indivíduos normis que tenh, pelo menos, um descendente
BIO 3E ul 07 07.01. Pr determinr se um crcterístic genétic é dominnte ou recessiv trvés d interpretção de um genelogi, deve-se procurr um cruzmento entre indivíduos normis que tenh, pelo menos, um descendente
A respeito das flores, que são estruturas exclusivas das gimnospermas e das angiospermas, considere as afirmações
 21 BIOLOGIA A respeito ds flores, que são estruturs exclusivs ds gimnosperms e ds ngiosperms, considere s firmções ixo. I Podem ou não ser hermfrodits. II Tods possuem ovário contendo um ou mis óvulos.
21 BIOLOGIA A respeito ds flores, que são estruturs exclusivs ds gimnosperms e ds ngiosperms, considere s firmções ixo. I Podem ou não ser hermfrodits. II Tods possuem ovário contendo um ou mis óvulos.
Métodos utilizados em genética mendeliana
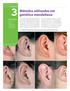 Cpítulo 3 Neste cpítulo Cruzmento- -teste. Noções de probbilidde. Construção de heredogrms. Métodos utilizdos em genétic mendelin O modelo experimentl desenvolvido por Gregor Mendel pr estudr trnsmissão
Cpítulo 3 Neste cpítulo Cruzmento- -teste. Noções de probbilidde. Construção de heredogrms. Métodos utilizdos em genétic mendelin O modelo experimentl desenvolvido por Gregor Mendel pr estudr trnsmissão
Resoluções das atividades
 LIVRO BIOLOGI Resoluções ds tividdes Sumário Cpítulo Pré-Mendelismo e Genétic Mendelin... Cpítulo Redescobert do trblho de Mendel, mono-hibridismo e estudo de heredogrms... Cpítulo Hernç utossômic monogênic,
LIVRO BIOLOGI Resoluções ds tividdes Sumário Cpítulo Pré-Mendelismo e Genétic Mendelin... Cpítulo Redescobert do trblho de Mendel, mono-hibridismo e estudo de heredogrms... Cpítulo Hernç utossômic monogênic,
Aula 8: Gramáticas Livres de Contexto
 Teori d Computção Segundo Semestre, 2014 ul 8: Grmátics Livres de Contexto DINF-UTFPR Prof. Ricrdo Dutr d Silv Veremos gor mneir de gerr s strings de um tipo específico de lingugem, conhecido como lingugem
Teori d Computção Segundo Semestre, 2014 ul 8: Grmátics Livres de Contexto DINF-UTFPR Prof. Ricrdo Dutr d Silv Veremos gor mneir de gerr s strings de um tipo específico de lingugem, conhecido como lingugem
CPV O cursinho que mais aprova na GV
 O cursinho que mis prov n GV FGV Administrção 04/junho/006 MATEMÁTICA 0. Pulo comprou um utomóvel fle que pode ser bstecido com álcool ou com gsolin. O mnul d montdor inform que o consumo médio do veículo
O cursinho que mis prov n GV FGV Administrção 04/junho/006 MATEMÁTICA 0. Pulo comprou um utomóvel fle que pode ser bstecido com álcool ou com gsolin. O mnul d montdor inform que o consumo médio do veículo
Cap. 19: Linkage Dois pares de genes localizados no mesmo par de cromossomos homólogos
 Cp. 19: Linkge Dois pres de genes loclizdos no mesmo pr de cromossomos homólogos Equipe de iologi Linkge Genes ligdos: ocorrem qundo dois ou mis genes estão loclizdos no mesmo cromossomo. Esses genes não
Cp. 19: Linkge Dois pres de genes loclizdos no mesmo pr de cromossomos homólogos Equipe de iologi Linkge Genes ligdos: ocorrem qundo dois ou mis genes estão loclizdos no mesmo cromossomo. Esses genes não
Biologia Fascículo 09 Juvenal Carlos Schalch
 iologi Fscículo 09 Juvenl Crlos Schlch Índice Genétic...1 Exercícios...7 Grito...10 Genétic Nomencltur genétic genótipo: é o ptrimônio genético de um indivíduo, representdo pelo conjunto de seus genes.
iologi Fscículo 09 Juvenl Crlos Schlch Índice Genétic...1 Exercícios...7 Grito...10 Genétic Nomencltur genétic genótipo: é o ptrimônio genético de um indivíduo, representdo pelo conjunto de seus genes.
COPEL INSTRUÇÕES PARA CÁLCULO DA DEMANDA EM EDIFÍCIOS NTC 900600
 1 - INTRODUÇÃO Ests instruções têm por objetivo fornecer s orientções pr utilizção do critério pr cálculo d demnd de edifícios residenciis de uso coletivo O referido critério é plicável os órgãos d COPEL
1 - INTRODUÇÃO Ests instruções têm por objetivo fornecer s orientções pr utilizção do critério pr cálculo d demnd de edifícios residenciis de uso coletivo O referido critério é plicável os órgãos d COPEL
Gabarito - Matemática Grupo G
 1 QUESTÃO: (1,0 ponto) Avlidor Revisor Um resturnte cobr, no lmoço, té s 16 h, o preço fixo de R$ 1,00 por pesso. Após s 16h, esse vlor ci pr R$ 1,00. Em determindo di, 0 pessos lmoçrm no resturnte, sendo
1 QUESTÃO: (1,0 ponto) Avlidor Revisor Um resturnte cobr, no lmoço, té s 16 h, o preço fixo de R$ 1,00 por pesso. Após s 16h, esse vlor ci pr R$ 1,00. Em determindo di, 0 pessos lmoçrm no resturnte, sendo
Uma roda gigante tem 10m de raio e possui 12 assentos, igualmente espaçados, e gira no sentido horário.
 Questão PROVA FINAL DE MATEMÁTICA - TURMAS DO O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - OUTUBRO DE. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Um rod
Questão PROVA FINAL DE MATEMÁTICA - TURMAS DO O ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - OUTUBRO DE. ELABORAÇÃO: PROFESSORES OCTAMAR MARQUES E ADRIANO CARIBÉ. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Um rod
COLÉGIO NAVAL 2016 (1º dia)
 COLÉGIO NAVAL 016 (1º di) MATEMÁTICA PROVA AMARELA Nº 01 PROVA ROSA Nº 0 ( 5 40) 01) Sej S som dos vlores inteiros que stisfzem inequção 10 1 0. Sendo ssim, pode-se firmr que + ) S é um número divisíel
COLÉGIO NAVAL 016 (1º di) MATEMÁTICA PROVA AMARELA Nº 01 PROVA ROSA Nº 0 ( 5 40) 01) Sej S som dos vlores inteiros que stisfzem inequção 10 1 0. Sendo ssim, pode-se firmr que + ) S é um número divisíel
Matemática. Resolução das atividades complementares. M13 Progressões Geométricas
 Resolução ds tividdes complementres Mtemátic M Progressões Geométrics p. 7 Qul é o o termo d PG (...)? q q? ( ) Qul é rzão d PG (...)? q ( )? ( ) 8 q 8 q 8 8 Três números reis formm um PG de som e produto
Resolução ds tividdes complementres Mtemátic M Progressões Geométrics p. 7 Qul é o o termo d PG (...)? q q? ( ) Qul é rzão d PG (...)? q ( )? ( ) 8 q 8 q 8 8 Três números reis formm um PG de som e produto
a FICHA DE AVALIAÇÃO FORMATIVA 9.º ANO
 Cristin Antunes Mnuel Bispo Pul Guindeir FICHA DE AVALIAÇÃO FORMATIVA 9.º ANO Escol Turm N.º Dt Grupo I Documento I É um serviço de tendimento telefónico de Trigem, Aconselhmento e Encminhmento, Assistênci
Cristin Antunes Mnuel Bispo Pul Guindeir FICHA DE AVALIAÇÃO FORMATIVA 9.º ANO Escol Turm N.º Dt Grupo I Documento I É um serviço de tendimento telefónico de Trigem, Aconselhmento e Encminhmento, Assistênci
b para que a igualdade ( ) 2
 DATA DE ENTREGA: 0 / 06 / 06 QiD 3 8º ANO PARTE MATEMÁTICA. (,0) Identifique o monômio que se deve multiplicr o monômio 9 5 8 b c. 5 b pr obter o resultdo. (,0) Simplifique s expressões bixo. ) x + x(3x
DATA DE ENTREGA: 0 / 06 / 06 QiD 3 8º ANO PARTE MATEMÁTICA. (,0) Identifique o monômio que se deve multiplicr o monômio 9 5 8 b c. 5 b pr obter o resultdo. (,0) Simplifique s expressões bixo. ) x + x(3x
1º semestre de Engenharia Civil/Mecânica Cálculo 1 Profa Olga (1º sem de 2015) Função Exponencial
 º semestre de Engenhri Civil/Mecânic Cálculo Prof Olg (º sem de 05) Função Eponencil Definição: É tod função f: R R d form =, com R >0 e. Eemplos: = ; = ( ) ; = 3 ; = e Gráfico: ) Construir o gráfico d
º semestre de Engenhri Civil/Mecânic Cálculo Prof Olg (º sem de 05) Função Eponencil Definição: É tod função f: R R d form =, com R >0 e. Eemplos: = ; = ( ) ; = 3 ; = e Gráfico: ) Construir o gráfico d
64 5 y e log 2. 32 5 z, então x 1 y 1 z é igual a: c) 13 e) 64 3. , respectivamente. Admitindo-se que E 1 foi equivalente à milésima parte de E 2
 Resolução ds tividdes complementres Mtemátic M Função Logrítmic p. (UFSM-RS) Sejm log, log 6 e log z, então z é igul : ) b) c) e) 6 d) log log 6 6 log z z z z (UFMT) A mgnitude de um terremoto é medid
Resolução ds tividdes complementres Mtemátic M Função Logrítmic p. (UFSM-RS) Sejm log, log 6 e log z, então z é igul : ) b) c) e) 6 d) log log 6 6 log z z z z (UFMT) A mgnitude de um terremoto é medid
Desvio do comportamento ideal com aumento da concentração de soluto
 Soluções reis: tividdes Nenhum solução rel é idel Desvio do comportmento idel com umento d concentrção de soluto O termo tividde ( J ) descreve o comportmento de um solução fstd d condição idel. Descreve
Soluções reis: tividdes Nenhum solução rel é idel Desvio do comportmento idel com umento d concentrção de soluto O termo tividde ( J ) descreve o comportmento de um solução fstd d condição idel. Descreve
DESAFIOS. π e. π <y < π, satisfazendo seny = 8 x
 DESAFIOS ENZO MATEMÁTICA 01-(FUVEST) Sejm x e y dois números reis, com 0
DESAFIOS ENZO MATEMÁTICA 01-(FUVEST) Sejm x e y dois números reis, com 0
U N I V E R S I D A D E F E D E R A L D E M I N A S G E R A I S
 U N I V E R S I D A D E F E D E R A L D E M I N A S G E R A I S QUÍMICA 2 1 - Este Cderno de Prov contém cinco questões, que ocupm um totl de onze págins, numerds de 4 14.. Cso hj lgum problem, solicite
U N I V E R S I D A D E F E D E R A L D E M I N A S G E R A I S QUÍMICA 2 1 - Este Cderno de Prov contém cinco questões, que ocupm um totl de onze págins, numerds de 4 14.. Cso hj lgum problem, solicite
EXPOENTE. Podemos entender a potenciação como uma multiplicação de fatores iguais.
 EXPOENTE 2 3 = 8 RESULTADO BASE Podeos entender potencição coo u ultiplicção de ftores iguis. A Bse será o ftor que se repetirá O expoente indic qunts vezes bse vi ser ultiplicd por el es. 2 5 = 2. 2.
EXPOENTE 2 3 = 8 RESULTADO BASE Podeos entender potencição coo u ultiplicção de ftores iguis. A Bse será o ftor que se repetirá O expoente indic qunts vezes bse vi ser ultiplicd por el es. 2 5 = 2. 2.
ATIVIDADES DE RECUPERAÇÃO PARALELA 2º Trimestre. 3 ano DISCIPLINA: BIOLOGIA B
 ATIVIDADES DE RECUPERAÇÃO PARALELA 2º Trimestre 3 ano DISCIPLINA: BIOLOGIA B Observações: 1- Antes de responder às atividades, releia o material entregue sobre Sugestão de Como Estudar. 2 - Os exercícios
ATIVIDADES DE RECUPERAÇÃO PARALELA 2º Trimestre 3 ano DISCIPLINA: BIOLOGIA B Observações: 1- Antes de responder às atividades, releia o material entregue sobre Sugestão de Como Estudar. 2 - Os exercícios
1. A tabela mostra a classificação das ondas eletromagnéticas em função das suas frequências.
 1. A tbel mostr clssificção ds onds eletromgnétics em função ds sus frequêncis. Região do espectro eletromgnético Onds de rádio Fix de frequênci (Hz) Micro-onds 9,0 10 Infrvermelho Visível Ultrviolet Rios
1. A tbel mostr clssificção ds onds eletromgnétics em função ds sus frequêncis. Região do espectro eletromgnético Onds de rádio Fix de frequênci (Hz) Micro-onds 9,0 10 Infrvermelho Visível Ultrviolet Rios
PROVA DE MATEMÁTICA DA UNESP VESTIBULAR 2012 1 a Fase RESOLUÇÃO: Profa. Maria Antônia Gouveia.
 PROVA DE MATEMÁTICA DA UNESP VESTIBULAR 01 1 Fse Prof. Mri Antôni Gouvei. QUESTÃO 83. Em 010, o Instituto Brsileiro de Geogrfi e Esttístic (IBGE) relizou o último censo populcionl brsileiro, que mostrou
PROVA DE MATEMÁTICA DA UNESP VESTIBULAR 01 1 Fse Prof. Mri Antôni Gouvei. QUESTÃO 83. Em 010, o Instituto Brsileiro de Geogrfi e Esttístic (IBGE) relizou o último censo populcionl brsileiro, que mostrou
Professores Edu Vicente e Marcos José Colégio Pedro II Departamento de Matemática Potências e Radicais
 POTÊNCIAS A potênci de epoente n ( n nturl mior que ) do número, representd por n, é o produto de n ftores iguis. n =...... ( n ftores) é chmdo de bse n é chmdo de epoente Eemplos =... = 8 =... = PROPRIEDADES
POTÊNCIAS A potênci de epoente n ( n nturl mior que ) do número, representd por n, é o produto de n ftores iguis. n =...... ( n ftores) é chmdo de bse n é chmdo de epoente Eemplos =... = 8 =... = PROPRIEDADES
Simbolicamente, para. e 1. a tem-se
 . Logritmos Inicilmente vmos trtr dos ritmos, um ferrment crid pr uilir no desenvolvimento de cálculos e que o longo do tempo mostrou-se um modelo dequdo pr vários fenômenos ns ciêncis em gerl. Os ritmos
. Logritmos Inicilmente vmos trtr dos ritmos, um ferrment crid pr uilir no desenvolvimento de cálculos e que o longo do tempo mostrou-se um modelo dequdo pr vários fenômenos ns ciêncis em gerl. Os ritmos
Material envolvendo estudo de matrizes e determinantes
 E. E. E. M. ÁREA DE CONHECIMENTO DE MATEMÁTICA E SUAS TECNOLOGIAS PROFESSORA ALEXANDRA MARIA º TRIMESTRE/ SÉRIE º ANO NOME: Nº TURMA: Mteril envolvendo estudo de mtrizes e determinntes INSTRUÇÕES:. Este
E. E. E. M. ÁREA DE CONHECIMENTO DE MATEMÁTICA E SUAS TECNOLOGIAS PROFESSORA ALEXANDRA MARIA º TRIMESTRE/ SÉRIE º ANO NOME: Nº TURMA: Mteril envolvendo estudo de mtrizes e determinntes INSTRUÇÕES:. Este
BIOLOGIA. 08. O desenho ilustra os cromossomos em uma fase da divisão celular e seus respectivos alelos.
 BIOLOGIA CURSO APOIO 08. O desenho ilustra os cromossomos em uma fase da divisão celular e seus respectivos alelos. a) Qual fase da divisão celular está representada? Justifique sua resposta. b) Ao final
BIOLOGIA CURSO APOIO 08. O desenho ilustra os cromossomos em uma fase da divisão celular e seus respectivos alelos. a) Qual fase da divisão celular está representada? Justifique sua resposta. b) Ao final
Aula 5 Reprodução das Angiospermas
 Aula 5 Reprodução das Angiospermas Nas angiospermas, o esporófito é formado por raízes, caule, folhas, flores, frutos e sementes. As flores são folhas modificadas, preparadas para a reprodução das angiospermas.
Aula 5 Reprodução das Angiospermas Nas angiospermas, o esporófito é formado por raízes, caule, folhas, flores, frutos e sementes. As flores são folhas modificadas, preparadas para a reprodução das angiospermas.
Vestibular UFRGS 2013 Resolução da Prova de Matemática
 Vestibulr UFRG 0 Resolução d Prov de Mtemátic 6. Alterntiv (C) 00 bilhões 00. ( 000 000 000) 00 000 000 000 0 7. Alterntiv (B) Qundo multiplicmos dois números com o lgrismo ds uniddes igul 4, o lgrismo
Vestibulr UFRG 0 Resolução d Prov de Mtemátic 6. Alterntiv (C) 00 bilhões 00. ( 000 000 000) 00 000 000 000 0 7. Alterntiv (B) Qundo multiplicmos dois números com o lgrismo ds uniddes igul 4, o lgrismo
1 Distribuições Contínuas de Probabilidade
 Distribuições Contínus de Probbilidde São distribuições de vriáveis letóris contínus. Um vriável letóri contínu tom um numero infinito não numerável de vlores (intervlos de números reis), os quis podem
Distribuições Contínus de Probbilidde São distribuições de vriáveis letóris contínus. Um vriável letóri contínu tom um numero infinito não numerável de vlores (intervlos de números reis), os quis podem
Fluxo Gênico. Desvios de Hardy-Weinberg. Estimativas de Fluxo gênico podem ser feitas através de dois tipos de métodos:
 Desvios de Hrdy-Weinberg cslmento preferencil Mutção Recombinção Deriv Genétic Fluo gênico Fluo Gênico O modelo de Hrdy-Weinberg consider pens um únic populção miori ds espécies tem váris populções locis
Desvios de Hrdy-Weinberg cslmento preferencil Mutção Recombinção Deriv Genétic Fluo gênico Fluo Gênico O modelo de Hrdy-Weinberg consider pens um únic populção miori ds espécies tem váris populções locis
QUESTÃO 01. QUESTÃO 02.
 PROVA DE MATEMÁTICA DO O ANO _ EM DO COLÉGIO ANCHIETA BA. ANO 6 UNIDADE III PRIMEIRA AVALIAÇÃO. ELABORAÇÃO: PROFESSOR OCTAMAR MARQUES. PROFESSORA MARIA ANTÔNIA GOUVEIA. QUESTÃO. Quntos inteiros são soluções
PROVA DE MATEMÁTICA DO O ANO _ EM DO COLÉGIO ANCHIETA BA. ANO 6 UNIDADE III PRIMEIRA AVALIAÇÃO. ELABORAÇÃO: PROFESSOR OCTAMAR MARQUES. PROFESSORA MARIA ANTÔNIA GOUVEIA. QUESTÃO. Quntos inteiros são soluções
Trigonometria FÓRMULAS PARA AJUDÁ-LO EM TRIGONOMETRIA
 Trigonometri é o estudo dos triângulos, que contêm ângulos, clro. Conheç lgums regrs especiis pr ângulos e váris outrs funções, definições e trnslções importntes. Senos e cossenos são dus funções trigonométrics
Trigonometri é o estudo dos triângulos, que contêm ângulos, clro. Conheç lgums regrs especiis pr ângulos e váris outrs funções, definições e trnslções importntes. Senos e cossenos são dus funções trigonométrics
Genética Conceitos Básicos
 Genética Conceitos Básicos O que é genética? É o estudo dos genes e de sua transmissão para as gerações futuras. É dividida em: Genética Clássica Mendel (1856 1865) Genética Moderna Watson e Crick (1953).
Genética Conceitos Básicos O que é genética? É o estudo dos genes e de sua transmissão para as gerações futuras. É dividida em: Genética Clássica Mendel (1856 1865) Genética Moderna Watson e Crick (1953).
a) sexto b) sétimo c) oitavo d) nono e) décimo
 1 INSPER 16/06/013 Seu Pé Direito ns Melhores Fculddes 1. Nos plnos seguir, estão representds dus relções entre s vriáveis x e y: y = x e y = x, pr x 0.. Em um sequênci, o terceiro termo é igul o primeiro
1 INSPER 16/06/013 Seu Pé Direito ns Melhores Fculddes 1. Nos plnos seguir, estão representds dus relções entre s vriáveis x e y: y = x e y = x, pr x 0.. Em um sequênci, o terceiro termo é igul o primeiro
UNIVERSIDADE FEDERAL DE JUIZ DE FORA PROVA DE BIOLOGIA- VESTIBULAR 2007 ABERTA
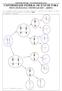 Vestiulndo We Pge www.vestiulndowe.com.r UNIVERSIDDE FEDERL DE JUIZ DE FOR PROV DE IOLOGI- VESTIULR 2007 ERT 01) O esquem ixo ilustr de form sintétic o processo de formção de gmets (meiose) de um indivíduo
Vestiulndo We Pge www.vestiulndowe.com.r UNIVERSIDDE FEDERL DE JUIZ DE FOR PROV DE IOLOGI- VESTIULR 2007 ERT 01) O esquem ixo ilustr de form sintétic o processo de formção de gmets (meiose) de um indivíduo
POLINÔMIOS. Definição: Um polinômio de grau n é uma função que pode ser escrita na forma. n em que cada a i é um número complexo (ou
 POLINÔMIOS Definição: Um polinômio de gru n é um função que pode ser escrit n form P() n n i 0... n i em que cd i é um número compleo (ou i 0 rel) tl que n é um número nturl e n 0. Os números i são denomindos
POLINÔMIOS Definição: Um polinômio de gru n é um função que pode ser escrit n form P() n n i 0... n i em que cd i é um número compleo (ou i 0 rel) tl que n é um número nturl e n 0. Os números i são denomindos
ESTÁTICA DO SISTEMA DE SÓLIDOS.
 Definições. Forçs Interns. Forçs Externs. ESTÁTIC DO SISTEM DE SÓLIDOS. (Nóbreg, 1980) o sistem de sólidos denomin-se estrutur cuj finlidde é suportr ou trnsferir forçs. São quels em que ção e reção, pertencem
Definições. Forçs Interns. Forçs Externs. ESTÁTIC DO SISTEM DE SÓLIDOS. (Nóbreg, 1980) o sistem de sólidos denomin-se estrutur cuj finlidde é suportr ou trnsferir forçs. São quels em que ção e reção, pertencem
Semelhança e áreas 1,5
 A UA UL LA Semelhnç e áres Introdução N Aul 17, estudmos o Teorem de Tles e semelhnç de triângulos. Nest ul, vmos tornr mis gerl o conceito de semelhnç e ver como se comportm s áres de figurs semelhntes.
A UA UL LA Semelhnç e áres Introdução N Aul 17, estudmos o Teorem de Tles e semelhnç de triângulos. Nest ul, vmos tornr mis gerl o conceito de semelhnç e ver como se comportm s áres de figurs semelhntes.
As bactérias operárias
 A U A UL LA As bactérias operárias Na Aula 47 você viu a importância da insulina no nosso corpo e, na Aula 48, aprendeu como as células de nosso organismo produzem insulina e outras proteínas. As pessoas
A U A UL LA As bactérias operárias Na Aula 47 você viu a importância da insulina no nosso corpo e, na Aula 48, aprendeu como as células de nosso organismo produzem insulina e outras proteínas. As pessoas
QUESTÃO 01. O lado x do retângulo que se vê na figura, excede em 3cm o lado y. O valor de y, em centímetros é igual a: 01) 1 02) 1,5 03) 2
 PROV ELBORD PR SER PLICD ÀS TURMS DO O NO DO ENSINO MÉDIO DO COLÉGIO NCHIET-B EM MIO DE. ELBORÇÃO: PROFESSORES OCTMR MRQUES E DRINO CRIBÉ. PROFESSOR MRI NTÔNI C. GOUVEI QUESTÃO. O ldo x do retângulo que
PROV ELBORD PR SER PLICD ÀS TURMS DO O NO DO ENSINO MÉDIO DO COLÉGIO NCHIET-B EM MIO DE. ELBORÇÃO: PROFESSORES OCTMR MRQUES E DRINO CRIBÉ. PROFESSOR MRI NTÔNI C. GOUVEI QUESTÃO. O ldo x do retângulo que
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA B DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 735) 1ª FASE 23 DE JUNHO 2015 GRUPO I
 PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA B DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 735) 1ª FASE 23 DE JUNHO 2015 GRUPO I 1. A função objetivo é o lucro e é dd por L(x, y) = 30x + 50y. Restrições: x 0
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA B DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 735) 1ª FASE 23 DE JUNHO 2015 GRUPO I 1. A função objetivo é o lucro e é dd por L(x, y) = 30x + 50y. Restrições: x 0
Faculdade de saúde Pública. Universidade de São Paulo HEP-5705. Epidemiologia I. Estimando Risco e Associação
 1 Fuldde de súde Públi Universidde de São Pulo HEP-5705 Epidemiologi I Estimndo Riso e Assoição 1. De 2.872 indivíduos que reeberm rdioterpi n infâni em deorrêni de presentrem o timo umentdo, 24 desenvolverm
1 Fuldde de súde Públi Universidde de São Pulo HEP-5705 Epidemiologi I Estimndo Riso e Assoição 1. De 2.872 indivíduos que reeberm rdioterpi n infâni em deorrêni de presentrem o timo umentdo, 24 desenvolverm
Nome: N.º: endereço: data: Telefone: PARA QUEM CURSA A 1 a SÉRIE DO ENSINO MÉDIO EM Disciplina: MaTeMÁTiCa
 Nome: N.º: endereço: dt: Telefone: E-mil: Colégio PARA QUEM CURSA A SÉRIE DO ENSINO MÉDIO EM 05 Disciplin: MTeMÁTiC Prov: desfio not: QUESTÃO 6 O Dr. Mni Aco not os números trvés de um código especil.
Nome: N.º: endereço: dt: Telefone: E-mil: Colégio PARA QUEM CURSA A SÉRIE DO ENSINO MÉDIO EM 05 Disciplin: MTeMÁTiC Prov: desfio not: QUESTÃO 6 O Dr. Mni Aco not os números trvés de um código especil.
Prova 3 Matemática QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. QUESTÕES OBJETIVAS GABARITO 3
 Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo MATEMÁTICA 0 Considere n um número nturl.
Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo MATEMÁTICA 0 Considere n um número nturl.
Prova 3 Matemática QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. QUESTÕES OBJETIVAS GABARITO 2
 Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo MATEMÁTICA 0 Colocm-se qutro cubos de
Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo MATEMÁTICA 0 Colocm-se qutro cubos de
Prova 3 Matemática QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. QUESTÕES OBJETIVAS GABARITO 4
 Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo MATEMÁTICA 0 Considere s funções f e
Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo MATEMÁTICA 0 Considere s funções f e
U N I V E R S I D A D E F E D E R A L D E M I N A S G E R A I S
 U N I V E R S I D A D E F E D E R A L D E M I N A S G E R A I S FILOSOFIA 2 1 - Este Cderno de Prov contém questões, que ocupm um totl de págins, numerds de 3 6.. Cso hj lgum problem, solicite deste Cderno.
U N I V E R S I D A D E F E D E R A L D E M I N A S G E R A I S FILOSOFIA 2 1 - Este Cderno de Prov contém questões, que ocupm um totl de págins, numerds de 3 6.. Cso hj lgum problem, solicite deste Cderno.
Prova 3 Matemática QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. QUESTÕES OBJETIVAS GABARITO 1
 Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo GABARITO MATEMÁTICA 0 Considere equção
Prov Mtemátic QUESTÕES OBJETIVAS QUESTÕES APLICADAS A TODOS OS CANDIDATOS QUE REALIZARAM A PROVA ESPECÍFICA DE MATEMÁTICA. UEM Comissão Centrl do Vestibulr Unificdo GABARITO MATEMÁTICA 0 Considere equção
PROJETO DE CONSTRUÇÃO DE FOSSA BIODISGESTORA
 PROJETO DE CONSTRUÇÃO DE FOSSA BIODISGESTORA Acdêmicos: Adenilton Sntos Moreir 123 RESUMO Este rtigo present um projeto de foss biodigestor, que será executdo pelo utor do mesmo, su principl finlidde é
PROJETO DE CONSTRUÇÃO DE FOSSA BIODISGESTORA Acdêmicos: Adenilton Sntos Moreir 123 RESUMO Este rtigo present um projeto de foss biodigestor, que será executdo pelo utor do mesmo, su principl finlidde é
Citologia das alterações leucocitárias
 Citologi ds lterções leucocitáris Principis lterções leucocitáris recionis o Infecções bcterins e processos inflmtórios gudos: frequentemente há leucocitose com desvio à esquerd gerlmente esclondo nesss
Citologi ds lterções leucocitáris Principis lterções leucocitáris recionis o Infecções bcterins e processos inflmtórios gudos: frequentemente há leucocitose com desvio à esquerd gerlmente esclondo nesss
Formas Quadráticas. FUNÇÕES QUADRÁTICAS: denominação de uma função especial, definida genericamente por: 1 2 n ij i j i,j 1.
 Forms Qudrátics FUNÇÕES QUADRÁTICAS: denominção de um função especil, definid genericmente por: Q x,x,...,x x x x... x x x x x... x 1 n 11 1 1 1 1n 1 n 3 3 nn n ou Qx,x,...,x 1 n ij i j i,j1 i j n x x
Forms Qudrátics FUNÇÕES QUADRÁTICAS: denominção de um função especil, definid genericmente por: Q x,x,...,x x x x... x x x x x... x 1 n 11 1 1 1 1n 1 n 3 3 nn n ou Qx,x,...,x 1 n ij i j i,j1 i j n x x
1. VARIÁVEL ALEATÓRIA 2. DISTRIBUIÇÃO DE PROBABILIDADE
 Vriáveis Aletóris 1. VARIÁVEL ALEATÓRIA Suponhmos um espço mostrl S e que cd ponto mostrl sej triuído um número. Fic, então, definid um função chmd vriável letóri 1, com vlores x i2. Assim, se o espço
Vriáveis Aletóris 1. VARIÁVEL ALEATÓRIA Suponhmos um espço mostrl S e que cd ponto mostrl sej triuído um número. Fic, então, definid um função chmd vriável letóri 1, com vlores x i2. Assim, se o espço
FUNCIONAL ENTORNO ELEMENTOS DE ENTORNO, CONSIDERANDO OS ATRIBUTOS DO LUGAR - MASSAS TOPOGRAFIA #8. fonte imagem: Google Earth
 FUNCIONL ENTORNO IDENTIFICR RELÇÃO DO EDIFÍCIO COM OS ELEMENTOS DE ENTORNO, CONSIDERNDO OS TRIBUTOS DO LUGR - MSSS EDIFICDS, RELÇÕES DE PROXIMIDDE, DIÁLOGO, INTEGRÇÃO OU UTONOMI O ENTORNO D CSH #9 É COMPOSTO
FUNCIONL ENTORNO IDENTIFICR RELÇÃO DO EDIFÍCIO COM OS ELEMENTOS DE ENTORNO, CONSIDERNDO OS TRIBUTOS DO LUGR - MSSS EDIFICDS, RELÇÕES DE PROXIMIDDE, DIÁLOGO, INTEGRÇÃO OU UTONOMI O ENTORNO D CSH #9 É COMPOSTO
1 As grandezas A, B e C são tais que A é diretamente proporcional a B e inversamente proporcional a C.
 As grndezs A, B e C são tis que A é diretmente proporcionl B e inversmente proporcionl C. Qundo B = 00 e C = 4 tem-se A = 5. Qul será o vlor de A qundo tivermos B = 0 e C = 5? B AC Temos, pelo enuncido,
As grndezs A, B e C são tis que A é diretmente proporcionl B e inversmente proporcionl C. Qundo B = 00 e C = 4 tem-se A = 5. Qul será o vlor de A qundo tivermos B = 0 e C = 5? B AC Temos, pelo enuncido,
Apostila De Matemática GEOMETRIA: REVISÃO DO ENSINO FUNDAMENTAL, PRISMAS E PIRÂMIDES
 posti De Mtemátic GEOMETRI: REVISÃO DO ENSINO FUNDMENTL, PRISMS E PIRÂMIDES posti de Mtemátic (por Sérgio Le Jr.) GEOMETRI 1. REVISÃO DO ENSINO FUNDMENTL 1. 1. Reções métrics de um triânguo retânguo. Pr
posti De Mtemátic GEOMETRI: REVISÃO DO ENSINO FUNDMENTL, PRISMS E PIRÂMIDES posti de Mtemátic (por Sérgio Le Jr.) GEOMETRI 1. REVISÃO DO ENSINO FUNDMENTL 1. 1. Reções métrics de um triânguo retânguo. Pr
Acoplamento. Tipos de acoplamento. Acoplamento por dados. Acoplamento por imagem. Exemplo. É o grau de dependência entre dois módulos.
 Acoplmento É o gru de dependênci entre dois módulos. Objetivo: minimizr o coplmento grndes sistems devem ser segmentdos em módulos simples A qulidde do projeto será vlid pelo gru de modulrizção do sistem.
Acoplmento É o gru de dependênci entre dois módulos. Objetivo: minimizr o coplmento grndes sistems devem ser segmentdos em módulos simples A qulidde do projeto será vlid pelo gru de modulrizção do sistem.
CPV 82% de aprovação na ESPM em 2011
 CPV 8% de provção n ESPM em 0 Prov Resolvid ESPM Prov E 0/julho/0 MATEMÁTICA. Considerndo-se que x = 97, y = 907 e z =. xy, o vlor d expressão x + y z é: ) 679 b) 58 c) 7 d) 98 e) 77. Se três empds mis
CPV 8% de provção n ESPM em 0 Prov Resolvid ESPM Prov E 0/julho/0 MATEMÁTICA. Considerndo-se que x = 97, y = 907 e z =. xy, o vlor d expressão x + y z é: ) 679 b) 58 c) 7 d) 98 e) 77. Se três empds mis
GEOMETRIA ESPACIAL. 1) O número de vértices de um dodecaedro formado por triângulos é. 2) O número de diagonais de um prisma octogonal regular é
 GEOMETRIA ESPACIAL 1) O número de vértices de um dodecedro formdo por triângulos é () 6 (b) 8 (c) 10 (d) 15 (e) 0 ) O número de digonis de um prism octogonl regulr é () 0 (b) (c) 6 (d) 40 (e) 60 ) (UFRGS)
GEOMETRIA ESPACIAL 1) O número de vértices de um dodecedro formdo por triângulos é () 6 (b) 8 (c) 10 (d) 15 (e) 0 ) O número de digonis de um prism octogonl regulr é () 0 (b) (c) 6 (d) 40 (e) 60 ) (UFRGS)
SERVIÇO PÚBLICO FEDERAL Ministério da Educação
 SERVIÇO PÚBLICO FEDERAL Ministério d Educção Universidde Federl do Rio Grnde Universidde Abert do Brsil Administrção Bchreldo Mtemátic pr Ciêncis Sociis Aplicds I Rodrigo Brbos Sores . Mtrizes:.. Introdução:
SERVIÇO PÚBLICO FEDERAL Ministério d Educção Universidde Federl do Rio Grnde Universidde Abert do Brsil Administrção Bchreldo Mtemátic pr Ciêncis Sociis Aplicds I Rodrigo Brbos Sores . Mtrizes:.. Introdução:
PERSPECTIVA. ciências. Sugestão de avaliação. Coleção Perspectiva
 PERSPECTIVA Coleção Perspectiva ciências 8 Sugestão de avaliação Professor, esta sugestão de avaliação corresponde ao segundo bimestre escolar ou às Unidades 3 e 4 do Livro do Aluno. Avaliação Ciências
PERSPECTIVA Coleção Perspectiva ciências 8 Sugestão de avaliação Professor, esta sugestão de avaliação corresponde ao segundo bimestre escolar ou às Unidades 3 e 4 do Livro do Aluno. Avaliação Ciências
CONTROLE DO METABOLISMO GENES
 CONTROLE DO METABOLISMO GENES 10/06/15 1º ANO - BIOLOGIA 1 ESTRUTURA DO GENE Segmentos (pedaços) da molécula de DNA, o constituinte dos nossos cromossomos, onde estão inscritas receitas (códigos genéticos)
CONTROLE DO METABOLISMO GENES 10/06/15 1º ANO - BIOLOGIA 1 ESTRUTURA DO GENE Segmentos (pedaços) da molécula de DNA, o constituinte dos nossos cromossomos, onde estão inscritas receitas (códigos genéticos)
Primeira Lei de Mendel e probabilidade associada à Genética 37
 Unidde GENÉTIC sexo feminino sexo msculino crinç indivíduo de sexo desconhecido Primeir Lei de Mendel e proilidde ssocid à Genétic 7 um csl Psso psso. -II, -I, c-iii, d-iv.. Sim. Dus populções geneticmente
Unidde GENÉTIC sexo feminino sexo msculino crinç indivíduo de sexo desconhecido Primeir Lei de Mendel e proilidde ssocid à Genétic 7 um csl Psso psso. -II, -I, c-iii, d-iv.. Sim. Dus populções geneticmente
1 Assinale a alternativa verdadeira: a) < <
 MATEMÁTICA Assinle lterntiv verddeir: ) 6 < 7 6 < 6 b) 7 6 < 6 < 6 c) 7 6 < 6 < 6 d) 6 < 6 < 7 6 e) 6 < 7 6 < 6 Pr * {} temos: ) *, * + e + * + ) + > + + > ) Ds equções (I) e (II) result 7 6 < ( 6 )
MATEMÁTICA Assinle lterntiv verddeir: ) 6 < 7 6 < 6 b) 7 6 < 6 < 6 c) 7 6 < 6 < 6 d) 6 < 6 < 7 6 e) 6 < 7 6 < 6 Pr * {} temos: ) *, * + e + * + ) + > + + > ) Ds equções (I) e (II) result 7 6 < ( 6 )
ÁLGEBRA LINEAR Equações Lineares na Álgebra Linear EQUAÇÃO LINEAR SISTEMA LINEAR GEOMETRIA DA ESQUAÇÕES LINEARES RESOLUÇÃO DOS SISTEMAS
 EQUAÇÃO LINEAR SISTEMA LINEAR GEOMETRIA DA ESQUAÇÕES LINEARES RESOLUÇÃO DOS SISTEMAS Equção Liner * Sej,,,...,, (números reis) e n (n ) 2 3 n x, x, x,..., x (números reis) 2 3 n Chm-se equção Liner sobre
EQUAÇÃO LINEAR SISTEMA LINEAR GEOMETRIA DA ESQUAÇÕES LINEARES RESOLUÇÃO DOS SISTEMAS Equção Liner * Sej,,,...,, (números reis) e n (n ) 2 3 n x, x, x,..., x (números reis) 2 3 n Chm-se equção Liner sobre
Transporte de solvente através de membranas: estado estacionário
 Trnsporte de solvente trvés de membrns: estdo estcionário Estudos experimentis mostrm que o fluxo de solvente (águ) em respost pressão hidráulic, em um meio homogêneo e poroso, é nálogo o fluxo difusivo
Trnsporte de solvente trvés de membrns: estdo estcionário Estudos experimentis mostrm que o fluxo de solvente (águ) em respost pressão hidráulic, em um meio homogêneo e poroso, é nálogo o fluxo difusivo
Física Geral e Experimental I (2011/01)
 Diretori de Ciêncis Exts Lbortório de Físic Roteiro Físic Gerl e Experimentl I (/ Experimento: Cinemátic do M. R. U. e M. R. U. V. . Cinemátic do M.R.U. e do M.R.U.V. Nest tref serão borddos os seguintes
Diretori de Ciêncis Exts Lbortório de Físic Roteiro Físic Gerl e Experimentl I (/ Experimento: Cinemátic do M. R. U. e M. R. U. V. . Cinemátic do M.R.U. e do M.R.U.V. Nest tref serão borddos os seguintes
PROFESSOR: EQUIPE DE MATEMÁTICA
 PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES MATEMÁTICA ª SÉRIE ENSINO MÉDIO ============================================================================================= Questões de Vestibulr: Polinômios
PROFESSOR: EQUIPE DE MATEMÁTICA BANCO DE QUESTÕES MATEMÁTICA ª SÉRIE ENSINO MÉDIO ============================================================================================= Questões de Vestibulr: Polinômios
PROPOSTA DE RESOLUÇÃO DA PROVA DE MATEMÁTICA B DO ENSINO SECUNDÁRIO (CÓDIGO DA PROVA 735) 1ª FASE 23 DE JUNHO 2015 GRUPO I
 Associção de Professores de Mtemátic Contctos: Ru Dr. João Couto, n.º 27-A 1500-236 Lisbo Tel.: +351 21 716 36 90 / 21 711 03 77 Fx: +351 21 716 64 24 http://www.pm.pt emil: gerl@pm.pt PROPOSTA DE RESOLUÇÃO
Associção de Professores de Mtemátic Contctos: Ru Dr. João Couto, n.º 27-A 1500-236 Lisbo Tel.: +351 21 716 36 90 / 21 711 03 77 Fx: +351 21 716 64 24 http://www.pm.pt emil: gerl@pm.pt PROPOSTA DE RESOLUÇÃO
COMENTÁRIO DA PROVA DE BIOLOGIA
 COMENTÁRIO DA PROVA DE BIOLOGIA A prova de Biologia da UFPR apresentou uma boa distribuição de conteúdos ao longo das nove questões. O grau de dificuldade variou entre questões médias e fáceis, o que está
COMENTÁRIO DA PROVA DE BIOLOGIA A prova de Biologia da UFPR apresentou uma boa distribuição de conteúdos ao longo das nove questões. O grau de dificuldade variou entre questões médias e fáceis, o que está
facebook/ruilima
 MATEMÁTICA UFPE ( FASE/008) 01. Sej áre totl d superfície de um cubo, e y, o volume do mesmo cubo. Anlise s firmções seguir, considerndo esss informções. 0-0) Se = 5 então y = 7. 1-1) 6y = 3 -) O gráfico
MATEMÁTICA UFPE ( FASE/008) 01. Sej áre totl d superfície de um cubo, e y, o volume do mesmo cubo. Anlise s firmções seguir, considerndo esss informções. 0-0) Se = 5 então y = 7. 1-1) 6y = 3 -) O gráfico
De acordo com a segunda lei de Mendel, assinale o que for correto, no que ser refere ao cálculo referente aos tipos de gametas formados por um
 De acordo com a segunda lei de Mendel, assinale o que for correto, no que ser refere ao cálculo referente aos tipos de gametas formados por um indivíduo. 01) Considerando-se um indivíduo AaBbcc pode-se
De acordo com a segunda lei de Mendel, assinale o que for correto, no que ser refere ao cálculo referente aos tipos de gametas formados por um indivíduo. 01) Considerando-se um indivíduo AaBbcc pode-se
REVISÃO Lista 12 Geometria Analítica., então r e s são coincidentes., então r e s são perpendiculares.
 NOME: ANO: º Nº: PROFESSOR(A): An Luiz Ozores DATA: REVISÃO List Geometri Anlític Algums definições y Equções d ret: by c 0, y mb, y y0 m( 0) e p q Posições de dus rets: Dds s rets r : y mr br e s y ms
NOME: ANO: º Nº: PROFESSOR(A): An Luiz Ozores DATA: REVISÃO List Geometri Anlític Algums definições y Equções d ret: by c 0, y mb, y y0 m( 0) e p q Posições de dus rets: Dds s rets r : y mr br e s y ms
Cartilha Explicativa. Segurança para quem você ama.
 Crtilh Explictiv Segurnç pr quem você m. Bem-vindo, novo prticipnte! É com stisfção que recebemos su desão o Fmíli Previdênci, plno desenhdo pr oferecer um complementção de posentdori num modelo moderno
Crtilh Explictiv Segurnç pr quem você m. Bem-vindo, novo prticipnte! É com stisfção que recebemos su desão o Fmíli Previdênci, plno desenhdo pr oferecer um complementção de posentdori num modelo moderno
CINÉTICA QUÍMICA CINÉTICA QUÍMICA. Lei de Velocidade
 CINÉTICA QUÍMICA Lei de Velocidde LEIS DE VELOCIDADE - DETERMINAÇÃO Os eperimentos em Cinétic Químic fornecem os vlores ds concentrções ds espécies em função do tempo. A lei de velocidde que govern um
CINÉTICA QUÍMICA Lei de Velocidde LEIS DE VELOCIDADE - DETERMINAÇÃO Os eperimentos em Cinétic Químic fornecem os vlores ds concentrções ds espécies em função do tempo. A lei de velocidde que govern um
5) Para b = temos: 2. Seja M uma matriz real 2 x 2. Defina uma função f na qual cada elemento da matriz se desloca para a posição. e as matrizes são:
 MATEMÁTIA Sej M um mtriz rel x. Defin um função f n qul cd elemento d mtriz se desloc pr posição b seguinte no sentido horário, ou sej, se M =, c d c implic que f (M) =. Encontre tods s mtrizes d b simétrics
MATEMÁTIA Sej M um mtriz rel x. Defin um função f n qul cd elemento d mtriz se desloc pr posição b seguinte no sentido horário, ou sej, se M =, c d c implic que f (M) =. Encontre tods s mtrizes d b simétrics
b) Justifique sua resposta. Resolução a) A afirmação não é válida. b) Os vírus são parasitas obrigatórios de células procarióticas
 1 BIOLOGIA Devido ao fato de serem muito simples em termos de organização, podemos afirmar que os vírus provavelmente tiveram sua origem antes do surgimento das primeiras células procarióticas. a) A afirmação
1 BIOLOGIA Devido ao fato de serem muito simples em termos de organização, podemos afirmar que os vírus provavelmente tiveram sua origem antes do surgimento das primeiras células procarióticas. a) A afirmação
PROVA DE MATEMÁTICA - TURMAS DO
 PROVA DE MATEMÁTICA - TURMAS DO o ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - MARÇO DE 0. ELABORAÇÃO: PROFESSORES ADRIANO CARIBÉ E WALTER PORTO. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 0. (UDESC SC)
PROVA DE MATEMÁTICA - TURMAS DO o ANO DO ENSINO MÉDIO COLÉGIO ANCHIETA-BA - MARÇO DE 0. ELABORAÇÃO: PROFESSORES ADRIANO CARIBÉ E WALTER PORTO. PROFESSORA MARIA ANTÔNIA C. GOUVEIA Questão 0. (UDESC SC)
Material Teórico - Módulo de Razões e Proporções. Proporções e Conceitos Relacionados. Sétimo Ano do Ensino Fundamental
 Mteril Teórico - Módulo de Rzões e Proporções Proporções e Conceitos Relciondos Sétimo Ano do Ensino Fundmentl Prof. Frncisco Bruno Holnd Prof. Antonio Cminh Muniz Neto Portl OBMEP 1 Introdução N ul nterior,
Mteril Teórico - Módulo de Rzões e Proporções Proporções e Conceitos Relciondos Sétimo Ano do Ensino Fundmentl Prof. Frncisco Bruno Holnd Prof. Antonio Cminh Muniz Neto Portl OBMEP 1 Introdução N ul nterior,
CONCURSO DE SELEÇÃO 2003 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO
 CONCURSO DE SELEÇÃO 003 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO 41100 0$7(0É7,&$ RESOLUÇÃO PELA PROFESSORA MARIA ANTÔNIA CONCEIÇÃO GOUVEIA $ LOXVWUDomR TXH VXEVWLWXL D RULJLQDO GD TXHVWmR H DV GDV UHVROXo}HV
CONCURSO DE SELEÇÃO 003 UNIVERSIDADE FEDERAL DO RIO DE JANEIRO 41100 0$7(0É7,&$ RESOLUÇÃO PELA PROFESSORA MARIA ANTÔNIA CONCEIÇÃO GOUVEIA $ LOXVWUDomR TXH VXEVWLWXL D RULJLQDO GD TXHVWmR H DV GDV UHVROXo}HV
4 π. 8 π Considere a função real f, definida por f(x) = 2 x e duas circunferência C 1 e C 2, centradas na origem.
 EFOMM 2010 1. Anlise s firmtivs bixo. I - Sej K o conjunto dos qudriláteros plnos, seus subconjuntos são: P = {x K / x possui ldos opostos prlelos}; L = {x K / x possui 4 ldos congruentes}; R = {x K /
EFOMM 2010 1. Anlise s firmtivs bixo. I - Sej K o conjunto dos qudriláteros plnos, seus subconjuntos são: P = {x K / x possui ldos opostos prlelos}; L = {x K / x possui 4 ldos congruentes}; R = {x K /
, então ela é integrável em [ a, b] Interpretação geométrica: seja contínua e positiva em um intervalo [ a, b]
![, então ela é integrável em [ a, b] Interpretação geométrica: seja contínua e positiva em um intervalo [ a, b] , então ela é integrável em [ a, b] Interpretação geométrica: seja contínua e positiva em um intervalo [ a, b]](/thumbs/39/18525051.jpg) Interl Deinid Se é um unção de, então su interl deinid é um interl restrit à vlores em um intervlo especíico, dimos, O resultdo é um número que depende pens de e, e não de Vejmos deinição: Deinição: Sej
Interl Deinid Se é um unção de, então su interl deinid é um interl restrit à vlores em um intervlo especíico, dimos, O resultdo é um número que depende pens de e, e não de Vejmos deinição: Deinição: Sej
07 AVALIAÇÃO DO EFEITO DO TRATAMENTO DE
 07 AVALIAÇÃO DO EFEITO DO TRATAMENTO DE SEMENTES NA QUALIDADE FISIOLOGICA DA SEMENTE E A EFICIENCIA NO CONTROLE DE PRAGAS INICIAIS NA CULTURA DA SOJA Objetivo Este trblho tem como objetivo vlir o efeito
07 AVALIAÇÃO DO EFEITO DO TRATAMENTO DE SEMENTES NA QUALIDADE FISIOLOGICA DA SEMENTE E A EFICIENCIA NO CONTROLE DE PRAGAS INICIAIS NA CULTURA DA SOJA Objetivo Este trblho tem como objetivo vlir o efeito
ALGEBRA LINEAR AUTOVALORES E AUTOVETORES. Prof. Ademilson
 LGEBR LINER UTOVLORES E UTOVETORES Prof. demilson utovlores e utovetores utovlores e utovetores são conceitos importntes de mtemátic, com plicções prátics em áres diversificds como mecânic quântic, processmento
LGEBR LINER UTOVLORES E UTOVETORES Prof. demilson utovlores e utovetores utovlores e utovetores são conceitos importntes de mtemátic, com plicções prátics em áres diversificds como mecânic quântic, processmento
A FAMÍLIA SILVA E SEUS GENES. Os filhos são diferentes, mas todos são Silva. Saiba como! ALBINO PIGMENTADO PROCEDIMENTO
 A FAMÍLIA SILVA E SEUS GENES Os filhos são diferentes, mas todos são Silva. Saiba como! ALBINO PIGMENTADO PROCEDIMENTO PROCEDIMENTO PARTE 1 Determinação dos genótipos dos pais 1.1. Observar a aparência
A FAMÍLIA SILVA E SEUS GENES Os filhos são diferentes, mas todos são Silva. Saiba como! ALBINO PIGMENTADO PROCEDIMENTO PROCEDIMENTO PARTE 1 Determinação dos genótipos dos pais 1.1. Observar a aparência
Universidade Federal do Rio Grande FURG. Instituto de Matemática, Estatística e Física IMEF Edital 15 - CAPES MATRIZES
 Universidde Federl do Rio Grnde FURG Instituto de Mtemátic, Esttístic e Físic IMEF Editl - CAPES MATRIZES Prof. Antônio Murício Medeiros Alves Profª Denise Mri Vrell Mrtinez Mtemátic Básic pr Ciêncis Sociis
Universidde Federl do Rio Grnde FURG Instituto de Mtemátic, Esttístic e Físic IMEF Editl - CAPES MATRIZES Prof. Antônio Murício Medeiros Alves Profª Denise Mri Vrell Mrtinez Mtemátic Básic pr Ciêncis Sociis
CPV O Cursinho que Mais Aprova na GV
 CPV O Cursinho que Mis Aprov n GV FGV ADM 04/dezembro/016 MATEMÁTICA APLICADA 01. ) Represente grficmente no plno crtesino função: P(t) = t 4t + 10 se t 4 1 t se t > 4 Se função P(t), em centens de reis,
CPV O Cursinho que Mis Aprov n GV FGV ADM 04/dezembro/016 MATEMÁTICA APLICADA 01. ) Represente grficmente no plno crtesino função: P(t) = t 4t + 10 se t 4 1 t se t > 4 Se função P(t), em centens de reis,
AULA 1. 1 NÚMEROS E OPERAÇÕES 1.1 Linguagem Matemática
 1 NÚMEROS E OPERAÇÕES 1.1 Lingugem Mtemátic AULA 1 1 1.2 Conjuntos Numéricos Chm-se conjunto o grupmento num todo de objetos, bem definidos e discerníveis, de noss percepção ou de nosso entendimento, chmdos
1 NÚMEROS E OPERAÇÕES 1.1 Lingugem Mtemátic AULA 1 1 1.2 Conjuntos Numéricos Chm-se conjunto o grupmento num todo de objetos, bem definidos e discerníveis, de noss percepção ou de nosso entendimento, chmdos
Quantidade de oxigênio no sistema
 EEIMVR-UFF Refino dos Aços I 1ª Verificção Junho 29 1. 1 kg de ferro puro são colocdos em um forno, mntido 16 o C. A entrd de oxigênio no sistem é controld e relizd lentmente, de modo ir umentndo pressão
EEIMVR-UFF Refino dos Aços I 1ª Verificção Junho 29 1. 1 kg de ferro puro são colocdos em um forno, mntido 16 o C. A entrd de oxigênio no sistem é controld e relizd lentmente, de modo ir umentndo pressão
FUNÇÕES. Mottola. 1) Se f(x) = 6 2x. é igual a (a) 1 (b) 2 (c) 3 (d) 4 (e) 5. 2) (UNIFOR) O gráfico abaixo. 0 x
 FUNÇÕES ) Se f() = 6, então f ( 5) f ( 5) é igul () (b) (c) 3 (d) 4 (e) 5 ) (UNIFOR) O gráfico bio 0 () não represent um função. (b) represent um função bijetor. (c) represent um função não injetor. (d)
FUNÇÕES ) Se f() = 6, então f ( 5) f ( 5) é igul () (b) (c) 3 (d) 4 (e) 5 ) (UNIFOR) O gráfico bio 0 () não represent um função. (b) represent um função bijetor. (c) represent um função não injetor. (d)
CÁLCULO E INSTRUMENTOS FINANCEIROS I (2º ANO)
 GESTÃO DE EMPRESAS CÁLCULO E INSTRUMENTOS FINANCEIROS I (2º ANO) Exercícios Amortizção de Empréstimos EXERCÍCIOS DE APLICAÇÃO Exercício 1 Um empréstimo vi ser reembolsdo trvés de reembolsos nuis, constntes
GESTÃO DE EMPRESAS CÁLCULO E INSTRUMENTOS FINANCEIROS I (2º ANO) Exercícios Amortizção de Empréstimos EXERCÍCIOS DE APLICAÇÃO Exercício 1 Um empréstimo vi ser reembolsdo trvés de reembolsos nuis, constntes
81,9(56,'$'( )('(5$/ '2 5,2 '( -$1(,52 &21&8562 '( 6(/(d 2 0$7(0É7,&$
 81,9(56,'$'( )('(5$/ ' 5, '( -$1(,5 &1&856 '( 6(/(d 0$7(0É7,&$ -867,),48( 7'$6 $6 68$6 5(667$6 De um retângulo de 18 cm de lrgur e 48 cm de comprimento form retirdos dois qudrdos de ldos iguis 7 cm, como
81,9(56,'$'( )('(5$/ ' 5, '( -$1(,5 &1&856 '( 6(/(d 0$7(0É7,&$ -867,),48( 7'$6 $6 68$6 5(667$6 De um retângulo de 18 cm de lrgur e 48 cm de comprimento form retirdos dois qudrdos de ldos iguis 7 cm, como
Resoluções das atividades
 Resoluções ds tividdes Começo de convers A velocidde ds notícis Resposts pessois. É possível pontr indicdores numéricos comuns à relidde ds mídis sociis, tis como: quntidde de comprtilhmentos, número de
Resoluções ds tividdes Começo de convers A velocidde ds notícis Resposts pessois. É possível pontr indicdores numéricos comuns à relidde ds mídis sociis, tis como: quntidde de comprtilhmentos, número de
Soluções tampão. EFEITO TAMPÃO: é a resistência de uma solução a mudanças de. concentração de íons hidrogênio ao se adicionar pequenas
 Soluções tmpão EFEITO TAMPÃO: é resistênci de um solução mudnçs de concentrção de íons hidrogênio o se dicionr pequens quntiddes de ácido ou bse. Um solução que tem ess propriedde é chmd de SOLUÇÃO TAMPÃO.
Soluções tmpão EFEITO TAMPÃO: é resistênci de um solução mudnçs de concentrção de íons hidrogênio o se dicionr pequens quntiddes de ácido ou bse. Um solução que tem ess propriedde é chmd de SOLUÇÃO TAMPÃO.
LISTA DE EXERCÍCIOS Questões de Vestibulares. e B = 2
 LISTA DE EXERCÍCIOS Questões de Vestiulres ) UFBA 9 Considere s mtries A e B Sendo-se que X é um mtri simétri e que AX B, determine -, sendo Y ( ij) X - R) ) UFBA 9 Dds s mtries A d Pode-se firmr: () se
LISTA DE EXERCÍCIOS Questões de Vestiulres ) UFBA 9 Considere s mtries A e B Sendo-se que X é um mtri simétri e que AX B, determine -, sendo Y ( ij) X - R) ) UFBA 9 Dds s mtries A d Pode-se firmr: () se
Análise de Circuitos Trifásicos Desequilibrados Utilizando-se Componentes Simétricas
 Análise de Circuitos Trifásicos Desequilibrdos Utilizndo-se Componentes Simétrics Prof. José Rubens Mcedo Jr. Exercício: Um determind crg trifásic, ligd em estrel flutunte, é limentd pels seguintes tensões
Análise de Circuitos Trifásicos Desequilibrdos Utilizndo-se Componentes Simétrics Prof. José Rubens Mcedo Jr. Exercício: Um determind crg trifásic, ligd em estrel flutunte, é limentd pels seguintes tensões
Unidade 7. Reprodução e hereditariedade
 Unidade 7 Reprodução e hereditariedade O ESTUDO DA HEREDITARIEDADE Teoria da pré-formação ou Progênese: dentro de cada semente (gameta) existiam miniaturas de seres humanos, chamados homúnculos. Gregor
Unidade 7 Reprodução e hereditariedade O ESTUDO DA HEREDITARIEDADE Teoria da pré-formação ou Progênese: dentro de cada semente (gameta) existiam miniaturas de seres humanos, chamados homúnculos. Gregor
- Nosso corpo é formado por inúmeras estruturas macro e microscópicas;
 CAPÍTULO 01 A CÉLULA - Nosso corpo é formado por inúmeras estruturas macro e microscópicas; - O funcionamento interligado e harmonioso dessas estruturas mantém o corpo vivo, em funcionamento; A ORGANIZAÇÃO
CAPÍTULO 01 A CÉLULA - Nosso corpo é formado por inúmeras estruturas macro e microscópicas; - O funcionamento interligado e harmonioso dessas estruturas mantém o corpo vivo, em funcionamento; A ORGANIZAÇÃO
