Complementos de Cálculo Diferencial
|
|
|
- Renata Franca Raminhos
- 7 Há anos
- Visualizações:
Transcrição
1 Matemática - 009/0 - Comlementos de Cálculo Diferencial 47 Comlementos de Cálculo Diferencial A noção de derivada foi introduzida no ensino secundário. Neste teto retende-se relembrar algumas de nições e resultados já conhecidos e comlementar os conhecimentos adquiridos com vista ao cálculo integral que será dado no caítulo seguinte. Anteriormente foram estudadas as funções trigonométricas e resectivas derivadas, mas não foram estudadas as funções inversas das funções trigonométricas. Aqui serão aresentadas as funções inversas das quatro rinciais funções trigonométricas, seno, co-seno, tangente e cotagente, ara as quais serão também calculadas as derivadas. Ao longo deste caítulo todas as funções consideradas são funções reais de variável real. Revisões Algumas derivadas conhecidas: Se c R e f () c, então f 0 () 0 (a derivada de uma função constante é 0) Para R, ( ) 0 (e ) 0 e Para a R +, (a ) 0 a ln a (ln ) 0 (sin ) 0 cos (cos ) 0 sin (tan ) 0 cos (cot ) 0 sin Observação: Lembrando que, ara b > 0 e a qualquer e que, se a > 0; a b a b () a a, () constata-se que a fórmula da derivada de ; R, também se alica a derivadas de funções do tio () e (). Eemlos:. Se f (), então f 0 () ( 0 ) 0
2 Matemática - 009/0 - Comlementos de Cálculo Diferencial 48. Se f () 4 ; então f 0 ()! Relações trigonométricas tan sin cos, cot tan cos sin Fórmula fundamental da trigonometria cos + sin Se cos 6 0, cos + tan, cos + tan Se sin 6 0, sin + cot, sin + cot cos ( + ) cos cos sin sin cos ( ) cos cos + sin sin sin ( + ) cos sin + cos sin sin ( ) cos sin cos sin cos () cos sin sin () cos sin cos sin sin cos cos cos + cos cos sin ( + ) + sin ( ) cos ( ) + cos ( + ) Alguns valores das funções trigonométricas 0 6 0o 4 45o 60o 90o 80 o 90o sin 0 0 cos 0 0 tan 0 nd 0 nd cot nd 0 nd 0
3 Matemática - 009/0 - Comlementos de Cálculo Diferencial 49 Regras de derivação De nição: Uma função é diferenciável em R se tiver derivada nita em : Teorema: Se uma função f é diferenciável em R, então f é contínua em : Derivada do roduto escalar: Se k R e f é uma função diferenciável num onto R, então a função kf também é diferenciável em e: (kf) 0 () k (f 0 ()) Eemlo: ( ) 0 ( ) 0 () 6: Derivada da soma e do roduto: Se f e g são funções diferenciáveis em R, então as funções f + g e f g também são diferenciáveis em e: Derivada da soma: (f + g) 0 () f 0 () + g 0 () [abreviadamente (f + g) 0 f 0 + g 0 ] Derivada do roduto: (f g) 0 () f 0 () g () + f () g 0 () [abreviadamente (fg) 0 f 0 g + fg 0 ] Eemlos:. Se f () e g () então: (f + g) 0 () ( + ) 0 ( ) 0 + () A derivada de q () é q 0 () () 0 + (8) Se f () e e g () ln então: (f + g) 0 () (e + ln ) 0 (e ) 0 + (ln ) 0 e + (f g) 0 () (e ln ) 0 (e ) 0 ln + e (ln ) 0 e ln + e e ln + 4. Se f () sin e g () cos então: (f + g) 0 () (sin + cos ) 0 (sin ) 0 + (cos ) 0 cos sin
4 Matemática - 009/0 - Comlementos de Cálculo Diferencial 50 (f g) 0 () (sin cos ) 0 (sin ) 0 cos + sin (cos ) 0 cos cos + sin ( sin ) cos sin Derivada do cociente: Se f e g são funções diferenciáveis em R e se g () 6 0, então f também é diferenciável em e: g 0 f () f 0 () g () g f () g 0 () (g ()) [abreviadamente 0 f f 0 g fg 0 ] g g Eemlos:. Se f () ln e g () então: 0 0 f () ln g () (ln )0 ln () 0 ln ln. Através da regra da derivada do cociente odemos deduzir a derivada da função tan. De facto, se f () sin e g () cos então f () g () sin tan : Assim, cos 0 sin (tan ) 0 () cos (sin )0 cos sin (cos ) 0 (cos ) cos cos sin ( sin ) cos cos + sin cos cos Derivada da função comosta: Se f e g são funções, f diferenciável em R e g diferenciável em f (), então a função g f é diferenciável no onto e: (g f) 0 () g 0 (f ()) f 0 () Eemlos:. Sejam f () ln e g () : Então (a) (g f) () g (f ()) (ln ) e (ln ) 0 ln : (ln ) 0 ln (b) (f g) () f (g ()) ln ( ) e (ln ( )) 0 : ( ) 0
5 Matemática - 009/0 - Comlementos de Cálculo Diferencial 5. Seja h () cos : Considerando as funções f () e g () cos veri ca-se que h f g: Então: h 0 () ( cos ) 0 (cos ) 0 (cos ) (cos ) 0 sin cos A artir da regra da derivada da função comosta odem-se deduzir eressões gerais ara as derivadas de muitas funções. Eemlos:. Seja f () uma função qualquer. Para R, qual é a derivada def ()? Esta função é a comosição de f () com a função g () : Usando a regra da derivação da função comosta obtemos (f () ) 0 f () f 0 (). Seja f () uma função qualquer. Para calcular a derivada de ln f () ; basta observar que ln f () é a comosição de f () com a função g () ln. Pela regra (ln f ()) 0 f () f 0 () f 0 () f () Resumimos as fórmulas assim obtidas na seguinte tabela (que já inclui as derivadas das funções trigonométricas inversas que deduziremos de seguida): Se é uma variável: Derivadas Se f é uma função: ( ) 0 ; R (f ) 0 f :f 0 ; R (e ) 0 e e f 0 e f :f 0 (a ) 0 a ln a; a R + a f 0 a f : ln a:f 0 ; a R + (ln ) 0 (ln f) 0 f 0 f (sin ) 0 cos (sin f) 0 cos f:f 0 (cos ) 0 sin (cos f) 0 sin f:f 0 (tan ) 0 (tan f) 0 f 0 cos cos f (cot ) 0 sin (cot f) 0 f 0 sin f (arcsin ) 0 (arcsin f) 0 f 0 f (arccos ) 0 (arccos f) 0 (arctan ) 0 + (arctan f) 0 f 0 (arccot ) 0 + (arccot f) 0 f 0 f + f f 0 + f
6 Matemática - 009/0 - Comlementos de Cálculo Diferencial 5 Funções trigonométricas inversas Função inversa da função seno Seja f () sin Domínio: R Contradomínio: [ ; ] sin Como a função seno não é injectiva, ara de nir a inversa temos de restringir h a função a um intervalo em que seja injectiva. Para isso escolhemos o intervalo ; i, no qual a função seno é estritamente crescente e assume todos os valores do seu contradomínio. Ao valor da função inversa do seno num onto deste intervalo chama-se habitualmente arco cujo seno é ; simbolicamente arcsin : Como sin e arcsin são funções inversas, é claro que sin (arcsin ) : Tem-se então: f () arcsin Domínio: [ ; ] h Contradomínio: ; i arcsin
7 Matemática - 009/0 - Comlementos de Cálculo Diferencial 5 Função inversa da função co-seno Seja f () cos Domínio: R Contradomínio: [ ; ] cos Também neste caso, ara de nir a função inversa temos de restringir a função co-seno a um intervalo em que seja injectiva. Para isso escolhemos o intervalo [0; ], no qual a função co-seno é estritamente decrescente e assume todos os valores do seu contradomínio. Ao valor da função inversa do co-seno num onto deste intervalo chama-se habitualmente arco cujo co-seno é ; simbolicamente arccos : Como cos e arccos são funções inversas, é claro que cos (arccos ) : Tem-se então: f () arccos Domínio: [ ; ] Contradomínio: [0; ] arccos
8 Matemática - 009/0 - Comlementos de Cálculo Diferencial 54 Função inversa da tangente: Seja f () tan n (ou f () tg ) o Domínio: R + k : k Z Contradomínio: R tan Neste i caso, ara calcular a função inversa da tangente, efectuamos a sua restrição ao intervalo ; h no qual a função é estritamente crescente e assume todos os valores do seu contradomínio. Ao valor da função inversa da tangente num onto deste intervalo chamase habitualmente arco cuja tangente é ; simbolicamente arctan ou arctg : Como tan e arctan são funções inversas, é claro que tan (arctan ) : Tem-se então: f () arctan (ou f () arctg ) Domínio: R i Contradomínio: ; h arctan
9 Matemática - 009/0 - Comlementos de Cálculo Diferencial 55 Função inversa da cotangente: f () cot (ou f () cotg ) Domínio: R fk : k Zg Contradomínio: R cot Neste caso, ara calcular a função inversa da cotangente, efectuamos a sua restrição ao intervalo ]0; [ no qual a função é estritamente decrescente e assume todos os valores do seu contradomínio. Ao valor da função inversa da tangente num onto deste intervalo chama-se habitualmente arco cuja cotangente é ; simbolicamente arccot ou arccotg : Como cot e arccot são funções inversas, é claro que cot (arccot ) : Tem-se então: f () arccot (ou f () arccotg ) Domínio: R Contradomínio: ]0; [ arccot
10 Matemática - 009/0 - Comlementos de Cálculo Diferencial 56 Derivada da função inversa O teorema que se enuncia de seguida ermite calcular a derivada da função inversa de uma função dada a artir da derivada da função inicial. Derivada da função inversa: Seja I um intervalo real, f : I! R uma função monótona e contínua e f : f (I)! R a inversa de f: Se f é diferenciável num onto I e f 0 () 6 0; então f é diferenciável em f () e: f 0 () f 0 (f ()) () Eemlos: Os eemlos que aresentamos mostram como utilizar este teorema no cálculo de derivadas já conhecidas.. Vamos calcular a derivada da função ln usando o facto de ser a função inversa de f () e : Com é sabido f 0 () e : Neste caso f () ln : Alicando a fórmula () obtemos: (ln ) 0 f 0 () f 0 (f ()) e (ln ). Vamos calcular a derivada da função usando o facto de ser a função inversa de f () : Com é sabido f 0 () : Neste caso f () : Alicando a fórmula () obtemos: 0 ( ) 0 f 0 () f 0 (f ()) Derivadas das funções trigonométricas inversas arcsin Se f () sin então f 0 () cos e f () arcsin. Alicando a fórmula () da ágina 56, obtém-se: arccos (arcsin ) 0 cos (arcsin ) # ver g. 48 sin (arcsin ) Se f () cos então f 0 () sin e f () arcsen. Alicando a fórmula () da ágina 56, obtém-se: (arccos ) 0 sin (arccos ) # ver g. 48 cos (arccos )
11 Matemática - 009/0 - Comlementos de Cálculo Diferencial 57 arctan Se f () tan então f 0 () cos e f () arctan. Alicando a fórmula () da ágina 56, obtém-se: (arctan ) 0 cos (arctan ) # ver g tan (arctan ) + arccot Se f () cot então f 0 () da ágina 56, obtém-se: sen e f () arccot. Alicando a fórmula () (arccot ) 0 sin (arccot ) # ver g cot (arccot ) + Conclusão: (arcsin ) 0 (arccos ) 0 (arctan ) 0 + (arccot ) 0 +
Complementos de Cálculo Diferencial
 MTDI I - 7/8 - Comlementos de Cálculo Diferencial 34 Comlementos de Cálculo Diferencial A noção de derivada foi introduzida no ensino secundário. Neste caítulo retende-se relembrar algumas de nições e
MTDI I - 7/8 - Comlementos de Cálculo Diferencial 34 Comlementos de Cálculo Diferencial A noção de derivada foi introduzida no ensino secundário. Neste caítulo retende-se relembrar algumas de nições e
Continuidade de uma função
 Continuidade de uma função Consideremos f : D f uma função real de variável real (f.r.v.r.) e a um ponto de acumulação de D f que pertence a D f. Diz-se que a função f é contínua em a se lim f x f a. x
Continuidade de uma função Consideremos f : D f uma função real de variável real (f.r.v.r.) e a um ponto de acumulação de D f que pertence a D f. Diz-se que a função f é contínua em a se lim f x f a. x
Capítulo 1 Funções reais de uma variável 1.2 Funções trigonométricas inversas
 As funções trigonométricas seno, coseno, tangente e cotangente não são funções injetivas, não sendo portanto invertíveis nos respetivos domínios. Para definir as respetivas funções inversas tem de se considerar
As funções trigonométricas seno, coseno, tangente e cotangente não são funções injetivas, não sendo portanto invertíveis nos respetivos domínios. Para definir as respetivas funções inversas tem de se considerar
Trigonometria e funções trigonométricas. Funções trigonométricas O essencial
 Trigonometria e funções trigonométricas Funções trigonométricas O essencial Funções seno e cosseno Designa-se por função seno (respetivamente, função cosseno) e representa-se por sin ou sen (respetivamente,
Trigonometria e funções trigonométricas Funções trigonométricas O essencial Funções seno e cosseno Designa-se por função seno (respetivamente, função cosseno) e representa-se por sin ou sen (respetivamente,
Notas sobre primitivas
 Matemática - 8/9 - Notas sobre primitivas 57 Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo I a uma função F cuja derivada
Matemática - 8/9 - Notas sobre primitivas 57 Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo I a uma função F cuja derivada
7.1 Regras Básicas de Derivação. 7.2 Principais Notações. 01. regra da soma: [f (x) + g (x)] 0 = f 0 (x) + g 0 (x)
![7.1 Regras Básicas de Derivação. 7.2 Principais Notações. 01. regra da soma: [f (x) + g (x)] 0 = f 0 (x) + g 0 (x) 7.1 Regras Básicas de Derivação. 7.2 Principais Notações. 01. regra da soma: [f (x) + g (x)] 0 = f 0 (x) + g 0 (x)](/thumbs/64/50953812.jpg) 7. Regras Básicas e Derivação 0. regra a soma: [f () + g ()] 0 = f 0 () + g 0 () 0. regra a iferença [f () g ()] 0 = f 0 () g 0 () 0. regra o routo [f () :g ()] 0 = f () g 0 () + f 0 () g () 04. regra
7. Regras Básicas e Derivação 0. regra a soma: [f () + g ()] 0 = f 0 () + g 0 () 0. regra a iferença [f () g ()] 0 = f 0 () g 0 () 0. regra o routo [f () :g ()] 0 = f () g 0 () + f 0 () g () 04. regra
1. FUNÇÕES REAIS DE VARIÁVEL REAL
 1 1 FUNÇÕES REAIS DE VARIÁVEL REAL 11 Funções trigonométricas inversas 111 As funções arco-seno e arco-cosseno Como as funções seno e cosseno não são injectivas em IR, só poderemos definir as suas funções
1 1 FUNÇÕES REAIS DE VARIÁVEL REAL 11 Funções trigonométricas inversas 111 As funções arco-seno e arco-cosseno Como as funções seno e cosseno não são injectivas em IR, só poderemos definir as suas funções
MAT146 - Cálculo I - Derivada das Inversas Trigonométricas
 MAT46 - Cálculo I - Derivada das Inversas Trigonométricas Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos anteriormente que as funções trigonométricas não são inversíveis, mas
MAT46 - Cálculo I - Derivada das Inversas Trigonométricas Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos anteriormente que as funções trigonométricas não são inversíveis, mas
A. Funções trigonométricas directas
 A. Funções trigonométricas directas As funções seno, cosseno, tangente e cotangente são contínuas e periódicas nos respectivos domínios. Todas elas são funções não injectivas e, portanto, não possuem inversa.
A. Funções trigonométricas directas As funções seno, cosseno, tangente e cotangente são contínuas e periódicas nos respectivos domínios. Todas elas são funções não injectivas e, portanto, não possuem inversa.
Notas sobre primitivas
 MTDI I - 007/08 - Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo I a uma função F cuja derivada
MTDI I - 007/08 - Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo I a uma função F cuja derivada
Notas sobre primitivas
 Análise Matemática I - Engenharia Topográ ca - 9/- Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo
Análise Matemática I - Engenharia Topográ ca - 9/- Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo
7.1 Mudança de Variável (método de substituição)
 7. Mudança de Variável (método de substituição) 0. 0. 0. 05. 07. 08. 0... e 5 (res. e 5 =5 + C) sen a (res. a cos a + C; a 6= 0) sen () 7 (res. cotg + C) (res. jln 7j + C) tan (res. ln jcos j + C) cot
7. Mudança de Variável (método de substituição) 0. 0. 0. 05. 07. 08. 0... e 5 (res. e 5 =5 + C) sen a (res. a cos a + C; a 6= 0) sen () 7 (res. cotg + C) (res. jln 7j + C) tan (res. ln jcos j + C) cot
Jaime Carvalho e Silva. Princípios de Análise Matemática Aplicada. Suplemento
 Jaime Carvalho e Silva Princípios de Análise Matemática Aplicada Suplemento 2002/2003 2 Departamento de Matemática Universidade de Coimbra Contacto com o autor: jaimecs@mat.uc.pt Página de apoio: http://www.mat.uc.pt/~jaimecs/index_aulas.html
Jaime Carvalho e Silva Princípios de Análise Matemática Aplicada Suplemento 2002/2003 2 Departamento de Matemática Universidade de Coimbra Contacto com o autor: jaimecs@mat.uc.pt Página de apoio: http://www.mat.uc.pt/~jaimecs/index_aulas.html
Regras Básicas de Derivação
 Regras Básicas e Derivação. regra a soma: (u + kv) = u + kv, k constante 2. regra a iferença: (u + v) = u + v 3. regra o prouto: (u v) = u v + u v u u v u v 4. regra o quociente: = v v 2 5. regra a caeia:
Regras Básicas e Derivação. regra a soma: (u + kv) = u + kv, k constante 2. regra a iferença: (u + v) = u + v 3. regra o prouto: (u v) = u v + u v u u v u v 4. regra o quociente: = v v 2 5. regra a caeia:
Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].
![Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3]. Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].](/thumbs/100/144026914.jpg) Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Limites e continuidade
 Limites e continuidade Limite (finito) de uma função em a Salvo indicação em contrário, quando nos referimos a uma função estamos sempre a considerar funções reais de variável real (f.r.v.r.), ou seja,
Limites e continuidade Limite (finito) de uma função em a Salvo indicação em contrário, quando nos referimos a uma função estamos sempre a considerar funções reais de variável real (f.r.v.r.), ou seja,
Derivando fun»c~oes trigonom etricas
 Aula 1 Derivando fun»c~oes trigonom etricas Nesta aula estaremos deduzindo derivadas de fun»c~oes trigonom etricas. Estaremos tamb em aresentando as fun»c~oes trigonom etricas inversas e deduzindo suas
Aula 1 Derivando fun»c~oes trigonom etricas Nesta aula estaremos deduzindo derivadas de fun»c~oes trigonom etricas. Estaremos tamb em aresentando as fun»c~oes trigonom etricas inversas e deduzindo suas
Cálculo diferencial. Motivação - exemplos de aplicações à física
 Cálculo diferencial Motivação - eemplos de aplicações à física Considere-se um ponto móvel sobre um eio orientado, cuja posição em relação à origem é dada, em função do tempo, pela função s. st posição
Cálculo diferencial Motivação - eemplos de aplicações à física Considere-se um ponto móvel sobre um eio orientado, cuja posição em relação à origem é dada, em função do tempo, pela função s. st posição
Cálculo Diferencial e Integral I 1 o Sem. 2015/16 - LEAN, LEMat, MEQ FICHA 8
 Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem. 05/6 - LEAN, LEMat, MEQ FICHA 8 Regra de Cauchy. Estudo de funções. a. a) b 0 é uma indeterminação do tipo
Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem. 05/6 - LEAN, LEMat, MEQ FICHA 8 Regra de Cauchy. Estudo de funções. a. a) b 0 é uma indeterminação do tipo
Instituto Politécnico de Bragança Escola Superior de Tecnologia e Gestão. Análise Matemática I 2003/04
 Instituto Politécnico de Bragança Escola Superior de Tecnologia e Gestão Análise Matemática I 00/0 Ficha Prática nº Parte III Função Eponencial Função Logaritmo Funções trigonométricas directas e inversas
Instituto Politécnico de Bragança Escola Superior de Tecnologia e Gestão Análise Matemática I 00/0 Ficha Prática nº Parte III Função Eponencial Função Logaritmo Funções trigonométricas directas e inversas
Matemática Licenciatura - Semestre Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa. Diferenciabilidade.
 1 Matemática Licenciatura - Semestre 2010.1 Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa Diferenciabilidade Funções Trigonométricas Inicialmente, observe pela gura que para ângulos 0
1 Matemática Licenciatura - Semestre 2010.1 Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa Diferenciabilidade Funções Trigonométricas Inicialmente, observe pela gura que para ângulos 0
4 Cálculo Diferencial
 4 Cálculo Diferencial 1 (Eercício IV1 de [1]) Calcule as derivadas das funções: a) tg, b) +cos 1 sen, c) e arctg, d) e log, e) sen cos tg, f) (1 + log ), g) cos(arcsen ) h) (log ), i) sen Derive: a) arctg
4 Cálculo Diferencial 1 (Eercício IV1 de [1]) Calcule as derivadas das funções: a) tg, b) +cos 1 sen, c) e arctg, d) e log, e) sen cos tg, f) (1 + log ), g) cos(arcsen ) h) (log ), i) sen Derive: a) arctg
Matemática /09 - Produto Interno 32. Produto Interno
 Matemática - 2008/09 - Produto Interno 32 Produto Interno A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass. Neste capítulo
Matemática - 2008/09 - Produto Interno 32 Produto Interno A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass. Neste capítulo
A derivada da função inversa
 A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
Ficha de Problemas n o 6: Cálculo Diferencial (soluções) 2.Teoremas de Rolle, Lagrange e Cauchy
 Ficha de Problemas n o 6: Cálculo Diferencial soluções).teoremas de Rolle, Lagrange e Cauchy. Seja f) = 3 e. Então f é contínua e diferenciável em R. Uma vez que f) = +, f0) = conclui-se do Teorema do
Ficha de Problemas n o 6: Cálculo Diferencial soluções).teoremas de Rolle, Lagrange e Cauchy. Seja f) = 3 e. Então f é contínua e diferenciável em R. Uma vez que f) = +, f0) = conclui-se do Teorema do
DERIVADA. A Reta Tangente
 DERIVADA A Reta Tangente Seja f uma função definida numa vizinança de a. Para definir a reta tangente de uma curva = f() num ponto P(a, f(a)), consideramos um ponto vizino Q(,), em que a e traçamos a S,
DERIVADA A Reta Tangente Seja f uma função definida numa vizinança de a. Para definir a reta tangente de uma curva = f() num ponto P(a, f(a)), consideramos um ponto vizino Q(,), em que a e traçamos a S,
Capítulo 6 - Integral Inde nida
 Caítulo - Integral Inde nida. Calcule as integrais inde nidas abaio usando integração imediata ou o método da substituição. e d (j) e d d e ( ) (k) d d arctan (l) ( ) d d sec tg (m) d ln d e (n) ( e )
Caítulo - Integral Inde nida. Calcule as integrais inde nidas abaio usando integração imediata ou o método da substituição. e d (j) e d d e ( ) (k) d d arctan (l) ( ) d d sec tg (m) d ln d e (n) ( e )
4 Cálculo Diferencial
 4 Cálculo Diferencial 1. (Eercício IV.1 de [1]) Calcule as derivadas das funções: a) tg, b) +cos 1 sen, c) e arctg, d) e log2, e) sen cos tg, f) 2 (1 + log ), g) cos(arcsen ) h) (log ), i) sen 2. 2. Derive:
4 Cálculo Diferencial 1. (Eercício IV.1 de [1]) Calcule as derivadas das funções: a) tg, b) +cos 1 sen, c) e arctg, d) e log2, e) sen cos tg, f) 2 (1 + log ), g) cos(arcsen ) h) (log ), i) sen 2. 2. Derive:
1. Polinómios e funções racionais
 Um catálogo de funções. Polinómios e funções racionais Polinómios e funções racionais são funções que se podem construir usando apenas as operações algébricas elementares. Recordemos a definição: Definição
Um catálogo de funções. Polinómios e funções racionais Polinómios e funções racionais são funções que se podem construir usando apenas as operações algébricas elementares. Recordemos a definição: Definição
Processo Seletivo Estendido 2017
 Processo Seletivo Estendido 07 Professor: Fernando de Ávila Silva Departamento de Matemática - UFPR. Converta de graus para radianos: a 0 b 0 c 5 d 5 e 70 f 70 g 5 h 700 i 080 j. Converta de radianos para
Processo Seletivo Estendido 07 Professor: Fernando de Ávila Silva Departamento de Matemática - UFPR. Converta de graus para radianos: a 0 b 0 c 5 d 5 e 70 f 70 g 5 h 700 i 080 j. Converta de radianos para
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Resolução do Eame / Testes de Recuperação I.. (, val.)determine os ites das seguintes sucessões convergentes (i) u n n + n n e n + n, (ii) v n n + π n Resolução: i) A sucessão
Cálculo Diferencial e Integral I Resolução do Eame / Testes de Recuperação I.. (, val.)determine os ites das seguintes sucessões convergentes (i) u n n + n n e n + n, (ii) v n n + π n Resolução: i) A sucessão
Derivada da função composta, derivada da função inversa, derivada da função implícita e derivada de funções definidas parametricamente.
 Análise Matemática - 007/008.5.- Derivada da função composta, derivada da função inversa, derivada da função implícita e derivada de funções definidas parametricamente. Teorema.31 Derivada da Função Composta
Análise Matemática - 007/008.5.- Derivada da função composta, derivada da função inversa, derivada da função implícita e derivada de funções definidas parametricamente. Teorema.31 Derivada da Função Composta
MatemáticaI Gestão ESTG/IPB Departamento de Matemática 28
 Cap. Funções Reais de variável Real MatemáticaI Gestão ESTG/IPB Departamento de Matemática 8. Conjuntos de Números,,3 Números Naturais,,, 0,,, Números Inteiros a : a, b, b 0 Números Racionais b Irracionais
Cap. Funções Reais de variável Real MatemáticaI Gestão ESTG/IPB Departamento de Matemática 8. Conjuntos de Números,,3 Números Naturais,,, 0,,, Números Inteiros a : a, b, b 0 Números Racionais b Irracionais
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LEA, LEM, LEAN, MEAer, MEMec o Semestre de 006/007 6 a Aula Prática Soluções e algumas resoluções abreviadas. a) Como e é crescente, com contradomínio ]0, + [, o contradomínio
Cálculo Diferencial e Integral I LEA, LEM, LEAN, MEAer, MEMec o Semestre de 006/007 6 a Aula Prática Soluções e algumas resoluções abreviadas. a) Como e é crescente, com contradomínio ]0, + [, o contradomínio
Por outras palavras, iremos desenvolver a operação inversa da derivação conhecida por primitivação.
 RIMITIVS Definições No caítulo anterior, centramos a nossa atenção no seguinte roblema: dada uma função, determinar a sua função derivada Neste caítulo, vamos considerar o roblema inverso, ou seja, determinar
RIMITIVS Definições No caítulo anterior, centramos a nossa atenção no seguinte roblema: dada uma função, determinar a sua função derivada Neste caítulo, vamos considerar o roblema inverso, ou seja, determinar
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: 500 - MATEMÁTICA DISCIPLINA: Matemática A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: 500 - MATEMÁTICA DISCIPLINA: Matemática A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias
P L A N I F I C A Ç Ã O A N U A L
 P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: Matemática DISCIPLINA: Matemática A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias ANO:11º
P L A N I F I C A Ç Ã O A N U A L DEPARTAMENTO: MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS ÁREA DISCIPLINAR: Matemática DISCIPLINA: Matemática A NÍVEL DE ENSINO: Secundário CURSO: Ciências e Tecnologias ANO:11º
1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:
![1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com: 1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:](/thumbs/68/59802332.jpg) Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
Gr aficos de Fun c oes Elementares
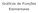 Gráficos de Funções Elementares O gráfico de uma f.r.v.r. é uma curva ou uma união de curvas. Para a sua determinação é necessário conhecer o comportamento da função. Entre os vários aspectos da teoria
Gráficos de Funções Elementares O gráfico de uma f.r.v.r. é uma curva ou uma união de curvas. Para a sua determinação é necessário conhecer o comportamento da função. Entre os vários aspectos da teoria
Resolução dos Exercícios sobre Derivadas
 Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
Universidade de Trás-os-Montes e Alto Douro. Biomatemática/ Matemática I FOLHAS PRÁTICAS
 Universidade de Trás-os-Montes e Alto Douro Biomatemática/ Matemática I FOLHAS PRÁTICAS Licenciaturas em Arquitectura Paisagista, Biologia e Geologia (ensino) e Biologia (cientíco) Ano lectivo 004/005
Universidade de Trás-os-Montes e Alto Douro Biomatemática/ Matemática I FOLHAS PRÁTICAS Licenciaturas em Arquitectura Paisagista, Biologia e Geologia (ensino) e Biologia (cientíco) Ano lectivo 004/005
CÁLCULO I. Figura 1: Círculo unitário x2 + y 2 = 1
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula no 05: Funções Logarítmica, Exponencial e Hiperbólicas. Objetivos da Aula De nir as funções trigonométricas, trigonométricas
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula no 05: Funções Logarítmica, Exponencial e Hiperbólicas. Objetivos da Aula De nir as funções trigonométricas, trigonométricas
0.1 Função Inversa. Notas de Aula de Cálculo I do dia 07/06/ Matemática Profa. Dra. Thaís Fernanda Mendes Monis.
 Notas de Aula de Cálculo I do dia 07/06/03 - Matemática Profa. Dra. Thaís Fernanda Mendes Monis. 0. Função Inversa Definição. Uma função f : A C é injetiva se f(x) f(y) para todo x y, x, y A. Seja f :
Notas de Aula de Cálculo I do dia 07/06/03 - Matemática Profa. Dra. Thaís Fernanda Mendes Monis. 0. Função Inversa Definição. Uma função f : A C é injetiva se f(x) f(y) para todo x y, x, y A. Seja f :
FICHA 11 - SOLUÇÕES. b a f(x)g(x)dx b a g(x)dx M,
 Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I - o Sem 07/8 - LEGM, MEC FICHA - SOLUÇÕES a = f/; b = f; c / = f/ Começe por aplicar o Teorema de Weierstrass a f
Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I - o Sem 07/8 - LEGM, MEC FICHA - SOLUÇÕES a = f/; b = f; c / = f/ Começe por aplicar o Teorema de Weierstrass a f
Funções Trigonométricas. A função Seno. Função Seno. Função Seno: Propriedades. f : R R. = medida algébrica do. CD(f ) = R, Im(f ) = [ 1, 1].
![Funções Trigonométricas. A função Seno. Função Seno. Função Seno: Propriedades. f : R R. = medida algébrica do. CD(f ) = R, Im(f ) = [ 1, 1]. Funções Trigonométricas. A função Seno. Função Seno. Função Seno: Propriedades. f : R R. = medida algébrica do. CD(f ) = R, Im(f ) = [ 1, 1].](/thumbs/100/146875047.jpg) Funções Trigonométricas função Seno Função Seno Função Seno: ropriedades (a) sen( + π) = sen() R R f () = sen() segmento (b) sen() = sen( ) Se está no primeiro ou segundo quadrante então sen() é positivo.
Funções Trigonométricas função Seno Função Seno Função Seno: ropriedades (a) sen( + π) = sen() R R f () = sen() segmento (b) sen() = sen( ) Se está no primeiro ou segundo quadrante então sen() é positivo.
Seno e cosseno de arcos em todos os. quadrantes
 Trigonometria Seno e cosseno de arcos em todos os quadrantes Seno e cosseno de arcos em todos os quadrantes Exemplo: Vamos determinar X, com 0 x < 2π tal que sen x = - 1 2. Seno e cosseno de arcos em todos
Trigonometria Seno e cosseno de arcos em todos os quadrantes Seno e cosseno de arcos em todos os quadrantes Exemplo: Vamos determinar X, com 0 x < 2π tal que sen x = - 1 2. Seno e cosseno de arcos em todos
Derivadas. Slides de apoio sobre Derivadas. Prof. Ronaldo Carlotto Batista. 21 de outubro de 2013
 Cálculo 1 ECT1113 Slides de apoio sobre Derivadas Prof. Ronaldo Carlotto Batista 21 de outubro de 2013 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados
Cálculo 1 ECT1113 Slides de apoio sobre Derivadas Prof. Ronaldo Carlotto Batista 21 de outubro de 2013 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados
Limite e Continuidade
 Matemática Licenciatura - Semestre 200. Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa Limite e Continuidade Neste caítulo aresentaremos as idéias básicas sobre ites e continuidade de
Matemática Licenciatura - Semestre 200. Curso: Cálculo Diferencial e Integral I Professor: Robson Sousa Limite e Continuidade Neste caítulo aresentaremos as idéias básicas sobre ites e continuidade de
CÁLCULO I. Figura 1: Círculo unitário x2 + y 2 = 1
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Aula no 04: Funções Trigonométricas, Logarítmica, Exponencial e Hiperbólicas. Objetivos
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Aula no 04: Funções Trigonométricas, Logarítmica, Exponencial e Hiperbólicas. Objetivos
3 Funções reais de variável real (Soluções)
 3 Funções reais de variável real (Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y
3 Funções reais de variável real (Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y
A inversa da função seno
 UFF/GMA Notas de aula de MB-I Maria Lúcia/Marlene 015-1 PARTE III FUNÇÕES TRIGONOMÉTRICAS INVERSAS Funções inversas. O que isso significa? A cada valor da imagem corresponde um e só um valor do domínio
UFF/GMA Notas de aula de MB-I Maria Lúcia/Marlene 015-1 PARTE III FUNÇÕES TRIGONOMÉTRICAS INVERSAS Funções inversas. O que isso significa? A cada valor da imagem corresponde um e só um valor do domínio
Exercícios sobre Trigonometria
 Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Universidade Federal Fluminense Campus do Valonguinho Instituto de Matemática e Estatística Departamento de Matemática Aplicada - GMA Prof Saponga uff Rua Mário Santos Braga s/n 400-40 Niterói, RJ Tels:
Aula 15. Integrais inde nidas. 15.1 Antiderivadas. Sendo f(x) e F (x) de nidas em um intervalo I ½ R, dizemos que
 Aula 5 Integrais inde nidas 5. Antiderivadas Sendo f() e F () de nidas em um intervalo I ½, dizemos que F e umaantiderivada ou uma rimitiva de f, emi, sef 0 () =f() ara todo I. Ou seja, F e antiderivada
Aula 5 Integrais inde nidas 5. Antiderivadas Sendo f() e F () de nidas em um intervalo I ½, dizemos que F e umaantiderivada ou uma rimitiva de f, emi, sef 0 () =f() ara todo I. Ou seja, F e antiderivada
CÁLCULO I. 1 Primitivas. Objetivos da Aula. Aula n o 18: Primitivas. Denir primitiva de uma função; Calcular as primitivas elementares.
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 8: Primitivas. Objetivos da Aula Denir primitiva de uma função; Calcular as primitivas elementares. Primitivas Em alguns problemas, é necessário
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 8: Primitivas. Objetivos da Aula Denir primitiva de uma função; Calcular as primitivas elementares. Primitivas Em alguns problemas, é necessário
MAT001 Cálculo Diferencial e Integral I
 1 MAT001 Cálculo Diferencial e Integral I RESUMO DA AULA TEÓRICA 4 Livro do Stewart: Apêndice D e Seção 16 FUNÇÕES TRIGONOMÉTRICAS O círculo trigonométrico e arcos orientados Num plano cartesiano, considere
1 MAT001 Cálculo Diferencial e Integral I RESUMO DA AULA TEÓRICA 4 Livro do Stewart: Apêndice D e Seção 16 FUNÇÕES TRIGONOMÉTRICAS O círculo trigonométrico e arcos orientados Num plano cartesiano, considere
Derivada. Aula 09 Cálculo Diferencial. Professor: Éwerton Veríssimo
 Derivada Ala 09 Cálclo Dierencial Proessor: Éwerton Veríssimo Derivada: Conceito Físico Taa de Variação A dosagem de m medicamento pode variar conorme o tempo de tratamento do paciente. O desgaste das
Derivada Ala 09 Cálclo Dierencial Proessor: Éwerton Veríssimo Derivada: Conceito Físico Taa de Variação A dosagem de m medicamento pode variar conorme o tempo de tratamento do paciente. O desgaste das
Valores e vectores próprios
 Valores e Vectores Prórios - Matemática II- /5 Valores e vectores rórios De nem-se valores e vectores rórios aenas ara matrizes quadradas, elo que, ao longo deste caítulo e quando mais nada seja eseci
Valores e Vectores Prórios - Matemática II- /5 Valores e vectores rórios De nem-se valores e vectores rórios aenas ara matrizes quadradas, elo que, ao longo deste caítulo e quando mais nada seja eseci
Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005. Cálculo I. Caderno de Exercícios 4
 Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005 Cálculo I Caderno de Eercícios 4 Limites, continuidade e diferenciabilidade de funções; fórmulas de Taylor e MacLaurin; estudo de funções.
Faculdade de Economia Universidade Nova de Lisboa Primavera 2004/2005 Cálculo I Caderno de Eercícios 4 Limites, continuidade e diferenciabilidade de funções; fórmulas de Taylor e MacLaurin; estudo de funções.
MAT 103 Complementos de Matemática para Contabilidade e Administração Prova 2 D 26 de Junho de 2008
 MAT 103 Complementos de Matemática para Contabilidade e Administração Prova D 6 de Junho de 008 Nome: RG: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos. Assinale as alternativas
MAT 103 Complementos de Matemática para Contabilidade e Administração Prova D 6 de Junho de 008 Nome: RG: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos. Assinale as alternativas
MAT 103 Complementos de Matemática para Contabilidade e Administração Prova 2 C 26 de Junho de 2008
 MAT 103 Complementos de Matemática para Contabilidade e Administração Prova C 6 de Junho de 008 Nome: RG: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos. Assinale as alternativas
MAT 103 Complementos de Matemática para Contabilidade e Administração Prova C 6 de Junho de 008 Nome: RG: Assinatura: Instruções A duração da prova é de uma hora e quarenta minutos. Assinale as alternativas
Produto interno no espaço vectorial R n
 ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
Processo Seletivo Estendido 2016 LISTA FUNÇ~OES - 6
 Processo Seletivo Estendido 0 LISTA FUNÇ~OES - Professor: Fernando de Ávila Silva Departamento de Matemática - UFPR Esta lista foi inicialmente elaborada pelo professor Aleandre Trovon UFPR. A presente
Processo Seletivo Estendido 0 LISTA FUNÇ~OES - Professor: Fernando de Ávila Silva Departamento de Matemática - UFPR Esta lista foi inicialmente elaborada pelo professor Aleandre Trovon UFPR. A presente
CÁLCULO I Ano Lectivo o Semestre
 Faculdade de Economia da Universidade Nova de Lisboa CÁLCULO I Ano Lectivo 6-7 - o Semestre CORRECÇÃO EXAME a ÉPOCA Gruo a) A frase é falsa or dois motivos: - Função com derivada contém o caso em que as
Faculdade de Economia da Universidade Nova de Lisboa CÁLCULO I Ano Lectivo 6-7 - o Semestre CORRECÇÃO EXAME a ÉPOCA Gruo a) A frase é falsa or dois motivos: - Função com derivada contém o caso em que as
TÉCNICAS DE DIFERENCIAÇÃO13
 TÉCNICAS DE DIFERENCIAÇÃO3 Gil da Costa Marques 3. Introdução 3. Derivada da soma ou da diferença de funções 3.3 Derivada do produto de funções 3.4 Derivada de uma função composta: a Regra da Cadeia 3.5
TÉCNICAS DE DIFERENCIAÇÃO3 Gil da Costa Marques 3. Introdução 3. Derivada da soma ou da diferença de funções 3.3 Derivada do produto de funções 3.4 Derivada de uma função composta: a Regra da Cadeia 3.5
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL UEMS SEGUNDA LICENCIATURA EM INFORMÁTICA. Função Composta e Função Inversa NOVA ANDRADINA MS
 UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL UEMS SEGUNDA LICENCIATURA EM INFORMÁTICA Função Composta e Função Inversa NOVA ANDRADINA MS UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL UEMS SEGUNDA LICENCIATURA
UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL UEMS SEGUNDA LICENCIATURA EM INFORMÁTICA Função Composta e Função Inversa NOVA ANDRADINA MS UNIVERSIDADE ESTADUAL DE MATO GROSSO DO SUL UEMS SEGUNDA LICENCIATURA
Prova de Avaliação de MATEMÁTICA. Identi que claramente os grupos e as questões a que responde.
 Provas Especialmente Adequadas Destinadas a Avaliar a Capacidade para a Frequência dos Cursos Superiores do Instituto Politécnico de Leiria dos Maiores de 3 Anos 017 Prova de Avaliação de MATEMÁTICA Identi
Provas Especialmente Adequadas Destinadas a Avaliar a Capacidade para a Frequência dos Cursos Superiores do Instituto Politécnico de Leiria dos Maiores de 3 Anos 017 Prova de Avaliação de MATEMÁTICA Identi
1.1 Domínios & Regiões
 1. CAMPOS ESCALARES CÁLCULO 2-2018.2 1.1 Domínios & Regiões 1. Esboce o conjunto R do plano R 2 dada abaixo e determine sua fronteira. Classi que R em: aberto, fechado, itado, compacto, ou conexo. (a)
1. CAMPOS ESCALARES CÁLCULO 2-2018.2 1.1 Domínios & Regiões 1. Esboce o conjunto R do plano R 2 dada abaixo e determine sua fronteira. Classi que R em: aberto, fechado, itado, compacto, ou conexo. (a)
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
 MATEMÁTICA II Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari amanda.perticarrari@unesp.br Generalidades Aplicação: integrais cujos integrandos são compostos de: produtos; funções trigonométricas;
MATEMÁTICA II Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari amanda.perticarrari@unesp.br Generalidades Aplicação: integrais cujos integrandos são compostos de: produtos; funções trigonométricas;
3 Limites e Continuidade(Soluções)
 3 Limites e Continuidade(Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y = log y
3 Limites e Continuidade(Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y = log y
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B33 Limites e Derivadas Prof a. Graça Luzia Dominguez Santos
 UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B Limites e Derivadas Prof a Graça Luzia Dominguez Santos LISTA DE EXERCÍCIOS( Questões de Provas a UNIDADE) Derivada
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B Limites e Derivadas Prof a Graça Luzia Dominguez Santos LISTA DE EXERCÍCIOS( Questões de Provas a UNIDADE) Derivada
Exame de Matemática II - Curso de Arquitectura
 Exame de Matemática II - Curso de Arquitectura o semestre de 7 de Julho de 7 Resonsável Henrique Oliveira a Parte. Considere a seguinte função f R! R de nida or f(x ; x ; x ) (x sin (x ) ; x ; x cos (x
Exame de Matemática II - Curso de Arquitectura o semestre de 7 de Julho de 7 Resonsável Henrique Oliveira a Parte. Considere a seguinte função f R! R de nida or f(x ; x ; x ) (x sin (x ) ; x ; x cos (x
Cálculo Diferencial e Integral I 1 o Sem. 2016/17 - LEAN, MEMat, MEQ FICHA 11 - SOLUÇÕES
 Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem 06/7 - LEAN, MEMat, MEQ FICHA - SOLUÇÕES Teorema Fundamental do Cálculo Regra de Barrow Integração por partes
Instituto Superior Técnico Departamento de Matemática Cálculo Diferencial e Integral I o Sem 06/7 - LEAN, MEMat, MEQ FICHA - SOLUÇÕES Teorema Fundamental do Cálculo Regra de Barrow Integração por partes
Universidade de Mogi das Cruzes UMC. Cálculo Diferencial e Integral II Parte II
 Cálclo Diferencial e Integral II Página Universidade de Mogi das Crzes UMC Campos Villa Lobos Cálclo Diferencial e Integral II Parte II Engenharia Civil Engenharia Mecânica marilia@mc.br º semestre de
Cálclo Diferencial e Integral II Página Universidade de Mogi das Crzes UMC Campos Villa Lobos Cálclo Diferencial e Integral II Parte II Engenharia Civil Engenharia Mecânica marilia@mc.br º semestre de
Instituto Superior Técnico - 1 o Semestre 2006/2007 Cálculo Diferencial e Integral I LEA-pB, LEM-pB, LEN-pB, LEAN, MEAer e MEMec
 Instituto Superior Técnico - o Semestre 006/007 Cálculo Diferencial e Integral I LEA-pB, LEM-pB, LEN-pB, LEAN, MEAer e MEMec a Ficha de eercícios para as aulas práticas 3-4 Novembro de 006. Determine os
Instituto Superior Técnico - o Semestre 006/007 Cálculo Diferencial e Integral I LEA-pB, LEM-pB, LEN-pB, LEAN, MEAer e MEMec a Ficha de eercícios para as aulas práticas 3-4 Novembro de 006. Determine os
MÓDULO 45 TRIGONOMETRIA II. Ciências da Natureza, Matemática e suas Tecnologias MATEMÁTICA. 1. Considere a equação. (3 2 cos 2 x) 1 + tg 2. 6 tg = 0.
 Ciências da Natureza, Matemática e suas Tecnologias MATEMÁTICA. Considere a equação TRIGONOMETRIA II ( cos ) + tg MÓDULO 5 tg = 0. a) Determine todas as soluções no intervalo [0, [. b) Para as soluções
Ciências da Natureza, Matemática e suas Tecnologias MATEMÁTICA. Considere a equação TRIGONOMETRIA II ( cos ) + tg MÓDULO 5 tg = 0. a) Determine todas as soluções no intervalo [0, [. b) Para as soluções
Produto interno no espaço vectorial R n
 ALGA - 00/0 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
ALGA - 00/0 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
Matemática I - 2 a Parte: Cálculo Diferencial e Integral real
 Matemática I - 2 a Parte: Cálculo Diferencial e Integral real Ana Rita Martins Católica Lisbon 1 o Semestre 2012/2013 1 / 99 Funções Uma função é uma correspondência f entre dois conjuntos A e B, que a
Matemática I - 2 a Parte: Cálculo Diferencial e Integral real Ana Rita Martins Católica Lisbon 1 o Semestre 2012/2013 1 / 99 Funções Uma função é uma correspondência f entre dois conjuntos A e B, que a
Planificação Anual Matemática 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2016/2017 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 72 3º 36 Total: 186 1º Período Total de
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2016/2017 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 72 3º 36 Total: 186 1º Período Total de
A derivada da função inversa, o Teorema do Valor Médio e Máximos e Mínimos - Aula 18
 A derivada da função inversa, o Teorema do Valor Médio e - Aula 18 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 10 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014106
A derivada da função inversa, o Teorema do Valor Médio e - Aula 18 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 10 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014106
CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2010/11 2 a FICHA DE EXERCÍCIOS - PARTE 2
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 010/11 a FICHA DE EXERCÍCIOS - PARTE I. Representação gráfica
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 010/11 a FICHA DE EXERCÍCIOS - PARTE I. Representação gráfica
IST-2010/11-1 o Semestre-MArq Matemática I 1 o TESTE (VERSÃO A) 6 de Novembro de 2010
 IST-00/- o Semestre-MArq Matemática I o TESTE (VERSÃO A) 6 de Novembro de 00 Nome: Número: Sala: O teste que vai realizar tem a duração de hora e 0 minutos e consiste de 5 roblemas. Os roblemas,, e 4 deverão
IST-00/- o Semestre-MArq Matemática I o TESTE (VERSÃO A) 6 de Novembro de 00 Nome: Número: Sala: O teste que vai realizar tem a duração de hora e 0 minutos e consiste de 5 roblemas. Os roblemas,, e 4 deverão
Derivadas. Capítulo O problema da reta tangente
 Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este conceito relaciona-se com o problema de determinar a reta tangente
Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este conceito relaciona-se com o problema de determinar a reta tangente
Produto interno, externo e misto de vectores
 MTDI I - 00/08 - Produto Interno Produto interno, externo e misto de vectores A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass.
MTDI I - 00/08 - Produto Interno Produto interno, externo e misto de vectores A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass.
Capítulo 5 Derivadas
 Departamento de Matemática - ICE - UFJF Disciplina MAT54 - Cálculo Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este
Departamento de Matemática - ICE - UFJF Disciplina MAT54 - Cálculo Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este
cotg ( α ) corresponde ao valor da abcissa do
 Capítulo II: Funções Reais de Variável Real 59 Função co-tangente Seja α um ângulo representado no círculo trigonométrico. ( α ) corresponde ao valor da abcissa do ponto que resulta de projectar o lado
Capítulo II: Funções Reais de Variável Real 59 Função co-tangente Seja α um ângulo representado no círculo trigonométrico. ( α ) corresponde ao valor da abcissa do ponto que resulta de projectar o lado
x + 2 > 1 (x 2)(x + 2) x + 2 > e
 Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
2. Tipos de funções. Funções pares e ímpares Uma função f é par se é simétrica em relação ao eixo y, isto é, f( x) = f(x).
 1. Algumas funções básicas 2. Tipos de funções Funções pares e ímpares Uma função f é par se é simétrica em relação ao eio y, isto é, f( ) = f(). Eemplos: A função f() = n onde n inteiro positivo é par?
1. Algumas funções básicas 2. Tipos de funções Funções pares e ímpares Uma função f é par se é simétrica em relação ao eio y, isto é, f( ) = f(). Eemplos: A função f() = n onde n inteiro positivo é par?
Planificação Anual Matemática A 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática A 11º Ano Ano letivo 2017 / 2018 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 60 3º 48 Total: 186 1º Período Total
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática A 11º Ano Ano letivo 2017 / 2018 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 78 2º 60 3º 48 Total: 186 1º Período Total
DISTRIBUIÇÃO DOS DOMÍNIOS POR PERÍODO
 DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS Planificação Anual da Disciplina de Matemática 11.º ano Ano Letivo de 2016/2017 Manual adotado: Máximo 11 Matemática A 11.º ano Maria Augusta Ferreira
DEPARTAMENTO DE MATEMÁTICA E CIÊNCIAS EXPERIMENTAIS Planificação Anual da Disciplina de Matemática 11.º ano Ano Letivo de 2016/2017 Manual adotado: Máximo 11 Matemática A 11.º ano Maria Augusta Ferreira
REVISÃO DE CONCEITOS BÁSICOS
 Carlos Aurélio Nadal Doutor em Ciências Geodésicas Professor Titular do Departamento de Geomática - Setor de Ciências da Terra Unidades de medidas que utilizavam o corpo humano 2,54cm 30,48cm 0,9144m 66cm
Carlos Aurélio Nadal Doutor em Ciências Geodésicas Professor Titular do Departamento de Geomática - Setor de Ciências da Terra Unidades de medidas que utilizavam o corpo humano 2,54cm 30,48cm 0,9144m 66cm
Matemática. Lic. em Enologia, 2009/2010
 Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Trigonometria Funções Trigonométricas
 Trigonometria Funções Trigonométricas imagem: [ -, ] Prof. FUNÇÕES TRIGONOMÉTRICAS f(x) = sen x y f(x) = R R Imagem: [-,] Período: 3 0 0 0 x - 3 - período imagem: [ -, ] Prof. FUNÇÕES TRIGONOMÉTRICAS f(x)
Trigonometria Funções Trigonométricas imagem: [ -, ] Prof. FUNÇÕES TRIGONOMÉTRICAS f(x) = sen x y f(x) = R R Imagem: [-,] Período: 3 0 0 0 x - 3 - período imagem: [ -, ] Prof. FUNÇÕES TRIGONOMÉTRICAS f(x)
Matemática Ensino Médio Anotações de aula Trigonometira
 Matemática Ensino Médio Anotações de aula Trigonometira Prof. José Carlos Ferreira da Silva 2016 1 ÍNDICE Trigonometria Introdução... 04 Ângulos na circunferência...04 Relações trigonométricas no triângulo
Matemática Ensino Médio Anotações de aula Trigonometira Prof. José Carlos Ferreira da Silva 2016 1 ÍNDICE Trigonometria Introdução... 04 Ângulos na circunferência...04 Relações trigonométricas no triângulo
MAT 111 Cálculo Diferencial e Integral I. Prova 2 14 de Junho de 2012
 MAT 111 Cálculo Diferencial e Integral I Prof. Paolo Piccione Prova 2 14 de Junho de 2012 Nome: Número USP: Assinatura: Instruções A duração da prova é de duas horas. Assinale as alternativas corretas
MAT 111 Cálculo Diferencial e Integral I Prof. Paolo Piccione Prova 2 14 de Junho de 2012 Nome: Número USP: Assinatura: Instruções A duração da prova é de duas horas. Assinale as alternativas corretas
MAT 111 Cálculo Diferencial e Integral I. Prova 2 14 de Junho de 2012
 MAT 111 Cálculo Diferencial e Integral I Prof. Paolo Piccione Prova 2 14 de Junho de 2012 Nome: Número USP: Assinatura: Instruções A duração da prova é de duas horas. Assinale as alternativas corretas
MAT 111 Cálculo Diferencial e Integral I Prof. Paolo Piccione Prova 2 14 de Junho de 2012 Nome: Número USP: Assinatura: Instruções A duração da prova é de duas horas. Assinale as alternativas corretas
Substituição Trigonométrica
 Universidade Federal do ABC Aula 18 Substituição Trigonométrica BCN0402-15 FUV SUBSTITUIÇÃO TRIGONOMÉTRICA Substituição Trigonométrica Introdução: Um exemplo A área de um círculo ou uma elipse é dada por
Universidade Federal do ABC Aula 18 Substituição Trigonométrica BCN0402-15 FUV SUBSTITUIÇÃO TRIGONOMÉTRICA Substituição Trigonométrica Introdução: Um exemplo A área de um círculo ou uma elipse é dada por
- Recursos educacionais utilizados: notebook associado ao projetor multimídia; uso do programa geogebra.
 Formação Continuada Para Professores de Matemática CECIERJ / SEEDUC-RJ Colégio: Colégio Estadual Stella Matutina Professor: Eduardo Basílio Robba Matrícula: 0091003-9 Modalidade / Nível de Ensino: 1º ano
Formação Continuada Para Professores de Matemática CECIERJ / SEEDUC-RJ Colégio: Colégio Estadual Stella Matutina Professor: Eduardo Basílio Robba Matrícula: 0091003-9 Modalidade / Nível de Ensino: 1º ano
Unidade 6. Fun»c~oes trigonom etricas Regras de L'Hopital. 6.1 Pequena revis~ao de trigonometria Trigonometria geom etrica
 Unidade 6 Fun»c~oes trigonom etricas Regras de L'Hopital Agora estaremos fazendo uma pequena revis~ao de fun»c~oes trigonom etricas e apresentando suas derivadas. Estaremos estudando tamb em um m etodo
Unidade 6 Fun»c~oes trigonom etricas Regras de L'Hopital Agora estaremos fazendo uma pequena revis~ao de fun»c~oes trigonom etricas e apresentando suas derivadas. Estaremos estudando tamb em um m etodo
Planificação Anual Matemática 11º Ano
 ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2018 / 2019 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 72 2º 72 3º 36 Total: 180 1º Período Total
ESCOLA SECUNDÁRIA/3 RAINHA SANTA ISABEL 402643 ESTREMOZ Planificação Anual Matemática 11º Ano Ano letivo 2018 / 2019 PERÍODO Nº de AULAS PREVISTAS (45 min) 1º 72 2º 72 3º 36 Total: 180 1º Período Total
1. Arcos de mais de uma volta. Vamos generalizar o conceito de arco, admitindo que este possa dar mais de uma volta completa na circunferência.
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Trigonometria II Prof.: Rogério
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: FUNDAMENTOS DE MATEMÁTICA Trigonometria II Prof.: Rogério
