Derivadas. Slides de apoio sobre Derivadas. Prof. Ronaldo Carlotto Batista. 21 de outubro de 2013
|
|
|
- Mateus Vidal Borges
- 5 Há anos
- Visualizações:
Transcrição
1 Cálculo 1 ECT1113 Slides de apoio sobre Derivadas Prof. Ronaldo Carlotto Batista 21 de outubro de 2013
2 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados como único material didático. O conteúdo apresentado aqui está no capítulo 4 do livro Cálculo A, Flemming & Gonçalves, 6ª Ed (livro texto); ou ainda, alternativamente, no capítulo 3 do livro Cálculo, George B. Thomas, Vol. 2, 11º Ed.
3 Noção Intuitiva de Derivada A noção intuitiva de derivada aparece, por exemplo, se quisermos determinar o ângulo α que a reta tangente a uma função f (x) em um ponto x 1 D f reta secante que passa por (x 1, f (x 1 )) e (x 2, f (x 2 )) tem: tg (α) = f x = f (x 2) f (x 1 ) x 2 x 1. faz com a horizontal. A
4 Noção Intuitiva de Derivada A noção intuitiva de derivada aparece, por exemplo, se quisermos determinar o ângulo α que a reta tangente a uma função f (x) em um ponto x 1 D f reta secante que passa por (x 1, f (x 1 )) e (x 2, f (x 2 )) tem: tg (α) = f x = f (x 2) f (x 1 ) x 2 x 1. faz com a horizontal. A Tomando x 2 = x 1 + x, e fazendo x tender a zero, teremos α da reta tangente em x 1 dada por: f (x 1 + x) f (x 1 ) tg (α) = lim. x 0 x
5 Noção Intuitiva de Derivada A noção intuitiva de derivada aparece, por exemplo, se quisermos determinar o ângulo α que a reta tangente a uma função f (x) em um ponto x 1 D f reta secante que passa por (x 1, f (x 1 )) e (x 2, f (x 2 )) tem: tg (α) = f x = f (x 2) f (x 1 ) x 2 x 1. faz com a horizontal. A Tomando x 2 = x 1 + x, e fazendo x tender a zero, teremos α da reta tangente em x 1 dada por: f (x 1 + x) f (x 1 ) tg (α) = lim. x 0 x Generalizando para qualquer x D f, denimos a derivada de uma função f (x) por df (x) dx = f f (x + h) f (x) = lim. h 0 h
6 Noção Intuitiva de Derivada - Exemplos Exemplo 1: Determine o ângulo que reta f (x) = 2 + x faz com a horizontal.
7 Noção Intuitiva de Derivada - Exemplos Exemplo 1: Determine o ângulo que reta f (x) = 2 + x faz com a horizontal. Exemplo 2: Determine o ângulo que reta tangente da função f (x) = x 2 + 2x no ponto x = 1 faz com a horizontal.
8 Noção Intuitiva de Derivada Seja a posição de uma partícula dada pela função: x (t) = x 0 + v 0 t a 0t 2. Tomando o seguinte limite, dx dt = x x (t + h) x (t) = v (t) = lim h 0 h temos a velocidade instantânea da partícula: v (t) = v 0 + a 0 t.,
9 Noção Intuitiva de Derivada Seja a posição de uma partícula dada pela função: x (t) = x 0 + v 0 t a 0t 2. Tomando o seguinte limite, dx dt = x x (t + h) x (t) = v (t) = lim h 0 h temos a velocidade instantânea da partícula: v (t) = v 0 + a 0 t. De forma análoga, podemos denir a aceleração instantânea, 2 x dv dt = d dt 2 v (t + h) v (t) = a (t) = lim = a 0 h 0 h
10 Quando a derivada não existe? A derivada de uma função é denida em função de um limite, portanto se tal limite não existir em algum ponto do domínio da função dizemos que a função não é derivável.
11 Quando a derivada não existe? A derivada de uma função é denida em função de um limite, portanto se tal limite não existir em algum ponto do domínio da função dizemos que a função não é derivável. Exemplo: Seja f (x) = x 1, mostre porque em x = 1 f (x + h) f (x) lim h 0 h.
12 Quando a derivada não existe? A derivada de uma função é denida em função de um limite, portanto se tal limite não existir em algum ponto do domínio da função dizemos que a função não é derivável. Exemplo: Seja f (x) = x 1, mostre porque em x = 1 f (x + h) f (x) lim h 0 h. Note que f (x) é contínua, mas não é derivável.
13 Continuidade de Funções Deriváveis Vimos que uma função contínua não é necessariamente derivável. Contudo, pode-se provar que Theorem Uma função derivável é contínua.
14 Regras de derivação Sejam f, g e h funções deriváveis e c uma constante real, valem as seguintes regras de derivação: 1 Produto de função por constante: f (x) = c g (x), f (x) = c g (x) 2 Derivada da soma: f = g + h, f = g + h 3 Derivada do produto: f = g h f = g h + g h 4 Derivada do quociente: f = g/h f = g h g h h 2
15 Regras de derivação de funções 1 Função Constante: f (x) = c, f (x) = 0 2 Função Potência: f (x) = x n, com n 0 e racional f (x) = nx n 1 3 Função Polinomial: f (x) = a 0 + a 1 x + a 2 x a n x n, com n 0 e natural
16 Regras de derivação de funções 1 Função Constante: f (x) = c, f (x) = 0 2 Função Potência: f (x) = x n, com n 0 e racional f (x) = nx n 1 3 Função Polinomial: f (x) = a 0 + a 1 x + a 2 x a n x n, com n 0 e natural f (x) = a 1 + 2a 2 x + 3a 3 x na n x n 1
17 Exemplos Determine as derivadas das funções abaixo Exemplo 1: f (x) = x 3 + 2x 1
18 Exemplos Determine as derivadas das funções abaixo Exemplo 1: f (x) = x 3 + 2x 1 Exemplo 2: f (x) = ( 3x 4 + 2x 2) x 2
19 Exemplos Determine as derivadas das funções abaixo Exemplo 1: f (x) = x 3 + 2x 1 Exemplo 2: f (x) = ( 3x 4 + 2x 2) x 2 Exemplo 3: f (x) = x 3 2x 2 3x 8
20 Exemplos Determine as derivadas das funções abaixo Exemplo 1: f (x) = x 3 + 2x 1 Exemplo 2: f (x) = ( 3x 4 + 2x 2) x 2 Exemplo 3: f (x) = x 3 2x 2 3x 8 Essas funções não são deriváveis em algum ponto, se sim onde?
21 Regra da Cadeia Sejam y = g (u) e u = f (x) funções deriváveis. A Regra da Cadeia estabelece que dy dx = dy du du dx. Note que a função y = g (u) = g (f (x)) é uma função composta de g com f.
22 Regra da Cadeia Sejam y = g (u) e u = f (x) funções deriváveis. A Regra da Cadeia estabelece que dy dx = dy du du dx. Note que a função y = g (u) = g (f (x)) é uma função composta de g com f. A Regra da Cadeia pode ser demonstrada avaliando o seguinte limite: dy dx = lim g (f (x + h)) g (f (x)) h 0 h
23 Regra da Cadeia Exemplos Usando a Regra da Cadeia determine a derivada das seguintes funções Exemplo 1: f (x) = ( ) x x 1
24 Regra da Cadeia Exemplos Usando a Regra da Cadeia determine a derivada das seguintes funções Exemplo 1: f (x) = ( ) x x 1 Exemplo 2: f (x) = g (x) h (x)
25 Regra da Cadeia Exemplos Usando a Regra da Cadeia determine a derivada das seguintes funções Exemplo 1: f (x) = ( ) x x 1 Exemplo 2: Exemplo 3: f (x) = g (x) h (x) f (x) = 3x + 2 2x + 1
26 Regra da Cadeia Exemplos Exemplo 4: ( 3x + 2 f (x) = 2x + 1 ) 5
27 Regra da Cadeia Exemplos Exemplo 4: ( 3x + 2 f (x) = 2x + 1 ) 5 Exemplo 5: f (x) = 5 x 2 + 3
28 Regra da Cadeia Exemplos Exemplo 4: ( 3x + 2 f (x) = 2x + 1 ) 5 Exemplo 5: Exemplo 6: f (x) = 5 x f (x) = (1 x 2 ) 3/2
29 Derivada da função exponencial A derivada da função f (x) = a x, com a > 0 e a 1 é dada pelo seguinte limite d a x+h a x ) = dx (ax lim h 0 h.
30 Derivada da função exponencial A derivada da função f (x) = a x, com a > 0 e a 1 é dada pelo seguinte limite d a x+h a x ) = dx (ax lim h 0 h. Usando o seguinte limite fundamental a h 1 lim h 0 h = ln (a), temos que d dx (ax ) = a x ln (a).
31 Derivada da função logarítmica A derivada da função f (x) = log a x com a > 0 e a 1 é dada pelo seguinte limite d dx (log a log x) = a (x + h) log a x lim. h 0 h Usando o seguinte limite fundamental lim u ± ( u ) u = e podemos mostrar que d dx (log a x) = 1 x log a e
32 F. Exp. e Log. Exemplos básicos Determine as derivadas das seguinte funções: Exemplo 1: f (x) = 2 x e g (x) = log 2 x
33 F. Exp. e Log. Exemplos básicos Determine as derivadas das seguinte funções: Exemplo 1: f (x) = 2 x e g (x) = log 2 x Exemplo 2: f (x) = e x e g (x) = lnx
34 F. Exp. e Log. Exemplos Determine as derivadas das seguinte funções: Exemplo 1: f (x) = 3 2x 2 +3x 1
35 F. Exp. e Log. Exemplos Determine as derivadas das seguinte funções: Exemplo 1: Exemplo 2: f (x) = 3 2x 2 +3x 1 ( ) x + 1 f (x) = exp x 1
36 F. Exp. e Log. Exemplos Determine as derivadas das seguinte funções: Exemplo 1: Exemplo 2: Exemplo 3: f (x) = 3 2x 2 +3x 1 f (x) = exp ( ) x + 1 x 1 ) f (x) = log 2 (3x 2 + 7x 1
37 Derivada da função seno A derivada da função sen (x) é dada por: d dx sen (x + h) sen (x) (senx) = lim. h 0 h Usando o seguinte limite fundamental podemos mostrar que sen (u) lim u 0 u = 1, d (senx) = cosx dx
38 Derivada da função cosseno A derivada da função cos (x) é dada por: d dx cos (x + h) cos (x) (cosx) = lim. h 0 h Usando o seguinte limite fundamental podemos mostrar que sen (u) lim u 0 u = 1, d (cosx) = senx. dx
39 Derivada das demais funções trigonométricas Como as demais funções trigonométricas são denidas em função das funções seno e cosseno, basta usarmos as regras de derivação para determinar suas derivadas. Por exemplo: tg (x) = sen (x) cos (x), então, usando a regra do quociente temos d dx cos 2 (x) + sen 2 (x) tg (x) = cos 2 (x) d dx tg (x) = sec2 (x). = 1 cos 2 (x),
40 Derivada das demais funções trigonométricas De forma análoga podemos determinar: d sec (x) = dx d cotg (x) = dx d cosec (x) = dx
41 Derivada das demais funções trigonométricas De forma análoga podemos determinar: d sec (x) = sec (x) tg (x) dx d dx cotg (x) = cosec2 (x) d cosec (x) = cosec (x) cotg (x) dx
42 Derivada das funções trigonométricas Exemplos Determine a derivadas das seguintes funções: Exemplo 1: ( f (x) = sen x 3 + x 2)
43 Derivada das funções trigonométricas Exemplos Determine a derivadas das seguintes funções: Exemplo 1: ( f (x) = sen x 3 + x 2) Exemplo 2: ( ) f (x) = cos x 3 + 3
44 Derivada das funções trigonométricas Exemplos Determine a derivadas das seguintes funções: Exemplo 1: ( f (x) = sen x 3 + x 2) Exemplo 2: ( ) f (x) = cos x Exemplo 3: ( f (x) = sec (x) ) sen x 2
45 Derivada de funções hiperbólicas As funções seno e cosseno hiperbólicas são denidas por: e senh (x) = e x e x 2 cosh (x) = e x + e x. 2
46 Derivada de funções hiperbólicas As funções seno e cosseno hiperbólicas são denidas por: e senh (x) = e x e x 2 cosh (x) = e x + e x. Dadas essas denições, determine d dx senh (x) e d dx 2 cosh (x).
47 Derivada de funções hiperbólicas As funções seno e cosseno hiperbólicas são denidas por: e senh (x) = e x e x 2 cosh (x) = e x + e x. Dadas essas denições, determine d Respostas: dx senh (x) e d dx 2 cosh (x). d senh (x) = cosh (x) e d dx cosh (x) = senh (x) dx
48 Derivada de Função Inversa Seja u = f (x) e v = f 1 (x). Sabemos que u (v) = f ( f 1 (x) ) = x, então du dx = du dv dv dx = 1. Como isso podemos podemos determinar a derivada da função inversa v por: dv dx = ( ) 1 du. dv
49 Derivada de Função Inversa Seja u = f (x) e v = f 1 (x). Sabemos que u (v) = f ( f 1 (x) ) = x, então du dx = du dv dv dx = 1. Como isso podemos podemos determinar a derivada da função inversa v por: Exemplo: dv dx = ( ) 1 du. Seja u = x 2, determine sua inversa e a derivada desta. dv
50 Derivada das funções trigonométricas inversas Tomando u = sen (x), com D u = [ π 2, π 2 ] temos I u = [ 1, 1], e podemos denir sua inversa v = u 1 = arcsen (x). Então a derivada de v é dada por:
51 Derivada das funções trigonométricas inversas Tomando u = sen (x), com D u = [ π 2, π 2 ] temos I u = [ 1, 1], e podemos denir sua inversa v = u 1 = arcsen (x). Então a derivada de v é dada por: dv dx = ( ) 1 d sen (v) = dv 1 cos (v) = 1 1 sen 2 (v),
52 Derivada das funções trigonométricas inversas Tomando u = sen (x), com D u = [ π 2, π 2 ] temos I u = [ 1, 1], e podemos denir sua inversa v = u 1 = arcsen (x). Então a derivada de v é dada por: dv dx = ( ) 1 d sen (v) = dv 1 cos (v) = 1 1 sen 2 (v), note que sen (v) = sen (arcsen (x)) = x, portanto d dx arcsen (x) = 1 1. x 2
53 Derivada das funções trigonométricas inversas De forma análoga podemos determinar d dx arcsen (x) = 1 1, x < x 1 2 d dx arccos (x) = 1 1, x < x 1 2 d dx arctg (x) = x 2 d 1 arccotg (x) = dx 1 + x 2 d dx arcsec (x) = 1 x, x > 1 x 2 1 d dx arccosec (x) = 1 x, x > 1 x 2 1
54 Derivadas de ordem superior Com frequência é preciso saber a segunda ou terceira derivada de uma função. Por exemplo, para determinar a força à qual que está sujeita uma partícula cuja posição em função do tempo é: x (t) = x v 0 (t t 0 ) + x 0, 2 e (t t0)/t0 com t t 0. Da Segunda Lei de Newton (em uma dimensão), sabemos que 2 x F = ma = m dv dt = m d dt, 2 portanto, calculando a derivada segunda de x (t) podemos determinar a força.
55 Derivadas de ordem superior Com frequência é preciso saber a segunda ou terceira derivada de uma função. Por exemplo, para determinar a força à qual que está sujeita uma partícula cuja posição em função do tempo é: x (t) = x v 0 (t t 0 ) + x 0, 2 e (t t0)/t0 com t t 0. Da Segunda Lei de Newton (em uma dimensão), sabemos que 2 x F = ma = m dv dt = m d dt, 2 portanto, calculando a derivada segunda de x (t) podemos determinar a força. Nesse caso temos F = m 2 (t 0 ) 2 x 0e (t t0)/t0.
56 Derivação Implícita Seja uma função F (x, y) = 0, diz-se que uma função y = f (x) é denida implicitamente por F se F (x, f (x)) = 0.
57 Derivação Implícita Seja uma função F (x, y) = 0, diz-se que uma função y = f (x) é denida implicitamente por F se F (x, f (x)) = 0. Exemplo 1: Seja F (x, y) = x 2 + y 1 = 0, verique se 2 y = 2 (1 x 2 ) é denida implicitamente por F. Se sim, determine dy/dx.
58 Derivação Implícita Seja uma função F (x, y) = 0, diz-se que uma função y = f (x) é denida implicitamente por F se F (x, f (x)) = 0. Exemplo 1: Seja F (x, y) = x 2 + y 1 = 0, verique se 2 y = 2 (1 x 2 ) é denida implicitamente por F. Se sim, determine dy/dx. Exemplo 2: Seja F (x, y) = y 2 + x 2 4 = 0, com y 0. Determine dy/dx implicitamente e também explicitamente.
59 Diferencial Seja uma função f = f (x), seu diferencial é dado por df = f dx. Um exemplo sicamente interessante de diferencial está relacionado com a massa contida numa esfera de densidade constante ρ 0. Neste caso, a massa contida até um raio r é dada por: M = 4π 3 r 3 ρ 0. Então o diferencial tem a seguinte expressão: dm = 4πρ 0 r 2 dr. Conhecendo esta expressão, podemos generalizar para o caso de uma densidade dependente do raio: dm = 4πρ (r) r 2 dr.
Derivada - Parte 2 - Regras de derivação
Derivada - Parte 2 - Wellington D. Previero previero@utfpr.edu.br http://paginapessoal.utfpr.edu.br/previero Universidade Tecnológica Federal do Paraná - UTFPR Câmpus Londrina Wellington D. Previero Derivada
Limites. Slides de apoio sobre Limites. Prof. Ronaldo Carlotto Batista. 7 de outubro de 2013
Cálculo 1 ECT1113 Slides de apoio sobre Limites Prof. Ronaldo Carlotto Batista 7 de outubro de 2013 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados
Limites, continuidade e diferenciação de funções
Matemática 1 Semanas 9, 10 e 11 Professor Luiz Claudio Pereira Faculdade de Planaltina Universidade de Brasília Material Previsto para três semanas 113018 (UNB) Luiz Claudio Pereira 2017 1 / 100 Limites,
CÁLCULO I. 1 Derivada de Funções Elementares
CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o : Derivada das Funções Elementares. Regras de Derivação. Objetivos da Aula Apresentar a derivada das funções elementares; Apresentar
Pré-Cálculo ECT2101 Slides de apoio Funções II
Pré-Cálculo ECT2101 Slides de apoio Funções II Prof. Ronaldo Carlotto Batista 8 de abril de 2017 Funções Trigonométricas As funções trigonométricas são denidas no círculo unitário: sen (θ) = y r, cos (θ)
DERIVADA. A Reta Tangente
DERIVADA A Reta Tangente Seja f uma função definida numa vizinança de a. Para definir a reta tangente de uma curva = f() num ponto P(a, f(a)), consideramos um ponto vizino Q(,), em que a e traçamos a S,
MAT146 - Cálculo I - Derivada das Inversas Trigonométricas
MAT46 - Cálculo I - Derivada das Inversas Trigonométricas Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos anteriormente que as funções trigonométricas não são inversíveis, mas
AT3-1 - Unidade 3. Derivadas e Aplicações 1. Cálculo Diferencial e Integral. UAB - UFSCar. Bacharelado em Sistemas de Informação
AT3-1 - Unidade 3 1 Cálculo Diferencial e Integral Bacharelado em Sistemas de Informação UAB - UFSCar 1 Versão com 34 páginas 1 / 34 Tópicos de AT3-1 1 Uma noção intuitiva Caracterização da derivada Regras
MAT146 - Cálculo I - Derivada de funções polinomiais, regras de derivação e derivada de funções trigonométricas
MAT146 - Cálculo I - Derivada de funções polinomiais, regras de derivação e derivada de funções trigonométricas Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos que uma função
Diferenciabilidade de função de uma variável
Capítulo 6 Diferenciabilidade de função de uma variável Um conceito importante do Cálculo é o de derivada, que é um ite, como veremos na definição. Fisicamente o conceito de derivada está relacionado ao
Ana Carolina Boero. Página: Sala Bloco A - Campus Santo André
Funções de uma variável real a valores reais E-mail: ana.boero@ufabc.edu.br Página: http://professor.ufabc.edu.br/~ana.boero Sala 512-2 - Bloco A - Campus Santo André Funções de uma variável real a valores
A derivada da função inversa
A derivada da função inversa Sumário. Derivada da função inversa............... Funções trigonométricas inversas........... 0.3 Exercícios........................ 7.4 Textos Complementares................
Derivadas. Incremento e taxa média de variação
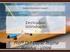Derivadas Incremento e taxa média de variação Consideremos uma função f, dada por y f (x). Quando x varia de um valor inicial de x para um valor x, temos o incremento em x. O símbolo matemático para a
CÁLCULO I. Iniciaremos com o seguinte exemplo: u 2 du = cos x + u3 3 + C = cos3 x
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aulas n o 9: Técnicas de Integração II - Integrais Trigonométricas e Substituição Trigonométrica Objetivos da Aula Calcular integrais de potências
CÁLCULO I. Figura 1: Círculo unitário x2 + y 2 = 1
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Aula no 04: Funções Trigonométricas, Logarítmica, Exponencial e Hiperbólicas. Objetivos
CÁLCULO I. Figura 1: Círculo unitário x2 + y 2 = 1
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula no 05: Funções Logarítmica, Exponencial e Hiperbólicas. Objetivos da Aula De nir as funções trigonométricas, trigonométricas
CÁLCULO I. Calcular integrais envolvendo funções trigonométricas; Apresentar a substituição trigonométrica. Iniciaremos com o seguinte exemplo:
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Prof. Emerson Veiga Prof. Tiago Coelho Aula n o 8: Integrais Trigonométricas. Substituição Trigonométrica. Objetivos da Aula Calcular
UNIVERSIDADE FEDERAL DE PERNAMBUCO
CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
CÁLCULO I. 1 A Função Logarítmica Natural. Objetivos da Aula. Aula n o 22: A Função Logaritmo Natural. Denir a função f(x) = ln x;
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 22: A Função Logaritmo Natural Objetivos da Aula Denir a função f(x) = ln x; Calcular limites, derivadas e integral envolvendo a função
Derivadas. Capítulo O problema da reta tangente
Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este conceito relaciona-se com o problema de determinar a reta tangente
MAT Aula 12/ 23/04/2014. Sylvain Bonnot (IME-USP)
MAT 0143 Aula 12/ 23/04/2014 Sylvain Bonnot (IME-USP) 2014 1 Resumo: 1 Site: http://www.ime.usp.br/~sylvain/courses.html 2 Hoje: correção da prova + derivadas. 3 Derivadas: definição de f (a) e equação
1) = 4 +8) =7 4 +8) 5 4) 8. Derivada da Função Composta (Regra da Cadeia)
8. Derivada da Função Composta (Regra da Cadeia) Regra da Cadeia (primeira notação): Se e são funções diferenciáveis e = é a função composta definida por )=), então é diferenciável e é dada por )=) = ).
Derivada. Aula 09 Cálculo Diferencial. Professor: Éwerton Veríssimo
Derivada Ala 09 Cálclo Dierencial Proessor: Éwerton Veríssimo Derivada: Conceito Físico Taa de Variação A dosagem de m medicamento pode variar conorme o tempo de tratamento do paciente. O desgaste das
Derivadas 1
www.matematicaemexercicios.com Derivadas 1 Índice AULA 1 Introdução 3 AULA 2 Derivadas fundamentais 5 AULA 3 Derivada do produto e do quociente de funções 7 AULA 4 Regra da cadeia 9 www.matematicaemexercicios.com
Para ilustrar o conceito de limite, vamos supor que estejamos interessados em saber o que acontece à
Limite I) Noção intuitiva de Limite Os limites aparecem em um grande número de situações da vida real: - O zero absoluto, por eemplo, a temperatura T C na qual toda a agitação molecular cessa, é a temperatura
CÁLCULO I. Conhecer a interpretação geométrica da derivada em um ponto. y = f(x 2 ) f(x 1 ). y x = f(x 2) f(x 1 )
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 0: Taxa de Variação. Derivadas. Reta Tangente. Objetivos da Aula Denir taxa de variação média e a derivada como a taxa
A derivada da função inversa, o Teorema do Valor Médio e Máximos e Mínimos - Aula 18
A derivada da função inversa, o Teorema do Valor Médio e - Aula 18 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 10 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014106
Capítulo 5 Derivadas
Departamento de Matemática - ICE - UFJF Disciplina MAT54 - Cálculo Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este
Resolução dos Exercícios sobre Derivadas
Resolução dos Eercícios sobre Derivadas Eercício Utilizando a idéia do eemplo anterior, encontre a reta tangente à curva = 0 e = y = nos pontos onde Vamos determinar a reta tangente à curva y = nos pontos
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL APOSTILA DE CÁLCULO. Realização:
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL APOSTILA DE CÁLCULO Realização: Fortaleza, Fevereiro/2010 1. LIMITES 1.1. Definição Geral Se os valores de f(x) puderem
CÁLCULO I Aula 08: Regra da Cadeia. Derivação Implícita. Derivada da Função Inversa.
CÁLCULO I Aula 08: Regra da Cadeia.. Função Inversa. Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará 1 2 3 Teorema (Regra da Cadeia) Sejam g(y) e y = f (x) duas funções deriváveis,
CÁLCULO I Aula 03: Funções Logarítmicas, Exponenciais e
CÁLCULO I Aula 03: s, e. Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará 1 2 3 4 A Seja x > 0. Denimos a função logarítmica natural como sendo a função dada pela medida da área
Nome: Gabarito Data: 28/10/2015. Questão 01. Calcule a derivada da função f(x) = sen x pela definição e confirme o resultado
Fundação Universidade Federal de Pelotas Departamento de Matemática e Estatística Curso de Licenciatura em Matemática - Diurno Segunda Prova de Cálculo I Prof. Dr. Maurício Zan Nome: Gabarito Data: 8/0/05.
Tópico 4. Derivadas (Parte 1)
Tópico 4. Derivadas (Parte 1) 4.1. A reta tangente Para círculos, a tangencia é natural? Suponha que a reta r da figura vá se aproximando da circunferência até tocá-la num único ponto. Na situação da figura
CÁLCULO I. Estabelecer a relação entre continuidade e derivabilidade; Apresentar a derivada das funções elementares. f f(x + h) f(x) c c
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 11: Derivada de uma função. Continuidade e Derivabilidade. Derivada das Funções Elementares. Objetivos da Aula Denir
Limites e continuidade
Limites e continuidade Limite (finito) de uma função em a Salvo indicação em contrário, quando nos referimos a uma função estamos sempre a considerar funções reais de variável real (f.r.v.r.), ou seja,
7.1 Regras Básicas de Derivação. 7.2 Principais Notações. 01. regra da soma: [f (x) + g (x)] 0 = f 0 (x) + g 0 (x)
![7.1 Regras Básicas de Derivação. 7.2 Principais Notações. 01. regra da soma: [f (x) + g (x)] 0 = f 0 (x) + g 0 (x)](/thumbs/64/50953812.jpg "7.1 Regras Básicas de Derivação. 7.2 Principais Notações. 01. regra da soma: [f (x) + g (x)] 0 = f 0 (x) + g 0 (x)")
7. Regras Básicas e Derivação 0. regra a soma: [f () + g ()] 0 = f 0 () + g 0 () 0. regra a iferença [f () g ()] 0 = f 0 () g 0 () 0. regra o routo [f () :g ()] 0 = f () g 0 () + f 0 () g () 04. regra
Integrais indefinidas
Integrais indefinidas que: Sendo f(x) e F(x) definidas em um intervalo I R, para todo x I, dizemos F é uma antiderivada ou uma primitiva de f, em I, se F (x) = f(x) Exemplos: F(x) = x é uma antiderivada
Derivada. Capítulo Retas tangentes e normais Número derivado
Capítulo 3 Derivada 3.1 Retas tangentes e normais Vamos considerar o problema que consiste em traçar a reta tangente e a reta normal a uma curvay= f(x) num determinado ponto (a,f(a)) da curva. Por isso
UNIVERSIDADE FEDERAL DE PERNAMBUCO. Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos
CÁLCULO L NOTAS DA DÉCIMA OITAVA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos a primeira técnica de integração: mudança
Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para. em p = 9
Exercícios - Limite e Continuidade-1 Exercício 1 Dê o valor, caso exista, que a função deveria assumir no ponto dado para ser contínua: (a) f(x) = x2 16 x 4 (b) f(x) = x3 x x em p = 4 em p = 0 (c) f(x)
Capítulo 6 - Derivação de Funções Reais de Variável Real
Capítulo 6 - Derivação de Funções Reais de Variável Real Carlos Balsa balsa@ipb.pt Departamento de Matemática Escola Superior de Tecnologia e Gestão de Bragança Matemática I - 1 o Semestre 2010/2011 Matemática
DERIVADA. Definição: A reta tangente a uma curva y = f(x) em um ponto P(a, f(a)), é a reta por P que tem a inclinação
61 DERIVADA O problema de encontrar a reta tangente a uma curva e o problema para encontrar a velocidade de um objeto envolvem determinar o mesmo tipo de limite. Este tipo especial de limite é chamado
A Derivada. Derivadas Aula 16. Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil
Derivadas Aula 16 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 04 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014104 - Engenharia Mecânica A Derivada Seja x = f(t)
Respostas sem justificativas não serão aceitas. Além disso, não é permitido o uso de aparelhos eletrônicos. x x = lim.
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL 1-2017.2 1A VERIFICAÇÃO DE APRENDIZAGEM - TURMA GEA Nome Legível RG CPF Respostas sem
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B33 Limites e Derivadas Prof a. Graça Luzia Dominguez Santos
UNIVERSIDADE FEDERAL DA BAHIA INSTITUTO DE MATEMÁTICA DEPARTAMENTO DE MATEMÁTICA MAT B Limites e Derivadas Prof a Graça Luzia Dominguez Santos LISTA DE EXERCÍCIOS( Questões de Provas a UNIDADE) Derivada
CÁLCULO I. Reconhecer, através do gráco, a função que ele representa; (f + g)(x) = f(x) + g(x). (fg)(x) = f(x) g(x). f g
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 03: Operações com funções. Funções Polinominais, Racionais e Trigonométricas Objetivos da Aula Denir operações com funções; Apresentar algumas
Slides de apoio: Funções I
Pré-Cálculo ECT2101 Slides de apoio: Funções I Prof. Ronaldo Carlotto Batista 10 de março de 2017 Produto Cartesiano Denição Sejam dois conjuntos não vazios A e B, o produto cartesiano entre A e B é dado
Cálculo Diferencial e Integral I
Provas e listas: Cálculo Diferencial e Integral I Período 204.2 Sérgio de Albuquerque Souza 4 de maio de 205 UNIVERSIDADE FEDERAL DA PARAÍBA CCEN - Departamento de Matemática http://www.mat.ufpb.br/sergio
A derivada (continuação) Aula 17
A derivada (continuação) Aula 17 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 08 de Abril de 2014 Primeiro Semestre de 2014 Turma 2014106 - Engenharia Mecânica Teorema
CÁLCULO DIFERENCIAL E INTEGRAL. Prof. Rodrigo Carvalho
CÁLCULO DIFERENCIAL E INTEGRAL LIMITES Uma noção intuitiva de Limite Considere a unção () = 2 + 3. Quando assume uma ininidade de valores, aproimando cada vez mais de zero, 2 + 3 assume uma ininidade de
Aula n o 29:Técnicas de Integração: Integrais Trigonométricas - Substituição Trigonométrica
CÁLCULO I Aula n o 29:Técnicas de Integração: Integrais Trigonométricas - Substituição Trigonométrica Prof. Edilson Neri Júnior Prof. André Almeida 1 Integrais Trigonométricas Iniciaremos com o seguinte
Respostas sem justificativas não serão aceitas. Além disso, não é permitido o uso de aparelhos eletrônicos. x 1 x 1. 1 sen x 1 (x 2 1) 2 (x 2 1) 2 sen
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL - 07. A VERIFICAÇÃO DE APRENDIZAGEM - TURMA EL Nome Legível RG CPF Respostas sem justificativas
Substituição trigonométrica hiperbólica. Esta é a última aula do segundo módulo da disciplina Cálculo II. Isso
MÓDULO - AULA 30 Aula 30 Técnicas de integração Miscelânea Esta é a última aula do segundo módulo da disciplina Cálculo II. Isso significa que você está completando boa parte desta jornada. Você já enfrentou
CÁLCULO I. 1 Primitivas. Objetivos da Aula. Aula n o 18: Primitivas. Denir primitiva de uma função; Calcular as primitivas elementares.
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 8: Primitivas. Objetivos da Aula Denir primitiva de uma função; Calcular as primitivas elementares. Primitivas Em alguns problemas, é necessário
4.1 Funções Deriváveis
4. Funções Deriváveis 4.A Em cada caso, encontre a derivada da função y = f (), usando a de nição. (a) y = + (b) y = 3 (c) y = 5 (d) y = 3 (e) y = +
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Derivada e Diferencial de uma Função Professora Renata Alcarde Sermarini Notas de aula
(x 1) 2 (x 2) dx 42. x5 + x + 1
I - Integrais Indefinidas ā Lista de Cálculo I - POLI - 00 Calcule as integrais indefinidas abaixo. Para a verificação das resposta lembre-se que f(x)dx = F (x), k IR F (x) = f(x), x D f.. x7 + x + x dx.
velocidade média = distância tempo = s(t 0 + t) s(t 0 )
Universidade do Estado do Rio de Janeiro Cálculo I e Cálculo Diferencial I - Professora: Mariana G. Villapouca Aula 3 - Derivada Taxa de variação: Sejam f : I R e x 0 I. f(x) r x0 rx f = f(x) f(x) = =
MATEMÁTICA II. Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari
MATEMÁTICA II Profa. Dra. Amanda Liz Pacífico Manfrim Perticarrari amanda@fcav.unesp.br CONSIDERAÇÕES INICIAIS Considere a função f x : R R tal que y = f(x). Então: Derivada: Mede a taxa de variação de
Derivada de algumas funções elementares
Universidade de Brasília Departamento de Matemática Cálculo 1 Derivada de algumas funções elementares Vamos lembrar que a função f é derivável no ponto x = a se existe o limite f f(x) f(a) f(a+) f(a) (a).
Cálculo diferencial. Motivação - exemplos de aplicações à física
Cálculo diferencial Motivação - eemplos de aplicações à física Considere-se um ponto móvel sobre um eio orientado, cuja posição em relação à origem é dada, em função do tempo, pela função s. st posição
5.1 Noção de derivada. Interpretação geométrica de derivada.
Capítulo V Derivação 5 Noção de derivada Interpretação geométrica de derivada Seja uma unção real de variável real Deinição: Chama-se taa de variação média de uma unção entre os pontos a e b ao quociente:
CÁLCULO I Aula 11: Limites Innitos e no Innito. Assíntotas. Regra de l'hôspital.
Limites s CÁLCULO I Aula 11: Limites s e no... Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará Limites s 1 Limites no 2 Limites s 3 4 5 Limites s Denição Seja f uma função denida
Aplicações de Derivadas. Prof. Ronaldo Carlotto Batista. 25 de outubro de 2013
Cálculo 1 ECT1113 Aplicações de Derivadas Prof. Ronaldo Carlotto Batista 25 de outubro de 2013 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados como
CÁLCULO I. 1 Aproximações Lineares. Objetivos da Aula. Aula n o 16: Aproximações Lineares e Diferenciais. Regra de L'Hôspital.
CÁLCULO I Prof Marcos Diniz Prof André Almeida Prof Edilson Neri Júnior Prof Emerson Veiga Prof Tiago Coelho Aula n o 6: Aproimações Lineares e Diferenciais Regra de L'Hôspital Objetivos da Aula Denir
4.-1 Funções Deriváveis
4.- Funções Deriváveis 4.A Em cada caso, encontre a derivada da função y = f (), usando a de nição. (a) y = + (b) y = 3 (c) y = 5 (d) y = 3 (e) y = +
da dx = 2 x cm2 /cm A = (5 t + 2) 2 = 25 t t + 4
Capítulo 13 Regra da Cadeia 13.1 Motivação A área A de um quadrado cujo lado mede x cm de comprimento é dada por A = x 2. Podemos encontrar a taxa de variação da área em relação à variação do lado: = 2
1 Definição de Derivada
Departamento de Computação é Matemática Cálculo I USP- FFCLRP Prof. Rafael A. Rosales 5 de março de 2014 Lista 5 Derivada 1 Definição de Derivada Eercício 1. O que é f (a)? Eplique com suas palavras o
Índice. AULA 6 Integrais trigonométricas 3. AULA 7 Substituição trigonométrica 6. AULA 8 Frações parciais 8. AULA 9 Área entre curvas 11
www.matematicaemexercicios.com Integrais (volume ) Índice AULA 6 Integrais trigonométricas 3 AULA 7 Substituição trigonométrica 6 AULA 8 Frações parciais 8 AULA 9 Área entre curvas AULA Volumes 3 www.matematicaemexercicios.com
Bases Matemáticas Continuidade. Propriedades do Limite de Funções. Daniel Miranda
Daniel De modo intuitivo, uma função f : A B, com A,B R é dita contínua se variações suficientemente pequenas em x resultam em variações pequenas de f(x), ou equivalentemente, se para x suficientemente
MAT2453- Cálculo Diferencial e Integral para Engenharia I - POLI 1o. Semestre de a. Lista de Exercícios. x cos x. x 1+ x 4 dx 12. sec x dx 15.
MAT45- Cálculo Diferencial e Integral para Engenharia I - POLI o. Semestre de - a. Lista de Eercícios I - Integrais Indefinidas Calcule as integrais indefinidas abaio: 7 + +.. e. cos 7 4. tg 7 sen 5. 6.
Limites de Funções. Bases Matemáticas. 2 o quadrimestre de o quadrimestre de / 57
2 o quadrimestre de 2017 2 o quadrimestre de 2017 1 / Visão Geral 1 Limites Finitos Limite para x ± 2 Limites infinitos Limite no ponto Limite para x ± 3 Continuidade Definição e exemplos Resultados importantes
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior
Objetivos da Aula CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 4: Aproximações Lineares e Diferenciais. Regra de L Hôspital. Definir e calcular a aproximação linear
12 AULA. ciáveis LIVRO. META Estudar derivadas de funções de duas variáveis a valores reais.
1 LIVRO Diferen- Funções ciáveis META Estudar derivadas de funções de duas variáveis a valores reais. OBJETIVOS Estender os conceitos de diferenciabilidade de funções de uma variável a valores reais. PRÉ-REQUISITOS
Capítulo 1. Funções e grácos
Capítulo 1 Funções e grácos Denição 1. Sejam X e Y dois subconjuntos não vazios do conjunto dos números reais. Uma função de X em Y ou simplesmente uma função é uma regra, lei ou convenção que associa
Derivadas das Funções Trigonométricas Inversas
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS UNIVERSITÁRIO DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGICAS CURSO DE ENGENHARIA CIVIL DISCIPLINA: CÁLCULO DIFERENCIAL E INTEGRAL I Derivadas das Funções
Apostila de Cálculo I
Limites Diz-se que uma variável tende a um número real a se a dierença em módulo de -a tende a zero. ( a ). Escreve-se: a ( tende a a). Eemplo : Se, N,,,4,... quando N aumenta, diminui, tendendo a zero.
MAT 1351 : Cálculo para Funções de Uma Variável Real I. Sylvain Bonnot (IME-USP)
MAT 1351 : Cálculo para Funções de Uma Variável Real I Sylvain Bonnot (IME-USP) 2016 1 Limites of differences: como tratar Exemplos: 2 Como trabalhar com ites infinitos: somas e produtos Somas: 1. (+ )
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 09: Regras de Derivação Objetivos da Aula Apresentar e aplicar as regras operacionais de derivação; Derivar funções utilizando diferentes
Lista de Férias. 6 Prove a partir da definição de limite que: a) lim. (x + 6) = 9. 1 Encontre uma expressão para a função inversa: b) lim
Lista de Férias Bases Matemáticas/FUV Encontre uma epressão para a função inversa: + 3 a) 5 2 + e b) e c) 2 + 5 d) ln( + 3) 6 Prove a partir da definição de ite que: a) 3 ( + 6) = 9 b) = c) 2 = 4 2 d)
Derivadas. Derivadas. ( e )
Derivadas (24-03-2009 e 31-03-2009) Recta Tangente Seja C uma curva de equação y = f(x). Para determinar a recta tangente a C no ponto P de coordenadas (a,f(a)), i.e, P(a, f(a)), começamos por considerar
Cálculo. Artur Rodrigues. Como definido no ultimo material, podemos considerar a derivada como a seguinte expressão:
Cálculo Artur Rodrigues Como definido no ultimo material, podemos considerar a derivada como a seguinte expressão: = lim x 0 f (x+ x) f (x) x Essa é a definição formal de derivada e usando-a você poderá
MAT2453- Cálculo Diferencial e Integral para Engenharia I - POLI 1 o Semestre de a Lista de Exercícios. sen 3 x cos x. x dx 11. sec x dx 15.
MAT45- Cálculo Diferencial e Integral para Engenharia I - POLI o Semestre de - a Lista de Eercícios I - Integrais Indefinidas Calcule as integrais indefinidas abaio: 7 + +.. 7 5. 6. 9. tg. e. tg sec 7..
Trigonometria e funções trigonométricas. Funções trigonométricas O essencial
Trigonometria e funções trigonométricas Funções trigonométricas O essencial Funções seno e cosseno Designa-se por função seno (respetivamente, função cosseno) e representa-se por sin ou sen (respetivamente,
CÁLCULO I. 1 Concavidade. Objetivos da Aula. Aula n o 19: Concavidade. Teste da Segunda Derivada. Denir concavidade de uma função;
CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 19: Concavidade. Teste da Segunda Derivada. Objetivos da Aula Denir concavidade de uma função; Denir ponto de inexão;
Integrais indefinidas
Integrais indefinidas que: Sendo f() e F() definidas em um intervalo I R, para todo I, dizemos F é uma antiderivada ou uma primitiva de f, em I, se F () = f() F() = é uma antiderivada (primitiv de f()
Funções Elementares. Sadao Massago. Maio de Alguns conceitos e notações usados neste texto. Soma das funções pares é uma função par.
Funções Elementares Sadao Massago Maio de 0. Apresentação Neste teto, trataremos rapidamente sobre funções elementares. O teto não é material completo do assunto, mas é somente uma nota adicional para
x 2 + (x 2 5) 2, x 0, (1) 5 + y + y 2, y 5. (2) e é positiva em ( 2 3 , + ), logo x = 3
Página 1 de 4 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral I - MAC 118 Gabarito segunda prova - Escola Politécnica / Escola de Química - 13/06/2017 Questão 1: (2 pontos) Determinar
Capítulo 1. Limites nitos. 1.1 Limite nito num ponto
Capítulo 1 Limites nitos 1.1 Limite nito num ponto Denição 1. Seja uma função f : D f R R, x y = f(x, e p R tal que p D f ou p é um ponto da extremidade de D f. Dizemos que a função f possui ite nito no
Cálculo 1 A Turma F1 Prova VS
Cálculo 1 A 017. Turma F1 Prova VS Nome (MAIÚSCULO): Matrícula: O IMPORTANTE É O RACIOCÍNIO, PORTANTO DEIXE-O TODO NA PROVA. RESPOSTAS SEM AS DEVIDAS JUSTIFICATIVAS SERÃO DESCONSIDERADAS. (1) Encontre
Continuidade de uma função
Continuidade de uma função Consideremos f : D f uma função real de variável real (f.r.v.r.) e a um ponto de acumulação de D f que pertence a D f. Diz-se que a função f é contínua em a se lim f x f a. x
CÁLCULO I. 1 Funções Exponenciais e Logarítmicas
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 05: Funções Logarítmica, Exponencial e Hiperbólicas. Objetivos da Aula Denir as funções logarítmica, exponencial e hiperbólicas;
TÉCNICAS DE DIFERENCIAÇÃO13
TÉCNICAS DE DIFERENCIAÇÃO3 Gil da Costa Marques 3. Introdução 3. Derivada da soma ou da diferença de funções 3.3 Derivada do produto de funções 3.4 Derivada de uma função composta: a Regra da Cadeia 3.5
CÁLCULO I. 1 Concavidade. Objetivos da Aula. Aula n o 18: Concavidade. Teste da Segunda Derivada. Denir concavidade do gráco de uma função;
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 18: Concavidade. Teste da Segunda Derivada. Objetivos da Aula Denir concavidade do gráco de uma função; Denir ponto de
Derivada da função composta, derivada da função inversa, derivada da função implícita e derivada de funções definidas parametricamente.
Análise Matemática - 007/008.5.- Derivada da função composta, derivada da função inversa, derivada da função implícita e derivada de funções definidas parametricamente. Teorema.31 Derivada da Função Composta
Universidade de Mogi das Cruzes UMC. Cálculo Diferencial e Integral II Parte II
Cálclo Diferencial e Integral II Página Universidade de Mogi das Crzes UMC Campos Villa Lobos Cálclo Diferencial e Integral II Parte II Engenharia Civil Engenharia Mecânica marilia@mc.br º semestre de