Fundamentos de Análise II
|
|
|
- Aline Veiga Braga
- 6 Há anos
- Visualizações:
Transcrição
1 Universidade Federal de Minas Gerais Educação a Distância 2013 Fundamentos de Análise II Paulo Cupertino de Lima
2
3 Fundamentos de Análise II
4
5 Paulo Cupertino de Lima Fundamentos de Análise II Belo Horizonte CAED-UFMG 2013
6 UNIVERSIDADE FEDERAL DE MINAS GERAIS Profº Clélio Campolina Diniz Reitor Profª Rocksane de Carvalho Norton Vice-Reitoria Profª Antônia Vitória Soares Aranha Pró Reitora de Graduação Profº André Luiz dos Santos Cabral Pró Reitor Adjunto de Graduação CENTRO DE APOIO DE EDUCAÇÃO À DISTÂNCIA Profº Fernando Selmar Rocha Fidalgo Diretor de Educação a Distância Prof º Wagner José Corradi Barbosa Coordenador da UAB/UFMG Profº Hormindo Pereira de Souza Junior Coordenador Adjunto da UAB/UFMG EDITORA CAED-UFMG Profº Fernando Selmar Rocha Fidalgo CONSELHO EDITORIAL Profª. Ângela Imaculada Loureiro de Freitas Dalben Profº. Dan Avritzer Profª. Eliane Novato Silva Profº. Hormindo Pereira de Souza Profª. Paulina Maria Maia Barbosa Profª. Simone de Fátima Barbosa Tófani Profª. Vilma Lúcia Macagnan Carvalho Profº. Vito Modesto de Bellis Profº. Wagner José Corradi Barbosa COLEÇÃO EAD MATEMÁTICA Coordenador: Dan Avritzer LIVRO: Fundamentos de Análise II Autores: Paulo Cupertino de Lima Revisão: Jussara Maria Frizzera Projeto Gráfico: Departamento de Design - CAED Formatação: Sérgio Luz Dados Internacionais de Catalogação na Publicação (CIP) (Luciana de Oliveira M. Cunha, CRB-6/2725) L732f Lima, Paulo Cupertino de Fundamentos de análise II / Paulo Cupertino de Lima. Belo Horizonte : CAED-UFMG, p. : il. p&b. ; 27 cm. Inclui bibliografia. ISBN Funções (Matemática). 2. Ensino a distância. I. Universidade Federal de Minas Gerais. II. Título. CDD 515 CDU 517.5
7 Sumário Apresentação...7 Nota do Editor...9 Aula 1 - Funções de variável real A definição de função de uma variável real Imagem e pré-imagem de uma função Funções crescentes e funções decrescentes A inversa de uma função Exercícios Limite de uma função real Definição de ite de uma função Propriedades do ite O Teorema do Sanduiche Limites laterais de uma função Limites infinitos Limites no infinito Exercícios Continuidade Definição de continuidade Propriedades da continuidade O Teorema do Valor Extremo O Teorema do Valor Intermediário Exercícios Diferenciabilidade Definição da derivada Propriedades da derivada A Regra da Cadeia Máximos e mínimos Pontos críticos O Teorema do Valor Médio Exercícios... 70
8 5 As funções exponenciais Introdução Definição da função exponencial Propriedades das funções exponenciais As funções exponenciais são contínuas A derivada de e x As funções logarítmicas Definição das funções logaritmicas Derivadas de funções logaritmicas Propriedades das funções logaritmicas Noções de Topologia Conjuntos abertos Conjuntos fechados Pontos de acumulação Conjuntos compactos O teorema de Heine-Borel Exercícios Referências...105
9 apresentação Este livro foi escrito para ser utilizado no curso de Licenciatura em Matemática à distância oferecido pela UFMG. Tendo em vista que este livro é destinado a cursos à distância, o texto possui características específicas para assim ser utilizado. Neste livro introduzimos os conceitos de funções crescentes e funções decrescentes e de inversa de uma função. Falamos sobre ite, continuidade e diferenciabilidade de funções de uma variável real. Definimos as funções exponenciais e logaritmicas e introduzimos algumas noções de topologia. Na Aula 1 introduzimos o conceito inversa de uma função, mostramos que uma função é bijetiva se, e somente se, ela tiver inversa. Introduzimos os conceitos de funções crescente e decrescente e mostramos que estas são injetivas. Na Aula 2 introduzimos o conceito de ite de uma função, mostramos as suas propriedades, provamos o Teorema do Sanduiche e damos várias aplicações do mesmo. Falamos sobre ites infinitos e de ites no infinito. A partir da definição calculamos os ites de algumas funções elementares, tais como polinômios, funções trigonométricas e a raiz quadrada. Na Aula 3 introduzimos o conceito de continuidade e provamos as suas propriedades. Mostramos que algumas funções elementares, tais como polinômios, razão de polinômios, as funções trigonométricas e a raiz quadrada são contínuas. Mostramos que a composta de funções contínuas é uma função contínua. Provamos que funções contínuas em intervalos fechados e itados são itadas, provamos os Teoremas do Valor Intermediário e do Valor Extremo. Na Aula 4 introduzimos o conceito de derivada e mostramos as suas propriedades. A partir da definição, calculamos as derivadas de várias funções. Provamos a Regra da Cadeia e demos vários exemplos de aplicações da mesma. Introduzimos os conceitos de máximo e mínimo locais e globais, bem como o conceito de pontos críticos. Provamos os Teoremas de Fermat, de Rolle e do Valor Médio. Descrevemos como calcular os valores máximo e mínimo globais de uma função contínua num intervalo fechado e itado. Damos várias aplicações do Teorema do Valor Médio. 9
10 Na Aula 5 definimos as funções exponeciais a x, onde a é um número real positivo e diferente de 1. Mais precisamente, mostramos que se (r n ) for uma sequência qualquer de números racionais convergindo para x, então a sequência (a r n) é convergente e o seu ite não depende de (r n ), com isso definimos a x como o ite da sequência (a r n). Mostramos as propriedades da função a x, que ela é contínua, injetiva e sobrejetiva, e calculamos a sua derivada. Na Aula 6 definimos a inversa da função a x, ou seja, a função log a x, e mostramos as propriedades desta função. Calculamos as derivadas das funções logaritmicas. Na Aula 7 damos algumas noções de topologia, ou seja, os conceitos de conjuntos aberto, fechado e compacto e de pontos de acumulação. Mostramos que o supremo e o ínfimo de um conjunto compacto pertencem ao mesmo. Mostramos a generalização Teorema dos Intervalos Encaixantes para conjuntos compactos. Provamos o Teorema de Heine-Borel. 10
11 nota do editor A Universidade Federal de Minas Gerais atua em diversos projetos de Educação a Distância, que incluem atividades de ensino, pesquisa e extensão. Dentre elas, destacam-se as ações vinculadas ao Centro de Apoio à Educação a Distância (CAED), que iniciou suas atividades em 2003, credenciando a UFMG junto ao Ministério da Educação para a oferta de cursos a distância. O CAED-UFMG (Centro de Apoio à Educação a Distância da Universidade Federal de Minas Gerais), Unidade Administrativa da Pró-Reitoria de Graduação, tem por objetivo administrar, coordenar e assessorar o desenvolvimento de cursos de graduação, de pós-graduação e de extensão na modalidade a distância, desenvolver estudos e pesquisas sobre educação a distância, promover a articulação da UFMG com os polos de apoio presencial, como também produzir e editar livros acadêmicos e/ou didáticos, impressos e digitais, bem como a produção de outros materiais pedagógicos sobre EAD. Em 2007, diante do objetivo de formação inicial de professores em serviço, foi criado o Programa Pró-Licenciatura com a criação dos cursos de graduação a distância e, em 2008, com a necessidade de expansão da educação superior pública, foi criado pelo Ministério da Educação o Sistema Universidade Aberta do Brasil UAB. A UFMG integrou-se a esses programas, visando apoiar a formação de professores em Minas Gerais, além de desenvolver um ensino superior de qualidade em municípios brasileiros desprovidos de instituições de ensino superior. Atualmente, a UFMG oferece, através do Pró-licenciatura e da UAB, cinco cursos de graduação, quatro cursos de pós-graduação lato sensu, sete cursos de aperfeiçoamento e um de atualização. Como um passo importante e decisivo, o CAED-UFMG decidiu, no ano de 2011, criar a Editora CAED-UFMG como forma de potencializar a produção do material didático a ser disponibilizado para os cursos em funcionamento. Fernando Selmar Rocha Fidalgo Editor 11
12 1 Funções de variável real
13 AULA1: FUNÇÕES DE VARIÁVEL REAL OBJETIVOS Ao final dessa aula, o aluno deverá ser capaz de: 1. Compreender os conceitos de função de uma variável real e de pré-imagem de uma função. 2. Compreender os conceitos de funções crescentes e decrescentes e de inversa de uma função. 1.1 A definição de função de uma variável real No curso de Fundamentos de Análise I, vimos a definição de uma função f : A B, onde A e B eram conjuntos arbitrários, chamados de domínio e contradomínio de f, respectivamente. Neste curso estaremos interessados num caso particular em que A e B são subconjuntos de R, portanto f assumirá valores reais, por isso dizemos que f é uma função real. É importante ficar claro que para definirmos uma função precisamos especificar não só a regra que a define, mas também o seu domínio, pois para uma mesma regra, ao considerarmos diferentes domínios, teremos diferentes funções. Por exemplo, f : R R, dada por f (x) =x 2 e g : (1, 1) R, dada por g(x) = x 2,são funções diferentes, pois os seus domínios são diferentes. Há situações em que especificamos apenas a regra que define a função f ; neste caso estará implícito que o seu domínio é o maior subconjunto de R, para o qual a regra faça sentido, ou seja, f (x) éumnúmero real. Por exemplo, para f (x) = x, o maior subconjunto de R, para o qual f está definida é [0, ). Já a função f (x) =1/x está definida para todo x = 0, enquanto a função f (x) =ln x está definida para todo x > 0. Exemplo 1.1. A função f : R R, definida por f (x) =x, é bijetiva. De fato, dados x, y R, se x = y, temos f (x) =x = y = f (y), portanto f (x) = f (y) e concluimos que f é injetiva. Por outro lado, dado y R, se tomarmos x = y, teremos f (x) =x = y, o que mostra que para todo y R a equação f (x) =y, sempre tem solução, portanto, f é sobrejetiva. Como f é injetiva e sobrejetiva, ela é bijetiva. Exemplo 1.2. Af: R R, definida por f (x) =x 3, é injetiva e sobrejetiva. aula 1: Funções de variável real 13
14 De fato, suponha que x 1 x 2, digamos x 1 < x 2, mostraremos que f (x 1 ) f (x 2 ). Como f (x 2 ) f (x 1 )=x 3 2 x3 1 =(x 2 x 1 )(x x 2x 1 + x 2 1 ), e x 1 x 2, segue-se que f (x 1 )= f (x 2 ) se, e somente se, x x 2x 1 + x 2 1 = 0. Temos duas possibilidades: x 1 x 2 0 ou x 1 x 2 < 0, no primeiro caso, temos x x 2x 1 + x 2 1 x2 1 + x2 2 > 0, no segundo caso temos x2 2 + x 2x 1 + x 2 1 =(x 2 x 1 ) 2 x 1 x 2 x 1 x 2 > 0, portanto, em ambos os casos temos, x x 2x 1 + x 2 1 > 0, logo f (x 2 ) f (x 1 ) > 0, com isso concluimos que f é injetiva. Vimos na Aula 5 do curso de Fundamentos de Análise I que dado y 0, que existe um (único) número real x, denotado por 3 y, tal que x 3 = y. Por outro lado, se y < 0, tome x = 3 y, então x 3 = y = y. Logo, para todo y R, existe x R, tal que x 3 = y, o que mostra que a imagem de f é igual ao seu contradomínio, portanto, f é sobrejetiva. Lembramos que o gráfico de uma função f : A B é o conjunto dos pontos {(x, f (x)) : x A}. (1.1) Se A e B forem subconjuntos de R, a representação dos pontos de (1.1) no plano é uma curva. Por exemplo, se f : R R, for definida por f (x) =x 2, o seu gráfico é o conjunto {(x, x 2 ) : x R}, o qual está representado na Figura 1.1. y f (x) =x 2 y = b x Figura 1.1: O gráfico de f (x) =x 2, x R. 14 Fundamentos de Análise II
15 No caso em que A e B são subconjuntos de R, podemos dar uma interpretação geométrica para os conceitos de injetividade, sobrejetividade e bijetividade. Uma função f : A B é injetiva, se para todo b B, a reta y = b intersecta o gráfico de f no máximo em um ponto. Por outro lado, f será sobrejetiva, se para todo b B, a reta y = b intersecta o gráfico de f em pelo menos num ponto. Portanto, f será bijetiva se, e somente se, para todo b B, a reta y = b intersecta o gráfico de f em exatamente um ponto. A função f : R R, definida por f (x) =x 2,não é injetiva, pois para todo b > 0 a reta y = b intersecta o seu gráfico em dois pontos (±b, b 2 ). Ela também não é sobrejetiva, pois se b < 0, a reta y = b não intersecta o gráfico de f, pois f (x) 0, para todo x. Note que a função g : [0, ) R, definida por g(x) =x 2, é injetiva mas não é sobrejetiva; por quê? Além disso, a função h : [0, ) [0, ), definida por h(x) =x 2, é injetiva e sobrejetiva; por quê? 1.2 Imagem e pré-imagem de uma função Definição 1.1. Dada uma função f : A B, se M A, denotamos por f (M) ={ f (a) : a M}, chamado de imagem de M por f. Dado N B, definimos f 1 (N) ={x A : f (x) N}. O conjunto f 1 (N) é chamado de pré-imagem ou imagem inversa de N pela função f. Vale a pena ressaltar que na definição acima o símbolo f 1 não representa a inversa de f, a qual será definida na Definição 1.4. Exemplo 1.3. Seja f : {a, b, c} {1, 2, 3, 4}, definida por f (a) =2, f (b) =4, f (c) =1. Então f ({a, b} = {2, 4} ef 1 ({1, 2}) ={a, c} ef 1 ({3}) =. Exemplo 1.4. Seja f : R R, definida por f (x) =x 2, então f ([ 1, 3)) = [0, 9) e f 1 [1, 4] =[ 2, 1] [1, 2]. Nos dois teoremas seguintes, os conjuntos A e B são bem gerais, não precisando ser subconjuntos de R. Teorema 1.1. Dada uma função f : A B, sejam M, N B. Então f 1 (M N) = f 1 (M) f 1 (N). aula 1: Funções de variável real 15
16 Prova. Suponha que x f 1 (M N), então, f (x) M N, ou seja, f (x) M e f (x) N, portanto x f 1 (M) e x pertence a f 1 (N), logo, x f 1 (M) f 1 (N), o que mostra que f 1 (M N) f 1 (M) f 1 (N). (1.2) Por outro lado, se x f 1 (M) f 1 (N), então x f 1 (M) e x f 1 (N), portanto f (x) M e f (x) N, logo f (x) pertence a M N, consequentemente x f 1 (M N). Disso concluimos que f 1 (M) f 1 (N) f 1 (M N). (1.3) De (1.2) e (1.3), concluimos a demonstração do teorema. Teorema 1.2. Dada uma função f : A B, sejam M, N A. Então f (M N) = f (M) f (N). Prova. Suponha que y f (M N), então y = f (x), onde x M N, portanto x M ou x N, se x M, então y f (M), se x N, então y f (N), de qualquer forma y f (M) f (N), portanto f (M N) f (M) f (N). (1.4) Por outro lado, se y f (M) f (N), então y f (M) ou y pertence a f (N). Se y f (M), então existe x M, tal que y = f (x), se y f (N), existe x N, tal que y = f (x). De qualquer forma, existe x M N, tal que f (x) =y, ou seja, y f (M N), isto mostra que f (M) f (N) f (M N). (1.5) De (1.4) e (1.5), concluimos a demonstração do teorema. 1.3 Funções crescentes e funções decrescentes Definição 1.2. Seja I um intervalo da reta, podendo ele ser a reta toda, dizemos que uma função f : I R é crescente em I, se para todo x 1, x 2 I, com x 1 < x 2, tivermos f (x 1 ) < f (x 2 ). Teorema 1.3. Se f for crescente em I, então f é injetiva em I. Prova. Suponha que f seja crescente em I e sejam x 1, x 2 I, com x 1 x 2, afirmamos que f (x 1 ) f (x 2 ). Como x 1 e x 2 são diferentes, temos uma das seguintes possibilidades: (i) x 1 < x 2 ou (ii) x 2 < x 1. Como f é crescente em I, no caso (i) temos f (x 1 ) < f (x 2 ) e no caso (ii) temos f (x 2 ) < f (x 1 ), portanto f (x 1 ) f (x 2 ). 16 Fundamentos de Análise II
17 Por indução podemos mostrar que para quaisquer números reais a e b e inteiro positivo n, temos a n b n =(a b)(a n 1 + a n 2 b + a n 3 b b n 1 ), (1.6) usaremos este resultado nos três exemplos seguintes. Exemplo 1.5. Seja n um inteiro positivo e f : [0, ) R, definida por Então f é crescente. De fato, em virtude de (1.6), temos f (x) =x n. f (x 2 ) f (x 1 ) = x2 n xn 1 = (x 2 x 1 )(x2 n 1 + x2 n 2 x x1 n 1 ). Portanto se x 2 > x 1 0, então f (x 2 ) > f (x 1 ), o que mostra que f é crescente. Exemplo 1.6. Seja n um inteiro positivo e g : [0, ) [0, ), definida por Então g é crescente. g(x) =x 1/n. De fato, suponha que x 2 > x 1, então tendo em vista (1.6), podemos escrever x 2 x 1 = g(x 2 ) n g(x 1 ) n = (g(x 2 ) g(x 1 )) ( g(x 2 ) n 1 + g(x 2 ) n 2 g(x 1 )+...+ g(x 1 ) n 1). (1.7) Como x 2 > x 1, então x 2 x 1 > 0. Como g(x) > 0 para x > 0eg(0) =0, segue g(x 2 ) > 0eg(x 1 ) 0, logo g(x 2 ) n 1 + g(x 2 ) n 2 g(x 1 )+...+ g(x 1 ) n 1 > 0. Portanto de (1.7), concluimos que o que mostra que g é crescente. g(x 2 ) g(x 1 ) > 0, Exemplo 1.7. Sejam m, n inteiros positivos e h : [0, ) R definida por Então h é crescente. h(x) =x m/n ( (x m ) 1/n ). aula 1: Funções de variável real 17
18 De fato, note que h(x) =g( f (x)). Suponha que x 2 > x 1 0, como a função f é crescente, temos f (x 1 ) < f (x 2 ) e como g é crescente, temos g( f (x 1 )) < g( f (x 2 )), portanto h(x 1 ) < h(x 2 ), o que mostra que h é crescente. Definição 1.3. Seja I R, dizemos que uma função f : I R é decrescente em I, se para todos x 1, x 2 I com x 1 < x 2 tivermos f (x 1 ) > f (x 2 ). Exercício 1.1. Mostre que se f for decrescente em I, então f é injetiva em I. Na Aula 4 estudaremos a derivada de uma função e veremos que ela nos dá informações sobre os intervalos de crescimento e de decrescimento de uma função derivável. 1.4 A inversa de uma função Definição 1.4. Dada uma função f : A B, dizemos que f tem inversa, se existir uma função g : B A, tal que ( f g)(x) =x, x B e (g f )(x) =x, x A. Usamos a notação f 1, para denotar a a inversa de f. Exemplo 1.8. Seja f : R R, definida por f (x) =x + 1. Mostre que g : R R, definida por g(x) =x 1 é a inversa de f. Solução. Seja g(x) =x 1, então para todo x R, temos f (g(x)) = f (x 1) =(x 1)+1 = x e g( f (x)) = g(x + 1) =(x + 1) 1 = x. 18 Fundamentos de Análise II
19 O aluno deve estar perguntando como foi encontrada a inversa de f no exemplo anterior. O que fizemos foi o seguinte: da equação y = x + 1 podemos encontrar x em função de y e temos x = y 1; ou seja, a inversa de f é a função que f 1 (y) = g(y) =y 1. Como é comum usarmos x como a variável independente, substituimos x por y e y por x nesta equação e temos que f 1 (x) =g(x) =x 1. Em geral, se quisemos encontrar a inversa de y = f (x), consideramos a equação x = f (y) e desta tentamos encontrar y em função de x, a qual será f 1 (x). Quase nunca é possível resolver a equação x = f (y), mesmo no caso mais simples que possamos imaginar em que f (y) é um polinômio. Exercício 1.2. Encontre a fórmula para a função inversa das funções abaixo. (i) f (x) =x (ii) f : R { 3/2} R {2}, definida por f (x) = 4x 1 2x+3. Teorema 1.4. Sejam S, T conjuntos e f : S T uma função. Mostre que f é bijetiva se, e somente se, f tem inversa. Prova. Suponha que f seja bijetiva, mostraremos que f tem inversa. De fato, dado qualquer y T, existe x S, tal que f (x) =y, pois f é sobrejetiva e este x é único, pois f é injetiva. Isto nos permite definir g : T S, por g(y) =x, onde x éoúnico elemento de S, tal que f (x) =y. Por construção ( f g)(y) = f (g(y)) = f (x) =y, para todo y T e (g f )(x) =g( f (x)) = g(y) =x, para todo x S. Ou seja, g = f 1. Reciprocamente, suponha que f tenha uma inversa, a qual denotaremos por g. Mostraremos que f é sobrejetiva e injetiva. De fato, dado y T, temos f (g(y)) = y, seja x S, definido por x = g(y), então f (x) = f (g(y)) = y, logo é f é sobrejetiva. Tome x, x S, tal que x x, afirmamos que f (x) f (x ), caso contrário, teríamos x = g( f (x)) = g( f (x )) = x, o que seria um absurdo, portanto f é injetiva. Definição 1.5. Seja A um subconjunto de R, tal que se x A, então x A. Dizemos que f : A R é uma função par, se f ( x) = f (x), para todo x A. Se f ( x) = f (x), para todo x A, dizemos que f é uma função ímpar. Exemplo 1.9. As funções cos xex 2 são pares e as funções sen xex 3 são funções ímpares, quando definidas na reta toda ou num intervalo ( a, a), onde a > 0. aula 1: Funções de variável real 19
20 Exemplo Se f for ímpar, então f (0) =0. De fato, como f é impar, f (0) = f ( 0) = f (0), logo f (0) = f (0), ou seja, 2 f (0) =0, o que implica f (0) =0. 20 Fundamentos de Análise II
21 1.5 Exercícios Exercício 1.3. Seja f : A B uma função injetiva e seja C a imagem de f. Por que a função g : A C, definida por g(x) = f (x) para todo x A, é bijetiva? Exercício 1.4. A função f (x) = x + 1, x R, é injetiva? Exercício 1.5. Mostre que a função f : R {2} R {1}, definida por é bijetiva e encontre a sua inversa. f (x) = x x 2, Exercício 1.6. Mostre que a função f : R [ 1, ), definida por é sobrejetiva, mas não é injetiva. f (x) =x 2 + 2x, Exercício 1.7. Encontre as inversas das seguintes funções: (1) f (x) = 10 3x, x 10/3, (2) f (x) =2x 3 + 3, (3) f (x) =(2x + 8) 3. Exercício 1.8. Mostre que as funções abaixo são bijetivas e encontre as suas inversas. (1) f : R {2} R {5}, definida por f (x) = 5x+1 x 2, (2) f : R { 3/2} R {2}, definida por f (x) = 4x 1 2x+3. Exercício 1.9. (Revisão) Diga se as afirmações abaixo são verdadeiras ou falsas, justificando a sua opção. (1) Existe uma função bijetiva f : N Q, (2) Existe uma função bijetiva f : N R, (3) Existe uma função bijetiva f : {1, 2,..., n} P({1, 2,..., n}). aula 1: Funções de variável real 21
22 2 Limite de uma função real
23 AULA2: LIMITE DE UMA FUNÇÃO REAL OBJETIVOS Ao final dessa aula, o aluno deverá ser capaz de: 1. Compreender o conceito de ite de uma função, as suas propriedades e as suas implicações. 2. Calcular ites a partir da definição. 3. Aplicar o Teorema do Sanduiche. 4. Compreender os conceitos de ites infinitos e de ites no infinito, bem como calculá-los. 2.1 Definição de ite de uma função Definição 2.1. Dado um número real x o, dizemos que um conjunto V é uma vizinhança de x o, se existir algum número real α > 0, tal que (x o α, x o + α) V. Se de uma vizinhança de x o retirarmos o ponto x o, dizemos que o conjunto obtido é uma vizinhança deletada de x o. Em particular o conjunto dos x, tais que 0 < x x o < α, o qual é precisamente (x o α, x o ) (x o, x o + α) é um exemplo de vizinhança deletada de x o. Na definição de ite, a qual será dada nesta aula, estaremos interessados em saber o que acontece com uma função f (x) para valores de x próximos de x o, mas x x o. Em outras palavras, a funcão precisa estar definida numa vizinhança delatada de x o. Por exemplo, embora a função sen x x não esteja definida para x = 0, nada nos impede de perguntarmos o que acontece a ela, a medida em que tomamos x cada vez mais próximos de 0. Por exemplo, poderíamos perguntar se os valores desta função estão ficando cada vez mais próximos de um número real L. Consideraremos, por exemplo, a seguinte função: f (x) = x2 1 x 1. Embora x = 1não faça parte do seu domínio, ela está definida para todo x 1, portanto podemos perguntar o que acontece com os valores de f (x), a medida em que x fica cada vez mais próximo de 1. É claro que para todo x 1, podemos escrever (x 1)(x + 1) f (x) = = x + 1, x 1 o que é equivalente a f (x) 2 = x 1. Portanto, se tomarmos x cada vez mais próximos de 1, os valores de f (x) ficam cada vez mais próximos de 2. Em particular, se quisermos, por exemplo, que Aul a 2 Limite de uma função real 23
24 f (x) 2 < 10 15, basta que tomemos 0 < x 1 < A fim de formalizarmos o que foi dito, acima temos duas noções de proximidade: a primeira é a proximidade de f (x) do valor 2, a qual é medida por f (x) 2. A segunda é a proximidade de x ao ponto x = 1, a qual é medida por x 1. Por isso introduziremos dois números positivos ɛ e δ, o primeiro mede a proximidade de f (x) ao 2, e o segundo mede a proximidade de x a 1. No presente caso, dado ɛ > 0, se tomarmos δ = ɛ, então sempre que 0 < x 1 < δ, teremos f (x) 2 = x 1 < δ = ɛ. Resumindo o que foi dito acima, dado arbitrariamente ɛ > 0, mostramos que existe um δ > 0, tal que se 0 < x 1 < δ, então f (x) 2 < ɛ. No presente caso, uma possível escolha é tomarmos δ = ɛ. Em virtude disso, dizemos que o ite de f (x) quando x tende a 1 é 2 e escrevemos ou seja, f (x) =2, x 1 x 2 1 x 1 x 1 = 2. Definição 2.2. Seja f uma função definida numa vizinhança deletada do ponto x o. Se existir um número real L, de modo que para todo ɛ > 0, exista um δ > 0, tal que f (x) L < ɛ, sempre que 0 < x x o < δ, dizemos que o ite de f (x) quando x tende a x o é L e escrevemos x x o f (x) =L. Embora no exemplo que consideramos acima tomamos δ = ɛ, em geral, a dependência de δ com ɛ pode ser complicada. Teorema 2.1. (Unicidade do ite) Seja f definida numa vizinhança delatada de x = x o. Se x xo f (x) existir ele é único. Prova. Suponha que f (x) =L e f (x) =M, mostraremos que L = M. Se x xo x xo tivéssemos L = M, digamos L < M, na definição de ite tomaríamos ɛ = M L 2. Para este ɛ, como f (x) =L, existiria δ 1 > 0, tal que se 0 < x x o < δ 1, x xo então teríamos f (x) L < ɛ. Visto que f (x) =M, existiria δ 2 > 0, tal que se x xo 0 < x x o < δ 2, então teríamos f (x) M < ɛ. Se tomarmos δ = min{δ 1, δ 2 }, então para 0 < x x o < δ, teríamos f (x) L < ɛ e também f (x) M < ɛ,o que equivale dizer que f (x) (L ɛ, L + ɛ) e f (x) (M ɛ, M + ɛ), o que seria um absurdo, pois estes intervalos são disjuntos. 24 Fundamentos de Análise II
25 Exemplo 2.1. Suponha que x xo f (x) exista. Então para todo ɛ > 0 e toda constante positiva k, existe δ > 0, tal que se 0 < x x o < δ, então f (x) L < kɛ. De fato, dados arbitrariamente ɛ e k positivos, seja ɛ = kɛ. Na definição de ite, para este valor de ɛ, existe δ > 0, tal que se 0 < x x o < δ, então f (x) L < ɛ, ou seja, f (x) L < kɛ. Em muitas situações aplicaremos o resultado do exemplo acima fazendo k = 1/2 ou k = 1/3; mas outras escolhas do valor de k também serão consideradas e, dependerá do problema. Exercício 2.1. Seja f (x) =c, para todo x, onde c é uma constante. Usando ɛ e δ, mostre que para todo x o, temos x x o f (x) =c, Exercício 2.2. Seja f (x) =x, para todo x. Usando ɛ e δ, mostre que para todo x o, temos x x o f (x) =x o. Exemplo 2.2. Seja f (x) =2x + 3, mostraremos a partir da definição que para todo x o R. x x o f (x) =2x o + 3, De fato, dado ɛ > 0, tome δ = ɛ/2, portanto, se 0 < x x o < δ, temos f (x) (2x o + 3) = 2 x x o < 2δ = 2 ɛ 2 = ɛ, o que mostra que x xo f (x) =2x o + 3. Aul a 2 Limite de uma função real 25
26 Exercício 2.3. Demonstre cada afirmação usando ɛ e δ. (a) x/5 = 3/5. x 3 ( (b) 4 3x ) = 7. x 5 5 (c) x 3 x 2 + x 12 x 3 (d) x 0 x 2 = 0. (e) x 2 x 3 = 8. = 7. Exercício 2.4. Seja f (x) = { 0, se x for racional 1, se x for irracional. Mostre que x 0 f (x) não existe. Sugestão: Note que em qualquer vizinhança deletada de x = 0 existem números racionais e números irracionais. Na definição de ite tome ɛ = 1/2. Exercício 2.5. Encontre um número δ > 0, tal que se x 2 < δ, então 4x 8 < ɛ, onde ɛ = Exemplo 2.3. Suponha que f (x) exista e seja c uma constante qualquer. Então x xo ( ) (cf(x)) = c f (x). x x o x x o De fato, seja L = f (x). Dado ɛ > 0, em virtude do Exercício 2.1, existe δ > 0, x xo tal que 0 < x x o < δ implica f (x) L < ɛ 1+ c, portanto cf(x) cl = c f (x) L < c ɛ 1 + c < ɛ, 26 Fundamentos de Análise II
27 o que mostra que x xo (cf(x)) = cl. Teorema 2.2. Suponha que x xo f (x) exista, então existem constantes positivas K e α, tais que se 0 < x x o < α, então f (x) K. Prova. Seja L = x xo f (x). Na definição de ite, tome ɛ = 1, então existe α positivo, tal que se 0 < x x o < α, temos f (x) L < 1, isto juntamente com a desigualdade triangular implicam que f (x) = ( f (x) L)+L f (x) L + L < 1 + L. Fazendo K = L + 1, concluimos a nossa demonstração. O teorema acima diz que se x xo f (x) existir, então f tem que ser itada numa vizinhança deletada de x o ; em particular, se uma função não for itada numa vizinhança deletada de x o, então x xo f (x) não pode existir. Exemplo 2.4. Para todo x o > 0, temos De fato, dado ɛ > 0, tome x x o x = xo. { xo δ = min 2, } x o ɛ. Se tomarmos 0 < x x o < δ, então x > x o δ, como δ x o 2, temos x > x o 2 > 0, portanto x estará no domínio da função x. Por outro lado, x x o = x x o = x x o x + xo x + xo < x x o xo < δ xo ɛ, na última desigualdade usamos que δ x o ɛ. Exercício 2.6. Mostre que x xo f (x) =L se, e somente se, x x o f (x) L = 0. Aul a 2 Limite de uma função real 27
28 Exemplo 2.5. Se então x x o g(x) =M, x x o g(x) = M. De fato, o caso em que M = 0 deixamos para o aluno no Exercício 2.6; portanto, a seguir vamos assumir que M = 0. Como g(x) = M, fazendo ɛ = M x xo 2, encontramos δ 1 > 0, tal que se 0 < x x o < δ 1, então ou seja, M M 2 g(x) M < M 2, < g(x) < M + M 2. (2.1) Da primeira desigualdade de (2.1) concluimos que se M > 0, então g(x) > M 2. Por outro lado, da segunda desigualdade de (2.1) concluimos que se M < 0, então g(x) < M 2. Portanto, g(x) e M têm o mesmo sinal se 0 < x x o < δ 1, em particular nesta vizinhança deletada temos g(x) M = g(x) M, (2.2) Como x xo g(x) =M, dado ɛ > 0, existe δ 2 > 0, tal que se 0 < x x o < δ 2, então g(x) M < ɛ. (2.3) Seja δ = {δ 1, δ 2 }, em virtude de (2.2) e (2.3), se 0 < x x o < δ temos g(x) M = g(x) M < ɛ. Exemplo 2.6. Suponha que x xo g(x) =MeM = 0. Então existe α > 0, tal que se 0 < x x o < α, temos g(x) > M 2. De fato, se fizermos α = δ 1, onde δ 1 foi encontrado no exercício anterior, para 0 < x x o < α, valem as seguintes afirmações: (i) se M > 0, então g(x) > M 2 (ii) se M < 0, então g(x) < M 2 M g(x) > 2, g(x) > M Fundamentos de Análise II
29 Teorema 2.3. Suponha que x xo g(x) = 0. Mostre que 1 x x o g(x) = 1 x xo g(x). Prova. Seja x xo g(x) =M, onde M = 0. No Exemplo 2.6, vimos que existe α > 0, tal que se 0 < x x o < α, então teremos g(x) > M 2, o que é equivalente a 1 M g(x) < 2 M 2. (2.4) Dado ɛ > 0, como x xo g(x) =M, existe δ > 0 (o qual tomaremos menor do que α), tal que se 0 < x x o < δ, então g(x) M < ɛm2 2. (2.5) Portanto, se 0 < x x o < δ, valem as relações (2.4) e (2.5), logo 1 g(x) 1 M = g(x) M 1 M g(x) < ɛ M M 2 = ɛ. 2.2 Propriedades do ite Em geral calcular os ites a partir da definição pode ser muito técnico; o que mostraremos a seguir são as propriedades dos ites, com as quais podemos calcular ites de funções mais complicadas, a partir do conhecimento de ites de funções mais simples. Teorema 2.4. Sejam f e g funções definidas numa vizinhança deletada de x = x o e suponha que f (x) e g(x) existam. Então valem as propriedades abaixo. x xo x xo (i) Para toda constante c, temos x x o (cf(x)) = c ( ) f (x) x x o (ii) ( f (x)+g(x)) = f (x)+ g(x). x xo x xo x xo ( )( ) (iii) ( f (x)g(x)) = f (x) g(x). x xo x x o x x o (iv) Se x xo g(x) = 0, então x x o f (x) f (x) g(x) = x xo g(x). x x o. Aul a 2 Limite de uma função real 29
30 Prova. Sejam L = x xo f (x) e M = x xo g(x). A propriedade (i) já foi provada no Exemplo 2.3. A seguir provaremos a propriedade (ii). Como f (x) =L e g(x) =M, x x o x xo dado ɛ > 0, existe δ > 0, tal que se 0 < x x o < δ, então f (x) L < 2 ɛ e g(x) M < 2 ɛ, isto juntamente com a desigualdade triangular implicam que ( f (x)+g(x)) (L + M) = ( f (x) L)+(g(x) M) f (x) L + g(x) M o que mostra a propriedade (ii). < ɛ 2 + ɛ 2 = ɛ, A seguir mostraremos a propriedade (iii). Seja dado ɛ > 0. Como x xo g(x) existe, pelo Teorema 2.2 existem constantes positivas α e K, tais que 0 < x x o < α, implica que g(x) K. (2.6) Como f (x) =L, existe δ 1 > 0 (assumiremos δ 1 < α), tal que se 0 < x x o < x xo δ 1, então f (x) L < ɛ 2K. (2.7) Da mesma forma, como g(x) =M, existe um δ > 0 (assumiremos δ < δ 1 ), x xo tal que se 0 < x x o < δ, então ɛ g(x) M < 2( L + 1). (2.8) Portanto, se 0 < x x o < δ, então valem (2.6), (2.7) e (2.8); portanto, da desigualdade triangular, temos ( f (x)g(x)) (LM) = ( f (x) L)g(x) +L(g(x) M) f (x) L g(x) + L g(x) M < ɛ 2K K + ɛ 2( L + 1) L < ɛ 2 + ɛ 2 = ɛ, 30 Fundamentos de Análise II
31 o que mostra a propriedade (iii). A propriedade (iv) é uma consequência do Teorema 2.3 e da propriedade (iii). Exemplo 2.7. Combinando-se as propriedades (i) e (ii), segue por indução que se os ites f 1 (x),..., f n (x) existirem, então para quaisquer constantes c 1,...,c n, x xo x xo temos n n x x o c i f i (x) = c i f i (x). x xo i=1 i=1 Exemplo 2.8. Da propriedade (iii), segue por indução que se os ites f 1 (x),..., x xo f n (x) existirem, então x x o ( ) ( ) ( f 1 (x)... f n (x)) = f 1 (x)... f n (x). x x o x x o x x o Exemplo 2.9. Seja seja P(x) uma função polinomial. Usando o Exercício 2.2 e os Exemplos (2.7) (2.8), concluimos que P(x) =P(x o ). x x o Exemplo Sejam P(x) eq(x) funções polinomiais, com Q(x o ) 0. Usando o Exercício (2.9) e a propriedade (iv), concluimos que Exemplo P(x) x x o Q(x) = P(x o) Q(x o ). x 2 (x2 + 2x + 1) =( 2) 2 + 2( 2)+1 = 1. Exemplo ( )( ) x 1 (x2 + 1)(x 3 2x 5) = x 1 (x2 + 1) x 1 (x3 2x 5) = (( 1) 2 + 1)(( 1) 3 2( 1) 5) = 8. Exemplo x 3 + 4x + 3 x 0 x 2 1 = x 0 (x3 + 4x + 3) x 0 (x2 1) = 3 1 = 3. Aul a 2 Limite de uma função real 31
32 2.3 O Teorema do Sanduiche Teorema 2.5. (Teorema do Sanduiche) Sejam f, g e h funções definidas numa vizinhaça deletada de x = x o, na qual g(x) f (x) h(x). Se x xo g(x) =L = x xo h(x), então f (x) =L. x x o Prova. Como g(x) = L = h(x), dado ɛ > 0 existe δ > 0 tal que se x xo x xo 0 < x x o < δ, temos g(x) L < ɛ e h(x) L < ɛ. Destas desigualdades temos L ɛ < g(x) e h(x) < L + ɛ, respectivamente. Portanto L ɛ < g(x) f (x) h(x) < L + ɛ, ou seja, L ɛ < f (x) < L + ɛ, logo f (x) L < ɛ. O que mostra que x xo f (x) = L. Exemplo Do Teorema do Sanduiche, segue que ( π ) x 3 + x 2 sen = 0. x x 0 De fato, para todo x = 0 temos ( sen πx ) 1, além disso, x 3 + x 2 = x 1 + x. Se nos restringirmos a x pequenos, digamos 0 < x < 1, então, 0 < x + 1 < 2, como a função x é crescente, segue-se que 1 + x < 2, portanto, x 3 + x 2 = x 1 + x 2 x. Logo, ( π ) 0 x 3 + x 2 sen 2 x x como 0 = 0 e 2 x = 0, das desigualdades acima e do Teorema do x 0 x 0 Sanduiche concluímos que ( π ) x 3 + x 2 sen = 0, x 0 x o que é equivalente a x 3 + x 2 sen x 0 ( π ) = 0. x Teorema 2.6. Sejam f e g definidas numa vizinhança deletada de x = x o na qual g(x) K, onde K é uma constante positiva. Mostre que se x xo f (x) = 0, então x x o ( f (x)g(x)) = Fundamentos de Análise II
33 Prova. Como g(x) K, temos 0 f (x)g(x) K f (x). (2.9) Como K f (x) = 0 e 0 = 0, de (2.9) e do Teorema do Sanduiche, temos x xo x xo f (x)g(x) = 0, o que é equivalente a ( f (x)g(x)) = 0. x x o x xo Exercício 2.7. Usando as identidades trigonométricas: cos(a ± b) =cos a cos b sen a sen b mostre que sen (a ± b) =sen a cos b ± sen b cos a ( ) ( ) x xo x + xo cos x cos x o = 2sen sen 2 2 (2.10) ( ) x xo sen x sen x o = 2 sen 2 ( x + xo cos 2 ). (2.11) y 1 P B O A x Figura 2.1: A área hachurada na figura corresponde à área de um setor circular que subentende um ângulo de x radianos, onde 0 < x < π/2. Aul a 2 Limite de uma função real 33
34 Da Figura 2.1 temos as seguintes desigualdades: ou seja, o que é equivalente a Área( OAP) Área(setorOAP) Área( OAB), sen x 2 cos x sen x x x 2 tg x 2, 1, (2.12) para todo 0 < x < π/2. Como as funções 1, cos x e sen x x são pares, concluimos que as desigualdades em (2.12) valem para 0 < x < π/2. Teorema 2.7. Temos os seguinte ites: cos x = cos x o, (2.13) x x o sen x x 0 x = 1, (2.14) sen x = senx o. (2.15) x x o Prova. Como a função seno é itada por 1, então para todos x e x o reais, temos ( ) x + sen xo 1 2 e de (2.10) temos para 0 < x x o < π. sen ( x x o ) 2 1, x x o 2 De (2.11), (2.12) e das duas desigualdades acima, temos ( ) ( ) cos x cos x o = x 2sen xo x + xo sen 2 2 sen ( x x o ) ( ) 2 = 2 x x o x + 2 sen xo 2 x x o 2 x x o, 34 Fundamentos de Análise II
35 para 0 < x x o < π. Da desigualdade acima e do Teorema do Sanduiche concluimos que x x o cos x = cos x o, com isso provamos (2.13). De (2.13) cos x = cos 0 = 1, x 0 isto juntamente com (2.12) e do Teorema do Sanduiche implicam (2.14). Como a função cosseno é itada por 1, segue de (2.10), (2.12) e de (2.11) que ( ) ( ) senx senx o = x 2 sen xo x + xo cos 2 2 sen ( x x o ) ( ) 2 = 2 x x o x + 2 cos xo 2 x x o 2 x x o, para 0 < x x o < π. Da desigualdade acima e do Teorema do Sanduiche concluimos que x x o senx = senx o, com isso provamos (2.15). Exercício 2.8. Sejam f (x) eg(x) duas funções definidas numa vizinhança de x = x o, tais que f (x) =g(x), para todo x x o e suponha que f (x) =L. O que podemos dizer de g(x)? x xo x xo 2.4 Limites laterais de uma função Se uma função f (x) estiver definida para valores de x próximos porém maiores do que x o, podemos perguntar o que acontece com os valores de f (x) quando aproximamos de x o pela direita, ou seja, através de x > x o. Isto nos leva à noção de ite lateral à direita. De maneira análoga, se uma função estiver definida para valores próximos porém menores do que x o, podemos perguntar o que acontece com f (x) quando nos aproximamos de x o por valores de x < x o e isto nos leva a noção de ite lateral à esquerda. Se uma função f estiver definida numa vizinhança deletada de um ponto x o, podemos considerar os ites laterais à direita e à esquerda e perguntarmos se eles existem e, em caso afirmativo, se eles são iguais. Aul a 2 Limite de uma função real 35
36 Definição 2.3. Suponha que f esteja definida para valores de x próximos e maiores do que x o. Se para todo ɛ > 0 existir um δ > 0, tal que f (x) L < ɛ, sempre que x (x o, x o + δ), dizemos que o ite lateral à direita de f quando x tende a x o é L e escrevemos x x + o f (x) =L. Definição 2.4. Suponha que f esteja definida para valores de x próximos e menores do que x o. Se para todo ɛ > 0 existir um δ > 0, tal que f (x) L < ɛ, sempre que x (x o δ, x o ), dizemos que o ite lateral à esquerda de f quando x tende a x o é L e escrevemos x x o f (x) =L. Teorema 2.8. Seja f uma função definida numa vizinhança deletada de x = x o. Então x x o f (x) =L se, e somente se, x x + o f (x) =L = x x o f (x). Prova. Suponha que f (x) = L. Dado ɛ > 0, então existe δ > 0, tal que x xo f (x) L < ɛ sempre que 0 < x x o < δ, mas 0 < x x o < δ é equivalente a x (x o δ, x o ) (x o, x o + δ), portanto temos o seguinte: (i) sempre que x (x o δ, x o ) teremos f (x) L < ɛ e (ii) sempre que x (x o, x o + δ) teremos f (x) L < ɛ. De (i) temos que x xo Suponha que x x + o f (x) =L e de (ii) x x + o f (x) =L = x x o f (x). f (x) =L. Tome ɛ > 0, como x x + o f (x) =L, existe δ 1 > 0, tal que se x (x o, x o + δ 1 ), temos f (x) L < ɛ. Da mesma forma, como f (x) =L, existe δ 2 > 0, tal x xo que se x (x o δ 2, x o ), temos f (x) L < ɛ. Seja δ = min{δ 1, δ 2 }, então sempre que tivermos x (x o, x o + δ) ou x (x o δ, x o ), teremos f (x) L < ɛ. Em outras palavras se 0 < x x o < δ, teremos f (x) L < ɛ. O teorema acima diz que o ite de f (x) quando x tende a x o existirá se, e somente se, os ites laterais existirem e tiverem o mesmo valor. Exemplo Seja f (x) = x x, então x 0 f (x) =+1 e f (x) = 1. + x 0 36 Fundamentos de Análise II
37 De fato Portanto e f (x) = x 0 { 1, se x > 0 1, se x < 0. f (x) = 1 = 1 x 0 f (x) = 1 = 1, x 0 + x 0 + como f (x) = f (x), concluímos que f (x) não existe. x 0 x 0 + x 0 Exercício 2.9. Suponha que =L e que exista δ > 0 tal que g(x) 0, x 0 +g(x) para x (0, δ). Mostre que L 0. Exercício Suponha que =L e que exista δ > 0 tal que g(x) 0, x 0 +g(x) para x (0, δ). Mostre que L 0. Exercício Suponha que =L e que exista δ > 0 tal que g(x) 0, x 0 g(x) para x ( δ,0). Mostre que L 0. Exercício Suponha que =L e que exista δ > 0 tal que g(x) 0, x 0 g(x) para x ( δ,0). Mostre que L Limites infinitos Considere a função f (x) = 1, cujo o gráfico se encontra na Figura 2.2. Dado x um número M > 0, não importa quão grande ele seja, podemos encontrar uma vizinhança deletada de x = 0, na qual f (x) > M. De fato, se fizermos δ = M 1, se 0 < x < δ, teremos f (x) = 1 > 1 x δ = M. Neste caso dizemos que o ite de f (x) quando x tende a zero é infinito e escrevemos x x o f (x) =+. Aul a 2 Limite de uma função real 37
38 y y = M x Figura 2.2: O gráfico de f (x) = 1 x. Definição 2.5. Seja f definida numa vizinhança deletada de x = x o. Se para todo M > 0 existir um δ > 0, tal que f (x) > M, sempre que 0 < x x o < δ, dizemos que o ite de f (x) quando x tende a x o é infinito e escrevemos f (x) =+. x x o Exercício Suponha que f (x) =+ e g(x) =c, onde c é uma constante. Mostre que ( f (x)+g(x)) = +. x xo x xo x xo Exercício Suponha que x xo f (x) =+ e x xo g(x) =c, onde c é uma constante postiva. Mostre que x xo ( f (x)g(x)) = +. Definição 2.6. Seja f definida numa vizinhança deletada de x = x o. Se para todo M < 0 existir um δ > 0, tal que f (x) < M, sempre que 0 < x x o < δ, dizemos que o ite de f (x) quando x tende a x o é menos infinito e escrevemos f (x) =. x x o 38 Fundamentos de Análise II
39 y y = M > 0 x y = M < 0 Figura 2.3: O gráfico de f (x) = 1 x. Exercício Seja f (x) = 1. Mostre que f (x) =. x x Definição 2.7. Se para todo M > 0 existir um δ > 0, tal que f (x) > M, sempre que x (x o, x o + δ), dizemos que o ite lateral à direita f (x) quando x tende a x o é mais infinito e escrevemos x x + o f (x) =+. Definição 2.8. Se para todo M > 0 existir um δ > 0, tal que f (x) > M, sempre que x (x o δ, x o ), dizemos que o ite lateral à esquerda f (x) quando x tende a x o é infinito e escrevemos x x o f (x) =+. Exercício Baseado nas duas definições anteriores, em termos de M e de δ, o que significaria dizer que f (x) = e f (x) =? x x o + x xo Aul a 2 Limite de uma função real 39
40 2.6 Limites no infinito y x 2 1 x 2 +1 x Figura 2.4: O gráfico de f (x) = x2 1 x Muitas vezes a função considerada está definida na reta toda ou numa semi-reta e queremos saber qual é o comportamento dela quando x fica muito grande, positiva e ou negativamente. Por exemplo, seja cujo gráfico é mostrado na Figura 2.4. f (x) = x2 1 x 2 + 1, A seguir mostraremos que podemos fazer com que f (x) fique tão próximo de 1 quanto desejarmos, bastando que tomemos x grande. Note que portanto Logo, dado ɛ > 0, seja f (x) = x2 1 x = (x2 + 1) 2 x f (x) 1 = 2 x x o = max{1, 2/ɛ}, o que significa dizer que x o 1ex o 2 ɛ. = 1 2 x 2 + 1, Logo, se x > x o, teremos x > 2 ɛ e x > 1. Como x > 1, então x 2 > x > x o 2 ɛ, portanto x > x 2 = x 2 > x > x o 2 ɛ, ou seja, 2 x < ɛ. 40 Fundamentos de Análise II
41 Consequentemente, f (x) 1 = 2 x < ɛ. Resumindo, mostramos que dado ɛ > 0, existe x o > 0, tal que se x > x o, temos f (x) 1 < ɛ. Definição 2.9. Dizemos que o ite de f (x) quando x tende para mais infinito é L e escrevemos f (x) =L, x + se para todo ɛ > 0 existir x o > 0, tal que x > x o implica f (x) L < ɛ. Exemplo Pela discussão que fizemos no início desta seção concluímos que x + x 2 1 x = 1. Exemplo onde n é um inteiro positivo. x + 1 x n = 0, De fato, dado ɛ > 0, tome x o = n 1 ɛ, como a função x n é crescente, se x > x o, temos x n > x n o, portanto, 1 x n < 1 x n o = ɛ, logo f (x) 0 = 1 x n < ɛ. Definição Dizemos que o ite de f (x) quando x tem para menos infinito é L e escrevemos f (x) =L, x se para todo ɛ > 0 existir x o < 0, tal que x < x o implica f (x) L < ɛ. Exemplo Pela discussão que fizemos no início desta seção concluímos que Exemplo x x + ( x 2 1 x) =0 x 2 1 x = 1. Aul a 2 Limite de uma função real 41
42 De fato, para x 1, temos x 2 1 x = = = ( x 2 1 x)( x x) x2 1 + x 1 x2 1 + x 1 x2 1 + x < 1 x. Portanto, dado ɛ > 0, seja x o = max{1, 1 ɛ }, então se x > x o, x 2 1 x < 1 x < 1 = ɛ. x o Exercício A partir da definição, mostre que (a) x (b) x + 4x 2 5x + 1 2x 2 + 7x 4 = 2, 3x 2 x + 1 x 3 5x + 3 = 0, 4x (c) 3 + x + 5 x 7x 4 =+. 42 Fundamentos de Análise II
43 2.7 Exercícios Exercício Prove que se f (x) =3 e g(x) =2, então x a x a (a) (3 f (x)+g(x) 2 )=13 x a (b) (1/g(x)) = 1/2 x a (c) 3 f (x)+8g(x) =5. x a Exercício Encontre os ites abaixo. (a) x 2 (2x 3 3x + 4), x (b) 3 + 2x 2 1, x 2 5 3x ( 1 (c) x 0 x 1 ) x 2, + x x 3 (d) x 9 x 9, x (e), x 0 x ( f ) x sen (1/x) x + sen (2x) (g), x 0 2x x (h) 3 3x 2 + 2x, x 2 x 2 (i) x 1 x 3 1 x 2 x. (Sugestão: faça a mudança de variáveis u = 1/x), Aul a 2 Limite de uma função real 43
44 3 Continuidade
45 AULA3: CONTINUIDADE OBJETIVOS Ao final dessa aula, o aluno deverá ser capaz de: 1. Compreender o conceito de continuidade, as suas propriedades e as suas implicações. 2. Mostrar que uma função é contínua a partir da definição. 3. Compreender os Teoremas do Valor Intermediário e do Valor Extremo e saber aplicá-los. 3.1 Definição de continuidade Definição 3.1. Seja f uma função definida numa vizinhança do ponto x = x o, dizemos que f é contínua em x o se, e somente se, (i) x xo f (x) existir e (ii) x xo f (x) = f (x o ). Na Figura 3.1 temos dois gráficos. No da esquerda mostramos uma função f (x) que não é contínua em x = 0, pois f (x) não existe. No gráfico da direita f (x) x 0 não é contínua em x = 0, pois embora f (x) exista, ele não é igual ao valor x 0 f (0). y y y = f (x) y = f (x) x x Figura 3.1: Exemplos de funções descontínuas em x = 0. AUla 3: Continuidade 45
46 Exemplo 3.1. Seja f (x) uma função polinômial de grau n, ou seja f (x) =a n x n a 1 x + a o, onde a 1,...,a n são constantes e a n 0. Vimos no Exercício 2.9 que x xo f (x) = f (x o ), para todo x o, portanto funções polinômiais são contínuas em todos os pontos. Exercício 3.1. Seja f : R R, tal que f (λx) =λ n f (x), para todo λ e todo x reais, onde n é um inteiro positivo fixo. Mostre que f é contínua. Sugestão. Note que f (x) = f (x.1) =x n f (1). 3.2 Propriedades da continuidade Teorema 3.1. Sejam f e g funções contínuas em x = x o e c uma constante, então as seguintes funções são contínuas em x o : f cf, f + g, f g, fg e g (se g(x o) 0). O teorema acima é uma consequência imediata do Teorema 2.4; porquê? Exemplo 3.2. Em virtude do Teorema acima e do Exemplo 3.1, concluimos que se P(x) eq(x) são funções polinômiais e Q(x o ) 0, então P(x) Q(x) também será contínua em x o; porquê? Exemplo 3.3. Pelo Teorema 2.7 temos sen x = sen x o e cos x = cos x o, x x o x xo para todo x o. Portanto, as funções seno e cosseno são contínuas em todos os pontos. Logo, do Teorema 3.1, as funções tg x = sen cos x x e sec x = cos 1 x são contínuas em todos os pontos onde o cosseno não se anula, ou seja, x o (2n+1)π 2, onde n é inteiro. Da mesma forma, as funções cotg x = sen cos x x e cossec x = sen 1 x são contínuas em todos os pontos onde o seno não se anula, ou seja, x o nπ. Exemplo 3.4. A função g(x) = x cos x x3 +1 é contínua para todo x. x 2 +3 De fato, as funções cos x e x contínuas para todo x, o mesmo acontece com o produto delas, ou seja, x cos x. Sendo x cos x e x contínuas para todo x, o mesmo acontece com a soma destas duas funções, ou seja, x cos x x é uma função contínua para todo x. A função x é contínua em todos os pontos e não tem zeros em R. Como g(x) é a razão de duas funções contínuas para todo x e o seu denominador nunca se anula, segue-se que g(x) é contínua para todo x. 46 Fundamentos de Análise II
47 Exercício 3.2. Para que valores de x a função f (x) = x3 5x+1 x cos x vale x π f (x)? é contínua? Quanto Exercício 3.3. Mostre que a função f (x) = x é contínua em todos os pontos. Exercício 3.4. Se f for contínua em x = x o, mostre que existem constantes K e δ positivos, tais que f (x) K, para todo x em (x o δ, x o + δ). Sugestão: Veja a demonstração do Teorema 2.2. Exercício 3.5. Seja f : (a, b) R contínua em x = x o e (x n ) uma sequência tal que x n (a, b) para todo n e n x n = x o. Mostre que n f (x n )= f (x o ). Exercício 3.6. Seja f (x) = { x 2 + 1, x 0 x + b, x > 0, onde b é uma constante. É possível tomarmos b, tal que f seja contínua em todos os pontos? Em caso afirmativo, qual deve ser o valor de b? Exercício 3.7. Seja f (x) = { sen x x, x 0 a, x = 0, onde a é uma constante. É possível tomarmos a, tal que f seja contínua em todos os pontos? Em caso afirmativo, qual deve ser o valor de a? AUla 3: Continuidade 47
48 Exercício 3.8. Encontre valores de a e b, de modo que a função x 2 4 x 2 se x < 2 f (x) = ax 2 bx + 3, se 2 x < 3 2x a + b, se x 3 seja contínua em todos os pontos. Exercício 3.9. Explique porque a função f : [0, ) R, definida por { x 2 x f (x) = x 2 1, se x 1 1, se x = 1 é descontínua em x = 1. Exercício Mostre que a função { x f (x) = 4 sen (1/x), se x 0 0, se x = 0 é contínua em x = 0. Definição 3.2. Seja f definida num conjunto contendo um intervalo da forma [x o, x o + α), onde α > 0. Dizemos que f (x) é contínua à direita de x o se x x + o f (x) = f (x o ). Definição 3.3. Seja f definida num conjunto contendo um intervalo da forma (x o α, x o ], onde α > 0. Dizemos que f (x) é contínua à esquerda de x o se x x o f (x) = f (x o ). Dizemos que f : A R é contínua em A, se f for contínua em todos os pontos de A. Fica implícito que se x o não for um ponto interior de A (veja Definição 7.1), a continuidade é à direita ou à esquerda de x o, aquela que fizer sentido. Por exemplo, se A =[a, b], dizemos que f é contínua em A se f for contínua em (a, b), for contínua à direita em x = a e contínua à esquerda em x = b. 48 Fundamentos de Análise II
49 Exercício Mostre que f é contínua em x o se, e somente se, f for contínua à direita e à esquerda de x o. Exemplo 3.5. A função x é contínua para todo x 0. De fato, no Exercício 2.4, vimos que x = xo, x x o para todo x o > 0; portanto x é contínua para x > 0. Por outro lado, dado ɛ > 0, tome N, tal que 1 N < ɛ, o que é possível, pois a sequência ( 1 n ) converge para zero. Suponha que 0 < x < 1 N, como a função x é crescente, então x 0 = x < 1 N < ɛ, logo x 0 + x = 0 = 0, o que mostra que x é contínua à direita em x = 0. Portanto x é contínua para todo x 0. Teorema 3.2. Seja f for contínua em x = x o ef(x o ) = 0, mostre que existe um δ > 0, tal que o sinal de f (x) não muda no intervalo (x o δ, x o + δ). Prova. Suponha que f (x o ) > 0. Na definição de continuidade, tome ɛ = f (x o) 2, então existe δ > 0, tal que se x x o < δ, implica f (x) f (x o ) f (x o) 2, ou seja, em particular f (x) f (x o) 2 > 0. Se f (x o ) < 0, faça 1 2 f (x o) f (x) 3 2 f (x o), (3.1) g(x) = f (x), então g é contínua em x o e g(x o ) > 0, logo valem as desigualdades de (3.1) para a função g, ou seja, dado ɛ > 0, existe δ > 0, tal que se x x o < δ implica 1 2 g(x o) g(x) 3 2 g(x o), multiplicando estas desigualdades por 1, encontramos 3 2 f (x o) f (x) 1 2 f (x o), AUla 3: Continuidade 49
50 em particular, f (x) f (x o) 2 < 0. No Teorema 3.2, se f for contínua em x = x o e se f (x o ) > d, então existe um δ > 0, tal que f (x) > d em (x o δ, x o + δ). Da mesma forma, se f (x o ) < d, então existe um δ > 0, tal que f (x) < d em (x o δ, x o + δ). Basta que consideremos a função g(x) = f (x) d, a qual é contínua em x o enão se anula neste ponto. Do Teorema 3.2 podemos encontrar um δ > 0, para o qual podemos trocar o intervalo aberto (x o δ, x o + δ) pelo intervalo fechado [x o δ, x o + δ]; por quê? Exercício Suponha que f seja contínua à direita em x = x o e que f (x o ) = 0, mostre que existe δ > 0, tal que o sinal de f não muda para x [x o, x o + δ). Exercício Suponha que f seja contínua à esquerda em x = x o e que f (x o ) = 0, mostre existe δ > 0, tal que o sinal de f não muda para x (x o δ, x o ]. Nos dois exercícios anteriores, se f for contínua à direita em x o e se f (x o ) > d, então existe um δ > 0, tal que f (x) > d em [x o, x o + δ]. Da mesma forma, se f (x o ) < d, então existe um δ > 0, tal que f (x) < d em [x o, x o + δ]. Valem comentários similares se f for contínua à esquerda em x o. Teorema 3.3. Seja f contínua em x = ae x xo g(x) =a, então f (g(x)) = f (a), x x o ou seja, ( ) f (g(x)) = f g(x). x x o x x o Em particular, se g(x) for contínua em x o, então a composta f g também será contínua em x o. Prova. Considere a composta y = f (u), onde u = g(x). Dado ɛ > 0, como f (u) é contínua em u = a, existe α > 0, tal que se u a < α, temos f (u) f (a) < ɛ. Como x xo g(x) = a, existe δ > 0, tal que se 0 < x x o < δ, temos g(x) a < α. Portanto, se 0 < x x o < δ, temos f (g(x)) f (a) < ɛ. 50 Fundamentos de Análise II
Limites de Funções. Bases Matemáticas. 2 o quadrimestre de o quadrimestre de / 57
 2 o quadrimestre de 2017 2 o quadrimestre de 2017 1 / Visão Geral 1 Limites Finitos Limite para x ± 2 Limites infinitos Limite no ponto Limite para x ± 3 Continuidade Definição e exemplos Resultados importantes
2 o quadrimestre de 2017 2 o quadrimestre de 2017 1 / Visão Geral 1 Limites Finitos Limite para x ± 2 Limites infinitos Limite no ponto Limite para x ± 3 Continuidade Definição e exemplos Resultados importantes
Limites. 2.1 Limite de uma função
 Limites 2 2. Limite de uma função Vamos investigar o comportamento da função f definida por f(x) = x 2 x + 2 para valores próximos de 2. A tabela a seguir fornece os valores de f(x) para valores de x próximos
Limites 2 2. Limite de uma função Vamos investigar o comportamento da função f definida por f(x) = x 2 x + 2 para valores próximos de 2. A tabela a seguir fornece os valores de f(x) para valores de x próximos
(versão preliminar) exceto possivelmente para x = a. Dizemos que o limite de f(x) quando x tende para x = a é um numero L, e escrevemos
 LIMITE DE FUNÇÕES REAIS JOSÉ ANTÔNIO G. MIRANDA versão preinar). Revisão: Limite e Funções Continuas Definição Limite de Seqüências). Dizemos que uma seqüência de números reais n convergente para um número
LIMITE DE FUNÇÕES REAIS JOSÉ ANTÔNIO G. MIRANDA versão preinar). Revisão: Limite e Funções Continuas Definição Limite de Seqüências). Dizemos que uma seqüência de números reais n convergente para um número
1. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R
 . Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
. Funções Reais de Variável Real Vamos agora estudar funções definidas em subconjuntos D R com valores em R, i.e. f : D R R D x f(x). Uma função é uma regra que associa a cada elemento x D um valor f(x)
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL APOSTILA DE CÁLCULO. Realização:
 UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL APOSTILA DE CÁLCULO Realização: Fortaleza, Fevereiro/2010 1. LIMITES 1.1. Definição Geral Se os valores de f(x) puderem
UNIVERSIDADE FEDERAL DO CEARÁ CENTRO DE TECNOLOGIA PROGRAMA DE EDUCAÇÃO TUTORIAL APOSTILA DE CÁLCULO Realização: Fortaleza, Fevereiro/2010 1. LIMITES 1.1. Definição Geral Se os valores de f(x) puderem
Universidade Federal de Pelotas. Instituto de Física e Matemática Pró-reitoria de Ensino. Módulo de Limites. Aula 01. Projeto GAMA
 Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
Universidade Federal de Pelotas Instituto de Física e Matemática Pró-reitoria de Ensino Atividades de Reforço em Cálculo Módulo de Limites Aula 0 208/ Projeto GAMA Grupo de Apoio em Matemática Ideia Intuitiva
A = B, isto é, todo elemento de A é também um elemento de B e todo elemento de B é também um elemento de A, ou usando o item anterior, A B e B A.
 Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
Capítulo 1 Números Reais 1.1 Conjuntos Numéricos Um conjunto é uma coleção de elementos. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos
CÁLCULO I. Apresentar e aplicar a Regra de L'Hospital.
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o : Limites Innitos e no Innito. Assíntotas. Regra de L'Hospital Objetivos da Aula Denir ite no innito e ites innitos; Apresentar alguns tipos
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o : Limites Innitos e no Innito. Assíntotas. Regra de L'Hospital Objetivos da Aula Denir ite no innito e ites innitos; Apresentar alguns tipos
CÁLCULO I Aula 05: Limites Laterais. Teorema do Valor Intermediário. Teorema do Confronto. Limite Fundamental Trigonométrico.
 s Laterais CÁLCULO I Aula 05: s Laterais.... Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará s Laterais 1 s Laterais 2 3 4 s Laterais Considere a função de Heaviside, denida
s Laterais CÁLCULO I Aula 05: s Laterais.... Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará s Laterais 1 s Laterais 2 3 4 s Laterais Considere a função de Heaviside, denida
LIMITES E CONTINIDADE
 MATEMÁTICA I LIMITES E CONTINIDADE Prof. Dr. Nelson J. Peruzzi Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Parte 2 Limites Infinitos Definição de vizinhança e ite Limites laterais Limite de função
MATEMÁTICA I LIMITES E CONTINIDADE Prof. Dr. Nelson J. Peruzzi Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Parte 2 Limites Infinitos Definição de vizinhança e ite Limites laterais Limite de função
Fundamentos de Análise I
 Universidade Federal de Minas Gerais Educação a Distância 2013 Fundamentos de Análise I Paulo Cupertino de Lima Fundamentos de Análise I Paulo Cupertino de Lima Fundamentos de Análise I Belo Horizonte
Universidade Federal de Minas Gerais Educação a Distância 2013 Fundamentos de Análise I Paulo Cupertino de Lima Fundamentos de Análise I Paulo Cupertino de Lima Fundamentos de Análise I Belo Horizonte
Aula 7 Os teoremas de Weierstrass e do valor intermediário.
 Os teoremas de Weierstrass e do valor intermediário. MÓDULO - AULA 7 Aula 7 Os teoremas de Weierstrass e do valor intermediário. Objetivo Compreender o significado de dois resultados centrais a respeito
Os teoremas de Weierstrass e do valor intermediário. MÓDULO - AULA 7 Aula 7 Os teoremas de Weierstrass e do valor intermediário. Objetivo Compreender o significado de dois resultados centrais a respeito
Aula 5 Limites infinitos. Assíntotas verticais.
 MÓDULO - AULA 5 Aula 5 Limites infinitos. Assíntotas verticais. Objetivo lim Compreender o significado dos limites infinitos lim f(x) = ±, f(x) = ± e lim f(x) = ± + Referências: Aulas 34 e 40, de Pré-Cálculo,
MÓDULO - AULA 5 Aula 5 Limites infinitos. Assíntotas verticais. Objetivo lim Compreender o significado dos limites infinitos lim f(x) = ±, f(x) = ± e lim f(x) = ± + Referências: Aulas 34 e 40, de Pré-Cálculo,
MATEMÁTICA I LIMITE. Profa. Dra. Amanda L. P. M. Perticarrari
 MATEMÁTICA I LIMITE Profa. Dra. Amanda L. P. M. Perticarrari amanda@fcav.unesp.br Parte 1 Limites Definição de vizinhança e ite Limites laterais Limite de função real com uma variável real Teorema da existência
MATEMÁTICA I LIMITE Profa. Dra. Amanda L. P. M. Perticarrari amanda@fcav.unesp.br Parte 1 Limites Definição de vizinhança e ite Limites laterais Limite de função real com uma variável real Teorema da existência
Aula 22 O teste da derivada segunda para extremos relativos.
 O teste da derivada segunda para extremos relativos. MÓDULO 2 - AULA 22 Aula 22 O teste da derivada segunda para extremos relativos. Objetivo: Utilizar a derivada segunda para determinar pontos de máximo
O teste da derivada segunda para extremos relativos. MÓDULO 2 - AULA 22 Aula 22 O teste da derivada segunda para extremos relativos. Objetivo: Utilizar a derivada segunda para determinar pontos de máximo
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 06: Continuidade de Funções Objetivos da Aula Definir função contínua; Reconhecer uma função contínua através do seu gráfico; Utilizar as
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 06: Continuidade de Funções Objetivos da Aula Definir função contínua; Reconhecer uma função contínua através do seu gráfico; Utilizar as
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo. Módulo I: Cálculo Diferencial e Integral Limite e Continuidade
 Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Limite e Continuidade Professora Renata Alcarde Sermarini Notas de aula do professor Idemauro
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Limite e Continuidade Professora Renata Alcarde Sermarini Notas de aula do professor Idemauro
Funções potência da forma f (x) =x n, com n N
 Folha 1 Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções potência da forma f (x) =x n, com n N Parte 08 Parte 8 Matemática Básica 1
Folha 1 Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções potência da forma f (x) =x n, com n N Parte 08 Parte 8 Matemática Básica 1
Aula 05 - Limite de uma Função - Parte I Data: 30/03/2015
 bras.png Cálculo I Logonewton.png Aula 05 - Limite de uma Função - Parte I Data: 30/03/2015 Objetivos da Aula: Definir limite de uma função Definir limites laterias Apresentar as propriedades operatórias
bras.png Cálculo I Logonewton.png Aula 05 - Limite de uma Função - Parte I Data: 30/03/2015 Objetivos da Aula: Definir limite de uma função Definir limites laterias Apresentar as propriedades operatórias
Ementa detalhada até agora
 Ementa detalhada até agora de Setembro de 07. (3/07): Introdução aos números reais: soma, produto, opostos, inversos,(o inverso de a só existe quando a 0). Demostração do fato que a 0 = 0, regra dos sinais,
Ementa detalhada até agora de Setembro de 07. (3/07): Introdução aos números reais: soma, produto, opostos, inversos,(o inverso de a só existe quando a 0). Demostração do fato que a 0 = 0, regra dos sinais,
MAT001 Cálculo Diferencial e Integral I
 1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
1 MAT001 Cálculo Diferencial e Integral I GEOMETRIA ANALÍTICA Coordenadas de pontos no plano cartesiano Distâncias entre pontos Sejam e dois pontos no plano cartesiano A distância entre e é dada pela expressão
UNIVERSIDADE FEDERAL DE PERNAMBUCO. Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos
 CÁLCULO L NOTAS DA DÉCIMA OITAVA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos a primeira técnica de integração: mudança
CÁLCULO L NOTAS DA DÉCIMA OITAVA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a noção de integral indefinidada. Também discutiremos a primeira técnica de integração: mudança
4.1 Preliminares. 1. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = 1=x; x 6= 0 (c) f (x) = 1= p x; x > 0:
 4. FUNÇÕES DERIVÁVEIS ANÁLISE NO CORPO R - 208. 4. Preinares. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = =x; x 6= 0 (c) f (x) = = p x; x > 0: 2. Mostre que
4. FUNÇÕES DERIVÁVEIS ANÁLISE NO CORPO R - 208. 4. Preinares. Em cada caso, use a de nição para calcular f 0 (x) : (a) f (x) = x 3 ; x 2 R (b) f (x) = =x; x 6= 0 (c) f (x) = = p x; x > 0: 2. Mostre que
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
1 Limites e Conjuntos Abertos
 1 Limites e Conjuntos Abertos 1.1 Sequências de números reais Definição. Uma sequência de números reais é uma associação de um número real a cada número natural. Exemplos: 1. {1,2,3,4,...} 2. {1,1/2,1/3,1/4,...}
1 Limites e Conjuntos Abertos 1.1 Sequências de números reais Definição. Uma sequência de números reais é uma associação de um número real a cada número natural. Exemplos: 1. {1,2,3,4,...} 2. {1,1/2,1/3,1/4,...}
AULA 1 Introdução aos limites 3. AULA 2 Propriedades dos limites 5. AULA 3 Continuidade de funções 8. AULA 4 Limites infinitos 10
 Índice AULA 1 Introdução aos limites 3 AULA 2 Propriedades dos limites 5 AULA 3 Continuidade de funções 8 AULA 4 Limites infinitos 10 AULA 5 Limites quando numerador e denominador tendem a zero 12 AULA
Índice AULA 1 Introdução aos limites 3 AULA 2 Propriedades dos limites 5 AULA 3 Continuidade de funções 8 AULA 4 Limites infinitos 10 AULA 5 Limites quando numerador e denominador tendem a zero 12 AULA
CÁLCULO I. Reconhecer, através do gráco, a função que ele representa; (f + g)(x) = f(x) + g(x). (fg)(x) = f(x) g(x). f g
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 03: Operações com funções. Funções Polinominais, Racionais e Trigonométricas Objetivos da Aula Denir operações com funções; Apresentar algumas
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 03: Operações com funções. Funções Polinominais, Racionais e Trigonométricas Objetivos da Aula Denir operações com funções; Apresentar algumas
Capítulo 1. Funções e grácos
 Capítulo 1 Funções e grácos Denição 1. Sejam X e Y dois subconjuntos não vazios do conjunto dos números reais. Uma função de X em Y ou simplesmente uma função é uma regra, lei ou convenção que associa
Capítulo 1 Funções e grácos Denição 1. Sejam X e Y dois subconjuntos não vazios do conjunto dos números reais. Uma função de X em Y ou simplesmente uma função é uma regra, lei ou convenção que associa
CÁLCULO I Aula 11: Limites Innitos e no Innito. Assíntotas. Regra de l'hôspital.
 Limites s CÁLCULO I Aula 11: Limites s e no... Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará Limites s 1 Limites no 2 Limites s 3 4 5 Limites s Denição Seja f uma função denida
Limites s CÁLCULO I Aula 11: Limites s e no... Prof. Edilson Neri Júnior Prof. André Almeida Universidade Federal do Pará Limites s 1 Limites no 2 Limites s 3 4 5 Limites s Denição Seja f uma função denida
Cálculo II - B profs.: Heloisa Bauzer Medeiros e Denise de Oliveira Pinto 1 2 o semestre de 2017 Aulas 6 e 7 Limites e Continuidade
 Cálculo II - B profs.: Heloisa Bauzer Medeiros e Denise de Oliveira Pinto 2 o semestre de 207 Aulas 6 e 7 Limites e Continuidade Estas duas aulas envolvem detalhes muito técnicos. Por essa razão, serão
Cálculo II - B profs.: Heloisa Bauzer Medeiros e Denise de Oliveira Pinto 2 o semestre de 207 Aulas 6 e 7 Limites e Continuidade Estas duas aulas envolvem detalhes muito técnicos. Por essa razão, serão
Derivadas. Capítulo O problema da reta tangente
 Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este conceito relaciona-se com o problema de determinar a reta tangente
Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este conceito relaciona-se com o problema de determinar a reta tangente
MAT146 - Cálculo I - Derivada de funções polinomiais, regras de derivação e derivada de funções trigonométricas
 MAT146 - Cálculo I - Derivada de funções polinomiais, regras de derivação e derivada de funções trigonométricas Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos que uma função
MAT146 - Cálculo I - Derivada de funções polinomiais, regras de derivação e derivada de funções trigonométricas Alexandre Miranda Alves Anderson Tiago da Silva Edson José Teixeira Vimos que uma função
CÁLCULO I. 1 Velocidade Instantânea. Objetivos da Aula. Aula n o 04: Limites e Continuidade. Denir limite de funções; Calcular o limite de uma função;
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 04: Limites e Continuidade Objetivos da Aula Denir ite de funções; Calcular o ite de uma função; Utilizar as propriedades operatórias do
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 04: Limites e Continuidade Objetivos da Aula Denir ite de funções; Calcular o ite de uma função; Utilizar as propriedades operatórias do
Capítulo Topologia e sucessões. 7.1 Considere o subconjunto de R 2 : D = {(x, y) : xy > 1}.
 Capítulo 7 Introdução à Análise em R n 7. Topologia e sucessões 7. Considere o subconjunto de R 2 : D = {(x, y) : > }.. Indique um ponto interior, um ponto fronteiro e um ponto exterior ao conjunto D e
Capítulo 7 Introdução à Análise em R n 7. Topologia e sucessões 7. Considere o subconjunto de R 2 : D = {(x, y) : > }.. Indique um ponto interior, um ponto fronteiro e um ponto exterior ao conjunto D e
CÁLCULO I. 1 Derivada de Funções Elementares
 CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o : Derivada das Funções Elementares. Regras de Derivação. Objetivos da Aula Apresentar a derivada das funções elementares; Apresentar
CÁLCULO I Prof. Marcos Diniz Prof. Edilson Neri Prof. André Almeida Aula n o : Derivada das Funções Elementares. Regras de Derivação. Objetivos da Aula Apresentar a derivada das funções elementares; Apresentar
CONTINUIDADE E LIMITES INFINITOS
 MATEMÁTICA I CONTINUIDADE E LIMITES INFINITOS Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Continuidade de Funções Definição Tipos de Descontinuidade Propriedades Parte 2 Limites Infinitos Definição
MATEMÁTICA I CONTINUIDADE E LIMITES INFINITOS Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Continuidade de Funções Definição Tipos de Descontinuidade Propriedades Parte 2 Limites Infinitos Definição
3. Limites e Continuidade
 3. Limites e Continuidade 1 Conceitos No cálculo de limites, estamos interessados em saber como uma função se comporta quando a variável independente se aproxima de um determinado valor. Em outras palavras,
3. Limites e Continuidade 1 Conceitos No cálculo de limites, estamos interessados em saber como uma função se comporta quando a variável independente se aproxima de um determinado valor. Em outras palavras,
Resumo das aulas dos dias 4 e 11 de abril e exercícios sugeridos
 MAT 1351 Cálculo para funções uma variável real I Curso noturno de Licenciatura em Matemática 1 semestre de 2016 Docente: Prof. Dr. Pierluigi Benevieri Resumo das aulas dos dias 4 e 11 de abril e exercícios
MAT 1351 Cálculo para funções uma variável real I Curso noturno de Licenciatura em Matemática 1 semestre de 2016 Docente: Prof. Dr. Pierluigi Benevieri Resumo das aulas dos dias 4 e 11 de abril e exercícios
Bases Matemáticas Continuidade. Propriedades do Limite de Funções. Daniel Miranda
 Daniel De modo intuitivo, uma função f : A B, com A,B R é dita contínua se variações suficientemente pequenas em x resultam em variações pequenas de f(x), ou equivalentemente, se para x suficientemente
Daniel De modo intuitivo, uma função f : A B, com A,B R é dita contínua se variações suficientemente pequenas em x resultam em variações pequenas de f(x), ou equivalentemente, se para x suficientemente
MAT154: Cálculo 1. Beatriz Ribeiro, Flaviana Ribeiro e Reginaldo Braz. Departamento de Matemática - UFJF. Versão: fevereiro de 2018
 MAT54: Cálculo Beatriz Ribeiro, Flaviana Ribeiro e Reginaldo Braz Departamento de Matemática - UFJF Versão: fevereiro de 208 0 Baseada na apostila da professora Maria Julieta Ventura Carvalho de Araújo.
MAT54: Cálculo Beatriz Ribeiro, Flaviana Ribeiro e Reginaldo Braz Departamento de Matemática - UFJF Versão: fevereiro de 208 0 Baseada na apostila da professora Maria Julieta Ventura Carvalho de Araújo.
Derivadas 1 DEFINIÇÃO. A derivada é a inclinação da reta tangente a um ponto de uma determinada curva, essa reta é obtida a partir de um limite.
 Derivadas 1 DEFINIÇÃO A partir das noções de limite, é possível chegarmos a uma definição importantíssima para o Cálculo, esta é a derivada. Por definição: A derivada é a inclinação da reta tangente a
Derivadas 1 DEFINIÇÃO A partir das noções de limite, é possível chegarmos a uma definição importantíssima para o Cálculo, esta é a derivada. Por definição: A derivada é a inclinação da reta tangente a
Cálculo Diferencial e Integral I. Jair Silvério dos Santos * Professor Dr. Jair Silvério dos Santos 1
 MATEMATICA APLICADA A NEGÓCIOS 3, 0 (200) Cálculo Cálculo Diferencial e Integral I LIMITES LATERAIS Jair Silvério dos Santos * Professor Dr Jair Silvério dos Santos Teorema 0 x x 0 Dada f : A R R uma função
MATEMATICA APLICADA A NEGÓCIOS 3, 0 (200) Cálculo Cálculo Diferencial e Integral I LIMITES LATERAIS Jair Silvério dos Santos * Professor Dr Jair Silvério dos Santos Teorema 0 x x 0 Dada f : A R R uma função
Questão 4 (2,0 pontos). Defina função convexa (0,5 pontos). Seja f : I R uma função convexa no intervalo aberto I. Dado c I (qualquer)
 DM IMECC UNICAMP, Análise I, Prof. Marcelo M. Santos Exame Final, 15/07/2009 Aluno: RA: Ass.: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha as suas resoluções
DM IMECC UNICAMP, Análise I, Prof. Marcelo M. Santos Exame Final, 15/07/2009 Aluno: RA: Ass.: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha as suas resoluções
26 CAPÍTULO 4. LIMITES E ASSÍNTOTAS
 Capítulo 4 Limites e assíntotas 4.1 Limite no ponto Considere a função f(x) = x 1 x 1. Observe que esta função não é denida em x = 1. Contudo, fazendo x sucientemente próximo de 1 (mais não igual a1),
Capítulo 4 Limites e assíntotas 4.1 Limite no ponto Considere a função f(x) = x 1 x 1. Observe que esta função não é denida em x = 1. Contudo, fazendo x sucientemente próximo de 1 (mais não igual a1),
Capítulo 1. Limites nitos. 1.1 Limite nito num ponto
 Capítulo 1 Limites nitos 1.1 Limite nito num ponto Denição 1. Seja uma função f : D f R R, x y = f(x, e p R tal que p D f ou p é um ponto da extremidade de D f. Dizemos que a função f possui ite nito no
Capítulo 1 Limites nitos 1.1 Limite nito num ponto Denição 1. Seja uma função f : D f R R, x y = f(x, e p R tal que p D f ou p é um ponto da extremidade de D f. Dizemos que a função f possui ite nito no
Aula 3 Propriedades de limites. Limites laterais.
 Propriedades de ites. Limites laterais. MÓDULO - AULA 3 Aula 3 Propriedades de ites. Limites laterais. Objetivos Estudar propriedades elementares de ites, tais como: soma, produto, quociente e confronto.
Propriedades de ites. Limites laterais. MÓDULO - AULA 3 Aula 3 Propriedades de ites. Limites laterais. Objetivos Estudar propriedades elementares de ites, tais como: soma, produto, quociente e confronto.
Matemática I. 1 Propriedades dos números reais
 Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Matemática I 1 Propriedades dos números reais O conjunto R dos números reais satisfaz algumas propriedades fundamentais: dados quaisquer x, y R, estão definidos a soma x + y e produto xy e tem-se 1 x +
Enumerabilidade. Capítulo 6
 Capítulo 6 Enumerabilidade No capítulo anterior, vimos uma propriedade que distingue o corpo ordenado dos números racionais do corpo ordenado dos números reais: R é completo, enquanto Q não é. Neste novo
Capítulo 6 Enumerabilidade No capítulo anterior, vimos uma propriedade que distingue o corpo ordenado dos números racionais do corpo ordenado dos números reais: R é completo, enquanto Q não é. Neste novo
Lista de Exercícios da Primeira Semana Análise Real
 Lista de Exercícios da Primeira Semana Análise Real Nesta lista, a n, b n, c n serão sempre sequências de números reais.. Mostre que todo conjunto ordenado com a propriedade do supremo possui a propriedade
Lista de Exercícios da Primeira Semana Análise Real Nesta lista, a n, b n, c n serão sempre sequências de números reais.. Mostre que todo conjunto ordenado com a propriedade do supremo possui a propriedade
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
CÁLCULO L1 NOTAS DA QUINTA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Iniciamos a aula definindo as funções trigonométricas e estabelecendo algumas de suas propriedades básicas. A seguir, calcularemos
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão Lista 1. Números Naturais
 Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 01 Lista 1 Números Naturais 1. Demonstre por indução as seguintes fórmulas: (a) (b) n (j 1) = n (soma dos n primeiros ímpares).
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 01 Lista 1 Números Naturais 1. Demonstre por indução as seguintes fórmulas: (a) (b) n (j 1) = n (soma dos n primeiros ímpares).
Fundação Universidade Federal de Pelotas Curso de Licenciatura em Matemática Disciplina de Análise II - Prof. Dr. Maurício Zahn Lista 01 de Exercícios
 Fundação Universidade Federal de Pelotas Curso de Licenciatura em Matemática Disciplina de Análise II - Prof Dr Maurício Zahn Lista 01 de Eercícios 1 Use a definição de derivada para calcular a derivada
Fundação Universidade Federal de Pelotas Curso de Licenciatura em Matemática Disciplina de Análise II - Prof Dr Maurício Zahn Lista 01 de Eercícios 1 Use a definição de derivada para calcular a derivada
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo
 Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Derivada e Diferencial de uma Função Professora Renata Alcarde Sermarini Notas de aula
Escola Superior de Agricultura Luiz de Queiroz Universidade de São Paulo Módulo I: Cálculo Diferencial e Integral Derivada e Diferencial de uma Função Professora Renata Alcarde Sermarini Notas de aula
Funções. Matemática Básica. O que é uma função? O que é uma função? Folha 1. Humberto José Bortolossi. Parte 07. Definição
 Folha 1 Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções Parte 07 Aula 9 Matemática Básica 1 Aula 9 Matemática Básica 2 O que é uma
Folha 1 Matemática Básica Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções Parte 07 Aula 9 Matemática Básica 1 Aula 9 Matemática Básica 2 O que é uma
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior
 Objetivos da Aula CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 4: Aproximações Lineares e Diferenciais. Regra de L Hôspital. Definir e calcular a aproximação linear
Objetivos da Aula CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 4: Aproximações Lineares e Diferenciais. Regra de L Hôspital. Definir e calcular a aproximação linear
CÁLCULO I. Estabelecer a relação entre continuidade e derivabilidade; Apresentar a derivada das funções elementares. f f(x + h) f(x) c c
 CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 11: Derivada de uma função. Continuidade e Derivabilidade. Derivada das Funções Elementares. Objetivos da Aula Denir
CÁLCULO I Prof. Marcos Diniz Prof. André Almeida Prof. Edilson Neri Júnior Aula n o 11: Derivada de uma função. Continuidade e Derivabilidade. Derivada das Funções Elementares. Objetivos da Aula Denir
MATEMÁTICA I FUNÇÕES. Profa. Dra. Amanda L. P. M. Perticarrari
 MATEMÁTICA I FUNÇÕES Profa. Dra. Amanda L. P. M. Perticarrari amanda.perticarrari@unesp.br Conteúdo Função Variáveis Traçando Gráficos Domínio e Imagem Família de Funções Funções Polinomiais Funções Exponenciais
MATEMÁTICA I FUNÇÕES Profa. Dra. Amanda L. P. M. Perticarrari amanda.perticarrari@unesp.br Conteúdo Função Variáveis Traçando Gráficos Domínio e Imagem Família de Funções Funções Polinomiais Funções Exponenciais
Questão 3. a) (1,5 pontos). Defina i) conjunto aberto, ii) conjunto
 DM IMECC UNICAMP Análise I Prof. Marcelo M. Santos Prova de Segunda Chamada, 08/07/2009 Aluno: Assinatura: RA: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha
DM IMECC UNICAMP Análise I Prof. Marcelo M. Santos Prova de Segunda Chamada, 08/07/2009 Aluno: Assinatura: RA: Observações: Tempo de prova: 100min; Justifique sucintamente todas as suas afirmações; Disponha
Pré-Cálculo. Humberto José Bortolossi. Aula de maio de Departamento de Matemática Aplicada Universidade Federal Fluminense
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Aula 11 28 de maio de 2010 Aula 11 Pré-Cálculo 1 A função raiz quadrada f : [0, + ) [0, + ) x y
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Aula 11 28 de maio de 2010 Aula 11 Pré-Cálculo 1 A função raiz quadrada f : [0, + ) [0, + ) x y
Capítulo 5 Derivadas
 Departamento de Matemática - ICE - UFJF Disciplina MAT54 - Cálculo Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este
Departamento de Matemática - ICE - UFJF Disciplina MAT54 - Cálculo Capítulo 5 Derivadas Este capítulo é sobre derivada, um conceito fundamental do cálculo que é muito útil em problemas aplicados. Este
AULA 1: PRÉ-CÁLCULO E FUNÇÕES
 MATEMÁTICA I AULA 1: PRÉ-CÁLCULO E FUNÇÕES Prof. Dr. Nelson J. Peruzzi Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Conjuntos numéricos A reta real Intervalos Numéricos Valor absoluto de um número
MATEMÁTICA I AULA 1: PRÉ-CÁLCULO E FUNÇÕES Prof. Dr. Nelson J. Peruzzi Profa. Dra. Amanda L. P. M. Perticarrari Parte 1 Conjuntos numéricos A reta real Intervalos Numéricos Valor absoluto de um número
Notas Sobre Sequências e Séries Alexandre Fernandes
 Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Notas Sobre Sequências e Séries 2015 Alexandre Fernandes Limite de seqüências Definição. Uma seq. (s n ) converge para a R, ou a R é limite de (s n ), se para cada ɛ > 0 existe n 0 N tal que s n a < ɛ
Derivadas Parciais Capítulo 14
 Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS 14.2 Limites e Continuidade Nesta seção, aprenderemos sobre: Limites e continuidade de vários tipos de funções. LIMITES E CONTINUIDADE Vamos comparar o
Derivadas Parciais Capítulo 14 DERIVADAS PARCIAIS 14.2 Limites e Continuidade Nesta seção, aprenderemos sobre: Limites e continuidade de vários tipos de funções. LIMITES E CONTINUIDADE Vamos comparar o
Objetivos. Estudar a derivada de certas funções.
 Funções deriváveis MÓDULO 1 - AULA 9 Aula 9 Funções deriváveis Objetivos Compreender a noção de função derivável Referências: Aulas 15 e 16, de Pré-Cálculo, e aulas 2, 3, 4 e 5 Estudar a derivada de certas
Funções deriváveis MÓDULO 1 - AULA 9 Aula 9 Funções deriváveis Objetivos Compreender a noção de função derivável Referências: Aulas 15 e 16, de Pré-Cálculo, e aulas 2, 3, 4 e 5 Estudar a derivada de certas
Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].
![Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3]. Apresente todos os cálculos e justificações relevantes. a) Escreva A e B como intervalos ou união de intervalos e mostre que C = { 1} [1, 3].](/thumbs/100/144026914.jpg) Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
Instituto Superior Técnico Departamento de Matemática 1. o TESTE DE CÁLCULO DIFERENCIAL E INTEGRAL I - Versão A LEAN, LEMat, MEQ 1. o Sem. 2016/17 12/11/2016 Duração: 1h0m Apresente todos os cálculos e
3 AULA. Séries de Números Reais LIVRO. META Representar funções como somas de séries infinitas. OBJETIVOS Calcular somas de infinitos números reais.
 LIVRO Séries de Números Reais META Representar funções como somas de séries infinitas. OBJETIVOS Calcular somas de infinitos números reais. PRÉ-REQUISITOS Seqüências (Aula 02). Séries de Números Reais.
LIVRO Séries de Números Reais META Representar funções como somas de séries infinitas. OBJETIVOS Calcular somas de infinitos números reais. PRÉ-REQUISITOS Seqüências (Aula 02). Séries de Números Reais.
Escalas em Gráficos. Pré-Cálculo. Cuidado! Cuidado! Humberto José Bortolossi. Parte 4. Um círculo é desenhado como uma elipse.
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Escalas em Gráficos Parte 4 Parte 4 Pré-Cálculo 1 Parte 4 Pré-Cálculo 2 Cuidado! Cuidado! Um círculo
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Escalas em Gráficos Parte 4 Parte 4 Pré-Cálculo 1 Parte 4 Pré-Cálculo 2 Cuidado! Cuidado! Um círculo
= 2 sen(x) (cos(x) (b) (7 pontos) Pelo item anterior, temos as k desigualdades. sen 2 (2x) sen(4x) ( 3/2) 3
 Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Problema (a) (3 pontos) Sendo f(x) = sen 2 (x) sen(2x), uma função π-periódica, temos que f (x) = 2 sen(x) cos(x) sen(2x) + sen 2 (x) 2 cos(2x) = 2 sen(x) (cos(x) sen(2x) + sen(x) cos(2x) ) = 2 sen(x)
Integrais indefinidas
 Integrais indefinidas que: Sendo f(x) e F(x) definidas em um intervalo I R, para todo x I, dizemos F é uma antiderivada ou uma primitiva de f, em I, se F (x) = f(x) Exemplos: F(x) = x é uma antiderivada
Integrais indefinidas que: Sendo f(x) e F(x) definidas em um intervalo I R, para todo x I, dizemos F é uma antiderivada ou uma primitiva de f, em I, se F (x) = f(x) Exemplos: F(x) = x é uma antiderivada
Funções monótonas. Pré-Cálculo. Atividade. Funções crescentes. Parte 3. Definição
 Pré-Cálculo Departamento de Matemática Aplicada Universidade Federal Fluminense Funções monótonas Parte 3 Funções crescentes Pré-Cálculo 1 Atividade Pré-Cálculo 2 Dizemos que uma função f : D C é crescente
Pré-Cálculo Departamento de Matemática Aplicada Universidade Federal Fluminense Funções monótonas Parte 3 Funções crescentes Pré-Cálculo 1 Atividade Pré-Cálculo 2 Dizemos que uma função f : D C é crescente
CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS. k + e 1 x, x > 0 f(x) = x cos 1, x > 0
 Instituto Superior Técnico Departamento de Matemática CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS I. Continuidade de Funções. 1) Considere a função f :
Instituto Superior Técnico Departamento de Matemática CÁLCULO DIFERENCIAL E INTEGRAL I LMAC, MEBIOM, MEFT 1 o SEM. 2014/15 2 a FICHA DE EXERCÍCIOS I. Continuidade de Funções. 1) Considere a função f :
UNIVERSIDADE FEDERAL DO ABC. 1 Existência e unicidade de zeros; Métodos da bissecção e falsa posição
 UNIVERSIDADE FEDERAL DO ABC BC1419 Cálculo Numérico - LISTA 1 - Zeros de Funções (Profs. André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda) 1 Existência e unicidade de zeros; Métodos
UNIVERSIDADE FEDERAL DO ABC BC1419 Cálculo Numérico - LISTA 1 - Zeros de Funções (Profs. André Camargo, Feodor Pisnitchenko, Marijana Brtka, Rodrigo Fresneda) 1 Existência e unicidade de zeros; Métodos
Derivadas. Slides de apoio sobre Derivadas. Prof. Ronaldo Carlotto Batista. 21 de outubro de 2013
 Cálculo 1 ECT1113 Slides de apoio sobre Derivadas Prof. Ronaldo Carlotto Batista 21 de outubro de 2013 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados
Cálculo 1 ECT1113 Slides de apoio sobre Derivadas Prof. Ronaldo Carlotto Batista 21 de outubro de 2013 AVISO IMPORTANTE Estes slides foram criados como material de apoio às aulas e não devem ser utilizados
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA. Medida e Probabilidade
 UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
UNIVERSIDADE FEDERAL DE PERNAMBUCO DEPARTAMENTO DE ESTATÍSTICA Medida e Probabilidade Aluno: Daniel Cassimiro Carneiro da Cunha Professor: Andre Toom 1 Resumo Este trabalho contem um resumo dos principais
Propriedades das Funções Contínuas
 Propriedades das Funções Contínuas Prof. Doherty Andrade 2005- UEM Sumário 1 Seqüências 2 1.1 O Corpo dos Números Reais.......................... 2 1.2 Seqüências.................................... 5
Propriedades das Funções Contínuas Prof. Doherty Andrade 2005- UEM Sumário 1 Seqüências 2 1.1 O Corpo dos Números Reais.......................... 2 1.2 Seqüências.................................... 5
Análise Real. IF Sudeste de Minas Gerais. Primeiro semestre de Prof: Marcos Pavani de Carvalho. Marcos Pavani de Carvalho
 IF Sudeste de Minas Gerais Prof: Primeiro semestre de 2014 Proposição: É uma afirmação que pode ser classificada em verdadeira ou falsa, mas que faça sentido. Exemplo: Sejam as proposições: A: A soma dos
IF Sudeste de Minas Gerais Prof: Primeiro semestre de 2014 Proposição: É uma afirmação que pode ser classificada em verdadeira ou falsa, mas que faça sentido. Exemplo: Sejam as proposições: A: A soma dos
Pré-Cálculo. Humberto José Bortolossi. Parte 1. Departamento de Matemática Aplicada Universidade Federal Fluminense. Parte 1 Pré-Cálculo 1
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Parte 1 Parte 1 Pré-Cálculo 1 Apresentação do curso Parte 1 Pré-Cálculo 2 Conteúdo do curso Números
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Parte 1 Parte 1 Pré-Cálculo 1 Apresentação do curso Parte 1 Pré-Cálculo 2 Conteúdo do curso Números
Respostas sem justificativas não serão aceitas. Além disso, não é permitido o uso de aparelhos eletrônicos. x x = lim.
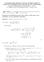 UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL 1-2017.2 1A VERIFICAÇÃO DE APRENDIZAGEM - TURMA GEA Nome Legível RG CPF Respostas sem
UNIVERSIDADE FEDERAL RURAL DE PERNAMBUCO UNIDADE ACADÊMICA DO CABO DE SANTO AGOSTINHO CÁLCULO DIFERENCIAL E INTEGRAL 1-2017.2 1A VERIFICAÇÃO DE APRENDIZAGEM - TURMA GEA Nome Legível RG CPF Respostas sem
PARTE 5 LIMITE. 5.1 Um Pouco de Topologia
 PARTE 5 LIMITE 5.1 Um Pouco de Topologia Vamos agora nos preparar para definir ite de funções reais de várias variáveis reais. Para isto, precisamos de alguns conceitos importantes. Em primeiro lugar,
PARTE 5 LIMITE 5.1 Um Pouco de Topologia Vamos agora nos preparar para definir ite de funções reais de várias variáveis reais. Para isto, precisamos de alguns conceitos importantes. Em primeiro lugar,
Limites de funções algumas propriedades
 Limites de funções algumas propriedades Good girls go to heaven; Bad girls go everywhere. Frase de pára-choque de caminhão americano, que diz algo como Garotas bem comportadas vão para o céu; Garotas sapecas
Limites de funções algumas propriedades Good girls go to heaven; Bad girls go everywhere. Frase de pára-choque de caminhão americano, que diz algo como Garotas bem comportadas vão para o céu; Garotas sapecas
Análise Matemática I 1 o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI)
 Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Análise Matemática I o Exame (Grupos I, II, III, IV, V e VI) 2 o Teste (Grupos IV, V e VI) Campus da Alameda 5 de Janeiro de 2003 LEC, LET, LEN, LEM, LEMat, LEGM Apresente todos os cálculos e justificações
Diferenciabilidade de função de uma variável
 Capítulo 6 Diferenciabilidade de função de uma variável Um conceito importante do Cálculo é o de derivada, que é um ite, como veremos na definição. Fisicamente o conceito de derivada está relacionado ao
Capítulo 6 Diferenciabilidade de função de uma variável Um conceito importante do Cálculo é o de derivada, que é um ite, como veremos na definição. Fisicamente o conceito de derivada está relacionado ao
Cálculo I -A- Humberto José Bortolossi. Departamento de Matemática Aplicada Universidade Federal Fluminense. Parte de novembro de 2013
 Folha 1 Cálculo I -A- Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Parte 16 13 de novembro de 2013 Parte 16 Cálculo I -A- 1 Aproximações lineares (afins)
Folha 1 Cálculo I -A- Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Parte 16 13 de novembro de 2013 Parte 16 Cálculo I -A- 1 Aproximações lineares (afins)
Funções. Pré-Cálculo. O que é uma função? O que é uma função? Humberto José Bortolossi. Parte 2. Definição
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções Parte 2 Parte 2 Pré-Cálculo 1 Parte 2 Pré-Cálculo 2 O que é uma função? O que é uma função?
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções Parte 2 Parte 2 Pré-Cálculo 1 Parte 2 Pré-Cálculo 2 O que é uma função? O que é uma função?
Capítulo 1. f : A B. elementos A com elementos de B ilustradas nos seguintes diagramas.
 Capítulo 1 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Capítulo 1 Funções Sejam A e B conjuntos não vazios. Uma função com domínio A e contradomínio B é uma regra f que a cada elemento em A associa um único elemento em B. A notação usual para uma função f
Propriedades das Funções Contínuas e Limites Laterais Aula 12
 Propriedades das Funções Contínuas e Limites Laterais Aula 12 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 27 de Março de 2014 Primeiro Semestre de 2014 Turma 2014106 -
Propriedades das Funções Contínuas e Limites Laterais Aula 12 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 27 de Março de 2014 Primeiro Semestre de 2014 Turma 2014106 -
Limites infinitos e limites no infinito Aula 15
 Propriedades dos ites infinitos Limites infinitos e ites no infinito Aula 15 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 03 de Abril de 2014 Primeiro Semestre de 2014
Propriedades dos ites infinitos Limites infinitos e ites no infinito Aula 15 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 03 de Abril de 2014 Primeiro Semestre de 2014
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L NOTAS DA DÉCIMA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a Regra de L Hôpital, que será utilizada para solucionar indeterminações de ites de qualquer
CÁLCULO L NOTAS DA DÉCIMA TERCEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos a Regra de L Hôpital, que será utilizada para solucionar indeterminações de ites de qualquer
UNIVERSIDADE FEDERAL DO OESTE DO PARÁ PRÓ-REITORIA DE ENSINO DE GRADUAÇÃO INSTITUTO DE ENGENHARIA E GEOCIENCIAS-IEG PROGRAMA DE COMPUTAÇÃO
 1 UNIVERSIDADE FEDERAL DO OESTE DO PARÁ PRÓ-REITORIA DE ENSINO DE GRADUAÇÃO INSTITUTO DE ENGENHARIA E GEOCIENCIAS-IEG PROGRAMA DE COMPUTAÇÃO NOTAS DE AULA DA DISCIPLINA DE CÁLCULO 1 MATERIAL EM CONSTRUÇÃO
1 UNIVERSIDADE FEDERAL DO OESTE DO PARÁ PRÓ-REITORIA DE ENSINO DE GRADUAÇÃO INSTITUTO DE ENGENHARIA E GEOCIENCIAS-IEG PROGRAMA DE COMPUTAÇÃO NOTAS DE AULA DA DISCIPLINA DE CÁLCULO 1 MATERIAL EM CONSTRUÇÃO
O limite trigonométrico fundamental
 O ite trigonométrico fundamental Meta da aula Continuar a apresentação de ites de funções. Objetivo Ao final desta aula, você deverá ser capaz de: Calcular ites usando o ite trigonométrico fundamental.
O ite trigonométrico fundamental Meta da aula Continuar a apresentação de ites de funções. Objetivo Ao final desta aula, você deverá ser capaz de: Calcular ites usando o ite trigonométrico fundamental.
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
CÁLCULO L NOTAS DA NONA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos as funções logaritmo e exponencial e calcularemos as suas derivadas. Também estabeleceremos algumas propriedades
1. Polinómios e funções racionais
 Um catálogo de funções. Polinómios e funções racionais Polinómios e funções racionais são funções que se podem construir usando apenas as operações algébricas elementares. Recordemos a definição: Definição
Um catálogo de funções. Polinómios e funções racionais Polinómios e funções racionais são funções que se podem construir usando apenas as operações algébricas elementares. Recordemos a definição: Definição
3 Funções reais de variável real (Soluções)
 3 Funções reais de variável real (Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y
3 Funções reais de variável real (Soluções). a) Como e é crescente, com contradomínio ]0, + [, o contradomínio de f é ]e, + [. Para > 0 e y ] e, + [, temos Logo, a inversa de f é f () = y e = y = log y
Provas de Análise Real - Noturno - 3MAT003
 Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Provas de 2006 - Análise Real - Noturno - 3MAT003 Matemática - Prof. Ulysses Sodré - Londrina-PR - provas2006.tex 1. Definir a operação ϕ entre os conjuntos A e B por ϕ(a, B) = (A B) (A B). (a) Demonstrar
Funções monótonas. Pré-Cálculo. Funções decrescentes. Funções crescentes. Humberto José Bortolossi. Parte 3. Definição. Definição
 Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções monótonas Parte 3 Parte 3 Pré-Cálculo 1 Parte 3 Pré-Cálculo 2 Funções crescentes Funções
Pré-Cálculo Humberto José Bortolossi Departamento de Matemática Aplicada Universidade Federal Fluminense Funções monótonas Parte 3 Parte 3 Pré-Cálculo 1 Parte 3 Pré-Cálculo 2 Funções crescentes Funções
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA DÉCIMA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos o Teorema do Valor Médio e algumas de suas conseqüências como: determinar os intervalos de
CÁLCULO L1 NOTAS DA DÉCIMA PRIMEIRA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, apresentaremos o Teorema do Valor Médio e algumas de suas conseqüências como: determinar os intervalos de
