Transformação da deformação
|
|
|
- Maria Fernanda de Vieira Capistrano
- 7 Há anos
- Visualizações:
Transcrição
1 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Transformação da deformação Introdução: O estado geral das deformações em um ponto de um corpo. Deformação Normal: ( ε x, ε, ε z ) Deformação por Cisalhamento: ( γ, γ γ ) xz, Esses seis componentes tendem a deformar cada face de um elemento material Variam de acordo com a orientação do elemento No laboratório as medidas são feitas através de extensômetros. Estado Plano de Deformações ( ε x,ε ) Dois componentes de deformação normal ( γ ) Um componente de deformação por cisalhamento z Figura 1. Estado Plano de Deformações. Observações: O estado plano de deformações não causa um estado plano de tensões e vice-versa. 1
2 Figura. Equações Gerais de Transformação para o Estado Plano de Deformações Objetivos: Estabelecer equações de transformação que podem ser usadas para determinar os componentes de deformação normal e por cisalhamento x, em um ponto, desde que os componentes de deformação x, sejam conhecidos. Convenção de sinal: Deformação Normal e por Cisalhamento Determinação de ε x' Figura 3. Convenção de Sinais. dx = dx' cosθ d = dx' senθ (1) Se ε x > 0 (Figura 4.b) Alongamento de dx é ε xdx Alongamento de dx é ε x dx cosθ Se ε 0 (Figura 4.c) Alongamento de d é ε d Alongamento de dx é ε d senθ >
3 Figura 4. Se dx é fixo Deslocamento γ d para a direita do topo da linha d (Figura 4.d) Alongamento de dx é γ dc osθ Somando-se os três alongamentos: Mas, δx' = ε dx cosθ + ε d senθ γ d cosθ () x + 3
4 δx' ε x' = (3) dx' Substituindo-se (1) em (3) ε = ε cos θ + ε sen θ γ senθ cosθ (4) x ' x + A equação de transformação da deformação para determinar γ x' ' é desenvolvida considerando-se a intensidade da rotação que cada segmento de reta dx e d sofre quando submetido aos componentes da deformação ε, ε γ. Utilizando-se (1) e (5). Figura 4.e. x, δ' α = (5) dx' δ' = ε dx senθ + ε d cosθ γ dsenθ (6) x ( ε + ε ) senθ cosθ γ sen θ α = (7) x Como mostra a Figura 4.e a reta d gira β. Podemos determinar esse ângulo por uma análise semelhante, ou simplesmente substituindo-se θ por θ + 90 e assim tem-se: ( ε + ε ) senθ cosθ γ cos θ β = (8) x γ x ' ' = α β (9) Dessa forma, as equações de transformação da deformação de um elemento orientado com ângulo θ como mostram a Figura 5 são: ε x + ε ε x ε γ ε x ' = + cos( θ ) + sen( θ ) (10) γ x' ' ε x ε γ = sen( θ ) + cos( θ ) (11) Para determinar ε, basta substituir θ por ( + 90) ' θ em (10) e assim tem-se: ε x + ε ε x ε γ ε ' = cos( θ ) sen( θ ) (1) Faça uma comparação com as equações do estado plano de tensão 4
5 Figura 5. Deformações Principais: Deformações normais sem deformações por cisalhamento tg ( θ ) p γ = (13) ε ε x ε x + ε ε x ε γ 1, ε = ± + (14) Deformação por Cisalhamento Máxima no Plano tg ε x ε θ = c (15) γ ( ) γ ε x ε γ = ± + max noplano (16) ε med ε x + ε = (17) Circulo de Mohr Estado Plano de Deformações As equações (10) e (11) podem ser escritas na forma Onde: ( ε ) + = R γ ε x méd (18) 5
6 ε méd ε x + ε = (19) R= ε x ε γ + (0) Centro do círculo fica no ponto (,0 ) ε. méd Construção do Círculo 1. Estabelecer um sistema de coordenadas tal que a abscissa represente a deformação normal ε, com sentido positivo para a direita e a ordenada represente metade do valor da deformação por cisalhamento, γ /, com sentido positivo para baixo.. Determinar o centro do círculo C, que está localizado no eixo ε a uma distância ε = ε + ε da origem. méd ( ) x 3. Marcar o ponto de referência A ( ) x, γ ε. 4. Conectar o ponto A ao ponto C e determinar o raio R pelo triângulo sombreado. 5. Uma vez determinado R, traçar o círculo Figura 6. Deformações Principais 1. As deformações principais, ε 1 e ε são as coordenadas dos pontos B e D na Figura 7.a onde γ / = 0. 6
7 . Determinar a orientação do plano sobre o qual ε 1 atua pelo círculo calculando θ p1 por meio de trigonometria (medido no sentido anti-horário a partir da reta de referência radial CA até a reta CB). Figura 7.a. Lembrar que a rotação de θ p1 deve ser na mesma direção, a partir do eixo de referência do elemento x para o eixo x. Figura 7.b. Figura 7. Deformações por Cisalhamento Máximo no Plano 1. A deformação normal média e a metade da deformação por cisalhamento máxima no plano são determinadas como coordenadas E e F. Figura 7.a. Calcular θ s1 por meio de trigonometria (medido no sentido horário a partir da reta de referência radial CA até a Reta CE). Deformações no plano arbitrário 1. Para um plano especificado por um ângulo θ utiliza-se trigonometria para se calcular a deformação normal e por cisalhamento.. O ângulo conhecido θ do eixo x é medido no círculo como θ. 3. Se for necessário saber o valor de ε ', determiná-lo calculando-se a coordenada ε do ponto Q. A reta CQ localiza-se a 180º de CP e, desse modo, representa uma rotação de 90º do eixo x. 7
8 Exercícios: 1. O estado de deformação no ponto do suporte tem componentes ε x = 00( 10 ), ε = 50( 10 ), γ = 175( 10 ). Usar as equações de transformação da deformação para determinar as deformações planas equivalentes em um o elemento orientado a θ = 0 no sentido anti-horário em relação à posição original. Esquematizar no plano x- o elemento distorcido em virtude dessas deformações Figura8. ε x' = , ε ' = , γ x' ' = resp: ( ) ( ) ( ). O elemento infinitesimal que representa um ponto do material está sujeito ao estado plano de deformações ε x = 500( 10 ), ε = 300( 10 ), γ = 00( 10 ), o qual tende a torcê-lo como mostra a Figura 9.a. Determinar as deformações equivalentes que atuam sobre um elemento orientado a 30º no sentido horário em relação a posição original. Solução: Figuras 9.b e 9.c Resp: x' = 13( 10 ) ' = 13,4 10 Figura 9. ε, ε ( ), γ = 793( ) x' ' 10 8
9 3. O elemento infinitesimal que representa um ponto do material está sujeito ao estado plano de deformações ε x = 350( 10 ), ε = 00( 10 ), γ = 80( 10 ), o qual tende a torcê-lo como mostra a Figura 11.a. Determinar as deformações principais no ponto e a orientação do elemento a elas correspondente. Figura 11. Solução: Figura 11.b Resp. θ = 353( ) o o p 4,14 e 85, 9 ε 1 10, ε x' = ε 4. O estado plano de deformações em um ponto é representado pelos componentes ε x = 50( 10 ), ε = 150( 10 ) e γ = 10( 10 ). Determinar as deformações principais e a orientação do elemento. Solução: Figura 1. ε 1 = 59 10, ε = , θ p1 = 8, 35 Resp: ( ) ( ) o 5. O estado plano de deformações em um ponto é representado pelos componentes ε x = 50( 10 ), ε = 150( 10 ) e γ = 10( 10 ). Determinar as deformações por cisalhamento máximas no plano e a orientação do elemento. o Resp: γ = 418 ( 10 ), ε = 50( 10 ), θ = 36, x' ' méd s1 6 9
10 5. O estado plano de deformações em um ponto é representado pelos componentes ε x = 300( 10 ), ε = 100( 10 ) e γ = 100( 10 ). Determinar o estado de deformação de um elemento orientado a 0º no sentido horário em relação a posição informada. Resp: ε = 309( 10 ), γ = 5( 10 ), ε = 91,3( ) x' x' ' ' 10 Obs: Estudar os exercícios resolvidos do prof. Duran. Referências Bibliográficas: 1. BEER, F.P. e JOHNSTON, JR., E.R. Resistência dos Materiais, 3.º Ed., Makron Books, Gere, J. M. Mecânica dos Materiais, Editora Thomson Learning 3. HIBBELER, R.C. Resistência dos Materiais, 3.º Ed., Editora Livros Técnicos e Científicos, 000. Observações: 1- O presente texto é baseado nas referências citadas. - Todas as figuras se encontram nas referências citadas. 10
Tensão de Cisalhamento Máxima Absoluta
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensão de Cisalhamento
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensão de Cisalhamento
Capítulo 7 Transformação de deformação no plano
 Capítulo 7 Transformação de deformação no plano Resistência dos Materiais I SLIDES 08 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Transformar as componentes
Capítulo 7 Transformação de deformação no plano Resistência dos Materiais I SLIDES 08 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com Objetivos do capítulo Transformar as componentes
Objetivo: Determinar a equação da curva de deflexão e também encontrar deflexões em pontos específicos ao longo do eixo da viga.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Deflexão de Vigas Objetivo:
RESISTÊNCIA DOS MATERIAIS 2 Marcel Merlin dos Santos
 6/0/07 RESISTÊNIA DOS MATERIAIS Marcel Merlin dos Santos ÍRULO DE MOHR O estado plano de tensões pode ser representado por uma solução gráfica. Além disso, essa abordagem nos permitirá visualizar como
6/0/07 RESISTÊNIA DOS MATERIAIS Marcel Merlin dos Santos ÍRULO DE MOHR O estado plano de tensões pode ser representado por uma solução gráfica. Além disso, essa abordagem nos permitirá visualizar como
Carregamentos Combinados
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Carregamentos Combinados
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Carregamentos Combinados
Aula 06 - Estudo de Deformações, Normal e por Cisalhamento.
 Aula 06 - Estudo de Deformações, Normal e por Cisalhamento. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Deformação Quando uma força é aplicada a um corpo, tende a mudar a forma e o tamanho
Aula 06 - Estudo de Deformações, Normal e por Cisalhamento. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Deformação Quando uma força é aplicada a um corpo, tende a mudar a forma e o tamanho
RESISTÊNCIA DOS MATERIAIS 2 Marcel Merlin dos Santos
 03/11/017 RESISTÊNIA DOS MATERIAIS Marcel Merlin dos Santos TENSÃO EM EIXOS QUE SE DEVE À ARGA AXIAL E À TORÇÃO Ocasionalmente os eios circulares são submetidos a efeitos combinados de carga aial e torção.
03/11/017 RESISTÊNIA DOS MATERIAIS Marcel Merlin dos Santos TENSÃO EM EIXOS QUE SE DEVE À ARGA AXIAL E À TORÇÃO Ocasionalmente os eios circulares são submetidos a efeitos combinados de carga aial e torção.
Capítulo 6 Círculo de Mohr para tensões
 Capítulo 6 Círculo de Mohr para tensões Resistência dos Materiais I SLIDES 07 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com 6.4 Círculo de Mohr - Tensão no plano Consiste na solução
Capítulo 6 Círculo de Mohr para tensões Resistência dos Materiais I SLIDES 07 Prof. MSc. Douglas M. A. Bittencourt prof.douglas.pucgo@gmail.com 6.4 Círculo de Mohr - Tensão no plano Consiste na solução
Aula 03 Tensão; Tensão Normal Média em uma barra com carga axial
 Aula 03 Tensão; Tensão Normal Média em uma barra com carga axial Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Conceito de Tensão Representa a intensidade da força interna sobre um plano específico
Aula 03 Tensão; Tensão Normal Média em uma barra com carga axial Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Conceito de Tensão Representa a intensidade da força interna sobre um plano específico
São as vigas que são fabricadas com mais de um material.
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões em Vigas Tópicos
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões em Vigas Tópicos
Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período
 UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
Figura 9.1: Corpo que pode ser simplificado pelo estado plano de tensões (a), estado de tensões no interior do corpo (b).
 9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
9 ESTADO PLANO DE TENSÕES E DEFORMAÇÕES As tensões e deformações em um ponto, no interior de um corpo no espaço tridimensional referenciado por um sistema cartesiano de coordenadas, consistem de três componentes
RESISTÊNCIA DOS MATERIAIS
 Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. Beer E. Russell Johnston, Jr. Análise de Tensões no Estado Plano Capítulo 6 Análise de Tensões no Estado Plano 6.1 Introdução 6. Estado Plano
Terceira Edição CAPÍTULO RESISTÊNCIA DOS MATERIAIS Ferdinand P. Beer E. Russell Johnston, Jr. Análise de Tensões no Estado Plano Capítulo 6 Análise de Tensões no Estado Plano 6.1 Introdução 6. Estado Plano
MECÂNICA DOS SÓLIDOS DEFORMAÇÕES
 MECÂNICA DOS SÓLIDOS DEFORMAÇÕES Prof. Dr. Daniel Caetano 2019-1 Objetivos Conhecer os tipos de deformação e deslocamentos Saber estimar valor da deformação nas formas normal/axial e por cisalhamento Calcular
MECÂNICA DOS SÓLIDOS DEFORMAÇÕES Prof. Dr. Daniel Caetano 2019-1 Objetivos Conhecer os tipos de deformação e deslocamentos Saber estimar valor da deformação nas formas normal/axial e por cisalhamento Calcular
Estado duplo ou, Estado plano de tensões.
 Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra
Estado duplo ou, Estado plano de tensões. tensão que atua em um ponto é função do plano pelo qual se faz o estudo. Esta afirmação pode ficar mais clara quando analisa, por exemplo, um ponto de uma barra
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO
 Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
Resistência dos Materiais 2 AULA 5-6 TRANSFORMAÇÃO DA DEFORMAÇÃO PROF.: KAIO DUTRA Estado Plano de Deformações O estado geral das deformações em determinado ponto de um corpo é representado pela combinação
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
Resistência dos. Materiais. Capítulo 2. - Elasticidade Linear 2
 Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Resistência dos Materiais - Elasticidade Linear Acetatos baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva Índice Carregamento Genérico:
Tensões de Flexão nas Vigas
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões de Flexão nas Vigas
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Tensões de Flexão nas Vigas
MECÂNICA GERAL EQUILÍBRIO TRIDIMENSIONAL DE PONTO MATERIAL. Prof. Dr. Daniel Caetano EXERCÍCIOS:
 MECÂNICA GERAL EXERCÍCIOS: EQUILÍBRIO TRIDIMENSIONAL DE PONTO MATERIAL Prof. Dr. Daniel Caetano 2019-1 Objetivos Exercitar os conceitos de problemas de equilíbrio de ponto material em três dimensões Material
MECÂNICA GERAL EXERCÍCIOS: EQUILÍBRIO TRIDIMENSIONAL DE PONTO MATERIAL Prof. Dr. Daniel Caetano 2019-1 Objetivos Exercitar os conceitos de problemas de equilíbrio de ponto material em três dimensões Material
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 01 Teoria das Tensões Eng. Civil Augusto Romanini
Notas de aula prática de Mecânica dos Solos II (parte 8)
 1 Notas de aula prática de Mecânica dos Solos II (parte 8) Helio Marcos Fernandes Viana Conteúdo da aula prática Exercício relacionado ao traçado do ciclo de Mohr para um elemento (ou pequena parte) de
1 Notas de aula prática de Mecânica dos Solos II (parte 8) Helio Marcos Fernandes Viana Conteúdo da aula prática Exercício relacionado ao traçado do ciclo de Mohr para um elemento (ou pequena parte) de
Coordenadas Polares. Exemplos: Representar em um sistema de coordenadas polares, os seguintes pontos: d) P 4,
 Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano, as coordenadas são números
Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano, as coordenadas são números
Resistência dos Materiais 2 AULA 3-4 TRANSFORMAÇÃO DE TENSÕES
 Resistência dos Materiais 2 AULA 3-4 TRANSFORMAÇÃO DE TENSÕES PROF.: KAIO DUTRA Transformação no Estado Plano de Tensões O estado geral de tensão em um ponto é caracterizado por seis componentes independentes
Resistência dos Materiais 2 AULA 3-4 TRANSFORMAÇÃO DE TENSÕES PROF.: KAIO DUTRA Transformação no Estado Plano de Tensões O estado geral de tensão em um ponto é caracterizado por seis componentes independentes
Coordenadas Polares. Exemplos: Representar em um sistema de coordenadas polares, os seguintes pontos: d) P 4,
 Cálculo II Profa. Adriana Cherri 1 Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano,
Cálculo II Profa. Adriana Cherri 1 Coordenadas Polares Existem vários sistemas de coordenadas que mostram a posição de um ponto em um plano. O sistema de coordenadas polares é um deles. No sistema cartesiano,
Dep. de Engenharia Elétrica Curso de Especialização Engenharia Elétrica / Instrumentação. Tópicos abordados:
 Dep. de Engenharia Elétrica Curso de Especialização Engenharia Elétrica / Instrumentação Tópicos abordados: 1.Introdução 2.Extensômetros 3.Tipos de Extensômetros 4.Ponte de Wheatstone 5.Configurações de
Dep. de Engenharia Elétrica Curso de Especialização Engenharia Elétrica / Instrumentação Tópicos abordados: 1.Introdução 2.Extensômetros 3.Tipos de Extensômetros 4.Ponte de Wheatstone 5.Configurações de
A integral definida Problema:
 A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
A integral definida Seja y = f(x) uma função definida e limitada no intervalo [a, b], e tal que f(x) 0 p/ todo x [a, b]. Problema: Calcular (definir) a área, A,da região do plano limitada pela curva y
Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período
 UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
UNIVERSIDADE DO ESTADO DO RIO DE JANEIRO INSTITUTO POLITÉCNICO Graduação em Engenharia Mecânica Disciplinas: Mecânica dos Materiais 2 6º Período E Dinâmica e Projeto de Máquinas 2-10º Período Professor:
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II
 UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 04 Teoria das deformações Eng. Civil Augusto Romanini
UNIVERSIDADE DO ESTADO DE MATO GROSSO CAMPUS DE SINOP FACULDADE DE CIÊNCIAS EXATAS E TECNOLÓGIAS CURSO DE ENGENHARIA CIVIL MECÂNICA DOS SÓLIDOS II Aula 04 Teoria das deformações Eng. Civil Augusto Romanini
Aula 06 Introdução e Equilíbrio de um corpo deformável
 Aula 06 Introdução e Equilíbrio de um corpo deformável Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Resistência dos Materiais Definição: É um ramo da mecânica que estuda as relações entre
Aula 06 Introdução e Equilíbrio de um corpo deformável Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Resistência dos Materiais Definição: É um ramo da mecânica que estuda as relações entre
Resistência dos Materiais I
 Resistência dos Materiais I Luciano Pessanha Moreira, D.Sc. Professor Associado Departamento de Engenharia Mecânica Escola de Engenharia Metalúrgica Industrial de Volta Redonda Universidade Federal Fluminense
Resistência dos Materiais I Luciano Pessanha Moreira, D.Sc. Professor Associado Departamento de Engenharia Mecânica Escola de Engenharia Metalúrgica Industrial de Volta Redonda Universidade Federal Fluminense
Flexão Vamos lembrar os diagramas de força cortante e momento fletor
 Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Flexão Vamos lembrar os diagramas de força cortante e momento fletor Elementos longos e retos que suportam cargas perpendiculares a seu eixo longitudinal são denominados vigas. Vigas são classificadas
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M é
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia de Computação 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M é
PME Mecânica dos Sólidos II 6 a Lista de Exercícios
 Eercícios Sugeridos (Livro Teto) PME-3211 - Mecânica dos Sólidos II 6 a Lista de Eercícios Referência: Gere, J.M. & Goodno, B.J., Mecânica dos Materiais, Cengage Learning, 2010, 858 p. Deformação Plana:
Eercícios Sugeridos (Livro Teto) PME-3211 - Mecânica dos Sólidos II 6 a Lista de Eercícios Referência: Gere, J.M. & Goodno, B.J., Mecânica dos Materiais, Cengage Learning, 2010, 858 p. Deformação Plana:
Capítulo1 Tensão Normal
 - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Referências Bibliográficas:
- UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA PROFESSORA: SALETE SOUZA DE OLIVEIRA BUFFONI DISCIPLINA: RESISTÊNCIA DOS MATERIAIS Referências Bibliográficas:
1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional = 4200 knm²
 CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
CE2 ESTABILIDADE DAS CONSTRUÇÕES II LISTA DE EXERCÍCIOS PREPARATÓRIA PARA O ENADE 1) Determine a energia de deformação (energia interna) da estrutura abaixo. Rigidez flexional 42 knm² Formulário: equação
Capítulo 7 Transformações de Tensão e Deformação. O Círculo de Mohr. Grupo 9:
 Capítulo 7 Transformações de Tensão e Deformação O Círculo de Mohr André P. Santos Edward O. Schaden Pedro G. Rubira Túlio J. Silva Grupo 9: RA:070166 RA:060316 RA:073592 RA:072544 Transformação do Estado
Capítulo 7 Transformações de Tensão e Deformação O Círculo de Mohr André P. Santos Edward O. Schaden Pedro G. Rubira Túlio J. Silva Grupo 9: RA:070166 RA:060316 RA:073592 RA:072544 Transformação do Estado
DEPARTAMENTO DE ENGENHARIA MECÂNICA. ) uma base ortonormal positiva de versores de V. Digamos que a lei de transformação do operador T seja dada por:
 PME-00 - Mecânica dos Sólidos a ista de Exercícios Apresentar as unidades das seguintes grandezas, segundo o Sistema nternacional de Unidades (S..: a comprimento (l; i rotação (θ; b força concentrada (P;
PME-00 - Mecânica dos Sólidos a ista de Exercícios Apresentar as unidades das seguintes grandezas, segundo o Sistema nternacional de Unidades (S..: a comprimento (l; i rotação (θ; b força concentrada (P;
Nota de aula 8 - Estado Plano de Tensões - Resistência dos Materiais II
 Nota de aula 8 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 011 Flávia Bastos
Nota de aula 8 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 011 Flávia Bastos
Torção Não-Uniforme - UNIVERSIDADE FEDERAL FLUMINENSE ESCOLA DE ENGENHARIA INDUSTRIAL METALÚRGICA DE VOLTA REDONDA SALETE SOUZA DE OLIVEIRA BUFFONI
 - UNIVERSIDADE FEDERA FUMINENSE ESCOA DE ENGENHARIA INDUSRIA MEAÚRGICA DE VOA REDONDA SAEE SOUZA DE OIVEIRA BUFFONI RESISÊNCIA DOS MAERIAIS orção Não-Uniforme A barra não precisa ser prismática e os torques
- UNIVERSIDADE FEDERA FUMINENSE ESCOA DE ENGENHARIA INDUSRIA MEAÚRGICA DE VOA REDONDA SAEE SOUZA DE OIVEIRA BUFFONI RESISÊNCIA DOS MAERIAIS orção Não-Uniforme A barra não precisa ser prismática e os torques
Aula 16 - Elementos esta0camente indeterminados carregados com torque.
 Aula 16 - Elementos esta0camente indeterminados carregados com torque. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Conceito Um eixo carregado com torque pode ser classificado como esta4camente
Aula 16 - Elementos esta0camente indeterminados carregados com torque. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Conceito Um eixo carregado com torque pode ser classificado como esta4camente
Aula 08 - Carga Axial e Princípio de Saint- Venant.
 Aula 08 - Carga Axial e Princípio de Saint- Venant. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Carga Axial A tubulação de perfuração de petróleo suspensa no guindaste da perfuratriz está
Aula 08 - Carga Axial e Princípio de Saint- Venant. Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Carga Axial A tubulação de perfuração de petróleo suspensa no guindaste da perfuratriz está
Deformação. Deformação. Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele.
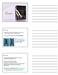 Capítulo 2: Adaptado pela prof. Dra. Danielle Bond Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele. Essas mudanças são denominadas deformações. Note as posições
Capítulo 2: Adaptado pela prof. Dra. Danielle Bond Sempre que uma força é aplicada a um corpo, esta tende a mudar a forma e o tamanho dele. Essas mudanças são denominadas deformações. Note as posições
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 03 de Julho de Prof o. E.T.
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Civil + Física 0 de Julho de 2014 - Prof o ETGalante 1 (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo O ponto M
Aula 4. Coordenadas polares. Definição 1. Observação 1
 Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Aula Coordenadas polares Nesta aula veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana Embora os sistemas cartesianos sejam muito utilizados, há curvas
Capítulo 19. Coordenadas polares
 Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Capítulo 19 Coordenadas polares Neste capítulo, veremos que há outra maneira de expressar a posição de um ponto no plano, distinta da forma cartesiana. Embora os sistemas cartesianos sejam muito utilizados,
Exercícios de Coordenadas Polares Aula 41
 Revisão - Métodos de Integração e Exercícios de Coordenadas Polares Aula 41 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 24 de Junho de 2014 Primeiro Semestre de 2014 Turma
Revisão - Métodos de Integração e Exercícios de Coordenadas Polares Aula 41 Alexandre Nolasco de Carvalho Universidade de São Paulo São Carlos SP, Brazil 24 de Junho de 2014 Primeiro Semestre de 2014 Turma
UFABC - Universidade Federal do ABC. ESTO Mecânica dos Sólidos I. as deformações principais e direções onde elas ocorrem.
 UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
UFABC - Universidade Federal do ABC ESTO008-13 Mecânica dos Sólidos I Sétima Lista de Exercícios Prof. Dr. Wesley Góis CECS Prof. Dr. Cesar Freire - CECS Estudo das Deformações 1. Segundo as direções a,b
Capítulo X Parte I Momentos de Inércia
 Universidade Federal Fluminense - UFF Escola de Engenharia de Volta Redonda EEMVR Departamento de Ciências Eatas Capítulo X Parte Momentos de nércia Profa. Salete Souza de Oliveira Home: http://www.professores.uff.br/salete
Universidade Federal Fluminense - UFF Escola de Engenharia de Volta Redonda EEMVR Departamento de Ciências Eatas Capítulo X Parte Momentos de nércia Profa. Salete Souza de Oliveira Home: http://www.professores.uff.br/salete
Geometria Analítica. Cônicas. Prof Marcelo Maraschin de Souza
 Geometria Analítica Cônicas Prof Marcelo Maraschin de Souza É o lugar geométrico dos pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante. Considere dois pontos distintos
Geometria Analítica Cônicas Prof Marcelo Maraschin de Souza É o lugar geométrico dos pontos de um plano cuja soma das distâncias a dois pontos fixos desse plano é constante. Considere dois pontos distintos
Jorge M. V. Capela, Marisa V. Capela. Araraquara, SP
 Cônicas e Equações Quadráticas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Parábolas 2 3 4 5 Introdução Parábolas Parábolas
Cônicas e Equações Quadráticas Jorge M. V. Capela, Marisa V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Parábolas 2 3 4 5 Introdução Parábolas Parábolas
Material Teórico - Módulo: Vetores em R 2 e R 3. Produto Vetorial. Terceiro Ano - Médio
 Material Teórico - Módulo: Vetores em R 2 e R 3 Produto Vetorial Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto Nesta aula, estudaremos uma operação definida
Material Teórico - Módulo: Vetores em R 2 e R 3 Produto Vetorial Terceiro Ano - Médio Autor: Prof. Angelo Papa Neto Revisor: Prof. Antonio Caminha M. Neto Nesta aula, estudaremos uma operação definida
Resistência dos Materiais
 - Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
- Flexão Acetatos e imagens baseados nos livros: - Mechanics of Materials - Beer & Jonhson - Mecânica e Resistência dos Materiais V. Dias da Silva - Resistência dos Materiais, R.C. Hibbeler Índice Flexão
PME Mecânica dos Sólidos I 4 a Lista de Exercícios
 ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ENGENHARIA MECÂNICA PME-300 - Mecânica dos Sólidos I 4 a Lista de Eercícios 1) Seja o tensor das deformações em um dado ponto de um sólido
ESCOLA POLITÉCNICA DA UNIVERSIDADE DE SÃO PAULO DEPARTAMENTO DE ENGENHARIA MECÂNICA PME-300 - Mecânica dos Sólidos I 4 a Lista de Eercícios 1) Seja o tensor das deformações em um dado ponto de um sólido
Resistência dos Materiais
 Capítulo 3: Tensões em Vasos de Pressão de Paredes Finas Coeficiente de Dilatação Térmica Professor Fernando Porto Resistência dos Materiais Tensões em Vasos de Pressão de Paredes Finas Vasos de pressão
Capítulo 3: Tensões em Vasos de Pressão de Paredes Finas Coeficiente de Dilatação Térmica Professor Fernando Porto Resistência dos Materiais Tensões em Vasos de Pressão de Paredes Finas Vasos de pressão
Matemática 3 Módulo 3
 Matemática Módulo COMENTÁRIOS ATIVIDADES PARA SALA 1. Lembrando... Se duas figuras são semelhantes, temos: 1 A = k; 1 = k, em que R 1 e R são medidas lineares A e A 1 e A são as áreas. Círculo I IV. =
Matemática Módulo COMENTÁRIOS ATIVIDADES PARA SALA 1. Lembrando... Se duas figuras são semelhantes, temos: 1 A = k; 1 = k, em que R 1 e R são medidas lineares A e A 1 e A são as áreas. Círculo I IV. =
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Ambiental 03 de Julho de Prof o. E.T.Galante
 Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Ambiental 03 de Julho de 2014 - Prof o. E.T.Galante 1. (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo. O ponto M
Universidade Federal de Mato Grosso do Sul - UFMS VGA - 2 a Prova - Engenharia Ambiental 03 de Julho de 2014 - Prof o. E.T.Galante 1. (2,0 pontos) Na gura acima ABCDEF GH é um paralelepípedo. O ponto M
Flexão. Tensões na Flexão. e seu sentido é anti-horário. Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras.
 Flexão Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras. O estudo da flexão que se inicia, será dividido, para fim de entendimento, em duas partes: Tensões na flexão; Deformações
Flexão Estudar a flexão em barras é estudar o efeito dos momentos fletores nestas barras. O estudo da flexão que se inicia, será dividido, para fim de entendimento, em duas partes: Tensões na flexão; Deformações
Pontifícia Universidade Católica do Rio de Janeiro / PUC-Rio Departamento de Engenharia Mecânica. ENG1705 Dinâmica de Corpos Rígidos.
 Pontifícia Universidade Católica do Rio de Janeiro / PUC-Rio Departamento de Engenharia Mecânica ENG1705 Dinâmica de Corpos Rígidos (Período: 2016.1) Notas de Aula Capítulo 1: VETORES Ivan Menezes ivan@puc-rio.br
Pontifícia Universidade Católica do Rio de Janeiro / PUC-Rio Departamento de Engenharia Mecânica ENG1705 Dinâmica de Corpos Rígidos (Período: 2016.1) Notas de Aula Capítulo 1: VETORES Ivan Menezes ivan@puc-rio.br
FESP Faculdade de Engenharia São Paulo Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr.
 CE2 Estabilidade das Construções II FESP Faculdade de Engenharia São Paulo Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Nome: Matrícula: Assinale a(s) avaliação(ões) que perdeu: A1 A2
CE2 Estabilidade das Construções II FESP Faculdade de Engenharia São Paulo Prof. Douglas Pereira Agnelo Prof. Dr. Alfonso Pappalardo Jr. Nome: Matrícula: Assinale a(s) avaliação(ões) que perdeu: A1 A2
Teoria das Estruturas I - Aula 08
 Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Teoria das Estruturas I - Aula 08 Cálculo de Deslocamentos em Estruturas Isostáticas (1) Trabalho Externo das Cargas e Energia Interna de Deformação; Relações entre Energia de Deformação e Esforços Internos;
Mecânica Geral. Prof. Evandro Bittencourt (Dr.) Engenharia de Produção e Sistemas UDESC. 27 de fevereiro de 2008
 Mecânica Geral Prof Evandro Bittencourt (Dr) Engenharia de Produção e Sistemas UDESC 7 de fevereiro de 008 Sumário 1 Prof Evandro Bittencourt - Mecânica Geral - 007 1 Introdução 11 Princípios Fundamentais
Mecânica Geral Prof Evandro Bittencourt (Dr) Engenharia de Produção e Sistemas UDESC 7 de fevereiro de 008 Sumário 1 Prof Evandro Bittencourt - Mecânica Geral - 007 1 Introdução 11 Princípios Fundamentais
Aula 08 - Tensão de Cisalhamento Média
 Aula 08 - Tensão de Cisalhamento Média Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Tensão de Cisalhamento Sob a ação de forças de tração P, a barra e a junta irão exercer uma pressão cortante
Aula 08 - Tensão de Cisalhamento Média Prof. Wanderson S. Paris, M.Eng. prof@cronosquality.com.br Tensão de Cisalhamento Sob a ação de forças de tração P, a barra e a junta irão exercer uma pressão cortante
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida
 CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 2: Aproximações Lineares e Diferenciais Objetivos da Aula Definir e calcular a aproximação linear de uma função derivável; Conhecer e determinar
CÁLCULO I Prof. Edilson Neri Júnior Prof. André Almeida Aula n o 2: Aproximações Lineares e Diferenciais Objetivos da Aula Definir e calcular a aproximação linear de uma função derivável; Conhecer e determinar
Deduza a Equação de Onda que representa uma onda progressiva unidimensional, numa corda de massa M e comprimento L.
 Deduza a Equação de Onda que representa uma onda progressiva unidimensional, numa corda de massa M e comprimento L. Esquema do problema Consideremos uma corda longa, fixa nas extremidades, por onde se
Deduza a Equação de Onda que representa uma onda progressiva unidimensional, numa corda de massa M e comprimento L. Esquema do problema Consideremos uma corda longa, fixa nas extremidades, por onde se
Matemática B Intensivo V. 2
 Matemática Intensivo V. Eercícios ) ) C ( ) (5 7) Usando a fórmula do ponto médio: X + X Y + Y C + 5 + 7 6 8 ( ) ERRT: considere (6 ). Temos d () d (C). ssim: ( 6) + ( b ) ( ) + ( 6 b) 9 + b 9 + b b +
Matemática Intensivo V. Eercícios ) ) C ( ) (5 7) Usando a fórmula do ponto médio: X + X Y + Y C + 5 + 7 6 8 ( ) ERRT: considere (6 ). Temos d () d (C). ssim: ( 6) + ( b ) ( ) + ( 6 b) 9 + b 9 + b b +
Resistência dos Materiais AULA 1-2: TENSÃO
 Resistência dos Materiais AULA 1-2: TENSÃO PROF.: KAIO DUTRA Bibliografia Resistência dos Materiais HIBBELER, R.C. Introdução A resistência dos materiais é um ramo da mecânica que estuda as relações entre
Resistência dos Materiais AULA 1-2: TENSÃO PROF.: KAIO DUTRA Bibliografia Resistência dos Materiais HIBBELER, R.C. Introdução A resistência dos materiais é um ramo da mecânica que estuda as relações entre
Programa Princípios Gerais Forças, vetores e operações vetoriais
 Programa Princípios Gerais Forças, vetores e operações vetoriais Representação gráfica de vetores Graficamente, um vetor é representado por uma flecha: a intensidade é o comprimento da flecha; a direção
Programa Princípios Gerais Forças, vetores e operações vetoriais Representação gráfica de vetores Graficamente, um vetor é representado por uma flecha: a intensidade é o comprimento da flecha; a direção
LOM Introdução à Mecânica dos Sólidos. Parte 3. Estado plano de tensão. Tensões em tubos e vasos de pressão de parede fina
 LOM 3081 - Parte 3. Estado plano de tensão. Tensões em tubos e vasos de pressão de parede fina DEMAR USP Professores responsáveis: Viktor Pastoukhov, Carlos A.R.P. Baptista Ref. 1: F.P. BEER, E.R. JOHNSTON,
LOM 3081 - Parte 3. Estado plano de tensão. Tensões em tubos e vasos de pressão de parede fina DEMAR USP Professores responsáveis: Viktor Pastoukhov, Carlos A.R.P. Baptista Ref. 1: F.P. BEER, E.R. JOHNSTON,
Elementos de Matemática
 Elementos de Matemática Exercícios de Trigonometria - atividades didáticas de 2007 Versão compilada no dia 23 de Maio de 2007. Departamento de Matemática - UEL Prof. Ulysses Sodré E-mail: ulysses@matematica.uel.br
Elementos de Matemática Exercícios de Trigonometria - atividades didáticas de 2007 Versão compilada no dia 23 de Maio de 2007. Departamento de Matemática - UEL Prof. Ulysses Sodré E-mail: ulysses@matematica.uel.br
Esta é só uma amostra do livro do Prof César Ribeiro.
 Esta é só uma amostra do livro do Prof César Ribeiro Para adquirir este (e outros livros do autor) vá ao site: http://wwwescolademestrescom/dicasemacetes Conheça também nosso Blog: http://blogescolademestrescom
Esta é só uma amostra do livro do Prof César Ribeiro Para adquirir este (e outros livros do autor) vá ao site: http://wwwescolademestrescom/dicasemacetes Conheça também nosso Blog: http://blogescolademestrescom
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2014-2 Objetivos Compreender a deformação por torção Compreender os esforços de torção Determinar distribuição de tensões de cisalhamento
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2014-2 Objetivos Compreender a deformação por torção Compreender os esforços de torção Determinar distribuição de tensões de cisalhamento
Tensões associadas a esforços internos
 Tensões associadas a esforços internos Refs.: Beer & Johnston, Resistência dos ateriais, 3ª ed., akron Botelho & archetti, Concreto rmado - Eu te amo, 3ª ed, Edgard Blücher, 2002. Esforços axiais e tensões
Tensões associadas a esforços internos Refs.: Beer & Johnston, Resistência dos ateriais, 3ª ed., akron Botelho & archetti, Concreto rmado - Eu te amo, 3ª ed, Edgard Blücher, 2002. Esforços axiais e tensões
3ª série do Ensino Médio Turma 1º Bimestre de 2017 Data / / Escola Aluno
 AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 3ª série do Ensino Médio Turma 1º Bimestre de 2017 Data / / Escola Aluno EM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Avaliação da Aprendizagem em Processo
AVALIAÇÃO DA APRENDIZAGEM EM PROCESSO Matemática 3ª série do Ensino Médio Turma 1º Bimestre de 2017 Data / / Escola Aluno EM 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Avaliação da Aprendizagem em Processo
Halliday & Resnick Fundamentos de Física
 Halliday & Resnick Fundamentos de Física Mecânica Volume 1 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
Halliday & Resnick Fundamentos de Física Mecânica Volume 1 www.grupogen.com.br http://gen-io.grupogen.com.br O GEN Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
carga do fio: Q. r = r p r q figura 1
 Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito. Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio. Dados do problema
Uma carga Q está distribuída uniformemente ao longo de um fio reto de comprimento infinito. Determinar o vetor campo elétrico nos pontos situados sobre uma reta perpendicular ao fio. Dados do problema
Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II
 Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 010 Flávia Bastos
Nota de aula 9 - Estado Plano de Tensões - Resistência dos Materiais II Flávia Bastos (retirado da apostila do Prof. Elson Toledo) MAC - Faculdade de Engenharia - UFJF o. semestre de 010 Flávia Bastos
x = 4 2sen30 0 = 4 2(1/2) = 2 2 e y = 4 2 cos 30 0 = 4 2( 3/2) = 2 6.
 CURSO DE PRÉ CÁLCULO ONLINE - PET MATEMÁTICA / UFMG LISTA DE EXERCÍCIOS RESOLVIDOS: Exercício 1 Calcule o valor de x e y indicados na figura abaixo. Solução: No triângulo retângulo ABD, temos que AD mede
CURSO DE PRÉ CÁLCULO ONLINE - PET MATEMÁTICA / UFMG LISTA DE EXERCÍCIOS RESOLVIDOS: Exercício 1 Calcule o valor de x e y indicados na figura abaixo. Solução: No triângulo retângulo ABD, temos que AD mede
Apresentação da Disciplina MECÂNICA APLICADA. Prof. André Luis Christoforo.
 Objetivos da Estática: 01 Universidade Federal de São Carlos Departamento de Engenharia Civil - DECiv Apresentação da Disciplina MECÂNICA APICADA Prof. André uis Christoforo christoforoal@yahoo.com.br
Objetivos da Estática: 01 Universidade Federal de São Carlos Departamento de Engenharia Civil - DECiv Apresentação da Disciplina MECÂNICA APICADA Prof. André uis Christoforo christoforoal@yahoo.com.br
peso da barra: P = 15 N; comprimento do segmento AO: D A = 1 m; comprimento do segmento BO: D B = 0,5 m.
 Uma barra AOB homogênea de secção constante cujo peso é de 15 N é dobrada segundo um ângulo reto em O de maneira que AO = 1 m e BO = 0,5 m. Suspende-se a barra pelo ponto O, determinar: a) O ângulo α formado
Uma barra AOB homogênea de secção constante cujo peso é de 15 N é dobrada segundo um ângulo reto em O de maneira que AO = 1 m e BO = 0,5 m. Suspende-se a barra pelo ponto O, determinar: a) O ângulo α formado
Capítulo 2 Vetores. 1 Grandezas Escalares e Vetoriais
 Capítulo 2 Vetores 1 Grandezas Escalares e Vetoriais Eistem dois tipos de grandezas: as escalares e as vetoriais. As grandezas escalares são aquelas que ficam definidas por apenas um número real, acompanhado
Capítulo 2 Vetores 1 Grandezas Escalares e Vetoriais Eistem dois tipos de grandezas: as escalares e as vetoriais. As grandezas escalares são aquelas que ficam definidas por apenas um número real, acompanhado
Relações Material Propriedade
 - UNIVRSIDAD FDRAL FLUMINNS SCOLA D NGNHARIA INDUSTRIAL MTALÚRGICA D VOLTA RDONDA PROFSSORA: SALT SOUZA D OLIVIRA BUFFONI DISCIPLINA: RSISTÊNCIA DOS MATRIAIS Relações Material Propriedade Lei de Hooke
- UNIVRSIDAD FDRAL FLUMINNS SCOLA D NGNHARIA INDUSTRIAL MTALÚRGICA D VOLTA RDONDA PROFSSORA: SALT SOUZA D OLIVIRA BUFFONI DISCIPLINA: RSISTÊNCIA DOS MATRIAIS Relações Material Propriedade Lei de Hooke
CÁLCULO VETORIAL E GEOMETRIA ANALÍTICA
 04 CÁLCULO VETORIAL E GEOMETRIA ANALÍTICA CAPÍTULO 0 TRANSLAÇÃO E ROTAÇÃO DE EIXOS TRANSLAÇÃO DE EIXOS NO R Sejam e O os eixos primitivos, do Sistema Cartesiano de Eixos Coordenados com origem O(0,0).
04 CÁLCULO VETORIAL E GEOMETRIA ANALÍTICA CAPÍTULO 0 TRANSLAÇÃO E ROTAÇÃO DE EIXOS TRANSLAÇÃO DE EIXOS NO R Sejam e O os eixos primitivos, do Sistema Cartesiano de Eixos Coordenados com origem O(0,0).
6. Calcular as equações paramétricas de uma reta s que passa pelo ponto A(1, 1, 1) e é ortogonal x 2
 Lista 2: Retas, Planos e Distâncias - Engenharia Mecânica Professora: Elisandra Bär de Figueiredo x = 2 + 2t 1. Determine os valores de m para que as retas r : y = mt z = 4 + 5t sejam: (a) ortogonais (b)
Lista 2: Retas, Planos e Distâncias - Engenharia Mecânica Professora: Elisandra Bär de Figueiredo x = 2 + 2t 1. Determine os valores de m para que as retas r : y = mt z = 4 + 5t sejam: (a) ortogonais (b)
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2013-1 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2013-1 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
(atualizado em 12/07/2014)
 ENG285 4ª Unidade 1 (atualizado em 12/07/2014) Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para
ENG285 4ª Unidade 1 (atualizado em 12/07/2014) Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para
Capítulo 12. Ângulo entre duas retas no espaço. Definição 1. O ângulo (r1, r2 ) entre duas retas r1 e r2 é assim definido:
 Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
Capítulo 1 1. Ângulo entre duas retas no espaço Definição 1 O ângulo (r1, r ) entre duas retas r1 e r é assim definido: (r1, r ) 0o se r1 e r são coincidentes, se as retas são concorrentes, isto é, r1
ENG285 4ª Unidade 1. Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais.
 ENG285 4ª Unidade 1 Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para seção retangular: I =. Para
ENG285 4ª Unidade 1 Fonte: Arquivo da resolução da lista 1 (Adriano Alberto), Slides do Prof. Alberto B. Vieira Jr., RILEY - Mecânica dos Materiais. Momento de Inércia (I) Para seção retangular: I =. Para
Resistência dos Materiais. Aula 6 Estudo de Torção, Transmissão de Potência e Torque
 Aula 6 Estudo de Torção, Transmissão de Potência e Torque Definição de Torque Torque é o momento que tende a torcer a peça em torno de seu eixo longitudinal. Seu efeito é de interesse principal no projeto
Aula 6 Estudo de Torção, Transmissão de Potência e Torque Definição de Torque Torque é o momento que tende a torcer a peça em torno de seu eixo longitudinal. Seu efeito é de interesse principal no projeto
UNIVERSIDADE FEDERAL DE PERNAMBUCO
 CÁLCULO L1 NOTAS DA VIGÉSIMA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, consideraremos mais uma técnica de integração, que é conhecida como substituição trigonométrica. Esta técnica pode
CÁLCULO L1 NOTAS DA VIGÉSIMA AULA UNIVERSIDADE FEDERAL DE PERNAMBUCO Resumo. Nesta aula, consideraremos mais uma técnica de integração, que é conhecida como substituição trigonométrica. Esta técnica pode
Análise Vetorial na Engenharia Elétrica
 nálise Vetorial na Engenharia Elétrica ula 13/03/09 1.3 - Medida algébrica de um segmento Segmento: um segmento é determinado por um par ordenado d de pontos. figura 1.8 apresenta um segmento Figura 1.8
nálise Vetorial na Engenharia Elétrica ula 13/03/09 1.3 - Medida algébrica de um segmento Segmento: um segmento é determinado por um par ordenado d de pontos. figura 1.8 apresenta um segmento Figura 1.8
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I
 RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2012-2 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
RESISTÊNCIA DOS MATERIAIS II TORÇÃO PARTE I Prof. Dr. Daniel Caetano 2012-2 Objetivos Compreender o que é a deformação por torção Compreender os esforços que surgem devido à torção Determinar distribuição
Material by: Caio Guimarães (Equipe Rumoaoita.com) Referência: cadernos de aula: Professor Eduardo Wagner
 Material by: Caio Guimarães (Equipe Rumoaoita.com) Referência: cadernos de aula: Professor Eduardo Wagner 3 - Parábolas Definição 1.1: Dados um ponto no plano F e uma reta d no plano, é denominada Parábola
Material by: Caio Guimarães (Equipe Rumoaoita.com) Referência: cadernos de aula: Professor Eduardo Wagner 3 - Parábolas Definição 1.1: Dados um ponto no plano F e uma reta d no plano, é denominada Parábola
Controle de Obras Mecânica dos solos
 Controle de Obras Mecânica dos solos Diagrama de Mohr Critérios de ruptura 1 Considerações Preliminares: Forças em um ponto: - peso próprio - forças externas Várias forças agindo na massa do solo: 2 1
Controle de Obras Mecânica dos solos Diagrama de Mohr Critérios de ruptura 1 Considerações Preliminares: Forças em um ponto: - peso próprio - forças externas Várias forças agindo na massa do solo: 2 1
Sumário e Objectivos. Lúcia M.J.S. Dinis 2007/2008. Mecânica dos Sólidos Aula 5 1
 Sumário e Objectivos Sumário: Deformações sobre um plano. Valores Estacionários das Deformações. Compatibilidade das Deformações. Construção de Mohr para Deformações. Roseta de Extensómetros. Objectivos
Sumário e Objectivos Sumário: Deformações sobre um plano. Valores Estacionários das Deformações. Compatibilidade das Deformações. Construção de Mohr para Deformações. Roseta de Extensómetros. Objectivos
FUNÇÕES TRIGONOMÉTRICAS. Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica
 FUNÇÕES TRIGONOMÉTRICAS Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica Teorema de Pitágoras Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma
FUNÇÕES TRIGONOMÉTRICAS Teorema de Pitágoras Razões trigonométricas Circunferência trigonométrica Teorema de Pitágoras Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma
Cálculo Diferencial e Integral 2: Integrais Duplas
 Cálculo Diferencial e Integral 2: Integrais Duplas Jorge M. V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Integrais Duplas sobre Retângulos 2 3 Lembrete:
Cálculo Diferencial e Integral 2: Integrais Duplas Jorge M. V. Capela Instituto de Química - UNESP Araraquara, SP capela@iq.unesp.br Araraquara, SP - 2017 1 Integrais Duplas sobre Retângulos 2 3 Lembrete:
Física Geral Grandezas
 Física Geral Grandezas Grandezas físicas possuem um valor numérico e significado físico. O valor numérico é um múltiplo de um padrão tomado como unidade. Comprimento (m) Massa (kg) Tempo (s) Corrente elétrica
Física Geral Grandezas Grandezas físicas possuem um valor numérico e significado físico. O valor numérico é um múltiplo de um padrão tomado como unidade. Comprimento (m) Massa (kg) Tempo (s) Corrente elétrica
