AULA Exercícios. DETERMINAR A EXPRESSÃO GERAL E A MATRIZ DE UMA TL CONHECIDAS AS IMAGENS DE UMA BASE DO
|
|
|
- Flávio Ramalho Sequeira
- 6 Há anos
- Visualizações:
Transcrição
1 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno resolvendo os problemas apresentados na bibliografia sem consulta prévia das soluções propostas análise comparativa entre as suas resposta e a respostas propostas e posterior eposição junto do docente de todas as dúvidas associadas. ÓPICOS ercícios. UL. ercícios. DRMINR XPRSSÃO GRL MRIZ D UM L CONHCIDS S IMGNS D UM S DO SU DOMÍNIO.. Considere-se a transformação linear () ( ). Vamos determinar a epressão geral de isto é : R R tal que () ( ) e ( ) ( ) R Sendo e então logo () () Prof. José maral LG
2 Pelo que ( ) ficando assim determinada a epressão geral de : ( ) ( ).. Dada a transformação linear : R R tal que ( e ) ( ) e ( e ) ( ) escreva a matriz da transformação. Sendo a matriz canónica da transformação dada por [ e ) ( e )] imediato temos de (.. Seja : R R uma transformação linear tal que () () ( ) ( ) ( ) ( ) Determine a representação matricial de relativamente à base canónica de epressão de z ( ) ( z ) R. R e a Designando por a matriz canónica da transformação temos z ( ) ( z ) logo escrevendo a equação matricial das equações acima resulta Prof. José maral LG
3 I Sendo z ( ) ( z ) temos z z ( ) + z ( z + z).. Seja : R R uma transformação linear tal que ( ) ( ) () ( ) Justifique a eistência e unicidade da transformação. Determine a representação matricial de e a epressão de ( ) ( ) R. Uma aplicação linear cujo domínio é um espaço vectorial de dimensão finita fica perfeitamente definida quando se conhecem as imagens dos vectores de uma qualquer base desse domínio eistindo uma e só uma transformação que relaciona os dois conjuntos de vectores. Designando por a matriz canónica da transformação temos ( ) ( ) logo escrevendo a equação matricial das equações acima resulta Sendo ( ) ( ) temos Prof. José maral LG
4 Prof. José maral LG ( ) ( ) DRMINR MRIZ D UM L DD SU XPRSSÃO GRL.5. Seja ) ( f uma função de R R tal que + doptando a notação matricial podemos escrever e ainda função ) ( f considerada sendo uma transformação matricial é uma transformação linear ) ( sendo a matriz da transformação.6. Determine as matrizes canónicas das transformações ) ( ) ( ) ( ) ( + + ) ( ) ( + Conhecida a epressão analítica da transformação a determinação da matriz canónica da transformação é imediata. Para ) ( ) ( ) ( temos logo
5 Procedendo de modo análogo para ( ) ( + + ) temos: e para ) ( + ) (.7. Dada a transformação linear : R R definida por z ( ) (+ z z) screva a matriz da transformação em relação à base canónica de R. Designando por a matriz canónica da transformação temos z ( ) (+ z z) + z z z ( z ) Logo.8. Dada a transformação linear : R R definida por ( ) ( ) screva a matriz da transformação em relação à base canónica de {( )()( } R e à base de Usando a matriz calculada verifique se o vector ( ) pertence à imagem de. R Prof. José maral LG
6 Podemos começar por calcular a matriz canónica da transformação. emos ( ) ( ) Logo Podemos agora calcular a matriz da transformação em relação à base canónica de e à base de ( )()(. tendendo ao diagrama R { } R [ ] [ ] M [ ] temos pelo que [ ] [ ] M M [ ] ( M ) Dado que M tem por colunas os vectores da base {( )()( } escritos na base canónica temos M m alternativa e mais rapidamente podemos atender a que Prof. José maral LG
7 ( M ) M Resolvendo os dois sistemas de equações em simultâneo temos logo tenda-se a que o vector ( ) está escrito na base canónica. partir da matriz é imediato verificar que não pertence à imagem de dado que o sistema é impossível Para tirar conclusões utilizando a matriz atenda-se a que e pelo que [ ] [ ] [ ] M [ ] [ ] [ ] ( M ) [ ] [ ] [ ] M M Resolvendo o sistema tiraríamos a mesma conclusão (aliás o sistema é o mesmo dado que obviamente M e [ ] [ ]..9. Dada a transformação linear : R R definida por z ( ) ( + ) Prof. José maral LG
8 omando a mesma base no domínio e no contradomínio escreva a matriz da transformação em relação à base de R {( )( )( } tenda-se ao diagrama [ ] [ ] M M [ ] [ ] temos logo Sendo e pelo que temos [ ] [ ] ( ) [ ] [ ] M M ( M ) M ( M ) M M z ( ) ( + ) + z Prof. José maral LG
9 ( M ) M Note que a relação acima pode ser escrita na forma M M pelo que alternativamente temos resolvendo os sistemas de equações em simultâneo o mesmo resultado de modo mais epedito MISCLÂNS... m R e R é possível fazer uma representação geométrica simples do efeito da aplicação de uma transformação linear quer se considere que os pares ou ternos ordenados são representativos de pontos ou de vectores. m R n a interpretação do resultado da aplicação de uma transformação linear é idêntica embora a sua representação geométrica não seja possível. a) Seja : R R a transformação linear ( ) Figura. emos então transformação u e. Da aplicação da matriz da a qualquer objecto de R resulta uma imagem que corresponde ao seu simétrico relativamente ao eio dos ( ) ( ) Prof. José maral LG
10 b) Seja : R R a transformação linear ( ) u cos( θ) sen( θ) sen( θ) cos( θ) em que θ é um ângulo medido no sentido directo. Cada uma das colunas da matriz de transformação resulta da aplicação da transformação a cada um dos vectores da base canónica de R e e e cos( θ) sen( θ) [ ( ) ( ) ] sen( θ) cos( θ) e e emos assim que cos( θ) sen( θ) cos( θ) ( e ) sen() θ cos() θ sen() θ e cos( θ) sen( θ) sen( θ) ( e ) sen( θ) cos( θ) cos( θ) mbos os vectores da base canónica de R sofrem uma rotação de θ no sentido directo. m resultado da aplicação de uma transformação com matiz Figura. cos( θ) sen( θ) sen( θ) cos( θ) todos os objectos do plano sofrem uma rotação de θ no sentido directo. matriz é por isso chamada matriz de rotação em R... Considere o endomorfismo que tomando um vector ( z ) R o reflecte em relação ao plano z e depois o projecta ortogonalmente sobre o plano z (num referencial z ortonormado). screva a matriz de em relação à base canónica de R e determine todos os vectores ( z ) R tais que z ( ) ( ). Sendo em R a matriz de refleão em relação ao plano z e a matriz de projecção sobre o plano z Prof. José maral LG
11 temos z ( ) z z ( z) Os vectores ( z ) R tais que z ( ) ( ) são as soluções do sistema ou seja ( ) R. z.. Considere a transformação linear : R R que transforma o paralelogramo da figura a) no paralelogramo da figura b). Qual das seguintes matrizes pode ser a matriz da transformação em causa asta atender a que ( ) ( ) a) Ora sendo ( ) e e ( e) temos ( e ) pelo que das matrizes candidatas a única que pode ser a matriz da transformação em causa é a matriz. b) scolhendo dois vectores linearmente independentes por eemplo u () e u () temos ( u ) ( ) e ( u ) () pelo que sendo Prof. José maral LG
12 Prof. José maral LG [ ] [ ] u u u Genericamente [ ][ ] u u >> u[ ]'; >> u[ ]'; >> [- -]'; >> [ ]'; >> [ ]*inv([u u]) -/ -/ COMPOSIÇÃO D RNSFORMÇOS LINRS.. Sendo : R R uma refleão sobre o plano z u u u ) ( : S R R uma rotação de π θ sobre o eio do zz
13 v S( ) S cos( θ) sen( θ) sen( ) cos( ) θ θ U : R R uma epansão de k. 5 r U( v) v U.5.5 v.5 composição de U com S com r V ( u) U( S( ( u)) ( U S )( u) u é uma transformação linear V : R R com matriz de transformação V U S U ou seja S r V ( u) V u.5.5 u.5 Saliente-se que a composição de transformações lineares não é comutativa (basta atender ao facto de se efectuar à custa de um produto matricial)... Dada a transformação linear : R R definida por z ( ) ( + z + z z + ) Prof. José maral LG
14 screva a matriz da transformação em relação à base canónica de R. Considere a base {( )()( ) } de R e seja S : R R a transformação linear cuja matriz em relação à base e à base canónica de R é S Determine a epressão geral de S e determine ( S )( ). matriz da transformação em relação à base canónica de R sendo z ( ) ( + z + z z + ) + z + z z + z é matriz de mudança da base {( )()( ) } R é tendendo ao diagrama para a base canónica de M [ ] [ ] S M S [ ] temos Prof. José maral LG
15 ( ) S M S M S S M S S logo a matriz da transformação S em relação às bases canónicas de S MS ou seja a epressão geral de S é Sz ( ) S( z ) z ( + + z + ) R e R é Finalmente para ( S )( ) temos ( S )( ) S Prof. José maral LG
16 RNSFORMÇÃO LINR INVRS.5 Sendo : R R uma rotação de θ π sobre o eio do zz ( u) u cos( π ) sen( π ) sen( π ) cos( π ) u u a sua transformação inversa tem matriz de transformação u ( ) cos( π ) sen( π ) sen( π ) cos( π ) ou seja como seria de esperar uma rotação de θ π. MISCLÂN..6. Dada a transformação linear : R R tal que () () ( ) ( ) ( ) ( ) a) Determine a matriz que representa em relação às bases canónicas dos dois espaços e ainda a matriz que representa em relação à base canónica de R e à base de ( )( )( )( ). R { } b) Justifique que cada uma seguintes afirmações é verdadeira: b.) ( ) Img( ). b.) ( ) ker( ) b.) () ( ) b.) não é sobrejectiva nem injectiva. Prof. José maral LG
17 b.5) dim(img( )) c) Indique bases para ker( ) e Img( ). d) Determine z ( ) ( z ) R. a) m relação às bases canónicas dos dois espaços resulta directamente do enunciado para a matriz que representa : m relação à base canónica de R e à base de ( )( )( )( ) temos atendendo ao diagrama { } R [ ] [ ] M [ ] que Sendo temos: M ( M ) M M Prof. José maral LG
18 Pelo que resolvendo o sistema temos: M b) Qualquer das 5 alíneas pode ser respondida rapidamente por inspecção da definição da transformação linear. Dado que () () ( ) ( ) ( ) ( ) temos: b.) Logo ( ) Img( ). + + b.) Logo ( ) ker( ). + + b.) Prof. José maral LG
19 b.) transformação é injectiva sse Nuc( ) ( ) ker( ) logo não é injectiva.. Vimos em b.) que transformação é sobrejectiva sse dim(im( )) dim( ). Sendo : R R é: dim(im( )) n e dim( ) m logo a transformação não é sobrejectiva. b.5) Por inspecção da matriz é imediato que a a e a colunas são linearmente dependentes sendo independentes da a logo dim(img( )). c) Podemos calcular uma base para ker( ) procurado as soluções do sistema homogéneo. emos logo z z z O vector ( ) constitui uma base de ker( ) Podemos calcular uma base para Img( ) calculando uma base de col( ) lin( ). emos Os vectores ( ) e ( ) constituem uma base de Img( ). d) emos logo z z ( ) z z z + z ( z) ( z z + z) ( z) R Prof. José maral LG
AULA Exercícios. DETERMINAR A EXPRESSÃO GERAL E A MATRIZ DE UMA TL CONHECIDAS AS IMAGENS DE UMA BASE DO
 Note bem: a leitra destes apontamentos não dispensa de modo algm a leitra atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo alno resolvendo
Note bem: a leitra destes apontamentos não dispensa de modo algm a leitra atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo alno resolvendo
Ficha de Trabalho 08 Transformações Lineares. (Aulas 19 a 22).
 F I C H A D E R A B A L H O 0 8 Ficha de rabalho 08 ransformações Lineares. (Aulas 19 a ). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto
F I C H A D E R A B A L H O 0 8 Ficha de rabalho 08 ransformações Lineares. (Aulas 19 a ). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto
AULA Exercícios. DEMONSTRAR QUE UMA TRANSFORMAÇÃO É LINEAR Se A é uma matriz real m n e. u R, a aplicação T : R R tal que
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
AULA 13 { } 13. Exercícios. DETERMINAR UMA BASE DE UM SUBESPAÇO Determinar uma base do subespaço de
 Prof. Isabel Matos & José Amaral ALGA A - 6--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R ma ve que qualquer conjunto de
Prof. Isabel Matos & José Amaral ALGA A - 6--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R ma ve que qualquer conjunto de
AULA 13 { } 13. Exercícios. DETERMINAR UMA BASE DE UM SUBESPAÇO Determinar uma base do subespaço de
 Prof. Isabel Matos & José Amaral ALGA A - 8--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R W ma ve que qualquer conjunto
Prof. Isabel Matos & José Amaral ALGA A - 8--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R W ma ve que qualquer conjunto
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Ficha de Trabalho 06 e 07
 Ficha de rabalho 06 e 07 Produto Interno. (Aulas 1 a 18). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto interno. Norma. Desigualdade de
Ficha de rabalho 06 e 07 Produto Interno. (Aulas 1 a 18). Produto interno em R n. Vectores livres: Ângulo de dois vectores. Vectores ortogonais. Vectores em R n : Produto interno. Norma. Desigualdade de
Resolução do 1 o Teste - A (6 de Novembro de 2004)
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Ano Lectivo de 2004/2005 Resolução do 1 o Teste - A (6 de Novembro de 2004) 1 Considere o subconjunto
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Ano Lectivo de 2004/2005 Resolução do 1 o Teste - A (6 de Novembro de 2004) 1 Considere o subconjunto
AULA 13 { } 13. Exercícios. DETERMINAR UMA BASE DE UM SUBESPAÇO Determinar uma base do subespaço de
 Prof Isabel Matos & José Amaral ALGA A3-7--8 3 ercícios DTRMINAR MA BAS D M SBSPAÇO 3 Determinar uma base do subespaço de 4 R { } 4 3 4 (,,, ) (,,, ) : ( ) ( ) L u u u u R ma ve que qualquer conjunto de
Prof Isabel Matos & José Amaral ALGA A3-7--8 3 ercícios DTRMINAR MA BAS D M SBSPAÇO 3 Determinar uma base do subespaço de 4 R { } 4 3 4 (,,, ) (,,, ) : ( ) ( ) L u u u u R ma ve que qualquer conjunto de
Lista 6: transformações lineares.
 Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
Lista 6: transformações lineares. 1) Diga, justificando, quais das seguintes funções constituem transformações lineares. a) T : R 2 R 2 tal que T (x 1, x 2 ) = (x 1 + x 2, 3x 1 x 2 ) b) T : R 2 R 2 tal
1. Considere a seguinte matriz dos vértices dum triângulo D = 0 2 3
 INSTITUTO SUPERIOR TÉCNICO - DEPARTAMENTO DE MATEMÁTICA 7 a LISTA DE PROBLEMAS E EXERCÍCIOS DE ÁLGEBRA LINEAR LEIC-Taguspark, LERCI, LEGI, LEE 1 o semestre 2006/07 - aulas práticas de 2006-12-04 e 2006-12-06
INSTITUTO SUPERIOR TÉCNICO - DEPARTAMENTO DE MATEMÁTICA 7 a LISTA DE PROBLEMAS E EXERCÍCIOS DE ÁLGEBRA LINEAR LEIC-Taguspark, LERCI, LEGI, LEE 1 o semestre 2006/07 - aulas práticas de 2006-12-04 e 2006-12-06
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
Nota de aula: Transformações Lineares
 Nota de aula: Transformações Lineares Prof. Rebello out/99 rev. out/ São aplicações entre espaços vetoriais, isto é, funções onde tanto o domínio como o contra domínio são espaços vetoriais, portanto todas
Nota de aula: Transformações Lineares Prof. Rebello out/99 rev. out/ São aplicações entre espaços vetoriais, isto é, funções onde tanto o domínio como o contra domínio são espaços vetoriais, portanto todas
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução da Repetição do 2º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 2º Teste 30 de Junho de 2014 Ano Lectivo: 2013-2014 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 2º Teste 30 de Junho de 2014 Ano Lectivo: 2013-2014 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç ALGA Álgebra
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do 2º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 2º Teste 11 de Junho de 2013 Ano Lectivo: 2012-2013 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 2º Teste 11 de Junho de 2013 Ano Lectivo: 2012-2013 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
ÁLGEBRA LINEAR A FICHA 2
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral
 Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Módulo 9 ALGA I. Operadores auto-adjuntos (simétricos e hermitianos). Teorema espectral Contents 9.1 Operadores auto-adjuntos (simétricos e hermitianos) 136 9. Teorema espectral para operadores auto-adjuntos...........
Álgebra Linear - Exercícios resolvidos
 Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
AULA Exercícios O sistema de equações lineares. tem a matriz completa. , pelo que
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
Nota de aula: Transformações Lineares
 Nota de aula: Transformações Lineares Prof. Rebello out/99 rev. mai/0 São aplicações entre espaços vetoriais, isto é, funções onde tanto o domínio como o contra domínio são espaços vetoriais, portanto
Nota de aula: Transformações Lineares Prof. Rebello out/99 rev. mai/0 São aplicações entre espaços vetoriais, isto é, funções onde tanto o domínio como o contra domínio são espaços vetoriais, portanto
ficha 6 espaços lineares com produto interno
 Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
TRANSFORMAÇÕES LINEARES
 1 TRANSFORMAÇÕES LINEARES Cristianeguedes.pro.br/cefet Transformação Linear 2 Definição: Sejam U e V dois espaços vetoriais reais. Uma função T (ou aplicação) é denominada Transformação Linear de U em
1 TRANSFORMAÇÕES LINEARES Cristianeguedes.pro.br/cefet Transformação Linear 2 Definição: Sejam U e V dois espaços vetoriais reais. Uma função T (ou aplicação) é denominada Transformação Linear de U em
Introdução à Geometria
 Introdução à Geometria - 2007-2008 Algumas noções 1. Norma de um vector Seja E um espaço vectorial real de dimensão finita E munido de um produto interno (u, v) u v. Dado um vector v E chama-se norma ou
Introdução à Geometria - 2007-2008 Algumas noções 1. Norma de um vector Seja E um espaço vectorial real de dimensão finita E munido de um produto interno (u, v) u v. Dado um vector v E chama-se norma ou
Ficha de Trabalho 09 e 10
 Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
AULA Exercícios. VERIFICAR SE UM VECTOR É UMA COMBINAÇÃO LINEAR DE UM CONJUNTO DE VECTORES.
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Indicação de uma possível resolução do exame
 Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
GAAL - Terceira Prova - 15/junho/2013. Questão 1: Analise se a afirmação abaixo é falsa ou verdadeira:
 GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
GAAL - Terceira Prova - /junho/3 SOLUÇÕES Questão : Analise se a afirmação abaio é falsa ou verdadeira: [ A matriz A é diagonalizável SOLUÇÃO: Sabemos que uma matriz n n é diagonalizável se ela possuir
TÓPICOS. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -1
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do Exame (Época de Recurso) 15 de Julho de 2015; 10:00 Ano Lectivo: 2014-2015 Semestre: Verão Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 006/07 5 a Lista: Ortogonalidade Nos exercícios em que n~ao é especificado o produto interno, considere o produto interno
Álgebra Linear e Geometria Analítica em R 3
 Módulo 2 Álgebra Linear e Geometria Analítica em R 3 Neste segundo módulo vamos generalizar os conceitos aprendidos no módulo 1, e também no ensino secundário, estudando Álgebra Linear e Geometria Analítica
Módulo 2 Álgebra Linear e Geometria Analítica em R 3 Neste segundo módulo vamos generalizar os conceitos aprendidos no módulo 1, e também no ensino secundário, estudando Álgebra Linear e Geometria Analítica
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
TÓPICOS. Exercícios. Determinando a matriz escalonada reduzida equivalente
 Note bem: a leitra destes apontamentos não dispensa de modo algm a leitra atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo alno resolvendo
Note bem: a leitra destes apontamentos não dispensa de modo algm a leitra atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo alno resolvendo
Aplicação da Álgebra Linear à Geometria (1/2) 1. Geometria a m: rectas e planos
 30 a : aula (1h) 19/05/2010 Aplicação da Álgebra Linear à Geometria (1/2) 30-1 Instituto Superior Técnico 2010 2 o semestre Álgebra Linear 1 o ano das Lics em Engenharia Informática e de Computadores e
30 a : aula (1h) 19/05/2010 Aplicação da Álgebra Linear à Geometria (1/2) 30-1 Instituto Superior Técnico 2010 2 o semestre Álgebra Linear 1 o ano das Lics em Engenharia Informática e de Computadores e
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
10 a Lista de Exercícios
 Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores
 Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores Teoria dos Sinais e dos Sistemas O procedimento de Gram-Schmidt: definição, exemplos e aplicações Artur Ferreira {arturj@isel.pt}
Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores Teoria dos Sinais e dos Sistemas O procedimento de Gram-Schmidt: definição, exemplos e aplicações Artur Ferreira {arturj@isel.pt}
Matriz de mudança de coordenadas: S B1!B 2. (como se faz e para que serve) transformação linear. (como se faz e para que serve)
 Matriz de mudança de coordenadas: S B!B (como se faz e para que serve) Transformação linear A matriz de T em relação às bases B e B 0 : M(T ; B; B 0 ) (como se faz e para que serve) As 3 formas (equivalentes)
Matriz de mudança de coordenadas: S B!B (como se faz e para que serve) Transformação linear A matriz de T em relação às bases B e B 0 : M(T ; B; B 0 ) (como se faz e para que serve) As 3 formas (equivalentes)
Instituto Politécnico de Bragança Escola Superior de Tecnologia e Gestão. Análise Matemática I 2003/04
 Instituto Politécnico de Bragança Escola Superior de Tecnologia e Gestão Análise Matemática I 00/0 Ficha Prática nº Parte III Função Eponencial Função Logaritmo Funções trigonométricas directas e inversas
Instituto Politécnico de Bragança Escola Superior de Tecnologia e Gestão Análise Matemática I 00/0 Ficha Prática nº Parte III Função Eponencial Função Logaritmo Funções trigonométricas directas e inversas
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS COIMBRA 12º ANO DE ESCOLARIDADE MATEMÁTICA A
 ESCOLA SECUNDÁRIA COM º CICLO D. DINIS COIMBRA º ANO DE ESCOLARIDADE MATEMÁTICA A Tarefa nº do plano de trabalho nº 7. Considere a função f() -. a. Encontre a epressão analítica da função inversa de f.
ESCOLA SECUNDÁRIA COM º CICLO D. DINIS COIMBRA º ANO DE ESCOLARIDADE MATEMÁTICA A Tarefa nº do plano de trabalho nº 7. Considere a função f() -. a. Encontre a epressão analítica da função inversa de f.
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:
![1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com: 1. Matrizes. 1. Dê um exemplo, em cada alínea, de uma matriz A = [a ij ] m n com:](/thumbs/68/59802332.jpg) Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
Matemática Licenciatura em Biologia 4 / 5. Matrizes.. Dê um eemplo, em cada alínea, de uma matriz A = [a ij ] m n com: m =, n = cuja soma das entradas principais seja. (b) m = n = 4 com a a e a 4 = a 4.
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 2012/2013
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do Exame (Época Normal) 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
ÁLGEBRA LINEAR E GEOMERIA ANALÍICA Resolução do Exame (Época Normal) 04 de Fevereiro de 2015; 19:00 Ano Lectivo: 2014-2015 Semestre: Inverno Aceda aqui à página de ALGA ISEL è ADMat Secção de Álgebra ç
RESISTÊNCIA DOS MATERIAIS II MOMENTO DE INÉRCIA
 RESISTÊNCIA DOS MATERIAIS II MOMENTO DE INÉRCIA Prof. Dr. Daniel Caetano 2013-2 Objetivos Apresentar os conceitos: Momento de inércia Momento polar de inércia Produto de Inércia Eios Principais de Inércia
RESISTÊNCIA DOS MATERIAIS II MOMENTO DE INÉRCIA Prof. Dr. Daniel Caetano 2013-2 Objetivos Apresentar os conceitos: Momento de inércia Momento polar de inércia Produto de Inércia Eios Principais de Inércia
Preparação para o Cálculo
 Preparação para o Cálculo Referencial cartesiano Representação gráfica Um referencial cartesiano é constituído por duas rectas perpendiculares (fias), com ponto de intersecção O: O diz-se a origem do referencial;
Preparação para o Cálculo Referencial cartesiano Representação gráfica Um referencial cartesiano é constituído por duas rectas perpendiculares (fias), com ponto de intersecção O: O diz-se a origem do referencial;
Nota: Turma: MA 327 Álgebra Linear. Terceira Prova. Boa Prova! Primeiro Semestre de T o t a l
 Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
Turma: Nota: MA 327 Álgebra Linear Primeiro Semestre de 26 Terceira Prova Nome: RA: Questões Pontos Questão 1 Questão 2 Questão 3 Questão 4 Questão 5 T o t a l Boa Prova! Questão 1. 2. Pontos) Seja U um
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL REGIME NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA º FREQUÊNCIA de Janeiro de 8 Duração:
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL REGIME NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA º FREQUÊNCIA de Janeiro de 8 Duração:
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Colectânea de Exercícios
 ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - o Ano 08 - Época especial Proposta de resolução Caderno... Como A e B são acontecimentos equiprováveis, temos que P A P B E como A e B são acontecimentos independentes,
Prova Escrita de MATEMÁTICA A - o Ano 08 - Época especial Proposta de resolução Caderno... Como A e B são acontecimentos equiprováveis, temos que P A P B E como A e B são acontecimentos independentes,
Apontamentos III. Espaços euclidianos. Álgebra Linear aulas teóricas. Lina Oliveira Departamento de Matemática, Instituto Superior Técnico
 Apontamentos III Espaços euclidianos Álgebra Linear aulas teóricas 1 o semestre 2017/18 Lina Oliveira Departamento de Matemática, Instituto Superior Técnico Índice Índice i 1 Espaços euclidianos 1 1.1
Apontamentos III Espaços euclidianos Álgebra Linear aulas teóricas 1 o semestre 2017/18 Lina Oliveira Departamento de Matemática, Instituto Superior Técnico Índice Índice i 1 Espaços euclidianos 1 1.1
Cap. 0. Cálculo tensorial
 Cap. 0. Cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores. Álgebra tensorial 3. ensores cartesianos em D simétricos
Cap. 0. Cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores. Álgebra tensorial 3. ensores cartesianos em D simétricos
2º Teste de Mecânica Aplicada II
 MEAer / MEMEc / LEAN Ano Lectivo de 2012/2013 Instituto Superior Técnico 23 de Abril de 2013 2º Teste de Mecânica Aplicada II Este teste é constituído por 3 problemas e tem a duração de uma hora e meia.
MEAer / MEMEc / LEAN Ano Lectivo de 2012/2013 Instituto Superior Técnico 23 de Abril de 2013 2º Teste de Mecânica Aplicada II Este teste é constituído por 3 problemas e tem a duração de uma hora e meia.
Resolução do efólio B
 Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
J. Delgado - K. Frensel - L. Crissaff Geometria Analítica e Cálculo Vetorial
 178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
178 Capítulo 10 Equação da reta e do plano no espaço 1. Equações paramétricas da reta no espaço Sejam A e B dois pontos distintos no espaço e seja r a reta que os contém. Então, P r existe t R tal que
Prova Escrita de MATEMÁTICA A - 12o Ano Época especial
 Prova Escrita de MATEMÁTICA A - o Ano 08 - Época especial Proposta de resolução Caderno... Como A e B são acontecimentos equiprováveis, temos que P A P B E como A e B são acontecimentos independentes,
Prova Escrita de MATEMÁTICA A - o Ano 08 - Época especial Proposta de resolução Caderno... Como A e B são acontecimentos equiprováveis, temos que P A P B E como A e B são acontecimentos independentes,
Produto interno, externo e misto
 Produto interno, externo e misto Definição: Chama-se norma (ou comprimento) do vector u ao comprimento do segmento de recta [OP ] e representa-se por u. Definição: Sejam a = OA e b = OB dois vectores não
Produto interno, externo e misto Definição: Chama-se norma (ou comprimento) do vector u ao comprimento do segmento de recta [OP ] e representa-se por u. Definição: Sejam a = OA e b = OB dois vectores não
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Esmeralda Sousa Dias. (a) (b) (c) Figura 1: Ajuste de curvas a um conjunto de pontos
 Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
Universidade de Aveiro Departamento de Electrónica, Telecomunicações e Informática. Transformações 2D
 Universidade de Aveiro Departamento de Electrónica, Telecomunicações e Informática Transformações 2D Computação Visual Beatriz Sousa Santos, Joaquim Madeira Transformações 2D Posicionar, orientar e escalar
Universidade de Aveiro Departamento de Electrónica, Telecomunicações e Informática Transformações 2D Computação Visual Beatriz Sousa Santos, Joaquim Madeira Transformações 2D Posicionar, orientar e escalar
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 2018
 GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
Um curso rápido de ALGA apenas em R 2
 Módulo 1 Um curso rápido de ALGA apenas em R 2 Neste primeiro módulo vamos retomar alguns conceitos ensinados no ensino secundário, e fazer uma ponte para os assuntos mais sofisticados que precisamos de
Módulo 1 Um curso rápido de ALGA apenas em R 2 Neste primeiro módulo vamos retomar alguns conceitos ensinados no ensino secundário, e fazer uma ponte para os assuntos mais sofisticados que precisamos de
EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003. Funções reais de várias variáveis
 EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003 Funções reais de várias variáveis 1. Faça um esboço de alguns conjuntos de nível das seguintes funções: (a) f (x,y) = 1 + x + 3y, (x,y)
EXERCÍCIOS DE ELEMENTOS DE MATEMÁTICA II (BQ, CTA, EFQ, Q) 2002/2003 Funções reais de várias variáveis 1. Faça um esboço de alguns conjuntos de nível das seguintes funções: (a) f (x,y) = 1 + x + 3y, (x,y)
Álgebra Linear I - Aula Bases Ortonormais e Matrizes Ortogonais
 Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Álgebra Linear I - Aula 19 1. Bases Ortonormais e Matrizes Ortogonais. 2. Matrizes ortogonais 2 2. 3. Rotações em R 3. Roteiro 1 Bases Ortonormais e Matrizes Ortogonais 1.1 Bases ortogonais Lembre que
Produto interno, externo e misto de vectores
 MTDI I - 00/08 - Produto Interno Produto interno, externo e misto de vectores A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass.
MTDI I - 00/08 - Produto Interno Produto interno, externo e misto de vectores A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass.
Produto interno no espaço vectorial R n
 ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
Matemática. Lic. em Enologia, 2009/2010
 Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
7 Formas Quadráticas
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
AULA Transformações lineares de R n em R m Composição de transformações lineares.
 Note bem: a leitra destes apotametos ão dispesa de modo algm a leitra ateta da bibliografia pricipal da cadeira Chama-se a ateção para a importâcia do trabalho pessoal a realizar pelo alo resoledo os problemas
Note bem: a leitra destes apotametos ão dispesa de modo algm a leitra ateta da bibliografia pricipal da cadeira Chama-se a ateção para a importâcia do trabalho pessoal a realizar pelo alo resoledo os problemas
7 Formas Quadráticas
 Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Prova Escrita de MATEMÁTICA A - 12o Ano a Fase
 Prova Escrita de MATEMÁTICA A - o Ano 006 - a Fase Proposta de resolução GRUPO I. Como, pela observação da figura podemos constatar que os gráficos das duas funções se intersetam num ponto de ordenada
Prova Escrita de MATEMÁTICA A - o Ano 006 - a Fase Proposta de resolução GRUPO I. Como, pela observação da figura podemos constatar que os gráficos das duas funções se intersetam num ponto de ordenada
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Aula Orientação do espaço. Observação 1
 Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
Aula 14 Nesta aula vamos definir dois novos produtos entre vetores do espaço, o produto vetorial e o produto misto. Para isso, primeiro vamos apresentar o conceito de orientação. 1. Orientação do espaço
Lista de Exercícios de Cálculo 3 Primeira Semana
 Lista de Exercícios de Cálculo 3 Primeira Semana Parte A 1. Se v é um vetor no plano que está no primeiro quadrante, faz um ângulo de π/3 com o eixo x positivo e tem módulo v = 4, determine suas componentes.
Lista de Exercícios de Cálculo 3 Primeira Semana Parte A 1. Se v é um vetor no plano que está no primeiro quadrante, faz um ângulo de π/3 com o eixo x positivo e tem módulo v = 4, determine suas componentes.
Bases de subespaços. 5 a : aula prática (1.30h) e 08-04/2010 Bases de subespaços 5-1
 a : aula prática (.h) - e 8-/ Bases de subespaços - Instituto Superior Técnico o semestre Álgebra Linear o ano da Lics.em Engenharia Informática e de Computadores e Engenharia Química Bases de subespaços
a : aula prática (.h) - e 8-/ Bases de subespaços - Instituto Superior Técnico o semestre Álgebra Linear o ano da Lics.em Engenharia Informática e de Computadores e Engenharia Química Bases de subespaços
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial
 TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Exercícios de Cálculo p. Informática, Ex 1-1 Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar
 Eercícios de Cálculo p. Informática, 2006-07 Números Reais. E - Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar o número dado: 7 a) b) 6 7 c) 2.(3) = 2.33 d) 2 3 e)
Eercícios de Cálculo p. Informática, 2006-07 Números Reais. E - Nas alíneas seguintes use os termos inteiro, racional, irracional, para classificar o número dado: 7 a) b) 6 7 c) 2.(3) = 2.33 d) 2 3 e)
4. Tensores cartesianos em 3D simétricos
 4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
GAAL - Exame Especial - 12/julho/2013. Questão 1: Considere os pontos A = (1, 2, 3), B = (2, 3, 1), C = (3, 1, 2) e D = (2, 2, 1).
 GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
GAAL - Exame Especial - /julho/3 SOLUÇÕES Questão : Considere os pontos A = (,, 3), B = (, 3, ), C = (3,, ) e D = (,, ) (a) Chame de α o plano que passa pelos pontos A, B e C e de β o plano que passa pelos
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
TRANSFORMAÇÕES LINEARES
 ransformação Linear RNSFORMÇÕES LINERES Sejam e espaços vetoriais reais Dizemos que uma função : é uma transformação linear se a função preserva as operações de adição e de multiplicação por escalar, isto
ransformação Linear RNSFORMÇÕES LINERES Sejam e espaços vetoriais reais Dizemos que uma função : é uma transformação linear se a função preserva as operações de adição e de multiplicação por escalar, isto
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
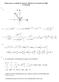 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Problemas de Álgebra Linear
 Problemas de Álgebra Linear Curso: Engenharia Aeroespacial o Semestre 203/204 Prof Paulo Pinto http://wwwmathistutlpt/ ppinto/ Conteúdo Sistemas de equações lineares e álgebra matricial Álgebra de matrizes
Problemas de Álgebra Linear Curso: Engenharia Aeroespacial o Semestre 203/204 Prof Paulo Pinto http://wwwmathistutlpt/ ppinto/ Conteúdo Sistemas de equações lineares e álgebra matricial Álgebra de matrizes
