Ficha de Exercícios nº 3
|
|
|
- Arthur Vidal de Almada
- 7 Há anos
- Visualizações:
Transcrição
1 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação linear? a). b). c) 0 1. d) ( ). 2 Qual das seguintes afirmações é verdadeira? a) Uma transformação linear de domínio pode ter como contradomínio um conjunto constituído apenas por um vector não nulo. b) A aplicação que transforma cada objecto na soma das suas imagens segundo duas transformações lineares é uma transformação linear. c) A intersecção dos conjuntos de imagens de duas transformações lineares com domínio e o mesmo espaço de chegada pode ser. d) Todas as transformações lineares com o mesmo espaço de partida e espaço de chegada são invertíveis. 3 T e f são duas transformações lineares, de para, cujas matrizes de transformação, na base canónica, são comutativas. Qual das seguintes afirmações é necessariamente verdadeira? a) T e f têm os mesmos valores próprios. b) Os núcleos de T e f são o mesmo. c) As transformações compostas Tof e fot são iguais. d) T e f são transformações inversas. 1
2 Ficha de Exercícios nº 3 4 O espaço próprio associado a um valor próprio de uma transformação linear T, cuja matriz de transformação na base canónica é diagonalizável, é *+. Das seguintes, qual pode ser a imagem de segundo T, escrita numa base de vectores próprios de T? a). b). c). d). 5 T e f são duas transformações lineares, de para, cujos valores próprios são reais. O que pode garantidamente afirmar sobre a transformação composta Tof? a) Pode não ser uma transformação linear. b) A sua matriz de transformação na base canónica não é diagonalizável. c) É a mesma transformação que fot. d) Os vectores próprios comuns a T e a f são seus vectores próprios. 6 é uma matriz diagonalizável, cujos valores próprios são reais. O que pode garantidamente afirmar sobre A? a) É simétrica. b) Todos os seus valores próprios têm multiplicidade algébrica 1. c) Tem determinante diferente de 0. d) Pode ter um único valor próprio distinto. 7 T é uma transformação linear, cuja matriz de transformação na base canónica, A, comuta com uma matriz não singular, V, cujas colunas são vectores próprios de A. O que pode garantidamente afirmar sobre A? a) É não singular. b) É ortogonal. c) É diagonal. d) É idempotente. 2
3 Ficha de Exercícios nº 3 8 Qual das seguintes afirmações é verdadeira? a) Uma forma quadrática pode ser semi-definida positiva e semi-definida negativa. b) Se a matriz associada a uma forma quadrática for o quadrado de uma outra matriz, a forma quadrática pode ser definida negativa. c) Se a matriz associada a uma forma quadrática for singular, a forma quadrática pode ser definida positiva. d) Se uma forma quadrática não envolver termos cruzados, não pode ser semidefinida positiva, nem semi-definida negativa. 9 Q é uma forma quadrática não nula cuja matriz associada é idempotente. Qual é, garantidamente, a classificação de Q? a) Definida positiva. b) Semi-definida positiva. c) Indefinida. d) Definida negativa. 10 Q é a forma quadrática que representa, para cada vector de, o quadrado da soma das suas coordenadas. Qual das seguintes mudanças de variável não permite representar Q sem termos cruzados? a). /. b). /. c). /. d). /. 3
4
5 Nova School of Business and Economics Álgebra Linear Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação linear? a). A resposta é incorrecta: Linear na soma: [ ] Linear na multiplicação por números reais: : (. ), (. ). Conclusão: T é uma transformação linear. b). A resposta é incorrecta: Linear na soma: [ ] Linear na multiplicação por números reais: : (. ),. - 1
6 ... (. ). Conclusão: T é uma transformação linear. c) 0 1. A resposta é incorrecta: 0 1 Linear na soma:, - [ ] [ ] [ ] [ ] Linear na multiplicação por números reais: : (. ), (. ). Conclusão: T é uma transformação linear. d) ( ). A resposta é correcta: ( ) Linear na soma:, -, -, -, -, -, -, -, - Linear na multiplicação por números reais: : 2
7 ,. -,. -., -., -.,. -., - Conclusão: T não é uma transformação linear. Resposta correcta: d) 2 Qual das seguintes afirmações é verdadeira? a) Uma transformação linear de domínio pode ter como contradomínio um conjunto constituído apenas por um vector não nulo. A afirmação é falsa. Se uma transformação, T, tiver domínio e como contra-domínio o conjunto * +,, então a imagem de todos os seus objectos é a mesma,. Se isto acontecer, T não é uma transformação linear: Linear na soma: Linear na multiplicação por números reais: : (. )... (. ). Conclusão: T não é uma transformação linear. b) A aplicação que transforma cada objecto na soma das suas imagens segundo duas transformações lineares é uma transformação linear. A afirmação é verdadeira. Basicamente, é preciso provar que a soma de duas transformações lineares é uma transformação linear. Chamemos a duas transformações lineares quaisquer e. A sua soma, T, é uma aplicação que a cada objecto comum a e, x, faz corresponder um outro vector,, que é a soma das imagens de x segundo e, ou seja,. Vamos provar que, sendo e transformações lineares, ou seja, lineares na soma e lineares na multiplicação por números reais, T também é:, e transformações lineares 3
8 4 Linear na soma:, Linear na multiplicação por números reais: : (. ) (. ) (. )...., -.. (. ). Conclusão: T é uma transformação linear. c) A intersecção dos conjuntos de imagens de duas transformações lineares com domínio e o mesmo espaço de chegada pode ser. A afirmação é falsa. Todas as transformações lineares com domínio têm como objecto o vector nulo deste espaço. E a imagem do vector nulo, segundo qualquer transformação linear, é o vector nulo do espaço de chegada. De facto: ( ) (. ). Mas se duas transformações lineares contêm, nos conjunto das suas imagens, o vector nulo do seu espaço de chegada, a intersecção destes conjuntos não pode ser o conjunto vazio, já que inclui este vector nulo. d) Todas as transformações lineares com o mesmo espaço de partida e espaço de chegada são invertíveis. A afirmação é falsa. Se uma transformação é invertível, então os seus espaços de partida e de chegada são iguais, pois caso contrário será impossível definir uma transformação que a cada vector do espaço de chegada da transformação original faça corresponder o vector do espaço de partida que lhe deu origem. Mas se o espaço de partida e o espaço de chegada de uma transformação forem o mesmo, não é garantido que a transformação seja invertível. Basta pensar na transformação, de para, definida por. Nesta transformação, qualquer vector de tem a mesma imagem,, o que significa que T não é injectiva (porque tem pelo menos 2 objectos com a mesma imagem). Não sendo injectiva, não é invertível. De facto, se existisse, teria que ter, como imagem de, o objecto que o originou segundo T. Mas, no caso desta transformação linear, não houve um objecto único a originar, mas uma infinidade de vectores: todos os de. Logo, segundo, o vector teria que ter mais do que uma imagem, o que é incompatível com o facto de ser uma transformação. Por outro lado, sabemos que, se uma transformação T tiver inversa,, então as matrizes de transformação destas duas transformações, na mesma base, são inversas. Mas se A, a matriz de transformação de T na
9 base canónica não tiver inversa, não existe matriz de transformação de canónica, o que significa que não existe. De facto: na base * +, Resposta correcta: b) 3 T e f são duas transformações lineares, de para, cujas matrizes de transformação, na base canónica, são comutativas. Qual das seguintes afirmações é necessariamente verdadeira? a) T e f têm os mesmos valores próprios. b) Os núcleos de T e f são o mesmo. c) As transformações compostas Tof e fot são iguais. d) T e f são transformações inversas. A transformação composta Tof é a transformação que calcula imagens em 2 etapas. Primeiro, faz corresponder a cada objecto de f uma imagem segundo esta transformação. Depois, trata cada uma destas imagens como objectos de T e faz-lhes corresponder a sua imagem segundo T:, - A transformação composta fot usa T e f por outra ordem. Primeiro, transforma cada objecto de T na sua imagem segundo esta transformação e depois transforma o vector resultante na sua imagem segundo f:, - Chamemos a A e B as matrizes de transformação de T e f, respectivamente, na base canónica. Matricialmente, podemos descrever o processo Tof da seguinte forma: cada vector x é multiplicado, à esquerda, por B, para se obter a sua imagem segundo f, o vector Bx. Depois, este vector é multiplicado, à esquerda, por A, para se obter a sua imagem segundo T. O vector obtido no final do processo é ABx. Assim,. Já o processo fot segue os seguintes passos, na forma matricial: cada vector x é multiplicado por A, à esquerda, originando a sua imagem segundo T, o vector Ax, que depois é multiplicado por B, à esquerda, para que se encontre a sua imagem segundo f, gerando-se no fim o vector BA. Logo,. Mas se A e B são comutativas, sabemos que a ordem pela qual são 5
10 multiplicadas é irrelevante para o resultado obtido, pelo que. Mas isto signfica que e as transformações compostas Tof e fot são iguais. Resposta correcta: c) 4 O espaço próprio associado a um valor próprio de uma transformação linear T, cuja matriz de transformação na base canónica é diagonalizável, é *+. Das seguintes, qual pode ser a imagem de segundo T, escrita numa base de vectores próprios de T? a). b). c). d). Se T tem como vectores próprios associados a um valor próprio o conjunto de múltiplos de, então T é uma transformação linear de para. Sendo a sua matriz de transformação na base canónica, chamemos-lhe A, é diagonalizável, sabemos que podemos encontrar uma base do seu espaço de partida,, constituída por vectores próprios de A, sendo que o número de vectores próprios associados a cada valor próprio, de entre os escolhidos, é igual à multiplicidade (geométrica ou algébrica, neste caso é irrelvante, porque, sendo A diagonalizável, são iguais) desse valor próprio. Sendo o espaço próprio (conjunto de vectores próprios) associado a um valor próprio de A, chamemos-lhe, *+, sabemos que a multiplicidade (algébrica e geométrica) de é 1, tal como a dimensão de *+. Assim, ao formarmos uma base de constituída por vectores próprios de A, temos que escolher um vector não nulo pertencente a *+, ou seja, um múltiplo de, que podemos designar genericamente como.,. Chamando V a esta base, sabemos que *. +, sendo e vectores próprios associado aos outros (ou outro) vectores próprios de A (claro que o vector. pode estar noutra ordem, mas tem sempre que pertencer a V). Sendo um vector próprio de T associado a, sabemos que a sua imagem, na base canónica, é o múltiplo de resultante da multiplicação de por :. Queremos agora saber as suas coordenadas na base V. Para isso, temos que saber como escrevê-lo como uma combinação linear dos vectores da base V, ou seja, temos que encontrar os valores únicos de, e (únicos porque V é uma base de, o que significa que há apenas uma combinação linear dos seus vectores que permite gerar cada vector deste espaço) que resolvem a seguinte equação:.,. - 6
11 Uma solução para esta equação é óbvia:, e. Sendo e V uma base de, sabemos faz sentido e é a única. Desta forma, as coordenadas de. na base V são. /, que dependem do valor próprio e do múltiplo de escolhido para formar a base V. Logo, de entre as hipóteses de resposta, a única possível é. Note-se que estas coordenadas apenas são possíveis se, aquando da formação da base V, se escolher o múltiplo do como 1º vector. Resposta correcta: c) 5 T e f são duas transformações lineares, de para, cujos valores próprios são reais. O que pode garantidamente afirmar sobre a transformação composta Tof? a) Pode não ser uma transformação linear. A resposta é incorrecta. Se T e f são transformações lineares, logo lineares na soma e na multiplicação por números reais e compatíveis para composição, a transformação composta Tof tem que ser linear. Sabendo que a transformação composta Tof transforma cada objecto de f na correspondente imagem, transformando o vector daqui resultante na sua imagem segundo T, ou seja, que, -, a prova é a seguinte:, -, T e f transformações lineares Linear na soma:, -, -, -, -, -, - Linear na multiplicação por números reais: : (. ), (. )-., -.., - (. ). Conclusão: Tof é uma transformação linear. b) A sua matriz de transformação na base canónica não é diagonalizável. A resposta é incorrecta. Basta pensar em T e f como sendo representadas, na base canónica, respectivamente, pelas matrizes 0 1 e 0 1. Sabemos que a transformação composta Tof é representada, na base canónica, pela matriz 0 1. Esta matriz é diagonalizável não só por ser simétrica, mas também por ser diagonal (o que implica que os seus valores próprios são os seus elementos da diagonal principal e a matriz que resulta do processo da sua diagonalização é a própria matriz). 7
12 c) É a mesma transformação que fot. A resposta é incorrecta. Já sabemos que Tof e fot são a mesma transformação se (e só se, é fácil demonstrá-lo) as matrizes que as representam numa base forem comutativas. Não sendo estas matrizes comutativas, fot e Tof são duas transformações lineares diferentes. d) Os vectores próprios comuns a T e a f são seus vectores próprios. A resposta é correcta. De facto, qualquer vector que, quando transformado quer em T, quer em f, resulta num múltiplo de si próprio, também o fará quando transformado em Tof. Chamemos a x um vector próprio de T e de f, associado ao valor próprio no caso de T e no caso de f. Podemos então dizer que. e que.. Agora, basta lembrarmo-nos que T é linear na multiplicação por números reais para provarmos que x é vector próprio de Tof:, - (. ).. Não só provámos que, se x for vector próprio de T e f associado aos valores próprios e, respectivamente, também é vector próprio de Tof, como provámos que o valor próprio que lhe está associado na transformação composta é o produto dos valores próprios que lhe estavam associados em cada uma das transformações originais:. Resposta correcta: d) 6 é uma matriz diagonalizável, cujos valores próprios são reais. O que pode garantidamente afirmar sobre A? 8 a) É simétrica. A resposta é incorrecta. Todas as matrizes simétricas são diagonalizáveis, mas nem todas as matrizes diagonalizáveis são simétricas. Qualquer matriz cujos valores próprios têm multiplicidades algébrica e geométrica iguais é diagonalizável. Por exemplo, a matriz 0 1 tem como valores próprios 1 e 2, cada um com multiplicidade algébrica igual a 1 (porque são raízes únicas do polinómio característico, ). Os espaços próprios de A são *+ e *+ associados, respectivamente aos valores próprios 1 e 2, o que significa que ambos os valores próprios têm multiplicidade geométrica 1 (porque os espaços próprios que lhes estão associados têm dimensão 1). Desta forma, tanto para o valor próprio 1 como para o valor próprio 2, a multiplicidade algébrica é igual à geométrica o que significa que A é diagonalizável e é possível construir uma base de com vectores próprios de A. Por exemplo, * +. b) Todos os seus valores próprios têm multiplicidade algébrica 1. A resposta é incorrecta. Para A ser diagonalizável, é necessário que todos os seus valores próprios tenham multiplicidades algébrica e geométrica iguais. Não é necessário que qualquer uma destas multiplicidades seja 1. Por exemplo, a matriz identidade (2x2),
13 0 1, tem um valor próprio, 1, com multiplicidade algébrica 2. O espaço próprio que lhe está associado é, que tem dimensão 2, pelo que a multiplicidade geométrica do seu valor próprio é 2. Logo, I é diagonalizável e é possível construir uma base de com vectores próprios de I. Por exemplo, * +. c) Tem determinante diferente de 0. A resposta é incorrecta. O determinante de uma matriz iguala o produto dos seus valores próprios, repetidos um número de vezes igual à sua multiplicidade algébrica. Se o determinante de uma matriz é diferente de 0, é garantido que nenhum dos seus valores próprios é 0. Mas esta condição não é necessária para a matriz ser diagonalizável. Por exemplo, a matriz 0 1 tem como valores próprios 0 e 2 (os dois têm multiplicidade algébrica 1) e, por isso, determinante nulo. Contudo, os espaços próprios que lhes estão associados são, respectivamente, *+ e *+, dois espaços com dimensão 1, pelo que a multiplicidade geométrica de ambos os valores próprios é 1. Logo, A é diagonalizável e é possível construir uma base de com vectores próprios de A. Por exemplo, * +. d) Pode ter um único valor próprio distinto. A resposta é correcta. Para uma matriz ser diagonalizável, os seus valores próprios têm que ter multiplicidades algébrica e geométrica iguais. Mas isto não significa que tenha que haver mais do que 1. Por exemplo, a matriz identidade (2x2), 0 1, tem um único valor próprio, 1, com multiplicidade algébrica 2. O espaço próprio que lhe está associado é, cuja dimensão é 2, pelo que a sua multiplicidade geométrica é 2. Logo, I é diagonalizável e é possível construir uma base de com vectores próprios de I. Por exemplo, * +. Resposta correcta: d) 7 T é uma transformação linear, cuja matriz de transformação na base canónica, A, comuta com uma matriz não singular, V, cujas colunas são vectores próprios de A. O que pode garantidamente afirmar sobre A? a) É não singular. b) É ortogonal. c) É diagonal. d) É idempotente. V é uma matriz não singular, logo com determinante não nulo e, por isso, quadrada, (nxn). É por isso constituída por n colunas que são vectores de, que formam um conjunto linearmente independente (já que o determinante de V não é 0) e são, por isso (e porque 9
14 qualquer conjunto de n vectores de um espaço vectorial de dimensão n geram esse espaço) uma base de. Sendo estes vectores vectores próprios de A, sabemos que é possível construir uma base de com vectores próprios de A e, por isso, A é diagonalizável. Logo, é possível diagonalizar A, encontrando uma matriz cujas colunas sejam uma base de de vectores próprios de A, como é, por exemplo, V. Diagonalizamos A, calculando e sabendo que, ao fazê-lo, será uma matriz diagonal, cujos elementos da diagonal principal são os valores próprios, pela ordem correspondente à escolhida aquando da construcção da base de vectores próprios de A. Por outro lado, A e V comutam, o que quer dizer que. Tendo esta igualdade em conta, bem como aquela decorrente da diagonalização de A, ficamos com: Ou seja, neste caso, A é não só diagonalizável, como também igual à matriz diagonal originada pela sua diagonalização. Logo, podemos afirmar que A é uma matriz diagonal. Repare-se que A não tem que ser não singular, ortogonal, nem idempotente, como nos mostra a matriz 0 1, singular, não ortogonal e não idempotente e que comuta com 0 1, cujas colunas formam uma base de constituída por vectores próprios de A. Resposta correcta: d) 8 Qual das seguintes afirmações é verdadeira? 10 a) Uma forma quadrática pode ser semi-definida positiva e semi-definida negativa. A afirmação é verdadeira. Uma forma quadrática em n variáveis é semi-definida positiva se, avaliada em qualquer vector de, for não negativa. É semi-definida negativa se for sempre não positiva. Mas é possível que as duas condições sejam preenchidas. Se uma forma quadrática for nula em qualquer vector de, é sempre não negativa e não positiva. De facto, repare-se que a forma quadrática nula, em 2 variáveis, preenche estas condições. Podemos confirmar este facto, passando a forma quadrática para a forma matricial,, e constantando que a matriz A tem um único vector próprio que é não negativo e, ao mesmo tempo, não positivo: 0. b) Se a matriz associada a uma forma quadrática for o quadrado de uma outra matriz, a forma quadrática pode ser definida negativa. A afirmação é falsa. Se uma matriz estiver associada a, o quadrado de A, é garantidamente semi-definida positiva (pode também ser definida positiva, mas não deixa de ser semi-definida positiva). De facto, se A está associada a uma forma quadrática, é simétrica e, por isso, todos os seus valores próprios são reais. Cada valor próprio de é o quadrado de um valor próprio de A. Sendo o quadrado de qualquer número um número não
15 negativo (pode ser 0, se o número for 0), sabemos que todos os valores próprios de maiores ou iguais a 0. Quer isto dizer que a forma quadrática associada a é forçosamente semi-definida positiva. Se nenhum valor próprio de A for 0, podemos também dizer que a forma quadrática associada a próprios positivos. são é definida positiva, porque esta matriz terá todos os valores c) Se a matriz associada a uma forma quadrática for singular, a forma quadrática pode ser definida positiva. A afirmação é falsa. Uma matriz singular é uma matriz não invertível, cujo determinante é 0. Sendo o determinante de uma matriz o produto dos seus valores próprios, repetidos um número de vezes igual à sua multiplicidade algébrica, sabemos que, se for 0, um dos valores próprios da matriz será também 0. Mas se uma matriz tem um valor próprio nulo, não pode ser definida positiva (nem definida negativa), podendo, isso sim, ser semi-definida positiva, semi-definida negativa, ou indefinida. d) Se uma forma quadrática não envolver termos cruzados, não pode ser semidefinida positiva, nem semi-definida negativa. A afirmação é falsa. Uma forma quadrática em n variáveis semi-definida positiva é um polinómio constituído apenas por termos de grau 2 que é não negativo, para qualquer vector de. Mesmo não tendo termos cruzados, pode perfeitamente ser sempre maior ou igual a 0. Primeiro, porque é óbvio que pode ser definida positiva, como acontece, por exemplo, com a forma quadrática (que é obviamente sempre positiva, com a excepção do vector nulo de, que anula qualquer forma quadrática), sendo, por isso, semi-definida positiva (se a forma quadrática é sempre positiva, também é verdade que é sempre não negativa). Depois, porque pode ser estritamente semi-definida positiva (no sentido em que não é definida positiva). De facto, mesmo não tendo termos cruzados, pode ser possível anulá-la num vector não nulo. É o que se passa, por exemplo, com a forma quadrática. Apesar de não contemplar nenhum termo envolvendo a variável y, esta deve ser incluída nos vectores a aplicar a Q. Desta forma, qualquer vector da forma anula esta forma quadrática, sendo, por isso, Q semi-definida positiva. O mesmo raciocínio se aplica à classificação semi-definida negativa. Resposta correcta: a) 9 Q é uma forma quadrática não nula cuja matriz associada é idempotente. Qual é, garantidamente, a classificação de Q? a) Definida positiva. b) Semi-definida positiva. c) Indefinida. d) Definida negativa. 11
16 Sabemos que Q não é a forma quadrática nula, pelo que tem pelo menos um valor próprio não nulo. Para além disso, a matriz que lhe está associada, chamemos-lhe A, é idempotente, o que significa que. Sendo os valores próprios de o quadrado dos valores próprios de A, estes valores próprios são o quadrado de si próprios ( representa um valor próprio): * + Assim, A pode ter como valores próprios apenas 0 e 1. Tendo pelo menos um valor próprio não nulo, sabemos que 1 será sempre valor próprio de A. Já 0 pode ser ou não. Podemos desta forma garantir que os valores próprios de A são não negativos, não sendo possível afirmar que são positivos. É por isso possível afirmar que Q é semi-definida positiva (se o seu único valor próprio for 1, como acontece com a matriz identidade de qualquer dimensão, Q é definida positiva, não sendo por isso que deixa de ser semi-definida positiva). Resposta correcta: b) 10 Q é a forma quadrática que representa, para cada vector de, o quadrado da soma das suas coordenadas. Qual das seguintes mudanças de variável não permite representar Q sem termos cruzados? a). /. b). /. 12 c). /. d). /. Primeiro, encontremos a expressão de e representemo-la na forma matricial:, Q é uma forma quadrática que tem 1 termo cruzado, e, por isso, a matriz que lhe está associada não é uma matriz diagonal. Contudo, é possível efectuar uma mudança de variável, de forma a que Q, nessa nova variável, não apresente termos cruzados. De facto, chamemos à nova variável e definamos a mudança de variável da seguinte forma:, sendo V uma matriz (2x2). Resta saber que matriz poderá ser V, para que a forma quadrática na nova variável não tenha, de facto, termos cruzados (ou para que a matriz associada à forma quadrática nesta variável seja diagonal). Lembrando-nos da representação matricial de Q e da mudança de variável a efectuar, ficamos com: Desta forma, a matriz associada a Q na nova variável é. Resta garantir que é uma matriz diagonal. Sabemos que, sendo A simétrica, é diagonalizável, o que significa que é
17 possível obter uma matriz diagonal a partir de A. Para isso, é necessário encontrar uma base de constituída por vectores próprios de A e construir uma matriz, chamemos-lhe, cujas colunas são estes mesmos vectores. Ao fazermos isto, obtemos a matriz diagonal, (que tem na diagonal principal os valores próprios de A, pela ordem correspondente à ordem pela qual os vectores próprios de A foram escolhidos para colunas de V), através do produto. Se conseguirmos garantir que (ou seja, que V é ortogonal), então e a matriz de Q na variável é diagonal. Mas uma matriz é ortogonal se e só se as suas colunas são vectores ortonormados (mutuamente ortogonais e de norma 1). Por isso, se, durante a diagonalização de A, escolhermos para colunas de V vectores que não só são vectores próprios de A, mas ainda ortonormados, garantimos que V é ortogonal. Se isto for verdade: Vamos então calcular os valores próprios de A: Agora, os seus vectores próprios: { { * + * + * { { * + * + *+ Já sabemos que os vectores próprios associados a são os múltiplos de e os vectores próprios associados a são os múltiplos de. Precisamos agora de escolher um vector de e outro de que tenham norma 1 e sejam ortogonais. Sendo A simétrica (o que acontece em todas as matrizes associadas a formas quadráticas), sabemos que a valores próprios diferentes de A correspondem vectores próprios ortogonais. Logo, qualquer vector de é ortogonal a qualquer vector de. Por outro lado, sabemos que se multiplicarmos um vector próprio de A por qualquer número real, continuamos a ter um vector próprio de A, pelo que, depois de escolher um vector de e outro de podemos multiplicá-los pelo inverso da sua norma, obtendo desta forma vectores ortonormados. Agora, as hipóteses de escolha de vectores de e de são infinitas. Chamemos, ao vector escolhido de, e, ao proveniente de,, com e diferentes de 0 (caso contrário, um dos vectores escolhidos é o vector nulo e os vectores escolhidos não podem formar uma base de, por serem linearmente dependentes). Multiplicando cada um pelo inverso da sua norma, obtemos os seguintes vectores: 13
18 ( ). / {. /. / ( ). / {. /. / Estes resultados significam que, independentemente dos vectores escolhidos de e de, os vectores ortonormados a ser usados serão o. / ou o. / e o. / ou o. / (qualquer combinação, por qualquer ordem, funciona). Chamemos aos vectores escolhidos, respectivamente, e. Assim, a matriz V, cujas colunas serão os vectores a e b terá a forma [ ]. Logo, 0 1. Resta saber qual a mudança de variáveis associada a esta matriz V. Dissemos que, para chegar à forma quadrática na nova variável, faríamos a mudança de variável. Mas, se isto é verdade, então: [ ] 0 1 [ ] [ ] [ ] A primeira coordenada da nova variável será uma combinação linear das duas coordenadas da variável original, cujos coeficientes são as coordenadas do vector a. A segunda coordenada também será uma combinação linear das mesmas coordenadas, mas com coeficientes iguais às coordenadas do vector b. Desta forma, esta é a lista de todas as mudanças de variável que permitem eliminar o termo cruzado de Q:. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. /. / 14
19 Repare-se que, enquanto que nas primeiras 4 mudanças de variável, o 1º vector escolhido pertencia a e o segundo a, nas outras, a ordem foi revertida. Assim, equanto que, para as primeiras 4 mudanças de variável, a forma quadrática na nova variável é, [ ], para as outras, a forma é, [ ]. Resposta correcta: c) 15
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
7 Formas Quadráticas
 Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
7 Formas Quadráticas
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Ficha de Exercícios nº 1
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
(2008/2009) Espaços vectoriais. Matemática 1º Ano - 1º Semestre 2008/2009. Mafalda Johannsen
 Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
Ficha de Exercícios nº 2
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 2 Matrizes, Determinantes e Sistemas de Equações Lineares 1 O produto de duas matrizes, A e B, é a matriz nula (mxn). O que pode
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 2 Matrizes, Determinantes e Sistemas de Equações Lineares 1 O produto de duas matrizes, A e B, é a matriz nula (mxn). O que pode
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
 MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
ficha 4 valores próprios e vectores próprios
 Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Ficha de Trabalho 09 e 10
 Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
Álgebra Linear I - Aula 20
 Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Álgebra Linear I - Aula 20 1 Matrizes diagonalizáveis Exemplos 2 Forma diagonal de uma matriz diagonalizável 1 Matrizes diagonalizáveis Exemplos Lembramos que matriz quadrada a 1,1 a 1,2 a 1,n a 2,1 a
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
2009/2010-2º SEMESTRE- 2ª ÉPOCA EXAME DE ÁLGEBRA LINEAR (1303) 16 de Junho de Respostas
 Grupo 1 1- Considere o conjunto S 3 definido por: S x 1,x 2,x 3 3 : x 1 x 2 x 3 0 1.1- Mostre que S éumsub-espaço de 3. Determine a dimensão de S exibindo uma base B de S. [1/20] 1.2- Qual é o complemento
Grupo 1 1- Considere o conjunto S 3 definido por: S x 1,x 2,x 3 3 : x 1 x 2 x 3 0 1.1- Mostre que S éumsub-espaço de 3. Determine a dimensão de S exibindo uma base B de S. [1/20] 1.2- Qual é o complemento
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Valores e vectores próprios
 Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0
![Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0 Q1. Considere as bases: der 2 e der 3, respectivamente. Seja T :R 2 R 3 a transformação linear Temos que T(1,2) é igual a: [T] BC = 1 0](/thumbs/93/113642308.jpg) Q. Considere as bases: B = { (,),(, ) }, C = { (,,),(,,),(,,) }, der e der, respectivamente. Seja T :R R a transformação linear cuja matriz em relação às bases B e C é: [T] BC =. Temos que T(,) é igual
Q. Considere as bases: B = { (,),(, ) }, C = { (,,),(,,),(,,) }, der e der, respectivamente. Seja T :R R a transformação linear cuja matriz em relação às bases B e C é: [T] BC =. Temos que T(,) é igual
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
Resolução do efólio B
 Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Álgebra Linear I - Aula Forma diagonal de uma matriz diagonalizável
 Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Álgebra Linear I - Aula 18 1 Forma diagonal de uma matriz diagonalizável 2 Matrizes ortogonais Roteiro 1 Forma diagonal de uma matriz diagonalizável Sejam A uma transformação linear diagonalizável, β =
Cálculo Diferencial e Integral 2 Formas Quadráticas
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Cálculo Diferencial e Integral 2 Formas Quadráticas 1 Formas quadráticas Uma forma quadrática em R n é um polinómio do
Multiplicidade geométrica
 Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
Valores e Vectores Próprios - ALGA - /5 Multiplicidade geométrica Chama-se multiplicidade geométrica de um valor próprio ao grau de indeterminação do sistema (A I n ) X : O grau de indeterminação de corresponde
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
Provas. As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor.
 Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
Provas As notas da primeira e segunda prova já foram digitadas no Minha UFMG. Caso você não veja sua nota, entre em contato com o professor. Terceira prova. Sábado, 15/junho, 10:00-12:00 horas, ICEx. Diagonalização
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
Parte 3 - Produto Interno e Diagonalização
 Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
[ ] EXEMPLOS: Muitas vezes precisamos montar uma Matriz a partir de uma lei geral. Analise os exemplos a seguir:
![[ ] EXEMPLOS: Muitas vezes precisamos montar uma Matriz a partir de uma lei geral. Analise os exemplos a seguir: [ ] EXEMPLOS: Muitas vezes precisamos montar uma Matriz a partir de uma lei geral. Analise os exemplos a seguir:](/thumbs/52/30426431.jpg) MATRIZES CONCEITO: Um conjunto de elementos algébricos dispostos em uma tabela retangular com linhas e colunas é uma Matriz. A seguir, vemos um exemplo de Matriz de 3 linhas e 4 colunas, e que representaremos
MATRIZES CONCEITO: Um conjunto de elementos algébricos dispostos em uma tabela retangular com linhas e colunas é uma Matriz. A seguir, vemos um exemplo de Matriz de 3 linhas e 4 colunas, e que representaremos
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
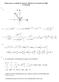 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
. Repare que ao multiplicar os vetores (-1,1) e
 Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
Álgebra Linear II P1-2014.2 Obs: Todas as alternativas corretas são as representadas pela letra A. 1 AUTOVETORES/ AUTOVALORES Essa questão poderia ser resolvida por um sistema bem chatinho. Mas, faz mais
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
MAT Geometria Analítica Licenciatura em Matemática
 MAT010 - Geometria Analítica Licenciatura em Matemática 3 ā Prova - 29/06/2009 Nome: N ō USP: Instruções: 1- Preencha o cabeçalho a caneta. 2- A prova pode ser resolvida a lápis. 3- Justifique suas afirmações.
MAT010 - Geometria Analítica Licenciatura em Matemática 3 ā Prova - 29/06/2009 Nome: N ō USP: Instruções: 1- Preencha o cabeçalho a caneta. 2- A prova pode ser resolvida a lápis. 3- Justifique suas afirmações.
ÁLGEBRA LINEAR A FICHA 6. Por definição do determinante de uma matriz 3 3, tem-se det A = 7.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial
 TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
Espaços Vectoriais. Espaços Vectoriais
 Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Métodos Matemáticos II
 Sumário Métodos Matemáticos II Nuno Bastos Licenciatura em Tecnologias e Design Multimédia Escola Superior de Tecnologia de Viseu Gabinete 4 nbastos@mat.estv.ipv.pt http://www.estv.ipv.pt/paginaspessoais/nbastos.
Sumário Métodos Matemáticos II Nuno Bastos Licenciatura em Tecnologias e Design Multimédia Escola Superior de Tecnologia de Viseu Gabinete 4 nbastos@mat.estv.ipv.pt http://www.estv.ipv.pt/paginaspessoais/nbastos.
Notas para o Curso de Algebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009
 Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Notas para o Curso de Álgebra Linear Il Dayse Haime Pastore 20 de fevereiro de 2009 2 Sumário 1 Matrizes e Sistemas Lineares 5 11 Matrizes 6 12 Sistemas Lineares 11 121 Eliminação Gaussiana 12 122 Resolução
Análise Complexa e Equações Diferenciais Guia 9 João Pedro Boavida. 23 a 30 de Novembro
 Análise Complexa e Equações Diferenciais Guia 9 24 de Novembro de 2 Este guia explica vários exemplos de determinação de formas de Jordan e cálculo de exponenciais de matrizes, bem como alguns outros exemplos
Análise Complexa e Equações Diferenciais Guia 9 24 de Novembro de 2 Este guia explica vários exemplos de determinação de formas de Jordan e cálculo de exponenciais de matrizes, bem como alguns outros exemplos
2012/2013-1º SEMESTRE- 1ª ÉPOCA EXAME DE ÁLGEBRA LINEAR (1303) 2 de Janeiro de 2013
 / - º SEMESTRE- ª ÉPOCA EXAME DE ÁLGEBRA LINEAR () de Janeiro de Grupo - Considere o conjunto C t,,t : t..- Mostre que C é um sub-espaço de. [/].- Mostre que qualquer vector z C é uma combinação linear
/ - º SEMESTRE- ª ÉPOCA EXAME DE ÁLGEBRA LINEAR () de Janeiro de Grupo - Considere o conjunto C t,,t : t..- Mostre que C é um sub-espaço de. [/].- Mostre que qualquer vector z C é uma combinação linear
5. Seja A uma matriz qualquer. Assinale a afirmativa
 UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
UFRJ Instituto de Matemática Disciplina: Algebra Linear II - MAE 125 Professor: Bruno, Gregório, Luiz Carlos, Mario, Milton, Monique e Umberto Data: 12 de julho de 2013 Terceira Prova 1. Considere no espaço
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear I - Lista 12. Matrizes semelhantes. Diagonalização. Respostas
 Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
Álgebra Linear I - Lista 12 Matrizes semelhantes. Diagonalização Respostas 1) Determine quais das matrizes a seguir são diagonalizáveis. Nos caso afirmativos encontre uma base de autovetores e uma forma
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Definição de Matrizes. Exemplos. Definição de Ordem de Uma Matriz. Exemplos. Representação Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz
Álgebra Linear e Geometria Analítica. Valores Próprios e Vectores Próprios
 Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
TÓPICOS. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -1
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Álgebra Linear I - Aula 22
 Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 2012/2013
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
10 a Lista de Exercícios
 Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Sistemas de Equações Lineares
 Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
Matrizes e Determinantes
 Aula 10 Matrizes e Determinantes Matrizes e Determinantes se originaram no final do século XVIII, na Alemanha e no Japão, com o intuito de ajudar na solução de sistemas lineares baseados em tabelas formadas
Aula 10 Matrizes e Determinantes Matrizes e Determinantes se originaram no final do século XVIII, na Alemanha e no Japão, com o intuito de ajudar na solução de sistemas lineares baseados em tabelas formadas
Primeira prova de Álgebra Linear - 06/05/2011 Prof. - Juliana Coelho
 Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
Primeira prova de Álgebra Linear - 6/5/211 Prof. - Juliana Coelho JUSTIFIQUE SUAS RESPOSTAS! Questões contendo só a resposta, sem desenvolvimento ou justificativa serão desconsideradas! QUESTÃO 1 (2, pts)
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear. Professor Alessandro Monteiro. 1º Sábado - Matrizes - 11/03/2017
 º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
º Sábado - Matrizes - //7. Plano e Programa de Ensino. Matrizes. Exemplos. Ordem de Uma Matriz. Exemplos. Representação 7. Matriz Genérica m x n 8. Matriz Linha 9. Exemplos. Matriz Coluna. Exemplos. Diagonal
Ficha de Revisão. Nova School of Business and Economics Álgebra Linear
 Nova School of Business and Economics Álgebra Linear Ficha de Revisão 1 Três amigos, o Xavier, o Yuri e a Zulmira tinham pouco que fazer, porque já tinha acabado a Floribella. Então decidiram ir para uma
Nova School of Business and Economics Álgebra Linear Ficha de Revisão 1 Três amigos, o Xavier, o Yuri e a Zulmira tinham pouco que fazer, porque já tinha acabado a Floribella. Então decidiram ir para uma
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
Renato Martins Assunção
 Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Análise Numérica Renato Martins Assunção DCC - UFMG 2012 Renato Martins Assunção (DCC - UFMG) Análise Numérica 2012 1 / 84 Equação linear Sistemas de equações lineares A equação 2x + 3y = 6 é chamada linear
Notas em Álgebra Linear
 Notas em Álgebra Linear 1 Pedro Rafael Lopes Fernandes Definições básicas Uma equação linear, nas variáveis é uma equação que pode ser escrita na forma: onde e os coeficientes são números reais ou complexos,
Notas em Álgebra Linear 1 Pedro Rafael Lopes Fernandes Definições básicas Uma equação linear, nas variáveis é uma equação que pode ser escrita na forma: onde e os coeficientes são números reais ou complexos,
ÁLGEBRA LINEAR A FICHA 2
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
2012/2013-2º SEMESTRE- 2ª ÉPOCA EXAME DE ÁLGEBRA LINEAR (1303) 4 de Julho de 2013
 1- Um n-simplex é um conjunto S n n definido por: S n x 1,x 2,...,x n n : x 1 x 2... x n 1,x 1 0,x 2 0,...,x n 0. 1.1- Desenhe S 3 x 1,x 2,x 3 3 : x 1 x 2 x 3 1,x 1 0,x 2 0,x 3 0. [1/20] 1.2- Qual é o
1- Um n-simplex é um conjunto S n n definido por: S n x 1,x 2,...,x n n : x 1 x 2... x n 1,x 1 0,x 2 0,...,x n 0. 1.1- Desenhe S 3 x 1,x 2,x 3 3 : x 1 x 2 x 3 1,x 1 0,x 2 0,x 3 0. [1/20] 1.2- Qual é o
ficha 6 espaços lineares com produto interno
 Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Inversão de Matrizes
 Inversão de Matrizes Prof. Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2015.2 21 de
Inversão de Matrizes Prof. Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2015.2 21 de
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear I - Aula 19
 Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
Álgebra Linear I - Aula 19 1. Matrizes diagonalizáveis. 2. Matrizes diagonalizáveis. Exemplos. 3. Forma diagonal de uma matriz diagonalizável. 1 Matrizes diagonalizáveis Uma matriz quadrada T = a 1,1 a
5. Seja R : R 3 R 3 uma rotação em torno do eixo gerado por (0, 0, 1). Suponha que R mande o vetor
 Universidade Federal do Rio de Janeiro Instituto de Matemática Disciplina: Álgebra Linear II Professor: Bruno Costa, Cesar Niche, Francesco Noseda, Luiz Carlos Guimarães, Mário de Oliveira, Milton Ramirez,
Universidade Federal do Rio de Janeiro Instituto de Matemática Disciplina: Álgebra Linear II Professor: Bruno Costa, Cesar Niche, Francesco Noseda, Luiz Carlos Guimarães, Mário de Oliveira, Milton Ramirez,
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0
![1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0 1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0](/thumbs/77/76694592.jpg) 1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
LISTA DE EXERCÍCIOS 2017
 CURSO LISTA DE EXERCÍCIOS 2017 DISCIPLINA ESTUDANTE PROFESSOR (A) DATA Questão 1) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas
CURSO LISTA DE EXERCÍCIOS 2017 DISCIPLINA ESTUDANTE PROFESSOR (A) DATA Questão 1) Um aluno registrou as notas bimestrais de algumas de suas disciplinas numa tabela. Ele observou que as entradas numéricas
(a) (1,5) Obtenha os autovalores e autovetores de L. (b) (1,0) A matriz de L em relação à base canônica de M 2 2 é diagonalizável? Explique.
 Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
Nome do(a) estudante(a): ALI0001(PRO11-0A) Prova IV 8/06/016 Prof. Helder G. G. de Lima ˆ Identifique-se em todas as folhas. ˆ Mantenha o celular e os demais equipamentos eletrônicos desligados durante
4. Tensores cartesianos em 3D simétricos
 4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
(c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
 Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
P3 de Álgebra Linear I
 P3 de Álgebra Linear I 2008.2 Data: 14 de Novembro de 2008. Gabarito. 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Considere uma transformação linear T : R 3 R 3 tal que existem vetores
P3 de Álgebra Linear I 2008.2 Data: 14 de Novembro de 2008. Gabarito. 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Considere uma transformação linear T : R 3 R 3 tal que existem vetores
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
Lista 1: sistemas de equações lineares; matrizes.
 Lista : sistemas de equações lineares; matrizes. Obs. As observações que surgem no fim desta lista de exercícios devem ser lidas antes de resolvê-los. ) Identifique as equações que são lineares nas respectivas
Lista : sistemas de equações lineares; matrizes. Obs. As observações que surgem no fim desta lista de exercícios devem ser lidas antes de resolvê-los. ) Identifique as equações que são lineares nas respectivas
Geometria Analítica e Álgebra Linear
 UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
Esmeralda Sousa Dias. (a) (b) (c) Figura 1: Ajuste de curvas a um conjunto de pontos
 Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
Mínimos quadrados Esmeralda Sousa Dias É frequente ser necessário determinar uma curva bem ajustada a um conjunto de dados obtidos experimentalmente. Por exemplo, suponha que como resultado de uma certa
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Lista 2 - Resolução. 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os.
 GAN00140 Álgebra Linear 018.1 Prof a. Ana Maria Luz F. do Amaral Lista - Resolução 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os. 1 a) b) 1 3 0 0 1 /. 1 1/ 1
GAN00140 Álgebra Linear 018.1 Prof a. Ana Maria Luz F. do Amaral Lista - Resolução 1. Verifique se os produtos abaixo estão bem definidos e, em caso afirmativo, calcule-os. 1 a) b) 1 3 0 0 1 /. 1 1/ 1
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Matemática Matrizes e Determinantes
 . (Unesp) Um ponto P, de coordenadas (x, y) do a plano cartesiano ortogonal, é representado pela matriz 5. (Unicamp) Considere a matriz M b a, onde coluna assim como a matriz coluna b a e b são números
. (Unesp) Um ponto P, de coordenadas (x, y) do a plano cartesiano ortogonal, é representado pela matriz 5. (Unicamp) Considere a matriz M b a, onde coluna assim como a matriz coluna b a e b são números
1 Auto vetores e autovalores
 Auto vetores e autovalores Os autovalores de uma matriz de uma matriz n n são os n números que resumem as propriedades essenciais daquela matriz. Como esses n números realmente caracterizam a matriz sendo
Auto vetores e autovalores Os autovalores de uma matriz de uma matriz n n são os n números que resumem as propriedades essenciais daquela matriz. Como esses n números realmente caracterizam a matriz sendo
