Ficha de Revisão. Nova School of Business and Economics Álgebra Linear
|
|
|
- Maria do Mar Balsemão Caldas
- 6 Há anos
- Visualizações:
Transcrição
1 Nova School of Business and Economics Álgebra Linear Ficha de Revisão 1 Três amigos, o Xavier, o Yuri e a Zulmira tinham pouco que fazer, porque já tinha acabado a Floribella. Então decidiram ir para uma pista de skate, estranhamente para fazer skate. Quando chegaram, ficaram maravilhados com a pista que até tinha indicadas algumas medidas: A 13 m 5 m 5 m Como se pode ver pela figura, a rampa tem um comprimento de 13 m e uma largura de 5m e quem a desce avança 5 m em relação à parede que suporta a pista. Já a pensar em pessoas que gostam muito de Álgebra Linear, a Junta de Freguesia da Abóboda (onde está construída a pista), deixou um ponto preto no chão e recomenda que seja considerado, para todos os efeitos, a origem do referencial de. O Xavier, uma pessoa à frente do seu tempo, disse: E se considerássemos a rampa como sendo parte de um plano de? a) Seguindo a ideia do Xavier (vá-se lá saber porquê), encontre um vector normal ao plano. b) Utilizando este vector e um ponto do plano, encontre a equação cartesiana do plano. c) A Zulmira, que não é pessoa para ficar calada, acrescentou: O conjunto de pontos deste plano é um subespaço vectorial de. Mostre que a Zulmira é mais bolos e não tinha razão. d) O Yuri, que ainda não tinha dito nada, resolveu dizer: O plano não é um subespaço vectorial, mas se eu pegar numa bulldozer e empurrar a rampa para baixo, subtraindo à cota (3ª coordenada) de todos os seus pontos um certo valor, passa a sê-lo. Sabendo que o Yuri tinha razão, descubra que valor é este. 1
2 Ficha de Revisão e) Por acaso ia a passar na rua uma bulldozer (o que acontece muito) e fez o que o Yuri sugeriu, pelo que o plano que contém a rampa passou a ser um subespaço vectorial. Indique uma base e a dimensão deste subespaço. f) Depois desta operação, o Xavier, que continuava com pouco que fazer, foi para o ponto A da figura (não se esqueça que todos os pontos sofreram uma translacção), pegou num iô-iô e deixou-o descer até ao ponto posto pela Junta de Freguesia (que também desceu). De repente, lembrou-se: O fio do iô-iô, como está agora, é parte de uma recta de, que é um subespaço vectorial. A dimensão do subespaço vectorial correspondente à intersecção da recta com o plano da rampa (depois de baixada) é 0. Recorrendo ao Teorema das Dimensões, justifique esta afirmação. 2 Enquanto estiveram na rampa de skate, o Xavier, o Yuri e a Zulmira aproveitaram para fazer um campeonato de estilo e pediram ao Walter para os pontuar, com pontos positivos ou negativos. No fim, o Walter disse: Não vos vou dizer quantos pontos é que dei a cada um, mas vou dar-vos algumas pistas: Se subtraírem aos pontos do Xavier os do Yuri e os da Zulmira, ficam com -4 pontos. A soma dos vossos pontos é 6. Se multiplicarem os pontos do Xavier por 2, os do Yuri por 2 e os da Zulmira por a e somarem as 3 parcelas, ficam com b pontos. a) O a e o b, que o Walter não quis revelar eram, respectivamente, 3 e 15. Quais foram as pontuações de cada um? b) A Zulmira, que queria ver se conseguia saber as pontuações, afirmou, mesmo sem saber: Eu sei que o b é 12. O Walter não achou graça e pensou Se a Zulmira acha que o b é 12, vou indicar-lhes um a que lhes dá mais do que uma solução para o problema. Descubra o a em que o Walter estava a pensar e indique o conjunto de soluções que resolvem o problema com este a e b. c) O Yuri, depois de perceber que não conseguia resolver o problema com a informação dada pelo Walter, resolveu arriscar: Eu sei que o a é 2. Desta vez, o Walter ainda fez pior: Agora vez vou dar-lhes um b que torna o problema impossível de ser resolvido. Que valores é que pode tomar o b em que o Walter pensou? 3 Depois de se despedirem do Walter, sem nunca terem sabido as pontuações, os três amigos foram para uma sala de jogos. Encontraram uma máquina que tinha 3 entradas para moedas e por baixo, 3 saídas. Não dizia quais eram as regras, só pedia para se introduzir moedas em cada uma das entradas e esperar pelo que saísse. Os três resolveram experimentá-la, ficando o Xavier com a entrada da esquerda, o Yuri com a do meio e a Zulmira a da direita. Primeiro, introduziram 1 Euro cada um. Ao Xavier saíram 2 Euros, ao Yuri 1 e à Zulmira não saiu nada. Depois, o Xavier introduziu 1 Euro, o Yuri 2 e a Zulmira nada. Ao Xavier saíram 3 Euros e ao Yuri e à Zulmira não saiu nada. 2
3 Ficha de Revisão Na terceira jogada, o Xavier introduziu 2 Euros e o Yuri e a Zulmira nada. Saiu a todos o que tinham introduzido. A Zulmira, mesmo sem ter ganho dinheiro, percebeu: Esta máquina opera uma transformação linear sobre o dinheiro dos 3 jogadores. a) Sabendo que desta vez a Zulmira tinha razão, calcule quanto é que sairia a cada um dos jogadores, se todos jogassem 2 Euros. b) Indique o espaço de partida, o espaço de chegada e a expressão geral da transformação linear operada pela máquina. c) Calcule a matriz que representa esta transformação linear na base canónica. d) A Zulmira, que não ficou contente com o resultado do jogo, afirmou: Deviam inventar um jogo que transformasse todos os resultados do jogo que nós jogámos no dinheiro introduzido ao princípio, ou seja, que operasse a transformação inversa da deste jogo. É possível encontrar uma transformação linear que faça o que a Zulmira pretende? e) O Xavier lembrou-se de dizer: Não há duas maneiras diferentes de introduzir dinheiro que dêm o mesmo resultado. Tem razão? (lembre-se que uma transformação linear é injectiva se e só se { }, ou seja, se o único ponto que é transformado no vector nulo é o próprio vector nulo.) f) O Yuri quis saber quais eram os conjuntos de valores introduzidos que se transformavam, através do jogo, em múltiplos de si próprios. Descubra se estes conjuntos de valores existem e, caso existam, quais os múltiplos que lhes estão associados. g) Para acabar, verifique se é possível construir outra máquina que opera o mesmo jogo que esta, mas que trabalha com Dólares Canadianos, tanto na entrada como na saída, de maneira a que a matriz que representa a transformação que opera seja diagonal. 3
4
5 Nova School of Business and Economics Álgebra Linear 1 Três amigos, o Xavier, o Yuri e a Zulmira tinham pouco que fazer, porque já tinha acabado a Floribella. Então decidiram ir para uma pista de skate, estranhamente para fazer skate. Quando chegaram, ficaram maravilhados com a pista que até tinha indicadas algumas medidas: A 13 m 5 m 5 m Como se pode ver pela figura, a rampa tem um comprimento de 13 m e uma largura de 5m e quem a desce avança 5 m em relação à parede que suporta a pista. Já a pensar em pessoas que gostam muito de Álgebra Linear, a Junta de Freguesia da Abóboda (onde está construída a pista), deixou um ponto preto no chão e recomenda que seja considerado, para todos os efeitos, a origem do referencial de. O Xavier, uma pessoa à frente do seu tempo, disse: E se considerássemos a rampa como sendo parte de um plano de? a) Seguindo a ideia do Xavier (vá-se lá saber porquê), encontre um vector normal ao plano. Como o plano pertence a, precisamos de 2 vectores não paralelos que sejam a diferença de pontos do plano. Para isso, precisamos de 3 pontos não colineares do plano. Observando a figura, podemos encontrar as coordenadas de 4 pontos do plano (A, B, C e D): 1
6 A B 13 m O 5 m C 5 m D Representando a abcissa, ordenada e cota do ponto por, respectivamente,, e :, { { { ( ) Qualquer vector do tipo de exemplo: é um vector normal ao plano (excluindo o vector nulo). Por ( ) b) Utilizando este vector e um ponto do plano, encontre a equação cartesiana do plano. Sendo qualquer ponto do plano, um ponto específico do plano e um vector normal ao plano, a equação normal do plano é: Utilizando, por exemplo, o ponto e o vector : [ ] ( ) ( ) 2
7 Equação cartesiana do plano: Alternativamente, sabemos que a equação cartesiana do plano é do tipo, em que, e são as coordenadas de um vector normal ao plano. Sabendo que o plano tem que passar, por exemplo, pelo ponto, ou seja, que as coordenadas do ponto têm que respeitar a equação do plano, temos que: Equação cartesiana do plano: c) A Zulmira, que não é pessoa para ficar calada, acrescentou: O conjunto de pontos deste plano é um subespaço vectorial de. Mostre que a Zulmira é mais bolos e não tinha razão. O plano pode ser descrito da seguinte forma: { } { } {( ) } Podemos desde logo afirmar que este plano não é um subespaço vectorial, porque não contém a origem (basta observar a figura e constatar que o ponto demarcado pela junta de Freguesia não pertence à rampa). De qualquer maneira, podemos ver que características é que o plano não tem e que o impedem de ser um subespaço vectorial: Não vazio: echado para a soma: ( ) ( ) ( ) ( ) ( ) ( ) echado para a multiplicação por escalares: ( ) ( ) ( ) ( ) 3
8 d) O Yuri, que ainda não tinha dito nada, resolveu dizer: O plano não é um subespaço vectorial, mas se eu pegar numa bulldozer e empurrar a rampa para baixo, subtraindo à cota (3ª coordenada) de todos os seus pontos um certo valor, passa a sê-lo. Sabendo que o Yuri tinha razão, descubra que valor é este. Sabemos que um conjunto é um subespaço vectorial só se contiver a origem do espaço em que se encontra. Subtraindo 12 unidades à cota do ponto, transformamo-lo na origem: Se subtrairmos 12 unidades a todos os pontos do plano, obtemos o plano, paralelo a, mas que passa por outros pontos: A equação cartesiana de é facilmente encontrada: { } { } {( ) } Vamos confirmar que é um subespaço vectorial: Não vazio: echado para a soma: ( ) ( ) ( ) ( ) ( ) echado para a multiplicação por escalares: ( ) ( ) ( ) e) Por acaso ia a passar na rua uma bulldozer (o que acontece muito) e fez o que o Yuri sugeriu, pelo que o plano que contém a rampa passou a ser um subespaço vectorial. Indique uma base e a dimensão deste subespaço. {( ) } { ( ) } {( ) } Sabemos que é gerado pelos vectores ( ) e. Caso estes dois vectores formem um conjunto linarmente independente, são uma base de. Vamos testar a sua independência linear: 4
9 [ ] (porque a matriz já se encontra no formato em escada por linhas e tem 2 linhas não nulas e 2 pivots {( ) } é linearmente independente {( ) } f) Depois desta operação, o Xavier, que continuava com pouco que fazer, foi para o ponto A da figura (não se esqueça que todos os pontos sofreram uma translacção), pegou num iô-iô e deixou-o descer até ao ponto posto pela Junta de Freguesia (que também desceu). De repente, lembrou-se: O fio do iô-iô, como está agora, é parte de uma recta de, que é um subespaço vectorial. A dimensão do subespaço vectorial correspondente à intersecção da recta com o plano da rampa (depois de baixada) é 0. Recorrendo ao Teorema das Dimensões, justifique esta afirmação. O fio do iô-iô é parte de uma recta vertical, cujos pontos têm abcissa e ordenada nula. A sua equação cartesiana é, por isso,. Recta : { } { } { } { } { } A soma directa do plano com a recta,, é o conjunto de pontos que pode ser obtido somando cada ponto de com cada ponto de. Um possível sistema de vectores geradores de é constituído pelos vectores que pertencem às bases destes conjuntos: {( ) } Vamos averiguar se este é um conjunto linearmente independente (em caso afirmativo, constitui uma base de ): {( ) } De acordo com o Teorema das Dimensões: 5
10 O único subespaço com dimensão nula é aquele constituído apenas pelo vector nulo. Vamos confirmar que a intersecção de com é o vector nulo:, { ( ) ( ) { { 2 Enquanto estiveram na rampa de skate, o Xavier, o Yuri e a Zulmira aproveitaram para fazer um campeonato de estilo e pediram ao Walter para os pontuar, com pontos positivos ou negativos. No fim, o Walter disse: Não vos vou dizer quantos pontos é que dei a cada um, mas vou dar-vos algumas pistas: Se subtraírem aos pontos do Xavier os do Yuri e os da Zulmira, ficam com -4 pontos. A soma dos vossos pontos é 6. Se multiplicarem os pontos do Xavier por 2, os do Yuri por 2 e os da Zulmira por a e somarem as 3 parcelas, ficam com b pontos. a) O a e o b, que o Walter não quis revelar eram, respectivamente, 3 e 15. Quais foram as pontuações de cada um? O problema pode ser representado por um sistema de equações lineares. Denominando os pontos atribuídos ao Xavier por, aqueles atribuídos ao Yuri por e os recebidos pela Zulmira por, temos o seguinte sistema: { [ ] * + [ ] Vamos construir a matriz aumentada e reduzi-la ao formato em escada por linhas: [ ] [ ] [ ] Substituindo e pelos seus valores, obtemos a seguinte matriz: [ ] Podemos agora classificar o sistema (sabendo que operações de eliminação de Gauss não alteram o rank de uma matriz e notando que, depois de reduzidas ao formato em escada por linhas, tanto como têm 3 linhas não nulas): O sistema é possível e determinado Para resolver o sistema, podemos utilizar a Regra de Cramer: 6
11 Alternativamente, podemos resolver o sistema por eliminação de Gauss: [ ] [ ] [ ] [ ] [ ] De qualquer forma, a solução do sistema é o vector. b) A Zulmira, que queria ver se conseguia saber as pontuações, afirmou, mesmo sem saber: Eu sei que o b é 12. O Walter não achou graça e pensou Se a Zulmira acha que o b é 12, vou indicar-lhes um a que lhes dá mais do que uma solução para o problema. Descubra o a em que o Walter estava a pensar e indique o conjunto de soluções que resolvem o problema com este a e b. Substituindo pelo valor indicado pela Zulmira, obtemos a seguinte matriz: [ ] Agora, temos que dar um valor a para que o sistema seja possível e indeterminado. Sabendo que, tanto como vão ter sempre as duas primeiras linhas linearmente independentes, qualquer que seja o valor de, o rank destas matrizes vai ser não inferior a 7
12 2. Como queremos que o rank das duas matrizes seja igual e menor do que o número de variáveis do sistema, 3, temos que garantir que ambas as matrizes têm apenas duas linhas não nulas no formato em escada por linhas: O sistema é possível e indeterminado Vamos resolver o sistema com, começando por calcular o número de variáveis livres (ou a dimensão do subespaço constituído pelas soluções do sistema homogéneo que lhe está associado): N mero de variáveis livres Vamos agora resolver o sistema homogéneo associado, com a preocupação de resolver as suas equações em função de uma das variáveis (porque o sistema tem uma variável livre): { { { { } { } { } { } Agora, encontramos uma solução particular para o sistema original, dando um valor a 1 das variáveis (já que o sistema tem 1 variável livre) e encontrando o valor que as outras devem ter para que o sistema seja resolvido (podemos escolher, por exemplo): { { { { A solução geral do sistema é simplesmente a soma da solução particular encontrada com a solução do sistema homogéneo associado: c) O Yuri, depois de perceber que não conseguia resolver o problema com a informação dada pelo Walter, resolveu arriscar: Eu sei que o a é 2. Desta vez, o Walter ainda fez pior: Agora vez vou dar-lhes um b que torna o problema impossível de ser resolvido. Que valores é que pode tomar o b em que o Walter pensou? Substituindo 8 pelo valor indicado pelo Yuri, obtemos a seguinte matriz: [ ] Agora, temos que dar um valor a para que o sistema seja impossível. Sabendo que vai ter as 2 primeiras linhas linearmente independentes e nenhum conjunto de 3 linhas linearmente independentes (porque qualquer conjunto de 3 linhas, em, vai conter o vector nulo) e que vai ter as duas primeiras linhas linearmente independentes, qualquer que seja o valor de, o rank da primeira vai ser 2 e o da outra não inferior a 2. Como queremos que o rank de seja inferior ao de, temos que garantir que tem 3 linhas não nulas no formato em escada por linhas: O sistema é impossível
13 3 Depois de se despedirem do Walter, sem nunca terem sabido as pontuações, os três amigos foram para uma sala de jogos. Encontraram uma máquina que tinha 3 entradas para moedas e por baixo, 3 saídas. Não dizia quais eram as regras, só pedia para se introduzir moedas em cada uma das entradas e esperar pelo que saísse. Os três resolveram experimentá-la, ficando o Xavier com a entrada da esquerda, o Yuri com a do meio e a Zulmira a da direita. Primeiro, introduziram 1 Euro cada um. Ao Xavier saíram 2 Euros, ao Yuri 1 e à Zulmira não saiu nada. Depois, o Xavier introduziu 1 Euro, o Yuri 2 e a Zulmira nada. Ao Xavier saíram 3 Euros e ao Yuri e à Zulmira não saiu nada. Na terceira jogada, o Xavier introduziu 2 Euros e o Yuri e a Zulmira nada. Saiu a todos o que tinham introduzido. A Zulmira, mesmo sem ter ganho dinheiro, percebeu: Esta máquina opera uma transformação linear sobre o dinheiro dos 3 jogadores. a) Sabendo que desta vez a Zulmira tinha razão, calcule quanto é que sairia a cada um dos jogadores, se todos jogassem 2 Euros. Podemos pensar nos valores introduzidos por cada um dos jogadores como sendo coordenadas de pontos de. Assim, denominemos o valor introduzido pelo Xavier por, o dinheiro jogado pelo Yuri por e aquilo que a Zulmira insere na máquina por. Assim, temos: Vamos ver se os 3 objectos cuja imagem é conhecida são linarmente independentes: Os vectores são linearmente independentes e são uma base de (o espaço de partida da transformação linear operada por esta máquina), pois quaisquer 3 vectores linearmente independentes de são uma base deste espaço. Sendo uma base de, é possível escrever qualquer vector deste espaço como uma combinação linear destes 3 vectores. Vamos ver quais as coordenadas do vector nesta base: { { { Sabendo estas coordenadas, basta aplicar o conceito de transformação linear: [ ] 9
14 b) Indique o espaço de partida, o espaço de chegada e a expressão geral da transformação linear operada pela máquina. Vamos aplicar o mesmo raciocínio a um vector geral de : { { { ( ) ( ) * ( ) ( ) + ( ) ( ) ( ) ( ) ( ) ( ) A transformação linear transforma vectores de em vectores do mesmo espaço: c) Calcule a matriz que representa esta transformação linear na base canónica. { } { [ ] [ ] * + 10
15 [ ] A matriz de transformação na base canónica,, não é mais do que a matriz cujas colunas são as imagens dos vectores da base canónica. d) A Zulmira, que não ficou contente com o resultado do jogo, afirmou: Deviam inventar um jogo que transformasse todos os resultados do jogo que nós jogámos no dinheiro introduzido ao princípio, ou seja, que operasse a transformação inversa da deste jogo. É possível encontrar uma transformação linear que faça o que a Zulmira pretende? A Zulmira quer saber se a transformação linear operada pela máquina é invertível. Sabemos que uma transformação linear é invertível se e só se a matriz que a representa também for: transformação linear inversa e) O Xavier lembrou-se de dizer: Não há duas maneiras diferentes de introduzir dinheiro que dêm o mesmo resultado. Tem razão? (lembre-se que uma transformação linear é injectiva se e só se { }, ou seja, se o único ponto que é transformado no vector nulo é o próprio vector nulo). Sabendo que uma transformação linear é injectiva (ou seja, a cada imagem corresponde um e um só objecto) se e só se o seu núcleo é constituído apenas pelo vector nulo, apenas precisamos de calcular o núcleo da transformação: { } { } { } { } { } { } { } { } não é injectiva, logo há pelo menos uma imagem que corresponde a mais do que um objecto e, portanto, há duas maneiras diferentes de introduzir dinheiro que dão o mesmo resultado. f) O Yuri quis saber quais eram os conjuntos de valores introduzidos que se transformavam, através do jogo, em múltiplos de si próprios. Descubra se estes conjuntos de valores existem e, caso existam, quais os múltiplos que lhes estão associados. O Yuri quis saber, basicamente, quais os vectores e valores próprios desta transformação: [ ] [ ] : 11
16 [ ] * + [ ] { { { } { } { } { } : [ ] * + [ ] {, { } { } { } { } Há dois tipos de vectores próprios: os múltiplos do vector, associados ao valor próprio 1 e os múltiplos do vector, associados ao valor próprio 0. g) Para acabar, verifique se é possível construir outra máquina que opera o mesmo jogo que esta, mas que trabalha com Dólares Canadianos, tanto na entrada como na saída, de maneira a que a matriz que representa a transformação que opera seja diagonal. Aqui, é preciso descobrir se é possível construir o seguinte esquema da mesma transformação linear em bases diferentes, tal que seja uma matriz diagonal: A B A ser possível, é uma base de constituída por vectores próprios de e tem na diagonal principal os valores próprios de. Portanto, basta saber se existem ou não 3 vectores próprios independentes de. Para tal, basta analisar as multiplicidades algébrica e geométrica dos valores próprios de : multiplicidade de ( ) como raíz do polin mio característico multiplicidade de ( ) como raíz do polin mio característico 12
17 Como as multiplicidades algébrica e geométrica de diferem, não é possível encontrar uma base de de vectores próprios de e, por isso, não é possível diagonalizar esta matriz. 13
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Sistemas de Equações Lineares e Equações Vectoriais Aula 2 Álgebra Linear Pedro A. Santos
 Sistemas de Equações Lineares e Equações Vectoriais Aula 2 Álgebra Linear MEG Operações Elementares Trocar a posição de duas equações Multiplicar uma equação por uma constante diferente de zero Não alteram
Sistemas de Equações Lineares e Equações Vectoriais Aula 2 Álgebra Linear MEG Operações Elementares Trocar a posição de duas equações Multiplicar uma equação por uma constante diferente de zero Não alteram
Ficha de Exercícios nº 1
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
(2008/2009) Espaços vectoriais. Matemática 1º Ano - 1º Semestre 2008/2009. Mafalda Johannsen
 Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
ÁLGEBRA LINEAR A FICHA 2
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Teste 1 de Matemática I - Curso de Arquitectura
 Teste de Matemática I - Curso de Arquitectura de Outubro de 9 - Teste B Resolva por eliminação de Gauss e descreva geometricamente o conjunto de soluções dos sistemas em R < x + y + z = (a) ( val) x +
Teste de Matemática I - Curso de Arquitectura de Outubro de 9 - Teste B Resolva por eliminação de Gauss e descreva geometricamente o conjunto de soluções dos sistemas em R < x + y + z = (a) ( val) x +
Os Quatro Subespaços Fundamentais
 Álgebra Linear e Geometria Analítica Texto de apoio Professor João Soares 7 páginas Universidade de Coimbra 26 de Novembro de 29 Os Quatro Subespaços Fundamentais Seja A uma matriz m n de elementos reais.
Álgebra Linear e Geometria Analítica Texto de apoio Professor João Soares 7 páginas Universidade de Coimbra 26 de Novembro de 29 Os Quatro Subespaços Fundamentais Seja A uma matriz m n de elementos reais.
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear - Exercícios resolvidos
 Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
Exercício 1: Álgebra Linear - Exercícios resolvidos Sejam E = L({(1, 1, 1), (1, 2, 2)}) e F = L({(, 1, 1), (1, 1, 2)}). a) Determine a dimensão de E + F. b) Determine a dimensão de E F. Resolução: a) Temos
ÁLGEBRA LINEAR. Exame Final
 UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DE AVEIRO DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR Exame Final 9/0/00 DURAÇÃO: 3 horas Nome: N o Aluno: Observação: Declaro que desisto: (Justifique sempre as suas respostas) Folha. (4,0
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA
 UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
UNIVERSIDADE DO ALGARVE ESCOLA SUPERIOR DE TECNOLOGIA LICENCIATURA EM ENGENHARIA CIVIL/TOPOGRÁFICA REGIMES DIURNO/NOCTURNO - º SEMESTRE - º ANO - 7 / 8 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA EXAME DE ÉPOCA
{ 1 2 3, 2 4 6, T
 Ficha de rabalho 0 e 05 Espaços Vectoriais. (Aulas 9 a 1). Vectores em n. Vectores livres. Vectores em 2 e. Vectores em n. Vectores iguais. Soma de vectores. Produto de um escalar por um vector. Notação
Ficha de rabalho 0 e 05 Espaços Vectoriais. (Aulas 9 a 1). Vectores em n. Vectores livres. Vectores em 2 e. Vectores em n. Vectores iguais. Soma de vectores. Produto de um escalar por um vector. Notação
ESPAÇOS LINEARES (ou vetoriais)
 Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Álgebra Linear- 1 o Semestre 2018/19 Cursos: LEIC A Lista 3 (Espaços Lineares) ESPAÇOS LINEARES (ou vetoriais) Notações: Seja A uma matriz e S um conjunto de vetores Núcleo de A: N(A) Espaço das colunas
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Álgebra Linear Semana 05
 Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
Álgebra Linear Semana 5 Diego Marcon 4 de Abril de 7 Conteúdo Interpretações de sistemas lineares e de matrizes invertíveis Caracterizações de matrizes invertíveis 4 Espaços vetoriais 5 Subespaços vetoriais
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
ÁLGEBRA LINEAR. Base e Dimensão de um Espaço Vetorial. Prof. Susie C. Keller
 ÁLGEBRA LINEAR Base e Dimensão de um Espaço Vetorial Prof. Susie C. Keller Base de um Espaço Vetorial Um conjunto B = {v 1,..., v n } V é uma base do espaço vetorial V se: I) B é LI II) B gera V Base de
ÁLGEBRA LINEAR Base e Dimensão de um Espaço Vetorial Prof. Susie C. Keller Base de um Espaço Vetorial Um conjunto B = {v 1,..., v n } V é uma base do espaço vetorial V se: I) B é LI II) B gera V Base de
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial
 TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Álgebra Linear e Geometria Analítica. 7ª aula
 Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
Álgebra Linear e Geometria Anaĺıtica. Espaços Vetoriais Reais
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 4 Espaços Vetoriais Reais Definição de espaço vetorial real [4 01] O conjunto
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
Resolução do efólio B
 Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Resolução do efólio B Álgebra Linear I Código: 21002 I. Questões de escolha múltipla. Em cada questão de escolha múltipla apenas uma das afirmações a), b), c), d) é verdadeira. Indique-a marcando no quadrado
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
exercícios de álgebra linear 2016
 exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
exercícios de álgebra linear 206 maria irene falcão :: maria joana soares Conteúdo Matrizes 2 Sistemas de equações lineares 7 3 Determinantes 3 4 Espaços vetoriais 9 5 Transformações lineares 27 6 Valores
Indicação de uma possível resolução do exame
 Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Valores e vectores próprios
 ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
ALGA - Eng Civil e EngTopográ ca - ISE - / - Valores e vectores próprios 5 Valores e vectores próprios Neste capítulo, sempre que não haja especi cação em contrário, todas as matrizes envolvidas são quadradas
Matemática. Lic. em Enologia, 2009/2010
 Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Álgebra Linear e Geometria Analítica. Valores Próprios e Vectores Próprios
 Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Material Teórico - Módulo Matrizes e Sistemas Lineares. Sistemas Lineares - Parte 2. Terceiro Ano do Ensino Médio
 Material Teórico - Módulo Matrizes e Sistemas Lineares Sistemas Lineares - Parte 2 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto 1 A representação
Material Teórico - Módulo Matrizes e Sistemas Lineares Sistemas Lineares - Parte 2 Terceiro Ano do Ensino Médio Autor: Prof Fabrício Siqueira Benevides Revisor: Prof Antonio Caminha M Neto 1 A representação
3 a Lista para auto-avaliação (com um exercício resolvido)
 Álgebra Linear Cursos: Engenharia Civil, Engenharia de Minas, Engenharia do Território 1 ō ano/1 ō Semestre 21/211 3 a Lista para auto-avaliação (com um exercício resolvido) 1. Indique a característica
Álgebra Linear Cursos: Engenharia Civil, Engenharia de Minas, Engenharia do Território 1 ō ano/1 ō Semestre 21/211 3 a Lista para auto-avaliação (com um exercício resolvido) 1. Indique a característica
Álgebra Linear AL. Luiza Amalia Pinto Cantão. Depto. de Engenharia Ambiental Universidade Estadual Paulista UNESP
 Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Álgebra Linear AL Luiza Amalia Pinto Cantão Depto de Engenharia Ambiental Universidade Estadual Paulista UNESP luiza@sorocabaunespbr Espaços Vetoriais 1 Definição; 2 Subespaços; 3 Combinação Linear, dependência
Teste de avaliação (Versão B) Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 0º ANO DE MATEMÁTICA A 2-03 - 2007 Teste de avaliação (Versão B) Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 0º ANO DE MATEMÁTICA A 2-03 - 2007 Teste de avaliação (Versão B) Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
2009/2010-2º SEMESTRE- 2ª ÉPOCA EXAME DE ÁLGEBRA LINEAR (1303) 16 de Junho de Respostas
 Grupo 1 1- Considere o conjunto S 3 definido por: S x 1,x 2,x 3 3 : x 1 x 2 x 3 0 1.1- Mostre que S éumsub-espaço de 3. Determine a dimensão de S exibindo uma base B de S. [1/20] 1.2- Qual é o complemento
Grupo 1 1- Considere o conjunto S 3 definido por: S x 1,x 2,x 3 3 : x 1 x 2 x 3 0 1.1- Mostre que S éumsub-espaço de 3. Determine a dimensão de S exibindo uma base B de S. [1/20] 1.2- Qual é o complemento
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática
 UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
UNIVERSIDADE FEDERAL DE VIÇOSA Centro de Ciências Exatas Departamento de Matemática 2 a Lista - MAT 137 - Introdução à Álgebra Linear II/2005 1 Resolva os seguintes sistemas lineares utilizando o Método
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Teste 1 de Matemática I - Curso de Arquitectura
 Teste 1 de Matemática I - Curso de Arquitectura 8 de Outubro de 9 - Teste A 1 Resolva por eliminação de Gauss e descreva geometricamente o conjunto de soluções dossistemasemr : x + y + z = (a) (1 val)
Teste 1 de Matemática I - Curso de Arquitectura 8 de Outubro de 9 - Teste A 1 Resolva por eliminação de Gauss e descreva geometricamente o conjunto de soluções dossistemasemr : x + y + z = (a) (1 val)
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática 3 a Lista - MAT 137 - Introdução à Álgebra Linear 2017/II 1. Sejam u = ( 4 3) v = (2 5) e w = (a b).
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 2012/2013
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ficha 4 valores próprios e vectores próprios
 Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Formação Continuada Nova Eja. Plano de Ação II INTRODUÇÃO
 Nome: Armando dos Anjos Fernandes Formação Continuada Nova Eja Plano de Ação II Regional: Metro VI Tutor: Deivis de Oliveira Alves Este plano de ação contemplará as unidades 29 e 30. Unidade 29 I - Matrizes
Nome: Armando dos Anjos Fernandes Formação Continuada Nova Eja Plano de Ação II Regional: Metro VI Tutor: Deivis de Oliveira Alves Este plano de ação contemplará as unidades 29 e 30. Unidade 29 I - Matrizes
G2 de Álgebra Linear I
 G2 de Álgebra Linear I 2013.1 17 de Maio de 2013. Gabarito 1) Considere a transformação linear T : R 3 R 2 definida por: T (1, 1, 0) = (2, 2, 0), T (0, 1, 1) = (1, 0, 0) T (0, 1, 0) = (1, 1, 0). (a) Determine
G2 de Álgebra Linear I 2013.1 17 de Maio de 2013. Gabarito 1) Considere a transformação linear T : R 3 R 2 definida por: T (1, 1, 0) = (2, 2, 0), T (0, 1, 1) = (1, 0, 0) T (0, 1, 0) = (1, 1, 0). (a) Determine
TÓPICOS. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -1
 Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Note bem: a leitura destes apontamentos não dispensa de modo algum a leitura atenta da bibliografia principal da cadeira Chama-se a atenção para a importância do trabalho pessoal a realizar pelo aluno
Álgebra Linear. 8 a Lista: a) Use o processo de ortogonalização de Gram Schmidt para construir uma base ortonormada para W.
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais, Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07 8 a Lista: Nos exercícios em que n~ao se especifica
Expansão linear e geradores
 Espaços Vectoriais - ALGA - 004/05 Expansão linear e geradores Se u 1 ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u 1 ; u ;
Espaços Vectoriais - ALGA - 004/05 Expansão linear e geradores Se u 1 ; u ; :::; u n são vectores de um espaço vectorial V; como foi visto atrás, alguns vectores de V são combinação linear de u 1 ; u ;
6. Verifique detalhadamente que os seguintes conjuntos são espaços vetoriais(com a soma e produto por escalar usuais):
 a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
a Lista. Sejam u = ( 4 ) v = ( 5) e w = (a b). Encontre a e b tais que (a)w = u + v (b)w = 5v (c)u + w = u v. Represente os vetores acima no plano cartesiano.. Sejam u = (4 ) v = ( 4) e w = (a b c). Encontre
Sistemas de equações lineares
 Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Matemática II - / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a
Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática
 1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
1 Universidade Federal de Viçosa Centro de Ciências Exatas e Tecnológicas Departamento de Matemática Lista 4 - MAT 137 -Introdução à Álgebra Linear 2017/II 1. Entre as funções dadas abaixo, verifique quais
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
x 1 + b a 2 a 2 : declive da recta ;
 - O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
- O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
GAAL Exercícios 6: Umas soluções
 GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
GAAL Exercícios 6: Umas soluções. Quais dos seguintes vetores são combinação linear de u = (5, 3, ), v = (, 4, 3), w = (, 8, 7)? (a) (, 2, 5) (b) (, 2, 8) (c) ( 2, ) (d) (, 2, 3). O conjunto {u, v, w}
Álgebra Linear e Geometria Anaĺıtica. Matrizes e Sistemas de Equações Lineares
 universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
universidade de aveiro departamento de matemática Álgebra Linear e Geometria Anaĺıtica Agrupamento IV (ECT, EET, EI) Capítulo 1 Matrizes e Sistemas de Equações Lineares Geometria anaĺıtica em R 3 [1 01]
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 2018
 GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
Álgebra linear e geometria analítica
 27//29 o teste Álgebra linear e geometria analítica OCV Instruç~oes escolha n exercícios e responda em Portugu^es.. (2 valores) Determine uma equação cartesiana da recta que passa pelos pontos (, ) e (
27//29 o teste Álgebra linear e geometria analítica OCV Instruç~oes escolha n exercícios e responda em Portugu^es.. (2 valores) Determine uma equação cartesiana da recta que passa pelos pontos (, ) e (
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
7 Formas Quadráticas
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
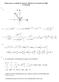 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
G2 de Álgebra Linear I
 G de Álgebra Linear I 7. Gabarito ) Considere o conjunto de vetores W = {(,, ); (, 5, ); (,, ); (3,, ); (, 3, ); (,, )}. (a) Determine a equação cartesiana do sub-espaço vetorial V gerado pelos vetores
G de Álgebra Linear I 7. Gabarito ) Considere o conjunto de vetores W = {(,, ); (, 5, ); (,, ); (3,, ); (, 3, ); (,, )}. (a) Determine a equação cartesiana do sub-espaço vetorial V gerado pelos vetores
Notas em Álgebra Linear
 Notas em Álgebra Linear 1 Pedro Rafael Lopes Fernandes Definições básicas Uma equação linear, nas variáveis é uma equação que pode ser escrita na forma: onde e os coeficientes são números reais ou complexos,
Notas em Álgebra Linear 1 Pedro Rafael Lopes Fernandes Definições básicas Uma equação linear, nas variáveis é uma equação que pode ser escrita na forma: onde e os coeficientes são números reais ou complexos,
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA
 FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
FACULDADE DE ENGENHARIA DA UNIVERSIDADE DO PORTO LEEC EXERCÍCIOS DE ÁLGEBRA Exercícios vários. Considere o conjunto C =, e a operação binária definida por a b = min(a, b). O conjunto C é, relativamente
Sistemas de Equações Lineares
 Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Espaços Vectoriais. Espaços Vectoriais
 Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Espaços Vectoriais Espaço vectorial sobre um corpo V - conjunto não vazio de objectos, chamados vectores F - conjunto de escalares, com estrutura de corpo Em V definimos duas operações: - adição de elementos
Ficha de Trabalho 09 e 10
 Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
Ficha de Trabalho 09 e 0 Diagonalização. (Aulas a 6). Diagonalização. Valores e vectores próprios. Equação característica. Matrizes semelhantes. Matriz diagonalizável. Factorização PDP -. Diagonalização
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A Teste de avaliação Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A 0 05 007 Teste de avaliação Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A 0 05 007 Teste de avaliação Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas quatro alternativas,
1 a LISTA DE EXERCÍCIOS Sistemas de Equações Lineares e Matrizes Álgebra Linear - 1 o Semestre /2018 Engenharia Aeroespacial
 1 a LISTA DE EXERCÍCIOS Sistemas de Equações Lineares e Matrizes Álgebra Linear - 1 o Semestre - 217/218 Engenharia Aeroespacial Problema 1 Calcule A 2 2B + I, ( ( 2 1 onde A =, B =, e I é a matriz identidade
1 a LISTA DE EXERCÍCIOS Sistemas de Equações Lineares e Matrizes Álgebra Linear - 1 o Semestre - 217/218 Engenharia Aeroespacial Problema 1 Calcule A 2 2B + I, ( ( 2 1 onde A =, B =, e I é a matriz identidade
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução da Repetição do 1º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste Realizado em 01 de Fevereiro de 2012 Ano Lectivo: 2011-2012 Semestre: Inverno ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução da Repetição do 1º Teste Realizado em 01 de Fevereiro de 2012 Ano Lectivo: 2011-2012 Semestre: Inverno ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Maria da Graça Marcos Marisa João Guerra Pereira de Oliveira Alcinda Maria de Sousa Barreiras
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Maria da Graça Marcos Marisa João Guerra Pereira de Oliveira Alcinda Maria de Sousa Barreiras EDIÇÃO, DISTRIBUIÇÃO E VENDAS SÍLABAS & DESAFIOS - UNIPESSOAL LDA. NIF:
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Maria da Graça Marcos Marisa João Guerra Pereira de Oliveira Alcinda Maria de Sousa Barreiras EDIÇÃO, DISTRIBUIÇÃO E VENDAS SÍLABAS & DESAFIOS - UNIPESSOAL LDA. NIF:
(Todos os cursos da Alameda) Paulo Pinto
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Resumo das Aulas Teóricas de 2 o Semestre 2004/2005 (Todos os cursos da Alameda) Paulo Pinto Álgebra Linear Conteúdo Sistemas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Resumo das Aulas Teóricas de 2 o Semestre 2004/2005 (Todos os cursos da Alameda) Paulo Pinto Álgebra Linear Conteúdo Sistemas
Álgebra Linear 1 o Teste
 Instituto Superior Técnico Departamento de Matemática 1 o Semestre 2008-2009 6/Janeiro/2008 Prova de Recuperação Álgebra Linear 1 o Teste MEMec, MEAer Nome: Número: Curso: Sala: A prova que vai realizar
Instituto Superior Técnico Departamento de Matemática 1 o Semestre 2008-2009 6/Janeiro/2008 Prova de Recuperação Álgebra Linear 1 o Teste MEMec, MEAer Nome: Número: Curso: Sala: A prova que vai realizar
Sistemas de equações lineares
 ALGA- / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b
ALGA- / - Sistemas de Equações Lineares Sistemas de equações lineares Introdução Uma equação linear nas incógnitas ou variáveis x ; x ; :::; x n é uma expressão da forma: a x + a x + ::: + a n x n = b
Aulas Teóricas de Álgebra Linear
 Aulas Teóricas de Álgebra Linear Instituto Superior Técnico - o Semestre 009/00 MEAmbi - MEBiol Matrizes De nição Uma matriz A, do tipo m n (m por n), é uma tabela de mn números dispostos em m linhas e
Aulas Teóricas de Álgebra Linear Instituto Superior Técnico - o Semestre 009/00 MEAmbi - MEBiol Matrizes De nição Uma matriz A, do tipo m n (m por n), é uma tabela de mn números dispostos em m linhas e
Profs. Alexandre Lima e Moraes Junior 1
 Raciocínio Lógico-Quantitativo para Traumatizados Aula 07 Matrizes, Determinantes e Solução de Sistemas Lineares. Conteúdo 7. Matrizes, Determinantes e Solução de Sistemas Lineares...2 7.1. Matrizes...2
Raciocínio Lógico-Quantitativo para Traumatizados Aula 07 Matrizes, Determinantes e Solução de Sistemas Lineares. Conteúdo 7. Matrizes, Determinantes e Solução de Sistemas Lineares...2 7.1. Matrizes...2
G2 de Álgebra Linear I
 G2 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Suponha
G2 de Álgebra Linear I 2008.1 Gabarito 1) Decida se cada afirmação a seguir é verdadeira ou falsa e marque COM CANETA sua resposta no quadro a seguir. Itens V F N 1.a x 1.b x 1.c x 1.d x 1.e x 1.a) Suponha
ALGA I. Representação matricial das aplicações lineares
 Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
Módulo 6 ALGA I Representação matricial das aplicações lineares Contents 61 Matriz de uma aplicação linear 76 62 Cálculo do núcleo e imagem 77 63 Matriz da composta 78 64 GL(n Pontos de vista passivo e
AULA 13 { } 13. Exercícios. DETERMINAR UMA BASE DE UM SUBESPAÇO Determinar uma base do subespaço de
 Prof. Isabel Matos & José Amaral ALGA A - 8--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R W ma ve que qualquer conjunto
Prof. Isabel Matos & José Amaral ALGA A - 8--9. Eercícios. DETERMINAR MA ASE DE M SESPAÇO... Determinar uma base do subespaço de R { } (,,, ) (,,, ) : ( ) ( ) L u u u u R W ma ve que qualquer conjunto
2012/2013-1º SEMESTRE- 1ª ÉPOCA EXAME DE ÁLGEBRA LINEAR (1303) 2 de Janeiro de 2013
 / - º SEMESTRE- ª ÉPOCA EXAME DE ÁLGEBRA LINEAR () de Janeiro de Grupo - Considere o conjunto C t,,t : t..- Mostre que C é um sub-espaço de. [/].- Mostre que qualquer vector z C é uma combinação linear
/ - º SEMESTRE- ª ÉPOCA EXAME DE ÁLGEBRA LINEAR () de Janeiro de Grupo - Considere o conjunto C t,,t : t..- Mostre que C é um sub-espaço de. [/].- Mostre que qualquer vector z C é uma combinação linear
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO
 ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO Matemática 10º ANO Novembro 004 Ficha de Trabalho nº 4 - Conjuntos de pontos e condições Distância entre dois pontos Mediatriz de um segmento de recta Circunferência
ESCOLA SECUNDÁRIA DE ALBERTO SAMPAIO Matemática 10º ANO Novembro 004 Ficha de Trabalho nº 4 - Conjuntos de pontos e condições Distância entre dois pontos Mediatriz de um segmento de recta Circunferência
Aula 5 - Produto Vetorial
 Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Aula 5 - Produto Vetorial Antes de iniciar o conceito de produto vetorial, precisamos recordar como se calculam os determinantes. Mas o que é um Determinante? Determinante é uma função matricial que associa
Álgebra Linear Exercícios Resolvidos
 Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
Álgebra Linear Exercícios Resolvidos Agosto de 001 Sumário 1 Exercícios Resolvidos Uma Revisão 5 Mais Exercícios Resolvidos Sobre Transformações Lineares 13 3 4 SUMA RIO Capítulo 1 Exercícios Resolvidos
CM 005 Álgebra Linear: Prova 1 22 de Setembro de 2016
 CM 5 Álgebra Linear: Prova 1 22 de Setembro de 216 Orientações gerais 1) As soluções devem conter o desenvolvimento e ou justicativa. Questões sem justicativa ou sem raciocínio lógico coerente não pontuam.
CM 5 Álgebra Linear: Prova 1 22 de Setembro de 216 Orientações gerais 1) As soluções devem conter o desenvolvimento e ou justicativa. Questões sem justicativa ou sem raciocínio lógico coerente não pontuam.
Álgebra Linear Semana 02
 Álgebra Linear Semana 2 Diego Marcon 3 de Abril de 27 Conteúdo Vetores Representação matricial para sistemas Lineares 3 2 Combinações lineares de vetores 4 3 Sistemas lineares e combinações lineares das
Álgebra Linear Semana 2 Diego Marcon 3 de Abril de 27 Conteúdo Vetores Representação matricial para sistemas Lineares 3 2 Combinações lineares de vetores 4 3 Sistemas lineares e combinações lineares das
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Espaços Euclidianos. Espaços R n. O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais:
 Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Espaços Euclidianos Espaços R n O conjunto R n é definido como o conjunto de todas as n-uplas ordenadas de números reais: R n = {(x 1,..., x n ) : x 1,..., x n R}. R 1 é simplesmente o conjunto R dos números
Teste de avaliação (Versão A) Grupo I
 ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A 09-03 - 007 Teste de avaliação (Versão A) Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
ESCOLA SECUNDÁRIA COM 3º CICLO D. DINIS 10º ANO DE MATEMÁTICA A 09-03 - 007 Teste de avaliação (Versão A) Grupo I As cinco questões deste grupo são de escolha múltipla. Para cada uma delas são indicadas
Geometria Analítica e Álgebra Linear
 UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
Colectânea de Exercícios
 ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
ÁLGEBRA Colectânea de Exercícios P. Milheiro de Oliveira 1998/1999 Departamento de Engenharia Civil Faculdade de Engenharia da Universidade do Porto A presente colectânea de exercícios foi elaborada para
Escola Secundária de Lousada. Ficha de Trabalho de Matemática do 9.º Ano N.º
 Escola Secundária de Lousada Ficha de Trabalho de Matemática do 9.º Ano N.º Assunto: Preparação para o 3º Teste de Avaliação Lições nº e Data: /0/01 Apresentação dos Conteúdos e Objectivos para o 3º Teste
Escola Secundária de Lousada Ficha de Trabalho de Matemática do 9.º Ano N.º Assunto: Preparação para o 3º Teste de Avaliação Lições nº e Data: /0/01 Apresentação dos Conteúdos e Objectivos para o 3º Teste
. (1) Se S é o espaço vetorial gerado pelos vetores 1 e,0,1
 QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
QUESTÕES ANPEC ÁLGEBRA LINEAR QUESTÃO 0 Assinale V (verdadeiro) ou F (falso): (0) Os vetores (,, ) (,,) e (, 0,) formam uma base de,, o espaço vetorial gerado por,, e,, passa pela origem na direção de,,
Material Teórico - O Plano Cartesiano e Sistemas de Equações. Sistemas de Equações do Primeiro Grau com Duas Incógnitas
 Material Teórico - O Plano Cartesiano e Sistemas de Equações Sistemas de Equações do Primeiro Grau com Duas Incógnitas Sétimo Ano do Ensino Fundamental Prof Francisco Bruno Holanda Prof Antonio Caminha
Material Teórico - O Plano Cartesiano e Sistemas de Equações Sistemas de Equações do Primeiro Grau com Duas Incógnitas Sétimo Ano do Ensino Fundamental Prof Francisco Bruno Holanda Prof Antonio Caminha
