4. Tensores cartesianos em 3D simétricos
|
|
|
- Giulia Amarante Branco
- 5 Há anos
- Visualizações:
Transcrição
1 4. Tensores cartesianos em D simétricos 4.1 Valores e vectores próprios ou valores e direcções principais Em D não é possível deduzir as fórmulas que determinam os valores e as direcções principais na forma puramente analítica, como em D. Por essa razão é necessário determinar os valores principais, usando a definição que faz parte da disciplina Álgebra linear. Os valores principais são os valores que asseguram que eiste uma solução não-trivial v da equação abaio. T I v 0 Em D, a equação matricial acima corresponde a três equações algébricas lineares homogéneas para as três incógnitas que são as componentes do vector v, T v, v, v, e onde ainda eiste o parâmetro. As referidas equações são algébricas, porque não envolvem funções trigonométricas, nem outras semelhantes; são lineares porque as incógnitas aparecem apenas com epoente um, e são homogéneas porque todos os termos contêm uma das incógnitas e assim o lado direito de cada equação é nulo. Sabe-se que este sistema de equações tem sempre uma solução trivial,, um vector em que cada componente é nula, independente do valor. A solução não-trivial, a solução em que pelo menos uma das componentes do vector v é diferente de zero, eiste apenas quando o determinante da matriz formada pelos coeficientes do sistema é nulo. Neste caso, a solução não-trivial não está unicamente definida, mas eistem infinitas soluções linearmente dependentes. Os números que asseguram a nulidade do determinante da matriz de coeficientes chamamse valores próprios (principais). A cada um desses valores eistem infinitas soluções de vector v que se chamam direcções (vectores) próprios (principais). 4. Determinação e propriedades Analisando o determinante da matriz de coeficientes, obtém-se: det T Ty T z T I det Ty Ty Tyz Tz Tyz Tz T Ty Tz TTy TyTz TTz Tyz Tz Ty T T T T T T T T T T T T y yz z yz y z z y T T T T T T T T T T T T y yz z yz y z z y
2 Como a epressão iguala-se ao zero, costuma-se apresentar com o sinal trocado: T Ty Tz TTy TyTz TTz Tyz Tz Ty T T T T T T T T T T T T y yz z yz y z z y 0 Esta equação chama-se, equação característica. A equação característica é uma equação cúbica, por isso tem três raízes. As raízes podem ser simples, ou uma dupla e uma simples. O caso de uma raiz tripla será abordado posteriormente. Em todos os casos pode-se comprovar que as raízes são números reais, devido ao facto de T ser simétrico. Os coeficientes da equação característica são invariantes fundamentais. I1 I I 0 Assim, analogamente como em D: I1 T Ty Tz corresponde ao traço de T I T T T T T T T T T T T T ao determinante de y yz z yz y z z y T. I T T T T T T T T T é na realidade a soma de sub-determinantes diagonais y y z z yz z y T Ty T T Ty T z yz de segunda ordem,, I T T T T T T em que o primeiro termo y y z z yz z obtém-se cortando a terceira linha e a terceira coluna, o segundo termo cortando a segunda linha e coluna, e o último termo cortando a primeira linha e coluna. Assim, os invariantes I, I, I correspondem à soma de sub-determinantes diagonais de primeira, segunda e 1 terceira ordem. Em alternativa, os invariantes fundamentais são também chamados invariante linear, quadrático e cúbico. Note-se que por eemplo os valores principais são também invariantes, mas neste caso não fundamentais. Eiste uma forma analítica que define as raízes. Para isso introduz-se um ângulo auiliar na forma 1 I 9I I 7I arccos / I1 I depois as raízes calculam-se de: I I I cos j, j 0,1, 1 j Para a utilização correcta da fórmula acima tem que se ter cuidado com o ângulo. Quando usado em radianos, soma-se com /, quando usado em graus, soma-se com 10º.
3 Pode-se ainda comprovar que aplicando a metodologia de D ao D, os resultados finais verificam as fórmulas já deduzidas. det T T T I T T T Ty Ty y det y y y y y traço det 0 T T T T T T T I1 I Aplicando a fórmula que calcula raízes de uma equação quadrática: T T T T 4 I1 I1 y y 1, I Tm TTy Ty T Ty TT y Tm Ty Tm R 4 Depois de resolver os valores principais, estes por convenção ordenam-se de acordo com a grandeza T1 T T. Assim T 1 corresponde ao valor principal máimo,, ao valor máimo de todas as possíveis componentes normais para todas as possíveis rotações do referencial. T corresponde ao valor principal mínimo, ao valor mínimo de todas as possíveis componentes normais para todas as possíveis rotações do referencial, e T é o valor principal intermédio. As componentes do tensor no referencial principal são assim T princ T T T, tal como em D os valores fora da diagonal (valores tangenciais) são nulos. A matriz de componentes chama-se neste caso, a matriz canónica. Sabendo os valores principais pode proceder-se ao cálculo das direcções principais. Este cálculo tem que ser, em princípio, feito para cada valor principal separadamente. Para isso um valor calculado, por eemplo T i onde i=1, ou, substitui-se no sistema de equações T Ti I v 0 i T Ti Ty T v z 0 i Ty Ty Ti Tyz vy 0 T i z Tyz Tz T i v 0 z
4 Já se sabe que o determinante do sistema é nulo e por isso eistem infinitas soluções nãotriviales. Quando o valor T i é uma raiz simples, pode comprovar-se que o sistema acima está composto por duas equações linearmente independentes e que a terceira é já dependente das outras duas,, que o posto da matriz de coeficientes é igual a dois. Neste caso eiste uma liberdade na definição de componentes do vector principal correspondente, e consequentemente todas as soluções do sistema formam apenas uma única direcção. Por outras palavras, se o vector não-trivial sistema definem-se por procedimento de cálculo. i i v resolve o sistema, depois todas as soluções do v onde é qualquer número real. Isso permite definir o No primeiro passo pode arbitrar-se qualquer componente do vector i v por qualquer número diferente de zero. Habitualmente escolhe-se um número simples, por eemplo i v 1. No segundo passo pode escolher-se quaisquer duas equações e substituir nelas o valor i arbitrado v 1. Isso forma duas equações não homogéneas que têm uma única solução para as duas restantes componentes do vector i v : i i v e v. No terceiro passo, a equação não utilizada serve para a verificação do cálculo. Este processo pode repetir-se para cada valor principal simples. Pode comprovar-se que tal como em D, as direcções principais são mutuamente ortogonais. Isso pode facilitar o cálculo. Por eemplo, no caso de três raízes simples da equação característica, podem calcular-se duas direcções principais pelo método descrito acima e a terceira direcção via produto eterno. Antes de fazer o produto eterno, convém verificar a ortogonalidade das direcções calculadas pelo produto interno. Por eemplo, sabendo os vectores 1 v e v 1 1 1, é válido v v v v v v 0 y y z z Esta verificação pode fazer-se para qualquer forma dos vectores calculados,, se for conveniente pode-se alterar o vector calculado para y i z v usando qualquer número diferente de zero, ou normalizar. O terceiro vector calcula-se pelo produto eterno. Neste caso a ordem de multiplicação deve seguir a regra de mão direita v v v 1 porque os vectores calculados usam-se para definir o referencial principal e este tem que ser directo. Usando vectores normalizados, o terceiro vector também sairá unitário. Depois de calcular v, o sistema
5 T T Ty T v z 0 T T T T v 0 y y yz y T z Tyz Tz T v 0 z serve para verificação. Para definir o referencial principal, tal como em D, é mais habitual usar a base do referencial,, vectores normalizados. Neste caso usa-se a designação vectores base formam a matriz de rotação 1 e e e R e e e e e e 1 e, e e No caso eplicado acima, onde se teve cuidado na ordem de multiplicação para cumprir a regra de mão direita, já se sabe que o determinante da matriz de rotação vale +1. No caso de dúvida, pode calcular-se o determinante para a verificação. Se o determinante valer -1, é necessário virar um dos vectores base ao contrário. Da disciplina de Álgebra linear, sabe-se que mudando os sinais numa linha, muda o sinal do determinante. Com esta regra conseguemse atingir os sentidos dos vectores base pretendidos e manter o valor do determinante +1. e. Os Em casos ecepcionais é necessário introduzir alterações no procedimento descrito acima. Por eemplo, no caso do tensor definido pelas componentes no referencial 0yz T Pode calcular-se que o valor principal máimo é 150 e este valor é simples. Para calcular o primeiro vector principal constrói-se o sistema v vy v 0 z Neste caso o posto matricial equivale a dois, tal como dito, mas verifica-se que a primeira linha na matriz é uma multiplicação da segunda , , 87 60
6 Isso significa que não há liberdade na escolha das equações porque a primeira é igual à segunda,, não podem ser escolhidas as primeiras duas equações, mas por eemplo a primeira e a terceira, ou a segunda e a terceira. Isso podia detectar-se durante a resolução, 1 arbitrando v v 480v 688 v v y z y z 87vy 60vz z z v 60v Como o resultado corresponde à identidade, isso significa que há infinitas soluções. Como se sabe que a solução tem que ser única, pode concluir-se que não podem ser escolhidas as primeiras duas equações, mas por eemplo a primeira e a terceira, ou a segunda e a terceira. Assim v 480v 688 v v y z y z 60vy 145vz vz 145vz ,1vz 480 vz 0 e por isso v, 1 4 y v 1,,0 1 4 T Este eemplo eplicou o que fazer quando a escolha de equações não dá o resultado esperado. A resolução do problema era por alteração da selecção das equações. Note-se que neste caso não se chegou à contradição, mas sim, à identidade, à identificação insuficiente. Os vectores principais foram definidos como vectores não-triviales, o que não impede que uma das componentes seja nula. Este caso foi demostrado no problema anterior. Facilmente chegase à conclusão que no primeiro passo do método de resolução, onde se arbitra uma das componentes por um número diferente de zero, pode-se introduzir uma contradição. 1 1 Arbitrando no problema anterior v 1 em vez de v 1, têm-se z
7 v 516v 480 v v y y 480v 60vy , v v 145 que é contradição. Como se sabe que a solução tem que ser única, sem contradições, pode concluir-se que a escolha da componente não estava correcta. Na realidade eistem apenas duas opções, o valor nulo ou diferente de zero, porque esta propriedade mantém-se, qualquer que seja a multiplicação. Se o valor não nulo conduziu à contradição, significa que este valor tem que ser nulo. Em alternativa, e no caso de dúvida, bastava arbitrar outra componente do vector e repetir a resolução das equações. 4. Casos particulares 4.4 Valores etremos fora da diagonal 4.5 O tensor de inércia 5. Análise tensorial
Tensores cartesianos. Grandezas físicas como funções de posição e/ou de tempo
 ensores cartesianos Quantidades (grandeas) físicas: Classificação: Escalares Vectores ensores de segunda ordem... ensores de ordem ero ensores de primeira ordem ensores de segunda ordem... Relacionadas
ensores cartesianos Quantidades (grandeas) físicas: Classificação: Escalares Vectores ensores de segunda ordem... ensores de ordem ero ensores de primeira ordem ensores de segunda ordem... Relacionadas
Cap. 1. Tensores cartesianos, cálculo tensorial, aplicação aos momentos de inércia
 Cap. 1. ensores cartesianos, cálculo tensorial, aplicação aos momentos de inércia 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores.
Cap. 1. ensores cartesianos, cálculo tensorial, aplicação aos momentos de inércia 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores.
Cap. 0. Cálculo tensorial
 Cap. 0. Cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores. Álgebra tensorial 3. ensores cartesianos em D simétricos
Cap. 0. Cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores. Álgebra tensorial 3. ensores cartesianos em D simétricos
2.1 Translação, rotação e deformação da vizinhança elementar Variação relativa do comprimento (Extensão)
 Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
Cap.. Deformação 1. Deslocamento. Gradiente de deformação.1 ranslação, rotação e deformação da vizinhança elementar 3. ensor de deformação de agrange 4. ensor das pequenas deformações 4.1 Caracter tensorial
ÁLGEBRA LINEAR A FICHA 2
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 7/Out/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Matrizes: Inversão e Formas
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
G3 de Álgebra Linear I 11.1 Gabarito 1) Seja A : R 3 R 3 uma transformação linear cuja matriz na base canônica é 4 [A] = 4. 4 (a) Determine todos os autovalores de A. (b) Determine, se possível, uma forma
P4 de Álgebra Linear I de junho de 2005 Gabarito
 P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
P4 de Álgebra Linear I 25.1 15 de junho de 25 Gabarito 1) Considere os pontos A = (1,, 1), B = (2, 2, 4), e C = (1, 2, 3). (1.a) Determine o ponto médio M do segmento AB. (1.b) Determine a equação cartesiana
6 Valores e Vectores Próprios de Transformações Lineares
 Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
Nova School of Business and Economics Prática Álgebra Linear 6 Valores e Vectores Próprios de Transformações Lineares 1 Definição Valor próprio de uma transformação linear ( ) Número real (ou complexo)
7 Formas Quadráticas
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Cap. 1. Tensores cartesianos, cálculo tensorial
 Cap. 1. ensores cartesianos, cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores. Álgebra tensorial 3. ensores cartesianos
Cap. 1. ensores cartesianos, cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores 1.3 Definição dos tensores. Álgebra tensorial 3. ensores cartesianos
G3 de Álgebra Linear I
 G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
G de Álgebra Linear I 7 Gabarito ) Considere a transformação linear T : R R cuja matriz na base canônica E = {(,, ), (,, ), (,, )} é [T] E = a) Determine os autovalores de T e seus autovetores correspondentes
Tópicos para a resolução do exame de Álgebra de 11 de Janeiro de 2000 (1ª Chamada)
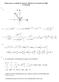 6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
6 & ' 6 a Tópicos para a resolução do eame de Álgebra de de Janeiro de 000 (ª Chamada) Im z z - - z Re b c d ( artg ) ( artg ) ; 9 6 ; z e z e e z e 6 6 p e z e z z ( )e ( ) e ( ) ( ) i z z z z z 6 Re(
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC
 Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
Universidade Federal de Alagoas UFAL Centro de Tecnologia - CTEC Programa de Pós-Graduação em Engenharia Civil - PPGEC Introdução à Mecânica do Contínuo Tensores Professor: Márcio André Araújo Cavalcante
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
G4 de Álgebra Linear I 013.1 8 de junho de 013. Gabarito (1) Considere o seguinte sistema de equações lineares x y + z = a, x z = 0, a, b R. x + ay + z = b, (a) Mostre que o sistema é possível e determinado
G3 de Álgebra Linear I
 G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
G3 de Álgebra Linear I 2.2 Gabarito ) Considere a matriz 4 N = 4. 4 Observe que os vetores (,, ) e (,, ) são dois autovetores de N. a) Determine uma forma diagonal D de N. b) Determine uma matriz P tal
Tensores Cartesianos
 Tensores Cartesianos Mecânica II Notas de apoio à disciplina de Mecânica II Vitor Leitão Departamento de Engenharia Civil e Arquitectura Instituto Superior Técnico Lisboa, 2011 vitor@civil.ist.utl.pt -
Tensores Cartesianos Mecânica II Notas de apoio à disciplina de Mecânica II Vitor Leitão Departamento de Engenharia Civil e Arquitectura Instituto Superior Técnico Lisboa, 2011 vitor@civil.ist.utl.pt -
ADA 1º BIMESTRE CICLO I 2018 MATEMÁTICA 2ª SÉRIE DO ENSINO MÉDIO
 ADA º BIMESTRE CICLO I 08 MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO ITEM DA ADA Um sistema de equações pode ser usado para representar situações-problemas da matemática ou do dia-a-dia. Assinale a alternativa
ADA º BIMESTRE CICLO I 08 MATEMÁTICA ª SÉRIE DO ENSINO MÉDIO ITEM DA ADA Um sistema de equações pode ser usado para representar situações-problemas da matemática ou do dia-a-dia. Assinale a alternativa
Sumário e Objectivos. 2007/2008 Lúcia M.J.S.Dinis. Mecânica dos Sólidos 2ªAula
 Sumário e Objectivos Sumário: Equações de Equilíbrio de Forças e Momentos. Mudança de Eixos de Referência. Tensões Principais e Direcções Principais. Invariantes das Tensões. Tensor Hidrostático ou Isotrópico.
Sumário e Objectivos Sumário: Equações de Equilíbrio de Forças e Momentos. Mudança de Eixos de Referência. Tensões Principais e Direcções Principais. Invariantes das Tensões. Tensor Hidrostático ou Isotrópico.
(2008/2009) Espaços vectoriais. Matemática 1º Ano - 1º Semestre 2008/2009. Mafalda Johannsen
 Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
Espaços vectoriais Matemática 1º Ano 1º Semestre 2008/2009 Capítulos Características de um Espaço Vectorial Dimensão do Espaço Subespaço Vectorial Combinação Linear de Vectores Representação de Vectores
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 2018
 GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
GEOMETRIA II EXERCÍCIOS RESOLVIDOS - ABRIL, 08 ( Seja a R e f(x, y ax + ( ay. Designe por C a a cónica dada por f(x, y 0. (a Mostre que os quatro pontos (±, ± R pertencem a todas as cónicas C a (independentemente
7 Formas Quadráticas
 Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Nova School of Business and Economics Prática Álgebra Linear 1 Definição Forma quadrática em variáveis Função polinomial, de grau, cuja expressão tem apenas termos de grau. Ex. 1: é uma forma quadrática
Ficha de Exercícios nº 3
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 3 Transformações Lineares, Valores e Vectores Próprios e Formas Quadráticas 1 Qual das seguintes aplicações não é uma transformação
2.1 Translação, rotação e deformação da vizinhança elementar. 4.3 Significado físico das pequenas deformações
 Sebenta da Disciplina MMC, Zuzana Dimitrovová, DEC/FC/UNL, 016 Cap. 4. Deformação 1. Deslocamento. Gradiente de deslocamento.1 ranslação, rotação e deformação da vizinhança elementar. Significado físico
Sebenta da Disciplina MMC, Zuzana Dimitrovová, DEC/FC/UNL, 016 Cap. 4. Deformação 1. Deslocamento. Gradiente de deslocamento.1 ranslação, rotação e deformação da vizinhança elementar. Significado físico
Cap. 3. Tensão. 1. Existência das forças internas. 2. Princípio das tensões de Euler e Cauchy. 3. Vector das tensões no ponto P
 Cap. 3. Tensão 1. Existência das forças internas 2. Princípio das tensões de Euler e Cauchy 3. Vector das tensões no ponto P 3.1 Componentes cartesianas 3.2 Componentes intrínsecas 4. Tensor das tensões
Cap. 3. Tensão 1. Existência das forças internas 2. Princípio das tensões de Euler e Cauchy 3. Vector das tensões no ponto P 3.1 Componentes cartesianas 3.2 Componentes intrínsecas 4. Tensor das tensões
Resistência dos Materiais 2003/2004 Curso de Gestão e Engenharia Industrial
 1/1 Resistência dos Materiais 3/4 Curso de Gestão e Engenharia Industrial 4ª Aula Duração - Horas Data - de Outubro de 3 Sumário: Mudança de Eixos de Referência. Tensões Principais e Direcções Principais.
1/1 Resistência dos Materiais 3/4 Curso de Gestão e Engenharia Industrial 4ª Aula Duração - Horas Data - de Outubro de 3 Sumário: Mudança de Eixos de Referência. Tensões Principais e Direcções Principais.
1 Espaços Vectoriais
 Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
Nova School of Business and Economics Apontamentos Álgebra Linear 1 Definição Espaço Vectorial Conjunto de elementos que verifica as seguintes propriedades: Existência de elementos: Contém pelo menos um
ficha 6 espaços lineares com produto interno
 Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
Exercícios de Álgebra Linear ficha espaços lineares com produto interno Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico o semestre 011/1 Notação
x 1 + b a 2 a 2 : declive da recta ;
 - O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
- O que é a Álgebra Linear? 1 - É a Álgebra das Linhas (rectas). Equação geral das rectas no plano cartesiano R 2 : a 1 x 1 + a 2 = b Se a 2 0, = a 1 a 2 x 1 + b a 2 : m = a 1 : declive da recta ; a 2
Indicação de uma possível resolução do exame
 Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Eame de Álgebra Linear e Geometria Analítica Eng Electrotécnica e Eng Mecânica 3 de Janeiro de 7 Duração horas, Tolerância 5 minutos (Sem consulta) Indicação de uma possível resolução do eame Considere
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Produto interno no espaço vectorial R n
 ALGA - 00/0 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
ALGA - 00/0 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Sistemas Retangulares
 Sistemas Retangulares Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2015.1 9 de julho
Sistemas Retangulares Márcio Nascimento Universidade Estadual Vale do Acaraú Centro de Ciências Exatas e Tecnologia Curso de Licenciatura em Matemática Disciplina: Álgebra Matricial - 2015.1 9 de julho
Geometria Analítica e Álgebra Linear
 UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
UNIFEI - Universidade Federal de Itajubá campus Itabira Geometria Analítica e Álgebra Linear Parte 1 Matrizes 1 Introdução A teoria das equações lineares desempenha papel importante e motivador da álgebra
P2 de Álgebra Linear I Data: 10 de outubro de Gabarito
 P2 de Álgebra Linear I 2005.2 Data: 10 de outubro de 2005. Gabarito 1 Decida se cada afirmação a seguir é verdadeira ou falsa. Itens V F N 1.a F 1.b V 1.c V 1.d F 1.e V 1.a Considere duas bases β e γ de
P2 de Álgebra Linear I 2005.2 Data: 10 de outubro de 2005. Gabarito 1 Decida se cada afirmação a seguir é verdadeira ou falsa. Itens V F N 1.a F 1.b V 1.c V 1.d F 1.e V 1.a Considere duas bases β e γ de
Gabarito P2. Álgebra Linear I ) Decida se cada afirmação a seguir é verdadeira ou falsa.
 Gabarito P2 Álgebra Linear I 2008.2 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Se { v 1, v 2 } é um conjunto de vetores linearmente dependente então se verifica v 1 = σ v 2 para algum
Gabarito P2 Álgebra Linear I 2008.2 1) Decida se cada afirmação a seguir é verdadeira ou falsa. Se { v 1, v 2 } é um conjunto de vetores linearmente dependente então se verifica v 1 = σ v 2 para algum
Instituto Superior Técnico Departamento de Matemática Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 18/Nov/2003 ÁLGEBRA LINEAR A REVISÃO DA PARTE III Parte III - (a) Ortogonalidade Conceitos: produto
Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc..
 Introdução a vetor Professor Fiore O que são grandezas? Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc.. O que são
Introdução a vetor Professor Fiore O que são grandezas? Chamamos de grandezas coisas que podem ser medidas. Por exemplo, tempo, área, volume, temperatura, velocidade, aceleração, força, etc.. O que são
Instituto Superior Técnico Departamento de Matemática Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A
 Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Instituto uperior Técnico Departamento de Matemática ecção de Álgebra e Análise Última actualização: 3/Dez/2003 ÁLGEBRA LINEAR A REVIÃO DA PARTE IV Parte IV - Diagonalização Conceitos: valor próprio, vector
Geometria Analítica. Números Reais. Faremos, neste capítulo, uma rápida apresentação dos números reais e suas propriedades, mas no sentido
 Módulo 2 Geometria Analítica Números Reais Conjuntos Numéricos Números naturais O conjunto 1,2,3,... é denominado conjunto dos números naturais. Números inteiros O conjunto...,3,2,1,0,1, 2,3,... é denominado
Módulo 2 Geometria Analítica Números Reais Conjuntos Numéricos Números naturais O conjunto 1,2,3,... é denominado conjunto dos números naturais. Números inteiros O conjunto...,3,2,1,0,1, 2,3,... é denominado
MATRIZES, DETERMINANTES E SISTEMAS LINEARES SISTEMAS LINEARES
 MATRIZES, DETERMINANTES E SISTEMAS LINEARES SISTEMAS LINEARES SISTEMAS LINEARES Equação linear Equação linear é toda equação da forma: a 1 x 1 + a 2 x 2 + a 3 x 3 +... + a n x n = b em que a 1, a 2, a
MATRIZES, DETERMINANTES E SISTEMAS LINEARES SISTEMAS LINEARES SISTEMAS LINEARES Equação linear Equação linear é toda equação da forma: a 1 x 1 + a 2 x 2 + a 3 x 3 +... + a n x n = b em que a 1, a 2, a
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1
 ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ALGEBRA LINEAR 1 RESUMO E EXERCÍCIOS* P1 *Exercícios de provas anteriores escolhidos para você estar preparado para qualquer questão na prova. Resoluções em VETORES Um vetor é uma lista ordenada de números
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 2012/2013
 ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
ESCOLA SUPERIOR DE TECNOLOGIA DE SETÚBAL DEPARTAMENTO DE MATEMÁTICA ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA TÓPICOS DE RESOLUÇÃO do Teste Final 0/0 A) B) C) D) [,0]. Considere as seguintes a rmações: I. ~x
- identificar operadores ortogonais e unitários e conhecer as suas propriedades;
 DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
DISCIPLINA: ELEMENTOS DE MATEMÁTICA AVANÇADA UNIDADE 3: ÁLGEBRA LINEAR. OPERADORES OBJETIVOS: Ao final desta unidade você deverá: - identificar operadores ortogonais e unitários e conhecer as suas propriedades;
ficha 5 transformações lineares
 Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Exercícios de Álgebra Linear ficha 5 transformações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12 5 Notação
Aulas práticas de Álgebra Linear
 Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
Ficha 3 Aulas práticas de Álgebra Linear Licenciatura em Engenharia Naval e Oceânica Mestrado Integrado em Engenharia Mecânica 1 o semestre 2018/19 Jorge Almeida e Lina Oliveira Departamento de Matemática,
G4 de Álgebra Linear I
 G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
G4 de Álgebra Linear I 27.1 Gabarito 1) Considere a base η de R 3 η = {(1, 1, 1); (1,, 1); (2, 1, )} (1.a) Determine a matriz de mudança de coordenadas da base canônica para a base η. (1.b) Considere o
Seja f um endomorfismo de um espaço vectorial E de dimensão finita.
 6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
6. Valores e Vectores Próprios 6.1 Definição, exemplos e propriedades Definição Seja f um endomorfismo de um espaço vectorial E, com E de dimensão finita, e seja B uma base arbitrária de E. Chamamos polinómio
Parte 1 - Matrizes e Sistemas Lineares
 Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Parte 1 - Matrizes e Sistemas Lineares Matrizes: Uma matriz de tipo m n é uma tabela com mn elementos, denominados entradas, e formada por m linhas e n colunas. A matriz identidade de ordem 2, por exemplo,
Álgebra Linear I - Aula 22
 Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Álgebra Linear I - Aula 1. Bases Ortonormais.. Matrizes Ortogonais. 3. Exemplos. 1 Bases Ortonormais Lembre que uma base β é ortogonal se está formada por vetores ortogonais entre si: para todo par de
Ficha de Exercícios nº 1
 Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Nova School of Business and Economics Álgebra Linear Ficha de Exercícios nº 1 Espaços Vectoriais 1 Qual das seguintes afirmações é verdadeira? a) Um espaço vectorial pode ter um número ímpar de elementos.
Álgebra Linear e Geometria Analítica. Valores Próprios e Vectores Próprios
 Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Álgebra Linear e Geometria nalítica Valores Próprios e Vectores Próprios Será assim para todos os vectores? R α α, Será assim para todos os vectores? Definição: Seja um número real e uma matriz quadrada
Análise de Tensões. Universidade Federal de Alagoas Centro de Tecnologia Curso de Engenharia Civil
 Universidade Federal de Alagoas Centro de Tecnologia Curso de Engenharia Civil Disciplina: Mecânica dos Sólidos Código: ECIV3 rofessor: Eduardo Nobre Lages Análise de Tensões Maceió/AL Agosto/14 Motivação
Universidade Federal de Alagoas Centro de Tecnologia Curso de Engenharia Civil Disciplina: Mecânica dos Sólidos Código: ECIV3 rofessor: Eduardo Nobre Lages Análise de Tensões Maceió/AL Agosto/14 Motivação
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial
 TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
TESTE FINAL DE ÁLGEBRA LINEAR 18 de Janeiro de 2017 Instituto Superior Técnico - Engenharia Aeroespacial Nome: Número: O que vai fazer? Só T1+T2 Só T3 T1+T2 e T3 Problema a b c d lalala Problema a b c
Lista de Álgebra Linear Aplicada
 Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
Lista de Álgebra Linear Aplicada Matrizes - Vetores - Retas e Planos 3 de setembro de 203 Professor: Aldo Bazán Universidade Federal Fluminense Matrizes. Seja A M 2 2 (R) definida como 0 0 0 3 0 0 0 2
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Matemática I. Capítulo 3 Matrizes e sistemas de equações lineares
 Matemática I Capítulo 3 Matrizes e sistemas de equações lineares Objectivos Matrizes especiais e propriedades do produto de matrizes Matriz em escada de linhas Resolução de sistemas de equações lineares
Matemática I Capítulo 3 Matrizes e sistemas de equações lineares Objectivos Matrizes especiais e propriedades do produto de matrizes Matriz em escada de linhas Resolução de sistemas de equações lineares
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO
 INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-458 Álgebra Linear para Engenharia II Terceira Lista de Eercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Seja V um espaço vetorial
INSTITUTO DE MATEMÁTICA E ESTATÍSTICA UNIVERSIDADE DE SÃO PAULO MAT-458 Álgebra Linear para Engenharia II Terceira Lista de Eercícios - Professor: Equipe da Disciplina EXERCÍCIOS 1. Seja V um espaço vetorial
Matemática C Semiextensivo v. 4
 Semietensivo v Eercícios ), aplicando o teorema de Laplace na ª coluna, temos que: A + A + A + A + + ( ) + ( ) ( + + + + ) + ( + + + 9 + ) + ) para qualquer valor de A + A + A + A + ( ) ( ) + ( ), ou seja,
Semietensivo v Eercícios ), aplicando o teorema de Laplace na ª coluna, temos que: A + A + A + A + + ( ) + ( ) ( + + + + ) + ( + + + 9 + ) + ) para qualquer valor de A + A + A + A + ( ) ( ) + ( ), ou seja,
Sistemas de Equações Lineares
 Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Capítulo 2 Sistemas de Equações Lineares 21 Generalidades Chamamos equação linear nas variáveis (incógnitas) x 1, x 2, x 3,, x n uma igualdade da forma a a 1 x 1 + a 2 x 2 + a 3 x 3 + + a n x n = b Os
Produto interno no espaço vectorial R n
 ALGA - 008/09 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
ALGA - 008/09 - Produto interno 8 Produto interno no espaço vectorial R n A noção de produto interno de vectores foi introduzida no ensino secundário, para vectores de R e R : Neste capítulo generaliza-se
Parte 3 - Produto Interno e Diagonalização
 Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
Parte 3 - Produto Interno e Diagonalização Produto Escalar: Sejam u = (u 1,..., u n ) e v = (v 1,..., v n ) dois vetores no R n. O produto escalar, ou produto interno euclidiano, entre esses vetores é
CAPÍTULO 2 CÁLCULO VECTORIAL Grandezas escalares e vectoriais. Noção de Vector. As grandezas físicas podem ser escalares ou vectoriais.
 CAPÍTULO CÁLCULO VECTORIAL.1. Grandeas escalares e vectoriais. Noção de Vector. As grandeas físicas podem ser escalares ou vectoriais. As grandeas massa, comprimento, tempo ficam completamente definidas
CAPÍTULO CÁLCULO VECTORIAL.1. Grandeas escalares e vectoriais. Noção de Vector. As grandeas físicas podem ser escalares ou vectoriais. As grandeas massa, comprimento, tempo ficam completamente definidas
Produto Misto, Determinante e Volume
 15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
15 Produto Misto, Determinante e Volume Sumário 15.1 Produto Misto e Determinante............ 2 15.2 Regra de Cramer.................... 10 15.3 Operações com matrizes............... 12 15.4 Exercícios........................
EXERCÍCIOS DE ÁLGEBRA LINEAR
 IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
IST - 1 o Semestre de 016/17 MEBiol, MEAmbi EXERCÍCIOS DE ÁLGEBRA LINEAR FICHA - Vectores e valores próprios 1 1 Vectores e valores próprios de transformações lineares Dada uma transformação linear T V!
ÁLGEBRA LINEAR A FICHA 6. Por definição do determinante de uma matriz 3 3, tem-se det A = 7.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Produto interno, externo e misto de vectores
 MTDI I - 00/08 - Produto Interno Produto interno, externo e misto de vectores A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass.
MTDI I - 00/08 - Produto Interno Produto interno, externo e misto de vectores A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para vectores com duas ou três coordenadass.
Cap. 1. Tensores cartesianos, cálculo tensorial
 Sebenta da Disciplina MMC, Zuzana Dimitrovová, DEC/FC/UNL, 016 Cap. 1. ensores cartesianos, cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores
Sebenta da Disciplina MMC, Zuzana Dimitrovová, DEC/FC/UNL, 016 Cap. 1. ensores cartesianos, cálculo tensorial 1. Quantidades físicas 1.1 ipos das quantidades físicas 1. Descrição matemática dos tensores
Produto interno no espaço vectorial R n
 ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
ALGA - Eng.Civil e Eng. Topográ ca - ISE - 00/0 - Produto Interno Produto interno no espaço vectorial R n A noção de produto interno (ou escalar) de vectores foi introduzida no ensino secundário, para
Métodos Numéricos - Notas de Aula
 Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares,
Métodos Numéricos - Notas de Aula Prof a Olga Regina Bellon Junho 2007 Introdução Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares,
LTDA APES PROF. RANILDO LOPES SITE:
 Matemática Aplicada - https://ranildolopes.wordpress.com/ - Prof. Ranildo Lopes - FACET 1 Faculdade de Ciências e Tecnologia de Teresina Associação Piauiense de Ensino Superior LTDA APES PROF. RANILDO
Matemática Aplicada - https://ranildolopes.wordpress.com/ - Prof. Ranildo Lopes - FACET 1 Faculdade de Ciências e Tecnologia de Teresina Associação Piauiense de Ensino Superior LTDA APES PROF. RANILDO
UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CAMPUS AVANÇADO DE NATAL CURSO DE CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR
 UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CAMPUS AVANÇADO DE NATAL CURSO DE CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROFESSOR: MARCELO SILVA 1. Introdução No ensino fundamental você estudou
UNIVERSIDADE DO ESTADO DO RIO GRANDE DO NORTE CAMPUS AVANÇADO DE NATAL CURSO DE CIÊNCIA DA COMPUTAÇÃO DISCIPLINA: ÁLGEBRA LINEAR PROFESSOR: MARCELO SILVA 1. Introdução No ensino fundamental você estudou
ALGA - Eng. Civil e Eng. Topográ ca - ISE / Geometria Analítica 89. Geometria Analítica
 ALGA - Eng. Civil e Eng. Topográ ca - ISE - 011/01 - Geometria Analítica 9 Geometria Analítica A noção de recta em R e R ; tal como a noção de plano em R já foram abordados no ensino secundário. Neste
ALGA - Eng. Civil e Eng. Topográ ca - ISE - 011/01 - Geometria Analítica 9 Geometria Analítica A noção de recta em R e R ; tal como a noção de plano em R já foram abordados no ensino secundário. Neste
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA. Resolução do 2º Teste
 ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 2º Teste 11 de Junho de 2013 Ano Lectivo: 2012-2013 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução
ÁLGEBRA LINEAR E GEOMETRIA ANALÍTICA Resolução do 2º Teste 11 de Junho de 2013 Ano Lectivo: 2012-2013 Semestre: Verão ISEL è ADM Secção de Álgebra ç ALGA Álgebra Linear e Geometria Analítica - Resolução
Exercícios de Álgebra Linear 2 o Semestre 2008/2009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC
 Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
Exercícios de Álgebra Linear o Semestre 008/009 LEIC, LEGM, LMAC, MEFT, MEBiom e MEC João Ferreira Alves/Ricardo Coutinho Sistemas de Equações Lineares e Matrizes Exercício Resolva por eliminação de Gauss
POLINÕMIOS E EQUAÇÕES POLINOMIAIS 2016
 POLINÕMIOS E EQUAÇÕES POLINOMIAIS 06. (Unicamp 06) Considere o polinômio cúbico p() a, onde a é um número real. a) No caso em que p() 0, determine os valores de para os quais a matriz A abaio não é invertível.
POLINÕMIOS E EQUAÇÕES POLINOMIAIS 06. (Unicamp 06) Considere o polinômio cúbico p() a, onde a é um número real. a) No caso em que p() 0, determine os valores de para os quais a matriz A abaio não é invertível.
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE MAIO DE 2017
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
Marcelo M. Santos DM-IMECC-UNICAMP msantos/
 Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Universidade Estadual de Maringá - Departamento de Matemática Cálculo Diferencial e Integral: um KIT de Sobrevivência 0 anos c Publicação Eletrônica do KIT http://www.dma.uem.br/kit Identificação de Cônicas
Notas sobre primitivas
 MTDI I - 007/08 - Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo I a uma função F cuja derivada
MTDI I - 007/08 - Notas sobre primitivas Notas sobre primitivas Seja f uma função real de variável real de nida num intervalo real I: Chama-se primitiva de f no intervalo I a uma função F cuja derivada
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS LINEARES
 EQUAÇÕES DIFERENCIAIS ORDINÁRIAS LINEARES Na disciplina de Análise Matemática, logo ao início de certos cursos de licenciatura, é usual tratar, entre outros temas, o das equações diferenciais, sejam ordinárias
EQUAÇÕES DIFERENCIAIS ORDINÁRIAS LINEARES Na disciplina de Análise Matemática, logo ao início de certos cursos de licenciatura, é usual tratar, entre outros temas, o das equações diferenciais, sejam ordinárias
a) 4x 10 = 0, onde x é a incógnita e 4 é 10 são os coeficientes. b) x + 3 = 4x + 8
 Equação do 1º Grau Introdução Equação é uma sentença matemática aberta epressa por uma igualdade envolvendo epressões matemáticas. Uma equação é composta por incógnitas e coeficientes (esses são conhecidos).
Equação do 1º Grau Introdução Equação é uma sentença matemática aberta epressa por uma igualdade envolvendo epressões matemáticas. Uma equação é composta por incógnitas e coeficientes (esses são conhecidos).
Espaços vectoriais reais
 ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
ALGA - 00/0 - Espaços Vectoriais 49 Introdução Espaços vectoriais reais O que é que têm em comum o conjunto dos pares ordenados de números reais, o conjunto dos vectores livres no espaço, o conjunto das
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 6 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE UMA
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... GRÁFICO DA FUNÇÃO DO º GRAU... IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 6 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE UMA
MAT2457 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 2015
 MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
MAT27 ÁLGEBRA LINEAR PARA ENGENHARIA I Gabarito da 2 a Prova - 1 o semestre de 201 Nesta prova considera-se fixada uma orientação do espaço e um sistema de coordenadas Σ (O, E) em E 3, em que E é uma base
Curso Satélite de. Matemática. Sessão n.º 1. Universidade Portucalense
 Curso Satélite de Matemática Sessão n.º 1 Universidade Portucalense Conceitos Algébricos Propriedades das operações de números reais Considerem-se três números reais quaisquer, a, b e c. 1. A adição de
Curso Satélite de Matemática Sessão n.º 1 Universidade Portucalense Conceitos Algébricos Propriedades das operações de números reais Considerem-se três números reais quaisquer, a, b e c. 1. A adição de
Todos os exercícios sugeridos nesta apostila se referem ao volume 1. MATEMÁTICA I 1 FUNÇÃO DO 1º GRAU
 FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... 5 GRÁFICO DA FUNÇÃO DO º GRAU... 5 IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 7 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE
FUNÇÃO IDENTIDADE... FUNÇÃO LINEAR... FUNÇÃO AFIM... 5 GRÁFICO DA FUNÇÃO DO º GRAU... 5 IMAGEM... COEFICIENTES DA FUNÇÃO AFIM... ZERO DA FUNÇÃO AFIM... 7 FUNÇÕES CRESCENTES OU DECRESCENTES... 7 SINAL DE
Nota importante: U é a matriz condensada obtida no processo de condensação da matriz
 Decomposição P T LU A denominada decomposição P T L U é um processo que pode ser extremamente útil no cálculo computacional, na resolução de sistemas de equações lineares. Propriedade Seja A uma matriz
Decomposição P T LU A denominada decomposição P T L U é um processo que pode ser extremamente útil no cálculo computacional, na resolução de sistemas de equações lineares. Propriedade Seja A uma matriz
UFSC Matrizes. Prof. BAIANO
 UFSC Matrizes Prof. BAIANO Matrizes Classifique como Verdadeiro ou Falso ( F ) Uma matriz é dita retangular, quando o número de linhas é igual ao número de colunas. ( F ) A matriz identidade é aquela em
UFSC Matrizes Prof. BAIANO Matrizes Classifique como Verdadeiro ou Falso ( F ) Uma matriz é dita retangular, quando o número de linhas é igual ao número de colunas. ( F ) A matriz identidade é aquela em
Agenda do Dia Aula 14 (19/10/15) Sistemas Lineares: Introdução Classificação
 Agenda do Dia Aula 14 (19/10/15) Sistemas Lineares: Introdução Classificação Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares. Um
Agenda do Dia Aula 14 (19/10/15) Sistemas Lineares: Introdução Classificação Sistemas Lineares Sistemas lineares são sistemas de equações com m equações e n incógnitas formados por equações lineares. Um
10 a Lista de Exercícios
 Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Álgebra Linear Licenciaturas: Eng. Biológica, Eng. Ambiente, Eng. Química, Química 1 ō ano 2004/05 10 a Lista de Exercícios Problema 1. Decida quais das expressões seguintes definem um produto interno.
Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores
 Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores Teoria dos Sinais e dos Sistemas O procedimento de Gram-Schmidt: definição, exemplos e aplicações Artur Ferreira {arturj@isel.pt}
Instituto Superior de Engenharia de Lisboa Engenharia Informática e de Computadores Teoria dos Sinais e dos Sistemas O procedimento de Gram-Schmidt: definição, exemplos e aplicações Artur Ferreira {arturj@isel.pt}
CDI-II. Resumo das Aulas Teóricas (Semana 5) 1 Extremos de Funções Escalares. Exemplos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Resumo das Aulas Teóricas (Semana 5) 1 Etremos de Funções Escalares. Eemplos Nos eemplos seguintes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Prof. Gabriel Pires CDI-II Resumo das Aulas Teóricas (Semana 5) 1 Etremos de Funções Escalares. Eemplos Nos eemplos seguintes
Álgebra Linear e Geometria Analítica. 7ª aula
 Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
Álgebra Linear e Geometria Analítica 7ª aula ESPAÇOS VECTORIAIS O que é preciso para ter um espaço pç vectorial? Um conjunto não vazio V Uma operação de adição definida nesse conjunto Um produto de um
com 3 Incógnitas A interseção do plano paralelo ao plano yz, passando por P, com o eixo x determina a coordenada x.
 Interpretação Geométrica de Sistemas Lineares com 3 Incógnitas Reginaldo J. Santos Departamento de Matemática Instituto de Ciências Eatas Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi
Interpretação Geométrica de Sistemas Lineares com 3 Incógnitas Reginaldo J. Santos Departamento de Matemática Instituto de Ciências Eatas Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi
Álgebra linear e geometria analítica
 27//29 o teste Álgebra linear e geometria analítica OCV Instruç~oes escolha n exercícios e responda em Portugu^es.. (2 valores) Determine uma equação cartesiana da recta que passa pelos pontos (, ) e (
27//29 o teste Álgebra linear e geometria analítica OCV Instruç~oes escolha n exercícios e responda em Portugu^es.. (2 valores) Determine uma equação cartesiana da recta que passa pelos pontos (, ) e (
Aula 19 Operadores ortogonais
 Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
Operadores ortogonais MÓDULO 3 AULA 19 Aula 19 Operadores ortogonais Objetivos Compreender o conceito e as propriedades apresentadas sobre operadores ortogonais. Aplicar os conceitos apresentados em exemplos
QUESTÕES ANPEC CÁLCULO A VÁRIAS VARIÁVEIS. 5. Em cada opção assinale se falsa ou verdadeira:
 QUESTÕES ANPEC CÁLCULO A VÁRIAS VARIÁVEIS QUESTÃO Calcule o comprimento do vetor z e que minimiza o valor da função QUESTÃO Ache os valores de e correspondentes ao máimo da função 0 0 e satisfazem a equação
QUESTÕES ANPEC CÁLCULO A VÁRIAS VARIÁVEIS QUESTÃO Calcule o comprimento do vetor z e que minimiza o valor da função QUESTÃO Ache os valores de e correspondentes ao máimo da função 0 0 e satisfazem a equação
