MA14 - Aritmética Lista 1. Unidades 1 e 2
|
|
|
- Ana Luísa Stachinski Barreto
- 7 Há anos
- Visualizações:
Transcrição
1 MA14 - Aritmética Lista 1 Unidades 1 e 2 Abramo Hefez PROFMAT - SBM 05 a 11 de agosto 2013
2 Unidade 1 1. Mostre, por indução matemática, que, para todo n N {0}, a) 8 3 2n + 7 b) 9 10 n n Mostre que, para todo n N {0}, a) n n+2 b) n n+1 c) n n+1 3. Sejam a, b Z. a) Se a b, mostre que, para todo n N, n 2, a n b n a b = an 1 + a n 2 b + + ab n 2 + b n 1. b) Se a + b 0, mostre que, para todo n N, a 2n+1 + b 2n+1 = a 2n a 2n 1 b + ab 2n 1 + b 2n. a + b c) Se a + b 0, mostre que para todo n N, a 2n b 2n a + b = a 2n 1 a 2n 2 b + + ab 2n 2 b 2n 1. PROFMAT - SBM Aritmética - Lista 1 - Unidades 1 e 2 slide 2/5
3 Unidade 1 - Continuação 4. Para quais valores de a N a) a 2 a 3 + 4? b) a + 3 a 3 3? c) a + 2 a 4 + 2? d) a + 2 a 4 + 2a 3 + a 2 + 1? 5. Mostre que, para todos a, m, n Z, m > n 0 = a 2n + 1 a 2m Mostre, para todo n N, que n 2 (n + 1) n Mostre, para todo a Z, que a) 2 a 2 a b) 3 a 3 a c) 5 a 5 a d) 7 a 7 a PROFMAT - SBM Aritmética - Lista 1 - Unidades 1 e 2 slide 3/5
4 Unidade 2 1. a) Mostre que um número natural a é par se, e somente se, a n é par, qualquer que seja n N. b) Mostre que a n ± a m é sempre par, quaisquer que sejam n, m N. c) Mostre que, se a e b são ímpares, então a 2 + b 2 é divisível por 2 mas não divisível por Quais são os números que, quando divididos por 5, deixam resto igual a) à metade do quociente? b) ao quociente? c) ao dobro do quociente? d) ao triplo do quociente? 3. Seja n um número natural. Mostre que um, e apenas um, número do terno abaixo é divisível por 3. n, n + 10, n + 23 PROFMAT - SBM Aritmética - Lista 1 - Unidades 1 e 2 slide 4/5
5 Unidade 2 - Continuação 4. a) Mostre que, se um número a não é divisível por 3, então a 2 deixa resto 1 na divisão por 3. b) A partir desse fato, prove que, se a e b são inteiros tais que 3 divide a 2 + b 2, então a e b são divisíveis por O resto da divisão do inteiro N por 20 é 8. Qual é o resto da divisão de N por 5? 6. Ache o menor múltiplo de 5 que deixa resto 2 quando dividido por 3 e por 4. PROFMAT - SBM Aritmética - Lista 1 - Unidades 1 e 2 slide 5/5
6 MA14 - Aritmética Lista 2 Unidades 3 e 4 Abramo Hefez PROFMAT - SBM 12 a 18 de agosto 2013
7 Unidade 3 1. Um certo número de três algarismos na base 10 aumenta de 36 se permutarmos os dois algarismos da direita, e diminui de 270 se permutarmos os dois algarismos da esquerda. O que acontece ao número se permutarmos os dois algarismos extremos? 2. Critério de divisibilidade por uma potência de 2 Seja dado um número a, representado na base 10 por a = a n a n 1... a 0. Usando o fato de que 2 k 10 k, mostre que 2 k divide a se, e somente se, o número a k 1... a 1 a 0 é divisível por 2 k. Em particular, a é divisível por 2 se, e somente se, a 0 é 0, 2, 4, 6 ou 8; também, a é divisível por 4 se, e somente se, a 1 a 0 é divisível por Escolha um número abc de três algarismos no sistema decimal, de modo que os algarismos das centenas a e o das unidades c difiram de, pelo menos, duas unidades. Considere os números abc e cba e subtraia o menor do maior, obtendo o número xyz. A soma de xyz com zyx vale Justifique esse fato. PROFMAT - SBM Aritmética - Lista 2 - Unidades 3 e 4 slide 2/5
8 Unidade 3 - Continuação 4. Seja dado o número na base 10; escreva-o nas seguintes bases: 2, 7, 12 e O número está na base 7; escreva-o nas bases 5 e Um número na base 10 escreve-se 37; em que base escrever-se-á 52? 7. Considere 73 na base 10; em que base ele escrever-se-á 243? 8. Escreva a tabuada na base 5. Use-a para calcular [132] 5 + [413] 5 e [23] 5 [342] Utilize o método do Exemplo 4.10 para calcular PROFMAT - SBM Aritmética - Lista 2 - Unidades 3 e 4 slide 3/5
9 Unidade 3 - Continuação 10. Escreva: a) O número 2 n 1 na base 2. b) O número bn 1 b 1 na base b. 11. Sendo a = [a n... a 1 a 0 ] b, mostre que o número a (a a n ) é divisível por b 1. PROFMAT - SBM Aritmética - Lista 2 - Unidades 3 e 4 slide 4/5
10 Unidade 4 1. Determine, em cada caso apresentado abaixo, se a posição é segura ou insegura. a) b) c) d) 2. Determine qual das seguintes situações iniciais no Jogo de Nim permite ao primeiro jogador traçar uma estratégia vencedora. a) (12, 14, 15), b) (7, 9, 14), c) (7, 9, 15, 17). Em tal caso faça uma jogada que lhe será favorável. PROFMAT - SBM Aritmética - Lista 2 - Unidades 3 e 4 slide 5/5
11 MA14 - Aritmética Lista 3 Unidades 5 e 6 Abramo Hefez PROFMAT - SBM 19 a 25 de agosto 2013
12 Unidade 5 1. Para cada par de números naturais a e b dados abaixo, ache (a, b) e determine números inteiros m e n tais que (a, b) = ma + nb. a) 637 e b) 648 e c) 551 e 874 d) e Seja n N. Mostre que a) (n, 2n + 1) = 1; b) (n + 1, n 2 + n + 1) = 1; c) (2n + 1, 9n + 4) = 1; d) (n! + 1, (n + 1)! + 1) = Mostre que (a, a 2 + na + b) b, quaisquer que sejam a, b, n N. 4. Seja dado a Z \ { 1}. a) Se m N, mostre que ( a 2m ) 1 a + 1, a + 1 = (a + 1, 2m). PROFMAT - SBM Aritmética - Lista 3 - Unidades 5 e 6 slide 2/6
13 Unidade 5 - Continuação b) Se m N {0}, mostre que ( a 2m a + 1 ), a + 1 = (a + 1, 2m + 1). 5. Calcule ( 3 a) 40 ) , 35 1 ( 2 40 ) + 1 c) , ( b) 6 d) ), 6 ( , ). 6. Sejam a e n números naturais com a 1. Mostre que (a 1) 2 a n 1 a 1 n. PROFMAT - SBM Aritmética - Lista 3 - Unidades 5 e 6 slide 3/6
14 Unidade 6 1. Sejam a, b, d Z com d 0. Mostre que se I (a, b) = dz, então d = (a, b). 2. Mostre que a) se (a, b) = 1, a c e b c, então ab c. b) se (a, b) = 1, então (ac, b) = (c, b). c) (ac, b) = 1 se, e somente se, (a, b) = (c, b) = 1. d) (a, b) = (a, d) = (c, b) = (c, d) = 1 se, e somente se, (ac, bd) = 1. e) se (a, b) = 1, então (a n, b m ) = 1, para todos n, m N {0}. 3. Para todos a, b Z e todo n N, mostre que (a n, b n ) = (a, b) n. 4. a) Mostre que, se n é ímpar, então n(n 2 1) é divisível por 24. b) Mostre que 24 divide n(n 2 1)(3n + 2) para todo n N. PROFMAT - SBM Aritmética - Lista 3 - Unidades 5 e 6 slide 4/6
15 Unidade 6 - Continuação 5. a) Mostre que n 5 n é divisível por 30. b) Mostre que n 5 e n possuem o mesmo algarismo das unidades. 6. Mostre que se a e b não são ambos nulos, então a bc se, e a somente se, (a, b) c. 7. Sejam a e b dois números inteiros com (a, b) = 1. a) Mostre que (b + a, b a) é 1 ou 2. b) Mostre que (a + b, a 2 + b 2 ) é 1 ou Mostre que, se a, b, x, y Z, com ax + by = (a, b), então, (x, y) = Sejam a e b dois números naturais com (a, b) = 1. Mostre que a b se é par. então é ímpar. Vale a recíproca? (a, b) (a, b) PROFMAT - SBM Aritmética - Lista 3 - Unidades 5 e 6 slide 5/6
16 Unidade 6 - Continução 10. Um prédio possui duas escadarias, uma delas com 780 degraus e a outra com 700 degraus. Sabendo que os degraus das duas escadas só estão no mesmo nível quando conduzem a um andar, descubra quantos andares tem o prédio. 11. Calcule (1 116, 984, 855). 12. Mostre que se três números inteiros são tais que dois deles são coprimos, então eles são coprimos. Mostre que não vale a recíproca; isto é, exiba três números inteiros coprimos mas que não são dois a dois coprimos. PROFMAT - SBM Aritmética - Lista 3 - Unidades 5 e 6 slide 6/6
17 MA14 - Aritmética Lista 4 Unidades 7 e 8 Abramo Hefez PROFMAT - SBM
18 Unidade 7 1. Calcule o mmc dos pares de números: a) 38, 46; b) 35, 75; c) 235, a) Mostre que [ca, cb] = c [a, b]. b) Se m é um múltiplo comum positivo de a e b, mostre que ( m m = [a, b] a, m ) = 1. b c) Se r e s não são nulos e ra = sb > 0, mostre que ra (r, s) = sb = [a, b]. (r, s) 3. Sejam a, b, c três números naturais. Mostre que abc = [a, b, c](ab, ac, bc). PROFMAT - SBM Aritmética - Lista 4 - Unidades 7 e 8 slide 2/7
19 Unidade 7 - Continuação 4. Seja n N; calcule [n 2 + 1, n + 1]. 5. Mostre que a) (a, b) = [a, b] a = b, a, b N. b) [a n, b n ] = [a, b] n, a, b Z, n N. 6. Sejam a, b Z ambos não nulos. Considere o conjunto M(a, b) = az bz = {x Z; m, n Z tais que x = ma e x = nb}. a) Mostre que [a, b] = min (M(a, b) N). b) Mostre que M(a, b) = [a, b]z. 7. Sejam d, m N. Mostre que uma condição necessária e suficiente para que existam a, b Z tais que (a, b) = d e [a, b] = m é que d m. PROFMAT - SBM Aritmética - Lista 4 - Unidades 7 e 8 slide 3/7
20 Unidade 7 - Continuação 8. Sejam a 1,..., a n Z \ {0}. Mostre que (a i, a j ) = 1, i j [a 1,..., a n ] = a 1 a n. 9. Mostre que [a 1, a 2,..., a n 1, a n ] = [[a 1, a 2,..., a n 1 ], a n ]. PROFMAT - SBM Aritmética - Lista 4 - Unidades 7 e 8 slide 4/7
21 Unidade 8 1. Resolva em Z as equações: a) 90X + 28Y = 22 b) 50X 56Y = 74 c) 40X 65Y = 135 d) 8X 13Y = Para quais valores de c em N a equação 10X + 14Y = c não possui soluções em N {0}? 3. Resolva em N {0} as equações: a) 16X + 7Y = 601 b) 30X + 17Y = 201 c) 47X + 29Y = 1288 d) 8X + 13Y = Dispondo de R$100, 00, quais são as quantias que se podem gastar comprando selos de R$5, 00 e de R$7, 00? 5. Determine os múltiplos naturais de 11 e de 9 cuja soma é igual a a) 79 b) 80 c) Determine o menor inteiro positivo que tem restos 11 e 35 quando dividido, respectivamente, por 37 e 48. PROFMAT - SBM Aritmética - Lista 4 - Unidades 7 e 8 slide 5/7
22 Unidade 8 - Continuação 7. Numa criação de coelhos e galinhas, contaram-se 400 pés. Quantas são as galinhas e quantos são os coelhos, sabendo que a diferença entre esses dois números é a menor possível? 8. Subindo uma escada de dois em dois degraus, sobra um degrau. Subindo a mesma escada de três em três degraus, sobram dois degraus. Determine quantos degraus possui a escada, sabendo que o seu número é múltiplo de 7 e está compreendido entre 40 e (ENC 2002) Em certo país, as cédulas são de $4 e $7. Com elas, é possível pagar, sem troco, qualquer quantia inteira a) a partir de $11, inclusive. b) a partir de $18, inclusive. c) ímpar, a partir de $7, inclusive. d) que seja $1 maior do que um múltiplo de $3. e) que seja $1 menor do que um múltiplo de $5. PROFMAT - SBM Aritmética - Lista 4 - Unidades 7 e 8 slide 6/7
23 Unidade 8 - Continuação 10. De quantas maneiras pode-se comprar selos de R$3, 00 e de R$5, 00 de modo que se gaste R$50, 00? 11. Sejam a 1, a 2,..., a n, c Z. Mostre que a equação a 1 X 1 + a 2 X a n X n = c possui soluções inteiras se, e somente se, (a 1, a 2,..., a n ) c. PROFMAT - SBM Aritmética - Lista 4 - Unidades 7 e 8 slide 7/7
24 MA14 - Aritmética Lista 5 Unidades 10 e 11 Abramo Hefez PROFMAT - SBM 9 a 15 de setembro 2013
25 Unidade Sejam a, m, n N, a > 1. Mostre que a n 1 a m 1 se, e somente se, n m. 2. Sejam n, m N com n m e m n (a m + 1, a n + 1) = a n Sejam a, m, n N, com m > n. Mostre que ( a 2 m 1, a 2n + 1 ) = a 2n + 1. ímpar. Se a N, mostre que 4. Calcule a) ( , ) b) ( , ) c) ( , ) PROFMAT - SBM Aritmética - Lista 5 - Unidades 10 e 11 slide 2/4
26 Unidade 10 - Continuação 5. Seja (M n ) n a sequência definida por M n = 2 n 1. Mostre que a) 3 M n se, e somente se, n é par. b) 5 M n se, e somente se, n é múltiplo de 4. c) 9 M n se, e somente se, n é múltiplo de 6. PROFMAT - SBM Aritmética - Lista 5 - Unidades 10 e 11 slide 3/4
27 Unidade Mostre que, se na sequência de Fibonacci existir um termo divisível por um número natural m, então, existem infinitos tais termos. 2. Na sequência de Fibonacci, mostre que a) u m é par se, e somente se, m é divisível por 3. b) u m é divisível por 5 se, e somente se, m é divisível por 5. c) u m é divisível por 13 se, e somente se, m é divisível por Na sequência de Fibonacci, mostre que a) u m é divisível por 21 sempre que m for divisível por 8. b) u m é divisível por 8 sempre que m for divisível por 6. PROFMAT - SBM Aritmética - Lista 5 - Unidades 10 e 11 slide 4/4
28 MA14 - Aritmética Lista 6 Unidades 12 e 13 Abramo Hefez PROFMAT - SBM
29 Unidade Ache os possíveis valores de n, m N {0} de modo que o número 9 m 10 n tenha: a) 27 divisores b) 243 divisores. 2. Qual é a forma geral dos números naturais que admitem: a) um só divisor além de 1 e dele próprio? b) um número primo de divisores? 3. Sejam a, b N, com (a, b) = 1. Mostre que, se ab é um quadrado, então a e b são quadrados. Generalize para ab uma potência r-ésima. 4. Seja m N. Pode o número m(m + 1) ser a sétima potência de um número natural? (Generalize.) 5. (ENC-2002) Qual é o menor valor do número natural n que torna n! divisível por 1000? 6. Mostre que a soma de todos os números naturais menores ou iguais a n divide o seu produto se, e somente se, n + 1 é composto. PROFMAT - SBM Aritmética - Lista 6 - Unidades 12 e 13 slide 2/5
30 Unidade 12 - Continuação 7. Usando a caracterização de mdc e mmc de dois números naturais a e b através da fatoração em primos desses números, prove que (a, b)[a, b] = ab. 8. Mostre que todo número primo p > 2 escreve-se de modo único como diferença de dois quadrados. 9. Seja p > 1 um número natural com a seguinte propriedade: Se p divide o produto de dois números naturais quaisquer, então p divide um dos fatores. Mostre que p é necessariamente primo. 10. Mostre que, se n e m são dois números naturais não nulos tais que (n, m) = 1, então d(nm) = d(n)d(m). 11. Mostre que, se n é composto, então o n-ésimo número de Fibonacci u n é composto. PROFMAT - SBM Aritmética - Lista 6 - Unidades 12 e 13 slide 3/5
31 Unidade Mostre que 42 a 7 a para todo número natural a. 2. Ache o resto da divisão de 12 p 1 por p quando p é primo. 3. Mostre que, para todo n N, é natural o número 3 5 n n n. 4. Mostre que, para todo n N, 15 3n 5 + 5n 3 + 7n. 5. Seja n N. Mostre que a) Se 5 n, 5 n 1, 5 n + 1, então 5 n b) Se 7 n, 7 n 1, 7 n 3 + 1, então 7 n 2 + n Sejam a N. Mostre que 7 a 18 1, se (a, 7) = 1. Generalize. 7. Um terno de primos é dito de primos trigêmeos se for da forma p, p + 2 e p + 4. Mostre que 3, 5 e 7 é o único terno de primos trigêmeos. PROFMAT - SBM Aritmética - Lista 6 - Unidades 12 e 13 slide 4/5
32 Unidade 13 - Continuação 8. Mostre que a 12 b 12 é divisível por 13, se a e b são primos com 13. Mostre também que é divisível por 91, se a e b são primos com 91. PROFMAT - SBM Aritmética - Lista 6 - Unidades 12 e 13 slide 5/5
33 MA14 - Aritmética Lista 7 Unidades 15 e 16 Abramo Hefez PROFMAT - SBM
34 Unidade 15 Problemas 1.1 a 1.7 do Capítulo 8, Seção 1. Unidade 16 Problemas 2.1 a 2.6 do Capítulo 8, Seção 2. PROFMAT - SBM Aritmética - Lista 7 - Unidades 15 e 16 slide 2/2
35 MA14 - Aritmética Lista 8 Unidades 17 e 18 Abramo Hefez PROFMAT - SBM
36 Unidade 17 - Capítulo 8, Seção Ache a decomposição em fatores primos de 50! e determine com quantos zeros termina esse número a) Ache as maiores potências de 2 e de 5 que dividem 1000!. b) Determine com quantos zeros termina o número 1000!. c) Ache a maior potência de 104 que divide 1000!. d) Ache o menor número natural n tal que 5 7 n!. ( ) (Profmat 2011) É possível repartir exatamente 528 objetos entre 49 pessoas? Mostre que não há nenhum número natural n tal que 3 7 seja a maior potência de 3 que divida n! Mostre que, se m, n N são tais que (m, n) = 1, então, (m + n 1)! m!n! N. PROFMAT - SBM Aritmética - Lista 8 - Unidades 17 e 18 slide 2/7
37 8.3.6 a) Mostre que, para todo n N, tem-se que 2 n n!. b) Mostre que 2 n 1 n! se, e somente se, existe m N tal que n = 2 m. c) Determine todos os números naturais n tais que 2 n 2 n!. d) Se r N, determine todos os números naturais n tais que 2 n r n! Sejam n, m N; mostre que (nm)! é divisível por [(n!) m, (m!) n ] Para todo n N, mostre que (n!) (n 1)! divide (n!)! Seja m, n N, com n m 1. Mostre que é inteiro o número ( ) (n, m) n n m PROFMAT - SBM Aritmética - Lista 8 - Unidades 17 e 18 slide 3/7
38 Exercícios Suplementares 8.S.1 Mostre que 2 n divide (2n)!. Mostre que, geralmente, o produto de 2n números naturais consecutivos é divisível por 2 n. 8.S.2 Mostre que 2 n (n + 1)(n + 2) (2n), mas 2 n+1 (n + 1)(n + 2) (2n). 8.S.3 Mostre que n!2 n 3 n divide (3n)!. ( ) 8.S.4 Se 1 r p n p n com E p (r) = k, mostre que é divisível r por p n k, mas não por p n k+1. 8.S.5 Mostre que , mas que PROFMAT - SBM Aritmética - Lista 8 - Unidades 17 e 18 slide 4/7
39 Unidade 18 - Capítulo 9, Seção Sejam a, p N, com p primo. Mostre que, se a 2 1 mod p, então a 1 mod p ou a 1 mod p Ache o resto da divisão a) de 7 10 por 51 b) de por 11 c) de 5 21 por 127 d) de por 17 e) de ( ) 21 por 8 f) de por 3 g) de 1! + 2! + + (10 10 )! por (ENC 98) O resto da divisão de por 5 é: (A) 0 (B) 1 (C) 2 (D) 3 (E) Para todo n N, mostre que a) 101 6n 1 é divisível por 70; b) 19 8n 1 é divisível por Determine o resto da divisão por 7 do número a) b) c) d) PROFMAT - SBM Aritmética - Lista 8 - Unidades 17 e 18 slide 5/7
40 9.1.6 Determine o resto da divisão por 4 do número a) b) Determine o algarismo das unidades do número Ache os algarismos das centenas e das unidades do número Mostre, para todo n N, que a) 10 2n 1 mod 11 b) 10 2n+1 1 mod (ENC 2000) Se x 2 1 mod 5, então, (A) x 1 mod 5 (B) x 2 mod 5 (C) x 4 mod 5 (D) x 1 mod 5 ou x 4 mod 5 (E) x 2 mod 5 ou x 4 mod 5 PROFMAT - SBM Aritmética - Lista 8 - Unidades 17 e 18 slide 6/7
41 Suponha que m = p α 1 1 pαr r. Mostre que a b mod m a b mod p α i i, i = 1,..., r Ache o menor número natural que deixa restos 5, 4, 3 e 2 quando dividido, respectivamente, por 6, 5, 4 e Mostre que a soma dos quadrados de quatro números naturais consecutivos nunca pode ser um quadrado. PROFMAT - SBM Aritmética - Lista 8 - Unidades 17 e 18 slide 7/7
42 MA14 - Aritmética Lista 9 Unidades 19 e 20 Abramo Hefez PROFMAT - SBM
43 Unidade 19 - Capítulo 9, Seção a) Usando o fato de que 100 é divisível por 4, 25 e 100, ache critérios de divisibilidade por 4, 25 e 100. b) Considerando que 1000 é divisível por 8, 125 e 1000, ache critérios de divisibilidade por 8, 125 e Mostre que um número natural na base 10 é divisível por 6 se, e somente se, a soma do algarismo da unidade com o quádruplo de cada um dos outros algarismos é divisível por Usando o fato de que mod 7, mod 11, mod 13, prove o seguinte critério de divisibilidade por 7, 11 e 13: Um número natural n = n r... n 2 n 1 n 0, escrito na base 10, é divisível por 7, 11 ou 13, se, e somente se, n 2 n 1 n 0 n 5 n 4 n 3 + n 8 n 7 n 6 n 11 n 10 n mod 7, n 2 n 1 n 0 n 5 n 4 n 3 + n 8 n 7 n 6 n 11 n 10 n mod 11 e PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 2/9
44 9.2.4 Analisando a tabela do Exemplo 2.14 (do livro texto), determine os números de Fibonacci que são divisíveis por 8, por 11, por 13 ou por Mostre que um número da forma a n = 2 n 1 (2 n 1) para n > 2 é congruente a 1 módulo 9. Conclua que todo número perfeito par maior do que 6, assim como a soma de seus algarismos, é da forma 9k + 1. Sugestão. Utilize as fórmulas do Problema e indução Mostre que se n 2, então o número de Fermat F n tem algarismo da unidade igual a a) Mostre que para todo n 1 tem-se que F n 5 mod 12. b) Mostre que nenhum número de Fermat pode ser um quadrado ou um cubo. PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 3/9
45 9.2.8 Seja a N com a > 1. Considere a sequência α(a, n) = an 1 a 1. a) Mostre que α(a, n) 0 mod (a 1) se, e somente se, a 1 n. b) Mostre que α(a, n) 0 mod (a + 1) se, e somente se, n é par. c) Enuncie esses resultados para a = 10. PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 4/9
46 Unidade 20 - Capítulo 10, Seções 1 e Ache o resto da divisão de a) 5 60 por 26 b) por Mostre que, se m > 2, então ϕ(m) é par Mostre que, se p é um número primo, então, para todo a Z e para todo k N, tem-se que a k(p 1)+1 a mod p a) Mostre que (i, m) = 1 1 i < m i = 1 2 m ϕ(m). b) Mostre que, se m 1,..., m ϕ(m) é um sistema reduzido de resíduos módulo m, então m divide m m ϕ(m). PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 5/9
47 Resolva em m N as equações a) ϕ(m) = 12 b) ϕ(m) = 8 c) ϕ(m) = 16 d) ϕ(m) = Supondo que (a, m) = (a 1, m) = 1, mostre que 1 + a + a a ϕ(m) 1 0 mod m Mostre que, se ϕ(m) = 2 r, para algum r N, então m é um produto de uma potência de 2 e de primos de Fermat distintos. Essa equação aparece na resolução dada por Gauss do problema clássico da construtibilidade com régua e compasso dos poĺıgonos regulares inscritos numa circunferência Supondo que (m, n) = 1, mostre que m ϕ(n) + n ϕ(m) 1 mod nm. PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 6/9
48 Sejam a, m Z, com m > 1, tais que (a, m) = 1. Mostre que, se n 1 n 2 mod ϕ(m), então a n 1 a n 2 mod m Mostre que 2730 n 13 n, para todo n Z Sejam a Z e n, r N, com (r, n) = 1. Mostre que no conjunto {a, a + r,..., a + (n 1)r }, há exatamente ϕ(n) números primos com n Quais são os possíveis restos da divisão de a 100, onde a Z, quando dividido por 125? PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 7/9
49 Mostre que o número primo p é o menor inteiro maior do que 1 que divide o número (p 1)! Mostre que, se p > 2 é um número primo, então a) p (p 2)! 1 b) p (p 3)! (p 1)/ Seja p > 3 um número primo. a) Mostre que p! e (p 1)! 1 são primos entre si. b) Prove que, se n N e n (p 1)! 1 mod p!, então os p 2 inteiros que precedem n e os p inteiros que sucedem n são compostos Seja p um número primo e a N. Mostre que a) a p + (p 1)!a 0 mod p b) (p 1)!a p + a 0 mod p Seja p um número primo tal que p 3 mod 4. Mostre que [( ) p 1 2!] 1 mod p. 2 PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 8/9
50 Seja p um número primo ímpar e seja N = (p 2). Mostre que N 1 mod p ou N 1 mod p Seja p um número primo ímpar. Mostre que a) (p 2) (p 1) 2 mod p; b) se p 1 mod 4, então (p 1) 2 1 mod p; c) se p 3 mod 4, então (p 1) 2 1 mod p. PROFMAT - SBM Aritmética - Lista 9 - Unidades 19 e 20 slide 9/9
51 MA14 - Aritmética Lista 10 Unidades 21 e 22 Abramo Hefez PROFMAT - SBM
52 Unidade 21 - Capítulo 11, Seções 1 e Pode o dobro de um número natural deixar resto igual a 9 quando dividido por 26? E quando dividido por 25? Resolva, quando possível, as congruências: a) 3X 5 mod 7; b) 6X 21 mod 18; c) 12X 36 mod 28; d) 12X 36 mod 28; e) 151X 11 mod Seja p um número primo e seja a um número inteiro tal que p a. Mostre que a única solução módulo p da congruência ax b mod p é x = a p 2 b Sejam a, m Z, com m > 2 e (a, m) = 1. Mostre que a única solução módulo m da congruência ax b mod m é x = a ϕ(m) 1 b Mostre que a congruência X mod 7 não possui soluções. Conclua que a equação X 2 7Y 2 14X + 7Y 6 = 0 não admite soluções inteiras. PROFMAT - SBM Aritmética - Lista 10 - Unidades 21 e 22 slide 2/7
53 Ache todos os números inteiros que deixam restos 2, 3 e 4 quando divididos por 3, 4 e 5, respectivamente Ache o menor número natural que deixa restos 1, 3 e 5 quando dividido por 5, 7 e 9, respectivamente Dispomos de uma quantia de x reais menor do que Se distribuirmos essa quantia entre 11 pessoas, sobra R$1, 00; se a distribuirmos entre 12 pessoas, sobram R$2, 00 e se a distribuirmos entre 13 pessoas, sobram R$3, 00. De quantos reais dispomos? Um macaco, ao subir uma escada de dois em dois degraus, deixa de sobra um degrau; ao subir de três em três degraus, sobram dois degraus; e ao subir de cinco em cinco degraus, sobram três degraus. Quantos degraus possui a escada, sabendo que o número de degraus está entre 150 e 200? Resolva o sistema: 3X 1 mod 7, 5X 2 mod 11, 4X 3 mod 13. PROFMAT - SBM Aritmética - Lista 10 - Unidades 21 e 22 slide 3/7
54 Levando em consideração que 2275 = , resolva a congruência 3X 11 mod Resolva o sistema: X 2 mod 3, X 3 mod 4, X 4 mod 5, X 5 mod Resolva o sistema: X 2 mod 3, X 3 mod 4, X 4 mod 5, X 2 mod (Yi Shing, aprox. 700d.C.) Ache os inteiros que deixam restos 1, 2, 5 e 5 quando divididos respectivamente por 2, 3, 6 e Sejam F 1,..., F n os n primeiros números de Fermat. Mostre que existe um número natural N tal que F i divide N + i 1 para i = 1,..., n. PROFMAT - SBM Aritmética - Lista 10 - Unidades 21 e 22 slide 4/7
55 Unidade 22 - Capítulo 11, Seção Seja {a 1,..., a m } um sistema completo de resíduos módulo m. a) Mostre que se a é um inteiro, então {a 1 + a,..., a m + a} é um sistema completo de resíduos módulo m. b) Se (a, m) = 1, então {a a 1,..., a a m } é um sistema completo de resíduos módulo m. Mostre que vale a recíproca. c) Se p é primo e a um inteiro que não é múltiplo de p, mostre que a p 1 1 mod p (Pequeno Teorema de Fermat). d) Mostre que se (r, m) = 1, então {a, a + r,..., a + (m 1)r} é um sistema completo de resíduos módulo m. Sugestão. (para c) Considere os dois sistemas completos de resíduos mod p: {0, 1,..., p 1} e {0, a 1,..., a(p 1)} e note que 1 (p 1) a p 1 1 (p 1) mod p. PROFMAT - SBM Aritmética - Lista 10 - Unidades 21 e 22 slide 5/7
56 Construa as tabelas da adição e da multiplicação para Z 6 e Z Ache os elementos invertíveis de Z 6, Z 7, Z 8 e Z Ache os inversos de a) [5] em Z 6 b) [3], [4] e [5] em Z 7 c) [3], [5], e [7] em Z 8 d) [5], [4] e [8] em Z 9 e) [1 951] em Z f) [3], [5] e [7] em Z a) Seja {a 1,..., a ϕ(m) } um sistema reduzido de resíduos módulo m. Mostre que se (a, m) = 1, então {a a 1,..., a a ϕ(m) } é um sistema reduzido de resíduos módulo m. b) Utilize o item anterior para dar uma outra demonstração do Teorema de Euler. PROFMAT - SBM Aritmética - Lista 10 - Unidades 21 e 22 slide 6/7
57 Considere Z m para m > 2. Mostre que (a) Z m tem um número par de elementos invertíveis; (b) se [a] é invertível, então [a] é invertível e [a] [a]. (c) Mostre que a soma dos elementos invertíveis de Z m é igual a [0]. (d) Mostre que a soma de todos os elementos de um sistema reduzido qualquer de resíduos módulo m é sempre múltiplo de m (Enade 2008) No anel dos inteiros módulo 12, R = Z 12, (A) não há divisores de zero. (B) todo elemento não nulo é invertível. (C) o subconjunto dos elementos invertíveis forma um subanel de R. (D) a multiplicação não é comutativa. (E) há exatamente quatro elementos invertíveis. PROFMAT - SBM Aritmética - Lista 10 - Unidades 21 e 22 slide 7/7
MA14 - Aritmética Unidade 15 - Parte 1 Resumo. Congruências
 MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
MA14 - Aritmética Unidade 15 - Parte 1 Resumo Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do assunto.
MAT Álgebra I para Licenciatura 2 a Lista de exercícios
 MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MAT0120 - Álgebra I para Licenciatura 2 a Lista de exercícios 1. Quais são os números de cifras iguais que são divisíveis por 3? Idem, por 9? Idem por 11? 2. Determinar mmc (56, 72) e mmc (119, 272). 3.
MA14 - Aritmética Unidade 22 Resumo. Aritmética das Classes Residuais
 MA14 - Aritmética Unidade 22 Resumo Aritmética das Classes Residuais Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 22 Resumo Aritmética das Classes Residuais Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Lista 2 - Álgebra I para Computação - IME -USP -2011
 Lista 2 - Álgebra I para Computação - IME -USP -2011 (A) Relações de Equivalência e Quocientes 1. Seja N = {0, 1, 2,...} o conjunto dos números naturais e considere em X = N N a seguinte relação: (a, b)
Lista 2 - Álgebra I para Computação - IME -USP -2011 (A) Relações de Equivalência e Quocientes 1. Seja N = {0, 1, 2,...} o conjunto dos números naturais e considere em X = N N a seguinte relação: (a, b)
Matemática Discreta. Introdução à Teoria de Números - Exercícios 1 o ano /2011
 Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
Lic. em Ciências da Computação Matemática Discreta Introdução à Teoria de Números - Exercícios 1 o ano - 2010/2011 1. Determine o quociente e o resto na divisão de: (a) 310156 por 197; (b) 32 por 45; (c)
(Ciência de Computadores) 2005/ Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação
 Álgebra (Ciência de Computadores) 2005/2006 Números inteiros 1. Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação (a) {inteiros positivos impares}; (b) {inteiros negativos pares};
Álgebra (Ciência de Computadores) 2005/2006 Números inteiros 1. Diga quais dos conjuntos seguintes satisfazem o Princípio de Boa Ordenação (a) {inteiros positivos impares}; (b) {inteiros negativos pares};
MATEMÁTICA 1 MÓDULO 2. Divisibilidade. Professor Matheus Secco
 MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
MATEMÁTICA 1 Professor Matheus Secco MÓDULO 2 Divisibilidade 1. DIVISIBILIDADE 1.1 DEFINIÇÃO: Dizemos que o inteiro a é divisível pelo inteiro b (ou ainda que a é múltiplo de b) se existe um inteiro c
Este material é apenas um resumo de parte do conteúdo da disciplina.
 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 11 - Seção 1.3 do livro texto da disciplina: Aritmética, A. Hefez,
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 11 - Seção 1.3 do livro texto da disciplina: Aritmética, A. Hefez,
ALGORITMO DE EUCLIDES
 Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
Sumário ALGORITMO DE EUCLIDES Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Máximo Divisor Comum 2 Algoritmo
MA14 - Aritmética Unidade 1 Resumo. Divisibilidade
 MA14 - Aritmética Unidade 1 Resumo Divisibilidade Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
MA14 - Aritmética Unidade 1 Resumo Divisibilidade Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
MATEMÁTICA MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA. Professor Matheus Secco
 MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
MATEMÁTICA Professor Matheus Secco MÓDULO 8 DIVISIBILIDADE E CONGRUÊNCIA 1. DIVISIBILIDADE Definição: Sejam a, b inteiros com a 0. Diz-se que a divide b (denota-se por a b) se existe c inteiro tal que
MA14 - Aritmética Unidade 20 Resumo. Teoremas de Euler e de Wilson
 MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 20 Resumo Teoremas de Euler e de Wilson Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Aritmética. Somas de Quadrados
 Aritmética Somas de Quadrados Carlos Humberto Soares Júnior PROFMAT - SBM Objetivo Determinar quais números naturais são soma de dois quadrados. PROFMAT - SBM Aritmética, Somas de Quadrados slide 2/14
Aritmética Somas de Quadrados Carlos Humberto Soares Júnior PROFMAT - SBM Objetivo Determinar quais números naturais são soma de dois quadrados. PROFMAT - SBM Aritmética, Somas de Quadrados slide 2/14
MA14 - Aritmética Unidade 15 - Parte 2 Resumo
 MA14 - Aritmética Unidade 15 - Parte 2 Resumo Aplicações de Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante
MA14 - Aritmética Unidade 15 - Parte 2 Resumo Aplicações de Congruências Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante
MA14 - Aritmética Unidade 3. Divisão nos Inteiros (Divisibilidade)
 MA14 - Aritmética Unidade 3 Divisão nos Inteiros (Divisibilidade) Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 3 Divisão nos Inteiros (Divisibilidade) Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
Roteiro da segunda aula presencial - ME
 PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
PIF Enumerabilidade Teoria dos Números Congruência Matemática Elementar Departamento de Matemática Universidade Federal da Paraíba 29 de outubro de 2014 PIF Enumerabilidade Teoria dos Números Congruência
Atividade Especial Revisão
 9 Atividade Especial Revisão 1 Unidade 9 Esta unidade será dedicada à resolução de uma lista de problemas sobre a matéria até agora desenvolvida. 1. (a) Quantos múltiplos de 5 existem no intervalo [1,
9 Atividade Especial Revisão 1 Unidade 9 Esta unidade será dedicada à resolução de uma lista de problemas sobre a matéria até agora desenvolvida. 1. (a) Quantos múltiplos de 5 existem no intervalo [1,
Aritmética dos Restos. Problemas com Congruências. Tópicos Adicionais
 Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
Aritmética dos Restos Problemas com Congruências Tópicos Adicionais Aritmética dos Restos Problemas com Congruências 1 Exercícios Introdutórios Exercício 1. inteiro n Prove que n 5 + 4n é divisível por
MA14 - Aritmética Unidade 1 Resumo. Divisibilidade
 MA14 - Aritmética Unidade 1 Resumo Divisibilidade Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
MA14 - Aritmética Unidade 1 Resumo Divisibilidade Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio do
Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 42
 1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
1 / 42 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 42 1 Combinatória 2 3 Grafos 3 / 42 Capítulo 2 4 / 42 Axiomática dos Inteiros Sejam a e b inteiros. Designaremos
XIX Semana Olímpica de Matemática. Nível 3. Polinômios Ciclotômicos e Congruência Módulo p. Samuel Feitosa
 XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
XIX Semana Olímpica de Matemática Nível 3 Polinômios Ciclotômicos e Congruência Módulo p Samuel Feitosa O projeto da XIX Semana Olímpica de Matemática foi patrocinado por: Semana Olímpica 2016 Polinômios
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado Para cada número inteiro a definimos a = {x Z; x a mod n} Como
MA14 - Aritmética Unidade 6 - Parte 3 Resumo
 MA14 - Aritmética Unidade 6 - Parte 3 Resumo A Equação Pitagórica Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 6 - Parte 3 Resumo A Equação Pitagórica Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero.
 Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Lista 1 - Teoria de Anéis - 2013 Professor: Marcelo M.S. Alves Data: 03/09/2013 obs: i) Salvo menção em contrário, anel = anel comutativo com unidade. ii) O conjunto dos naturais inclui o zero. 1. Os conjuntos
Introdução à Teoria dos Números Notas de Aulas 3 Prof Carlos Alberto S Soares
 Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números 2018 - Notas de Aulas 3 Prof Carlos Alberto S Soares 1 Números Primos e o Teorema Fundamental da Aritmética Em notas anteriores já definimos os números primos, isto é, números
Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II
 1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
1 Introdução à Teoria dos Números - Notas 4 Tópicos Adicionais II. 1 O Anel dos Inteiros Módulo n Consideremos um número natural n 2 fixado. Para cada número inteiro a definimos a = {x Z; x a mod n}. Como
Tópicos de Matemática Elementar
 Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Tópicos de Matemática Elementar 2 a série de exercícios 2004/05. A seguinte prova por indução parece correcta, mas para n = 6 o lado esquerdo é igual a 2 + 6 + 2 + 20 + 30 = 5 6, enquanto o direito é igual
Polos Olímpicos de Treinamento. Aula 6. Curso de Teoria dos Números - Nível 2. Congruências II. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências II Na aula de hoje, aprenderemos um dos teoremas mais importantes do curso: o pequeno teorema
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências II Na aula de hoje, aprenderemos um dos teoremas mais importantes do curso: o pequeno teorema
Aritmética dos Restos. Pequeno Teorema de Fermat. Tópicos Adicionais
 Aritmética dos Restos Pequeno Teorema de Fermat Tópicos Adicionais Aritmética dos Restos Pequeno Teorema de Fermat 1 Exercícios Introdutórios Exercício 1. Encontre os restos da divisão de 2 24 por a) 5
Aritmética dos Restos Pequeno Teorema de Fermat Tópicos Adicionais Aritmética dos Restos Pequeno Teorema de Fermat 1 Exercícios Introdutórios Exercício 1. Encontre os restos da divisão de 2 24 por a) 5
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão Lista 1. Números Naturais
 Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 01 Lista 1 Números Naturais 1. Demonstre por indução as seguintes fórmulas: (a) (b) n (j 1) = n (soma dos n primeiros ímpares).
Universidade Federal de Santa Maria Departamento de Matemática Curso de Verão 01 Lista 1 Números Naturais 1. Demonstre por indução as seguintes fórmulas: (a) (b) n (j 1) = n (soma dos n primeiros ímpares).
, com k 1, p 1, p 2,..., p k números primos e α i, β i 0 inteiros, as factorizações de dois números inteiros a, b maiores do que 1.
 Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Como seria de esperar, o Teorema Fundamental da Aritmética tem imensas consequências importantes. Por exemplo, dadas factorizações em potências primas de dois inteiros, é imediato reconhecer se um deles
Congruências I. Por exemplo, 7 2 (mod 5), 9 3 (mod 6), 37 7 (mod 10) mas 5 3 (mod 4). Veja que a b (mod m) se, e somente se, m a b.
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências I Definição 1. Dizemos que os inteiros a e b são congrentes módulo m se eles deixam o mesmo
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 6 Congruências I Definição 1. Dizemos que os inteiros a e b são congrentes módulo m se eles deixam o mesmo
Matemática para Ciência de Computadores
 Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
Matemática para Ciência de Computadores 1 o Ano - LCC & ERSI Luís Antunes lfa@ncc.up.pt DCC-FCUP Complexidade 2002/03 1 Inteiros e divisão Definição: Se a e b são inteiros com a 0, dizemos que a divide
MA14 - Aritmética Unidade 2 Resumo. Divisão Euclidiana
 MA14 - Aritmética Unidade 2 Resumo Divisão Euclidiana Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte da disciplina e o seu estudo não garante o domínio do assunto. O material
MA14 - Aritmética Unidade 2 Resumo Divisão Euclidiana Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte da disciplina e o seu estudo não garante o domínio do assunto. O material
NÚMEROS INTEIROS. Álgebra Abstrata - Verão 2012
 NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
NÚMEROS INTEIROS PROF. FRANCISCO MEDEIROS Álgebra Abstrata - Verão 2012 Faremos, nessas notas, uma breve discussão sobre o conjunto dos números inteiros. O texto é basicamente a seção 3 do capítulo 1 de
UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática
 UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática Segunda Lista de Exercícios de ITN: Números Inteiros Prof. Marnei Luis Mandler Segundo
UDESC - Universidade do Estado de Santa Catarina CCT - Centro de Ciências Tecnológicas DMAT - Departamento de Matemática Segunda Lista de Exercícios de ITN: Números Inteiros Prof. Marnei Luis Mandler Segundo
01. D e m o n s t r a r q u e s e. 02. Mostre que se a 1 a2
 Série Professor(a) Aluno(a) Rumo ao ITA Marcelo Mendes Sede Turma Turno Data N / / Ensino Pré-Universitário TC Matemática Revisão de Álgebra OSG.: 85/0 Exercícios de Fixação 0. Encontre os valores das
Série Professor(a) Aluno(a) Rumo ao ITA Marcelo Mendes Sede Turma Turno Data N / / Ensino Pré-Universitário TC Matemática Revisão de Álgebra OSG.: 85/0 Exercícios de Fixação 0. Encontre os valores das
Este material é apenas um resumo de parte do conteúdo da disciplina.
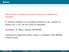 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
Aviso Este material é apenas um resumo de parte do conteúdo da disciplina. O material completo a ser estudado encontra-se no Capítulo 10 - Seções 10.1 e 10.2 do livro texto da disciplina: Aritmética, A.
Resolução dos Exercícios 31/05-09/06.
 Resolução dos Exercícios 31/05-09/06. 1. Seja A um domínio de integridade. Mostre que todo subgrupo finito de U(A) é cíclico. Seja K o corpo de frações de A. Então A é um subanel de K (identificado com
Resolução dos Exercícios 31/05-09/06. 1. Seja A um domínio de integridade. Mostre que todo subgrupo finito de U(A) é cíclico. Seja K o corpo de frações de A. Então A é um subanel de K (identificado com
MA14 - Unidade 1 Divisibilidade Semana de 08/08 a 14/08
 MA14 - Unidade 1 Divisibilidade Semana de 08/08 a 14/08 Neste curso, consideraremos o conjunto dos números naturais como sendo o conjunto N = {0, 1, 2, 3,... }, denotando por N o conjunto N \ {0}. Como
MA14 - Unidade 1 Divisibilidade Semana de 08/08 a 14/08 Neste curso, consideraremos o conjunto dos números naturais como sendo o conjunto N = {0, 1, 2, 3,... }, denotando por N o conjunto N \ {0}. Como
1. Conhecendo-se somente os produtos AB e AC, calcule A = X 2 = 2X. 3. Mostre que se A e B são matrizes que comutam com a matriz M = 1 0
 Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Lista de exercícios. AL. 1 sem. 2015 Prof. Fabiano Borges da Silva 1 Matrizes Notações: 0 para matriz nula; I para matriz identidade; 1. Conhecendo-se somente os produtos AB e AC calcule A(B + C) B t A
Teorema de Tales. MA13 - Unidade 8. Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria.
 Teorema de Tales MA13 - Unidade 8 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Proporcionalidade 1. Dizemos que o segmento x é a quarta proporcional
Teorema de Tales MA13 - Unidade 8 Resumo elaborado por Eduardo Wagner baseado no texto: A. Caminha M. Neto. Geometria. Coleção PROFMAT Proporcionalidade 1. Dizemos que o segmento x é a quarta proporcional
Números Primos, MDC e MMC. O próximo teorema nos diz que os primos são as peças fundamentais dos números inteiros:
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 4 Números Primos, MDC e MMC. Definição 1. Um inteiro p > 1 é chamado número primo se não possui um divisor d
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 4 Números Primos, MDC e MMC. Definição 1. Um inteiro p > 1 é chamado número primo se não possui um divisor d
Programação Acadêmica de 2011 Semestre 1
 Programação Acadêmica de 2011 Semestre 1 U = Unidade (Em cada semana haverá duas unidades a serem estudadas para cada disciplina) P = Aula Presencial A programação de cada disciplina prevê 12 aulas presenciais
Programação Acadêmica de 2011 Semestre 1 U = Unidade (Em cada semana haverá duas unidades a serem estudadas para cada disciplina) P = Aula Presencial A programação de cada disciplina prevê 12 aulas presenciais
PLANEJAMENTO ANUAL / TRIMESTRAL 2012 Conteúdos Habilidades Avaliação
 COLÉGIO LA SALLE BRASÍLIA Disciplina: Matemática Trimestre: 1º Números Naturais: - Sistema de numeração - Adição e subtração - Multiplicação e divisão - Traduzir em palavras números representados por algarismos
COLÉGIO LA SALLE BRASÍLIA Disciplina: Matemática Trimestre: 1º Números Naturais: - Sistema de numeração - Adição e subtração - Multiplicação e divisão - Traduzir em palavras números representados por algarismos
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 2018.1 Gabarito Questão 01 [ 1,25 ::: (a)=0,50; (b)=0,75 ] Isótopos radioativos de um elemento químico estão sujeitos a um processo de decaimento
Polos Olímpicos de Treinamento. Aula 7. Curso de Teoria dos Números - Nível 2. Aula de Revisão e Aprofundamento. Prof.
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 7 Aula de Revisão e Aprofundamento Observação 1. É recomendável que o professor instigue seus alunos a pensarem
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 7 Aula de Revisão e Aprofundamento Observação 1. É recomendável que o professor instigue seus alunos a pensarem
1. O que podemos dizer sobre a imagem da função. f : Z Z, f(x) = x 2 + x + 1?
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
INSTRUÇÕES. Esta prova é individual e sem consulta à qualquer material.
 OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
OPRM 07 Nível 3 (Ensino Médio) Primeira Fase 09/06/7 ou 0/06/7 Duração: 3 horas Nome: Escola: Aplicador(a): INSTRUÇÕES Escreva seu nome, o nome da sua escola e nome do APLICADOR nos campos acima. Esta
QUESTÃO 18 QUESTÃO 19
 Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSA O 8 Ọ ANO DO ENSINO FUNDAMENTAL EM 016 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 16 A soma de três números naturais múltiplos
Nome: N.º: endereço: data: Telefone: E-mail: Colégio PARA QUEM CURSA O 8 Ọ ANO DO ENSINO FUNDAMENTAL EM 016 Disciplina: MaTeMÁTiCa Prova: desafio nota: QUESTÃO 16 A soma de três números naturais múltiplos
INTEIROS. Luciana Santos da Silva Martino. lulismartino.wordpress.com PROFMAT - Colégio Pedro II. 25 de agosto de 2017
 Sumário REPRESENTAÇÃO DOS NÚMEROS INTEIROS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Sistemas de Numeração
Sumário REPRESENTAÇÃO DOS NÚMEROS INTEIROS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 25 de agosto de 2017 Sumário 1 Sistemas de Numeração
MA14 - Aritmética Unidade 9 Resumo. Teorema Fundamental Da Aritmética
 MA14 - Aritmética Unidade 9 Resumo Teorema Fundamental Da Aritmética Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 9 Resumo Teorema Fundamental Da Aritmética Abramo Hefez PROFMAT - SBM Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
1 Conjuntos, Números e Demonstrações
 1 Conjuntos, Números e Demonstrações Definição 1. Um conjunto é qualquer coleção bem especificada de elementos. Para qualquer conjunto A, escrevemos a A para indicar que a é um elemento de A e a / A para
1 Conjuntos, Números e Demonstrações Definição 1. Um conjunto é qualquer coleção bem especificada de elementos. Para qualquer conjunto A, escrevemos a A para indicar que a é um elemento de A e a / A para
Polos Olímpicos de Treinamento. Aula 1. Curso de Teoria dos Números - Nível 2. Divisibilidade I. Samuel Barbosa Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Samuel Barbosa Feitosa Aula 1 Divisibilidade I Teorema 1. (Algoritmo da Divisão) Para quaisquer inteiros positivos a e b, existe um
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Samuel Barbosa Feitosa Aula 1 Divisibilidade I Teorema 1. (Algoritmo da Divisão) Para quaisquer inteiros positivos a e b, existe um
Note-se que pelo Teorema de Euler. a φ(n) 1 (mod n) logo existe k nas condições da definição acima e. Raízes Primitivas. Ordem de um elemento
 Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Ordem de um elemento Definição Sejam a e n inteiros tais que m.d.c.(a, n) = 1. O menor inteiro positivo k tal que tal que a k 1 (mod n) diz-se a ordem de a módulo n e representa-se por ord n (a). Note-se
Módulo de Números Naturais. Divisibilidade e Teorema da Divisão Euclideana. 8 ano E.F.
 Módulo de Números Naturais. Divisibilidade e Teorema da Divisão Euclideana. 8 ano E.F. Módulo de Números Naturais. Divisibilidade e Teorema da Divisão Euclideana. 1 Exercícios Introdutórios Exercício 1.
Módulo de Números Naturais. Divisibilidade e Teorema da Divisão Euclideana. 8 ano E.F. Módulo de Números Naturais. Divisibilidade e Teorema da Divisão Euclideana. 1 Exercícios Introdutórios Exercício 1.
LISTA DE EXERCÍCIOS DE MATEMÁTICA PRODUTOS NOTÁVEIS E FATORAÇÃO ALGÉBRICA. 1 - A soma de uma sequência de números ímpares, começando do
 LISTA DE EXERCÍCIOS DE MATEMÁTICA PRODUTOS NOTÁVEIS E FATORAÇÃO ALGÉBRICA 1 - A soma de uma sequência de números ímpares, começando do 1, é sempre igual a um número quadrado perfeito. Com base nessa informação,
LISTA DE EXERCÍCIOS DE MATEMÁTICA PRODUTOS NOTÁVEIS E FATORAÇÃO ALGÉBRICA 1 - A soma de uma sequência de números ímpares, começando do 1, é sempre igual a um número quadrado perfeito. Com base nessa informação,
é uma proposição verdadeira. tal que: 2 n N k, Φ(n) = Φ(n + 1) é uma proposição verdadeira. com n N k, tal que:
 Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
Matemática Discreta 2008/09 Vítor Hugo Fernandes Departamento de Matemática FCT/UNL Axioma (Princípio da Boa Ordenação dos Números Naturais) O conjunto parcialmente (totalmente) ordenado (N, ), em que
deve ter a forma 2 3 5, com a, b e c inteiros, 0 a 8, é dessa forma. Cada um dos outros números possui um fator primo diferente de 2, 3 e 5.
 XXXII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (Ensino Médio) GABARITO GABARITO NÍVEL 1) E 6) C 11) E 16) D 1) E ) B 7) B 1) C 17) E ) C ) E 8) D 1) D 18) A ) B 4) E 9) D 14) A 19) C 4) E
XXXII OLIMPÍADA BRASILEIRA DE MATEMÁTICA PRIMEIRA FASE NÍVEL (Ensino Médio) GABARITO GABARITO NÍVEL 1) E 6) C 11) E 16) D 1) E ) B 7) B 1) C 17) E ) C ) E 8) D 1) D 18) A ) B 4) E 9) D 14) A 19) C 4) E
1. Múltiplos e divisores
 Escola Básica de Santa Marinha Matemática 2009/2010 7º Ano Síntese dos conteúdos Números e operações 1 Múltiplos e divisores Múltiplo de um número é todo o número que se obtém multiplicando o número dado
Escola Básica de Santa Marinha Matemática 2009/2010 7º Ano Síntese dos conteúdos Números e operações 1 Múltiplos e divisores Múltiplo de um número é todo o número que se obtém multiplicando o número dado
MATEMÁTICA MÓDULO 1 TEORIA DOS NÚMEROS 1. DIVISIBILIDADE 1.1. DEFINIÇÃO 1.2. CRITÉRIOS DE DIVISIBILIDADE
 TEORIA DOS NÚMEROS 1. DIVISIBILIDADE Neste momento inicial, nosso interesse será em determinar quando a divisão entre dois números inteiros é exata, ou seja, quando o resto da divisão é 0. Antes de mais
TEORIA DOS NÚMEROS 1. DIVISIBILIDADE Neste momento inicial, nosso interesse será em determinar quando a divisão entre dois números inteiros é exata, ou seja, quando o resto da divisão é 0. Antes de mais
a) Falsa. Por exemplo, para n = 2, temos 3n = 3 2 = 6, ou seja, um número par.
 Matemática Unidade I Álgebra Série - Teoria dos números 01 a) Falsa. Por exemplo, para n =, temos 3n = 3 = 6, ou seja, um número par. b) Verdadeira. Por exemplo, para n = 1, temos n = 1 =, ou seja, um
Matemática Unidade I Álgebra Série - Teoria dos números 01 a) Falsa. Por exemplo, para n =, temos 3n = 3 = 6, ou seja, um número par. b) Verdadeira. Por exemplo, para n = 1, temos n = 1 =, ou seja, um
Equações Diofantinas II
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 1 Equações Diofantinas II Continuaremos nosso estudo das equações diofantinas abordando agora algumas equações
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível Prof. Samuel Feitosa Aula 1 Equações Diofantinas II Continuaremos nosso estudo das equações diofantinas abordando agora algumas equações
Curso Turno Disciplina Carga Horária Licenciatura Plena em Noturno Matemática Elementar I 60h
 1 Curso Turno Disciplina Carga Horária Licenciatura Plena em Noturno Matemática Elementar I 60h Matemática Aula Período Data Coordenador 3.1 1. a 06/06/2006 (terça feira) Tempo Estratégia Descrição (Arte)
1 Curso Turno Disciplina Carga Horária Licenciatura Plena em Noturno Matemática Elementar I 60h Matemática Aula Período Data Coordenador 3.1 1. a 06/06/2006 (terça feira) Tempo Estratégia Descrição (Arte)
1 Congruências e aritmética modular
 1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
1 Congruências e aritmética modular Vamos considerar alguns exemplos de problemas sobre números inteiros como motivação para o que se segue. 1. O que podemos dizer sobre a imagem da função f : Z Z, f(x)
Polos Olímpicos de Treinamento. Aula 9. Curso de Teoria dos Números - Nível 2. O Teorema de Euler. Prof. Samuel Feitosa
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 2 Prof. Samuel Feitosa Aula 9 O Teorema de Euler Nesta aula, obteremos uma generalização do teorema de Fermat. Definição 1. Dado n N,
Aula 4 - Números Primos, MDC e MMC
 Polos Olímpicos de Treinamento Intensivo (POTI) Curso de Teoria dos Números - Nível Aula 4 - Números Primos, MDC e MMC Prof. Samuel Feitosa Arquivo Original 1 1 Documento:...gaia/educacional/matematica/teoria
Polos Olímpicos de Treinamento Intensivo (POTI) Curso de Teoria dos Números - Nível Aula 4 - Números Primos, MDC e MMC Prof. Samuel Feitosa Arquivo Original 1 1 Documento:...gaia/educacional/matematica/teoria
Primeiro Desao Mestre Kame
 Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
Primeiro Desao Mestre Kame Alan Anderson 8 de julho de 2017 O propósito dessa lista é gerar uma intuição numérica das demonstrações abstratas do teoremas famosos de Teoria dos números, de modo que alguns
NÚMEROS ESPECIAIS. Luciana Santos da Silva Martino. lulismartino.wordpress.com PROFMAT - Colégio Pedro II
 Sumário NÚMEROS ESPECIAIS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 27 de outubro de 2017 Sumário 1 Primos de Fermat, de Mersenne e em
Sumário NÚMEROS ESPECIAIS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 27 de outubro de 2017 Sumário 1 Primos de Fermat, de Mersenne e em
Se mdc(a,m) = 1, como a é invertível módulo m, a equação. ax b (mod m)
 Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Polos Olímpicos de Treinamento Curso de Teoria dos Números - Nível 3 Carlos Gustavo Moreira Aula 8 Equações lineares módulo n e o teorema chinês dos restos 1 Equações Lineares Módulo m Se mdc(a,m) = 1,
Produtos Notáveis. Vejamos alguns exemplos para diversos produtos notáveis que auxiliarão na formação de ideias para problemas futuros mais difíceis.
 Polos Olímpicos de Treinamento Curso de Álgebra - Nível Prof. Marcelo Mendes Aula Produtos Notáveis Vários problemas de Álgebra para alunos do Ensino Fundamental utilizam Produtos Notáveis, que são identidades
Polos Olímpicos de Treinamento Curso de Álgebra - Nível Prof. Marcelo Mendes Aula Produtos Notáveis Vários problemas de Álgebra para alunos do Ensino Fundamental utilizam Produtos Notáveis, que são identidades
Semana Olímpica 2019
 Semana Olímpica 2019 Prof a Ana Paula Chaves apchaves.math@gmail.com Nível 1 Congruência 1. Divisibilidade e Aritmética Modular Um dos tópicos mais fundamentais da teoria dos números é, sem dúvidas, a
Semana Olímpica 2019 Prof a Ana Paula Chaves apchaves.math@gmail.com Nível 1 Congruência 1. Divisibilidade e Aritmética Modular Um dos tópicos mais fundamentais da teoria dos números é, sem dúvidas, a
Programa Combinatória Aritmética Racional MATEMÁTICA DISCRETA. Patrícia Ribeiro. Departamento de Matemática, ESTSetúbal 2018/ / 52
 1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
1 / 52 MATEMÁTICA DISCRETA Patrícia Ribeiro Departamento de Matemática, ESTSetúbal 2018/2019 2 / 52 Programa 1 Combinatória 2 Aritmética Racional 3 Grafos 3 / 52 Capítulo 1 Combinatória 4 / 52 Princípio
Funções - Terceira Lista de Exercícios
 Funções - Terceira Lista de Exercícios Módulo - Números Reais. Expresse cada número como decimal: a) 7 b) c) 9 0 5 5 e) 3 7 0 f) 4 g) 8 7 d) 7 8 h) 56 4. Expresse cada número decimal como uma fração na
Funções - Terceira Lista de Exercícios Módulo - Números Reais. Expresse cada número como decimal: a) 7 b) c) 9 0 5 5 e) 3 7 0 f) 4 g) 8 7 d) 7 8 h) 56 4. Expresse cada número decimal como uma fração na
Teorema Chinês dos Restos. Tópicos Adicionais
 Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Teorema Chinês dos Restos Teorema Chinês dos Restos Tópicos Adicionais Tópicos Adicionais Teorema Chinês dos Restos 1 Exercícios Introdutórios Exercício 1. Para cada um dos itens abaixo, encontre o menor
Módulo de Progressões Aritméticas. Soma dos termos de uma P.A. 1 a série E.M. Professores Tiago Miranda e Cleber Assis
 Módulo de Progressões Aritméticas Soma dos termos de uma PA 1 a série EM Professores Tiago Miranda e Cleber Assis Progressões Aritméticas Soma dos termos de uma PA 1 Exercícios Introdutórios Exercício
Módulo de Progressões Aritméticas Soma dos termos de uma PA 1 a série EM Professores Tiago Miranda e Cleber Assis Progressões Aritméticas Soma dos termos de uma PA 1 Exercícios Introdutórios Exercício
Matemática Discreta. Fundamentos e Conceitos da Teoria dos Números. Universidade do Estado de Mato Grosso. 4 de setembro de 2017
 Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Matemática Discreta Fundamentos e Conceitos da Teoria dos Números Professora Dr. a Donizete Ritter Universidade do Estado de Mato Grosso 4 de setembro de 2017 Ritter, D. (UNEMAT) Matemática Discreta 4
Funções - Primeira Lista de Exercícios
 Funções - Primeira Lista de Exercícios Vers~ao de 0/03/00 Recomendações Não é necessário o uso de teoremas ou resultados complicados nas resoluções. Basta que você tente desenvolver suas idéias. Faltando
Funções - Primeira Lista de Exercícios Vers~ao de 0/03/00 Recomendações Não é necessário o uso de teoremas ou resultados complicados nas resoluções. Basta que você tente desenvolver suas idéias. Faltando
Números Naturais Representação, Operações e Divisibilidade. Múltiplos e Divisores. Tópicos Adicionais
 Números Naturais Representação, Operações e Divisibilidade Múltiplos e Divisores Tópicos Adicionais Números Naturais Representação, Operações e Divisibilidade Múltiplos e Divisores 1 Exercícios Introdutórios
Números Naturais Representação, Operações e Divisibilidade Múltiplos e Divisores Tópicos Adicionais Números Naturais Representação, Operações e Divisibilidade Múltiplos e Divisores 1 Exercícios Introdutórios
Triângulos retângulos com lados inteiros: Procurando as hipotenusas
 MATEMÁTICA UNIVERSITÁRIA n o 41 Dezembro/2006 pp. 1 10 Triângulos retângulos com lados inteiros: Procurando as hipotenusas José F. Andrade 1 Introdução O objetivo principal deste artigo é determinar os
MATEMÁTICA UNIVERSITÁRIA n o 41 Dezembro/2006 pp. 1 10 Triângulos retângulos com lados inteiros: Procurando as hipotenusas José F. Andrade 1 Introdução O objetivo principal deste artigo é determinar os
Programação Acadêmica de 2012 Semestre 1 Turma 2011
 Programação Acadêmica de 2012 Semestre 1 Turma 2011 U = Unidade (Em cada semana haverá duas unidades a serem estudadas para cada disciplina) P = Aula Presencial A bibliografia está indicada ao final. Os
Programação Acadêmica de 2012 Semestre 1 Turma 2011 U = Unidade (Em cada semana haverá duas unidades a serem estudadas para cada disciplina) P = Aula Presencial A bibliografia está indicada ao final. Os
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. ENQ Gabarito. a(x x 0) = b(y 0 y).
 MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016.1 Gabarito Questão 01 [ 1,00 ::: (a)=0,50; (b)=0,50 ] (a) Seja x 0, y 0 uma solução da equação diofantina ax + by = c, onde a, b são inteiros
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 016.1 Gabarito Questão 01 [ 1,00 ::: (a)=0,50; (b)=0,50 ] (a) Seja x 0, y 0 uma solução da equação diofantina ax + by = c, onde a, b são inteiros
CENTRO EDUCACIONAL GIRASSOL TD de Matemática Prof.: Tiago Rodrigues
 CENTRO EUCACIONAL GIRASSOL T de Matemática Prof.: Tiago Rodrigues proftiagorodrigues@gmail.com IVISIBILIAE E RESTO. Introdução O assunto divisibilidade no Conjunto dos Inteiros ( ) é extremamente importante
CENTRO EUCACIONAL GIRASSOL T de Matemática Prof.: Tiago Rodrigues proftiagorodrigues@gmail.com IVISIBILIAE E RESTO. Introdução O assunto divisibilidade no Conjunto dos Inteiros ( ) é extremamente importante
x é igual a: 07. (Colégio Naval) No conjunto R dos números reais, qual será o 01. (PUC) O valor de m, de modo que a equação
 0. (PUC) O valor de m, de modo que a equação 5 m m 0 b) c) d) 0. Quantos valores de satisfazem a equação a) b) c) d) 5 e) 0 Prof. Paulo Cesar Costa tenha uma das raízes igual a, é: ( ). 07. (Colégio Naval)
0. (PUC) O valor de m, de modo que a equação 5 m m 0 b) c) d) 0. Quantos valores de satisfazem a equação a) b) c) d) 5 e) 0 Prof. Paulo Cesar Costa tenha uma das raízes igual a, é: ( ). 07. (Colégio Naval)
MATEMÁTICA. Aula 4. Professor : Dêner Rocha. Monster Concursos 1
 MATEMÁTICA Aula 4 Professor : Dêner Rocha Monster Concursos 1 Divisibilidade Critérios de divisibilidade São critérios que nos permite verificar se um precisarmos efetuar grandes divisões. número é divisível
MATEMÁTICA Aula 4 Professor : Dêner Rocha Monster Concursos 1 Divisibilidade Critérios de divisibilidade São critérios que nos permite verificar se um precisarmos efetuar grandes divisões. número é divisível
Hewlett-Packard CONJUNTOS NUMÉRICOS. Aulas 01 a 08. Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos
 Hewlett-Packard CONJUNTOS NUMÉRICOS Aulas 01 a 08 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 2019 Sumário CONJUNTOS NUMÉRICOS... 2 Conjunto dos números Naturais... 2 Conjunto dos números
Hewlett-Packard CONJUNTOS NUMÉRICOS Aulas 01 a 08 Elson Rodrigues, Gabriel Carvalho e Paulo Luiz Ramos Ano: 2019 Sumário CONJUNTOS NUMÉRICOS... 2 Conjunto dos números Naturais... 2 Conjunto dos números
ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ]
![ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ] ENQ Gabarito MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL. Questão 01 [ 1,25 ]](/thumbs/67/56480825.jpg) MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 017 Gabarito Questão 01 [ 1,5 ] Encontre as medidas dos lados e ângulos de dois triângulos ABC diferentes tais que AC = 1, BC = e A BC = 0 Considere
MESTRADO PROFISSIONAL EM MATEMÁTICA EM REDE NACIONAL ENQ 017 Gabarito Questão 01 [ 1,5 ] Encontre as medidas dos lados e ângulos de dois triângulos ABC diferentes tais que AC = 1, BC = e A BC = 0 Considere
Módulo: aritmética dos restos. Divisibilidade e Resto. Tópicos Adicionais
 Módulo: aritmética dos restos Divisibilidade e Resto Tópicos Adicionais Módulo: aritmética dos restos Divisibilidade e resto 1 Exercícios Introdutórios Exercício 1. Encontre os inteiros que, na divisão
Módulo: aritmética dos restos Divisibilidade e Resto Tópicos Adicionais Módulo: aritmética dos restos Divisibilidade e resto 1 Exercícios Introdutórios Exercício 1. Encontre os inteiros que, na divisão
MA14 - Aritmética Unidade 5 Resumo. Máximo Divisor Comum
 MA14 - Aritmética Unidade 5 Resumo Máximo Divisor Comum Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
MA14 - Aritmética Unidade 5 Resumo Máximo Divisor Comum Abramo Hefez PROFMAT - SBM Julho 2013 Aviso Este material é apenas um resumo de parte do conteúdo da disciplina e o seu estudo não garante o domínio
11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA
 Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Teoria de Números 11.1) Noções Elementares 11.2) MDCs e algoritmos de Euclides 11.3) Aritmética modular 11.4) Aplics da MD: O sistema criptográfico RSA Material extraído dos livros-textos (Cormen( Cormen)
Proposição 0 (Divisão Euclidiana): Dados a b, b b * existem q, r b unicamente determinados tais que 0 r < b e a = bq + r
 "!$#%& '!)( * +-,/.10 2/3"456387,:9;2 .1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos
"!$#%& '!)( * +-,/.10 2/3"456387,:9;2 .1?/@.1, ACB DFEHG IJDLK8MHNLK8OHP Q RTSVUVWYXVZ\[^]_W Este artigo se roõe a ser uma referência sobre os temas citados no título, que aarecem naturalmente em diversos
1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0
![1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0 1.3 Matrizes inversas ] [ 0 1] = [ ( 1) ( 1) ] = [1 0](/thumbs/77/76694592.jpg) 1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
1.3 Matrizes inversas Definição: Seja A uma matriz de ordem k n, a matriz B de ordem n k é uma inversa à direita de A, se AB = I. A Matriz C de ordem n k é uma inversa à esquerda de A, se CA = I. Exemplo
CURSO ANUAL DE MATEMÁTICA VOLUME 1
 CURSO ANUAL DE MATEMÁTICA VOLUME ) SISTEMA DE NUMERAÇÃO DECIMAL O sistema de numeração que usamos é o sistema de numeração decimal, pelo fato de contarmos os elementos em grupos de dez. Dezenas cada grupo
CURSO ANUAL DE MATEMÁTICA VOLUME ) SISTEMA DE NUMERAÇÃO DECIMAL O sistema de numeração que usamos é o sistema de numeração decimal, pelo fato de contarmos os elementos em grupos de dez. Dezenas cada grupo
Lista de Exercícios 05 Álgebra Matricial
 Lista de Exercícios 05 Álgebra Matricial - 016.1 1. Determine a quantidade desconhecida em cada uma das expressões: ( ) ( ) ( ) T 0 3 x + y + 3 3 w (a) 3.X = (b) = 6 9 4 0 6 z. Uma rede de postos de combustíveis
Lista de Exercícios 05 Álgebra Matricial - 016.1 1. Determine a quantidade desconhecida em cada uma das expressões: ( ) ( ) ( ) T 0 3 x + y + 3 3 w (a) 3.X = (b) = 6 9 4 0 6 z. Uma rede de postos de combustíveis
DIVISÃO NOS INTEIROS. Luciana Santos da Silva Martino. lulismartino.wordpress.com PROFMAT - Colégio Pedro II
 Sumário DIVISÃO NOS INTEIROS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 18 de agosto de 2017 Sumário 1 Divisibilidade 2 Divisão Euclidiana
Sumário DIVISÃO NOS INTEIROS Luciana Santos da Silva Martino lulismartino.wordpress.com lulismartino@gmail.com PROFMAT - Colégio Pedro II 18 de agosto de 2017 Sumário 1 Divisibilidade 2 Divisão Euclidiana
Universidade do Minho
 Teórica n o 1 2007-02-22 Apresentação do docente e da disciplina. Algumas revisões de teoria de números elementar. O algoritmo de Euclides estendido; demonstração do teorema que fundamenta o algoritmo.
Teórica n o 1 2007-02-22 Apresentação do docente e da disciplina. Algumas revisões de teoria de números elementar. O algoritmo de Euclides estendido; demonstração do teorema que fundamenta o algoritmo.
Ficha de Trabalho 02 Sistemas. Matriz Inversa. (Aulas 4 a 6).
 F I C H A D E R A B A L H O 0 Ficha de rabalho 0 Sistemas. Matriz Inversa. (Aulas 4 a 6). Sistemas de equações lineares. Equação linear. Sistema de equações lineares. Equação matricial. Soluções do sistema.
F I C H A D E R A B A L H O 0 Ficha de rabalho 0 Sistemas. Matriz Inversa. (Aulas 4 a 6). Sistemas de equações lineares. Equação linear. Sistema de equações lineares. Equação matricial. Soluções do sistema.
