ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE
|
|
|
- Lucas Palma Vieira
- 5 Há anos
- Visualizações:
Transcrição
1 Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE Séries de Fourier (1 Desenvova em série de Fourier as seguintes funções: (a f : [ 1, 1] R definida por 1 se 1 x f(x = +1 se < x 1 ; (b f : [ π, π] R definida por f(x = cos (x sin 3 (x. Resoução: (a A série de Fourier da função f é da forma onde a + (a n cos(nπx + b n sin(nπx a n = b n = f(x cos(nπx dx para n, f(x sin(nπx dx para n 1. Como f é uma função ímpar, todos os a n s são zero e b n = = 1 1 f(x sin(nπx dx sin(nπx dx = nπ (cos nπ cos = ( 1n nπ = 4 nπ se n é ímpar, se n é par. Logo, a série de Fourier de f é n ímpar 4 nπ sin(nπx = n= 4 sin((n + 1πx. (n + 1π
2 AMIV FICHA SUPLEMENTAR 5 Comentário: Como a função f é seccionamente diferenciáve em [ 1, 1], a sua série de Fourier converge em [ 1, 1] para f(x se x ] 1, [ ou x ], 1[ 1 se x ] 1, [ = se x = ou x = ±1 se x = ou x = ±1 1 se x ], 1[ Nos pontos da forma x = k Z, a série converge para porque este vaor é a média dos imites aterais nestes pontos da extensão de f a R como função periódica de período : im x 1 f(x = im f(x = 1 e im f(x = x 1 x 1 + im f(x = 1. x 1 + (b A série de Fourier da função f é da forma a + (a n cos(nx + b n sin(nx Uma vez que o desenvovimento de Fourier é único, quaquer desenvovimento que obtenhamos para f em termos das funções base 1, cos(nx e sin(nx será o desenvovimento de Fourier de f. Ora tem-se cos x = 1 + cos(x e, pea fórmua de DeMoivre, = cos(x Im ( (cos x + i sin x 3 = Im(cos(3x + i sin(3x 3 cos x sin x sin 3 x = sin(3x 3(1 sin x sin x sin 3 x = sin(3x sin 3 x = 3 4 sin x 1 4 sin(3x portanto o desenvovimento de Fourier de f é cos(x 3 4 sin x sin(3x isto é, a = 1, a = 1, a n = para n, e b 1 = 3 4, b 3 = 1 4, b n = para n 1, 3. ( Desenvova as seguintes funções em série de Fourier: e x se x 1 (a f(x = e x se 1 x < ; (b f : [ π, π] R definida por f(x = sin 4 x ; x se x < (c f(x =. se x
3 AMIV FICHA SUPLEMENTAR 5 3 (3 Desenvova a função f : [, π] R definida por f(x = e x em série de senos. Resoução: A série de senos da função f é da forma b n sin(nx onde, para n 1 se tem b n = π Logo, a série de senos de f é π π f(x sin(nx dx = e x sin(nx dx π = ( π π Im e ( 1+inx dx ( = π Im e ( 1+inx π 1 + in = ( e π π Im ( 1 n in = n (1 e π ( 1 n π(1 + n n (1 e π ( 1 n π(1 + n sin(nx. (4 Seja um número rea positivo. Desenvova a função f : [, ] R definida por x se x f(x = x se < x em série de cosenos. Resoução: A série de cosenos da função f é da forma a + a n cos ( nπx onde, para n se tem Assim, a n = ( a = x dx + f(x cos nπx dx ( x dx =
4 4 AMIV FICHA SUPLEMENTAR 5 e, para n 1, a n = ( = + ( x cos ( nπx x nπ sin ( nπx ( x nπ dx + sin ( nπx ( x cos ( nπx dx nπ sin ( nπx dx ( = nπ sin ( ( nπ + nπ sin ( nπx dx n π cos ( nπx nπ sin ( ( nπ n π cos ( nπx ( ( = cos nπ ( n π 1 cos(nπ + cos nπ ( ( = cos nπ n π 1 ( 1 n Tendo em conta que cos ( nπ = se n é ímpar 1 se n = 4k para agum inteiro k 1 se n = 4k + tem-se 8 se n = 4k + a n = n π caso contrário Portanto a série de cosenos de f é ( (4k + π cos (4k+πx k= (5 Desenvova as seguintes funções em série de cosenos: 1 se x < 1 (a f(x = x se 1 para x [, 1]; x 1 (b f(x = cos x sin x para x [, π]. (6 Desenvova as seguintes funções em série de senos: (a f(x = 1 para x [, 1]; (b f(x = (π xx para x [, π]; (c f(x = 55 4x para x [, 1]; (d f(x = x(x 1 para x [, 1]. Comentário: As respostas às primeiras três aĺıneas deste exercício estão contidas nas resouções dos exercícios 1, 13 e 9 respectivamente.
5 AMIV FICHA SUPLEMENTAR 5 5 Equações do caor, de Lapace e das ondas (7 Seja c um parâmetro rea positivo. Recorrendo ao método de separação de variáveis, determine a soução do seguinte probema para a equação das ondas u = c u t x u(t, = u(t, 1 = u(, x =, (, x = 1 t para t e para x [, 1] (satisfazendo a equação diferencia para < x < 1. Resoução: para as quais Peo método de separação de variáveis, procura-se souções da EDP da forma u(t, x = T (tx(x, t T (tx(x = T ( (tx(x e x T (tx(x = T (tx ( (x. Substituindo na equação, e assumindo que T (tx(x, fica T ( (tx(x = c T (tx ( (x T ( (t T (t }} k = c X( (x X(x }} k onde cada um dos membros tem que ser uma constante rea k (porque o membro esquerdo não depende de x, o membro direito não depende de t e ees têm que ser iguais. Para que a condição na fronteira, T (tx( = T (tx(1 =, seja satisfeita por uma soução não identicamente nua, tem que ser X( = X(1 = (já que, se X( ou X(1, teria que ser T (t =, t. A soução gera de X ( (x = k c X(x é, consoante os casos, k X(x = c 1 e c x + c e k c x se k > X(x = c 1 + c x se k = X(x = c 1 cos( k c x + c sin( k c x se k <. Quando k, a única soução X(x que satisfaz a condição na fronteira é a soução identicamente nua, ou seja, nesses casos, X( = X(1 = = c 1 = c =. Quando k <, a condição X( = impõe c 1 = e depois a condição X(1 = impõe a uma soução não identicamente nua que k sin( =. c Esta condição pode ser satisfeita por uma soução não identicamente nua desde que k = nπ, n = 1,, 3,... c
6 6 AMIV FICHA SUPLEMENTAR 5 ou seja, é Para k <, a soução gera de A condição inicia k = c n π, n = 1,, 3,... T ( (t = kt (t T (t = c 1 cos( kt + c sin( kt. T (X(x = impõe que seja T ( = para que a soução não seja identicamente nua. Quando T (t é uma combinação inear de sin e cos como acima, tem que então ser c 1 =. Obtêm-se assim todas as seguintes souções para o probema de vaor na fronteira conjugado com a primeira condição inicia: u n (t, x = sin(cnπt }} T (t sin(nπx, n = 1,, 3,... }} X(x definidas para t e para x [, 1]. Por inearidade, quaquer combinação inear finita desta souções é ainda soução e, mais geramente, quaquer série d n u n (t, x é uma soução forma. Para que a soução mais gera da forma acima satisfaça a segunda condição inicia tem que ser Como a condição fica n t (, x = 1, t d n n t = 1. t= = cnπ cos(cnπt sin(nπx, d n cnπ sin(nπx = 1. Para encontrar as constantes d n adequadas, desenvove-se a função 1 em série de senos. Isso é equivaente a estender esta função ao intervao [ 1, 1] como função ímpar, e desenvover a extensão em série de Fourier, trabaho esse que foi feito no exercício 1 onde se encontrou que a série de senos para a função 1 é n ímpar 4 nπ sin(nπx = n= 4 sin((n + 1πx. (n + 1π Logo, os d n s devem ser quando n é par e devem satisfazer d n cnπ = 4 nπ
7 AMIV FICHA SUPLEMENTAR 5 7 quando n é ímpar. Concui-se que a série que dá a soução forma do probema posto é n ímpar 4 cn sin(cnπt sin(nπx π = n= 4 c(n + 1 sin (c(n + 1πt sin((n + 1πx. π (8 Use o método de separação de variáveis para determinar a soução do seguinte probema de vaor na fronteira para a equação de Lapace: para x π e y π. Resoução: forma u + u = x y u(x, = u(x, π = u(, y = u(π, y = sin(y Peo método de separação de variáveis, procura-se souções do probema da u(x, y = X(xY (y. Substituindo na equação obtém-se, para X(xY (y, X ( (xy (y + X(xY ( (y = X( (x X(x Concui-se que existe k R ta que X ( (x X(x Para que a condição na fronteira = k = Y ( (y Y (y X(xY ( = X(xY (π = = Y ( (y Y (y seja satisfeita por uma soução não identicamente nua, tem que ser A equação Y ( = Y (π = Y ( (y + ky (y = só tem souções não identicamente nuas que verifiquem a condição fronteira Y ( = Y (π = se k >. Nesse caso, a soução gera é Y (y = c 1 cos( ky + c sin( ky A condição Y ( = impica c 1 = e a condição Y (π = impôe sin( kπ = k = n para agum n inteiro Para que a soução não seja identicamente nua, tem que ser n e caramente basta considerar n >. A soução gera da equação é X ( (x n X(x = X(x = c 1 e nx + c e nx
8 8 AMIV FICHA SUPLEMENTAR 5 Para uma soução não identicamente nua, a condição na fronteira X(Y (y = impica X( = c 1 + c = c = c 1 peo que ( e nx e nx X(x = c 1 = c 1 sinh(nx Obtêm-se assim as seguintes souções que verificam todas as condições na fronteira excepto possivemente a que foi imposta para x = π: u n (x, y = sinh(nx sin(ny, n = 1,, 3,... definidas para x π e y π. Por inearidade obtem-se a soução forma d n u n (x, y Para que esta série satisfaça a condição fronteira que resta devemos ter d n u n (π, y = sin y d n sinh(nπ sin(ny = sin y Concui-se que d n = para n e que d = 1 sinh(π. Isto é, a soução do probema do enunciado é u(x, y = 1 sinh(x sin(y. sinh(π
9 AMIV FICHA SUPLEMENTAR 5 9 (9 Considere a equação do caor t = u α x, onde α é um parâmetro rea positivo, t e x [, L]. Uma soução estacionária da equação do caor é uma soução que não depende do tempo, t. (a Mostre que todas as souções estacionárias da equação do caor são ineares em x, i.e., são funções da forma u(x = ax + b. (b Determine uma soução estacionária para a equação do caor com a seguinte condição na fronteira: u(t, = T 1 e u(t, L = T. (c Ache uma soução da equação do caor (verificando a equação diferencia para < x < L com as seguintes condições de fronteira e inicia u(, x = 75 u(t, =, u(t, 1 = 6. Sugestão: Considere souções da forma u(t, x = v(x + w(t, x, onde v(x é uma soução estacionária do probema com condição na fronteira: u(t, = e u(t, 1 = 6. Resoução: (a Seja u(x uma soução estacionária da equação do caor. equação, obtém-se cuja soução gera é = α u ( u(x = c 1 + c x, Substituindo u(x na que é uma função inear. (b Procura-se os coeficientes c 1 e c tais que a correspondente soução estacionária, u(x = c 1 + c x, satisfaça u( = c 1 = T 1 u(l = c 1 + c L = T. A soução deste sistema inear é c 1 = T 1 c = T T 1 L. Encontra-se então a seguinte soução estacionária para a equação do caor com a condição na fronteira dada: u(x = T 1 + T T 1 L (c De acordo com a sugestão, procura-se uma soução da forma x. u(t, x = v(x + w(t, x,
10 1 AMIV FICHA SUPLEMENTAR 5 onde v(x é uma soução estacionária do probema da aĺınea (b tomando T 1 =, T = 6 e L = 1. Então v(x = + 4x, e w(t, x = u(t, x v(x terá de ser uma soução do probema homogéneo w ( t = α w x w(t, = w(t, 1 =. Apica-se o método de separação de variáveis na pesquisa de souções de ( : procurase souções da forma T (tx(x, para as quais t T (tx(x = T (tx(x x T (tx(x = T (tx ( (x. Substituindo na equação, e assumindo que T (tx(x, fica T (tx(x = α T (tx ( (x T (t T (t }} k e = α X( (x X(x }} k onde cada um dos membros tem que ser uma constante rea k (porque o membro esquerdo não depende de x, o membro direito não depende de t e ees têm que ser iguais. A soução gera de T (t = kt (t é A soução gera de T (t = ce kt com c R. X ( (x k α X(x = é, consoante os casos, k X(x = c 1 e α x + c e k α x se k > X(x = c 1 + c x se k = X(x = c 1 cos( k α x + c sin( k α x se k <. Para que a condição homogénea na fronteira, T (tx( = T (tx(1 =, seja satisfeita por uma soução não identicamente nua, tem que ser X( = X(1 = (já que, se X( ou X(1, teria que ser T (t =, t. Quando k, a única soução X(x que satisfaz esta condição na fronteira é a soução identicamente nua, ou seja, nesses casos, X( = X(1 = = c 1 = c =. Quando k <, a condição X( = impõe c 1 = e depois a condição X(1 = impõe a uma soução não identicamente nua que k sin( α =.
11 AMIV FICHA SUPLEMENTAR 5 11 Esta condição pode ser satisfeita por uma soução não identicamente nua desde que k = nπ, n = 1,, 3,... α ou seja, k = n π α, n = 1,, 3,... Obtêm-se assim todas as seguintes souções para o probema homogéneo ( : w n (t, x = e n π α t }} T (t sin(nπx, n = 1,, 3,... }} X(x definidas para t e para x [, 1]. Por inearidade, quaquer combinação inear finita desta souções é ainda soução e, mais geramente, quaquer série uniformemente convergente da forma b n w n (t, x é ainda soução. Obtêm-se assim as seguintes funções que verificam todas as condições do probema posto excepto a condição inicia: + 4x + b n w n (t, x. Finamente, impondo a condição inicia, u(, x = 75, terá que ser + 4x + b n w n (, x = 75, ou seja, b n sin(nπx = 55 4x. Para encontrar as constantes b n adequadas, desenvove-se a função 55 4x em série de senos. Isso é equivaente a estender esta função ao intervao [ 1, 1] como função ímpar, e desenvover a extensão em série de Fourier. Os coeficientes a n de uma função ímpar anuam-se e os coeficientes b n, para n 1, são dados por b n = = = f(x sin(nπx dx f(x sin(nπx dx (55 4x sin(nπx dx [ = 55 cos(nπx + 4x cos(nπx 4 sin(nπx ] 1 nπ nπ n π = [ 55 ( 1n nπ ] nπ + 4( 1n nπ = 11 3( 1n nπ.
12 1 AMIV FICHA SUPLEMENTAR 5 Concui-se que a soução forma do probema posto é 11 3( 1 + 4x + n nπ e n π α t sin(nπx. Comentário: O probema anterior diz respeito à evoução da distribuição de temperatura numa barra situada entre os pontos x = e x = L. No instante inicia todos os pontos da barra estão à mesma temperatura (75 e as temperaturas nas extremidades são mantidas constantes igua a em x = e a 6 na extremidade x = 1. (1 (11 (1 Determine a soução do seguinte probema para a equação do caor: = 4 u t x se x 1 u(x, = 75 se 1 < x (, t = (, t = x x para t e x (satisfazendo a equação diferencia para < x <. Seja c um parâmetro rea positivo. Determine a soução do seguinte probema de vaor na fronteira para a equação das ondas: u = c u t x u(x, = x cos ( πx t (x, = u(, t = u(1, t = para t e x 1 (satisfazendo a equação diferencia para < x < 1. Use o método de separação de variáveis para determinar uma soução do seguinte probema para a equação de Lapace: para x 1, y 1. u + u x y x = y (x, = y (, y = sin(πy (x, 1 = x (1, y = Método de separação de variáveis (a Determine as souções para t e para x [, π] de (13 t = u x u u(t, = u(t, π = (satisfazendo a equação diferencia para x ], π[. (b Determine a soução que satisfaz a condição inicia u(, x = (π xx. Resoução: (a Peo método de separação de variáveis, procura-se souções da EDP da forma u(t, x = T (tx(x,
13 AMIV FICHA SUPLEMENTAR 5 13 para as quais t T (tx(x = T (tx(x e x T (tx(x = T (tx ( (x. Substituindo na equação, e assumindo que T (tx(x, fica T (tx(x = T (tx ( (x T (tx(x T (t T (t }} k = X( (x 1 X(x }} k onde cada um dos membros tem que ser uma constante rea k (porque o membro esquerdo não depende de x, o membro direito não depende de t e ees têm que ser iguais. A soução gera de T (t = kt (t é A soução gera de T (t = ce kt com c R. X ( (x (k + 1X(x = é, consoante os casos, X(x = c 1 e k+1x + c e k+1x se k + 1 > X(x = c 1 + c x se k + 1 = X(x = c 1 cos( k 1x + c sin( k 1x se k + 1 <. Para que a condição na fronteira, T (tx( = T (tx(π =, seja satisfeita por uma soução não identicamente nua, tem que ser X( = X(π = (já que, se X( ou X(π, teria que ser T (t =, t. Quando k + 1, a única soução X(x que satisfaz esta condição na fronteira é a soução identicamente nua, ou seja, nesses casos, X( = X(π = = c 1 = c =. Quando k + 1 <, a condição X( = impõe c 1 = e depois a condição X(π = impõe a uma soução não identicamente nua que sin( k 1π =. Esta condição pode ser satisfeita por uma soução não identicamente nua desde que k 1π = nπ, n = 1,, 3,... ou seja, k = 1 n, n = 1,, 3,... Obtêm-se assim todas as seguintes souções para o probema de vaor na fronteira dado: u n (t, x = e (1+n t }} sin(nx, n = 1,, 3,... }} T (t X(x
14 14 AMIV FICHA SUPLEMENTAR 5 definidas para t e para x [, π]. Por inearidade, quaquer combinação inear finita destas souções é ainda soução e, mais geramente, quaquer série b n u n (t, x é uma soução forma. (b Para que a soução gera da forma acima satisfaça a condição inicia tem que ser ou seja, u(, x = (π xx, b n u n (, x = (π xx, b n sin(nx = (π xx. Para encontrar as constantes b n adequadas, desenvove-se a função (π xx em série de senos. Isso é equivaente a estender esta função ao intervao [ π, π] como função ímpar, e desenvover a extensão em série de Fourier. Os coeficientes da série são b n = π = π π (π xx sin(nx dx x sin(nx dx π π x sin(nx dx = [ x n cos(nx + 1 sin(nx ] π n [ π x x n cos(nx + sin(nx + cos(nx n n 3 = 4 n 3 π [1 ( 1n ] ] π = 8 n 3 π se n é ímpar se n é par (onde as primitivas foram obtidas por primitivação por partes, uma vez no primeiro integra e duas no segundo. Logo, a soução pretendida é n ímpar 8 n 3 π e (1+n t sin(nx = n= 8 (n π e (1+(n+1 t sin((n + 1x.
15 AMIV FICHA SUPLEMENTAR 5 15 (a Determine as souções para t e para x [, 1] de (14 t = u x + u u(t, =, u(t, 1 = sin 1 (satisfazendo a equação diferencia para x ], 1[. (b Determine a soução que satisfaz a condição inicia u(, x = 3 sin(πx 7 sin(4πx + sin x. Resoução: (a A soução gera deste probema com condições não homogéneas pode ser obtida somando a uma soução particuar do probema não homogéneo a soução gera do probema homogéneo associado. Vai-se procurar uma soução particuar entre as souções estacionárias, i.e., que não dependem do tempo t. Em resumo, procura-se escrever a soução gera na forma u(t, x = v(x + w(t, x, onde v(x é uma soução particuar estacionária do probema dado e w(t, x é a soução gera do probema homogéneo w ( t = w + w x w(t, = w(t, 1 =. Soução particuar estacionária: Substituindo v(x na equação, obtém-se cuja soução gera é = v ( + v v(x = c 1 cos x + c sin x. Para que a condição em x =, v( =, seja satisfeita, tem que ser c 1 =. Depois para que a condição em x = 1, v(1 = sin 1, seja satisfeita, tem que ser c = 1. Concui-se que v(x = sin x é uma soução particuar (estacionária do probema não homogéneo. Soução gera homogénea: Peo método de separação de variáveis, procura-se souções do probema homogéneo ( da forma w(t, x = T (tx(x, para as quais t T (tx(x = T (tx(x e x T (tx(x = T (tx ( (x. Substituindo na equação, e assumindo que T (tx(x, fica T (tx(x = T (tx ( (x + T (tx(x T (t T (t }} k = X( (x + 1 X(x }} k onde cada um dos membros tem que ser uma constante rea k (porque o membro esquerdo não depende de x, o membro direito não depende de t e ees têm que ser iguais.
16 16 AMIV FICHA SUPLEMENTAR 5 A soução gera de é A soução gera de T (t = kt (t T (t = ce kt com c R. X ( (x (k 1X(x = é, consoante os casos, X(x = c 1 e k 1x + c e k 1x se k 1 > X(x = c 1 + c x se k 1 = X(x = c 1 cos( 1 kx + c sin( 1 kx se k 1 <. Para que a condição na fronteira, T (tx( = T (tx(1 =, seja satisfeita por uma soução não identicamente nua, tem que ser X( = X(1 = (já que, se X( ou X(1, teria que ser T (t =, t. Quando k 1, a única soução X(x que satisfaz esta condição na fronteira é a soução identicamente nua, ou seja, nesses casos, X( = X(1 = = c 1 = c =. Quando k 1 <, a condição X( = impõe c 1 = e depois a condição X(1 = impõe a uma soução não identicamente nua que sin( 1 k =. Esta condição pode ser satisfeita por uma soução não identicamente nua desde que 1 k = nπ, n = 1,, 3,... ou seja, k = 1 n π, n = 1,, 3,... Obtêm-se assim todas as seguintes souções para o probema homogéneo ( : w n (t, x = e (1 n π t }} T (t sin(nπx, n = 1,, 3,... }} X(x definidas para t e para x [, 1]. Por inearidade, quaquer combinação inear finita desta souções é ainda soução e, mais geramente, quaquer série b n w n (t, x é uma soução forma. Soução gera: sin x + b n w n (t, x. (b Para que a soução gera da forma acima satisfaça a condição inicia tem que ser u(, x = 3 sin(πx 7 sin(4πx + sin x, b n w n (, x = 3 sin(πx 7 sin(4πx,
17 AMIV FICHA SUPLEMENTAR 5 17 ou seja, b n sin(nπx = 3 sin(πx 7 sin(4πx. As constantes b n adequadas são b = 3, b 4 = 7, todos os outros b n s são zero. (A função 3 sin(πx 7 sin(4πx já é dada em série de Fourier. A soução pretendida é sin x + 3e (1 4π t sin(πx 7e (1 16π t sin(4πx. (a Cacue a série de Fourier da função f(x = x(x 1 para x [ 1, 1]. (b Recorrendo ao método de separação de variáveis, determine as souções para t e para x [, 1] de (15 u t + + u = u t x u(t, = u(t, 1 =. (c Determine a soução que satisfaz a condição inicia u(, x = sin(πx e t (, x = x(x 1. (16 (a Cacue a série de Fourier da função f : R R definida por ( πx f(x = sin. (b Recorrendo ao método de separação de variáveis, determine as souções para t e para x [, 1] de t = u x x (t, = x (t, 1 =. (c Determine a soução que satisfaz a condição inicia u(, x = sin ( πx.
18 18 AMIV FICHA SUPLEMENTAR 5 Transformada de Lapace (17 Utiizando a transformada de Lapace, resova o seguinte probema de vaor inicia: y ( 5ẏ + 4y = e t y( = 1, ẏ( = 1. Resoução: Seja Y (s a transformada de Lapace da soução y(t. Apicando a transformada de Lapace, a equação fica Ly ( } 5Lẏ} + 4Y (s = Le t } ( s Y (s sy( ẏ( 5 (sy (s y( + 4Y (s = 1 s s Y (s 5sY (s + 4Y (s s + 6 = 1 s ( s 5s + 4 Y (s = 1 s + s 6 Y (s = 1 (s (s 5s+4 + s 6 s 5s+4. Para reconhecer esta função como a transformada de Lapace de uma combinação de funções eementares, decompõe-se em fracções simpes. Cácuos auxiiares: Quanto à primeira parcea de Y (s, tem-se s 5s + 4 = s = 1 ou s = 4 1 (s 1(s (s 4 = A s 1 + B s + C s 4 1 = A(s (s 4 + B(s 1(s 4 + C(s 1(s. Quando s = 1, obtém-se que A = 1 3 ; quando s =, obtém-se que B = 1 ; quando s = 4, obtém-se que C = 1 6. Logo, (s (s 5s + 4 = 3 s 1 s + 6 s 4. Quanto à segunda parcea de Y (s, tem-se s 6 s 5s+4 = s 4 (s 1(s 4 = 1 s 1 (s 1(s 4 1 (s 1(s 4 = D s 1 + E s 4 1 = D(s 4 + E(s 1. Quando s = 1, obtém-se que D = 1 3 ; quando s = 4, obtém-se que E = 1 3. Assim, s 6 s 5s + 4 = 1 s s 1 3 s 4. Continuação da resoução: De acordo com os cácuos auxiiares, Y (s = 1 3 s 1 1 s s s s 1 3 s 4 = s 1 1 s 1 s 4 = Le t } 1 Let } 1 Le4t }
19 AMIV FICHA SUPLEMENTAR 5 19 peo que y(t = e t 1 et 1 e4t. (18 Sabendo que y = y(t satisfaz a equação diferencia y ( ẏ + y = f(t e que a transformada de Lapace de y(t é dada por Y (s = (s 1(s (s 1, determine f e as condições iniciais de y(t, ou seja, os vaores de y( e ẏ(. Resoução: Soução 1: Apicando a transformada de Lapace, a equação fica Ly ( } Lẏ} + Y (s = Lf(t} ( s Y (s sy( ẏ( (sy (s y( + Y (s = Lf(t} ( s s + 1 Y (s sy( ẏ( = Lf(t} (s 1 ( (s 1(s (s 1 = Lf(t} + ẏ( + sy( s = Lf(t} + ẏ( + sy( s+1 = Lf(t} donde se concui que e t = f(t 1 = ẏ( = y( porque a transformada de Lapace de uma função não pode incuir termos da forma a + bs. Portanto, f(t = e t, ẏ( = 1 e y( =. Soução : Sabendo que Y (s = (s 1(s (s 1, pode-se cacuar y(t desenvovendo a expressão da direita em fracções simpes. Cácuos auxiiares: (s 1(s 1 = (s 1 (s + 1 (s 1(s 1 = A s 1 + B (s 1 + C s + 1 = A(s 1(s B(s C(s 1 Quando s = 1, obtém-se que B = 1; quando s = 1, obtém-se que C = 1. Derivando a expressão acima, = A(s 1 + A(s B + C(s 1,
20 AMIV FICHA SUPLEMENTAR 5 e avaiando, por exempo, em s = 1, obtém-se que A = 1. Logo, donde se concui que Como os vaores em são: Y (s = 1 s s+1 + (s 1 = 1 Let } + 1 Le t } d ds Let } = 1 Let } + 1 Le t } + Lte t } y(t = 1 et + 1 e t + te t. ẏ(t = 3 et 1 e t + te t, y( = = e ẏ( = 3 1 = 1. A função f(t pode ser cacuada substituindo y(t na equação: peo que y ( ẏ + y y ( (t = 7 et + 1 e t + te t, = ( 7 et + 1 e t + te t ( 3 et 1 e t + te t + ( 1 et + 1 e t + te t = e t. (19 Utiizando a transformada de Lapace, resova o seguinte probema de vaor inicia: y ( 4ẏ + 4y = f(t y( =, ẏ( =, onde f(t = te t, se t 1 te t + (t 1e (t 1, se t 1. ( Utiizando a transformada de Lapace, resova o seguinte probema de vaor inicia: y ( + ẏ + y = (t 3H 3 (t y( =, ẏ( = 1, onde H 3 (t =, se t 3 1, se t 3.
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE 2A - 15 DE JUNHO DE DAS 11H. Apresente e justifique todos os cálculos. dy dt = y t t ; y(1) = 1.
 Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE A - 5 DE JUNHO DE 9 - DAS H ÀS :3H Apresente e justifique todos os cácuos.
Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE A - 5 DE JUNHO DE 9 - DAS H ÀS :3H Apresente e justifique todos os cácuos.
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática Disciplina: Cálculo Diferencial e Integral IV Unidades: Escola Politécnica e Escola de Quimica Código: MAC 48 a
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática Disciplina: Cálculo Diferencial e Integral IV Unidades: Escola Politécnica e Escola de Quimica Código: MAC 48 a
2 ō Semestre 2015/2016
 Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0
Questão 1: (2.0 pontos) (a) (1.0 ponto) Obtenha os cinco primeiros termos da série de Taylor da função f(x) = cos x em.
 Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
ANÁLISE MATEMÁTICA IV FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Universidade Tecnológica Federal do Paraná Câmpus Francisco Beltrão
 Equações Diferenciais Parciais Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke Equações Diferenciais Parciais Uma equação diferencial parcial (EDP) é uma equação envolvendo uma ou mais
Equações Diferenciais Parciais Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke Equações Diferenciais Parciais Uma equação diferencial parcial (EDP) é uma equação envolvendo uma ou mais
c + 1+t 2 (1 + t 2 ) 5/2 dt e 5 2 ln(1+t2 )dt (1 + t 2 ) 5/2 dt (c 5/2 + (1 + t 2 ) 5/2 (1 + t 2 ) 5/2 dt ϕ(t) = (1 + t 2 ) 5/2 (1 + t).
 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
Séries de Fourier. Matemática Aplicada. Artur M. C. Brito da Cruz. Escola Superior de Tecnologia Instituto Politécnico de Setúbal 2014/2015 1
 Séries de Fourier Matemática Aplicada Artur M. C. Brito da Cruz Escola Superior de Tecnologia Instituto Politécnico de Setúbal 14/15 1 1 versão 16 de Dezembro de 17 Conteúdo 1 Séries de Fourier...............................
Séries de Fourier Matemática Aplicada Artur M. C. Brito da Cruz Escola Superior de Tecnologia Instituto Politécnico de Setúbal 14/15 1 1 versão 16 de Dezembro de 17 Conteúdo 1 Séries de Fourier...............................
EQUAÇÕES DIFERENCIAIS: MÉTODOS DE SÉRIES II
 EQUAÇÕES DIFERENCIAIS: MÉTODOS DE SÉRIES II MAURICIO A. VILCHES Departamento de Anáise - IME UERJ 2 Copyright by Mauricio A. Viches Todos os direitos reservados Proibida a reprodução parcia ou tota 3 PREFÁCIO
EQUAÇÕES DIFERENCIAIS: MÉTODOS DE SÉRIES II MAURICIO A. VILCHES Departamento de Anáise - IME UERJ 2 Copyright by Mauricio A. Viches Todos os direitos reservados Proibida a reprodução parcia ou tota 3 PREFÁCIO
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA. MATEMÁTICA APLICADA 1 o SEMESTRE 2016/2017
 3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Departamento de Matemática da Universidade de Aveiro
 Departamento de Matemática da Universidade de Aveiro ANÁLISE MATEMÁTICA II 7/8 Folha 4 - soluções: Séries de Fourier; notação complexa. Vamos mostrar que se f e g são funções periódicas de período T, fg
Departamento de Matemática da Universidade de Aveiro ANÁLISE MATEMÁTICA II 7/8 Folha 4 - soluções: Séries de Fourier; notação complexa. Vamos mostrar que se f e g são funções periódicas de período T, fg
36 a Aula AMIV LEAN, LEC Apontamentos
 36 a Aula 004113 AMIV EAN, EC Apontamentos (RicardoCoutinho@mathistutlpt) 361 Equação do Calor não homogénea Considere-se o problema do calor numa barra de comprimento ecomconstante dedifusão térmica k,
36 a Aula 004113 AMIV EAN, EC Apontamentos (RicardoCoutinho@mathistutlpt) 361 Equação do Calor não homogénea Considere-se o problema do calor numa barra de comprimento ecomconstante dedifusão térmica k,
SEGUNDA PROVA DE EDB - TURMA M
 SEGUNDA PROVA DE EDB - TURMA M Prof. MARCELO MARCHESIN -/1/7 (13:-1: DPTO. DE MATEMÁTICA, UFMG. RESOLUÇÃO E CRITÉRIOS 1. (11, ptos Sabendo-se que u n (x, y = c n senh( nπx nπy b sen( b para n = 1,,...
SEGUNDA PROVA DE EDB - TURMA M Prof. MARCELO MARCHESIN -/1/7 (13:-1: DPTO. DE MATEMÁTICA, UFMG. RESOLUÇÃO E CRITÉRIOS 1. (11, ptos Sabendo-se que u n (x, y = c n senh( nπx nπy b sen( b para n = 1,,...
x 2 y 6xy + 10y = 0, x > 0 y(1) = 1, y(2) = 18.
 Gabarito da a Prova Unificada de Cálculo IV Dezembro de a Questão: (. pts) Resolva o problema de contorno: x y 6xy + y =, x > y() =, y() = 8. Solução: Como se trata de uma equação de Euler, a solução geral
Gabarito da a Prova Unificada de Cálculo IV Dezembro de a Questão: (. pts) Resolva o problema de contorno: x y 6xy + y =, x > y() =, y() = 8. Solução: Como se trata de uma equação de Euler, a solução geral
Suponhamos que f é uma função que pode ser representada por uma série trigonométrica da forma. ) + B nsen( 2nπx )]. (2)
![Suponhamos que f é uma função que pode ser representada por uma série trigonométrica da forma. ) + B nsen( 2nπx )]. (2) Suponhamos que f é uma função que pode ser representada por uma série trigonométrica da forma. ) + B nsen( 2nπx )]. (2)](/thumbs/67/57907746.jpg) Séries de Fourier Os fenómenos periódicos aparecem nas mais variadas situações: ondas de som, movimento da erra, batimento cardíaco,... Frequentemente uma função periódica pode ser representada por meio
Séries de Fourier Os fenómenos periódicos aparecem nas mais variadas situações: ondas de som, movimento da erra, batimento cardíaco,... Frequentemente uma função periódica pode ser representada por meio
Questão 1: (2.5 pontos) f(x) =
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 07/07/010 Questão 1: (.5 pontos Seja
Página 1 de 7 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 07/07/010 Questão 1: (.5 pontos Seja
1 [35] (O jogo dos 7 erros.) Considere a equação de advecção-difusão unidimensional
![1 [35] (O jogo dos 7 erros.) Considere a equação de advecção-difusão unidimensional 1 [35] (O jogo dos 7 erros.) Considere a equação de advecção-difusão unidimensional](/thumbs/75/72920630.jpg) TT1 Matemática Aplicada II Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P1, 23 nov 212 Prof. Nelson uís Dias NOME: GABARITO Assinatura: 1 [35] (O jogo dos 7 erros.) Considere
TT1 Matemática Aplicada II Curso de Engenharia Ambiental Departamento de Engenharia Ambiental, UFPR P1, 23 nov 212 Prof. Nelson uís Dias NOME: GABARITO Assinatura: 1 [35] (O jogo dos 7 erros.) Considere
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Corda Elástica Presa Somente em uma das Extremidades
 Corda Elástica Presa Somente em uma das Extremidades Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi 5 de outubro de 2010 2 Vamos determinar
Corda Elástica Presa Somente em uma das Extremidades Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi 5 de outubro de 2010 2 Vamos determinar
Análise Complexa e Equações Diferenciais 2 ō Semestre 2012/2013
 Análise Complexa e Equações Diferenciais ō Semestre 1/13 ō Teste Versão A (Cursos: LEAN, LEMat, LMAC, MEAer, MEAmbi, MEBiom, MEBiol, MEFT, MEMec, MEQ) 5 de Maio de 13, 11h Duração: 1h 3m 1. Considere o
Análise Complexa e Equações Diferenciais ō Semestre 1/13 ō Teste Versão A (Cursos: LEAN, LEMat, LMAC, MEAer, MEAmbi, MEBiom, MEBiol, MEFT, MEMec, MEQ) 5 de Maio de 13, 11h Duração: 1h 3m 1. Considere o
Nesta seção começamos o estudo das equações diferenciais a derivadas parciais, abreviadamente. da onda da onda ocorre é no problema da corda vibrante.
 Seção 18: Equação da Onda Nesta seção começamos o estudo das equações diferenciais a derivadas parciais, abreviadamente EDP s. Começamos pela equação da onda. Um exemplo de situação em que a equação da
Seção 18: Equação da Onda Nesta seção começamos o estudo das equações diferenciais a derivadas parciais, abreviadamente EDP s. Começamos pela equação da onda. Um exemplo de situação em que a equação da
FEUP - MIEEC - Análise Matemática 1
 FEUP - MIEEC - Análise Matemática Resolução da a Chamada - de Janeiro de 9 Respostas a perguntas diferentes em folhas diferentes Justifique cuidadosamente todas as respostas. Não é permitida a utilização
FEUP - MIEEC - Análise Matemática Resolução da a Chamada - de Janeiro de 9 Respostas a perguntas diferentes em folhas diferentes Justifique cuidadosamente todas as respostas. Não é permitida a utilização
ANÁLISE MATEMÁTICA IV LEEC SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS EDO S. disponível em
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualiação: //003 ANÁLISE MATEMÁTICA IV LEEC RESOLUÇÃO DA FICHA 3 SÉRIES, SINGULARIDADES, RESÍDUOS E PRIMEIRAS
Polinómio e série de Taylor
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA II - o Semestre 05/06 Exercícios Suplementares (Eng a Física Tecnológica, Matemática Aplicada e Computação
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Equações Diferenciais com Derivadas Parciais
 1/13 Equações Diferenciais com Derivadas Parciais Chamam-se equações principais da física matemática às seguintes equações diferenciais com derivadas parciais de segunda ordem: 2/13 2 u t 2 = a 2 2 u x
1/13 Equações Diferenciais com Derivadas Parciais Chamam-se equações principais da física matemática às seguintes equações diferenciais com derivadas parciais de segunda ordem: 2/13 2 u t 2 = a 2 2 u x
TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER
 TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER Transformada integral Em Física Matemática há pares de funções que satisfazem uma expressão na forma: F α = a b f t K α, t dt f t = A função F( ) é denominada
TRANSFORMADAS INTEGRAIS LAPLACE E FOURIER Transformada integral Em Física Matemática há pares de funções que satisfazem uma expressão na forma: F α = a b f t K α, t dt f t = A função F( ) é denominada
TEMPO DE PROVA: 2h30. 1 se 0 x < 1, 0 se 1 x 2. f(x) =
 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito seg. prova unificada - Escola Politécnica / Escola de Química - 1/06/018 Questão 1: (.5 pontos) Seja f : [0,] R a função
Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito seg. prova unificada - Escola Politécnica / Escola de Química - 1/06/018 Questão 1: (.5 pontos) Seja f : [0,] R a função
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Análise Complexa e Equações Diferenciais
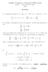 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))
![GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1)) GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))](/thumbs/97/131760884.jpg) GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 1 NÚMEROS E FUNÇÕES COMPLEXAS (1) Calcule i, i e i e represente estes números geometricamente.
Análise Matemática II - 1 o Semestre 2001/ o Exame - 25 de Janeiro de h
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Análise Matemática II - 1 o Semestre 2001/2002 2 o Exame - 25 de Janeiro de 2001-9 h Todos os cursos excepto Eng. Civil,
Equações Diferenciais Ordinárias de Ordem Superior a Um
 Capítulo 2 Equações Diferenciais Ordinárias de Ordem Superior a Um 2.1 EDOs lineares homogéneas de ordem dois. Redução de ordem. Exercício 2.1.1 As seguintes equações diferenciais de 2 a ordem podem ser
Capítulo 2 Equações Diferenciais Ordinárias de Ordem Superior a Um 2.1 EDOs lineares homogéneas de ordem dois. Redução de ordem. Exercício 2.1.1 As seguintes equações diferenciais de 2 a ordem podem ser
Podemos utilizar o cálculo do determinante para nos auxiliar a encontrar a inversa de uma matriz, como veremos à seguir.
 O cácuo da inversa de uma matriz quadrada ou trianguar é importante para ajudar a soucionar uma série probemas, por exempo, a computação gráfica, na resoução de probemas de posicionamento de juntas articuadas
O cácuo da inversa de uma matriz quadrada ou trianguar é importante para ajudar a soucionar uma série probemas, por exempo, a computação gráfica, na resoução de probemas de posicionamento de juntas articuadas
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1. (1) Descreva as regiões do plano complexo definidas por z i c z, onde c é um número real não negativo.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 1 NÚMEROS COMPLEXOS E FUNÇÕES COMPLEXAS Números Complexos 1) Descreva as regiões
d [xy] = x arcsin x. dx + 4x
![d [xy] = x arcsin x. dx + 4x d [xy] = x arcsin x. dx + 4x](/thumbs/65/53462517.jpg) Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
u t = c 2 u xx, (1) u(x, 0) = 1 (0 < x < L) Solução: Utilizando o método de separação de variáveis, começamos procurando uma solução u(x, t) da forma
 Seção 9: Equação do Calor Consideremos um fluxo de calor em uma barra homogênea, construída de um material condutor de calor, em que as dimensões da seção lateral são pequenas em relação ao comprimento.
Seção 9: Equação do Calor Consideremos um fluxo de calor em uma barra homogênea, construída de um material condutor de calor, em que as dimensões da seção lateral são pequenas em relação ao comprimento.
sica- Matemática tica e a equação diferencial parcial que descreve o fluxo de calor
 A Equação de Calor Uma das EDP s clássica da FísicaF sica- Matemática tica e a equação diferencial parcial que descreve o fluxo de calor em um corpo sólido. s E uma aplicação mais recente é a que descreve
A Equação de Calor Uma das EDP s clássica da FísicaF sica- Matemática tica e a equação diferencial parcial que descreve o fluxo de calor em um corpo sólido. s E uma aplicação mais recente é a que descreve
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Breve resolução do e-fólio B
 ÁLGEBRA LINEAR I 22 Breve resoução do e-fóio B I. Questões de escoha mútipa. d), pois o vetor nuo pertence a quaquer subespaço, e a intersecção de 2 subespaços ainda é um subespaço. 2. c), os 3 vetores
ÁLGEBRA LINEAR I 22 Breve resoução do e-fóio B I. Questões de escoha mútipa. d), pois o vetor nuo pertence a quaquer subespaço, e a intersecção de 2 subespaços ainda é um subespaço. 2. c), os 3 vetores
INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE TÉCNICA DE LISBOA. Guia do ensaio de laboratório para as disciplinas:
 INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE TÉCNICA DE LISBOA Guia do ensaio de aboratório para as discipinas: Transmissão de Caor e Transmissão de Caor e Massa I Anáise da transferência de caor em superfícies
INSTITUTO SUPERIOR TÉCNICO UNIVERSIDADE TÉCNICA DE LISBOA Guia do ensaio de aboratório para as discipinas: Transmissão de Caor e Transmissão de Caor e Massa I Anáise da transferência de caor em superfícies
Instituto de Matemática - IM-UFRJ Cálculo Diferencial e Integral IV - MAC248 Primeira prova - Unificada - 29/04/2019
 Página Questão : (.5 pontos é (condicionalmente ou absolutamente convergente, ou di-. Determine se a série vergente. Instituto de Matemática - IM-UFRJ Primeira prova - Unificada - 9/04/09 TEMPO DE PROVA:
Página Questão : (.5 pontos é (condicionalmente ou absolutamente convergente, ou di-. Determine se a série vergente. Instituto de Matemática - IM-UFRJ Primeira prova - Unificada - 9/04/09 TEMPO DE PROVA:
SÉRIES DE FOURIER. Fabio Cardoso D Araujo Martins, Fernando Sergio Cardoso Cunha, Paula Rodrigues. Ferreira Alves, Rafael Caveari Gomes
 SÉRIES DE FOURIER Fabio Cardoso D Araujo Martins, Fernando Sergio Cardoso Cunha, Paula Rodrigues Ferreira Alves, Rafael Caveari Gomes UFF - Universidade Federal Fluminense Neste artigo mostramos com diversos
SÉRIES DE FOURIER Fabio Cardoso D Araujo Martins, Fernando Sergio Cardoso Cunha, Paula Rodrigues Ferreira Alves, Rafael Caveari Gomes UFF - Universidade Federal Fluminense Neste artigo mostramos com diversos
Reginaldo J. Santos. Universidade Federal de Minas Gerais 22 de novembro de 2007
 Séries de Fourier e Equações Diferenciais Parciais Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.r/~regi de novemro de 7 Sumário Séries de
Séries de Fourier e Equações Diferenciais Parciais Reginaldo J. Santos Departamento de Matemática-ICE Universidade Federal de Minas Gerais http://www.mat.ufmg.r/~regi de novemro de 7 Sumário Séries de
TEMPO DE PROVA: 2h30 Questão 1: (2.5 pontos) Estude a convergência, convergência absoluta ou divergência das séries abaixo. ( 1) m m.
 Instituto de Matemática - IM/UFRJ Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 26/09/208 TEMPO DE PROVA: 2h30 Questão : (2.5 pontos) Estude a convergência, convergência absoluta
Instituto de Matemática - IM/UFRJ Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 26/09/208 TEMPO DE PROVA: 2h30 Questão : (2.5 pontos) Estude a convergência, convergência absoluta
u(0; y) = u(1; y) = u(x; 0) = 0 8 x ; se 0 x < x ; se
 Instituto Tecnológico de Aeronáutica / Departamento de Matemática / o. Fund / 009. LISTA NEGRA DE MAT-4 (Apenas para auxiliar nos estudos para o exame). (i) Em cada um dos casos (edp hiperbólica, parabólica
Instituto Tecnológico de Aeronáutica / Departamento de Matemática / o. Fund / 009. LISTA NEGRA DE MAT-4 (Apenas para auxiliar nos estudos para o exame). (i) Em cada um dos casos (edp hiperbólica, parabólica
Na figura abaixo, a balança está em equilíbrio e as três melancias têm o mesmo peso. Nessas condições, qual é o peso (em kg) de cada melancia?
 A UUL AL A 5 Introdução à ágebra Na figura abaixo, a baança está em equiíbrio e as três meancias têm o mesmo peso. Nessas condições, qua é o peso (em ) de cada meancia? Para pensar 3 Uma barra de rapadura
A UUL AL A 5 Introdução à ágebra Na figura abaixo, a baança está em equiíbrio e as três meancias têm o mesmo peso. Nessas condições, qua é o peso (em ) de cada meancia? Para pensar 3 Uma barra de rapadura
33 a Aula AMIV LEAN, LEC Apontamentos
 33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
Instituto de Matemática - UFRJ Cálculo 1 Segunda Prova 16 de Novembro de 2017
 Instituto de Matemática - UFRJ Segunda Prova 6 de Novembro de 7. ( pontos) Jurema tem uma folha de cartolina retangular com dimensões cm 4 cm. Ela gostaria de fazer uma caixa sem tampa cortando quadrados
Instituto de Matemática - UFRJ Segunda Prova 6 de Novembro de 7. ( pontos) Jurema tem uma folha de cartolina retangular com dimensões cm 4 cm. Ela gostaria de fazer uma caixa sem tampa cortando quadrados
Instituto Politécnico de Tomar Escola Superior de Tecnologia de Tomar Área Interdepartamental de Matemática
 Instituto Politécnico de Tomar Escola Superior de Tecnologia de Tomar Área Interdepartamental de Matemática Análise Numérica Licenciaturas em Engenharia Ambiente,Civil e Química I - Equações Não Lineares.
Instituto Politécnico de Tomar Escola Superior de Tecnologia de Tomar Área Interdepartamental de Matemática Análise Numérica Licenciaturas em Engenharia Ambiente,Civil e Química I - Equações Não Lineares.
Caderno de Exercícios
 Caderno de Exercícios Orlando Ferreira Soares Índice Caracterização de Sinais... Caracterização de Sistemas...0 Sistemas LIT - Convolução...5 Série de Fourier para Sinais Periódicos Contínuos...0 Transformada
Caderno de Exercícios Orlando Ferreira Soares Índice Caracterização de Sinais... Caracterização de Sistemas...0 Sistemas LIT - Convolução...5 Série de Fourier para Sinais Periódicos Contínuos...0 Transformada
t 2 se t 0 Determine a expansão em série de potências para a função F (x) = ( 1) n y2n (2n)!, ( 1) n t4n (2n)! (2n)! ( 1) n t4n 2 dt = ( 1) n t 4n 2 )
 MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
Capítulo 4 Condução Bidimensional em Regime Estacionário. Prof. Dr. Santiago del Rio Oliveira
 Capítulo 4 Condução Bidimensional em Regime Estacionário Prof. Dr. Santiago del Rio Oliveira 4. Considerações Gerais A distribuição de temperaturas é caracterizada por duas coordenadas espaciais, ou seja:
Capítulo 4 Condução Bidimensional em Regime Estacionário Prof. Dr. Santiago del Rio Oliveira 4. Considerações Gerais A distribuição de temperaturas é caracterizada por duas coordenadas espaciais, ou seja:
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Cálculo Diferencial e Integral I Complementos ao texto de apoio às aulas. Amélia Bastos, António Bravo Julho 24 Introdução O texto apresentado tem por objectivo ser um complemento ao texto de apoio ao
Álgebra Linear e Geometria Analítica
 Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Instituto Politécnico de Viseu Escola Superior de Tecnologia Departamento: Matemática Álgebra Linear e Geometria Analítica Curso: Engenharia Electrotécnica Ano: 1 o Semestre: 1 o Ano Lectivo: 007/008 Ficha
Segunda Lista de Exercícios de Física Matemática I Soluções (Séries de Fourier) IFUSP - 28 Março { 1 se 0 x < h f(x) = 0 se h x < 2π, Sf(x) =
 Segunda Lista de Exercícios de Física Matemática I Soluções (Séries de Fourier) IFUSP - 28 Março 29 Exercício Seja f : R R uma função periódica tal que { se x < h f(x) = se h x
Segunda Lista de Exercícios de Física Matemática I Soluções (Séries de Fourier) IFUSP - 28 Março 29 Exercício Seja f : R R uma função periódica tal que { se x < h f(x) = se h x
Sist. Lin. I. Sistemas Lineares Introdução Definições Geometria Resolução Equivalência Eliminação de Gauss Após Escalonamento. Sist. Lin.
 Motivação - 1 o Exempo 1 a Parte Pauo Godfed Marco Cabra Probema: há dois tipos de moeda, indistinguíveis exceto peo peso As de materia X pesam 10 g cada e as de materia Y, 0 g cada Se um conjunto de 100
Motivação - 1 o Exempo 1 a Parte Pauo Godfed Marco Cabra Probema: há dois tipos de moeda, indistinguíveis exceto peo peso As de materia X pesam 10 g cada e as de materia Y, 0 g cada Se um conjunto de 100
Método dos Deslocamentos
 Método dos Desocamentos formuação matemática do método das forças e dos desocamentos é bastante semehante, devendo a escoha do método de anáise incidir num ou noutro conforme seja mais vantajoso O método
Método dos Desocamentos formuação matemática do método das forças e dos desocamentos é bastante semehante, devendo a escoha do método de anáise incidir num ou noutro conforme seja mais vantajoso O método
d [xy] = x cos x. dx y = sin x + cos x + C, x
![d [xy] = x cos x. dx y = sin x + cos x + C, x d [xy] = x cos x. dx y = sin x + cos x + C, x](/thumbs/66/55981826.jpg) Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Séries de Fourier. Universidade Tecnológica Federal do Paraná Câmpus Francisco Beltrão. Cálculo Diferencial e Integral 4A
 Séries de Fourier Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke As séries de Fourier são a ferramente básica para se representar as funções periódicas, as quais desempenham um importante
Séries de Fourier Câmpus Francisco Beltrão Disciplina: Prof. Dr. Jonas Joacir Radtke As séries de Fourier são a ferramente básica para se representar as funções periódicas, as quais desempenham um importante
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de 2010
 Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS
 FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS Maio 12, 2008 2 Contents 1. Complementos de Álgebra Linear 3 1.1. Determinantes 3 1.2. Valores e vectores próprios 5 2. Análise em
FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS Maio 12, 2008 2 Contents 1. Complementos de Álgebra Linear 3 1.1. Determinantes 3 1.2. Valores e vectores próprios 5 2. Análise em
3 Estática das estruturas planas
 STÁTI 3674 27 3 stática das estruturas panas 3.1 ácuo das reações vincuares - apoios 3.1.1 ondições de equiíbrio estático O equiíbrio estático de uma estrutura bidimensiona (a estrutura considerada, as
STÁTI 3674 27 3 stática das estruturas panas 3.1 ácuo das reações vincuares - apoios 3.1.1 ondições de equiíbrio estático O equiíbrio estático de uma estrutura bidimensiona (a estrutura considerada, as
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
COMPLEMENTOS DE MATEMÁTICA MÓDULO 1. Equações Diferenciais com Derivadas Parciais
 Complementos de Matemática 1 COMPLEMENTOS DE MATEMÁTICA MÓDULO 1 Séries de Fourier Equações Diferenciais com Derivadas Parciais Complementos de Matemática 2 Jean Baptiste Joseph Fourier (1768-1830) viveu
Complementos de Matemática 1 COMPLEMENTOS DE MATEMÁTICA MÓDULO 1 Séries de Fourier Equações Diferenciais com Derivadas Parciais Complementos de Matemática 2 Jean Baptiste Joseph Fourier (1768-1830) viveu
Setor de Tecnologia - TC Engenharia Ambiental Prova Final. Matemática Aplicada II
 Universidade Federal do Paraná Matemática Aplicada II Setor de Tecnologia - TC Engenharia Ambiental 2014-1 Curitiba, 14.07.2014 Prova Final Matemática Aplicada II Tobias Bleninger Departamento de Engenharia
Universidade Federal do Paraná Matemática Aplicada II Setor de Tecnologia - TC Engenharia Ambiental 2014-1 Curitiba, 14.07.2014 Prova Final Matemática Aplicada II Tobias Bleninger Departamento de Engenharia
Resolução das equações
 Resolução das equações Equação de Difusão (calor) (1D) Equação de ondas (corda virante) (1D) Equação de Laplace (2D) - Difusão térmica em estado estacionário (2D e 3 D); - Função potencial de uma partícula
Resolução das equações Equação de Difusão (calor) (1D) Equação de ondas (corda virante) (1D) Equação de Laplace (2D) - Difusão térmica em estado estacionário (2D e 3 D); - Função potencial de uma partícula
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
ANÁLISE MATEMÁTICA IV EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN. tet + t
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
MAT CÁLCULO 2 PARA ECONOMIA. Geometria Analítica
 MT0146 - CÁLCULO PR ECONOMI SEMESTRE DE 016 LIST DE PROBLEMS Geometria nalítica 1) Sejam π 1 e π os planos de equações, respectivamente, x + y + z = e x y + z = 1. Seja r a reta formada pela interseção
MT0146 - CÁLCULO PR ECONOMI SEMESTRE DE 016 LIST DE PROBLEMS Geometria nalítica 1) Sejam π 1 e π os planos de equações, respectivamente, x + y + z = e x y + z = 1. Seja r a reta formada pela interseção
Análise matricial de estruturas não-lineares usando o Método de Newton.
 Anáise matricia de estruturas não-ineares usando o Método de Newton. Exercício Computaciona - MAP3121 1 Primeiro probema 1.1 Descrição da estrutura não-inear Considere um sistema formado por três barras
Anáise matricia de estruturas não-ineares usando o Método de Newton. Exercício Computaciona - MAP3121 1 Primeiro probema 1.1 Descrição da estrutura não-inear Considere um sistema formado por três barras
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
As combinações. combinatória que envolviam o princípio multiplicativo e as permutações.
 Acesse: http://fuvestibuar.com.br/ AUUL AL A As combinações Até agora você estudou probemas de anáise combinatória que envoviam o princípio mutipicativo e as permutações. Introdução Se observar os probemas
Acesse: http://fuvestibuar.com.br/ AUUL AL A As combinações Até agora você estudou probemas de anáise combinatória que envoviam o princípio mutipicativo e as permutações. Introdução Se observar os probemas
Equações diferenciais com derivadas parciais
 Equações diferenciais p. 1/49 Equações diferenciais com derivadas parciais Alexander Plakhov e Luís Descalço Universidade de Aveiro Equações diferenciais p. 2/49 Equações e separação das variáveis Equações
Equações diferenciais p. 1/49 Equações diferenciais com derivadas parciais Alexander Plakhov e Luís Descalço Universidade de Aveiro Equações diferenciais p. 2/49 Equações e separação das variáveis Equações
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas
 Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas LCE0176 - Cálculo e Matemática Aplicados às Ciências Biológicas Professora: Clarice G. B. Demétrio
Universidade de São Paulo Escola Superior de Agricultura Luiz de Queiroz Departamento de Ciências Exatas LCE0176 - Cálculo e Matemática Aplicados às Ciências Biológicas Professora: Clarice G. B. Demétrio
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Representação e Análise de Sistemas Dinâmicos Lineares Componentes Básicos de um Sistema de Controle
 Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Representação e Análise de Sistemas Dinâmicos Lineares 1 Introdução 11 Componentes Básicos de um Sistema de Controle Fundamentos matemáticos 1 Singularidades: Pólos e zeros Equações diferencias ordinárias
Primitivação de funções reais de variável real
 Capítulo 3 Sugere-se a seguinte bibliografia adicional que completa o estudo a efectuar nas aulas teóricas e nas aulas práticas: Maria Aldina C. Silva e M. dos Anjos F. Saraiva. Primitivação. Edições Asa,
Capítulo 3 Sugere-se a seguinte bibliografia adicional que completa o estudo a efectuar nas aulas teóricas e nas aulas práticas: Maria Aldina C. Silva e M. dos Anjos F. Saraiva. Primitivação. Edições Asa,
Equações Diferenciais B. Prof. Paulo Cupertino de Lima Departamento de Matemática - UFMG
 Equações Diferenciais B Prof. Paulo Cupertino de ima Departamento de Matemática - UFMG 1 Conteúdo 1 Séries de Fourier 4 1.1 Séries de Fourier de Funções Pares e Ímpares...................... 9 1. Cálculo
Equações Diferenciais B Prof. Paulo Cupertino de ima Departamento de Matemática - UFMG 1 Conteúdo 1 Séries de Fourier 4 1.1 Séries de Fourier de Funções Pares e Ímpares...................... 9 1. Cálculo
Seção 29 Ortogonalidade das funções de Bessel Membrana circular
 Seção 9 Ortogonalidade das funções de Bessel Membrana circular Vamos considerar o problema de determinar vibrações livres de uma membrana presa pelo bordo tambor), conhecidos o deslocamento e a velocidade
Seção 9 Ortogonalidade das funções de Bessel Membrana circular Vamos considerar o problema de determinar vibrações livres de uma membrana presa pelo bordo tambor), conhecidos o deslocamento e a velocidade
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
Setor de Tecnologia - TC Engenharia Ambiental Prova Final. Matemática Aplicada II
 Universidade Federal do Paraná Matemática Aplicada II Setor de Tecnologia - TC Engenharia Ambiental 2015-1 Curitiba, 10.07.2015 Prova Final Matemática Aplicada II Tobias Bleninger Departamento de Engenharia
Universidade Federal do Paraná Matemática Aplicada II Setor de Tecnologia - TC Engenharia Ambiental 2015-1 Curitiba, 10.07.2015 Prova Final Matemática Aplicada II Tobias Bleninger Departamento de Engenharia
Problema de Dirichlet no Círculo e em Regiões Circulares
 Problema de Dirichlet no Círculo e em Regiões Circulares Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi 5 de outubro de 2010 2 Vamos
Problema de Dirichlet no Círculo e em Regiões Circulares Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi 5 de outubro de 2010 2 Vamos
38 a Aula AMIV LEAN, LEC Apontamentos
 38 a ula 2004.12.17 MIV LEN, LEC pontamentos (Ricardo.Coutinho@math.ist.utl.pt) 38.1 Equilíbrio da equação do calor e da equação das ondas Quer na equação do calor u t = k lap u, quer na equação das ondas
38 a ula 2004.12.17 MIV LEN, LEC pontamentos (Ricardo.Coutinho@math.ist.utl.pt) 38.1 Equilíbrio da equação do calor e da equação das ondas Quer na equação do calor u t = k lap u, quer na equação das ondas
5.1. Simulações para o Campo Magnético Gerado por um Ímã Permanente.
 Simuações. No presente capítuo são apresentadas simuações referentes ao comportamento de parâmetros importantes para o desenvovimento do transdutor de pressão. As simuações foram eaboradas com o objetivo
Simuações. No presente capítuo são apresentadas simuações referentes ao comportamento de parâmetros importantes para o desenvovimento do transdutor de pressão. As simuações foram eaboradas com o objetivo
GOVERNO DO ESTADO DE MATO GROSSO SECRETARIA DE ESTADO DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO
 0) Responda aos itens. GOVERNO DO ESTADO DE MATO GROSSO SECRETARIA DE ESTADO DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO FACET Faculdade de Ciências Exatas e Tecnológicas Avaliação 5/04/06
0) Responda aos itens. GOVERNO DO ESTADO DE MATO GROSSO SECRETARIA DE ESTADO DE CIÊNCIA E TECNOLOGIA UNIVERSIDADE DO ESTADO DE MATO GROSSO FACET Faculdade de Ciências Exatas e Tecnológicas Avaliação 5/04/06
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
NOTAS DE AULA DE ELETROMAGNETISMO
 UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA NOTAS DE AULA DE ELETROMAGNETISMO Prof. Dr. Helder Alves Pereira Outubro, 2017 - CONTEÚDO DAS AULAS NAS TRANSPARÊNCIAS
UNIVERSIDADE FEDERAL DE CAMPINA GRANDE CENTRO DE ENGENHARIA ELÉTRICA E INFORMÁTICA NOTAS DE AULA DE ELETROMAGNETISMO Prof. Dr. Helder Alves Pereira Outubro, 2017 - CONTEÚDO DAS AULAS NAS TRANSPARÊNCIAS
EQUAÇÕES DIFERENCIAIS PARCIAIS: ESTUDO DE CASO
 1 EQUAÇÕES DIFERENCIAIS PARCIAIS: ESTUDO DE CASO Bruno Claudino dos Santos, Viviane Colucci, Vitória Maria Almeida Teodoro de Oliveira, Felipe Borino Giroldo, eticia Darlla Cordeiro. Universidade Tecnológica
1 EQUAÇÕES DIFERENCIAIS PARCIAIS: ESTUDO DE CASO Bruno Claudino dos Santos, Viviane Colucci, Vitória Maria Almeida Teodoro de Oliveira, Felipe Borino Giroldo, eticia Darlla Cordeiro. Universidade Tecnológica
