Análise Complexa e Equações Diferenciais 1 ō Semestre 2016/2017
|
|
|
- Luiz Felipe Flores
- 5 Há anos
- Visualizações:
Transcrição
1 Análise Complexa e Equações Diferenciais 1 ō Semestre 016/017 ō Teste Versão A (Cursos: MEBiol, MEQ 17 de Dezembro de 016, 10h [,0 val 1 Considere a equação diferencial e t + y e t + ( 1 + ye t dy dt 0 Determine um fator integrante que dependa apenas da variável t e resolva o problema de valor inicial y(0 0 indicando o intervalo máximo de definição da solução Chamemos M(t, y e t + y e t e N(t, y 1 + ye t A equação é então M(t, y + N(t, y dy dt 0, e não é exacta pois M y 1 N t ye t Como sugerido no enunciado, procuramos agora um factor integrante µ µ(t, ou seja, tal que multiplicando toda a equação por µ, ela se reduza a uma equação exacta Para isso, µ tem necessariamente de satisfazer a equação µm y µn t µ(t M y dµ dt N + µ(t N t, ou seja, ( M dµ dt y N t N(t, y µ(t, pelo que existe um tal factor integrante µ, só função de t, se o termo função apenas de t E, de facto, ( M y N t N(t, y 1 + ye t 1, 1 + ye t ( M y N t N(t,y for também donde o factor integrante µ µ(t satisfaz a equação diferencial ordinária, linear homogénea, dµ dt µ, e daqui concluímos que poderemos escolher µ(t e t
2 Multiplicando então toda a equação inicial dada por e t obtemos a nova equação equivalente (agora evidentemente exacta e t + ye t + ( e t + y dy dt 0 Existe, portanto, um potencial Φ(t, y, definido em R, tal que { Φ t et + ye t Φ y et + y Primitivando a primeira destas equações em ordem a t obtém-se Φ(t, y et + yet t + α(y, e substituindo na segunda equação podemos obter o termo α(y que resta: O potencial é assim dado por e t + α (y e t + y α (y y α(y y + c, c R e a solução na forma impĺıcita por Φ(t, y et + yet t + y + c, Φ(t, y c e t + ye t 4t + y c (e t + y 4t c, com c arbitrário em R Finalmente, usamos a condição inicial para determinar o valor de c, específico para o problema de valor inicial em questão: c (e 0 + y( , concluindo-se assim que a solução do PVI, na forma impĺıcita, é dada por (e t + y 4t 1 Esta equação permite explicitar y como função de t Assim, tem-se (e t + y(t 4t 1 e t + y(t ± 1 + 4t y(t e t ± 1 + 4t Por fim, substituindo t 0 e usando a condição inicial, imediatamente se conclui que, dos dois sinais possíveis na raiz quadrada, a solução do PVI corresponde ao sinal positivo y(t e t t O intervalo máximo de definição da solução é, evidentemente, t 14 [,, onde y é C 1 Relembramos que, apesar da raíz quadrada estar definida em t 1 4, ela não é diferenciável nesse ponto e por isso este não faz parte do intervalo máximo de definição de y como solução da equação diferencial ordinária
3 Considere a matriz A [ 1 1 [1,5 val [1,0 val (a Calcule e At (b Determine uma solução particular para o sistema x Ax + (0, e t (a Começamos por determinar os valores e vectores próprios da matriz A O seu polinómio característico det(a λi tem raízes: det(a λi 0 ( λ λ ±i λ ± i Donde se conclui que os dois valores próprios são complexos, necessariamente conjugados Basta-nos agora calcular os vectores próprios associados a apenas um dos valores próprios, por exemplo λ +i, porque sabemos que para λ i os vectores próprios são também conjugados Assim, det(a λiv 0 [ i 1 1 i [ v1 v [ 0 0 Os vectores próprios associados a λ + i são, portanto, da forma [ [ v1 1 α i v v iv 1 Conclui-se imediatamente que para λ i serão [ [ v1 1 α i v A matriz A é assim diagonalizável, usando estes dois tipos de vectores próprios, linearmente independentes, como nova base Assim, A SΛS 1, com [ 1 1 S i i e [ + i 0 0 i Por fim, e At Se Λt S 1 e assim [ [ [ e At 1 1 e (+it 0 1 i i 0 e ( it 1 i 1 1 i [ e (+it +e ( it e(+it e ( it i e (+it e ( it e (+it +e ( it i [ e t cos t e t sen t e t sen t e t cos t
4 (b Uma solução particular do sistema não homogéneo pode ser obtida pelo correspondente termo da fórmula da variação das constantes ˆ e At e At b(tdt, o que, substituindo pela exponencial matricial calculada na aĺınea anterior, e pelo termo não homogéneo do sistema dado b(t (0, e t dá [ e t cos t e t ˆ [ sen t e t cos t e t sen t e t sen t e t cos t e t sen t e t cos t [ e t cos t e t ˆ [ sen t sen t e t sen t e t dt cos t cos t [ e t cos t e t [ sen t cos t e t sen t e t cos t sen t [ e t 0 [ 0 e t dt 3 Considere a equação diferencial sendo g(t uma função contínua em R y + y g(t [1,0 val [1,5 val (a Determine a solução geral da equação no caso em que g(t 0 (b Determine a solução da equação que verifica y(0 y (0 0 no caso em que g(t 5 sen t + 8t (a Neste caso a equação é homogénea e pode escrever-se como D y + Dy 0 D(D + y 0 A solução geral desta equação homogénea, de segunda ordem, ou seja, o conjunto de todas as possíveis soluções, constitui um espaço vectorial de dimensão dois Pelo que podemos obtê-la por combinação linear arbitrária de duas soluções linearmente independentes (ie uma base do espaço das soluções Pela factorização anterior concluimos que os valores próprios do polinómio característico são λ 0 e λ, pelo que duas soluções linearmente indepentes serão y(t 1 e y(t e t O espaço gerado por esta base, ou seja, a solução geral da equação, será assim dada por com c 1, c R constantes reais arbitrárias y(t c 1 + c e t, (b Para resolver este problema de valor inicial, para a equação não homogénea, utilizamos o método dos aniquiladores A função sen t corresponde à existência dos valores próprios complexos (necessariamente conjugados i e i, portanto o seu aniquilador é (D i(d + i (D + 1 A função t corresponde à repetição dupla do valor próprio zero, ou seja é (evidentemente aniquilada por D Assim, o aniquilador do termo não homogéneo g(t 5 sen t + 8t é D (D + 1
5 Aplicando este aniquilador a ambos os membros da equação não homogénea dada, obtemos a equação homogénea aumentada cuja solução geral é D 3 (D + 1(D + y 0, y(t c 1 + c e t + c 3 t + c 4 t + c 5 cos t + c 6 sen t De todos estes termos, os dois primeiros já sabemos, pela aĺınea anterior, que correspondem à solução geral homogénea, pela que uma solução particular da equação não homogénea corresponderá a y p (t c 3 t + c 4 t + c 5 cos t + c 6 sen t, com as constantes c 3, c 4, c 5 e c 6 convenientemente escolhidas equação original, e notando que Assim, substituindo na y p(t c 4 c 5 cos t c 6 sen t, e que obtemos y p(t c 3 + c 4 t c 5 sen t + c 6 cos t, (c 4 + c 3 + (4c 4 t + (c 6 c 5 cos t + ( c 6 c 5 sen t 5 sen t + 8t, donde resulta o sistema c 4 + c 3 0 4c 4 8 c 6 c 5 0 c 6 c 5 5 e daqui se conclui que c 3, c 4, c 5 e c 6 1, ou seja a solução particular é e a solução geral não homogénea é y p (t t + t cos t sen t, y(t c 1 + c e t t + t cos t sen t, com c 1, c R Resta finalmente acertar estas duas últimas constantes de forma a que a solução y satisfaça a condição inicial Para isso e y(0 0 c 1 + c 0, y (0 0 c 1 0, donde se conclui que c 1 7/ e c 3/, pelo que a solução do problema de valor inicial é y(t 7 3 e t t + t cos t sen t [1,0 val 4 (a Determine o desenvolvimento em série de senos da função { x se 0 x < π f(x 0 se π x π
6 [1,0 val Estude a convergência pontual da série em R (b Resolva o problema de valor inicial e valores na fronteira u t (t + cos u t x 0 < x < π, t > 0 u(t, 0 u(t, π 0 t > 0 u(0, x f(x 0 < x < π (a Para escrever a função f, definida em [0, π como uma série de Fourier de senos, começamos por considerar o prolongamento ímpar de f ao intervalo [ π, 0 Obtemos assim uma função ímpar em [ π, π pelo que a correspondente série de Fourier, com L π, terá os correspondentes coeficientes dos cosenos iguais a zero, e os dos senos Mas f(x 0 para x [π, π pelo que b n ˆ π f(x sen dx π 0 ˆ π b n 1 x sen dx π 0 4 ( [ π x cos nπ 0 4 ( ( nπ π cos nπ n 4 ( ( nπ π cos nπ Assim, a série de Fourier de senos de f é n0 ( 4 ( nπ cos n ˆ π 0 [ sen n sen ( nπ πn sen ( nπ cos π 0 sen dx Como o prolongamento ímpar de f, em [ π, π, é seccionalmente C 1, com descontinuidades em x ±π, o teorema da convergência pontual das séries de Fourier garante que a correspondente série de senos converge, em cada x [ π, π, para 0 se π < x π π se x π π se x π x se x < π Nos restantes pontos de x R a série converge para o prolongamento periódico, de período 4π, desta função (b Observamos que a equação diferencial parcial dada, assim como as condições de fronteira, são homogéneas É válido, por isso, o princípio da sobreposição, ou seja, funções obtidas por combinações lineares arbitrárias de soluções da equação e das condições de fronteira ainda as satisfazem
7 Vamos por isso usar o método de separação de variáveis, construindo soluções gerais por combinação linear (eventualmente infinita de soluções mais simples, da forma u(t, x T (tx(x, para 0 x π e t 0 Substituindo na equação diferencial parcial obtemos T (tx(x (t + cos tt (tx (x T (t (t + cos tt (t X (x X(x Esta igualdade só é possivel se as funções dos dois lados da igualdade, de variáveis diferentes x e t, forem ambas iguais a uma constante, digamos λ Portanto é equivalente ao sistema seguinte, onde λ é um número real qualquer { T (t λ(t + cos tt (t X (x λx(x 0 A primeira equação é uma equação linear homogénea para T (t, cuja solução geral é T (t Ae λ(t +sen t com A R A expressão para as soluções da segunda equação depende do sinal de λ Temos Be λx + Ce λx se λ > 0 X(x Bx + C se λ 0 B cos λx + C sen λx se λ < 0 onde B, C são constantes reais As condições de fronteira homogéneas u(t, 0 u(t, π 0 para as soluções da forma T (tx(x não nulas dizem que T (tx(0 T (tx(π 0 { X(0 0 X(π 0 Impondo estas condições às soluções X(x determinadas acima temos (i Para λ > 0: { B + C 0 Be λπ + Ce λπ 0 { B 0 C 0 (ii Para λ 0: (iii Para λ < 0: { C 0 Bπ + C 0 { B 0 C 0 { B 0 B cos λπ + C sen λπ 0 { B 0 C 0 ou λπ nπ donde obtemos as soluções não nulas X(x C sen ( nx com n 1,,, para λ n 4 As soluções não triviais da equação diferencial da forma T (tx(x que satisfazem as condições de fronteira são portanto as funções da forma com A R e n 1,, A sen e n 4 (t +sen t
8 Procuramos agora uma solução formal para a equação e condição inicial que seja uma combinação linear infinita das soluções obtidas acima: u(x, t c n sen e n 4 (t +sen t n1 Substituindo esta expressão na condição inicial u(0, x f(x obtemos c n sen f(x n1 pelo que os coeficientes c n são os coeficientes da série de senos obtida na aĺınea anterior Sendo assim c n 4 ( ( nπ cos ( nπ n πn sen e portanto a solução é u(t, x n1 ( 4 ( nπ cos n πn sen ( nπ sen e n 4 (t +sen t [1,0 val 5 Considere a constante real α e a matriz A [ α 1 0 Determine para que valores de α R todas as soluções do sistema x Ax são limitadas, para t R + Os valores próprios da matriz A dada são, em termos de α dados por det(a λi 0 λ + λ + α 0 λ 1 ± 1 α Será o sinal da parte real destes dois valores próprios que determina se a correspondente exponencial será crescente, decrescente ou constante, e portanto se as soluções serão ilimitadas ou limitadas Em resumo, procuramos α para o qual os valores próprios tenham parte real menor ou igual a zero Estudando os diferentes casos em detalhe, em primeiro lugar, para α < 0, tem-se que 1 α > 1 e consequentemente, dos dois valores próprios λ α e λ α, este último λ é positivo As soluções da forma e λ t v serão evidentemente ilimitadas para t > 0, donde neste caso não se verifica a condição exigida Para α 0 os dois valores próprios são λ 1 e λ 0 Como são diferentes, os seus respectivos vectores próprios, digamos v 1 e v, são linearmente independentes e a solução geral do sistema será uma combinação linear de e t v 1 e v, ambas limitadas em t > 0 (a primeira porque converge para zero, quando t e a segunda por ser constante A solução geral será, por isso, também limitada Para 0 < α < 1 os dois valores próprios λ α e λ α são reais, diferentes e ambos negativos A solução geral, combinação linear de e λ 1t v 1 e e λ t v, é limitada em t > 0 porque converge para zero, quando t
9 Para α 1 os dois valores próprios são iguais λ 1 λ 1, mas a multiplicidade geométrica (ou seja, o número de vectores próprios independentes associados a este único valor próprio é apenas 1, porque a matriz A não é diagonal Neste caso, como explicado anteriormente, a exponencial matricial e At, obtida com recurso à forma canónica de Jordan, fará surgir, além de termos da forma e t, outros da forma te t Ambos convergem para zero, quando t pelo que estas soluções também são limitadas em t > 0 Por fim, para α > 1, tem-se que 1 α < 0 e portanto os valores próprios são complexos conjugados 1 ± i α 1 Neste caso, a parte real dos valores próprios é negativa pelo que as soluções, além dos termos oscilatórios (senos e cosenos de ( α 1t resultantes da componente imaginária dos valores próprios, terão também presente o termo e t que fará as respectivas soluções convergir para zero, quando t pelo que estas soluções também são limitadas em t > 0 Conclui-se assim que todas as soluções do sistema x Ax são limitadas, para t R +, quando α 0
Análise Complexa e Equações Diferenciais 2 ō Semestre 2013/2014
 Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
Análise Complexa e Equações Diferenciais 2 ō Semestre 213/21 Cursos: 2 ō Teste, versão A LEIC, MEEC, LEMat, MEAer, MEBiol, MEQ, MEAmbi 31 de Maio de 21, 11h3 [1,5 val. 1. Considere a equação diferencial
c + 1+t 2 (1 + t 2 ) 5/2 dt e 5 2 ln(1+t2 )dt (1 + t 2 ) 5/2 dt (c 5/2 + (1 + t 2 ) 5/2 (1 + t 2 ) 5/2 dt ϕ(t) = (1 + t 2 ) 5/2 (1 + t).
 Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Análise Complexa e Equações Diferenciais 2 o Semestre 206/207 3 de junho de 207, às 9:00 Teste 2 versão A MEFT, MEC, MEBiom, LEGM, LMAC, MEAer, MEMec, LEAN, LEMat [,0 val Resolva os seguintes problemas
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015
 Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
Análise Complexa e Equações Diferenciais 2 o Semestre 2014/2015 (Cursos: 2 o Teste, versão A LEAN, LEGM, LMAC, MEBiom, MEC, MEFT, MEMec) 30 de Maio de 2015, 9h Duração: 1h 30m INSTRUÇÕES Não é permitida
2 ō Semestre 2015/2016
 Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
Análise Complexa e Equações Diferenciais ō Semestre 15/16 ō Teste, versão A (Cursos: LEIC-A, MEAmbi, MEBiol, MEQ) 1 (a) Resolva o problema de valor inicial 8 de Maio de 16, 11h 3m Duração: 1h 3m y +6x+4xy
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS. Apresente e justifique todos os cálculos
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTES DE RECUPERAÇÃO A - 6 DE JUNHO DE 9 - DAS H ÀS :3H Teste Apresente e justifique
Análise Complexa e Equações Diferenciais 2 ō Semestre 2012/2013
 Análise Complexa e Equações Diferenciais ō Semestre 1/13 ō Teste Versão A (Cursos: LEAN, LEMat, LMAC, MEAer, MEAmbi, MEBiom, MEBiol, MEFT, MEMec, MEQ) 5 de Maio de 13, 11h Duração: 1h 3m 1. Considere o
Análise Complexa e Equações Diferenciais ō Semestre 1/13 ō Teste Versão A (Cursos: LEAN, LEMat, LMAC, MEAer, MEAmbi, MEBiom, MEBiol, MEFT, MEMec, MEQ) 5 de Maio de 13, 11h Duração: 1h 3m 1. Considere o
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV o Teste do 1 o semestre de 04/05 cursos: LEAm, LEBl, LEQ, LQ, LEIC, LEM, LEMat, LEGM, LEAN e LEC
21 de Junho de 2010, 9h00
 Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
Análise Complexa e Equações Diferenciais ō Semestre 009/00 ō Teste \ ō Exame - Versão A (Cursos: Todos) de Junho de 00, 9h00 Duração: Teste - h 30m, Exame - 3h INSTRUÇÕES Não é permitida a utilização de
( x)(x 2 ) n = 1 x 2 = x
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
Página 1 de 7 Instituto de Matemática - IM/UFRJ Gabarito prova final unificada - Escola Politécnica / Escola de Química - 10/12/2009 Questão 1: (.0 pontos) (a) (1.0 ponto) Seja a função f(x) = x, com x
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 6 SÉRIES DE FOURIER E MÉTODO DE SEPARAÇÃO DAS VARIÁVEIS 1 Determine o desenvolvimento em série
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática
 Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática Disciplina: Cálculo Diferencial e Integral IV Unidades: Escola Politécnica e Escola de Quimica Código: MAC 48 a
Universidade Federal do Rio de Janeiro Instituto de Matemática Departamento de Matemática Disciplina: Cálculo Diferencial e Integral IV Unidades: Escola Politécnica e Escola de Quimica Código: MAC 48 a
Análise Complexa e Equações Diferenciais Exame B de 30 de junho de 2014 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec
 Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Análise Complexa e Equações Diferenciais Exame B de 3 de junho de 4 Cursos: LEAN, LMAC, MEBiom, MEFT, MEMec [ val.] RESOLUÇÃO INÍCIO DA PRIMEIRO PARTE. Considere a função u(x, y) = 3xy x 3. (a) Escreva
Sistemas de Equações Diferenciais Lineares
 Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
Capítulo 9 Sistemas de Equações Diferenciais Lineares Agora, estamos interessados em estudar sistemas de equações diferenciais lineares de primeira ordem: Definição 36. Um sistema da linear da forma x
ANÁLISE MATEMÁTICA IV EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN. tet + t
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV FICHA 4 EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ESCALARES E FORMAS CANÓNICAS DE JORDAN () Determine
EXAMES DE ANÁLISE MATEMÁTICA III
 EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
EXAMES DE ANÁLISE MATEMÁTICA III Jaime E. Villate Faculdade de Engenharia Universidade do Porto 22 de Fevereiro de 1999 Resumo Estes são alguns dos exames e testes da disciplina de Análise Matemática III,
x 2 y 6xy + 10y = 0, x > 0 y(1) = 1, y(2) = 18.
 Gabarito da a Prova Unificada de Cálculo IV Dezembro de a Questão: (. pts) Resolva o problema de contorno: x y 6xy + y =, x > y() =, y() = 8. Solução: Como se trata de uma equação de Euler, a solução geral
Gabarito da a Prova Unificada de Cálculo IV Dezembro de a Questão: (. pts) Resolva o problema de contorno: x y 6xy + y =, x > y() =, y() = 8. Solução: Como se trata de uma equação de Euler, a solução geral
depende apenas da variável y então a função ṽ(y) = e R R(y) dy
 Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
Formulario Equações Diferenciais Ordinárias de 1 a Ordem Equações Exactas. Factor Integrante. Dada uma equação diferencial não exacta M(x, y) dx + N(x, y) dy = 0. ( ) 1. Se R = 1 M N y N x depende apenas
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE 2A - 15 DE JUNHO DE DAS 11H. Apresente e justifique todos os cálculos. dy dt = y t t ; y(1) = 1.
 Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE A - 5 DE JUNHO DE 9 - DAS H ÀS :3H Apresente e justifique todos os cácuos.
Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS TESTE A - 5 DE JUNHO DE 9 - DAS H ÀS :3H Apresente e justifique todos os cácuos.
GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))
![GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1)) GABARITO DA 2 a PROVA - CÁLCULO IV 1 0 PERÍODO a Questão:(valor 2.0) (a) O gráfico de f é esboçado na Figura 1. (b) Temos que: + [x]2 1 ((1))](/thumbs/97/131760884.jpg) GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
GABARITO DA a PROVA - CÁLCULO IV 0 PERÍODO 009 a Questão:(valor.0) (a) O gráfico de f é esboçado na Figura. (b) Cálculo de a 0. Temos que: a 0 = f (x)dx = a 0 = { dx + } dx = a 0 = { } [x] + [x] = a 0
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Programa de Pós-Graduação em Matemática Aplicada Prova Escrita - Processo Seletivo 2017/2 - Mestrado
 UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Programa de Pós-Graduação em Matemática Aplicada Prova Escrita - Processo Seletivo 27/2 - Mestrado A prova é composta de 6 (seis) questões, das quais o candidato
UFRGS INSTITUTO DE MATEMÁTICA E ESTATÍSTICA Programa de Pós-Graduação em Matemática Aplicada Prova Escrita - Processo Seletivo 27/2 - Mestrado A prova é composta de 6 (seis) questões, das quais o candidato
Exercício: Identifique e faça um esboço do conjunto solução da. 3x xy + y 2 + 2x 2 3y = 0
 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 + 2 3xy + y 2 + 2x 2 3y = 0 Motivação Exercício: Identifique e faça um esboço do conjunto solução da equação 3x 2 +
Matemática 2. Teste Final. Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
 Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
Matemática 2 Lic. em Economia, Gestão e Finanças Data: 4 de Julho de 2017 Duração: 1H Teste Final Atenção: Esta prova deve ser entregue ao fim de 1 Hora. Deve justificar detalhadamente todas as suas respostas.
8.1-Equação Linear e Homogênea de Coeficientes Constantes
 8- Equações Diferenciais Lineares de 2 a Ordem e Ordem Superior As equações diferenciais lineares de ordem n são aquelas da forma: y (n) + a 1 (x) y (n 1) + a 2 (x) y (n 2) + + a n 1 (x) y + a n (x) y
8- Equações Diferenciais Lineares de 2 a Ordem e Ordem Superior As equações diferenciais lineares de ordem n são aquelas da forma: y (n) + a 1 (x) y (n 1) + a 2 (x) y (n 2) + + a n 1 (x) y + a n (x) y
Álgebra Linear. Curso: Engenharia Electrotécnica e de Computadores 1 ō ano/1 ō S 2006/07
 Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
Álgebra Linear Curso: Engenharia Electrotécnica e de Computadores ō ano/ ō S 6/7 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES Sistemas de equações lineares. Quais das seguintes equações
33 a Aula AMIV LEAN, LEC Apontamentos
 33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
33 a Aula 24.12.3 AMIV EAN, EC Apontamentos (Ricardo.Coutinho@math.ist.utl.pt) 33.1 Soluções da equação do calor sem restrições. De acordo com leis gerais da teoria do calor temos a seguinte equação que
Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas.
 Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
Capítulo 6 Definição (6.1): Definimos equação diferencial como uma qualquer relação entre uma função e as suas derivadas. Definição (6.2): Seja e uma função real incógnita definida num intervalo aberto.
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
LEEC Exame de Análise Matemática 3 0 de Janeiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utilização de máquina de calcular O tempo para a realização desta prova é de horas
3 a Avaliação Parcial - Álgebra Linear
 3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
3 a Avaliação Parcial - Álgebra Linear - 016.1 1. Considere a função T : R 3 R 3 dada por T(x, y, z) = (x y z, x y + z, x y z) e as bases de R 3 B = (1, 1, 1), (1, 0, 1), ( 1,, 0)} (a) Encontre [T] B B.
Análise Matemática IV
 . Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
. Análise Matemática IV o Exame - 9 de Janeiro de 006 LEA, LEC, LEEC, LEFT, LEN e LMAC Resolução y 4y + 4y = e t (D ) y = e t (D ) 3 y = 0 y = c e t + c te t + c 3 t e t, c, c, c 3 R. Substituindo estas
INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA. MATEMÁTICA APLICADA 1 o SEMESTRE 2016/2017
 3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
3 de janeiro de 7 Instruções: INSTITUTO POLITÉCNICO DE SETÚBAL ESCOLA SUPERIOR DE TECNOLOGIA DEPARTAMENTO DE MATEMÁTICA MATEMÁTICA APLICADA o SEMESTRE 6/7 Resolução do o Teste Duração: hm É obrigatória
Introdução às Equações Diferenciais e Ordinárias
 Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
Introdução às Equações Diferenciais e Ordinárias - 017. Lista - EDOs lineares de ordem superior e sistemas de EDOs de primeira ordem 1 São dadas trincas de funções que são, em cada caso, soluções de alguma
de Coeficientes Constantes
 Seção 12: Equações Diferenciais Lineares não Homogêneas de Coeficientes Constantes O objetivo desta seção é estudar as equações lineares não homogêneas de coeficientes constantes No entanto, a versão do
Seção 12: Equações Diferenciais Lineares não Homogêneas de Coeficientes Constantes O objetivo desta seção é estudar as equações lineares não homogêneas de coeficientes constantes No entanto, a versão do
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de 2010
 Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
Gabarito da Prova Final Unificada de Cálculo IV Dezembro de a Questão: (5 pts) Dentre as três séries alternadas abaixo, diga se convergem absolutamente, se convergem condicionalmente ou se divergem Justifique
36 a Aula AMIV LEAN, LEC Apontamentos
 36 a Aula 004113 AMIV EAN, EC Apontamentos (RicardoCoutinho@mathistutlpt) 361 Equação do Calor não homogénea Considere-se o problema do calor numa barra de comprimento ecomconstante dedifusão térmica k,
36 a Aula 004113 AMIV EAN, EC Apontamentos (RicardoCoutinho@mathistutlpt) 361 Equação do Calor não homogénea Considere-se o problema do calor numa barra de comprimento ecomconstante dedifusão térmica k,
Questão 1: (2.0 pontos) (a) (1.0 ponto) Obtenha os cinco primeiros termos da série de Taylor da função f(x) = cos x em.
 Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Página de 7 Instituto de Matemática - IM/UFRJ Gabarito da prova final unificada - Escola Politécnica / Escola de Química - 0/07/009 Questão :.0 pontos a.0 ponto Obtenha os cinco primeiros termos da série
Álgebra Linear. Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente 1 ō ano/1 ō Semestre 2006/07
 Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear Cursos: Química, Engenharia Química, Engenharia de Materiais,Engenharia Biológica, Engenharia do Ambiente ō ano/ ō Semestre 2006/07 a Lista: SISTEMAS DE EQUAÇÕES LINEARES E ÁLGEBRA DE MATRIZES
Álgebra Linear para MBiol MAmb
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Álgebra Linear para MBiol MAmb Teste 3 22 de Dezembro de 212 Duração: 9 minutos Resolução da versão A (1. val.) 1. Considere
d [xy] = x cos x. dx y = sin x + cos x + C, x
![d [xy] = x cos x. dx y = sin x + cos x + C, x d [xy] = x cos x. dx y = sin x + cos x + C, x](/thumbs/66/55981826.jpg) Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Instituto de Matemática e Estatística da USP MAT2455 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - 2o. Semestre 2011-21/11/2011 Turma A Questão 1. a) (1,0 ponto) Determine a solução geral
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
Cálculo Diferencial e Integral I Eame - Parte I - de Julho de 8 LERC, LEGI, LEE, LEIC-T Número: Nome: valores a) valores b) valores 3 4 valores 4 valores 5 a) 3 valores 5 b) 3 valores 6 valores páginas
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec
 Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
Análise Complexa e Equações Diferenciais 2 o Semestre 2013/14 Cursos: LEAN, MeMec M Paluch Aulas 28 33 7 23 de Abril de 2014 Exemplo de uma equação diferencial A Lei de Newton para a propagação de calor,
SEGUNDA PROVA DE EDB - TURMA M
 SEGUNDA PROVA DE EDB - TURMA M Prof. MARCELO MARCHESIN -/1/7 (13:-1: DPTO. DE MATEMÁTICA, UFMG. RESOLUÇÃO E CRITÉRIOS 1. (11, ptos Sabendo-se que u n (x, y = c n senh( nπx nπy b sen( b para n = 1,,...
SEGUNDA PROVA DE EDB - TURMA M Prof. MARCELO MARCHESIN -/1/7 (13:-1: DPTO. DE MATEMÁTICA, UFMG. RESOLUÇÃO E CRITÉRIOS 1. (11, ptos Sabendo-se que u n (x, y = c n senh( nπx nπy b sen( b para n = 1,,...
d [xy] = x arcsin x. dx + 4x
![d [xy] = x arcsin x. dx + 4x d [xy] = x arcsin x. dx + 4x](/thumbs/65/53462517.jpg) Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Instituto de Matemática e Estatística da USP MAT456 - Cálculo Diferencial e Integral IV para Engenharia 3a. Prova - o. Semestre 01-6/11/01 Turma A Questão 1. a (1,0 ponto Determine a solução geral da equação
Questão 1: (2.5 pontos) f(x) =
 Página 1 de 7 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 07/07/010 Questão 1: (.5 pontos Seja
Página 1 de 7 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito prim. prova unificada - Escola Politécnica / Escola de Química - 07/07/010 Questão 1: (.5 pontos Seja
1 A Equação Fundamental Áreas Primeiras definições Uma questão importante... 7
 Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Conteúdo 1 4 1.1- Áreas............................. 4 1.2 Primeiras definições...................... 6 1.3 - Uma questão importante.................. 7 1 EDA Aula 1 Objetivos Apresentar as equações diferenciais
Diagonalização. Operador diagonalizável
 Operador linear Diagonalização Se T: V V for uma transformação linear definida no espaço vectorial V, então T designa-se por operador linear. A representação matricial de um operador linear depende da
Operador linear Diagonalização Se T: V V for uma transformação linear definida no espaço vectorial V, então T designa-se por operador linear. A representação matricial de um operador linear depende da
Matrizes Semelhantes e Matrizes Diagonalizáveis
 Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Diagonalização Matrizes Semelhantes e Matrizes Diagonalizáveis Nosso objetivo neste capítulo é estudar aquelas transformações lineares de R n para as quais existe pelo menos uma base em que elas são representadas
Álgebra Linear. Determinantes, Valores e Vectores Próprios. Jorge Orestes Cerdeira Instituto Superior de Agronomia
 Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
Álgebra Linear Determinantes, Valores e Vectores Próprios Jorge Orestes Cerdeira Instituto Superior de Agronomia - 200 - ISA/UTL Álgebra Linear 200/ 2 Conteúdo Determinantes 5 2 Valores e vectores próprios
ÁLGEBRA LINEAR A FICHA 7
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 3/Dez/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Cálculo de Valores Próprios
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 3/Dez/3 ÁLGEBRA LINEAR A FICHA SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Cálculo de Valores Próprios
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE MAIO DE 2017
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 3 7 DE MAIO DE 27 A = 2 2 2 A matriz tem como valor próprio λ = 2 (triplo. Para os vectores próprios: { z = y + z = v = A matriz não é diagonalizável,
ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE
 Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE Séries de Fourier (1 Desenvova
Instituto Superior Técnico Departamento de Matemática Secção de Ágebra e Anáise ANÁLISE MATEMÁTICA IV FICHA SUPLEMENTAR 5 EQUAÇÕES DIFERENCIAIS PARCIAIS E TRANSFORMADA DE LAPLACE Séries de Fourier (1 Desenvova
Curso: Engenharia Ambiental. Disciplina: Equações Diferenciais Ordinárias. Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2
 Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
Curso: Engenharia Ambiental Disciplina: Equações Diferenciais Ordinárias Professora: Dr a. Camila N. Boeri Di Domenico NOTAS DE AULA 2 11. EQUAÇÕES DIFERENCIAIS ORDINÁRIAS DE 2º ORDEM y (x) = f (x,y,y
ÁLGEBRA LINEAR I - MAT0032
 UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
UNIVERSIDADE FEDERAL DA INTEGRAÇÃO LATINO-AMERICANA Instituto Latino-Americano de Ciências da Vida e Da Natureza Centro Interdisciplinar de Ciências da Natureza ÁLGEBRA LINEAR I - MAT32 12 a Lista de exercícios
ANÁLISE MATEMÁTICA IV FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise ANÁLISE MATEMÁTICA IV E FICHA 3 TEOREMA DOS RESÍDUOS EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM ( Seja f a função definida
Polinômios de Legendre
 Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
Seção 5: continuação do método de resolução por séries de potências Na Seção foi exposto informalmente, através de exemplos, o método de resolução de equações diferenciais ordinárias por séries de potências.
ficha 1 matrizes e sistemas de equações lineares
 Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Exercícios de Álgebra Linear ficha matrizes e sistemas de equações lineares Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2/2
Interbits SuperPro Web
 1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
1 (Ita 018) Uma progressão aritmética (a 1, a,, a n) satisfaz a propriedade: para cada n, a soma da progressão é igual a n 5n Nessas condições, o determinante da matriz a1 a a a4 a5 a 6 a a a 7 8 9 a)
Universidade Federal do Pará Instituto de Tecnologia. Cálculo III. Campus de Belém Curso de Engenharia Mecânica
 Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
Universidade Federal do Pará Instituto de Tecnologia Cálculo III Prof. Dr. Jorge Teófilo de Barros Lopes Campus de Belém Curso de Engenharia Mecânica Universidade Federal do Pará Instituto de Tecnologia
xy + y = 0. (1) Portanto a solução geral de (1) é a família de hipérboles y = C x,
 Seção 4: Equações Exatas Fator Integrante Introduzimos a idéia de equação exata, através de dois exemplos simples. Note que nesses dois exemplos, além de exata, a EDO também é separável, podendo alternativamente
Seção 4: Equações Exatas Fator Integrante Introduzimos a idéia de equação exata, através de dois exemplos simples. Note que nesses dois exemplos, além de exata, a EDO também é separável, podendo alternativamente
Aula 5 Equação Diferencial de Segunda Ordem Linear e Coeficientes constantes:
 Aula 5 Equação Diferencial de Segunda Ordem Linear e Coeficientes constantes: caso não Homogêneo Vamos estudar as equações da forma: ay + by + cy = G(x), onde G(x) é uma função polinomial, exponencial,
Aula 5 Equação Diferencial de Segunda Ordem Linear e Coeficientes constantes: caso não Homogêneo Vamos estudar as equações da forma: ay + by + cy = G(x), onde G(x) é uma função polinomial, exponencial,
Análise Complexa e Equações Diferenciais 1 o Semestre 2012/2013
 Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Análise Complexa e Equações Diferenciais 1 o Semestre 01/013 Cursos: 1 o Teste Versão A LEGM, LEMat, MEAer, MEAmbi, MEBiol, MEC, MEEC, MEQ) 3 de Novembro de 01, 8h Duração: 1h 30m 1. Considere a função
Equações Diferenciais (M2011)
 Equações Diferenciais (M2011) ICruz - FCUP Aula 16-16 abr 18 (ICruz - FCUP) Equações Diferenciais (M2011) Aula 16-16 abr 18 1 / 12 Estabilidade de pontos de equilíbrio de sistemas LHCC No caso de sistemas
Equações Diferenciais (M2011) ICruz - FCUP Aula 16-16 abr 18 (ICruz - FCUP) Equações Diferenciais (M2011) Aula 16-16 abr 18 1 / 12 Estabilidade de pontos de equilíbrio de sistemas LHCC No caso de sistemas
ÁLGEBRA LINEAR A FICHA 6. Por definição do determinante de uma matriz 3 3, tem-se det A = 7.
 Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Instituto Superior Técnico Departamento de Matemática Secção de Álgebra e Análise Última actualização: 20/Nov/2003 ÁLGEBRA LINEAR A FICHA 6 SOLUÇÕES SUMÁRIAS DOS EXERCÍCIOS ÍMPARES Propriedades dos Determinantes
Análise Complexa e Equações Diferenciais 1 ō Semestre 2014/2015
 Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Análise Complexa e Equações Diferenciais ō Semestre /205 (Curso: ō Teste MEAer de Novembro de, 9h. Considere a função u: R 2 R definida pela expressão onde a, b são parâmetros reais. u(x, y = ax 3 + bxy
Aulas práticas de Álgebra Linear
 Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
Ficha Matrizes e sistemas de equações lineares Aulas práticas de Álgebra Linear Mestrado Integrado em Engenharia Eletrotécnica e de Computadores o semestre 6/7 Jorge Almeida e Lina Oliveira Departamento
ANÁLISE MATEMÁTICA IV
 Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Instituto Superior Técnico Departamento de Matem tica SecÁ o de Álgebra e Análise ANÁLISE MATEMÁTICA IV 1 o Teste Cursos: LCI, LEAmb, LEBL, LEGM, LEIC, LEM, LEMat, LEMG, LEQ, LQ Justifique cuidadosamente
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ
 Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Aula 1 Análise Complexa e Equações Diferenciais 2 o Semestre 2018/19 Cursos: LEIC-A MEBiol MEAmbi MEEC MEQ Michael Paluch Instituto Superior Técnico Universidade de Lisboa 18 Fevereiro de 2019 Método de
Corda Elástica Presa Somente em uma das Extremidades
 Corda Elástica Presa Somente em uma das Extremidades Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi 5 de outubro de 2010 2 Vamos determinar
Corda Elástica Presa Somente em uma das Extremidades Reginaldo J. Santos Departamento de Matemática-ICEx Universidade Federal de Minas Gerais http://www.mat.ufmg.br/~regi 5 de outubro de 2010 2 Vamos determinar
LEEC Exame de Análise Matemática 3
 LEEC Exame de Análise Matemática 3 5 de Fevereiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utiliação de máquina de calcular O tempo para a realiação desta prova é de horas
LEEC Exame de Análise Matemática 3 5 de Fevereiro de 005 Justifique cuidadosamente todas as respostas Não é permitida a utiliação de máquina de calcular O tempo para a realiação desta prova é de horas
ORDINÁRIAS. Víctor Arturo Martínez León
 INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
INTRODUÇÃO ÀS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS Víctor Arturo Martínez León September 3, 2017 Súmario 1 Equações diferenciais lineares de primeira ordem 2 2 Equações diferenciais lineares de segundo ordem
Parte II. Análise funcional II
 Parte II Análise funcional II 12 Capítulo 5 Produto de Operadores. Operadores inversos Neste capítulo vamos introduzir a noção de produto de operadores assim como a de operador invertível. Para tal precisamos
Parte II Análise funcional II 12 Capítulo 5 Produto de Operadores. Operadores inversos Neste capítulo vamos introduzir a noção de produto de operadores assim como a de operador invertível. Para tal precisamos
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (variáveis independentes), envolvendo
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE NOVEMBRO DE dt + a 0(t)y = 0
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 24 16 DE NOVEMBRO DE 2016 EQUAÇÕES LINEARES HOMOGÉNEAS DE ORDEM SUPERIOR A DOIS São da forma a n (t) dn y dt n + a n 1(t) dn 1 y dt n 1 + + a 1(t)
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 24 16 DE NOVEMBRO DE 2016 EQUAÇÕES LINEARES HOMOGÉNEAS DE ORDEM SUPERIOR A DOIS São da forma a n (t) dn y dt n + a n 1(t) dn 1 y dt n 1 + + a 1(t)
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes
 Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
Seção 15: Sistema de Equações Diferenciais Lineares Homogêneas com Coeficientes Constantes Muitos problemas de física envolvem diversas equações diferenciais. Na seção 14, por exemplo, vimos que o sistema
Análise Complexa e Equações Diferenciais
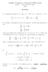 Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
Análise Complexa e Equações Diferenciais Exame - 9 de Janeiro de 8 MEC Resolução. A imagem da região { z C : Rz < e 3 8 < Iz < 8} por z e z é { z C : < z < e 3 } 4 < argz
TEMPO DE PROVA: 2h30. 1 se 0 x < 1, 0 se 1 x 2. f(x) =
 Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito seg. prova unificada - Escola Politécnica / Escola de Química - 1/06/018 Questão 1: (.5 pontos) Seja f : [0,] R a função
Instituto de Matemática - IM/UFRJ Cálculo Diferencial e Integral IV - MAC48 Gabarito seg. prova unificada - Escola Politécnica / Escola de Química - 1/06/018 Questão 1: (.5 pontos) Seja f : [0,] R a função
Equações Diferenciais Noções Básicas
 Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
Equações Diferenciais Noções Básicas Definição: Chama-se equação diferencial a uma equação em que a incógnita é uma função (variável dependente) de uma ou mais variáveis (independentes), envolvendo derivadas
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de T ( p(x) ) = p(x + 1) p(x), (a) 8, (b) 5, (c) 0, (d) 3, (e) 4.
 MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
MAT2458 ÁLGEBRA LINEAR PARA ENGENHARIA II 2 a Prova - 2 o semestre de 218 Q1. Considere a transformação linear T : P 3 (R) P 2 (R), dada por T ( p(x) ) = p(x + 1) p(x), para todo p(x) P 3 (R), e seja A
ficha 4 valores próprios e vectores próprios
 Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Exercícios de Álgebra Linear ficha 4 valores próprios e vectores próprios Exercícios coligidos por Jorge Almeida e Lina Oliveira Departamento de Matemática, Instituto Superior Técnico 2 o semestre 2011/12
Análise Complexa e Equações Diferenciais Guia 8 João Pedro Boavida. 16 a 23 de Novembro
 Análise Complexa e Equações Diferenciais Guia 8 Este guia explica como resolver os problemas do guia 7 Explica também vários aspectos mais técnicos sobre equações lineares em R n, com os quais eu prefiro
Análise Complexa e Equações Diferenciais Guia 8 Este guia explica como resolver os problemas do guia 7 Explica também vários aspectos mais técnicos sobre equações lineares em R n, com os quais eu prefiro
(c) apenas as afirmações (II) e (III) são necessariamente verdadeiras;
 Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
Q1. Considere o espaço vetorial R 4 munido do seu produto interno usual. Sejam B uma base de R 4, A M 4 (R) uma matriz e T : R 4 R 4 a transformação linear tal que [T ] B = A. Considere as seguintes afirmações:
MAT Álgebra Linear para Engenharia II - Poli 2 ō semestre de ā Lista de Exercícios
 MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
MAT 2458 - Álgebra Linear para Engenharia II - Poli 2 ō semestre de 2014 1 ā Lista de Exercícios 1. Verifique se V = {(x, y) x, y R} é um espaço vetorial sobre R com as operações de adição e de multiplicação
Prova: Usando as definições e propriedades de números reais, temos λz = λx + iλy e
 Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Lista Especial de Exercícios de Física Matemática I Soluções (Número complexo, sequência de Cauchy, função exponencial e movimento hamônico simples) IFUSP - 8 de Agosto de 08 Exercício Se z x + iy, x,
Matemática Computacional - 2 o ano LEMat e MEQ
 Instituto Superior Técnico Departamento de Matemática Secção de Matemática Aplicada e Análise Numérica Matemática Computacional - o ano LEMat e MEQ Exame/Teste - 1 de Janeiro de 1 - Parte I (1h3m) 1. Considere
Instituto Superior Técnico Departamento de Matemática Secção de Matemática Aplicada e Análise Numérica Matemática Computacional - o ano LEMat e MEQ Exame/Teste - 1 de Janeiro de 1 - Parte I (1h3m) 1. Considere
FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS
 FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS Maio 12, 2008 2 Contents 1. Complementos de Álgebra Linear 3 1.1. Determinantes 3 1.2. Valores e vectores próprios 5 2. Análise em
FOLHAS DE PROBLEMAS DE MATEMÁTICA II CURSO DE ERGONOMIA PEDRO FREITAS Maio 12, 2008 2 Contents 1. Complementos de Álgebra Linear 3 1.1. Determinantes 3 1.2. Valores e vectores próprios 5 2. Análise em
(x, y) = 0. Análise Complexa e Equações Diferenciais 2 o Semestre 2016/ de abril de 2017, às 9:00 Teste 1 versão A
 Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Análise Complexa e Equações Diferenciais 2 o Semestre 26/27 22 de abril de 27, às 9: Teste versão A. Considere a função definida em R 2 por em que a e b são constantes reais. MEFT, MEC, MEBiom, LEGM, LMAC,
Sistemas Lineares Periódicos: Teoria de Floquet
 Sistemas Lineares Periódicos: eoria de Floquet Considere o sistema linear homogêneo e periódico ẋ = A(t)x, (1) onde R t A(t) M n (R)(ou M n (C)) é contínua e periódica, isto é, existe > 0 tal que A(t +
Sistemas Lineares Periódicos: eoria de Floquet Considere o sistema linear homogêneo e periódico ẋ = A(t)x, (1) onde R t A(t) M n (R)(ou M n (C)) é contínua e periódica, isto é, existe > 0 tal que A(t +
x + 2 > 1 (x 2)(x + 2) x + 2 > e
 Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
Instituto Superior Técnico Departamento de Matematica TESTES DE RECUPERAÇÃO DE CDI I O SEM. / DURAÇÃO: H/H VERSÃO A LEMAT, LEAN, MEBIOL, MEQ, MEAMBI E LMAC, MEBIOM, MEFT RESOLUÇÃO. (,5 val.) (a) (,9 val.)
Forma Canônica de Matrizes 2 2
 Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
Forma Canônica de Matrizes Slvie Olison Kamphorst Departamento de Matemática - ICE - UFMG Versão. - Novembro 5 a b Seja A c d induzida por A uma matriz real e seja T a transformação operador linear de
IST-TAGUS PARQUE-2007/08-2 o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO
 IST-TAGUS PARQUE-007/08- o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM. Diga, justi cando, se as seguintes
IST-TAGUS PARQUE-007/08- o SEMESTRE ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS EQUAÇÕES DIFERENCIAIS ORDINÁRIAS EXERCÍCIOS DE REVISÃO EQUAÇÕES DIFERENCIAIS DE PRIMEIRA ORDEM. Diga, justi cando, se as seguintes
ALGA I. Bases, coordenadas e dimensão
 Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Módulo 5 ALGA I. Bases, coordenadas e dimensão Contents 5.1 Bases, coordenadas e dimensão............. 58 5.2 Cálculos com coordenadas. Problemas......... 65 5.3 Mudanças de base e de coordenadas..........
Cálculo Diferencial e Integral I
 Cálculo Diferencial e Integral I LEE, LEIC-T, LEGI e LERC - o semestre - / de Junho de - 9 horas I ( val.). (5, val.) Determine o valor dos integrais: x + (i) x ln x dx (ii) (9 x )( + x ) dx (i) Primitivando
Cálculo Diferencial e Integral I LEE, LEIC-T, LEGI e LERC - o semestre - / de Junho de - 9 horas I ( val.). (5, val.) Determine o valor dos integrais: x + (i) x ln x dx (ii) (9 x )( + x ) dx (i) Primitivando
Convergência em espaços normados
 Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
Chapter 1 Convergência em espaços normados Neste capítulo vamos abordar diferentes tipos de convergência em espaços normados. Já sabemos da análise matemática e não só, de diferentes tipos de convergência
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA DE ABRIL DE 2011
 ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 27 18 DE ABRIL DE 2011 y 2y + y 2y = 0 O polinómio característico é r 3 2r 2 + r 2, que tem r = 2 como raiz. Obtemos então r 3 2r 2 + r 2 = (r 2) (r
ANÁLISE COMPLEXA E EQUAÇÕES DIFERENCIAIS AULA TEÓRICA 27 18 DE ABRIL DE 2011 y 2y + y 2y = 0 O polinómio característico é r 3 2r 2 + r 2, que tem r = 2 como raiz. Obtemos então r 3 2r 2 + r 2 = (r 2) (r
Matemática Computacional - 2 o ano LEMat e MEQ
 Instituto Superior Técnico Departamento de Matemática Secção de Matemática Aplicada e Análise Numérica Matemática Computacional - o ano LEMat e MEQ Exame/Teste - 5 de Fevereiro de - Parte I (h3m). Considere
Instituto Superior Técnico Departamento de Matemática Secção de Matemática Aplicada e Análise Numérica Matemática Computacional - o ano LEMat e MEQ Exame/Teste - 5 de Fevereiro de - Parte I (h3m). Considere
Matemática. Lic. em Enologia, 2009/2010
 Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
Universidade de Trás-os-Montes e Alto Douro Matemática Lic. em Enologia, 009/00 a Parte: Álgebra Linear Vectores em R n e em C n. Sejam u = (, 7,, v = ( 3, 0, 4 e w = (0, 5, 8. Calcule: a 3u 4v b u + 3v
t 2 se t 0 Determine a expansão em série de potências para a função F (x) = ( 1) n y2n (2n)!, ( 1) n t4n (2n)! (2n)! ( 1) n t4n 2 dt = ( 1) n t 4n 2 )
 MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
MAT456 - Cálculo Diferencial e Integral IV para Engenharia Escola Politecnica - a. Prova - 8// Turma A a Questão (,) a) Seja cos (t ) f(t) = t se t se t = Determine a expansão em série de potências para
Valores e vectores próprios
 Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Valores e vectores próprios Álgebra Linear C (Engenharia Biológica) 0 de Dezembro de 006 Conteúdo Motivação e definições Propriedades 4 3 Matrizes diagonalizáveis 5 Motivação e definições Considere a matriz
Vamos revisar alguns fatos básicos a respeito de séries de potências
 Seção 4 Revisão sobre séries de potências Vamos revisar alguns fatos básicos a respeito de séries de potências a n (x x ) n, que serão úteis no estudo de suas aplicações à resolução de equações diferenciais
Seção 4 Revisão sobre séries de potências Vamos revisar alguns fatos básicos a respeito de séries de potências a n (x x ) n, que serão úteis no estudo de suas aplicações à resolução de equações diferenciais
Nesta seção começamos o estudo das equações diferenciais a derivadas parciais, abreviadamente. da onda da onda ocorre é no problema da corda vibrante.
 Seção 18: Equação da Onda Nesta seção começamos o estudo das equações diferenciais a derivadas parciais, abreviadamente EDP s. Começamos pela equação da onda. Um exemplo de situação em que a equação da
Seção 18: Equação da Onda Nesta seção começamos o estudo das equações diferenciais a derivadas parciais, abreviadamente EDP s. Começamos pela equação da onda. Um exemplo de situação em que a equação da
